1 Introduction

Nonlinear dynamical systems are known to exhibit a rich variety of long-term behaviours such as limit cycles, quasiperiodic and chaotic motion. In a complex dynamical system, several equilibrium states or other attractors may coexist for a given set of system parameters which is known as multistability. Multistable systems are seen in laser physics [1], condensed-matter physics [2], electronic oscillators [3] etc. and biological systems namely population dynamics [4], neuroscience [5] and climate dynamics [6]. Multistability is naturally found in weakly dissipative systems [7], delay systems [8] and coupled systems [9]. The dynamics of multistable systems are extremely sensitive to the initial state due to the coexistence of different attractors and as a result very small perturbations of the initial state might cause a large change in the final state. The mechanisms behind multistable behaviour of many natural systems are not completely known. Understanding the rules behind multistability behaviour of a dynamical system remains one of the fundamental problems of dynamical systems theory. In extreme multistability, the number of coexisting attractors is infinite. Techniques for designing extreme multistable systems had been reported by Sun et al [10]. In their technique, the choice of coupling plays the vital role. In this work, our motivation is to identify some universal mechanisms that lead to multistability and to prove rigorously under what circumstances the phenomenon may occur.

Synchronization of two or more coupled nonlinear systems is a fundamental concept of nonlinear dynamics. Many synchronization techniques [12,13,14,15,16] were proposed since the pioneering work of Pecora and Carroll [11] in 1990. Recently, Hens et al [17] have shown that the coexistence of infinitely many attractors in two-coupled m-dimensional system will be possible if \((m-1)\) variables of the two systems are completely synchronized and one of them keeps a constant difference between them. In other words, Hens et al [17] proposed the partial synchronization technique for constructing multistable systems. Pal et al [18] reported the multistable behaviour of coupled Lorenz–Stenflo systems. But all previous researchers used coupled identical dynamical systems for designing multistable systems. Most of the researchers have not considered the spatial variation of dynamical behaviours for designing multistability systems. In real-world physical, electrical, chemical, social and biological systems, multistable behaviour may arise due to the interaction of two or more different dynamical systems and at the same time there may be variation of the dynamical systems in different spatial points. We can incorporate the spatial variation of dynamical systems in the most simple way by assuming two different dynamical systems for two different spatial points and then observe how multistability can be designed by coupling them. Therefore, it is worth investigating multistability generation procedure by coupling two different dynamical systems.

In this work, we propose schemes for designing multistable systems by coupling two different dynamical systems and using active control. The section-wise split of the paper is as follows. In §2 a scheme for designing multistable systems coupling two different dynamical systems of the same order via active control is discussed. In §3, the proposed scheme is illustrated by coupling a Lorenz and a Lu system. In §4, the numerical simulation results are presented to show the effectiveness of the proposed scheme. Finally, conclusion is drawn in §5.

2 Design of multistable systems by coupling two different dynamical systems

Consider two different n-dimensional dynamical systems of the following type:

$$\begin{aligned} \dot{x}_1= & {} f_1(x_1,x_2,x_3,\ldots ,x_n),\nonumber \\ \dot{x}_2= & {} f_2(x_1,x_2,x_3,\ldots ,x_n),\nonumber \\ \dot{x}_3= & {} f_3(x_1,x_2,x_3,\ldots ,x_n),\nonumber \\ ....&..&.............................,\nonumber \\ \dot{x}_n= & {} f_n(x_1,x_2,x_3,\ldots ,x_n) \end{aligned}$$
(1)

and

$$\begin{aligned} \dot{y}_1= & {} g_1(y_1,y_2,y_3,\ldots ,y_n),\nonumber \\ \dot{y}_2= & {} g_2(y_1,y_2,y_3,\ldots ,y_n),\nonumber \\ \dot{y}_3= & {} g_3(y_1,y_2,y_3,\ldots ,y_n),\nonumber \\ ....&..&.............................,\nonumber \\ \dot{y}_n= & {} g_n(y_1,y_2,y_3,\ldots ,y_n). \end{aligned}$$
(2)

Now, we couple two different dynamical systems of the above type in the following way:

$$\begin{aligned} \dot{x}_1= & {} f_1(x_1,x_2,x_3,\ldots ,x_n)\nonumber \\&+\,u_1( x_1,x_2,x_3,\ldots ,x_n;y_1,y_2,y_3,\ldots ,y_n),\nonumber \\ \dot{x}_2= & {} f_2(x_1,x_2,x_3,\ldots ,x_n)\nonumber \\&+\,u_2( x_1,x_2,x_3,\ldots ,x_n;y_1,y_2,y_3,\ldots ,y_n),\nonumber \\ \dot{x}_3= & {} f_3(x_1,x_2,x_3,\ldots ,x_n)\nonumber \\&+\,u_3( x_1,x_2,x_3,\ldots ,x_n;y_1,y_2,y_3,\ldots ,y_n),\nonumber \\ ....&..&.............................,\nonumber \\ \dot{x}_n= & {} f_n(x_1,x_2,x_3,\ldots ,x_n)\nonumber \\&+\,u_n( x_1,x_2,x_3,\ldots ,x_n;y_1,y_2,y_3,\ldots ,y_n) \end{aligned}$$
(3)

and

$$\begin{aligned} \dot{y}_1= & {} g_1(y_1,y_2,y_3,\ldots ,y_n)\nonumber \\&+\,v_1( x_1,x_2,x_3,\ldots ,x_n;y_1,y_2,y_3,\ldots ,y_n),\nonumber \\ \dot{y}_2= & {} g_2(y_1,y_2,y_3,\ldots ,y_n)\nonumber \\&+\,v_2( x_1,x_2,x_3,\ldots ,x_n;y_1,y_2,y_3,\ldots ,y_n),\nonumber \\ \dot{y}_3= & {} g_3(y_1,y_2,y_3,\ldots ,y_n)\nonumber \\&+\,v_3( x_1,x_2,x_3,\ldots ,x_n;y_1,y_2,y_3,\ldots ,y_n),\nonumber \\ ....&..&.............................,\nonumber \\ \dot{y}_n= & {} g_n(y_1,y_2,y_3,\ldots ,y_n)\nonumber \\&+\,v_n( x_1,x_2,x_3,\ldots ,x_n;y_1,y_2,y_3,\ldots ,y_n), \end{aligned}$$
(4)

where \(u_{1},u_{2},u_{3},\ldots ,u_{n}\) and \(v_{1},v_{2},v_{3},\ldots ,v_{n}\) are the controllers. We define synchronization error between systems (3) and (4) as \(e_i=y_i-x_i,i=1,2,\ldots ,n\). Now, we obtain the error dynamical system as follows:

$$\begin{aligned} \dot{e}_1= & {} g_1(y_1,y_2,y_3,\ldots ,y_n)\nonumber \\&-f_1(x_1,x_2,x_3,\ldots ,x_n)+v_1-u_1,\nonumber \\ \dot{e}_2= & {} g_2(y_1,y_2,y_3,\ldots ,y_n)\nonumber \\&-f_2(x_1,x_2,x_3,\ldots ,x_n)+v_2-u_2,\nonumber \\ \dot{e}_3= & {} g_3(y_1,y_2,y_3,\ldots ,y_n)\nonumber \\&-f_3(x_1,x_2,x_3,\ldots ,x_n)+v_3-u_3,\nonumber \\ ....&..&.............................,\nonumber \\ \dot{e}_n= & {} g_n(y_1,y_2,y_3,\ldots ,y_n)\nonumber \\&-f_n(x_1,x_2,x_3,\ldots ,x_n)+v_n-u_n. \end{aligned}$$
(5)

We choose the controllers \(u_{1},u_{2},u_{3},\ldots ,u_{n}\) and \(v_{1},v_{2},v_{3},\ldots ,v_{n}\) in such a way that the coupled system becomes multistable.

Now, according to our scheme, a multistable system can be designed by choosing \(u_{1},u_{2},u_{3},\ldots ,u_{n}\) and \(v_{1},v_{2},v_{3},\ldots ,v_{n}\) in such way that i \((1 \le i\le n-1)\) number of state variables keep constant difference and \((n-i)\) number of state variables synchronize. Therefore, we choose \(u_{1},u_{2},u_{3},\ldots ,u_{n}\) and \(v_{1},v_{2},v_{3},\ldots ,v_{n}\) in such a way that

$$\begin{aligned}&\dot{e}_1=0,\nonumber \\&\dot{e}_2=0,\nonumber \\&\dot{e}_3=0,\nonumber \\&...\,..\,...,\nonumber \\&\dot{e}_i=0,\nonumber \\&\dot{e}_{i+1}=-e_ {i+1},\nonumber \\&\dot{e}_{i+2}=-e_{i+2},\nonumber \\&......\,..\,.......,\nonumber \\&\dot{e}_n=-e_n, \end{aligned}$$
(6)

where \(1\le i\le n-1\). Then, for such a choice, the coupled systems (3) and (4) as a whole may show multistability. Now we choose the function \(L=(e_{i+1}^2+e_{i+2}^2 +e_{i+3}^2+\cdots +e_{n}^2)/2 \) as a Lyapunov function and observe that

$$\begin{aligned} \dot{L}= & {} e_{i+1}\dot{e}_{i+1}+e_{i+2}\dot{e}_{i+2}+e_{i+3}\dot{e}_{i+3}+\cdots +e_{n}\dot{e}_{n}\nonumber \\= & {} -e_{i+1}^2-e_{i+2}^2 -e_{i+3}^2-\cdots -e_{n}^2. \end{aligned}$$
(7)

Hence, the errors \(e_{i+1},e_{i+2},e_{i+3},\ldots ,e_{n}\) must tend to zero, i.e., \(y_{i+1}=x_{i+1}\), \(y_{i+2}=x_{i+2}\),...,\(y_{n}=x_{n}\) as \(t\rightarrow \infty \) and \({e_1},{e_2},{e_3},\ldots ,{e_i} \) become constants of motion.

Therefore, \(y_{1}=x_{1}+c_{1},y_{2}=x_{2}+c_{2},y_{3}=x_{3}+c_{3},\ldots ,y_{i}=x_{i}+c_{i}\) and \(y_{i+1}=x_{i+1}\), \(y_{i+2}=x_{i+2},\ldots ,y_{n}=x_{n}\). Here, \(c_1,c_2,\ldots ,c_i\) are differences between the initial conditions of the two coupled systems. Now, the dynamics of the coupled systems (3) and (4) are equivalent to the following modified system:

$$\begin{aligned} \dot{x}_1= & {} f_1(x_1,x_2,\ldots ,x_n)+u_1( x_1,x_2,\ldots ,x_n;\nonumber \\&x_1+c_1,\ldots ,x_i+c_i,x_{i+1},\ldots ,x_n),\nonumber \\ \dot{x}_2= & {} f_2(x_1,x_2,\ldots ,x_n)+u_2( x_1,x_2,\ldots ,x_n;\nonumber \\&x_1+c_1,\ldots ,x_i+c_i,x_{i+1},\ldots ,x_n),\nonumber \\ \dot{x}_3= & {} f_3(x_1,x_2,\ldots ,x_n)+u_3( x_1,x_2,\ldots ,x_n;\nonumber \\&x_1+c_1,\ldots ,x_i+c_i,x_{i+1},\ldots ,x_n),\nonumber \\ ....&..&.............................,\nonumber \\ \dot{x}_n= & {} f_n(x_1,x_2,\ldots ,x_n)+u_n( x_1,x_2,\ldots ,x_n;\nonumber \\&x_1+c_1,\ldots ,x_i+c_i,x_{i+1},\ldots ,x_n), \end{aligned}$$
(8)

where \(c_1,c_2,c_3,\ldots ,c_i\) are initial condition-dependent constants. The coupled systems (3) and (4) show multistable behaviour if dynamics of system (8) changes qualitatively with the variation of \(c_1,c_2,c_3,\ldots ,c_i\). Notice that we have chosen \(\dot{e}_1= \dot{e}_2=\cdots =\dot{e}_i=0\), and in general \(\dot{e}_1,\dot{e}_2,\ldots ,\dot{e}_i\) may be chosen as any polynomial functions of \(e_{i+1},e_{i+2},e_{i+3},\ldots ,e_{n}\).

3 Illustration of our technique of coupling Lorenz and Lu systems

In this section, we shall discuss the proposed technique for designing multistable systems by coupling Lorenz and Lu systems. The famous Lorenz system is the following

$$\begin{aligned} \dot{x}= & {} a(y-x),\nonumber \\ \dot{y}= & {} cx-xz-y,\nonumber \\ \dot{z}= & {} xy-bz, \end{aligned}$$
(9)

where \(a,b,c >0\) are the parameters. The Lu system is described by

$$\begin{aligned} \dot{x}= & {} \rho (y-x),\nonumber \\ \dot{y}= & {} -xz+\gamma y,\nonumber \\ \dot{z}= & {} xy-\mu z, \end{aligned}$$
(10)

where \(\rho , \gamma \) and \(\mu \) are the positive parameters.

In this section, we shall discuss two different schemes for generating multistable systems by coupling Lorenz and Lu systems.

Fig. 1
figure 1

Phase diagram of system (14) when \(a=10, c=25, b=8/3\) for (a) \(z_{20}=10\) and (b) \(z_{20}=-5\).

Full size image

Scheme I:

In this scheme, we make two corresponding variables of the two systems to synchronize and one variable to keep constant difference. We couple a Lorenz and a Lu system in the following way:

$$\begin{aligned} \dot{x}_1= & {} a(y_1-x_1)+w_1(t),\nonumber \\ \dot{y}_1= & {} cx_1-x_1z_1-y_1+w_2(t),\nonumber \\ \dot{z}_1= & {} x_1y_1-bz_1+w_3(t),\nonumber \\ \dot{x}_2= & {} \rho (y_2-x_2)+u_1(t), \nonumber \\ \dot{y}_2= & {} -x_2z_2+\gamma y_2+u_2(t),\nonumber \\ \dot{z}_2= & {} x_2y_2-\mu z_2+u_3(t). \end{aligned}$$
(11)

We choose controllers \(w_i(t)\) and \(u_i(t),i=1,2,3\) such that the above system becomes multistable. We construct the governing equations for the synchronization errors \(e_1=x_2-x_1, e_2=y_2-y_1, e_3=z_2-z_1\) as

$$\begin{aligned} \dot{e}_1= & {} \rho (y_2-x_2)-a(y_1-x_1)+u_1(t)-w_1(t),\nonumber \\ \dot{e}_2= & {} -x_2z_2+\gamma y_2-cx_1+x_1z_1+y_1+u_2(t)-w_2(t),\nonumber \\ \dot{e}_3= & {} x_2y_2-\mu z_2-x_1y_1+bz_1+u_3(t)-w_3(t). \end{aligned}$$
(12)

Now the controllers \(u_i(t)\) and \(w_i(t)\); \(i=1,2,3\) are selected as

Hence the error system becomes

$$\begin{aligned} \dot{\mathbf{e}}= & {} A\mathbf{e}, \end{aligned}$$
(13)

where

$$\begin{aligned} \mathbf{e}=\left( \begin{array}{ccc} e_1\\ e_2 \\ e_3\end{array}\right) \quad \mathrm {and} \quad A=\left( \begin{array}{c@{\quad }c@{\quad }c} -1 &{} 0 &{} 0\\ 0 &{} -1 &{} 0 \\ \gamma &{} \rho &{} 0\end{array}\right) . \end{aligned}$$

From (13) it is clear that \(e_1,e_2\rightarrow 0\) as \(t\rightarrow \infty \) and \(\dot{e_3}=\gamma e_1+\rho e_2\), i.e., \(e_3=\hbox { constant }=k\). Hence \(z_{20}-z_{10}=k\), i.e., \(z_{20}=z_{10}+k,\) where k is a constant, depends on the initial conditions of the full system. Therefore, the dynamics of system (11) is equivalent to the following three-dimensional systems:

$$\begin{aligned} \dot{x}_1= & {} a(y_1-x_1),\nonumber \\ \dot{y}_1= & {} (c-z_{20})x_1-2x_1z_1-y_1,\nonumber \\ \dot{z}_1= & {} x_1y_1-bz_1. \end{aligned}$$
(14)

System (11) is a multistable system if the dynamical behaviour of system (14) changes qualitatively with the variation of the value of \(z_{20}\).

Scheme II:

In this scheme, we design multistable system synchronizing one variable and keeping two variables at constant difference. Here, we consider the coupled Lorenz and Lu systems in the following manner:

$$\begin{aligned} \dot{x}_1= & {} a(y_1-x_1)+u_{11},\nonumber \\ \dot{y}_1= & {} cx_1-x_1z_1-y_1+u_{12},\nonumber \\ \dot{z}_1= & {} x_1y_1-bz_1+u_{13},\nonumber \\ \dot{x}_2= & {} \rho (y_2-x_2)+u_{21},\nonumber \\ \dot{y}_2= & {} -x_2z_2+\gamma y_2+u_{22},\nonumber \\ \dot{z}_2= & {} x_2y_2-\mu z_2+u_{23}. \end{aligned}$$
(15)

We choose \(u_{11}, u_{12}, u_{13}\) and \(u_{21}, u_{22}, u_{23}\) as \(u_{11}=\rho (y_2-x_2), u_{12}=\gamma y_2-x_2z_2+y_2, u_{13}=x_2y_2-\mu z_2\) and \(u_{21}=a(y_2-x_1), u_{22}=cx_1-x_1z_1+y_2, u_{23}=y_1(x_1-a-\rho )+(a+\rho )y_2+bz_1\). We construct the governing equations for the synchronization errors as

$$\begin{aligned} \dot{e}_1= & {} ae_2,\nonumber \\ \dot{e}_2= & {} -e_2,\nonumber \\ \dot{e}_3= & {} (a+\rho )e_2. \end{aligned}$$
(16)

Therefore, from (16) it is clear that \(e_2\rightarrow 0\) as \(t\rightarrow \infty \) i.e., \(y_2=y_1\) and \(\dot{e}_1=0,\dot{e}_3=0\) implies that \(x_{20}=x_{10}+k_1\) and \(z_{20}=z_{10}+k_2,\) where \(k_1\) and \(k_2\) are constants that depend on the initial conditions of the full system. Therefore, the dynamics of the system of eq. (15) is equivalent to the following three-dimensional system:

$$\begin{aligned} \dot{x}_1= & {} (a+\rho )(y_1-x_1)-\rho x_{20},\nonumber \\ \dot{y}_1= & {} (c-z_{20})x_1-2x_1z_1+\gamma y_1-x_{20}z_1-x_{20}z_{20},\nonumber \\ \dot{z}_1= & {} 2x_1y_1-(b+\mu )z_1+x_{20}y_1-\mu z_{20}. \end{aligned}$$
(17)

System (15) is a multistable system if the dynamical behaviour of system (17) changes qualitatively with the variation of \(x_{20}\) and \(z_{20}\).

Fig. 2
figure 2

Bifurcation diagram of sytem (14) with respect to \(z_{20}\) for \(a=10, c=25\) and \(b={8}/{3}\).

Full size image
Fig. 3
figure 3

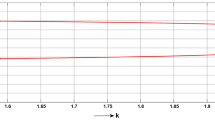
Variation of maximum Lyapunov exponent of system (14) with respect to \(z_{20}\) for \(a=10, c=25\) and \(b=8/3\).

Full size image
Fig. 4
figure 4

Phase diagram of the six-dimensional coupled system (inducing all the controllers) of system (15) for \(\rho =30, a=10, c=30, b=8/3, \gamma =10, \mu =3 \) with respect to xy plane, (a) for the initial conditions \( x_{10}=1.0, y_{10}=1.0, z_{10}=1.0, x_{20}=2.5, y_{20}=1.0, z_{20}=-5\) and (b) for the initial conditions \(x_{10}=1.0, y_{10}=1.0, z_{10}=1.0, x_{20}=2.5, y_{20}=1.0, z_{20}=3\).

Full size image

4 Numerical simulation results

Fig. 5
figure 5

Phase diagram of system (17) for \(\rho =30, a=10, c=30, b={8}/{3}, \gamma =10, \mu =3, x_{20}=3\) and \(z_{20}=-5\).

Full size image
Fig. 6
figure 6

Bifurcation diagram of system (17) with respect to \(x_{20}\) for \(\rho =30, a=10, c=30, b={8}/{3}, \gamma =10, \mu =3 \) and \(z_{20}=-5\).

Full size image
Fig. 7
figure 7

Variation of maximum Lyapunov exponent with respect to \(x_{20}\) for \(\rho =30, a=10, c=30, b={8}/{3}, \gamma =10, \mu =3 \) and \(z_{20}=-5\).

Full size image
Fig. 8
figure 8

Phase diagram of system (17) for \(\rho =30, a=10, c=30, b={8}/{3}, \gamma =10, \mu =3, x_{20}=1\) and \(z_{20}=-5\).

Full size image
Fig. 9
figure 9

Bifurcation diagram of system (17) with respect to \(z_{20}\) for \(\rho =30, a=10, c=30, b={8}/{3}, \gamma =10, \mu =3\) and \(x_{20}=5\).

Full size image

In this section, we present numerical simulation results to show the effectiveness of our theoretical results using MATLAB R2009b. In figure 1, phase diagram of system (14) is plotted in the xy plane for different values of \(z_{20}\), e.g., \(z_{20}=10\) and \(z_{20}=-5\) when \(a=10, c=25\) and \(b={8}/{3}\). Bifurcation diagram of system (14) with respect to \(z_{20}\) for the above set of parameters is shown in figure 2. Since \(z_{20}\) is completely an initial condition-dependent parameter, system (14) has qualitatively different dynamical behaviour with the variation of \(z_{20}\) which is clear from figures 1 and 2. Variation of maximum Lyapunov exponent of system (14) with respect to \(z_{20}\) is depicted in figure 3 which again establishes the existence of qualitatively different dynamical behaviour with the variation of initial conditions. We draw the phase diagram of the six-dimensional coupled system (inducing all the controllers) for \(\rho =30, a=10, c=30, b=8/3, \gamma =10, \mu =3 \) with respect to xy plane for the initial conditions \( x_{10}=1.0, y_{10}=1.0, z_{10}=1.0, x_{20}=2.5, y_{20}=1.0, z_{20}=-5\) in figures 4a and 4b for the initial conditions \(x_{10}=1.0, y_{10}=1.0, z_{10}=1.0, x_{20}=2.5, y_{20}=1.0, z_{20}=3\). In figure 5, the phase diagram is plotted for the same set of parameters and for the initial conditions \(x_{20}=3\), \(y_{20}=1\) and \(z_{20}=5\). We present the bifurcation diagram of system (17) with respect to \(x_{20}\) in figure 6 for \(\rho =30, a=10, c=30, b=8/3, \gamma =10, \mu =3 \) and \(z_{20}=-5\). Variation of maximum Lyapunov exponent with respect to \(x_{20}\) for system (17) is plotted in figure 7. Figure 5 matches with the result of figures 6 and 7. In figure 8, we draw the phase diagram of system (17) for \(x_{20}=1\), \(y_{20}=1\) and \(z_{20}=-5\) and lastly in figure 9 we draw the bifurcation diagram of system (17) with respect to \(z_{20}\) for \(\rho =30, a=10, c=30, b=8/3, \gamma =10, \mu =3 \) and by taking the initial condition \(x_{20}=5\). Here the result of figure 8 is consistent with result of figure 9. Therefore, the above numerical simulation results show that the newly proposed scheme can successfully design multistable systems.

5 Conclusion

We have proposed a generalized scheme for designing multistable systems coupling two different dynamical systems of the same dimension via active control. Designing partial synchronization of states between the coupled systems and finding some completely initial condition-dependent constants of motion are the key concepts for designing multistability here. Basically, in the proposed scheme, complete synchronization of i number (\(1\le i \le m-1\)) of state variables occur and at the same time constant difference between j (\(1\le j\le m-1\), \(i+j=m\)) number of state variables of the coupled systems exist. We illustrate our scheme by coupling Lorenz and Lu systems. Existence of multistable behaviour is established with the help of phase diagrams, bifurcation diagrams and maximum Lyapunov exponents variation with respect to the completely initial condition-dependent constants of motion. We have also presented the variation of maximum Lyapunov exponents with the variation of initial conditions. If we couple two dynamical systems of same dimension in such a way that the corresponding state variables of the coupled systems keep constant differences, then this kind of coupling can produce multistability. This proposed scheme may be very useful to design real-world physical, electrical, chemical, social and biological systems with multistable behaviour and it may also be helpful to understand the basic mechanisms of many natural multistable systems.