1 Introduction

It is held that the long-range forces in the Universe are produced by scalar fields. Since long, scalar–tensor theories of gravitation have been of focal interest in many areas of gravitational physics and cosmology. Einstein’s theory of general relativity does not seem to resolve some of the important problems in cosmology such as dark matter or the missing matter. The scalar–tensor theories, being viable alternatives to general relativity, provide convenient set of representations for the observational limits on possible deviations from general relativity. The most widely accepted and possibly the best motivated theory in which a scalar field shares the stage of gravitation is that of Brans and Dicke [1]. The scalar–tensor theories of gravitation involving dimensionless scalar fields have also been extensively studied by fairly a large number of eminent workers. Saez–Ballester [2] developed a scalar–tensor theory in which the matter is coupled with a dimensionless scalar field ϕ in a simple manner. The ϕ-coupling provided a satisfactory description of the weak fields in which antigravity regime appears in spite of the dimensionless behaviours of the scalar field. This theory suggests a possible way to solve the missing mass problem in a non-flat FRW models. Saez [3] presented a non-singular zero curvature FRW model and found that there is an antigravity regime which can act either at the beginning of the inflationary epoch or before. The cosmological models based on scalar fields have a long history for exploring possible inflationary scenario and for describing dark energy. In recent years, cosmological model with a scalar field is the most natural basis for inflationary models. Scalar fields explains the existence of the effective cosmological constant at the early stages of the cosmic evolution.

The discovery of expansion of the Universe stands as a major breakthrough of the observational cosmology. Survey of cosmological distant type-Ia supernove [4–6] indicated the presence of a new unaccounted for dark energy (DE) that opposes the self-attractions of matter and accelerates the expansion of the Universe. Astrophysical observations indicate that expansion of the Universe is driven by an exotic energy with large negative pressure which is known as dark energy. In spite of all the evidences, dark energy is still a challenging problem in theoretical physics. High-precision measurements of the expansion of Universe are required to understand how the expansion rate changes over time. In general relativity, the evolution of the Universe is parametrized by the cosmological equation of state (the relationship between temperature, pressure, combined matter, energy and vacuum energy density for any region of space). Measuring the equation of state parameter for dark energy is one of the biggest efforts in observational cosmology today. The DE has conventionally been characterized by equation of state (EoS) parameter ω = p/ρ, which is not necessarily constant, where ρ is the energy density and p is the pressure of the Universe. The simplest DE candidate is the vacuum energy (ω = −1), which is mathematically equivalent to the cosmological constant Λ. The other conventional alternatives, which can be described by minimally coupled scalar fields, are quintessence (ω ≥ −1), phantom (ω ≤ −1) and quintom (that can cross from phantom region to quintessence region as evolved), chaplygin gas, tachyon etc. [7,8]. However, it is a function of time or red-shift in general [9]. For instance, quintessence models involving scalar fields give rise to the time-dependent EoS parameter [10,11].

In recent years, several researchers [12–19] have shown keen interest in studying the Universe with variable EoS. In all these models, DE is handled as an isotropic fluid. However, there is no a priori reason to assume that the DE is isotropic in nature. In principle, the EoS parameter of DE may be generalized by determining the EoS parameter separately on each spatial axis in a consistent way with the considered metric, because the energy density is a scalar quantity but the pressure is a vectorial quantity. Such DE candidates can also be studied in the context of vectorial fields and such candidates have been proposed by several researchers [20–25]. The cosmological data from large-scale structures [26] and type-Ia supernova [27] observations do not rule out the possibility of an anisotropic DE [28].

For instance, quintessence models involving scalar fields give to time-dependent EoS parameter ω [29,30]. Amirhashchi et al [31] and Pradhan et al [32] have discussed a Bianchi type-VI DE model with a variable EoS parameter. Ray et al [33], Kumar [34] and Pradhan et al [35] are some of the researchers who have investigated dark energy models with variable EoS parameter in different physical contexts. Yadav and Saha [36] have obtained an LRS Bianchi-I anisotropic cosmological model where dark energy is dominated. Shri Ram et al [37] have discussed the field equations in Saez–Ballester theory of gravitation for Bianchi type-V model filled with viscous fluid together with heat flow. Rao et al [38] have obtained Bianchi type-I dark energy in the scalar–tensor theory of Saze and Ballester. Recently, Naidu et al [39,40] have discussed dark energy models of a locally rotationally symmetric Bianchi type-II and Bianchi-III respectively in Saez–Ballester scalar–tensor theory of gravitation with variable EoS parameter. It deserves mention that Jamil et al [41] have investigated the generalized Saez–Ballester scalar–tensor theory of gravity via Noether gauge symmetry in the background of Bianchi type-I cosmological space–time.

Motivated by this study, we have investigated hypersurface-homogeneous anisotropic dark energy cosmological models with variable EoS parameter in Saez–Ballester theory of gravitation.

2 Metric and field equations

Stewart and Ellis [42] have obtained some general solutions to the Einstein’s field equations in the case of a perfect fluid distribution satisfying a barotropic equation of state for the hypersurface-homogeneous space–time given by the metric

$$ \mathrm{d}s^{2}= \mathrm{d}t^{2}-A^{2}(t) \mathrm{d}x^{2}-B^{2}(t)\left[\mathrm{d}y^{2} + {\Sigma}^{2}(y, K)\mathrm{d}z^{2}\right], $$
(1)

where \( \sum (y,K)= \sin y \), y, \(\sinh y\), respectively, when K = 1,0,−1. These are spaces having a group of motions G 4 on V 3, which are locally rotationally symmetric (LRS). For the metric (1), Hajj-Boutros [43] procured a method of generating exact solution to the field equations in the case of a perfect fluid not satisfying an equation of state. Verma and Shri Ram [44] studied model (1) with a bulk-viscous term and found some exact solutions.

The field equations in scalar–tensor theory, proposed by Saez and Ballester [2] are

$$ R_{\mu\nu}-\frac{1}{2}R g_{\mu\nu}-\pi \phi^{r}{}\left( {}\phi_{,\mu}\phi_{,\nu}-\frac{1}{2}g_{\mu\nu}\phi_{,\alpha}\phi^{,\alpha}{}\right)=-T_{\mu\nu}, $$
(2)

where π is a dimensionless coupling constant and T μν is the energy–momentum tensor of a perfect fluid defined by

$$ T_{\mu\nu}=(\rho + p)u_{\mu} u_{\nu} - p g_{\mu \nu}, $$
(3)

where ρ is the energy density, p is the pressure and u μ is the velocity four-vector of the fluid. In comoving coordinate system u μ is given by

$$ u^{\mu}=(0, 0, 0, 1). $$
(4)

The scalar field ϕ satisfies the equation

$$ 2\phi^{r}\phi^{;\alpha}_{;\alpha}+r\phi^{r-1}\phi_{,~\alpha}\phi^{, \alpha}=0. $$
(5)

Here r is an arbitrary constant, comma and semicolon denote ordinary and covariant derivative respectively.

The simplest generalization of the EoS parameter of the perfect fluid may be to determine the EoS parameter separately on each spatial axis by preserving the diagonal form of the energy–momentum tensor in a consistent way with the considered metric. Therefore, the energy–momentum tensor of the fluid is given as

$$ T^{\mu}_{\nu}=\text{diag}[{T^{1}_{1}}, {T^{2}_{2}}, {T^{3}_{3}}, {T^{4}_{4}}]. $$
(6)

For an anisotropic fluid, the energy–momentum tensor can be taken as

$$\begin{array}{@{}rcl@{}} T^{\mu}_{\nu}&=& \text{diag}[ -p_{x}, -p_{y}, -p_{z}, \rho] \\ & =& \text{diag}[-\omega_{x}, -\omega_{y}, -\omega_{z}, 1] {\rho}, \end{array} $$
(7)

where p x , p y and p z are the pressure and ω x , ω y , ω z are the directional EoS parameters along the x-, y- and z-axes respectively. We parametrized the deviation from isotropy by setting ω x = ω and then introducing skewness parameters γ and δ which are the deviation from ω on y- and z-axes respectively. Here, ω, γ and δ are not necessarily constants and can be functions of time. Again, as \({T^{2}_{2}}={T^{3}_{3}}\), we have γ = δ. Then eq. (7) can be customized to the metric (1) by

$$ T^{\mu}_{\nu} =\text{diag}[ -\omega, -(\omega+\gamma), -(\omega+\gamma), 1] {\rho}. $$
(8)

In a comoving coordinate system u i = (1,0,0,0), field equation (2) for the metric (1) and the energy–momentum tensor eq. (8) read as

$$ \frac{ 2 \dot{A}}{A}\frac{\dot{B}}{B}+ \frac{\dot{B}^{2}}{B^{2}}+\frac{K}{B^{2}} +\frac{1}{2} \pi \phi^{r} \dot {\phi^{2}}= \rho, $$
(9)
$$ \frac{2 \ddot{B}}{B}+ \frac{\dot{B}^{2}}{B^{2}}+\frac{K}{B^{2}} -\frac{1}{2} \pi \phi^{r} \dot {\phi^{2}}=-\omega \rho , $$
(10)
$$ \frac{\ddot{B}}{B}+ \frac{\ddot{A}}{A}+\frac{\dot{A}}{A}\frac{\dot{B}}{B} -\frac{1}{2} \pi \phi^{r} \dot {\phi^{2}} =- (\omega +\gamma) \rho , $$
(11)
$$ \ddot{\phi}+\dot{\phi}\left( \frac{\dot{A}}{A}+2\frac{\dot{B}}{B}\right)+\frac{r}{2\phi}{\dot{\phi}}^{2}=0, $$
(12)

where the dot denotes differentiation with respect to the cosmic time t.

The anisotropy of the expansion can be parametrized after defining the directional Hubble parameter and the mean Hubble parameter of the expansion. The directional Hubble parameters in the direction of x, y and z for the metric defined in eq. (1) may be defined as follows:

$$ H_{1}=\frac{\dot{A}}{A},\quad H_{2}=H_{3}=\frac{\dot{B}}{B}. $$
(13)

The spatial volume for model (1) is given by

$$ V=AB^{2}. $$
(14)

We define a = (AB 2)1/3 as the average scale factor so that the Hubble parameter is anisotropic and may be defined as

$$ H = \frac{\dot a}{a}=\frac{1}{3}\left( \frac{\dot{A}}{A}+\frac{2 \dot{B}}{B}\right). $$
(15)

The scalar expansion 𝜃, shear scalar σ 2 and the average anisotropy parameter A m are defined as

$$ \theta = \frac{\dot{A}}{A}+\frac{2 \dot{B}}{B}, $$
(16)
$$ \sigma^{2} =\frac{1}{2} \sigma_{ij} \sigma^{ij}=\frac{1}{3}\left( \frac{\dot{A}}{A}- \frac{\dot{B}}{B}\right)^{2}, $$
(17)
$$ A_{m}= \frac{1}{3}\sum\left( \frac{\Delta H_{i}}{H}\right)^{2}, $$
(18)

where ΔH i = H i −H (i = 1,2,3). H i (1,2,3) represents the directional Hubble parameter in the direction of x, y and z, respectively. A m = 0 corresponds to isotropic expansion. The space approaches isotropy, in the case of diagonal energy–momentum tensor (T 0i = 0, where i = 1, 2, 3) if A m → 0, V →\(+\infty \) and T 00>0 (ρ>0) as \(t\rightarrow + \infty \) [45].

Using eqs (13) and (15), the average anisotropy parameter eq. (18) can be reduced to

$$ A_{m}=\frac{2}{9}\left( \frac{H_{x}-H_{y}}{H}\right)^{2}. $$
(19)

From (10) and (11), we get

$$ \frac{\dot{A}}{A}-\frac{\dot{B}}{B}=\frac{\lambda}{V}+\frac{1}{V}\int\left( \frac{K}{B^{2}}-\gamma \rho\right) V\mathrm{d}t, $$
(20)

where λ is the real constant of integration and the term with γ is the term that arises due to the possible intrinsic anisotropy of the fluid. Finally, using eq. (20) in (19) we obtain the anisotropy parameter of the expansion,

$$ A_{m}=\frac{2}{9 H^{2}}\left[\lambda+\int\left( \frac{K}{B^{2}}-\gamma \rho\right) V\mathrm{d}t\right] V^{-2}. $$
(21)

Choosing γ = 0, the anisotropy parameter for hypersurface-homogeneous model in the presence of a perfect fluid is reduced to

$$ A_{m}=\frac{2}{9 H^{2}}\left[\lambda+ K \int \frac{V}{B^{2}}\mathrm{d}t\right] V^{-2}. $$
(22)

The integral term in (21) vanishes for

$$ \gamma=\frac{K}{\rho B^{2}}, $$
(23)

which further leads to the following energy–momentum tensor:

$$ T^{\mu}_{\nu} = \text{diag}{\kern-2.5pt}\left[ -1,\omega, \omega+\frac{K}{\rho B^{2}}, \omega+\frac{K}{\rho B^{2}}\right]{\kern-2.5pt}{\rho}, $$
(24)

where the anisotropy parameter (21) reduces to

$$ A_{m}=\frac{2\lambda }{9H^{2}} V^{-2}. $$
(25)

Using the energy–momentum tensor (24), the field equations (9)–(11) now read as

$$ \frac{ 2 \dot{A}}{A}\frac{\dot{B}}{B}+ \frac{\dot{B}^{2}}{B^{2}} +\frac{1}{2} \pi \phi^{r} \dot {\phi^{2}}= \rho -\frac{K}{B^{2}}=(1-\gamma)\rho, $$
(26)
$$ \frac{2 \ddot{B}}{B}+ \frac{\dot{B}^{2}}{B^{2}}+\frac{K}{B^{2}} -\frac{1}{2} \pi \phi^{r} \dot {\phi^{2}}=-\omega \rho , $$
(27)
$$ \frac{\ddot{B}}{B}+ \frac{\ddot{A}}{A}+\frac{\dot{A}}{A}\frac{\dot{B}}{B} +\frac{K}{B^{2}}-\frac{1}{2} \pi \phi^{r} \dot {\phi^{2}} =- \omega \rho. $$
(28)

The quadrature expression for the dimensionless scalar field function ϕ, from eq. (12), is found as

$$ \phi=\left[\frac{h(r+2)}{2}\int{\frac{\mathrm{d}t}{a^{3}}}\right]^{{2}/{(r+2)}}, $$
(29)

where h is an arbitrary constant.

3 Solutions of field equations

We are at liberty to make some assumptions as we have more unknown A, B, ρ, ω, γ, δ and ϕ with lesser number of field eqs (26)–(28) and (12) to determine them. For the complete determination of these field equations, we use a special law of variation of Hubble parameter proposed by Bermann [46] that gives a constant negative deceleration parameter model of the Universe. Now we consider the constant negative deceleration parameter defined by

$$ q=-\frac{a \ddot{a}}{\dot{a}^{2}}. $$
(30)

Here the constant is taken as negative for an accelerating model of the Universe.

The solution of eq. (30) yields

$$ a= \left( c_{1}t+c_{2}\right)^{1/(1+q)}, $$
(31)

where c 1 and c 2 are constants of integration. This equation implies that the condition of expansion is 1 + q>0.

From eqs (27) and (28), we get

$$ \frac{\dot{B}}{B} -\frac{\dot{A}}{A} =\frac{\lambda}{V}=\frac{\lambda}{a^{3}}. $$
(32)

Using eqs (15), (31) and (32), we obtain the solutions for the scale factors as follows:

$$\begin{array}{@{}rcl@{}} A&=& l_{1}{}\left( c_{1}t+c_{2}\right)^{1/(1+q)}\\ && \times\exp \left\{\frac{-2\lambda (1+q)}{3c_{1}(q-2)} (c_{1}t+c_{2})^{{(q-2)}/{(1+q)}}\right\}, \end{array} $$
(33)
$$\begin{array}{@{}rcl@{}} B&=& l_{2}{}\left( c_{1}t+c_{2}\right)^{1/(1+q)}\\ &&\times\exp \left\{\frac{\lambda (1+q)}{3c_{1}(q-2)} (c_{1}t+c_{2})^{{(q-2)}/{(1+q)}}\right\}, \end{array} $$
(34)

where l 1 and l 2 are integration constants related by \(l_{1}{l_{2}^{2}}=1\).

The metric of the solutions is therefore

$$\begin{array}{@{}rcl@{}} \mathrm{d}s^{2}&=&-\mathrm{d}t^{2}+{l_{1}^{2}}(c_{1}t+c_{2})^{{2}/{(1+q)}}\\ && \times\exp{}\left\{\frac{-4\lambda(1+q)}{3c_{1}(q-2)}(c_{1}t+c_{2})^{{(q-2)}/{(1+q)}}\right\}\mathrm{d}x^{2}\\ &&+\,{l_{2}^{2}}(c_{1}t+c_{2})^{{2}/{(1+q)}}\\ &&\times\exp{}\left\{\frac{2\lambda(1+q)}{3c_{1}(q-2)}(c_{1}t+c_{2})^{{(q-2)}/{(1+q)}}\right\}\\ && \times~(\mathrm{d}y^{2}+{\Sigma}^{2}(y,k)\mathrm{d}z^{2}). \end{array} $$
(35)

Using the transformation

$$ T=c_{1}t+c_{2},\quad X=l_{1}x,\quad Y=l_{2}y,\quad Z=l_{2}z $$
(36)

the model (35) can be written in the form

$$\begin{array}{@{}rcl@{}} \mathrm{d}s^{2}&=&-\mathrm{d}T^{2}+T^{{2}/{(1+q)}}\\ &&\times \exp{}\left\{\frac{-4\lambda(1+q)}{q-2}T^{{(q-2)}/{(1+q)}}\right\}\mathrm{d}x^{2}\\ &&+\,T^{{2}/{(1+q)}}\exp\left\{\frac{2\lambda(1+q)}{q-2}T^{{(q-2)}/{(1+q)}}\right\}\\ &&\times~(\mathrm{d}y^{2}+{\Sigma}^{2}\mathrm{d}z^{2}). \end{array} $$
(37)

The solution for the scalar function ϕ, from eq. (29), is obtained by

$$\begin{array}{@{}rcl@{}} \phi=\left[\frac{\phi_{0}(r+2)(1+q)}{2(q-2)}T^{{(q-2)}/{(1+q)}}\right]^{{2}/{(r+2)}}, \end{array} $$
(38)

where ϕ 0 is an arbitrary constant.

For the derived line element (37), the energy density has the following expression:

$$\begin{array}{@{}rcl@{}} \rho &=& \frac{3}{(1+q)^{2} T^{2}} +\frac{3\pi h^{2}+10\lambda^{2}}{6 T^{{6}/{(1+q)}}}+\frac {K}{T^{{2}/{(1+q)}}} \\ &&\times\exp{}{\left\{\frac{-2 \lambda (1+q)}{3(q-2)} T^{{(q-2)}/{(1+q)}}\right\}}. \end{array} $$
(39)

The deviation-free part of the EoS parameter is given by

$$\begin{array}{@{}rcl@{}} \omega &=& -\frac{1}{\rho}\left[\frac{1-2q}{(1+2q)^{2} T^{2}} +\frac{3\pi h^{2}-2\lambda^{2}}{6 T^{{6}/{(1+q)}}}+\frac {K}{T^{{2}/{(1+q)}}} \right.\\ &&\times\left.\exp{}{\left\{\frac{-2 \lambda (1+q)}{3(q-2)} T^{{(q-2)}/{(1+q)}}\right\}}\right] \end{array} $$
(40)

which is negative if π>(2λ 2/3h 2). The skewness parameter (γ) has the value

$$\begin{array}{@{}rcl@{}} \gamma = \frac{K}{\rho T^{{2}/{(1+q)}}} \exp{\{ -2 \lambda (1+q) T^{{(q-4)}/{(1+q)}}\}}. \end{array} $$
(41)

Thus the line element (37) represents a hypersurface-homogeneous cosmological model with anisotropic dark energy in Saez–Ballester theory of gravitation. The deceleration parameter is always negative indicating the accelerating Universe.

4 Results and discussions

The directional Hubble parameters for model (37) are

$$ H_{1}=\frac{1}{(1+q)t}-\frac{2\lambda}{3t^{{3}/{(1+q)}}}, $$
(42)
$$ H_{2}=H_{3}=\frac{1}{(1+q)t}+\frac{\lambda}{3t^{{3}/{(1+q)}}}. $$
(43)

The mean Hubble parameter is given by

$$ H=\frac{1}{(1+q)t}. $$
(44)

The dynamical scalars 𝜃 and σ 2 are obtained as

$$ \theta=\frac{3}{(1+q)t}, $$
(45)
$$ \sigma^{2}=\frac{\lambda^{2}}{3t^{{6}/{(1+q)}}}. $$
(46)

After a little manipulation of eq. (19) and using eqs (42)–(44), we get

$$ A_{m}=\frac{2\lambda(1+q)^{2}}{9t^{{(4-2q)}/{(1+q)}}}, $$
(47)

where parameter A m , being infinite at T = 0, is a decreasing function of time which tends to zero as T →\(\infty \). We also observe that σ/𝜃 tends to zero as T →\(\infty \). Therefore, the model approaches isotropy for large values of T. The scalar field ϕ contributes significantly to the energy density and EoS parameter.

We now present models for K = 0, 1 and −1.

Model I

When K = 0, the model (37) reduces to

$$\begin{array}{@{}rcl@{}} \mathrm{d}s^{2}&=& -\mathrm{d}T^{2}+T^{{2}/{(1+q)}}\\ &&\times\exp{\kern-3.5pt}\left\{\frac{-4\lambda(1+q)}{q-2}T^{{(q-2)}/{(1+q)}}\right\}\mathrm{d}X^{2}\\ &&+\,T^{{2}/{(1+q)}}\exp{\kern-3.5pt}\left\{\frac{2\lambda(1+q)}{q-2}T^{{(q-2)}/{(1+q)}}\right\}\\ &&\times\,(\mathrm{d}Y^{2}+Y^{2}\mathrm{d}Z^{2}). \end{array} $$
(48)

For this model, the energy density and EoS parameter are given by

$$\begin{array}{@{}rcl@{}} \rho=\frac{3}{(1+q)^{2}T^{2}}+\frac{3\bar{\omega}h^{2}+10\lambda^{2}}{6T^{{6}/{(1+q)}}}, \end{array} $$
(49)
$$\begin{array}{@{}rcl@{}} \omega=-\frac{1}{\rho}\left[\frac{1-2q}{(1+2q)^{2}T^{2}}+\frac{3\bar{\omega}h^{2}-2\lambda^{2}}{6T^{{6}/{(1+q)}}}\right]. \end{array} $$
(50)

From eq. (41), we see that γ = 0 which means that the model (48) represents a model with isotropic dark energy.

Model II

When K = 1, the model (37) becomes

$$\begin{array}{@{}rcl@{}} \mathrm{d}s^{2}&=& -\mathrm{d}T^{2}+T^{{2}/{(1+q)}}\\ &&\times\exp{\kern-3.5pt}\left\{{\frac{-4\lambda(1+q)}{q-2}}T^{{(q-2)}/{(1+q)}}\right\}\mathrm{d}X^{2}\\ &&+\,T^{{2}/{(1+q)}}\exp{\kern-3.5pt}\left\{\frac{2\lambda(1+q)}{q-2}T^{{(q-2)}/{(1+q)}}\right\}\\ &&\times\,(\mathrm{d}Y^{2}+\sin^{2}Y\mathrm{d}Z^{2}) \end{array} $$
(51)

corresponding to the cosmological model with anisotropic dark energy. The expressions for the energy density and EoS parameter can be obtained from eqs (39) and (40) by putting K = 1.

Model III

When K = −1, model (37) is

$$\begin{array}{@{}rcl@{}} \mathrm{d}s^{2}&=& -\mathrm{d}T^{2}+T^{{2}/{(1+q)}}\\ &&\times\exp{\kern-3.2pt}\left\{\frac{-4\lambda(1+q)}{q-2}T^{{(q-2)}/{(1+q)}}\right\}\mathrm{d}X^{2}\\ &&+\,T^{{2}/{(1+q)}}\exp{\kern-3.2pt}\left\{\frac{2\lambda(1+q)}{q-2}T^{{(q-2)}/{(1+q)}}\right\}\\ &&\times~(\mathrm{d}Y^{2}+\sinh^{2}y\, \mathrm{d}Z^{2}). \end{array} $$
(52)

The energy density and the EoS parameter for this model are given as

$$\begin{array}{@{}rcl@{}} \rho&=&\frac{3}{(1+q)^{2}T^{2}}+\frac{3\bar{\omega}h^{2}+10\lambda^{2}}{6T^{{6}/{(1+q)}}}-\frac{1}{T^{{2}/{(1+q)}}}\\ &&\times\exp{\kern-3.1pt}\left\{\frac{-2\lambda(1+q)}{3(q-2)}T^{{(q-2)}/{(1+q)}}\right\}. \end{array} $$
(53)

The deviation-free part of the EoS parameter is given by

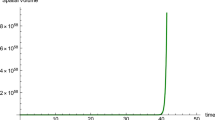
$$\begin{array}{@{}rcl@{}} \omega&=&-\frac{1}{\rho}\left[\frac{1-2q}{(1+q)^{2}T^{2}}+\frac{3\bar{\omega}h^{2}-2\lambda^{2}}{6T^{{6}/{(1+q)}}}-\frac{1}{T^{{2}/{(1+q)}}}\right.\\ &&\left.\times\exp{}\left\{\frac{-2\lambda(1+q)}{3(q-2)}T^{{(q-2)}/{(1+q)}}\right\}\right]. \end{array} $$
(54)

In eqs (53) and (54), the first two terms dominate over the third term and therefore ρ > 0 and ω < 0. Thus, model (54) represents an anisotropic accelerating Universe dominated by dark energy (figures 1 and 2).

Figure 1
figure 1

Plots of energy density (ρ) vs. cosmic time (t).

Full size image
Figure 2
figure 2

Plots of EoS (ω) vs. cosmic time.

Full size image

5 Conclusions

In this paper we have obtained exact solutions of the field equations for hypersurface-homogeneous space–times in the presence of anisotropic dark energy in Saez–Ballester theory of gravitation by applying the variation law for generalized Hubble parameter that yields a negative value of deceleration parameter. For K = 0, the model represents an accelerating Universe with isotropic dark energy, whereas for K = 1 and −1 the models represent accelerating Universe with anisotropic dark energy, which eventually isotropize for large time. For these models, spatial scale factors and the volume scalar vanish at the initial time T = 0. The energy density is infinite at this initial epoch. At this epoch, the dynamical parameters 𝜃, σ and A m are all infinite. Therefore, these models have Big-Bang singularity at T = 0.As T →\(\infty \) the scale factor diverges and ρ tends to zero. The dynamical parameters 𝜃, σ and A m decrease with cosmic time and vanish as T →\(\infty \). The scalar field ϕ contributes significantly to the energy density and the EoS parameter ω.