1 Introduction

Quantum entanglement is a property of correlations between two or more quantum systems [1] and it plays an important role in quantum information theory. It is worth mentioning here, that quantum entanglement has many applications in the emerging technologies of quantum computing and cryptography [2,3] and has been used to realize quantum teleportation experimentally [4]. Also, it has been used in other important applications such as superdense coding [5] and quantum metrology [6]. Several entanglement measures such as concurrence [7], entanglement of formation [8], tangle [9] and negativity [10] have been proposed in pure and mixed states. In this regard, the concurrence and negativity are used as entanglement measures for a mixed state, but for a pure state, the von Neumann entropy of density matrix can also be used as a measure of entanglement [11]. All these measures are used to test whether a given quantum state is separable or entangled. Certain physical phenomena are observed as a result of an entanglement measure such as the ‘entanglement sudden death’ (ESD) and ‘entanglement sudden birth’ (ESB) [12] is the formation of entanglement where the initial unentangled qubits can be entangled after a certain finite evolution time. The coherent field is a type of electromagnetic field which has a minimum uncertainty and it is more of a classical field than being quantum [13]. Other states of the electromagnetic field, such as squeezed states, even and odd coherent states and so on, do not have minimum uncertainty and they are non- classical states, and have more applications in quantum communications and weak signal detection [14].

Considering the motion of the atoms, the Tavis–Jaynes–Cummings model (TJCM) with two moving atoms has been investigated [15] and the researchers have shown that the ESD and ESB [16] have also been experimentally observed for entangled photon pairs [17] and the atom ensembles [18]. In addition to those, the entanglement of two moving atoms interacting with a single-mode field via a three-photon process is also investigated [19]. The von Neumann entropy measurement is used to measure the amount of entanglement between two moving atoms and a strongly squeezed field via four-photon transitions [20] and the researchers have shown ESD and ESB. The geometric phase of a moving three-level atom interacting with the field initially prepared in a coherent and even coherent state has been investigated [21], where the results show that the atomic motion and the type of coherent state play important roles in the dynamic geometric phase. In this investigation, we focus on the study of entanglement between moving and non-moving two two-level atoms interacting with a single-mode radiation field via multiphoton process (kth photon) within a closed system and our main aim is to look for some important phenomena such as ESD and ESB for the system under consideration and investigate the effects of atomic motion parameter p, the photon transition parameter k, the atomic position 𝜃 and the arbitrary constant r. Also, we want to be convinced whether these parameters have a real effect on the interaction system or not.

This paper is organized as follows. In §2 the basic equations and relations for the system under consideration are given. In §3 the entanglement measures like the von Neumann entropy, concurrence, negativity and atoms–field tangle are investigated. In §4 the results are discussed. The main conclusion is summarized in §5.

2 Basic equations and relations

We consider a cavity of length L, containing two identical atoms moving with velocity v j for the jth atomic velocity, and the atomic motion is restricted in the z direction. We consider that the atoms in their motion take the shape of the cosine curve. The shape function of the cavity field-mode f(z j ) (j = A, B atoms) denote the mode structure of the jth atom and take the following form [22]

$$ f(z_{j})\rightarrow f(v_{j}t)=\cos \left( \frac{pv_{j}\pi t}{L}\right) , $$
(1)

where p represents the atomic motion parameter. These two moving atoms interact with the single-mode quantized radiation field in a closed system. In other words, there are no external fields (or external effects) that can act on the system. The interaction Hamiltonian of the two moving atoms interacting with a single-mode quantized electromagnetic field via multiphoton transitions process (i.e., kth photon), in the rotating wave approximation (RWA) can be given as [23] (set \(\hbar =1\))

$$ \hat{H}_{\mathrm{I}}={\sum\limits}_{j=1}^{2}\lambda_{j}f(v_{j}t)\left( \hat{a}^{k}\hat{\sigma}_{+}^{(j)}+\hat{a}^{\dagger k}\hat{\sigma}_{-}^{(j)}\right) , $$
(2)

where \(\hat {\sigma }_{\pm }^{(j)}\) are the Pauli spin operators for the jth atom, \(\hat {a}(\hat {a}^{\dagger } )\) is the annihilation(creation) operator denoting the cavity mode, λ j is the atom–field coupling constant of the jth atom and k is the transition parameter. Let A, B and F denote the first atom, second atom and the radiation field, respectively. Considering that the two atoms have the same velocity, f(z A)=f(z B), we assume that the two atoms are initially in an entangled state and the field in the general coherent state, thus is

$$\begin{array}{@{}rcl@{}} |{\Psi}_{\text{AB}F}\!\left( 0\right) \rangle &=& |{\Psi}_{\mathrm{AB\!}}\!\left( 0\right) \rangle \otimes |{\Psi}_{F}\!\left( 0\right) \rangle\\ &=& \sum\limits_{n=0}^{\infty} B_{n,r} \left[ \cos\theta |e_{1},e_{2},n\rangle + \sin \theta |g_{1},g_{2},n\rangle \right], \end{array} $$
(3)

where

$$B_{n,r}=\frac{q_{n}\!\left( 1+r\left( -1\right)^{n}\right)} {\sqrt{\left( 1+r^{2}+r\mathrm{e}^{-2n}\right)} }, $$

where r is an arbitrary constant having three values r = 0,1, and −1, representing a coherent state, even coherent state and odd coherent state, respectively, and q n is the coherent amplitude for the coherent field having the value [21]

$$q_{n}=\frac{\alpha^{n}}{\sqrt{n!}}\exp \left( \frac{ -\left\vert \alpha \right\vert^{2}}{2}\right). $$

Hence, using the above initial conditions to obtain the wave function of the whole system |Ψ(t)〉 at t ≥ 0 it can be easily evaluated as

$$\begin{array}{@{}rcl@{}} |{\Psi} (t) \rangle &=&\sum\limits_{n=0}^{\infty} [\psi_{1}(n,k,t)|e_{1},e_{2},n\rangle +\psi_{2}(n,k,t)|e_{1},g_{2},n+k\rangle \\ &&+\psi_{3}(n,k,t)|g_{1},e_{2},n+k\rangle +\psi_{4}(n,k,t)|g_{1},g_{2},n+2k\rangle ], \end{array} $$
(4)

where

$$\begin{array}{@{}rcl@{}} \psi_{1}(n,k,t) &=&\frac{B_{n,r}}{n!(n+2k)!+[\left( n+k\right) !]^{2}}[\cos \theta \!\left\{ n!(n+2k)!+[\left( n+k\right) !]^{2} \right\} \\ &&\times\cos \left( \xi_{n}t\right) +\left( n+k\right) !\sqrt{n!\left( n+2k\right) !}\sin \theta \left\{ \cos \left( \xi_{n}t\right) -1\right\} ], \end{array} $$
(5)
$$\begin{array}{@{}rcl@{}} \psi_{2}(n,k,t)=\psi_{3}(n,k,t)=\frac{-iB_{n,r}\gamma \left( t\right) \sin \left( \xi_{n}t\right)} {\xi_{n}}\left[ \sqrt{\frac{\left( n+k\right) !}{n!} }\cos \theta \right. \\ &&{\kern-6.5pc}\left. +\sqrt{\frac{\left( n+2k\right) !}{\left( n+k\right) !}}\sin \theta \right] , \end{array} $$
(6)
$$\begin{array}{@{}rcl@{}} \psi_{4}(n,k,t)\!\! &=&\! \frac{B_{n,r}}{n!(n\,+\,2k)!\,+\,[\left( n\,+\,k\right) !]^{2}}[\sin \theta\! \left\{ n!(n \,+\, 2k)!\cos \left( \xi_{n}t\right) \,+\, [\left( n\!\,+\,k\right) !]^{2}\right\} \\ &&+\left( n+k\right) !\sqrt{n!\left( n+2k\right) !}\cos \theta \left\{ \cos \left( \xi_{n}t\right) \!-1\right\} ],\! \end{array} $$
(7)
$$ \xi_{n}=\gamma \left( t\right) \sqrt{\frac{2n!\left( n+2k\right) !+2[\left( n+k\right) !]^{2}}{n!\left( n+k\right)!}}, $$
(8)

and

$$ \gamma \left( t\right) ={{\int}_{0}^{t}}f(vt^{\prime} )\mathrm{d}t^{\prime} =\frac{ L}{pv\pi} \sin \left( \frac{pv\pi t}{L}\right) . $$
(9)

Thus, one can obtain the atomic density matrix \(\hat {\rho }_{\text {AB}}\left (t\right ) \) as

$$ \hat{\rho}_{\text{AB}}\left( t\right) =\text{Tr}_{F}(\hat{\rho}_{\text{AB}F}\left( t\right) )=\left( \begin{array}{cccc} \rho_{11} & \rho_{12} & \rho_{13} & \rho_{14} \\ \rho_{21} & \rho_{22} & \rho_{23} & \rho_{24} \\ \rho_{31} & \rho_{32} & \rho_{33} & \rho_{34} \\ \rho_{41} & \rho_{42} & \rho_{43} & \rho_{44} \end{array} \right) , $$
(10)

where

$$ \rho_{ii}=\sum\limits_{n=0}^{\infty} \left\vert \psi_{i}(n,k,t)\right\vert^{2},\quad~~~ i=1,2,3,4, $$
(11)

are atomic occupation probabilities of levels |e 1, e 2〉, |e 1, g 2〉, |g 1, e 2〉 and |g 1, g 2〉, respectively, and

$$\begin{array}{@{}rcl@{}} \rho_{12} &=&\sum\limits_{n=0}^{\infty} \psi_{1}(n+k,k,t)\psi_{2}^{\ast} (n,k,t), \\ \rho_{13} &=&\sum\limits_{n=0}^{\infty} \psi_{1}(n+k,k,t)\psi_{3}^{\ast} (n,k,t), \\ \rho_{14} &=&\sum\limits_{n=0}^{\infty} \psi_{1}(n+2k,k,t)\psi_{4}^{\ast} (n,k,t), \\ \rho_{23} &=&\sum\limits_{n=0}^{\infty} \psi_{2}(n,k,t)\psi_{3}^{\ast} (n,k,t), \\ \rho_{24} &=&\sum\limits_{n=0}^{\infty} \psi_{2}(n+k,k,t)\psi_{4}^{\ast} (n,k,t), \\ \rho_{34} &=&\sum\limits_{n=0}^{\infty} \psi_{3}(n+k,k,t)\psi_{4}^{\ast} (n,k,t), \\ \rho_{il} &=&\rho_{li}^{\ast} . \end{array} $$
(12)

In the following section, we use the relations obtained earlier to investigate the entanglement measures using certain statistical aspects such as von Neumann entropy, concurrence, negativity and the atoms–field tangle for the system under consideration.

3 Entanglement measures

To investigate the entanglement for the TJCM, numerous measures of quantum entanglement that quantify the amount of entanglement are adopted. In this study the four chosen entanglement measures are concurrence, negativity, von Neumann entropy measure and the atoms–field tangle. These entanglement measures are discussed in the following sections.

3.1 The von Neumann entropy

The quantum (von Neumann) entropy is used for studying the entanglement of pure states. Now, we want to investigate the amount of entanglement between two atoms with a field by using the two atoms density matrix given by eq. (10). Two-atom von Neumann entropy takes the form [11]

$$ S_{\text{AB}}(t) =-\text{Tr}\left( \hat{\rho}_{\text{AB}}\left( t\right) \ln \hat{\rho} _{\text{AB}}\left( t\right) \right) =-\sum\limits_{j=1}^{4}\eta_{j}\left( t\right) \ln \eta_{j}(t), $$
(13)

where η j (t) is the eigenvalue of \(\hat {\rho }_{\text {AB}}(t)\).

The entanglement between two atoms and the field can be measured by the tangle. The tangle of three qubits in terms of concurrence is termed as the three-way tangle [9]. For the present system tangle τ AB−F (t) is given by [24]

$$ \tau_{\text{AB}-F}(t)=2\left[ 1-\text{Tr}(\rho_{\text{AB}}(t))^{2}\right], $$
(14)

where ρ AB(t) is the atomic density matrix which is defined in eq. (10).

It is observed that for the system under study the tangle shows the same behaviour as the von Neumann entropy during time evolution.

3.2 Concurrence and negativity

It is worth mentioning that, an entanglement between the atoms A and B exists regardless of the presence of a field, and the optimal measures to quantify the degree of entanglement between these atoms are concurrence and negativity. In the case of two-qubit [25,26] mixed state defined in eq. (10), an analytical solution was developed by Wootters in terms of concurrence [27] and the concurrence is given by

$$ C_{\text{AB}}(t) =\max \!\!\left\{ 0,\sqrt{\lambda_{1}}-\sqrt{\lambda_{2}} -\sqrt{\lambda_{3}}-\sqrt{\lambda_{4}}\right\} , $$
(15)

where λ i is the eigenvalue of the non-Hermitian matrix \(\hat { \rho }_{\text {AB}}(t) \tilde {\rho }(t) \) and listed in the decreasing order of \(\hat {\rho }_{\text {AB}}(t) \tilde {\rho }(t)\). \(\tilde {\rho }(t) \) is the spin-flipped state of the density operator \(\hat {\rho }_{\text {AB}}(t)\),

$$ \tilde{\rho}\left( t\right) =\left( \hat{\sigma}_{y}\otimes \hat{\sigma}_{y}\right) \left( \hat{\rho}_{\text{AB}}(t) \right)^{\ast} \left( \hat{\sigma}_{y}\otimes \hat{\sigma}_{y}\right) , $$
(16)

where \(\left (\hat {\rho }_{\text {AB}}(t) \right )^{\ast } \) is the conjugate of eq. (10) and \(\hat {\sigma }_{y}\) is the Pauli spin operator. The concurrence has zero value, i.e., C AB(t)=0 for unentangled atoms, whereas C AB(t)=1 for the maximally entangled atoms. Negativity, the other measure of entanglement is based on the Peres–Horodecki criterion [28,29] (PPT criterion). We calculate the partial transposition of the density matrix in eq. (10) with respect to the first atom A as

$$ \hat{\rho}^{\mathrm{T}_{\mathrm{A}}}\left( t\right) =\left( \begin{array}{cccc} \rho_{11} & \rho_{12} & \rho_{31} & \rho_{32} \\ \rho_{21} & \rho_{22} & \rho_{41} & \rho_{42} \\ \rho_{31} & \rho_{14} & \rho_{33} & \rho_{34} \\ \rho_{23} & \rho_{24} & \rho_{43} & \rho_{44} \end{array} \right) , $$
(17)

where \(\hat {\rho }^{\mathrm {T}_{\mathrm {A}}}(t) \) denotes the partial transpose of \( \hat {\rho }_{\text {AB}}(t) \) with respect to the first atom A, the trace-normalized operator is defined to have the matrix elements [30]

$$ \left\langle i_{\mathrm{A}},j_{\mathrm{B}}\!\left\vert \hat{\rho}^{\mathrm{T}_{\mathrm{A}}}\left( t\right) \right\vert k_{\mathrm{A}},l_{\mathrm{B}}\right\rangle =\left\langle k_{\mathrm{A}},j_{\mathrm{B}}\!\left\vert \hat{\rho}_{\text{AB}}(t) \right\vert i_{\mathrm{A}},l_{\mathrm{B}}\right\rangle. $$
(18)

Thus, the negativity is defined as

$$ N_{\text{AB}}(t)=\max \left( 0,-2\sum\limits_{m}\beta_{m}\right) , $$
(19)

where the sum is taken over the negative values, β m of relation (17). For the pure state, like in the case of concurrence, N AB(t) = 1 for maximally entangled atoms and N AB(t) = 0 is for unentangled atoms.

4 Numerical results and discussion

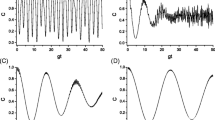
In this section, we obtain the numerical results which describe the dynamics of the quantum system for the interaction between moving and stationary two two-level atoms with a general coherent field (i.e., r = 0) or with an even coherent field as a special case of the general coherent field (i.e., r = 1), all from relation (3). The numerical results are represented using the entanglement measures such as the von Neumann entropy S AB, concurrence C AB, the negativity N AB and the atoms–field tangle given by relations (13), (14), (15) and (19), respectively, and we consider the effects of different parameters such as the number of photon transitions k, the atomic motion parameter p, the atomic position 𝜃 and the arbitrary constant r, as the coherent parameter α = 6 and the results are shown in figures 1–4. On the other hand, we present a comparison between the general coherent field (r = 0) and even coherent field (r = 1) because the fields interact with two identical atoms which are initially prepared in two atomic superposition states (i.e., 𝜃 = 0 and π/3) by controlling an arbitrary constant r, and this interaction results in the phenomena, ESD and ESB. However, in figures 1–4 the statistical quantities like the von Neumann entropy S AB (solid line), the concurrence C AB and the negativity N AB (dashed line) are plotted with the scaled time t and the first observation is that the concurrence and the negativity give the same result, i.e., C AB=N AB, for all cases under consideration.

Figure 1
figure 1

The time evolution of the von Neumann entropy S AB(t) (solid line), concurrence C AB(t) (dashed line) for two two-level atoms interacting with a coherent field (i.e. r = 0) in (a, c) and an even coherent field (i.e. r = 1) (b, d). The other parameters are α = 6 and k = 1. When the atomic motion parameter p is neglected, the atoms are initially in an excited state for 𝜃 = 0 in (a, b) but in (c, d) the atoms are initially in an entangled state for 𝜃 = π/3.

Full size image
Figure 2
figure 2

The same as in figure 1, but for k = 2.

Full size image
Figure 3
figure 3

The same as figure 1, but the atomic motion parameter is considered (p = 1).

Full size image
Figure 4
figure 4

The same as figure 2, but the atomic motion parameter is considered p = 1.

Full size image

The mechanism of interaction between the general coherent field or the even coherent field with the excited atoms is the transition of one photon (i.e., k = 1) in the absence of the atomic motion which are represented in figures 1a and 1b. In figure 1a, we can observe the excited atoms interacting with a general coherent field for r = 0 and this interaction gives an opposite relation between the behaviour of S AB and C AB implying that the atoms–field entanglement is minimum and atom–atom entanglement is maximum and the interaction is reverse at 0 ≤ t ≤ 3π, but S AB and C AB show irregular and non-periodic behaviour with the time evolution t because t≥3π. This behaviour is considered chaotic. In figure 1b, the excited atoms interact only with the even coherent states, and take the same behaviour as in figure 1a but with different oscillations in the time interval 2π ≤ t ≤ 4π, and the amplitudes for S AB and C AB are limited between 0.2 and 0.9. Figure 1c exhibits the maximum value of S AB increasing with the time evolution t because the atoms are in superposition state and there is death of entanglement between atoms in C AB as π/2 ≤ t ≤ 5π. Also, at the moment t = 5π, there is the fast appearance of ESB in concurrence, the maximum value of which is 0.55, then abruptly falls to zero at 7π resulting in ESD. We have noted that the ESD and ESB decrease with the time evolution t, such that the system in the interval 0 ≤ t ≤ 20π is in the entangled state, but since t≥20π, the interaction system will have chaotic behaviour. The even coherent field interacting with the entangled atoms and exhibiting the same behaviour for S AB and C AB are shown in figure 1d but with different oscillations in the time interval 3π−𝜖 ≤ t ≤ 3π+𝜖, where 𝜖≪1 and the amplitudes for these oscillations are between 0 and 0.8.

In figure 2, we can see the effect of the two-photon transitions on the interaction between two atoms and field with the same initial conditions as in figure 1. Figure 2a depicts that, the interaction system exhibits a regular periodic and an opposite behaviour between atoms and the field which is represented by S AB and C AB, occurring in the periodic interval m π (m = 1, 2, 3, ...). Besides, for every periodic time t = m π, we detected that S AB=C AB=0. At this particular moment, the system is in the separable state and A–B and atoms–field entanglements are absent. But, as r = 1 as in figure 2b, the results show that the even coherent field shows the same behaviour and gives the same information for the general coherent field in the interaction with the excited atoms but in a shorter periodic time m π/2 (m = 1, 2, ...). On the other hand, we note in figure 2c that the dynamical system exhibits a regular periodic behaviour in periodic interval m π (m = 1, 2,...) for S AB, the concurrence C AB exhibits a ESD for the range m π/2 ≤ t ≤ (m+1)π/2 (m = 0,1,2,...) and in the same range, the von Neumann entropy S AB describes that there is a maximum value between two minimum values. Furthermore, C AB reveals the ESB and ESD at the periodic time for the range (m π/2)−𝜖 ≤ t ≤ (m π/2)+𝜖, where 𝜖≪1. The results in figure 2d show the same behaviour but with different time intervals, the concurrence predicts the appearance of ESB and ESD at the periodic time for the range (m π/4) − 𝜖 ≤ t ≤ (m π/4)+𝜖, where 𝜖≪1 (m = 1,2,...). Also, there is a death entanglement in C AB at periodic interval m π/4 (m = 1,2,...). On the other hand, the von Neumann entropy S AB has a regular periodic behaviour for the periodic interval m π/2 (m = 1,2,...), all in the absence of motion of atomic centre-of-mass.

Further, we investigate the interaction system in the presence of the atomic motion by setting p = 1 and the results are presented in figures 3 and 4 using the same parameters as in figures 1 and 2. In figures 3a and 3b, it is noticed that there is a regular periodic behaviour in periodic intervals m π (m = 1,2,...) for both C AB and S AB. Also, there is a separable state, i.e., C AB=S AB=0, in the same periodic time m π (m = 1,2,...), and the system is in the entangled state at the maximum value of the von Neumann entropy is 0.66 for r = 0 as seen in figure 3a. But, as r = 1, the maximum value for S AB equals one with more oscillations which appear in figure 3b for S AB. In figures 3c and 3d as the system is in a mixed state by setting 𝜃 = π/3, we have found that the dynamical system of the atomic motion exhibits a regular opposite and periodic behaviour in periodic intervals m π (m = 1,2,...) for both C AB and S AB. Also, S AB shows that there is a separable state between two moving atoms with the general coherent field in figure 3c and with the even coherent field in figure 3d for periodic time m π (m = 1,2,...) and there are more oscillations in figure 3d because r = 1.

However, figure 4 depicts important features for moving atoms and pairs of photons. In figures 4a and 4b, the same behaviour is observed for both the general coherent field and even coherent field in the interaction with the excited moving atoms where both C AB and S AB exhibit regular and opposite periodic behaviour between them for the periodic time m π (m = 1,2,...) and the results show that there is a separable state, i.e., C AB=S AB=0, as t = m π (m = 1,2,...). Also, the von Neumann entropy and concurrence have maximum values entangled equal to 1 and 0.5, respectively. Furthermore, if the atoms are initially in mixed state, i.e., 𝜃 = π/3, we observe a regular periodic behaviour for periodic interval m π (m = 1,2,...) for both r = 0 and 1 in figures 4c and 4d. Besides, we have obtained the ESD and ESB presented by the evolution of the concurrence in the periodic interval m π (m = 1,2,...), where in figure 4d the ESD appears three times in every periodic interval m π (m = 1,2,...) in the case of even coherent field state (i.e. r = 1).

5 Conclusion

We have studied the moving and non-moving atom–atom entanglement and the entanglement between two atoms with the coherent and even coherent fields. We have focussed our attention on the effects of initial state setting of the two atoms on the entanglement of each atom and field. Our results show that some new important and interesting features such as entanglement sudden birth and sudden death can be obtained when the two atoms are initially in the entangled state. On the other hand, we have found that the system becomes separable at the periodic time. Also, the results show that the even coherent field shows the same behaviour of the general coherent field with different oscillations bccause the interaction depends on one-photon process.

It is well known that the study of the physical properties of the atom–field interaction is an important topic in quantum optics and information. In this regard, our results show that the interaction between two atoms and the field in the presence of atomic motion provides a more elaborate structure than in the absence of atomic motion. An important future investigation will be the study of the effect of decoherence of the dynamics of even and odd coherent fields interacting with two atoms in the presence of decoherence, considering phase damping.