Viscosity: From air to hot nuclei

Abstract

After a brief review of the history of viscosity from classical to quantal fluids, a discussion of how the shear viscosity η of a finite hot nucleus is calculated directly from the width and energy of the giant dipole resonance (GDR) of the nucleus is given in this paper. The ratio η/s with s being the entropy volume density, is extracted from the experimental systematic of GDR in copper, tin and lead isotopes at finite temperature T. These empirical results are compared with the results predicted by several independent models, as well as with almost model-independent estimations. Based on these results, it is concluded that the ratio η/s in medium and heavy nuclei decreases with increasing T to reach $(1.3 - 4) \times \hbar /(4\pi k_{\mathrm {B}})$ at T = 5 MeV, which is almost the same as that obtained for quark-gluon plasma at T > 170 MeV.

1 Introduction

The recent observations of the charged particle elliptic flow and jet quenching in ultrarelativistic Au–Au and Pb–Pb collisions at the Relativistic Heavy Ion Collider (RHIC) at Brookhaven National Laboratory (BNL) [1] and Large Hadron Collider (LHC) at CERN [2] have been the key experimental discoveries in the creation and study of quark-gluon plasma (QGP). The analysis of the data obtained from the hot and dense system produced in these experiments revealed that the strongly interacting matter formed in these collisions is a nearly perfect fluid with extremely low specific viscosity (the ratio η/s where η is the shear viscosity and s is entropy volume density). In the verification of the condition for applying hydrodynamics to nuclear system, it turned out that the quantum mechanical uncertainty principle requires a finite viscosity for any thermal fluid. In this respect, one of the most fascinating theoretical findings has been the conjecture by Kovtun, Son and Starinets (KSS) that the specific viscosity η/s is bound below for all fluids, i.e., the value η/s=1/(4π k _B) is the universal lower bound (the KSS bound or KSS unit) [3]. The QGP fluid produced at RHIC has η/s≃ (1.5–2.5) KSS units. Given this conjectured universality, there has been an increasing interest in calculating η/s in different systems.

For finite nuclei, the first calculations by Auerbach and Shlomo within the Fermi liquid drop model (FLDM) estimated η/s within (4–19) and (2.5–12.5) times the KSS bound for heavy and light nuclei, respectively [4]. Given the large uncertainty in such estimations, it has been proposed to calculate the shear viscosity η, the entropy density s, and the ratio η/s directly from the most recent and accurate experimental systematics of the giant dipole resonance’s (GDR) widths in hot nuclei. These results will be presented in this paper after a brief review of the study of viscosity in classical fluids and QGP.

2 A brief history of viscosity

The word ‘viscosity’ is derived from the Latin word ‘viscum album’ meaning mistletoe, whose berries have a sticky juice which was used in ancient times for trapping small animals or birds. Viscosity is the resistance of a fluid, which is being deformed by a stress. In other words, it is the ‘thickness’ or internal friction of a fluid. In this sense, water is thin and honey is thick.

Matter consists of three primary states: solid, liquid, and gas. In a solid the intermolecular attractions keep its molecules in fixed spatial relationships, whereas in a liquid these attractions keep molecules in proximity, but not in fixed relationships. Molecules of a gas are separated and intermolecular attractions have little effect on their respective motion. Plasma is a gas of charged particles. Amongst these three states of matter, liquid and gas are fluids, i.e., they continually deform (flow) under an applied shear stress. The resistance of a fluid to the applied shear stress is called shear (dynamic) viscosity. If the shear stress of magnitude F is applied to a layer of fluid with area A, the shear viscosity η of the fluid is defined as the proportional factor, which relates F to the gradient ∂ u/∂ y of the local fluid velocity u in the direction perpendicular to u, i.e., F/A=η ∂ u/∂ y. The unit of η is poise (P), named after Jean Léonard Marie Poiseuille (1797–1869), French physician and physiologist, who studied non-turbulent flow of liquids through pipes, such as blood flow in capillaries and veins: 1 P =0.1 Pa s =1 g/(cm s), 1 cP =1 mPa s =0.001 Pa s. The values of viscosity are different for various substances: 0.02 cP for air at 18^∘C, 1 cP for water at 20^∘C, 2000–10000 cP for honey, 23×10¹⁰ cP for pitch at 20^∘C, (1–3) ×10¹² cP for an atomic nucleus at absolute zero temperature (−273.15^∘C), or in the order of 10¹⁴ cP for lead glass at 500^∘C and QGP at 4×10^{12 ∘}C.

In 1860, James Clerk Maxwell (1831–1879) showed that viscosity of a gas, which he called the ordinary coefficient of internal friction, can be obtained by density ρ of molecules (e.g., 1.3 g/l for air), mean free path $\bar {l}$ (65 nm for air), and average velocity $\bar {v}$ of molecules (250 m/s for air), i.e., $\eta = 1/3\rho \bar {l}\bar {v}$ [5]. Because the mean free path is inversely proportional to the density, i.e., a decrease of pressure by 1/2 reduces the density by 1/2 but increases the mean free path by 2, Maxwell concluded that viscosity of a gas is independent of its pressure (or density), a conclusion which he could hardly believe. This conclusion was known as Maxwell’s law. Maxwell also found that viscosity of a gas increases with temperature T. This conclusion also went against the common sense based on experience with liquids at that time. He decided to test these predictions himself. Finally, the results obtained in 1886 by Maxwell the experimentalist confirmed the predictions by Maxwell the theorist, which show viscosity of air η = 0.01878(1 + a T) cP at pressure between 0.017 and 1 atm.

In contrast with gas, ‘viscosity of a liquid is a very tough nut to crack’, as has been commented by E M Purcell (1912–1997). It cannot be related to the mean free path because of the strong attractions between its molecules. For a liquid flowing through tubes, the following Poiseuille’s law holds:

$$ \eta = \frac{\pi r^{4} Pt}{8VL}, $$

(1)

where t is the elapsed time in which a liquid of volume V under the hydrostatic pressure P travels a distance L through a tube of radius r.

A significant contribution in fluid dynamics was made by Navier and Stokes with the Navier–Stokes equation, which describes the fluid motion in space,

$$ \rho \left(\frac{\partial\mathbf{v}}{\partial{t}} + \mathbf{v}~\nabla~\mathbf{v}\right) =-\nabla\mathbf{p} + \eta\nabla^{2}~\mathbf{v} + \mathbf{f}~, $$

(2)

where the left-hand side, which is the density multiplied by the sum of unsteady acceleration ∂ v/∂ t and convective acceleration v∇v, defines the inertial force per unit volume, and the right-hand side includes the divergence of stress, which consists of the pressure gradient −∇p shear stress η∇² v, and other forces f. In the world of very small Reynolds numbers Re=ρ v d/η with d being the characteristic dimension of the object, v its relative velocity in the fluid, ρ density of the fluid, i.e., for very large viscosity η (for microorganism, sperm, lava, paint, viscous polymer, etc.), the inertial forces are negligible and the flows obey the Stokes equation (Stokes law).

Two notable experiments were carried out to determine the viscosity of pitch. The first one begun in 1930 at University of Queensland (Australia), which won the Guinness record as the longest continuously running laboratory experiment and 2005’s Ig Nobel prize. Between 1930 and November 2000 eight drops have fallen, making an approximated average of 1 drop every 9 years. The second experiment started at Trinity College in Dublin (UK) 14 years later, where a pitch drop was successfully filmed for the first time on July 11, 2013 [6]. The viscosity of pitch was found to be 230 billions times that of water.

3 Universal lower bound conjecture for shear viscosity

According to Maxwell’s and Poiseuille’s laws, viscosity of a fluid can be infinite, such as that of an ideal gas, but cannot be zero. Purcell has noticed, in the Chemical Rubber Handbook, that ‘there is almost no liquid with viscosity much lower than that of water.’ He pointed out that viscosities have a big range, but they seem to ‘stop at the same place’ [7]. So, viscosity of liquids can be very large as that of pitch, but it cannot be too small. This leads to the search for the lower bound of viscosity.

In 1936, by assuming that the frequency of molecule collisions in liquids is k _B T/h, Henry Eyring (1901–1981) found that η≃h ρexp[E/(R T)], where E is the activation Gibbs energy of flow required to remove molecules within the fluid from their energetically most favourable state to the activated state, h is the Planck’s constant, and R is the gas constant. This relation shows that at infinite T, viscosity goes to h ρ. Obviously, the meaningful quantity is η/n rather than η. However, because the particle number is not conserved for relativistic fluids, it is better to consider η/s, where s is the entropy volume density. From the Maxwell’s law and the uncertainty relation, one finds $\rho \bar {v}\bar {l}\geq \hbar$ so that $\eta /s\geq \hbar /k_{\mathrm {B}}$ because s∼ρ k _B. But this cannot be taken as the lower bound for η/s because the kinetic theory is not reliable in the quantum regime $\eta /s\sim \hbar /k_{\mathrm {B}}$. Therefore, other methods are needed to determine the minimum ratio of η/s.

In 2005, by using string theory, Kovtun, Son and Starinets conjectured that the value

$$ \eta/s = \hbar/(4\pi k_{\mathrm{B}}) = 5.24\times 10^{-23}~\text{MeV~s} $$

(3)

is the universal lower bound for all fluids [3]. This is called the KSS limit. The physical meaning of this lower bound conjecture comes from the wave–particle duality, according to which a particle is also a wave with the De Broglie’s wavelength λ= ℏ/p. The KSS conjecture means that the shortest mean free path of a particle is its wavelength, otherwise a particle does not have enough time to exist as ‘a particle’. The KSS conjecture (3) is fundamental in the sense that its right-hand side is model-independent, contains only fundamental physical constants, and connects three branches of physics, namely fluid dynamics, thermodynamics, and quantum mechanics.

No experimental evidence of a fluid that violates this conjecture has ever been found so far. All known fluids in nature have the ratio η/s above the KSS bound. For example, the ratio η/s is found to be around 380 KSS units for water at 1 bar pressure and 25^∘C, and 9 KSS for liquid helium including the superfluid one. The recent experimental data from RHIC (Brookhaven National Laboratory) and LHC (CERN) have revealed that the matter formed in ultrarelativistic heavy-ion Au–Au collisions with $\sqrt {s_{NN}} =$ 200 GeV at T>T _c∼ 175 MeV and Pb–Pb collisions with $\sqrt {s_{NN}} = 5.4$ TeV is a nearly perfect liquid with an extremely ‘low’ specific viscosity, i.e., η/s≃ 1.5–2.5 KSS.

4 Shear viscosity of hot nuclei

From the concept of collective theories, one of the fundamental explanations for the giant resonance damping is the friction term (or viscosity) of the neutron and proton fluids. By using the Green–Kubo’s relation, in [8] an exact expression of shear viscosity η(T) has been derived at finite T in terms of the GDR parameters at zero and finite T as

$$ \eta(T)=\eta(0)\frac{\Gamma(T)}{\Gamma(0)} \frac{E_{\mathrm{\text{GDR}}}(0)^{2}+[{\Gamma}(0)/2]^{2}}{E_{\mathrm{\text{GDR}}}(T)^{2}+[{\Gamma}(T)/2]^{2}}~. $$

(4)

There exists a wealth of experimental data for GDR width Γ(T) and energy E _GDR(T) in medium and heavy nuclei [9]. The damping of hot GDR has also been studied theoretically in the last three decades. These results can be used in eq. (4) to predict the value of shear viscosity η(T) provided η(0) is known. In [10], the two-body viscosity was employed under the assumption of a rigid nuclear boundary to fit the data of isovector and isoscalar giant resonances at T=0. A value η(0)≃1u≃ 0.016 TP (terapoise) has been found, where u = 10⁻²³ MeV s fm⁻³. The analysis of nuclear fission data based on the two-body collisions [11] gives η(0) in the range of (0.6–1.2)u or (0.01–0.02) TP. In this paper, the value η(0) = 1u, extracted in [10], is adopted as a parameter in combination with the lower and upper bounds, equal to 0.6u and 1.2u, respectively, obtained in [11] and applied here as error bars. As for the GDR width and energy, the phonon damping model (PDM) [12,13] is employed, whose predictions are compared with those obtained by using the experimental data [14–21] and other theoretical models such as the adiabatic model (AM) [22], phenomenological thermal shape fluctuation model (pTSFM) [23], and Fermi liquid drop model (FLDM) [4].

4.1 Phonon damping model

The PDM employs a model Hamiltonian, which consists of an independent single-particle (quasiparticle) field, GDR phonon field, and the coupling between them. The Woods–Saxon potentials for spherical nuclei at T=0 are used to obtain single-particle energies. These single-particle spectra span a large space from around −40 MeV upto around 17–20 MeV. They are kept unchanged with T based on the results of the temperature-dependent self-consistent Hartree–Fock calculations, which showed that the single-particle energies are not sensitive to the variation of T upto T∼ 5–6 MeV in medium and heavy nuclei. The GDR width Γ(T) is given as the sum of the quantal width, Γ_Q, and thermal width, Γ_T:

$$ {\Gamma}(T)={\Gamma}_{\mathrm{Q}}+{\Gamma}_{\mathrm{T}}~. $$

(5)

In the presence of superfluid pairing, the quantal and thermal widths are given as [13]

$$ {\Gamma}_{\mathrm{Q}}=2\pi {F_{1}^{2}}\sum\limits_{\text{ph}}[u_{\text{ph}}^{(+)}]^{2}(1-n_{\mathrm{p}}-n_{\mathrm{h}}) \delta[E_{\text{GDR}}(T)-E_{\mathrm{p}}-E_{\mathrm{h}}]~, $$

(6)

$$ {\Gamma}_{\mathrm{T}}=2\pi {F_{2}^{2}}\sum\limits_{s>s^{\prime}}[v_{ss^{\prime}}^{(-)}]^{2}(n_{s^{\prime}}-n_{s}) \delta[E_{\text{GDR}}(T)-E_{s}+E_{s^{\prime}}]~, $$

(7)

where (s s ^′) stands for (p p ^′) and (h h ^′) with p and h denoting the orbital angular momenta j _p and j _h for particles and holes, respectively. Functions $u_{\text {ph}}^{(+)}$ and $v_{ss^{\prime }}^{(-)}$ are combinations of the Bogoliubov coefficients u _j , v _j , namely $u_{\text {ph}}^{(+)}=u_{\mathrm {p}}v_{\mathrm {h}}+v_{\mathrm {p}}u_{\mathrm {h}}$ and $v_{ss^{\prime }}^{(-)}=u_{s}u_{s^{\prime }}-v_{s}v_{s^{\prime }}$. The quantal width is caused by coupling of the GDR vibration (phonon) to non-collective ph configurations with the factors (1−n _p−n _h), whereas the thermal width arises due to coupling of the GDR phonon to pp and hh configurations including the factors $(n_{s}-n_{s^{\prime }})$ with (s,s ^′)=(h,h ^′) or (p,p ^′). The quasiparticle occupation number n _j has the shape of a Fermi-Dirac (FD) distribution $n_{j}^{\text {FD}}=[\exp (E_{j}/T)+1]^{-1}$, smoothed with a Breit–Wigner kernel, whose width is equal to the quasiparticle damping with the quasiparticle energy $E_{j}=\sqrt {(\epsilon _{j}-\lambda )^{2}+{\Delta }(T)^{2}}$. Here 𝜖 _j , λ, and Δ(T) are the (neutron or proton) single-particle energy, chemical potential, and pairing gap, respectively. When the quasiparticle damping is small, as usually is the case for GDR in medium and heavy nuclei, the Breit–Wigner-like kernel can be replaced with the δ-function so that the quasiparticle occupation number n _j can be approximated with the Fermi–Dirac (FD) distribution $n_{j}\simeq n_{j}^{\text {FD}}$ of non-interacting quasiparticles. The PDM predicts a slight decrease of the quantal width (in agreement with the finding that the Landau and spreading widths of GDR do not change much with T), and a strong increase of the thermal width with increasing T, as well as a saturation of the total width at T≥ 4–5 MeV in tin and lead isotopes [12] in agreement with experimental systematics [16–21].

For the open-shell nuclei, in the presence of strong thermal fluctuations, the pairing gap Δ(T) of a finite nucleus does not collapse at the critical temperature T _c, corresponding to the superfluid–normal phase transition predicted by the BCS theory for infinite systems, but decreases monotonically as T increases [24–26]. The effect due to thermal fluctuations of quasiparticle numbers, which smooths out the superfluid–normal phase transition, is taken into account by using Δ(T) obtained as the solution of the modified BCS (MBCS) equations [25]. The use of the MBCS thermal pairing gap Δ(T) for ¹²⁰Sn leads to a nearly constant GDR width or even a slightly decreasing one at T≤1 MeV [13] in agreement with the data of [19].

Within the PDM, the GDR strength function is calculated in terms of the GDR spectral intensity J _q (ω)=−2Im[G _R(ω)]/[exp(ω/T)−1] with G _R(ω) being the retarded Green function associated with the GDR. Its final form reads as $J_{q}(\omega )={f^{\text {BW}}(\omega , \omega _{q}^{\prime },2\gamma _{q})}[\mathrm {e}^{\omega /T}-1]^{-1}$ with $\omega ^{\prime }_{q}=\omega _{q}+P_{q}(\omega )$, where ω _q is the unperturbed phonon energy, P _q (ω) is the polarization operator arised due to coupling of GDR phonon to ph, pp and hh configurations. The GDR energy is defined as the solution of the equation ω−ω _q −P _q (ω)=0 at which one obtains Γ(T)=2γ _q in eq. (5).

4.2 Entropy density

The entropy density (entropy per volume V) is calculated as

$$ s = \frac{S}{V} = \rho\frac{S}{A} $$

(8)

with the nuclear density ρ=0.16 fm⁻³. The entropy S at temperature T is calculated by integrating the Clausius definition of entropy as

$$ S = {{\int}_{0}^{T}}\frac{1}{\tau}\frac{\partial\mathcal{E}}{\partial\tau}\mathrm{d}\tau~, $$

(9)

where $\mathcal {E}$ is the total energy of the system at temperature τ, which is evaluated microscopically within the PDM or macroscopically by using the Fermi gas formula, $\mathcal {E} = \mathcal {E}_{0} + aT^{2}$, within the FLDM.

By taking the thermal average of the PDM Hamiltonian and applying eq. (9), it follows that

$$ S=S_{\mathrm{F}}+S_{\mathrm{B}}~, $$

(10)

where S _F and S _B are the entropies of the quasiparticle and phonon fields, respectively. The entropy S _α (α=F,B) is given in units of Boltzmann constant k _B as

$$ S_{\alpha}^{\text{PDM}} = -\sum\limits_{j}N_{j}[p_{j}\ln p_{j}\pm (1\mp p_{j})\ln(1\mp p_{j})]~, $$

(11)

where p _j =n _j are the quasiparticle occupation numbers (α=F) or phonon occupation numbers p _j =ν _j (α=B), the upper (lower) sign is for quasiparticles (phonons), N _j =2j+1 and 1 for α=F and B, respectively. For α=F, the index j denotes the single-particle energy level, corresponding to the orbital angular momentum j, whereas for α=B, it corresponds to that of GDR phonon. As the quasiparticle (single-particle) damping is negligible for heavy nuclei, it is neglected in the present calculations of entropy S _F for the sake of simplicity, assuming $n_{j} = n_{j}^{\text {FD}}$. Regarding the phonon occupation number for the GDR, it is approximated with the Bose–Einstein distribution ν _GDR≃νGDR B=[exp(E _GDR/T)−1]⁻¹ in the present calculations. This gives the upper bound for the entropy, hence the lowest bound for the ratio η/s, estimated within the PDM. Indeed, for the GDR (q = GDR), the phonon occupation number ν _q , is given by the Bose–Einstein distribution νGDRB = [exp(E _GDR/T)−1]⁻¹ smoothed with a Breit–Wigner kernel, whose width is equal to the GDR width, i.e., ν _GDR < νGDRB. Given E _GDR≫T, it turns out, however, that S _B≪S _F so that in all the cases considered, one has S≃S _F. E.g., for ¹²⁰Sn with E _GDR≃ 15.5 MeV and FWHM around 14 MeV at T = 5 MeV [12], one finds νGDRB≃0.009, which gives a negligible value 0.051 for S _B as compared to S _F≃ 109 (in units of k _B).

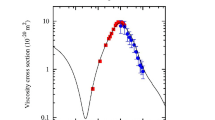
In figure 1a–1c are the GDR widths predicted by the PDM, AM, pTSFM, and FLDM are shown as functions of temperature T in comparison with the experimental systematics [14–21], which are also recorded in [9]. The PDM predictions agree very well with the experimental systematics for all the three nuclei ⁶³Cu, ¹²⁰Sn, and ²⁰⁸Pb. The AM fails to describe the GDR width at low T for ¹²⁰Sn because thermal pairing was not included in the AM calculations, while it slightly overestimates the width for ²⁰⁸Pb (the AM prediction for GDR width for ⁶³Cu is not available). The predictions by the pTSFM is qualitatively similar to those by the AM, although to achieve this agreement the pTSFM needs to use Γ(0)=5 MeV for ⁶³Cu and 3.8 MeV for ¹²⁰Sn, i.e., substantially smaller than the experimental values of around 7 and 4.9 MeV for ⁶³Cu and ¹²⁰Sn, respectively. This model also produces the width saturation similar to that predicted by the PDM, although for ⁶³Cu the width obtained within the pTSFM at T>3 MeV is noticeably smaller than that predicted by the PDM. The widths obtained within the FLDM fit the data fairy well upto T≃2.5 MeV. However, they do not saturate at high T, but increases sharply with T, and break down at T _c < 4 MeV. At T > 2.5 MeV the dependence on η(0) starts to show up in the FLDM results for the GDR widths, which are 18.3, 17.5, and 17 MeV for η ₀≡η(0) = 0.6, 1.0, and 1.2u, respectively, for ⁶³Cu at T=3 MeV. The corresponding differences between the widths obtained by using these values of η(0) for ¹²⁰Sn and ²⁰⁸Pb are slightly smaller. The values of the critical temperature T _c, starting from which the FLDM width becomes imaginary, are 3.58, 3.72, 3.83 MeV by using η(0)=0.6u, 1.0u, and 1.2u, respectively, for ⁶³Cu. For ¹²⁰Sn the corresponding values for T _c are 3.77, 3.94, and 4.1 MeV, whereas for ²⁰⁸Pb they are 3.42, 3.54, and 3.65 MeV, respectively. At these values of T _c, the ratio η(T _c)/η(0) is smaller than 3.5.

Figure 1

FWHM of GDR as functions of T for ⁶³Cu (a), ¹²⁰Sn (b), and ²⁰⁸Pb (c) in comparison with the experimental systematics for copper (Cu⁵⁹ [14] and Cu⁶³ [15]), tin (by Bracco et al [16], Enders et al [17], Baumann et al [18], Heckmann et al [19], and Kelly et al [20]), and lead (Pb²⁰⁸ [18] and Pb²⁰⁰ [21]) regions. The notations for the theoretical curves are given in (a) and (b). The corresponding entropies as functions of T are shown in (d)–(f).

4.3 Entropy

In figures 1d–1f the entropies obtained by using the microscopic expressions (10) and (11) and the empirical ones extracted from the Fermi-gas formula by using the empirical values for the level-density parameter a are compared. The microscopic entropy includes pairing for open shell nuclei. For ⁶³Cu, although pairing is not included in the calculation of the GDR width, the finite-temperature BCS pairing with blocking by the odd proton is taken into account for the entropy to ensure its vanishing value at low T (compare the thick dotted line obtained by including the BCS pairing and the thin dotted line obtained without pairing in figure 1d). For ¹²⁰Sn, the MBCS theory [25] is required to reproduce the GDR width depletion at T≤1 MeV in the nucleus due to the non-vanishing thermal pairing gap above the temperature of the BCS superfluid–normal phase transition (thick solid line in figure 1b). So the MBCS thermal pairing gap is also included in the calculation of the entropy. For the closed-shell nucleus ²⁰⁸Pb, the quasiparticle entropy S _F in eq. (11) becomes the single-particle entropy because of the absence of pairing. The good agreement between the results of microscopic calculations and the empirical extraction indicates that the level-density parameter for ⁶³Cu within the temperature interval 0.7 < T < 2.5 MeV can be considered to be temperature-independent and equal to a=63/8.8≃7.16 MeV⁻¹, whereas for ¹²⁰Sn and ²⁰⁸Pb the level-density parameter varies significantly with T [18]. The Fermi-gas entropy S ^FG=2a T with a constant level-density parameter a fits best the microscopic and empirical results with A/a=8.8 MeV for ⁶³Cu and 11 MeV for ¹²⁰Sn and ²⁰⁸Pb.

The predictions for the shear viscosity η and the ratio η/s by several theoretical models, namely the PDM, pTSFM, AM, and FLDM for ⁶³Cu, ¹²⁰Sn, and ²⁰⁸Pb are plotted as functions of T in figure 2 in comparison with the empirical results. The latter are extracted from the experimental systematics for GDR widths and energies in tin and lead regions [9] by using eq. (4). It is seen in figure 2 that the predictions by the PDM have the best overall agreement with the empirical results. It produces an increase of η(T) with T upto 3–3.5 MeV and a saturation of η(T) within (2–3)u at higher T (with η(0)=1u, u=10⁻²³ MeV s fm⁻³). The ratio η/s decreases sharply with increasing T upto T∼1.5 MeV, starting from which the decrease gradually slows down to reach 2–3 KSS units at T=5 MeV. The FLDM has a similar trend as that of the PDM upto T∼ 2–3 MeV, but at higher T (T> 3 MeV for ¹²⁰Sn or 2 MeV for ²⁰⁸Pb) it produces an increase of both η and η/s with T. At T=5 MeV, the FLDM model predicts the ratio η/s within (3.7–6.5) KSS units, which are roughly 1.5–2 times larger than the PDM predictions. The AM and pTSFM show similar trend for η and η/s. However, in order to obtain such similarity, η(0) in the pTSFM calculations has to be reduced to 0.72u instead of 1u. They overestimate η at T < 1.5 MeV.

Figure 2

Shear viscosity η(T) (a–c) and ratio η/s (d–f) as functions of T for nuclei in copper (a, d), tin (b, e), and lead (c, f) regions. The thick solid lines and gray areas are the PDM predictions for ⁶³Cu (a, d), ¹²⁰Sn (b, e), and ²⁰⁸Pb (c, f) by using η(0)=1u and 0.6u≤η(0)≤1.2u, respectively, with u=10⁻²³ MeV s fm⁻³.

A model-independent estimation for the high-T limit of the ratio η/s can also be inferred directly from eq. (4). Assuming that, at the highest T _max≃ 5–6 MeV where the GDR can still exist, the GDR width Γ(T) cannot exceed Γ_max≃3Γ(0)≃0.9E _GDR(0) [10], and E _GDR(T)≃E _GDR(0), from eq. (4) η _max≃2.551×η(0). By noticing that, S _F→2Ωln2 at T→∞ because n _j → 1/2, where ${\Omega }={\sum }_{j}(j+1/2)$ for the spherical single-particle basis or sum of all doubly-degenerate levels for the deformed basis and that the particle-number conservation requires A=Ω because all single-particle occupation numbers are equal to 1/2, one obtains the high-T limit of entropy density s _max=2ρln2≃0.222(k _B). Dividing η _max by s _max yields high-T limit (or lowest bound) for η/s in finite nuclei, i.e., $({\eta }/{s})_{\min }\simeq 2.2^{+0.4}_{-0.9}$ KSS units, where the empirical values for $\eta (0) = 1.0^{+0.2}_{-0.4}~u$ are used [10,11]. Based on these results, one can conclude that the values of η/s for medium and heavy nuclei at T=5 MeV is in between 1.3 and 4.0 KSS units, which are about 3–5 times smaller (and of much less uncertainty) than the values between 4 and 19 KSS units predicted by the FLDM for heavy nuclei [4], where the same lower value η(0)=0.6u was used.

5 Conclusions

In the present paper, a brief review of the study of viscosity in physics is given with the latest developments in QGP and hot nuclei, where the ratio η/s has been estimated. The KSS conjecture of the lower bound limit for η/s has prompted the attempts of predicting the values of this ratio for various substances including atomic nuclei.

For hot nuclei, by using the Kubo relation and the fluctuation–dissipation theorem, the shear viscosity η and the ratio η/s have been extracted from the experimental systematics for the GDR widths in copper, tin and lead regions at T≠0, and compared with the theoretical predictions by four independent theoretical models. The calculations adopt the value $\eta (0)=1.0_{-0.4}^{+0.2}\times u$ (u=10⁻²³ MeV s fm⁻³) as a parameter, which has been extracted by fitting the giant resonances at T=0 [10] and fission data [11]. The analysis of numerical calculations show that the shear viscosity η increases between 0.5u and 2.5u with increasing T from 0.5 upto T≃ 3–3.5 MeV for η(0)=1u. At higher T the PDM, AM, and pTSFM predict saturation, or at least a very slow increase of η, whereas the FLDM shows a continuous strong increase of η, with T. At T=5 MeV, the PDM estimates η between 1.3u and 3.5u.

All theoretical models predict a decrease of the ratio η/s with increasing T upto T≃ 2.5 MeV. At higher T, the PDM, AM, and pTSFM show a continuous decrease of η/s, whereas the FLDM predicts an increase of η/s, with increasing T. The PDM fits best the empirical values for η/s extracted at 0.7 ≤T≤ 3.2 MeV for all the three nuclei, ⁶³Cu, ¹²⁰Sn, and ²⁰⁸Pb. At T=5 MeV, the values of η/s predicted by the PDM reach $3^{+0.63}_{-1.2}$, $2.8^{+0.5}_{-1.1}$, and $3.3^{+0.7}_{-1.3}$ KSS units for ⁶³Cu, ¹²⁰Sn, and ²⁰⁸Pb, respectively. Combining these results with the model-independent estimation for the high-T limit of η/s, which is $2.2^{+0.4}_{-0.9}$ KSS units, one can conclude that the value of η/s for medium and heavy nuclei at T=5 MeV is between 1.3 and 4.0 KSS units, which is about 3–5 times smaller (and of much less uncertainty) than the value between 4 and 19 KSS units predicted by the FLDM for heavy nuclei, where the same lower value η(0)=0.6u was used. By using the same upper value η(0)=2.5u as in [4], instead of η(0)=1.2u, the interval for η/s becomes 1.3–8.3 KSS units, whose uncertainty of 7 KSS units is still smaller than that predicted by the FLDM (15 KSS units). This estimation also indicates that nucleons inside a hot nucleus at T=5 MeV has nearly the same ratio η/s as that of QGP, around 1.5–2.5 KSS units, at T>170 MeV discovered at RHIC and LHC.