Effects of length-dependent positive feedback on length distributions of microtubules undergoing hydrolysis

Abstract

Despite a rapid turnover of subunits, how cells control the lengths of cytoskeletal filaments (such as microtubules) is a fundamental question in cell biology. Here, we theoretically investigate how microscopic processes affect the length distributions of multiple microtubules growing stochastically in a shared subunit pool. In particular, we consider length-dependent positive feedback on filament growth and the chemical conversion from GTP-tubulin to GDP-tubulin (hydrolysis) inside a filament. We found different dynamical regimes for a single filament by simulating a model of microtubule kinetics, where both bimodal and unimodal (bell-shaped) length distributions emerge in the steady state. More significantly, the length distributions of multiple filaments were not unimodal, predicting a collective effect for more than one filament. Interestingly, when length distributions were bimodal, we also observed bistable toggling of individual lengths. Therefore, regulation of biophysical parameters (e.g., hydrolysis rate and feedback strength) can lead to length diversity in an ensemble of multiple microtubules.

1 Introduction

A fascinating fact of cell biology is that subcellular filamentous structures (such as cytoskeletal filaments) regulate their size distributions despite a rapid turnover of their building blocks (Mohapatra et al. 2016). It is still elusive how cells may achieve such length control. Experiments found that the size of a mitotic spindle and its essential constituent, microtubules, scale with cytoplasmic volume (Winey et al. 1995; Good et al. 2013; Hazel et al. 2013). This raised the idea that depletion of a limiting subunit pool can regulate the lengths of microtubules by balancing their polymerization and depolymerization processes on average (Goehring and Hyman 2012; Mohapatra et al. 2016). Experiments with other organelles (e.g., centrosomes, the nucleolus, Golgi bodies, etc.) also suggest that a limiting subunit pool can play a central role in regulating the sizes of many subcellular structures (Weber and Brangwynne 2015; Marshall 2016; Amiri et al. 2020).

On the contrary, a recent theoretical study (Mohapatra et al. 2017) predicted that a limiting subunit pool alone could not control the lengths of multiple filaments since subunits can freely diffuse between filaments, leading to large length fluctuations and power-law length distributions in general. Nevertheless, this physical argument holds when filaments undergo reversible (or equilibrium) assembly and disassembly dynamics in a shared subunit pool. It is well known that microtubule-associated proteins and molecular motors can regulate growth kinetics in a length-dependent manner, essentially leading to feedback mechanisms and breaking the reversibility in dynamics (Varga et al. 2006; Gardner et al. 2011; Bowne-Anderson et al. 2015; Hibbel et al. 2015). Moreover, subunits in a microtubule remain in two distinct chemical states (GTP-tubulins and GDP-tubulins), and nonequilibrium (i.e., almost unidirectional) conversion from GTP-tubulin to GDP-tubulin happens inside a filament, a process known as ‘hydrolysis’ (Desai and Mitchison 1997; Jonathon 2001). Therefore, a question arises: how do these nonequilibrium processes (such as hydrolysis and length-dependent feedback) affect the length distributions of microtubules?

The hydrolysis causes interesting length fluctuations in microtubules due to the difference in GTP- and GDP-state-dependent kinetic rates. For instance, microtubules grow by assembling GTP-tubulins, but GTP converts to GDP (by releasing phosphate) inside the filament. In addition, the disassembly rate of a GDP-subunit is much higher than a GTP-subunit ($\sim$10- to 1000-fold difference) (Desai and Mitchison 1997; Jonathon 2001). Consequently, microtubule lengths can stochastically switch between phases of sharp shrinkages (called ‘catastrophe’) and rapid growth (called ‘rescue’) depending on whether the growing filament tip is made of unstable GDP-subunits or relatively stable GTP-subunits, respectively (Mitchison and Kirschner 1984; Drechsel and Kirschner 1994). This phenomenon is known as ‘dynamic instability’, which serves biological functions such as ‘search and capture’ of kinetochores and spindle positioning during chromosome segregation (Gopalakrishnan and Govindan 2011; Banigan et al. 2015; Chatterjee et al. 2021). Moreover, theoretical studies have shown that the collective force generated by growing microtubules pushing against a barrier becomes non-additive due to hydrolysis (Das et al. 2014a, b).

In vivo, the hydrolysis and length-dependent feedback may act together for robust regulation of filament lengths. For example, experiments have shown that kinesin-Kip2 motors promote growth via length-dependent positive feedback and also inhibit hydrolysis-induced catastrophes in length (Hibbel et al. 2015). These motors walk along the microtubule lattice progressively and enhance the subunit assembly as they reach the growing tip; thus, more motors bind to longer filaments, effectively leading to positive feedback. On the other hand, previous theoretical studies on filament length regulation via feedback often did not explicitly include hydrolysis as a microscopic kinetic process (Govindan et al. 2008;  Hough et al. 2009; Johann et al. 2012; Melbinger et al. 2012; Mohapatra et al. 2016; Rank et al. 2018).

In this study, we asked how the presence of length-dependent positive feedback along with  hydrolysis affects length distributions in a limiting subunit pool. We simulated a detailed model involving kinetic processes of GTP/GDP-state-dependent polymerization, depolymerization, and hydrolysis at the subunit level. In addition, we incorporated length-dependent positive feedback on the polymerization rate. However, we did not explicitly consider any motor or regulatory protein-based interactions; instead, we implemented the feedback in a coarse-grained manner to extract general predictions of length distributions. First, for a single filament, variation of feedback strength and hydrolysis rate led to various dynamical regimes in the steady state. We found a ‘no growth’ state with exponential length distributions and states with unimodal (bell-shaped) and bimodal distributions. More interestingly, we observed no unimodal distribution for more than one filament. Thus, although the single-filament length distribution was unimodal in a broad parameter regime, multi-filament distributions became distinctively bimodal, signifying an emerging collective property. Accordingly, we observed that filaments stochastically toggled between high and low length states, leading to length diversity. Moreover, our simulations predict testable shapes of the length distributions when using experimentally measured parameter values suitable for microtubules.

2 Model

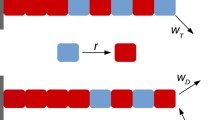
We generalized a published model of microtubule kinetics (Brun et al. 2009; Ranjith et al. 2009; Sumedha and Chakraborty 2011; Padinhateeri et al. 2012; Bowne-Anderson et al. 2013; Das et al. 2014a; Aparna et al. 2017) by including length-dependent feedback and a finite subunit pool. This model implemented hydrolysis as a random process happening at any subunit inside a filament, as found in experiments (Christian et al. 2016). The subunits can be in GTP or GDP bound states associated with different rate parameters (figure 1). Inside a filament, a GTP-subunit converts into a GDP-subunit at a rate h (hydrolysis rate), while the reverse process (GDP $\rightarrow$ GTP) takes place via nucleotide exchange at a rate $k_{ne}$ in the pool. The filaments grow from F number of nucleating centers by assembling GTP-subunits. Following Banerjee and Banerjee (2020), we incorporated length-dependent positive feedback on the assembly rate. The assembly rate of the i-th filament is $r_{T}^{i}= r_{T0} (N - l_1 -l_2 - \cdots l_F) (1+l_i)^\alpha$ when the filament tip has a GTP subunit. Here N is the total number of subunits, $\alpha (\ge 0)$ is the feedback strength, and filament lengths are denoted by $l_1, l_2, \ldots , l_F$, respectively, in units of monomers. Similarly, the assembly rate of the i-th filament is given by $r_{D}^{i}= r_{D0} (N - l_1 -l_2 - \cdots l_F) (1+l_i)^\alpha$ when the terminal subunit is GDP-tubulin. As in Aparna et al. (2017), we assumed $r_{D0}=r_{T0}/100$, since experiments suggest that a microtubule is much less likely to polymerize if its terminal subunit is GDP-tubulin due to the structural differences between GTP- and GDP-tubulins (Mandelkow et al. 1991; Brouhard and Rice 2014). Finally, a GTP-tubulin and a GDP-tubulin can disassemble from a filament at constant rates, $\gamma _T$ and $\gamma _D$, respectively. Note that $\gamma _D{>\!\!\!\!>} \gamma _T$ for microtubules (table 1), leading to length catastrophes (Desai and Mitchison 1997; Jonathon 2001).

Figure 1

A schematic of our model showing two microtubules growing from two nucleation centers (blue boxes) in a shared subunit pool. Arrows show different kinetic processes (as described in section 2). Note that a GTP-tubulin (green) coverts into a GDP-tubulin (orange) irreversibly and randomly inside a filament (at a hydrolysis rate, h), while the reverse conversion (GDP-tubulin $\rightarrow$ GTP-tubulin) happens in the pool (rate, $k_{ne}$). The subunit assembly and disassembly rates depend on the GTP/GDP states of the terminal subunits ($r_T$, $r_D$, $\gamma _T$ and $\gamma _D$, respectively). Also, the assembly rates ($r_T$ and $r_D$) are assumed to depend on the respective filament lengths ($l_i$), as shown in the box; but disassembly rates are constants ($\gamma _T$ and $\gamma _D$). Here, N denotes the total subunit number, and $\alpha (\ge 0)$ represents the feedback strength. Thus, the term $(N-l_1-l_2)$ represents a competitive effect due to a finite subunit pool, while the term $(1+ l_i)^\alpha$ represents a coarse-grained nonlinear increase of the assembly rate with the respective lengths.

Table 1 Parameter values for microtubule kinetics found from literature (Carlier and Pantaloni 1981; Brylawski and Caplow 1983; Mitchison 1992; Desai and Mitchison 1997; Jonathon  2001) (see the discussion on parameter choice in  the appendix)

The model described above includes the microscopic hydrolysis process, and it is more detailed than heavily coarse-grained two-state models of microtubules (Hill and Chen 1984; Dogterom and Leibler 1993; Zelinski and Kierfeld 2013). This explicit modeling of hydrolysis (that produces kinetic heterogeneity) can lead to emerging properties in length distributions for multiple filaments, as we discuss next. On the other hand, although a single microtubule comprises 13 protofilaments, our model visualizes one microtubule as a single filament, as done in previous studies (Sumedha and Chakraborty 2011; Padinhateeri et al. 2012; Bowne-Anderson et al. 2013; Das et al. 2014a; Aparna et al. 2017). Nevertheless, more detailed models exist with explicit multi-protofilament nature (VanBuren et al. 2002; Molodtsov et al. 2005; Margolin et al. 2012; Jemseena and Gopalakrishnan 2013), which are computationally expensive. But our level of coarse-graining allowed us to simulate multiple filaments in a computationally efficient way with a minimal set of parameters. Moreover, our ‘random hydrolysis’ model was shown to capture experimentally observed features of ‘length versus time’ data, including catastrophes (Aparna et al. 2017).

3 Results

We simulated the model using the Gillespie algorithm with realistic parameter values estimated from in vitro experiments on microtubules (table 1 and Appendix A and B for detailed discussions on the simulation method). We first obtained stochastic trajectories (length versus time) for individual filaments and then calculated the steady-state distributions of individual lengths after sampling over many such trajectories. In simulations, we started with zero lengths of the filaments and ran the simulations until the system reached a steady state. We assumed that the steady state was reached when both the mean and variance of individual lengths stabilized over time, and we took data for lengths after this condition was met.

3.1 Different dynamical regimes emerge for a single filament with distinct length distributions

We first calculated the length distribution of a single filament for a wide range of hydrolysis rate (h) and feedback strength ($\alpha$). We found that qualitatively distinct dynamical regimes can emerge, as shown in the ‘phase diagram’ of figure 2. When the hydrolysis rate is very high, and the feedback strength is low (large h and small $\alpha$), the filament could not essentially grow since the dominance of hydrolysis makes the filaments mostly  of GDP-tubulins with a very high disassembly rate (table 1). As a result, the distribution became exponential in this ‘no growth’ phase (figure 2i, ii). On the other hand, at high $\alpha$ and low h, the filament length quickly reached a high steady value due to the dominance of the positive feedback over hydrolysis. In this case, the filament length became close to the maximum limit set by the pool size with small fluctuations around the mean, and consequently, the distribution was Poisson-like, i.e., sharply peaked with a small width (figure 2iii, iv). In between these regimes, we found bimodal length distributions, and the length toggled between a higher value (close to the pool size) and a lower value (close to zero) (figure 2v–vii). Here, the hydrolysis-induced sharp catastrophes in length were countered by the positive feedback-mediated rapid rescues of length. Finally, between the ‘bimodal’ and ‘exponential’ regimes, we noticed transitory shapes characterized by long-tailed distributions (figure 2viii). Here, the length trajectory mostly stayed near zero but exhibited occasional rescue events producing probability weights towards  higher lengths (figure 2ix).

Figure 2

Different dynamical regimes with distinct length distributions for a single filament: The ‘phase diagram’ in the parameter space of hydrolysis rate (h) and feedback strength ($\alpha$) is shown in the middle. With increasing $\alpha$, length distributions transition from an exponential (green triangles) to a bimodal shape (blue dots) and finally to a unimodal Poisson-like shape (brown diamonds). Transitory shapes of long-tailed distributions (magenta upside-down triangles) were also observed. Specific examples of distinct distributions with corresponding length trajectories are shown (i–ix). In particular, the regime with bimodal distribution exhibited length toggling (see the zoomed-in trajectory in vi). We used a pool size $N=1000$, and other parameters were taken from table 1.

3.2 Emergence of bimodal length distributions for two filaments

We next focused on the individual length distribution of a filament in a two-filament system. Similar to the single-filament case, we found that length distributions showed a transition from exponential to bimodal shape with increasing feedback strength, and between these regimes, transitory long-tailed distributions also appeared (figure 3A). However, an interesting point to note here is that we did not find any unimodal distributions like the single-filament case (compare figures 2 and 3A), signifying a collective property. In certain parameter regimes (high $\alpha$ and low h), a unimodal distribution for a single filament can become a bimodal distribution when filament number is increased—see figure 3B, C, where a specific point in the parameter-space of h and $\alpha$ is shown as an example. Corresponding length trajectories of the two filaments showed a ‘win–loss’ scenario, where a randomly selected filament stays long for a considerable amount of time (figure 3B, inset), ensuring a bimodal distribution of individual lengths when sampled over an ensemble. In contrast, the single-filament trajectory reached a high steady value (figure 3C, inset).

Figure 3

Emergence of bimodal length distribution and length toggling in a two-filament system: (A) Different regimes in the parameter space of hydrolysis rate (h) and feedback strength ($\alpha$), showing the exponential (green triangles), bimodal (blue dots), and long-tailed distributions (magenta upside-down triangles) of individual lengths in a two-filament system. Note that no regime exhibits unimodal distributions like the single-filament case (compared with figure 2). (B, C) Individual length distributions in two-filament (B) and single-filament (C) systems are shown as examples for a specific point ($h=0.0001/$s, $\alpha =0.45$) in the ($h,\alpha$) parameter space. In panel B, note the concentrated but significantly high probability weight near the zero length. Correspondingly, the length trajectories in the two-filament system exhibit a win–loss behavior, i.e., one of the filament lengths always stays near the pool size ($N=1000$), while the other one is close to zero (inset, B). However, the single-filament length reaches the steady maximum value (inset, C). (D–F) Individual length trajectories (shown in red and blue) in a two-filament system are plotted for increasing feedback strength (at a fixed h). At low $\alpha$, the lengths stochastically toggle (D, E); while at high $\alpha$, a win–loss scenario emerges (F). Nevertheless, all length distributions corresponding to panels D–F are bimodal (see figure 5). The pool size was $N=1000$, and other parameters were taken from table 1.

We further found individual length toggling in the two-filament system (see the trajectories in figure 3D). When the GTP-cap is stochastically lost in one of the filaments, it shrinks sharply, but the other one grows rapidly due to the positive feedback. When the longer filament reaches the maximum length, it may again stochastically go to the ‘catastrophic’ phase, giving the other one a chance to grow. Interestingly, the residence time in the high (or low) length state increased on average with increasing feedback strength, ultimately giving rise to a win–loss scenario (figure 3D–F). When $\alpha$ is very high, the residence time can be so large that the longer filament stays long for a sufficiently large time and does not come close to zero on realistic timescales (in comparison to the division timescale of about an hour in budding yeast cells). A similar situation (i.e., a changeover from size oscillation to a win–loss scenario) can arise when the pool size (N) is increased systematically (at a fixed h and $\alpha$), as shown in Banerjee and Banerjee (2020).

3.3 Bimodal length distributions in multi-filament systems

Since multiple microtubules are commonly present inside a cell, the question remains if the bimodal distributions of individual lengths can be observed in multi-filament systems for realistic parameter choices. Although we kept a small pool size ($N=1000$) so far, a suitable pool size could be at least an order of magnitude higher. It was estimated in a recent in vitro experiment on microtubules (Rank et al. 2018) that around 26000 tubulin subunits are available per filament (also see the discussion in the appendix). We, therefore, used $N=25000$ and $h=0.3/$s (as in table 1) for our simulations to check if realistic choices of parameters can lead to the emergence of bimodality for multiple filaments.

As shown in figure 4, the bimodal length distributions indeed emerged for more than one filament, although the single-filament length distribution was unimodal. Interestingly, all distributions for more than one filament were, in fact, trimodal—two modes were mildly present near the maximum length. Nevertheless, the significantly higher probability weight remained near zero and the maximum length (close to the net pool size), effectively leading to bimodal shapes. This point can be further clarified if we compare the length trajectories (corresponding to the distributions shown in figure 4), where win–loss scenarios were consistently observed for multiple filaments (figure 6). We further checked up to ten filaments that the bimodality carried forward (data not shown).

Figure 4

Bimodal distributions for multiple filaments: Steady-state distributions of individual lengths are shown up to four filaments. Note the mild appearance of two modes near the maximum length for more than one filament. Here we used $N=25000, h=0.3/$s, and $\alpha =0.1$, while we took other parameters from table 1.

However, the question remains if the inclusion of hydrolysis and feedback changes the nature of the length distributions fundamentally. To investigate this explicitly, we compared the length distributions in different scenarios: (1) in the absence of both hydrolysis and feedback and (2) when either hydrolysis or feedback was ‘switched off’ in the model (figure 7). First, without hydrolysis and feedback (i.e., $h= \alpha = 0$), the distributions were uniform for two filaments and power-law for three or more filaments (figure 7A–C). This is consistent with a recent theoretical study (Mohapatra et al. 2017), which predicted that the limiting subunit pool cannot control the lengths of a set of ‘equilibrium’ filaments undergoing reversible processes of assembly and disassembly. Inclusion of either hydrolysis or  feedback breaks the reversibility. When only  feedback was introduced (i.e., $h=0$, but $\alpha$ is nonzero), it was sufficient to induce bistability for multiple filaments. However, both modes of the bimodal distributions were extremely narrowly concentrated in the ‘high’ and ‘zero’ length states, signifying win–loss scenarios (figure 7D–F). On the other hand, when only  hydrolysis was present (i.e., h is nonzero and $\alpha =0$), the length distributions for more than one filament became ‘long-tailed’, suggesting large length fluctuations (figure 7G–I). Finally, in the presence of both  hydrolysis and feedback (i.e., h and $\alpha$ both are nonzero), the multi-filament length distributions are prominently bimodal with significant probability weights around each mode (figure 4). Interestingly, the single filament distribution was unimodal in all the above cases (figures 4 and 7A,D,G). This analysis highlights how collective effects of hydrolysis and feedback can give rise to length diversity in an ensemble of filaments.

4 Conclusion and discussion

Although a limiting pool of subunits can control the sizes of many subcellular structures (Goehring and Hyman 2012), a recent theoretical study showed that a limiting subunit pool could not regulate lengths of biofilaments growing through assembly and disassembly of subunits (Mohapatra et al. 2017). However, cytoskeletal filaments like microtubules employ length-sensing mechanisms using microtubule-associated proteins to achieve robust control on lengths (Varga et al. 2006; Bowne-Anderson et al. 2015; Hibbel et al. 2015). Such protein regulators effectively create length-dependent feedback on the assembly/disassembly rates. Another crucial feature often ignored in modeling is that microtubules are made of heterogeneous subunits (GTP-tubulins and GDP-tubulins), and a chemical conversion from the GTP-tubulin to GDP-tubulin (called hydrolysis) takes place randomly inside a filament (Desai and Mitchison 1997; Jonathon 2001). The hydrolysis essentially makes a filament unstable since the disassembly rate of GDP-tubulins is much greater than the GTP-tubulins. Also, the hydrolysis is almost irreversible inside a microtubule, implying nonequilibrium filament dynamics with crucial implications. How hydrolysis-induced kinetic heterogeneity and length-dependent feedback mechanisms affect microtubule length distribution is still poorly understood. Some theoretical models on feedback-mediated length regulation of biofilaments omitted to explicitly include hydrolysis as a kinetic process (Govindan et al. 2008;  Hough et al. 2009; Johann et al. 2012; Melbinger et al. 2012; Mohapatra et al. 2016; Rank et al. 2018).

In this study, we investigated how  hydrolysis and length-dependent feedback act together to regulate the length distributions of microtubules. In particular, motivated by a recent experiment on kinesin-Kip2-mediated microtubule growth (Hibbel et al. 2015), we implemented length-dependent positive feedback on the filament assembly rate in a coarse-grained way. Simultaneously, we took account of hydrolysis as a microscopic random process in our model (figure 1). Simulations of our model revealed different kinetic regimes for a single filament upon variation of the hydrolysis rate and feedback strength (figure 2). The distributions became exponential when hydrolysis dominated over positive feedback (i.e., at a high hydrolysis rate and low feedback strength). Conversely, if positive feedback dominated over hydrolysis (at a low hydrolysis rate and high feedback strength), the distribution was unimodal and sharply peaked. In between these regimes, we found bimodal and transitory long-tailed shapes of length distributions.

More importantly, although the kinetic regimes for two filaments were almost similar to the single-filament case, there was an important distinction (figure 3A). We found no parameter regimes showing unimodal distributions for more than one filament (figures 3A–C and 4). This collective effect signifies that a shared subunit pool among many filaments can lead to length diversity in the presence of hydrolysis and positive feedback. Moreover, bimodal distributions were generally characterized by bistable length toggling (figures 2vi and 3D, E). Interestingly, such size oscillations gradually gave rise to a win–loss scenario in the two-filament system as the feedback strength was increased (figure 3D–F). In this case, the residence time in the higher- or lower-length state increased with increasing feedback strength, and consequently, only one filament stayed longer for a considerable time, and the other one could not grow. As expected, such a win–loss scenario also led to bimodal distributions when sampled over an ensemble (figures 3B and 5). These results also hold for more than two filaments (see figures 4 and 6).

A few theoretical studies investigated the length distributions of many microtubules in a confined space that mimics a cell boundary (Gregoretti et al. 2006; Cassimeris et al. 2018). In contrast to our predictions, these studies found exponential length distributions. However, Cassimeris et al. (2018) used a coarse-grained two-state model that ignored the detailed microscopic kinetics of hydrolysis as in our model, although the two-state nature ensured a dynamic instability-like feature. These theoretical studies did not also consider any feedback mechanisms. On the other hand, a recent in vitro experiment found a long-tailed length distribution of microtubules, neither an exponential nor a Gaussian (Jeune-Smith and Hess 2010). However, this experiment used microtubules growing from both ends, and other processes like shearing and annealing were also present.

Finally, the question arises whether our prediction of bimodal length distributions can be tested at least in vitro. For example, to assess the role of hydrolysis, one can compare length distributions of microtubules made from the almost non-hydrolyzable analog of GTP-tubulins (GMPCPP tubulins) with normal microtubules. Distributions can also be tested in the presence and absence of molecular motors that create positive feedback (as in Hibbel et al. 2015), maintaining a limiting pool condition. In this context, we note that a recent in vitro experiment found bimodal length distributions of microtubules in a limiting pool of Kip3 motors and tubulin subunits (Rank et al. 2018). In this case, Kip3 motors walk towards the growing tip of a microtubule and help in the disassembly of tubulins. However, longer filaments have a lower concentration of Kip3 near the growing end, thereby reducing the Kip3-dependent disassembly process and effectively leading to positive feedback. In this experiment, however, microtubules were grown from the non-hydrolyzable GMPCPP subunits, suggesting that the positive feedback was sufficient to observe bimodality (consistent with our observation in figure 7D–F).

It is to be noted that we have incorporated the positive feedback in a coarse-grained manner (similar to Banerjee and Banerjee 2020), which can correspond to different molecular processes at the microscopic level. For instance, kinesin-Kip2 motors are known to promote the microtubule assembly rate as the motors reach the growing plus end of the microtubule walking along the microtubule lattice (Hibbel et al. 2015). On the other hand, the Kip3 motors promote the disassembly of tubulins from the growing tip. However, in this case, the disassembly rate can decrease nonlinearly with the length since longer filaments have a lower concentration of Kip3 motors on them (Rank et al. 2018). This again gives rise to effective positive feedback. Keeping these examples in mind, we used simple coarse-grained models, ignoring the detailed interactions between motors and microtubules.

Nevertheless, a general feedback mechanism can affect other processes, not only the subunit assembly. As described above, the Kip3 motors can effectively reduce the disassembly rates in a length-dependent manner. We, therefore, investigated a similar model with length-dependent positive feedback on the disassembly rates, where the disassembly rates decrease nonlinearly with increasing filament lengths (appendix C). In this case, we again found bimodal length distributions for more than one filament as an emerging collective effect of the hydrolysis and the feedback (figure 8). Thus, our qualitative conclusions remain the same.

Together, our study establishes that both hydrolysis rate and feedback strength act as ‘biophysical knobs’ that can be tuned to obtain length diversity in an ensemble of multiple microtubules. Moreover, the insights gained from our study can be relevant for other types of biofilaments such as actin filaments and their prokaryotic homolog ParM filaments, which also undergo ATP hydrolysis and are controlled by protein-mediated feedback mechanisms (Fujiwara et al. 2002;  Garner et al. 2004; Antkowiak et al. 2019).

Appendices

Appendix A: Parameter choices for microtubules

As summarized in table 1, the rate constants were taken from in vitro experiments on microtubules. In particular, the polymerization rate is generally reported in experiments as a second-order rate constant ($k_0$) expressed in units of µM⁻¹ s⁻¹. This rate refers to filament assembly at a constant tubulin concentration (i.e., unlimited subunit pool). Following Mohapatra et al. (2017), we normalized this rate by the pool size to obtain a first-order rate constant (in units of s⁻¹) as $r_{T0} = k_0 C/N = k_0 / (N_A V)$. Here, C is the molar concentration of subunits (i.e., $C=N/(N_A V)$), N is the total number of subunits, V is the volume available per filament, and $N_A$ is the Avogadro number.

From the literature, we found the value of the second-order rate constant as $k_0 \approx 3.2$ µM⁻¹ s⁻¹ (Desai and Mitchison 1997 ; Jonathon 2001). A recent in vitro experiment (Rank et al. 2018) also estimated that the volume available per filament in a typical experimental condition was roughly $V \approx 1.66$ µM³. Therefore, we estimated: $r_{T0} = (3.2 \times 10^6) /(6.023 \times 10^{23} \times 1.66 \times 10^{-15}) \approx 0.003$ s⁻¹.

Realistic estimate of the pool size: In a recent in vitro experiment (Rank et al. 2018), by comparing the concentrations of free tubulins and the assembled tubulins in the microtubules, the authors estimated that roughly 2000 tubulin dimers are available per protofilament at 2 µM tubulin concentration. Therefore, in a typical in vitro experiment, the total number of tubulins available per filament is around 26000 $(2000 \times 13)$, as one microtubule is generally made of 13 protofilaments. We thus used the pool size $N=25000$ in figure 4 to observe bimodal length distributions of microtubules.

Appendix B: Simulation method

We used the Gillespie algorithm to simulate the stochastic processes occurring in the system. Each filament has three possible reactions: assembly, disassembly, and hydrolysis. One more reaction is the conversion of GDP-tubulin to GTP-tubulin via nucleotide exchange, which can randomly happen in the pool. Therefore, in a system of F-number of filaments, the total number of possible reactions is $R_{tot}=3F+1$. The kinetic processes can be summarized by the following set of reactions:

${R_1}$::

$l_i\xrightarrow {{r_T}^i} l_i+1$ (if tip-subunit is GTP-bound) $\xrightarrow {{r_D}^i} l_i+1$ (if tip-subunit is GDP-bound)

${R_2}:$:

$l_i \xrightarrow {{\gamma _T}} l_i-1$ (if tip-subunit is GTP-bound) $\xrightarrow {{\gamma _D}} l_i-1$ (if tip-subunit is GDP-bound)

${R_3}:$:

GTP-subunit $\xrightarrow {{K_h}}$ GDP-subunit

${R_4}:$:

GDP-subunit $\xrightarrow {{K_{ne}}}$ GTP-subunit

Here, $l_i$ denote the length of the i-th filament in units of monomers. The assembly rate is a function of lengths and is also dependent on the chemical states: $r_{T}^{i}= r_{T0}(N -\sum _{i=1}^{F} l_i)(1+l_i)^\alpha$ and $r_{D}^{i}= r_{D0}(N -\sum _{i=1}^{F} l_i)(1+l_i)^\alpha$, respectively (figures 5 and 6).

Figure 5

Distributions of individual lengths for a two-filament system are plotted corresponding to the length trajectories shown in figure 3D–F. Note that both the length toggling and win–loss scenarios in the trajectories led to bimodal distributions. Parameters were the same as in figure 3.

Figure 6

Length versus time trajectories corresponding to the distributions in figure 4. Individual lengths were shown in different colors for multi-filament systems. The parameters were $N=25000$, $h=0.3/$s, $\alpha =0.1$, and others were from table 1.

Note that the state-switching reactions $R_3$ and $R_4$ are of first order. Hence, the propensity of the hydrolysis is $K_h = h\, {n_{GTP}}^i(t)$ , where ${n_{GTP}}^i$ is the instantaneous number of GTP-subunits inside the i-th filament. Similarly, the propensity of the nucleotide exchange process happening in the pool is $K_{ne}$=$k_{ne}\, {n_{GDP}}^{pool}(t)$, where ${n_{GDP}}^{pool}$ is the instantaneous number of GDP-subunits in the pool. Finally, $\gamma _T$ and $\gamma _D$ are constant disassembly rates.

The Gillespie algorithm uses two random numbers $r_1$ and $r_2$ to determine which reaction will occur and at what time. According to the Gillespie algorithm, the instantaneous state of the system (at a time t) determines the time for the next reaction at a time $t+\tau$, where the time-increment is given by $\tau =\frac{1}{A_0}\ln {(1/r_1)}$. Here, $A_0=\sum _{i=1}^{R_{tot}} A_i$ is the sum of all propensities. Moreover, the m-th reaction will be chosen to occur at a time $t+\tau$ if $\sum _{i=1}^{m-1} A_i\le r_2A_0 < \sum _{i=1}^{m} A_i$. Iterating the above steps, the stochastic dynamics of the filaments were simulated.

Appendix C: A modified model with length-dependent disassembly rates

In our main model (figure 1), we have considered length-dependent positive feedback on the subunit assembly rate, while the disassembly rates were constants. In contrast, we here investigate how length-dependent feedback on the disassembly rates can affect the filament length distributions. As before, the assembly rates of i-th filament are given by $r_{T}^{i}= r_{T0}(N - l_1 -l_2 - \cdots l_F)$ and $r_{D}^{i}= r_{D0}(N - l_1 -l_2 - \cdots l_F)$, corresponding to the presence of GTP- or GDP-tubulin at the filament-tip, respectively. These rates merely represent a competitive effect due to a finite subunit pool. Additionally, the disassembly rates are given by $\gamma _T=\gamma _{T0}{l_i}^\beta$ and $\gamma _D=\gamma _{D0}{l_i}^\beta$ for the disassembly of GTP- and GDP-tubulins respectively. Here, $\beta$ is a negative parameter, representing the positive feedback strength, as the disassembly rate decreases nonlinearly with length. Simulating this model, we again found bimodal length distributions for more than one filament (figure 8). Therefore, our qualitative conclusions remain the same as inferred from the main model (figures 7 and 8).

Figure 7

Length distributions for different values of feedback strength ($\alpha$) and hydrolysis rate (h). (A–C) Length distributions for one to three filaments in the absence of feedback and hydrolysis. Panel B is a uniform and panel C is a power law distribution. (D–F) Distributions in the absence of hydrolysis but with finite feedback.The single-filament distribution is unimodal, and multi-filament distributions are sharply bimodal. (G–I) With hydrolysis (but without feedback), the single-filament distribution is skewed, whereas others are long-tailed. The pool size is $N=25000$ and other parameters were from table 1.

Figure 8

Length distributions for multiple filaments when disassembly rates decrease with filament lengths (see appendix C for the detailed model). The steady-state distributions of individual lengths are shown up to three filaments. Similar to figure 4, multi-filament distributions are bimodal. The parameters were $N=25000$, $h=0.3/$s, $\beta =-0.1$, and others were from table 1.