1 Introduction

Study of nonlinear phenomena is a prominent topic from a mathematical as well as a physical point of view because of its massive contribution in aerodynamics, space science, cosmology, rocket science, theory of relativity, interplanetary motion and many more (Karman 1941; Moschetti 1987; Wang et al. 2019). In the present scenario, many researchers and scientists are studying the theory of nonlinear waves with the help of partial differential equations describing the existence of these waves in certain mediums. The conservation laws of gas dynamics, electrodynamics, hydrodynamics and other branches of mechanics are typically characterized by quasilinear system of PDEs or system of such equations. Hyperbolic systems, in particular, represent the proper mathematical model for a host of a variety of wave propagation phenomena in Whitham (2011).

Many researchers have studied the nonlinear waves in one-dimensional system. In stellar environments, shock waves, such as those produced by a core-collapse supernova explosion, are transformed into radiation-mediated shocks. Such shocks form when photons collide with matter like electrons, and the downstream of these shocks is dominated by radiation energy density rather than thermal energy density. The relativistic shock wave is a particular example of an astrophysical shock wave, in which the velocity of shocks is the non-negligible fraction of the speed of light. Shock formation in black hole accretion is also expected to be a general phenomenon because shock waves in rotating and non-rotating flows are convincingly capable of converting a significant amount of gravitational energy (see Horowitz & Itzhaki 1999). Das (2002) explored the possibility of shock formation in black hole accretion discs and observed that standing shocks are a crucial component of accretion discs near non-rotating black hole. When we look at two-dimensional problem, it becomes more complicated. In two-dimensional form, it is very difficult to find the solution and to analyse the study. To explain the phenomena ranging from atomic explosions in the Earth’s atmosphere to supernova explosions and active galactic nuclei (Zel’Dovich et al. 1967; Weaver 1976), the shock wave theory has been used continuously. The investigation of shock wave in van der Waals gas flow has great consideration of engineers and scientists due to its important role in the study of several areas like atmospheric science, oceanography, astrophysics, hypervelocity impact, hypersonic flow and aerodynamics. Some authors have explored the analysis of shock wave propagation in various gas regimes and discussed different physical features of these propagating waves (Pandey 2015; Srivastava et al. 2020, 2021, 2022). Jagadeesh (2008) has studied the various features of the shock wave theory, described the innovative shock wave applications in industries and science, and shown that shock waves can enhance the temperature, pressure and other flow variables, which experience rapid changes. Also, the shock wave phenomenon is widespread in radiation gas dynamics because radiation effects are crucial in extremely high-speed flow, where shock waves usually occur. The study of propagation of small disturbances in a radiating gas has been previously examined by Marshak (1958), Vincenti & Baldwin (1962), Lick (1964), Sharma et al. (1987), Chaturvedi et al. (2019a, 2019b, 2022) and Chauhan (2022). The study of shock is most common in the interstellar medium. In stellar environments, shock waves often form due to collisions of photons with electrons of the matter (Mostafavi & Zank 2018; Shweta et al. 2023). Furthermore, Singh et al. (1988, 2010, 2011, 2012), Chaturvedi & Singh (2021) and Chaturvedi et al. (2022) used the wavefront analysis method to analyse the phenomenon of shock-wave formation in a 2-D steady supersonic flow of a radiating gas and described the behavior of propagating waves and their flow patterns. Menon & Sharma (1981) examined the flattening and steepening of characteristic wavefronts in planar and non-planar plasma motion in perfect gas and the magnetic field effect on wave propagation and have illustrated that the disturbance propagated into the medium obeys the Bernoulli-type differential equation. Whitham (1956) has proposed a method to study the propagation and decay of weak shock wave produced by explosions and by bodies in supersonic flight. The relativistic shock is an example of the astrophysical shock (see Bykov & Treumann 2011). The problem of a shock wave in a real gas with presence of magnetic field has been studied by many researchers in the past. In recent decades, many studies have been available in the literature on the propagation of magnetic shock waves and applications in many industrial and scientific researches and developments. The propagation of wave and its behavior always depend on the flow variables and the medium chosen for the flow unless the motion of the wave need a medium for the flow. The behavior of the flow changes with respect to the constraint considered. The strength of the wave depends on the Mach number, which is the ratio of flow speed to sound speed. Here, we consider the steady flow, therefore, we do not consider the time dependence of the flow variables. In this paper, we consider the transverse magnetic field; one may use an oblique shock wave to generalize this problem to get different results as in Wang & Wu (2022). Sahu (2020) and Srivastava et al. (2022) studied the propagation of cylindrical and spherical shock waves non-ideal gas with conductive as well as radiative heat fluxes in magnetogasdynamics under the presence of magnetic field.

The issues of radiative energy transmission in fluids stand out enough to be noticed in recent decades as a result of speeding up bodies through the atmosphere and extremely high temperatures achieved by gases in motion. Significant efforts have been made to study interaction problems between the gasdynamic field and the radiation field, and a new title ‘Radiation Gasdynamics’, has been proposed for this subject. The new advancements in space innovation have necessitated an in-depth investigation of the consequences of the effect of thermal radiation on the flow field of extremely high-temperature gas. In many technological developments, such as space vehicle re-entry, temperature of the gas is so high that thermal radiation becomes a critical factor in determining the flow field. The effect of thermal radiation in gas dynamics is an excellent example of an interdisciplinary research activity that necessitates the practical application of the following crucial physical science fields: quantum mechanics, fluid mechanics and statistical mechanics (with stress on quantitative spectroscopic investigations; Scala & Sampson 1963; Pai 1966; Pai & Tsao 1966).

Purpose of the present study is to analyse the simultaneous effect of radiative heat transfer and the imperfectness (non-idealness) of the gas on the flow pattern of the discontinuities propagated under the presence of magnetic field. It seems worthwhile to give a broader discussion of these effects for wave propagation problems in general and to investigate all the various possibilities that may arise in astrophysics. In the previous studies (see Chaturvedi & Singh 2021; Chaturvedi et al. 2022), no one has been analysed the supersonic flow in non-ideal magnetogasdynamic regime in the presence of radiation effect. In this paper, we study the behavior of the flow in ideal and non-ideal cases and compare the difference between the flow patterns and the physical changes that took place.

The complete structure of this paper is organized into sections as follows: In Section 2, we transformed the governing equations into matrix form to determine the characteristic curves that represent the propagation of the waves. In Section 3, we introduced new coordinates and derive the transport equations, which describe the evolutionary process of the propagating waves. In Section 4, we have analysed the behavior of the waves for plane and axisymmetric cases and determined the condition for the shock formation. Section 5 refers to the consequences of various parameter effects on the shock-formation process and its deformation. The last section is the conclusion of the entire work of this paper.

2 Governing equations and its characteristic formulation

In this section, to describe the propagation of nonlinear wave in gasdynamics, we considered the following hyperbolic system of quasilinear partial differential equations, which governs the two-dimensional steady supersonic flow of van der Waals gas in magnetogasdynamics under the effect of radiative heat transfer as in Chaturvedi & Singh (2021) and Jeffrey (1976):

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{l} u\partial _x\varrho + v\partial _y\varrho + \varrho \left( \partial _x u+\partial _y v + \dfrac{mv}{y} \right) =0,\\ \varrho u\partial _x u + \varrho v\partial _y u + (\partial _x p+\partial _x h) =0, \\ \varrho u\partial _x v + \varrho v\partial _y v + (\partial _y p+\partial _y h) =0, \\ u\partial _x p + v\partial _y p - \dfrac{\gamma p}{\varrho (1-b\varrho )} (u \partial _x \varrho + v \partial _y \varrho )\\ \quad + (\gamma -1)q =0,\\ u\partial _x h + v\partial _y h + \varrho e^{2} \left( \partial _x u + \partial _y v + \dfrac{mv}{y} \right) =0, \end{array}\right. \end{aligned} \end{aligned}$$
(1)

where x, y are spatial coordinates, \(\varrho \) is the density of the gas and u and v are the velocities in x and y directions, respectively. p represents the pressure and h is the magnetic pressure, which is defined as \(h={\omega H^{2}}/{2}\). Here, \(\omega \) and H denote the magnetic permeability and transverse magnetic field, respectively. q represents the rate of energy loss by the gas per unit volume through radiation and it is defined as \(q=4k\sigma (T^{4}-T_{b}^{4})\), where k is the Planck mean absorption coefficient, which is a function of density \(\varrho \) and temperature T of the gas. \(\sigma \) denotes the Stefan–Boltzmann constant and \(T_{b}\) is the uniform temperature of the body along which the flow is investigated. \(\gamma \) is the specific heat ratio of the gas. The energy loss \(q=4k\sigma T^{4}\) caused by the radiating gas has been enhanced by \(q=-4k\sigma T_{b}^{4}\), resulting in an infinite optically thin gas with no radiating boundary. The boundary wall having uniform temperature \(T_{b}\) has no energy loss or gain due to the radiating gas. \(e= ({2h}/{\varrho })^{{1}/{2}}\) is Alfvén speed. m is a constant such that \(m=0\) for planar flow and \(m=1\) for cylindrically axisymmetric flow.

In matrix form, Equation (1) can be written as:

$$\begin{aligned} V_{x}+MV_{y}+N=0. \end{aligned}$$
(2)

Here, the subscript x and y signify the partial derivatives in x and y directions. V and N are column vectors and M is a square matrix of order 5 given below:

$$\begin{aligned} V&= \begin{pmatrix} \varrho \\ u \\ v \\ p \\ h \end{pmatrix},\hspace{0.1cm} N= \frac{1}{(u^{2}-c^{2})}\nonumber \\&\qquad \qquad \quad \quad \times \begin{pmatrix} \frac{ \varrho muv}{y} + \frac{ (\gamma -1)q}{u} \\ \frac{ -mv}{y}c^{2} -\frac{ (\gamma -1)q}{\varrho } \\ 0 \\ \frac{ \varrho muv }{y}a^{2} + \frac{ (\gamma -1)q}{u}(u^{2}-e^{2})\\ \frac{ \varrho muv}{y}e^{2} + \frac{ (\gamma -1)q}{u}e^{2} \end{pmatrix} \end{aligned}$$
(3)

and the non-zero entries of the matrix \(M= (M^{ij})_{5\times 5}\) are as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} M^{11}= \dfrac{v}{u}, M^{12}= -\dfrac{\varrho v}{(u^{2}-c^{2})}, M^{13}= \dfrac{\varrho u}{(u^{2}-c^{2})},\\ M^{14}= M^{15} = \dfrac{v}{u(u^{2}-c^{2})}, M^{22}= \dfrac{uv}{(u^{2}-c^{2})},\\ M^{23}= -\dfrac{c^{2}}{(u^{2}-c^{2})}, M^{24}= M^{25}= -\dfrac{v}{\varrho (u^{2}-c^{2})},\\ M^{33} = \dfrac{v}{u}, M^{34}=M^{35} = \dfrac{1}{\varrho u}, M^{42}=-\dfrac{\varrho va^{2}}{(u^{2}-c^{2})},\\ M^{43}=\dfrac{\varrho ua^{2}}{(u^{2}-c^{2})}, M^{44}=\dfrac{v(u^{2}-e^{2})}{u(u^{2}-c^{2})},\\ M^{45}=\dfrac{va^{2}}{u(u^{2}-c^{2})}, \\ M^{52}=-\dfrac{\varrho ve^{2}}{(u^{2}-c^{2})}, M^{53}=\dfrac{\varrho ue^{2}}{(u^{2}-c^{2})},\\ M^{54}=\dfrac{ve^{2}}{u(u^{2}-c^{2})}, M^{55}=\dfrac{v(u^{2}-a^{2})}{u(u^{2}-c^{2})}, \end{array}\right. } \end{aligned}$$
(4)

where

$$\begin{aligned} a=\left( \frac{\gamma p}{\varrho (1-b\varrho )}\right) ^{{1/2}} \end{aligned}$$

is speed of sound for a non-ideal gas and \(c= (a^{2}+e^{2})^{1/2}\) is the magneto-sonic speed.

Let \(\mu ^{i}\) denotes the eigenvalue of the matrix M and \(l^{i}\) denotes the corresponding left eigenvector, where \(1\le i \le 5\). Eigenvalues of M are given as:

$$\begin{aligned}&\mu ^{(1,2)} = \frac{uv\pm c^{2}\left( \frac{M^{2}(1-b\varrho )}{\varepsilon }-1 \right) ^{ \frac{1}{2}}}{(u^{2}-c^{2})}, \nonumber \\&\mu ^{(3,4,5)}=\frac{v}{u}. \end{aligned}$$
(5)

Here,

$$\begin{aligned} M=\frac{(u^{2}+v^{2})^{{1}/{2}}}{d} \end{aligned}$$

represents the upstream flow Mach number, b is the parameter of non-idealness and \(d=( {\gamma p}/{\varrho })^{{1}/{2}}\) is the speed of sound for ideal gas. The Alfvén number \(\varepsilon \) is defined as \(\varepsilon =1+({e^{2}}/{a^{2}})\), which is 1 for non-magnetic case and >1 for magnetic case.

The left eigenvectors \(l^{i}\) of the corresponding eigenvalues \(\mu ^{i}\) are given as:

$$\begin{aligned} {\left\{ \begin{array}{ll} l^{(1)}= \begin{pmatrix} 0 &{} 1 &{} -\dfrac{u}{v} &{} -\dfrac{1}{\varrho v}\left( \dfrac{M^{2}(1-b\varrho )}{\varepsilon }-1 \right) ^{\frac{1}{2}} &{} 0 \end{pmatrix},\\ l^{(2)}= \begin{pmatrix} 0 &{} 1 &{} -\dfrac{u}{v} &{} \dfrac{1}{\varrho v}\left( \dfrac{M^{2}(1-b\varrho )}{\varepsilon }-1 \right) ^{\frac{1}{2}} &{} 0 \end{pmatrix},\\ l^{(3)}= \begin{pmatrix} 1 &{} 0 &{} 0 &{} -\dfrac{1}{a^{2}} &{} 0 \end{pmatrix},\\ l^{(4)}= \begin{pmatrix} 0 &{} 1 &{} \dfrac{v}{u} &{} \dfrac{\varepsilon }{\varrho u} &{} 0 \end{pmatrix},\\ l^{(5)}= ( \begin{array}{@{}ccccc@{}} 0 &{} 0 &{} 0 &{} (1-\varepsilon ) &{} 1 \end{array}) . \end{array}\right. } \end{aligned}$$

Equation (5) shows that all eigenvalues of the matrix M are real for supersonic flow \((M> 1)\), therefore, system (2) is hyperbolic in nature. Also, from Equation (5), it can be noticed that system (2) have two families of characteristic curves along:

$$\begin{aligned} \frac{dy}{dx} = \frac{uv\pm c^{2}\left( \frac{M^{2}(1-b\varrho )}{\varepsilon }-1 \right) ^{ \frac{1}{2}}}{(u^{2}-c^{2})}, \end{aligned}$$

which represents the waves propagating in opposite directions with the characteristic speed \(\mu ^{(1,2)}\).

3 Transport equations for discontinuities

In this section, we shall derive the transport equations for the evolution of weak discontinuities in V as they move along the initial wavefront, which will be used for further study of the growth and decay behavior of shock wave. We assume that the initial wave front \(\psi (x,y)=0\), is described by the characteristic curve \(\mu ^{(1)}\), such that it passes through the point \((x_{0},y_{0})\). Further, we consider that the initial wavefront \(\psi (x,y)=0\), moving with uniform velocity \(u_{0}\) in x-direction and \(v_{0}=0\) in y-direction, density \(\varrho _{0}\), pressure \(p_{0}\) and temperature \(T_{0}=T_{b}\). Here, we have used the suffix ‘0’ to signify the value of the variables in the region ahead of the wavefront \(\psi (x,y)=0\).

Now, we transform the coordinates x and y into curvilinear coordinates \(\psi \) and \({\bar{y}}\) by using the following transformation (Jeffrey 1976):

$$\begin{aligned} {\left\{ \begin{array}{ll} \psi _{x}+\mu ^{(1)}\psi _{y}=0,\\ \psi (x, y_{0})=x-x_{0},\\ y={\bar{y}}. \end{array}\right. } \end{aligned}$$
(6)

Then, \(\psi \) has the property that is positive (negative) behind (ahead of) the leading characteristic on which \(\psi =0\).

Using the coordinate transformation (6) and multiplying Equation (2) by \(l^{(i)}\) from left side, (2) reduces into the following form:

$$\begin{aligned}&l^{(i)}V_{\psi }+\frac{\mu ^{(1)}\mu ^{(i)}}{\mu ^{(1)}-\mu ^{(i)}}x_{\psi }l^{(i)}V_{{\bar{y}}}+ \frac{\mu ^{(1)}}{\mu ^{(1)}-\mu ^{(i)}}x_{\psi }l^{(i)}\nonumber \\&N=0, \end{aligned}$$
(7)

where i is unsummed and \(x_{\psi }={1}/{\psi _{x}}\) is the Jacobian of the transformation.

V and \(V_{{\bar{y}}}\) are continuous across the wavefront \(\psi (x,y)=0\) and we use the subscript ‘0’ to denote the values of V and \(V_{{\bar{y}}}\) at the wavefront. On the other hand, \(V_{\psi }\) and \(x_{\psi }\) are discontinuous across the \(\psi (x,y)=0\). Evaluating Equation (7) by putting the values of i \((i=2,3,4,5)\) behind the wavefront, we obtain:

$$\begin{aligned}&\varrho _{\psi }=\frac{1}{a_{0}^{2}}p_{\psi }, \end{aligned}$$
(8)
$$\begin{aligned}&u_{\psi }=-\frac{\varepsilon _{0}}{\varrho _{0}u_{0}}p_{\psi },\end{aligned}$$
(9)
$$\begin{aligned}&v_{\psi }=\frac{1}{\varrho _{0}u_{0}}\left( \frac{M_{0}^{2}(1-b\varrho _{0})}{\varepsilon _{0}}-1 \right) ^{\frac{1}{2}}p_{\psi },\end{aligned}$$
(10)
$$\begin{aligned}&h_{\psi }=(\varepsilon _{0}-1)p_{\psi }. \end{aligned}$$
(11)

Taking \(i=1\) in (7) and differentiating with respect to \(\psi \), then evaluating it behind the wavefront \(\psi (x,y)=0\), we get:

$$\begin{aligned}&c_{0}a_{0}\varepsilon _{0}^{\frac{1}{2}} \left( \frac{M_{0}^{2}(1-b\varrho _{0})}{\varepsilon _{0}} -1\right) ^{\frac{1}{2}}p_{\psi {\bar{y}}}+u_{0} \varrho _{0}c_{0}a_{0}\varepsilon _{0}^{\frac{1}{2}} v_{\psi {\bar{y}}}\nonumber \\&\quad +\frac{mu_{0}\varrho _{0}}{{\bar{y}}}a_{0}^{2} v_{\psi }+\frac{(\gamma -1)}{u_{0}}(u_{0}^{2}-e_{0}^{2})q_{\psi }=0. \end{aligned}$$
(12)

Equation of state for non-ideal gas is:

$$\begin{aligned} p(1-b\varrho )=\varrho RT, \end{aligned}$$
(13)

where R is the gas constant. In view of (13), differentiating \(q=4k\sigma (T^{4}-T_{b}^{4})\) with respect to \(\psi \) and evaluating it behind \(\psi =0\), we obtain:

$$\begin{aligned} q_{\psi }=\frac{16(\gamma -1)k\sigma T_{b}^{4}}{\varrho _{0}a_{0}^{2}(1-b\varrho _{0})}. \end{aligned}$$
(14)

Inserting the value of \(v_{\psi }\) and \(q_{\psi }\) from Equations (10) and (14) in (12), we have:

$$\begin{aligned} p_{\psi {\bar{y}}}+ \left( \frac{m}{2{\bar{y}}}+ \Phi \Theta _{0}\right) \varepsilon _{0}^{-1}p_{\psi }=0, \end{aligned}$$
(15)

where

$$\begin{aligned} \Phi =\frac{8(\gamma -1)k}{\Omega } \end{aligned}$$

denotes the measure of thermal radiation,

$$\begin{aligned} \Omega =\frac{\varrho _{0}a_{0}^{3}}{(\gamma -1)\sigma T_{b}^{4}} \end{aligned}$$

represents the rate of the convective energy flux and

$$\begin{aligned} \Theta _{0}=\frac{\varepsilon _{0}\left( \frac{M_{0}^{2}(1-b\varrho _{0})}{\varepsilon _{0}}-1 \right) +1}{M_{0}(1-b\varrho _{0})^{\frac{1}{2}}\left( \frac{M_{0}^{2}(1-b\varrho _{0})}{\varepsilon _{0}}-1 \right) ^{\frac{1}{2}}}. \end{aligned}$$

Further, along \(\psi = \textrm{constant}\), we have:

$$\begin{aligned} x_{{\bar{y}}} = \frac{(u^{2}-a^{2}\varepsilon )}{uv+a^{2} \varepsilon \left( \frac{M^{2}(1-b\varrho )}{\varepsilon }-1 \right) ^{\frac{1}{2}}}. \end{aligned}$$
(16)

Integrating Equation (15) with respect to \({\bar{y}}\), we get:

$$\begin{aligned} p_{\psi }= p_{\psi _{0}}\left( \frac{y_{0}}{{\bar{y}}} \right) ^{\frac{m\varepsilon _{0}^{-1}}{2}}e^{\Phi \xi _{0}(y_{0}-{\bar{y}})}, \end{aligned}$$
(17)

where \(\xi _{0}=\Theta _{0}\varepsilon _{0}^{-1}\) and \(p_{\psi _{0}}\) denotes the limiting value of \(p_{\psi }\) along \(\psi =0\) as \({\bar{y}}\rightarrow y_{0}\).

Taking derivative of (16) with respect to \(\psi \) and evaluating it behind the wavefront \(\psi =0\) and using (17), we obtain:

$$\begin{aligned} x_{\psi {\bar{y}}}&=\frac{2\varepsilon _{0}(1-\varepsilon _{0})-(\gamma +\varepsilon _{0}+{\bar{b}}(1-\varepsilon _{0}))M_{0}^{2}}{2\varrho _{0}\varepsilon _{0}c_{0}^{2} \left( \frac{M_{0}^{2}(1-{\bar{b}})}{\varepsilon _{0}}-1 \right) ^{\frac{1}{2}}}\nonumber \\&\quad \times \left( \frac{y_{0}}{{\bar{y}}}\right) ^{\frac{m\varepsilon _{0}^{-1}}{2}} e^{\Phi \xi _{0}(y_{0}-{\bar{y}})}p_{\psi _{0}}, \end{aligned}$$
(18)

where, \({\bar{b}}\) is defined as \({\bar{b}}=b\varrho _{0}\). Equations (15) and (18) are the transport equations for the discontinuities \(p_{\psi }\) and \(x_{\psi }\), which will be used to analyse the flow pattern and behavior of the waves propagating into the disturbed region.

4 Behavior of propagating waves

Integrating Equation (18) with respect to \({\bar{y}}\), we have:

$$\begin{aligned}&x_{\psi }=1+ \frac{2\varepsilon _{0}(1-\varepsilon _{0})- (\gamma +\varepsilon _{0}+{\bar{b}}(1-\varepsilon _{0})) M_{0}^{2}}{2\varrho _{0}\varepsilon _{0}c_{0}^{2} \left( \frac{M_{0}^{2}(1-{\bar{b}})}{\varepsilon _{0}}-1 \right) ^{\frac{1}{2}}}\nonumber \\&\quad \times (y_{0})^{\frac{m\varepsilon _{0}^{-1}}{2}} e^{\Phi \xi _{0}y_{0}}p_{\psi _{0}}\int _{y_{0}}^{y} (z)^{-\frac{m\varepsilon _{0}^{-1}}{2}} e^{-\Phi \xi _{0}z} dz. \end{aligned}$$
(19)

In the above Equation (19), we have used the boundary condition \(x_{\psi -{0}}=x_{\psi }|_{\psi =0^{-}}=x_{\psi }|_{\psi =0^{+}}=1\).

We consider \(y=\kappa (x)\) to be the body contour equation in which the tangent to it remains parallel to the velocity of the streamline at the leading edge of the body. Along the stream line, we have:

$$\begin{aligned} \frac{dy}{dx}=\frac{v}{u}. \end{aligned}$$
(20)

Taking derivative of (20) with respect to \(\psi \) and evaluating it behind \(\psi =0\), we obtain:

$$\begin{aligned} v_{\psi _{0}}=u_{0}\kappa _{0}^{\prime \prime }, \end{aligned}$$
(21)

where \(\kappa _{0}^{\prime \prime }\) is the curvature of the top of the body.

In view of (10) and (21), (19) can be written into the following form:

$$\begin{aligned}&x_{\psi }=1+\frac{2\varepsilon _{0}(1-\varepsilon _{0}) -(\gamma +\varepsilon _{0}+{\bar{b}}(1-\varepsilon _{0})) M_{0}^{2}}{2\varepsilon _{0} (M_{0}^{2}(1-{\bar{b}})-\varepsilon _{0})}\nonumber \\&\quad {\times }(y_{0})^{\frac{m\varepsilon _{0}^{-1}}{2}} M_{0}^{2}(1{-}{\bar{b}})\kappa _{0}^{\prime \prime } e^{\Phi \xi _{0}y_{0}}\int _{y_{0}}^{y} (z)^{{-}\frac{m\varepsilon _{0}^{-1}}{2}}e^{{-}\Phi \xi _{0}z} dz. \end{aligned}$$
(22)

In Equation (22), since \(x_{\psi }\) is the Jacobian of the transformation at just behind \(\psi =0\), so that if for some \(y=y_{z}\), Jacobian vanishes, then the neighboring characteristics of the family \(\psi =\textrm{constant}\) will intersect on the wavefront \(\psi =0\) and this will cause to develop a discontinuity in the solution V of the system (2) in the form of a shock wave. In this case, if we consider \(V_{\psi }\) is finite at \(y=y_{z}\) as \(x_{\psi }=0\), then, just behind the wavefront \(\psi =0\), \(V_{x}=({V_{\psi }}/{x_{\psi }})\) will be infinite, which describes the wave propagation phenomenon.

Fig. 1
figure 1

Convergence of the characteristics for supersonic planar and axisymmetric flow.

Full size image

Now, we shall discuss the significance of Equation (22) and describe the supersonic flow of discontinuities propagated into the medium and its behavior for different values of m i.e., \(m=0\) for plane beak case and \(m=1\) for sharp-edged ring case. This phenomenon has been shown in Figure 1.

Case I. Planar flow (\(m=0\)): For \(m=0\), Equation (22) takes the form:

$$\begin{aligned} x_{\psi }=1-\frac{\kappa _{b}^{\prime \prime }(0)}{\Lambda }[1-e^{-\Phi \xi _{0}(y-y_{0})}] , \end{aligned}$$
(23)

where \(\Lambda = 2\Phi \xi _{0}\varepsilon _{0}[ M_{0}^{2}(1-{\bar{b}})-\varepsilon _{0}] [ (\gamma +\varepsilon _{0}+{\bar{b}}(1-\varepsilon _{0}))M_{0}^{2}-2\varepsilon _{0}(1-\varepsilon _{0})M_{0}^{2}(1-{\bar{b}})] ^{-1}>0 \) and \(\kappa _{b}^{\prime \prime }(0)\) stands for the value of radius of curvature at the tip of the body, where the contour of the body starts bending. As we earlier mention that the formation of shock depends on the Jacobian \(x_{\psi }\) i.e., when \(x_{\psi }\) vanishes, shock will form. From Equation (19), it is clearly observed that \(x_{\psi }\) will vanish on the leading wavefront for \(y_{0}<y\), which is possible only when \(\kappa _{b}^{\prime \prime }(0)>0\) with \(\kappa _{b}^{\prime \prime }(0)>\Lambda \). When \(\kappa _{b}^{\prime \prime }(0)\le \Lambda \), this is the case where \(x_{\psi }\) remains positive for \(y_{0}<y\) and resulting from that, the shock formation is not possible on the leading wavefront. Thus, we see that \(\Lambda \) plays an important role in shock formation. It represents a critical level in such a manner that whenever the radius of curvature \(\kappa _{b}^{\prime \prime }(0)\) surpasses this level at the tip of the body, shock will form at a finite distance far from the body.

Now, at the wavefront \(x_{\psi }=0\), we have \(v_{x}= {v_{\psi }}/{x_{\psi }}\). From Equations (8), (14) and (23) for \(m=0\), we obtain:

$$\begin{aligned} v_{x}=\frac{c_{0}M_{0}(1-{\bar{b}})^{\frac{1}{2}} \kappa _{b}^{\prime \prime }(0)e^{-\Phi \xi _{0}(y-y_{0})}}{\varepsilon _{0}^{\frac{1}{2}}\left[ 1- \frac{\kappa _{b}^{\prime \prime }(0)}{\Lambda } (1-e^{-\Phi \xi _{0}(y-y_{0})})\right] }. \end{aligned}$$
(24)

Equation (24) describes the evolutionary process of the propagating waves. Since, for \(\kappa _{b}^{\prime \prime }(0)>0\) with the condition \(\kappa _{b}^{\prime \prime }(0)>\Lambda \), shock will form and the corresponding shock formation distance \(y=y_{z}\) is given by:

$$\begin{aligned} y_{z}=y_{0}+\frac{1}{\Phi \xi _{0}}\log {\left\{ \frac{\kappa _{b}^{\prime \prime }(0)}{\kappa _{b}^{\prime \prime }(0)-\Lambda }\right\} }. \end{aligned}$$
(25)

In Equation (24), the denominator becomes zero, while the numerator remains finite, indicating that the velocity gradient at the wavefront \(\psi =0\) becomes unbounded at a distance \(y=y_{z}\), resulting in the termination of the wave into a shock wave. Equation (25) shows that this behavior coincides with the vanishing of \(x_{\psi }\). The wave remains compressive in case \(\kappa _{b}^{\prime \prime }(0)\le \Lambda \), but the velocity gradient does not steepen. In contrast, \(v_{x}\) along the wavefront \(\psi =0\) diminishes or it becomes stationary according as \(\kappa _{b}^{\prime \prime }(0)<\Lambda \) or \(\kappa _{b}^{\prime \prime }(0)=\Lambda \), respectively, and in this case, shock will not form on the leading wavefront \(\psi =0\).

Case II. Axisymmetric flow (m \(=\) 1): In this case, we consider that \(y=y_{z}(x)\) represents a ring-shaped body with a sharp-edged inlet, which initiates the initial perturbation running both inwards and outwards along the characteristic lines.

For \(m=1\), Equation (22) can be rewritten as:

$$\begin{aligned}&x_{\psi }=1- \frac{[ -2\varepsilon _{0}(1-\varepsilon _{0}) +(\gamma +\varepsilon _{0}+{\bar{b}}(1-\varepsilon _{0}))M_{0}^{2}] }{2\varepsilon _{0} ( M_{0}^{2}(1-{\bar{b}})-\varepsilon _{0} ) }\nonumber \\&\qquad \times (y_{0})^{\frac{\varepsilon _{0}^{-1}}{2}} M_{0}^{2}(1-{\bar{b}})\kappa _{z}^{\prime \prime }(0) e^{\Phi \xi _{0}y_{0}}\pi , \end{aligned}$$
(26)

where

$$\begin{aligned} \pi =\int _{y_{0}}^{y} (z)^{-\frac{\varepsilon _{0}^{-1}}{2}} e^{-\Phi \xi _{0}z} dz. \end{aligned}$$

It is clear from Equation (26) that for \(y>y_{0}\), the quantity within the square bracket is always positive and <1. As a result, if \(\kappa _{z}^{\prime \prime }(0)\) is positive and exceeds the critical value \(\pi ^{-1}\), the Jacobian \(x_{\psi }\) will vanish, resulting in the formation of shock. On the other hand, if \(\kappa _{z}^{\prime \prime }(0)\le \pi ^{-1}\), the value of \(x_{\psi }\) will always be >1, indicating that no shock will ever form on the leading wavefront. Tables 1 and 2 show the value of \(\pi \) for magnetic and non-magnetic cases for different values of \(\Phi \), respectively.

5 Results and discussion

In this section, we shall discuss the various parameter effects on the propagating waves and discuss the possibilities of shock formation for both the cases (plane beak case and sharp-edged ring case). From (24), we see that for \(M_{0}\sim \varepsilon _{0}\), shock formation distance is given by:

$$\begin{aligned}&y_{z}\sim y_{0}\\&-\frac{2\left[ \frac{M_{0}^{2}(1-{\bar{b}})}{\varepsilon _{0}}-1\right] }{[ (\gamma +\varepsilon _{0}+{\bar{b}}(1-\varepsilon _{0})) \varepsilon _{0}^{2}-2\varepsilon _{0}(1-\varepsilon _{0})] (1-{\bar{b}})}, \end{aligned}$$

whereas for \(M_{0}\gg \varepsilon _{0}\),

$$\begin{aligned} y_{z}\sim y_{0}-\frac{2\varepsilon _{0} }{[ (\gamma +\varepsilon _{0}+{\bar{b}}(1-\varepsilon _{0})) M_{0}^{2}-2\varepsilon _{0}(1-\varepsilon _{0})]}. \end{aligned}$$
Table 1 Variation in the value of \(\pi \) for magnetic ideal and non-ideal cases.
Full size table
Table 2 Variation in the value of \(\pi \) for non-magnetic ideal and non-ideal cases.
Full size table

It can be observed from the above expression that the shock formation distance is a function of the Mach number \(M_{0}\) i.e., if we increase the value of the Mach number, corresponding to this increment, shock formation distance decreases. Hence, for increasing the value of the Mach number, the time for the shock formation will reduce.

Fig. 2
figure 2

Effect of thermal radiation on the shock formation distance with (a) \(\varepsilon _{0}=1.6\), \(b=0.1\), \(y=1.4\) and (b) \(\varepsilon _{0}=1.6\), \(b=0.1,\) \(y=1.67\).

Full size image

Since \(\kappa _{b}^{\prime \prime }(0)<0\) corresponds to the situation when the shape of the body has expansive corner at \(x=0\). Therefore, for \(|\kappa _{b}^{\prime \prime }(0)|\ge \Lambda \), 24 yields:

$$\begin{aligned} v_{x}&\,=\, \frac{-2\Phi \xi _{0}\varepsilon _{0}^{2}c_{0}\left[ \frac{M_{0}^{2}(1-{\bar{b}})}{\varepsilon _{0}}-1\right] }{[ (\gamma +\varepsilon _{0}+{\bar{b}}(1-\varepsilon _{0}))M_{0}^{2} -2\varepsilon _{0}(1-\varepsilon _{0})]M_{0}}\nonumber \\&\quad \quad \times \frac{e^{-\Phi \xi _{0}(y-y_{0})}}{1-e^{-\Phi \xi _{0}(y-y_{0})}}. \end{aligned}$$
(27)

From Equation (27), we can determine the velocity gradient at the head of a Prandtl–Meyer expansion flow.

5.1 Analysis of the effects of thermal radiation on shock formation process

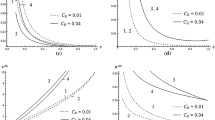
In this section, we shall discuss the consequences of the effect of thermal radiation on the shock formation distance and investigate the evolutionary process of the propagating waves. Figure 2 depicts the effect of thermal radiation on the shock formation distance for (a) \(\gamma =1.4\) and (b) \(\gamma =1.67\). From Figure 2(a), we observe that as we increase the value of parameter \(\Phi \), shock formation distance will increase and leads to increase in the time for the formation of shock. Also, we noticed that as the Mach number increases, the shock formation distance decreases, resulting in an early shock formation. Thus, the behavior of the propagation process under the thermal radiation effect and Mach number effect is opposite. A similar result can be seen from Figure 2(b), which shows the thermal radiation effect for \(\gamma =1.67\). If we compare the results shown in Figure 2(a and b), we observed that as we increase the value of \(\gamma \), shock formation distance decreases, resulting in an early shock formation i.e., \(y_{z}\) is a decreasing function of \(\gamma \).

5.2 Analysis of an increase in the value of magnetic parameter \(\varepsilon _{0}\)

Figure 3(a and b) shows the magnetic field effect on the shock formation distance for \(\gamma =1.4\) and \(\gamma =1.67\), respectively. Figure 3(a) reveals that an increase in the value of \(\varepsilon _{0}\) enhances the shock formation distance. For non-magnetic case \((\varepsilon _{0}=1.0)\), shock forms later as compared to magnetic case. Similarly, in Figure 3(b), we see that as we increase the value of \(\varepsilon _{0}\), shock forms earlier. Also, if we increase the value of \(\gamma \), shock formation distance decreases i.e., an increase in the value of the parameter \(\gamma \) leads to decrease in the time for shock formation. In Figure 3(a and b), we found that the flatness of the curve increases as an increase in the Mach number. Thus, the behavior of the propagating waves under the effect of magnetic field and Mach number are same i.e., for increasing the value of Mach number or magnetic field parameter \(\varepsilon _{0}\), shock formation distance \(y_{z}\) decreases. In the non-magnetic case, shock formation distance \(y_{z}\) decreases rapidly as compared to the magnetic case.

5.3 Analysis of an increase in the value of non-ideal parameter \({\bar{b}}\)

Figure 4(a and b) shows the effect of non-ideal on the shock formation distance for \(\gamma =1.4\) and \(\gamma =1.67\), respectively. In Figure 4(a), it can be noticed that an increase in the value of non-ideal parameter \({\bar{b}}\) causes to decrease the shock formation distance \(y_{z}\) i.e., increase in the value of \({\bar{b}}\) reduces the time for shock formation. Figure 4(b) shows the similar phenomenon as observed from Figure 4(a), which is for \(\gamma =1.4\). Further, for increasing the value of \(\gamma \) decrease in \(y_{z}\) and an early shock will form. Thus, we see that the effect of magnetic field strength and the parameter of non-idealness are similar, whereas in the case of thermal radiation, we get different result. Hence, we found that an increase in the value of parameter \(\varepsilon _{0}\) or \({\bar{b}}\) causes to increase the formation process of shock and increase in the value of \(\Phi \) or Mach number \(M_{0}\) enhances the shock-formation distance.

Fig. 3
figure 3

Effect of magnetic field on the shock formation distance with (a) \(\phi =0.8\), \(b=0.1\), \(y=1.4\) and (b) \(\phi =0.8\), \(b=0.1\), \(y=1.67\).

Full size image
Fig. 4
figure 4

Effect of non-idealness on the shock formation distance with (a) \(\phi =0.8\), \(\varepsilon _{0}=1.6, y=1.4\) and (b) \(\phi =0.8, \,\varepsilon _{0}=0.1, y=1.67\).

Full size image

6 Summary and conclusions

The present study deals with the combined effect of non-idealness and the radiative heat transfer effect on the propagation of shock wave. The optically thin approximation treats the effect of thermal radiation. We have described what physical changes take place when we change (increase or decrease) the values of the parameters required for the motion. The fundamental differential equation (transport equations) governing the growth and decay of disturbances propagated into the medium is obtained using the wavefront analysis method, which determines the distance at which the characteristic curves intersect, and the conditions that ensure no shock will ever form on the wavefront. It is found that the shock formation completely relies on the upstream flow Mach number \(M_{0}\), the magnetic field parameter \(\varepsilon _{0}\) and initial body curvature \(\eta \), which may be either \(\kappa _{b}^{\prime \prime }(0)^{-1}\) or \(\kappa _{z}^{\prime \prime }(0)^{-1}\), non-ideal parameters b and \(\Phi \), which represent the importance of thermal radiation. It is observed that the presence of a magnetic field and non-idealness reduces the time for shock formation i.e., increasing the magnetic field strength and the value of the non-ideal parameter causes shock to form earlier, whereas increasing the value of the Boltzmann number delays the formation process of shock. In the absence of thermal radiation parameter i.e., \((\Phi = 0)\), the results obtained in this study is similar with the results reported in the recent work by Chaturvedi & Singh (2021). Moreover, the results analysed in this paper are in close agreement with the results analysed by the authors in Sharma et al. (1987), Singh et al. (2010, 2011, 2012) and Chaturvedi et al. (2019a).