Approximate analytical solution for shock wave in rotational axisymmetric perfect gas with azimuthal magnetic field: Isothermal flow

Abstract

The propagation of cylindrical shock wave in rotational axisymmetric perfect gas under isothermal flow condition with azimuthal magnetic field is investigated. Distributions of gas dynamical quantities are discussed. The density, magnetic pressure, azimuthal fluid velocity and axial fluid velocity are assumed to be varying according to power law with distance from the axis of symmetry in the undisturbed medium. Approximate analytical solutions are obtained by expanding flow variables in power series. Zeroth-order and first-order approximations are discussed with the aid of power series method. Solutions for zeroth-order approximation are constructed in approximate analytical form. The effect of flow parameters namely: shock Cowling number $C_{0}$, ambient density variation index q and adiabatic exponent $\gamma$ are studied on the flow variables. Consideration of magnetic pressure increases the total energy of disturbance of zeroth order while with increase in ambient density variation index or adiabatic exponent, the total energy of disturbance decreases.

1 Introduction

The study of cylindrical shock wave in the presence of magnetic field in a rotating medium has enormous applications. Some of the applications include explosion of long thin wire, experiments on pinch effect, exploding wire, to certain axially symmetric hypersonic problems such as the shock envelope behind fast meteor or missile and many more.

Taylor (1950a, b) studied formation of a blast wave formed by a very intense explosion. Sakurai (1953, 1954) extended the work of Taylor (1950a, b) to the case of plane and cylindrical shock wave and using power series method, he obtained the first and second approximations to the solution in Sakurai (1953, 1954) respectively. An important role is played by magnetic fields in a number of astrophysical situations. The various industrial and astrophysical processes involve applied external magnetic fields (Hartmann 1998; Balick & Frank 2002). Nath and Vishwakarma (2014) obtained similarity solutions for the flow behind a magnetogasdynamic shock in a non-ideal gas with heat conduction and radiation heat-flux.

The assumption of isothermal flow is physically realistic, when radiation heat transfer effects are implicitly present. As the shock propagates, the temperature behind it increases and becomes very large so that there is intense transfer of energy by radiation. This causes the temperature gradient to approach zero, that is, the dependent temperature becomes uniform behind the shock front and the flow becomes isothermal (Laumbach & Probstein 1970; Sachdev & Ashraf 1971; Korobeinikov 1976; Zhuravskaya & Levin 1996; Nath 2011). Lerche (1979, 1981) developed mathematical theory of one-dimensional isothermal blast waves in a magnetic field. Purohit (1974) and Singh and Vishwakarma (1983) have studied homothermal flows behind a spherical shock wave in a self-gravitating gas.

The processes occurring in the outer atmospheres of stars or planets are significantly affected by their rotation due to which the explosions in rotating gas atmospheres are of definite astrophysical interest. Chaturani (1971) studied the propagation of cylindrical shock wave through a gas having solid body rotation.

There are other types of self-similar ansatz. The first one describes the dispersive solutions which can be found in Barna and Matyas (2013, 2015). In Barna and Matyas (2015), the analytical self-similar solutions of the Oberbeck–Boussinesq equations are obtained. They also have applied a completely different approach, namely the two-dimensional generalization of the self-similar ansatz which is well known for one dimension, for more than half a century (Sedov 1959; Baraneblatt 1979; Zełdovich & Raizer 1968). In Barna and Matyas (2013), analytical solution for the one-dimensional compressible Euler equation with heat conduction and with different kind of equation of state is obtained. Firstly, they tried to obtain the self-similar physically important diffusive solutions. If such solutions are not found, then they obtain the traveling wave solutions. These dispersive type solutions decay in time.

Second is the blowup type which can be found in Suzuki (2013). There the irrotational blowup of the solution to compressible Euler equation is obtained. Initially, the author examined the validity of physical laws such as conservation of mass and energy and also the decay of total pressure. He observed the non-existence of global-in-time irrotational solution with positive mass. These kind of solutions however explode in finite time.

In the present work, we have studied the problem of propagation of a one-dimensional unsteady isothermal flow behind a cylindrical shock wave in axisymmetric rotating perfect gas under the influence of azimuthal magnetic field. The medium is considered to obey ideal gas law. Barna and Matyas (2013) obtained analytical solution for compressible Euler equation in one dimension with heat conduction without considering the effect of magnetic field and rotation of the medium. Nath (2011) obtained self-similar solutions for the flow behind the magnetogasdynamic strong cylindrical shock wave generated by a moving piston in a rotational axisymmetric perfect gas under isothermal flow condition. The author has used the approach of Sedov (1959) to transform the fundamental equations of motion into a system of ordinary differential equations and the boundary condition into a non-dimensional form. In Nath (2011), the numerical solutions of the system of ODE’s are obtained by the Range–Kutta method of fourth order. In our problem, the approach of Sakurai (1953) has been used and approximate analytical solutions for the zeroth order approximation are obtained. The benefit of this approach over Sedov’s (1959) dimensional analysis approach is that by using Sakurai’s (1953) approach, we are able to obtain the solution in analytical form while in Nath (2011), they obtained the numerical solution using Sedov’s (1959) approach.

The importance of constructing analytical or exact solutions in mathematical physics and applied mathematics is that they can be used to classify and understand the nonlinear phenomena. Fundamental equations of motion (1)–(6) are coupled non-linear partial differential equations which are very difficult to solve; even there is no direct method to obtain the exact solutions of these type of equations. Thus, Sakurai’s approach is a way to find the approximate analytical solutions of these equations. Sakurai’s blast-wave analysis is capable of yielding results of any desired degree of accuracy; however there is a great deal of work involved in carrying out the required computations. Sakurai obtained the first approximation in analytical form (see Sakurai 1953) and the second approximation using numerical method (see Sakurai 1954). Also, Swigart (1960) extended the work of Sakurai (1953, 1954) to include third-order terms for the case of cylindrical symmetry. He used the first and second approximations obtained by Sakurai (1953, 1954) and obtained the coefficient of third-order by numerical integration. Freeman (1968) in his work extended the analysis of Sakurai (1953) to include variable-energy flows with particular reference to cylindrical spark channel formation. Freeman (1968) also pointed out that the second approximation does not yield results of sufficient accuracy for weak blast waves. In this work, we have obtained zeroth-order approximate analytical solution of the problem using power series expansion of the flow variables, i.e. we used the approach of Sakurai (1953). The present work is an extension to the work of Sakurai (1953) in the case of cylindrical shock, including the effects of magnetic field in rotational axisymmetric perfect gas for isothermal flow. Also the components of vorticity vector are taken into account. Following Taylor (1950a) and Sakurai (1953), solutions are obtained by expanding the flow variables in the power series of $(C/U)^{2}$, where C is the sound of speed in the undisturbed fluid and U is the propagation velocity of the shock wave. The zeroth-order approximate solutions are constructed in Section 5. The ordinary differential equations for the first-order approximation to the flow variables and the boundary conditions are also presented. The density, magnetic pressure, azimuthal and axial components of fluid velocity are assumed to vary according to the power law in ambient medium. The effect of Cowling number $C_{0}$, ambient density variation index q and adiabatic exponent $\gamma$ on the physical quantities are shown in Table 1 and Figures 1 and 2.

Table 1 Values of n and zeroth approximation of total energy $J_{0}$ for different values of $\gamma$, $C_{0}$ and q.

2 Equations of motion and boundary conditions

The fundamental equations governing the one-dimensional unsteady isothermal flow behind a cylindrical shock in rotational axisymmetric perfect gas with azimuthal magnetic field are (Nath 2011, 2012a, 2014a; Singh & Vishwakarma 1983; Nath & Singh 2017)

$$\begin{aligned}&\dfrac{\partial \rho }{\partial t} + u \dfrac{\partial \rho }{\partial r} + \rho \dfrac{\partial u}{\partial r} + \dfrac{ u \rho }{r} = 0, \end{aligned}$$

(1)

$$\begin{aligned}&\dfrac{\partial u}{\partial t} + u \dfrac{\partial u}{\partial r} + \dfrac{1}{\rho } \left[ \dfrac{\partial p}{\partial r} + \dfrac{\partial h}{\partial r} +\dfrac{2 h}{r} \right] - \dfrac{v^{2}}{r}=0, \end{aligned}$$

(2)

$$\begin{aligned}&\dfrac{\partial h}{\partial t} + u \dfrac{\partial h}{\partial r} + 2 h \dfrac{\partial u}{\partial r} = 0, \end{aligned}$$

(3)

$$\begin{aligned}&\dfrac{\partial v}{\partial t}+ u \dfrac{\partial v}{\partial r}+\dfrac{uv}{r}=0,\end{aligned}$$

(4)

$$\begin{aligned}&\dfrac{\partial w}{\partial t}+ u \dfrac{\partial w}{\partial r}=0,\end{aligned}$$

(5)

$$\begin{aligned}&\dfrac{\partial T}{\partial r}=0, \end{aligned}$$

(6)

where $\rho$ denotes the density; u, v and w denote the radial, azimuthal and axial components of fluid velocity $\vec {X}$; p denotes the pressure; h denotes the magnetic pressure defined by $h=\mu H^{*2}/2$, $\mu$ is the magnetic permeability and $H^{*}$ is the azimuthal magnetic field; r and t are independent space and time coordinates; T is the temperature.

Fig. 1

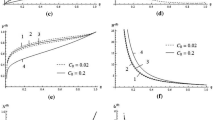
Dispersal of zeroth approximate solution of the flow variables in the region behind the cylindrical shock front for $\gamma =5/3$. (a) Radial fluid velocity $F^{(0)}$; (b) density $D^{(0)}$; (c) pressure $P^{(0)}$; (d) magnetic pressure $H^{(0)}$; (e) azimuthal fluid velocity $V^{(0)}$; (f) axial fluid velocity $W^{(0)}$; (g) $l_{\theta }^{(0)}$; (h) $l_{z}^{(0)}$: 1. $C_{0}=0.01, q=-1.7$; 2. $C_{0}=0.01, q=-1.82$; 3. $C_{0}=0.04, q=-1.7$; 4. $C_{0}=0.04, q=-1.82$.

Fig. 2

Dispersal of zeroth approximate solution of the flow variables in the region behind the cylindrical shock front for $C_{0}=0.01$ and $q=-1.7$. (a) Radial fluid velocity $F^{(0)}$; (b) density $D^{(0)}$; (c) pressure $P^{(0)}$; (d) magnetic pressure $H^{(0)}$; (e) azimuthal fluid velocity $V^{(0)}$; (f) axial fluid velocity $W^{(0)}$; (g) $l_{\theta }^{(0)}$; (h) $l_{z}^{(0)}$.

Let the radius of the shock front be given by $R=R(t)$, and $U\left( =\frac{\mathrm{d}R}{\mathrm{d}t}\right)$ be the propagation velocity of the shock front. The flow variables immediately ahead of the shock front are

$$\begin{aligned} \rho= & {} \rho _{0}=\rho ^{*} R^{q},~~ u=u_{0}=0,~~ h=h_{0}=h^{*} R^{-\beta _{1}}, \nonumber \\ v= & {} v_{0}=v^{*} R^{\alpha _{1}},~~w=w_{0}=w^{*} R^{\alpha _{2}}, \end{aligned}$$

(7)

where $\rho ^{*}$, q, $h^{*}$, $\beta _{1}$, $v^{*}$, $\alpha _{1}$, $w^{*}$ and $\alpha _{2}$ are constants and subscript ’0’ denotes the condition just ahead of the shock front.

The vorticity vector ${\bar{\zeta }}=\dfrac{1}{2} \mathrm{curl} \vec {X}$ has the following components:

$$\begin{aligned} \zeta _{r}=0, \quad \zeta _{\theta }=-\dfrac{1}{2}\dfrac{\partial w}{\partial r}, \quad \zeta _{z}=\dfrac{1}{2r}\dfrac{\partial (rv)}{\partial r}, \end{aligned}$$

(8)

where ${\bar{\zeta }}=\zeta _{r}{\hat{e}}_{r}+\zeta _{\theta }{\hat{e}}_{\theta }+\zeta _{z}{\hat{e}}_{z}$.

For self-similar solutions (Sedov 1959), the shock velocity is assumed to vary as

$$\begin{aligned} U^{2}=B^{2} R^{-\alpha }, \end{aligned}$$

(9)

where B and $\alpha$ are constants.

The equation of state and internal energy for ideal gas are

$$\begin{aligned} p=\Gamma \rho T; \qquad e=\dfrac{p}{(\gamma -1)\rho }, \end{aligned}$$

(10)

where $\Gamma$ is the gas constant, e is the internal energy per unit mass of the gas and $\gamma$ denotes the adiabatic exponent. Rankine–Hugoniot conditions across the shock are given as (Nath 2011; Nath & Singh 2017)

$$\begin{aligned}&\rho _{0} U=\rho _{1} (U-u_{1}) , \end{aligned}$$

(11)

$$\begin{aligned}&H^{*}_{0} U=H^{*}_{1} (U-u_{1}), \end{aligned}$$

(12)

$$\begin{aligned}&\rho _{0} U^{2} + p_{0} + \dfrac{1}{2} \mu H_{0}^{*2}=\rho _{1} (U-u_{1})^{2} +p_{1} + \dfrac{1}{2} \mu H_{1}^{*2},\end{aligned}$$

(13)

$$\begin{aligned}&\dfrac{1}{2} U^{2} + \dfrac{\gamma }{(\gamma -1)}\dfrac{p_{0}}{\rho _{0}}+\dfrac{\mu H_{0}^{*2}}{\rho _{0}}-\dfrac{Q_{0}}{\rho _{0} U}=\dfrac{1}{2} (U-u_{1})^{2} \nonumber \\&\quad + \dfrac{\gamma }{(\gamma -1)}\dfrac{p_{1}}{\rho _{1}}+\dfrac{\mu H_{1}^{*2}}{\rho _{1}}-\dfrac{Q_{1}}{\rho _{0} U}, \end{aligned}$$

(14)

$$\begin{aligned}&v_{0}=v_{1},\end{aligned}$$

(15)

$$\begin{aligned}&w_{0}=w_{1}, \end{aligned}$$

(16)

where subscript ‘1’ denotes the conditions immediately behind the shock front. We have $\rho _{1}=(\rho )_{r=R}$, $p_{1}=(p)_{r=R}$, $u_{1}=(u)_{r=R}$, $h_{1}=(h)_{r=R}$, $v_{1}=(v)_{r=R}$ and $w_{1}=(w)_{r=R}$ at the shock front $(r=R(t))$, and Q is the radiation heat flux. Substituting these values in Equations (11)–(16), we get conditions across the shock front as

$$\begin{aligned}&(\rho )_{r=R}=\dfrac{\rho _{0}}{\beta }, \end{aligned}$$

(17)

$$\begin{aligned}&(h)_{r=R}=\dfrac{h_{0}}{\beta ^{2}},\end{aligned}$$

(18)

$$\begin{aligned}&[U-(u)_{r=R}]=U \beta ,\end{aligned}$$

(19)

$$\begin{aligned}&(p)_{r=R}= p_{0} + h_{0} + \rho _{0} U^{2} - (h)_{r=R} - \rho _{0} U^{2} \beta , \end{aligned}$$

(20)

$$\begin{aligned}&(v)_{r=R}=v_{0}, \end{aligned}$$

(21)

$$\begin{aligned}&(w)_{r=R}=w_{0}, \end{aligned}$$

(22)

where $\beta$ is the density ratio across the shock front. To obtain solution using power series, we need to obtain boundary conditions in terms of $\big (\frac{C}{U}\big )^{2}(=\!\!\!\phi )$. As in Whitham (1958), the expression for $\beta$ $(0<\beta <1)$ is obtained as

$$\begin{aligned}&\dfrac{(\gamma -1)}{2}+\left( \dfrac{C}{U}\right) ^{2}-\dfrac{1}{2}\beta ^{2}(\gamma -1)\nonumber \\&\quad +\dfrac{(Q_{1}-Q_{0})\left\{ \dfrac{C^{2}}{\gamma U^{2}}+(1-\beta ) \right\} (\gamma -1)}{U (p)_{r=R} }=\beta \left( \dfrac{C}{U}\right) ^{2}\nonumber \\&\quad +\,\gamma \beta (1-\beta ). \end{aligned}$$

(23)

In the above Equation (23), $(Q_{1}-Q_{0})$ is assumed to be negligible in comparison to the product of $(p)_{r=R}$ and U (Nath 2015, 2016). Therefore, Equation (23) reduces to the form

$$\begin{aligned}&\dfrac{(\gamma -1)}{2}+\left( \dfrac{C}{U}\right) ^{2}-\dfrac{1}{2}\beta ^{2}(\gamma -1)\nonumber \\&\quad =\beta \left( \dfrac{C}{U}\right) ^{2}+\gamma \beta (1-\beta ). \end{aligned}$$

(24)

Thus from Equation (24), we get the expression for $\beta$ as

$$\begin{aligned} \beta =\dfrac{(\gamma -1)}{(\gamma +1)}\left[ 1+\dfrac{2}{(\gamma -1)}\left( \dfrac{C}{U}\right) ^{2}\right] . \end{aligned}$$

(25)

Using Equation (25), the shock jump conditions (17)–(22) become

$$\begin{aligned}&(\rho )_{r=R}=\dfrac{(\gamma +1)}{(\gamma -1)} \dfrac{\rho _{0}}{\left\{ 1+\dfrac{2}{(\gamma -1)}\left( \dfrac{C}{U}\right) ^{2}\right\} }, \end{aligned}$$

(26)

$$\begin{aligned}&(u)_{r=R}=\dfrac{2}{(\gamma +1)} U \left\{ 1-\left( \dfrac{C}{U}\right) ^{2}\right\} , \end{aligned}$$

(27)

$$\begin{aligned}&(p)_{r=R}=\dfrac{2 \rho _{0} U^{2}}{(\gamma +1)} \left\{ 1-\dfrac{(\gamma -1)}{2 \gamma }\left( \dfrac{C}{U}\right) ^{2}\right\} \nonumber \\&\quad +\dfrac{C_{0} \rho _{0} U^{2}}{2}-\dfrac{1}{2}\dfrac{(\gamma +1)^{2}}{(\gamma -1)^{2}} \dfrac{C_{0} \rho _{0} U^{2}}{\left\{ 1+ \dfrac{2}{(\gamma -1)}\left( \dfrac{C}{U}\right) ^{2}\right\} ^{2}},\end{aligned}$$

(28)

$$\begin{aligned}&(h)_{r=R}=\dfrac{1}{2} \dfrac{(\gamma +1)^{2}}{(\gamma -1)^{2}}\dfrac{C_{0} \rho _{0} U^{2}}{\left\{ 1+ \dfrac{2}{(\gamma -1)}\left( \dfrac{C}{U}\right) ^{2}\right\} ^{2}}, \end{aligned}$$

(29)

$$\begin{aligned}&(v)_{r=R}=v_{0},\end{aligned}$$

(30)

$$\begin{aligned}&(w)_{r=R}=w_{0}, \end{aligned}$$

(31)

where $C^{2}=\frac{\gamma p_{0}}{\rho _{0}}$ is the square of the speed of sound and $C_{0}=\frac{2 h_{0}}{\rho _{0} U^{2}}$ is the shock Cowling number. For $C_{0}$ to be constant, it is necessary that $\beta _{1}+q-\alpha =0$.

The energy balance equation is given by

$$\begin{aligned} E_{T}= & {} \int _{0}^{R} \left\{ \dfrac{1}{2} (u^{2}+v^{2}+w^{2}-(v_{0}^{2}+w_{0}^{2})) \right. \nonumber \\&\left. + \dfrac{1}{(\gamma -1)}\left( \dfrac{p}{\rho }-\dfrac{p_{0}}{\rho _{0}} \right) + \left( \dfrac{h}{\rho }-\dfrac{h_{0}}{\rho _{0}} \right) \right\} \rho r \mathrm{d}r ,\nonumber \\ \end{aligned}$$

(32)

where $E_{T}$ expresses the explosion energy per unit area of the surface of the shock front for cylinder of unit length.

Consider the relation

$$\begin{aligned} \int _{0}^{R} \dfrac{\rho }{\rho _{0}} r \mathrm{d}r=\dfrac{R^{2}}{2}, \end{aligned}$$

(33)

which is obtained from the Lagrangian equation of continuity. Using (32) and (33), we obtain

$$\begin{aligned}&E_{T}=\int _{0}^{R} \left\{ \dfrac{1}{2} \rho (u^{2}+v^{2}+w^{2}) + \dfrac{1}{(\gamma -1)} p + h \right\} r \mathrm{d}r\nonumber \\&-\dfrac{p_{0}}{(\gamma -1)}\dfrac{R^{2}}{2}-h_{0}\dfrac{R^{2}}{2}-\dfrac{1}{2}(v_{0}^{2}+w_{0}^{2})\rho _{0}\dfrac{R^{2}}{2}. \end{aligned}$$

(34)

Using Equations (6) and (10), we obtain

$$\begin{aligned} \dfrac{p}{(p)_{r=R}}=\dfrac{\rho }{(\rho )_{r=R}}. \end{aligned}$$

(35)

3 Similarity transformation

On the part of r and t, new independent variables $\eta$ and $\phi$ are proposed as

$$\begin{aligned} \dfrac{r}{R}=\eta ; \qquad \left( \dfrac{C}{U}\right) ^{2}=\phi . \end{aligned}$$

(36)

Expressing the physical quantities in the form

$$\begin{aligned}&u=U F(\eta ,\phi ), \end{aligned}$$

(37)

$$\begin{aligned}&\rho =\rho _{0} D(\eta ,\phi ),\end{aligned}$$

(38)

$$\begin{aligned}&p=p_{0} \left( \dfrac{U}{C}\right) ^{2} P(\eta ,\phi )= p_{0} P(\eta ,\phi )/\phi , \end{aligned}$$

(39)

$$\begin{aligned}&h=p_{0} \left( \dfrac{U}{C}\right) ^{2} H(\eta ,\phi )= p_{0} H(\eta ,\phi )/\phi , \end{aligned}$$

(40)

$$\begin{aligned}&v=U V(\eta ,\phi ),\end{aligned}$$

(41)

$$\begin{aligned}&w=U W(\eta ,\phi ), \end{aligned}$$

(42)

where F, D, P, H, V and W are functions of non-dimensional variables $\eta$ and $\phi$. Using Equations (36), (37), we obtain

$$\begin{aligned}&\dfrac{\partial }{\partial r}=\dfrac{1}{R} \dfrac{\partial }{\partial \eta }, \end{aligned}$$

(43)

$$\begin{aligned}&\dfrac{D}{Dt}=\dfrac{U}{R} \left\{ (F-\eta )\dfrac{\partial }{\partial \eta } + \lambda \phi \dfrac{\partial }{\partial \phi } \right\} , \end{aligned}$$

(44)

where $\lambda =R (\mathrm{d}\phi /\mathrm{d}R)/\phi$ and $\lambda$ is a function of $\phi$ only.

To obtain Equations (45)–(49), substituting (37)–(44) into the fundamental Equations (1)–(5), we have

$$\begin{aligned}&(F-\eta ) D_{\eta } + \lambda \phi D_{\phi } + D \left( F_{\eta } +\dfrac{F}{\eta } \right) +q D=0, \end{aligned}$$

(45)

$$\begin{aligned}&D \left\{ (F-\eta ) F_{\eta } + \lambda \phi F_{\phi } - \dfrac{\lambda F}{2} \right\} \nonumber \\&\quad + \dfrac{1}{\gamma } \left\{ P_{\eta }+H_{\eta }+\dfrac{2H}{\eta }\right\} -\dfrac{V^{2} D}{\eta }=0, \end{aligned}$$

(46)

$$\begin{aligned}&(F-\eta ) H_{\eta } -\lambda H+ \lambda \phi H_{\phi } + 2 H F_{\eta } + q H=0, \end{aligned}$$

(47)

$$\begin{aligned}&(F-\eta )V_{\eta }+\lambda \phi V_{\phi }+\dfrac{FV}{\eta }-\dfrac{\lambda }{2}V=0,\end{aligned}$$

(48)

$$\begin{aligned}&(F-\eta )W_{\eta }+\lambda \phi W_{\phi }-\dfrac{\lambda }{2}W=0, \end{aligned}$$

(49)

where the subscripts $\eta$ and $\phi$ refer to differentiation with respect to $\eta$ and $\phi$ respectively.

Using Equations (37)–(42) in Equation (34), we obtain

$$\begin{aligned} \phi \left( \dfrac{R_{0}}{R}\right) ^{2}= & {} J -\dfrac{\phi }{2(\gamma -1)}-\dfrac{C_{0} \gamma }{4}-\dfrac{\gamma }{4}\left( \dfrac{v^{*2}}{B^{2}}+\dfrac{w^{*2}}{B^{2}}\right) ,\nonumber \\ \end{aligned}$$

(50)

where

$$\begin{aligned} J=\int _{0}^{1} \small {\left\{ \dfrac{\gamma D (F^{2}+V^{2}+W^{2})}{2} + \dfrac{P}{(\gamma -1)} + H\right\} \eta \mathrm{d}\eta },\nonumber \\ \end{aligned}$$

(51)

and $R_{0}=\left( \frac{E_{T}}{p_{0}}\right) ^{\frac{1}{2}}$ with dimension of length.

Using transformations (37)–(42), Equations (26)–(31) become

$$\begin{aligned}&F(1,\phi )=\dfrac{2 (1-\phi )}{(\gamma +1)}, \end{aligned}$$

(52)

$$\begin{aligned}&D(1,\phi )=\dfrac{(\gamma +1)}{(\gamma -1)}\left\{ 1+\dfrac{2}{(\gamma -1)} \phi \right\} ^{-1}, \end{aligned}$$

(53)

$$\begin{aligned}&P(1,\phi )=\dfrac{2 \gamma }{(\gamma +1)}\left\{ 1-\dfrac{(\gamma -1)}{2 \gamma }\phi \right\} \nonumber \\&\quad +\dfrac{C_{0} \gamma }{2}-\dfrac{\gamma C_{0} (\gamma +1)^{2}}{2 (\gamma -1)^{2}}\left\{ 1+\dfrac{2 \phi }{(\gamma -1)}\right\} ^{-2}, \end{aligned}$$

(54)

$$\begin{aligned}&H(1,\phi )=\dfrac{1}{2}\dfrac{(\gamma +1)^{2}}{(\gamma -1)^{2}}\gamma C_{0} \left\{ 1+\dfrac{2}{(\gamma -1)}\phi \right\} ^{-2}, \end{aligned}$$

(55)

$$\begin{aligned}&V(1,\phi )=\dfrac{v^{*}(\rho ^{*}C_{0})^{1/2}}{(2h^{*})^{1/2}},\end{aligned}$$

(56)

$$\begin{aligned}&W(1,\phi )=\dfrac{w^{*}(\rho ^{*}C_{0})^{1/2}}{(2h^{*})^{1/2}}, \end{aligned}$$

(57)

where $\alpha _{1}=\alpha _{2}=\dfrac{-\alpha }{2}$.

Using Equations (35), (38), (39), (53) and (54), we obtain

$$\begin{aligned} P(\eta )=&\left[ \dfrac{2 \gamma (\gamma -1)}{(\gamma +1)^{2}}\left\{ 1+\dfrac{2 \phi }{(\gamma -1)}-\dfrac{(\gamma -1) \phi }{2 \gamma }-\dfrac{\phi ^{2}}{ \gamma }\right\} \right. \nonumber \\&+\dfrac{C_{0} \gamma (\gamma -1)}{2 (\gamma +1)}+\dfrac{C_{0} \gamma \phi }{(\gamma +1)}-\dfrac{C_{0} \gamma (\gamma +1)}{2 (\gamma -1)}\nonumber \\&\left. \left\{ 1-\dfrac{2 \phi }{(\gamma -1)}+\dfrac{4 \phi ^{2}}{(\gamma -1)^{2}}+\cdots \right\} \right] D(\eta ). \end{aligned}$$

(58)

Differentiating Equation (50) with respect to $\phi$, we obtain the expression for $\lambda$ as

$$\begin{aligned} \lambda =\dfrac{(q+2)\left[ J -\dfrac{\phi }{2(\gamma -1)}-\dfrac{\gamma C_{0}}{4} -\dfrac{\gamma }{4}\left( \dfrac{v^{*2}}{B^{2}}+\dfrac{w^{*2}}{B^{2}}\right) \right] }{J-\phi \left( \dfrac{dJ}{d\phi }\right) -\dfrac{\gamma C_{0}}{4}-\dfrac{\gamma }{4}\left( \dfrac{v^{*2}}{B^{2}}+\dfrac{w^{*2}}{B^{2}}\right) }.\nonumber \\ \end{aligned}$$

(59)

The non-dimensional components of the vorticity vector $l_{r}=\frac{\zeta _{r}}{(U/R)}$, $l_{\theta }=\frac{\zeta _{\theta }}{(U/R)}$, $l_{z}=\frac{\zeta _{z}}{(U/R)}$ are given by

$$\begin{aligned}&l_{r}=0, \end{aligned}$$

(60)

$$\begin{aligned}&l_{\theta }=-\dfrac{1}{2}W_{\eta },\end{aligned}$$

(61)

$$\begin{aligned}&l_{z}=\dfrac{1}{2 \eta }(V+ \eta V_{\eta }). \end{aligned}$$

(62)

4 Solution construction in power series in $\phi$

When the shock wave is formed, the shock front velocity U becomes larger than the sound velocity C for strong shock and $\phi =\left( \frac{C}{U}\right) ^{2}$ is considered to be small there. To construct the solution, the non-dimensional flow variables F, P, D, H, V and W can be expanded in power series in $\phi$ as

$$\begin{aligned}&F= F^{(0)} + \phi F^{(1)} + \phi ^{2} F^{(2)} +\cdots +\phi ^{k} F^{(k)} +\cdots , \nonumber \\&D= D^{(0)} + \phi D^{(1)} + \phi ^{2} D^{(2)} +\cdots +\phi ^{k} D^{(k)} +\cdots ,\nonumber \\&P= P^{(0)} + \phi P^{(1)} + \phi ^{2} P^{(2)} +\cdots +\phi ^{k} P^{(k)} +\cdots , \nonumber \\&H= H^{(0)} + \phi H^{(1)} + \phi ^{2} H^{(2)}+\cdots +\phi ^{k} H^{(k)} +\cdots , \nonumber \\&V= V^{(0)} + \phi V^{(1)} + \phi ^{2} V^{(2)}+\cdots +\phi ^{k} V^{(k)} +\cdots ,\nonumber \\&W= W^{(0)} + \phi W^{(1)} + \phi ^{2} W^{(2)}+\cdots +\phi ^{k} W^{(k)} +\cdots , \end{aligned}$$

(63)

where $F^{(k)}$, $D^{(k)}$, $P^{(k)}$, $H^{(k)}$, $V^{(k)}$ and $W^{(k)}$ are all functions of $\eta$ only and $(k=0,1,2,3,\ldots )$.

Inserting (63) into expression (51), we get

$$\begin{aligned} J=J_{0} (1+ \sigma _{1} \phi + \sigma _{2} \phi ^{2}+\sigma _{3} \phi ^{3}+\cdots ), \end{aligned}$$

(64)

where

$$\begin{aligned} J_{0}= & {} \int _{0}^{1} \left\{ \dfrac{\gamma }{2} D^{(0)} [(F^{(0)})^{2}+(V^{(0)})^{2}+(W^{(0)})^{2}] \right. \nonumber \\&\left. + \dfrac{1}{(\gamma -1)} P^{(0)} + H^{(0)}\right\} \eta \mathrm{d}\eta ,\end{aligned}$$

(65)

$$\begin{aligned} \sigma _{1} J_{0}= & {} \int _{0}^{1} \left\{ \dfrac{\gamma }{2} D^{(1)} [(F^{(0)})^{2}+(V^{(0)})^{2}+(W^{(0)})^{2}] \right. \nonumber \\&+\gamma [F^{(0)} F^{(1)}+V^{(0)} V^{(1)}+W^{(0)} W^{(1)}] D^{(0)}\nonumber \\&\left. + \dfrac{1}{(\gamma -1)} P^{(1)} + H^{(1)}\right\} \eta \mathrm{d}\eta , \end{aligned}$$

(66)

and so on. Using (64) in (50), we get

$$\begin{aligned}&\phi \left( \dfrac{R_{0}}{R}\right) ^{2}=J_{0} \left\{ \left[ 1-\dfrac{C_{0} \gamma }{4 J_{0}}-\dfrac{\gamma }{4 J_{0}}\left( \dfrac{v^{*2}}{B^{2}}+\dfrac{w^{*2}}{B^{2}}\right) \right] \right. \nonumber \\&\quad \left. + \left[ \sigma _{1}-\dfrac{1}{2 J_{0} (\gamma -1)} \right] \phi + \sigma _{2} \phi ^{2}+\cdots \right\} . \end{aligned}$$

(67)

Using (36), (67) becomes

$$\begin{aligned}&\left( \dfrac{C}{U}\right) ^{2}\left( \dfrac{R_{0}}{R}\right) ^{2}=J_{0} \left\{ \left[ 1-\dfrac{C_{0} \gamma }{4 J_{0}}-\dfrac{\gamma }{4 J_{0}}\left( \dfrac{v^{*2}}{B^{2}}+\dfrac{w^{*2}}{B^{2}}\right) \right] \right. \nonumber \\&\qquad \left. + \left( \sigma _{1}-\dfrac{1}{2 J_{0} (\gamma -1)} \right) \left( \dfrac{C}{U}\right) ^{2} + \sigma _{2} \left( \dfrac{C}{U}\right) ^{4}+\cdots \right\} .\nonumber \\ \end{aligned}$$

(68)

By using (59) and (64), $\lambda$ in Equation (59) may be expressed as

$$\begin{aligned} \lambda =(q+2)[1+\lambda _{1}\phi + \lambda _{2}\phi ^{2}+\cdots ], \end{aligned}$$

(69)

where

$$\begin{aligned}&\lambda _{1}=\dfrac{\sigma _{1}-\dfrac{1}{2J_{0} (\gamma -1)}}{1-\dfrac{\gamma C_{0}}{4 J_{0}}-\dfrac{\gamma }{4 J_{0}}\left( \dfrac{v^{*2}}{B^{2}}+\dfrac{w^{*2}}{B^{2}}\right) } ,\\&\lambda _{2}=\dfrac{2\sigma _{2}}{1-\dfrac{\gamma C_{0}}{4 J_{0}}-\dfrac{\gamma }{4 J_{0}}\left( \dfrac{v^{*2}}{B^{2}}+\dfrac{w^{*2}}{B^{2}}\right) } ,\ldots \end{aligned}$$

and so on. Now, substituting (63) and (69) in Equations (45)–(49) and comparing the like powers of $\phi$ on both sides, we obtain the following system of equations: For the zeroth power of $\phi$, we have the following set of equations:

$$\begin{aligned}&(F^{(0)}-\eta ) D_{\eta }^{(0)} + D^{(0)}\left( F_{\eta }^{(0)}+\dfrac{F^{(0)}}{\eta } \right) +q D^{(0)}=0, \end{aligned}$$

(70)

$$\begin{aligned}&(F^{(0)}-\eta ) D^{(0)} F_{\eta }^{(0)}+\dfrac{1}{\gamma }\left( P_{\eta }^{(0)}+H_{\eta }^{(0)}+\dfrac{2 H^{(0)}}{\eta }\right) \nonumber \\&\quad -\dfrac{(q+2)}{2}F^{(0)} D^{(0)}-\dfrac{D^{(0)} (V^{(0)})^{2}}{\eta }=0, \end{aligned}$$

(71)

$$\begin{aligned}&P^{(0)}=\left[ \dfrac{2 \gamma (\gamma -1)}{(\gamma +1)^{2}}-\dfrac{2 \gamma ^{2} C_{0}}{(\gamma ^{2}-1)}\right] D^{(0)},\end{aligned}$$

(72)

$$\begin{aligned}&(F^{(0)}-\eta ) H_{\eta }^{(0)}-2 H^{(0)} + 2 H^{(0)} F_{\eta }^{(0)}=0, \end{aligned}$$

(73)

$$\begin{aligned}&(F^{(0)}-\eta ) V_{\eta }^{(0)} +\dfrac{1}{\eta } F^{(0)} V^{(0)}-\dfrac{(q+2)}{2}V^{(0)}=0,\end{aligned}$$

(74)

$$\begin{aligned}&(F^{(0)}-\eta ) W_{\eta }^{(0)}-\dfrac{(q+2)}{2}W^{(0)}=0. \end{aligned}$$

(75)

For the first power of $\phi$, we have the following set of equations

$$\begin{aligned}&(F^{(0)}-\eta ) D_{\eta }^{(1)} + F^{(1)} D_{\eta }^{(0)}+(q+2) D^{(1)}\nonumber \\&\quad +D^{(0)}\left( F_{\eta }^{(1)}+\dfrac{ F^{(1)}}{\eta }\right) + D^{(1)}\left( F_{\eta }^{(0)}+\dfrac{ F^{(0)}}{\eta }\right) \nonumber \\&\quad +q D^{(1)}=0, \end{aligned}$$

(76)

$$\begin{aligned}&F^{(1)}D^{(0)}F_{\eta }^{(0)}+(F^{(0)}-\eta )(D^{(1)}F_{\eta }^{(0)} +D^{(0)}F_{\eta }^{(1)})\nonumber \\&\quad +(q+2)F^{(1)}D^{(0)}-\dfrac{(q+2)}{2}[F^{(0)}D^{(1)}\nonumber \\&\quad +F^{(1)}D^{(0)}+\lambda _{1}F^{(0)}D^{(0)}]\nonumber \\&\quad +\dfrac{1}{\gamma }\left[ P_{\eta }^{(1)}+H_{\eta }^{(1)}+\dfrac{2 H^{(1)}}{\eta }\right] \nonumber \\&\quad -\dfrac{1}{\eta }[D^{(1)}(V^{(0)})^{2}+2V^{(0)}V^{(1)}D^{(0)}]=0, \end{aligned}$$

(77)

$$\begin{aligned}&P^{(1)}=\left[ \dfrac{2 \gamma (\gamma -1)}{(\gamma +1) ^{2}}\left\{ \dfrac{2}{(\gamma -1)}-\dfrac{(\gamma -1)}{2 \gamma }\right\} \right. \nonumber \\&\quad \left. +\dfrac{C_{0} \gamma }{(\gamma +1)}+\dfrac{C_{0} \gamma (\gamma +1)}{(\gamma -1)^{2}}\right] D^{(0)}\nonumber \\&\quad +\left[ \dfrac{2 \gamma (\gamma -1)}{(\gamma +1)^{2}}+\dfrac{C_{0} \gamma (\gamma -1)}{2 (\gamma +1)}-\dfrac{C_{0} \gamma (\gamma +1)}{2 (\gamma -1)} \right] D^{(1)}, \end{aligned}$$

(78)

$$\begin{aligned}&(F^{(0)}-\eta )H_{\eta }^{(1)}-(q+2)\lambda _{1} H^{(0)}+F^{(1)}H_{\eta }^{(0)} \nonumber \\&\quad +2H^{(0)}F_{\eta }^{(1)}+2H^{(1)} F_{\eta }^{(0)}+q H^{(1)}=0 , \end{aligned}$$

(79)

$$\begin{aligned}&(F^{(0)}-\eta )V_{\eta }^{(1)}+F^{(1)}V_{\eta }^{(0)}+(q+2)V^{(1)}\nonumber \\&\quad +\dfrac{1}{\eta }[F^{(0)}V^{(1)}+F^{(1)}V^{(0)}]\nonumber \\&\quad -\dfrac{(q+2)}{2} [\lambda _{1}V^{(0)}+V^{(1)}]=0, \end{aligned}$$

(80)

$$\begin{aligned}&(F^{(0)}-\eta )W_{\eta }^{(1)}+F^{(1)}W_{\eta }^{(0)}+(q+2)W^{(1)}\nonumber \\&\quad -\dfrac{(q+2)}{2}[\lambda _{1}W^{(0)}+W^{(1)}]=0. \end{aligned}$$

(81)

Using (63) in Equations (52)–(57), we obtain the shock jump conditions for zeroth power of $\phi$ as

$$\begin{aligned} F^{(0)}(1)&=\dfrac{2}{(\gamma +1)}, \quad D^{(0)}(1)=\dfrac{(\gamma +1)}{(\gamma -1)},\nonumber \\ P^{(0)}(1)&=\dfrac{2 \gamma }{(\gamma +1)}+\dfrac{C_{0} \gamma }{2}-\dfrac{\gamma C_{0} (\gamma +1)^{2}}{2 (\gamma -1)^{2}},\nonumber \\ H^{(0)}(1)&=\dfrac{1}{2}\gamma C_{0} \dfrac{(\gamma +1)^{2}}{(\gamma -1)^{2}},\nonumber \\ V^{(0)}(1)&=\dfrac{v^{*}(\rho ^{*}C_{0})^{1/2}}{(2h^{*})^{1/2}},\quad W^{(0)}(1)=\dfrac{w^{*}(\rho ^{*}C_{0})^{1/2}}{(2h^{*})^{1/2}}. \end{aligned}$$

(82)

The shock jump conditions for first power of $\phi$ are obtained as

$$\begin{aligned} F^{(1)}(1)&= \dfrac{-2}{(\gamma +1)}, \quad D^{(1)}(1)=-\dfrac{2(\gamma +1)}{(\gamma -1)^{2}}, \nonumber \\ P^{(1)}(1)&= \dfrac{-(\gamma -1)}{(\gamma +1)}+\dfrac{2 \gamma C_{0} (\gamma +1)^{2}}{ (\gamma -1)^{3}}, \nonumber \\ H^{(1)}(1)&= \dfrac{-2 \gamma C_{0} (\gamma +1)^{2}}{(\gamma -1)^{3}},\quad V^{(1)}(1)=0,\nonumber \\ W^{(1)}(1)&=\,0. \end{aligned}$$

(83)

The first step of the solution of the problem under consideration is to solve the system of ODEs (70)–(75) for $F^{(0)}$, $P^{(0)}$, $D^{(0)}$, $H^{(0)}$, $V^{(0)}$ and $W^{(0)}$ with the boundary conditions (82). We obtain the zeroth-order approximations to the solutions of the shock waves in the form

$$\begin{aligned} u&=U F^{(0)}(\eta ),\quad \rho =\rho _{0} D^{(0)}(\eta ),\nonumber \\ p&=p_{0} (U/C)^{2} P^{(0)}(\eta ), \nonumber \\ h&=p_{0} (U/C)^{2} H^{(0)}(\eta ),\quad v=U V^{(0)}(\eta ),\nonumber \\ w&=U W^{(0)}(\eta ). \end{aligned}$$

(84)

We obtain zeroth-order approximation to $J_{0}$ from (65) by substituting the values of $F^{(0)}$, $P^{(0)}$, $D^{(0)}$, $H^{(0)}$, $V^{(0)}$ and $W^{(0)}$.

Similarly to obtain the first-order approximation to the solution, we need to substitute the zeroth-order approximations $F^{(0)}$, $P^{(0)}$, $D^{(0)}$, $H^{(0)}$, $V^{(0)}$ and $W^{(0)}$ in Equations (76)–(81) to obtain a system of ordinary differential equations which involve an indeterminate parameter $\lambda _{1}$.

5 The zeroth-order approximation

We rewrite Equations (70)–(75) in the following form:

$$\begin{aligned}&D_{\eta }^{(0)}/D^{(0)}=\left( F_{\eta }^{(0)} +\dfrac{F^{(0)}}{\eta }+q\right) /(\eta -F^{(0)}) , \end{aligned}$$

(85)

$$\begin{aligned}&(F^{(0)}-\eta ) D^{(0)} F_{\eta }^{(0)}+\dfrac{1}{\gamma }\left( P_{\eta }^{(0)}+H_{\eta }^{(0)}+\dfrac{2 H^{(0)}}{\eta }\right) \nonumber \\&\quad -\dfrac{(q+2)}{2}F^{(0)} D^{(0)}-\dfrac{D^{(0)} (V^{(0)})^{2}}{\eta }=0, \end{aligned}$$

(86)

$$\begin{aligned}&P^{(0)}=\left[ \dfrac{2 \gamma (\gamma -1)}{(\gamma +1)^{2}}-\dfrac{4 \gamma ^{2} C_{0}}{2 (\gamma ^{2}-1)}\right] D^{(0)} ,\end{aligned}$$

(87)

$$\begin{aligned}&H_{\eta }^{(0)}/H^{(0)}=(2 F_{\eta }^{(0)}-2)/(\eta -F^{(0)}), \end{aligned}$$

(88)

$$\begin{aligned}&V_{\eta }^{(0)}/V^{(0)}=\dfrac{1}{(\eta -F^{(0)})} \left[ \dfrac{F^{(0)}}{\eta }-\dfrac{(q+2)}{2}\right] , \end{aligned}$$

(89)

$$\begin{aligned}&W_{\eta }^{(0)}/W^{(0)}=\dfrac{1}{(F^{(0)}-\eta )}\dfrac{(q+2)}{2}. \end{aligned}$$

(90)

Using Equations (85), (87) and (88) in Equation (86), we obtain

$$\begin{aligned}&F_{\eta }^{(0)}=\dfrac{\dfrac{(\eta -F^{(0)})}{\eta }D^{(0)}(V^{(0)})^{2}+\dfrac{(q+2)}{2}(\eta -F^{(0)})F^{(0)}D^{(0)}}{\left[ \dfrac{2(\gamma -1)}{(\gamma +1)^{2}}-\dfrac{2 \gamma C_{0}}{(\gamma ^{2}-1)}\right] D^{(0)}+\dfrac{2 H^{(0)}}{\gamma }-(\eta -F^{(0)})^{2}D^{(0)}}\nonumber \\&\qquad -\dfrac{\left[ \dfrac{2(\gamma -1)}{(\gamma +1)^{2}}-\dfrac{2 \gamma C_{0}}{(\gamma ^{2}-1)}\right] D^{(0)}\left( \dfrac{F^{(0)}}{\eta }+q\right) +\dfrac{2 H^{(0)}}{\gamma }-\dfrac{2 H^{(0)}(\eta -F^{(0)})}{\eta \gamma }}{\left[ \dfrac{2(\gamma -1)}{(\gamma +1)^{2}}-\dfrac{2 \gamma C_{0}}{(\gamma ^{2}-1)}\right] D^{(0)}+\dfrac{2 H^{(0)}}{\gamma }-(\eta -F^{(0)})^{2}D^{(0)}}. \end{aligned}$$

(91)

Using Equation (82), the above Equation (91) becomes

$$\begin{aligned}&F_{\eta }^{(0)}(1)=\dfrac{\dfrac{v^{*2}\rho ^{*}C_{0}}{2 h^{*}}+\dfrac{(q+2)}{(\gamma +1)}-\dfrac{(\gamma +1)}{(\gamma -1)}\left[ \dfrac{2(\gamma -1)}{(\gamma +1)^{2}}-\dfrac{2 \gamma C_{0}}{(\gamma ^{2}-1)}\right] \left[ \dfrac{2}{(\gamma +1)}+q\right] -\dfrac{C_{0} (\gamma +1)}{(\gamma -1)}+\dfrac{C_{0} (\gamma +1)^{2}}{(\gamma -1)^{2}}}{\left[ \dfrac{2(\gamma -1)}{(\gamma +1)^{2}}-\dfrac{2 \gamma C_{0}}{(\gamma ^{2}-1)}\right] \dfrac{(\gamma +1)}{(\gamma -1)}+\dfrac{C_{0}(\gamma +1)^{2}}{(\gamma -1)^{2}}-\dfrac{(\gamma -1)}{(\gamma +1)}}.\nonumber \\ \end{aligned}$$

(92)

Also from (60)–(62) and using (89) and (90), the non-dimensional components of the vorticity vector for zeroth order approximation are obtained as

$$\begin{aligned}&l_{r}^{(0)}=0, \end{aligned}$$

(93)

$$\begin{aligned}&l_{\theta }^{(0)}=\dfrac{1}{4}(q+2)\dfrac{W^{(0)}}{(\eta -F^{(0)})}, \end{aligned}$$

(94)

$$\begin{aligned}&l_{z}^{(0)}=\dfrac{1}{2 \eta }\left[ V^{(0)}+\dfrac{(q+2) \eta V^{(0)}}{2 (F^{(0)}-\eta )}-\dfrac{F^{(0)}V^{(0)}}{(F^{(0)}-\eta )}\right] . \end{aligned}$$

(95)

Following Taylor (1950a), the approximate solution of $F^{(0)}$ of F is supposed to be of the form

$$\begin{aligned} F^{(0)}(\eta )=\dfrac{\eta }{\gamma }+A \eta ^{n}, \end{aligned}$$

(96)

where A and n are constants. Using Equations (96) and (82), the constant A is given by

$$\begin{aligned} A=\dfrac{(\gamma -1)}{\gamma (\gamma +1)}. \end{aligned}$$

(97)

Substituting the value of $F_{\eta }^{(0)}$ at $\eta =1$ from (92) in (96), and using value of A from Equation (97), we obtain the value of n as

$$\begin{aligned} n= & {} \dfrac{\gamma (\gamma +1)}{(\gamma -1)}\nonumber \\&\times \left\{ \dfrac{\dfrac{v^{*2}\rho ^{*}C_{0}}{2 h^{*}}+\dfrac{(q+2)}{(\gamma +1)}-\dfrac{(\gamma +1)}{(\gamma -1)}\left[ \dfrac{2(\gamma -1)}{(\gamma +1)^{2}}-\dfrac{2 \gamma C_{0}}{(\gamma ^{2}-1)}\right] \left( \dfrac{2}{(\gamma +1)}+q\right) -\dfrac{C_{0} (\gamma +1)}{(\gamma -1)}+\dfrac{C_{0}(\gamma +1)^{2}}{(\gamma -1)^{2}}}{\left[ \dfrac{2(\gamma -1)}{(\gamma +1)^{2}}-\dfrac{2 \gamma C_{0}}{(\gamma ^{2}-1)}\right] \dfrac{(\gamma +1)}{(\gamma -1)}+\dfrac{C_{0}(\gamma +1)^{2}}{(\gamma -1)^{2}}-\dfrac{(\gamma -1)}{(\gamma +1)}}-\dfrac{1}{\gamma }\right\} .\nonumber \\ \end{aligned}$$

(98)

Further substituting Equation (96) with values of A and n from (97) and (98) into Equations (85) and (87)–(90), these equations are integrated to yield

$$\begin{aligned}&D^{(0)}(\eta )=\dfrac{(\gamma +1)}{(\gamma -1)}\eta ^{\left\{ \dfrac{(2+q \gamma )}{(\gamma -1)} \right\} }\nonumber \\&\quad \left[ \dfrac{\gamma }{\gamma +1-\eta ^{n-1}} \right] ^{\left\{ \dfrac{(2+q \gamma )}{(n-1)(\gamma -1)}+\dfrac{(n+1)}{(n-1)} \right\} }, \end{aligned}$$

(99)

$$\begin{aligned}&P^{(0)}(\eta )=\left[ \dfrac{2\gamma (\gamma -1)}{(\gamma +1)^{2}}-\dfrac{2 \gamma ^{2} C_{0}}{(\gamma ^{2}-1)}\right] D^{(0)}(\eta ),\end{aligned}$$

(100)

$$\begin{aligned}&H^{(0)}(\eta )=\dfrac{\gamma C_{0} (\gamma +1)^{2}}{2 (\gamma -1)^{2}}\eta ^{-2} \left[ \dfrac{\gamma }{\gamma +1-\eta ^{n-1}}\right] ^{2},\end{aligned}$$

(101)

$$\begin{aligned}&V^{(0)}(\eta )=\dfrac{v^{*}(\rho ^{*}C_{0})^{1/2}}{(2h^{*})^{1/2}}\nonumber \\&\quad \left[ \dfrac{\gamma }{\gamma +1-\eta ^{n-1}}\right] ^{\left\{ \dfrac{2-\gamma (q+2)}{2(\gamma -1)(n-1)}+\dfrac{1}{(n-1)} \right\} }\nonumber \\&\qquad \eta ^{\left\{ \dfrac{2-\gamma (q+2)}{2(\gamma -1)}\right\} },\end{aligned}$$

(102)

$$\begin{aligned}&W^{(0)}(\eta )=\dfrac{w^{*}(\rho ^{*}C_{0})^{1/2}}{(2h^{*})^{1/2}}\nonumber \\&\quad \left[ \dfrac{\gamma }{\gamma +1-\eta ^{n-1}}\right] ^{\dfrac{\gamma (q+2)}{2(\gamma -1)(1-n)}}\eta ^{\dfrac{-\gamma (q+2)}{2(\gamma -1)}}, \end{aligned}$$

(103)

where the boundary conditions (82) are used to determine the integration constants.

6 The first-order approximation

In this section, we shall derive the system of differential equations for the first-order approximation $F^{(1)}$, $P^{(1)}$, $D^{(1)}$, $H^{(1)}$, $V^{(1)}$, $W^{(1)}$ to the flow variables F, P, D, H, V and W. We have the system of Equations (76)–(81) and the boundary conditions (83).

Splitting $F^{(1)}$, $P^{(1)}$, $D^{(1)}$, $H^{(1)}$, $V^{(1)}$ and $W^{(1)}$ as

$$\begin{aligned} F^{(1)}= & {} F_{1}^{(1)}+\lambda _{1}F_{2}^{(1)},\quad D^{(1)}=D_{1}^{(1)}+\lambda _{1}D_{2}^{(1)}, \nonumber \\ P^{(1)}= & {} P_{1}^{(1)}+\lambda _{1}P_{2}^{(1)}, \nonumber \\ H^{(1)}= & {} H_{1}^{(1)}+\lambda _{1}H_{2}^{(1)},\quad V^{(1)}=V_{1}^{(1)}+\lambda _{1}V_{2}^{(1)},\nonumber \\ W^{(1)}= & {} W_{1}^{(1)}+\lambda _{1}W_{2}^{(1)}, \end{aligned}$$

(104)

and using (104) in (76)–(81), we get two set of equations for $F_{1}^{(1)}$, $P_{1}^{(1)}$, $D_{1}^{(1)}$, $H_{1}^{(1)}$, $V_{1}^{(1)}$, $W_{1}^{(1)}$ and $F_{2}^{(1)}$, $P_{2}^{(1)}$, $D_{2}^{(1)}$, $H_{2}^{(1)}$, $V_{2}^{(1)}$, $W_{2}^{(1)}$, independent of $\lambda _{1}$.

For zeroth power of $\lambda _{1}$, we have the set of equations

$$\begin{aligned}&(F^{(0)}-\eta )D_{1\eta }^{(1)}+F_{1}^{(1)}D_{\eta }^{(0)}+(q+2)D_{1}^{(1)}\nonumber \\&\quad +D^{(0)}\left[ F_{1\eta }^{(1)}+\dfrac{F_{1}^{(1)}}{\eta }\right] +D_{1}^{(1)}\left[ F_{\eta }^{(0)}+\dfrac{F^{(0)}}{\eta }\right] \nonumber \\&\quad +qD_{1}^{(1)}=0, \end{aligned}$$

(105)

$$\begin{aligned}&F_{1}^{(1)}D^{(0)}F_{\eta }^{(0)}+(F^{(0)}-\eta )[D_{1}^{(1)}F_{\eta }^{(0)} +D^{(0)}F_{1\eta }^{(1)}]\nonumber \\&\quad +(q+2)D^{(0)}F_{1}^{(1)}-\dfrac{(q+2)}{2}[F_{1}^{(1)}D^{(0)}+F^{(0)}D_{1}^{(1)}] \nonumber \\&\quad +\dfrac{1}{\gamma }\left[ P_{1\eta }^{(1)}+H_{1\eta }^{(1)}+\dfrac{2 H_{1}^{(1)}}{\eta }\right] \nonumber \\&\quad -\dfrac{1}{\eta }[V^{(0)2}D_{1}^{(1)}+2V^{(0)}D^{(0)}V_{1}^{(1)}]=0, \end{aligned}$$

(106)

$$\begin{aligned}&P_{1}^{(1)}=\left[ \dfrac{2 \gamma (\gamma -1)}{(\gamma +1) ^{2}}\left\{ \dfrac{2}{(\gamma -1)}-\dfrac{(\gamma -1)}{2 \gamma }\right\} \right. \nonumber \\&\quad \left. +\dfrac{C_{0} \gamma }{(\gamma +1)}+\dfrac{C_{0} \gamma (\gamma +1)}{(\gamma -1)^{2}}\right] D^{(0)}\nonumber \\&\quad +\left[ \dfrac{2 \gamma (\gamma -1)}{(\gamma +1)^{2}}+\dfrac{C_{0} \gamma (\gamma -1)}{2 (\gamma +1)}-\dfrac{C_{0} \gamma (\gamma +1)}{2 (\gamma -1)} \right] D_{1}^{(1)}, \end{aligned}$$

(107)

$$\begin{aligned}&(F^{(0)}-\eta )H_{1\eta }^{(1)}+F_{1}^{(1)}H_{\eta }^{(0)} +2H^{(0)}F_{1\eta }^{(1)}+\nonumber \\&\quad +2H_{1}^{(1)}F_{\eta }^{(0)}+q H_{1}^{(1)}=0, \end{aligned}$$

(108)

$$\begin{aligned}&(F^{(0)}-\eta )V_{1\eta }^{(1)}+F_{1}^{(1)}V_{\eta }^{(0)} +(q+2)V_{1}^{(1)}\nonumber \\&\quad +\dfrac{1}{\eta }[F^{(0)}V_{1}^{(1)}+F_{1}^{(1)}V^{(0)}] -\dfrac{(q+2)}{2}V_{1}^{(1)}=0, \end{aligned}$$

(109)

$$\begin{aligned}&F_{1}^{(1)}W_{\eta }^{(0)}+(F^{(0)}-\eta )W_{1\eta }^{(1)} +\dfrac{(q+2)}{2}W_{1}^{(1)}=0, \end{aligned}$$

(110)

and for first power of $\lambda _{1}$, we have

$$\begin{aligned}&(F^{(0)}-\eta )D_{2\eta }^{(1)}+F_{2}^{(1)}D_{\eta }^{(0)} +(q+2)D_{2}^{(1)}\nonumber \\&\quad +D^{(0)}\left[ F_{2\eta }^{(1)} +\dfrac{F_{2}^{(1)}}{\eta }\right] +D_{2}^{(1)}\left[ F_{\eta }^{(0)} +\dfrac{F^{(0)}}{\eta }\right] \nonumber \\&\quad +qD_{2}^{(1)}=0, \end{aligned}$$

(111)

$$\begin{aligned}&F_{2}^{(1)}D^{(0)}F_{\eta }^{(0)}+(F^{(0)}-\eta )[D_{2}^{(1)} F_{\eta }^{(0)}+D^{(0)}F_{2\eta }^{(1)}]\nonumber \\&\quad +(q+2)D^{(0)}F_{2}^{(1)} -\dfrac{(q+2)}{2}[F_{2}^{(1)}D^{(0)}\nonumber \\&\quad +F^{(0)}D_{2}^{(1)}+F^{(0)}D^{(0)}] \nonumber \\&\quad +\dfrac{1}{\gamma }\left[ P_{2\eta }^{(1)}+H_{2\eta }^{(1)}+\dfrac{2 H_{2}^{(1)}}{\eta }\right] \nonumber \\&\quad -\dfrac{1}{\eta }[V^{(0)2}D_{2}^{(1)}+2V^{(0)}D^{(0)}V_{2}^{(1)}]=0, \end{aligned}$$

(112)

$$\begin{aligned}&P_{2}^{(1)}=\left[ \dfrac{2 \gamma (\gamma -1)}{(\gamma +1)^{2}} +\dfrac{C_{0} \gamma (\gamma -1)}{2(\gamma +1)}-\dfrac{C_{0} \gamma (\gamma +1)}{2(\gamma -1)}\right] D_{2}^{(1)},\end{aligned}$$

(113)

$$\begin{aligned}&(F^{(0)}-\eta )H_{2\eta }^{(1)}-(q+2)H^{(0)}+F_{2}^{(1)}H_{\eta }^{(0)}\nonumber \\&\quad +2H^{(0)}F_{2\eta }^{(1)}+2H_{2}^{(1)}F_{\eta }^{(0)}+q H_{2}^{(1)}=0,\end{aligned}$$

(114)

$$\begin{aligned}&(F^{(0)}-\eta )V_{2\eta }^{(1)}+F_{2}^{(1)}V_{\eta }^{(0)}+(q+2)V_{2}^{(1)}\nonumber \\&\quad +\dfrac{1}{\eta }[F^{(0)}V_{2}^{(1)}+F_{2}^{(1)}V^{(0)}]\nonumber \\&\quad -\dfrac{(q+2)}{2}[V_{2}^{(1)}+V^{(0)}]=0, \end{aligned}$$

(115)

$$\begin{aligned}&F_{2}^{(1)}W_{\eta }^{(0)}+(F^{(0)}-\eta )W_{2\eta }^{(1)}-\dfrac{(q+2)}{2}[W_{2}^{(1)}\nonumber \\&\quad +W^{(0)}]+(q+2)W_{2}^{(1)}=0. \end{aligned}$$

(116)

Substituting the values from (104) in (83) and equating to zero the coefficient of zeroth and first power of $\lambda _{1}$, we obtain

$$\begin{aligned} F_{1}^{(1)}(1)&=\dfrac{-2}{(\gamma +1)},\quad D_{1}^{(1)}(1)=\dfrac{-2(\gamma +1)}{(\gamma -1)^{2}},\nonumber \\ P_{1}^{(1)}(1)&=\dfrac{-(\gamma -1)}{(\gamma +1)}+\dfrac{2 \gamma C_{0} (\gamma +1)^{2}}{(\gamma -1)^{3}},\nonumber \\ H_{1}^{(1)}(1)&=\dfrac{-2 \gamma C_{0} (\gamma +1)^{2}}{(\gamma -1)^{3}},\quad V_{1}^{(1)}(1)=0, \nonumber \\ W_{1}^{(1)}(1)&=0 \end{aligned}$$

(117)

and

$$\begin{aligned} F_{2}^{(1)}(1)= & {} 0,\quad D_{2}^{(1)}(1)=0,\quad P_{2}^{(1)}(1)=0,\quad \nonumber \\ H_{2}^{(1)}(1)= & {} 0,\quad V_{2}^{(1)}(1)=0, \quad W_{2}^{(1)}(1)=0. \end{aligned}$$

(118)

By using (96), (99)–(103), (117) and (118), the system of Equations (105)–(110) for $F_{1}^{(1)}$, $D_{1}^{(1)}$, $P_{1}^{(1)}$, $H_{1}^{(1)}$, $V_{1}^{(1)}$, $W_{1}^{(1)}$ and the system of Equations (111)–(116) for $F_{2}^{(1)}$, $D_{2}^{(1)}$, $P_{2}^{(1)}$, $H_{2}^{(1)}$, $V_{2}^{(1)}$, $W_{2}^{(1)}$ can be integrated numerically. After substituting the values of $F_{1}^{(1)}$, $D_{1}^{(1)}$, $P_{1}^{(1)}$, $H_{1}^{(1)}$, $V_{1}^{(1)}$, $W_{1}^{(1)}$ and $F_{2}^{(1)}$, $D_{2}^{(1)}$, $P_{2}^{(1)}$, $H_{2}^{(1)}$, $V_{2}^{(1)}$, $W_{2}^{(1)}$ obtained above in (66), we have the following equation to determine $\lambda _{1}$,

$$\begin{aligned} \lambda _{1}=\dfrac{I_{1}-\dfrac{1}{2(\gamma -1)}}{J_{0}-\dfrac{\gamma C_{0}}{4}-\dfrac{\gamma }{4}\left( \dfrac{v^{*2}+w^{*2}}{B^{2}}\right) -I_{2}}, \end{aligned}$$

(119)

where

$$\begin{aligned} I_{1}= & {} \int _{0}^{1} \left\{ \dfrac{\gamma }{2} D_{1}^{(1)} [(F^{(0)})^{2}+(V^{(0)})^{2}+(W^{(0)})^{2}]\right. \\&+\gamma [F^{(0)}F_{1}^{(1)}+V^{(0)}V_{1}^{(1)}+W^{(0)}W_{1}^{(1)}]D^{(0)}\\&\left. +\dfrac{1}{(\gamma -1)}P_{1}^{(1)}+ H_{1}^{(1)}\right\} \eta \mathrm{d}\eta , \end{aligned}$$

and

$$\begin{aligned} I_{2}= & {} \int _{0}^{1} \left\{ \dfrac{\gamma }{2} D_{2}^{(1)} [(F^{(0)})^{2}+(V^{(0)})^{2}+(W^{(0)})^{2}]\right. \\&+\gamma [F^{(0)}F_{2}^{(1)}+V^{(0)}V_{2}^{(1)}+W^{(0)}W_{2}^{(1)}]D^{(0)}\\&\left. +\dfrac{1}{(\gamma -1)}P_{2}^{(1)}+ H_{2}^{(1)}\right\} \eta \mathrm{d}\eta . \end{aligned}$$

With the above values of $\lambda _{1}$ and $F_{1}^{(1)}$, $D_{1}^{(1)}$, $P_{1}^{(1)}$, $H_{1}^{(1)}$, $V_{1}^{(1)}$, $W_{1}^{(1)}$ and $F_{2}^{(1)}$, $D_{2}^{(1)}$, $P_{2}^{(1)}$, $H_{2}^{(1)}$, $V_{2}^{(1)}$, $W_{2}^{(1)}$ we can calculate $F^{(1)}$, $D^{(1)}$, $P^{(1)}$, $H^{(1)}$, $V^{(1)}$, $W^{(1)}$ using (104).

7 Results and discussion

In the case of zeroth order approximate analytical solution, the distributions of the flow variables radial fluid velocity $F^{(0)}$, density $D^{(0)}$, pressure $P^{(0)}$, magnetic pressure $H^{(0)}$, azimuthal fluid velocity $V^{(0)}$ and axial fluid velocity $W^{(0)}$, are drawn using Equations (96) and (99)–(103) and are shown in Figures 1(a)–(f). The zeroth approximation of non-dimensional components of vorticity vector $l_{\theta }^{(0)}$ and $l_{z}^{(0)}$, are drawn using Equations (94) and (95) respectively and are illustrated in Figures 1(g)–(h). The values of shock Cowling number $C_{0}$ are taken to be 0.01, 0.04; and the values of ambient density variation index q to be $-1.7, -1.82$ for calculations. The values of adiabatic exponent $\gamma$ are taken to be as 5/3 and 4/3. For fully ionized gas $\gamma = 5/3$ and for relativistic gases $\gamma = 4/3$, which are applicable to the interstellar medium. These two values of $\gamma$ mark the most general range of values seen in real stars.

The effect of shock Cowling number $C_{0}$, ambient density variation index q and adiabatic exponent $\gamma$ for cylindrical shock on the zeroth approximate solution of physical quantities are illustrated in Table 1 and Figures 1 and 2. Table 1 exhibits the values of n and zeroth approximation for total energy of disturbance $J_{0}$ in case of cylindrical shock for different values of $C_{0}$, q and $\gamma$. From Table 1, it is obtained that with increase in $C_{0}$ or q, the value of n decreases; whereas with increase in $\gamma$, the value of n increases. Also it is obtained that due to consideration of magnetic pressure, the total energy of disturbance for zeroth order increases, i.e. the shock strength decreases; whereas increase in ambient density variation index or adiabatic exponent decreases the total energy of disturbance for zeroth order, i.e. there is increase in shock strength. Figures 1 and 2 exhibit the distribution of zeroth order analytical solutions of flow variables radial fluid velocity $F^{(0)}$, density $D^{(0)}$, pressure $P^{(0)}$, magnetic pressure $H^{(0)}$, azimuthal fluid velocity $V^{(0)}$, axial fluid velocity $W^{(0)}$ and non-dimensional components of vorticity vector $l_{\theta }^{(0)}$ and $l_{z}^{(0)}$ for different values of $\gamma$, $C_{0}$ and q. From Figures 1 and 2, it is shown that as we move inwards from the shock front towards the axis of symmetry, the radial fluid velocity, azimuthal fluid velocity and axial component of vorticity vector $l_{z}^{(0)}$ decrease and tend to zero; whereas density, pressure, magnetic pressure, axial fluid velocity and azimuthal component of voticity vector $l_{\theta }^{(0)}$ increase. From Figure 1, it is obtained that variation in values of $C_{0}$ and q have similar effects on flow variables: pressure, azimuthal and axial components of fluid velocity and azimuthal component of vorticity vector $l_{\theta }^{(0)}$. However increase in value of $\gamma$ has reverse effect on pressure, axial fluid velocity and azimuthal component of vorticity vector $l_{\theta }^{(0)}$ as the effect of $C_{0}$ or q on these flow variables.

The importance of constructing analytical or exact solutions in mathematical physics and applied mathematics is that they can be used to classify and understand the nonlinear phenomena. The potential applications of this study could include analysis of data from exploding wire experiments, and axially symmetric hypersonic flow problems associated with meteors or re-entry vehicles (see Hutchens 1995; Nath 2012b, 2014b, 2015).

The higher order approximate analytical solutions can be obtained by using the approach of Sakurai (1954). However, in most of the cases, the first order or higher order solutions cannot be obtained analytically. For obtaining first- or higher-order solutions, implementation of a numerical scheme is required which requires the complete solution of zeroth order equations.

7.1 Effects of increase in value of shock Cowling number $C_{0}$ on zeroth approximate solution of flow variables

Magnetic pressure, azimuthal fluid velocity, axial fluid velocity, azimuthal and axial components of vorticity vector $l_{\theta }^{(0)}$ and $l_{z}^{(0)}$ increase with increase in $C_{0}$ (see Figures 1(d)–(h)); whereas pressure decreases (see Figure 1(c)). There is slight increase in radial fluid velocity (see Figure 1(a)) with increase in $C_{0}$. Density is not affected with variation in $C_{0}$ (see Figure 1(b)).

7.2 Effects of increase in value of ambient density variation index q on on zeroth approximate solution of flow variables

The azimuthal fluid velocity, axial fluid velocity and azimuthal component of vorticity vector $l_{\theta }^{(0)}$ increase (see Figure 1(e)–(g)) with increase in q; whereas density and pressure decrease (see Figure 1(b),(c)) with increase in q. A small change in q does not affect radial fluid velocity significantly (see Figure 1(a)). The magnetic pressure is not affected with variation in q (see Figure 1(d)). The axial component of vorticity vector $l_{z}^{(0)}$ increases in general (see Figure 1(h)).

7.3 Effects of increase in value of adiabatic exponent $\gamma$ on zeroth approximate solution of flow variables

With increase in $\gamma$, the flow variables radial fluid velocity, magnetic pressure, axial fluid velocity and azimuthal component of vorticity vector $l_{\theta }^{(0)}$ decrease (see Figures 2(a), (d), (f), (g)); whereas pressure and azimuthal fluid velocity increase (see Figure 2(c), (e)). Density decreases near shock but increases as we move inwards from the shock to the axis of symmetry (see Figure 2(b)). The axial component of vorticity vector $l_{z}^{(0)}$ decreases near shock but increases near the axis of symmetry as we move inwards from shock to the axis of symmetry (see Figure 2(h)).

8 Conclusions

In the present problem, we have obtained the zeroth order approximate analytical solutions for cylindrically symmetric motion of a magnetogasdynamic shock in axisymmetric perfect gas under isothermal flow condition. The approximate analytical representation and the distribution of the flow variables are obtained. Pre-supposing the gas dynamical model for cylindrical geometry, under the influence of azimuthal magnetic field in a rotating medium can be fruitful for the study of experiments on pinch effect, exploding wires, and so forth. Study of cylindrical shock waves is not only associated with the explosion of a long thin wire but also to certain axially symmetrical hypersonic flow problems, such as the shock envelope behind a fast meteor, or missile (see Lin 1954). From the present study, we can conclude the following:

• (i) The increase in value of $C_{0}$ increases the magnetic pressure, azimuthal fluid velocity, axial fluid velocity, $l_{\theta }^{(0)}$ and $l_{z}^{(0)}$; however it decreases the pressure.

• (ii) Increase in value of q has similar effect as that of ambient magnetic pressure on flow variables pressure, azimuthal fluid velocity, axial fluid velocity and $l_{\theta }^{(0)}$.

• (iii) Increase in value of $\gamma$ has reverse effect as that of ambient magnetic pressure on flow variables pressure, magnetic pressure, axial fluid velocity and $l_{\theta }^{(0)}$.

• (iv) From the figures, it obtained that as we move inwards from the shock front towards the axis of symmetry, the radial fluid velocity, azimuthal fluid velocity and axial component of vorticity vector $l_{z}^{(0)}$ decrease and tend to zero; whereas density, pressure, magnetic pressure, axial fluid velocity and azimuthal component of vorticity vector $l_{\theta }^{(0)}$ increase.

• (v) Consideration of magnetic pressure increases the total energy of disturbance of zeroth order while with increase in ambient density variation index or adiabatic exponent, the total energy of disturbance decreases.