1 Introduction

Many observational evidences such as data from type Ia supernovae (Riess et al. 1998; Perlmutter et al. 1999a; 2003; de Bernardis et al. 2000), Cosmic Microwave Background (CMB) (Spergel et al. 2003, 2007) and Sloan Digital Sky Survey (SDSS) (Tegmark et al. 2004a, b) have suggested to accept the fact that the universe is currently experiencing a phase of accelerated expansion. This expansion is due to unknown energy having negative pressure called dark energy (DE). The DE equation of state is \(p=\omega _D \rho \), where \(\omega _D ({<}0)\) is not necessarily constant. There are many candidates of DE such as cosmological constant \(\Lambda \, (\omega _D ={-}1)\) (Carroll 2001; Perlmutter et al. 2003; Astier et al. 2006), quintessence (Wetterich 1988; Ratra & Peebles 1988), K-essence (Chiba et al. 2000; Armendariz-Picon et al. 2001), phantom (Caldwell et al. 2003; Nojiri et al. 2006), quintom (Feng et al. 2005), tachyon (Padmanabhan 2002; Bagla et al. 2003; Guo & Zhang 2004; Copeland et al. 2005), holographic DE (Li 2004; Wang et al. 2005; Makarenko & Myagky 2018; Santhi et al. 2018), agegraphic DE (Cai 2007; Wei & Cai 2008), two fluid DE (Chirde & Shekh 2016; Katore & Kapse 2018), anisotropic DE (Akarsu & Kilinc 2010; Katore & Sancheti 2011; Katore & Hatkar 2015; Pawar & Solanke 2014; Mahanta & Sharma 2017) and many others.

In recent years, attention has been paid to the so-called ‘scalar-tensor gravity’, as the Einstein theory of gravity is having some problems in finding gravity accurately on all scales. One of the problems concerning general relativity was that it could not describe the accelerated expansion of the universe accurately (Perlmutter et al. 1999a, b; Riess et al. 2004). Besides, it is inconsistent with Mach’s principle. The scalar tensor theory by Brans and Dicke (1961) accommodates the Mach’s principle and it can pass the experimental tests from the solar system (Bertotti et al. 2003) and provide an explanation for the accelerated expansion of the universe (Mathiazhagan & Johri 1984; La & Steinhardt 1989; Das & Banerjee 2008). Recently, Reddy and Lakshmi (2015), Rao and Prasanthi (2016), Singh and Dewri (2016) and Naidu et al. (2018) have studied the cosmological models in the Brans–Dicke (BD) theory of gravitation.

The Friedmann–Robertson–Walker (FRW) cosmological models play an important role in cosmology. These models are established on the basis of isotropy and homogeneity of the universe. The FRW universe with two fluid DE has been extensively studied by several authors. Zang (2005) investigated an interacting two-fluid scenario for quintom DE. The tachyon cosmology in interacting and non-interacting cases in non-flat FRW universe was studied by Setare et al. (2009). An interacting and non-interacting two-fluid scenario for DE with constant deceleration parameter has been studied by Pradhan et al. (2011). An interacting two-fluid scenario for DE has been investigated by Amirhashchi et al. (2011a). Amirhashchi et al. (2011b) proposed an interacting and non-interacting two-fluid scenario for DE models with time-dependent deceleration parameter. Harko and Lobo (2011) investigated the possibility that dark matter is a mixture of two non-interacting perfect fluid with different four velocities and thermodynamics parameter. The two-fluid scenarios for DE models in an FRW universe have been studied by Saha et al. (2012). Amirhashchi et al. (2013) studied interacting two-fluid viscous DE models in a non-flat universe. Reddy and Santhi (2013) studied the evolution of two-fluid scenario for DE model in scalar-tensor theory of gravitation formulated by Saez and Ballester. Motivated by the above discussions, in this paper, we have considered the spatially homogeneous and isotropic FRW universe filled with barotropic fluid and DE in BD theory of gravitation.

This paper is organized as follows. In Section 2, we have proposed the metric and field equations for FRW space-time in the BD theory. The solutions of the field equations are obtained in Section 3. In Section 4, we have discussed the physical and geometrical properties of the derived models. Finally, conclusions are made in Section 5.

2 The metric and Brans–Dicke field equations

The line element for the homogeneous and isotropic FRW space-time is given by

$$\begin{aligned} \mathrm{d}s^{2}=-\mathrm{d}t^{2}+a^{2}(t)\left[ {\frac{\mathrm{d}r^{2}}{1\!-\!kr^{2}}\!+\! r^{2}(\mathrm{d}\theta ^{2}\!+\! \sin ^{2}\theta \mathrm{d}\Phi ^{2})} \right] , \end{aligned}$$
(1)

where \(a\left( t \right) \) is the scale factor and k is the curvature constant, \(k=-1, \,k=0,\,k=+1\) indicate open, flat and closed universe respectively.

The BD field equations are

$$\begin{aligned}&R_{ij} -\frac{1}{2}g_{ij} R-{\bar{\omega }}\varphi ^{-2}\left( {\varphi _{,i} \varphi _{,j} -\frac{1}{2}g_{ij} \varphi ^{,k}\varphi _{,k} } \right) \nonumber \\&\quad -\,\varphi ^{-1}(\varphi _{i;j} -g_{ij} \varphi _{;k}^{,k} )=\varphi ^{-1}(T_{ij} ) \end{aligned}$$
(2)

and

$$\begin{aligned} \phi _{;k}^k =\frac{T}{3+2{\bar{\omega }}}, \end{aligned}$$
(3)

where R is the Ricci scalar, \(R_{ij} \) is the Ricci tensor, \(\varphi \) is the BD scalar field, \({\bar{\omega }}\) is the BD parameter and T is the trace of energy momentum tensor \(T_{ij} \). For the line element (1), the field equations (2) and (3) lead to the following set of equations:

$$\begin{aligned} \frac{p_{\mathrm{tot}} }{\varphi }= & {} -\left( {2\frac{{\ddot{a}}}{a}+\frac{\dot{a}^{2}}{a^{2}}+\frac{k}{a^{2}}+\frac{\bar{{\omega }}}{2}\frac{\dot{\varphi }^{2}}{\varphi ^{2}}+\frac{\ddot{\varphi }}{\varphi }+2\frac{\dot{a}}{a}\frac{\dot{\varphi }}{\varphi }} \right) ,\nonumber \\ \end{aligned}$$
(4)
$$\begin{aligned} \frac{\rho _{\mathrm{tot}} }{\varphi }= & {} 3\frac{\dot{a}^{2}}{a^{2}}+3\frac{k}{a^{2}}-\frac{\bar{{\omega }}}{2}\frac{\dot{\varphi }^{2}}{\varphi ^{2}}+3\frac{\dot{a}}{a}\frac{\dot{\varphi }}{\varphi } \end{aligned}$$
(5)

and

$$\begin{aligned} {\ddot{\varphi }}+3\frac{\dot{a}}{a}\dot{\varphi }=\frac{\rho _{\mathrm{tot}} -3p_{\mathrm{tot}} }{3+2{\bar{\omega }}}, \end{aligned}$$
(6)

where \(p_{\mathrm{tot}} =p_m +p_D \) and \(\rho _{\mathrm{tot}} =\rho _m +\rho _D.\) Here \(p_m \) and \(\rho _m \) are the pressure and energy densities of the barotropic fluid respectively, whereas \(p_D \) and \(\rho _D \) are the pressure and energy densities of the dark fluid respectively.

The energy conservation equation \(T_{;j}^{ij} =0\) leads to

$$\begin{aligned} {{\dot{\rho }}}_{\mathrm{tot}} +3\frac{\dot{a}}{a}(\rho _{\mathrm{tot}} +p_{\mathrm{tot}} )=0. \end{aligned}$$
(7)

The equation of state (EoS) parameters of the barotropic fluid and dark energy are given by

$$\begin{aligned} \omega _m =\frac{p_m }{\rho _m } \quad \mathrm{and} \quad \omega _D =\frac{p_D }{\rho _D}. \end{aligned}$$
(8)

Here the EoS parameter is assumed to be a constant with values \(\,0,\,\frac{1}{3}\) and \(+1\) for dust, radiation and stiff matter dominated universe respectively. In general, it is a function of time or redshift.

We have assumed that there is no interaction between DE and barotropic fluid. Therefore, the energy conservation equation (7) leads to

$$\begin{aligned} {\dot{\rho }}_m +3\frac{\dot{a}}{a}(1+\omega _m )\rho _m =0 \end{aligned}$$
(9)

and

$$\begin{aligned} {\dot{\rho }}_D +3\frac{\dot{a}}{a}(1+\omega _D )\rho _D =0. \end{aligned}$$
(10)

Using Equation (9), the energy density for barotropic fluid is given by

$$\begin{aligned} \rho _m =\rho _0 a^{-3(1+\omega _m )}, \end{aligned}$$
(11)

where \(\rho _0 \) is an integrating constant.

3 Solutions of field equations

There are three linearly independent equations (4)–(6) having six variables. The system is thus initially undetermined and we need additional constraint to solve it. In order to solve these field equations, we first assume the power-law relation between scale factor a and scalar field \(\varphi \) (Pimentel 1985; Johri & Desikan 1994) as \(\varphi \propto a^{\varepsilon },\) where \(\varepsilon \) is any integer, which implies that

$$\begin{aligned} \varphi =\varphi _0 \,a^{\varepsilon }, \end{aligned}$$
(12)

where \(\varphi _0 \,>0\) is the constant of proportionality.

Here we have discussed three models.

3.1 Model-I (Constant deceleration parameter)

We apply the special law of variation for the generalized Hubble’s parameter, which leads to constant value of deceleration parameter q. We consider that the mean Hubble parameter H is related to the scale factor a by the relation (Berman 1983; Agrawal & Pawar 2017; Chirde & Shekh 2018)

$$\begin{aligned} H=Da^{-m}, \end{aligned}$$
(13)

where \(D>0\) and \(m\ge 0\) are constants.

From Equation (13), we obtain

$$\begin{aligned} \dot{a}=Da^{-m+1} \end{aligned}$$
(14)

and

$$\begin{aligned} {\ddot{a}}=-D^{2}(m-1)a^{-2m+1}. \end{aligned}$$
(15)

Here we obtain two cases, Case-I for \(m\ne 0\) and Case-II for \(m=0\).

3.1.1 Case-I: For \(m\ne 0\) (i.e. power-law volumetric expansion).    Integrating Equation (14), we obtain

$$\begin{aligned} a=(mDt+c_1 )^{\frac{1}{m}}, \end{aligned}$$
(16)

where \(c_1 \) is the constant of integration.

Using Equations (13), (14) and (15), the deceleration parameter q is given by

$$\begin{aligned} q=-\frac{{\ddot{a}}}{aH^{2}}=m-1. \end{aligned}$$
(17)

The sign of q indicates whether the model inflates or not. The positive sign of q corresponds to the decelerating universe whereas the negative sign indicates the accelerating universe. From Equation (17), it is observed that the deceleration parameter q is negative in power-law model for \(0<m<1\). This indicates that the universe is accelerating throughout the evolution of the universe. For \(m>1\), the deceleration parameter q is positive, hence the universe is decelerating. For \(m=1,\) the deceleration parameter \(q=0\) which corresponds to the expansion with constant speed, which is not consistent with the present observations. Therefore, we restrict the value of m to \(0<m<1\) in order to get an accelerating universe.

Using Equations (12) and (16), the Brans–Dicke scalar field \(\varphi \) is given by

$$\begin{aligned} \varphi =\varphi _0 (mDt+c_1 )^{\frac{\varepsilon }{m}}. \end{aligned}$$
(18)

From Equations (11) and (16), the energy density for barotropic fluid is obtained as

$$\begin{aligned} \rho _m =\rho _0 (mDt+c_1 )^{-\frac{3}{m}\left( {1+\omega _m } \right) }. \end{aligned}$$
(19)

The energy density for DE can be obtained by using Equations (5) and (16) as

$$\begin{aligned} \rho _D= & {} \varphi _0 (mDt+c_1 )^{\frac{\varepsilon }{m}}\nonumber \\&\left\{ 3\left( {1-\frac{\bar{{\omega }}}{6}\varepsilon ^{2}+\varepsilon } \right) (mDt+c_1 )^{-2}\right. \nonumber \\&\left. +3k(mDt\!+\!c_1 )^{\frac{-2}{m}} \right\} -\!\rho _0 (mDt+c_1 )^{-\frac{3}{m}\left( {1\!+\!\omega _m } \right) }.\nonumber \\ \end{aligned}$$
(20)

The pressure \(p_D \) of DE using Equation (4) is given by

$$\begin{aligned} p_D= & {} -\varphi _0 (mDt+c_1 )^{\frac{\varepsilon }{m}}\nonumber \\&\left\{ D^{2} \left( {3-2m+\left( {1+\frac{\bar{{\omega }}}{2}} \right) \varepsilon ^{2}-(m-2)\varepsilon } \right) \right. \nonumber \\&\left. \times (mDt+c_1 )^{-2}+k(mDt+c_1 )^{\frac{-2}{m}} \right\} \nonumber \\&-\,\omega _m \rho _0 (mDt+c_1 )^{-\frac{3}{m}\left( {1+\omega _m } \right) }. \end{aligned}$$
(21)

Using Equations (20) and (21), we obtain the EoS parameter \(\omega _D \) of DE as

$$\begin{aligned}&\omega _D\! =\!-\frac{\left\{ {\begin{array}{l} \varphi _0 (mDt+c_1 )^{\frac{\varepsilon }{m}}\left\{ {D^{2}\left( {3-2m+\left( {1+\frac{\bar{{\omega }}}{2}} \right) \varepsilon ^{2}-(m-2)\varepsilon } \right) (mDt+c_1 )^{-2}+k(mDt+c_1 )^{\frac{-2}{m}}} \right\} \\ +\omega _m \rho _0 (mDt+c_1 )^{-\frac{3}{m}\left( {1+\omega _m } \right) } \\ \end{array}} \right\} }{\varphi _0 (mDt\!+\!c_1 )^{\frac{\varepsilon }{m}}\left\{ {3\left( {1\!-\frac{\bar{{\omega }}}{6}\varepsilon ^{2}\!+\!\varepsilon } \right) (mDt+c_1 )^{-2}+3k(mDt+c_1 )^{\frac{-2}{m}}} \right\} -\rho _0 (mDt+c_1 )^{-\frac{3}{m}\left( {1+\omega _m } \right) }}. \end{aligned}$$
(22)

The barotropic matter energy density parameter \(\Omega _m \) and dark energy density parameter \(\Omega _D \) are respectively given by

$$\begin{aligned} \Omega _m =\frac{\rho _m }{3H^{2}}=\frac{\rho _0 (mDt+c_1 )^{-\frac{3}{m}\left( {1+\omega _m } \right) +2}}{3D^{2}} \end{aligned}$$
(23)

and

$$\begin{aligned} \Omega _D =\frac{\rho _D }{3H^{2}}=\frac{\left\{ {\begin{array}{l} \varphi _0 (mDt+c_1 )^{\left( {\frac{\varepsilon }{m}+2} \right) }\left\{ {3\left( {1-\frac{\bar{{\omega }}}{6}\varepsilon ^{2}+\varepsilon } \right) (mDt+c_1 )^{-2}+3k(mDt+c_1 )^{\frac{-2}{m}}} \right\} \\ -\rho _0 (mDt+c_1 )^{-\frac{3}{m}(1+\omega _m )+2} \\ \end{array}} \right\} }{3D^{2}}.\qquad \qquad \qquad \qquad \end{aligned}$$
(24)

Using Equations (23) and (24), the total energy density parameter is obtained as

$$\begin{aligned} \Omega =\Omega _m +\Omega _D =\frac{\varphi _0 (mDt+c_1 )^{\left( {\frac{\varepsilon }{m}+2} \right) }\left\{ {3\left( {1-\frac{\bar{{\omega }}}{6}\varepsilon ^{2}+\varepsilon } \right) (mDt+c_1 )^{-2}+3k(mDt+c_1 )^{\frac{-2}{m}}} \right\} }{3D^{2}}.\qquad \qquad \qquad \qquad \end{aligned}$$
(25)

The distance modulus curve for power-law volumetric expansion model. The distance modulus curve is stated as

$$\begin{aligned} \mu =5\log d_L +25, \end{aligned}$$
(26)

where \(d_L \) is the luminosity distance, which is calculated by

$$\begin{aligned} d_L =r_1 (1+z)a_0. \end{aligned}$$
(27)

Here z is the redshift parameter, \(r_1 \) is the radial co-ordinate and \(a_0 \) is the present scale factor.

We assume that \(T=mDt+c_1 \). Therefore, Equation (8) can be written as

$$\begin{aligned} a=T^{m_1 }, \end{aligned}$$
(28)

where \(m_1 =\frac{1}{m}\).

For determination of the radial co-ordinate \(r_1 \), we assume that a phantom emitted by a source with co-ordinate \((r,T_1 )\) is received at a time \(T_0 \) by an observer located at \(r=0\). Then we determine \(r_1 \) from following relation:

$$\begin{aligned} r_1 =\int \limits _{T_1 }^{T_0 } {\frac{\mathrm{d}T}{a}}. \end{aligned}$$
(29)

Solving Equations (26) to (29), we obtain the expression for distance modulus \(\mu \) in terms of the redshift parameter z as

$$\begin{aligned} \mu =&5\log \left( {\frac{D}{(1\!-\!m_1 )H_0 }(1\!+\!z)^{m_1 }((1+z)^{1-m_1 }\!-1)} \right) \nonumber \\&+25, \end{aligned}$$
(30)

where \(H_0\) is in unit of \(\mathrm{km}\,\mathrm{s}^{-1}\,\mathrm{Mpc}^{-1}\).

3.1.2 Case-II: For \(m=0\) (i.e. exponential volumetric expansion).   Integrating Equation (14), we obtain

$$\begin{aligned} a=c_2 \mathrm{e}^{Dt}, \end{aligned}$$
(31)

where \(c_2 >0\) is the constant of integration.

Using Equations (13), (14) and (15), the deceleration parameter q is given by

$$\begin{aligned} q=-1. \end{aligned}$$
(32)

The Brans–Dicke scalar field \(\varphi \) is given by

$$\begin{aligned} \varphi =\varphi _0 (c_2 \mathrm{e}^{Dt})^{\varepsilon }. \end{aligned}$$
(33)

Using Equation (32), the energy density of the barotropic matter, energy density of DE and the pressure of DE are respectively given by

$$\begin{aligned} \rho _m= & {} \rho _0 (c_2 \mathrm{e}^{Dt})^{-3\left( {1+\omega _m } \right) }, \end{aligned}$$
(34)
$$\begin{aligned} \rho _D= & {} \varphi _0 (c_2 \mathrm{e}^{Dt})^{\varepsilon }\left\{ 3D^{2}\left( {1-\frac{\bar{{\omega }}}{6}\varepsilon ^{2}+\varepsilon } \right) \right. \nonumber \\&\left. +\,3k(c_2 \mathrm{e}^{Dt})^{-2} \right\} -\rho _0 (c_2 \mathrm{e}^{Dt})^{-3\left( {1+\omega _m } \right) }, \end{aligned}$$
(35)
$$\begin{aligned} p_D= & {} -\varphi _0 (c_2 \mathrm{e}^{Dt})^{\varepsilon }\left\{ D^{2}\left( {3+\frac{\bar{{\omega }}}{2}\varepsilon ^{2}+\varepsilon \left( {\varepsilon +2} \right) } \right) \right. \nonumber \\&\left. +\,k(c_2 \mathrm{e}^{Dt})^{-2} \right\} -\omega _m \rho _0 (c_2 \mathrm{e}^{Dt})^{-3\left( {1+\omega _m } \right) }. \end{aligned}$$
(36)

Using Equations (35) and (36), we obtain the EoS parameter \(\omega _D \) of DE as

$$\begin{aligned} \omega _D =-\frac{\varphi _0 (c_2 \mathrm{e}^{Dt})^{\varepsilon }\left\{ {D^{2}\left( {3+\frac{\bar{{\omega }}}{2}\varepsilon ^{2}+\varepsilon (\varepsilon +2)} \right) +k(c_2 \mathrm{e}^{Dt})^{-2}} \right\} +\omega _m \rho _0 (c_2 \mathrm{e}^{Dt})^{-3\left( {1+\omega _m } \right) }}{\varphi _0 (c_2 \mathrm{e}^{Dt})^{\varepsilon }\left\{ {3D^{2}\left( {1-\frac{\bar{{\omega }}}{6}\varepsilon ^{2}+\varepsilon } \right) +3k(c_2 \mathrm{e}^{Dt})^{-2}} \right\} -\rho _0 (c_2 \mathrm{e}^{Dt})^{-3\left( {1+\omega _m } \right) }}. \end{aligned}$$
(37)

The barotropic matter energy density parameter and the dark energy density parameter are respectively given by

$$\begin{aligned} \Omega _m =\frac{\rho _0 (c_2 \mathrm{e}^{Dt})^{-3\left( {1+\omega _m } \right) }}{3D^{2}} \end{aligned}$$
(38)

and

$$\begin{aligned} \Omega _D =\frac{\varphi _0 (c_2 \mathrm{e}^{Dt})^{\varepsilon }\left\{ {3D^{2}\left( {1-\frac{\bar{{\omega }}}{6}\varepsilon ^{2}+\varepsilon } \right) +3k(c_2 \mathrm{e}^{Dt})^{-2}} \right\} -\rho _0 (c_2 \mathrm{e}^{Dt})^{-3\left( {1+\omega _m } \right) }}{3D^{2}}. \end{aligned}$$
(39)

Using Equations (38) and (39), the total energy density parameter takes the form

$$\begin{aligned} \Omega =\frac{\varphi _0 (c_2 \mathrm{e}^{Dt})^{\varepsilon }\left\{ {3D^{2}\left( {1\!-\frac{\bar{{\omega }}}{6}\varepsilon ^{2}+\varepsilon } \right) \!+\!3k(c_2 \mathrm{e}^{Dt})^{-2}} \right\} }{3D^{2}}. \end{aligned}$$
(40)

The distance modulus curve for exponential expansion model. We have

$$\begin{aligned} a=c_2 \mathrm{e}^{Dt}. \end{aligned}$$
(41)

For determination of \(r_1 \), we assume that a phantom emitted by a source with co-ordinate \((r,t_1 )\) is received at a time \(t_0 \) by an observer located at \(r=0\). Then we determine \(r_1 \) from the following relation:

$$\begin{aligned} r_1 =\int \limits _{t_1 }^{t_0 } {\frac{\mathrm{d}t}{a}}. \end{aligned}$$
(42)

Solving Equations (27), (28), (41) and (42), we obtain the expression for distance modulus \(\mu \) in terms of the redshift parameter z as

$$\begin{aligned} \mu =5\log \left( {\frac{1}{H_0 }(1+z)z} \right) +25. \end{aligned}$$
(43)

3.2 Model-II (Hybrid law)

We use the hybrid expansion law (Akarsu et al. 2014) for the scale factor a as

$$\begin{aligned} a\left( t \right) =nt^{\alpha }\mathrm{e}^{\beta t}, \end{aligned}$$
(44)

where \(n,\,\alpha \) and \(\beta \) are positive constants. Equation (44) gives the exponential law when \(\alpha =0\) and the power-law when \(\beta =0.\)

The deceleration parameter q is given by

$$\begin{aligned} q=-1+\frac{\alpha }{\left( {\alpha +\beta t} \right) ^{2}}. \end{aligned}$$
(45)

The Brans–Dicke scalar field \(\varphi \) is given by

$$\begin{aligned} \varphi =\varphi _0 (nt^{\alpha }\mathrm{e}^{\beta t})^{\varepsilon }. \end{aligned}$$
(46)

Using Equation (44), the energy density of the barotropic matter, energy density of DE and pressure of DE are respectively given by

$$\begin{aligned} \rho _m= & {} \rho _0 (nt^{\alpha }\mathrm{e}^{\beta t})^{-3\left( {1+\omega _m } \right) }, \end{aligned}$$
(47)
$$\begin{aligned} \rho _D= & {} \varphi _0 (nt^{\alpha }\mathrm{e}^{\beta t})^{\varepsilon }\left\{ 3\left( {1-\frac{\bar{{\omega }}}{6}\varepsilon ^{2}+\varepsilon } \right) \left( {\frac{\alpha +\beta t}{t}} \right) ^{2}\right. \nonumber \\&\left. +\frac{3k}{(nt^{\alpha }\mathrm{e}^{\beta t})^{2}} \right\} -\,\rho _0 (nt^{\alpha }\mathrm{e}^{\beta t})^{-3\left( {1+\omega _m } \right) }, \end{aligned}$$
(48)
$$\begin{aligned} p_D= & {} -\varphi _0 (nt^{\alpha }\mathrm{e}^{\beta t})^{\varepsilon }\left\{ \left( {3+\left( {1+\frac{\bar{{\omega }}}{2}} \right) \varepsilon ^{2}+2\varepsilon } \right) \right. \nonumber \\&\left. \times \left( {\frac{\alpha +\beta t}{t}} \right) ^{2}-\frac{\alpha \left( {\varepsilon +2} \right) }{t^{2}}+\frac{k}{(nt^{\alpha }\mathrm{e}^{\beta t})^{2}} \right\} \nonumber \\&-\omega _m \rho _0 (nt^{\alpha }\mathrm{e}^{\beta t})^{-3\left( {1+\omega _m } \right) }. \end{aligned}$$
(49)

Using Equations (48) and (49), we obtain the EoS parameter \(\omega _D \) of DE as

$$\begin{aligned} \omega _D =-\frac{\varphi _0 (nt^{\alpha }\mathrm{e}^{\beta t})^{\varepsilon }\left\{ {\left( {3+\left( {1+\frac{\bar{{\omega }}}{2}} \right) \varepsilon ^{2}+2\varepsilon } \right) \left( {\frac{\alpha +\beta t}{t}} \right) ^{2}-\frac{\alpha (\varepsilon +2)}{t^{2}}+\frac{k}{(nt^{\alpha }\mathrm{e}^{\beta t})^{2}}} \right\} +\omega _m \rho _0 (nt^{\alpha }\mathrm{e}^{\beta t})^{-3\left( {1+\omega _m } \right) }}{\varphi _0 (nt^{\alpha }\mathrm{e}^{\beta t})^{\varepsilon }\left\{ {3\left( {1-\frac{\bar{{\omega }}}{6}\varepsilon ^{2}+\varepsilon } \right) \left( {\frac{\alpha +\beta t}{t}} \right) ^{2}+\frac{3k}{(nt^{\alpha }\mathrm{e}^{\beta t})^{2}}} \right\} -\rho _0 (nt^{\alpha }\mathrm{e}^{\beta t})^{-3\left( {1+\omega _m } \right) }}.\qquad \quad \,\, \end{aligned}$$
(50)

The expression for barotropic matter energy density parameter and dark energy density parameter are respectively given by

$$\begin{aligned} \Omega _m =\frac{\rho _0 (nt^{\alpha }\mathrm{e}^{\beta t})^{-3\left( {1+\omega _m } \right) }}{3\left( {\frac{\alpha +\beta t}{t}} \right) ^{2}}, \end{aligned}$$
(51)

and

$$\begin{aligned} \Omega _D \!=\frac{\varphi _0 (nt^{\alpha }\mathrm{e}^{\beta t})^{\varepsilon }\left\{ {3\left( {1-\frac{\bar{{\omega }}}{6}\varepsilon ^{2}+\varepsilon } \right) \left( {\frac{\alpha +\beta t}{t}} \right) ^{2}+\frac{3k}{(nt^{\alpha }\mathrm{e}^{\beta t})^{2}}} \right\} -\rho _0 (nt^{\alpha }\mathrm{e}^{\beta t})^{-3\left( {1+\omega _m } \right) }}{3\left( {\frac{\alpha +\beta t}{t}} \right) ^{2}}. \end{aligned}$$
(52)

Using Equations (51) and (52), the total energy density parameter takes the form

$$\begin{aligned} \Omega {=}\frac{\varphi _0 (nt^{\alpha }\mathrm{e}^{\beta t})^{\varepsilon }\left\{ {3\left( {1\!\!-\!\frac{\bar{{\omega }}}{6}\varepsilon ^{2}\!+\!\varepsilon } \right) \left( {\frac{\alpha \!+\! \beta t}{t}} \right) ^{2}\!\!+\!\frac{3k}{(nt^{\alpha }\mathrm{e}^{\beta t})^{2}}} \right\} }{3\left( {\frac{\alpha {+}\beta t}{t}} \right) ^{2}}. \end{aligned}$$
(53)

3.3 Model-III (special form of deceleration parameter)

Here we consider the deceleration parameter form proposed by Singha and Debnath (2009) as

$$\begin{aligned} q=-\frac{{\ddot{a}}a}{\dot{a}}=-1+\frac{\gamma }{1+a^{\gamma }}, \end{aligned}$$
(54)

where \(\gamma >0\) is a constant.

Solving Equation (54), we obtain

$$\begin{aligned} a=\left( {\exp \left( {\gamma c_3 t} \right) -1} \right) ^{\frac{1}{\gamma }}, \end{aligned}$$
(55)

where \(c_3 >0\) is the constant of integration.

The Brans–Dicke scalar field \(\varphi \) is given by

$$\begin{aligned} \varphi =\varphi _0 \left( {\exp \left( {\gamma c_3 t} \right) -1} \right) ^{\frac{\varepsilon }{\gamma }}. \end{aligned}$$
(56)

Using Equation (55), the energy density of the barotropic matter, energy density of DE and pressure of DE are respectively given by

$$\begin{aligned}&\rho _m =\rho _0 (\exp (\gamma c_3 t)-1)^{-\frac{3}{\gamma }(1+\omega _m )}, \end{aligned}$$
(57)
$$\begin{aligned}&\rho _D =\varphi _0 (\exp (\gamma c_3 t)-1)^{\frac{\varepsilon }{\gamma }}\left\{ {\frac{3c_3 ^{2}\left( {1-\frac{\bar{{\omega }}}{6}\varepsilon ^{2}+\varepsilon } \right) \exp (2\gamma c_3 t)}{(\exp (\gamma c_3 t)-1)^{2}}+3k(\exp (\gamma c_3 t)-1)^{\frac{-2}{\gamma }}} \right\} \nonumber \\&-\rho _0 (\exp (\gamma c_3 t)-1)^{-\frac{3}{\gamma }(1+\omega _m )}, \end{aligned}$$
(58)
$$\begin{aligned}&p_D =-\varphi _0 (\exp (\gamma c_3 t)-1)^{\frac{\varepsilon }{\gamma }}\left\{ \frac{c_3 ^{2}\left( {3-2\gamma +\frac{\bar{{\omega }}}{2}\varepsilon ^{2}+\left( {2-\gamma } \right) \varepsilon } \right) \exp (2\gamma c_3 t)}{(\exp (\gamma c_3 t)-1)^{2}}\right. \nonumber \\&\quad \left. +\frac{2c_3 ^{2}\gamma \exp (\gamma c_3 t)}{(\exp (\gamma c_3 t)-1)}+k(\exp (\gamma c_3 t)-1)^{\frac{-2}{\gamma }} \right\} \nonumber \\&\qquad -\,\omega _m \rho _0 (\exp (\gamma c_3 t)-1)^{-\frac{3}{\gamma }(1+\omega _m )}. \end{aligned}$$
(59)

Using Equations (58) and (59), we obtain the EoS parameter \(\omega _D \) of DE as

$$\begin{aligned} \omega _D \!=\!-\!\frac{\left\{ {\begin{array}{l} \varphi _0 (\exp (\gamma c_3 t)-1)^{\frac{\varepsilon }{\gamma }}\left\{ {\frac{c_3 ^{2}\left( {3-2\gamma +\frac{\bar{{\omega }}}{2}\varepsilon ^{2}+(2-\gamma )\varepsilon } \right) \exp (2\gamma c_3 t)}{(\exp (\gamma c_3 t)-1)^{2}}+\frac{2c_3 ^{2}\gamma \exp (\gamma c_3 t)}{(\exp (\gamma c_3 t)-1)}+k(\exp (\gamma c_3 t)-1)^{\frac{-2}{\gamma }}} \right\} \\ +\omega _m \rho _0 (\exp (\gamma c_3 t)-1)^{-\frac{3}{\gamma }(1+\omega _m )} \\ \end{array}} \right\} }{\left\{ {\varphi _0 (\exp (\gamma c_3 t)\!-\!1)^{\frac{\varepsilon }{\gamma }}\left\{ {\frac{3c_3 ^{2}\left( {1-\frac{\bar{{\omega }}}{6}\varepsilon ^{2}+\varepsilon } \right) \exp (2\gamma c_3 t)}{(\exp (\gamma c_3 t)\!-\!1)^{2}}\!+\!3k(\exp (\gamma c_3 t)\!-\!1)^{\frac{-2}{\gamma }}} \right\} -\rho _0 (\exp (\gamma c_3 t)\!-\!1)^{-\frac{3}{\gamma }(1+\omega _m )}} \right\} }.\nonumber \\ \end{aligned}$$
(60)

The expression for matter energy density parameter and dark energy density parameter are given by

$$\begin{aligned} \Omega _m =\frac{\rho _0 \left( {\exp \left( {\gamma c_3 t} \right) -1} \right) ^{2-\frac{3}{\gamma }\left( {1+\omega _m } \right) }}{3c_3 ^{2}\exp \left( {2\gamma c_3 t} \right) } \end{aligned}$$
(61)

and

$$\begin{aligned} \Omega _D =\frac{1}{3c_3 ^{2}\exp \left( {2\gamma c_3 t} \right) }\left\{ {\begin{array}{l} \varphi _0 \left( {\exp \left( {\gamma c_3 t} \right) -1} \right) ^{2+\frac{\varepsilon }{\gamma }}\left\{ {\frac{3c_3 ^{2}\left( {1-\frac{\bar{{\omega }}}{6}\varepsilon ^{2}+\varepsilon } \right) \exp \left( {2\gamma c_3 t} \right) }{\left( {\exp \left( {\gamma c_3 t} \right) -1} \right) ^{2}}+3k\left( {\exp \left( {\gamma c_3 t} \right) -1} \right) ^{\frac{-2}{\gamma }}} \right\} \\ -\rho _0 \left( {\exp \left( {\gamma c_3 t} \right) -1} \right) ^{2-\frac{3}{\gamma }\left( {1+\omega _m } \right) } \\ \end{array}} \right\} .\qquad \quad \, \end{aligned}$$
(62)

Using Equations (61) and (62), the total energy density parameter takes the form

$$\begin{aligned} \Omega =\frac{\varphi _0 \left( {\exp \left( {\gamma c_3 t} \right) -1} \right) ^{2+\frac{\varepsilon }{\gamma }}}{3c_3 ^{2}\exp \left( {2\gamma c_3 t} \right) }\left\{ {\frac{3c_3 ^{2}\left( {1-\frac{\bar{{\omega }}}{6}\varepsilon ^{2}+\varepsilon } \right) \exp \left( {2\gamma c_3 t} \right) }{\left( {\exp \left( {\gamma c_3 t} \right) -1} \right) ^{2}}+3k\left( {\exp \left( {\gamma c_3 t} \right) -1} \right) ^{\frac{-2}{\gamma }}} \right\} .\qquad \qquad \qquad \qquad \qquad \, \end{aligned}$$
(63)

4 Results and discussion

The physical and geometrical behaviours of the above models are as follows:

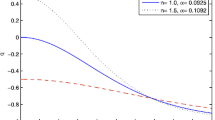
(i) The deceleration parameter \(\left( q\right) .\) The evolution of the deceleration parameter for power-law model (\(m=1/2)\), exponential model (\(m=0)\), hybrid law model (\(\alpha =1,\beta =1)\) and special form of deceleration parameter model (\(\gamma =3/2)\) is shown in Figure 1. It is found that the universe has been accelerating throughout the evolution of the universe in the power-law model for \(0<m<1\) and in the exponential model for \(m=0\), whereas the universe accelerates after an epoch of deceleration in the hybrid law model and special form of deceleration parameter model. For \(\gamma =3/2\), the deceleration parameter q is in the range \(-1\le q\le 0.5\) (shaded region in Figure 1) which matches with the observations (Perlmutter et al. 1998, 1999a, 2003; Riess et al. 1998, 2004; Tonry et al. 2003; Clocchiatti 2006).

Fig. 1
figure 1

Evolution of the deceleration parameter q.

Full size image

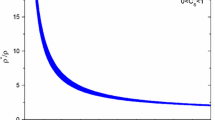
(ii) Energy density of the barotropic fluid \(\left( {\rho _m}\right) .\) The evolution of the energy density \(\rho _m \) of the barotropic fluid for all models is shown in Figure 2. It has been observed that when \(t\rightarrow 0\), in the power-law model, \(\rho _m \rightarrow \rho _0 c_1 ^{-3/m(1+\omega _m )}\), \(a\rightarrow c_1^{1/m} \), \(p_m \rightarrow \rho _0 \omega _m c_1 ^{-3/m(1+\omega _m )}\) and in the exponential model, \(\rho _m \rightarrow \rho _0 c_2 ^{-3/m(1+\omega _m )}\), \(a\rightarrow c_2 \), \(p_m \rightarrow \rho _0 \omega _m c_2 ^{-3/m(1+\omega _m )}\) which signify that there is no Big-Bang type of singularity. When \(t\rightarrow 0\), in both hybrid law and special form of deceleration parameter models, \(\rho _m \rightarrow \infty \), \(a\rightarrow 0\), \(p_m \rightarrow \infty \) which signify that there is a Big-Bang type of singularity. For all the models, \(\rho _m \rightarrow 0\), \(a\rightarrow \infty \), \(p_m \rightarrow 0\) when \(t\rightarrow \infty \) which implies that the models reduce to vacuum after very late time t.

Fig. 2
figure 2

Evolution of energy density \(\rho _m \) for \(m=0.5,D=c_1 =c_2 =c_3 =n=\alpha =\beta =\gamma =1\), \(\rho _0 =10\) and \(\omega _m =0.\)

Full size image
Fig. 3
figure 3

Evolution of DE EoS parameter \(\omega _D \) for \(m=0.5,\varepsilon =0.132124, \phi _0 =\bar{{\omega }}=D=c_1 =c_2 =c_3 =n=\alpha =\beta =\gamma =1\), \(\rho _0 =10\), \(k=\omega _m =0.\)

Full size image
Fig. 4
figure 4

Evolution of statefinder parameters s vs. r.

Full size image
Table 1 Comparison between the results of observed data and present models.
Full size table

(iii) Equation of state parameter of DE \(\left( {\omega _D}\right) .\) Figure 3 shows the evolution of EoS parameter of DE for power-law expansion, exponential expansion, hybrid law and special form of deceleration parameter. For all these models, at some finite time, the EoS parameter attains a constant value. In power-law expansion model (for \(m=0.5)\), \(\omega _D \) starts from the phantom region (\(\omega _D <-1)\) after some finite t attains the value \(\omega _D =-1\) (cosmological constant) and then it enters in the quintessence region \(\left( {-1<\omega _D <-1/3} \right) \). In case of exponential expansion model, hybrid expansion law model and special form of deceleration parameter model \(\omega _D \) starts from the phantom region (\(\omega _D <-1)\) after some finite t attains the value \(\omega _D \approx -1\) and remains the same for later time. Combining Planck data (Ade 2016) with other astrophysical data including Type Ia supernovae, the equation of state of dark energy is constrained to \(\omega _D =-1.006\pm 0.045.\) Hence in our models, the EoS parameter is consistent with these observations.

(iv) Statefinder parameters \(\left( {r,s} \right) .\) A different DE model has emerged to explain the accelerating expansion of the universe until now. We need a thorough investigation to differentiate these DE models. Sahni et al. (2003) introduced the parameter pair \(\left\{ {r,s} \right\} \), i.e., the so-called ‘statefinder’. The statefinder pair \(\left\{ {r,s} \right\} \) is defined as follows:

Fig. 5
figure 5

The plot of distance modulus \(\mu \) vs. redshift z.

Full size image
$$\begin{aligned} r=\frac{{\dddot{a}}}{aH^{3}} \quad \mathrm{and} \quad s=\frac{r-1}{3(q-1/2)} \end{aligned}$$

The statefinder is a ‘geometrical’ diagnostic in the sense that it depends upon the expansion factor and hence upon the metric describing space-time. Trajectories in the \(r-s\) plane corresponding to different cosmological models exhibit qualitatively different behaviours.

The statefinder parameters r and s for power-law model (i.e., model for \(m\ne 0)\) are given by

$$\begin{aligned}&r=(m-1)(2m-1) \quad \mathrm{and}\\&s=\frac{2\left( {(1-m)(1-2m)-1} \right) }{3(2m-3)}. \end{aligned}$$

The statefinder parameters r and s for exponential model (i.e., model for \(m=0)\) are given by

$$\begin{aligned} r=1\,\mathrm{and}\,s=0. \end{aligned}$$

The statefinder parameters r and s for hybrid law model are given by

$$\begin{aligned} r= & {} 1+\frac{2\alpha }{\left( {\alpha +\beta t} \right) ^{3}}-\frac{3\alpha }{\left( {\alpha +\beta t} \right) ^{2}}\,\mathrm{and }\\ s= & {} \frac{2\left( {2\alpha -3\alpha \left( {\alpha +\beta t} \right) } \right) }{\left( {2\alpha -3\left( {\alpha +\beta t} \right) ^{2}} \right) \left( {\alpha +\beta t} \right) }. \end{aligned}$$

The statefinder parameters r and s for special form of deceleration parameter model are given by

$$\begin{aligned} r= & {} 1+\frac{\gamma ^{2}-3\gamma }{1+a^{\gamma }}+\frac{\gamma ^{2}}{\left( {1+a^{\gamma }} \right) ^{2}}\,\mathrm{and }\\ s= & {} \frac{2\left( {\gamma ^{2}+\left( {\gamma ^{2}-3\gamma } \right) \left( {1+a^{\gamma }} \right) } \right) }{3\left( {1+a^{\gamma }} \right) \left( {2\gamma -3\left( {1+a^{\gamma }} \right) } \right) }. \end{aligned}$$

Figure 4 shows the evolving trajectory of this scenario in the \(r-s\) plane which is quite different from those of the other DE models. We hope that precise observations in future can determine these statefinder parameters and consequently explore the nature of DE.

(v) The distance modulus curve for Model-I. In the present analysis, we analysed 29 data sets out of the recently released 38 data sets of supernova Ia in the range \(0.014<z<1.551\). The comparison between observed distance modulus \(\mu \) and calculated distance modulus \(\mu \) are shown in Table 1 and Figure 5. It is found that the distance modulus curve of the derived Model-I (power-law and exponential models) fit well with the observational data (see Table 1 and Figure 5) and which are physically realistic.

5 Conclusion

In this article, we have investigated the spatially homogeneous and isotropic Friedmann–Robertson–Walker (FRW) universe filled with barotropic fluid and dark energy in the framework of the Brans–Dicke theory of gravitation. The field equations have been solved by using the following assumptions: (i) law of variation for Hubble’s parameter, (ii) hybrid expansion law, and (iii) special form of the deceleration parameter. Some physical and geometrical behaviour of the models are also discussed. It is found that there is no Big-Bang type of singularity for constant deceleration parameter models whereas there is a Big-Bang type of singularity in both hybrid law and special form of deceleration parameter models. It is observed that the EoS parameter \(\omega _D \) is consistent with the observations made by the Planck data (Ade 2016) with Type Ia supernovae which restricts that it should be \(\omega _D =-1.006\pm 0.045\). If \(\varphi \rightarrow 1\), the power-law model reduced to results of Pradhan (2011) and the hybrid expansion law model reduced to the results of Amirhashchi et al. (2011a) (for particular values of constants). Statefinder diagnostic is applied to each model in order to distinguish our DE model with other existing DE models. Among all the derived models, the best suitable standard cosmological model according to recent cosmological observations is the model with special form of deceleration parameter.