Circular restricted three-body problem when both the primaries are heterogeneous spheroid of three layers and infinitesimal body varies its mass

Abstract

The circular restricted three-body problem, where two primaries are taken as heterogeneous oblate spheroid with three layers of different densities and infinitesimal body varies its mass according to the Jeans law, has been studied. The system of equations of motion have been evaluated by using the Jeans law and hence the Jacobi integral has been determined. With the help of system of equations of motion, we have plotted the equilibrium points in different planes (in-plane and out-of planes), zero velocity curves, regions of possible motion, surfaces (zero-velocity surfaces with projections and Poincaré surfaces of section) and the basins of convergence with the variation of mass parameter. Finally, we have examined the stability of the equilibrium points with the help of Meshcherskii space–time inverse transformation of the above said model and revealed that all the equilibrium points are unstable.

1 Introduction

The restricted problem with many perturbations is an interesting problem in the celestial mechanics and space dynamics since many decades. Many researchers have studied the restricted problem of three-body with different perturbations as different shapes of the primaries, solar radiation pressure, P–R drag, variable mass, etc. Szebehely (1967) explained the dynamical behaviour of the bodies in his book ‘theory of orbits’. Sharma and Subba Rao (1975) numerically investigated the location of libration points for 19 systems of astronautical interest by taking the primaries as oblate bodies. Then they showed that the eccentricity and synodic period of these orbits are the function of oblateness. They also revealed that the orbits around libration points performed a different trend. Murray (1994) investigated the location and stability of the five equilibrium points in the planar circular restricted three-body problem under the effect of different drag forces. Khanna and Bhatnagar (1999) studied the existence and stability of libration points in the restricted three-body problem when the smaller primary is a triaxial rigid body and the bigger one an oblate spheroid when the equatorial plane of both the bodies are coinciding with the plane of motion. They have found five equilibrium points in which two are triangular and three are collinear. They also observed that the collinear equilibrium points are unstable while triangular equilibrium points are stable and have long or short periodic elliptical orbits. Idrisi and Taqvi (2013) investigated the existence and stability of five equilibrium points which lie on the arc of the unit circle with centre at bigger primary. They observed that all the equilibrium points are unstable. Ansari (2017) studied the effect of albedo on the motion of infinitesimal body in circular restricted three-body problem when all the bodies vary their masses. Using Meshcherskii transformations, he evaluated the equations of motion by which he has drawn the locations of equilibrium points, periodic orbits, Poincaré surfaces of section and basins of attraction in four cases. He also examined the stability of equilibrium points and found that all the equilibrium points are unstable. Shalini & Abdullah (2016) and Shalini et al. (2017) investigated the existence, linear stability and non-linear stability of equilibrium points in the restricted three-body problem when the smaller primary is a heterogeneous triaxial rigid body with N-layer. They found that the non-collinear libration points are stable. Suraj et al. (2014, 2018) studied the stationary solution of the planar restricted three-body problem when both the primaries are heterogeneous oblate spheroid with three layers of different densities and source of radiation as well. They have found five equilibrium points in which two are triangular points and three are collinear ones. They also observed that collinear points are unstable while triangular points are stable.

Many researchers have studied these problems with variable mass (Jeans 1928; Meshcherskii 1952; Shrivastava & Ishwar 1983; Lichtenegger 1984; Singh and Ishwar 1984; Singh & Ishwar 1985; Singh 2003; Singh & Leke 2010; Lukyanov 2009; Zhang et al. 2012; Abouelmagd & Mostafa 2015; Ansari & Alam 2016). Some researchers have investigated the basins of attractions (Ansari 2017; Suraj et al. 2018; Zotos 2016, 2017; Zotos & Suraj 2018).

This paper arranged as follows: In section 2, we have described the model of the problem and then evaluated the system of equations of motion of the infinitesimal variable mass under the effect of heterogeneous spheroid primaries and we have also determined the Jacobi integral. In the sections 3–9, we have plotted the equilibrium points in different planes (in-plane and out-of-planes), the zero-velocity curves, regions of motion, zero-velocity surfaces with projections, Poincaré surfaces of section and the basins of convergence through Mathematica software. After examining the stability of the equilibrium points, we have concluded the problem in section 10.

2 Description of the model and equations of motion

Let (Oxyz) be the barycentric rotating coordinate system with angular velocity $\omega$ about the z-axis. Here, we have considered the primaries of masses $m_1$ and $m_2$ as heterogeneous spheroid with three layers of different densities and the third infinitesimal body varies its mass according to Jean’s law. The primaries are moving in circular orbits around their common center of mass which is taken as origin O, in the same plane. The axes of the heterogeneous spheroid coincide with the rotating coordinate system. The third infinitesimal body m(t) is moving in the space under the influence of these two heterogeneous primaries but not influencing them. Let the coordinates of $m_1$, $m_2$ and m(t) be $(x_1,0,0),$ $(x_2,0,0)$ and (x, y, z) in the space as described in Fig. 1.

The potential of the heterogeneous spheroid $m_\mathrm{p}$ at the point m(t) is

$$\begin{aligned} \Omega _\mathrm{p} = -\frac{G m_\mathrm{p}}{r_\mathrm{p}}-\frac{G f_\mathrm{p}}{2r_\mathrm{p}^{3}}-\frac{3G f_\mathrm{p} z^2}{2r_\mathrm{p}^{5}}, \end{aligned}$$

where G is the gravitational constant, $r_\mathrm{p}^{2} = (x-x_\mathrm{p})^2 +y^2+z^2,$

$$\begin{aligned} f_\mathrm{p} = \frac{4\pi }{3}\sum _{q = 1}^{3}\{(\rho _{q}^{ p}-\rho _{q+1}^{ p})(a_{q}^{ p})^2 (c_{q}^{ p})\sigma _{q}^{ p}\}, \end{aligned}$$

where $\rho _{q}^{ p}$ and $a_{q}^{p}, c_{q}^{ p}$ are the densities and semi-axes of the heterogeneous spheroids respectively, and

$$\begin{aligned} \sigma _{q}^{ p} = \frac{(a_{q}^{ p})^2-(c_{q}^{ p})^2}{5}\,\, \hbox {(oblateness factor)}. \end{aligned}$$

$\rho _{4}^{ p} = 0$ $(p = 1, 2)$ is the fourth layer’s densities (Suraj et al. 2018).

Following the procedure of Abouelmagd & Mostafa (2015), we can write the equations of motion of infinitesimal variable-mass m(t) in the rotating co-ordinates when it has zero-momentum, and the variation of mass is non-isotropic and originates from one point as

Fig. 1

(a) Geometric configuration of the problem. (b) The shape of heterogeneous spheroid with three layers.

$$\begin{aligned} \left\{ \begin{array}{l} \frac{\dot{m}(t)}{m(t)}(\dot{x}- n y)+(\ddot{x}-2n \dot{y}) = V_{x}, \\ \frac{\dot{m}(t)}{m(t)}(\dot{y}+ n x)+(\ddot{y}+2 n\dot{x}) = V_{y},\\ \frac{\dot{m}(t)}{m(t)} \dot{z}+\ddot{z} = V_{z}, \end{array} \right. \end{aligned}$$

(1)

where

$$\begin{aligned} V= & {} \frac{n^2}{2}(x^2+ y^2)+ \frac{G m_1}{r_1}+\frac{G f_1}{2r_{1}^{3}}+\frac{3G f_1 z^2}{2r_{1}^{5}} \nonumber \\&+\frac{G m_2}{r_2}+\frac{G f_2}{2r_{2}^{3}}+\frac{3G f_2 z^2}{2r_{2}^{5}}. \end{aligned}$$

(2)

Here dot represents differentiation with respect to time t. $V_x, V_y$ and $V_z$ are partial differentiations of V with respect to x, y and z respectively. n is the modulus of the angular velocity $\omega$.

For dimensionless variables, we choose the unit of mass and length such that $(m_1+m_2=1),$ the sum of their masses and the distance between the primaries $(R = 1)$ are unity. Also t is so chosen that $G = 1.$ Let $0 < \mu = \frac{m_2}{m_1+m_2} \le \frac{1}{2}$, the mass ratio and $m_1 = (1-\mu ).$ The co-ordinates of $m_1$ and $m_2$ will be $(\mu , 0, 0)$ and $(\mu -1, 0, 0)$ respectively. Hence equations (1) and (2) reduce to

$$\begin{aligned} \left\{ \begin{array}{l} \frac{\dot{m}(t)}{m(t)}(\dot{x}- n y)+(\ddot{x}-2n \dot{y}) = W_{x}, \\ \frac{\dot{m}(t)}{m(t)}(\dot{y}+ n x)+(\ddot{y}+2 n\dot{x}) = W_{y},\\ \frac{\dot{m}(t)}{m(t)} \dot{z}+\ddot{z} = W_{z}, \end{array} \right. \end{aligned}$$

(3)

where

$$\begin{aligned} \left\{ \!\!\begin{array}{l} W = \frac{n^2}{2}(x^2+ y^2)+ \frac{1-\mu }{r_1}+\frac{f_1}{2r_{1}^{3}}+\frac{3f_1 z^2}{2r_{1}^{5}}+\frac{\mu }{r_2} \\ \qquad \quad +\frac{f_2}{2r_{2}^{3}}+\frac{3 f_2 z^2}{2r_{2}^{5}},\\ r_{1}^{2} = (x-\mu )^2 +y^2+z^2, r_{2}^{2} = (x-\mu +1)^2\\ \qquad \quad +y^2+z^2,\\ f_p = \frac{4\pi }{3}\sum _{q = 1}^{3}\{(\delta _{q}^{p}-\delta _{q+1}^{p})(A_{q}^{p})^2 (C_{q}^{p})\sigma _{q}^{p}\},\\ \delta = \frac{\rho _{q}^{p}}{m_1 + m_2}, A_q^p = \frac{a_{q}^{p}}{R}, C_q^p = \frac{c_{q}^{p}}{R}, \\ \sigma _{q}^{p}= \frac{(a_{q}^{p})^2-(c_{q}^{p})^2}{5R^2}, (p = 1, 2), \\ n = 1 + \frac{3f_3}{4}, \\ f_3 \!=\! \frac{\sum _{q = 1}^{3}\{(\delta _{q}^{1} \delta _{q}^{2}-\delta _{q+1}^{1}\delta _{q+1}^{2})(A_{q}^{1})^2 (C_{q}^{1})(A_{q}^{2})^2 (C_{q}^{2})(\sigma _{q}^{1}+\sigma _{q}^{2})\}}{\sum _{q = 1}^{3}\{(\delta _{q}^{1}-\delta _{q+1}^{1})(A_{q}^{1})^2 (C_{q}^{1})\}\sum _{q = 1}^{3}\{(\delta _{q}^{2}-\delta _{q+1}^{2})(A_{q}^{2})^2 (C_{q}^{2})\}}. \end{array} \right. \end{aligned}$$

(4)

The system (3) is the equations of motion of the restricted three-body problem when the primaries are heterogeneous spheroid and the infinitesimal mass varies its mass with respect to time t. Hence, we will use Jean’s law as

$$\begin{aligned} \frac{\mathrm{d}m(t)}{\mathrm{d}t}=-\lambda _{1}m(t). \end{aligned}$$

(5)

where $\lambda _1$ is the variation parameter which is a constant. And the space–time transformations are

$$\begin{aligned} \alpha= & {} \epsilon ^{\frac{1}{2}} x, \beta =\epsilon ^{\frac{1}{2}} y, \gamma =\epsilon ^{\frac{1}{2}} z, \mathrm{d}\tau = \mathrm{d}t,\\ l_{i}= & {} \epsilon ^{\frac{1}{2}}r_{i},\quad (i=1,2), \end{aligned}$$

where $\epsilon =\frac{m(t)}{m_0},$ which will be less than unity when the mass decreases and more than unity when the mass increases. $m_0$ is the initial mass of the infinitesimal body.

Therefore,

$$\begin{aligned} \left\{ \begin{array}{l} \frac{\mathrm{d} \epsilon }{\mathrm{d}t} = -\lambda _1 \epsilon , \\ \dot{x} \!=\! \epsilon ^{-1/2} (\alpha '\!+\!\frac{\lambda _1}{2}\alpha ),\quad \ddot{x} \!=\! \epsilon ^{-1/2} (\alpha ''\!+\!\lambda _1 \alpha ' \!+\!\frac{\lambda ^{2}_{1}}{4}\alpha ),\\ \dot{y} \!=\! \epsilon ^{-1/2} (\beta '\!+\!\frac{\lambda _1}{2}\beta ), \quad \ddot{y} \!=\! \epsilon ^{-1/2} (\beta ''\!+\!\lambda _1 \beta ' \!+\! \frac{\lambda ^{2}_{1}}{4}\beta ), \\ \dot{z} \!=\! \epsilon ^{-1/2} (\gamma '\!+\!\frac{\lambda _1}{2}\gamma ),\quad \ddot{z} \!=\! \epsilon ^{-1/2} (\gamma ''\!+\!\lambda _1 \gamma ' \!+\! \frac{\lambda ^{2}_{1}}{4}\gamma ), \end{array} \right. \end{aligned}$$

(6)

where dot $(\cdot )$ and prime $(')$ represent the differentiation with respect to t and $\tau$ respectively. Also $\frac{\mathrm{d}}{{\mathrm{d}}t}=\frac{\mathrm{d}}{{\mathrm{d}}\tau }.$

Finally, the equations of motion of the infinitesimal variable mass become

$$\begin{aligned} \left\{ \begin{array}{l} \ddot{\alpha }-2 n \dot{\beta } = U_{\alpha },\\ \ddot{\beta }+2n\dot{\alpha } = U_{\beta },\\ \ddot{\gamma } = U_{\gamma }, \end{array} \right. \end{aligned}$$

(7)

where

$$\begin{aligned} \left\{ \!\!\begin{array}{l} U =\frac{n^2}{2}(\alpha ^2+\beta ^2)+\frac{\lambda _{1}^2}{8}(\alpha ^2+\beta ^2+\gamma ^2)\\ \qquad +\epsilon ^{3/2}\{\frac{1-\mu }{l_1}+\frac{\epsilon f_1}{l_{1}^{3}}+\frac{3 \epsilon f_1 \gamma ^2}{2l_{1}^{5}}+ \frac{\mu }{l_2}+\frac{\epsilon f_2}{l_{2}^{3}}+\frac{3 \epsilon f_2 \gamma ^2}{2l_{2}^{5}}\},\\ l_{1}^{2}=(\alpha -\mu \epsilon ^{1/2} )^{2}+\beta ^{2}+\gamma ^{2}, \\ l_{2}^{2}=(\alpha -(\mu -1) \epsilon ^{1/2} )^{2}+\beta ^{2}+\gamma ^{2}. \end{array} \right. \end{aligned}$$

(8)

The corresponding Jacobian integral of the system (7) can be written as

$$\begin{aligned} \dot{\alpha }^2 +\dot{\beta }^2+\dot{\gamma }^2 =2 U - C- 2\int _{t_0}^{t} \frac{\partial U}{\partial t} \mathrm{d}t, \end{aligned}$$

(9)

where $\dot{\alpha }$, $\dot{\beta }$ and $\dot{\gamma }$ are the velocity components and C is the Jacobian constant which is conserved and related to the total energy of the system. The curve for given values of the energy integral is restricted in its motion to regions in which $2U(\alpha ,\beta , \gamma )\ge C,$ and all other regions are prohibited to the third infinitesimal body, i.e. it has zero velocities in these regions.

3 Equilibrium points

The location of equilibrium points can be obtained by solving the right hand sides of system (7) when all the derivatives (with respect to t) of the left-hand sides are to be zero, i.e., $\dot{\alpha }=\ddot{\alpha }=\dot{\beta }=\ddot{\beta }=\dot{\gamma }=\ddot{\gamma } = 0$. Hence we get

$$\begin{aligned} {\left\{ \begin{array}{ll} U_\alpha = 0, ~~~~~~~~~~~~~~~~~~ (10\mathrm{a})\\ U_\beta = 0, ~~~~~~~~~~~~~~~~~~ (10\mathrm{b}) \\ U_\gamma = 0, ~~~~~~~~~~~ (10\mathrm{c}) \end{array}\right. } \end{aligned}$$

Fig. 2

Locations of equilibrium points in the $\alpha -\beta$ plane: For (a) $\epsilon = 1.3$ (black), (b) $\epsilon = 1$ (red), (c) $\epsilon = 0.6$ (blue), (d) $\epsilon = 0.3$ (green), (e) Combined figures of (a), (b), (c) and (d).

Fig. 3

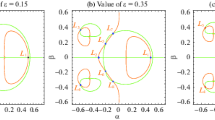
Locations of equilibrium points in the $\alpha -\gamma$ plane: (a) for $\epsilon = 1.3$ (black), $\epsilon = 0.6$ (blue), $\epsilon = 0.3$ (green). (b) The zoomed part of figure (a), (c) $\epsilon = 1$ (red). The red points which are bigger indicate the positions of the primaries in all the figures.

Fig. 4

Locations of equilibrium points in the $\beta -\gamma$ plane: (a) for $\epsilon = 1.3$ (black), $\epsilon = 0.6$ (blue), $\epsilon = 0.3$ (green), (b) for $\epsilon = 1$ (red).

Fig. 5

Zero-velocity curves (a) in the $\alpha -\beta$-plane, (b) in the $\alpha -\gamma$-plane, (c) in the $\beta -\gamma$-plane, all at $\epsilon = 1.3$ corresponding to the Jacobian constants.

Fig. 6

Regions of motion in the $\alpha -\beta$ plane corresponding to (a) $C_{L_{4,5}}$ (black regions), (b) $C_{L_{3}}$ (red regions), (c) $C_{L_{1}}$ (blue regions), $C_{L_{2}}$ (green regions).

Fig. 7

Regions of motion in the $\alpha -\gamma$ plane corresponding to (a) $C_{L_{4,5}}$ (black regions), (b) $C_{L_{3}}$ (red regions), (c) $C_{L_{1}}$ (blue regions), (d) $C_{L_{2}}$ (green regions).

Fig. 8

Regions of motion in the $\beta -\gamma$ plane corresponding to (a) $C_{L_{4,5}}$ (black regions), (b) $C_{L_{1,3}}$ (red regions), (c) $C_{L_{2}}$ (green regions).

where

$$\begin{aligned} U_\alpha= & {} n^2 \alpha + \frac{\alpha \lambda _1^2}{4}\nonumber \\&-\, \epsilon ^{\frac{3}{2}}\left\{ \frac{15 f_2 \gamma ^2 \epsilon (\alpha - \sqrt{\epsilon }(-1 + \mu ))}{2(\beta ^2 + \gamma ^2 + (\alpha - \sqrt{\epsilon } (-1 + \mu ))^2)^{\frac{7}{2}}}\right. \nonumber \\&+\frac{3 f_2 \epsilon (\alpha - \sqrt{\epsilon }(-1 + \mu ))}{2(\beta ^2 + \gamma ^2 + (\alpha - \sqrt{\epsilon } (-1 + \mu ))^2)^{\frac{5}{2}}}\nonumber \\&+\frac{\mu (\alpha -\sqrt{\epsilon }(-1 + \mu ))}{(\beta ^2 + \gamma ^2 + (\alpha - \sqrt{\epsilon } (-1 + \mu ))^2)^{\frac{3}{2}}}\nonumber \\&+\frac{15 f_1 \gamma ^2 \epsilon (\alpha - \sqrt{\epsilon } \mu )}{2(\beta ^2 + \gamma ^2 + (\alpha - \sqrt{\epsilon } \mu )^2)^{\frac{7}{2}}}\nonumber \\&+\frac{3 f_1 \epsilon (\alpha -\sqrt{\epsilon } \mu )}{2(\beta ^2 + \gamma ^2 + (\alpha -\sqrt{\epsilon } \mu )^2)^{\frac{5}{2}}}\nonumber \\&\left. +\frac{(1-\mu ) (\alpha - \sqrt{\epsilon } \mu )}{(\beta ^2 + \gamma ^2 + (\alpha - \sqrt{\epsilon } \mu )^2)^{\frac{3}{2}}}\right\} , \end{aligned}$$

(11)

$$\begin{aligned} U_\beta= & {} n^2 \beta + \frac{\beta \lambda _1^2}{4}\nonumber \\&-\, \epsilon ^{\frac{3}{2}}\left\{ \frac{15 f_2 \gamma ^2 \epsilon \beta }{2(\beta ^2 + \gamma ^2 + (\alpha -\sqrt{\epsilon } (-1 + \mu ))^2)^{\frac{7}{2}}}\right. \nonumber \\&+\frac{3 f_2 \epsilon \beta }{2(\beta ^2 + \gamma ^2 + (\alpha - \sqrt{\epsilon } (-1 + \mu ))^2)^{\frac{5}{2}}}\nonumber \\&+\frac{\mu \beta }{(\beta ^2 + \gamma ^2 + (\alpha - \sqrt{\epsilon } (-1 + \mu ))^2)^{\frac{3}{2}}}\nonumber \\&+\frac{15 f_1 \gamma ^2 \epsilon \beta }{2(\beta ^2 + \gamma ^2 + (\alpha - \sqrt{\epsilon } \mu )^2)^{\frac{7}{2}}} \nonumber \\&+\frac{3 f_1 \epsilon \beta }{2(\beta ^2 + \gamma ^2 + (\alpha -\sqrt{\epsilon } \mu )^2)^{\frac{5}{2}}}\nonumber \\&\left. +\frac{(1-\mu ) \beta }{(\beta ^2 + \gamma ^2 + (\alpha -\sqrt{\epsilon }\mu )^2)^{\frac{3}{2}}}\right\} , \end{aligned}$$

(12)

$$\begin{aligned} U_\gamma= & {} \frac{\gamma \lambda _1^2}{4}\!-\! \epsilon ^{\frac{3}{2}}\left\{ \frac{15 f_2 \gamma ^3 \epsilon }{2(\beta ^2 \!+\! \gamma ^2 \!+\! (\alpha -\sqrt{\epsilon } (-1 \!+\! \mu ))^2)^{\frac{7}{2}}}\right. \nonumber \\&+\frac{3 f_2 \epsilon \gamma }{2(\beta ^2 + \gamma ^2 + (\alpha - \sqrt{\epsilon } (-1 + \mu ))^2)^{\frac{5}{2}}}\nonumber \\&+\frac{\mu \gamma }{(\beta ^2 + \gamma ^2 + (\alpha - \sqrt{\epsilon } (-1 + \mu ))^2)^{\frac{3}{2}}}\nonumber \\&+\frac{15 f_1 \gamma ^3 \epsilon }{2(\beta ^2 + \gamma ^2 + (\alpha - \sqrt{\epsilon } \mu )^2)^{\frac{7}{2}}} \nonumber \\&+\frac{3 f_1 \epsilon \gamma }{2(\beta ^2 + \gamma ^2 + (\alpha -\sqrt{\epsilon } \mu )^2)^{\frac{5}{2}}} \nonumber \\&\left. +\frac{(1-\mu ) \gamma }{(\beta ^2 + \gamma ^2 + (\alpha -\sqrt{\epsilon }\mu )^2)^{\frac{3}{2}}}\right\} , \end{aligned}$$

(13)

$$\begin{aligned} U_{\alpha \alpha }= & {} n^2 + \frac{ \lambda _1^2}{4}\nonumber \\&+\, \epsilon ^{\frac{3}{2}}\left\{ -\frac{15 f_2 \gamma ^2 \epsilon }{2(\beta ^2 + \gamma ^2 + (\alpha -\sqrt{\epsilon } (-1 + \mu ))^2)^{\frac{7}{2}}}\right. \nonumber \\&-\frac{3 f_2 \epsilon }{2(\beta ^2 + \gamma ^2 + (\alpha -\sqrt{\epsilon } (-1 + \mu ))^2)^{\frac{5}{2}}} \nonumber \\&+ \frac{105 f_2 \gamma ^2 \epsilon (\alpha - \sqrt{\epsilon }(-1 + \mu ))^2}{2(\beta ^2 + \gamma ^2 + (\alpha - \sqrt{\epsilon } (-1 + \mu ))^2)^{\frac{9}{2}}}\nonumber \\&+\frac{15 f_2 \epsilon (\alpha -\sqrt{\epsilon }(-1 + \mu ))^2}{2(\beta ^2 + \gamma ^2 + (\alpha -\sqrt{\epsilon } (-1 + \mu ))^2)^{\frac{7}{2}}}\nonumber \\&-\frac{\mu }{(\beta ^2 + \gamma ^2 + (\alpha -\sqrt{\epsilon } (-1 + \mu ))^2)^{\frac{3}{2}}}\nonumber \\&+\frac{3\mu (\alpha -\sqrt{\epsilon }(-1 + \mu ))^2}{(\beta ^2 + \gamma ^2 + (\alpha -\sqrt{\epsilon } (-1 + \mu ))^2)^{\frac{5}{2}}}\nonumber \\&+\frac{105 f_1 \gamma ^2 \epsilon (\alpha -\sqrt{\epsilon } \mu )^2}{2(\beta ^2 + \gamma ^2 + (\alpha -\sqrt{\epsilon } \mu )^2)^{\frac{9}{2}}}\nonumber \\&-\frac{15 f_1 \epsilon \gamma ^2}{2(\beta ^2 + \gamma ^2 + (\alpha -\sqrt{\epsilon } \mu )^2)^{\frac{7}{2}}}\nonumber \\&-\frac{(1-\mu )}{(\beta ^2 + \gamma ^2 + (\alpha -\sqrt{\epsilon } \mu )^2)^{\frac{3}{2}}}\nonumber \\&+\frac{15 f_1 \epsilon (\alpha -\sqrt{\epsilon } \mu )^2}{2(\beta ^2 + \gamma ^2 + (\alpha -\sqrt{\epsilon } \mu )^2)^{\frac{7}{2}}}\nonumber \\&+\frac{3 f_1 \epsilon }{2(\beta ^2 + \gamma ^2 + (\alpha -\sqrt{\epsilon }\mu )^2)^{\frac{5}{2}}} \nonumber \\&\left. +\frac{3(1-\mu ) (\alpha - \sqrt{\epsilon } \mu )^2}{(\beta ^2 + \gamma ^2 + (\alpha - \sqrt{\epsilon } \mu )^2)^{\frac{5}{2}}}\right\} , \end{aligned}$$

(14)

$$\begin{aligned} U_{\alpha \beta }= & {} U_{\beta \alpha } \!=\! \epsilon ^{\frac{3}{2}}\left\{ \frac{105 f_2 \gamma ^2 \beta \epsilon (\alpha - \sqrt{\epsilon }(-1 + \mu ))}{2(\beta ^2 + \gamma ^2 + (\alpha \!-\! \sqrt{\epsilon } (-1 + \mu ))^2)^{\frac{9}{2}}}\right. \nonumber \\&+\frac{15 f_2 \epsilon \beta (\alpha -\sqrt{\epsilon }(-1 + \mu ))}{2(\beta ^2 + \gamma ^2 + (\alpha -\sqrt{\epsilon } (-1 + \mu ))^2)^{\frac{7}{2}}}\nonumber \\&+\frac{3\mu \beta (\alpha -\sqrt{\epsilon }(-1 + \mu ))}{(\beta ^2 + \gamma ^2 + (\alpha -\sqrt{\epsilon } (-1 + \mu ))^2)^{\frac{5}{2}}}\nonumber \\&+\frac{105 f_1 \gamma ^2 \beta \epsilon (\alpha -\sqrt{\epsilon } \mu )}{2(\beta ^2 + \gamma ^2 + (\alpha -\sqrt{\epsilon } \mu )^2)^{\frac{9}{2}}}\nonumber \\&+\frac{15 f_1 \epsilon \beta (\alpha -\sqrt{\epsilon } \mu )}{2(\beta ^2 + \gamma ^2 + (\alpha -\sqrt{\epsilon } \mu )^2)^{\frac{7}{2}}}\nonumber \\&\left. +\frac{3(1-\mu )\beta (\alpha - \sqrt{\epsilon } \mu )}{(\beta ^2 + \gamma ^2 + (\alpha -\sqrt{\epsilon } \mu )^2)^{\frac{5}{2}}}\right\} , \end{aligned}$$

(15)

$$\begin{aligned} U_{\beta \beta }= & {} n^2 + \frac{ \lambda _1^2}{4}\nonumber \\&+ \epsilon ^{\frac{3}{2}}\left\{ -\frac{15 f_2 \gamma ^2 \epsilon }{2(\beta ^2 + \gamma ^2 + (\alpha -\sqrt{\epsilon } (-1 + \mu ))^2)^{\frac{7}{2}}}\right. \nonumber \\&-\frac{3 f_2 \epsilon }{2(\beta ^2 + \gamma ^2 + (\alpha -\sqrt{\epsilon } (-1 + \mu ))^2)^{\frac{5}{2}}}\nonumber \\&+ \frac{105f_2\gamma ^2 \epsilon \beta ^2}{2(\beta ^2 + \gamma ^2 + (\alpha - \sqrt{\epsilon } (-1 + \mu ))^2)^{\frac{9}{2}}}\nonumber \\&+\frac{15 f_2 \epsilon \beta ^2}{2(\beta ^2 + \gamma ^2 + (\alpha -\sqrt{\epsilon } (-1 + \mu ))^2)^{\frac{7}{2}}}\nonumber \\&-\frac{\mu }{(\beta ^2 + \gamma ^2 + (\alpha -\sqrt{\epsilon } (-1 + \mu ))^2)^{\frac{3}{2}}}\nonumber \\&+\frac{3\mu \beta ^2}{(\beta ^2 + \gamma ^2 + (\alpha -\sqrt{\epsilon } (-1 + \mu ))^2)^{\frac{5}{2}}}\nonumber \\&+\frac{105 f_1 \gamma ^2 \epsilon \beta ^2}{2(\beta ^2 + \gamma ^2 + (\alpha -\sqrt{\epsilon } \mu )^2)^{\frac{9}{2}}}\nonumber \\&-\frac{15 f_1 \epsilon \gamma ^2}{2(\beta ^2 + \gamma ^2 + (\alpha -\sqrt{\epsilon } \mu )^2)^{\frac{7}{2}}}\nonumber \\&-\frac{(1-\mu )}{(\beta ^2 + \gamma ^2 + (\alpha -\sqrt{\epsilon } \mu )^2)^{\frac{3}{2}}}\nonumber \\&+\frac{15 f_1 \epsilon \beta ^2}{2(\beta ^2 + \gamma ^2 + (\alpha -\sqrt{\epsilon } \mu )^2)^{\frac{7}{2}}}\nonumber \\&+\frac{3 f_1 \epsilon }{2(\beta ^2 + \gamma ^2 + (\alpha -\sqrt{\epsilon }\mu )^2)^{\frac{5}{2}}} \nonumber \\&\left. +\frac{3(1-\mu ) \beta ^2}{(\beta ^2 + \gamma ^2 + (\alpha - \sqrt{\epsilon }\mu )^2)^{\frac{5}{2}}}\right\} . \end{aligned}$$

(16)

The second order derivatives of U, i.e., $U_{\alpha \alpha },$ $U_{\alpha \beta },$ $U_{\beta \alpha },$ $U_{\beta \beta },$ will be used in the basins of the convergence section. All the calculations are made for fixed value of $\mu = 0.3,$ $\lambda _1 = 0.2,$ $f_1 = 9.83933\times 10^{-18},$ $f_2 = 1.58302\times 10^{-7},$ $f_3 = 3.13153\times 10^{-8}.$

3.1 In-plane equilibrium points ($\alpha -\beta$ plane)

The solutions of equations $10(\mathrm{a})$ and $10(\mathrm{b})$ will be the location of equilibrium points in the $\alpha -\beta$ plane. We have located the locations of equilibrium points at the different four values of mass parameters ($\epsilon = 1.3$, 1 ($\lambda _1 = 0$), 0.6, 0.3) by the graphs in Figures 2(a)–(d). In all the four cases, there are five equilibrium points in which three ($L_1$, $L_2$, $L_3$) are collinear and the other two ($L_4$, $L_5$) are non-collinear equilibrium points. From Fig. 2(e), we observed that as we decrease the values of the variation of mass parameter ($\epsilon$), all the five equilibrium points are moving towards the origin. The red points that are bigger indicate the location of the primaries.

3.2 Out-of-plane equilibrium points

In this section, we have drawn the equilibrium points in two cases: (i) $\alpha \ne 0,\ \beta =0,\ \gamma \ne 0$ and (ii) $\alpha =0,\ \beta \ne 0,\ \gamma \ne 0$.

In the first case, there exist at most five equilibrium points ($L_1$, $L_2$, $L_3,$ $L_4$, $L_5$) (Fig. 3) at four different values of variation of mass parameters. For the values of $\epsilon = 1.3, 0.6, 0.3$, there are five equilibrium points and for $\epsilon = 1$, there are three collinear equilibrium points only. It is observed from Figures 3(a), (b) and (c) that as the value of $\epsilon$ decreases, all the equilibrium points move toward the origin.

In the second case (Figures 4(a) and (b)), we get the same phenomenon of equilibrium points as in the first case.

4 Zero-velocity curves (ZVCs)

Equation (9) can be rewritten as

$$\begin{aligned} V^2 =2 U - C- 2\int _{t_0}^{t} \frac{\partial U}{\partial t} \mathrm{d}t, \end{aligned}$$

(17)

where V is the velocity of the infinitesimal body. For the possible motion, $V^2 \ge 0,$ therefore

$$\begin{aligned} 2 U - C- 2\int _{t_0}^{t} \frac{\partial U}{\partial t} \mathrm{d}t \ge 0. \end{aligned}$$

(18)

Using the methodology of Abouelmagd & Mostafa (2015), equation (18) can be written as

$$\begin{aligned} 2 U \ge C. \end{aligned}$$

(19)

Fig. 9

Zero-velocity surfaces with projections in the $\alpha -\beta$ plane at $\epsilon = 1.3$.

Fig. 10

Zero-velocity surfaces with projections in the $\alpha -\gamma$ plane at $\epsilon = 1.3$.

Fig. 11

Zero-velocity surfaces with projections in the $\beta -\gamma$ plane at $\epsilon = 1.3$.

Using the equation (19), we have plotted the zero-velocity curves for fixed value of $\epsilon = 1.3$ in all three planes, where C is the Jacobian constant which is conserved.

In all the three planes, we have found five equilibrium points at $\epsilon = 1.3,$ and then we have evaluated the values of various Jacobian constants corresponding to these equilibrium points, i.e., $C_{L_{1}},$ $C_{L_{2}},$ $C_{L_{3}},$ $C_{L_{4,5}}$.

In the $\alpha -\beta$-plane, we have found four different zero-velocity curves corresponding to each Jacobian constants (Fig. 5(a)). At the value of $C_{L_{1}},$ there are two parts of zero-velocity curves in which one is dumb-bell shaped and other one is cardioid shaped. Both the curves (blue color) intersect at $L_{1}.$ At the value of $C_{L_{2}},$ there are two parts of zero-velocity curves in which one is lemniscate with intersection point at $L_{2}$ and both the ovals of lemniscate are around the primaries and the other one is a circle with green color curves; it is also observed that all the equilibrium points are within the circle. At the value of $C_{L_{3}},$ there are two parts of zero-velocity curves (red colors) where both the curves are intersecting at $L_{3}.$ At the value of $C_{L_{4, 5}},$ there are two parts of zero-velocity curves (black colors) which have oval shapes with centers at $L_{4}$ and $L_{5}.$

In the $\alpha -\gamma$-plane, we have found four different zero-velocity curves corresponding to each Jacobian constants (Fig. 5(b)). At the value of $C_{L_{1}},$ there are two parts of zero-velocity curves (blue color) in which one is dumb-bell shaped and other one is $\alpha$-hyperbola shaped. These two curves intersect at $L_{1}.$ At the value of $C_{L_{2}},$ there are two parts of zero-velocity curves in which one is lemniscate shaped with intersection point at $L_{2}$ and another one is $\alpha$-hyperbola shaped with green color curves. At the value of $C_{L_{3}},$ we got red color zero-velocity curves with intersection point at $L_{3}.$ At the value of $C_{L_{4, 5}},$ we got $\gamma$-hyperbola with each part of the curve (black colors) around $L_{4}$ and $L_{5}.$

In the $\beta -\gamma$-plane, we have found four different zero-velocity curves corresponding to each Jacobian constants (Fig. 5(c)). At the value of $C_{L_{1,3}},$ there are two part of zero-velocity curves in red color with intersection points at $L_{1}$ and $L_{3}.$ At the value of $C_{L_{2}},$ we got $\beta$-hyperbola with the origin at $L_{2}$. At the value of $C_{L_{4, 5}},$ we got $\gamma$-hyperbola with each wing (black color) around $L_{4}$ and $L_{5}$ respectively. In all the figures, blue points and red points represent the locations of the equilibrium points and primaries, respectively.

5 Regions of possible motion

In this section, we have illustrated the regions of motion of infinitesimal body under the effect of heterogeneous spheroid and the variations of mass parameter of the infinitesimal body in three planes: $\alpha -\beta$ (Figures 6(a)–(d)), $\alpha -\gamma$ (Figures 7(a)–(d)) and $\beta -\gamma$ (Figures 8(a)–(c)). In all the figures, the color regions are the forbidden regions which increase as the value of the corresponding Jacobian constants increase; the infinitesimal body can move freely in the white regions.

6 Zero-velocity surfaces with projections (ZVSs)

The projections of the zero-velocity surfaces onto the configuration plane are known as Hill’s region because the boundaries of the Hill’s region are the zero-velocity curves which are the locus in the configuration plane where the kinetic energy is zero. We have drawn the zero-velocity surfaces with projections at the variation of mass parameter $\epsilon =1.3$ corresponding to the Jacobian constant C. The motion is possible only inside the shaded regions of the surfaces and we observed that the variation of mass parameter has great impact on the characteristics of the zero-velocity surfaces. It is also observed that as the values of the Jacobian constant increase, the region of surfaces increases (Figures 9, 10 and 11).

7 Poincaré surfaces of sections

We have drawn the Poincaré surfaces of section of motion of infinitesimal variable body under the effect of heterogeneous oblate spheroid with three layers of different densities at four different values of variation of mass parameters ($\epsilon =$ 1.3 (black), 1 (red), 0.6 (blue) and 0.3 (green)). From Figures 12(a) and (b), it is observed that as the value of variation of mass parameters decreases, the surfaces of sections shrink and is shifted to the left side in $\alpha -\alpha '$ whereas these curves expand and shift down in $\beta -\beta '$ when $\gamma = 0.$ From Figures 13(a) and (b), it is observed that these curves shrink in both $\alpha -\alpha '$ and $\gamma -\gamma '$ when $\beta = 0.$ On the other hand, from Figures 14(a) and (b), it is also observed that these curves shrink in both $\beta -\beta '$ and $\gamma -\gamma '$ when $\alpha = 0.$ From these figures, it is clear that the variation of mass parameters has great impact on the Poincaré surfaces of section.

Fig. 12

Poincaré surfaces of sections in (a) $\alpha -\alpha '$ and (b) $\beta -\beta '$ for $\epsilon = 1.3$ (black), $\epsilon = 1$ (red), $\epsilon = 0.6$ (blue), $\epsilon = 0.3$ (green).

Fig. 13

Poincaré surfaces of sections in (a) $\alpha -\alpha '$ and (b) $\gamma -\gamma '$ for $\epsilon = 1.3$ (black), $\epsilon = 1$ (red), $\epsilon = 0.6$ (blue), $\epsilon = 0.3$ (green).

Fig. 14

Poincaré surfaces of sections in (a) $\beta -\beta '$ and (b) $\gamma -\gamma '$ for $\epsilon = 1.3$ (black), $\epsilon = 1$ (red), $\epsilon = 0.6$ (blue), $\epsilon = 0.3$ (green).

8 Basins of convergence

Here, we have discussed the basins of attraction for the circular restricted three-body problem in which we have taken the primaries as heterogeneous oblate spheroid and infinitesimal body varies its mass with time by using the Newton–Raphson basins of attraction which is a fast, accurate and simple tool to solve the multivariate functions. The basin of convergence or converging region is composed of all the initial conditions that lead to specific equilibrium points. It is an issue of great importance to get the basins of convergence which reflect some important qualitative properties of the dynamical systems. Using this iterative method, we have drawn the basins of convergence for the variation of mass parameters $\epsilon = 1.3$ in three planes: $\alpha -\beta$ plane (Fig. 15(a)), $\alpha -\gamma$ plane (Fig. 15(b)) and $\beta -\gamma$ plane (Fig. 15(d)). The algorithm of our problem in the $\alpha -\beta$ plane when $\gamma = 0,$ is given by

$$\begin{aligned} \left\{ \begin{array}{c} \alpha _{n+1} =\alpha _{n} -\left( \frac{U_{\alpha } U_{\beta \beta } - U_{\beta } U_{\alpha \beta }}{U_{\alpha \alpha } U_{\beta \beta } - U_{\alpha \beta } U _{\beta \alpha }} \right) _{(\alpha _{n} ,\beta _{n} )} ,\\ \beta _{n+1} =\beta _{n} -\left( \frac{U_{\beta } U_{\alpha \alpha } - U_{\alpha } U_{\beta \alpha } }{U_{\alpha \alpha } U_{\beta \beta } - U_{\alpha \beta } U _{\beta \alpha }} \right) _{(\alpha _{n} ,\beta _{n} )} , \end{array}\right. \end{aligned}$$

(20)

where $\alpha _{n}$ and $\beta _{n}$ are the values of $\alpha$ and $\beta$ co-ordinates of the n-th step of the Newton–Raphson iterative process. If the initial point converges rapidly to one of the equilibrium points, then this point $(\alpha ,\ \beta )$ will be a member of the basin of convergence of the root. This process stops when the successive approximation converges to an attractor. We used color code for the classification of the equilibrium points on the planes.

In the $\alpha -\beta$-plane (Fig. 15(a)), we observed that the equilibrium points $L_1$, $L_2$, $L_3$ represent light blue color regions while $L_4$ and $L_5$ represent magenta and yellow color regions respectively. The basins of convergence corresponding to these five equilibrium points extend to infinity. In the $\alpha -\gamma$-plane (Fig. 15(b)), we got the lemniscate shape and the equilibrium points $L_1$, $L_2$, $L_3$ represent cyan color regions while $L_4$ and $L_5$ represent red color regions. The basins of convergence corresponding to these five equilibrium points extend to infinity. We can see a more clear view in Fig. 15(c) which is the zoomed part of the Fig. 15(b). In the $\beta -\gamma$-plane (Fig. 15(d)), we got the dumbbell shape and the equilibrium points $L_1$, $L_2$, $L_3$ represent cyan color regions while $L_4$ and $L_5$ represent red color regions. The basins of convergence corresponding to these five equilibrium points extend to infinity. We can see a more clear view in Fig. 15(e) which is the zoomed part of Fig. 15(d). In all the figures, the red points represent the locations of the primaries.

Fig. 15

Basins of convergence in the (a) $\alpha -\beta$ plane, (b) $\alpha -\gamma$ plane, (d) $\beta -\gamma$ plane and (c), (e) are the zoomed part of figures (b) and (d) respectively.

9 Stability of equilibrium points

In this section, we have examined the linear stability of the equilibrium points by giving the displacements $((\alpha _1,\beta _1,\gamma _1)<<1)$ to $(\alpha _0,\beta _0, \gamma _0)$ as

$$\begin{aligned} \left\{ \begin{array}{c} \alpha = \alpha _1 + \alpha _{0},\\ \beta = \beta _1 + \beta _{0},\\ \gamma = \gamma _1 + \gamma _0, \end{array}\right. \end{aligned}$$

(21)

where $(\alpha _0,\beta _0, \gamma _0)$ is the equilibrium point for a fixed value of time $t_0$. We can get the variational equations from the equations (7) and (21) as

$$\begin{aligned} \left\{ \begin{array}{l} \ddot{\alpha _1}-2n\dot{\beta _1} = (U_{\alpha \alpha })_0 \alpha _1 + (U_{\alpha \beta })_0 \beta _1 + (U_{\alpha \gamma })_0 \gamma _1,\\ \ddot{\beta _1}+2n\dot{\alpha _1} =(U_{\beta \alpha })_0 \alpha _1 + (U_{\beta \beta })_0 \beta _1 + (U_{\beta \gamma })_0 \gamma _1,\\ \ddot{\gamma _1} =(U_{\gamma \alpha })_0 \alpha _1 + (U_{\gamma \beta })_0 \beta _1 + (U_{\gamma \gamma })_0 \gamma _1, \end{array}\right. \end{aligned}$$

(22)

where the subscript ‘0’ in the system (22) represents the values at the equilibrium point $(\alpha _0,\beta _0, \gamma _0)$.

In the phase space, system (22) may be written as

$$\begin{aligned} \left\{ \begin{array}{l} \dot{\alpha _1} = \alpha _2,\quad \dot{\beta _1} = \beta _2,\quad \dot{\gamma _1} = \gamma _2,\\ \dot{\alpha _2}-2n \beta _2 = (U_{\alpha \alpha })_0 \alpha _1 + (U_{\alpha \beta })_0 \beta _1 + (U_{\alpha \gamma })_0 \gamma _1,\\ \dot{\beta _2}+2n \alpha _2 =(U_{\beta \alpha })_0 \alpha _1 + (U_{\beta \beta })_0 \beta _1 + (U_{\beta \gamma })_0 \gamma _1,\\ \dot{\gamma _2} =(U_{\gamma \alpha })_0 \alpha _1 + (U_{\gamma \beta })_0 \beta _1 + (U_{\gamma \gamma })_0 \gamma _1. \end{array}\right. \end{aligned}$$

(23)

At $\lambda _1 =0,$ system (22) reduces to a system with constant mass. For $\lambda _1>0,$ we can not determine the linear stability from ordinary method because the distances of the primaries to the equilibrium point ($\alpha _0$, $\beta _0$, $\gamma _0$) varies with time. Therefore, we use the Meshcherskii space–time inverse transformations.

Table 1 Co-ordinates of in-plane equilibrium points and the corresponding characteristic roots ($\alpha -\beta$-plane) when both the primaries are heterogeneous oblate spheroid with three layers of different densities, and infinitesimal body varies its mass.

Table 2 Co-ordinates of out-of-plane equilibrium points and the corresponding characteristic roots ($\alpha -\gamma$-plane) when both the primaries are heterogeneous oblate spheroid with three layers of different densities, and infinitesimal body varies its mass.

Table 3 Co-ordinates of out-of-plane equilibrium points and the corresponding characteristic roots ($\beta -\gamma$-plane) when both the primaries are heterogeneous oblate spheroid with three layers of different densities, and infinitesimal body varies its mass.

Using the Meshcherskii inverse transformations and putting

$$\begin{aligned} x'= & {} \epsilon ^{-1/2} \alpha _1,\ y'=\epsilon ^{-1/2} \beta _1,\ z' = \epsilon ^{-1/2} \gamma _1,\ \alpha _1' = \epsilon ^{-1/2} \alpha _2,\\ \beta _1'= & {} \epsilon ^{-1/2} \beta _2,\ \gamma _1' = \epsilon ^{-1/2} \gamma _2, \end{aligned}$$

the system (23) can be written in matrix form as

$$\begin{aligned} \left( {\begin{array}{c} \frac{\mathrm{d}x'}{\mathrm{d}t} \\ \frac{\mathrm{d}y'}{\mathrm{d}t} \\ \frac{\mathrm{d}z'}{\mathrm{d}t} \\ \frac{\mathrm{d} \alpha _1'}{\mathrm{d}t} \\ \frac{\mathrm{d}\beta _1'}{\mathrm{d}t} \\ \frac{\mathrm{d}\gamma _1'}{\mathrm{d}t} \\ \end{array}}\right) = A \times \left( \begin{array}{c} x' \\ y' \\ z' \\ \alpha _1' \\ \beta _1' \\ \gamma _1' \end{array}\right) , \end{aligned}$$

(24)

where

$$\begin{aligned} A=\left( \begin{array}{cccccc} \frac{\lambda _1}{2} &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad \frac{\lambda _1}{2} &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad \frac{\lambda _1}{2} &{}\quad 0 &{}\quad 0 &{}\quad 1 \\ (U_{\alpha \alpha })_0 &{}\quad (U_{\alpha \beta })_0 &{}\quad (U_{\alpha \gamma })_0 &{}\quad \frac{\lambda _1}{2} &{}\quad 2n &{}\quad 0 \\ (U_{\beta \alpha })_0 &{}\quad (U_{\beta \beta })_0 &{}\quad (U_{\beta \gamma })_0 &{}\quad -2n &{}\quad \frac{\lambda _1}{2} &{}\quad 0 \\ (U_{\gamma \alpha })_0 &{}\quad (U_{\gamma \beta })_0 &{}\quad (U_{\gamma \gamma })_0 &{}\quad 0 &{}\quad 0 &{}\quad \frac{\lambda _1}{2} \end{array}\right) . \end{aligned}$$

In this problem, the locations of both primaries are invariant and their distances to the equilibrium points are invariable. Therefore stability of (24) and (7) will be consistent with each other. Thus, stability of this solution depends on the existence of stable region of the equilibrium point, which in turn depends on the boundedness of the solution of linear and homogenous system of equation (24).

And hence, the characteristic equation of the coefficient matrix A is

$$\begin{aligned}&64\lambda ^6 - 192 \lambda ^5 \lambda _1 + \lambda ^4 (256 n^2 - 64 U_{\alpha \alpha } - 64 U_{\beta \beta } - 64 U_{\gamma \gamma } \nonumber \\&\quad + 240 \lambda _1^2) + \lambda ^3 (128 n U_{\alpha \beta } - 128 n U_{\beta \alpha } - 512 n^2 \lambda _1 \nonumber \\&\quad + 128 U_{\alpha \alpha } \lambda _1 + 128 U_{\beta \beta } \lambda _1 + 128 U_{\gamma \gamma } \lambda _1 - 160 \lambda _1^3)\nonumber \\&\quad + \lambda ^2 (-64 U_{\alpha \beta } U_{\beta \alpha } + 64 U_{\alpha \alpha } U_{\beta \beta } \nonumber \\&\quad - 64 U_{\alpha \gamma } U_{\gamma \alpha } - 64 U_{\gamma \beta } U_{\beta \gamma } \nonumber \\&\quad - 256 n^2 U_{\gamma \gamma } + 64 U_{\alpha \alpha } U_{\gamma \gamma } + 64 U_{\beta \beta } U_{\gamma \gamma } \nonumber \\&\quad - 192 n U_{\alpha \beta } \lambda _1 + 192 n U_{\beta \alpha } \lambda _1 + 384 n^2 \lambda _1^2 \nonumber \\&\quad - 96 U_{\alpha \alpha } \lambda _1^2 - 96 U_{\beta \beta } \lambda _1^2 - 96 U_{\gamma \gamma } \lambda _1^2 + 60 \lambda _1^4) \nonumber \\&\quad + \lambda (-128 n U_{\beta \gamma } U_{\gamma \alpha } + 128 n U_{\alpha \gamma } U_{\gamma \beta }\nonumber \\&\quad - 128 n U_{\alpha \beta } U_{\gamma \gamma } + 128 n U_{\beta \alpha }U_{\gamma \gamma } + 64 U_{\alpha \beta } U_{\beta \alpha } \lambda _1 \nonumber \\&\quad - 64 U_{\alpha \alpha } U_{\beta \beta } \lambda _1 + 64 U_{\alpha \gamma } U_{\gamma \alpha } \lambda _1 + 64 U_{\beta \gamma } U_{\gamma \beta } \lambda _1 \nonumber \\&\quad + 256 n^2 U_{\gamma \gamma } \lambda _1 - 64 U_{\alpha \alpha } U_{\gamma \gamma } \lambda _1 - 64 U_{\beta \beta } U_{\gamma \gamma } \lambda _1 \nonumber \\&\quad + 96 n U_{\alpha \beta } \lambda _1^2 - 96 n U_{\alpha \beta } \lambda _1^2 - 128 n^2 \lambda _1^3 + 32 U_{\alpha \alpha } \lambda _1^3 \nonumber \\&\quad + 32 U_{\beta \beta } \lambda _1^3 + 32 U_{\gamma \gamma } \lambda _1^3 - 12 \lambda _1^5) + (64 U_{\alpha \gamma } U_{\beta \beta } U{\gamma \alpha } \nonumber \\&\quad - 64 U_{\alpha \beta } U_{\beta \gamma } U_{\gamma \alpha } - 64 U_{\alpha \gamma } U_{\beta \alpha } U_{\gamma \beta } + 64 U_{\alpha \alpha } U_{\beta \gamma } U_{\gamma \beta }\nonumber \\&\quad + 64 U_{\alpha \beta } U_{\beta \alpha } U_{\gamma \gamma } - 64 U_{\alpha \alpha } U_{\beta \beta } U_{\gamma \gamma } + 64 n U_{\beta \gamma } U_{\gamma \alpha } \lambda _1 \nonumber \\&\quad - 64 n U_{\alpha \gamma } U_{\gamma \beta } \lambda _1 + 64 n U_{\alpha \beta } U_{\gamma \gamma } \lambda _1 - 64 n U_{\gamma \gamma } U_{\beta \alpha } \lambda _1 \nonumber \\&\quad - 16 U_{\alpha \beta } U_{\beta \alpha } \lambda _1^2 + 16 U_{\alpha \alpha } U_{\beta \beta } \lambda _1^2 - 16 U_{\alpha \gamma } U_{\gamma \alpha }\lambda _1^2 \nonumber \\&\quad - 16 U_{\beta \gamma } U_{\gamma \beta } \lambda _1^2 - 64 n^2 U_{\gamma \gamma } \lambda _1^2 + 16 U_{\alpha \alpha } U_{\gamma \gamma } \lambda _1^2 \nonumber \\&\quad +16 U_{\beta \beta } U_{\gamma \gamma } \lambda _1^2 - 16 n U_{\alpha \beta } \lambda _1^3 + 16 n U_{\beta \alpha } \lambda _1^3 + 16 n^2 \lambda _1^4 \nonumber \\&\quad - 4 U_{\alpha \alpha } \lambda _1^4 - 4 U_{\beta \beta } \lambda _1^4 - 4 U_{\gamma \gamma } \lambda _1^4 + \lambda _1^6)=0. \end{aligned}$$

(25)

The stability of the system depends upon the nature of the roots of the characteristic equation (25). And when some or all of the characteristic roots have positive real parts, the equilibrium point is unstable. The characteristic roots have been calculated at various values of the mass parameter $\epsilon$ in three planes and given in the Tables 1–3. We observed from the tables that there are at least one positive real root (marked in bold in the tables) or having positive real part corresponding to each equilibrium points. Therefore, all the equilibrium points either in-plane or out-of-planes are unstable.

10 Conclusion

We have investigated the effect of variation of mass of infinitesimal body in the circular restricted three-body problem with heterogeneous primaries having three layers with different densities. After deriving the equations of motion, we have evaluated the Jacobi-integral and then we have illustrated equilibrium points in different planes (in-plane and out-of-planes), zero-velocity curves, regions of motion, zero-velocity surfaces with projections, Poincaré surfaces of section and basins of convergence for the variation of mass parameters. We found at most five equilibrium points in all the planes except for $\epsilon = 1$ which is the case when the mass is constant (Suraj et al. 2018). We have plotted the zero-velocity curves, regions of motion, zero-velocity surfaces with projections corresponding to each equilibrium point by finding the Jacobian constant and got different figures for each Jacobian constant. We also have drawn the Poincaré surfaces of the section in three planes and observed that as the values of mass parameter decrease, the curves corresponding to each value shrink. Then we studied the basins of convergence in all three planes ($\alpha -\beta$, $\alpha -\gamma$ and $\beta -\gamma$) and we observed that all the basins formed by the attractors extend to infinity. Finally, we have examined the stability of the equilibrium points using Meshcherskii space–time inverse transformation and found that all the equilibrium points are unstable.

We also observed that the variation of mass parameters have great impact on the motion of the infinitesimal variable body in the circular restricted three-body problem when the primaries are heterogeneous oblate spheroid with three layers of different densities.

Furthermore, we can extend this work to four- and five-body problems.