1 Introduction

The tomographic intensity mapping of the neutral hydrogen (HI) distribution through redshifted HI 21-cm signal observation is an important probe of cosmological evolution and structure formation in the post-reionization epoch (Bharadwaj & Sethi 2001; Wyithe & Loeb 2009; Loeb & Wyithe 2008; Chang et al. 2008). The astrophysical processes in the epoch of reionization is now believed to have completed by redshift z∼6 (Fan et al. 2006). In the post-reionization era most of the neutral HI gas are housed in the Damped Ly- α (DLA) systems. These DLA clouds are the predominant source of the HI 21-cm signal. Intensity mapping involves a low resolution imaging of diffuse HI 21-cm radiation background without resolving the individual DLAs. Such a tomographic imaging shall naturally provide astrophysical and cosmological data regarding the large scale matter distribution, structure formation and background cosmic history in the post-reionization epoch (Chang et al. 2008; Wyithe 2008; Bharadwaj et al. 2009; Camera et al. 2013; Bull et al. 2015). Several functioning and upcoming radio interferometric arrays like Giant Metrewave Radio Telescope (GMRT)Footnote 1, the Ooty Wide Field Array (OWFA) (Ali & Bharadwaj 2014), the Canadian Hydrogen Intensity Mapping Experiment (CHIME)Footnote 2, the Meer-Karoo Array Telescope (MeerKAT)Footnote 3, the Square Kilometer Array (SKA)Footnote 4 are aimed towards detecting the cosmological 21-cm background radiation. Detecting the 21-cm signal, is however extremely challenging. This is primarily because of the large astrophysical foregrounds (Santos et al. 2005; Di Matteo et al. 2002; Ghosh et al. 2010) from galactic and extra-galactic sources which are several orders of magnitude greater than the signal.

Cross-correlating the 21-cm signal with other probes may be useful towards mitigating the severe effect of foreground contaminants and other systematic effects which plague the signal. The main advantage of cross-correlation is that the cosmological origin of the signal can only be ascertained only if it is detected with high statistical significance in cross-correlation. Cosmological parameter estimation often involves a joint analysis of two data sets and this would require not only the auto-correlation but also cross-correlation information. Further, the two different probes may focus on specific k-modes with high signal-to-noise ratio and in such cases the cross-correlation signal takes advantage of the different probes simultaneously. This has been studied extensively in the case of the BAO (Guha Sarkar & Bharadwaj 2013). It is to be noted that if the observations of the distinct probes are perfect, there shall be no new advantage of using the cross correlation. However, we expect the first generation observations of the redshifted HI 21-cm signal to have large systematic errors and foreground residuals. For a detection of the 21-cm signal and subsequent cosmological investigations, these measurements can be cross-correlated with other large scale structure tracers to yield information from the 21-cm signal which may not be possible to obtain using the low SNR auto correlation signal. In this article, we consider the cross-correlation of the 21-cm signal with the Ly- α flux distribution. On large scales, both the Ly- α forest absorbed flux and the redshifted 21-cm signal are believed to be biased tracers of the underlying Dark Matter (DM) distribution (McDonald 2003; Bagla et al. 2010; Guha Sarkar et al. 2012; Villaescusa-Navarro et al. 2014). The clustering of these signals, is then, directly related to the underlying dark matter power spectrum. We investigate the possibility of using the cross-correlation of the 21-cm signal and the Ly- α forest for cosmological parameter estimation, neutrino mass measurement, studying BAO features and primordial bispectrum. We also investigate the possibility of correlating the post-reionization 21-cm signal with CMBR maps like the weak lensing and ISW anisotropies.

2 Cross-correlation between cosmological signals (general formalism)

Consider two cosmological fields A(k) and B(k). These could, for example, represent two tracers of large scale structure. We define the cross correlation estimator \(\hat {E}\) as follows:

$$ \hat{E} = \frac{1}{2}\ [ A B^{*} \ + \ B A^{*} ]. $$
(1)

We note that A and B can be complex fields. We are interested in the variance

$$ \sigma_{\hat{E}}^{2} = \langle {\hat{E}}^{2} \rangle - {\ \langle \hat{E} \rangle}^{2}. $$
(2)

Noting that 〈A(k) A(k)〉=〈A(k) A ∗(−k)〉=0, we have

$$ \langle {\hat{E}}^{2} \rangle = \frac{1}{2} \ [ \langle AA^{*}\rangle \langle BB^{*}\rangle \ + \ {|\langle AB \rangle |}^{2} \ + \ 3 \ {|\langle AB^{*} \rangle |}^{2} ]. $$
(3)

Further, the term 〈A B〉 can be dropped since

$$ \langle A ({\mathbf{k}})B({\mathbf{k}}) \rangle = \langle A({\mathbf{k}}) B^{*}(-{ \mathbf{k}}) \rangle = C \delta_{{\mathbf{k}}, {-{\mathbf{k}}}}= 0. $$
(4)

This gives

$$ \sigma_{\hat{E}}^{2} = \langle{\hat{E}}^{2} \rangle - {\ \langle \hat{E} \ \rangle}^{2} = \ \frac{1}{2} [ \langle AA^{*}\rangle \langle BB^{*}\rangle \ + \ {|\langle AB \rangle |}^{2}]. $$
(5)

The variance is suppressed by a factor of N c for that many number of independent estimates. Thus, finally we have

$$ \sigma_{\hat{E}}^{2} = \frac{1}{2N_{c}} [ \langle AA^{*}\rangle \langle BB^{*}\rangle \ + \ {|\langle AB \rangle |}^{2} ]. $$
(6)

3 Cross-correlation of post-reionization 21-cm signal with Lyman- α forest

Neutral gas in the post-reionization epoch produces distinct absorption features in the spectra of background quasars (Rauch 1998). The Ly- α forest traces the HI density fluctuations along one-dimensional quasar lines-of-sight. The Ly- α forest observations finds several cosmological applications (Croft et al. 1999b; Mandelbaum et al. 2003; Lesgourgues et al. 2007; Croft et al. 1999a; McDonald & Eisenstein 2007; Gallerani et al. 2006). On large cosmological scales, the Ly- α forest and the redshifted 21-cm signal are, both expected to be biased tracers of the underlying dark matter (DM) distribution (McDonald 2003; Bagla et al. 2010; Guha Sarkar et al. 2012; Villaescusa-Navarro et al. 2014). This allows to study their cross clustering properties in n-point functions. Also the Baryon Oscillation Spectroscopic Survey (BOSS)Footnote 5 is aimed towards probing the dark energy through measurements of the BAO signature in Ly- α forest (Delubac et al. 2014). The availability of Ly- α forest spectra with high signal-to-noise ratio for a large number of quasars from the BOSS survey allows 3D statistics to be done with Ly- α forest data (Pâris et al. 2014; Slosar et al. 2011).

Detection these signals are observationally challenging. For the HI 21-cm, a detection of the signal requires careful modeling of the foregrounds (Ghosh et al. 2011; Alonso et al. 2015). Some of the difficulties faced by Ly- α observations include proper modelling of the continuum, fluctuations of the ionizing sources, poor modeling of the temperature-density relation (McDonald et al. 2001) and metal lines contamination in the spectra (Kim et al. 2007). The two signals are tracers of the underlying dark matter distribution. Thus they are correlated on large scales. However foregrounds and other systematics are uncorrelated between the two independent observations. Hence, the cosmological nature of a detected signal can be only ascertained in a cross-correlation. The 2D and 3D cross correlation of the redshifted HI 21-cm signal with other tracers such as the Ly- α forest, and the Lyman break galaxies have been proposed as a way to avoid some of the observational issues (Guha Sarkar et al. 2011; Villaescusa-Navarro et al. 2015). The foregrounds in HI 21-cm observations appear as noise in the cross correlation and hence, a significant degree foreground cleaning is still required for a detection.

We use δ T to denote the redshifted 21-cm brightness temperature fluctuations and \(\delta _{\mathcal {F}}\) as the fluctuation in the transmitted flux through the Ly- α forest. We write \(\delta _{\mathcal {F}}\) and δ T in Fourier space as

$$ \delta_{a}(\mathbf{r}) = \int \ \frac{\mathrm{d}^{3} {\mathbf{k}}}{(2\pi)^{3}} \ \mathrm{e}^{i {\mathbf{k}}. \mathbf{r}} {\Delta}_{a}({\mathbf{k}}) \,, $$
(7)

where \(a={\mathcal {F}}\) and T refer to the Ly- α forest transmitted flux and 21-cm brightness temperature respectively. On large scales, we may write

$$ {\Delta}_{a}({\mathbf{k}}) = C_{a} [1 + \beta_{a} \mu^{2}] {\Delta}({\mathbf{k}}), $$
(8)

where Δ(k) is the dark matter density contrast in Fourier space and μ denotes the cosine of the angle between the line-of-sight direction \(\hat {\mathbf {n}}\) and the wave vector (\( \mu = \hat {\mathbf {k}} \cdot \hat {\mathbf {n}}\)). β a is similar to the linear redshift distortion parameter. The corresponding power spectra are

$$ P_{a}(k, \mu)= {C_{a}^{2}} [1 + \beta_{a} \mu^{2}]^{2} P(k), $$
(9)

where P(k) is the dark matter power spectrum.

For the 21-cm brightness temperature fluctuations, we have

$$ C_{T} = 4.0 \, {\text{mK}} \, b_{T} \, {\bar{x}_{\text{HI}}}(1 + z)^{2}\left( \frac{{\Omega}_{b0} h^{2}}{0.02} \right) \left( \frac{0.7}{h} \right) \left( \frac{H_{0}}{H(z)} \right). $$
(10)

The neutral hydrogen fraction \({\bar {x}_{\text {HI}}}\) is assumed to be a constant with a value \( {\bar {x}_{\text {HI}}} = 2.45 \times 10^{-2}\) (Lanzetta et al. 1995; P’eroux et al. 2003; Noterdaeme et al. 2009). For the HI 21-cm signal, the parameter β T is the ratio of the growth rate of linear perturbations f(z) and the HI bias b T . The 21-cm bias is assumed to be a constant. This assumption of linear bias is supported by several independent numerical simulations (Bagla et al. 2010; Guha Sarkar et al. 2012) which shows that over a wide range of k modes, a constant bias model adequately describes the 21-cm signal for z<3. We have adopted a constant bias b T =2 from simulations (Bagla et al. 2010; Guha Sarkar et al. 2012; Villaescusa-Navarro et al. 2014). For the Ly- α forest, \(\beta _{\mathcal {F}}\) can not be interpreted in the usual manner as β T . This is because Ly- α transmitted flux and the underlying dark matter distribution (Slosar et al. 2011) do not have a simple linear relationship. The parameters \((C_{\mathcal {F}}, \beta _{\mathcal {F}})\) are independent of each other.

We adopt approximately \((C_{\mathcal {F}}, \beta _{\mathcal {F}}) \approx (-0.15, 1.11 )\) from the numerical simulations of Ly- α forest (McDonald 2003). We note that for cross-correlation studies the Ly- α forest has to be smoothed to the observed frequency resolution of the HI 21-cm frequency channels.

We now consider the 3D cross-correlation power spectrum of the HI 21-cm signal and Ly- α forest flux. We consider an observational survey volume V which on the sky plane consists of a patch L×L and of line-of-sight thickness l along the radial direction. We consider the flat sky approximation. The Ly- α flux fluctuations are now written as a 3-D field

$$ \delta_{\mathcal{F}}(\vec{r})= \left[ \ \frac{ {\mathcal{F}}(\vec{r}) - {\bar{\mathcal{F}}}}{{\bar{\mathcal{F}}}} \ \right]. $$
(11)

The observed quantity is \(\delta _{{\mathcal {F}} \mathrm {o}}(\vec {r}) =\delta _{{\mathcal {F}} \mathrm {o}}(\vec {r}) \times \rho (\vec {r}) \), where the sampling function \(\rho (\vec {r})\) is defined as

$$ \rho(\vec{r}) =\frac {{\sum}_{a} w_{a} \ {\delta_{D}^{2}}(\vec{r}_{\perp} - \vec{r}_{\perp a})} {l {\sum}_{a} w_{a}} $$
(12)

and is normalized to unity (\(\int \mathrm {d}V \rho (\vec {r}) = 1\)). The summation as before extends up to N. The weights w a shall, in general, be related to the pixel noise. However, for measurements of transmitted height SNR flux, the effect of the weight functions can be ignored. With this simplification we have used w a =1, so that \({\sum }_{a} w_{a} = N\). In Fourier space, we have

$$ {\Delta}_{\mathcal{F}}(\vec{k}) = {\int}_{-L/2}^{L/2} {\int}_{-L/2}^{L/2} {\int}_{-l/2}^{l/2} \mathrm{d}^{2}{\vec{r_{\perp}}} \mathrm{d}r_{\parallel} \ \mathrm{e}^{i \vec{k} \cdot \vec{r}} \ \delta_{\mathcal{F}}(\vec{r}). $$
(13)

One may relate \(\vec {k}_{\perp } \) to \(\vec {U}\) as \(\vec {k}_{\perp }= \frac { 2 \pi \vec {U}}{r}\). We have, in Fourier space,

$$ {\Delta}_{{\mathcal{F}} \mathrm{o}}(\vec{k}) = \tilde{\rho}(\vec{k}) \otimes {{\Delta}_{\mathcal{F}}}(\vec{k}) + {\Delta}_{\mathrm{N}\mathcal{F}}(\vec{k}), $$
(14)

where \(\tilde {\rho }\) is the Fourier transform of ρ and ⊗ denotes a convolution defined as

$$ \tilde{\rho}(\vec{k}) \otimes {{\Delta}_{\mathcal{F}}}(\vec{k}) = \frac{1}{V} {\sum}_{\vec{k}^{\prime}} \ \tilde{\rho}(\vec{k} - \vec{k}^{\prime}) {{\Delta}_{\mathcal{F}}}(\vec{k}^{\prime}). $$
(15)

\( {\Delta }_{N\mathcal {F}}(\vec {k})\) denotes a possible noise term. Similarly the 21-cm signal in Fourier space is written as

$$ {\Delta}_{{T} \mathrm{o}}(\vec{k}) = {\Delta}_{T}(\vec{k}) + {\Delta}_{NT}(\vec{k}), $$
(16)

where Δ N T is the corresponding noise.

The cross-correlation 3-D power spectrum \( P_{c} (\vec {k})\) for the two fields is defined as

$$ \langle {\Delta}_{{\mathcal{F}}}(\vec{k}) {\Delta}^{*}_{T}(\vec{k}^{\prime}) \rangle = V P_{c} (\vec{k}) \delta_{\vec{k}, \vec{k}^{\prime}} $$
(17)

Similarly, we define the two auto-correlation multi frequency angular power spectra, \( P_{T} (\vec {k})\) for 21-cm radiation and \(P_{\mathcal {F}}(\vec {k})\) for Lyman- α forest flux fluctuations as

$$ \langle {\Delta}_{T}(\vec{k}) {\Delta}^{*}_{T}(\vec{k}^{\prime}) \rangle = V P_{T} (\vec{k}) \delta_{\vec{k}, \vec{k}^{\prime}}, $$
(18)
$$ \langle {\Delta}_{\mathcal{F}}(\vec{k}) {\Delta}^{*}_{\mathcal{F}}(\vec{k}^{\prime}) \rangle = V P_{\mathcal{F}} (\vec{k}) \delta_{\vec{k}, \vec{k}^{\prime}}. $$
(19)

We define the cross-correlation estimator \(\hat {\mathcal {E}}\) as

$$ \hat{\mathcal{E}}(\vec{k}, \vec{k}^{\prime} ) = \frac{1}{2} [ {\Delta}_{{\mathcal{F}} \mathrm{o}}(\vec{k}) {\Delta}^{*}_{{T}\mathrm{o}}(\vec{k}^{\prime}) + {\Delta}^{*}_{{\mathcal{F}} \mathrm{o}}(\vec{k}) {\Delta}_{{T}\mathrm{o}}(\vec{k}^{\prime}) ]. $$
(20)

We are interested in the various statistical properties of this estimator. Using the definitions of \({\Delta }_{{\mathcal {F}}\mathrm {o}}(\vec {k})\) and \({\Delta }_{T\mathrm {o}}(\vec {k})\), we have the expectation value of \(\hat {\mathcal {E}}\) as

$$\begin{array}{@{}rcl@{}} {}\langle \hat{\mathcal{E}}(\vec{k}, \vec{k}^{\prime} ) \rangle &=& \frac{1}{2} \langle [\tilde{\rho}(\vec{k}) \otimes {{\Delta}_{\mathcal{F}}}(\vec{k}) + {\Delta}_{N\mathcal{F}}(\vec{k})] \times [ {\Delta}^{*}_{T}(\vec{k}^{\prime}) + {\Delta}^{*}_{NT}(\vec{k}^{\prime})] \rangle \\ &&+ \frac{1}{2} \langle [\tilde{\rho}^{*}(\vec{k}) \otimes {{\Delta}_{\mathcal{F}}}^{*}(\vec{k}) + {\Delta}_{N\mathcal{F}}^{*}(\vec{k})] \times [{\Delta}_{T}(\vec{k}^{\prime}) + {\Delta}_{NT}(\vec{k}^{\prime}) ] \rangle. \end{array} $$
(21)

We assume that the quasars are distributed in a random fashion, are not clustered and the different noises are uncorrelated. Further, we note that the quasars are assumed to be at a redshift different from the rest of the quantities and hence ρ is uncorrelated with both Δ T and \({\Delta }_{\mathcal {F}}\). Therefore we have

$$ \langle \hat{\mathcal{E}}(\vec{k}, \vec{k}^{\prime}) \rangle = \frac{1}{V} {\sum}_{\vec{k^{\prime\prime}}} \langle \tilde{\rho} (\vec{k} - \vec{k}^{\prime\prime}) \rangle \times V P_{\mathcal{F}T} (\vec{k}^{\prime\prime}) \delta_{\vec{k}^{\prime\prime}, \vec{k}^{\prime}}. $$
(22)

Noting that

$$ \langle \tilde{\rho}(\vec{k}) \rangle = \delta_{\vec{k}_{\perp},0}\delta_{\vec{k}_{\parallel},0}, $$
(23)

we have

$$ \langle \hat{\mathcal{E}}(\vec{k},\vec{k}^{\prime} ) \rangle = P_{\mathcal{F} T} (\vec{k}) \delta_{\vec{k}, \vec{k}^{\prime}}. $$
(24)

Thus, the expectation value of the estimator faithfully returns the quantity we are probing, namely the 3-D cross-correlation power spectrum \( P_{\mathcal {F}T} (\vec {k})\).

We next consider the variance of the estimator \(\hat {\mathcal {E}}\) defined as

$$ \sigma_{\hat{\mathcal{E}}}^{2} = \langle {\hat{\mathcal{E}}}^{2} \rangle - {\langle \hat{\mathcal{E}} \rangle} ^{2}, $$
(25)
$$\begin{array}{@{}rcl@{}} \sigma_{\hat{\mathcal{E}}}^{2} = \frac{1}{2} \langle {\Delta}_{{\mathcal{F}} \mathrm{o}} (\vec{k}) {\Delta}_{{\mathcal{F}} \mathrm{o}}^{*}(\vec{k}) \rangle \langle {\Delta}_{T\mathrm{o}} (\vec{k}^{\prime}) {\Delta}_{T\mathrm{o}}^{*}(\vec{k}^{\prime}) \rangle + \frac{1}{2} {| \langle {\Delta}_{{\mathcal{F}} \mathrm{o}} (\vec{k}) {\Delta}_{T\mathrm{o}}^{*} (\vec{k}^{\prime}) \rangle |}^{2} \end{array} $$
(26)

We saw that

$$ \langle {\Delta}_{{\mathcal{F}}\mathrm{o}} (\vec{k}) {\Delta}_{T\mathrm{o}}^{*} (\vec{k}^{\prime})\rangle = P_{\mathcal{F}T} (\vec{k}) \delta_{\vec{k}, \vec{k}^{\prime}} $$
(27)

and we note that

$$ \langle {\Delta}_{T\mathrm{o}} (\vec{k}) {\Delta}_{T\mathrm{o}}^{*} (\vec{k}) \rangle = V [ P_{T} (\vec{k}) + N_{T} (\vec{k})], $$
(28)

where N T is the 21-cm noise power spectrum. We also have for the Ly- α forest

$$ \langle {\Delta}_{{\mathcal{F}}\mathrm{o}} (\vec{k}) {\Delta}_{{\mathcal{F}} \mathrm{o}}^{*}(\vec{k}) \rangle = \langle \tilde{\rho}(\vec{k}) \otimes {{\Delta}_{\mathcal{F}}}(\vec{k}) \ \tilde{\rho}^{*}(\vec{k}) \otimes {{\Delta}_{\mathcal{F}}}^{*}(\vec{k}) \rangle + N_{\mathcal{F}} L^{2}, $$
(29)

where \( N_{\mathcal {F}}\) is the noise power spectrum corresponding to the Ly- α flux fluctuations. Using the relation

$$ \langle \tilde{\rho}(\vec{k}) \tilde{\rho}^{*}(\vec{k^{\prime}}) \rangle = \frac{1}{N} \delta_{\vec{k_{\perp}}, \ \vec{k^{\prime}_{\perp}}} \delta_{k_{\parallel,0}} \delta_{k^{\prime}_{\parallel,0}} + \left( 1 - \frac{1}{N}\right) \delta_{\vec{k}, 0} \delta_{\vec{k^{\prime}}, 0}, $$
(30)

we have

$$\begin{array}{@{}rcl@{}} {}\langle {\Delta}_{{\mathcal{F}}\mathrm{o}} (\vec{k}) {\Delta}_{{\mathcal{F}} \mathrm{o}}^{*}(\vec{k}) \rangle \,=\, \frac{1}{V^{2}} {\sum}_{\vec{k_{1}},\vec{k_{2}}} \langle \tilde{\rho}(\vec{k} \,-\, \vec{k}_{1}) \tilde{\rho}^{*}(\vec{k} \,-\, \vec{k}_{2})\rangle \langle {\Delta}_{\mathcal{F}}(\vec{k}_{1\perp}, k_{1\parallel}) {\Delta}_{\mathcal{F}}^{*}(\vec{k}_{2\perp}, k_{2\parallel})\rangle \end{array} $$
(31)

or

$$\begin{array}{@{}rcl@{}} \langle {\Delta}_{\mathcal{F}\mathrm{o}} (\vec{k}) {\Delta}_{\mathcal{F}\mathrm{o}}^{*}(\vec{k}) \rangle &=& \frac{1}{V^{2}} {\sum}_{\vec{k_{1}},\vec{k_{2}}} \delta_{(\vec{k}-\vec{k_{1}}),0} \delta_{(\vec{k}-\vec{k_{2}}),0}\\ &&+ \frac{1}{N} (\delta_{(\vec{k_{\perp}}-\vec{k_{1\perp}}),(\vec{k_{\perp}}-\vec{k_{2\perp}})} \delta_{({k_{\parallel}}-{k_{1\parallel}}),({k_{\parallel}}-{k_{2\parallel}})}) \\ &&\times \langle {\Delta}_{\mathcal{F}}(\vec{k}_{1\perp}, k_{1\parallel}) {\Delta}_{\mathcal{F}}^{*}(\vec{k}_{2\perp}, k_{2\parallel})\rangle \end{array} $$
(32)

This gives

$$\begin{array}{@{}rcl@{}} \sigma_{\hat{\mathcal{E}}}^{2} = \frac{1}{2} \left[ \frac{1}{N} {\sum}_{\vec{k_{\perp}}} P_{\mathcal{F}}(\vec{k}) + P_{\mathcal{F}}(\vec{k}) + N_{\mathcal{F}} \right] \times [ P_{T} (\vec{k}) + N_{T}] + \frac{1}{2} P_{\mathcal{F}T}^{2}. \end{array} $$
(33)

Writing the summation as an integral, we get

$$\begin{array}{@{}rcl@{}} \sigma_{\hat{\mathcal{E}}}^{2} = \frac{1}{2} \left[ \frac{1}{\bar{n}} \left( \int \mathrm{d}^{2} \vec{k_{\perp}} \ P_{\mathcal{F}}(\vec{k}) \right) + P_{\mathcal{F}}(\vec{k}) + N_{\mathcal{F}} \right] \times[ P_{T} (\vec{k}) + N_{T}] + \frac{1}{2} P_{\mathcal{F}T}^{2}, \end{array} $$

where \(\bar {n}\) is the angular density of quasars and \(\bar {n} = N/ L^{2}\). We assume that the variance \(\sigma ^{2}_{{\mathcal {F}} N}\) of the pixel noise contribution to \(\delta _{\mathcal {F}}\) is a constant and is same across all the quasar spectra whereby we have \(N_{\mathcal {F}} = {\sigma }^{2}_{{\mathcal {F}} N}/\bar {n}\) for its noise power spectrum. An uniform weighing scheme for all quasars is a good approximation when most of the spectra are measured with a sufficiently high SNR (McQuinn & White 2011). We have not incorporated quasar clustering which is supposed to be sub-dominant as compared to Poisson noise. In reality, the clustering would enhance the term \( (P^{\mathrm {1D}}_{\mathcal {F} \mathcal {F}}(k_{\parallel }) P^{\text {{2D}}}_{w} + N^{}_{\mathcal {F}})\) by a factor \((1 + {\bar n} C_{Q}(\mathbf {k}_{\perp }))\), where C Q (k ⊥) is the angular power spectrum of the quasars (Myers et al. 2007).

For a radio-interferometric measurement of the 21-cm signal, we have (McQuinn et al. 2006; Wyithe et al. 2008)

$$ N_{T} (k,\nu)=\frac{T_{\text{sys}}^{2}}{B t_{0}} \left( \frac{\lambda^{2}}{A_{\mathrm{e}}} \right)^{2} \frac{r_{\nu}^{2} L}{n_{b}(U,\nu)} $$
(34)

Here T sys denotes the system temperature. B is the observation bandwidth, t 0 is the total observation time, r ν is the comoving distance to the redshift z, n b (U,ν) is the density of baseline U, and A e is the effective collecting area of each antenna.

3.1 The cross correlation signal and constraints with SKA

We investigate the possibility of detecting the signal using the upcoming SKA-mid phase1 telescope and future Ly- α forest surveys with very high quasar number densities. Two separate telescopes named SKA-low and SKA-mid operating at two different frequency bands will be constructed in Australia and South Africa respectively in two phases. For this work, we consider the instruments SKA1-mid which will be built in phase 1. The instrument specifications such as the total number of antennae, antenna distribution, frequency coverage, total collecting area etc., have not been fixed yet and might change in future. We use the specifications considered in the ‘Baseline Design Document’ and ’SKA Level 1 Requirements (revision 6)’ which are available on the SKA websiteFootnote 6. We assume that the SKA1-mid will operate in the frequency range from 350 MHz to 14 GHz. It shall have 250 antennae of 7.5 m radius each. We use the baseline distribution given in figure 6 – blue line of Villaescusa-Navarro et al. (2015) for the calculation presented here. We note that, the baseline distribution used here is consistent with the projected antenna that layout distribution with 40, 54, 70, 81 and 100% of the total antennae that are assumed to be enclosed within 0.4, 1, 2.5, 4 and 100 km radius respectively.

The fiducial redshift of z=2.5 is justified since the quasar distribution peaks in the range 2<z<3. Only a smaller part of the quasar spectra corresponding to an approximate band Δz∼0.4 is used to avoid contamination from metal lines and quasar proximity effect. The cross-correlation can however only be computed in the region of overlap between the 21-cm signal and the Ly- α forest field.

Figure 1(a) shows the dimensionless redshift space 21-cm power spectrum (\({\Delta }^{2}_{T}(k_{\perp }, k_{||})=k^{3} P_{T}(k_{\perp }, k_{||})/2 \pi ^{2}\)) at z=2.5. We can see that the power spectrum is not circularly symmetric in the (k ||, k ⊥) plane. The asymmetry is related to the redshift space distortion parameter. Figure 1(b) shows the 21-cm and Ly- α cross-power spectrum.

Figure 1
figure 1

Figure shows the power spectrum in 3D redshift space at z=2.5. (a) The HI 21-cm power spectrum \({\Delta }_{T}^{2} = k^{3} P_{TT}(\mathbf {k})/ 2 \pi ^{2}\) and (b) the 3D cross-correlation power spectrum \( {\Delta }_{\mathrm {C}}^{2} = k^{3} P_{T \mathcal {F}}(\mathbf {k})/ 2 \pi ^{2}\). The redshift space distortion reveals the departure from spherical symmetry of the power spectrum (Guha Sarkar et al. 2012).

Full size image

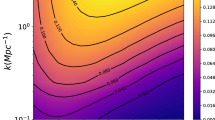
We first consider that a perfect foreground subtraction is achieved. The left panel of Fig. 2 shows the contours of SNR for the 21-cm auto correlation power spectrum for a 400 h observation and a total bandwidth of 32 MHz at a frequency 405.7 MHz. We have taken a bin (Δk,Δ𝜃)=(k/5,π/10). The SNR reaches the peak (>20) at intermediate value of (k ⊥,k ∥)=(0.4,0.4) Mpc−1. We find that 5σ detection is possible in the range 0.08≲k ⊥≲0.6 Mpc−1 and 0.1≲k ∥≲1.5 Mpc−1. The range for the 10σ detection is 0.12≲k ⊥≲0.5 Mpc−1 and 0.2≲k ∥≲1.2 Mpc−1. At lower values of k the noise is expected to be dominated by cosmic variance whereas, the noise is predominantly of instrumental origin at large k.

Figure 2
figure 2

The left panel shows SNR contours for the 21-cm auto-correlation power spectrum in redshift space at z=2.5. We have considered a 400 h observation at 405 MHz and assumed that complete foreground cleaning is done. The right panel shows the SNR contours for the cross-correlation signal (Guha Sarkar et al. 2012).

Full size image

The right panel of Fig. 2 shows the SNR contours for the Ly- α 21-cm cross-correlation power spectrum. For the 21-cm signal, a 400 h observation is considered. We have taken \(\bar n = 30\, \text {deg}^{-2}\), and the Ly- α spectra are assumed to be measured at a 2σ sensitivity level. We use β F to be 1.11 and overall normalization factor C F=−0.15 consistent with recent measurements (Slosar et al. 2011). Although the overall SNR for the cross-power spectrum is lower compared to the 21-cm auto power spectrum, 5σ detection is ideally possible for the 0.1≲k ⊥≲0.4 Mpc−1 and 0.1≲k ∥≲1 Mpc−1. The SNR peaks (> 10) at (k ⊥,k ∥)∼(0.2,0.3) Mpc−1. The error in the cross-correlation can be reduced either by increasing the QSO number density or by increasing the observing time for HI 21-cm survey. The QSO number density is already in the higher side for the BOSS survey that we consider. The only way to reduce the variance is to consider more observation time for HI 21-cm survey and enhance the volume of the survey.

3.2 Parameter estimation using cross-correlation

We now consider the precision at which we can constrain various model parameters using the Fisher matrix analysis. Figure 3 shows the 68.3,95.4 and 99.8% confidence contours obtained using the Fisher matrix analysis for the parameters \(A, \beta _{T}, \beta _{\mathcal {F}}, {\Omega }_{\Lambda }\). Table 1 summarizes the 1−σ error for these parameters. The parameters (ΩΛ,A) are constrained much better than \(\beta _{\mathcal {F}}\) and β T at 3.5% and 8%. The error projections presented here are for a single field of view radio observation. The noise scales as \( \sigma / \sqrt N\), where N is the number of pointings.

Figure 3
figure 3

The 68.3, 95.4 and 99.8% confidence ellipses for the parameters \(A, \beta _{T}, \beta _{\mathcal {F}}, {\Omega }_{\Lambda }\) (Guha Sarkar et al. 2012).

Full size image
Table 1 1−σ error on various cosmological parameters for a single field observation.
Full size table

We also consider conditional error on each of the parameters assuming that the other three are known. The projected 1−σ error in β T and \(\beta _{\mathcal {F}}\) are 8.5 and 4.5% respectively for single pointing. For 10 independent radio observations the conditional errors improve to 2.7, 1.4, 0.4 and 0.6% for β T , \(\beta _{\mathcal {F}}\), ΩΛ and A respectively. These constraints on the redshift space distortion parameters β from our cross-correlation analysis are found to be quite competitive with other cosmological probes (Font-Ribera et al. 2012; Slosar et al. 2011). Further, we note that higher density of QSOs and improved SNR for the individual QSO spectra shall also provide stronger constraints.

3.3 BAO imprint on the cross-correlation signal

The characteristic scale of the BAO is set by the acoustic horizon s at the epoch of recombination The comoving length-scale s defines an angular scale 𝜃 s = s[(1 + z)D A(z)]−1 in the transverse direction and a radial redshift interval Δz s = s H(z)/c, where D A(z) and H(z) are the angular diameter distance and Hubble parameter respectively. The comoving acousic horizon scale s=143 Mpc correspond to an angle 𝜃 s =1.38∘ and reshift interval Δz s =0.07 at redshift z=2.5. Measurement of 𝜃 s and Δz s separately, allows the determination of D A(z) and H(z) separately and thereby constrain background cosmological evolution. Here we consider the possibility of measurement of these two parameters from the imprint of BAO features on the cross-correlation power spectrum.

The Fisher matrix is given by (Guha Sarkar & Bharadwaj 2013)

$$ F_{i j} = \frac{V}{(2 \pi)^{3}} \int \, \, \frac{\mathrm{d}^{3} \mathbf{k}}{[P^{2}_{\mathcal{F}T}(\mathbf{k})+ P_{\mathcal{F} \mathcal{F} \mathrm{o}}(\mathbf{k}) P_{TT\mathrm{o}}(\mathbf{k})]} \frac{\partial P_{\mathcal{F} T}(\mathbf{k})}{\partial q_{i}} \frac{\partial P_{\mathcal{F} T}(\mathbf{k})}{\partial q_{j}}, $$
(35)

where q i refer to the cosmological parameters to be constrained. This BAO signal is mainly present at small k (large scales) with the first peak at roughly k∼0.045 Mpc−1. The subsequent oscillations are highly suppressed by k∼0.3 Mpc−1 which is within the limits of the k ⊥ and k ∥ integrals. We use P b = P−P c to isolate the purely baryonic features, and we use this in ∂ P(k)/∂ q i . Here, P c is the CDM power spectrum without the baryonic features. This gives

$$ P_{b}(\mathbf{k}) = \sqrt{8 \pi^{2}} A \, \frac{\sin x}{x} \, \exp \left[ - {\left( \frac{k}{k_{\text{silk}}} \right)}^{1.4} \right] \, \exp \left[{ - \left( \frac{k^{2}}{2 k_{\text{nl}}^{2}}\right)} \right] $$
(36)

where k silk and k nl denotes the scale of silk-damping and non-linearity respectively. We have used k nl=(3.07 h−1Mpc)−1 and k silk=(7.76 h−1Mpc)−1 from Seo & Eisenstein (2007). The quantity \( x = \sqrt { k_{\perp }^{2} s_{\perp }^{2} + k_{\parallel }^{2} s_{\parallel }^{2}}\), where s ⊥ and s ∥ corresponds to 𝜃 s and Δz s in units of distance. A is an overall normalization constant. The value of s is well constrained from CMBR data. Changes in D A and H(z) manifest as the corresponding changes in the values of s ⊥ and s ∥ respectively, and thus the fractional errors in s ⊥ and s ∥ correspond to fractional errors in D A and H(z) respectively. We choose \(q_{1} = \ln (s_{\perp }^{-1})\) and q 2= ln(s ∥) as the cosmological parameters to be constrained, and determine the precision at which it will be possible to measure these using the BAO imprint in the cross-correlation power spectrum. We use the formalism outlined in Seo & Eisenstein (2007), whereby we construct the 2−D Fisher matrix

$$ F_{ij} = V A^{2} \int \mathrm{d} k {\int}_{-1}^{1} \mathrm{d} \mu \frac{k^{2} \exp[-2 (k/k_{\text{silk}})^{1.4} - (k/k_{\text{nl}})^{2}]} {[P_{\mathcal{F}T}^{2}(k)+ P_{\mathcal{F} \mathcal{F}\mathrm{o}}(\mathbf{k}) P_{TT\mathrm{o}}(\mathbf{k})/F^{2}_{\mathcal{F} T}(\mu)]} f_{i}(\mu) f_{j}(\mu), $$
(37)
$$ F_{\mathcal{F}T}(\mu)= \frac{H(z)}{r^{2} c} C_{\mathcal{F}} C_{T} \, (1 + \beta_{\mathcal{F}} \mu^{2}) (1 + \beta_{T} \mu^{2}), $$
(38)

where f 1 = μ 2−1 and f 2 = μ 2. The Cramer–Rao bound \(\delta q_{i} = \sqrt {F^{-1}_{ii}}\) is used to calculate the maximum theoretical error in the parameter q i . A combined distance measure D V, also referred to as the ‘dilation factor’ (Eisenstein et al. 2005)

$$ D_{\mathrm{V}}(z)^{3} = (1 + z)^{2} D_{\mathrm{A}}(z) \frac{c z}{H(z)} $$
(39)

is often used as a single parameter to quantify BAO observations. We use \(\delta D_{\mathrm {V}}/ D_{\mathrm {V}} = \frac {1}{3} (4 F^{-1}_{11} + 4 F^{-1}_{12} + F^{-1}_{22} )^{0.5}\) to obtain the relative error in D V. The dilation factor is known to be particularly useful when the individual measurements of D A and H(z) have low signal-to-noise ratio.

The Fisher matrix formalism is used to determine the accuracy with which it will be possible to measure cosmological distances using this cross-correlation signal.

The limits \(\bar {n}_{\mathrm {Q}} \rightarrow \infty \) and N T →0, which correspond to \(P_{\mathcal {F} \mathcal {F}\mathrm {o}} \rightarrow P_{\mathcal {F} \mathcal {F}}\) and P T To→P T T , sets the cosmic variance–cosmic variance limit. In this limit, where the SNR depends only on the survey volume corresponding to the total field-of-view we have δ D V/D V=0.15%, δ H/H=0.25% and D A/D A=0.15% which are independent of any of the other observational details. The fractional errors decrease slowly beyond \(\bar {n}_{Q} \!>\! 50~\text {deg}^{-2}\) or N T <10−6 mK2. We find that parameter values \(\bar {n}_{Q} \sim 6 \, \text {deg}^{-2}\) and N T ∼4.7×10−5 mK2, attainable with BOSS and SKA1-mid are adequate for a 1% accuracy, whereas \(\bar {n}_{Q} \sim 2 \, \text {deg}^{-2}\) and N T ∼3×10−3 mK2 are adequate for ∼10 % accuracy in measurement of D V. With a BOSS-like survey, it is possible to achieve the fiducial value δ D V/D V=2.0% from the cross-correlation at N T = 2.9 × 10−4 mK2. The error varies slower than \(\sqrt {N_{T}}\) in the range N T =10−4 mK2 to N T =10−5 mK2. We have (δ D V/D V,δ D A/D A,δ H/H)=(1.3,1.5,1.3) % and (0.67,0.78,0.74) % at N T =10−4 mK2 and at N T =10−5 mK2, respectively. The errors do not significantly go down much further for N T <10−5 mK2, and we have (0.55,0.63,0.63) % at N T =10−6 mK2.

3.4 Constraints on neutrino mass

Free streaming of neutrinos causes a power suppression on large scales. This suppression of dark matter power spectrum shall imprint itself on the cross-correlation of Ly- α forest and 21-cm signal (Pal & Guha Sarkar 2016). We have suggested this as a possible way to constrain neutrino mass. We have considered a BOSS like Ly- α survey with a quasar density of 30 deg −2 with an average 3σ sensitivity for the measured spectra. We have also assumed a 21-cm intensity mapping experiment at a fiducial redshift z=2.5 corresponding to a frequency 406 MHz using a SKA1-mid like instrument with 250 dishes each of diameter 15 m. We have assumed \(({\kern -.3pt}{\Omega }_{\Lambda },{\Omega }_{m},{\Omega }_{r},h,\sum \nolimits _{i}m_{i}{\kern -.3pt})\;{=}\;({\kern -.3pt}0.6825,0.3175, 0.00005, 0.6711, 0.1~\text {eV}{\kern -.3pt})\)(Planck Collaboration et al. 2014) for this analysis. The Fisher matrix analysis using a two parameter (Ω m ⋅Ω ν ) shows that for a 10.000 h radio observation distributed over 25 pointings of 400 h each, the parameters Ω m and Ω ν are measurable at 0.321% and 3.671%, respectively (see Fig. 4). We find it significant that instead of a deep long duration observation in one small field-of-view, it is much better if one divides the total observation time over several pointings and thereby increasing survey volume. For 100 pointings each of 100 h one can get a 2.36% measurement of Ω ν . This is close to the cosmic variance limit at the fiducial redshift and the given observations. In the ideal limit, one may measure Ω ν at a 2.45% level which corresponds to a measurement of \(\sum m_{\nu }\) at the precision of (0.1±0.012) eV.

Figure 4
figure 4

68.3, 95.4 and 99.8 ellipse for 10000 h. Observations for 25 pointings with each pointing of 400 h. observations. The marginalized one-dimensional probability distribution function for Ω m and Ω ν are also shown (Pal & Guha Sarkar 2016).

Full size image

4 Cross-correlation with Lyman break galaxies

The cross-correlation between the HI 21-cm signal and the Lyman break galaxies is another important tool to probe the large scale structure of the Universe at post-reionization epoch. This has been studied recently (Villaescusa-Navarro et al. 2015) using a high resolution N-body simulation. Prospects for detecting such a signal using the SKA1-mid and SKA1-low telescopes together with a Lyman break galaxy spectroscopic survey with the same volume have also been investigated. It is seen that the cross power spectrum can be detected with SNR up to ∼10 times higher than the HI 21-cm auto power spectrum. Like in all other cross power spectrum, the Lyman break galaxy and the HI 21-cm cross power spectrum are expected to be extracted more reliably from the much stronger spectrally smoothed foreground contamination compared to the HI 21-cm auto power spectrum.

5 Cross-correlation of HI 21-cm signal with CMBR

5.1 Weak lensing

Gravitational lensing has the effect of deflecting the CMBR photons. This forms a secondary anisotropy in the CMBR temperature anisotropy maps (Lewis & Challinor 2006). The weak lensing of CMBR is a powerful probe of the universe at distances (z∼1100) far greater than any galaxy surveys. Measurement of the secondary CMBR anisotropies often uses the cross correlation of some relevant observable (related to the CMB fluctuations) with some tracer of the large scale structure (Hirata et al. 2004a, 2004b; Smith et al. 2007). For weak lensing statistics, the ‘convergence’ and the ‘shear’ fields quantify the distortion of the maps due to gravitational lensing. Convergence (κ) measures the lensing effect through its direct dependence on the gravitational potential along the line-of-sight and is thereby a direct probe of cosmology. The difficulty in precise measurement of lensing is the need for very high resolutions in the CMBR maps, since typical deflections over cosmological scales are only a few arcminutes. The non-Gaussianity imprinted by lensing on smaller scales allows a statistical detection for surveys with low angular resolution. Cross-correlation with traces, limits the effect of systematics thereby increasing the signal-to-noise. The weak lensing observables like convergence are constructed using various estimators involving the CMBR maps (T, E, B) (Seljak & Zaldarriaga 1999; Hu 2001; Hu & Okamoto 2002). The reconstructed convergence field can then be used for cross correlation.

We have probed the possibility of using the post-reionization HI as a tracer of large scale structure to detect the weak lensing (Guha Sarkar 2010) effects. We have studied the cross correlation between the fluctuations in the 21-cm brightness temperature maps and the weak lensing convergence field. We can probe the one dimensional integral effect of lensing at any intermediate redshift by tuning the observational frequency band for 21-cm observation. The cross-correlation power spectrum can hence independently quantify the cosmic evolution and structure formation at redshifts z≤6. The cross-correlation power spectrum may also be used to independently compare the various de-lensing estimators.

The distortions caused by the deflection is the quantity of study in weak lensing. At the lowest order, magnification of the signal is contained in the convergence. The convergence field is a line-of-sight integral of the matter over density δ given by (Van Waerbeke & Mellier 2003)

$$ \kappa(\hat{\mathbf{n}}) = \frac{3}{2} {\Omega}_{m0} {\left( \frac{H_{0}}{c} \right)}^{2} {\int}_{\eta_{0}}^{\eta_{LSS}} \mathrm{d}\eta F(\eta) \delta(\mathcal{D}(\eta)\hat{\mathbf{n}} , \eta) $$
(40)

and F(η) is given by

$$ F(\eta) = \frac {\mathcal{D}(\eta_{LSS} - \eta)\mathcal{D}(\eta)D_{+}(\eta)}{\mathcal{D}(\eta_{LSS}) a(\eta)}. $$
(41)

Here, D + denotes the growing mode of density contrast δ, and η L S S denotes the conformal time to the epoch of recombination. The comoving angular diameter distances \(\mathcal {D}(\chi ) = \chi \) for flat Universe, \(\mathcal {D}(\chi ) = \sin (K \chi ) / K \) for K=|1−Ω m −ΩΛ|1/2 H 0/c<0 and \(\mathcal {D}(\chi ) = \sinh (K \chi ) / K\) for K>0 Universe. The convergence power spectrum is defined as \( \langle a_{\ell m}^{\kappa } a_{\ell ^{\prime } m^{\prime }}^{\kappa *}\rangle = C_{\ell }^{\kappa } \delta _{\ell \ell ^{\prime }} \delta _{m m^{\prime }}\), where \(a_{\ell m}^{\kappa }\) are the expansion coefficients in spherical harmonic basis. The convergence auto-correlation power spectrum for large ℓ can be approximated as

$$ \mathcal{C}_{\ell}^{\kappa} \approx \frac{9}{4}{\Omega}_{m0}^{2} {\left( \frac{H_{0}}{c} \right)}^{4} \int \mathrm{d} \eta\frac{ F^{2}(\eta)} {\mathcal{D}^{2}(\eta)} P{\left( \frac{\ell}{\mathcal{D}(\eta)}\right)}. $$
(42)

The cross correlation angular power spectrum between the post-reionization HI 21-cm brightness temperature signal and the convergence field is given by

$$ {\mathcal{C}}_{\ell}^{\text{HI}-\kappa} = A (z_{\text{HI}}) \int \mathrm{d}k \left[ k^{2} P(k) {\mathcal{I}}_{\ell}(k r_{\text{HI}}) \int \mathrm{d} \eta F(\eta) j_{\ell}(kr)\right], $$
(43)

where P(k) is the dark matter power spectrum at z=0 , and

$$ {A}(z) = \frac{3}{\pi}{\Omega}_{m0} {\left( \frac{H_{0}}{c} \right)}^{2} \bar{T}(z)\bar{x}_{\text{HI}} D_{+}(z). $$
(44)

We note that the convergence field \(\kappa (\hat {\mathbf {n}})\), is not directly measurable in CMBR experiments. It is reconstructed from the CMBR maps through the use of various statistical estimators (Hanson et al. 2009; Kesden et al. 2003; Cooray & Kesden 2003). The cross-correlation angular power spectrum, \( \mathcal {C}_{\ell }^{\text {HI}-\kappa }\), does not de-lens the CMB maps directly. It uses the reconstructed cosmic shear fields, and is thereby very sensitive to the underlying tools of de-lensing, and the cosmological model. The cross-correlation angular power spectrum may provide a way to independently compare various de-lensing estimators.

The cross-correlation power spectrum follows the same shape as the matter power spectrum. The signal peaks at a particular ℓ which scales as ℓ∝r HI when the redshift is changed. The angular distribution of power clearly follows the underlying clustering properties of matter. The amplitude depends on several factors which are related to cosmological model and the HI distribution at z HI. The angular diameter distances also depends directly on the cosmological parameters. The cross-correlation signal may hence be used independently for joint estimation of cosmological parameters.

We shall now discuss the prospect of detecting the cross-correlation signal assuming a perfect foreground removal. The error in the cross-correlation signal is due to instrumental noise and sample variance. Sample variance however puts a limiting bound on the detectability. The cosmic variance for \(\mathcal {C}_{\ell }^{\text {HI}-\kappa } \) is given by

$$ \sigma_{\text{SV}}^{2} = \frac {\mathcal{C}_{\ell}^{\kappa} \mathcal{C}_{\ell}^{\text{HI}}}{(2\ell + 1){N_{c}}f_{\mathrm{s}} {\Delta}\ell}, $$
(45)

where f s is fraction of overlap portion of sky common to both observations and N c denotes the number of independent estimates of the signal.

In the ideal hypothetical possibility of a full sky 21-cm survey, we have f s=1, and Δℓ=1. The predicted S/N is found to be ∼2 and is not significantly high for detection which requires S/N≥3. Choosing Δℓ=10 for ℓ≤100 and Δℓ=100 for ℓ>100, we shall produce S/N>3. This establishes that, with full sky coverage and negligible instrumental noise, the binned cross-correlation power spectrum is not cosmic variance limited and it is detectable. The S/N estimate is based on HI observation at only one frequency. The 21-cm observations allow us to probe a continuous range of redshifts. This allows us to further increase the S/N by collapsing the signal from various redshifts. In principle, a broad band 21-cm experiment may further increase the S/N.

The S/N may be improved by collapsing the signal from different scales ℓ and thereby testing the feasibility of a statistically significant detection. The cumulated SNR up to a multipole ℓ is given by

$$ {\left( \frac{S}{N} \right)}^{2} = {\sum}_{0}^{\ell} \frac{(2\ell^{\prime} + 1) {N_{c}} f_{\mathrm{s}}{(\mathcal{C}_{\ell^{\prime}}^{\text{HI}-\kappa})}^{2}} {(\mathcal{C}_{\ell^{\prime}}^{\text{HI}} + N_{\ell^{\prime}}^{\text{HI}} )(\mathcal{C}_{\ell^{\prime}}^{\kappa} + N_{\ell^{\prime}}^{\kappa})} . $$
(46)

\( N_{\ell }^{\kappa }\) and \( N_{\ell }^{\text {HI}}\) denotes the noise power spectrum for κ and HI observations respectively. Ignoring the instrument noises, we note that there is a significant increase in the S/N by cumulating over multipoles ℓ. This implies that a statistically significant detection of \(\mathcal {C}_{\ell }^{\text {HI}-\kappa } \) is possible and the signal is not a limited cosmic variance. It is important to push instrumental noise to the limit set by cosmic variance for a detection of the signal. At the relevant redshifts of interest, it is possible to reach such low noise levels with SKA. It is however important to scan large parts of the sky thereby increasing the survey volume.

Instrumental noise plays an important role at large multipoles (small scale). For a typical CMB experiment, the noise power spectrum (Marian & Bernstein 2007; Smith et al. 2006) is given by \( N_{\ell } = \sigma ^{2}_{\text {pix}}{\Omega }_{\text {pix}}{ W_{\ell }}^{-2} \) , where different pixels have uncorrelated noise with variance \(\sigma ^{2}_{\text {pix}}= s^{2}/ t _{\text {pix}} \). Here s 2 and t pix are the pixel sensitivity and ‘time spent on the pixel’ respectively. Ωpix is the solid angle subtended per pixel and we use a Gaussian beam \( W_{\ell } = \exp [ { - \ell ^{2} \theta ^{2}_{\text {FWHM}}/ 16 \ln 2}] \).

For HI observations, the quantity of interest is the complex visibility which is used to estimate the power spectrum (Ali et al. 2008). For a radio telescope with N antennae, system temperature T sys, operating frequency ν and band width B, the noise correlation is given by

$$N_{\ell}^{\text{HI}} \propto \frac{1} {N (N - 1)}{ \left[ \frac{T_{\text{sys}}}{K} \right]}^{2} \frac{1}{T \sqrt{{\Delta \nu} B}}, $$

where T denotes the total observation time, and K is related to the effective collecting area of the antenna dish. Binning in ℓ also reduces the noise. The bin Δℓ=1/2π 2 𝜃 0 is chosen assuming a Gaussian beam of width 𝜃 0. With a SKA-like instrument (Ali et al. 2008), one can attain a noise level much lesser than the signal by increasing the observation time (in fact a 5000 h observation with the present SKA configuration is good enough) and also by increasing the radial distance probed by increasing the band width of the telescope. Being inversely related to the total number of antennae in the radio array, future designs may actually allow further reduction of the the system noise and achieve \( N_{\ell }^{\text {HI}} << \mathcal {C}_{\ell }^{\text {HI}}\). This establishes the detectability of the cross-correlation signal. We would like to conclude by noting that correlation between weak lensing fields and 21-cm maps, quantified through \( \mathcal {C}_{\ell }^{\text {HI}-\kappa }\) may allow independent means to estimate cosmological parameters and also test various estimators for CMBR delensing.

5.2 ISW effect

In an Universe, dominated by the cosmological constant, Λ , the expansion factor of the Universe, a, grows at a faster rate than the linear growth of density perturbations. This consequently implies that, the gravitational potential Φ∝−δ/a will decay. The ISW effect is caused by the change in energy of CMB photons as they traverse these time dependent potentials.

If the horizon size at the epoch of dark energy dominance (decay of the potential) is denoted by η Λ, then the ISW effect is suppressed on scales k≥2π/η Λ. This corresponds to an angular scale ℓ Λ=2π d/η Λ, where d is the angular diameter distance to the epoch of decay.

The ISW term is given by

$$ {\Delta} T(\hat{\mathbf{n}})^{\text{ISW}} = 2 T {\int}_{\eta_{\text{LSS}}}^{\eta_{0}} \mathrm{d}\eta \eta \, \dot{\Phi}(r \hat{\mathbf{n}},\eta). $$
(47)

The cross correlation angular power spectrum between HI 21-cm signal and ISW is given by Guha Sarkar et al. (2009)

$$ {\mathcal{C}}_{\ell}^{\text{HI--ISW}} = {\mathcal{K}}(z_{\text{HI}}) \int \mathrm{d}k (P(k) \mathcal{I}_{\ell}(k r_{\text{HI}}) {\int}_{\eta_{\text{LSS}}}^{\eta_{0}} \mathrm{d} \eta F(\eta) j_{\ell}(kr) ) $$
(48)

where P(k) is the present day dark matter power spectrum,

$$ \mathcal{K}(z) = -\bar{T}(z)\bar{x}_{\text{HI}} D_{+}(z) \frac{6 {H_{0}^{3}} {\Omega}_{m0}}{\pi c^{3}}, $$
(49)
$$ {\mathcal{I}}_{\ell}(x) = b j_{\ell}(x)- f \frac{\mathrm{d}^{2} j_{\ell}}{\mathrm{d}x^{2}} $$
(50)

and

$$ F(\eta) = \frac{D_{+} (f-1) H(z)}{H_{0}} $$
(51)

For large ℓ, we can use the Limber approximation (Limber 1954; Afshordi et al. 2004) which allows us to replace the spherical Bessel functions by Dirac deltas as

$$j_{\ell}(kr) \approx \sqrt{\frac{\pi}{2\ell+1}} \delta_{\text{D}}\left( \ell + \frac{1}{2} - kr\right), $$

whereby the angular cross-correlation power spectrum takes the simple scaling of the form

$$ \mathcal{C}_{\ell}^{\text{HI--ISW}} \sim \frac{\pi \mathcal{K} F} {2\ell^{2}} P\left( \frac{\ell}{r}\right), $$
(52)

where P(k) is the present day dark matter power spectrum and all the other terms on the right hand side. are evaluated at z HI. The dimensionless quantity f quantifies the growth of the dark matter perturbations, and the ISW effect is proportional to f−1. The term f−1 is a sensitive probe of dark energy. Here we estimate the viability of detecting the HI-ISW cross-correlation signal. Cosmic variance sets a limit in deciding whether the signals can be detected or not. Even in the cosmic variance limit at z∼1.0 with a 32-MHz observation, we find that S/N<0.45 for all z HI and ℓ and a statistically significant detection is not possible in such cases. It is possible to increase S/N collapsing of the signal at different multipoles ℓ. To test if a statistically significant detection is thus feasible, we have collapsed all multipoles less than ℓ to evaluate the cumulative S/N defined as (Cooray 2002; Adshead & Furlanetto 2008). We find that the contribution in the cumulated S/N comes from ℓ<50 at all redshifts 0.4<z<2. The cross-correlation signal is largest at z∼0.4 and is negligible for z>3. We further find that although there is an increase in S/N on collapsing the multipoles, it is still less than unity. This implies that a statistically significant detection is still not possible. Thus, probing a thin shell of HI does not allow us to detect a cross correlation, the signal being limited by the cosmic variance. A cumulated S/N of ∼1.6 is attained for redshift up to z=2 and there is hardly any increase in S/N on cumulating beyond this redshift. This is reasonable because the contribution from the ISW effect becomes smaller beyond the redshift z>2. This S/N is the theoretically calculated value for an ideal situation and is unattainable for most practical purposes. Incomplete sky coverage and foreground removal issues would actually reduce the S/N, and attaining a statistically significant level is not feasible.