1 Introduction

In 1975, Stephen Hawking (one of the world’s most famous physicists) made a shocking claim that when quantum mechanics is allied with general relativity, black holes (BHs) began to glow with Hawking Radiation (HR) (Hawking 1971, 1974, 1975, 1976). This emission consists of all sorts of massless/massive particles with different spins: spin- 0,1/2,1,…. Hawking’s prodigious calculations are based on a scenario that ubiquitous virtual particle pairs are continually being created near the event horizon of the BH due to vacuum fluctuations. Principally, these particles are created as a particle–antiparticle pair and immediately after they quickly annihilate each other. However, it is always possible that the one with negative energy (in order to conserve the total energy) falls into the BH while the other possessing the positive energy escapes to spatial energy as HR. Today, HR is also called the Bekenstein–Hawking radiation in virtue of Bekenstein’s remarkable contributions (Bekenstein 1972, 1973, 1974, 1975) to this phenomenon.

Since 1975, the studies concerning HR are being carried out. Until now, many different methods for the HR are proposed (the reader may refer to Gibbons & Hawking 1977a, b; Vanzo et al. 2011; Umetsu 2010; Kraus & Wilczek 1994, 1995 and references therein). Among them, the most fascinating quantum tunneling methods are Parikh and Wilczek’s null-geodesic method (Parikh & Wilczek 2000; Parikh 2002, 2004) and the semiclassical methods of Hamilton–Jacobi (Angheben et al. 2005; Srinivasan & Padmanabhan 1999; Shankaranarayanan et al. 2001; Kerner & Mann 2006) and Damour & Ruffini (1976). On the other hand, the HR of photons, scalar particles, massive vector bosons and fermions from various BHs have gained much attention in recent years (see, for example, Sakalli et al. 2012, 2014; Sakalli 2011; Mazharimousavi et al. 2010; Jiang 2007; Sakalli & Ovgun 2015a, b, c; Kerner & Mann 2008a, b; Yale & Mann 2009; Li & Chen 2015; Kruglov 2014a, b; Ovgun & Jusufi 2016; Jusufi & Ovgun 2016; Sakalli & Ovgun 2015d, 2016; Ovgun 2016; Frasca 2014; Valtancoli 2015; Cavalcanti & da Rocha 2016; Goswamia & Mohantya 2015; Ibungochouba Singh et al. 2016; Xie 2014; Yang et al. 2014). Furthermore, the information loss paradox (Giddings 1994; Varadarajan 2008; Hawking 2015) in the HR is one of the great puzzles for the physics community. Some theorists came forward with an idea to retrieve information from the BH encoded in the HR (Hawking et al. 2016; Hooft 1995, 1996; Dvali 2015; Lochan & Padmanabhan 2016; Stoica 2015; Kraus & Mathur 2015; Martin-Martinez & Louko 2015; Mann 2015; Calmet 2015; Perez 2015; Papadodimas & Raju 2014; Giddings & Shi 2014; Almheiri et al. 2013; Maldacena & Susskind 2013). However, this mystery has not been solved literally.

In 1970s, particle physicists realized that there is a very close link between two of the four fundamental forces (Davies 1986; Glashow 1961; Weinberg 1967; Salam 1968; Englert & Brout 1964; Higgs 1964; Guralnik et al. 1964) – the weak force and the electromagnetic force which is a single underlying force known as the electroweak force. The basic equations of the unified theory correctly describe the relationship between the electroweak force and its associated force-carrying particles (photons and the massive vector bosons ( W ± and Z)), except for a major glitch: all of these particles emerge without a mass! Although this is true for the photon, we know that the W ± and Z bosons must have mass, nearly hundred times that of a proton. The problem of spontaneously broken gauge theories in curved spacetime is well known in literature (Moniz et al. 1990; Troitsky 2012; Randall & Sundrum 1999; Arkani-Hamed et al. 1998; Witten 1981; Demir 1999, 2014). So far, the Higgs mechanism (Englert & Brout 1964; Higgs 1964) is the experimentally confirmed mechanism to solve the generation of mass problem in particle physics, which satisfies both the unitarity and the renormalization of the theory.

In this paper, a brief review for the derivation of the wave equation for the mass generating (massive and charged) scalar particles is given. Applying the resulting equation obtained for the general 4-dimensional static and spherically symmetric metric, we obtain the general radial integral solution for the action of Hamilton–Jacobi method. As a test bed we consider the dyonic Reissner–Nordström BH (DRNBH) (Chen et al. 2010) and compute its quantum tunneling rate by using the latter radial integral solution of the action. Finally, we show in detail how one recovers the original HR of the DRNBH from the quantum tunneling of the mass generating particles.

The paper is organized as follows. In section 2, we introduce the wave equation of a massive and charged mass generating scalar particle in a curved spacetime. Section 3 is devoted to computations of the quantum tunneling of the mass generating scalar particles from the DRNBH. While doing this, we are careful to increase our calculations generically. We draw our conclusions in section 4.

2 Wave equation of mass generating particles

In this section, we represent an expression for the wave equation of the mass generating particles. Their associated scalar fields are non-minimally coupled to gravity. The main idea underlying this mass generation mechanism is resplendently introduced in many textbooks (see, for instance, Peskin & Schroeder 1995; Langacker 2009).

For brevity, we initially use units \(\phantom {\dot {i}\!}G_{N}=c=\hbar =1\). One may write down the action of the interaction of the scalar fields with gravity (Moniz et al. 1990) as follows:

$$ S=\int d^{4}x\sqrt{-g}\left[\frac{\Re}{16\pi}-\xi\phi^{\dag}\phi\Re+(D_{\mu} \phi)^{\dag}D^{\mu}\phi-V(\phi)-\frac{1}{4}F_{\mu\nu}F^{\mu\nu}\right], $$
(1)

where R stands for the scalar curvature and F μ ν =∇ μ A ν −∇ ν A μ is the Maxwell field strength with the spin-1 gauge field A ν (electromagnetic vector potential). ξ denotes the dimensionless coupling constant which governs the non-minimal interaction of the scalar field ϕ ( ϕ † denotes the complex conjugate of ϕ) with gravity. In other words, the minimally coupled scalar fields correspond to ξ=0. It is worth noting that this coupling constant ξ can also be used to stabilize the vacuum expectation value \(\phantom {\dot {i}\!}y^{2}=\frac {v^{2}}{2}=\langle \phi ^{\dag } \phi \rangle \) near the event horizon of a BH (Demir 2014). The gauge-covariant derivative is given by

$$ D_{\mu}=\partial_{\mu}-ieA_{\mu}, $$
(2)

where e is the coupling constant (i.e. the Planck charge) of the electromagnetic vector potential A μ . The variation of the action (1) with respect to the metric tensor g μ ν leads to Einstein equations of motion as follows:

$$ \Re_{\mu\nu}-\frac{1}{2}\Re g_{\mu\nu}=-8\pi T_{\mu\nu}, $$
(3)

where T μ ν is the energy-momentum tensor. Its long expression can be seen in the study of Moniz et al. (1990). Significantly, when one applies the variation to the action (1) with respect to ϕ †, the following wave equation is obtained:

$$ \frac{1}{\sqrt{-g}}(\partial_{\mu}-ieA_{\mu})\left[\sqrt {-g}g^{\mu\nu}\left( \partial_{\nu}-ieA_{\nu}\right) \phi\right] +\xi \Re\phi+\partial_{\phi^{\dag}}V=0. $$
(4)

The mass generating potential was also defined in Moniz et al. (1990) as follows:

$$ V(\phi)=B+\tilde{m}^{2}\phi^{\dag}\phi+\lambda(\phi^{\dag}\phi)^{2}, $$
(5)

where B is an arbitrary constant and the coupling constant λ is dimensionless in the 4-dimensional spacetime. Without loss of generality, it is assumed that λ has a positive definite value. As clearly stated in Moniz et al. (1990), the vacuum expectation value must satisfy the condition of y 2≠0, which requires that V(ϕ) must have a minimum at ϕ ≠ 0. To obtain the bounded solution for the Hamiltonian, \(\phantom {\dot {i}\!}\tilde {m}^{2}\) must be negative since λ is positive. Due to this reason, we shift \(\phantom {\dot {i}\!}\tilde {m}^{2}\rightarrow -m^{2}\). Hence, using equation (5), we have

$$ \partial_{\phi^{\dag}}V=[-m^{2}+2\lambda(\phi^{\dag}\phi)] \phi. $$
(6)

After assigning the reduced Planck constant back to its original value \(\phantom {\dot {i}\!}\hslash \), equation (4) can be rewritten as

$$ \frac{1}{\sqrt{-g}}\left( \partial_{\mu}\! -\! i\frac{e}{\hslash}A_{\mu}\right)\left[\sqrt{-g}g^{\mu\nu}\left( \partial_{\nu}\! -\! i\frac{e}{\hslash}A_{\nu}\right) \phi\right] +\frac{1}{\hslash^{2}}[\xi\Re-m^{2} +2\lambda(\phi^{\dag}\phi)] \phi=0. $$
(7)

which is the wave equation of the mass generating particles with mass m and charge e in a curved spacetime. It is also important to know that whenever the scalar field ϕ is used for a Nambu–Goldstone boson in the gauge theory of spontaneous symmetry breaking, ξ is zero (Voloshin & Dolgov 1982). On the other hand, if the scalar field ϕ represents a composite particle, then the value of ξ is fixed by the dynamics of its components. In particular, ξ=1/6 in the large N approximation to the Nambu–Jona–Lasinio model (Hill & Salopek 1992). Moreover, in the Standard Model, the Higgs fields possess the values of ξ within the range of ξ≤0 and ξ≥1/6 (Hosotani 1985).

3 Quantum tunneling of mass generating particles from DRNBH

The line-element for the 4-dimensional generic static (spherically symmetric) BH metric is given by

$$ \mathrm{d}s^{2}=-F\mathrm{d}t^{2}+G^{-1}\mathrm{d}r^{2}+R(\mathrm{d}\theta^{2}+\sin^{2}\theta \mathrm{d}\varphi^{2}), $$
(8)

where the metric functions (F,G,R) are only the function of r. Any horizon r h should satisfy the condition of G(r h )=0 and r h is, in general, a function of the mass and charge of the BH. The Hawking temperature of a BH described by the metric (8) is given by (Fernando 2005)

$$ T_{\mathrm{H}}=\frac{1}{4\pi}\left. \left\vert \frac{\mathrm{d}g_{tt}}{\mathrm{d}r}\right\vert \sqrt{-g^{tt}g^{rr}}\right\vert_{r=r_{h}}=\frac{F^{\prime}\left( r_{h}\right)} {4\pi\sqrt{B\left( r_{h}\right)} }, $$
(9)

where \(\phantom {\dot {i}\!}B=\frac {F}{G}\) and the prime over a quantity denotes the derivative with respect to r. Furthermore, the Ricci scalar (Wald 1984) for the metric (8) can be found as

$$\begin{array}{@{}rcl@{}} \Re & =&\frac{1}{2F^{2}R^{2}}(-G^{\prime}F^{\prime}FR^{2}-2F^{\prime\prime} FGR^{2}+F^{^{\prime}2}GR^{2}- 2RGF^{\prime}R^{\prime}F\\ &&+\,R^{\prime2}F^{2}G-4R^{\prime\prime}F^{2} GR-2G^{\prime}R^{\prime}F^{2}R+4F^{2}R). \end{array} $$
(10)

In order to study the quantum tunneling of the mass generating particles from the generic BH (8), we use the WKB approximation and assume an ansatz for the scalar field ϕ as follows:

$$ \phi=c\exp\left( \frac{i}{\hbar}I(t,r,\theta,\varphi)\right), $$
(11)

where c is the amplitude of the wave and I stands for the classically forbidden action of the trajectory. Metric (8) admits two Killing vectors 〈∂ t , ∂ φ 〉, which show the existence of the symmetries. Therefore, one can assume a solution for the action as

$$ I=-Et+W(r)+j(\theta,\varphi)+C, $$
(12)

where E denotes energy, W(r) and j(𝜃,φ) are radial and angular functions, respectively. In equation (12), C is a complex constant.

Since A ν represents the electromagnetic vector potential, for a dyonic BH with electric and magnetic components one should have A ν =[A 0(r),0,0,A 1(𝜃)]. Under the guidance of the Hamilton–Jacobi method (Angheben et al. 2005), we first insert equations (11)–(13) in equation (7) and then consider the terms with the leading order of \(\phantom {\dot {i}\!}\hbar \). Thus, we obtain the following expression:

$$\begin{array}{@{}rcl@{}} && \sin^{2}\theta\{[(-G^{\prime}F^{\prime}-2F^{\prime\prime} G)F+F^{\prime2}G] R^{2}\\ &&\qquad-2[(G^{\prime}R^{\prime} -2+2GR^{\prime\prime}) F+GF^{\prime}R^{\prime}] FR+R^{\prime} F^{2}G\}\xi\\ &&-2FR\{[(-m^{2}-2\,\lambda c^{2}-GW^{\prime2})R-{j_{\theta}}^{2}] \mathrm{\sin}^{2}\theta-(eA_{1}-{j_{\varphi}})^{2})F\\ &&\qquad {\kern1pc} +R\mathrm{\sin}^{2}\theta E_{\text{net}}^{2}\}=0, \end{array} $$
(13)

where \(\phantom {\dot {i}\!}{j_{\theta }}=\frac {\partial j}{\partial \theta }\), \(\phantom {\dot {i}\!}{j_{\varphi }} =\frac {\partial j}{\partial \varphi }\) and E net = E + e A 0. From equation (13), we derive an integral solution for W(r) as follows:

$$ W_{\pm}=\pm\int\frac{1}{\sqrt{FG}}\left[\left( n_{1}F+n_{2}\right) \xi G+\frac{F}{R}n_{3}+E_{\text{net}}^{2}\right]^{\frac{1}{2}}\mathrm{d}r, $$
(14)

where

$$ n_{1}={\frac{2R^{\prime\prime}}{R}}+{\frac{G^{\prime}R^{\prime}-2}{GR}} -{\frac{1}{2}}\left( {\frac{R^{\prime}}{R}}\right)^{2}, $$
(15)
$$ n_{2}=\frac{F^{\prime2}}{2F}-\frac{F^{\prime}R^{\prime}}{R}-\frac{1}{2} \frac{G^{\prime}F^{\prime}}{G}-F^{\prime\prime}, $$
(16)
$$ n_{3}=(-2c^{2}\lambda-m^{2})R-{j_{\theta}}^{2}-\frac{(eA_{1}-{j_{\varphi}})^{2}}{\mathrm{\sin}^{2}\theta}. $$
(17)

Since \(\phantom {\dot {i}\!}G(r_{h_{+}})=0\), the near horizon form of equation (14) becomes

$$ W_{\pm}\approx\pm\int\sqrt{\frac{E_{\text{net}}^{2}R+Fn_{3}}{RFG}}\mathrm{d}r. $$
(18)

which is an essential expression for computing the quantum tunneling rate. Now, we test the above result obtained via the DRNBH geometry (Chen et al. 2010) whose metric functions and electromagnetic vector potential components are given by

$$ F=G=\frac{(r-r_{h_{+}}) (r-rh_{_{-}})} {r^{2}}, $$
(19)
$$ R=r^{2}, $$
(20)
$$ A_{0}=-\frac{Q}{r},\quad A_{1}=P\cos\theta, $$
(21)

where the physical quantities Q and P denote the DRNBH’s characteristic parameters: Q is the electric charge and P is the magnetic charge. The outer or event (\(\phantom {\dot {i}\!}r_{h_{+}}\)) and inner (\(\phantom {\dot {i}\!}r_{h_{-}}\)) horizons of the DRNBH are given by

$$ r_{h_{\pm}}=M\pm\sqrt{M^{2}-{\Theta}^{2}}, $$
(22)

where Θ2 = Q 2 + P 2. In equation (22), the parameter M represents the mass of the DRNBH. Since F = G, in equation (18), F n 3 → 0 around the event horizon. But, because of the vanishing term F n 3 one can immediately ask why does the particle’s mass m lose its effectiveness during the Hawking radiation? However, one can experience from previous studies (Vanzo et al. 2011) that the non-differential terms coupled to the wave function ϕ (for example, in equation (7), it corresponds to \(\phantom {\dot {i}\!}\frac {1}{\hslash ^{2}}[\xi \Re -m^{2} +2\lambda (\phi ^{\dag }\phi )] \phi \)) apart from the operator term acting on ϕ (like the Laplacian operator: \(\phantom {\dot {i}\!}\square \phi \)) always loses its efficiency near the horizon. That is why, for instance, the HR is independent of the particle’s mass (Liu et al. 2013; Jannes et al. 2011). Thus, equation (18) reduces to

$$ W_{\pm}\approx\pm\int\frac{E_{\text{net}}}{F}\mathrm{d}r. $$
(23)

Meanwhile, we now have \(\phantom {\dot {i}\!}E_{\text {net}}=E-\frac {eQ}{r_{h_{+}}}\). It is obvious that the above integrand possesses a simple pole at the event horizon. To evaluate integral (23), we first expand the metric function F as follows:

$$ F(r)=F^{\prime}(r_{h_{+}})(r-r_{h_{+}})+\Game(r-r_{h_{+}})^{2}. $$
(24)

Substituting the above expression into equation (23) and choosing the contour as a half loop going around the pole from left to right, one obtains

$$ W_{\pm} = \pm\,i\pi\frac{E_{\text{net}}}{F^{\prime}(r_{h_{+}})}. $$
(25)

Thus, the imaginary part of the action (12) becomes

$$ \operatorname{Im}I_{\pm}=\text{Im}~ C\pm\pi\frac{E_{\text{net}}}{F^{\prime}(r_{h_{+}})}. $$
(26)

Thence, we compute the probabilities of ingoing and outgoing particles tunneling the DRNBH horizon as

$$ P_{\text{in}}=\exp(-2\text{Im}~ I_{-})=\exp\left( -2\text{Im}~ C+2\pi\frac{E_{\text{net}}}{F^{\prime}\left( r_{h_{+}}\right)}\right), $$
(27)
$$ P_{\text{out}}=\exp(-2\text{Im}~ I_{+})=\exp\left( -2\text{Im}~ C-2\pi\frac{E_{\text{net}}}{F^{\prime}(r_{h_{+}})}\right). $$
(28)

Classically, having a BH is conditional on the no-reflection for the ingoing waves, which means full absorption: P in=1. This is possible simply by setting \(\phantom {\dot {i}\!}\text {Im}~ C=\pi \frac {E_{\text {net}}}{F^{\prime }\left (r_{h_{+}}\right )} \) (for similar and recent works, the reader is referred to Gohar & Saifullah 2013; Darabi et al. 2014; Sakalli & Gursel 2016 and references therein) which results in

$$ P_{\text{out}}=\exp\left( -4\pi\frac{E_{\text{net}}}{F^{\prime}(r_{h_{+}})}\right). $$
(29)

Consequently, we read the quantum tunneling rate for the DRNBH as

$$ {\Gamma}=\frac{P_{\text{out}}}{P_{\text{in}}}=\exp\left( -4\pi\frac{E_{\text{net}}}{F^{\prime} (r_{h_{+}})}\right). $$
(30)

Employing the Boltzmann formula Γ= exp(−E net/T) (Ryskin 2014), the surface temperature of the DRNBH can be computed as

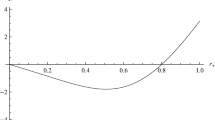
$$ T=\frac{F^{\prime}(r_{h_{+}})} {4\pi}=\frac{r_{h_{+}}-r_{h_{-}}} {r_{h_{+}}^{2}}=\frac{\sqrt{M^{2}-{\Theta}^{2}}}{2\pi\left( M+\sqrt {M^{2}-{\Theta}^{2}}\right)^{2}}, $$
(31)

which is exactly equal to the standard Hawking temperature of the DRNBH (Chen et al. 2010). Temperature versus mass plotting is depicted in Fig. 1 for M≥Θ. As it can be seen from Fig. 1, the locations of the peaks on the M-axis (which are very close to their associated starting mass value M initial=Θ: the extreme BH case, T=0) shift towards right with increasing M-value, however the peak values decrease when M initial gets higher values. Moreover, while M→∞,all the curves of the temperatures rapidly reach the curve of the Schwarzschild ( Θ=0) BH’s Hawking temperature, which goes to zero with increasing M-value.

Figure 1
figure 1

Plots of the temperature T vs. DRNBH mass M. The plots are governed by equation (31). The starting masses are governed by M initial=Θ.

Full size image

4 Conclusion

In this paper, we reviewed the derivation of the wave equation for the mass generating scalar particles in the concept of the spontaneous symmetry breaking theory. To this end, we introduced an action involving a non-minimal scalar field coupled to gravity. By using the Hamilton–Jacobi method with a suitable WKB ansatz, the quantum tunneling of the mass generating bosons from a generic static BH is thoroughly studied. We then obtained the general integral solution for the radial function (14) for the Hamilton–Jacobi action I. DRNBH geometry whose metric functions satisfy the equality F = G is considered as a test background for our computations. It is seen that scalar particle mass m, the non-minimal coupling constant ξ, and the potential constant λ are not decisive for the quantum tunneling rate, however the charge e is. In the semiclassical framework, we computed the probabilities of the ingoing and outgoing particles to get the quantum tunneling rate for the DRNBH. Finally, we managed to read the standard Hawking temperature of the DRNBH via the Boltzmann formula of the tunneling rate.

In future work, we plan to extend our analysis to a BH (might be a spherically non-symmetric) having F, which does not vanish at the event horizon F(r h )≠0. Because in such a case equation (18) may yield W ± values (having now the potential constant term λ) that the quantum tunneling rate can deviate from its pure thermal character (thermal radiations do not carry information, see for example, Parikh & Wilczek 2000) and give contribution to the information loss problem (Hawking 2015). We also aim to extend our analysis to the dynamic, rotating and higher/lower dimensional BHs. In this way, we will analyse the HR of the mass generating particles from various BHs.