Hawking radiation and particle dynamics in accelerating non-Kerr black holes

Abstract

In this article we study Hawking radiation and particle dynamics for the recently discovered accelerating non-Kerr black holes. A critical analysis of incoming and outgoing, charged and uncharged scalar and Dirac particles, has been done. The Hawking temperature of massive and massless Dirac particles has been found in the background of accelerating non-Kerr black holes. The centre of mass energy of colliding particles has also been calculated and presented graphically. The classical expression of action for the massive and massless charged fermions is also worked out. We have compared our results with those that exist in the literature.

1 Introduction

Classically, black holes are considered as a mysterious prison because anything that goes inside the hole never comes back. Therefore, the classical black hole can only grow bigger with time as it swallows everything and escape is not possible. In 1975, the astonishing discovery of Stephan Hawking [1] shook the existing theories as he demonstrated that black holes could actually radiate particles, quantum mechanically. These objects could shrink by losing energy and eventually evaporate by the emission of the so-called Hawking radiation [2,3,4,5,6,7]. But this discovery set up a long-standing puzzle that what happens to the information when the evaporation takes place? Other related issues have also been discussed in the literature [8, 9].

The notion of information loss during the process of radiation base on two pillars. Numerous results show that the the emission spectrum of black holes is entirely thermal and the no-hair theorem is valid [10, 11]. Since the thermal spectrum is completely determined by the parameter, temperature, therefore the outgoing radiation does not contain any information in pure thermal emission. Also, the no-hair theorem ensures that the geometry, outside a black hole, can be specified by its mass, charge and angular momentum. Thus the spacetime geometry does not have any significant information either. But if both the radiation and geometry do not carry any information then there must be no trace of collapsed matter left. The result of information loss is also in agreement with quantum mechanics.

But if we could show that there are few grains whose features are correlated with the collapsed matter, it will indicate that some information would have returned. So this moment reflects that both thermal emission and no-hair theorem cannot be considered at face value. If one of these conditions is strictly satisfied it could violate the conservation of energy. Hence the background geometry is considered to be fixed and conservation of energy is also not enforced during the radiation process. To ensure energy conservation, it was shown [10] that radiation could be entirely non-thermal and a black hole’s emission spectrum can be viewed as quantum tunneling of particles by taking the dynamical background geometry.

To study the tunneling effect, a well behaved coordinate system (Painlevé coordinate system) is introduced [10, 12], through which the behaviour of particles can be viewed across the horizon unlike the Schwarzschild metric (which is not regular at horizon). Thus the tunneling phenomenon provides an opportunity to study the emitted particles through Hawking radiation. In this approach, the imaginary part of the action is formulated for outgoing particles across the horizon. The tunneling probability is calculated for the particles coming from inside to outside the horizon. Then the expression for Hawking temperature of the hole using the Boltzmann factor [4, 13] is found. There are two different methods used in the literature to find imaginary part of the classical action: one is based on null geodesics while the other uses the Hamilton-Jacobi ansatz which is an extension of the complex path analysis [4, 12]. Initially, the tunneling approach was applied to the Schwarzschild black hole, and later, it was extended to a variety of charged, rotating and other black holes [14,15,16,17].

Several semi-classical approaches were employed to investigate the tunneling process of scalar and Dirac particles. The tunneling process of charged and uncharged Dirac particles for Gödel, Taub-NUT, Kerr and Kerr-Newman spacetimes has been studied [18,19,20]. This approach was extended to various three and four dimensional spacetimes [21,22,23,24,25,26,27,28,29,30] to investigate the process thoroughly. The tunneling probabilities of accelerating Kerr black holes by fermion and scalar particles with electric charge have also been studied [28,29,30,31] using WKB approximation. In this paper, we extend this study to the accelerating non-Kerr black holes.

Non-Kerr black holes were presented by Johannsen and Psaltis [11], which satisfy the no-hair theorem and one solution of some theory of gravity which is beyond Einstein’s general relativity. This spacetime is ideal to perform the strong field test of the no-hair theorem, and possesses novelty in itself because of its salient features. Firstly, it does not impose any restriction on rotation parameter a due to the presence of deformation parameter $\epsilon$. For the positive value of $\epsilon$, the non-Kerr black hole has two disconnected horizons for higher values of rotation parameter a and has no horizon for $a>M$. For the negative value of $\epsilon$, the horizon of non-Kerr black hole exists for any arbitrary a and topology of the horizon is toroidal. Because of these important features of the non-Kerr black holes, they have been studied extensively [32,33,34,35,36,37,38,39,40].

Accelerating and rotating frames are really important in black hole physics. In this paper, our focus is as to how tunneling occurs in non-Kerr black holes in the presence of acceleration and what are the effects of the acceleration parameter on Hawking temperature. We calculate the tunneling probabilities of charged, uncharged Dirac particles and scalar particles to work out the Hawking temperature. For this purpose, we employ the Hamilton-Jacobi anstaz using WKB approximation. In our approach, we use the Klein-Gordon equation (for the charged and uncharged scalar particles) and Dirac equation (for fermions) to find the tunneling probabilities of particles crossing the horizon. The centre of mass energy has also been studied for the charged accelerating non-Kerr black holes. This paper is arranged as follows. Section 2 introduces the mathematical structure of the background spacetime. In Sect. 3, quantum tunneling of Dirac uncharged and charged particles is studied. Section 4 deals with the tunneling phenomena and Hawking temperature for scalar particles. The expression for the centre of mass energy is found in Sect. 5 and concluding remarks are given in the last section.

2 Charged accelerating non-Kerr black hole

Johannsen and Psaltis [11] tested the gravity in the region of strong field by introducing a new metric. They started with a deformed Schwarzschild solution and applied the Newman-Janis transformation to obtain a deformed Kerr metric, which is now known as the non-Kerr spacetime. The accelerating non-Kerr metric in spherical coordinates (using the Plebański-Demiański metric) can be written as [41,42,43,44,45,46]

$$\begin{aligned} ds^{2}&=\frac{1}{\Omega ^{2}}\Big \{-\Big (\frac{Q}{\rho ^{2}}-\frac{a^{2}P\sin ^{2}\theta }{\rho ^{2}}\Big )\left( 1+h\right) dt^{2}+\frac{\rho ^{2}\left( 1+h\right) }{Q+a^2h\sin ^{2} \theta }dr^{2}+\frac{\rho ^{2}}{P} d\theta ^{2} \nonumber \\&\quad {+}\left[ \Bigg (\frac{P(r^{2}+a^{2})^{2} }{\rho ^{2}}{-}\frac{Qa^{2} \left( 1+h\right) \sin ^{2}\theta }{\rho ^{2}}\Bigg )\sin ^{2}\theta \right. \nonumber \\&\quad \left. +a^2 \sin ^4\theta \left( 2h+\frac{a^2 h\sin ^2\theta }{\rho ^{2} }\right) \right] d\phi ^{2}\Bigg \}\nonumber \\&\quad -\frac{2a \left[ P\left( r^{2}+a^{2}\right) {-}Q\right] \left( 1{+}h\right) \sin ^{2}\theta }{\rho ^{2}\Omega ^{2}}d\phi dt, \end{aligned}$$

(2.1)

where

$$\begin{aligned} \Omega= & {} -\alpha r\cos \theta {+}1, \end{aligned}$$

(2.2)

$$\begin{aligned} \rho ^{2}= & {} a^{2}\cos ^{2}\theta +r^{2} , \end{aligned}$$

(2.3)

$$\begin{aligned} P= & {} 1 +\alpha ^{2}\left( a^{2}+e^{2}\right) \cos ^{2}\theta -2\alpha M\cos \theta , \end{aligned}$$

(2.4)

$$\begin{aligned} Q= & {} (a^{2}+e^{2}+r^{2}-2Mr)(1-\alpha ^{2}r^{2}), \end{aligned}$$

(2.5)

$$\begin{aligned} h= & {} \frac{\epsilon M^3}{r^3}. \end{aligned}$$

(2.6)

Here a, M, $\alpha$ and $\epsilon$ denote the rotation, mass, acceleration and deformation parameter of the black hole, respectively. Now using the notation of Refs. [18, 29, 30], the above metric can be written as

$$\begin{aligned} ds^{2}=\frac{dr^{2}}{g(r,\theta )}-f(r,\theta )dt^{2}+\Sigma (r,\theta )d\theta ^{2}-2H(r,\theta )dtd\phi +K(r,\theta )d\phi ^{2} , \end{aligned}$$

(2.7)

where $g(r,\theta ),\ f(r,\theta ),\ \Sigma (r,\theta ), \ H(r,\theta )$ and $K(r,\theta )$ are defined below:

$$\begin{aligned} f(r,\theta )= & {} \left( \frac{Q-Pa^{2}\sin ^{2}\theta }{\rho ^{2}\Omega ^{2}}\right) \left( 1+h\right) , \end{aligned}$$

(2.8)

$$\begin{aligned} g(r,\theta )= & {} \frac{\Omega ^{2}\left( ah\sin ^2{\theta } +Q\right) }{\rho ^{2}(1+h)}, \end{aligned}$$

(2.9)

$$\begin{aligned} \Sigma (r,\theta )= & {} \frac{\rho ^{2}}{P\Omega ^{2}}, \end{aligned}$$

(2.10)

$$\begin{aligned} K(r,\theta )= & {} \left( \frac{P \left( a^2+r^2\right) ^2}{\rho ^{2}}-\frac{a^2 Q \sin ^2\theta (h+1)}{\rho ^{2} }\right) \sin ^2\theta \nonumber \\&+a^2 \sin ^4\theta \left( \frac{a^2 h \sin ^2\theta }{\rho ^{2}}+2 h\right) , \end{aligned}$$

(2.11)

$$\begin{aligned} H(r,\theta )= & {} {-}\frac{2a\sin ^{2}\theta \left[ P\left( r^{2}+a^{2}\right) {-}Q\right] \left( 1{+}h\right) }{\rho ^{2}\Omega ^{2}} . \end{aligned}$$

(2.12)

The equation $1/g_{rr}=0$ gives the horizon. It leads to two possibilities given as

$$\begin{aligned} \Omega ^{2}=0, \quad Q+a^2 h\sin ^2{\theta }=0. \end{aligned}$$

(2.13)

The first factor gives the accelerating horizon i.e. the horizon due to acceleration

$$\begin{aligned} r=\frac{1}{\alpha \cos \theta }. \end{aligned}$$

(2.14)

The outer horizon of accelerating non-Kerr black hole is denoted by $r_{+}$. The main difference between the present and earlier works comes from complexity of the event horizon equation. Here, this equation is of fifth order giving five roots: two are complex, one is negative and the other two are positive, which give us horizons. We have used the outer most root in our tunneling analysis. In the case of accelerating Kerr black holes [29, 30] we only have a quadratic equation from which roots can be calculated in exact form. In the present case of accelerating non-Kerr black holes we could only calculate the position of the horizon numerically which is $r_{+}=1.7923$. The function $F(r,\theta )$ and angular velocity at the outer horizon $\Omega _{H}$ are defined as [21]

$$\begin{aligned} F(r,\theta )= & {} \frac{H(r,\theta )+f(r,\theta )K(r,\theta )}{K(r,\theta )}, \end{aligned}$$

(2.15)

$$\begin{aligned} \Omega _{H}= & {} \frac{H(r_{+},\theta )}{K(r_{+},\theta )}. \end{aligned}$$

(2.16)

Using $f(r,\theta ),\ H(r,\theta )$ and $K(r,\theta )$ from Eqs. (2.8), (2.11) and (2.12), we obtain

$$\begin{aligned} F(r,\theta )= & {} \frac{(h+1)}{\Omega ^{2} \rho ^{2}}\Bigg (\frac{2 a^2 \rho ^{2} \left( a^4 P+2 a^2 P r^2+P r^4-Q\right) }{a^4 h \sin ^4\theta -a^2 \sin ^2\theta (h Q-2 h \rho ^{2} +Q)+P \left( a^2+r^2\right) ^2}\nonumber \\&+ Q-a^2 P\sin ^2\theta \Bigg ),\qquad \qquad \end{aligned}$$

(2.17)

$$\begin{aligned} \Omega _{H}= & {} \frac{2 a^2 (h+1) \left( a^4 P+2 a^2 P r^2+P r^4-Q\right) }{\Omega ^{2} \left( P \left( a^2+r^2\right) ^2+a^4 h \sin ^4\theta -a^2 \sin ^2\theta [h Q-2 h \rho ^{2} +Q]\right) }, \qquad \qquad \end{aligned}$$

(2.18)

where $r_{+}$ represents the event horizon of the accelerating non-Kerr black hole given by the solution of the second factor in Eq. (2.13). The calculations are done for the spin-up case. The calculations for the spin-down case are similar and there is a difference of sign only between the two cases.

3 Quantum tunneling of Dirac particles

In this section we will study the tunneling of uncharged and charged fermions. For this Dirac equations in the background of accelerating non-Kerr black holes.

3.1 Uncharged Dirac particles

We solve the Dirac equation to find the Hawking temperature at the outer horizon. The Dirac equation [18, 20] for fermions can be written in terms of the wave function $\Psi$ as

$$\begin{aligned} i \gamma ^{\mu }(D_{\mu })\Psi +\frac{m}{\hbar }\Psi =0. \end{aligned}$$

(3.1)

Here $\mu$ takes the values (0, 1, 2, 3), m is the mass of the fermion particles, $\hbar$ is the Planck constant and

$$\begin{aligned} D_{\mu }=\partial _{\mu }+\frac{1}{8}i ^{2}\Gamma _{\mu }^{\alpha \beta }[\Upsilon ^{\alpha },\Upsilon ^{\beta }]. \end{aligned}$$

(3.2)

where $\Gamma _{\mu }^{\alpha \beta }$ represent the Christoffel symbols and the $\gamma ^{\alpha }$ satisfy the commutative law

$$\begin{aligned}&[\gamma ^{\beta },\gamma ^{\alpha }]=-[\gamma ^{\alpha },\gamma ^{\beta }], \quad \alpha \ne \beta ,\nonumber \\ {}&0=[\gamma ^{\alpha },\gamma ^{\beta }],\quad \alpha =\beta . \end{aligned}$$

(3.3)

By giving variation to $\alpha$ and $\beta$, $D_{\mu }$ takes the form

$$\begin{aligned} D_{\mu }= & {} \partial _{\mu }+\frac{1}{8}i ^{2}\Bigg [\Gamma _{\mu }^{00}[\gamma ^{0},\gamma ^{0}]+\Gamma _{\mu }^{01}[\gamma ^{0},\gamma ^{1}]+\Gamma _{\mu }^{02}[\gamma ^{0},\gamma ^{2}]\nonumber \\&+\Gamma _{\mu }^{03}[\gamma ^{0},\gamma ^{03}]+\Gamma _{\mu }^{10}[\gamma ^{1},\gamma ^{0}] \nonumber \\&+\Gamma _{\mu }^{11}[\gamma ^{1},\gamma ^{1}]+\Gamma _{\mu }^{12}[\gamma ^{1},\gamma ^{2}]+\Gamma _{\mu }^{13}[\gamma ^{1},\gamma ^{3}]+\Gamma _{\mu }^{20}[\gamma ^{2},\gamma ^{0}]\nonumber \\&+\Gamma _{\mu }^{21}[\gamma ^{2},\gamma ^{1}] +\Gamma _{\mu }^{22}[\gamma ^{2},\gamma ^{2}] \nonumber \\&+\Gamma _{\mu }^{23}[\gamma ^{2},\gamma ^{3}]+\Gamma _{\mu }^{30}[\gamma ^{3},\gamma ^{0}]+\Gamma _{\mu }^{31}[\gamma ^{3},\gamma ^{1}]\nonumber \\&+\Gamma _{\mu }^{32}[\gamma ^{3},\gamma ^{2}]+\Gamma _{\mu }^{33}[\gamma ^{3},\gamma ^{3}]\Bigg ]. \end{aligned}$$

(3.4)

By using the commutative law, all the terms in Eq. (3.4) cancel out except $\partial _{\mu }.$ Thus Eq. (3.1) takes the form

$$\begin{aligned} \frac{m}{\hbar }\Psi +(i \gamma ^{r}\partial _{r}+i \gamma ^{t}\partial _{t}+i \gamma ^{\theta }\partial _{\theta }+i \gamma ^{\phi }\partial _{\phi })\Psi =0. \end{aligned}$$

(3.5)

We define the $\gamma ^{\alpha }$ for the metric (2.7)

$$\begin{aligned} \gamma ^{t}= & {} \sqrt{\frac{\Omega ^{2}\left[ P(a^{2}+r^{2})^{2}-Qa^{2}\sin ^{2}\theta \right] }{QP\rho ^{2}\left( 1+h\right) }}\gamma ^{0},\ \ \ \gamma ^{r}= \sqrt{\frac{\left( Q+a^2 h\sin ^2\theta \right) \Omega ^{2}}{\rho ^{2}}}\gamma ^{3},\nonumber \\ \gamma ^{\theta }= & {} \sqrt{\frac{P\Omega ^{2}}{\rho ^{2}}}\gamma ^{1}, \nonumber \\ \gamma ^{\phi }= & {} \frac{\rho \Omega \gamma ^{2}}{\sin \theta \sqrt{ \left[ P(a^{2}+r^{2})^{2}-a^{2}Q\sin ^{2}\theta \right] (1+h) }}\nonumber \\&+\frac{a(P(a^{2}+r^{2})-Q)\gamma ^{0}}{\sqrt{F(r,Q)}(P(a^{2}+r^{2})^{2}-a^{2}Q\sin ^{2}\theta )}. \end{aligned}$$

(3.6)

Here

$$\begin{aligned} \gamma ^{0}= & {} \left( \begin{array}{cc} 0 &{} I \\ -I &{} 0 \end{array} \right) ,\quad \gamma ^{1}=\left( \begin{array}{cc} 0 &{} \sigma ^{1} \\ \sigma ^{1} &{} 0 \end{array} \right) , \nonumber \\ \gamma ^{2}= & {} \left( \begin{array}{cc} 0 &{} \sigma ^{2} \\ \sigma ^{2} &{} 0 \end{array} \right) ,\quad \gamma ^{3}=\left( \begin{array}{cc} 0 &{} \sigma ^{3} \\ \sigma ^{3} &{} 0 \end{array} \right) . \end{aligned}$$

(3.7)

The Pauli sigma matrices ${\sigma ^{i} \quad (i=1,2,3)}$ are

$$\begin{aligned} \sigma ^{1}= & {} \left( \begin{array}{cc} 0 &{} 1 \\ 1 &{} 0 \end{array} \right) ,\quad \sigma ^{2}=\left( \begin{array}{cc} 0 &{} -i \\ i &{} 0 \end{array} \right) , \nonumber \\ \sigma ^{3}= & {} \left( \begin{array}{cc} 1 &{} 0 \\ 0 &{} -1 \end{array} \right) . \end{aligned}$$

(3.8)

The solutions for spin-up/spin-down cases can be respectively assumed to be of the form [20]

$$\begin{aligned} \Psi _{_{\uparrow }}(t,r,\theta ,\phi )=\left( \begin{array}{c} A(t,r,\theta ,\phi )\xi _{_{\uparrow }} \\ B(t,r,\theta ,\phi )\xi _{_{\uparrow }} \end{array} \right) \exp \left[ \frac{i }{\hbar }I_{\uparrow }(t,r,\theta ,\phi ) \right] , \nonumber \\ \Psi _{\downarrow }(t,r,\theta ,\phi )=\left( \begin{array}{c} C(t,r,\theta ,\phi )\xi _{\downarrow } \\ D(t,r,\theta ,\phi )\xi _{\downarrow } \end{array} \right) \exp \left[ \frac{i }{\hbar }I_{\downarrow }(t,r,\theta ,\phi ) \right] , \end{aligned}$$

(3.9)

where $I_{\uparrow }$ and $I_{\downarrow }$ denote the actions of the emitted particles for spin-up and spin-down cases, respectively. We shall discuss the spin-up case only since the spin-down case is similar except for a sign change. Here A, B, C and D are arbitrary functions of the coordinates $(t, r, \theta , \phi )$. Substituting Eq. (3.9) in Eq. (3.5) and taking leading order terms in $\hbar$ we obtain the following four equations after some algebra

$$\begin{aligned} 0= & {} Am-\left\{ \frac{\partial _{t}I_{\uparrow }}{\sqrt{F(r,\theta )}}+\sqrt{g(r,\theta )} \partial _{r}I_{\uparrow }+\frac{\Omega }{\sqrt{F(r,\theta )}}\partial _{\phi }I_{\uparrow }\right\} B, \end{aligned}$$

(3.10)

$$\begin{aligned} 0= & {} -\left\{ \sqrt{\frac{\Omega ^{2}P}{\rho ^{2}}}\partial _{\theta }I_{\uparrow }+\frac{i \Omega \rho }{\sin \theta \sqrt{\left[ P(a^{2}+r^{2})^{2}- a^{2}Q \sin ^{2}\theta \right] (1+h)}}\partial _{\phi }I_{\uparrow }\right\} B, \end{aligned}$$

(3.11)

$$\begin{aligned} 0= & {} Bm +\left\{ \frac{\partial _{t}I_{\uparrow }}{\sqrt{F(r,\theta )}}-\sqrt{g(r,\theta )}\partial _{r}I_{\uparrow }+\frac{\Omega }{\sqrt{F(r,\theta )}}\partial _{\phi }I_{\uparrow }\right\} A, \end{aligned}$$

(3.12)

$$\begin{aligned} 0= & {} -\left\{ \sqrt{\frac{\Omega ^{2}P}{\rho ^{2}}}\partial _{\theta }I_{\uparrow }+\frac{i \Omega \rho }{\sin \theta \sqrt{\left[ P(a^{2}+r^{2})^{2}- a^{2}Q \sin ^{2}\theta \right] (1+h)}}\partial _{\phi }I_{\uparrow }\right\} A. \nonumber \\ \end{aligned}$$

(3.13)

We apply the following ansatz for solving the above system of equations [21, 30]

$$\begin{aligned} I_{\uparrow }=J\phi -Et+W(r,\theta ), \end{aligned}$$

(3.14)

where E and J are the energy and angular momentum of the particle. With this substitution the above four equations become

$$\begin{aligned} 0= & {} Am -\left\{ \frac{-E}{\sqrt{F(r,\theta )}}+\sqrt{g(r,\theta )}W^{\prime }(r,\theta )+\frac{\Omega _HJ}{\sqrt{F(r,\theta )}}\right\} B, \end{aligned}$$

(3.15)

$$\begin{aligned} 0= & {} -\left\{ \sqrt{\frac{\Omega ^{2}P}{\rho ^{2}}}W_{\theta }(r,\theta ) +\frac{i \rho \Omega J}{\sin \theta \sqrt{\left[ P(a^{2}+r^{2})^{2}-a^{2}Q \sin ^{2}\theta \right] (1+h)}}\right\} B, \end{aligned}$$

(3.16)

$$\begin{aligned} 0= & {} Bm +\left\{ \frac{-E}{\sqrt{F(r,\theta )}}-\sqrt{g(r,\theta )}W^{\prime }(r,\theta )+\frac{\Omega _HJ}{\sqrt{F(r,\theta )}}\right\} A, \end{aligned}$$

(3.17)

$$\begin{aligned} 0= & {} -\left\{ \sqrt{\frac{\Omega ^{2}P}{\rho ^{2}}}W_{\theta }(r,\theta ) +\frac{i \Omega \rho J }{\sin \theta \sqrt{\left[ P(a^{2}+r^{2})^{2}- a^{2}Q \sin ^{2}\theta \right] (1+h)}}\right\} A. \nonumber \\ \end{aligned}$$

(3.18)

Using Taylor’s theorem in Eq. (2.9) and neglecting the squares and higher powers we obtain

$$\begin{aligned} g(r,\theta )=g(r_{+},\theta )+(r-r_{+})g_{r}(r_{+},\theta ). \end{aligned}$$

(3.19)

At the horizon

$$\begin{aligned} g(r_{+},\theta )=0. \end{aligned}$$

(3.20)

Thus Eq. (3.19) becomes

$$\begin{aligned} g(r,\theta )=(r-r_{+})g_{r}(r_{+},\theta ). \end{aligned}$$

(3.21)

Taking partial derivative of Eq. (2.9) with respect to r and evaluating at the horizon, we get

$$\begin{aligned} g_{r}(r_{+},\theta )= & {} \frac{\Omega ^2}{\rho ^2}\Bigg \{(1-\alpha ^{2}r_{+}^{2})(2r_{+}-2M)-2\alpha r_+ (a^2+r^2-2Mr)\nonumber \\&+a^2\epsilon M \sin ^2\theta \left[ \frac{1}{(a^2 \cos ^2\theta + r_{+}^{2} )^2}-\frac{4r_{+}^{2}}{(a^2 \cos ^2\theta +r_{+}^{2})^3}\right] \Bigg \}.\nonumber \\ \end{aligned}$$

(3.22)

Using Eq. (3.22) in Eq. (3.21) we get

$$\begin{aligned} g(r_+,\theta )= & {} (r-r_{+})\frac{\Omega ^2}{\rho ^2}\Bigg \{(1-\alpha ^{2}r_{+}^{2})(2r_{+}-2M)-2\alpha r_+ (a^2+r^2-2Mr)\nonumber \\&+a^2\epsilon M \sin ^2\theta \left[ \frac{1}{(a^2 \cos ^2\theta +r_{+}^{2})^2}-\frac{4r_{+}^{2}}{(a^2 \cos ^2\theta +r_{+}^{2})^3}\right] \Bigg \}. \end{aligned}$$

(3.23)

Now, expanding Eqs. (3.15) to (3.18) near the horizon of the black hole and using Eqs. (3.23) we get

$$\begin{aligned} 0= & {} Am-\left\{ \frac{-E}{\sqrt{F(r_{+},\theta )}}+\sqrt{(r-r_{+})g_{r}(r_{+},\theta )} W^{\prime }(r,\theta )+\frac{\Omega _HJ}{\sqrt{F(r_{+},\theta )}}\right\} B, \end{aligned}$$

(3.24)

$$\begin{aligned} 0= & {} -\left\{ \sqrt{\frac{\Omega ^{2}P}{\rho ^{2}}}W_{\theta }(r,\theta ) +\frac{i \rho \Omega _H }{\sin \theta \sqrt{\left[ P(a^{2}+r^{2})^{2}- a^{2}Q \sin ^{2}\theta \right] (1+h)}}J\right\} B, \end{aligned}$$

(3.25)

$$\begin{aligned} 0= & {} Bm +\left\{ \frac{-E}{\sqrt{F(r_{+},\theta )}}-\sqrt{(r-r_{+})g_{r}(r_{+},\theta )} W^{\prime }(r,\theta )+\frac{\Omega _HJ}{\sqrt{F(r_{+},\theta )}}\right\} A, \end{aligned}$$

(3.26)

$$\begin{aligned} 0= & {} -\left\{ \sqrt{\frac{\Omega ^{2}P}{\rho ^{2}}}W_{\theta }(r,\theta ) +\frac{i \rho \Omega _H}{\sin \theta \sqrt{\left[ P(a^{2}+r^{2})^{2}-Qa^{2} \sin ^{2}\theta \right] (1+h)}}J\right\} A. \nonumber \\ \end{aligned}$$

(3.27)

We neglect the equation which depends upon “$\theta$”. Although these equations could contribute to the (imaginary part) action, but its total contribution to the tunneling rate vanishes. Using Eq. (2.18) in Eqs. (3.24) and (3.26) we get

$$\begin{aligned} 0= & {} Am-\left[ \frac{-E+\Omega _{H}J}{\sqrt{F(r_{+},\theta )}}+\sqrt{ (r-r_{+})g_{r}(r_{+},\theta )}W^{\prime }(r,\theta )\right] B, \end{aligned}$$

(3.28)

$$\begin{aligned} 0= & {} +Bm+\left[ \frac{-E+\Omega _{H}J}{\sqrt{F(r_{+},\theta )}}-\sqrt{ (r-r_{+})g_{r}(r_{+},\theta )}W^{\prime }(r,\theta )\right] A. \end{aligned}$$

(3.29)

At the horizon we can further decompose $W(r,\theta )$. We shall also divide our solution into two parts, the massless and the massive cases.

3.1.1 The massless case

In this case we put $m=0$ in Eqs. (3.28)–(3.29), then two possible solutions could exist

$$\begin{aligned} B=0,\quad W^{\prime }(r)=W_{+}^{\prime }(r)=\frac{(E-\Omega _{H}J)}{ \sqrt{F(r_{+},\theta )}\sqrt{(r-r_{+})g_{r}(r_{+},\theta )}}. \end{aligned}$$

(3.30)

Eq. (3.29) become

$$\begin{aligned} A=0,\quad W^{\prime }(r)=W_{-}^{\prime }(r)=\frac{-(E-\Omega _{H}J)}{ \sqrt{F(r_{+},\theta )}\sqrt{(r-r_{+})g_{r}(r_{+},\theta )}}. \end{aligned}$$

(3.31)

Here prime is the notation of derivative with respect to r and $+/-$ corresponds to outgoing/incoming solution. To find the outgoing solution of the fermion particle i.e. $W_{+}(r)$ we integrate Eq. (3.30)

$$\begin{aligned} W_{+}(r)=\int \frac{(E-\Omega _{H}J)dr}{\sqrt{F(r_{+},\theta )g_{r}(r_{+},\theta )}\sqrt{(r-r_{+})}}. \end{aligned}$$

(3.32)

The above integrand diverges at $r=r_{+}$. By using the contour integration, we get

$$\begin{aligned} W_{+}(r)=\frac{2(i-1)(E-\Omega _{H}J)}{\sqrt{F(r_{+},\theta )g_{r}(r_{+},\theta )}}. \end{aligned}$$

(3.33)

Removing the $+$ subscript we can write

$$\begin{aligned} W(r)= & {} \frac{2(i-1)(E-\Omega _{H}J)}{\sqrt{F(r_{+},\theta )g_{r}(r_{+},\theta )}}, \nonumber \\ ImW= & {} \frac{2(E-\Omega _{H}J)}{\sqrt{F(r_{+},\theta )g_{r}(r_{+},\theta )}}. \end{aligned}$$

(3.34)

So the tunneling probabilities of fermions are given as [30]

$$\begin{aligned} Prob[out]\propto & {} \exp [-2Im I]=\exp [-2(Im W_{+}+Im\Theta )], \end{aligned}$$

(3.35)

$$\begin{aligned} Prob[in]\propto & {} \exp [-2Im I]=\exp [-2(Im W_{-}+Im\Theta )] \end{aligned}$$

(3.36)

Since $Im W_{+}=-Im W_{-}$, the resulting tunneling probability $\Gamma =\exp [-4Im W_{+}]$ becomes

$$\begin{aligned} \Gamma =\exp \left[ \frac{-8(E-\Omega _{H}J)}{\sqrt{F(r_{+},\theta )g_{r}(r_{+},\theta )}}\right] . \end{aligned}$$

(3.37)

Comparing this with the Boltzmann factor of energy, $\Gamma =\exp (-\beta E)$ where $\beta =1/T_{H}$, we get

$$\begin{aligned} T_{H}=\frac{\sqrt{F(r_{+},\theta )g_{r}(r_{+},\theta )}}{8}. \end{aligned}$$

(3.38)

This is the Hawking temperature for the accelerating non-Kerr black hole at the outer horizon which is decreasing for growing values of mass M over a certain range contrary to the accelerating Kerr black hole where temperature is decreasing throughout the range of M.

3.1.2 The massive case

In the massive case we shall eliminate the contribution of function $W^{\prime }(r,\theta )$ from Eqs. (3.28) and (3.29). We multiply Eq. (3.28) by A, Eq. (3.29) by B and then subtract these equations to obtain

$$\begin{aligned} A^{2}m-B^{2}m+2\frac{AB(E-J\Omega _{H})}{\sqrt{F(r_{+},\theta )} }=0. \end{aligned}$$

(3.39)

Multiplying the whole equation by the term $\sqrt{F(r_{+},\theta )}$ and dividing by $B^{2}$ we get

$$\begin{aligned}&m\sqrt{F(r_{+},\theta )}(A/B)^{2}+2(E-J\Omega _{H})(A/B)-m\sqrt{F(r_{+},\theta )}=0, \end{aligned}$$

(3.40)

$$\begin{aligned}&A/B =\frac{-(E-J\Omega _{H})\pm \sqrt{(E-J\Omega _{H})^{2}+m^{2}F_{r}(r_{+},\theta )(r-r_{+})}}{m\sqrt{F(r_{+},\theta )}}, \end{aligned}$$

(3.41)

where

$$\begin{aligned} \lim _{r\rightarrow r_{+}}(A/B)=\lim _{r\rightarrow r_{+}}\Big (\frac{-(E-J\Omega _{H})\pm \sqrt{(E-J\Omega _{H})^{2}+m^{2}F(r_{+},\theta )}}{m \sqrt{F(r_{+},\theta )}}\Big ). \end{aligned}$$

(3.42)

Now

$$\begin{aligned} \lim _{r\rightarrow r_{+}}A/B=\left\{ \begin{array}{c} 0 \\ -\infty \end{array} \right. , \end{aligned}$$

(3.43)

for the upper/lower sign respectively. Consequently, either $A/B\rightarrow 0$ or $A/B\rightarrow -\infty$ at the horizon, i.e. either $A\rightarrow 0$ or $B\rightarrow 0$. For $A\rightarrow 0$, the value of m can be found from Eq. (3.29) as,

$$\begin{aligned} m=-A/B[\frac{-E+J\Omega _{H}}{\sqrt{F(r_{+},\theta )}}-\sqrt{ g_{r}(r_{+},\theta )(r-r_{+})}W^{\prime }(r)]. \end{aligned}$$

(3.44)

Putting in Eq. (3.28) and simplifying we obtain

$$\begin{aligned} W_{r}(r,\theta )=W_{+}^{\prime }(r)=\frac{(E-J\Omega _{H})}{\sqrt{ g_{r}(r_{+},\theta )(r-r_{+})F(r_{+},\theta )}} (1+A^{2}/B^{2})/(1-A^{2}/B^{2}). \end{aligned}$$

(3.45)

Integrating with respect to r we have

$$\begin{aligned} W_{+}(r)=\int \frac{(E-J\Omega _{H})}{\sqrt{g_{r}(r_{+},\theta )(r-r_{+})F(r_{+},\theta )}}(1+A^{2}/B^{2})/(1-A^{2}/B^{2})dr. \end{aligned}$$

(3.46)

We see that at $r=r_{+}$ the integrand diverges. So, by using the contour integration technique, we get

$$\begin{aligned} W_{+}(r)=\frac{2(i-1)(E-\Omega _{H}J)}{\sqrt{F(r_{+},\theta )g_{r}(r_{+},\theta )}}. \end{aligned}$$

(3.47)

For $B\rightarrow 0$ we can simply rewrite the expression in terms of B/A to get

$$\begin{aligned} W_{r}(r,\theta )=W_{-}^{\prime }(r)=\frac{-(E-J\Omega _{H})}{\sqrt{ g_{r}(r_{+},\theta )(r-r_{+})F(r_{+},\theta )}} (1+B^{2}/A^{2})/(1+B^{2}/A^{2}),\nonumber \\ \end{aligned}$$

(3.48)

Integrating with respect to r and using Eq. (3.43) we obtain

$$\begin{aligned} W(r)=\frac{-2(i-1)(E-\Omega _{H}J)}{\sqrt{g_{r}(r_{+},\theta )F(r_{+},\theta )}}. \end{aligned}$$

(3.49)

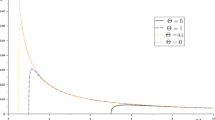
The spin-down case is same as the spin-up case, except for the difference of sign. The equations have the same form as in the spin-up case. The Hawking temperature (3.38) is recovered for both the cases (the massive and massless cases). Figure 1 shows that the Hawking temperature decay rapidly with the increase in certain range of mass. The temperature is plotted in the considered range of mass for accelerating non-Kerr black hole. The behaviour of the Hawking temperature for accelerating non-Kerr black hole is different from the accelerating Kerr. We see in Fig. 1 that the temperature has a critical point because it first decreases for large values of mass M upto a minimum and then it grows. On the other hand, if we put $h=0$ to examine the behaviour of the Hawking temperature of accelerating Kerr black hole, it only decreases.

Fig. 1

Hawking temperature against M for $a=0.2$, $\epsilon =-0.5$, $\theta =\pi /2$, $\alpha =0.3.$

3.2 Charged Dirac particles

To study the tunneling process of charged fermions, the Dirac equation with electric charge will be solved for accelerating non-Kerr black holes. The Dirac equation in covariant form with q (electric charge) is

$$\begin{aligned} i\gamma ^{\mu }\left( D_{\mu }-\frac{iq}{\hbar }A_{\mu }\right) \Psi +\frac{m }{\hbar }\Psi =0, \end{aligned}$$

(3.50)

where m represents the mass of the particles (fermions) and $D_{\mu }=\partial _{\mu }+\Omega _{\mu }$, where $\Omega _{\mu }=\frac{1}{2}i\Gamma _{\mu }^{\alpha \beta }\Sigma _{\alpha \beta }$, and $\Sigma _{\alpha \beta }$ is antisymmetric i.e. $\Sigma _{\alpha \beta } =\frac{1}{4}i\left[ \gamma ^{\alpha },\gamma ^{\beta } \right]$. The electromagnetic vector potential for these black holes is given by [43]

$$\begin{aligned} A=\frac{-er\left[ dt-a\sin ^{2}\theta d\phi \right] -g\cos \theta \left[ adt-\left( r^{2}+a^{2}\right) d\phi \right] }{r^{2}+a^{2}\cos ^{2}\theta }. \end{aligned}$$

(3.51)

Since the metric coefficients do not depend on the coordinates t and $\phi$, therefore, an ansatz [19, 20, 28] similar to the uncharged case, can be used. We use Taylor’s expansion of linear order for the terms $g\left( r,\theta \right)$ near the outer horizon, as has been done for uncharged particles [28]. Putting the values of $A_{t}(r_{+},\theta )$, $A_{\phi }( r_{+},\theta )$, $\Sigma (r_{+},\theta )$ and $K(r_{+},\theta )$ in Eq. (3.50) for the charged case, the following set of equations is obtained.

$$\begin{aligned} 0= & {} Am-\left[ \frac{\left( \Omega _{H}J-E+\frac{eqr_{+}}{\left( a^{2}+r^{2}\right) }\right) }{\sqrt{ F\left( r_{+},\theta \right) }}+\partial _{r}W \sqrt{\left( r-r_{+}\right) \partial _{r} g \left( r_{+},\theta \right) }\right] B, \end{aligned}$$

(3.52)

$$\begin{aligned} 0= & {} -\Bigg [ \sqrt{\frac{\Omega ^{2}\left( r_{+},\theta \right) P }{\rho ^{2}\left( r_{+},\theta \right) }}\partial _{\theta }W \nonumber \\&+\frac{i\Omega \left( r_{+},\theta \right) \rho \left( r_{+},\theta \right) }{\sqrt{\sin ^{2}\theta P\left( a^{2}+r_{+}^{2}\right) ^{2}}}\left( J-q\left( \frac{ ear_{+}\sin ^{2}\theta +g\left( a^{2}+r_{+}^{2}\right) \cos \theta }{ a^{2}\cos ^{2}\theta +r_{+}^{2} }\right) \right) \Bigg ]B, \end{aligned}$$

(3.53)

$$\begin{aligned} 0= & {} Bm +\left[ \frac{\left( \Omega _{H}J-E++\frac{eqr_{+}}{\left( a^{2}+r_{+}^{2}\right) }\right) }{\sqrt{ F\left( r_{+},\theta \right) }}-\sqrt{\left( r-r_{+}\right) \partial _{r}g\left( r_{+},\theta \right) }\partial _{r}W\right] A, \end{aligned}$$

(3.54)

$$\begin{aligned} 0= & {} -\Bigg [ \sqrt{\frac{\Omega ^{2}\left( r_{+},\theta \right) P}{\rho ^{2}\left( r_{+},\theta \right) }}\partial _{\theta }W \nonumber \\&+ \frac{i\Omega \left( r_{+},\theta \right) \rho \left( r_{+},\theta \right) }{\sqrt{P\left( a^{2}+r_{+}^{2}\right) ^{2}\sin ^{2}\theta }}\left( J-q\left( \frac{ g\left( r_{+}^{2}+a^{2}\right) \cos \theta +ear_{+}\sin ^{2}\theta }{ a^{2}\cos ^{2}\theta +r_{+}^{2}}\right) \right) \Bigg ]A.\nonumber \\ \end{aligned}$$

(3.55)

Now, $W(r,\theta )$ can be separated near the horizon of black hole as

$$\begin{aligned} W\left( r,\theta \right) =R\left( r\right) +\Theta \left( \theta \right) . \end{aligned}$$

(3.56)

We will solve Eqs. (3.52)–(3.55) for the massless case (i.e. $m=0$) first. Considering the above separation of $W(r,\theta )$ and $m=0$ we get

$$\begin{aligned} 0=-\left[ \frac{\left( \Omega _{H}J-E+\frac{eqr_{+}}{\left( a^{2}+r_{+}^{2}\right) }\right) }{\sqrt{ F\left( r_{+},\theta \right) }}+\sqrt{\left( r-r_{+}\right) \partial _{r}g\left( r_{+},\theta \right) }R^{\prime } \left( r\right) \right] B , \end{aligned}$$

which implies

$$\begin{aligned} R^{\prime } \left( r\right) = \frac{\left( -\Omega _{H}J+E-\frac{eqr_{+}}{\left( a^{2}+r_{+}^{2}\right) }\right) }{\sqrt{F(r,\phi )g_{r}(r,\phi )}\sqrt{(r-r_{+})} }=R^{\prime }_{+} \left( r\right) , \end{aligned}$$

(3.57)

where $R_{+}$ corresponds to the outgoing solution. In a similar pattern, the incoming solution can be obtained as

$$\begin{aligned} R^{\prime }\left( r\right) = -\frac{\left( -\Omega _{H}J+E-\frac{eqr_{+}}{\left( a^{2}+r_{+}^{2}\right) }\right) }{\sqrt{F(r,\phi )g_{r}(r,\phi )}\sqrt{(r-r_{+})} }=R^{\prime }_{-} \left( r\right) . \end{aligned}$$

(3.58)

The $R_{+}$ is

$$\begin{aligned} R_{+}(r) =\frac{2(i-1)\left( -\Omega _{H}J+E-\frac{eqr_{+}}{\left( a^{2}+ r_{+}^{2}\right) }\right) }{\sqrt{F(r_{+},\theta )g_{r}(r_{+},\theta )}}, \end{aligned}$$

(3.59)

and its imaginary part is

$$\begin{aligned} Im R_{+}=\frac{2\left( \Omega _{H}J+E-\frac{eqr_{+}}{\left( a^{2}+r_{+}^{2}\right) }\right) }{\sqrt{F(r_{+},\theta )g_{r}(r_{+},\theta )}}. \end{aligned}$$

(3.60)

Also,

$$\begin{aligned} Im R_{-}=-\frac{2\left( -\Omega _{H}J+E-\frac{eqr_{+}}{\left( a^{2}+r_{+}^{2}\right) }\right) }{\sqrt{F(r_{+},\theta )g_{r}(r_{+},\theta )}}, \end{aligned}$$

(3.61)

which shows that $Im R_{+}=- Im R_{-}$. Using Eq. (3.60), the expression $\Gamma =\exp \left[ -4Im R_{+}\right]$ becomes

$$\begin{aligned} \Gamma =\exp \left[ \frac{8}{\sqrt{F(r_{+},\theta ) g_{r}(r_{+},\theta )}}\left( -\Omega _{H}J+E-\frac{eqr_{+}}{\left( a^{2}+r_{+}^{2}\right) }\right) \right] . \end{aligned}$$

(3.62)

Comparing the above expression with $\Gamma =\exp [-\beta E]$, where $\beta = 1/T_H$, the Hawking temperature [4, 12] is found as

$$\begin{aligned} T_{H}=\frac{\sqrt{F(r_{+},\theta )g_{r}(r_{+},\theta )}}{8}. \end{aligned}$$

(3.63)

These result for the Kerr-Newman [18] and Reissner-Nordström black holes can be obtained from the above formulas by eliminating the effects of acceleration and rotation, from Eq. (3.62). It is possible here that for some specific values of E and J, Eqs. (3.60)–(3.62) could have the probabilities greater than 1, which is the violation of unitarity. However, this will not happen here because both the spatial and temporal parts contribute to the imaginary part $Im(E\Delta t)$ of the action [47, 48]. The (shifted) imaginary amount of time contributes to both the Prob[in] and Prob[out], and yields a correct value of $\Gamma$. Without this contribution, the Hawking temperature will be twice the original value [49, 50]. The case of massive particles ($m\ne 0$) gives the same value of temperature as in the massless case because both have the same behaviour near the horizon [28].

4 Quantum tunneling of scalar particles

This section deals with tunneling of charged and uncharged scalar particles for accelerating non-Kerr black hole. The tunneling probability and temperature will be found.

4.1 Uncharged scalar particles

In order to discuss quantum tunneling of scalar particles from accelerating non-Kerr black holes given in Eq. (2.7), we will solve the Klein-Gordon equation which is given as

$$\begin{aligned} g^{\mu \nu }\partial _{\mu }\partial _{\nu }\phi -\frac{m^{2}}{\hbar ^{2}} \Phi =0. \end{aligned}$$

(4.1)

The wave function $\Phi (t,r,\theta ,\phi )$ is defined as

$$\begin{aligned} \Phi (t,r,\theta ,\phi )=\exp (\frac{i }{\hbar } I(t,r,x^{a})+I_{1}(t,r,x^{a})+O(\hbar ), \end{aligned}$$

(4.2)

where $O(\hbar )$ is considered.

Using Eq. (4.2) in Eq. (4.1) we get

$$\begin{aligned} g^{\mu \nu }\left( \partial _{\mu }I\right) \left( \partial _{\nu }I\right) +m^{2}=0, \end{aligned}$$

(4.3)

where m, $g^{\mu \nu }$ and I represents the mass, the inverse of metric and the action of scalar particles. Expanding this equation and simplifying we get

$$\begin{aligned}&{-}\frac{\left( \partial _{t}I\right) ^{2}}{F\left( r,\theta \right) }{+}g\left( r,\theta \right) \left( \partial _{r}I\right) ^{2}-\frac{2H\left( r,\theta \right) }{F\left( r,\theta \right) K\left( r,\theta \right) }\left( \partial _{t}I\right) \left( \partial _{\phi }I\right) \nonumber \\&\quad +\frac{f\left( r,\theta \right) }{F\left( r,\theta \right) K\left( r,\theta \right) }\left( \partial _{\phi }I\right) ^{2}\nonumber \\&\quad {+}\frac{\left( \partial _{\theta }I\right) ^{2}}{\rho ^{2}\left( r,\theta \right) }{+}m^{2}=0, \end{aligned}$$

(4.4)

where the value of $F\left( r,\theta \right)$ is given by Eq. (2.17). We shall choose the following ansatz for the calculation of tunneling probability

$$\begin{aligned} I=-Et+W\left( r\right) +J\phi . \end{aligned}$$

(4.5)

Using Eq. (4.5) in Eq. (4.4) we obtain

$$\begin{aligned} -\frac{E^{2}}{F\left( r,\theta \right) }+g\left( r,\theta \right) W^{\prime \ 2}\left( r\right) +\frac{2H\left( r,\theta \right) }{F\left( r,\theta \right) K\left( r,\theta \right) } E J +\frac{ f\left( r,\theta \right) }{F\left( r,\theta \right) K\left( r,\theta \right) }J^{2}+m^{2}=0. \end{aligned}$$

(4.6)

After some algebra this takes the form

$$\begin{aligned}&{-}\frac{1}{F\left( r,\theta \right) }\left[ E-\frac{H\left( r,\theta \right) }{K\left( r,\theta \right) }J\right] ^{2} +\left[ \frac{f\left( r,\theta \right) }{F\left( r,\theta \right) }+\frac{H^{2}\left( r,\theta \right) }{F\left( r,\theta \right) K\left( r,\theta \right) }\right] \frac{J^{2}}{K\left( r,\theta \right) }\nonumber \\&\quad +g\left( r,\theta \right) W^{\prime \ 2}\left( r\right) +m^{2}=0. \end{aligned}$$

(4.7)

Here we will add and subtract the term $\frac{H^{2}\left( r,\theta \right) }{ F\left( r,\theta \right) K^{2}\left( r,\theta \right) }J^{2}$, to make the first term a complete square. So, this takes the form

$$\begin{aligned} -\frac{1}{F\left( r,\theta \right) }\left[ E-\frac{H\left( r,\theta \right) }{K\left( r,\theta \right) }J\right] ^{2}+\frac{J^{2}}{K\left( r,\theta \right) }+g\left( r,\theta \right) W^{\prime \ 2}\left( r\right) +m^{2}=0. \end{aligned}$$

(4.8)

Near the horizon $r=r_{+}$, Eq. (4.8) is expanded in the similar way as in the case of Dirac particles. Solving the above equation for $W\left( r\right)$ we get

$$\begin{aligned} W^{\prime \ 2}\left( r\right)= & {} \frac{1}{F(r_+, \theta )g_r(r_+, \theta )\left( r-r_{+}\right) }\left( E-\Omega _{H}J\right) ^{2}\nonumber \\&-\left( \frac{J^{2}}{K\left( r_{+},\theta \right) }+m^{2}\right) g_r(r_{+},\theta ) \left( r-r_{+}\right) . \end{aligned}$$

(4.9)

Taking square root and integrating yields

$$\begin{aligned} W_{\pm }\left( r\right)= & {} \pm \int \frac{dr}{\sqrt{F(r_+, \theta )g_r(r_+, \theta )\left( r-r_{+}\right) }}\nonumber \\&\times \sqrt{\left( E-\Omega _{H}J\right) ^{2}-\left( \frac{J^{2}}{K\left( r_{+},\theta \right) }+m^{2}\right) \frac{\left( r-r_{+}\right) }{g_r(r_{+},\theta )}}. \end{aligned}$$

(4.10)

Again noting that $r=r_{+}$ is a singularity in the above integrand, the contour integration method solves the above integral as

$$\begin{aligned} W_{+}(r)=\frac{2(i-1)(E-\Omega _{H}J)}{\sqrt{F(r_{+},\theta )g_{r}(r_{+},\theta )}}. \end{aligned}$$

(4.11)

The resulting tunneling probability is

$$\begin{aligned} \Gamma =\exp \left[ \frac{-8(E-\Omega _{H}J)}{\sqrt{F(r_{+},\theta )g_{r}(r_{+},\theta )}}\right] . \end{aligned}$$

(4.12)

Comparing this expression with $\Gamma =\exp (-\beta E)$ where $\beta =1/T_{H}$ gives the Hawking temperature

$$\begin{aligned} T_{H}=\frac{\sqrt{F(r_{+},\theta )g_{r}(r_{+},\theta )}}{8}. \end{aligned}$$

(4.13)

It can be noted that the Hawking temperature of scalar particles given in Eq. (4.13) is same as in the case of Dirac particles. Thus we recover the Hawking temperature at the outer horizon.

4.2 Charged scalar particles

This section studies the tunneling probability, at the outer horizon, of charged scalar particles from the accelerating non-Kerr black hole in the presence of charge. For the scalar field $\Phi$ and charge q, the Klein-Gordon equation can be written as

$$\begin{aligned} g^{\mu \nu } \left( \partial _{\nu }-\frac{iq}{\hbar }A_{\nu }\right) \left( \partial _{\mu }-\frac{iq}{\hbar }A_{\mu }\right) \Phi -\frac{m^{2}}{\hbar ^{2}}\Phi =0, \end{aligned}$$

(4.14)

where m, q, $g^{\mu \nu }$ and $A_{\mu }$ represent the mass of scalar particles, their charge, inverse metric tensor and vector potential (3.51) respectively. Using an ansatz similar to Eq. (4.5), as has been done earlier for the case of uncharged particles, the above equation becomes

$$\begin{aligned} g^{\mu \nu }\left( \partial _{\mu }I-qA_{\mu }\right) \left( \partial _{\nu }I-qA_{\nu }\right) +m^{2}=0. \end{aligned}$$

(4.15)

Substituting different quantities in the above and simplifying we have

$$\begin{aligned} 0= & {} -\frac{\left( \partial _{t}I-qA_{t}\right) ^{2}}{F\left( r,\theta \right) }+g\left( r,\theta \right) \left( \partial _{r}I\right) ^{2}-\frac{ 2H\left( r,\theta \right) }{F\left( r,\theta \right) K\left( r,\theta \right) }\left( \partial _{t}I-qA_{t}\right) \left( \partial _{\phi }I-qA_{\phi }\right) \nonumber \\&+\frac{f\left( r,\theta \right) }{F\left( r,\theta \right) K\left( r,\theta \right) }\left( \partial _{\phi }I-qA_{\phi }\right) ^{2}+\frac{ \left( \partial _{\theta }I\right) ^{2}}{\rho ^{2}\left( r,\theta \right) } +m^{2}. \end{aligned}$$

(4.16)

To solve this equation, we again use an action of the form given in Eq. (4.5) in the above equation and evaluate at the horizon. The functions which were defined in Sect. 2 have the following form in the vicinity of the outer horizon $r=r_{+}.$

$$\begin{aligned} F(r_{+},\theta )= & {} \frac{(h+1)}{\Omega ^{2} \rho ^{2}}\Bigg (\frac{2 a^2 \rho ^{2} \left( a^4 P+2 a^2 P r_{+}^2+P r_{+}^4-Q\right) }{a^4 h \sin ^4\theta -a^2 \sin ^2\theta (h Q-2 h \rho ^{2} +Q)+P \left( a^2+r_{+}^2\right) ^2}\nonumber \\&+ Q-a^2 P\sin ^2\theta \Bigg ), \end{aligned}$$

(4.17)

$$\begin{aligned} g\left( r,\theta \right)= & {} g_{r}\left( r_{+},\theta \right) \left( r-r_{+}\right) \nonumber \\= & {} \frac{\Omega ^2}{\rho ^2}\Bigg \{(1-\alpha ^{2}r_{+}^{2})(2r_{+}-2M)-2\alpha r_+ (a^2+r^2-2Mr)\nonumber \\&+a^2\epsilon M \sin ^2\theta \left[ \frac{1}{(a^2 \cos ^2\theta +r_{+}^{2})^2}-\frac{4r_{+}^{2}}{(a^2 \cos ^2\theta +r_{+}^{2} )^3}\right] \Bigg \}\left( r-r_{+}\right) ,\nonumber \\ \Omega _{H}= & {} \frac{2 a^2 (h+1) \left( a^4 P+2 a^2 P r_{+}^2+P r_{+}^4-Q\right) }{\Omega ^{2} \left( P \left( a^2+r_{+}^2\right) ^2+a^4 h \sin ^4\theta -a^2 \sin ^2\theta [h Q-2 h \rho ^{2} +Q]\right) }, \end{aligned}$$

(4.18)

$$\begin{aligned} K(r,\theta )= & {} \left( \frac{P \left( a^2+r_{+}^2\right) ^2}{\rho ^{2}}-\frac{a^2 Q \sin ^2\theta (h+1)}{\rho ^{2} }\right) \sin ^2\theta \nonumber \\&+a^2 \sin ^4\theta \left( \frac{a^2 h \sin ^2\theta }{\rho ^{2} }+2 h\right) , \end{aligned}$$

(4.19)

$$\begin{aligned} H(r,\theta )= & {} {-}\frac{2a\sin ^{2}\theta \left[ P\left( r_{+}^{2}+a^{2}\right) {-}Q\right] \left( 1{+}h\right) }{\rho ^{2}\Omega ^{2}}. \end{aligned}$$

(4.20)

Substituting the above values in Eq. (4.16) and expanding near the horizon $r=r_{+}$ we obtain

$$\begin{aligned} W^{\prime \ 2}\left( r\right)= & {} \frac{1}{F(r_+, \theta )g_r(r_+, \theta )\left( r-r_{+}\right) }\left( E-\Omega _{H}J-\frac{eqr_{+}}{\left( a^{2}+r_{+}^{2}\right) }\right) ^{2}\nonumber \\&-\left( \frac{\left( J-qA_{\phi }\right) ^{2}}{K\left( r_{+},\theta \right) }+m^{2}\right) g_r(r_{+},\theta ) \left( r-r_{+}\right) . \end{aligned}$$

(4.21)

Taking square root and integrating gives

$$\begin{aligned} W_{\pm }\left( r\right)= & {} \pm \int \frac{dr}{\sqrt{F(r_+, \theta )g_r(r_+, \theta )\left( r-r_{+}\right) }}\nonumber \\&\times \sqrt{\left( E-\Omega _{H}J-\frac{qer_{+}}{\left( r_{+}^{2}+a^{2}\right) }\right) ^{2}-\left( \frac{\left( J-qA_{\phi }\right) ^{2}}{K\left( r_{+},\theta \right) }+m^{2}\right) \frac{\left( r-r_{+}\right) }{g_r(r_{+},\theta )}}. \nonumber \\ \end{aligned}$$

(4.22)

Here $r=r_{+}$ is the singularity, therefore by using the residue theory, integration yields

$$\begin{aligned} W_{\pm }\left( r\right) =\pm \frac{2(i-1)\left( E-\Omega _{H}J-\frac{qer_{+}}{ \left( r_{+}^{2}+a^{2}\right) }\right) }{\sqrt{F(r_{+},\theta )g_{r}(r_{+},\theta )}}. \end{aligned}$$

(4.23)

or

$$\begin{aligned} Im W_{\pm }\left( r\right) =\pm \frac{2 \left( E-\Omega _{H}J-\frac{qer_{+}}{ \left( r_{+}^{2}+a^{2}\right) }\right) }{\sqrt{F(r_{+},\theta )g_{r}(r_{+},\theta )}}. \end{aligned}$$

(4.24)

Substituting $Im W_{+}$ in $\Gamma =\exp [-4Im W_{+}]$ we get the tunneling probability as

$$\begin{aligned} \Gamma =\exp \left[ \frac{8}{\sqrt{F(r_{+},\theta )g_{r}(r_{+},\theta )}}\left( E-\Omega _{H}J- \frac{qer_{+}}{\left( r_{+}^{2}+a^{2}\right) }\right) \right] . \end{aligned}$$

(4.25)

We observe that the scalar and Dirac particles have the same tunneling probabilities, which means that the emission rate for both the particles is same.

5 The centre of mass energy

Here we calculate the centre of mass energy $E_{CM}$ for the colliding particles, in the vicinity of the accelerating non-Kerr black hole, having equal masses i.e. $m_{1}=m_{2}=m_{0}$. The particles are falling from infinity with the same energies $E_{1}/m_{1}=E_{2}/m_{2}=1$ towards the black hole with angular momentum $L_{1}$ and $L_{2}$ (which are different). The motion of particles is considered in the equatorial plane i.e. ($\theta =\pi /2)$. Bañados, Silk and West (BSW) [51] have given the following expression for the $E_{CM}$ in both the curved and flat spacetimes.

$$\begin{aligned} \frac{E_{CM}^{2}}{2m_{0}^{2}}=1-g_{\mu \nu }u_{1}^{\mu }u_{2}^{\nu }, \end{aligned}$$

(5.1)

where $u_{1}^{\mu }$ =($\dot{t}_{1},\dot{r}_{1},\dot{\theta }_{1},\dot{\phi } _{1})$ and $u_{2}^{\mu }=$($\dot{t}_{2},\dot{r}_{2},\dot{\theta }_{2},\dot{\phi }_{2})$ are 4-velocities of both the particles. The derivative of components with respect to the proper time $\tau$ is represented by overdot. Since we have considered the equatorial plane, therefore, the derivative of $\theta$ vanishes i.e. $\dot{\theta }_{1}=\dot{\theta }_{2}=0.$ Varying the indices of $\mu$ and $\nu$ in Eq. (5.1) from 0-3, we have

$$\begin{aligned} \frac{E_{CM}^{2}}{2m_{0}^{2}}=1-\Big (g_{00}\dot{t}_{1}+g_{03}\dot{\phi } _{1}\Big )\dot{t}_{2}-g_{rr}\dot{r}_{1}\dot{r}_{2}-\dot{\phi }_{2}\Big (g_{t\phi }\dot{t}_{1} +g_{\phi \phi }\dot{\phi }_{1}\Big ). \end{aligned}$$

(5.2)

The 4-velocity components [52,53,54] of the particle having mass m are given in Appendix A in Eqs. (A.1)–(A.3). From these we find the expression for $E_{CM}^{2}$. Taking $a=0=\alpha ,$ in this expression, the centre of mass energy of the Schwarzschild black hole can be recovered. This expression shows that the centre of mass energy depends on the parameters of acceleration $\alpha$ and rotation a. The limiting form $r\rightarrow \infty$ of the above expression gives $E_{CM}=2m_{0},$ which is the same as found in flat spacetime for the colliding particles. Eq. (A.4) shows that the centre of mass energy is finite at horizon i.e. $r=$ $r_{+}$ for finite angular momenta $\pounds _{1}$ and $\pounds _{2}$ in the slow rotation limit. This expression diverges at $r=2M$. However, when we take the limit $r\rightarrow 2M,$ it is finite for finite values of $\pounds _{1}$ and $\pounds _{2}.$

Fig. 2

Graphs representing the behaviour of centre of mass energy against radius r for varying values of charge q and rotation parameter a with the values $\pounds _{1}=1.5$, $\pounds _{2}=-2.5$, $\alpha =0.1$ and $\epsilon =0.2$

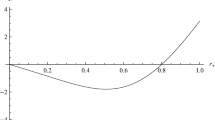
The centre of mass energy is plotted in Fig. 2. The plot on the left side shows that the energy has an inverse relation with the rotation parameter a. For growing values of a, the $E_{CM}$ is decreasing and the curves merge together for large radius. The right plot shows the effect of the charge parameter q on the energy. If the charge parameter increases, it enhances $E_{CM}$.

6 Conclusion

Black holes could emit Hawking radiations and eventually evaporate away in this process of radiation leaving nothing behind, over the time. These radiations have been studied extensively through Hawking radiation by using the null geodesic and Hamilton-Jacobi methods. In this paper we extend this approach to find the tunneling probabilities of fermions and scalar particles from accelerating non-Kerr black holes for massive and massless particles. We have observed an extra term of deformation parameter $\epsilon$ in the Hawking temperature in Eq. (4.1). When this parameter vanishes i.e. $\epsilon =0$, the results for accelerating and rotating black holes can be recovered [28,29,30]. Taking acceleration zero reduces this black hole to the Kerr-Newman, and the uncharged case recovers the results for the Kerr black hole. It is worth-noting that our results are independent of the nature of particles (scalar or fermions) and we obtain the same Hawking temperature in all the cases.

For the scalar particles, we have used the Klein-Gordon equation and noticed that tunneling probability of charged and uncharged fermions and scalar particles are same in both the massless and the massive cases which indicates that the emission rate of both the particles is same. In this study we have considered O(h) in the Klein-Gordon equation. This approach has two advantages: one is that we get back-reaction that provides a wide view of quantum process and radiations, and secondly, the grey-body effect can be further analysed, contrary to the approach used in Ref. [55], where $g_{tt}\rightarrow 0$ has been taken instead of $h\rightarrow 0$. These tunneling probabilities are used to determine the Hawking temperature. This temperature is plotted in Fig. 1 against mass and shows that for larger spin parameter a, the temperature of the black hole decreases rapidly.

Classically, only the outgoing particles confront the barrier but in semi-classical approach both the incoming and outgoing particles face the tunneling barrier i.e. the horizon. The tunneling probability of fermions particles is not depending on mass, rather it depends on the charge of the particle. Particularly, the total flux of fermions and scalars, emitted from the black hole as a result of quantum tunneling, can vanish for a critical value of mass, depending on the values of h. The centre of mass energy equation is also found and the limiting forms are also determined for the unbounded radius and for $r\rightarrow 2M$. The radial dependence of the centre of mass energy has also been shown in Fig. 2 for the rotation a and charge parameter q. The results show that arbitrarily high $E_{CM}$ can be achieved when the collision at horizon is considered. These results of Hawking temperature and $E_{CM}$ are reducible to the Kerr and Schwarzschild black holes by eliminating the effects of acceleration, rotation, deformation and charge parameters, accordingly.

A Four-velocity components

Here we give the 4-velocity components of the particle in Eq. (5.2)

$$\begin{aligned} \dot{t}= & {} \frac{2 a \mathcal {L} \left( -2 \alpha ^2 M r^3+2 M r+q^2 v+\alpha ^2 r^4\right) }{r^2 v \left( r (r-2 M)+q^2\right) }-\frac{r^5 \epsilon }{v \left( r (r-2 M)+q^2\right) \left( M^3 \epsilon +r^3\right) }\nonumber \\&\frac{1}{r^2 v^2 \left( r (r-2 M)+q^2\right) ^2 \left( M^3 \epsilon +r^3\right) }-\Bigg \{\epsilon \Bigg [4 q^4 v^2 \left( M^3 \epsilon +r^3\right) +8 q^2 r v\nonumber \\&+ \left( M \left( 2-2 \alpha ^2 r^2\right) +\alpha ^2 r^3\right) \left( M^3 \epsilon +r^3\right) +r^2\Bigg (-16 \alpha ^2 M r^6 v+16 M^2 r^3 v^2\nonumber \\&+\alpha ^2 r^7 \left( 4 \alpha ^2 r^2-1\right) +4 \alpha ^4 M^3 r^6 \epsilon -16 \alpha ^2 M^4 r^3 \epsilon v+16 M^5 \epsilon v^2\Bigg )\Bigg ]a^2\Bigg \}, \end{aligned}$$

(A.1)

$$\begin{aligned} \dot{\phi }= & {} \frac{\mathcal {L}}{r^2}-\frac{2 a \left( \epsilon \left( -2 \alpha ^2 M r^3+2 M r+q^2 v+\alpha ^2 r^4\right) \right) }{r^2 v \left( r (r-2 M)+q^2\right) }+\frac{1}{r^9 v \left( r (r-2 M)+q^2\right) }\nonumber \\&\Bigg \{\mathcal {L}\Bigg \{3 q^4 v^2 \left( M^3 \epsilon +r^3\right) +2 q^2 r v \Bigg (-6 M^4 \epsilon v\nonumber \\&+M^3 r \epsilon \left( 3 \alpha ^2 r^2+1\right) +r^2\Bigg [12 M^5 \epsilon v^2\nonumber \\&+12 M^2 r^3 v^2-12 \alpha ^2 M r^6 v+3 \alpha ^4 r^9+r^5+4 M^4 r \epsilon \left( -3 \alpha ^4 r^4+2 \alpha ^2 r^2+1\right) \nonumber \\&+M^3 r^2 \epsilon \left( 3 \alpha ^4 r^4+2 \alpha ^2 r^2-1\right) \Bigg ]\Bigg )a^2\Bigg \}\Bigg \}, \end{aligned}$$

(A.2)

$$\begin{aligned} \dot{r}^2= & {} \frac{\left( 1-\alpha ^2 r^2\right) \left( r (r-2 M)+q^2\right) \left( -\frac{r^5 \epsilon ^2}{v \left( r (r-2 M)+q^2\right) \left( M^3 \epsilon +r^3\right) }-\frac{\mathcal {L}^2}{r^2}-1\right) }{r^2 \left( \frac{M^3 \epsilon }{r^3}+1\right) }\nonumber \\&-\frac{4 a \left( \mathcal {L} \epsilon \left( q^2 v+\alpha ^2 r^4\right) \right) }{M^3 r \epsilon +r^4}+\frac{1}{r^2 \left( \frac{M^3 \epsilon }{r^3}+1\right) }\Bigg \{\left( \frac{M^3 \epsilon }{r^3}-\alpha ^2 r^2+1\right) \nonumber \\&\left( -\frac{r^5 \epsilon ^2}{v \left( r (r-2 M)+q^2\right) \left( M^3 \epsilon +r^3\right) }-\frac{\mathcal {L}^2}{r^2}-1\right) -\Bigg \{1-\alpha ^2 r^2\Bigg [\frac{1}{M^3 \epsilon +r^3}r^7\epsilon ^2\nonumber \\&\Bigg [4 q^4 v^2 (M^3 \epsilon +r^3)+8 q^2 r v(M (2-2 \alpha ^2 r^2)+\alpha ^2 r^3)(M^3 \epsilon +r^3)\nonumber \\&+r^2\Bigg [16 M^2 r^3 v^2-16 \alpha ^2 M r^6 v\alpha ^2 +r^7 \left( 4 \alpha ^2 r^2-1\right) +4 \alpha ^4 M^3 r^6 \epsilon -16 \alpha ^2 M^4 r^3 \epsilon v\nonumber \\&+16 M^5 \epsilon v^2\Bigg ]\Bigg ]\mathcal {L}^2 v +\left( r (r-2 M)+q^2\right) \Bigg [3 q^4 v^2 \left( M^3 \epsilon +r^3\right) +2 q^2 r v-6 M^4 \epsilon v\nonumber \\&+M^3 r \epsilon \left( 3 \alpha ^2 r^2+1\right) +M \left( 6 r^3-6 \alpha ^2 r^5\right) +3 \alpha ^2 r^6+r^2\Bigg (-12 \alpha ^2 M r^6+3 \alpha ^4 r^9\nonumber \\&+r^512 M^5 \epsilon v^2+12 M^2 r^3 v^2+v+4 M^4 r \epsilon \left( -3 \alpha ^4 r^4+2 \alpha ^2 r^2+1\right) +M^3 r^2 \epsilon \nonumber \\&\left( 3 \alpha ^4 r^4+2 \alpha ^2 r^2-1\right) \Bigg )\Bigg ]\Bigg ]\Bigg \}\left( /r^9 v^2 \left( r (r-2 M)+q^2\right) \right) \Bigg \}/a^2 \end{aligned}$$

(A.3)

where $\tau$, $\varepsilon =E/m$, $\pounds =L/m,$ represent the proper time, energy and angular momentum of the particle, respectively. The expression of the $E_{CM}$ from Eq. (5.2) is given as

$$\begin{aligned} E^2_{CM}= & {} \frac{2 m_0^2 \Bigg (4 a y_1 \epsilon \left( \frac{r^6 y_1 \left( -\frac{\mathcal {L}_1}{2 y_2}-\frac{\mathcal {L}_2}{3 y_2}\right) }{M^3 r \epsilon +r^4}+x \mathcal {L}_1\right) +\left( \frac{y_3 \left( M^3 \epsilon +r^3\right) }{r x}-\frac{r^5 \epsilon ^2}{x \left( M^3 \epsilon +r^3\right) }+1\right) \Bigg )}{r^2 y^2}\nonumber \\&+\frac{1}{2 r^9 \left( r (r-2 M)+q^2\right) ^3}\Bigg \{-\frac{2 r^7 \epsilon ^2 \left( r (r-2 M)+q^2\right) }{\left( \alpha ^2 r^2-1\right) ^2 \left( M^3 \epsilon +r^3\right) }\Bigg [4 q^4 \left( \alpha ^2 r^2-1\right) ^2\nonumber \\&+8 q^2 r \left( \alpha ^2 r^2-1\right) \left( M \left( 2-2 \alpha ^2 r^2\right) +\alpha ^2 r^3\right) \left( M^3 \epsilon +r^3\right) +r^2 \Bigg (- \left( \alpha ^2 r^2-1\right) \nonumber \\&16 M^5 \epsilon \left( \alpha ^2 r^2-1\right) ^2-16 \alpha ^2 M^4 r^3 \epsilon \left( \alpha ^2 r^2-1\right) +4 \alpha ^4 M^3 r^6 \epsilon +16 M^2 r^3\Bigg )\Bigg ]\nonumber \\&+\alpha ^2 r^7 \left( 4 \alpha ^2 r^2-1\right) -\frac{1}{\alpha ^2 r^2-1}2 \left( r (r-2 M)+q^2\right) ^2 \Bigg \{3 q^4 \left( \alpha ^2 r^2-1\right) ^2\nonumber \\&+2 q^2 r \alpha ^2 r^2-1 \left( -6 M^4 \epsilon \left( \alpha ^2 r^2-1\right) +M \left( 6 r^3-6 \alpha ^2 r^5\right) \right) r^2 \Bigg [r^5+3 \alpha ^4 r^9\nonumber \\&-12 \alpha ^2 M r^6 \left( \alpha ^2 r^2-1\right) +12 M^2 r^3 \left( \alpha ^2 r^2-1\right) ^2+12 M^5 \epsilon \left( \alpha ^2 r^2-1\right) ^2+4 M^4 r \epsilon \nonumber \\&\left( -3 \alpha ^4 r^4+2 \alpha ^2 r^2+1\right) \Bigg ]\Bigg \}+\Bigg \{-\frac{1}{y^2}\Bigg \{(-2+2 \alpha ^2 r^2-\frac{2 M^3 \epsilon }{r^3}\Bigg [1-\alpha ^2 r^2\Bigg [- \nonumber \\&+y_2 y_4 \Bigg ((2 y_4) \left( \frac{M^3 \epsilon }{r^3}-\alpha ^2 r^2+1\right) \Bigg \{1-\alpha ^2 r^2 \Bigg (\frac{1}{M^3 \epsilon +r^3}r^7 \epsilon ^2 \Bigg [4 q^4 \left( \alpha ^2 r^2-1\right) ^2 \nonumber \\&\left( M^3 \epsilon +r^3\right) +\left( M \left( 2-2 \alpha ^2 r^2\right) +\alpha ^2 r^3\right) (M^3 \epsilon +r^3)+r^2 \Bigg (-16 \alpha ^2 M r^6 \nonumber \\&\left( \alpha ^2 r^2-1\right) 16 M^5 \epsilon \left( \alpha ^2 r^2-1\right) ^2+4 \alpha ^4 M^3 r^6 \epsilon +16 M^2 r^3 \left( \alpha ^2 r^2-1\right) ^2\nonumber \\&+\alpha ^2 r^7 \left( 4 \alpha ^2 r^2-1\right) \Bigg )\Bigg ]+x[3 q^4 \left( \alpha ^2 r^2-1\right) ^2]\mathcal {L}_1^2 \Bigg )\Bigg \}/r^9 x^2\Bigg ]\Bigg ]\Bigg \}+ x^2 (2 y_3){}^2\Bigg \}\nonumber \\&-\frac{8\ 4 r^4 y_4 \mathcal {L}_1 \mathcal {L}_2 \epsilon ^2 }{(2 y_4) (3 y_4)}-\Bigg \{-\frac{4\ 4 y_2 \mathcal {L}_2^2 \epsilon ^2}{r^4}+y 3 y_3 \Bigg \{(3 (y_4)) \left( \frac{M^3 \epsilon }{r^3}-\alpha ^2 r^2+1\right) \nonumber \\&-\Bigg [1-\alpha ^2 r^2 \Bigg \{\frac{1}{M^3 \epsilon +r^3}r^7 \epsilon ^2 \Bigg (4 q^4+8 q^2 r \left( \alpha ^2 r^2-1\right) \Bigg (M \left( 2-2 \alpha ^2 r^2\right) \nonumber \\&+\alpha ^2 r^3\Bigg ) \left( M^3 \epsilon +r^3\right) +r^2 \Bigg (16 M^2 r^3-\left( \alpha ^2 r^2-1\right) +\alpha ^2 r^7 \left( 4 \alpha ^2 r^2-1\right) \nonumber \\&+16 M^5 \epsilon \left( \alpha ^2 r^2-1\right) ^2- \left( \alpha ^2 r^2-1\right) +4 \alpha ^4 M^3 r^6 \epsilon \Bigg )\Bigg )+x \Bigg (3 q^4 \left( \alpha ^2 r^2-1\right) ^2 \nonumber \\&\left( M^3 \epsilon +r^3\right) +2 q^2 r \alpha ^2 r^2-1 \Bigg (M \left( 6 r^3-6 \alpha ^2 r^5\right) +M^3 r \epsilon \left( 3 \alpha ^2 r^2+1\right) -6 M^4 \epsilon \nonumber \\&\left( \alpha ^2 r^2-1\right) \Bigg )+r^2 \Bigg (12 M^5 \epsilon \left( \alpha ^2 r^2-1\right) ^2\nonumber \\&+ \left( \alpha ^2 r^2-1\right) ^2-12 \alpha ^2 M r^6 \left( \alpha ^2 r^2-1\right) \nonumber \\&+3 \alpha ^4 r^9+r^5+4 M^4 r \epsilon \left( -3 \alpha ^4 r^4+2 \alpha ^2 r^2+1\right) \nonumber \\&+M^3 r^2 \epsilon \left( 3 \alpha ^4 r^4+2 \alpha ^2 r^2-1\right) \Bigg )\Bigg ) \nonumber \\&\mathcal {L}_2^2\Bigg \}\Bigg ]/r^9 x^2\Bigg \}\Bigg \}/(3 y_3)^2 \left( 1-\alpha ^2 r^2\right) \left( \alpha ^2 r^2-1\right) ^2\Bigg \}a^2 , \end{aligned}$$

(A.4)

where

$$\begin{aligned} x= & {} \left( \alpha ^2 r^2-1\right) \left( r (r-2 M)+q^2\right) ,\\ y= & {} q^2+r(r-2M)(1-r^2\alpha ^2),\\ z= & {} q^2-2Mr+r^2(r^2\alpha ^2-1),\\ y_1= & {} \sqrt{\frac{y \left( -\frac{r^5 \epsilon ^2}{z \left( M^3 \epsilon +r^3\right) }-\frac{\mathcal {L}_1^2}{r^2}-1\right) }{r^2 \left( \frac{M^3 \epsilon }{r^3}+1\right) }} \sqrt{\frac{y \left( -\frac{r^5 \epsilon ^2}{z \left( M^3 \epsilon +r^3\right) }-\frac{\mathcal {L}_2^2}{r^2}-1\right) }{r^2 \left( \frac{M^3 \epsilon }{r^3}+1\right) }},\\ y_2= & {} \frac{r^5 \epsilon ^2}{z \left( M^3 \epsilon +r^3\right) }+\frac{\mathcal {L}_1^2}{r^2}+1,\\ y_3= & {} \frac{r^5 \epsilon ^2}{z \left( M^3 \epsilon +r^3\right) }+\frac{\mathcal {L}_2^2}{r^2}+1,\\ y_4= & {} -2 \alpha ^2 M r^3+2 M r+q^2 \left( \alpha ^2 r^2-1\right) +\alpha ^2 r^4, \end{aligned}$$

and $\mathcal {L}_1$ and $\mathcal {L}_2$ represent angular momenta of the particles.