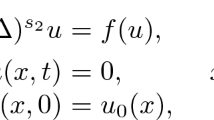A discrete algorithm for general weakly hyperbolic systems

Abstract

This paper studies the Cauchy problem for first order systems,

$$\begin{aligned} Lu \ =\ \partial _tu-\sum _{j=1}^dA_j(t,x)\partial _{x_j}u-B(t,x)u\ =\ f, \quad u(0,\cdot ) = g. \end{aligned}$$

(0.1)

Assume that for $\xi \in \mathbb {R}^d,$ $\sum A_j\xi _j$ has only real eigenvalues. For coefficients and Cauchy data sufficiently Gevrey regular the Cauchy problem has a unique sufficiently Gevrey regular solution. We prove stability and error estimates for the spectral Crank-Nicholson scheme. Approximate solutions can be computed with accuracy $\epsilon$ in $L^\infty ( [0,T]\times \mathbb {R}^d)$ with cost growing at most polynomially in $\epsilon ^{-1}$. The proofs uses pseudodifferential symmetrizers.

1 Introduction

1.1 Hyperbolic background

Consider the Cauchy problem (0.1). The coefficients $A_j$ and B are $m\times m$ complex matrix valued functions that are independent of x for x outside a fixed compact set in $\mathbb {R}^d$. Denote

$$\begin{aligned} A(t,x,\xi ) \ :=\ \sum _{j = 1}^dA_j(t,x)\xi _j. \end{aligned}$$

The operator is assumed to satisfy the very weak hyperbolicity condition,

$$\begin{aligned} \forall (t,x,\xi )\in \mathbb {R}\times \mathbb {R}^d\times \mathbb {R}^d, \quad \mathrm{Spectrum}\, A(t,x,\xi )\subset \mathbb {R}. \end{aligned}$$

(1.1)

This hypothesis is best understood by considering first the case where the coefficients are independent of t, x. In that case, the initial value problem is solved by Fourier transform indicated by a hat,

$$\begin{aligned} \widehat{u}(t,\xi ) \ =\ e^{t(iA(\xi ) + B)}\ \widehat{g}(\xi ). \end{aligned}$$

In the case $B=0$, the hypothesis implies that for all $\xi \in \mathbb {R}^d$

$$\begin{aligned} \big \Vert e^{ iA(\xi ) }\ \big \Vert _{ \mathrm{Hom}(\mathbb {C}^m)} \ \lesssim \ \langle \xi \rangle ^{m-1} , \quad \langle \xi \rangle := (1+|\xi |^2)^{1/2}. \end{aligned}$$

The Cauchy problem is well set in Sobolev spaces with at worst a loss of $m-1$ derivatives. For general B not zero one has the weaker estimate

$$\begin{aligned} \big \Vert e^{ iA(\xi ) + B }\ \big \Vert _{ \mathrm{Hom}(\mathbb {C}^m)} \ \lesssim \ e^{ c| \xi |^{(m-1)/m} } \langle \xi \rangle ^{m-1} . \end{aligned}$$

(1.2)

This estimate does not allow one to solve the initial value problem for $g\in C^\infty _0(\mathbb {R}^d)$. However, its subexponential growth shows that the Cauchy problem is well set in Gevrey spaces. Those spaces can be localized by Gevrey partitions of unity so provide a reasonable setting for the initial value problem (0.1). In the constant coefficient case, condition (1.1) is necessary and sufficient for Gevrey well posedness.

The operators hyperbolic in the sense of Petrowsky and Gårding [1] are characterized by the stronger estimate

$$\begin{aligned} \big \Vert e^{ iA(\xi ) + B }\ \big \Vert _{ \mathrm{Hom}(\mathbb {C}^m)} \ \lesssim \ \langle \xi \rangle ^{m-1} \end{aligned}$$

(1.3)

equivalent to Sobolev solvability with a loss of no more than $m-1$ derivatives.

Estimate (1.2) corresponds to a sort of instability at high frequency that is stronger than permitted for coefficient problems that are hyperbolic in the sense of Petrovsky and Gårding [1].

The remarkable fact is that provided that the coefficients of L are Gevrey regular, the Cauchy problem for L is well-posed in Gevrey classes if and only if (1.1) holds. The sufficiency is a result of Bronshtein [2]. The necessity is proved in the trio of articles [3,4,5]. In (1.1), no hypothesis is made about the singularities of the characteristic variety of L for t, x fixed, nor on how the geometry of that variety changes as t, x vary. The precise Gevrey regularity required does depend on such structures. Roughly, the more variable are the multiplicities the stronger is the required Gevrey regularity.

The present paper provides additional evidence that the weakly hyperbolic operators characterized by (1.1) deserve the right to be considered hyperbolic. We give an algorithm that computes approximate solutions with reasonable computational cost. The stability analysis of discrete approximations took flight in the the classic paper of Courant Friedrichs and Lewy [6] followed by the work of Von Neumann who showed that the Fourier Transform offered profound insights on the stability of discrete approximations. That pseudodifferential operators offered additional insights was observed by Kreiss, Yamaguti and Nogi and most importantly Lax and Nirenberg who discovered the sharp Gårding inequality for matrix symbol pseudodifferential operators for such an application. This result is crucial for our analysis too. An excellent overview of the classic results is presented in [7]. The proof of stability of our scheme is as difficult as any stability result that we know. The difficulty has two sources. The first is that the stability of the Cauchy problem is itself very difficult. There is no simple multiplier method. Second the stability is very weak so it is reasonable to suspect that it can be destroyed by replacing the problem by a discrete one.

1.2 Algorithm definition

Choose $\chi (x)\in C_0^{\infty }(\mathbb {R}^d)$ with $\chi =1$ in $|x|\le 2$ and $\chi =0$ for $|x|\ge 2\sqrt{2}$ such that $0\le \chi \le 1$. Denote $\chi _h(D)=\chi (h D)$. Define a family of spectral truncations of G by

$$\begin{aligned} G_h(t,x,D)=\chi _{2h} (D) \ \big (iA(t,x,D)+B(t,x)\big ) \chi _{2h}(D),\quad 0<h\le 1. \end{aligned}$$

(1.4)

The smoothing operators $G_h$ generate the ordinary differential operators $\partial _t-G_h$. The resulting ordinary differential equation is then approximated by the Crank-Nicholson scheme.

Definition 1.1

Define for $n\in \mathbb {Z}$,

$$\begin{aligned} G_h^n(x,D) = G_h(nk, x, D) = \chi (2hD) \, G(nk, x,D)\, \chi (2hD). \end{aligned}$$

The Crank–Nicholson scheme generating a sequence $\mathbb {N}\ni n \mapsto u_h^n$ intended to approximate $u_h(nk)$ is

$$\begin{aligned} \begin{aligned} \frac{u_h^{n+1}-u_h^{n}}{k}&=\ G^{n}_h\, \frac{u_h^{n+1}+u_h^{n}}{2} \ +\ \chi (2hD)f^{n}, \\ u^0_h(x)&=\ \chi (2h D)\,g,\quad f^n\,:=\,f(nk,\cdot ). \end{aligned} \end{aligned}$$

(1.5)

The uniform stability of the Cauchy problems for $\partial _tu =G_hu$ is proved in [8]. This equation has a symmetrizer $R_h=R^*_h$ with $0<c_h<R_h\le 1$. However as the spectral truncation grows the lower bound $c_h$ tends to zero.

Therefore, the straight forward stability arguments that would work for the Crank-Nicholson step, as in [9, 10] fail. The proof of stability must be at least as hard as the proof of the a priori estimates in [8]. Indeed they are more complicated. The main effort follows the strategy in [8]. We carefully control the additional errors from discretization in time. The Crank-Nicholson scheme is chosen because it is well adapted to estimates using a symmetrizer.

The precise stability result is Theorem 2.4. The proof that the approximations converge to the exact solution is Theorem 2.5.

For the very special case of operators of the form $u_{tt} = a(t) u_{xx}$ with nonnegative Gevrey a, the spectral Leap-Frog scheme is analysed in [11]. The computational cost estimates of [11] shows that the cost of computing with error $\epsilon$ grows no faster than polynomially in $\epsilon ^{-1}$. Virtually identical cost estimates work for our spectral Crank-Nicholson scheme. They are not repeated here.

Constant coefficient problems that are hyperbolic in the sense of Gårding and Petrowsky are more strongly hyperbolic than those studied in this paper. However variable coefficient operators whose frozen problems are hyperbolic in this sense need not inherit the Sobolev well posedness of the constant coefficient problems. Stability of difference approximations to constant coefficient problems hyperbolic in the sense of Gårding and Petrowsky have been studied in a number of works. We refer to [12] for a review of these.

2 Main theorems

2.1 Definition of the parameter $\theta$

First we formulate an important property which follows from the assumption (1.1). Define

$$\begin{aligned} {\mathcal {H}}_r(t,x,\xi ,y,\eta ;\epsilon ) = \sum _{|\alpha +\beta |\le r} \frac{\epsilon ^{|\alpha +\beta |}}{\alpha !\beta !} D_x^{\alpha }\partial _{\xi }^{\beta } A(t,x,\xi ) y^{\alpha }(-i\eta )^{\beta },\;\;D_{x_j}=-i\partial _{x_j} \end{aligned}$$

then from [8, Proposition 2.2] (see also [8, (2.3)]) it follows that for any compact set $K\subset \mathbb {R}^d$ and $T>0$ there are $\epsilon _0>0$, $c>0$ such that

$$\begin{aligned} \zeta ~\text{ is } \text{ an } \text{ eigenvalue } \text{ of }~{\mathcal {H}}_m(t,x,\xi ,y,\eta ;\epsilon ) \ \ \Longrightarrow \ \ |{\mathsf {Im}}\,\zeta |\le c\,|\epsilon | \end{aligned}$$

(2.1)

for any $x\in K$, $|\xi |\le 1$, $|(y,\eta )|\le 1$, $|\epsilon |\le \epsilon _0$, $|t|\le T$.

Following [8] introduce an integer $\theta$ defined as follows.

Hypothesis 2.1

The system is $\theta$ -regular with integer $0\le \theta \le m-1$ in the sense that for any $T>0$ and any compact $K\subset \mathbb {R}^d$ there exist $C>0$, $c>0$ and $\epsilon _0>0$ such that with $N=\max \{2\theta ,m\}$

$$\begin{aligned} \frac{\epsilon ^\theta }{C\, e^{cs\epsilon }} \le \big \Vert e^{is{\mathcal H_N(t,x,\xi ,y,\eta ;\epsilon )}} \big \Vert \le \frac{ C\, e^{cs\epsilon }}{\epsilon ^{\theta }} , \end{aligned}$$

(2.2)

for all $s\ge 0$, $0<\epsilon \le \epsilon _0$, $|\xi | \le 1$, $|(y,\eta )|\le 1$, $x\in K$, $|t|\le T$.

Remark 2.1

This definition of $\theta$-regularity is little bit more general than that of [8, Hypothesis 2.8]. Here ${\mathcal H}_r(t,x,\xi ,\xi , 0;\epsilon )$ coincides with ${\mathcal H}_r(t,x,\xi ; \epsilon )$ in [8].

Example 2.1

When (1.1) holds, Hypothesis 2.1 always holds with $\theta =m-1$. If $A(t,x,\xi )$ is uniformly diagonalizable then Hypothesis 2.1 holds with $\theta =0$ (for the proof see [8, Examples 2.9 and 2.10]).

Example 2.2

Suppose (1.1). Assume that there exists $T=T(t,x,\xi ,y,\eta ;\epsilon )$ with bounds on $\Vert T\Vert$ and $\Vert T^{-1}\Vert$ independent of $(t,x,\xi ,y,\eta ;\epsilon )$ such that $T^{-1}{\mathcal H}_mT$ is a direct sum $\oplus A_j$ where the size of $A_j$ is at most $\mu$. Then Hypothesis 2.1 holds with $\theta =\mu -1$ (for the proof see [8, Example 2.11]).

2.2 Recall the continuous case

Let

$$\begin{aligned} G(t,x,D)=iA(t,x,D)+B(t,x) \end{aligned}$$

then $Lu=f$ is written

$$\begin{aligned} \partial _t u=Gu+f. \end{aligned}$$

Denote

$$\begin{aligned} \langle {\xi }\rangle _{\ell }= \sqrt{\ell ^2+|\xi |^2} \ =\ \ell \sqrt{1\, +\, |\xi /\ell |^2} \end{aligned}$$

(2.3)

where $\ell \ge 1$ is a positive parameter. When $\ell =1$ we omit the suffix $\ell$ and write $\langle {\xi }\rangle _1=\langle {\xi }\rangle$.

Definition 2.1

If $1<s<\infty$, the function $a(x)\in C^{\infty }(\mathbb {R}^d)$ belongs to $G^{s}(\mathbb {R}^d)$ if there exist $C>0$, $A>0$ such that

$$\begin{aligned} \forall x\in {\mathbb R}^d,\quad \forall \alpha \in \mathbb {N}^d, \quad |\partial _x^{\alpha }a(x)| \ \le \ C A^{|\alpha |}|\alpha |!^s. \end{aligned}$$

Recall [8, Proposition 4.4].

Proposition 2.1

Suppose Hypothesis 2.1 is satisfied. Define

$$\begin{aligned} s= \frac{ 2+6\theta }{1+6\theta },\quad \rho =\frac{1}{s}, \quad \nu := \theta (1-\rho ). \end{aligned}$$

For some $1<s'\le s$ suppose that $A_j(t,x)$ (resp. B(t, x)) are lipschitzian (resp. continuous) in time uniformly on compact sets with values in $G^{s'}(\mathbb {R}^d)$. Then there exist $T>0$, ${\hat{c}}>0$, $C>0$ and $\ell _0>0$ such that for all u such that $e^{(T-{\hat{c}}\,t)\langle {D}\rangle _{\ell }^{\rho }}\partial _{t,x}^{\gamma }u\in L^1([0,T/{\hat{c}}];H^{\nu }(\mathbb {R}^d))$ for $|\gamma |\le 1$ one has

$$\begin{aligned} \begin{aligned}&\Vert \langle {D}\rangle ^{-\nu }_{\ell }e^{(T-{\hat{c}}\,t)\langle {D}\rangle _{\ell }^{\rho }}u\Vert ^2\le C\Vert \langle {D}\rangle _{\ell }^{\nu }e^{T\langle {D}\rangle _{\ell }^{\rho }}u(0)\Vert ^2\\&\quad +C\int _0^t\Vert \langle {D}\rangle _{\ell }^{-\nu }e^{(T-{\hat{c}}\,t')\langle {D}\rangle _{\ell }^{\rho }}(\partial _t-G)u(t')\Vert ^2dt' \end{aligned} \end{aligned}$$

(2.4)

for $0\le t\le T/{\hat{c}}$ and $\ell \ge \ell _0$.

This is a small improvement of [8, Proposition 4.4]. Here is a sketch of the easy proof: As noted in Remark 2.1 we use ${\mathcal H}_r(t,x,\xi ,y,\eta ; \epsilon )$ instead of ${\mathcal H}_r(t,x,\xi ;\epsilon )$ in [8] and make the same choice (3.16) below for $s, \epsilon , \xi ,y,\eta$ where $\chi _h\equiv 1$, $\chi _{2h}\equiv 1$ and ${\bar{\tau }}-\tau =T-at$. Therefore (3.17) below holds for $0\le T-at\le {\bar{\tau }}$ which gets rid off the constraint $T-at\ge c$ with some $c>0$ that we have assumed in [8]. This enables us to take $T_1=T$ in [8, Proposition 4.4]. In the estimate (2.4) the weight for Lu is improved from $\langle {D}\rangle _{\ell }^{3\nu }$ to $\langle {D}\rangle _{\ell }^{-\nu }$. That proof is also easy.

Corollary 2.2

There exist $T>0$, ${\hat{c}}>0$, $C>0$ and $\ell _0>0$ such that for all u satisfying $\partial _tu=Gu$ one has

$$\begin{aligned} \Vert \langle {D}\rangle ^{-\nu }_{\ell }e^{(T-{\hat{c}}\,t)\langle {D}\rangle ^{\rho }_{\ell }}u\Vert \le C\Vert \langle {D}\rangle ^{\nu }_{\ell }e^{T\langle {D}\rangle ^{\rho }_{\ell }}u(0)\Vert \end{aligned}$$

(2.5)

for $0\le t\le T/{\hat{c}}$ and $\ell \ge \ell _0$.

The proof of [8, Theorem 1.3] gives

Proposition 2.3

Assume the same assumption as in Proposition 2.1 and $e^{T\langle {D}\rangle ^{\rho }}g\in H^{\nu }(\mathbb {R}^d)$. Then there exists a unique u satisfying

$$\begin{aligned} \partial _tu=Gu, \quad t\in (0,T/{\hat{c}}),\quad u(0,\cdot )=g \end{aligned}$$

such that $e^{(T-{\hat{c}}\,t)\langle {D}\rangle ^{\rho }}u\in L^{\infty }([0,T/{\hat{c}}];H^{-\nu }(\mathbb {R}^d))$.

2.3 Stability and error estimates

The Crank–Nicholson scheme defined in (1.5) is equivalent to

$$\begin{aligned} \big ( I - \frac{k}{2}\, G^{n}_h\big ) u_h^{n+1} \ =\ \big ( I +\frac{k}{2}\, G^{n}_h\big )u_h^n \ +\ k\,\chi _{2h}\,f^{n}. \end{aligned}$$

(2.6)

Note that

$$\begin{aligned}&\big \Vert \frac{k}{2}\,G^n_h u \big \Vert \le \frac{k}{2}\,\big \Vert \langle {D}\rangle \chi _{2h}\langle {D}\rangle ^{-1}G(nk,x,D)\chi _{2h}u\big \Vert \\&\quad \le \frac{\sqrt{3}}{2}k\,h^{-1}\big \Vert \langle {D}\rangle ^{-1}G(nk,x,D)\chi _{2h}u\big \Vert \le {\bar{C}} k\,h^{-1}\Vert u\Vert \end{aligned}$$

where

$$\begin{aligned} {\bar{C}}=\frac{\sqrt{3}}{2}\sup _{0\le t\le T}\big \Vert \langle {D}\rangle ^{-1}G(t,x,D)\big \Vert _{{\mathcal L}(L^2,L^2)}. \end{aligned}$$

Assuming ${\bar{C}}\,k\,h^{-1}<1$ one has

$$\begin{aligned} \big ( I - \frac{k}{2}\, G^{n}_h\big )^{-1} \ =\ \sum _{j=0}^\infty \Big ( \frac{k}{2}\, G^{n}_h \Big )^j, \end{aligned}$$

(2.7)

and $u^{n+1}_h$ is given by

$$\begin{aligned} u^{n+1}_h = \big ( I - \frac{k}{2}\, G^{n}_h\big )^{-1} \Big ( \big ( I +\frac{k}{2}\, G^{n}_h\big )u^n_h \ +\ k\,\chi _{2h}\,f^{n} \Big ). \end{aligned}$$

Reasoning term by term in (2.7), $\big ( I - \frac{k}{2}\, G^{n}_h\big )^{-1}$ maps functions with spectrum in $\mathrm{supp}\,\chi _{2h}(\cdot )$ to themselves. Therefore,

$$\begin{aligned} \mathrm{supp}\, \mathcal {F}({u^n_h}) \ \subset \ \mathrm{supp}\,\chi _{2h}(\cdot ) . \end{aligned}$$

(2.8)

Theorem 2.4

Make the same assumption as in Proposition 2.1. Then there exist ${\bar{\tau }}>0$, ${\bar{\beta }}>0$, ${\bar{a}}>0$, ${\bar{h}}>0$ and $C>0$ such that the estimate

$$\begin{aligned}&\Vert \langle {D}\rangle ^{-\nu } e^{({\bar{\tau }}-{\bar{a}}t_n)\langle {D}\rangle ^{\rho }} u^n_h\Vert ^2\le C\Big (\Vert \langle {D}\rangle ^{\nu }e^{{\bar{\tau }}\langle {D}\rangle ^{\rho }}g\Vert ^2 +k\,\sum _{j=0}^{n-1}\Vert \langle {D}\rangle ^{-\nu }e^{({\bar{\tau }}-{\bar{a}}t_j)\langle {D}\rangle ^{\rho }}f^j\Vert ^2\Big )\\&\quad \le C\Big (\Vert \langle {D}\rangle ^{\nu }e^{{\bar{\tau }}\langle {D}\rangle ^{\rho }}g\Vert ^2 +\sup _{0\le j\le n-1}\Vert \langle {D}\rangle ^{-\nu }e^{({\bar{\tau }}-{\bar{a}}t_j)\langle {D}\rangle ^{\rho }}f^j\Vert ^2\Big ) \end{aligned}$$

holds for any $n\in \mathbb {N}$, $k>0, h>0$ satisfying $t_n=nk\le {\bar{\tau }}/{\bar{a}}$, $kh^{-1}\le {\bar{\beta }}$ and $0<h\le {\bar{h}}$ where $\nu =\theta (1-\rho )$.

A more precise estimate of the stability is given in Proposition 3.12.

Theorem 2.5

In addition to the assumption in Proposition 2.1, assume that $A_j(t,x)$ and B(t, x) are $C^1$ in time uniformly on compact sets with values in $G^{s'}(\mathbb {R}^d)$. Then there exist ${\bar{\tau }}>0$, ${\bar{\beta }}>0$, ${\bar{a}}>0$, ${\bar{h}}>0$ and $C>0$ such that for an exact solution u to (0.1) with Cauchy data g satisfying $\langle {D}\rangle ^{2+\nu }e^{{\bar{\tau }}\langle {D}\rangle ^{\rho }}g\in L^2$ one has

$$\begin{aligned} \Vert \langle {D}\rangle ^{-\nu }e^{({\bar{\tau }}-{\bar{a}}t_n)\langle {D}\rangle ^{\rho }}(u(t_n)-u^n_h)\Vert \le C\,(k+h)\Vert \langle {D}\rangle ^{2+\nu }e^{{\bar{\tau }}\langle {D}\rangle ^{\rho }}g\Vert \end{aligned}$$

and

$$\begin{aligned} \Vert e^{({\bar{\tau }}-{\bar{a}}t_n)\langle {D}\rangle ^{\rho }}(u(t_n)-u^n_h)\Vert \le C\,(k+h)h^{-\nu }\Vert \langle {D}\rangle ^{2+\nu }e^{{\bar{\tau }}\langle {D}\rangle ^{\rho }}g\Vert \end{aligned}$$

for any $n\in \mathbb {N}$, $k>0, h>0$ satisfying $t_n=nk\le {\bar{\tau }}/{\bar{a}}$, $kh^{-1}\le {\bar{\beta }}$ and $0<h\le {\bar{h}}$.

Corollary 2.6

With the same assumptions as in Theorem 2.5 there exist ${\bar{\tau }}>0$, ${\bar{\beta }}>0$, ${\bar{a}}>0$, ${\bar{h}}>0$ and $C>0$ such that for an exact solution u to (0.1) with Cauchy data g satisfying $\langle {D}\rangle ^{2+\nu }e^{{\bar{\tau }}\langle {D}\rangle ^{\rho }}g\in L^2$ one has

$$\begin{aligned} \Vert u(t_n)-u^n_h\Vert \le C\,(k+h)h^{-\nu }\Vert \langle {D}\rangle ^{2+\nu }e^{{\bar{\tau }}\langle {D}\rangle ^{\rho }}g\Vert \end{aligned}$$

for any $n\in \mathbb {N}$, $k>0, h>0$ satisfying $t_n=nk\le {\bar{\tau }}/{\bar{a}}$, $kh^{-1}\le {\bar{\beta }}$ and $0<h\le {\bar{h}}$.

Remark 2.2

Note that

$$\begin{aligned} \rho \ge \frac{1+6\theta }{2+6\theta } \quad \Longleftrightarrow \quad \rho \ge 3\nu +\frac{1}{2} \end{aligned}$$

(2.9)

so that one has $\rho \ge 3\nu +1/2$ under the assumption of Theorems 2.4 and 2.5.

3 Stability for the spectral Crank–Nicholson scheme

3.1 Spectral truncated weight for Crank–Nicholson scheme

Taking (1.5) into account define spectral truncated weights $W_h(t,D)$ by

$$\begin{aligned} W_h(t,\xi ) \ :=\ e^{(T-t)\langle {\xi }\rangle _{\ell }^{\rho }\chi _h(\xi )} \end{aligned}$$

and for $n\in \mathbb {N}$

$$\begin{aligned} W_h^n(\xi )\ :=\ W_h(ank,\xi ) \end{aligned}$$

where $a>0$ is a positive parameter which will be fixed later. In what follows we always assume that the parameters $a>0, k>0, \ell>0, h>0$ are constrained to satisfy

$$\begin{aligned} 0<h\le \ell ^{-1},\quad k\,h^{-1}\le 1/2\,{\bar{C}},\quad a\,k\,h^{-\rho } \le \log {2}/3. \end{aligned}$$

(3.1)

Since $a\langle {\xi }\rangle _{\ell }^{\rho }\chi _h\le 3\,a\, h^{-\rho }$ because $\langle {\xi }\rangle _{\ell }\le 3h^{-1}$ if $\chi _h(\xi )\ne 0$, it follows that

$$\begin{aligned} 1/2\le e^{-ak\langle {\xi }\rangle _{\ell }^{\rho }\chi _h}\le 1. \end{aligned}$$

(3.2)

Here recall [8, Definition 2.3].

Definition 3.1

For $0<\delta \le \rho \le 1$, the family $a(x,\xi ;\ell )\in C^{\infty }(\mathbb {R}^d\times \mathbb {R}^d)$ indexed by $\ell$ belongs to ${\tilde{S}}^m_{\rho ,\delta }$ if for all $\alpha$, $\beta \in \mathbb {N}^d$ there is $C_{\alpha \beta }$ independent of $\ell \ge 1,x,\xi$ such that

$$\begin{aligned} \big |\partial _x^{\beta }\partial _{\xi }^{\alpha }a(x,\xi ;\ell ) \big | \ \le \ C_{\alpha \beta }\ \langle {\xi }\rangle _\ell ^{m-\rho |\alpha |+\delta |\beta |}. \end{aligned}$$

Denote ${\tilde{S}}^m={\tilde{S}}^m_{1,0}$.

Since $|\partial _{\xi }^{\alpha }\chi _h|\le C_{\alpha }h^{|\alpha |}$ and $2h^{-1}\le \langle {\xi }\rangle _{\ell }\le 3h^{-1}$ on the support of $\partial _{\xi }^{\alpha }\chi _h$ for $|\alpha |\ge 1$ it is clear that $\chi _h\in {\tilde{S}}^0$.

We examine to what extent $W^n_h$ satisfies the Crank-Nicholson scheme (1.5).

Lemma 3.1

Assume (3.1) then one can write

$$\begin{aligned} \frac{W_h^{n+1}-W^n_h}{k}=-2\,a\,\omega _h\,\chi _h \frac{W^{n+1}_h+W^n_h}{2} \end{aligned}$$

(3.3)

where $\omega _h(\xi )\in {\tilde{S}}^{\rho }$ and

$$\begin{aligned} \langle {\xi }\rangle ^{\rho }_{\ell }/4\le \omega _h(\xi )\le \langle {\xi }\rangle _{\ell }^{\rho }. \end{aligned}$$

Proof

Denote

$$\begin{aligned} \frac{W_h^{n+1}-W^n_h}{k}=-2\,{\tilde{\omega }}_h \frac{W^{n+1}_h+W^n_h}{2} \end{aligned}$$

then it is clear that

$$\begin{aligned} {\tilde{\omega }}_h=\frac{1-e^{-ak\langle {\xi }\rangle ^{\rho }_{\ell }\chi _h}}{k}\,\frac{1}{1+e^{-ak\langle {\xi }\rangle ^{\rho }_{\ell }\chi _h}}. \end{aligned}$$

Since

$$\begin{aligned} \frac{1-e^{-ak\langle {\xi }\rangle ^{\rho }_{\ell }\chi _h}}{k}=a\langle {\xi }\rangle _{\ell }^{\rho }\chi _h\int _0^1e^{-ak\theta \langle {\xi }\rangle ^{\rho }_{\ell }\chi _h}d\theta \end{aligned}$$

one can define $\omega _h$ by

$$\begin{aligned} {\tilde{\omega }}_h=a\left( \langle {\xi }\rangle _{\ell }^{\rho }\int _0^1e^{-ak\theta \langle {\xi }\rangle ^{\rho }_{\ell }\chi _h} d\theta \,\frac{1}{1+e^{-ak\langle {\xi }\rangle ^{\rho }_{\ell }\chi _h}}\right) \chi _h=a\,\omega _h\,\chi _h. \end{aligned}$$

Then the first assertion is clear from (3.2). Note that

$$\begin{aligned} \big |\partial _{\xi }^{\alpha }\big (a\,k\langle {\xi }\rangle _{\ell }^{\rho }\chi _h \big )\big |\le C_{\alpha }\langle {\xi }\rangle _{\ell }^{-|\alpha |} \end{aligned}$$

(3.4)

because of (3.1). Therefore one has $|\partial _{\xi }^{\alpha }\omega _h|\le C_{\alpha }\, \langle {\xi }\rangle ^{\rho -|\alpha |}_{\ell }$. Using (3.2) this implies the second assertion. $\square$

3.2 Crank–Nicholson after conjugation

Note that $u^n_h$ satisfy

$$\begin{aligned} \forall \, n\in \mathbb {N},\quad \chi _hu^n_h=u^n_h \end{aligned}$$

(3.5)

thanks to (2.8). Assume that $u^n_h$ satisfies

$$\begin{aligned} \delta _ku^n_h=\frac{u^{n+1}_h-u^n_h}{k}=G^n_h(x,D)\ \frac{u^{n+1}_h+u^n_h}{2}+f^n \end{aligned}$$

(3.6)

where $\chi _hf^n=f^n$ is not necessarily assumed.

Consider a weighted energy $(R_h^nW^n_hu_h^n,\,W^n_hu_h^n)$ where $R^n_h$ is a symmetrizer that is symmetric $(R^n_h)^*=R^n_h$ and will be defined in Sect. 3.3 below. The discrete analog of $\partial _t (R_h^nW^n_hu_h^n,\,W^n_hu_h^n)$ is the time difference

$$\begin{aligned} \begin{aligned}&\delta _k(R^n_hW^n_h\,u^n_h,\,W^n_h\,u^n_h) \\&\quad = \frac{ (R^{n+1}_hW^{n+1}_h u^{n+1}_h,\,W^{n+1}_hu^{n+1}_h)-(R^{n}_hW^n_h u^{n}_h,\,W^n_hu^{n}_h)}{k}. \end{aligned} \end{aligned}$$

(3.7)

In what follows we omit the subscript h for ease of reading. Write (3.7) as

$$\begin{aligned} \frac{ (W^{n+1}R^{n}W^{n+1} u^{n+1} ,\, u^{n+1}) - (W^nR^{n}W^n u^{n} ,\, u^{n}) }{k} \ +\ (III), \end{aligned}$$

with

$$\begin{aligned} (III)\ :=\ \frac{ ((R^{n+1}-R^n)W^{n+1} u^{n+1},\,W^{n+1}u^{n+1})}{k}. \end{aligned}$$

(3.8)

The term (III) is an error term that will be estimated in Sect. 3.3. The first term is equal to

$$\begin{aligned}&\frac{ ((R^n{\bar{\delta }}_k{W^n}) u^{n+1},\, u^{n+1}) + ( (R^n{\bar{\delta }}_k{W^n})u^{n},\, u^{n}) }{2} \nonumber \\&\quad +\ \bigg (\Big (\frac{W^{n+1}R^{n}W^{n+1}+W^nR^{n}W^n}{2}\Big ) \Big (\frac{u^{n+1}+u^{n}}{2}\Big )\ ,\ \delta _ku^n \bigg ) \nonumber \\&\quad +\ \bigg ( \Big (\frac{W^{n+1}R^{n}W^{n+1}+W^nR^{n}W^n}{2}\Big )\ \delta _ku^n,\, \Big (\frac{u^{n+1}+u^{n}}{2}\Big ) \bigg ) \end{aligned}$$

(3.9)

where

$$\begin{aligned} R^n{\bar{\delta }}_k{W^n}=\frac{W^{n+1}R^nW^{n+1}-W^nR^nW^n}{k}. \end{aligned}$$

The first line of (3.9) is

$$\begin{aligned} (I)=\frac{ ((R^n{\bar{\delta }}_k{W^n})u^{n+1}, u^{n+1}) + ( (R^n{\bar{\delta }}_k{W^n})u^n, u^{n}) }{2}. \end{aligned}$$

(3.10)

Note that

$$\begin{aligned} \begin{aligned}&R^n{\bar{\delta }}_k{W^n} =\frac{W^{n+1}R^nW^{n+1}-W^nR^nW^n}{k}\\&\quad =\frac{1}{2}\,\frac{W^{n+1}-W^n}{k}R^n(W^{n+1}+W^n) +\frac{1}{2}\,(W^{n+1}+W^n)R^n\frac{W^{n+1}-W^n}{k}. \end{aligned} \end{aligned}$$

Using (3.3) and $\omega \chi _h\,W^m=W^m \omega \chi _h$ this becomes

$$\begin{aligned}&R^n{\bar{\delta }}_k{W^n} = -\frac{a}{2}\,(W^{n+1} +W^n)\,\omega \,\chi _hR^n (W^{n+1}+W^n)\\&\quad -\frac{a}{2}\,(W^{n+1}+W^n)R^n\, \omega \,\chi _h\,(W^{n+1}+W^n) . \end{aligned}$$

Therefore with $\Omega ^{n}=W^{n+1}+W^n$ one has, since $(R^n)^*=R^n$

$$\begin{aligned}&( (R^n{\bar{\delta }}_k{W^n})w, w)=-a\,{\mathsf {Re}}\, ( R^n\, \Omega ^n\, w, \,\omega \chi _h\, \Omega ^n w)\\&\quad =-a\,{\mathsf {Re}}\,(\omega \chi _h\, R^n\, \Omega ^n\, w, \, \Omega ^n w). \end{aligned}$$

Thus (I) yields

$$\begin{aligned} (I)\ =\ -\frac{a}{2}\sum _{j=0}^1\,{\mathsf {Re}}\, (\omega \chi _h\,R^n\,\, \Omega ^n\, u^{n+j},\Omega ^n\, u^{n+j}). \end{aligned}$$

Since $\chi _h\,\Omega ^n=\Omega ^n\,\chi _h$ and $\omega \chi _h=\chi _h \omega$ and using $\chi _hu^{n+j}=u^{n+j}$ that follows from (3.5) one has

$$\begin{aligned} (I)\ =\ -a\,\sum _{j=0}^1\,{\mathsf {Re}}\, (\omega \, R^n\, \Omega ^n u^{n+j},\,\Omega ^n u^{n+j}). \end{aligned}$$

(3.11)

The second line of (3.9) yields, with $U^n=u^{n+1}+u^n$

$$\begin{aligned}&\left( \left( \frac{W^{n+1}R^nW^{n+1}+W^n R^nW^n}{2}\right) \left( \frac{u^{n+1}+u^{n}}{2}\right) , \delta _ku^n \right) \\&\quad =\frac{1}{8}(R^nW^{n}U^n,\, W^{n}G^nU^n)+\frac{1}{8}(R^nW^{n+1}U^n,\, W^{n+1}G^nU^n)\\&\qquad +\frac{1}{4}(U^n,\, (W^{n+1}R^nW^{n+1}+W^n R^nW^n) f^n). \end{aligned}$$

Because of (3.6), this is equal to

$$\begin{aligned} \frac{1}{8}\sum _{j=0}^1( R^n\,W^{n+j} \,U^n,\, W^{n+j}\,G^n\,U^n) +\frac{1}{4}\sum _{j=0}^1(U^n, \,W^{n+j}R^n\,W^{n+j}f^n). \end{aligned}$$

Similarly the third line of (3.9) is

$$\begin{aligned}&\left( \frac{W^{n+1}R^nW^{n+1}+W^nR^{n}W^n}{2}\ \delta _ku^n,\, \frac{u^{n+1}+u^{n}}{2} \right) \\&\quad =\frac{1}{8}\sum _{j=0}^1(W^{n+j}\,G^n\,U^n,\, R^n\,W^{n+j}\,U^n) +\frac{1}{4}\sum _{j=0}^1&(W^{n+j}R^nW^{n+j} f^n,\, U^n). \end{aligned}$$

Therefore the sum of the second and the third lines of (3.9), denoted by (II), yields

$$\begin{aligned} \begin{aligned}&(II)=\frac{1}{4}\sum _{j=0}^1\,{\mathsf {Re}}\,( R^n \,W^{n+j} \,U^n,\, W^{n+j}\,G^n\,U^n)\\&\qquad \qquad +\frac{1}{2}\sum _{j=0}^1\,{\mathsf {Re}}\,(U^n, \,W^{n+j}R^n\,W^{n+j}f^n). \end{aligned} \end{aligned}$$

(3.12)

Recalling

$$\begin{aligned} \delta _k(R^nW^n\,u^n,\,W^n\,u^n)=(I)+(II)+(III) \end{aligned}$$

(3.13)

we have proved the following proposition.

Proposition 3.2

We have

$$\begin{aligned}&\delta _k(R^nW^n\,u^n,\,W^n\,u^n)=-a\,\sum _{j=0}^1\,{\mathsf {Re}}\, (\omega \, R^n\, \Omega ^n u^{n+j},\,\Omega ^n u^{n+j})\\&\quad +\frac{1}{4}\sum _{j=0}^1\,{\mathsf {Re}}\,( R^n\,W^{n+j} \,U^n,\, W^{n+j}\,G^n\,U^n) +\frac{1}{2}\sum _{j=0}^1\,{\mathsf {Re}}\,(U^n, \,W^{n+j}R^n\,W^{n+j}f^n)\\&\quad +\frac{((R^{n+1}-R^n)W^{n+1} u^{n+1},\,W^{n+1}u^{n+1})}{k} \end{aligned}$$

where $\Omega ^n:=W^{n+1}+W^n$ and $U^n:=u^{n+1}+u^n$.

3.3 Composition with $W^{\pm n}_h$ and definition of $R^n_h$

First recall Definition 2.4 from [8].

Definition 3.2

For $1<s$, $m\in \mathbb {R}$, the family $a(x,\xi ;\ell )\in C^{\infty }(\mathbb {R}^d\times \mathbb {R}^d )$ belongs to ${\tilde{S}}_{(s)}^m$ if there exist $C>0$, $A>0$ independent of $\ell \ge 1,x,\xi$ such that for all $\alpha$, $\beta \in \mathbb {N}^d$,

$$\begin{aligned} \big | \partial _x^{\beta }\partial _{\xi }^{\alpha }a(x,\xi ;\ell ) \big | \ \le \ C\,A^{|\alpha +\beta |}\ |\alpha +\beta |!^s\ \langle {\xi }\rangle _{\ell }^{m-|\alpha |} . \end{aligned}$$

We often write $a(x,\xi )$ for $a(x,\xi ;\ell )$ dropping the $\ell$. If $a(x,\xi )$ is the symbol of a differential operator of order m with coefficients $a_{\alpha }(x)\in G^{s}(\mathbb {R}^d)$ then $a(x,\xi )\in {\tilde{S}}^m_{(s)}$ because $|\partial _{\xi }^{\beta }\xi ^{\alpha }|\le CA^{|\beta |}|\beta |!\langle {\xi }\rangle _{\ell }^{|\alpha |-|\beta |}$ and $|\partial _x^{\beta }a_{\alpha }(x)|\le C_{\alpha }A_{\alpha }^{|\beta |}|\beta |!^s$ for any $\beta \in \mathbb {N}^d$.

Proposition 3.3

Suppose $1/2\le \rho <1$ and $s=1/\rho$ and let $A(x,\xi )$ be $m\times m$ matrix valued with entries in ${\tilde{S}}^1_{(s)}$ and $\partial _x^{\alpha }A(x,\xi )=0$ outside $|x|<R$ for some $R>0$ if $|\alpha |>0$. Define $m^*:={\max {\{\rho -k(1-\rho ),-1+\rho \}}}$. Then there is ${\bar{\tau }}>0$, $\ell _0>0$ such that

$$\begin{aligned} {\tilde{A}}(x,D)=e^{\tau \langle {D}\rangle _{\ell }^{\rho }\chi _h}A(x,D)e^{-\tau \langle {D}\rangle _{\ell }^{\rho }\chi _h} \end{aligned}$$

is a pseudodifferential operator with symbol given by

$$\begin{aligned} {\tilde{A}}(x,\xi )=\sum _{|\alpha |\le k}\frac{1}{\alpha !}D_x^{\alpha }A(x,\xi )\big (\tau \,\nabla _{\xi }(\langle {\xi }\rangle _{\ell }^{\rho }\chi _h)\big )^{\alpha }+R_k(x,\xi ) \end{aligned}$$

with $R_k\in {\tilde{S}}^{m^*}$ uniformly in $\tau$, $\ell$ constrained to satisfy

$$\begin{aligned} |\tau |\le {\bar{\tau }},\quad \ell \ge \ell _0. \end{aligned}$$

(3.14)

In particular ${\tilde{A}}(x,\xi )\in {\tilde{S}}^1$ uniformly in such $\tau$, $\ell$.

Remark 3.1

This proposition with $\chi _h\equiv 1$ is [8, Proposition 2.6]. The proof for the case $\chi _h\equiv 1$ works without any change for the case $\chi _h\in {\tilde{S}}^0$.

Choosing a smaller ${\bar{\tau }}>0$ if necessary one can assume that

$$\begin{aligned} {\bar{\tau }}\big |\nabla _{\xi }(\langle {\xi }\rangle _{\ell }^{\rho }\chi _h)\big | \ \le \ \langle {\xi }\rangle _{\ell }^{\rho -1}. \end{aligned}$$

In what follows we choose $T={\bar{\tau }}$ in the definition of $W(t,\xi )$ yielding

$$\begin{aligned} W(t,\xi ) \ =\ e^{({\bar{\tau }}-t)\langle {\xi }\rangle ^{\rho }_{\ell }\chi _h}. \end{aligned}$$

With $N=\max \{2\theta ,m\}$ denote

$$\begin{aligned} H( t,x,\xi , \tau ) \ =\ \sum _{|\alpha |\le N}\frac{1}{\alpha !} D_x^{\alpha }A(t,x,\xi ) \big (({\bar{\tau }}-\tau )\nabla _{\xi }(\langle {\xi }\rangle _{\ell }^{\rho }\chi _h)\big )^{\alpha } . \end{aligned}$$

Suppressing the subscript h for ease of reading, Proposition 3.3 shows that

$$\begin{aligned} W(\tau ,\xi )\#A(t,x,\xi )\#W^{-1}(\tau ,\xi ) \ =\ H(t,x,\xi ,\tau )+R,\quad R\in {\tilde{S}}^{m^*} . \end{aligned}$$

The choice of N guarantees that where $2\theta (1-\rho )+m^*\le \rho$. Define

$$\begin{aligned} H^h(t,x,\xi ,\tau ) \ =\ \chi _{2h}^2(\xi )H(t,x,\xi ,\tau ). \end{aligned}$$

Then, the definition of ${\mathcal H}_N$ implies that

$$\begin{aligned}&H^h(t,x,\xi ,\tau ) \nonumber \\&\quad =\chi _{2h}^2(\xi )\, \langle {\xi }\rangle _\ell \ {\mathcal H}_N\big ( t,x,\xi /\langle {\xi }\rangle _\ell , ({\bar{\tau }}-\tau )\nabla _{\xi }(\langle {\xi }\rangle _{\ell }^{\rho }\chi _h)/\langle {\xi }\rangle ^{\rho -1}_{\ell }, 0, \langle {\xi }\rangle _\ell ^{\rho -1} \big ). \end{aligned}$$

(3.15)

In (3.15) choose

$$\begin{aligned} \begin{aligned} s&=\chi _{2h}^2(\xi )\langle {\xi }\rangle _\ell , \quad \epsilon =\langle {\xi }\rangle _\ell ^{\rho -1}, \quad \xi =\xi /\langle {\xi }\rangle _\ell , \\ y&=({\bar{\tau }}-\tau )\nabla _{\xi }(\langle {\xi }\rangle _{\ell }^{\rho }\chi _h)/\langle {\xi }\rangle ^{\rho -1}_{\ell }, \quad \eta =0. \end{aligned} \end{aligned}$$

(3.16)

Using $0\le \chi _{2h}\le 1$, it follows from (2.2) that

$$\begin{aligned} \begin{aligned} \langle {\xi }\rangle _\ell ^{-\theta (1-\rho )} e^{-cs\langle {\xi }\rangle _\ell ^{\rho }}/C \ \le \ \big \Vert e^{isH^h(t,x,\xi ,\tau )} \big \Vert \le C \langle {\xi }\rangle _\ell ^{\theta (1-\rho )} e^{cs\langle {\xi }\rangle _\ell ^{\rho }} \end{aligned} \end{aligned}$$

(3.17)

for $|t|\le T$, $\ell \ge \ell _0$ where

$$\begin{aligned} 0\le \tau \le {\bar{\tau }},\quad 0< \epsilon =\langle {\xi }\rangle _{\ell }^{\rho -1} \le \ell ^{\rho -1}\le \ell _0^{\rho -1}=\epsilon _0. \end{aligned}$$

(3.18)

Following [8] define

$$\begin{aligned} M^h(t,x,\xi ,\tau ) \ =\ iH^h(t,x,\xi ,\tau ) \ -\ b\, \langle {\xi }\rangle _\ell ^{\rho } \end{aligned}$$

with a positive parameter $b>0$ that will be fixed later. Since $\Vert e^{sM^h(t,x,\xi ,\tau )}\Vert =e^{-bs\langle {\xi }\rangle _{\ell }^{\rho }}\Vert e^{isH^h(t,x,\xi ,\tau )}\Vert$, (3.17) implies

$$\begin{aligned} \langle {\xi }\rangle _{\ell }^{-\nu }\,e^{-c_1b\,s\langle {\xi }\rangle _{\ell }^{\rho }}/C\le \Vert e^{sM^h(t,x,\xi ,\tau )}\Vert \le C\,\langle {\xi }\rangle _{\ell }^{\nu }\,e^{-c_2b\,s\langle {\xi }\rangle _{\ell }^{\rho }} \end{aligned}$$

with $\nu =\theta (1-\rho )$ for $|t|\le T$ and $b\ge b_0$ with some $b_0>0$ where $c_1$, $c_2$ and $C>0$ are independent of $\ell$, h and b.

Introduce the symmetrizer

$$\begin{aligned} R_h(t,x,\xi ,\tau ) \ :=\ b\int _0^\infty \langle \xi \rangle ^\rho _\ell \big ( e^{sM^h(t,x,\xi ,\tau )}\big )^* \big ( e^{sM^h(t,x,\xi ,\tau )}\big ) ds . \end{aligned}$$

From [8, Theorem 3.1] it follows that

$$\begin{aligned} R_h(t,x,\xi ,\tau )\in {\tilde{S}}^{2\nu }_{\rho -\nu ,1-\rho +\nu },\quad b\,\partial _tR_h(t,x,\xi ,\tau )\in {\tilde{S}}^{3\nu +1-\rho }_{\rho -\nu ,1-\rho +\nu } \end{aligned}$$

under the constraint

$$\begin{aligned} b\,\ell ^{-(1-\rho )}\le 1 \end{aligned}$$

(3.19)

so that $b\,\langle {\xi }\rangle _{\ell }^{\rho -1}\le b\,\ell ^{-(1-\rho )}\le 1$. Recall [8, page 230] that

$$\begin{aligned} R_hM^h+(M^h)^*R_h =R_h\big (i\chi _{2h}^2H-b\langle {\xi }\rangle ^{\rho }_{\ell }\big )+\big (i\chi _{2h}^2H-b\langle {\xi }\rangle ^{\rho }_{\ell }\big )^*R_h=-b\,\langle {\xi }\rangle ^{\rho }_{\ell } \end{aligned}$$

that is

$$\begin{aligned} R_h(i\chi _{2h}^2H)+(i\chi _{2h}^2H)^*R_h=-b\,\langle {\xi }\rangle _{\ell }^{\rho }+2b\,\langle {\xi }\rangle _{\ell }^{\rho }\,R_h. \end{aligned}$$

(3.20)

Lemma 3.4

We have

$$\begin{aligned} \frac{b\,\big (R_h(t,x,\xi ,a(n+1)k)-R_h(t,x,\xi ,ank)\big )}{k\,a}\in {\tilde{S}}^{3\nu }_{\rho -\nu ,1-\rho +\nu } \end{aligned}$$

for $0\le t\le T$ uniformly in a, b, n, k, h under the constraint $ank\le {\bar{\tau }}$.

Proof

We show that

$$\begin{aligned} \big |\partial _x^{\beta }\partial _{\xi }^{\alpha }\partial _{\tau }R_h(t,x,\xi ,\tau )\big |\le C_{\alpha \beta }\,b^{-|\alpha +\beta |-1}\langle {\xi }\rangle _{\ell }^{3\nu +(1-\rho +\nu )|\beta |-(\rho -\nu )|\alpha |} \end{aligned}$$

(3.21)

with $C_{\alpha \beta }$ independent of b, h and $0\le \tau \le {\bar{\tau }}$. If (3.21) is proved then writing

$$\begin{aligned} R_h(t,x,\xi ,a(n+1)k)-R_h(t,x,\xi ,ank)=\int _{ank}^{ank+ak}\partial _{\tau }R_h(t,x,\xi ,\nu )d\nu \end{aligned}$$

the assertion follows immediately. To prove the estimate (3.21) we apply the same arguments in the proof of [8, Theorem 3.1]. First consider $\partial _{\tau }H(t,x,\xi ,\tau )$. Since

$$\begin{aligned} \partial _{\tau }H^h(t,x,\xi ,\tau )=-\chi _{2h}^2\sum _{1\le |\alpha |\le N}({\bar{\tau }}-\tau )^{|\alpha |-1}\frac{|\alpha |}{\alpha !} D_x^{\alpha }A(t,x,\xi ) \big (\nabla _{\xi }(\langle {\xi }\rangle _{\ell }^{\rho }\chi _h)\big )^{\alpha } \end{aligned}$$

it follows that

$$\begin{aligned} \big |\partial _x^{\beta }\partial _{\xi }^{\alpha }\partial _{\tau }H^h(t,x,\xi ,\tau )\big |\le C_{\alpha \beta }\langle {\xi }\rangle _{\ell }^{\rho -|\alpha |}. \end{aligned}$$

(3.22)

Denote

$$\begin{aligned} X(s;t,x,\xi ,\tau )=e^{sM^h(t,x,\xi ,\tau )}v,\;\;v\in \mathbb {C}^m,\quad X^{\alpha }_{\tau \beta }=\partial _x^{\beta }\partial _{\xi }^{\alpha }\partial _{\tau }X(t,x,\xi ,\tau ). \end{aligned}$$

Since

$$\begin{aligned} {\dot{X}}_{\tau }=M^hX_{\tau }+\partial _{\tau }H^hX,\quad X_{\tau }(0)=0 \end{aligned}$$

then (3.22) and Duhamel’s representation yields

$$\begin{aligned} \big |X_{\tau }\big |=\Big |\int _0^se^{(s-{\tilde{s}})M^h}(\partial _{\tau }H^h)Xd{\tilde{s}}\Big |\le C(s+\langle {\xi }\rangle _{\ell })\langle {\xi }\rangle _{\ell }^{\nu +\rho -1}E(s) \end{aligned}$$

where $E(s)=\langle {\xi }\rangle _{\ell }^{\nu }e^{-cb s\langle {\xi }\rangle _{\ell }^{\rho }}$. Repeating the same arguments in the proof of [8, Theorem3.1] one can prove

$$\begin{aligned} \big |X^{\alpha }_{\tau \beta }\big |\le C_{\alpha \beta }\,(s+\langle {\xi }\rangle _{\ell }^{-1})^{|\alpha |}(1+s\langle {\xi }\rangle _{\ell })^{|\beta |+1}\langle {\xi }\rangle _{\ell }^{\nu (|\alpha +\beta |+1)+\rho -1}E(s) \end{aligned}$$

from which we obtain (3.21) by exactly the same way as in the proof of [8, Theorem 3.1]. $\square$

Lemma 3.5

With $R_h^n(x,\xi ) \, :=\, R_h(nk,x,\xi ,ank)$, one has

$$\begin{aligned} \frac{b\,\big (R_h^{n+1}(x,\xi )-R_h^n(x,\xi )\big )}{k}\in {\tilde{S}}^{-2\nu +\rho }_{\rho -\nu ,1-\rho +\nu } \end{aligned}$$

for $0\le (n+1)k\le T$ uniformly in a, b, n, k, h under the constraint

$$\begin{aligned} ank\le {\bar{\tau }},\quad a\,\ell ^{-\rho /6}\le 1. \end{aligned}$$

(3.23)

Proof

Write

$$\begin{aligned}&R^{n+1}_h-R^n_h=R_h((n+1)k,x,\xi ,a(n+1)k)-R_h((n+1)k,x,\xi ,ank)\\&\quad +R_h((n+1)k,x,\xi ,ank)-R_h(nk,x,\xi ,ank). \end{aligned}$$

Express

$$\begin{aligned} R_h((n+1)k,x,\xi ,ank)-R_h(nk,x,\xi ,ank) =\int _{nk}^{nk+k}\partial _tR_h(t',x,\xi ,ank)dt' . \end{aligned}$$

Using $b\,\partial _tR_h(t,x,\xi ,\tau )\in {\tilde{S}}^{3\nu +1-\rho }_{\rho -\nu ,1-\rho +\nu }$, one obtains

$$\begin{aligned} \frac{b\,(R_h((n+1)k,x,\xi ,ank)-R_h(nk,x,\xi ,ank))}{k} \ \in \ {\tilde{S}}^{3\nu +1-\rho }_{\rho -\nu ,1-\rho +\nu } \end{aligned}$$

where $3\nu +1-\rho \le -2\nu +\rho$ in view of (2.2). For the term $R_h((n+1)k,x,\xi ,a(n+1)k)-R_h((n+1)k,x,\xi ,ank)$ we apply Lemma 3.4 to get

$$\begin{aligned} \frac{b\,\big (R_h((n+1)k,x,\xi ,a(n+1)k)-R_h((n+1)k,x,\xi ,ank)\big )}{k\,a}\in {\tilde{S}}^{3\nu }_{\rho -\nu ,1-\rho +\nu }. \end{aligned}$$

Here note that (2.9) implies $1/2>3\nu$ because $1>\rho \ge 3\nu +1/2$ and hence

$$\begin{aligned} \rho \ge 3\nu +1/2>6\nu . \end{aligned}$$

(3.24)

Then noting that $a\langle {\xi }\rangle _{\ell }^{3\nu }\le a\langle {\xi }\rangle ^{-\rho /6}_{\ell }\langle {\xi }\rangle ^{\rho -2\nu }_{\ell }\le a\,\ell ^{-\rho /6}\langle {\xi }\rangle ^{\rho -2\nu }_{\ell }$ one has

$$\begin{aligned} \frac{b\,\big (R_h((n+1)k,x,\xi ,a(n+1)k)-R_h((n+1)k,x,\xi ,ank)\big )}{k}\in {\tilde{S}}^{-2\nu +\rho }_{\rho -\nu ,1-\rho +\nu } \end{aligned}$$

under the constraint $a\,\ell ^{-\rho /6}\le 1$. Thus the proof is complete. $\square$

Definition 3.3

For a $m\times m$ complex matrix $\mathcal {M}=\mathcal {M}^*$, the notation $\mathcal {M}\gg 0$ means that for all $v\in \mathbb {C}^m$ one has $(\mathcal {M}v,\,v)_{\mathbb {C}^m}\ge 0$. For two such matrices, $\mathcal {M}_1\gg \mathcal {M}_2$ means that $\mathcal {M}_1-\mathcal {M}_2 \gg 0$.

Equation (3.17) yields for any $v\in \mathbb {C}^m$

$$\begin{aligned}&(R^n_h(x,\xi )v,v) = b \int _0^{\infty }\langle {\xi }\rangle _{\ell }^{\rho }\Vert e^{sM^h(nk,x,\xi ,ank)}v\Vert ^2\,ds\\&\quad \ge \ C^{-2}\,\Vert v\Vert ^2\langle {\xi }\rangle _{\ell }^{-2\nu } \int _0^{\infty }b\,\langle {\xi }\rangle _\ell ^{\rho }\,e^{-2c_1b\,s\langle {\xi }\rangle _\ell ^{\rho }}\,ds \ge c\, \langle {\xi }\rangle _\ell ^{-2\nu }\Vert v\Vert ^2. \end{aligned}$$

This is an important pointwise lower bound for the symbol

$$\begin{aligned} R^n_h(x,\xi ) \ \gg \ c\,\langle {\xi }\rangle _{\ell }^{-2\nu }I \end{aligned}$$

(3.25)

where c is independent of b, a, n, k, h constrained to satisfy (3.23) and (3.19).

3.4 Estimate of (I)

Suppressing the suffix h again, denote

$$\begin{aligned} { W}(\xi )=e^{-ak\langle {\xi }\rangle _{\ell }^{\rho }\chi _h} \end{aligned}$$

so that $W^{n+1}=W^nW$ where $1/2\le W\le 1$ and $W^{\pm 1}\in {\tilde{S}}^0$ which follows from (3.2) and (3.4). Consider ${\mathsf {Re}}(\omega \,R^n\,\Omega ^n\,w,\, \Omega ^n\,w)$. Write $\Omega ^n=W^{n+1}+W^n=(1+W)\,W^n$ and hence

$$\begin{aligned} {\mathsf {Re}}\,(\omega \,R^n\,\Omega ^n\,w,\Omega ^n\,w) \ =\ {\mathsf {Re}}\,\big ((1+W)\omega \,R^n(1+W)W^n\,w,\,W^n\,w\big ). \end{aligned}$$

Note that $R^n\in {\tilde{S}}^{2\nu }_{\rho -\nu ,1-\rho +\nu }$ uniformly for parameters satisfying the constraints (3.23) and (3.19).

Lemma 3.6

One can write

$$\begin{aligned} (1+W)\#\omega \#R^n\#(1+W)=(1+W)^2\,\omega \,R^n+iR_1^n+R_2^n \end{aligned}$$

with $(R_1^n)^*=R_1^n$ and $R_2^n\in {\tilde{S}}^{4\nu -\rho }_{\rho -\nu ,1-\rho +\nu }$.

Proof

Denote $f(\xi )=(1+W(\xi ))\omega (\xi )$ and $g(\xi )=1+W(\xi )$. Since one has $f(\xi )\in {\tilde{S}}^{\rho }\subset {\tilde{S}}^{\rho }_{\rho -\nu ,1-\rho +\nu }$ and $g(\xi )\in {\tilde{S}}^0\subset {\tilde{S}}^{0}_{\rho -\nu ,1-\rho +\nu }$ applying [13, Theorem 18.5.4] one can write

$$\begin{aligned}&\big ((1+W)\omega \big )\#R^n\#(1+W)=(1+W)^2\omega R^n\\&\quad +\frac{1}{2i}\sum _{|\alpha +\beta |=1}(-1)^{|\beta |}\partial _{\xi }^{\alpha } f\,(\partial _x^{\alpha +\beta }R^n)\,\partial _{\xi }^{\beta }g\\&\quad +\sum _{2\le |\alpha +\beta |<N}\frac{(-1)^{|\beta |}}{(2i)^{|\alpha +\beta |}\alpha !\beta !}\partial _{\xi }^{\alpha }f\,(\partial _x^{\alpha +\beta }R^n)\,\partial _{\xi }^{\beta }g+R_N \end{aligned}$$

where $R_N\in {\tilde{S}}^{2\nu +\rho -N(2\rho -1-2\nu )}_{\rho -\nu ,1-\rho +\nu }$.

Choose N so large that $2\nu +\rho -N(2\rho -1-2\nu )\le 4\nu -\rho$. The second term on the right-hand side, denoted by $iR_1^n$, clearly satisfies $(R_1^n)^*=R_1^n$ because $f(\xi )$ and $g(\xi )$ are real scalar symbols. Since $\partial _{\xi }^{\alpha }f\in {\tilde{S}}^{\rho -|\alpha |}_{\rho -\nu ,1-\rho +\nu }$ and $\partial _{\xi }^{\beta }g\in {\tilde{S}}^{-|\beta |}_{\rho -\nu ,1-\rho +\nu }$ it is clear that the third term on the right-hand side is in ${\tilde{S}}^{4\nu -\rho }_{\rho -\nu ,1-\rho +\nu }$. $\square$

Thanks to Lemma 3.6 we have

$$\begin{aligned}&{\mathsf {Re}}((1+ W)\, \omega R^n(1+W)W^n\,w,\,W^n\,w)\\&\quad \ge \ \big (\mathrm{Op}((1+W)^2\omega R^n)\,W^n\,w,\,W^n\,w\big ) -C\Vert \langle {D}\rangle _{\ell }^{2\nu -\rho /2}\,W^n\,w\Vert ^2. \end{aligned}$$

It follows from Lemma 3.1 and (3.25) that

$$\begin{aligned} (1+W)^2\omega R^n\gg c \big (\langle {\xi }\rangle _{\ell }^{\rho -2\nu }I+\langle {\xi }\rangle ^{\rho }_{\ell }R^n\big ),\quad (1+W)^2\omega R^n\in {\tilde{S}}^{2\nu +\rho }_{\rho -\nu ,1-\rho +\nu } \end{aligned}$$

with $c>0$ uniformly in the constrained parameters k, n, h, a, b. Note that

$$\begin{aligned} (1+W)^2\omega R^n \ \in \ S\big (\langle {\xi }\rangle _{\ell }^{2\nu +\rho },\, b^{-2}(\langle {\xi }\rangle _{\ell }^{2(1-\rho +\nu )}|dx|^2+\langle {\xi }\rangle _{\ell }^{-2(\rho -\nu )}|d\xi |^2\big ) \end{aligned}$$

since for any $k(\xi ) \in {\tilde{S}}^{q}$ one has

$$\begin{aligned} |\partial _{\xi }^{\alpha }k(\xi )|\le C_{\alpha }\langle {\xi }\rangle _{\ell }^{q-|\alpha |}\le C_{\alpha }\ell ^{-|\alpha |(1-\rho +\nu )}\langle {\xi }\rangle _{\ell }^{q-|\alpha |(\rho -\nu )} \end{aligned}$$

which is bounded by $C_{\alpha }b^{-|\alpha |}\langle {\xi }\rangle _{\ell }^{q-|\alpha |(\rho -\nu )}$ because of (3.19). Repeating the arguments proving [8, (4.6)] it follows from the sharp Gårding inequality [13, Theorem 18.6.7] that there is $\ell _0>0$ such that

$$\begin{aligned}&(\mathrm{Op} ((1+W)^2\omega R^n)\,W^n\,w,W^n\,w)\ge c\,\Vert \langle {D}\rangle _{\ell }^{-\nu +\rho /2}W^n\,w\Vert ^2\\&\quad +c\,(\mathrm{Op}(\langle {\xi }\rangle _{\ell }^{\rho }R^n)\,W^n\,w,W^n\,w)-Cb^{-2}\Vert \langle {D}\rangle _{\ell }^{-\rho /2+1/2+2\nu }W^n\,w\Vert ^2 \end{aligned}$$

for $\ell \ge \ell _0$. Since $-\nu +\rho /2\ge -\rho /2+1/2+2\nu$ by (2.9), choosing another $b_0$ if necessary one obtains

$$\begin{aligned} \begin{aligned}&(\mathrm{Op}((1 +W)^2\omega R^n)\,W^n\,w,\,W^n\,w)\\&\quad \ge c'\,\Vert \langle {D}\rangle _{\ell }^{-\nu +\rho /2}W^n\,w\Vert ^2 +c'\,(\mathrm{Op}(\langle {\xi }\rangle ^{\rho }_{\ell }R^n)\,W^n\,w,\,W^n\,w) \end{aligned} \end{aligned}$$

(3.26)

with $c'>0$ uniform for $\ell \ge \ell _0$ and $b\ge b_0$. From (2.9) again one sees that

$$\begin{aligned} \Vert \langle {D}\rangle _{\ell }^{2\nu -\rho /2}\,v\Vert ^2 \ \le \ C\ell ^{-1}\Vert \langle {D}\rangle _{\ell }^{-\nu +\rho /2}\,v\Vert ^2 \end{aligned}$$

and one concludes that choosing another $\ell _0$ if necessary

$$\begin{aligned}&{\mathsf {Re}}\,((1+W)\omega \,R^n\,(1+W)W^n\,w,\,W^n\,w)\\&\quad \ge c\,\Vert \langle {D}\rangle _{\ell }^{-\nu +\rho /2}W^n\,w\Vert ^2 +c\,(\mathrm{Op}(\langle {\xi }\rangle ^{\rho }_{\ell }R^n)\,W^n\,w,\,W^n\,w) \end{aligned}$$

with $c>0$ uniform for $\ell \ge \ell _0$ and $b\ge b_0$. Repeating the same arguments one obtains

$$\begin{aligned}&{\mathsf {Re}}\,((1+W^{-1})\,\omega \,R^n (1+W^{-1})\,W^{n+1}\,w,\,W^{n+1}w)\\&\quad \ge c\,\Vert \langle {D}\rangle _{\ell }^{-\nu +\rho /2}W^{n+1}\,w\Vert ^2 +c\,(\mathrm{Op}(\langle {\xi }\rangle ^{\rho }_{\ell }R^n)\,W^{n+1}\,w,\,W^{n+1}\,w). \end{aligned}$$

Summarizing we have

Lemma 3.7

There are $c>0$, $\ell _0$ and $b_0$ such that for $\ell \ge \ell _0$ and $b\ge b_0$ one has

$$\begin{aligned}&{\mathsf {Re}}\,( \omega \,R^n\,\Omega ^n\,w,\,\Omega ^n\,w)\\&\quad \ge c\,\left( \sum _{i=0}^1\Vert \langle {D}\rangle _{\ell }^{-\nu +\rho /2}\,W^{n+i}\,w\Vert ^2 +\big (\mathrm{Op}(\langle {\xi }\rangle ^{\rho }_{\ell }R^n)\,W^{n+i}\,w,\,W^{n+i}\,w\big )\right) . \end{aligned}$$

Lemma 3.7 together with (3.11) prove the following

Proposition 3.8

There exist $c>0$, $\ell _0>0$ and $b_0$ such that for $\ell \ge \ell _0$ and $b\ge b_0$ one has

$$\begin{aligned}&(I) \le -c\,a \mathop {\sum }_{\begin{array}{c} 0\le i\le 1\\ 0\le j\le 1 \end{array}} \Big ( \Vert \langle {D}\rangle _{\ell }^{-\nu +\rho /2}\,W^{n+i}\,u^{n+j}\Vert ^2\\&\qquad \quad + \big (\mathrm{Op}(\langle {\xi }\rangle ^{\rho }_{\ell }R^n)\,W^{n+i}\,u^{n+j},\,W^{n+i}\,u^{n+j}\big ) \Big ). \end{aligned}$$

From (3.25) one has $R^n\gg c\langle {\xi }\rangle ^{-2\nu }I$ and $\langle {\xi }\rangle ^{\rho }_{\ell }R^n\gg c\langle {\xi }\rangle ^{\rho -2\nu }I$ with some $c>0$ then repeating the same arguments proving (3.26) above there is $c>0$ such that

$$\begin{aligned} \begin{aligned}&(\mathrm{Op}(R^n)\,v,v)\ge c\,\Vert \langle {D}\rangle _{\ell }^{-\nu }\,v\Vert ^2,\\&\quad (\mathrm{Op}(\langle {\xi }\rangle ^{\rho }_{\ell }R^n)\,v,v)\ge c\,\Vert \langle {D}\rangle _{\ell }^{-\nu +\rho /2}\,v\Vert ^2 \end{aligned} \end{aligned}$$

(3.27)

for $b\ge b_0$. In particular $\mathrm{Op}(\langle {\xi }\rangle ^{\rho }_{\ell }R^n)$ is nonnegative hence

$$\begin{aligned} 2\big |(\mathrm{Op}(\langle {\xi }\rangle _{\ell }^{\rho }R^n)\,v,\,w)\big |\le \delta (\mathrm{Op}(\langle {\xi }\rangle _{\ell }^{\rho }R^n)\,v,\,v)+\delta ^{-1}(\mathrm{Op}(\langle {\xi }\rangle _{\ell }^{\rho }R^n)\,w,\,w) \end{aligned}$$

(3.28)

for any $\delta >0$.

3.5 Estimate of (II)

Consider the term ${\mathsf {Re}}\,(R^nW^{n}\,U^n,\,W^{n}\,G^n\,U^n)$. Recall $G^n=\chi _{2h}(iA(nk,x,D)+B(nk,x))\chi _{2h}$ and with $t_n=nk$

$$\begin{aligned} W^n\#A(t,x,\xi )\#W^{-n}=H(t,x,\xi ,at_n)+R(t,at_n),\quad R(t,at_n)\in {\tilde{S}}^{m^*} \end{aligned}$$

where

$$\begin{aligned} W^{-n}\ :=\ \big (W_h(at_n,\xi )\big )^{-n} \ =\ e^{-n({\bar{\tau }}-at_n)\langle {\xi }\rangle ^{\rho }_{\ell }\chi _h}. \end{aligned}$$

Then thanks to Proposition 3.3,

$$\begin{aligned}&W^n\,G^n\,W^{-n}=\chi _{2h}\,W^n(iA(t_n,x,D)+B(t_n,x))W^{-n}\,\chi _{2h}\\&\quad =\chi _{2h}(iH(t_n,x,D,at_n)+R(t_n,at_n))\chi _{2h}+\chi _{2h}\,W^nB(t_n,x)W^{-n}\,\chi _{2h}. \end{aligned}$$

Since $\chi _{2h}\in {\tilde{S}}^0$ and $H(t_n,x,\xi ,at_n)\in {\tilde{S}}^1$, one sees that

$$\begin{aligned} \chi _{2h}\#(iH(t_n,x,\xi ,at_n))\#\chi _{2h} \ =\ i\chi _{2h}^2H(t_n,x,\xi ,at_n)+{\tilde{R}}_n \end{aligned}$$

where ${\tilde{R}}_n\in {\tilde{S}}^0$ uniformly in all parameters satisfying $at_n=ank\le {\bar{\tau }}$. Define $K^n:={\tilde{R}}_n+\chi _{2h}\#R(t_n,at_n)\#\chi _{2h}+\chi _{2h}\#W^n\#B(t_n)\#W^{-n}\#\chi _{2h}$. Then

$$\begin{aligned} W^n\#G^n\#W^{-n}\ =\ i\chi _{2h}^2H(t_n,x,\xi ,at_n)\ +\ K^n(x,\xi ) \end{aligned}$$

so,

$$\begin{aligned} W^n\#G^n=(i\chi _{2h}^2H(t_n,x,\xi ,at_n)+K^n)\#W^n. \end{aligned}$$

(3.29)

In addition,

$$\begin{aligned} K^n\in {\tilde{S}}^{{\bar{m}}},\quad \mathrm{with} \quad {\bar{m}}=\max \{0,m^*\}. \end{aligned}$$

Note that $2\nu +{\bar{m}}\le \rho$ since $2\nu +{{m}^*}\le \rho$. Recall

$$\begin{aligned} R_h=b\int _0^{\infty }\langle {\xi }\rangle _{\ell }^{\rho }(e^{sM^h})^*e^{sM^h}ds,\quad M^h=i\chi _{2h}^2 H(t,x,\xi ,\tau )-b\,\langle {\xi }\rangle ^{\rho }_{\ell } \end{aligned}$$

and $R^n_h=R_h(t_n,x,\xi ,at_n)$ so that from (3.20) it follows that

$$\begin{aligned} \begin{aligned}&R^n(i\chi _{2h}^2H(t_n,x,\xi ,at_n))+(i\chi _{2h}^2 H (t_n,x,\xi ,at_n))^*R^n\\&\quad =-b\,\langle {\xi }\rangle _{\ell }^{\rho }+2b\,\langle {\xi }\rangle _{\ell }^{\rho }R^n. \end{aligned} \end{aligned}$$

(3.30)

In view of (3.29), denoting $H(t_n)=H(t_n,x,\xi ,at_n)$, one has

$$\begin{aligned}&2{\mathsf {Re}}\,(R^nW^{n}\, U^n,\,W^{n}\,G^n\,U^n)=2{\mathsf {Re}}\,(W^n\,U^n,\,R^nW^n\,G^n\,U^n)\\&\quad =2{\mathsf {Re}}\,(W^nU^n,\,R^n\,\mathrm{Op}(i\chi _{2h}^2H(t_n)+K^n)\,W^n\,U^n)\\&\quad =2{\mathsf {Re}}\,(R^n\,\mathrm{Op}(i\chi _{2h}^2H(t_n)+K^n)W^n\,U^n,\,W^n\,U^n)\\&\quad =(\mathrm{Op}(F)W^n\,U^n,\,W^n\,U^n). \end{aligned}$$

It follows from (3.30) that

$$\begin{aligned} F&=R^n\#(i\chi _{2h}^2H(t_n)+K^n)+(i\chi _{2h}^2H(t_n)+K^n)^*\#R^n\\&=-b\, \langle {\xi }\rangle ^{\rho }_{\ell } +2b\, \langle {\xi }\rangle ^{\rho }_{\ell }R^n+L^n+{\tilde{L}}^n, \end{aligned}$$

where $b\, L^n\in {\tilde{S}}^{1-\rho +3\nu }_{\rho -\nu ,1-\rho +\nu }$ and ${\tilde{L}}^n\in {\tilde{S}}^{2\nu +{\bar{m}}}_{\rho -\nu ,1-\rho +\nu }\subset {\tilde{S}}^{\rho }_{\rho -\nu ,1-\rho +\nu }$. Since $\rho \ge 1-\rho +3\nu$ taking another $b_0$ if necessary one concludes

$$\begin{aligned}&-b\,(\langle {D}\rangle _{\ell }^{\rho }\,W^n\,U^n,\,W^n\,U^n)+{\mathsf {Re}}(\mathrm{Op}(L^n+{\tilde{L}}^n )\,W^n\,U^n,\,W^n\,U^n)\\&\quad \le -\frac{b}{2}\Vert \langle {D}\rangle _{\ell }^{\rho /2}\,W^n\,U^n\Vert ^2 \end{aligned}$$

for $b\ge b_0$. Thanks to (3.28) one has

$$\begin{aligned} 2b\, (\mathrm{Op}(\langle {\xi }\rangle ^{\rho }_{\ell }R^n)\,W^n\,U^n,\,W^n\,U^n)\le 4\,b \sum _{j=0}^1(\mathrm{Op}((\langle {\xi }\rangle ^{\rho }_{\ell }R^n)\,W^n\,u^{n+j},\,W^n\,u^{n+j}). \end{aligned}$$

Combining these estimates one obtains for $b\ge b_0$,

$$\begin{aligned} \begin{aligned}&2\,{\mathsf {Re}}\,(R^nW^n\,U^n,\,W^n \,G^n\,U^n)\le -\frac{b}{2}\,\Vert \langle {D}\rangle _{\ell }^{\rho /2}\,W^n\,U^n\Vert ^2\\&\quad +4\,b \sum _{j=0}^1(\mathrm{Op}((\langle {\xi }\rangle ^{\rho }_{\ell }R^n)\,W^n\,u^{n+j},\,W^n\,u^{n+j}). \end{aligned} \end{aligned}$$

(3.31)

Next study ${\mathsf {Re}}\,(R^nW^{n+1}\,G^n\,U^n,\,W^{n+1}\,U^n)$.

Lemma 3.9

One has

$$\begin{aligned} W^{n+1}\#G^n\#W^{-(n+1)}=i\chi _{2h}^2H(t_n)+K^n+T^n,\quad \mathrm{with} \quad T^n\in {\tilde{S}}^{0}. \end{aligned}$$

Proof

Write $W^{n+1}\#G^n\#W^{-(n+1)}=W\#\big (W^n\#G^n\#W^{-n})\#W^{-1}$ so that

$$\begin{aligned} W^{n+1}\#G^n\#W^{-(n+1)}=W\#\big (i\chi _{2h}^2H(t_n)+K^n)\#W^{-1}. \end{aligned}$$

Since $W^{\pm 1}\in {\tilde{S}}^{0}$ and $H(t_n)\in {\tilde{S}}^1$ it is clear that

$$\begin{aligned} W\#(i\chi _{2h}^2H(t_n)+K^n)\#W^{-1}=i\chi _{2h}^2H(t_n)+K^n+T^n, \quad T^n\in {\tilde{S}}^{0}. \end{aligned}$$

This proves the lemma. $\square$

Lemma 3.9 implies that

$$\begin{aligned}&2\,{\mathsf {Re}}\,(R^n\,W^{n+1}G^n\,U^n,\,W^{n+1}\,U^n)\\&\quad =2\,{\mathsf {Re}}\,\big ((R^n\,\mathrm{Op}(i\chi _{2h}^2H(t_n)+K^n+T^n)\,W^{n+1}U^n,\,W^{n+1}U^n)\\&\quad =(\mathrm{Op}(F)W^{n+1}U^n,\,W^{n+1}U^n) \end{aligned}$$

with

$$\begin{aligned} F\ :=\ R^n\#(i\chi _{2h}^2H(t_n)+K^n+T^n)+(i\chi _{2h}^2H(t_n)+K^n+T^n)^*\#R^n. \end{aligned}$$

Since $R^n\#T^n+(T^n)^*\#R^n\in {\tilde{S}}^{2\nu }_{\rho -\nu ,1-\rho +\nu }$ and $\rho \ge 4\nu$ by (3.24) repeating the same arguments proving (3.31) one obtains for $b\ge b_0$

$$\begin{aligned} \begin{aligned}&2\,{\mathsf {Re}}\,(R^nW^{n+1}\,G^n\,U^n,\,W^{n+1}\,U^n)\le -\frac{b}{2}\,\Vert \langle {D}\rangle _{\ell }^{\rho /2}\,W^{n+1}\,U^n\Vert ^2\\&\quad +4\,b \sum _{j=0}^1(\mathrm{Op}((\langle {\xi }\rangle ^{\rho }_{\ell }R^n)\,W^{n+1}\,u^{n+j},\,W^{n+1}\,u^{n+j}). \end{aligned} \end{aligned}$$

(3.32)

Equations (3.31) and (3.32) yield the following lemma.

Lemma 3.10

There exist $b_0>0$ and $\ell _0>0$ such that for $b\ge b_0$ and $\ell \ge \ell _0$ one has

$$\begin{aligned}&\frac{1}{4}\sum _{j=0}^1\,{\mathsf {Re}}\,( R^n\,W^{n+j} \,U^n,\, W^{n+j} \,G^n\,U^n) \le -\frac{b}{16}\sum _{j=0}^1\Vert \langle {D}\rangle _{\ell }^{\rho /2}\,W^{n+j}\,U^n\Vert ^2\\&\quad +\frac{b}{2} \sum _{i=0}^1\sum _{j=0}^1\big (\mathrm{Op}(\langle {\xi }\rangle ^{\rho }_{\ell }R^n)\,W^{n+i}\,u^{n+j},\,W^{n+i}\,u^{n+j}\big ). \end{aligned}$$

Next estimate $\sum _{i=0}^1{\mathsf {Re}}\,(W^{n+i}R^nW^{n+i}f^n,\,U^n)$. Since $R^n\in {\tilde{S}}^{2\nu }_{\rho -\nu ,1-\rho +\nu }$, it follows that

$$\begin{aligned}&\big |\sum _{i=0}^1\big (W^{n+i}R^n W^{n+i}f^n,\, U^n\big )\big |\\&\quad \le \sum _{i=0}^1\Vert \langle {D}\rangle _{\ell }^{-\rho /2}\,R^nW^{n+i}f^n\Vert \Vert \langle {D}\rangle _{\ell }^{\rho /2}\,W^{n+i}U^n\Vert \\&\quad \le \frac{b}{16}\sum _{i=0}^1\Vert \langle {D}\rangle _{\ell }^{\rho /2}\,W^{n+i}\,U^n\Vert ^2 +\frac{C}{b}\sum _{i=0}^1\Vert \langle {D}\rangle _{\ell }^{2\nu -\rho /2}\,W^{n+i}\,f^n\Vert ^2 . \end{aligned}$$

Equation (3.24) implies that $-\nu >2\nu -\rho /2$ so

$$\begin{aligned}&\frac{1}{2}\sum _{i=0}^1{\mathsf {Re}}\,( W^{n+i} R^nW^{n+i}f^n,\,U^n) \nonumber \\&\quad \le \frac{b}{32}\sum _{i=0}^1\Vert \langle {D}\rangle _{\ell }^{\rho /2}\,W^{n+i}\,U^n\Vert ^2 +\frac{C}{b}\sum _{i=0}^1\Vert \langle {D}\rangle _{\ell }^{-\nu }\,W^{n+i}\,f^n\Vert ^2. \end{aligned}$$

(3.33)

Lemma 3.10 together with (3.12) and (3.33) yield the following proposition.

Proposition 3.11

There exist $C>0$, $b_0>0$ and $\ell _0>0$ such that for $b\ge b_0$ and $\ell \ge \ell _0$ one has

$$\begin{aligned} (II)\&\le \ -\frac{b}{32}\sum _{i=0}^1\Vert \langle {D}\rangle _{\ell }^{\rho /2}\, W^{n+i}\,U^n\Vert ^2\\&\quad +\frac{b}{2} \sum _{i=0}^1 \sum _{j=0}^1\big (\mathrm{Op}(\langle {\xi }\rangle ^{\rho }_{\ell }R^n)\,W^{n+i}\,u^{n+j},\,W^{n+i}\,u^{n+j}\big )\\&\quad +\frac{C}{b}\sum _{i=0}^1\Vert \langle {D}\rangle _{\ell }^{-\nu }\,W^{n+i}\,f^n\Vert ^2. \end{aligned}$$

3.6 Proof of Theorem 2.4

First choose $b={\bar{b}}$ and $\ell _1$ such that Propositions 3.8 and 3.11 and (3.27) hold with $b={\bar{b}}$ and $\ell \ge \ell _1$. Next choose $a={\bar{a}}$ such that $c\,{\bar{a}}\ge {\bar{b}}/2$ then taking (3.27) into account it follows from Propositions 3.8 and 3.11 that

$$\begin{aligned}&(I)+(II) \le -c\,{\bar{a} }\sum _{i=0}^1\sum _{j=0}^1\Vert \langle {D}\rangle _{\ell }^{-\nu +\rho /2}\,W^{n+i}\,u^{n+j}\Vert ^2 \nonumber \\&\quad -c'\,{\bar{b}}\sum _{i=0}^1\Vert \langle {D}\rangle _{\ell }^{\rho /2}\,W^{n+i}\,U^n\Vert ^2 +C{\bar{b}}^{-1}\sum _{i=0}^1\Vert \langle {D}\rangle _{\ell }^{-\nu }\,W^{n+i}\,f^n\Vert ^2. \end{aligned}$$

(3.34)

Finally we estimate (III). Thanks to Lemma 3.5 one has

(3.35)

Increase ${\bar{a}}$ if necessary so that $c\,{\bar{a}}\ge 2C'\,{\bar{b}}^{-1}$, in view of (3.34) and (3.35), recalling (3.13), we conclude that

$$\begin{aligned}&\delta _k(R^nW^nu^n,\,W^nu^n)\le -\frac{c}{2}{\bar{a}}\sum _{i=0}^1\sum _{j=0}^1\Vert \langle {D}\rangle _{\ell }^{-\nu +\rho /2}\,W^{n+i}\,u^{n+j}\Vert ^2 \nonumber \\&\quad -c'\,{\bar{b}}\sum _{i=0}^1\Vert \langle {D}\rangle _{\ell }^{\rho /2}\,W^{n+i}\,U^n\Vert ^2+C\,{\bar{b}}^{-1}\sum _{i=0}^1\Vert \langle {D}\rangle _{\ell }^{-\nu }\,W^{n+i}\,f^n\Vert ^2. \end{aligned}$$

(3.36)

Noting (3.23) and (3.19) we set

$$\begin{aligned} \ell _2\ :=\ \max {\{{\bar{a}}^{6/\rho },\, {\bar{b}}^{1/(1-\rho )},\, \ell _1\}}. \end{aligned}$$

In what follows we assume $\ell \ge \ell _2$. Taking (3.1) into account define

$$\begin{aligned} {\bar{\beta }} \ :=\ \min {\{1/2\,{\bar{C}},\,\log {2}/3\,{\bar{a}}\}}. \end{aligned}$$

Note that $\Vert \langle {D}\rangle _{\ell }^{-\nu }\,W^{n+1}\,f^n\Vert \le \Vert \langle {D}\rangle _{\ell }^{-\nu }\,W^{n}\,f^n\Vert$ thanks to (3.2). Summing (3.36) from 0 to $n-1$ yields

$$\begin{aligned}&(R^nW^nu^n,\,W^n u^n)+k\,\,\frac{c}{2}\,{\bar{a}}\sum _{p=0}^{n}\Vert \langle {D}\rangle _{\ell }^{-\nu +\rho /2}W^p u^p\Vert \nonumber \\&\quad \le \ (R\,W^0u^0,\, W^0u^0)+C\,k\sum _{p=0}^{n-1}\Vert \langle {D}\rangle _{\ell }^{-\nu }\,W^{p}\,f^p\Vert ^2. \end{aligned}$$

(3.37)

Since $W^p=e^{({\bar{\tau }}-{\bar{a}}t_p)\langle {D}\rangle _{\ell }^{\rho }\chi _h}$ with $\chi _h=1$ on $\mathrm{supp}\,\chi _{2h}$, and recalling (2.8), it follows from (3.27) and (3.37) that

$$\begin{aligned}&\Vert \langle {D}\rangle _{\ell }^{-\nu }\,e^{({\bar{\tau }}-{\bar{a}}t_n)\langle {D}\rangle _{\ell }^{\rho }}\, u^n\Vert ^2 +c\,k\,{\bar{a}}\sum _{p=0}^n\Vert \langle {D}\rangle _{\ell }^{-\nu +\rho /2}e^{({\bar{\tau }}-{\bar{a}}t_p)\langle {D}\rangle _{\ell }^{\rho }}u^p\Vert ^2 \\&\quad \le C\Vert \langle {D}\rangle _{\ell }^{\nu }\, e^{{\bar{\tau }}\langle {D}\rangle _{\ell }^{\rho }}u^0\Vert ^2 +C\,k\sum _{p=0}^{ n-1}\Vert \langle {D}\rangle _{\ell }^{-\nu }\,e^{({\bar{\tau }}-{\bar{a}}t_p)\langle {D}\rangle _{\ell }^{\rho }}f^p\Vert ^2. \end{aligned}$$

Equation (3.24) implies that $\rho /2-\nu >2\nu$ yielding the following proposition.

Proposition 3.12

There exist ${\bar{\tau }}>0$, ${\bar{a}}>0$, ${\bar{\beta }}>0$, $C>0$ and ${\bar{\ell }}\,(\ge \ell _2 )$ such that one has

$$\begin{aligned}&\Vert \langle {D}\rangle _{\ell }^{-\nu }e^{({\bar{\tau }}-{\bar{a}}t_n)\langle {D}\rangle _{\ell }^{\rho }}u^n\Vert ^2+k\,{\bar{a}}\sum _{p=0}^n\Vert \langle {D}\rangle _{\ell }^{2\nu }e^{({\bar{\tau }}-{\bar{a}}t_p)\langle {D}\rangle _{\ell }^{\rho }}u^p\Vert ^2 \nonumber \\&\quad \le C\Vert \langle {D}\rangle _{\ell }^{\nu }e^{{\bar{\tau }}\langle {D}\rangle _{\ell }^{\rho }}g\Vert ^2 +C\,k\,\sum _{p=0}^{ n-1}\Vert \langle {D}\rangle _{\ell }^{-\nu }e^{({\bar{\tau }}-{\bar{a}}t_p)\langle {D}\rangle _{\ell }^{\rho }}f^p\Vert ^2 \nonumber \\&\quad \le C\Vert \langle {D}\rangle _{\ell }^{\nu }e^{{\bar{\tau }}\langle {D}\rangle _{\ell }^{\rho }}g\Vert ^2 +C\,({\bar{\tau }}/{\bar{a}})\sup _{0\le p\le n-1}\Vert \langle {D}\rangle _{\ell }^{-\nu }e^{({\bar{\tau }}-{\bar{a}}t_p)\langle {D}\rangle _{\ell }^{\rho }}f^p\Vert ^2 \qquad \qquad \end{aligned}$$

(3.38)

for any $n\in \mathbb {N}$, $k>0, \ell>0, h>0$ satisfying $nk\le {\bar{\tau }}/{\bar{a}}$, $kh^{-1}\le {\bar{\beta }}$ and $h^{-1}\ge \ell \ge {\bar{\ell }}$.

Remark 3.2

To obtain Proposition 3.12 the spectral condition $\chi _{h}u^n=u^n$ is assumed while for $f^n$ no spectral condition is assumed.

Proof of Theorem 2.4

Fix $\ell ={\bar{\ell }}$ in Proposition 3.12. Since

$$\begin{aligned} \langle {\xi }\rangle ^{\rho }\le \langle {\xi }\rangle ^{\rho }_{{\bar{\ell }}}\le {\bar{\ell }}^{\rho }+\langle {\xi }\rangle ^{\rho },\quad \langle {\xi }\rangle \le \langle {\xi }\rangle _{{\bar{\ell }}}\le {\bar{\ell }}\,\langle {\xi }\rangle \end{aligned}$$

(3.39)

the proof is immediate. $\square$

4 Error estimates for the spectral Crank–Nicholson scheme

4.1 Continuous case revisited

Start by extending estimates (2.5) in Corollary 2.2 to $\partial _t^ju$ for $j=1,2$. It is clear that one can assume ${\bar{\tau }}\le T$ and ${\bar{a}}\ge {\hat{c}}$. Then it is easy to examine that Corollary 2.2 holds with $T={\bar{\tau }}$ and ${\hat{c}}={\bar{a}}$. Suppose $\partial _tu=Gu$. Write

$$\begin{aligned} \langle {D}\rangle _{\ell }^{\mu }G\langle {D}\rangle _{\ell }^{-\mu }=G+B_{\mu } \end{aligned}$$

so $\langle {D}\rangle _{\ell }^{\mu }u$ satisfies $\partial _t(\langle {D}\rangle _{\ell }^{\mu }u)=(G+B_{\mu })\langle {D}\rangle _{\ell }^{\mu }u$. The $B_\mu$ satisfy the following bounds.

Lemma 4.1

There is $A>0$ such that for any $\alpha , \beta \in \mathbb {N}^d$ one has

$$\begin{aligned} |\partial _{\xi }^{\alpha }\partial _x^{\beta }B_{\mu }(x,\xi )|\le C_{\alpha }A^{|\beta |}|\beta |!^s\langle {\xi }\rangle _{\ell }^{-|\alpha |}\langle {x}\rangle ^{-2d}. \end{aligned}$$

Proof

Up to a multiplicative constant $B_{\mu }$ is given by

$$\begin{aligned} B_{\mu }(x,\xi )&=\sum _{|\gamma |=1}\int e^{-iy\eta }\partial _{\eta }^{\gamma } \big (\langle {\xi +\eta /2}\rangle ^{\mu }\langle {\xi -\eta /2}\rangle ^{-\mu }\big )dyd\eta \\&\quad \times \int \partial _x^{\gamma }G(x+\theta y,\xi )d\theta . \end{aligned}$$

Therefore $\partial _{\xi }^{\alpha }\partial _x^{\beta }B_{\mu }$ is, after change of variables $x+\theta y\mapsto y$, $\theta ^{-1}\eta \mapsto \eta$, a sum of terms

$$\begin{aligned} \int e^{ix\eta }\partial _{\xi }^{\alpha '+\gamma }\big (\langle {\xi +\theta \eta /2}\rangle ^{\mu }\langle {\xi -\theta \eta /2}\rangle ^{-\mu }\big )dyd\eta \int e^{-iy\eta }\partial _{\xi }^{\alpha ''}\partial _x^{\gamma +\beta }G( y,\xi )d\theta \end{aligned}$$

with $\alpha '+\alpha ''=\alpha$. Recall that

$$\begin{aligned} \Big |\int e^{-iy\eta }\partial _{\xi }^{\alpha ''}\partial _x^{\gamma +\beta }G( y,\xi )d\theta \Big |\le C_{\alpha ''}\langle {\xi }\rangle _{\ell }^{1-|\alpha ''|}A^{|\beta |}|\beta |!^se^{-c\langle {\eta }\rangle ^{\rho }} \end{aligned}$$

with some $c>0$ (see [8, Lemma 6.2]). In addition, it is easy to see that

$$\begin{aligned} \big |\partial _{\eta }^{\delta }\partial _{\xi }^{\alpha '+\gamma }\big (\langle {\xi +\theta \eta /2}\rangle ^{\mu }\langle {\xi -\theta \eta /2}\rangle ^{-\mu }\big )\big |\le C_{\alpha ' \delta }\langle {\xi }\rangle _{\ell }^{-1-|\alpha '|}\langle {\eta }\rangle ^{2|\mu |+|\delta |+1+|\alpha '|}. \end{aligned}$$

Using $\langle {x}\rangle ^{2d}e^{ix\eta }=\langle {D_{\eta }}\rangle ^{2d}e^{ix\eta }$, an integration by parts in $\eta$ proves the assertion. $\square$

Thanks to Lemma 4.1 it follows from the proof of Proposition 3.3 that

$$\begin{aligned} e^{({\bar{\tau }}-{\bar{a}}t)\langle {\xi }\rangle _{\ell }^{\rho }}\#B_{\mu }\#e^{-({\bar{\tau }}-{\bar{a}}t)\langle {\xi }\rangle _{\ell }^{\rho }} \ \in \ {\tilde{S}}^0. \end{aligned}$$

Apply Corollary 2.2 to $\partial _tv=(G+B_{\mu })v$ with $v=\langle {D}\rangle _{\ell }^{\mu }u$ to find that choosing a smaller ${\bar{\tau }}>0$ and larger ${\bar{a}}>0$ and $\ell _0$ if necessary,

$$\begin{aligned} \Vert \langle {D}\rangle _{\ell }^{-\nu +\mu }e^{({\bar{\tau }}-{\bar{a}}t)\langle {D}\rangle _{\ell }^{\rho }}u(t)\Vert \le C \Vert \langle {D}\rangle _{\ell }^{\nu +\mu }e^{{\bar{\tau }}\langle {D}\rangle _{\ell }^{\rho }}u(0)\Vert \end{aligned}$$

(4.1)

for $0\le t\le {\bar{\tau }}/{\bar{a}}$ and $\ell \ge \ell _0$. Indeed in the proof of Proposition 2.1 the term B satisfies $e^{(T-{\hat{c}}t)\langle {\xi }\rangle _{\ell }^{\rho }}\#B\# e^{(T-{\hat{c}}t)\langle {\xi }\rangle _{\ell }^{\rho }}\in {\tilde{S}}^0$ so choosing ${\hat{c}}$ large, it is irrelevant. Write

$$\begin{aligned} \langle {D}\rangle _{\ell }^{\mu }e^{({\bar{\tau }}-{\bar{a}}t)\langle {D}\rangle _{\ell }^{\rho }}\partial _tu =\Big (e^{({\bar{\tau }}-{\bar{a}}t)\langle {D}\rangle _{\ell }^{\rho }}\,(G+B_{\mu })\,e^{-({\bar{\tau }}-{\bar{a}}t)\langle {D}\rangle _{\ell }^{\rho }}\Big )\langle {D}\rangle _{\ell }^{\mu }e^{({\bar{\tau }}-{\bar{a}}t)\langle {D}\rangle _{\ell }^{\rho }}u. \end{aligned}$$

Proposition 3.3 and Lemma 4.1 imply that $e^{({\bar{\tau }}-{\bar{a}}t)\langle {\xi }\rangle _{\ell }^{\rho }}\#(G+B_{\mu })\#e^{-({\bar{\tau }}-{\bar{a}}t)\langle {\xi }\rangle _{\ell }^{\rho }}\in {\tilde{S}}^1$. It follows that

$$\begin{aligned}&\Vert \langle {D}\rangle _{\ell }^{\mu }e^{({\bar{\tau }}-{\bar{a}}t)\langle {D}\rangle _{\ell }^{\rho }}\partial _tu(t)\Vert \ \le \ C'\Vert \langle {D}\rangle _{\ell }^{1+\mu }e^{({\bar{\tau }}-{\bar{a}}t)\langle {D}\rangle _{\ell }^{\rho }}u(t)\Vert \\&\quad \le \ C'C\Vert \langle {D}\rangle _{\ell }^{1+2\nu +\mu }e^{{\bar{\tau }}\langle {D}\rangle _{\ell }^{\rho }}u(0)\Vert \end{aligned}$$

from (4.1). Next assume that $A_j(t,x)$ and B(t, x) are $C^1$ in time uniformly on compact sets with values in $G^{s'}(\mathbb {R}^d)$. Since $\partial _t^2u=(\partial _tG)u+G\partial _tu$ repeating the same arguments one has

$$\begin{aligned}&\Vert \langle {D}\rangle _{\ell }^{\mu } e^{({\bar{\tau }}-{\bar{a}}t)\langle {D}\rangle _{\ell }^{\rho }}\partial _t^2u(t)\Vert \\&\quad \le \ C''\big (\Vert \langle {D}\rangle _{\ell }^{1+\mu }e^{({\bar{\tau }}-{\bar{a}}t)\langle {D}\rangle _{\ell }^{\rho }}u(t)\Vert \ +\Vert \langle {D}\rangle _{\ell }^{1+\mu }e^{({\bar{\tau }}-{\bar{a}}t)\langle {D}\rangle _{\ell }^{\rho }}\partial _tu(t)\Vert \big )\\&\quad \le \ C'''\Vert \langle {D}\rangle _{\ell }^{2+2\nu +\mu }e^{{\bar{\tau }}\langle {D}\rangle _{\ell }^{\rho }}u(0)\Vert . \end{aligned}$$

Choosing $\mu =-\nu +i$, $i=0,1,2$ one obtains the following lemma.

Lemma 4.2

Assume that $A_j(t,x)$ and B(t, x) are $C^1$ in time uniformly on compact sets with values in $G^{s'}(\mathbb {R}^d)$ and that $\partial _tu=Gu$. Then there exist $C>0$, $\ell _0>0$ such that

$$\begin{aligned} \Vert \langle {D}\rangle _{\ell }^{-\nu +i}e^{({\bar{\tau }}-{\bar{a}}t)\langle {D}\rangle _{\ell }^{\rho }}\partial _t^ju(t)\Vert \ \le \ C\Vert \langle {D}\rangle _{\ell }^{i+j+\nu }e^{{\bar{\tau }}\langle {D}\rangle _{\ell }^{\rho }}u(0)\Vert \end{aligned}$$

for $0\le t\le {\bar{\tau }}/{\bar{a}}$, $\ell \ge \ell _0$ and $0\le i,j\le 2$.

4.2 Error estimate for the spectral Crank–Nicholson scheme

Suppose that u(t, x) satisfies

$$\begin{aligned} \partial _tu(t,x)=G(t,x,D)u(t,x) \end{aligned}$$

(4.2)

where $G(t,x,D)=iA(t,x,D)+B(t,x)$. Denote ${\tilde{u}}=\chi _{2h} u$ so that $\chi _{h}{\tilde{u}}={\tilde{u}}$. Thus

$$\begin{aligned} \partial _t{\tilde{u}}=G{\tilde{u}}+f,\quad f=[\chi _{2h},G]u. \end{aligned}$$

(4.3)

Next estimate to what extent ${\tilde{u}}(t_n,x)$ satisfies the difference scheme. The error, denoted by $g(n)=g(n,\cdot )$, is given by

$$\begin{aligned} \frac{{\tilde{u}}(t_{n+1})-{\tilde{u}}(t_n)}{k} \ -\ G^n\,\frac{{\tilde{u}}(t_{n+1})+{\tilde{u}}(t_n)}{2} \ :=\ g(n) \end{aligned}$$

where $G^n=\chi _{2h}(iA(nk,x,D)+B(nk,x))\chi _{2h}$. Note that

$$\begin{aligned} \mathrm{supp}\,{\mathcal F}(g(n)) \ \subset \ \mathrm{supp}\,\chi _{2h}(\cdot ). \end{aligned}$$

(4.4)

The approximate solution $u^n=u^n_h$ satisfies

$$\begin{aligned} \frac{u^{n+1}-u^n}{k}-G^n\,\frac{u^{n+1}+u^n}{2}=0. \end{aligned}$$

At $t=0$ the approximate solution is equal to the spectral truncation of the exact solution, $u^0=\chi _{2h}g={\tilde{u}}(0)$.

Noting $\mathrm{supp}{\mathcal F}\big ({\tilde{u}}(t_n)-u^n\big )\subset \mathrm{supp}\,\chi _{2h}$ and hence $\chi _h({\tilde{u}}(t_n)-u^n)={\tilde{u}}(t_n)-u^n$, Proposition 3.12 implies

$$\begin{aligned} \Vert \langle {D}\rangle _{\ell }^{-\nu }\,W^n\,({\tilde{u}}(t_{n})-u^n)\Vert ^2 \ \le \ C\,k \sum _{l=0}^{ n-1} \Vert \langle {D}\rangle _{\ell }^{-\nu }\,W^l\,g(l)\Vert ^2 \end{aligned}$$

(4.5)

for any $t_n=kn\le {\bar{\tau }}/{\bar{a}}$.

Lemma 4.3

There is $C>0$ so that

$$\begin{aligned} \Vert \langle {D}\rangle _{\ell }^{-\nu }W^jg(j)\Vert \le C\,(k+h)\Vert \langle {D}\rangle ^{2+\nu }_{\ell }e^{{\bar{\tau }}\langle {D}\rangle ^{\rho }_{\ell }}u(0)\Vert \end{aligned}$$

for $0\le j\le n-1$ and $0\le t_n\le {\bar{\tau }}/{\bar{a}}$.

Proof

Use (4.3) to write

$$\begin{aligned} g(j) =g(j)-\big ({\tilde{u}}_t(t_j) - G(t_j){\tilde{u}}(t_j)-f(j)\big ). \end{aligned}$$

The triangle inequality yields

$$\begin{aligned}&\Vert \langle {D}\rangle _{\ell }^{-\nu }W^jg(j)\Vert \ \le \ \Big \Vert \langle {D}\rangle _{\ell }^{-\nu }W^j\Big (\frac{{\tilde{u}}(t_{j+1})-{\tilde{u}}(t_j)}{k} - {\tilde{u}}_t(t_j)\Big )\Big \Vert \nonumber \\&\quad +\Big \Vert \langle {D}\rangle _{\ell }^{-\nu }W^j\Big (G^j\Big (\frac{{\tilde{u}}(t_{j+1})+ {\tilde{u}}(t_j)}{2}-{\tilde{u}}(t_j)\Big )\Big )\Big \Vert \nonumber \\&\quad +\Vert \langle {D}\rangle _{\ell }^{-\nu }W^j\big (G(t_j)-G^j\big )\,{\tilde{u}}(t_j)\Vert +\Vert \langle {D}\rangle _{\ell }^{-\nu }W^jf(j)\Vert . \end{aligned}$$

(4.6)

Write

$$\begin{aligned} \langle {D}\rangle _{\ell }^{-\nu }W^j\left( \frac{{\tilde{u}}(t_{j+1})-{\tilde{u}}(t_j)}{k} - {\tilde{u}}_t(t_j)\right) =\frac{1}{k}\int _{t_j}^{t_{j+1}}ds\int _{t_j}^s\langle {D}\rangle _{\ell }^{-\nu }W^j\partial _t^2{\tilde{u}}(s')ds' \end{aligned}$$

and note that

$$\begin{aligned} W^j\partial _t^2{\tilde{u}}(s')=e^{{\bar{a}}(s'-t_j)\langle {D}\rangle _{\ell }^{\rho }\chi _h}e^{({\bar{\tau }}-{\bar{a}}s')\langle {D}\rangle _{\ell }^{\rho }\chi _h}\partial _t^2{\tilde{u}}(s'). \end{aligned}$$

Since $0\le s'-t_j\le k$ if $t_j\le s'\le t_{j+1}$ it follows from (3.2) that

$$\begin{aligned}&\Vert \langle {D}\rangle _{\ell }^{-\nu }W^j\partial _t^2{\tilde{u}}(s')\Vert \le 2\Vert \langle {D}\rangle _{\ell }^{-\nu }e^{({\bar{\tau }}-{\bar{a}}s')\langle {D}\rangle _{\ell }^{\rho }\chi _h}\partial _t^2{\tilde{u}}(s')\Vert \\&\quad \le 2\Vert \langle {D}\rangle _{\ell }^{-\nu }e^{({\bar{\tau }}-{\bar{a}}s')\langle {D}\rangle _{\ell }^{\rho }}\partial _t^2{ u}(s')\Vert \le C\Vert \langle {D}\rangle _{\ell }^{2+\nu }e^{{\bar{\tau }}\langle {D}\rangle _{\ell }^{\rho }}u(0)\Vert \end{aligned}$$

thanks to Lemma 4.2. Therefore one has

$$\begin{aligned} \left\| \langle {D}\rangle _{\ell }^{-\nu }W^j\left( \frac{{\tilde{u}}(t_{j+1})-{\tilde{u}}(t_j)}{k} - {\tilde{u}}_t(t_j)\right) \right\| \le C\,k\,\Vert \langle {D}\rangle _{\ell }^{2+\nu }e^{{\bar{\tau }}\langle {D}\rangle _{\ell }^{\rho }}u(0)\Vert . \end{aligned}$$

Turn to the second term on the right-hand side of (4.6). Use

$$\begin{aligned} \langle {D}\rangle _{\ell }^{-\nu }W^j\left( G^j\left( \frac{{\tilde{u}}(t_{j+1})+{\tilde{u}}(t_j)}{2}-{\tilde{u}}(t_j)\right) \right) =\frac{1}{2}\int _{t_j}^{t_{j+1}}\langle {D}\rangle _{\ell }^{-\nu }W^jG^j\partial _t{\tilde{u}}(s')ds' \end{aligned}$$

to write

$$\begin{aligned} \langle {D}\rangle _{\ell }^{-\nu }W^jG^j=\langle {D}\rangle _{\ell }^{-\nu }W^jG^jW^{-j}\big (W^{j}e^{-({\bar{\tau }}-{\bar{a}}s')\langle {D}\rangle _{\ell }^{\rho }\chi _h}\big )e^{({\bar{\tau }}-{\bar{a}}s')\langle {D}\rangle _{\ell }^{\rho }\chi _h}. \end{aligned}$$

Proposition 3.3 implies that $\langle {\xi }\rangle _{\ell }^{-\nu }\#W^j\#G^j\#W^{-j}\in {\tilde{S}}^{1-\nu }$. In addition, $W^je^{-({\bar{\tau }}-{\bar{a}}s')\langle {D}\rangle _{\ell }^{\rho }\chi _h}=e^{{\bar{a}}(s'-t_j)\langle {D}\rangle _{\ell }^{\rho }\chi _h}$ when $0\le s'-t_j\le k$. Repeat the same arguments as above to find

$$\begin{aligned} \Vert \langle {D}\rangle _{\ell }^{-\nu }W^jG^j\partial _t{\tilde{u}}(s')\Vert \ \le \ C\Vert \langle {D}\rangle _{\ell }^{2+\nu }e^{{\bar{\tau }}\langle {D}\rangle _{\ell }^{\rho }}u(0)\Vert \quad \mathrm{for} \quad t_j\le s'\le t_{j+1}. \end{aligned}$$

Then

$$\begin{aligned} \left\| \langle {D}\rangle _{\ell }^{-\nu }W^j\left( G^j\left( \frac{{\tilde{u}}(t_{j+1})+{\tilde{u}}(t_j)}{2}-{\tilde{u}}(t_j)\right) \right) \right\| \le C\,k\,\Vert \langle {D}\rangle _{\ell }^{2+\nu }e^{{\bar{\tau }}\langle {D}\rangle _{\ell }^{\rho }}u(0)\Vert . \end{aligned}$$

Next study the third and fourth term on the right-hand side of (4.6).

Lemma 4.4

Let $\alpha \ge 0$. There is $C>0$ such that

$$\begin{aligned} \Vert (I-\chi _{2 h})u\Vert \le C\,h^{\alpha }\Vert \langle {D}\rangle _{\ell }^{\alpha }u\Vert . \end{aligned}$$

Proof

Since $1-\chi _{2h}(\xi )=0$ unless $|\xi |\ge h^{-1}$ one has

$$\begin{aligned} \Vert (I-\chi _{2 h})u\Vert ^2&=\int (1-\chi _{2 h}(\xi ))^2\langle {\xi }\rangle ^{-2\alpha }_{\ell }\langle {\xi }\rangle _{\ell }^{2\alpha }|{\hat{u}}(\xi )|^2d\xi \\&\le Ch^{2\alpha }\int \langle {\xi }\rangle ^{2\alpha }_{\ell }|{\hat{u}}(\xi )|^2d\xi = C\Big (h^{\alpha }\Vert \langle {D}\rangle _{\ell }^{\alpha }u\Vert \Big )^2 \end{aligned}$$

which proves the assertion. $\square$

Since $G^j-G(t_j)=\chi _{2h}G(t_j)(\chi _{2h}-I)+(\chi _{2h}-I)G(t_j)$ one can write

$$\begin{aligned} \langle {D}\rangle _{\ell }^{-\nu }W^j(G^j-G(t_j))=\chi _{2h}\big (\langle {D}\rangle _{\ell }^{-\nu }W^jG(t_j)W^{-j}\big )(\chi _{2h}-I)W^j\\ +(\chi _{2h}-I)\big (\langle {D}\rangle _{\ell }^{-\nu }W^jG(t_j)W^{-j}\big )W^j. \end{aligned}$$

Using $\langle {\xi }\rangle _{\ell }^{-\nu }\#W^j\#G(t_j)\#W^{-j}\in {\tilde{S}}^{1-\nu }$ together with Lemma 4.4 one finds

$$\begin{aligned}&\Vert \langle {D}\rangle _{\ell }^{-\nu }W^j(G^j-G(t_j)){\tilde{u}}(t_j)\Vert \\&\quad \le C\,\Vert \langle {D}\rangle _{\ell }^{1-\nu }(\chi _{2h}-I)W^j{\tilde{u}}(t_j)\Vert +C\,h\,\Vert \langle {D}\rangle _{\ell }^{1-\nu }W^jG(t_j)W^{-j}W^j{\tilde{u}}(t_j)\Vert \\&\quad \le C'\,h\,\Vert \langle {D}\rangle _{\ell }^{2-\nu }W^j{\tilde{u}}(t_j)\Vert \le C'\,h\,\Vert \langle {D}\rangle _{\ell }^{2-\nu }e^{({\bar{\tau }}-{\bar{a}}t_j)\langle {D}\rangle _{\ell }^{\rho }}u(t_j)\Vert . \end{aligned}$$

Therefore by Lemma 4.2,

$$\begin{aligned} \Vert \langle {D}\rangle _{\ell }^{-\nu }W^j(G^j-G(t_j)){\tilde{u}}(t_j)\Vert \le C\,h\,\Vert \langle {D}\rangle _{\ell }^{2+\nu }e^{{\bar{\tau }}\langle {D}\rangle _{\ell }^{\rho }}u(0)\Vert . \end{aligned}$$

Turn to $f(j):=[\chi _{2h},G(t_j)]u(t_j)$. Since

$$\begin{aligned} {[}\chi _{2h},G(t_j)]=\chi _{2h}G(t_j)(I-\chi _{2h})-(I-\chi _{2h})G(t_j)\chi _{2h} \end{aligned}$$

repeating the same arguments as above one obtains that

$$\begin{aligned} \Vert \langle {D}\rangle _{\ell }^{-\nu }W^jf(j)\Vert \le C\,h\,\Vert \langle {D}\rangle _{\ell }^{2+\nu }e^{{\bar{\tau }}\langle {D}\rangle _{\ell }^{\rho }}u(0)\Vert . \end{aligned}$$

This finishes the proof of Lemma 4.3. $\square$

4.3 Proof of Theorem 2.5

Noting that $\mathrm{supp}{\mathcal {F}}\big ({\tilde{u}}(t_n)-u^n\big )\subset \mathrm{supp}\,\chi _{2h}$ and $\chi _h=1$ on the support of $\chi _{2h}$ it follows from (4.5) and Lemma 4.3 that

$$\begin{aligned}&\Vert \langle {D}\rangle _{\ell }^{-\nu }\,e^{({\bar{\tau }}-{\bar{a}}t_n)\langle {D}\rangle _{\ell }^{\rho }}\,({\tilde{u}}(t_{n})-u^n)\Vert \nonumber \\&\quad \le \ C\,\sqrt{{\bar{\tau }}/{\bar{a}}}\,(k+h)\Vert \langle {D}\rangle ^{2+\nu }_{\ell }e^{{\bar{\tau }}\langle {D}\rangle ^{\rho }_{\ell }}u(0)\Vert . \end{aligned}$$

(4.7)

Since $\langle {\xi }\rangle _{\ell }\le \sqrt{3}h^{-1}$ on the support of $\chi _{2h}$, (4.7) implies that

$$\begin{aligned} \Vert e^{({\bar{\tau }}-{\bar{a}}t_n)\langle {D}\rangle _{\ell }^{\rho }}\,({\tilde{u}}(t_{n})-u^n)\Vert \le C\,\sqrt{{\bar{\tau }}/{\bar{a}}}\,(k+h)h^{-\nu }\Vert \langle {D}\rangle ^{2+\nu }_{\ell }e^{{\bar{\tau }}\langle {D}\rangle ^{\rho }_{\ell }}u(0)\Vert . \end{aligned}$$

(4.8)

Finally estimate $\Vert \langle {D}\rangle _{\ell }^{-\nu }W^n(u(t_n)-{\tilde{u}}(t_n))\Vert$. Since $u(t_n)-{\tilde{u}}(t_n)=(1-\chi _{2h})u(t_n)$ the same arguments as above prove that

$$\begin{aligned} \Vert \langle {D}\rangle _{\ell }^{-\nu }\,e^{({\bar{\tau }}-{\bar{a}}t_n)\langle {D}\rangle _{\ell }^{\rho }}\,(u(t_n)-{\tilde{u}}(t_n))\Vert \ \le \ Ch^2\Vert \langle {D}\rangle _{\ell }^{2+\nu }e^{{\bar{\tau }}\langle {D}\rangle _{\ell }^{\rho }}u(0)\Vert . \end{aligned}$$

(4.9)

Similarly one has

$$\begin{aligned} \Vert e^{({\bar{\tau }}-{\bar{a}}t_n)\langle {D}\rangle _{\ell }^{\rho }}\,(u(t_n)-{\tilde{u}}(t_n))\Vert \ \le \ Ch^{2-\nu }\Vert \langle {D}\rangle _{\ell }^{2+\nu }e^{{\bar{\tau }}\langle {D}\rangle _{\ell }^{\rho }}u(0)\Vert . \end{aligned}$$

(4.10)

Combining (4.7), (4.8) and (4.9), (4.10) yields the following proposition.

Proposition 4.5

There exist ${\bar{\tau }}>0, {\bar{a}}>0, {\bar{\beta } }>0, C>0$ and ${\bar{\ell }}>0$ such that for any exact solution u to (4.2) with Cauchy data u(0) such that $\langle {D}\rangle ^{2+\nu }_{\ell }e^{{\bar{\tau }}\langle {D}\rangle _{\ell }^{\rho }}u(0)\in L^2$ one has

$$\begin{aligned} \Vert \langle {D}\rangle _{\ell }^{-\nu }e^{({\bar{\tau }}-{\bar{a}}t_n)\langle {D}\rangle _{\ell }^{\rho }}(u(t_n)-u^n)\Vert \le C\,(k+h)\Vert \langle {D}\rangle _{\ell }^{2+\nu }e^{{\bar{\tau }}\langle {D}\rangle _{\ell }^{\rho }}u(0)\Vert \end{aligned}$$

and

$$\begin{aligned} \Vert e^{({\bar{\tau }}-{\bar{a}}t_n)\langle {D}\rangle _{\ell }^{\rho }}(u(t_n)-u^n)\Vert \le C\,(k+h)h^{-\nu }\Vert \langle {D}\rangle _{\ell }^{2+\nu }e^{{\bar{\tau }}\langle {D}\rangle _{\ell }^{\rho }}u(0)\Vert \end{aligned}$$

for any $0\le t_n=nk\le {\bar{\tau }}/{\bar{a}}$, $kh^{-1}\le {\bar{\beta }}$ and $h^{-1}\ge \ell \ge {\bar{\ell }}$.

Remark 4.1

In order for a difference approximation to be accurate, the time discretization must be taken sufficiently fine [6]. Here Proposition 4.5 shows that one could constrain k to satisfy a CFL type condition $kh^{-1}\le {\bar{\beta }}$. More precisely, the proof shows that it suffices to constrain k to satisfy

$$\begin{aligned} kh^{-1}\le 1/2{\bar{C}},\quad kh^{-\rho }\le \log {2}/3{\bar{a}}. \end{aligned}$$

Proof of Theorem 2.5

Taking (3.39) into account it is enough to choose $\ell ={\bar{\ell }}$ in Proposition 4.5. $\square$