1 Introduction

The development of mathematical creativity is frequently seen as both a means and a goal in education. However, there is no consensus concerning the definition of mathematical creativity and its framework of study. Despite this conceptual ambiguity, educational research efforts were often oriented towards proposing frameworks for assessing creativity, especially through problem posing and problem solving.

Rather than looking for a summative indicator, in this paper we propose the construct of Geometry-problem-posing cognitive style as an expression of personal traits within mathematical competence and we use it to look at prospective teachers’ mathematical creativity. Specifically, we were interested in answering the following questions: what kind of tool could provide information about mathematical creativity of university students in problem-posing contexts? How could we assess students’ levels of creativity in this case?

The answers to these questions are drawn from explorations situated at the crossroads between careful analysis of students’ products from a mathematical point of view, and their interpretations using tools of cognitive psychology. Preliminary results of this study have been published in the Proceedings of the 9th Mathematical Creativity and Giftedness Conference (Singer et al. 2015b).

2 Theoretical framework

2.1 Cognitive style

Cognitive style has been defined as a stable dimension that delineates consistencies in how individuals process information across tasks (Ausburn and Ausburn 1978). In a comprehensive review, Kozhevnikov (2007) considers that cognitive styles represent relatively stable heuristics that individuals use to process information from their environment. These heuristics can be identified at multiple levels of information processing, from basic perception to metacognitive approaches, and they can be grouped according to the type of regulatory function they exert on processes ranging from automatic data encoding to conscious executive allocation of cognitive resources. In addition, a range of variables, such as intellectual abilities, previous experience, habits, and personality traits, influence the development of a particular cognitive style.

Cognitive styles mediate the relation between an individual and his or her environment, having an adaptive dialectic functioning. Thus, although styles are generally stable individual characteristics, they may also change or develop in response to specific environmental circumstances (Kozhevnikov 2007).

Although controversial, we refer further to Gregorc’s research because it played a role in inspiring the manner in which we analyzed our data and the way we have represented the results. Gregorc (1979, 1982) viewed learning style as a pattern composed of distinctive behaviors which serve as indicators of how a person learns from and adapts to his/her environment. Gregorc’s Mediation Ability Theory assumes that the human mind is an active and goal-oriented decision maker, and the model of learning style he developed is meant to express each individual’s unique capacities.

More recent research on cognitive styles tries to integrate patterns of cognitive behavior and personality features into meta-styles characterizing individual resources for self-monitoring and regulation of cognitive functioning (Riding 2001; Riding and Al-Sanabani 1998; Sternberg and Grigorenko 1997). Further data (e.g., Zhang and Sternberg 2001) revealed significant correlations among thinking styles, personality characteristics, socioeconomic status, and situational characteristics. In addition, a style manifestation may depend on the stylistic demands of a specific task (Kozhevnikov 2007).

The perspective presented above is appropriate for our research approach because it allows organizing our explorations towards structuring a tool that functions based on deducing cognitive traits through the analysis of students’ products. As master students enrolled in a mathematics program, it may be likely that, in many cases, the participants in our study had already consolidated specific cognitive styles that can be depicted by exposing these students to tasks that combine freedom and constraints so that their intellectual behavior is uncovered. However, in this paper, we are focused on a limited spectrum of cognitive features, more specifically those related to processing geometry problems in problem posing (PP) contexts.

As suggested by Borromeo Ferri and Kaiser (2003), mathematical thinking style can be reconstructed as a distinct psychological construct. Compared to the cited study, which uses a problem solving context, in the present paper we try to describe cognitive styles in a problem posing context, and to identify links between PP cognitive style and creativity. Such links might exist in students at university level: for example, Moutsios-Rentzos and Simpson (2010) found that a specific thinking style in mathematics university students can be identified, and that there exist some connections between studying mathematics at university level, and originality and freedom in thinking, i.e. connections between specific cognitive styles and creativity.

2.2 Creativity in PP contexts

Usually, creativity is studied starting from Torrance’s tests (Torrance 1974), which are based on four related components: fluency, flexibility, novelty, and elaboration. Starting from Torrance’s work, various frameworks for studying creativity have been generated, usually adapted to specific types of tasks and contexts.

Some researchers (e.g., Jay and Perkins 1997) claim that problem posing may stimulate creativity, possibly even more than problem solving. Singer et al. (2013, 2015a) advocate that problem posing can enhance students’ engagement in authentic mathematical activity and open students’ thinking towards new ideas and approaches.

In the present paper, we use a framework based on organizational theory to study creativity in a problem posing context (Pelczer et al. 2013; Singer et al. 2011; Singer 2012; Voica and Singer 2011, 2013, 2014). This framework relies on the concept of cognitive flexibility, described in terms of the following: cognitive variety, cognitive novelty, and changes in cognitive framing. In the problem-posing context, we consider that a student manifests cognitive flexibility when she or he poses different new problems starting from a given input (i.e., cognitive variety), generates new proposals that are far from the starting item (i.e., cognitive novelty), and is able to change his/her mental frame in solving problems or identifying/discovering new ones (i.e., change in cognitive framing). Thus, cognitive flexibility arises as a complex, non-linear interplay between these dimensions. Consequently, the construct of cognitive flexibility opens up the possibility of capturing different ways of being creative, namely through the differing loads on the three dimensions.

The sociological perspective of this framework has proved to be effective in PP contexts where problems reflect the process results not only as mathematical content, but also as the proposer’s attitudes and affect towards that content and context. This feature of the framework, of capturing aspects related to the proposer’s personality, represented for us a supplementary argument that it is relevant to be used in the study of creativity within the present research.

3 Methodology

3.1 Sample and data

Students-prospective teachers in their last year of a master’s program in Mathematics, participants in a course in Mathematics Education, were asked to pose problems starting from a context rich in geometrical properties. More precisely, the following task was presented to students:

To make students familiar with the given figure, but also to show that this figure offers a rich geometrical context, the teacher indicated and solved an example of a problem emerging from it:

Initially, six students (out of the eighteen students enrolled in this course) responded to the task. We repeated the call a year later, under identical circumstances (i.e., prospective teachers in mathematics, in their last year of a master’s program, and the same initial geometrical context and requirements). At this call, 7 students answered (out of the 9 students enrolled in the course). In all, in the two successive years, 13 students responded to the task, generating a total of 243 problems. Each of these students proposed at least 9 problems, and there is a student who generated 50 problems. These 13 students represent our sample.

After the primary processing of data, we addressed further questions and tasks to some of the students in the sample, for a better understanding of some aspects revealed during this process. In general, the added questions were of the following type:

  • How did you generate, starting from the given configuration, the figure on page…?

  • For your problem…, what additional elements are needed in the text in order to have a definite answer?

We included the problems provided by the students in this second phase in the analysis of their products. Finally, for better documenting their preferences, strengths and weaknesses, as well as their creative manifestations in other contexts, we compared the problem analysis with elements related to the meta-context (information about students’ academic performance, their teaching experience, class observations, etc.).

3.2 Criteria for data analysis

As discussed above, cognitive style refers to typical ways in which individuals organize their environment conceptually. The cognitive style is a hypothetical construct developed to explain the process of mediation between stimuli and responses.

Crespo (2003) uses the term “problem posing style” in relation to proposers’ views on and beliefs about mathematics problems and mathematical errors. Within the present research, the students generated products that revealed certain ways of perceiving and processing the given information, ways that can be better depicted from a good design of the parameters to be studied. We thus searched for criteria to characterize individual differences in geometry PP contexts. We identified three criteria, which are briefly described below.

Validity. For the validity criterion, we adapted the definitions used by Singer and Voica (2013) to the situation described in this paper. Thus, the students’ posed problems were analyzed in terms of their coherence and consistency.

The coherence of a problem refers to its syntax; more precisely it refers to the rules and principles that govern the structure of a mathematical problem (Singer and Voica 2015; Voica and Singer 2013). Within the context of this paper, the coherence is related to the explicit definition of the new elements added by the proposer to the initial configuration. A problem was considered as being coherent if its elements were defined explicitly or were marked on the drawing so as to avoid ambiguities.

The consistency of a problem refers to its semantics; more precisely, it refers to the existence of mathematically meaningful links among the elements of the problem. In the context of this paper, consistency also means a meaningful correlation of the new posed problems with the underlying configuration of the starting problem.

Geometric nature. The second criterion is a domain-specific one that takes into account the nature of the posed problems related to the geometrical context. We called this criterion the Geometric nature (GN) of the posed problems. The posed-problems GN is a bi-polar criterion, based on two opposite features: metric and qualitative. The metric posed problems are those that require finding sizes and the solving necessarily implies the use of specific computing formulas. The qualitative posed problems are those requiring the use of geometrical reasoning based on congruence without appealing to (explicit) metric calculations.

Conceptual dispersion. The third criterion captures the manner by which the filtering and processing of stimuli allows the environment to take on psychological meaning in a student’s mind. As compared to GN, which reflects the nature of the problem, this criterion reflects students’ personalized answers when facing the given task. We found that, in our sample, students’ strategies varied from a rigorously organized approach (named structured), to a random, fuzzy one (named entropic). For describing this spectrum of strategies, we introduced the term conceptual dispersion (CD) as a third criterion. This is also a bi-polar criterion, underlying two opposite features: structured versus entropic.

A student’s list of problems shows structured conceptual dispersion when the set of posed problems denotes an approach that is systematic, structured, planned, patterned, and rigorously organized. More specifically, this criterion is met when the student’s posed problems are organized within clearly defined structures, systematically exploiting a configuration, and incrementally going within sub-configurations.

We talk about an entropic conceptual dispersion when the set of posed problems shows an approach that is unsystematic, or arbitrary, and eventually extended beyond the given context. More specifically, this criterion is met when the student’s posed problems are disconnected to each other or to a prior mathematical model, denoting random distribution of ideas, with large leaps from one configuration to another.

The criteria described above may be thought of as independent in the sense that the classification of individuals on one criterion does not affect their classification based on another. By identifying these criteria, we found traits that could be used to describe students’ behavior in problem posing situations. We thus introduce the term geometry-problem-posing cognitive style to characterize individual differences in geometry PP contexts.

In general, we observed that as students started to apply a certain strategy, they followed it in a consequent manner. This reinforces the existence of a durable approach that goes beyond the specificity of posing a certain problem. It belongs to a bird’s eye view of the task—an aspect that suggests also considering a metacognitive dimension. Consequently, we needed to relate cognitive style to metacognitive functioning. A metacognitive dimension was discussed in the cognitive style literature (e.g., Kozhevnikov 2007), and it is consistent with our approach, as revealed by the data.

3.3 Problem classification: some relevant examples

To make more transparent the classification procedures based on the above three criteria, we include below, as examples, five of the problems posed by one of the students. (The problems were proposed in the listed order and refer to Fig. 1.) We selected these examples because we found in this list coming from the same student all types of needed exemplars for all the criteria. In addition, it was important to select examples from only one student to illustrate the CD criterion, which captures relations between problems from the same proposer.

Fig. 1
figure 1

The drawing used by one of the students as an iconic support for the posed problems

Full size image

Example 1: Prove that the diagonals of quadrilateral CEAE’ are orthogonal.

Example 2: Prove that FEO’O is a rectangular trapezoid.

Example 3: Prove that area of the triangle AOD is equal to OE2.

Example 4: Prove that EOʹ =  \(\frac{\sqrt 7 }{4}\) OC.

Example 5: Prove that the area of the triangle EOF is an irrational number.

All the five problems above are coherent (briefly, because the new intersection points that are referred in the problems are set out unambiguously on the figure) and task-consistent (briefly, because all these problems are connected to the given geometrical context). Problem 5 is coherent and task-consistent, but not mathematically consistent: the accuracy of this problem depends on the chosen measurement unit (by which one can express the sides of the square ABCD). More precisely, if the length of the side AB is a¸ then the area of the triangle EOF equals \(\frac{{a^{2} \sqrt 7 }}{20}\); therefore, if (for example) a = 1, then the area is expressed by an irrational number, and if \(a = \sqrt[4]{7}\), the area is expressed by a rational number. In other words, the mathematical model associated with this problem is not consistent.

We classified problems 1 and 2 as qualitative because their proofs use the congruence relationship and/or properties related to parallel or perpendicular straight lines. By comparison, problems 3, 4 and 5 were classified in the category of metric problems, because their proofs suppose computing lengths or areas based on the use of specific formulas.

We classified problems 2 and 4 in the category structured dispersion because they are derived from some previous problems (problem 2 is an immediate application of example 1), or from a recognizable model (problem 4 comes from the calculation of the height in an isosceles triangle). By comparison, we classified problems 1, 3 and 5 in the entropic dispersion category because they are independent of the same student’s previous proposals and the usable mathematical models are not a priori obvious.

3.4 Constructing the tools

The next difficulty was to find appropriate measures to match the criteria description with appropriate representations. Consequently, we assigned numerical values to the studied features. For the first criterion (concerning the validity of problems), the numerical characterization is simple: a problem is or is not coherent, or it is or is not mathematically consistent. Yet, the other two criteria required finer numerical characterizations that better capture both the specifics of each individual problem, and specifics of the entire list of problems. We further explain the design of the proposed tool.

3.4.1 Numerical values for the GN criterion

The second criterion—the geometry-specific nature of the posed problems (GN) refers to the content of the proposed problems. For the GN criterion, a problem was coded +1 if it was qualitative and −1 if it was a metric problem. Given the polarity involved, we did not used intermediary values: each problem was classified as either metric or qualitative.

The use of positive and negative values has no connotation in terms of quality assessment of the posed problems; these values are meant only to ensure the problems’ distribution on the two features of the bi-polar criterion GN, and the representation of these features on an orthogonal system of axes.

Next, we calibrated these raw measures with the total number of posed problems based on the arithmetical mean. Thus, the criterion led to two numerical values, expressing the relative weight of qualitative and metric problems in the set of the student’s posed problems.

In order to capture quantitatively the number of posed problems, (i.e. in order to link each problem, as an individual answer, to the list of all problems posed by a student) we divided, at the end, the numbers obtained in this process by the total number of posed problems. For the sake of a clearer representation, the previously obtained mean was conventionally multiplied by 10 to enlarge the drawing proportionally.

Therefore, we used the following formulas to obtain the two values of the features metric and qualitative used in the GN criterion:

$$\begin{aligned} Metric = - 10 \times \frac{{{\text{Number}}\,{\text{of}}\,{\text{metric}}\,{\text{problems}}}}{{{\text{Square}}\,{\text{of}}\,{\text{total}}\,{\text{number}}\,{\text{of}}\,{\text{posed}}\,{\text{problems}}}} \hfill \\ Qualitative = + 10 \times \frac{{{\text{Number}}\,{\text{of}}\,{\text{qualitative}}\,{\text{problems}}}}{{{\text{Square}}\,{\text{of}}\,{\text{total}}\,{\text{number}}\,{\text{of}}\,{\text{posed}}\,{\text{problems}}}} \hfill \\ \end{aligned}$$

3.4.2 Numerical values for the CD criterion

The third criterion—the Conceptual Dispersion of the posed problems (CD) reflects students’ personalized answers. This is a more sensitive criterion, which should capture more of each student’s personal approach, taking into account both the micro level of each posed problem and the macro level of his/her product in its entirety.

To better capture individual variation in the CD criterion, we nuanced its application. We associated with each student’s proposal a Dispersion Factor (DF), which characterizes each problem, and a Conceptual Dispersion Factor (CDF), which corresponds to the complete list of posed problems, viewed as a whole. We used these two factors to characterize numerically the conceptual dispersion features: structured and entropic.

The dispersion factor. For each problem, we determined its dispersion factor (DF) that represents the way in which the problem derives from the given configuration (and data). It is a composite factor that reflects, on the one hand, the way in which the problem connects to a mental model/previous problems, and, on the other hand, the way the student manipulates the initial given frame.

For the sake of a suggestive representation in an orthogonal system of axes, we associated each problem with the following: a positive value (conventionally taken as +1), if the posed problem is independent of any of the others in the list, and the mathematical model of the given configuration is integrated into consistent internalized developments; or a negative value (conventionally taken as −1), if the posed problem is an immediate derivation from an easily identifiable mathematical model that can be recognized either in the prior studied theory or in the previously posed problems. As in the GN criterion, the use of positive and negative values has no connotation in terms of quality assessment of the posed problems.

The frame manipulation factor. In the process of problem posing, students bring modifications to the initial geometrical context. The modified contexts are then used in the search for new relations. The nature and extent of modifications brought by students to the initial context was captured by a discrete scale that concerns the way a student manipulates the given frame.

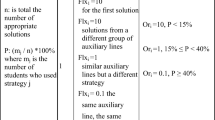
For entropic dispersion, we identified five frame manipulation degrees, as described in Table 1. For each of these, we associated a frame manipulation factor, varying from 0.1 to 0.5: in this case, the positivity of DF increases from stage 1 towards stage 5 (because of the multiplication by +1).

Table 1 The frame manipulation factors for entropic dispersion of posed problems
Full size table

For structured dispersion, the same discrete scale is applied for the initial frame manipulation, but the associated score is symmetrically disposed compared to the previous one (see Table 2). In this case, the negativity of DF decreases from stages 6 to 10 (because of multiplication by −1). We thus obtained a scale of ten frame-manipulation phases varying from −0.5 to + 0.5.

Table 2 The frame manipulation factors for structured dispersion of posed problems
Full size table

Finally, the obtained positive and negative scores for each problem from a proposed list were calibrated by dividing by the total number of posed problems in that list, in order to get a unitary measure of problems Dispersion Factor (pDF). Thus, the pDF results as a weighted mean of all the DFs of the posed problems for the two parameters: entropic problems dispersion factor (pDF + ) versus structured pDF (\(pDF_{ - }\)). In other words, we use the following formulas:

$$\begin{aligned} pDF_{ + } = \frac{{{\text{Sum}}\,{\text{of}}\,{\text{frame}}\,{\text{manipulation}}\,{\text{factors}}\,{\text{for}}\,{\text{entropic}}\,{\text{problems}}}}{{{\text{Total}}\,{\text{number}}\,{\text{of}}\,{\text{posed}}\,{\text{problems}}}} \hfill \\ pDF_{ - } = \frac{{{\text{Sum}}\,{\text{of}}\,{\text{frame}}\,{\text{manipulation}}\,{\text{factors}}\,{\text{for}}\,{\text{structured}}\,{\text{problems}}}}{{{\text{Total}}\,{\text{number}}\,{\text{of}}\,{\text{posed}}\,{\text{problems}}}} \hfill \\ \end{aligned}$$

The conceptual dispersion coefficient. In order to characterize the global parameter CD numerically, we introduced a conceptual dispersion coefficient (CDC). It provides a global assessment of the list of problems proposed by a student. To simplify the analysis, four stages on a discrete scale for CDC were considered, namely: structured, relatively structured, relatively entropic, and entropic. In order to allow a unifying representation for each of the student’s products, we conventionally assigned numerical values for the coefficients on this discrete CDC scale (i.e., 1.5; 2; 2.5; 3) so as to fulfill two conditions: to keep the result of multiplication of the coefficient with the Dispersion Factor smaller than 1, and to ensure equal distribution of the four stages on the CDC scale. A description of this CDC scale is presented in Table 3.

Table 3 The conceptual dispersion coefficient
Full size table

The numerical values for entropic and structured characteristics. The conceptual dispersion (CD) criterion allows a representation with two opposite directions, corresponding to entropic and structured features. In determining the numerical values corresponding to these characteristics, we use the following formulas:

$$\begin{aligned} Entropic{\mkern 1mu} ( = CD_{ + } ) = CDC \times pDF_{ + } \hfill \\ Structured{\mkern 1mu} ( = CD_{ - } ) = CDC \times pDF_{ - } \hfill \\ \end{aligned}$$

The number of posed problems implicitly occurs in computing the conceptual dispersion factors because they occur in the formulas for calculating the pDFs (pDF + and pDF −), which are obtained as weighted means relative to the total number of posed problems.

A note on choosing the coefficients. In the above formulas we used various coefficients, for example, for the following: the multiplication factor for metric and qualitative features; the ten frame-manipulation factors; the four conceptual-dispersion coefficients. The coefficients used in these formulas are multiplier constants, meaning that they keep the same value on all data sets. This allows us to choose these constants for convenience.

Once the system of constants is established, we can plot the data. The choices made for the constants are meant to lead to a more suggestive representation of data. Other choices for these values obviously lead to other graphical representations, but the results of the study (inferred based on these representations) are the same.

4 Results

4.1 A holistic view on the data

We organize the results based on the three criteria presented above.

The coherence-consistency criterion relates to the validity of the final product. Getting valid problems was a target pursued by almost all students in achieving their task. In total, 238 (i.e., 98 %) were coherent, out of the 243 generated problems. For the remaining 5 problems, the text was not sufficiently clear.

Six of the 243 posed problems were identified as not being consistent per se; except for these six problems, there are another 21 problems (9 %) that have been ranked as being not consistent relative to the task because they actually do not refer to the given geometric configuration. In total, 27 problems (i.e., 11 % of the 243) were classified as not being consistent.

A synthetic representation of the problems’ distribution relative to this criterion is presented in Fig. 2.

Fig. 2
figure 2

The posed-problem percent distribution according to the validity criterion

Full size image

The fact that most problems are coherent and consistent shows that the sample on which we did this analysis is valid: in PP tasks, a relatively low percentage of consistent and coherent problems may indicate that the task was not understood, or had a too high difficulty level, inappropriate for participants’ level. Consequently, we analyzed all the problems, even the non-valid ones, considering that some mistakes can be even more relevant in capturing personal-style accounts.

The 243 students’ posed problems have a balanced distribution with regard to the geometric nature criterion: a total of 141 problems (58 %) were been classified as metric, the remaining 102 posed problems (42 %) being qualitative. The balance is no longer preserved in terms of the conceptual dispersion criterion: 181 problems (74 %) were classified as structured, the remaining 62 problems (26 %) being entropic. These data give a holistic view of the sample, but they are not relevant as such. To get meaningful information, we have to analyze, first, particular cases, and then, to integrate these cases into a more fine-grained analysis.

4.2 Describing students’ proposals: nine relevant cases

In order to capture the manifestation of individual PP styles better, we present below brief descriptions of some students’ products. We have chosen nine cases that cover the entire sample in a relevant way.

4.2.1 The case of V.

V. initially posed 9 problems. He used elementary configurations; in each of his posed problems a circle and an inscribed quadrilateral were used. We classified all these problems as being task-related inconsistent.

We asked V. about his choice of using a single element from the initial configuration (i.e., the circle) instead of the whole figure (thus actually diluting the problem frame). His answer was that he self-imposed a constraint of posing simple problems. Yet, this seems rather to be a personal limitation and not the result of a self-imposed behavior during PP: When asked to pose problems considering a combination of elements from the given configuration, he was able to pose only a single problem which, again, was using only a circle from the initial context.

4.2.2 The case of L.

L. initially posed 14 problems. She used only “elementary configurations” to which she added initial data, so to have a coherent and consistent problem, if we were to appreciate it independently of the task. However, the ensemble of L.’s proposal is not consistent with the task frame. At our request to keep the combination of certain elements from the initial configuration (in order to ensure the consistency with the task), L. proposed three problems; we include one of them below (Fig. 3):

Fig. 3
figure 3

The drawing used by L

Full size image

For the inscribed circle in square ABCD, we trace the tangents that intersect the sides of the square in points Aʹ and A″, Bʹ and B″, Cʹ and C″, Dʹ and D″. Prove that triangles AAʹA″, BBʹB″, CCʹC″ and DDʹD″ are congruent, and that the quadrilateral determined by these tangents is a square.

In the above problem, the points to which the tangents are drawn are not specified, tacitly supposing that these are the middle points of the respective circular arcs. In general, her new posed problems show loose coherence, but they shift from metric to qualitative.

4.2.3 The case of P.

P. proposed a list of 10 problems, all of them coherent. In generating these problems, P. used a single drawing (Fig. 4), which started from the initial configuration, to which diverse supplementary constructions were added.

Fig. 4
figure 4

The drawing used by P

Full size image

The distinguishing element in this case, compared with others presented above, is the type of inconsistency. In fact, P. does not use the initial problem context in an authentic way: she thinks of learnt/previously-practiced models (as for example, a certain configuration of points on the sides of the triangle), then forcibly “implements” this configuration on the given one and applies a known result in formulating a problem, such as Ceva’s theorem. She applied this type of procedure in 4 out of the 10 posed problems. The remaining six can be solved by going through the first phase of the problem solving process—i.e. decoding.

All these elements suggest that P. ‘mimes’ problem posing: her problems are fully dependent on previously learnt mathematical models (even though some of them are quite advanced), and just transposed on the configuration.

4.2.4 The case of A.

A. proposed the most problems of all −50. All her problems are coherent and consistent and answer adequately to the task.

We were interested in looking into A.’s PP strategy, given that the number of the proposed problems was at least double that posed by the majority of students from the sample. A. explored one-by-one the configurations she ‘isolated’ from the given one. Each time her focus shifted to another aspect (a new sub-configuration), A. made a new drawing through which she accentuated certain aspects by coloring regions, bolding lines or marking details. For example, the drawings in Fig. 5 were made as support for the following problems:

Fig. 5
figure 5

Some of the drawings made by A

Full size image
  1. (a)

    Let S be the midpoint of the segment AF. Prove that OS =  \(\frac{AO}{2}\).

  2. (b)

    Prove that \(\angle CEO \equiv \angle CFO\) and that CO is the bisector of angle ECF.

  3. (c)

    Prove that the circle sector shaded area in the picture is \(\frac{{\pi R^{2} \cdot m(\angle EOF)}}{1440}\).

We hypothesize that the ‘personalized’ figures allowed A. to focus on those sub-configurations, and generate more formulations than peers did. In this way, she reduced the complexity of the initial figure by a simplification procedure that she applied systematically. This type of behavior individualizes her in our sample because the other students preferred to use a ‘global’ figure, or to use the same figure for more posed problems.

4.2.5 The case of D.

D. posed 33 problems. For all her problems, D. used a single figure (as P. did), on which she successively marked new elements. This ‘global’ drawing (Fig. 6) had a dual role: it replaced some text (a text that is reduced to a minimum possible—of the type AN = 4/5 AB), and it was used as a kind of graphic organizer. (The figure lists the lengths of segments, as they are calculated; this is why it is not very easy to follow it.). Many of the problems proposed by D. (27 out of 33) are of metric nature.

Fig. 6
figure 6

The drawing used by D

Full size image

4.2.6 The case of T.

T. posed 20 problems. All these problems were task-consistent, but 3 of them were not mathematically consistent.

As did P. and D., she used a single ‘global’ figure, for all proposals (Fig. 7), part of the problem data being specified only on the figure. Apparently, T. exploited the given configuration in the same way as D. did, but there is a major difference between the two students’ actions. While D. referred all measures to the side of the initial square, T. chose different reference systems: in 12 of the 20 problems, the requirement was to calculate a ratio (the compared measures being different each time).

Fig. 7
figure 7

The drawing used by T

Full size image

Her strategy in generating problems seems to be just that, namely, to express some measures as functions of other measures. When she abandoned this strategy, she proposed problems that were no longer consistent (see Example 5 in Sect. 3.3).

4.2.7 The case of C.

C. originally posed 19 problems, classified as coherent and consistent. In generating problems, C. had a metric approach: in most problems, the requirement referred to the calculation of a specified size. In the problems initially posed, C. did not generate new points: she only marked some points that naturally occurred in the initial configuration, as intersections of arcs and/or segments. The focus on various elements of the initial figure allowed her to redefine each time the framework on which she focused.

Once her attention focused on a frame, she explored (from a metric perspective) the new context and generated new problems, in this way. It seems that her process of generating problems was powered by the question “what else can be calculated?” As a result, the ‘frames’ were defined in these terms: she searched for triangles, circular sectors, and rectangles to calculate lengths, areas, arcs measures, or angles, resorting to known metric relationships.

Later, we asked C. to propose a way to complete the initial figure with new elements and to pose as many problems about the new configuration as she could. In response to this request, she made the drawing in Fig. 8a and, based on this configuration, posed 7 new problems.

Fig. 8
figure 8

Geometric configurations used by C

Full size image

We noticed that the requirement to extend the initial configuration helped C. to reframe. Although she persisted in posing metric problems, they are much more varied, referring (among others) to the minimal distance between arcs, or to negotiating a route without crossings on the same road (i.e., Eulerian path in a graph—see Fig. 8b).

4.2.8 The case of O.

O. posed 15 problems. She carefully defined any new element introduced in the geometric configuration, and she managed to generate only problems that are coherent and consistent. Out of the 15 problems, only two are likely to be metric (the framing of one is still questionable—it could also be considered as a qualitative problem).

O. had a different strategy for generating problems compared to the other students: she imagined a new configuration, formulated a problem, then she looked for other properties of the given geometric configuration. Moreover, O. emphasized the symmetry of the figure, in 5 of her posed problems, by using the configuration obtained by adding the circle of center C and radius CD: in this way, the figure became symmetrical, not only across the line AC, but also across the line BD (and about the center of the square). The qualitative properties of the figure (mainly based on symmetry) were therefore guiding O. in generating problems.

We have met the same strategy—using symmetry to imagine new configurations, in the case of C. There is, however, a major difference: while C. generated a new configuration by symmetry (Fig. 8a) and subsequently saw this configuration as being “rigid” (i.e., once generated, she could no longer modify it), O. proposed almost every time a new configuration. It seems that O. had a dynamic mode with which to perceive the given configuration—as also happened with D.

4.2.9 The case of I.

I. proposed 15 problems. She used one single drawing (Fig. 9) for all these problems. On this drawing, she completed the entire circle of center A and radius AB, built the arc of center C and radius CB, and marked other points, which occurred as intersections of lines and/or circles.

Fig. 9
figure 9

The drawing used by I

Full size image

With one exception, I. preferred to mark on the drawing the elements to which she referred (using colors to make the figure), instead of defining them in the problem text. All 15 problems were coherent and mathematically (and task) consistent. Only one of her problems was of metric type, all others being classified as qualitative.

Initially, she explored the symmetry properties of the given configuration: the first 9 problems highlight the figure symmetry across the diagonals AC and BD, or about the point O (square center). Later, she proposed ‘asymmetrical’ problems in which she requested, for example, to prove that the triangle CAE is acute-angled, or that m(ECA) > m(EAC).

The presence of these problems (in which symmetry is abandoned in favor of the order relationship) shows her predilection for comparative analyses. Her problem-generation process was driven by the question “what else can be compared”? As a result, she focused on a pair of elements of the figure (triangles, segments, or angles) and used ways to compare them (congruence, order, similarity). This strategy was used consistently, the first 13 problems being generated in this way. In the last two problems, she resumed the topic of the initial problem (i.e., 2 CE = AC) and proposes variations of it, concerning the area of quadrilateral CEAF.

5 Discussion

5.1 Representing the data

The tool presented above was applied to each student from our sample. More precisely:

  • For each posed problem: we determined the validity, we made a classification depending on the metric or qualitative nature, and we associated a frame manipulation factor;

  • For each list of problems: we determined the conceptual dispersion coefficient.

After applying the formulas specified in Sect. 3.4, we finally obtained the data presented in Table 4.

Table 4 The numerical characteristics of the GPP style for the students from the sample
Full size table

We represented these data as diagrams, in which, on the horizontal axis is the GN criterion, and on the vertical axis is the CD criterion; the diagrams corresponding to the 9 participants discussed above are shown in Fig. 10.

Fig. 10
figure 10

The graphical representations corresponding to nine of the students from the sample

Full size image

5.2 Differences in cognitive styles

In the diagrams of Fig. 10, the numbers on each axis associated with the GN and CD criteria determine a quadrilateral, which may be put in relation to a particular cognitive style in problem posing. The quadrilaterals obtained for the students in the sample have different shapes. The students’ preferences in PP evidenced by these representations show the existence of different PP cognitive styles. This variety of shapes is an additional argument that the above described criteria may be thought of as independent such that the position of individuals in one dimension does not affect their position in the other. This was visible in the nine analyzed cases; we found there a variety of combinations, with no dependence between the criteria.

Although all 9 diagrams are different, we tried to group them into several categories, within which we included diagrams with relatively similar shapes. In what follows, we briefly present these categories and discuss those students’ style in posing problems.

V.’s associated diagram (Fig. 10a) is concentrated towards metric and structured with zero value on the other dimensions. In addition, V.’s posed problems are not valid in the sense that his posed problems have only a loose link with the task, relying on a frame that conserves only disparate elements of the given context. The PP cognitive style of V. seems to be very particular—in fact, he did not pay attention to the task and retained only that he had to pose geometry problems.

The diagrams associated with L. (Fig. 10b), A. (Fig. 10d) and D. (Fig. 10e) are balanced relatively to the GN criterion (they are almost symmetrical across the vertical axis), but the effects are disproportionate relative to CD (with predisposition for structured). We now analyze the three students’ responses to the task in a holistic way. We observed in the case of L. the persistence of a strategy: although the new configuration keeps many of the complexities of the given problem, certain elements were excluded in favor of some new elements. The problems posed by L. retain the information from the given configuration partially (for example, the square) and denote a fuzzy selection of the problem contents. The strategies consisting in reformulation and synthesizing allowed A. to generate a big number of problems, denoting a good control of the frame associated with the initial configuration. She followed these strategies in a consistent manner to propose mainly metric problems, often linking them together. In the case of D., we can identify a diligently applied pattern. She used instruments specific to 1-D geometry (through calculations on the straight lines AC and BD) or 2-D (based on the symmetry in relation to the straight line AC and the use of certain metrical results) inside of a rigorously organized “program” driven by the question “what else can be calculated?”

The diagrams of P. (Fig. 10c), T. (Fig. 10f), and C. (Fig. 10g) have a balanced distribution on the criterion CD, but are disproportionate in relation to the criterion GN—predisposed to metric. A holistic analysis shows similar behaviors of the three students in solving the task. In the case of P., her strategy of implementing generic results on the given configuration was used for a part of her posed problems, but there exist also problems outside of this strategy. T. systematically exploited the given configuration, minimally completed with new points and segments, but she had moments during which she ‘jumped’ from one structure to another, highlighting new properties. In the case of C., we initially observed a ‘linear’ approach to the task; however, when we asked her to relate to the initial figure, she posed problems that were diverse, unconnected, highlighting new ideas (optimization problems, graph route problems, qualitative properties of geometrical figures).

The last two diagrams—i.e., the ones corresponding to O. (Fig. 10h) and to I. (Fig. 10i) form a special category. The diagrams show a predisposition for qualitative problems and entropic behavior in PP. We correlate this data with the holistic picture of how they proceeded to solve the task. O. and I. posed problems in which they used negation, or various relations (order, similarity, congruence), and the highlighted properties (open-ended type included) are varied.

Concluding this section, the information we gleaned from the diagrams are convergent with our observations and interpretations related to the analysis of students’ posed problems.

5.3 Diagrams and cognitive flexibility

The flowcharts of Fig. 10 highlight the existence of different geometric PP cognitive styles of students in our sample and show that the combination of the two criteria (GN and CD) allows the detection of personal manners in addressing the task, not imposed by the constraint of solving it correctly. The question we ask now is: What significance might these differences have in terms of mathematical creativity?

As stressed at the beginning, we analyze mathematical creativity based on a cognitive-flexibility framework, highlighting students’ behaviors on three components: cognitive variety, cognitive novelty, and changes in cognitive framing (Singer and Voica 2013; Voica and Singer 2013).

For cognitive variety, the indicator is the number of different posed problems. In the graphic representations, cognitive variety can be associated with the measure of the superior angle of the quadrilateral. Because the horizontal diagonal is smaller as the number of posed problems is higher, and the height of the top triangle is greater as the approach is more entropic (which is expressed by the variety of problems) we interpret cognitive variety in the following way: the sharper the superior angle, the greater the cognitive variety.

For cognitive novelty, the indicator is the amount of new proposals that are far from the given item. In the graphic representation, cognitive novelty can be associated with the measure of positive CD, because an entropic approach, based on an unsystematic, arbitrary, random selection of problem content and structure through a variety of problems bringing ideas from different unconnected zones, denotes novelty.

For cognitive framing, the indicator is the validity of posed problems. The proposal of valid problems (coherent and mathematically- and task-consistent) can be put in relation to an existing cognitive frame of the context in which it operates. If this frame is not set enough—as happens, for example, with V., the context is not understood and the posed problems are not valid.

For change in cognitive framing, the indicator is a student’s ability to change his/her mental frame in solving problems or identifying/discovering new ones. In the flowcharts, cognitive framing can be associated with the ratio between the vertical height of the superior triangle and the vertical height of the inferior triangle of the quadrilateral. In other words, when the module of the ratio between CD + and CD − is >1, this is a clue for a capacity for changing the cognitive frame, hence for creative behavior: the bigger the value of this ratio (>1), the larger the distance towards the initial frame.

Briefly expressed, a student is creative in the given context if the ratio between the area occupied by the quadrilateral in the first quadrant (qualitative–entropic) and the area occupied in any of the other quadrants is greater than 1. In addition, as a relative comparison, in the given context and within the given sample, the bigger the ratio between the area occupied by the quadrilateral in the first quadrant and the total area occupied in the other quadrants, the more creative the student is.

Therefore, looking at the flowcharts, we can estimate a degree of creativity for each of the students from our sample within the creativity framework described through cognitive flexibility.

5.4 GPP cognitive style as a tool to assess mathematical creativity

Within this study, we developed a tool that has the potential to give information about students’ creativity in problem posing contexts. In this section, we focus our discussion on the question: Is this a valid tool? To answer, we use two types of information about students in our sample. On the one hand, we interpret the diagrams from Fig. 10 within the cognitive flexibility discussion of Sect. 5.3; on the other hand, we use data collected from observing students’ behavior in class, in other contexts of learning, and data about their academic performance (evaluated against the performance of colleagues from the same master’s program: on average, in such a program 20 students are enrolled). We further analyze these comparisons.

V. had difficulty in understanding the proper task, which shows that he failed to develop a cognitive frame for this context. It is not accidental that his posed problems are not valid. Given this situation, it is meaningless to discuss changes in cognitive frame. The diagram positioning (Fig. 10a) suggests the absence of creative elements in his case. This conclusion is supported by observing V. in other learning contexts. On the academic level, V. is below average, having real difficulties in achieving a minimal understanding of mathematical concepts. In applying the mathematics, V. usually uses typical algorithms, proving (in the best case) a low level of creativity. It is interesting that V. is also an in-service teacher in a middle school (for 2 years now): he follows the master’s program in parallel with teaching, which is an exception to the rule. Perhaps the limited understanding of mathematical concepts overlapped with the need to teach mathematics at middle school level led him to focus on repetitive algorithms, which he also used as basis for solving the PP task.

In the case of L. (Fig. 10b) and D. (Fig. 10e), the module of the ratio between CD + and CD - has a low value (close to 0) and the top angle of the diagram is very flat. This shows that L. and D. do not go too far from the initial frame and cognitive variety is at a minimal level, indicating a low level of cognitive flexibility. In the case of D., this conclusion seems surprising because of the relatively large number of proposed problems (33); however, the shape of her diagram suggests limited cognitive variety and low level of cognitive novelty. We compared these findings with information about L. and D. obtained in other contexts. In both cases, we found an academic level below average and a cognitive behavior without personal initiatives, which indicates a low level of creativity. It is interesting that D. is also an in-service teacher (as in the case of V.); in her case, however, we have seen a particular skill in posing new problems starting from the given context, but most problems she posed are of a metric nature, suggesting an interest in the application of learned formulas and again, the concern for reproduction algorithms (which, actually, allows her to generate many problems very similar to one another).

A special case is A., who posed the biggest number of problems (50). The associated diagram (Fig. 10d) shows a balanced distribution on the GN criterion (metric versus qualitative problems) and the horizontal diagonal has a relatively small size, which indicates cognitive variety. On the other hand, the fact that the top angle of the diagram has a large size and (the module of) the ratio between CD + and CD − is <1 suggests an average level of cognitive novelty. These elements suggest the existence of cognitive flexibility at a moderate level. As a student, A. has above-average academic performances and manifests some ability in problem solving. The solutions she posed within the given task have nothing special, or ‘spectacular’: the general impression is that A. practiced problem-solving strategies without developing deep heuristics for problems and without making use of the stage of “looking back”. In a superficial examination, we would be tempted to consider her highly creative. Her diagram made us take a closer look at her work and reconsider that impression, leading to a more appropriate one.

The diagrams associated with P. (Fig. 10c), T. (Fig. 10f) and C. (Fig. 10g) are similar: an average value for the top angle measure, a ratio close to 1 between the CD + and CD −, and a higher value than in previous cases for CD +. All these indicate the existence of an above-average level of cognitive flexibility. We compare this statement with our class observations. In the case of C., the observations are consistent with this conclusion: on an academic level, C. is above average, and her interventions in other contexts of learning bring ‘something’ different, being sometimes “out of the box”, thereby confirming the diagram shape.

T. and P., however, represent special cases. In other learning situations, during the teaching course, T. did not come out at all, perhaps because of excessive shyness. When involved in activity and when she had to formulate an answer, no overcoming of routines was identified—i.e., change in cognitive framing. Therefore, in her case, the data obtained from different sources do not correlate. The same conclusion seems to apply to P.: she has medium academic level performance, and her interventions in learning contexts are sporadic, without bringing more quality, suggesting a rather low level of creativity—a result that seems contradictory to what the diagram indicates. Still, the mismatch can be due to insufficient observational data. In these cases, the diagrams may suggest the need for special attention to be given to some students who usually do not actively participate in the course.

The diagrams of O. (Fig. 10h) and I. (Fig. 10i) show the highest ratios between CD+ and CD-, and the measures of the top angles are small. In addition, the ratio between the areas occupied by the respective quadrilaterals in the first quadrant and the other quadrants are above 1. All these lead to the conclusion of a high level of cognitive novelty and cognitive variety for those students. These findings are consistent with our observations. O. and I. have above average academic performance. In problem solving activities, as well as in various other learning contexts (designed for teacher preparation), they have shown inventiveness and originality. Therefore, the highest level of creativity obtained in our sample for O. and I. by applying the developed tool is confirmed from both sources.

6 Conclusions

In this paper we investigated the problems posed in a given geometric context by a group of prospective mathematics teachers enrolled in a master’s program.

To detect students’ personal characteristics when involved in problem posing, we developed a tool to investigate students’ behaviors in this situation. We determined the validity of each posed problem (relative to its coherence and mathematical consistency), and we used two bi-polar criteria designed to detect personal manners in addressing the task: Geometric Nature (GN) of the posed problems (analyzed based on two opposite features: metric versus qualitative), and Conceptual Dispersion (CD) of the posed problems (analyzed based on two opposite features: structured versus entropic).

Numerical characterization of these features allowed us to associate each list of posed problems with a diagram of a quadrilateral shape. In this way, we recorded individual differences inside the sample and we identified a geometry-problem-posing cognitive style of each student from the sample.

Various geometric properties of the quadrilateral generated within the obtained charts were associated with the components of creativity based on the cognitive-flexibility framework used in this paper. Thus, cognitive variety can be associated with the measure of the superior angle of the quadrilateral; cognitive novelty can be associated with the measure of positive CD, i.e. with the height of the top triangle of the quadrilateral; cognitive framing can be associated with the ratio between the vertical height of the superior triangle and the vertical height of the inferior triangle of the quadrilateral. We noticed that, in the given context and within the given sample, the bigger the ratio between the area occupied by the quadrilateral in the first quadrant and the total area occupied in the other quadrants, the more creative the student is.

Our data converge on the fact that cognitive flexibility inversely correlates with a style that has dominance in metric GN and structured CD. Comparing data obtained within this study with information coming from other sources regarding the students’ creative behavior, we found that the shape of the PP cognitive style diagram can be a good predictor of students’ mathematical creativity in geometry-problem-posing situations. As a rough conclusion, a style that is closer to generating geometry problems with higher conceptual dispersion and qualitative rather than metric nature is more susceptible to belonging to a potentially creative person in mathematics.

Some limitations of this study should be taken into account. Thus, we cannot draw firm conclusions due to the small number of participants and to the fact that we have used a single task (even if it is complex). On the other hand, variations may occur in the administration of the proposed instruments, as long as there is no standardized system of recording the proposed parameters. However, in the teacher’s hand, such a tool can at least serve for a two-fold purpose: it could contribute to a better assessment of students’ capabilities, and it could draw attention towards some students who usually do not actively participate in the class, but who may happen to have high potential.

We intend to apply similar tasks with a larger sample and to analyze PP cognitive styles. We also intend to explore the validity of the developed tool across different types of PP tasks (not only related to geometry). Until then, we can conclude that, at least, students’ cognitive-style charts reveal different patterns of students’ knowledge organization and its emergence; further research will show whether those are sustained by converging evidence across tasks and mathematical domains.