Particle Swarm Optimization Variants for Solving Geotechnical Problems: Review and Comparative Analysis

Abstract

Optimization techniques have drawn much attention for solving geotechnical engineering problems in recent years. Particle swarm optimization (PSO) is one of the most widely used population-based optimizers with a wide range of applications. In this paper, we first provide a detailed review of applications of PSO on different geotechnical problems. Then, we present a comprehensive computational study using several variants of PSO to solve three specific geotechnical engineering benchmark problems: the retaining wall, shallow footing, and slope stability. Through the computational study, we aim to better understand the algorithm behavior, in particular on how to balance exploratory and exploitative mechanisms in these PSO variants. Experimental results show that, although there is no universal strategy to enhance the performance of PSO for all the problems tackled, accuracies for most of the PSO variants are significantly higher compared to the original PSO in a majority of cases.

1 Introduction

Engineering problems are challenging because, very often, they have a large number of design variables, are non-convex within their solution domains, contain multiple local minima in their search space, and involve multiple constraints. Global optimization algorithms allow us to handle these challenges when solving different types of engineering problems [1,2,3,4,5]. The complex nature of civil engineering problems has led to the use of optimization algorithms in a wide range of application areas such as earthquake engineering [6], structural engineering [7, 8], geotechnical engineering [9,10,11,12,13], transportation [14, 15], construction management [16, 17], and water resource engineering [18, 19].

Inconsistent behavior of soil and rock, as well as conditional reaction to different stimulations, have made geotechnical engineering problems difficult to solve with conventional optimization techniques. Artificial intelligence (AI) has thus become an alternative for solving such problems efficiently. The common approaches in geotechnical problems can be broadly categorized into analyzing (e.g., [20] and [21]), designing (e.g., [22]), predicting (e.g., [23]), and classification (e.g., [24]). One of the issues in analyzing problems is examining the stability of a given heterogeneous soil slope. A large number of studies have focused on finding the most critical failure surface of soil slopes [25]. Methods proposed to tackle this problem include the harmony search (HS) algorithm [26], support vector machine (SVM) [27], artificial neural network (ANN) [28], fuzzy logic [29,30,31], relevance vector machine [32], genetic algorithm (GA) [33], artificial bee colony (ABC) [34], gravitational search [35], ant colony optimization (ACO) [36], cuckoo search as well as other evolutionary-based optimization algorithms [37, 38].

Back analysis of different geotechnical problems has also attracted much attention from the AI community. For example, Ledesma et al. [39] estimated parameters in geotechnical back analysis based on a maximum likelihood approach. Wei [40] proposed to use particle swarm optimization (PSO) for back analysis in geotechnical engineering. Cheng et al. [41] utilized a hybrid approach for handling pile driving back analysis. Yu et al. [42] used an ANN for displacement back analysis of earth-rockfill dams. Hashash et al. [43] used optimization-based inverse analysis for excavation response. Rechea et al. [44] performed an inverse analysis for parameter identification in simulation of excavation support systems using optimization algorithms. Moreira et al. [45] used an evolution strategy for back analysis of geomechanical parameters in underground work.

In terms of designing geotechnical structures (e.g., retaining structures, shallow foundations, pile foundations), many studies have focused on finding optimal design of concrete retaining walls. For example, Camp and Akin [46] tackled the problem using a big bang-big crunch approach. Other methods used include the ACO [47], an enhanced charged system search algorithm [48], biogeography-based optimization algorithms [49], evolutionary optimization algorithms [50], and the teaching learning-based optimization algorithm [51]. Ponterosso and Fox [52] applied a GA for optimization of reinforced soil embankment. Basudhar et al. [53] studied the design of geosynthetic reinforced earth retaining walls. Basha and Babu [54] tackled the external stability of geosynthetic reinforced soil using a reliability-based approach. Manahiloh et al. [55] solved this problem by the HS algorithm. Ghiassian and Aladini [56] dealt with reinforced earth walls with metal strips using a GA. Kashani et al. [57] attempted to find optimum design of reinforced earth wall using evolutionary optimization algorithms.

When it comes to prediction related geotechnical engineering problems, several studies have used ANNs to model the capacities of axial and lateral loads of pile foundations [58,59,60,61,62,63,64]. Settlement and the load-settlement response of pile were predicted using ANNs by some other researchers [65,66,67]. Khajehzadeh et al. [68] found the optimum design of shallow foundation by means of gravitational search. Camp and Assadollahi [69] utilized a hybrid big bang-big crunch algorithm for shallow footing optimization. Gandomi and Kashani [70] explored the efficiency of a number of swarm intelligence-based algorithms for optimal cost design of shallow foundations. Other related applications include predicting liquefaction [71,72,73,74,75,76], mining [77, 78], rock mechanics [79, 80], site characterization [81], tunneling [82, 83], deep excavation [84], and classification problems [85,86,87].

In this paper, we focus on the PSO algorithm because of its wide applications in engineering optimization problems. PSO has drawn considerable attention in the field of civil engineering in general and geotechnical engineering in particular. We first provide a comprehensive review of the different applications of PSO on geotechnical engineering problems. Then, we employ PSO and its varaints to solve three benchmark geotechnical engineering problems, namely the slope stability, retaining wall, and shallow footing problems. Natural and artificial soil slopes as a prevalent structure in various construction projects, retaining walls as a kind of instrument for increasing the stability of unstable soil slopes, and shallow footing as one of the most impactful parts of a structure for conveying effective forces to the earth, are all of high importance in civil engineering.

Slope stability analysis examines the stableness of a soil slope by defining a factor of safety (FOS). This problem follows a nonlinear and nonconvex function with strong local minima within the solution domain [37], which makes finding the optimal solution using classical optimization algorithms nearly impossible. For the retaining wall and shallow footing problems, two key criteria have to be met during the design procedure: geotechnical stability and structural strength. Furthermore, the final costs of projects, as well as the volume of consumed materials, have to be minimized. Since the objective function engages a large number of design variables, satisfying the above-mentioned criteria is very difficult. Metaheuristic algorithms have proven to be helpful for handling these problems [88,89,90]. Our focus in this study is to assess the performance of the PSO variants, especially their information-sharing mechanisms in controlling exploration and exploitation. Through simulation experiments, we study the convergence histories and carry out statistical analysis over the results obtained.

The rest of this paper is organized as follows. In Sect. 2, we present an overview of PSO. In Sect. 3, we describe the geotechnical engineering problems in detail, including their objective functions. PSO algorithms are then discussed in Sect. 4. In Sect. 5, we review the application of PSO on a wide range of geotechnical engineering problems. In Sect. 6, simulation experiments and results are discussed. Finally, Sect. 7 concludes the work and suggests future research directions.

2 Particle Swarm Optimization Overview

PSO is one of the most popular metaheuristic algorithms, known for its ability to solve a variety of challenging problems [91,92,93,94]. Due to its stochastic nature, PSO produces varying solutions in each trial and is computationally more expensive than exact mathematical methods in general. A key issue here is to balance between diversification (exploration) and intensification (exploitation). A suitable trade-off between the two is essential for maximizing the algorithm’s performance [95]. In the following, some related work on PSO is presented and analyzed.

Shi and Eberhart [96] proposed an inertia weight w to balance intensification and diversification for the original PSO. Smaller values of w push PSO toward local search while larger values lead to global search. The main reason behind this is that large values of w decrease the independence of particles from the initial solutions and make them free to search new areas. Cognitive and social learning factors have also been proven to play a significant role in balancing global and local search. Increasing the cognitive coefficient provides more concentration on global search, and a large social coefficient strengthens local search.

Cui et al. [97] presented an improved PSO (IPSO) with three non-linear time-varying strategies for cognitive c₁ and social c₂ component adjustment. The underlying approach is based on providing more global search in the intial iterations and proceeding toward local search in the final iterations. Therefore, two of those three schemes proposed a decreasing pattern for cognitive coefficient and one proposed an increasing pattern. Comparison of the proposed decreasing routines with the original PSO and linear time-varying strategy exhibited slower convergence in the intial runs versus better convergence in the final iterations.

Ziyu and Dingxue [98] utilized an exponentially time-varying acceleration function for updating c₁ and c₂, resulting in a modified PSO (MPSO). This modification was successful in striking a balance between exploration and exploitation for solving some benchmark functions. However, results proved that this method may not be as consistent, since it failed to solve the Sphere benchmark function. Bao and Mao [99] applied an asymmetric time-varying trend for acceleration coefficient adjustment to the MPSO. In their study several patterns were proposed where the variation of c₁ and c₂ did not follow the same pace. Their proposal proved to be efficient in enhancing PSO.

A comprehensive learning particle swarm optimizer (CLPSO) was proposed by Liang et al. [100, 101]. Instead of following the global best solution (g_best), all particles’ best solutions (p_best) have the possibility to serve as an exemplar for updating the velocity. The main concept behind this is to benefit from sharing the achievements of all the particles. Comparison of the results obtained by CLPSO with several variations of PSO showed superiority of this algorithm in handling the tackled benchmark functions.

Ngo et al. [102] attempted to modify the particle motion based on selecting an exemplar other than the global best solution. In other words, all particles, from the best to the worst, have the chance of being a leader in the next iteration. They called their algorithm the extraordinary particle swarm optimization (EPSO). EPSO was tested over several constrained and unconstrained (i.e., unimodal and multimodal) functions, and its performance was assessed against other algorithms inclusing other PSO variants. Even though EPSO did not provide the best solutions, its results were close to the global optimum and considerably comparable to those generated by the best algorithms.

A more recent variant of PSO based on the comprehensive learning strategy can be found in the heterogeneous comprehensive learning particle swarm optimization (HCLPSO) algorithm [101]. In HCLPSO, the population is divided into two subpopulations, conducting exploration and exploitation independently without interfering with each other. Another improvement in HCLPSO is the use of adaptive control parameters in order to boost exploration and exploitation.

Other PSO variants include an evolutionary extension developed by Tillett et al. [103], known as Darwinian PSO (DPSO), which employs many swarms that work independently at any time; the fractional-order DPSO (FDPSO) proposed by Couceiro et al. [104], which employs fractional calculus for evaluating the velocity; and an improved random drift PSO (IRDPSO) by Elsayed et al. [105], which imitates the free electron model. The IRDPSO was based on two modifications applied to the original RDPSO: (1) adding a crossover operator; and (2) using local best instead of the mean best position.

3 Geotechnical Engineering Problems

3.1 Slope Stability Analysis

To examine the stability of a soil slope, valid trial slippery surfaces must be constructed by considering predefined rules. The critical failure surface has to be concave upward without fluctuation. In this paper, the proposed method by Cheng [106] is utilized to produce a valid slip surface, and the Morgenstern-Price method [107] is utilized to evaluate the FOS for every potential failure surface.

3.2 Retaining Wall Design

Concrete cantilever retaining wall is an important geotechnical structure because of a wide range of applications, massive and costly construction operations, and serious consequences of collapse. Successful functioning of retaining walls necessitates meeting the following geotechnical measures: (1) overturning safety factor (FOS_O); (2) sliding safety factor (FOS_S); (3) bearing capacity safety factor (FOS_B). In this study, the Mononobe–Okabe method is used to evaluate the active and passive forces under a seismic loading case [108]. For more details on the design procedure, see [12].

3.3 Shallow Footing Design

Another key geotechnical structure is the shallow foundation. Any structure or megastructure would be unable to successfully function unless the loads directed to the earth are effective. A foundation can be remodeled by the footing length (L), width (B), thickness (H), and depth from the ground to the bottom of the footing (D).

The final design must be checked for two fundamental criteria: geotechnical stability and structural strength. Geotechnical stability measures are bearing capacity and settlement. Additionally, a lot of structural requirements are defined based on ACI 318-05 [109] to guarantee enough strength for providing serviceability. These requirements can be listed as: one-way shear capacity, two-way shear capacity, flexural capacity, the column’s bearing capacity, dowels, and footing, and the reinforcement development length. More details on such restrictions and constraints can be found in ACI 318-05 [109] and Camp and Assadollahi [69, 88].

3.4 Objective Function Formulation

As a necessary part of working with an optimization algorithm, an objective function should be defined. In slope stability analysis, the value of FOS is considered as the fitness function in a minimization procedure.

However, for the retaining wall minimization problem, the final cost and weight of the structure are subject to Eqs. (1) and (2), respectively.

$$ f_{cost} = C_{s} W_{st} + C_{c} V_{c} $$

(1)

$$ f_{weight} = W_{st} + 100V_{c} \gamma_{c} $$

(2)

where C_s and C_c indicate unit costs of steel and concrete, respectively, W_st is the steel’s weight, V_c represents the concrete volume, and γ_c is the concrete unit weight scaled by a factor of 100 in a similar manner to Saribas and Erbatur [110].

For the shallow footing optimization problem, minimum cost design is considered based on Eq. (1).

4 Optimization Algorithms

4.1 Particle Swarm Optimization

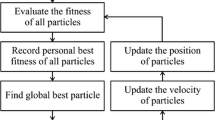
As a swarm intelligence algorithm, PSO imitates the collective behavior of a school of fish or birds [111]. In PSO, a group of particles searches the solution space via sharing their best-found information. Each particle schedules its next movement by taking its own best finding and the overall best achievement into account. PSO defines each particle’s position as follows:

$$ X_{i}^{t + 1} = X_{i}^{t} + V_{i}^{t + 1} $$

(3)

where $X_{i}^{t + 1}$ shows the the position of the ith particle in t + 1th iteration, $X_{i}^{t}$ indicates the current position (in tth iteration), and $V_{i}^{t + 1}$ is the velocity calculated for the t + 1th iteration.

Shi and Eberhart [96] proposed Eq. (4) for evaluating the velocity.

$$ V_{i}^{t + 1} = \omega V_{i}^{t} + C_{1} r_{1} (P_{i} - X_{i}^{t} ) + C_{2} r_{2} (P_{g} - X_{i}^{t} ) $$

(4)

In this equation, ω is the inertia weight within [0, 1.2] to balance exploration and exploitation, P_i and P_g are the personal and global bests of particles, respectively; C₁ and C₂ are constants typically set to a number in the interval of [0, 2], and r₁ and r₂ are random numbers in the interval of [0, 1].

4.2 Comprehensive Learning Particle Swarm Optimization

The CLPSO was proposed to improve exploratory and exploitative behavior in PSO [112]. By changing how the velocity is updated, the best experiences of all particles will be shared. Based on this method, for each dimension, a random number will be produced and compared to a learning probability function, P_ci. In the case of having a number lower than P_ci, the dth variable of P_i will be updated using other particles’ best-found solutions. Otherwise, their own best experience will be selected for updating P_i. The velocity term and probability function are defined by Eqs. (5) and (6), respectively.

$$ V_{i,t + 1}^{d} = wV_{i,t}^{d} + c \times rand_{i}^{d} \times (pbest_{{f_{i} (d)}}^{d} - X_{i,t}^{d} ) $$

(5)

where f_i(d)= [f_i(1), f_i(2),…, f_i(D)] indicates if the ith particle follows its own or others’ $pbest_{i}^{d}$ for each dimension d.

$$ P_{{C_{i} }} = a + b \times \frac{{\left( {\exp \left( {(10(i - 1))/(ps - 1)} \right) - 1} \right)}}{{\left( {\exp (10) - 1} \right)}} $$

(6)

In Eq. (6), ‘ps’ represents the population size, a = 0.05, and b = 0.45.

4.3 Heterogeneous Comprehensive Learning Particle Swarm Optimization

In continuing PSO improvement, a heterogeneous version of CLPSO was introduced with a different scheme for updating the velocity term [113]. In this method, the population is categorized into two separate subpopulations with different tasks: exploration and exploitation. The exploitation subpopulation uses Eq. (7) for updating the velocity while the exploration subpopulation will move to the next step accordingly:

$$ V_{i,t + 1}^{d} = \,wV_{i,t}^{d} + c_{1} \times r1_{i}^{d} \times (pbest_{{f_{i} (d)}}^{d} - X_{i,t}^{d} ) + c_{2} \times r2_{i}^{d} \times (gbest^{d} - X_{i,t}^{d} ) $$

(7)

where the inertia weight w decreases linearly with respect to run time from 0.99 to 0.2. A time-dependent acceleration factor, c, is defined, which varies between 1.5 and 3 to boost the exploration ability of sub-population-group 2. c₁ and c₂ in Eq. (7) are set within [0.5, 2.5] to improve the exploitation capacity.

Another important fact about HCLPSO is that the exploration subpopulation does not have access to the exploitation information. This way, HCLPSO prevents a rapid information flow. HCLPSO thus benefits from a satisfactory balance between exploration and exploitation.

4.4 Extraordinary Particle Swarm Optimization

In this algorithm, similar to many other efforts, the main focus is on balancing exploration and exploitation. By updating the particles’ movement directions based on their best-found solutions (p_best) and the global best (g_best), it is highly possible that the algorithm will face premature convergence and be trapped in a local optimum solution. On the other hand, using information from other individuals for producing new solutions enables the algorithm to explore the solution space with higher diversity. Taking this into account, Ngo et al. [102] proposed a new variant of PSO, the EPSO.

With EPSO, all the particles take part in updating the velocity term stochastically by the following equation:

$$ \vec{V}_{i,t + 1} = C(\vec{X}_{Ti,t} - \vec{X}_{i,t} ) $$

(8)

where X_Ti,t is the determined target of the ith particle at the tth iteration, and C is a combined coefficient including cognitive and social factors.

The utilized stochastic approach for selecting the target individual, X_Ti,t, follows the following basic rules:

• 1. the upper limitation of T_up is defined by a user-defined coefficient α multiplied by population size N_pop according to:

  $$ T_{up} = round(\alpha \times N_{pop} ) $$

  (9)

• 2. a target is randomly produced according to:

  $$ T = round(rand \times N_{pop} ) $$

  (10)

• 3. if the produced T in step 2 is between 0 and T_up, the particle will move toward the target using Eq. (10). Otherwise, it will move randomly.

4.5 Fractional-Order Darwinian PSO

Tillett et al. [103] proposed a new Darwinian-based variation of PSO called DPSO. In this algorithm, sub-swarms are formed and used in conjuction with the selection, as an evolutionary operator.

The most important feature of DPSO is enlisting the fundamental Darwinian theory of survival of the fittest to evade the local optima. DPSO tries to search the solution domain using different swarm sets, which work simultaneously in parallel for a given test problem. In 2012, Couceiro et al. [104], by implementing fractional calculus using Grünwald–Letnikov definition, proposed Eq. (11) for updating the velocity:

$$ \begin{aligned} v_{t + 1}^{n} & = \alpha v_{t}^{n} + \frac{1}{2}\alpha v_{t - 1}^{n} + \frac{1}{6}\alpha (1 - \alpha )v_{t - 2}^{n} + \frac{1}{24}\alpha (1 - \alpha )(2 - \alpha )v_{t - 3}^{n} + \rho_{1} r_{1} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{g}_{t}^{n} - x_{t}^{n} ) \\ & \quad + \rho_{2} r_{2} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{x}_{t}^{n} - x_{t}^{n} ) + \rho_{3} r_{3} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{n}_{t}^{n} - x_{t}^{n} ) \\ \end{aligned} $$

(11)

where α is a fractional coefficient, ρ₁, ρ₂, and ρ₃ assign weights to the inertial influence, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{g}_{t}^{n}$ is the global best, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{x}_{t}^{n}$, ${n}_{t}^{n}$ is the neighborhood best.

4.6 Improved Random Drift PSO

The RDPSO developed by Sun et al. [114] is an improved version of PSO in which a modified equation for velocity is proposed. In this algorithm, the velocity term uses the mean best position at each iteration to update the position. In fact, RDPSO mimics the free electron model in which the electron thermal motion and electric field cause random movements. Elsayed et al. [105] proposed an improved version of this algorithm called IRDPSO by taking two modifications into account: (1) adding a crossover operator to the original RDPSO; and (2) replacing the mean best position in the population with one of the locally optimal solutions obtained. The proposed velocity equation in IRDPSO is presented as follows:

$$ v_{t + 1}^{n} = \alpha \left(Y_{i,j}^{t - 1} - X_{i,j}^{t - 1} \right)\delta_{i,j}^{t} + \beta \left(Z_{i}^{t} - X_{i}^{t - 1} \right) $$

(12)

where $Y_{i,j}^{t - 1}$ is the jth element of the personal best position for particle i at iteration t − 1, α is the thermal coefficient, β is the drift coefficient, $\delta_{i,j}^{t}$ is a random number with a similar distribution to the jth element of particle i at iteration t, and $Z_{i}^{t}$ is the local focus position of i-th particle in t-th iteration.

4.7 Improved Particle Swarm Optimization Based on Dynamic Parameter Setting

The main parameters of PSO are the weighting factor (w), cognitive coefficient (c₁) and social coefficient (c₂). Similar to many other optimization algorithms, fine-tuning of these parameters will affect its performance especially in dealing with complex problems. The important fact in adjusting c₁ and c₂ is that a greater value of c₁ than c₂ guides the algorithm toward global search while a greater value of c₂ leads the algorithm toward local search. Besides, c₁ should be changed sharply to provide exploration and c₂ should be changed gently to strengthen PSO’s ability to evade from the local minima. Dynamic parameter settings have been proposed as an efficient alternative to reach an appropriate adjustment of acceleration coefficients (c₁ and c₂) [97,98,99]. In this paper, three improvements of PSO based on time-dependent parameter settings are utilized accordingly.

4.7.1 An Improved PSO equipped with Time-Varying Accelerator Coefficients

In 2008, an improved version of PSO was proposed by Cui et al. [97], based on a time-varying strategy for adjustment of c₁ and c₂, known as IPSO in short. They proposed three different non-linear methodologies for updating the cognitive coefficient: the upward, concave, and exponential functions. It is mentioned in the original study that the sum of c₁ and c₂ will be 3.0, therefore, by defining c₁ the relevant value of c₂ can be evaluated easily. Here, the following settings are considered for c₁ and c₂:

$$ c_{1} (t) = 2.5 + 2\left( {\frac{t}{T}} \right)^{2} - 2\left( {\frac{2t}{T}} \right)\text{,}\quad c_{2} (t) = 0.5 - 2\left( {\frac{t}{T}} \right)^{2} + 2\left( {\frac{2t}{T}} \right) $$

(13)

In Eq. (13), t shows the current iteration and T represents the predefined maximum iteration.

4.7.2 A Modified PSO with Adaptive Acceleration Coefficients

Considering the impact of acceleration coefficient in exploring the solution space effectively, Ziyu and Dingxue [98] proposed another modified version of PSO named TACPSO. TACPSO uses Eqs. (14) and (15) to encourage the algorithm toward global search in the initial iterations and more concentration on local search in the later iterations.

$$ c_{1} = c_{\hbox{min} } + (c_{\hbox{max} } - c_{\hbox{min} } ) \cdot \exp [ - (4k/G)^{2} ] $$

(14)

$$ c_{2} = c_{\hbox{max} } - (c_{\hbox{max} } - c_{\hbox{min} } ) \cdot \exp [ - (4k/G)^{2} ] $$

(15)

where G represents the maximum iteration time and k shows the present iterative time, and c_max and c_min are 2.5 and 0.5, respectively.

4.7.3 PSO with Asymmetric Time Varying Acceleration Coefficients

Another effort to enhance the effectiveness of PSO via a time-varying acceleration coefficient approach can be found in a study by Bao and Mao [99]. In this version of PSO, called MPSO, the acceleration is updated according to Eqs. (16) and (17):

$$ c_{1} = c_{1\hbox{max} } - k \times (c_{1\hbox{max} } - c_{1\hbox{min} } )/k_{\hbox{max} } $$

(16)

$$ c_{2} = c_{2\hbox{min} } + k \times (c_{2\hbox{max} } - c_{2\hbox{min} } )/k_{\hbox{max} } $$

(17)

where k is the current iteration and k_max is the maximum iteration. In this study, the parameter settings utilized in [30] are considered for Eqs. (16) and (17).

4.8 Autonomous Particle Groups for Particle Swarm Optimization

Autonomous particle groups for particle swarm optimization (AGPSO) is a new approach based on defining autonomous groups that explore the solution space independently [115]. AGPSO mimics the diverse obligations of individuals in a termite colony based on their different abilities and potentials. Mirjallili et al. [115] attempted to find a balance between diversification and intensification in their modified version of PSO by defining four groups of particles that explore the solution space autonomously. Similar to the original PSO, global best (g_best) and personal best (p_best) of the particles are evaluated at each iteration. Then, each group of particles will have their specific strategy for updating c₁ and c₂ [115]. After calculating c₁ and c₂, the velocities and positions of particles will be updated following the conventional PSO rules using Eqs. (3) and (4).

In this study, three different variations of AGPSO developed in the original paper [115], named AGPSO1, AGPSO2, and AGPSO3, are used. These versions are differentiated by different strategies for updating c₁ and c₂.

5 PSO Applications in Geotechnical Engineering

In this section, we provide a comprehensive review of the different applications of PSO algorithms for geotechnical engineering problems. In the following sub-sections, a detailed review is presented based on the following categories: slope stability, retaining walls, shallow foundations, pile foundations, reinforced soil, tunneling, and others.

5.1 Slope Stability

One of the most crucial challenges in geotechnical engineering is examining the stability of a slope. These structures are prevalent in many construction projects such as highways, mines, tunneling, embankments, etc. Hence, any fault in stability assessment of the slopes can end up in a catastrophic disaster. However, finding the most critical failure surface and its relevant FOS is a complicated task. Hui et al. [116] in 2004, used the PSO algorithm for finding the critical slip surface in soil slopes for the first time. In 2005, an improved version of PSO was proposed for slope stability analysis by Li et al. [117], in which a mutation operator was mounted to the original PSO.

Cheng et al. [118], in 2007, proposed a methodology for finding the non-circular slip surface in two-dimensional soil slopes. Such a consideration is more compatible with non-homogeneous soil slopes and will result in more realistic solutions. In their study, a limit-equilibrium based method by vertical slices was suggested for evaluating the FOS. They handled this problem by enlisting the original PSO and a modified version of PSO. Based on this modification, the number of flies for the particles became limited to a maximum band and better particles have more chances to fly more than once. The proposed methods were assessed over several benchmark case studies. Li et al. [119], in 2007, also proposed a discontinuous flying PSO to improve the performance of this algorithm and reduce the operation time for time expensive problems. The proposed algorithm was examined for analyzing a wide range of soil slopes. In another study by Cheng et al. [120] in 2007, six different heuristic algorithms were employed for handing slope stability problem, with the PSO demonstrating more stable performance among them. In this study, the authors proposed well-adjusted values for necessary parameters of PSO (i.e., inertia weight and stochastic weighting factors) by conducting a sensitivity analysis. Wang et al. [121] proposed a methodology using a finite element approach for evaluating the stability of a given soil slope. In this work a PSO algorithm was attributed to find the solution. In 2009, Tian et al. [122] attempted to handle the problem of finding minimum FOS based on the stress field resulting from a finite element simulation by means of the PSO algorithm. Li et al. [123], in 2009, proposed a combined method based on HS and PSO for finding the most critical failure surface of a soil slope. Khajehzadeh et al. [124, 125] incorporated uncertainties of the soil material into the FOS evaluations. In 2010, Li et al. [126] proposed an improvement on the PSO algorithm based on the same strategy utilized by Cheng et al. [118] and Li et al. [118]. Li and Chu [127], in 2011, used a hybrid approach based on PSO and HS to estimate the stability of 2D slope. In 2012, Kalatehjari et al. [128] utilized the PSO algorithm for exploring the stability of homogeneous soil slopes. Cheng et al. [41] developed a hybrid approach based on merging PSO and HS for slope stability optimization. Khajehzadeh et al. [129] concentrated on locating the critical slip surface in 2D soil slopes by enlisting a modified PSO algorithm. Based on this modification, the inertia weight decreased in the course of time. Furthermore, the content of a randomly chosen particle was shared for updating the velocity. In a study by Johari and Sahebkar [130] in 2013, the PSO algorithm was used to handle the problem of slope stability. Wang et al. [131] considered a limit equilibrium method based on the locations of the trailing edge and shear outlet; they considered the circular slip surface and utilized the PSO algorithm to solve the problem. In 2013, Khajehzadeh et al. [132] applied a modified version of PSO by considering a chaotic sequence for updating the inertia weight to analyze the 2D soil slope. Kalatehjari et al. [133] considered the effects of two different methods (i.e., conventional method (CM) and triple-point method (TPM)) for generating trial circular slip surface on the final results obtained by PSO in slope stability analysis. Kalatehjari et al. [134, 135] analyzed 3D soil slopes by an FEM-based model in PLAXIS coupled with the PSO algorithm. In 2015, Gandomi et al. [136] considered the problem of 2D soil slopes using some swarm intelligence-based algorithms among which PSO performed satisfactorily for handling the tackled problems. Li et al. [137] proposed a hybrid approach based on quantum-behaving PSO integrated with a least square SVM for slope stability analysis. Chen et al. [138] synchronized the standard landslide analysis program (STABL) with PSO for slope stability assessment. They tested the proposed methodology for handling homogeneous soil slopes considering different values for the inertia weight. Xue [139] developed a hybrid technique based on the least square SVM (LSSVM) and PSO algorithm for defining the stability of slopes. Their proposed methodology was validated through two numerical case studies. Kang et al. [140] conducted a reliability analysis of soil slopes based on the υ-SVM. Kang et al. [21] in another study used the LSSVM for reliability analysis of the soil slopes. The hyper-parameters of both υ-SVM and LSSVM were adjusted using PSO. Gordan et al. [141] attempted to solve the homogeneous slope stability problem using a combined PSO and ANN approach. In that study, 699 cases were simulated using GeoStudio software and their associated FOS was computed. Those case studies remodeled a wide range of possible conditions while varying the influential parameters such as slope height, gradient, cohesion, friction angle and peak ground acceleration. Moreover, Gordan et al. [141] studied the impact of stochastic weighting factors on the function of their proposed technique via sensitivity analysis. Reale et al. [142, 143] conducted comprehensive studies for reliability analysis of the soil slopes. In their study, the main aim was finding the location of the most critical failure surface with the minimum reliability index as well as finding all possible discrete failure mechanisms. To that end, the authors used two multimodal versions of PSO named locally informed PSO (LIPS) and standardized LIPS (SLIPS). Wang et al. [144] studied the stability of rock slopes during the excavation of the surface. They conducted a reliability analysis for this problem using the Monte Carlo method. In this study, a binary PSO was utilized for finding the minimum shear strength in a 3D shear zone. Johari and Mousavi [145] took the uncertainties of the effective parameters on soil slope stability (i.e., angle of shearing resistance (φ), cohesion intercept (c), and unit weight (γ) of soil) into account while height and inclination were frozen. Four limit equilibrium-based methods were utilized for FOS evaluation. In that study, PSO was assigned to automate the procedure of finding minimum reliability index. In one of the most recent studies, Pandit et al. [146] provided a review of the application of various deterministic and stochastic algorithms including PSO for slope stability analysis. Additionally, an overview of both deterministic and reliability analysis of the soil slope stability was provided. Sharma et al. [147] matched GeoStudio software with PSO for finding the most critical failure surface in 2D slopes. They considered the bishop method with circular slip surface in their study. Himanshu and Burman [148] studied locating the critical slip surface of slopes using PSO in 2019. In their study, Bishop’s method with a different number of vertical slices was utilized for evaluating the FOS based on seepage and seismic loading considerations. Koopialipoor et al. [149] compared the performance of ANN for handling the stability analysis of homogeneous soil slope affected by static and dynamic loads. They used four optimization algorithms, including the GA, PSO, imperialistic competitive algorithm, and artificial bee colony, for adjusting weight and bias of ANN. Luo et al. [150] developed a hybrid approach combining the PSO and cubist algorithm called PSO-CA to predict the stability of soil slopes. A comparative study was provided by applying other tools such as the SVM, k-nearest neighbor (kNN), and classification and regression trees (CART). Shinoda and Miyata [151] used the PSO algorithm for stability analysis of unreinforced and reinforced soil slopes, where a comprehensive sensitivity analysis was conducted on the effect of inertia weight, stochastic weighting factors, and the number of particles. Singh et al. [152] solved the problem of slope stability using three optimization algorithms, namely the GA PSO, and biogeography-based optimization (BBO) algorithm. Yuan and Moayedi [153] used multilayer perceptron (MLP) for classifying the soil slopes and failure recognition, where they combined several optimization algorithms (GA, PSO, ACO, BBO, evolutionary strategy, and probability-based incremental learning) with MLP. Table 1 summarizes the application of different techniques for evaluating the slope stability problem.

Table 1 Review of the application of PSO to slope stability problems

5.2 Retaining Wall

Retaining walls are important whenever dealing with a naturally unstable tranche is a concern in a construction project. However, due to their huge bulk, they cause extravagant expenses for any given project. Therefore, much effort has been devoted to the optimal design of retaining structures. Here we discuss those studies that used the PSO algorithm for handling the retaining wall optimization problem. Zhao and Ru [154] presented a hybrid method based on SVM and PSO for optimum design of retaining structures of deep pits. In 2009, Ahmadi-Nedushan and Varaee [155] applied the PSO algorithm for minimum-cost and minimum-weight design reinforced concrete cantilever retaining walls (RCC wall). Khajehzadeh et al. [156, 157] considered the optimal design of retaining walls using particle swarm optimization with passive congregation (PSOPC) and MPSO. In those studies, eight different design variables for describing a wall without a base shear key were considered. In 2012, Pei and Xia [158] applied some heuristic algorithms (GA, PSO, and simulated annealing (SA)), including a random direct search algorithm called the complex method (CM), to the problem of minimum-cost retaining wall optimization. In 2014, Kaveh and Soleimani [159] utilized improved harmony search (HIS), colliding bodies optimization (CBO) and democratic PSO (DPSO) for optimum design of retaining walls. In their study, the minimum cost design of the wall based on ACI 318-05 [109] considerations, was proposed. In 2015, Gandomi et al. [160] utilized four swarm intelligence-based algorithms for optimum design of retaining walls (PSO, FA, APSO, and CS), where the minimum-cost and minimum-weight analysis of the walls were considered based on the ACI 318-05 [109] rules. A short review of the application of PSO to retaining wall optimization is provided in Table 2.

Table 2 Review of the application of PSO to retaining wall optimization

5.3 Reinforced Soil

Due to the lack of tensile strength of soil materials, there are many cases where they cannot provide a satisfying demanding service. One solution in those conditions is utilizing reinforcements. In those situations, the cost of utilized reinforcements or finding an appropriate design would not be an easy task. Artificial intelligence-based techniques and in specific PSO have been the subject of many solutions in the literature. For instance, Li et al. [161] attempted to determine proper reinforcement parameters to provide stability of Zhongjiawu slope with lowest possible construction cost. In their study, a hybrid approach based on PSO and SVM handled an objective function based on construction cost. The stabilizing method in the mentioned investigation was the anti-sliding piles utilized for a high cut slope and FOS of the slope applied to the design procedure as a constraint. Shinoda and Miyata [162] conducted a probabilistic analysis of soil slopes affected by seismic loading, where the noncircular failure surface was considered based on the limit equilibrium method. PSO was selected for handling the objective function and evaluating the FOS while quasi-Monte Carlo simulation was tackled to conduct a probabilistic analysis. One of the most recent studies on the basis of reinforced soils was conducted by Yalcin et al. [163] in 2019. In their study, four optimization algorithms (i.e., GA, PSO, ABC, and DE) were enlisted to handle the optimum cost design of mechanically stabilized earth walls (MSEW) with geosynthetic. Three objectives were followed in this study to reach optimum cost design: (1) reinforcement type, (2) length, and (3) layout of MSEWs. The design procedure in the study was developed based on the Federal Highway Administration (FHWA) requirements. Sereshki and Derakhshani [164] considered the optimum design of MSEWs reinforced with metal strips using PSO, GWO, and salp swarm algorithm (SSA). FHWA regulation was again the foundation of the design procedure and the design variables were the length, width, thickness, vertical spaces, and horizontal spaces of reinforcements. Numerical simulations were conducted by resolving a case study presented by FHWA for four different heights of the wall with different combinations of soil specifications. As depicted in Table 3, Shinoda and Miyata [151] considered the stability analysis of reinforced slopes by applying PSO to a limit equilibrium-based procedure. Table 3 provides a review of the application of PSO to reinforced soil-related problems.

Table 3 Review of the application of PSO to reinforced soil

5.4 Shallow Foundation

Shallow foundation is one of the key elements that guarantees serviceability of any given structure by directing the effective loads to the earth. Many researchers have focused on different aspects of the problem of shallow foundation, though focus on their optimal cost design is a relatively new research area. In the following, we present a review of the different application of PSO to shallow foundation and how PSO was helpful in addressing the issue.

In 2010, Zhao and Yin [165] introduced a hybrid approach based on combining SVM and CPSO for predicting the shallow foundations’ bearing capacity. In their study, CPSO was utilized to adjust the hyper-parameters of SVM. The algorithm was trained using 50 datasets by considering ultimate bearing capacity based on some factors such as the width of footing, depth of footing, etc. Khajehzadeh et al. [124] examined PSO, PSOPC and MPSO for optimum design shallow foundations, and also proposed an improved version of PSO based on passive congregation where a randomly selected particle for updating the velocity term in addition to the best-found solutions would be considered. Modified PSO (MPSO) that utilizes a time-varying equation for inertia weight was proposed. The objective function was defined as the final cost of the footing.

In 2013, Jing et al. [166] utilized a hybrid approach based on an ANN and improved PSO to predict dam foundation uplift pressure. Marto et al. [167] proposed a hybrid predictive method based on the ANN for estimating the bearing capacity of shallow foundations, where PSO was utilized for the optimum hyper-parameter setting of ANN. 40 recorded samples in granular soils from full-scale axial compression load test on shallow foundations were chosen from the literature. Ultimate axial bearing capacity was defined as a function of footing length and width, embedded depth of the footing, average vertical effective stress of the soil, friction angle of the soil, and groundwater level. The optimum parameter setting of PSO and architecture of ANN was achieved by a sensitivity analysis. Nazir et al. [168] used a hybrid approach based on the ANN and PSO to predict the settlement of a shallow foundation on cohesionless soil. The decision variables were length, width, and depth of embedment in addition to friction angle, stiffness, and effective stress below footing. Eighty footing load tests on cohesionless soils collected from the literature to constitute the database.

Rezaei et al. [169] applied a GA- and PSO-based ANN for predicting the bearing capacity of thin-walled shallow foundations. 145 recorded test results in addition to some experimental tests by the authors provided the required datasets. Results declared a good performance of PSO-base ANN in handling this problem. In 2017, Debnath and Ghosh [170] utilized the PSO algorithm to solve limit equilibrium equations that govern the seismic bearing capacity of shallow foundations. The results were reported in a tabular form to be applicable for examining the seismic bearing capacity of any given shallow foundation. In 2018, Gandomi and Kashani [70] enlisted several swarm-intelligence-based algorithms for optimum cost design of shallow foundations. In the study, PSO, APSO, FA, LKH, whale optimization algorithm (WOA), antlion optimizer (ALO), grey wolf optimizer (GWO), moth-flame optimization algorithm (MFO), and teaching–learning-based optimization algorithm (TLBO) were analyzed. The design procedure was automated based on ACI 318-05 [109] requirements. Moayedi et al. [171] proposed several hybrid approaches for predicting the ultimate bearing capacity of shallow foundation on two-layered soil. The utilized algorithms were an ANN, combined GA, PSO, and differential evolution (DE) with ANN, adaptive neuro-fuzzy inference system (ANFIS), general regression neural network (GRNN), and feedforward neural network (FFNN). Input variables in the study were footing width, top and bottom soil layer properties, thickness of top layer, and width of foundation. Among all the utilized techniques ANN-PSO was the most efficient method. A summary of the application of PSO to shallow foundation is provided in Table 4.

Table 4 Review of the applications of PSO to shallow foundations

5.5 Pile Foundations

Pile foundations have numerous applications in a wide range of civil engineering projects where the shallow foundation is incapable of directing the effective force to the earth appropriately. Guo and Liu [172] utilized the PSO algorithm for analyzing the reliability of bearing capacity of multi-pile foundations. The reliability index was evaluated based on the first-order second-moment approach that minimizes the distance from the origin to the limit-state surface. Three numerical cases were studied, and the results were compared to Monte Carlo simulations. Ismail and Jeng [173] studied the prediction of single piles’ settlement using PSO based higher order neural network (HONN-PSO). Cheng et al. [41] proposed a hybrid approach based on HS and PSO to address the evaluation of pile capacity and pile driving’s control based on a back-analysis approach. Ismail et al. [174] applied a hybrid approach based on PSO and back propagation (BP) to predict the load-deformation behavior of piles. The predicted results based on this hybrid approach satisfactorily matched the actual data. Armaghani et al. [175] proposed a hybrid approach based on PSO and ANN to predict the bearing capacity of rock-socketed piles. The bearing capacity was attributed to soil length to socket length ratio, total length to diameter ratio, uniaxial compressive strength, and standard penetration test. The simulations results demonstrated that PSO-ANN had high reliability in estimating ultimate bearing capacity. Moayedi et al. [176] tried to predict friction capacity ratio in driven shafts using Adaptive Neuro-Fuzzy Inferences System (ANFIS). Their main focus was on optimizing the performance of ANFIS by incorporating GA and PSO in the training procedure. Table 5 tabulates the previous efforts on the application of PSO to pile foundations.

Table 5 Review of the application of PSO to pile foundations

5.6 Tunnels

Tunnel engineering is another field that has benefited from artificial intelligence to some extent. Xing et al. [177] automated the adaptive control of tunnel excavation using PSO. This procedure utilized to back-analyze rock mechanics parameters and to select the optimal construction schemes. Liu et al. [178] applied PSO based LSSVM to the problem of Optimal earth pressure balance control. This is done for shield tunneling. Jiang et al. [179] proposed an AI-based alternative for feedback analysis of tunnel construction, where a two-step procedure based on a combination of PSO and SVM was proposed for handling the problem. Annan and Zhiwu [180] applied an improved PSO (IPSO) to the problem of optimizing the supporting parameters (anchor and spay layer parameters) of metro tunnel. Bahmanikashkooli et al. [181] proposed utilizing the SPO algorithm for determining the critical depth of horseshoe cross-section channels. Conducting numerical simulations showed the efficiency of PSO in handling this problem. Hasanipanah et al. [182] developed a hybrid approach based on ANN and PSO for examining the surface settlement that might take place during tunneling. Hou et al. [83] utilized an exponential tuning mechanism for the inertia weight immune PSO (EAIW-IPSO) for selection of shield tunneling parameter values. A comparative study was provided by applying linear decreasing inertia weight particle swarm optimization (LDIW-PSO), random inertia weight particle swarm optimization (RIW-PSO), and exponentially decreasing inertia weight particle swarm optimization (EDIW-PSO) to this problem. Moosazadeh et al. [183] developed a combined algorithm based on PSO and ANN to assess the building damage caused by tunneling. A summary of different applications of PSO to tunnel related problems can be found in Table 6.

Table 6 Review of the application of PSO to tunnel problems

5.7 Miscellaneous Applications

Chen and Feng [184] attempted to automate back analysis of displacement to estimate rheological parameters of a soft and weak rock mass. To this end, a modified version of PSO with contracted ranges in search space and velocity (CSV-PSO) was considered for handling the problem. This modification was based on considering a parallel strategy where a parallel CSV-PSO with master–slave mode was developed called PCSV-PSO. Zhang [185] utilized a multi-objective approach to find a tradeoff between equipment and configurations of earthmoving operations. In 2009, Chen et al. [186] optimized the construction time of a secant pile wall. A comparative study based on the performance of self-organizing map-based optimization (SOMO) and PSO algorithms were considered for handling the problem. Zhao and Yin [187] estimated the geomechanical parameters based on back analysis approach and monitored displacements. They utilized a combined strategy based on SVM and PSO to handle the back-analysis approach. Jiang and Wan [188] proposed a methodology based on combining colony density PSO (CDPSO) and FLAC for optimizing the length and interval of anchor and the thickness of shotcreting, which consequently resulted in finding optimal cost and time. Yunkai et al. [189] proposed a prediction model for soil erosion using coupled SVM and PSO based on monitoring the data of sand production. Sadoghi Yazdi et al. [190] developed a model based on neuro-fuzzy model and PSO for calibration of soil parameters used in a linear elastic-hardening plastic constitutive model. This model was used in conjunction with the Drucker-Prager yield criterion. A short review of the above-mentioned studies is provided in Table 7.

Roshani and Farsadizadeh [191] utilized PSO for optimizing the dimension of clay core in non-homogeneous earth fill dams. Wan [192] utilised clustering analysis to generate landslide susceptibility maps for Shei Pa National Park in Miao Li, Taiwan. In the study, two different classifiers were used for handling the problem: (1) a combination of entropy-based classification (EBC) and K-mean with PSO (KPSO); and (2) self-organizing map (SOM). Zhang et al. [193] utilized hybrid moving boundary PSO (hm-PSO) for parameters identification in Barcelona Basic Model (BBM). This methodology presented an automatic back analysis approach that minimized the difference between examined and observed values on the cavity pressure-cavity strain curve. Piliounis and Lagaros [194] studied reliability analysis of geostructures using some metaheuristic optimization techniques. Choobbasti et al. [195] developed a hybrid method based on PSO and MLP to locate a trench layer around a pipeline to reach the minimum liquefaction potential. Mirzaei et al. [196] incorporated weighted LSSVM (WLS-SVM) and PSO algorithms to handle the optimal design of homogeneous dams with oblique and horizontal drains. Kutanaei and Choobbasti [197] enlisted a PSO algorithm-based method to examine combined effects of fibers and cement on the mechanical properties of sand. Nama et al. [198] addressed the problem of evaluating active earth pressure in retaining walls. They tried to automate this procedure using PSO, HS, and TLBO optimization algorithms. Hasanipanah et al. [199] presented a PSO-based approach to find a precise equation for predicting flyrock due to blasting. Samareh et al. [200] developed a predictive method based on a hybridized PSO and GA. In the study, peak particle velocity (PPV) resulting from mining blasts were examined with nonlinear regression and ANN. Yin et al. [9] investigated the performance of different optimization algorithms for identifying soil parameters. Fatty and Li [201] used PSO to handle back-analysis procedure and investigate uncertain geotechnical parameters for a rock slope. Hasheminejad et al. [204] employed a hybrid approach based on adaptive neural fuzzy inference system (ANFIS) and PSO for examining collapsibility of unsaturated soils. Bui et al. [23] combined PSO and MLP for predicting soil compression coefficient. Nguyen et al. [202] utilized ANFIS enhanced by PSO, hybrid ANN-PSO, and best first decision trees-based rotation forest (RFBFDT) for landslide spatial prediction. Zhang et al. [203] employed a mixed technique based extreme gradient boosting machine (XGBoost) and PSO for predicting ground vibration in open-pit mines caused by blasting. Xi et al. [205] used a combined algorithm based on PSO and ANN for hazard assessment of earthquake-made landslide in Ludian area, China.

Table 7 Review of the other applications of PSO in geotechnical engineering problems

6 Numerical Simulation

In this section, we report on the efficacy of FDPSO, IRDPSO, MPSO, IPSO, AGPSO, CLSPO, HCLPSO and EPSO examined through computational experiments based on problems of three different geotechnical categories: concrete cantilever retaining walls, shallow foundations, and slope stability. To this end, three computer programs have been developed to simulate the basis of our problems as fitness functions based on Das [206] and ACI 318-05 [109] in MATLAB (2012Ra). For the retaining walls, two objectives are considered: to minimize the final cost and final weight of the projects. Shallow footing optimization deals with minimizing the final cost. For slope stability, the value of factor of safety is minimized to find the most critical failure surface.

Final results using the above-mentioned algorithms are compared to those obtained by PSO. The final results are reported in the form of Best, Mean and standard deviation (SD) from a series of 101 runs for retaining wall and shallow footing and 20 runs for slope stability problems for each algorithm. Moreover, a non-parametric Friedman statistical test is utilized for ranking the algorithms’ performances based on their scores. The lower the scores, the better the performance of the algorithms. In the retaining wall and shallow footing problems, the population size of 50 and the number of iterations of 1000 were considered for all the algorithms. Besides, the slope stability problem was run with the population size of 50 and the number of iterations of 3000. The obtained results are collected in Tables 8–16 as well as Figs. 1–7. It is worth noting that the best-found observations are shown in bold.

6.1 Retaining Wall Minimum-Cost and Minimum-Weight Simulations

In this section, a 3 m wall presented as the first example in [11] is analyzed. This wall is affected by the nine combinations of seismic loading conditions. This example is resolved by eight variations of PSO. Based on the statistical results, the Mean and SD of each algorithm are tabulated in Tables 8 and 9, respectively. Rankings of the algorithms based on Friedman test results are presented in Tables 10 and 11.

Table 8 Mean and SD values in terms of cost for retaining wall numerical simulations

Table 9 Mean and SD values in terms of weight for retaining wall numerical simulations

Table 10 Friedman test scoring for minimum-cost design of retaining wall

Table 11 Friedman test scoring for minimum-weight design of retaining wall

Results of low-cost design reveal improvements to the PSO algorithm’s performance with both HCLPSO and EPSO. RDPSO recorded the poorest results while HCLPSO has the lowest values of Mean solutions. Also, although HCLPSO found lower values of Mean and SD over all the cases, there were also slight differences between the results obtained by HCLPSO and EPSO. In contrast, for the minimum-weight design, there was no uniform pattern in the performance of the evaluated algorithms. It can be seen clearly that although in some cases EPSO and HCLPSO overcome the original PSO, in most of the cases there was no considerable advancement provided by HCLPSO and EPSO. In other words, the three algorithms performed identically in most of the cases. Considering all the algorithms together, we can say that PSO variations other than HCLPSO and EPSO performed inefficiently in this case. Moreover, RDPSO again recorded the poorest results in this case. Reviewing the results presented in Tables 8 and 9, it can be seen that for low-cost design, HCLPSO has achieved the lowest mean values again, while for low-weight design there is no definite algorithm that would be the best over all the cases.

In Table 10, the Friedman ranking results for low-cost design show that HCLPSO had the lowest scores. EPSO ranked second in all the cases except for cases 3 and 6, where the original PSO performed better. On the contrary, the worst algorithm over all but cases 4 and 7 was RDPSO. For cases 4 and 7, the poorest results were provided by AGPSO3 and AGPSO2, respectively. The Friedman test results in Table 11 again show that there was no consistent pattern between the evaluated algorithms. For weight design of the wall, HCLPSO was the best in all cases except cases 2, 3, and 8 where PSO proved to be the best. Ignoring cases 2 and 9 in which CLPSO and MPSO were the weakest algorithms, respectively, RDPSO was the weakest algorithm in the remaining cases.

Reviewing the convergence rate plots in Figs. 1 and 2, we see a more moderate level of convergence for HCLPSO and EPSO than other variations of PSO. It can be observed that CLPSO could not converge to a valid solution until the latter iterations. Moreover, RDPSO and FDPSO reached solutions far away from the other algorithms’ results. Mean convergence results confirm the better performance of HCLPSO and EPSO.

Fig. 1

Convergence rate plots based on best solutions of retaining wall numerical simulation for minimum cost design. (Color figure online)

Fig. 2

Convergence rate plots based on best solutions of retaining wall numerical simulation for minimum weight design. (Color figure online)

Different loading combinations from the static loading case (case 1) to dynamical ones (cases 2–9) showed that, by applying the horizontal loading factor, the final design saw an increase in either the cost value or weight value. However, by applying and increasing the vertical components the final design was reduced from 0 in cases 1 and 2 to 0.15 in cases 4 and 5, respectively, and from 0.15 in cases 4 and 5 to 0.3 in cases 7 and 8, respectively. Lower costs and weights in the final design, by increasing the vertical coefficient of earthquake loading, may be observed in the presence of horizontal loading component k_h= 0.15. On the contrary, this reduction was not observed if the horizontal loading factor of 0.3 was applied to the wall.

6.2 Shallow Footing Minimum-Cost Design

For the shallow footing case study, a foundation situated on a cohesionless soil under two different loading cases studied by Gandomi and Kashani [70] was considered. In the first case, this footing was subjected to transmission of uniaxial forces resulting from the combination of dead and live loads equalling 650 kN and 350 kN, respectively. The final results are summarized in Table 12 based on the best, worst, mean, SD, and median values. In this case, as shown in Table 12, all the variations except CLPSO, FDPSO, RDPSO and EPSO had the lowest solution of $43,442.27, though it can be seen that EPSO registered a better record based on the lowest values of Mean and SD of $47,152.33 and $2076.14, respectively. From the results, it can also be concluded that most of the improved algorithms had better performance than PSO because of the lower values of mean, SD, and Median. Analyzing the Friedman test results presented in Table 13, it can be seen clearly that HCLPSO performed better than EPSO, and AGPSO3 was the second best algorithm. Moreover, most of the algorithms performed better than the original PSO.

Table 12 Design cost values for the shallow footing case I numerical simulations

Table 13 Friedman test scoring for minimum-cost design of shallow footing

For the second case, in addition to the vertical forces in the previous case, a moment was applied at the center of footing, which is a combination of the dead and live loads of 400 kN m and 150 kN m, respectively. In this case, PSO, CLPSO, and RDPSO failed to converge to a valid solution. AGPSO2, ISPO, and TACPSO obtained the lowest design of $71,225.33, while EPSO had the lowest values of Mean, SD, and Median of $72,601.88, $1461.44, and $72,102.83, respectively. The Friedman test assessment and ranking of the algorithms based on their performances confirmed that EPSO was the best algorithm thanks to its lower score (Table 14).

Table 14 Design cost values for the shallow footing case II numerical simulations

Convergence rate curves of the shallow footing simulation based on the mean results are shown in Figs. 3 and 4, respectively. As expected, Fig. 3 shows a fast convergence of PSO while other variations of PSO follow a gentler trend for convergence. The convergence pattern is a clear proof of stronger exploration in modified versions than the original PSO. In those figures, FDPSO and MPSO converged to the results far more than the optimal solutions. Original PSO, RDPSO, and CLSPO recorded weak performance in the first case study based on poor convergence and in the second case since they were unable to converge to the final solutions. According to the figures, EPSO and HCLPOS approached the final solution after the 100th iteration. The slower convergence rate of HCLPSO and EPSO in these cases proves the stronger exploration ability of HCLPSO and EPSO than other PSO variations.

Fig. 3

Convergence rate plot based on best solutions for foundation design case I. (Color figure online)

Fig. 4

Convergence rate plot based on best solutions for foundation design case II. (Color figure online)

6.3 Slope Stability Analysis Simulations

For the third numerical simulation, soil slope stability, which is one of the most complicated engineering problems was considered [26]. Three different soil slopes were resolved, as shown in Figs. 5, 6 and 7 borrowed from Arai and Tagyo [207], ACAD, a study by Donald et al. [208], and Zolfaghari et al. [209] as Cases I, II, and III, respectively. A brief comparison of the final results is shown in Table 15. Furthermore, the most critical slip surfaces of each slope are shown in Figs. 5, 6 and 7. In all of the case studies, we attempted to collect complicated slope samples in which a weak soil layer is situated between two stronger ones.

Fig. 5

Slope geometry and critical slip surface for case I. (Color figure online)

Fig. 6

Slope geometry and critical slip surface for case II. (Color figure online)

Fig. 7

Slope geometry and critical slip surface for case III. (Color figure online)

Table 15 Values of factor of safety for slope stability problems

The first example is the most straightforward case without sensible difference between the algorithms’ results. In this case, the lowest FOS were obtained by FDPSO and IPSO, while FDPSO performed better with lower values of Mean and SD. Based on the Friedman test results too, the lowest score were provided by FDPSO. All the PSO variations except RDPSO and CLPSO were better than the original PSO in this case based on their lower Mean values and Friedman scores. For the second case, a more complex problem with a band of weak soil layer sandwiched between two strong layers was tackled. It can be seen that the final solution of FOS was improved considerably. The lowest values of FOS acquired by AGPSO3 and TACPSO are nearly identical and better than other algorithms. However, the Mean value of TACPSO was less than AGPSO3. The worst performances were recorded by RDPSO, CLPSO, and original PSO, respectively.

The Friedman test results, however, indicate that TACPSO was the best algorithm with the lowest score in examples 2. The worst algorithm, in this case, was again RDPSO. In the third case, TACPSO outperformed other PSO variants based on the lowest values of Best, Mean and SD. The Friedman test results further confirmed the superiority of TACPSO over other algorithms, while the worst performance was provided by the original RDPSO (Table 16).

Table 16 Friedman test scoring for slope stability analysis

7 Conclusion

There were two major objectives of this paper. First, we aimed to provide a comprehensive review of the application of PSO algorithms to solve a wide range of geotechnical engineering problems. Second, we wanted to investigate the use of some variants of PSO, including FDPSO, IRDPSO, MPSO, IPSO, AGPSO, CLPSO, HCLPSO and EPSO, to solve three geotechnical engineering problems.

Review of the literature on the application of PSO to geotechnical problems indicated that this algorithm approches difficult problems in different ways. There are several cases where PSO algorithms have shown satisfying performance to address difficulties of these problems. On the other hand, some other challenging cases proved to be beyond PSO algorithms’ ability to find optimum solutions. In general two different strategies have been employed for using PSO to handle the problems: first, directly approaching the problems by consducting an optimization procedure; second, coupling with prective tools (e.g., ANN, SVM, etc.) for optimizing the hyper parameters. In addition, several reseachers have attempted to enhance PSO by proposing hybrid optimization algorithms or by introducing some modifications to PSO itself.

For the second objective, three different geotechnical engineering benchmark problems, which include the slope stability, retaining wall, and shallow footing problems, were tackled in this study. For the slope stability problem, the objective was to minimize the FOS against slipping, while for the retaining wall problem, two objectives—the total cost and weight minimization—were considered. For shallow footing, the total cost value was considered. All the three problems followed the stability criteria defined by ACI 318-05 [109], AASHTOO [108], and Das [206]. The algorithms’ performances were examined via comprehensive simulation experiments on cantilever concrete retaining walls affected by pseudo-static loading cases, shallow footing, and soil slope stability. Experiments on each algorithm were repeated 20 times for every slope stability problem instance and 101 times for the retaining wall and shallow footing problems. We reported the best-found solutions, means and standard deviations of the results, as well as the amount of diversity. Non-parametric Friedman tests were carried out to ascertain the statistical significance of the results obtained.

Our results have clearly demonstrated that most of the PSO variations are capable of solving the problems at hand well. Comparisons of the mean and standard deviation results for the retaining wall problem showed substantial improvements achieved by HCLPSO and EPSO over other PSO variants in terms of minimizing the cost and weight. HCLPSO was the best algorithm for cost minimization of the wall. Moreover, this algorithm was also successful in achieving better results than other methods in terms of weight minimization in most of the cases. Friedman test results confirmed that the improvements were significant. Despite the results obtained by the algorithms, in terms of minimizing the weight, appearing nearly identical to the original PSO in some cases, Friedman test results indicated that HCLPSO’s results were actually significantly better than the results provided by other algorithms. Shallow footing analysis has also shown significantly better performances of HCLPSO and EPSO over other variations of PSO based on the mean and standard deviation values as well as Friedman test results. For the slope stability problem though TACPSO performed better than other algorithms. TACPSO has obtained the lowest mean and standard deviation results in examples 2 and 3 while FDPSO emerged as the best performer in one of the case studies.

To sum up, balancing between exploration and exploitation is a necessary step to achieving the best possible performance of an optimization algorithm. This study reiterated this fact and showed that PSO variants can be successfully used to solve geotechnical engineering problems. It can be observed that most of the enlisted strategies for improving PSO’s performance were successful in improving the results provided by the original PSO. In our future work, we will further investigate the potential of improving these PSO variants and use them to solve other civil engineering problems.