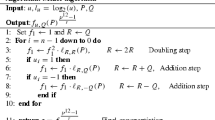Faster Beta Weil Pairing on BLS Pairing Friendly Curves with Odd Embedding Degree

Abstract

Since the advent of pairing-based cryptography, various optimization methods that increase the speed of pairing computations have been exploited, as well as new types of pairings. This paper extends the work of (Kinoshita and Suzuki Advances in Information and Computer Security - 15th International Workshop on Security, IWSEC 2020, Fukui, Japan, September 2-4, 2020, Proceedings, Lecture Notes in Computer Science, Springer, 2020) who proposed a new formula for the $\beta$-Weil pairing on curves with even embedding degree by eliminating denominators and exponents during the computation of the Weil pairing. We provide novel formulas suitable for the parallel computation for the $\beta$-Weil pairing on curves with odd embedding degree which involve vertical line functions useful for sparse multiplications. For computations we used Miller’s algorithm combined with storage and multifunction methods. Applying our framework to BLS-27, BLS-15 and BLS-9 curves at respectively the 256 bit, the 192 bit and the 128 bit security level, we obtain faster $\beta$-Weil pairings than the previous state-of-the-art constructions. The correctness of all the formulas and bilinearity of pairings obtained in this work is verified by a SageMath code.

1 Introduction

Pairings have first been studied in mathematical research areas such as algebraic number theory and algebraic geometry [2]. Then pairings on elliptic curves have attracted significant attention and have been applied to many cryptographic schemes, namely Boneh and Franklin’s identity based encryption scheme [3], Boneh, Lynn and Shacham’s short signature scheme [4] and Joux’s one round tripartite key exchange [5]. Before the advent of pairings one did not know how to effectively build up these protocols. A pairing is a bilinear map from the cartesian product of two abelian additive groups to an abelian multiplicative group. For instance, the Weil pairing e over the r-torsion E[r] of an elliptic curve E,  satisfies the following basic properties :

• e is bilinear i.e. for every $P_{1}, P_{2}, Q_{1}$ and $Q_{2}$ in E[r],  we have that $e(P_{1} + P_{2}, Q_{1})= e(P_{1}, Q_{1})\cdot e(P_{2}, Q_{1})$ and $e(P_{1}, Q_{1} + Q_{2})= e(P_{1}, Q_{1})\cdot e(P_{1}, Q_{2})$;

• e is non degenerate i.e. if $e(P, Q)=1$ for all $P\in E[r]$, then $Q=\mathcal {O},$ where $\mathcal {O}$ is the point at infinity;

• e is alternating i.e. $e(P, P)=1$ for all P in E[r].

The bilinearity is the most important property for building applications with cryptographic pairings. The very first pairings used in cryptography were the Weil and the Tate pairings [3, 6]. To date there are several variants of the Tate pairing and the most efficient candidate is the optimal Ate pairing [7]. On the other hand variants of the Weil pairing such as $\alpha$-Weil [8], $\beta$-Weil [8,9,10] and $\omega$-Weil pairings [11, 12] are elegant constructions tailored for parallel executions. Viewed in this angle, the $\beta$-Weil pairing is more efficient than the optimal Ate pairing [9, 10]. Moreover our motivation for computing the $\beta$-Weil pairing rather than the Tate pairing or its variants, is that it has no time-consuming final exponentiation and can be trivially parallelized [9]. The pairings can be implemented on a smart card, but due to the limited computing power and constrained memory there is a need to faster evaluate the pairings.

In this work, we focus on the $\beta$-Weil pairing defined over pairing-friendly elliptic curves with odd embedding degrees 9, 15 and 27. These curves admit twists of degree three which enable computations to be done in subfields and also lead to the denominator elimination technique. It is noticed in [13] that elliptic curves with embedding degree $k = 27$ are a suitable choice for computing product of pairings. Moreover, Barbulescu et al. showed that at the 256 bits security level, curve with $k=27$ seem to be the best choice for pairing efficiency [14]. Also in [10] Fouotsa et al. proposed a pairing denoted $\hat{\beta }_{k }$-pairing different from $\beta$-pairing which is more efficient than the optimal Ate pairing over BLS-15. Many works in the litterature have been carried out for faster evaluation of the pairings such as [15,16,17,18,19,20,21] including their security [22,23,24].

The original $\beta$-Weil pairing that we consider here is the generalised formula proposed by Fouotsa et al. in [10]. Their theoretical evaluation showed some limitations such as:

• The inversions of Miller’s functions which are very costly,

• The precomputation of some points $[p^i]P$ that underestimated the total cost of the $\beta$-Weil pairing,

• the $\beta$-Weil pairing was not tailored for multifunction technique, this technique extremely reduces the cost of squarings in the finite field.

Our main contribution is the extension of Kinoshita and Suzuki’s work [1] who proposed a formula for the $\beta$-Weil pairing on the curves with even embedding degree by eliminating the denominators and the exponents. But their formula to simplify the denominators does not work for odd embedding degrees. We then provide a novel formula for the $\beta$-Weil pairing on curves with odd embedding degrees which involve vertical line functions useful for sparse multiplications. To compute the new formula of our novel $\beta$-Weil pairing, we use Miller’s algorithm based on storage and multifunction techniques.

Whereas, storage technique consists of compute and store line functions for Miller’s loop that are reused to find another line functions for other Miller’s function, multifunction technique evaluates the product of n Miller’s functions and only requires a single squaring in the extension field per iteration instead of n squarings in the naive way. The idea of precomputation and storage of line functions and the exploitation of sparsity can be found in [25] and for multi-function technique see [26].

The correctness of the formulas for curves with embedding degrees 27, 15 and 9 are ensured by a SageMath script available at [27] and inspired by Aurore’s online SageMath repository for even embedding degree pairings. As applications we applied the variant of Miller’s algorithm with these formulas with the Miller loop parameters obtained by applying the recommendation in [28] and [29, 30]. The pairings over these curves are resistant to the STNFS attacks.

Detailed cost estimation of $\beta$-Weil pairing on BLS-27, BLS-15 and BLS-9 at respectively the 256, 192 and 128 bits level of security are provided. Our theoretical results reduce the number of multiplication operations on the prime field in $\beta$-Weil pairing for BLS family with $k=27,15$ and 9 about $44.78 \% ,$ $49.07 \%$ and $38.49 \% ,$ as well as the number of divisions of about $87.1 \%$ $78.8 \%$ and $61.2 \%$ respectively for serial computation. The optimal Ate pairing remains the fastest pairing in the serial computation. However, the proposed $\beta$-Weil pairing on curve with $k=15$ is competitive to optimal Ate pairing on the same curve. In the parallel computation with 3 processors, the $\beta$-Weil pairing on BLS-27,  BLS-15 and BLS-9 is faster than the optimal Ate pairing. For more details see Sect. 6, Appendix A.2.2 and Table 3.

This paper is organized as follows. The Sect. 2 summarises the mathematical background on Weil pairing over elliptic curves and recalls the idea of Kinoshita and Suzuki [1] to accelerate the $\beta$-Weil pairing computation. Sect. 3 provides a new formula of the $\beta$-Weil pairing on curves with odd embedding degrees. Sect. 4 describes storage and multifunction techniques. Sect. 5 estimates the theoretical cost of the basic and special operations of the pairing. Sects. 6 provides theoretical costs of computing, the new $\beta$-Weil pairing both in serial and parallel and sect. 7 compares our results with those done on previous works. Finally, Sect. 8 concludes the work.

2 Mathematical Preliminaries.

In this section, we define the Weil pairing as well as its variant called $\beta$-Weil pairing with some past results.

2.1 The Weil Pairing

Let E be an elliptic curve defined over $\mathbb {F}_{p}$, where p is a large prime number and let r be the largest prime number such that r divides $\#E(\mathbb {F}_{p})$. Let k be the smallest positive integer such that r divides $p^{k} - 1$. The integer k is called the embedding degree of E (with respect to r). For any $P \in E[r] ,$ we denote $f_{r,P}$ the rational function with divisor

$$\begin{aligned} div(f_{r,P}) = r[P] - r[\mathcal {O}]. \end{aligned}$$

The Weil pairing is defined as:

$$\begin{aligned} e_{W}: E(\mathbb {F}_{p^k})[r]\times E(\mathbb {F}_{p^k})[r] \longrightarrow \mu _{r} : (P,Q)\longmapsto (-1)^r\frac{f_{r,P}(Q)}{f_{r,Q}(P)}. \end{aligned}$$

The function $f_{r,P}$ is called the Miller function, it is obtained through Miller’s algorithm [17] based on the following relations. For all $a,b \in \mathbb {Z}$ and $P\in E[r],$

$$\begin{aligned} f_{1, P}= & {} 1, \end{aligned}$$

(2.1)

$$\begin{aligned} f_{a+b, P}= & {} f_{a, P}\cdot f_{b, P}\cdot h_{[a]P, [b]P}, \end{aligned}$$

(2.2)

$$\begin{aligned} f_{ab, P}= & {} f_{b, P}^a \cdot f_{a, [b]P}=f_{a, P}^b \cdot f_{b, [a]P}, \end{aligned}$$

(2.3)

where $h_{[a]P, [b]P}=l_{[a]P, [b]P}/\mathcal {V}_{[a+b]P}$ and $l_{[a]P, [b]P}$ is the straight line containing [a]P and [b]P and $\mathcal {V}_{[a+b]P}$ is the corresponding vertical line passing through $[a+b]P$.

The Weil pairing is composed of two executions of the Miller’s loop for the evaluation of $f_{r, P}(Q)$ and $f_{r, Q}(P).$ The efficiency of Miller’s loop highly depends on the choice of the elliptic curve and the system of coordinates of the elliptic curve. Pairing-friendly elliptic curves are curves allowing an efficient implementation of pairings. These curves are parametrized by polynomials p(x), r(x) and t(x) such that for a given security level, we find the corresponding value of x such that $\#E(\mathbb {F}_{p(x)})=p(x)+1-t(x)$ is divisible by r(x). The parameters p(x), r(x) and t(x) for elliptic curves with embedding degrees 9, 15 and 27 denoted as BLS-9,  BLS-15 and BLS-27 in [31] are respectively represented as polynomials as follows:

• BLS-27: $r(x)= \frac{1}{3}(x^{18} + x^{9} + 1),$ $p(x)= \frac{1}{3}(x-1)^2(x^{18} + x^{9} + 1)+x,$ $t(x)= x+1.$

• BLS-15: $r(x)= x^{8}-x^{7} + x^{5}-x^{4}+x^{3}-x + 1,$ $p(x)= \frac{1}{3}(x^{12}-2x^{11} + x^{10}+x^{7}-2x^{6}+x^5+x^2+x + 1),$ $t(x)= x+1.$

• BLS-9: $r(x)= \frac{1}{3}(x^{6} + x^{3} + 1),$ $p(x)= \frac{1}{4}((x+1)^2+\frac{1}{3}((x-1)^2(2x^{3} + 1)^2)),$ $t(x)= x+1.$

2.2 Previous Results on $\beta$-Weil Pairing Computation

The most efficient way to optimize a pairing is by using Miller’s algorithm which computes the rational function $f_{s, R}$ where, $s \in \mathbb {Z}$ and $R\in E[r].$ This rational function is called Miller’s function with divisor $div(f_{s, R})=s(R)-([s]R)-(s-1)(\mathcal {O}).$ Vercauteren [7] introduced the extended Miller function $f_{s,h, R}$ with divisor $div(f_{s,h, R})=\sum _{i=0}^{w}h_{i}(([p^i]R)-(\mathcal {O})),$ where $h(x)=\sum _{i=0}^{w}h_{i}x^i$ in $\mathbb {Z}[x]$ is the optimal polynomial obtained by using a lattice-based method such that $h(p)=0 \mod r.$ For $m =h(p)/r$ and $m\not \mid r,$ this extended Miller function is expressed as

$$\begin{aligned} f_{s,h, R}=\dfrac{f_{r, R}^m}{\prod _{j=0}^{w}f_{p^j, R}^{h_{j}}}. \end{aligned}$$

(2.4)

The extended Miller’s function was used to propose efficient variants of Ate pairing and Weil pairing such as optimal Ate pairing [7] and $\beta$-Weil pairing [8] on curves of even embedding degrees where the Miller’s loop length is reduced to $\log _{2}(x)$ iterations.

In [10], Fouotsa et al. extended the work of Aranha et al. [8] on the $\beta$-Weil pairing to curves with an odd embedding degree k. They provided the following formula.

Theorem 2.1

([10], Theorem 4). Let l be a proper divisor of k. There exists a polynomial $h(z)=\sum _{i=0}^{w}h_{i}z^{i}\in \mathbb {Z}[z]$ such that $| h_{i}|<r^{\frac{1}{\varphi (k)}}$ and $h(p)=rs$ so that the map

$$\begin{aligned} \beta _{k}: \mathbb {G}_{1}\times \mathbb {G}_{2} \rightarrow \mu _{r}: (P,Q)\mapsto \left( \prod _{i=0}^{e-1}\left( \dfrac{f_{p,h,Q}([p^i]P)}{f_{p,h,[p^i]P}(Q)}\right) ^{p^{e-1-i}}\right) ^{p^{l}-1}, \end{aligned}$$

is a pairing and $e=k/d$ where d is the twisted degree of the curve. More precisely, if $r\not \mid sp^{e-1-i}$ and $r\not \mid h_{j},$ for all $0\le i\le e-1$ and $1\le j\le w,$ then the map $\beta _{k}$ is non-degenerate.

Note that the final powering $p^l-1$ sends to 1 the multiplicative factors of the Miller’s function which lies in proper subfields of $\mathbb {F}_{p^k}.$

Remark 2.2

For curves of even embedding degrees, Aranha [8] et al. provided the following formula of the $\beta$-Weil pairing

$$\begin{aligned} \beta _{k} (P,Q)= \left( \prod _{i=0}^{e-1}\left( \dfrac{f_{p,h,Q}([p^i]P)}{f_{p,h,[p^i]P}(Q)}\right) ^{p^{e-1-i}}\right) ^{p^{k/2}-1}. \end{aligned}$$

To avoid denominators and exponents in the computation of $\beta$-Weil pairings for curves of even embedding degrees, Kinoshita et al. [1] considered the useful results in the following lemma.

Lemma 2.3

• 1. Elimination of the denominators (and thus an inversion) of the $\beta$-Weil pairing. In the context of an elliptic curve of even embedding degree, the following relations hold:

  $$\begin{aligned} f_{a,R}^{-1}=f_{a,-R} \qquad and \qquad f_{p,h,R}^{-1}=f_{p,h,-R} \end{aligned}$$

• 2. Elimination of the exponents of the $\beta$-Weil pairing. For any $P\in \mathbb {G}_{1}$ and $Q\in \mathbb {G}_{2}$ :

  $$\begin{aligned} f_{p,h,P}^{p^i}(Q)=f_{p,h,P} (\pi _{p^i}(Q))\qquad and \qquad f_{p,h,Q}^{p^i}(P)=f_{p,h,\pi _{p^i}(Q)} (P). \end{aligned}$$

Then they provided the simplified formula of the $\beta$-Weil pairing

$$\begin{aligned} \beta _{k}(P,Q)= \left( \prod _{i=0}^{e-1}f_{p,h,\pi _{p^{\delta _{i}}}(Q)}([p^i]P) \cdot f_{p,h,[p^i]\overline{P}}(\pi _{p^{\delta _{i}}}(Q))\right) ^{p^{k/2}-1} \end{aligned}$$

(2.5)

where, $\overline{P}=-P$ and $\delta _{i}=e-1-i.$

The first item of the Lemma 2.3 does not work on elliptic curves with odd embedding degrees. In the following we will derive an analogous lemma as well as the new $\beta$-Weil pairing on elliptic curves of odd embedding degrees.

3 New Formula for $\beta$-Weil Pairing

In this section we first provide a new general formula of $\beta$-Weil pairing on elliptic curves of odd embedding degrees. Then we give the explicit formulas of $\beta$-Weil pairing on BLS-27,  BLS-15 and BLS-9.

3.1 New Formula for $\beta$-Weil Pairing: the Case of Odd Embedding Degrees

The following lemma gives nice properties of the Miller’s function in the case of odd embedding degrees.

Lemma 3.1

For all $a\in \mathbb {Z}$ and $R\in E$, we obtain the following two relations:

• (i) $f_{a,R}^{-1}=f_{a,-R} \cdot \mathcal {V}_{[a]R} \cdot \mathcal {V}_{R}^{-a}.$

• (ii) $f_{p,h,R}^{-1}=f_{p,h,-R}\cdot \prod _{j=0}^{w}\mathcal {V}_{[p^j]R}^{-h_{j}}.$

Proof

• (i) From Eq. 2.3, We have that, $f_{a,R}^{-1}=\dfrac{f_{-1,R}^{a} \cdot f_{a,[-1]R}}{f_{-1,[a]R}}.$

  Since, $div(f_{-1,[a]R}) =-(([a]R)+([-a]R))-2(\mathcal {O})=div(\mathcal {V}_{[a]R}^{-1})$

  and $div(f_{-1,R}^a) =di(\mathcal {V}_{R}^{-a}).$ Then, $f_{a,R}^{-1}=f_{a,-R} \cdot \mathcal {V}_{[a]R} .\mathcal {V}_{R}^{-a}.$

• (ii) From Eq. 2.4, we have that $f_{p,h,R}=\dfrac{f_{rm,R}}{\prod _{i=1}^{w}f_{p^i,R}^{h_{i}}}.$ Taken this equation to power $-1$, it yields $f_{p,h,R}^{-1}=\dfrac{f_{rm,R}^{-1}}{\prod _{i=1}^{w}(f_{p^i,R}^{-1})^{h_{i}}}.$ Then from (i), $f_{p,h,R}^{-1}=\dfrac{f_{rm,-R} \cdot \mathcal {V}_{[rm]R} \cdot \mathcal {V}_{R}^{-rm}}{\prod _{i=1}^{w}\bigg (f_{p^i,-R}^{h_{i}} \cdot \mathcal {V}_{[p^i]R}^{h_{i}} \cdot \mathcal {V}_{R}^{-p^ih_{i}}\bigg )}=\dfrac{f_{rm,-R} }{\prod _{i=1}^{w}f_{p^i,-R}^{h_{i}} } \cdot \dfrac{\mathcal {V}_{[rm]R} \cdot \mathcal {V}_{R}^{-rm}}{\prod _{i=1}^{w}(\mathcal {V}_{[p^i]R}^{h_{i}}) \cdot \mathcal {V}_{R}^{-\sum _{j=0}^{w}h_{i}p^i}}.$ Since, $[r]R=\mathcal {O}$ and $\sum _{j=0}^{w}h_{j} p^j=r \cdot m,$ the result follows $f_{p,h,R}^{-1}=f_{p,h,-R} \cdot \prod _{j=0}^{w}\mathcal {V}_{[p^j]R}^{-h_{j}}.$

A straightforward application of Lemma 3.1 in the Theorem 2.1 gives the following theorem:

Theorem 3.2

For every curves of odd embedding degrees, the new formula of $\beta$-Weil pairing is given as follows

$$\begin{aligned} \beta _{k}(P,Q)= \left( \prod _{i=0}^{e-1}f_{p,h,\pi _{p^{\delta _{i}}}(Q)}([p^i]P) \cdot f_{p,h,[p^i]\overline{P}}(\pi _{p^{\delta _{i}}}(Q))\cdot \prod _{j=0}^{w}\mathcal {V}_{[p^{i+j}]P}^{-h_{j}}(\pi _{p^{\delta _{i}}}(Q))\right) ^{p^l-1}, \end{aligned}$$

(3.1)

where $\overline{P}=-P$ and $\delta _{i}=e-1-i$.

Corollary 3.3

For pairing-friendly curves of embedding degrees $k=27,15$ and 9,  the polynomial h(z) for the extended Miller’s function yields $h(z)=x-z,$ then $f_{p,h,P}= f_{x,P}$ and Eq. 3.1 becomes

$$\begin{aligned} \beta _{k}(P,Q)= \left( \prod _{i=0}^{e-1}f_{x,Q_{i}}(P_{i}) \cdot f_{x,\overline{P}_{i}}(Q_{i}) \cdot \mathcal {V}_{P_{i}}^{-x}(Q_{i}) \cdot \mathcal {V}_{P_{i+1}}(Q_{i})\right) ^{p^l-1}, \end{aligned}$$

(3.2)

where $P_{i}=[p^i]P$ and $Q_{i}=\pi _{p^{\delta _{i}}}(Q).$

Enge and Milan [32] proposed a variant of Miller’s algorithm (Algorithm 2) which evaluates the function $f_{x,P}$ or $f_{x,Q}$ for any seed x,  positive, negative, sparse, in binary and in $2-$NAF form, that is, $x = \sum _{i=0}^{n} s_{i}2^i$ with $s_{i}$ in $\{0,-1,1\}.$

Moreover, for a matter of efficiency, it is possible to find the parameters x,  so as to avoid the computation of $\mathcal {V}_{P_{i}}^{-x}(Q_{i}) .$ The simplified formulas in this case are given by corollary 3.4.

Corollary 3.4

The simplified formulas of the $\beta$-Weil pairing with $x=-2^n+\sum _{i=0}^{n-1}s_{i}2^i,$ or $x=2^n+\sum _{i=0}^{n-1}s_{i}2^i,$ where $s_{i}\in \{0,-1,1\},$ is

$$\begin{aligned} \beta _{k}(P,Q)= \left( \prod _{i=0}^{e-1}f_{x,Q_{i}}(P_{i})\cdot f_{-x,P_{i}}(Q_{i}) \cdot \mathcal {V}_{P_{i+1}}(Q_{i})\right) ^{p^l-1}, \end{aligned}$$

(3.3)

where $P_{i}=[p^i]P$ and $Q_{i}=\pi _{p^{\delta _{i}}}(Q).$

Proof

If $x<0,$ that is $x=-|x|$ since, $\overline{P}_{i}=-P_{i}$ then, $f_{x,\overline{P}_{i}}(Q_{i})= f_{-|x|,-P_{i}}(Q_{i}).$ From Eq. 2.3, $f_{-|x|,-P_{i}}(Q_{i})=f_{-1,-P_{i}}^{|x|}(Q_{i})\cdot f_{|x|,P_{i}}(Q_{i}).$ But, $f_{-1,-P_{i}}(Q_{i})=\mathcal {V}_{-P_{i}}^{-1}(Q_{i})$ and $\mathcal {V}_{-P_{i}}^{-1}(Q_{i})=\mathcal {V}_{P_{i}}^{-1}(Q_{i}),$ therefore $f_{x,\overline{P}_{i}}(Q_{i})=f_{|x|,P_{i}}(Q_{i})\cdot \mathcal {V}_{P_{i}}^{-|x|}(Q_{i})=f_{-x,P_{i}}(Q_{i})\cdot \mathcal {V}_{P_{i}}^{x}(Q_{i}).$

If $x>0,$ $f_{-x,P_{i}}(Q_{i})=f_{x,-P_{i}}(Q_{i})\cdot \mathcal {V}_{P_{i}}^{-x}(Q_{i})$ i.e $f_{x,\overline{P}_{i}}(Q_{i})=f_{-x,P_{i}}(Q_{i})\cdot \mathcal {V}_{P_{i}}^{x}(Q_{i}).$

For each case substitute, $f_{x,\overline{P}_{i}}(Q_{i})$ by $f_{-x,P_{i}}(Q_{i})\cdot \mathcal {V}_{P_{i}}^{x}(Q_{i})$ in Eq. 3.2 and it becomes Eq. 3.3.

Algorithm 1 computes $f_{x,Q}(P)$ for positive x,  whereas Algorithm 2 computes $f_{x,Q}(P)$ for negative x. In fact, $f_{x,Q}(P)=f_{-x,-Q}(P)\cdot \mathcal {V}_{Q}^{x}(P)$ and the Algorithm 2 computes $\mathcal {V}_{Q}^{x}(P)$ internally.

By direct analogy with Algorithm 1 and  2, exchanging P and Q gives two algorithms for computing Miller Lite function this is, $f_{x,P}(Q)$ for positive x and $f_{x,P}(Q)$ for negative x respectively. Note that the Miller Lite function is defined over $\mathbb {F}_{p}$ and evaluated at a point of $E(\mathbb {F}_{p^k}).$ Whereas the Full Miller function is defined over $\mathbb {F}_{p^k}$ and evaluated at a point of $E(\mathbb {F}_{p}).$

Remark 3.5

Lin et al. [33] first observed that, for every point S in $\mathbb {G}_{1}$ and R in $\mathbb {G}_{2}$, we have that

$$\begin{aligned} \frac{1}{\mathcal {V}_{R}(S)}=\frac{1}{x_{S}-x_{R}}=\frac{x^2_{S}+x_{S}x_{R}+x^2_{R}}{y^2_{S}-y^2_{R}} . \end{aligned}$$

This leads to the denominator elimination with cubic twist since, $y^2_{S}-y^2_{R}$ lies in a subfield. Then $\mathcal {V}_{R}^{-1}(S)$ can be replaced by

$$\begin{aligned} \mathcal {S}_{R}(S)=x^2_{S}+x_{S}x_{R}+x^2_{R}. \end{aligned}$$

(3.4)

3.2 Applications on BLS Curves: Explicit Formulas

In this subsection, we apply the proposed Formula 3.3 to BLS pairing friendly curves. BLS curves are available for several embedding degrees [31], in particular, the curves with embedding degrees $k=27, 15$ and $k=9$ named BLS-27,  BLS-15 and BLS-9 respectively. These curves have the form $y^2=x^3+b$ and admit a cubic twist.

Table 1 provides explicit formulas of $\beta$-Weil pairing on BLS-27,  BLS-15 and BLS-9 at different levels of security.

Table 1 New $\beta$-Weil pairing formulas on BLS curves. At 128-bit, 192-bit level of security the seeds provided come from the recommendation of Guillevic in [28]. At $256-$bit security level no seed is given for $k=27$ we then refer to [29]

These new formulas of the $\beta$-Weil pairing are more suitable for the storage and multifunction techniques as explained in the next section.

4 Storage and Multifunction Techniques For Fast Computation

The storage technique stores some line equations during the Miller’s algorithm in order to speed up the computation, whereas the multifunction technique reduces the number of squarings in the pairing computation.

4.1 Storage Technique

The computation of the Miller’s function $f_{s,Q}(P)$ can be performed in two steps: the first step consists of evaluating the line functions depending on Q, while the second step is to evaluate the line functions at P. Storage technique then computes and stores the line functions of the first step. As Algorithm 3 computes and stores all line functions of $f_{s,Q}$ or $f_{s,P},$ Algorithm 4 computes and stores line functions of $f_{s,\pi _{p^{i}}(Q)}$ by raising all the line functions of $f_{s,Q}$ to the power $p^i$.

We remark that, for $s>0,$ item 1 becomes $T=R$ and item 5 is $T=T+R.$

4.2 Multifunction Technique

After computing and storing all line functions, we compute the products of e Miller’s functions with the help of multifunction technique. The method only requires a single squaring in the extension field per doubling step instead of e squarings in the naive way. Algorithm 5 evaluates the product of e-multifunction.

By direct analogy with Algorithm 5 exchanging P and Q yields another algorithm for positive s.

To estimate the theoretical complexity of Algorithm 5, we need some notations:

• $G_{kj}$ cost of the multiplication by the line function $g_{k}[j],$

• $Subs(g_{kj})$ cost of substitution of $P_{k}$ in the line function $g_{k}[j],$

• $H_{kj}$ cost of the multiplication by the line function $h_{k}[j],$

• $Subs(h_{kj})$ cost of substitution of $Q_{k}$ in the line function $h_{k}[j],$

• $M_{S_{-Q_{i}}(P_{i})}$ cost of the multiplication by the line $S_{-Q_{i}}(P_{i}),$

• HW(x) the hamming weight of x, 

• $S_{k}$ cost of the squaring in $\mathbb {F}_{p^k}.$

Then, total operations cost of Algorithm 5 is given by

$$\begin{aligned} Cost_{Alg.~5}= & {} e\times cost_{S_{-Q_{i}}(P_{i})}+(e-1)\times M_{S_{-Q_{i}}(P_{i})}\nonumber \\&+\log _{2}(x)\times (S_{k}+e\times (G_{kj}+Subs(g_{kj})+H_{kj}+Subs(h_{kj})))\nonumber \\&+HW(x)\times e \times (G_{kj}+Subs(g_{kj})+H_{kj}+Subs(h_{kj})+M_{S_{-Q_{i}}(P_{i})}). \end{aligned}$$

(4.1)

5 Basic Operations for $\beta$-Weil on BLS Curves with Twisted Degree 3

Under this section, basic and special operations for the $\beta$-Weil pairing on BLS curves of cubic twist are computed.

Let M, S and I denote the cost of the multiplication, squaring and inversion in $\mathbb {F}_{p},$ whereas, $M_{k},$ $S_{k},$ $I_{k},$ $F_{p},$ $E_{x}$ denote the cost of the multiplication, squaring, inversion, $p-th$ Frobenius operation and the power of x in $F_{p^k}$ respectively. Let $I_{cyc}$ denote the cost of the inversion in the cyclotomic subgroup $G_{\phi _{k}}.$

5.1 Tower Extension

From Table 1, we have a specific value of x as well as the parameter p which defines the field $\mathbb {F}_{p}$ for each curve BLS-27,  BLS-15 and BLS-9. For efficient arithmetic, the extension field $\mathbb {F}_{p^{k}}$ ($k=27, 15, 9$) can be constructed as follows:

$$\begin{aligned} \mathbb {F}_{p^{k/3}}= & {} \mathbb {F}_{p^{i}}[\beta ]/(\beta ^{k/(3i)}-\alpha ),\\ \mathbb {F}_{p^k}= & {} \mathbb {F}_{p^{k/3}}[\omega ]/(\omega ^3-\beta ), \end{aligned}$$

where $\alpha$ is a primitive root in $\mathbb {F}_{p^{i}}$ and $i=1$ for $k=9, 15$ and $i=3$ for $k=27.$ We then derived the cited BLS curves $(E):y^2=x^3+b$ from the parameters p(x), r(x) and t(x) for the chosen value x (see table 1). The cubic twisted curve $E'$ of E and their isomorphic mapping $\psi _{3}$ are given as follows: $E': y^2=x^3+b\beta ^{2}$ and

$$\begin{aligned} \psi _{3}: E'(\mathbb {F}_{p^{k/3}})[r]\rightarrow & {} E(\mathbb {F}_{p^{k}})[r]\\ (x,y)\mapsto & {} (\omega ^{-2} x, \beta ^{-1} y). \end{aligned}$$

5.2 Elliptic Curve Doubling and Elliptic Curve Addition

Let us consider $T=(\omega ^{-2} x_{T'},\beta ^{-1} y_{T'}),$ $Q=(\omega ^{-2} x_{Q'},\beta ^{-1} y_{Q'})$ given in affine coordinates on the group $E(\mathbb {F}_{p^{k}})$ such that $T'=(x_{T'}, y_{T'})$ and $Q'=(x_{Q'}, y_{Q'})$ are on the twisted curve $E'$ defined over $\mathbb {F}_{p^{k/3}}.$ Let the elliptic curve doubling of T be $2T=(x_{2T},y_{2T})$ and $P=(x_{P},y_{P})$ where $x_{P},y_{P}\in \mathbb {F}_{p}.$

The formulas for computing the doubling and the corresponding line function in affine coordinates are obtained in [13] as follows:

• $\lambda _{T,T}=\frac{3x_{T}^2}{2y_{T}}=\frac{3\omega ^{-4}x_{T'}^2}{2\beta ^{-1} y_{T'}}=\frac{3x_{T'}^2}{2 y_{T'}}\omega ^{-1}=\lambda _{T',T'}\omega ^{-1},$ where $\lambda _{T',T'}=\frac{3x_{T'}^2}{2 y_{T'}}.$

• $x_{2T}=\lambda _{T,T}^2-2x_{T}=\lambda _{T',T'}^2\omega ^{-2}-2\omega ^{-2}x_{T'}=(\lambda _{T',T'}^2-2x_{T'})\omega ^{-2}=x_{2T'}\omega ^{-2},$ where $x_{2T'}=\lambda _{T',T'}^2-2x_{T'}.$

• $y_{2T}=\lambda _{T,T}(x_{T}-x_{2T})-y_{T}=\lambda _{T',T'}\omega ^{-1}(x_{T'}\omega ^{-2}-x_{2T'}\omega ^{-2})-y_{T'}\beta ^{-1}=[\lambda _{T',T'}(x_{T'}-x_{2T'})-y_{T'}]\beta ^{-1}=y_{2T'}\beta ^{-1}$ where $y_{2T'}=\lambda _{T',T'}(x_{T'}-x_{2T'})-y_{T'}.$

• $l_{T,T}(P)=x_{P}^2+x_{2T}x_{P}+x_{2T}^2-\lambda _{T,T}(y_{P}-y_{2T})=x_{P}^2+[(x_{2T'}^2+y_{2T'}\lambda _{T',T'})\beta ^{-1}-\lambda _{T',T'}y_{P}]\omega ^{-1}+x_{2T'}x_{P}\omega ^{-2}.$

When considering the affine coordinates $(x,y,t)=(x,y,x^2),$ the previous affine formulas are given by computing the following sequences of operations:

$A=3t_{T'},$ $B=\frac{1}{2y_{T'}},$ $C=A\cdot B,$ $x_{2T'}=C^2-2x_{T'},$ $y_{2T'}=C\cdot (x_{T'}-x_{2T'})-y_{T'},$ $D=x_{2T'}^2 ,$ $E=D\beta ^{-1}+ C\cdot (y_{2T'}\beta ^{-1}-y_{P}),$ $F= x_{2T'}\cdot x_{P} ,$ $x_{2T}=x_{2T'}\omega ^{-2},$ $y_{2T}=y_{2T'}\beta ^{-1},$ $l_{T,T}(P)=t_{P}+E\omega ^{-1}+F\omega ^{-2}.$ Therefore the doubling step and line evaluation cost $1I_{k/3}+3M_{k/3}+2S_{k/3}+\frac{k}{3}M.$ (See [13] for more explanation).

The elliptic curve addition step ($T\ne Q$) and line evaluation can also be optimized similarly to the above procedure. Let the elliptic curve addition of T and Q be $R=T+Q=(x_{R},y_{R}).$ The formulas for computing the point addition and the corresponding line function are obtained as follows:

• $\lambda _{T,Q}=\frac{y_{Q}-y_{T}}{x_{Q}-x_{T}}=\frac{y_{Q'}-y_{T'}}{x_{Q'}-x_{T'}}\beta ^{-1}\omega ^{2}=\frac{y_{Q'}-y_{T'}}{x_{Q'}-x_{T'}}\omega ^{-1}=\lambda _{T',Q'}\omega ^{-1},$ where $\lambda _{T',Q'}=\frac{y_{Q'}-y_{T'}}{x_{Q'}-x_{T'}}.$

• $x_{R}=\lambda _{T,Q}^2-x_{Q}-x_{T}=(\lambda _{T',Q'}^2-x_{Q'}-x_{T'})\omega ^{-2}=x_{R'}\omega ^{-2},$ where $x_{R'}=\lambda _{T',Q'}^2-x_{Q'}-x_{T'}.$

• $y_{R}=\lambda _{T,Q}(x_{T}-x_{R})-y_{T}=\lambda _{T',Q'}\omega ^{-1}(x_{T'}\omega ^{-2}-x_{R'}\omega ^{-2})-y_{T'}\beta ^{-1}=[\lambda _{T',Q'}(x_{T'}-x_{R'})-y_{T'}]\beta =y_{R'}\beta ^{-1}$ where $y_{R'}=\lambda _{T',Q'}(x_{T'}-x_{Q'})-y_{T'}.$

• $l_{T,Q}(P)=x_{P}^2+x_{R}x_{P}+x_{R}^2-\lambda _{T,Q}(y_{P}-y_{R})=x_{P}^2+[(x_{R'}^2+y_{R'}\lambda _{T',Q'})\beta ^{-1}-\lambda _{T',Q'}y_{P}]\omega ^{-1}+x_{R'}x_{P}\omega ^{-2}$

When considering the affine coordinates $(x,y,t)=(x,y,x^2),$ the previous affine formulas are given by computing sequence of operations:

$A=y_{Q'}-y_{T'},$ $B=\frac{1}{x_{Q'}-x_{T'}},$ $C=A\cdot B,$ $x_{R'}=C^2-x_{Q'}-x_{T'},$ $y_{R'}=C\cdot (x_{T'}-x_{R'})-y_{T'},$ $D=x_{R'}^2 ,$ $E=D\beta ^{-1}+C \cdot (y_{R'}\beta ^{-1}-y_{P}),$ $F= x_{R'}\cdot x_{P} ,$ $x_{R}=x_{R'}\omega ^{-2},$ $y_{R}=y_{R'}\beta ^{-1},$ $l_{T,Q}(P)=t_{P}+E\omega ^{-1}+F\omega ^{-2}.$ Therefore the addition step and line evaluation cost $1I_{k/3}+3M_{k/3}+2S_{k/3}+\frac{k}{3}M.$

5.3 Affine Sparse Multiplication and Projective Sparse Multiplication

The sparse multiplication reduces the cost of the multiplications in $\mathbb {F}_{p^{k}}$ for Miller’s algorithm.

Affine sparse multiplication. In affine coordinates, as we have previously seen, the line function obtained from the elliptic curve doubling and addition steps is

$$\begin{aligned} l(x,y)=x^2+(ay+b\beta ^{-1})\omega ^{-1}+cx\omega ^{-2} , \qquad (a,b, c \in \mathbb {F}_{p^{k/3}}), \end{aligned}$$

where $(x,y)\in \mathbb {F}_{p}\times \mathbb {F}_{p}.$ Since $\omega ^3=\beta ,$ then $\omega ^{-1}=\beta ^{-1}\omega ^2$ and $\omega ^{-2}=\beta ^{-1}\omega$ hence,

$$\begin{aligned} l(x,y)=A+B\omega +C\omega ^2 , \end{aligned}$$

(5.1)

where $A=x^2, B=cx\beta ^{-1}$ and $C=ay\beta ^{-1}+b\beta ^{-2}.$

The sparse multiplication consists of computing $f\cdot l(P)$ with f in $\mathbb {F}_{p^{k}}$ and it is evaluated through Algorithm 6.

The Affine Sparse Multiplication cost $5M_{k/3}+\frac{k}{3}M$ in the base field (instead of $6M_{k/3}$ multiplications with the Karatsuba formulas).

Moreover, the vertical line function from elliptic curve is given as follows

$$\begin{aligned} \mathcal {V}(x,y)=x-a, \end{aligned}$$

where a belongs to $\mathbb {F}_{p}.$ We substitute Q in the previous equation and obtain $\mathcal {V}(Q)=\beta ^{-1} x_{Q'}\omega -a.$ The sparse multiplication $f \cdot \mathcal {V}(Q)$ for f in $\mathbb {F}_{p^{k}}$ can be calculated by Algorithm 7.

The affine Sparse Multiplication cost $3M_{k/3}+2(\frac{k}{3}M)$ in the base field (instead of $6M_{k/3}$ multiplications with the Karatsuba formulas).

Projective sparse multiplication. In projective coordinates, the line function from elliptic curve doubling and addition steps is given in [34] as follows

$$\begin{aligned} l(x,y)=ax^2+bx+cy+d, \end{aligned}$$

where a, b, c and d are in $\mathbb {F}_{p}.$ The point $Q=(x,y)$ in $E(\mathbb {F}_{p^{k}})$ can be viewed as $\psi _{3}(Q')=(\omega ^{-2} x_{Q'}, \beta ^{-1} y_{Q'})$ for $Q'$ in $E(\mathbb {F}_{p^{k/3}}).$ We substitute Q in the previous equation and obtain $l(Q)=A+B\omega +C\omega ^2,$ where $A=cy_{Q'}\beta ^{-1}+d, B=bx_{Q'}\beta ^{-1}$ and $C=ax^2_{Q'}\beta ^{-2}$ are in $\mathbb {F}_{p^{k/3}}.$ We did not find an efficient computation method for the following multiplication $f \cdot l(Q)$ where $f\in \mathbb {F}_{p^{k}}.$

The inverse of the vertical line From Eq. 3.4, the inverse of the vertical line $1/\mathcal {V}_{Q}(P)$ becomes $\mathcal {S}_{Q}(P)=x_{P}^2+x_{Q}x_{P}+x_{Q}^2.$ For $Q=(\omega ^{-2}x_{Q'}, \beta ^{-1}y_{Q'}),$ with $(x_{Q'}, y_{Q'})$ in $E(\mathbb {F}_{p^{k/3}})$ we have, $\mathcal {S}_{Q}(P)=x_{P}^2+x_{Q'}x_{P}\omega ^{-2}+x_{Q'}^2(\beta \omega )^{-1}.$ This cost $1S_{k/3}+k/3 M.$

$p^i-$ th Frobenius map for the line function.

From Eq. 5.1 the line functions for computing $f_{x,Q}$ are represented as :

$$\begin{aligned} l(x,y)=A+B\omega +C\omega ^2 , \end{aligned}$$

where, $A\in \mathbb {F}_{p}$ and $B, C\in \mathbb {F}_{p^{k/3}}.$ The $p^i-$th Frobenius map is $l^{p^i}(x,y)=A+B^{p^i}\omega ^{p^i}+C\omega ^{2p^i},$ since $A\in \mathbb {F}_{p}.$ The cost of Frobenius map for the extension field element is at most the degree of field extension, so the cost of $p^i-$th Frobenius map for B and C are $2\frac{k}{3} M,$ since $B,C\in \mathbb {F}_{p^{k/3}}.$ Then for a given $\omega ^{p^i}$ and $\omega ^{2p^i},$ the $p^i-$th Frobenius map for line function cost $2\frac{k}{3} M.$

$p^i-$ th Frobenius map for a point Q.

$$\begin{aligned} \pi _{p^i}(Q)=\pi _{p^i}(\omega ^{-2}x_{Q'};\beta ^{-1} y_{Q'})=\big ((\omega ^{p^i})^{-2}x_{Q'}^{p^i};( \beta ^{p^i})^{-1}y_{Q'}^{p^i}\big ) \end{aligned}$$

For the given $\omega ^{-p^i}$ and $\beta ^{-p^i},$ the computational costs of $\pi _{p^i}(Q)$ is the total cost of the $p^i-$th Frobenius map for $x_{Q'}$ and $y_{Q'}.$

6 Application on BLS-27: Theoretical Costs of $\beta$-Weil Computation

We used the ideas of storage and multifunction techniques to evaluate the $\beta$-Weil pairing on BLS-27 either in serial or parallel computation.

Proposition 6.1

For pairing-friendly curves of embedding degrees $k=27,15$ and 9,  with the extended Miller function $h(z) = x - z$ such that $h(p)=0 \mod r,$ the relation $[p]P=[x]P$ holds, for any P in $\mathbb {G}_{1}$ or $\mathbb {G}_{2}$ of order r.

Proof

: By hypothesis, $h(p)=0 \mod r,$ then $x=p \mod r,$ and $[x]P= [p]P ,$ since P is of order r.

The proposed $\beta$-Weil pairing formula for BLS-27 in Table 1 is

$$\begin{aligned} \beta _{27}(P,Q)= & {} \Big [\prod _{i=0}^{8}(f_{x,Q_{i}}(P_{i})\cdot f_{-x,P_{i}}(Q_{i}) ) \cdot \prod _{i=0}^{8}\mathcal {V}_{P_{i+1}}(Q_{i}) \Big ] ^{p^{9}-1}. \end{aligned}$$

The basic operations used to evaluate the theoretical cost of the $\beta$-Weil pairing on BLS-27 are recapitulated in the following Table 2.

Table 2 Costs of arithmetic operations in a tower extension field $\mathbb {F}_{p^{27}}$ and special operations in the $\beta$-Weil pairing computations on BLS-27 in this work and [17]

6.1 Serial Computation of the $\beta$-Weil Pairing Over BLS-27

In the first paragraph, we evaluate the theoretical cost of the line functions for each of the Miller functions. In the second paragraph, we estimate the cost of $A=\prod _{i=0}^{8}(f_{x,Q_{i}}(P_{i})\cdot f_{-x,P_{i}}(Q_{i}) )$ using Algorithm 5 and the line functions previously obtained. After we evaluate the product of the vertical lines and end with the final powering $p^9-1.$

On the first hand, we compute in projective coordinates and store the line functions for each Miller-Lite function $f_{-x,P_{i}}$ where, $x=-2^{51}-2^{31}-2^{21}-2^8-2^4,$ and $P_{i}=[p^i]P.$ This is done through Algorithm 3: $CSL([p^i]P, -x)=h_{i}.$ Each Miller’s function is composed by 51 doubling steps (13M) and 4 mixed addition steps (16M). So for each $0\le i\le 8,$ the addition and doubling steps cost $51 \cdot 13 M+4\cdot 16 M= 727 M.$ Since $[p^i]P$ is equal to $[-xp^{i-1}]P$ (see Proposition 6.1) and that we obtain $[-xp^{i-1}]P$ after computing $CSL([p^{i-1}]P, -x),$ we do not need to compute again $[p^i]P.$ For mixed addition coordinate (see [34]), it is required to convert $[p^i]P=(X_{i}:Y_{i}:Z_{i})$ from projective to affine coordinates $(X_{i}\cdot Z_{i}^{-1}, Y_{i}\cdot Z_{i}^{-1})$ for a cost of $I+2M$ for each i $(1\le i\le 8).$ Note that for $i=0,$ $P_{0}=P$ is given in each coordinate. Hence, the total cost of all line functions computation for all Miller-Lite functions is $9\cdot 727 M+8(I+2M)= 6559 M+8 I .$

On the other hand, we compute in affine coordinates and store the line functions for computing $f_{x,Q}.$ This is done through Algorithm 3: $CSL(Q, x)=g_{0}.$ The Full Miller’s function is composed by 51 doubling steps $(233 M+I)$ and 4 mixed addition steps $(233 M+I).$ This yields $51(233 M+I)+4(233 M+I)=12815 M+55 I.$ From x is $-2^{51}-2^{31}-2^{21}-2^8-2^4 ,$ $f_{x,Q}$ is made of 55 line functions. Since the $p^i-$th Frobenius map for line function is 18M,  the cost of one $CSLFrob(g_{0}, i)$ execution for $f_{x,\pi _{p^{8-i}}(Q)}$ is $55\cdot 18M = 990 M.$ Therefore, the total cost of all line functions computation for all Full-Miller’s functions is $(12815 M+55 I)+8 \cdot 990 M= 20735 M+55 I.$

Hence, the total cost of all line functions computation for $A=\prod _{i=0}^{8}(f_{x,Q_{i}}(P_{i})\cdot f_{-x,P_{i}}(Q_{i}) )$ is $(6559 M+8 I) +(20735 M+55 I) =\mathbf{27294} M+ 63 I .$

Secondly, we evaluate all line functions at a given point and compute the product of Miller’s functions by using Algorithm 5. From Table 2, the computational costs of $\pi _{p^{i}}(Q)$ for $1\le i\le 8$ is $2\cdot 12 M+6\cdot 16 M =120 M.$ Since each $\mathcal {S}_{-Q_{i}}(P_{i})$ (Eq. 3.4) costs $S_{9}+9 M=34 M$ and the multiplication by $\mathcal {S}_{-Q_{i}}(P_{i})$ in $\mathbb {F}_{p^{27}}$ costs 189M. From Eq. 4.1, the execution cost for A is $9\cdot 34 M +8\cdot 189 M+51\cdot 125+51\cdot 9\cdot (189M+9M+216M+27M)+4\cdot 9\cdot (189M+9M+216M+27M+189M)=233292 M.$ Therefore the total cost is $120 M+ 233292 M=\mathbf{233412} M .$

Thirdly, we compute $B= A \cdot \prod _{i=0}^{8}\mathcal {V}_{P_{i+1}}(Q_{i}).$ To have B,  we multiply A by each $\mathcal {V}_{P_{i+1}}(Q_{i})$ for $0\le i\le 8$ for a cost of $9\cdot 126 M=\mathbf{1134} M$ (see Algorithm 7). There is no need to evaluate the point $P_{9}=[p^9]Q$ as we obtain $P_{9}$ after computing $f_{-x,P_{8}}.$

Finally, $(B)^{p^{9}-1}$ is made of one inversion, one multiplication and one $p^9-$Frobenius in $\mathbb {F}_{p^{27}},$ at the cost of $I_{27}+M_{27}+18 M=\mathbf{683} M+I .$

The total cost of serial computation of the $\beta$-Weil pairing is $(27294 M+63 I)+( 233412 M)+(1134 M )+(683 M+I)=\mathbf{262523} M+64 I .$

6.2 Parallel Computation of $\beta _{27}(P,Q)$ Using 3 Processors

Here we parallelise the evaluation of $\beta _{27}(P,Q)$ and find its theoretical cost. In the first step, each processor computes and stores 6 line functions. For step 2, each processor evaluates the stored line functions using the multifuction technique. Whereas step 3 computes the additional factors of $\beta _{27}(P,Q)$ and the last step combines each result. Since $P_{i}=[p^i]P$ and $Q_{i}=\pi _{p^{8-i}}(Q)$ for $0\le i \le 8,$

$$\begin{aligned} \beta _{27}(P,Q)= & {} \big [ f_{x,\pi _{p^8}(Q)}(P) \cdot f_{-x,P}(\pi _{p^8}(Q)) \cdot f_{x,\pi _{p^5}(Q)}(P_{3})\cdot f_{-x,P_{3}}(\pi _{p^5}(Q)) \cdot f_{x,\pi _{p^2}(Q)}(P_{6}) \\&\cdot \, f_{-x,P_{6}}(\pi _{p^2}(Q)) \cdot \mathcal {V}_{P_{1}}(\pi _{p^8}(Q))\cdot \mathcal {V}_{P_{4}}(\pi _{p^5}(Q))\cdot \mathcal {V}_{P_{7}}(\pi _{p^2}(Q))\\&\cdot \, f_{x,\pi _{p^7}(Q)}(P_{1})\cdot f_{-x,P_{1}}(\pi _{p^7}(Q)) \cdot f_{x,\pi _{p^4}(Q)}(P_{4}) \cdot f_{-x,P_{4}}(\pi _{p^4}(Q)) \cdot f_{x,\pi _{p}(Q)}(P_{7}) \\&\cdot \, f_{-x,P_{7}}(\pi _{p}(Q)) \cdot \mathcal {V}_{P_{2}}(\pi _{p^7}(Q))\cdot \mathcal {V}_{P_{5}}(\pi _{p^4}(Q))\cdot \mathcal {V}_{P_{8}}(\pi _{p}(Q))\\&\cdot \, f_{x,\pi _{p^6}(Q)}(P_{2})\cdot f_{-x,P_{2}}(\pi _{p^6}(Q))\cdot f_{x,\pi _{p^3}(Q)}(P_{5})\cdot f_{-x,P_{5}}(\pi _{p^3}(Q))\cdot f_{x,Q}(P_{8})\\&\cdot \, f_{-x,P_{8}}(Q) \cdot \mathcal {V}_{P_{3}}(\pi _{p^6}(Q))\cdot \mathcal {V}_{P_{6}}(\pi _{p^3}(Q))\cdot \mathcal {V}_{P_{9}}(Q)\big ]^{p^9-1}. \end{aligned}$$

That is,

$$\begin{aligned} \beta _{27}(P,Q)= & {} \big [\big \{ f_{x,\pi _{p^6}(Q)}(P) \cdot f_{-x,P}(\pi _{p^6}(Q)) \cdot f_{x,\pi _{p^3}(Q)}(P_{3})\cdot f_{-x,P_{3}}(\pi _{p^3}(Q)) \cdot f_{x,Q}(P_{6})\\&\cdot \, f_{-x,P_{6}}(Q) \cdot \mathcal {V}_{P_{1}}(\pi _{p^6}(Q))\cdot \mathcal {V}_{P_{4}}(\pi _{p^3}(Q))\cdot \mathcal {V}_{P_{7}}(Q)\big \}^{p^2}\\&\cdot \, \big \{f_{x,\pi _{p^6}(Q)}(P_{1})\cdot f_{-x,P_{1}}(\pi _{p^6}(Q)) \cdot f_{x,\pi _{p^3}(Q)}(P_{4}) \cdot f_{-x,P_{4}}(\pi _{p^3}(Q)) \cdot f_{x,Q}(P_{7})\\&\cdot \, f_{-x,P_{7}}(Q) \cdot \mathcal {V}_{P_{2}}(\pi _{p^6}(Q))\cdot \mathcal {V}_{P_{5}}(\pi _{p^3}(Q))\cdot \mathcal {V}_{P_{8}}(Q)\big \}^p\\&\cdot \, f_{x,\pi _{p^6}(Q)}(P_{2})\cdot f_{-x,P_{2}}(\pi _{p^6}(Q))\cdot f_{x,\pi _{p^3}(Q)}(P_{5})\cdot f_{-x,P_{5}}(\pi _{p^3}(Q))\cdot f_{x,Q}(P_{8})\\&\cdot \, f_{-x,P_{8}}(Q) \cdot \mathcal {V}_{P_{3}}(\pi _{p^6}(Q))\cdot \mathcal {V}_{P_{6}}(\pi _{p^3}(Q))\cdot \mathcal {V}_{P_{9}}(Q)\big ]^{p^9-1}. \end{aligned}$$

For parallel computation using 3 processors, $\beta _{27}(P,Q)$ can be regarded as

$$\begin{aligned} \beta _{27}(P,Q)=(X^{p^2}\cdot Y^p \cdot Z)^{p^{9}-1}, \end{aligned}$$

where

$$\begin{aligned} X= & {} f_{x,\pi _{p^6}(Q)}(P) \cdot f_{-x,P}(\pi _{p^6}(Q)) \cdot f_{x,\pi _{p^3}(Q)}(P_{3})\cdot f_{-x,P_{3}}(\pi _{p^3}(Q)) \cdot f_{x,Q}(P_{6}) \cdot f_{-x,P_{6}}(Q) \cdot H_{1},\\ Y= & {} f_{x,\pi _{p^6}(Q)}(P_{1})\cdot f_{-x,P_{1}}(\pi _{p^6}(Q)) \cdot f_{x,\pi _{p^3}(Q)}(P_{4}) \cdot f_{-x,P_{4}}(\pi _{p^3}(Q)) \cdot f_{x,Q}(P_{7})\cdot f_{-x,P_{7}}(Q) \cdot H_{2},\\ Z= & {} f_{x,\pi _{p^6}(Q)}(P_{2})\cdot f_{-x,P_{2}}(\pi _{p^6}(Q))\cdot f_{x,\pi _{p^3}(Q)}(P_{5})\cdot f_{-x,P_{5}}(\pi _{p^3}(Q))\cdot f_{x,Q}(P_{8})\cdot f_{-x,P_{8}}(Q) \cdot H_{3} \end{aligned}$$

and

$$\begin{aligned} H_{1}= & {} \mathcal {V}_{P_{1}}(\pi _{p^6}(Q))\cdot \mathcal {V}_{P_{4}}(\pi _{p^3}(Q))\cdot \mathcal {V}_{P_{7}}(Q),\\ H_{2}= & {} \mathcal {V}_{P_{2}}(\pi _{p^6}(Q))\cdot \mathcal {V}_{P_{5}}(\pi _{p^3}(Q))\cdot \mathcal {V}_{P_{8}}(Q),\\ H_{3}= & {} \mathcal {V}_{P_{3}}(\pi _{p^6}(Q))\cdot \mathcal {V}_{P_{6}}(\pi _{p^3}(Q))\cdot \mathcal {V}_{P_{9}}(Q). \end{aligned}$$

Step 1.

• 1. The $1^{st}$ processor computes and stores $CSL([p^i]P,-x)=h_{i}$ for $0\le i\le 8$ for a cost of $9\cdot 727 M +8(I+2 M)=6559 M+8 I$ and $CSL(Q,x)=g_{0}$ for a cost of $12815 M+55 I.$ The total cost is $\mathbf{19374} M+63 I .$

• 2. The $2^{nd}$ processor computes and stores $\pi _{p^3}(Q)$ and $CSL(\pi _{p^3}(Q),x)=g_{3}$ for a cost of $12M+12815 M+55 I=12827 M+55 I.$

• 3. The $3^{rd}$ processor computes and stores $\pi _{p^6}(Q)$ and $CSL(\pi _{p^6}(Q),x)=g_{6}$ for the same cost as the $2^{nd}$ processor.

Step 2.

• 1. From Eq. 4.1, the $1^{st}$ processor computes $X_{1}=EPM \big (\big [(g_{6},P_{0}), (g_{3},P_{3}), (g_{0},P_{6}),$

  $(h_{0},\pi _{p^6}(Q)), (h_{3},\pi _{p^3}(Q)), (h_{6},Q) \big ],x\big )$ for a cost of $3\cdot 34 M+2 \cdot 189 M+51 S_{27}+51 \cdot 3\cdot (189 M+9M+216 M+27 M)+4\cdot 3\cdot (189 M+9M+216 M+27 M+189 M) =\mathbf{81922} M .$

• 2. The $2^{nd}$ processor computes $Y_{2}=EPM \big (\big [(g_{6},P_{1}), (g_{3},P_{4}), (g_{0},P_{7}),(h_{1},\pi _{p^6}(Q)),$

  $(h_{4},\pi _{p^3}(Q)), (h_{7},Q) \big ],x\big )$ for the same cost as the $1^{st}$ processor.

• 3. The $3^{rd}$ processor computes $Z_{3}=EPM \big (\big [(g_{6},P_{2}), (g_{3},P_{5}), (g_{0},P_{8}),(h_{2},\pi _{p^6}(Q)),$

  $(h_{5},\pi _{p^3}(Q)), (h_{8},Q) \big ],x\big )$ for the same cost as the $1^{st}$ processor.

Step 3.

• 1. The $1^{st}$ processor computes $X=X_{1}\cdot H_{1}=X_{1}\cdot \mathcal {V}_{P_{1}}(\pi _{p^6}(Q))\cdot \mathcal {V}_{P_{4}}(\pi _{p^3}(Q))\cdot \mathcal {V}_{P_{7}}(Q)$ at cost of $3 \cdot 126 M=\mathbf{378} M .$

• 2. The $2^{nd}$ processor computes Y for the same cost as the $1^{st}$ processor.

• 3. The $3^{rd}$ processor computes Z for the same cost as the $1^{st}$ processor.

Step 4.

Since $\beta _{27}(P,Q)=((X^{p}\cdot Y)^p \cdot Z)^{p^{9}-1},$ in the final step one processor computes two $p-$ and one $p^9-$Frobenius maps, three multiplications and one inversion in $\mathbb {F}_{p^{27}}$ which yields $2 \cdot 26 M+18 M + 3 M_{27} +I_{27}=\mathbf{1167} M+I .$

The total cost of parallel computation of the $\beta$-Weil pairing using 3 processors is $(19374 M+63 I)+81922 M+378 M+(1167 M+I)=\mathbf{102841} M+64I .$

Similarly, in Appendix 1 we find the theoretical costs of the $\beta$-Weil pairing on the BLS-15,  BLS-9 curves.

7 Comparison

In this section, we compare the theoretical costs of the optimal Ate pairing (see Appendix B.2, B.2, B.2), the original $\beta$-Weil pairing (see Appendix A.2.2) and the proposed $\beta$-Weil pairing (Corollary 3.4) on the BLS-27,  BLS-15,  BLS-9 curves. The parallel computation of the optimal Ate pairing is obtained when parallelising the computation of Miller loop only [8], since to date there is not a way to parallelise the final exponentiation. Given that in the literature there is no parallel computation of the optimal Ate pairing on the aforementioned curves, we estimate the costs by dividing a Miller loop cost by the number of processors (see 8.1) and add this to the final exponentiation cost. Then our theoretical results reduce the number of multiplication operations on the prime field in $\beta$-Weil pairing for BLS family with $k=27.15$ and 9 about $44.78 \% ,$ $49.07 \%$ and $38.49\% ,$ as well as the number of divisions of about $87.1 \%$ $78.8 \%$ and $61.2 \%$ respectively for serial computation. The optimal Ate pairing when compared with the new $\beta$-Weil pairing in the sequential case, it is approx. $33\%$ more efficient for $k = 27$ and approx. $17\%$ more efficient for $k = 9.$ Also, the two pairing types for $k = 15$ have pretty much the same execution time. However, the proposed $\beta$-Weil pairing on curve with $k=15$ is competitive to optimal Ate pairing. Indeed, since the final exponentiation in the optimal Ate pairing is expensive and it is about 5, 4 and 2 times the Full Miller functions for $k=27, 15$ and 9 respectively with one extra Full Miller function the optimal Ate pairing is about 6, 5 and 3 times the Full Miller functions for $k=27, 15$ and 9 respectively. In the other hand without the Miller Lite functions and the simple final exponentiation, the new $\beta$-Weil pairing is made of 9, 5 and 3 the Full Miller functions that need to be evaluate by only one processor for $k=27, 15$ and 9 respectively. This explain the difference between the two pairings on the BLS-27,  BLS-15 and BLS-9.

In the parallel computation with 3 processors, the $\beta$-Weil pairing on BLS-27,  BLS-15 and BLS-9 is faster than the optimal Ate pairing. See the Table 3 for a complete comparison.

Table 3 Theoretical cost of the optimal Ate pairing, the original $\beta$-Weil pairing (without storage technique and multifunction technique) and the proposed $\beta$-Weil pairing

Table 4 gives the number of $\mathbb {F}_{p}$ elements required to store for the $\beta$-Weil pairing computation. The total storage of elements is determined by the following formula $a_{1}b_{1}c_{1}+a_{2}b_{2}c_{2},$ where,

• $a_{1}$ and $a_{2}$ are the number of stored extended Miller functions $f_{p,h,P_{i}}$ and $f_{p,h,Q_{i}}$ respectively,

• $b_{1}$ and $b_{2}$ are the number of stored lines in $f_{p,h,P_{i}}$ and $f_{p,h,Q_{i}}$ respectively,

• $c_{1}$ and $c_{2}$ are the number of $\mathbb {F}_{p}$ elements of line coefficients in $f_{p,h,P_{i}}$ and $f_{p,h,Q_{i}}$ respectively.

Table 4 Number of $\mathbb {F}_{p}$ elements required to be stored for our method

8 Conclusion

In this paper, we extended the work of Kinoshita and Suzuki [1] by providing a new formula for the $\beta$-Weil pairing on curves with odd embedding degrees. This formula involves vertical line functions useful for the sparse multiplications during Miller’s loop. For faster computation of the proposed $\beta$-Weil pairing we compute and store line functions for some Miller’s functions that are reused to find other line functions for other Miller’s functions. The multifunction technique evaluates the product of n Miller’s functions and only requires a single squaring in the extension field per iteration instead of n squarings in the naive way. Then our theoretical results give faster $\beta$-Weil computation on the BLS family with $k = 9, 15$ and 27 than the original $\beta$-Weil pairing on the same curves. The proposed $\beta$-Weil pairing on curve with $k=15$ is competitive to optimal Ate pairing. The implementation results of the proposed methods and the original $\beta$-Weil pairings on BLS$-9$, BLS$-15$ and BLS$-27$ curves are left for future work to confirm the theoretical results.

Appendices

Appendix A. Computation of the $\beta$-Weil Pairing Over BLS-15 and BLS-9

1.1 Evaluation of the New $\beta$-Weil Pairing Formula on BLS-15 Curve

Following the same process, we find the theoretical cost of the serial and the parallel computations of the $\beta$-Weil pairing on BLS-15 curve. The proposed $\beta$-Weil pairing formula for BLS-15 is given as

$$\begin{aligned} \beta _{15}(P,Q)=\left( \prod _{i=0}^{4}f_{x,Q_{i}}(P_{i})\cdot f_{-x,P_{i}}(Q_{i})\cdot \mathcal {V}_{P_{i+1}}(Q_{i})\right) ^{p^5-1} \end{aligned}$$

where $x=-2^{77} -2^{76} -2^{68} -2^{50} .$

Costs of arithmetic operations in the fields $\mathbb {F}_{p^{5}}$ and $\mathbb {F}_{p^{15}}$ can be found in [35] and [17]. Also, the special operations in the $\beta$-Weil pairing computations on BLS-15 curve can be obtained in [17] (sect. 5).

1.1.1 Serial Computation of the $\beta$-Weil Pairing Over BLS-15

Algorithm 3 computes and stores the line functions necessary to find $f_{-x,P_{i}},$ $i=0,1,2,3,4$ for a cost of $5(77 \cdot 13 M+3\cdot 16 M) +4(I+2 M)= \mathbf{5253} M+ 4 I .$ Also Algorithm 3 computes and stores the line functions for $f_{x,Q},$ for a cost of $77(95 M+ I)+3(95 M+ I)=\mathbf{7600} M + 80 I$. Whereas Algorithm 4 computes and stores the line functions for $f_{x,Q_{i}},$ $i=1,2,3,4$ for a cost of $4 \cdot 80 \cdot 10 M=\mathbf{3200} M ,$ where the $p^i-$th Frobenius map for line function is 10M.

Before using Algorithm 5 to find the product of Miller’s functions, we first compute $\pi _{p^{i}}(Q)$ for $1\le i\le 4$ for the cost of $4 \cdot 10 M=\mathbf{40} M .$ See Table 5 for the other computations.

Table 5 computational cost of Algorithm 5 for $\beta _{15}$ (see [35] and [17] for basic operations)

The total cost of the $\beta$-Weil pairing on BLS-15 is then $90477 M+ 85 I.$

1.1.2 Parallel Computation of the $\beta$-Weil Pairing Over BLS-15 Using 3 Processors

The parallel computation of $\beta _{15}(P,Q)$ with 3 processors of the $\beta$-Weil pairing on BLS-15 curve is defined as

$$\begin{aligned} \beta _{15}(P,Q)=(X^{p^2}\cdot Y\cdot Z)^{p^{5}-1}. \end{aligned}$$

Where

$$\begin{aligned} X= & {} f_{x,\pi _{p^2}(Q)}(P)\cdot f_{-x,P}(\pi _{p^2}(Q))\cdot f_{x,\pi _{p}(Q)}(P_{1})\cdot f_{-x,P_{1}}(\pi _{p}(Q))\cdot \mathcal {V}_{P_{1}}(\pi _{p^2}(Q))\cdot \mathcal {V}_{P_{2}}(\pi _{p}(Q)),\\ Y= & {} f_{x,\pi _{p^2}(Q)}(P_{2})\cdot f_{-x,P_{2}}(\pi _{p^2}(Q))\cdot f_{x,\pi _{p}(Q)}(P_{3})\cdot f_{-x,P_{3}}(\pi _{p}(Q))\cdot \mathcal {V}_{P_{3}}(\pi _{p^2}(Q))\cdot \mathcal {V}_{P_{4}}(\pi _{p}(Q)) \\ Z= & {} f_{x,Q}(P_{4})\cdot f_{-x,P_{4}}(Q) \cdot \mathcal {V}_{P_{5}}(Q) \end{aligned}$$

Step 1.

• 1. The $1^{st}$ processor computes $CSL([p^i]P,-x)=h_{i}$ for $0\le i\le 4$ for a cost of $5(77\cdot 13 M+3\cdot 16 M) +4(I+2 M)=\mathbf{5253} M+ 4 I$ and $CSL(Q,x)=g_{0}$ for a cost of $77(95 M+ I)+3(95 M+ I)= \mathbf{7600} M + 80 I$.

• 2. The $2^{nd}$ processor computes $\pi _{p}(Q)$ and $CSL(\pi _{p}(Q),x)=g_{1}$ for a cost of $10 M+ (7600 M + 80 I)= 7610 M + 80 I$.

• 3. The $3^{rd}$ processor computes $\pi _{p^2}(Q)$ and $CSL(\pi _{p^2}(Q),x)=g_{2}$ for a cost of $10 M+ (7600 M + 80 I)= 7610 M + 80 I$.

Step 2.

• 1. The $1^{st}$ processor computes $X_{1}=EPM \big (\big [(g_{2},P_{0}), (g_{1},P_{1}),(h_{0},\pi _{p^2}(Q)),$

  $(h_{1},\pi _{p}(Q)), \big ],x\big )$ as in the table 5, for a cost of $2\cdot 18M+ 1\cdot 70 M+77\cdot 78 M+77[2(70 M+5 M+78 M+15 M )]+3[2(70 M+5 M+78 M+15 M )+70 M]= \mathbf{33202} M .$ Also this processor computes $X=X_{1}\cdot \mathcal {V}_{P_{1}}(\pi _{p^2}(Q))\cdot \mathcal {V}_{P_{2}}(\pi _{p}(Q))$ for $2\cdot 49 M=\mathbf{98} M .$

• 2. The $2^{nd}$ processor computes $Y_{1}=EPM \big (\big [(g_{2},P_{2}), (g_{1},P_{3}), (h_{2},\pi _{p^2}(Q)),$

  $(h_{3},\pi _{p}(Q)) \big ],x\big )$ and $Y=Y_{1}\cdot \mathcal {V}_{P_{3}}(\pi _{p^2}(Q))\cdot \mathcal {V}_{P_{4}}(\pi _{p}(Q))$ for the same cost as the first processor.

• 3. The $3^{rd}$ processor computes $Z_{1}=EPM \big (\big [ (g_{0},P_{4}), (h_{4},Q) \big ],x\big )$ for a cost of $18M+77\cdot 78 M+77[(70 M+5 M+78 M+15 M )]+3[(70 M+5 M+78 M+15 M )+70 M]=19674 M$ Also this processor computes $Z=Z_{1}\cdot \mathcal {V}_{P_{5}}(Q)$ for 49M.

Step 3.

Since $\beta _{15}(P,Q)=(X^{p^2}\cdot Y \cdot Z)^{p^{5}-1},$ in the final step one processor computes one $p^2$ Frobenius map, three multiplications and one inversion in $\mathbb {F}_{p^{15}}$ which yields $14 M+3 M_{15} +I_{15}=\mathbf{513} M+I .$

The total cost of the parallel computation of the $\beta$-Weil pairing using 3 processors is $\mathbf{46666} M+ 85 I .$

1.2 Evaluation of the New $\beta$-Weil Pairing Formula on BLS-9 Curve

Similarly, we find the serial and the parallel computations of the $\beta$-Weil pairing on BLS-9. The proposed $\beta$-Weil pairing formula for BLS-9 is given as

$$\begin{aligned} \beta _{9}(P,Q)=\left( \prod _{i=0}^{2}f_{x,Q_{i}}(P_{i})\cdot f_{-x,P_{i}}(Q_{i})\cdot \mathcal {V}_{P_{i+1}}(Q_{i})\right) ^{p^3-1} \end{aligned}$$

where $x=-2^{74} -2^{72} -2^{46} -2^{31} .$

1.2.1 Serial Computation of the $\beta$-Weil Pairing Computations on the BLS-9

Algorithm 3 computes and stores the line functions necessary to find $f_{-x,P_{i}},$ $i=0,1,2$ for a cost of $3(74\cdot 13 M+3\cdot 16 M) +2(I+2 M)= \mathbf{3034M}+ 2I .$ Also Algorithm 3 computes and stores the line functions for $f_{x,Q},$ for a cost of $74(39 M+ I)+3(39 M+ I)=\mathbf{3003} M+77 I .$ Whereas Algorithm 4 computes and stores the line functions for $f_{x,Q_{i}},$ $i=1,2$ for a cost of $2\cdot 77\cdot 8 M=\mathbf{1232} M$.

Before using Algorithm 5 to find the product of Miller’s functions, we first compute $\pi _{p^{i}}(Q)$ for $i=1,2$ for the cost of $2\cdot 4 M=\mathbf{8} M .$ See Table 6 for the other computations.

Table 6 computational cost of Algorithm 5 for $\beta _{9}$ with the help of [17]

The total cost of the $\beta$-Weil pairing on the BLS-9 is then $26984 M+ 80I.$

1.2.2 Parallel Computation of $\beta _{9}(P,Q)$ Using 3 Processors

The parallel computation with 3 processors of the $\beta$-Weil pairing on the BLS-9 curve is defined as

$$\begin{aligned} \beta _{9}(P,Q)=(X^{p}\cdot Y \cdot Z)^{p^{3}-1} \end{aligned}$$

Where

$$\begin{aligned} X= & {} f_{x,\pi _{p}(Q)}(P) \cdot f_{-x,P}(\pi _{p}(Q)) \cdot \mathcal {V}_{P_{1}}(\pi _{p}(Q)),\\ Y= & {} f_{x,\pi _{p}(Q)}(P_{1}) \cdot f_{-x,P_{1}}(\pi _{p}(Q))\cdot \mathcal {V}_{P_{2}}(\pi _{p}(Q)),\\ Z= & {} f_{x,Q}(P_{2})\cdot f_{-x,P_{2}}(Q) \cdot \mathcal {V}_{P_{3}}(Q). \end{aligned}$$

Step 1.

• 1. The $1^{st}$ processor computes $CSL([p^i]P,-x)=h_{i}$ for $i=0,1,2$ for a cost of $3(74\cdot 13 M+3\cdot 16 M) +2(I+2 M)= 3034 M+ 2 I .$

• 2. The $2^{nd}$ processor computes $CSL(Q,x)=g_{0}$ for a cost of $74(39 M+ I)+3(39 M+ I)= 3003 M + 77 I.$

• 3. The $3^{rd}$ processor computes $\pi _{p}(Q)$ and $CSL(\pi _{p}(Q),x)=g_{1}$ for a cost of $4 M+ 3003 M + 77 I= \mathbf{3007} M + 77 I .$

Step 2.

• 1. The $1^{st}$ processor computes $X_{1}=EPM \big (\big [ (g_{1},P_{0}),(h_{0},\pi _{p}(Q)) \big ],x\big )$ as in Table 6, at a cost of $8M+74\cdot 25 M+74[(33 M+3 M+36 M+9 M )]+3[(33 M+3 M+36 M+9 M )+33 M]= \mathbf{8194} M .$ Also this processor computes $X=X_{1} \cdot \mathcal {V}_{P_{1}}(\pi _{p}(Q))$ for $\mathbf{24} M .$

• 2. The $2^{nd}$ processor computes $Y_{1}=EPM \big (\big [(g_{1},P_{1}), (h_{1},\pi _{p}(Q))\big ],x\big )$ and $Y=Y_{1}\cdot \mathcal {V}_{P_{2}}(Q_{1})$ for the same cost.

• 3. The $3^{rd}$ processor computes $Z_{1}=EPM \big (\big [(g_{0},P_{2}), (h_{2},Q)\big ],x\big )$ and $Z=Z_{1}\cdot \mathcal {V}_{P_{3}}(Q)$ for the same cost.

Step 3.

Since $\beta _{9}(P,Q)=((X^p\cdot Y \cdot Z)^{p^{3}-1},$ in the final step one processor computes one $p^3$ Frobenius map, three multiplications and one inversion in $\mathbb {F}_{p^{9}}$ which yields $6 M+3 M_{9} +I_{9}=\mathbf{189} M+I .$

The total cost of the parallel computation of the $\beta$-Weil pairing on BLS-9 using 3 processors is $\mathbf{11414} M+78 I .$

Appendix B. Original $\beta$-Weil Pairing on BLS Curves with Embedding Degree 27, 15 and 9.

In this section, we find the theoretical cost of the original $\beta$-Weil pairing computation on BLS-27,  BLS-15,  and BLS-9 curves without storage technique and multifunction technique.

The original $\beta$-Weil pairing (see theorem 2.1) on BLS-27 for seed $x=-2^{51}-2^{31}-2^{21}-2^{8}-2^4$ is given as:

$$\begin{aligned} \beta _{27}(P,Q)= & {} \prod _{i=0}^{8}\left( \dfrac{f_{x,Q}([p^i]P)}{ f_{x,[p^i]P}(Q)}\right) ^{(p^{8-i})(p^{9}-1)}\\= & {} \bigg [ \big ( f^{p^8}_{x,Q}(P)\cdot f^{p^7}_{x,Q}([p]P)\cdot f^{p^6}_{x,Q}([p^2]P)\cdot f^{p^5}_{x,Q}([p^3]P)\cdot f^{p^4}_{x,Q}([p^4]P)\\&\cdot \,f^{p^3}_{x,Q}([p^5]P)\cdot f^{p^2}_{x,Q}([p^6]P)\cdot f^{p}_{x,Q}([p^7]P)\cdot f_{x,Q}([p^8]P)\big )\\&\cdot \, \big ( f^{p^8}_{x,P}(Q)\cdot f^{p^7}_{x,[p]P}(Q)\cdot f^{p^6}_{x,[p^2]P}(Q)\cdot f^{p^5}_{x,[p^3]P}(Q)\cdot f^{p^4}_{x,[p^4]P}(Q)\\&\cdot \,f^{p^3}_{x,[p^5]P}(Q)\cdot f^{p^2}_{x,[p^6]P}(Q)\cdot f^{p}_{x,[p^7]P}(Q)\cdot f_{x,[p^8]P}(Q)\big )^{-1} \bigg ]^{p^9-1} \end{aligned}$$

1.1 Serial Computation

Original $\beta$-Weil pairing for serial computation are 9 Miller lite functions, 9 full Miller functions, 2 p, 2 $p^2,$ 2 $p^3,$ 2 $p^4,$ 2 $p^5,$ 2 $p^6,$ 2 $p^7,$ 2 $p^8,$ and 1 $p^9$ Frobenius maps, 18 multiplications, 2 inversions in $\mathbb {F}_{p^{27}}.$ From Algorithm 2, the cost of Miller Lite is $34M+51(125 M)+51(13 M +27 M +216 M)+4(16 M +27 M + 216M+216 M) = 21365 M.$ The cost of Full Miller is $34M+51(125 M)+51(233 M +I+9M +189 M)+4(233M +I+9M +189 M+189M) = 30870 M +55 I.$ The total cost is $9\cdot 21365 M+9(30870 M +55 I)+2(3\cdot 18 M+6\cdot 26 M)+18 M+ 18\cdot 216 M +2(I+449 M +62 S)=475463 M+497 I.$

Similarly, the computational cost of the original $\beta$-Weil pairing on BLS-15 given as $\beta _{15}(P,Q)= \prod _{i=0}^{4}\left( \dfrac{f_{x,Q}([p^i]P)}{ f_{x,[p^i]P}(Q)}\right) ^{(p^{4-i})(p^{5}-1)}$ with $x=-2^{77}-2^{76}-2^{68}-2^{50}$ is $5 Miller.Lite+5 Full.Miller+2(F_{1}+F_{2}+F_{3}+F_{4})+10 M_{15}+F_{5}+2 I_{15}=177657 M+401 I,$ where $Miller.Lite= 14747 M$ and $Full.Miller=20498 M+80 I.$

Also, the computational cost of the original $\beta$-Weil pairing on BLS-9 given as $\beta _{9}(P,Q)= \prod _{i=0}^{2}\left( \dfrac{f_{x,Q}([p^i]P)}{ f_{x,[p^i]P}(Q)}\right) ^{(p^{2-i})(p^{3}-1)}$ with $x=-2^{74}-2^{72}-2^{46}-2^{31}$ is $3 Miller.Lite+3 Full.Miller+2(F_{1}+F_{2})+6 M_{9}+F_{3}+2 I_{9}=43874 M+232I,$ where $Miller.Lite= 6441 M$ and $Full.Miller=7972 M+77 I.$

1.2 Parallel Computation of $\beta$-Weil Pairing on BLS-27 Using 3 Processors

$1^{st}$ processor computes

$\bigg (f^{p^8}_{x,Q}(P). f^{p^7}_{x,Q}([p]P)\cdot f^{p^6}_{x,Q}([p^2]P)\bigg )\cdot \bigg ( f^{p^8}_{x,P}(Q)\cdot f^{p^7}_{x,[p]P}(Q)\cdot f^{p^6}_{x,[p^2]P}(Q) \bigg )^{-1}$

$2^{nd}$ processor computes

$\bigg (f^{p^5}_{x,Q}([p^3]P)\cdot f^{p^4}_{x,Q}([p^4]P)\cdot f^{p^3}_{x,Q}([p^5]P)\bigg )\cdot \bigg ( f^{p^5}_{x,[p^3]P}(Q)\cdot f^{p^4}_{x,[p^4]P}(Q)\cdot f^{p^3}_{x,[p^5]P}(Q) \bigg )^{-1}$

$3^{rd}$ processor computes

$\bigg ( f^{p^2}_{x,Q}([p^6]P)\cdot f^{p}_{x,Q}([p^7]P)\cdot f_{x,Q}([p^8]P)\bigg )\cdot \bigg ( f^{p^2}_{x,[p^6]P}(Q)\cdot f^{p}_{x,[p^7]P}(Q)\cdot f_{x,[p^8]P}(Q) \bigg )^{-1}$

We see that, $3^{rd}$ processor’s cost is greater than $1^{st}$ and $2^{nd}$ processors’ cost because $3^{rd}$ processor require the extra computation of $[p^i]P$ $(1\le i\le 6)$ which does not require in $1^{st}$ and $2^{nd}$ processors. Therefore, the computational cost of the $3^{rd}$ processor is $cost.of.([p^6]P)+3 Miller.Lite+3 Full.MIller+2(F_{1}+F_{2})+5 M_{27}+I_{27}= 6\cdot 727 M+3(21365 M)+3(30870 M +55 I)+2( 26 M+26 M) + 5\cdot 216 M+(449 M+I)=162700 M+166 I.$ In the last step, one processor multiplies the three results of each processor and computes the $p^9-1$ power at a cost of $3\cdot 216 M+18M+(I+449 M)=1115 M+I.$ Therefore, the total cost is $163815 M+167 I.$

Appendix C: Computation of the Optimal Ate Pairing on BLS$-27$ Curve with a New Parameter

Remark 8.1

The method of [8] (section 3 page 6 ) for parallelizing the computation of the Miller function $f_{x, Q}$ is the following. We first write $x=2^{w}x_{1}+x_{0},$ where $x_{0}< 2^w.$ We obtain

$$\begin{aligned} f_{x, Q}= f^{2^w}_{x_{1}, Q} \cdot f_{2^w, x_{1}Q} \cdot f_{x_{0}, Q} \cdot \frac{l_{2^wx_{1}Q,x_{0}Q}}{V_{xQ}} \end{aligned}$$

Thus the computation of $f_{x, Q}$ can be parallelized by computing $f^{2^w}_{x_{1}, Q}$ on one processor, $f_{2^w, x_{1}Q}$ on a second processor and $f_{x_{0}, Q} \cdot \frac{l_{2^wx_{1}Q,x_{0}Q}}{V_{xQ}}$ on a third processor. This is the case where the three processors are independent. The parameter w should be carefully selected in order to balance the time of the three function computations. And if it is done in the right way we can estimate the cost one processor (the more costly) to be about $\frac{1}{3}$ of the initial Miller loop. Note that we can only parallelize the Miller function but not the final exponentiation.

The optimal Ate pairing on $BLS-27$ curve in [13] is given by:

$$\begin{aligned} e_{0}(Q,P)=f_{x,Q}(P)^{(p^{27}-1)/r}. \end{aligned}$$

For $x=-2^{51}-2^{31}-2^{21}-2^{8}-2^{4},$ the Miller loop executes 51 doubling steps, 4 addition steps, 51 squarings and 59 multiplications in $\mathbb {F}_{p^{27}}$. As in [17], the Miller loop cost of $M{27}=34M+51(233 M +I+9M )+4(233M +I+9M )+51(125 M)+59\cdot 189 M = 30870 M +55 I.$

The final exponentiation is divided into two parts: the easy part $A=f^{p^{9}-1}$ and the hard part $A^{d}$, where $d=(p^{18}+p^{9}+1)/r$.

the easy part is 1 $p^{9}-$Frobenius, 1 multiplications and 1 inversion in $\mathbb {F}_{p^{27}}$. That is $18 M+ 1 M_{27}+1 I_{27}=682M+I$. The element $d=(p^{18}p+^{9}+1)/r$, is decomposed as

$(x-1)^2\cdot (p^9+x^9+1)\cdot (p^8+x.p^7+...+x^7.p+x^8)+3.$ The evaluation of the hard part is as follows:

$A_{1}=A^{p^8}\cdot A^{xp^7}\cdot A^{x^2p^6}\cdot A^{x^3p^5}\cdot A^{x^4p^4}\cdot A^{x^5p^3}\cdot A^{x^6p^2}\cdot A^{x^7p}\cdot A^{x^8},$

$A_{2}=A_{1}^{(x-1)^2},$ $A_{3}=A_{2}^{x^9}\cdot A_{2}^{p^9}\cdot A_{2},$ $A_{4}=A^3\cdot A_{3}.$

The computation of the hard part requires 17 powers of x,  2 powers of $x-1,$ 11 multiplications in $\mathbb {F}_{p^{27}}$ and p, $p^2, p^3, p^4, p^5, p^6, p^7, p^8, p^9-$Frobenius maps. The negative coefficient in the value of x requires 19 inversions in the cyclotomic subgroup when raising to the power of x during the final exponentiation. (Note that $A^{-1} = A^{p^9}\cdot A^{p^{18}}$ and cost $2\cdot 18M+ 1 M_{27}=252 M$ ). The hard part then cost

$17(51 S_{27} + 4 M_{27})+2(51 S_{27} + 5 M_{27}) + 11 M_{27}+2\cdot 18M+6\cdot 26M+19 I_{G_{\varphi _{3}(p^9)}}= 145329 M .$ The computational cost of the optimal Ate pairing over $BLS-27-$curve is then $(31365 M +55 I) +(682M+I)+145329 M=\mathbf{176881} M+56I .$

Appendix D: Computation of the Optimal Ate Pairing on BLS-15 Curve with a New Parameter

Similarly, we evaluate $e_{0}(Q,P)=f_{x,Q}(P)^{(p^{15}-1)/r}$ with $x=-2^{77}-2^{76}-2^{68}-2^{50}$ on BLS-15 curve. The computational cost of Miller full is $20498 M +80 I$ and best cost of the final exponentiation is $9 E_{x}+2 E_{x-1}+12 M_{15}+S_{15}+I_{15}+3 I_{cyc}+3 F_{1}+F_{2}+F_{3}+F_{4}+2 F_{5}+F_{6}+F_{7}$ see [36]) for this we will add 11 cyclotomique inversion due to the negative parameter x. $E_{x}=77 S_{15}+3 M_{15},$ $E_{x-1}=77 S_{15}+4 M_{15}$ and $I_{cyc}=54 M.$ Thus the final exponentiation cost $70971 M+I$ and the computational cost of the optimal ate is then $91469 M+81I.$

Appendix E: Computation of the Optimal Ate Pairing on BLS-9 Curve with a New Parameter

We evaluate $e_{0}(Q,P)=f_{x,Q}(P)^{(p^{9}-1)/r}$ with $x=-2^{74}-2^{72}-2^{46}-2^{31}$ on BLS-9 curve. The computational cost of Miller full is $7972 M +77I$ and the optimal cost of the final exponentiation is $5 E_{x}+2 E_{x-1}+7 M_{9}+S_{9}+I_{9}+ F_{1}+F_{2}+2F_{3}$ see [36]) for this we will add 7 cyclotomique inversion due to the negative parameter x. $E_{x}=74 S_{9}+3 M_{9},$ $E_{x-1}=74 S_{9}+4 M_{9}$ and $I_{cyc}=33 M.$ Thus the final exponentiation cost $14393M+I$ and the computational cost of the optimal Ate is then $22365 M+78 I.$