Degree Upper Bounds for Involutive Bases

Abstract

The aim of this paper is to investigate upper bounds for the maximum degree of the elements of any minimal Janet basis of an ideal generated by a set of homogeneous polynomials. The presented bounds depend on the number of variables and the maximum degree of the generating set of the ideal. For this purpose, by giving a deeper analysis of the method due to Dubé (SIAM J Comput 19:750–773, 1990), we improve (and correct) his bound on the degrees of the elements of a reduced Gröbner basis. By giving a simple proof, it is shown that this new bound is valid for Pommaret bases, as well. Furthermore, based on Dubé’s method, and by introducing two new notions of genericity, so-called J-stable position and prime position, we show that Dubé’s (new) bound holds also for the maximum degree of polynomials in any minimal Janet basis of a homogeneous ideal in any of these positions. Finally, we study the introduced generic positions by proposing deterministic algorithms to transform any given homogeneous ideal into these positions.

1 Introduction

The concept of Gröbner bases along with the first algorithm to compute them were introduced by Bruno Buchberger in his PhD thesis [3, 4]. Since then many interesting applications of these bases have been found in Mathematics, science, and engineering. For example, we can point out their applications in the ideal membership problem, computing the dimension of an ideal, solving polynomial systems and so on. It is worth noting that establishing upper bounds for the degrees of the elements of a minimal Gröbner basis is very important for predicting the practical feasibility of the computations as well as for the complexity analysis of Gröbner bases computations, see [16].

To review the existing literature on degree upper bounds for Gröbner bases, let ${\mathcal {R}}$ be the polynomial ring ${\mathcal {K}}[x_1,\ldots , x_n]$ where ${\mathcal {K}}$ is a field of characteristic zero and let ${\mathcal {I}}\subset {\mathcal {R}}$ be an ideal generated by homogeneous polynomials of degree at most d. The doubly-exponential nature of degree upper bounds for Gröbner bases were established by Bayer, Möller, Mora and Giusti, see [21, Chapter 38]. Möller and Mora [20] derived the degree upper bound $(2d)^{(2n+2)^{n+1}}$ for any Gröbner basis of ${\mathcal {I}}$. At the same time, Giusti [11] presented the upper bound $(2d)^{2^{n-2}}$ for the degree of the reduced Gröbner basis w.r.t. the degree reverse lexicographic ordering of ${\mathcal {I}}$ provided that ${\mathcal {I}}$ is in generic position. Using a self-contained and constructive combinatorial argument, Dubé [6] proved the degree bound $2(d^2/2 + d)^{2^{n-1}}$. Finally, Mayr and Ritscher [18], following the method by Dubé, improved his bound to the dimension-dependent upper bound $2(1/2(d^{n-D}+d))^{2^{D-1}}$ for every reduced Gröbner basis of ${\mathcal {I}}$ where $D=\dim ({\mathcal {I}})$. It should be noted that in [14], dimension and depth depending upper bounds were exhibited for the Castelnuovo-Mumford regularity and the degrees of the elements of the reduced Gröbner basis of an ideal in generic position.

Since in this paper, we discuss degree upper bounds for involutive bases, let us step back and briefly review the literature on these bases. Involutive bases (which may be considered as a particular kind of non-reduced Gröbner bases) have their origin in the works by Janet [15] in the analysis of (linear) partial differential equations. By developing the methods by Pommaret [22], Zharkov and Blinkov introduced the notion of involutive polynomial bases [25]. Then, Gerdt and Blinkov [10] introduced the concepts of involutive division and involutive bases for polynomial ideals, and the theory of involutive bases led to an alternative approach to Buchberger’s algorithm.

In this paper, by giving a deeper analysis of Dubé’s method [6], we improve first Dubé’s bound to $O(1)d^{2^{n-2}}$ for the degrees of the elements of a Gröbner basis. In addition, we point out two flaws in the proof of his main result [6, Lemma 8.1]. We correct Dubé’s bound into the sharper bound $(d+1)^{2^{n-2}}$. Finally, we investigate degree upper bounds for Pommaret and Janet bases by introducing two new notions of genericity. It should be noted that we discuss these notions in more details by showing how one can transform a given ideal into these positions.

The structure of the paper is as follows. Section 2 recalls the basic notations and definitions used throughout this paper. Section 3 reviews the combinatorial approach proposed by Dubé [6] to provide a degree upper bound for a Gröbner basis. In Sect. 4, an improvement of Dubé’s bound is presented. Section 5 is devoted to the study of degree upper bounds for Pommaret bases. In Sects. 6 and 7, we introduce new generic positions, and show that any degree upper bound obtained for a Gröbner basis by applying Dubé’s approach holds for the Janet basis of an ideal in any of these generic positions. Finally, we discuss how one can transform a given ideal into any of these positions.

2 Preliminaries

In this section, we will briefly explain the basic notations and preliminaries that used in the subsequent sections. Let ${\mathcal {R}}={\mathcal {K}}[X]$ be the polynomial ring over an infinite field ${\mathcal {K}}$ where $X=\{x_{1},\dots ,x_{n}\}$. Furthermore, let ${\mathcal {M}}$ be the set of all monomials in ${\mathcal {R}}$ (a monomial is a power product of the elements of X). We consider a finite set of homogeneous polynomials $F=\{f_1,\ldots ,f_k\}\subset {\mathcal {R}}$ and the ideal ${\mathcal {I}}=\langle F \rangle$ generated by F. We denote the degree w.r.t. a variable $x_{i}$ of a polynomial $f\in {\mathcal {R}}$ by $\deg _{i}(f)$ and the total degree of f by $\deg (f)$. The maximum degree of the polynomials in F is denoted by d. The Krull dimension of the factor ring ${\mathcal {R}}/{\mathcal {I}}$, denoted by $D=\dim ({\mathcal {I}})$, is the number of elements of any maximal set $S\subseteq X$ such that ${\mathcal {I}}\cap {\mathcal {K}}[S]=\{0\}$. A prime ideal ${\mathcal {P}}$ is called a minimal prime ideal of ${\mathcal {I}}$, if ${\mathcal {I}}\subseteq {\mathcal {P}}$ and ${\mathcal {P}}$ is minimal with this property.

A typical example of a monomial ordering that we use in this paper is the degree reverse lexicographical ordering with $x_n\prec _{drl} \cdots \prec _{drl} x_1$. More precisely, for two monomials $x^{\alpha }$ and $x^{\beta }$ we write $x^{\alpha }\prec _{drl} x^{\beta }$ if either $\deg (x^{\alpha })<\deg (x^{\beta })$ or $\deg (x^{\alpha })=\deg (x^{\beta })$ and the right-most non-zero entry of $\beta -\alpha$ is negative. The leading monomial of a polynomial $0\ne f\in {\mathcal {R}}$, denoted by ${\mathrm{LM}}(f)$, is the greatest monomial appearing in f w.r.t. $\prec$ and its coefficient is called the leading coefficient of f, denoted by ${\mathrm{LC}}(f)$. The leading term of f is the product ${\mathrm{LT}}(f)={\mathrm{LC}}(f){\mathrm{LM}}(f)$. For $F\subset {\mathcal {R}}$, $\mathrm{LM}(F)$ stands for $\{\mathrm{LM}(f) \ | \ f\in F\}$. The leading monomial ideal of ${\mathcal {I}}$ is the monomial ideal ${\mathrm{LM}}({\mathcal {I}}) = \langle {\mathrm{LM}}(f) \ | \ 0\ne f \in {{\mathcal {I}}}\rangle$. A finite set $G \subset {{\mathcal {I}}}$ is called a Gröbner basis for ${\mathcal {I}}$ w.r.t. $\prec$, if ${\mathrm{LM}}({\mathcal {I}}) = \langle \mathrm{LM}(G) \rangle$. The remainder of division f by a Gröbner basis G w.r.t. $\prec$, is denoted by ${\text{ NF }}_{G}(f)$. For a Gröbner basis G, we let $N_{{\mathcal {I}}}=\{ {\text{ NF }}_{G}(f) \mid f\in {\mathcal {R}}\}$ be the ${\mathcal {K}}$-vector space generated by the set of all monomials u with $u\notin \langle \mathrm{LM}(G) \rangle$. We refer to [5] for more details on the theory of Gröbner bases. Now, let us review some definitions and results from the theory of involutive bases, see [9, 24] for more information.

Definition 2.1

An involutive division ${\mathcal {L}}$ is defined on ${\mathcal {M}}$, if for any nonempty finite set $U \subset {\mathcal {M}}$ and for any monomial $u \in U$, we can partition the set of variables X into two disjoint subsets $M_{{\mathcal {L}}}(u,U)$ of multiplicative variables and $NM_{{\mathcal {L}}}(u,U)$ of non-multiplicative variables such that for any $u_1,v_1 \in U$ the following conditions hold:

• 1. if $u_1{\mathcal {L}}(u_1,U) \cap v_1{\mathcal {L}}(v_1,U)\ne \emptyset$ then either $u_1 \in v_1{\mathcal {L}}(v_1,U)$ or $v_1 \in u{\mathcal {L}}(u_1,U)$,

• 2. if $v_1 \in u_1{\mathcal {L}}(u_1,U)$ then ${\mathcal {L}}(v_1,U)\subseteq {\mathcal {L}}(u_1,U)$,

• 3. if $u_1\in V$ and $V\subseteq U$ then ${\mathcal {L}}(u_1,U) \subseteq {\mathcal {L}}(u_1,V)$,

where for any monomial $u \in U$, ${\mathcal {L}}(u,U)$ denotes the subset of ${\mathcal {M}}$ consisting of all monomials in terms of $M_{{\mathcal {L}}}(u,U)$.

As classical examples of involutive divisions, we recall the definitions of the Janet and Pommaret divisions.

Definition 2.2

For a given finite set $U\subset {\mathcal {M}}$ of monomials and a given sequence of non-negative integers $d_{1},\ldots , d_{i}$ with $1\le i\le n$ define

$$\begin{aligned} {[}d_{1},\ldots ,d_{i}]=\lbrace u\in U \mid d_{j}=\deg _{j}(u), 1\le j \le i \rbrace . \end{aligned}$$

$x_{1}$ is Janet multiplicative (or shortly ${\mathcal {J}}$-multiplicative) for $u \in U$, if $\deg _{1}(u)=\max \lbrace \deg _{1}(v) \ \mid \ v \in U \rbrace$. For $i>1$, $x_{i}$ is ${\mathcal {J}}$-multiplicative for $u\in U$, if $\deg _{i}(u)=\max \lbrace \deg _{i}(v) \ \mid \ v \in [\deg _1(u),\ldots ,\deg _{i-1}(u)] \rbrace$.

Definition 2.3

For $u=x_{1}^{d_{1}}\cdots x_{k}^{d_{k}}$ with $d_{k}>0$, the integer k is called the class of u and is denoted by ${{\,\mathrm{cls}\,}}(u)$. The variables $x_{{{\,\mathrm{cls}\,}}(u)},\ldots ,x_n$ are Pommaret multiplicative (or shortly ${\mathcal {P}}$-multiplicative) for u. For $u=1$, all the variables are Pommaret multiplicative.

In the next example, the separation of variables is shown for Janet and Pommaret divisions.

Example 2.4

For $U=\{x_{1}x_{2},x_{3}\} \subset {\mathcal {K}}[x_{1},x_{2},x_{3}]$, we have

Monomial	$M_{{\mathcal {J}}}$	$NM_{{\mathcal {J}}}$	$M_{{\mathcal {P}}}$	$NM_{{\mathcal {P}}}$
$x_{1}x_{2}$	$x_{1},x_{2},x_{3}$		$x_{2},x_{3}$	$x_{1}$
$x_{3}$	$x_{2},x_{3}$	$x_{1}$	$x_{3}$	$x_{1},x_{2}$

Gerdt and Blinkov [10, Proposition 3.6] showed that both these divisions are involutive.

Definition 2.5

For a finite set $U\subset {\mathcal {M}}$ of monomials, the sets ${\mathcal {C}}(U)=\bigcup _{u\in U}u {\mathcal {M}}$ and ${\mathcal {C}}_{{\mathcal {L}}}(U)=\bigcup _{u \in U}u{\mathcal {L}}(u,U)$ are called, respectively, the cone and the ${\mathcal {L}}$ -involutive cone generated by U.

Definition 2.6

For a finite set $U\subset {\mathcal {M}}$ of monomials, a set ${\tilde{U}}$ with $U\subseteq {\tilde{U}}\subseteq {\mathcal {M}}$ is called an ${\mathcal {L}}$ -completion of U, if ${\mathcal {C}}(U)={\mathcal {C}}_{{\mathcal {L}}}({\tilde{U}})$. Furthermore, U is ${\mathcal {L}}$-complete or ${\mathcal {L}}$ -involutive, if it holds ${\mathcal {C}}_{{\mathcal {L}}}(U)={\mathcal {C}}(U)$. An involutive division ${\mathcal {L}}$ is said to be Nœtherian, if every finite set U possesses a finite ${\mathcal {L}}$-completion.

We are now in a position to introduce the concept of involutive bases. A finite set $F\subset {\mathcal {R}}$ is ${\mathcal {L}}$-autoreduced, if for any $f\in F$, no monomial occurring in f is ${\mathcal {L}}$-divisible by $\mathrm{LM}(F)\setminus \{\mathrm{LM}(f)\}$.

Definition 2.7

Let ${\mathcal {I}}\subset {\mathcal {R}}$ be an ideal and ${\mathcal {L}}$ an involutive division. Then an ${\mathcal {L}}$-autoreduced subset $G\subset {\mathcal {I}}$ is called an ${\mathcal {L}}$-involutive basis (or shortly an involutive basis) for ${\mathcal {I}}$, if for each $f\in {\mathcal {I}}$ there exists $g\in G$ so that $\mathrm{LM}(g)|_{{\mathcal {L}}} \mathrm{LM}(f)$.

According to the above definition, every involutive basis is a Gröbner basis for the ideal it generates. Furthermore, in [10, Proposition 4.5], it was shown that the Janet division is Nœtherian and it follows immediately from this property that every ideal has a (finite) Janet basis. Gerdt in [9] described an algorithmic approach to construct involutive bases. We shall point out that this process terminates in finitely many steps only for Nœtherian divisions. However, the following simple example illustrates that finite Pommaret bases do not exist in general.

Example 2.8

Let ${\mathcal {I}}=\langle x_{2} \rangle \subset {\mathcal {K}}[x_{1},x_{2}]$. The Pommaret basis of ${\mathcal {I}}$ is the infinite set $\{ x_{1}^{i}x_{2} \mid i\ge 0 \}$.

The third author in [23] explicitly related the ideals with finite Pommaret bases to the notion of genericity. For this, the notion of quasi stable position was introduced and it was shown that an ideal in such a position possesses a finite Pommaret basis.

Definition 2.9

A monomial ideal ${\mathcal {I}}\subset {\mathcal {R}}$ is quasi stable, if for any monomial $m\in {\mathcal {I}}$ and all positive integers i, j, s with $1 \le j < i\le n$, if $x^{s}_{i}\mid m$, there exists an integer $t \ge 0$ such that $x^{t}_{j} (m/x^{s}_{i})\in {\mathcal {I}}$. An ideal ${\mathcal {I}}\subset {\mathcal {R}}$ is called in quasi stable position, if $\mathrm{LM}({\mathcal {I}})$ w.r.t. $\prec$ is quasi stable.

Proposition 2.10

( [23, Proposition 4.4]) A homogeneous ideal ${\mathcal {I}}$ has a finite Pommaret basis, if and only if it is in quasi stable position.

Since ${\mathcal {K}}$ is infinite, then, for a given ideal, by applying a generic linear change of variables, one is able to transform the ideal into quasi stable position and in consequence the new ideal has a finite Pommaret basis, see [23] for more details.

3 Dubé’s Approach

In this section, we give a short review of Dubé’s [6] method which entails degree upper bound for Gröbner bases. For this, let us first recall some basic definitions from [6]. Let us denote by ${\text{ indet }}(u)$ the set of all variables appearing in the monomial $u\in {\mathcal {M}}$. For a finite set $F\subset {\mathcal {R}}$ of monomials, we set ${\text{ indet }}(F)=\bigcup _{u\in F}{\text{ indet }}(u)$.

Definition 3.1

Let ${\mathcal {T}}\subset {\mathcal {R}}$. The family $S_{1},\ldots ,S_{t}$ of subsets of ${\mathcal {T}}$ is said to be a direct decomposition of ${\mathcal {T}}$ if every $p \in {\mathcal {T}}$ can be uniquely expressed of the form $p=\sum _{i=1}^{r}p_{i}$ where $p_{i}\in S_{i}$ and $r\le t$. This property is indicated by the notation ${\mathcal {T}}=S_{1}\oplus S_{2}\oplus \cdots \oplus S_{m}$.

For example, ideal ${\mathcal {I}}=\langle x_{2} \rangle$ in Example  2.8 has a direct decomposition $S_{i}=\{x_{1}^{i}x_{2}^{j} \mid j\ge 1 \}$, $i\ge 0$. Also, for any ideal ${\mathcal {I}}$ we can decompose ${\mathcal {R}}={\mathcal {I}}\oplus N_{{\mathcal {I}}}$. For a homogeneous polynomial h and set $u\subseteq X$, the set $C(h,u)=\{ ah \ | \ a\in {\mathcal {R}}\ \text {and}\ {\text{ indet }}(a)\subseteq u \}$ is also called the cone presented by h and u.

Definition 3.2

Let $h_{1},\ldots ,h_{t}$ be homogeneous polynomials in ${\mathcal {R}}$, and $u_{1},\ldots ,u_{t}$ subsets of X. A finite set $P=\{ C(h_{1},u_{1}),\ldots ,C(h_{t},u_{t}) \}$ is called a cone decomposition of ${\mathcal {T}}\subset {\mathcal {R}}$ if the cones $C(h_{i},u_{i})$’s form a direct decomposition for ${\mathcal {T}}$.

If the set $F=\{f_1,\ldots ,f_k\}$ is a Janet basis for a given ideal ${\mathcal {I}}$ then, from properties of a Janet basis it follows that $\{ C(f_1,M_{{\mathcal {J}}}(\mathrm{LM}(f_k),\mathrm{LM}(F))), \ldots ,C(f_k,M_{{\mathcal {J}}}(\mathrm{LM}(f_k),\mathrm{LM}(F)))\}$ forms a cone decomposition for ${\mathcal {I}}$. For a cone decomposition P, we write $P^{+}=\{ C(h,u)\in P \mid u\ne \emptyset \}$.

Definition 3.3

Let k be a non-negative integer and P a cone decomposition. Then, P is called k-standard if the following conditions hold:

• 1. There is no cone $C(h,u)\in P^{+}$ with $\deg (h)<k$.

• 2. For each $C(g,u)\in P^{+}$ and $k\le d \le \deg (g)$, there exists $C(h,v)\in P^{+}$ with $\deg (h)=d$ and $\vert u \vert \ge \vert v\vert$.

By convention, if $P^{+}$ is the empty set, then P is k-standard for all k.

Example 3.4

Let ${\mathcal {I}}=\langle x_{1}x_{2}x_{3}, x_{1}x_{3}^{2}, x_{1}x_{4} \rangle \subset {\mathcal {K}}[x_{1},x_{2},x_{3},x_{4}]$. Then $C(1,\{x_{2},x_{3},x_{4}\})\oplus C(x_{1},\{ x_{1},x_{2} \})\oplus C(x_{1}x_{3},\{ x_{1} \})$ is a 0-standard cone decomposition for $N_{{\mathcal {I}}}$.

Definition 3.5

A cone decomposition P is called exact if it is k-standard for some k, and in addition for each d, there exists at most one $C(h,u)\in P^{+}$ with $\deg (h)=d$.

For example, one observes that the 0-standard cone decomposition in Example 3.4 is exact, as well.

Definition 3.6

The Macaulay constants of a k-exact cone decomposition P is defined to be:

$$\begin{aligned} {}b_{i}=\mathrm{min}\{ d\ge k \ | \ \forall \ C(h,u)\in P; \vert u\vert \ge i \Longrightarrow \deg (h)< d \}, \ \ \ \ \ i=0,\ldots ,n+1. \end{aligned}$$

We note as a simple observation that $b_{0}\ge b_{1}\ge \dots \ge b_{n+1}=k$. In Example 3.4, Macaulay constants for set $N_{{\mathcal {I}}}$ are $b_{0}=3, b_{1}=3, b_{2}=2, b_{3}=1, b_{4}=0$ and $b_{5}=0$.

Lemma 3.7

( [6, Lemma 6.1]) Let P be an exact cone decomposition, and $b_{0},\ldots ,b_{n+1}$ be the Macaulay constants of P. Then for each $i=1,\dots ,n$ and any given degree d with $b_{i+1}\le d< b_{i}$, there is exactly one cone $C(h,u)\in P^{+}$ such that $\deg (h)=d$ and in that cone $\vert u\vert =i$.

Now, we are ready to give the outline of the approach proposed by Dubé in [6].

• 1. Starting with a homogeneous generating set F for a given ideal ${\mathcal {I}}\subset {\mathcal {R}}$ and assume that d is the maximum degree of the polynomials in F.

• 2. Finding a 0-exact cone decomposition for $N_{{\mathcal {I}}}$ and also a direct decomposition of the form ${\mathcal {I}}=C(f,\{x_{1} \ldots ,x_{n}\})\oplus S$ such that $f\in F,\,\deg (f)=d$ and S is a d-exact cone decomposition.

• 3. Using Macaulay constants of these two exact cone decompositions to give a simple formulation for Hilbert functions of $N_{{\mathcal {I}}}$ and ${\mathcal {I}}$.

• 4. Using these Hilbert functions and applying the equality ${\mathcal {R}}={\mathcal {I}}\oplus N_{{\mathcal {I}}}$ to find a new upper bound for the Macaulay constants.

• 5. It was shown that this upper bound can be generalized for an arbitrary ideal generated by a set of polynomials of degree at most d.

Given an ideal, by applying the next algorithm, we are able to construct a 0-standard cone decomposition for $N_{\mathrm{LM}({\mathcal {I}})}$ w.r.t. a fixed monomial ordering. In the next algorithm, we assume that ${\mathcal {I}}$ is a monomial ideal.

Example 3.8

As a simple example, Split$(1,\{x_{1},x_{2}\},\{x_{1}^{2}x_{2},x_{1}x_{2}^{2},x_{2}^{3} \})$ returns (P, Q) with

$$\begin{aligned} P= & {} \big \{C(x_{2}^{3},\{x_{2}\}),C(x_{1}x_{2}^{2},\{x_{2}\}),C(x_{1}^{2} x_{2},\{x_{1},x_{2}\}) \big \} \\ Q= & {} \big \{C(1,\{x_{1}\}),C(x_{2},\emptyset ),C(x_{2}^{2},\emptyset ), C(x_{1}x_{2},\emptyset ) \big \}. \end{aligned}$$

It was proved in [6, Lemmata 4.3 and 4.4] that this algorithm terminates in finitely many steps and is correct. In addition, it was shown in [6, Lemma 4.10, Theorem 4.11] that if we have $(P,Q)=$ Split(h, u, F) then Q is a $\deg (h)$-standard cone decomposition. Now, given a homogeneous ideal ${\mathcal {I}}$, we give a pair of cone decompositions for ${\mathcal {I}}$ and $N_{{\mathcal {I}}}$. For this, let us assume that $(P,Q)=$ Split$(1,X,\mathrm{LM}(G))$ where G is a Gröbner basis for ${\mathcal {I}}$. It follows that Q is a 0-standard cone decomposition for $N_{{\mathcal {I}}}$ (note that here we use the fact that $N_{{\mathcal {I}}}=N_{\mathrm{LM}({\mathcal {I}})}$, see [5] for more information). Furthermore, we can conclude that P can provide a standard decomposition for ${\mathcal {I}}$. In [6], an algorithm was described to transform a k-standard cone decomposition into an k-exact cone decomposition. All together, we are able to construct a 0-exact cone decomposition for $N_{{\mathcal {I}}}$.

Let ${\mathcal {T}}$ be a ${\mathcal {K}}$-vector space so that the homogeneous components of any element of ${\mathcal {T}}$ belong to ${\mathcal {T}}$. The set of all homogeneous polynomials in ${\mathcal {T}}$ of degree i is denoted by ${\mathcal {T}}_{i}$. The Hilbert function of ${\mathcal {T}}$ at i, denoted by $\varphi _{{\mathcal {T}}}(i)$, is the dimension of ${\mathcal {T}}_{i}$ as a ${\mathcal {K}}$-vector space. Now, assume that P is an exact cone decomposition for a homogeneous ${\mathcal {K}}$-vector space ${\mathcal {T}}$ and $b_{0},\ldots ,b_{n+1}$ are Macaulay constants of P. Then, the Hilbert function of ${\mathcal {T}}$ can be expressed as follows:

$$\begin{aligned} \varphi _{{\mathcal {T}}}(z)=\sum _{C(h,u)\in P}\varphi _{C(h,u)}(z). \end{aligned}$$

For any $z\ge b_{0}$, each of the cones in $P^{+}$ has a Hilbert function described by the binomial coefficient

$$\begin{aligned} \varphi _{C(h,u)}(z)={z-\deg (h)+\vert u\vert -1\atopwithdelims ()\vert u\vert -1} \end{aligned}$$

and in consequence for $z\ge b_{0}$, we can write

$$\begin{aligned} \varphi _{{\mathcal {T}}}(z)=\sum _{C(h,u)\in P^{+}}{z-\deg (h)+\vert u \vert -1\atopwithdelims ()\vert u\vert -1}. \end{aligned}$$

By applying Lemma 3.7, for $z\ge b_{0}$ we have

$$\begin{aligned} \varphi _{{\mathcal {T}}}(z)=\sum _{j=1}^{n}\sum _{d=b_{j+1}}^{b_{j}-1}{z-d+j-1\atopwithdelims ()j-1}. \end{aligned}$$

Then, using a combinatorial argument, it was shown in [6, page 768] that for $z\ge b_{0}$ it holds

$$\begin{aligned} \varphi _{{\mathcal {T}}}(z)={z-b_{n+1}+n\atopwithdelims ()n}-1-\sum _{i=1}^{n}{z-b_{i}+i-1\atopwithdelims ()i}. \end{aligned}$$

(1)

The Hilbert function $\varphi _{{\mathcal {T}}}$ for $z\ge b_{0}$ can be represented by a unique polynomial, so-called the Hilbert polynomial of ${\mathcal {T}}$ and is denoted by ${\bar{\varphi }}_{{\mathcal {T}}}(z)$. Hence for $z\ge b_{0}$, $\varphi _{{\mathcal {T}}}(z)={\bar{\varphi }}_{{\mathcal {T}}}(z)$.

In [6, Lemma 7.1], it was proved that the Macaulay constants $b_{0},\dots ,b_{n}$ for ${\mathcal {T}}$ are uniquely determined if $b_{n+1}$ has been fixed. Summarizing, the Split algorithm returns a 0-standard cone decomposition Q for $N_{{\mathcal {I}}}$ where ${\mathcal {I}}$ is a homogeneous ideal. Furthermore, in [6, Theorem 4.11] it was shown that $t=1+\max \{ \deg (h) \mid C(h,u)\in Q \}$ is an upper bound for the degrees of the polynomials in any reduced Gröbner basis of the ideal ${\mathcal {I}}$. Finally, the construction of the exact cones shows that the Macaulay constant $b_{0}$ is greater than t, and according to [6, Lemma 7.2] $b_{0}$ remains an upper bound for degree of any reduced Gröbner basis of ${\mathcal {I}}$.

4 A New Upper Degree Bound for Gröbner Bases

In this section, by a deeper analysis of Dubé’s method, we give a more accurate upper bound for the degrees of the polynomials in any reduced Gröbner basis of a homogeneous ideal ${\mathcal {I}}$. For this, assume that we are given a 0-exact cone decomposition Q with the Macaulay constants $b_{0}\ge b_{1}\ge \cdots \ge b_{n+1}=0$ for $N_{{\mathcal {I}}}$. Then, the Hilbert function of $N_{{\mathcal {I}}}$ for $z\ge b_{0}$ equals

$$\begin{aligned} \varphi _{N_{{\mathcal {I}}}}(z)={z+n\atopwithdelims ()n}-1-\sum _{i=1}^{n}{z-b_{i}+i-1\atopwithdelims ()i}. \end{aligned}$$

Furthermore, if d is the maximum degree of a generating set of ${\mathcal {I}}$ then ${\mathcal {I}}=C(f,X)\oplus K'$ where $\deg (f)=d$ and $K'$ is a d-exact cone decomposition with the Macaulay constants $a_{0}\ge a_{1}\ge \cdots \ge a_{n+1}=d$. Then, for $z\ge a_{0}$ the Hilbert function of ${\mathcal {I}}$ is:

$$\begin{aligned} \varphi _{{\mathcal {I}}}(z)={z-d+n-1\atopwithdelims ()n-1}+{z-d+n\atopwithdelims ()n}-1-\sum _{i=1}^{n}{z-a_{i}+i-1\atopwithdelims ()i}. \end{aligned}$$

From the equality ${\mathcal {R}}={\mathcal {I}}\oplus N_{{\mathcal {I}}}$, for $z\ge \mathrm{max}\{a_{0},b_{0}\}$, we can write

$$\begin{aligned} \varphi _{{\mathcal {R}}}(z)= & {} {z+n-1\atopwithdelims ()n-1}\nonumber \\= & {} {z-d+n-1\atopwithdelims ()n-1}+{z-d+n\atopwithdelims ()n}+{z+n\atopwithdelims ()n}-2 \nonumber \\&-\sum _{i=1}^{n} \left[ {z-a_{i}+i-1\atopwithdelims ()i}+{z-b_{i}+i-1\atopwithdelims ()i}\right] . \end{aligned}$$

(2)

By considering both sides as polynomials in z and making equal the coefficients of the polynomials at the left and right hand sides, we try to find the desired upper bound. For this, and following the notations of [6], the backward difference operator $\nabla$, for any function f(x) is defined as $\nabla f(x):=f(x)-f(x-1)$, and inductively, for any j, $\nabla ^{j} f(x)=\nabla (\nabla ^{j-1}f(x))$. It is seen that the degree of univariate polynomial in (2) is $n-1$. Now to extract the coefficients of the polynomial in (2), it is enough to apply the operator $\nabla ^{j}$ to both sides of (2) for $j=0,\dots ,n-1$. Hence applying this operator to both sides of (2) and taking into account the identity $\nabla ^{j} {z+k\atopwithdelims ()n}={z+k-j\atopwithdelims ()n-j}$, for enough large value of z, we obtain:

$$\begin{aligned} {z+n-j-1\atopwithdelims ()n-j-1}= & {} {z-d+n-j-1\atopwithdelims ()n-j-1}+{z-d+n-j\atopwithdelims ()n-j}+{z+n-j\atopwithdelims ()n-j}\\&-\sum _{i=j}^{n}\left[ {z-a_{i}+i-j-1\atopwithdelims ()i-j}+{z-b_{i}+i-j-1\atopwithdelims ()i-j} \right] . \end{aligned}$$

For $i=j$ we have ${z-a_{i}+i-j-1\atopwithdelims ()i-j}+{z-b_{i}+i-j-1\atopwithdelims ()i-j}=2$ and in turn

$$\begin{aligned} {z+n-j-1\atopwithdelims ()n-j-1}= & {} {z-d+n-j-1\atopwithdelims ()n-j-1}+{z-d+n-j\atopwithdelims ()n-j}+{z+n-j\atopwithdelims ()n-j}-2\nonumber \\&-\sum _{i=j+1}^{n}\left[ {z-a_{i}+i-j-1\atopwithdelims ()i-j}+{z-b_{i}+i-j-1\atopwithdelims ()i-j} \right] . \end{aligned}$$

(3)

For simplicity, we denote the constant coefficient of ${z+k\atopwithdelims ()n}$ by:

$$\begin{aligned} l (k,n)= {\left\{ \begin{array}{ll} 1&{}\text {if }n=0\\ \dfrac{k(k-1)\cdots (k-n+1)}{n!}&{}\text {if }n\ne 0.\\ \end{array}\right. } \end{aligned}$$

So, comparing the constant coefficient of both sides of Equality (3), we get

$$\begin{aligned} 1= & {} l (-d+n-j-1,n-j-1)+ l (-d+n-j,n-j)-1\nonumber \\&-\sum _{i=j+1}^{n}\left[ l (-a_{i}+i-j-1,i-j)+ l (-b_{i}+i-j-1,i-j)\right] . \end{aligned}$$

(4)

For $j=n-1$, we have:

$$\begin{aligned} {}1= l (-d,0)+ l (-d+1,1)-1- l (-a_{n},1)- l (-b_{n},1)=1-d+1-1+a_{n}+b_{n}. \end{aligned}$$

Thus, $a_{n}+b_{n}=d$. On the other hand, we have $a_{n}\ge d$ and $b_{n}\ge 0$ which implies that $a_{n}=d$ and $b_{n}=0$. Using these properties, we can simplify Equality (4) as follows:

$$\begin{aligned} 1= & {} l (-d+n-j-1,n-j-1)+ l (-d+n-j,n-j)- l (-d+n-j-1,n-j)-1\\&-\sum _{i=j+1}^{n-1}\left[ l (-a_{i}+i-j-1,i-j)+ l (-b_{i}+i-j-1,i-j)\right] . \end{aligned}$$

From the equality $l (-d+n-j,n-j)- l (-d+n-j-1,n-j)= l (-d+n-j-1,n-j-1)$, it follows that:

$$\begin{aligned} 1= & {} 2 l (-d+n-j-1,n-j-1)-1\\&-\sum _{i=j+1}^{n-1}\left[ l (-a_{i}+i-j-1,i-j)+ l (-b_{i}+i-j-1,i-j)\right] . \end{aligned}$$

Let for each j, $c_{j}$ denote the sum $a_{j}+b_{j}$. Then, we can conclude that:

$$\begin{aligned} c_{j+1}= & {} -2 l (-d+n-j-1,n-j-1)+2\nonumber \\&+\sum _{i=j+2}^{n-1}\left[ l (-a_{i}+i-j-1,i-j)+ l (-b_{i}+i-j-1,i-j)\right] . \end{aligned}$$

(5)

For $j=n-2$, one observes that $c_{n-1}=-2 l (-d+1,1)+2=2d$. For $j=n-3$ we have:

$$\begin{aligned} c_{n-2}= & {} -2 l (-d+2,2)+2+ l (-a_{n-1}+1,2)+ l (-b_{n-1}+1,2)\\= & {} -2\dfrac{(d-1)(d-2)}{2}+2+\dfrac{a_{n-1}(a_{n-1}-1)}{2} +\dfrac{b_{n-1}(b_{n-1}-1)}{2}\\= & {} -d^{2}+2d+\dfrac{a_{n-1}^{2}+b_{n-1}^{2}}{2}\\\le & {} -d^{2}+2d+\dfrac{c_{n-1}^{2}}{2}=d^{2}+2d. \end{aligned}$$

Below, we state a simple helpful lemma which can be shown using calculus.

Lemma 4.1

Consider the function $f(x,y)=x^{n}+y^{n}$ where $n\in {\mathbb {N}},\,x+y=2d\,\,,x\ge d$ and $y\ge 0$. Then, the maximum and minimum values of f are $2^{n}d^{n}$ and $2d^{n}$, respectively.

Let us continue the above reasoning for $j=n-4$ and $j=n-5$. In fact, by studying different values of j, we try to predict the desired degree upper bound. For $j=n-4$, we have

$$\begin{aligned} c_{n-3}= & {} 2+2\dfrac{(d-1)(d-2)(d-3)}{6}+\dfrac{a_{n-2}^{2} +b_{n-2}^{2}}{2}+\dfrac{-a_{n-2}-b_{n-2}}{2}\\&+\dfrac{-a_{n-1}^{3}-b_{n-1}^{3}}{6}+\dfrac{a_{n-1}^{2} +b_{n-1}^{2}}{2}+\dfrac{-a_{n-1}-b_{n-1}}{3} \end{aligned}$$

By using Lemma 4.1 and this inequality, one gets $-c_{n-2}\le -c_{n-1}=-2d$ and in consequence

$$\begin{aligned} c_{n-3}\le & {} 2+2\dfrac{(d-1)(d-2)(d-3)}{6}+\dfrac{(d^{2}+2d)^{2}}{2}+\dfrac{-2d}{2}\\&+\dfrac{-2d^{3}}{6}+\dfrac{4d^{2}}{2}+\dfrac{-2d}{3} =\dfrac{1}{2}d^{4}+2d^{3}+2d^{2}+2d. \end{aligned}$$

Finally, for $j=n-5$ by a similar argument, we can obtain:

$$\begin{aligned} c_{n-4}\,\,\le \,\, \dfrac{1}{8}d^{8}+d^{7}+3d^{6}+5d^{5}+\dfrac{85}{12}d^{4}+ 6d^{3}+\dfrac{35}{12}d^{2}+2d. \end{aligned}$$

We are now in a position to set up an induction to show that for each $j=1,\dots ,n-1$, there exists a univariate polynomial ${\mathcal {F}}_{j}(d)\in {\mathbb {Q}}[d]$ such that $c_{j}\le {\mathcal {F}}_{j}(d)$ and $\deg ({\mathcal {F}}_{j})=2^{n-j-1}$.

Lemma 4.2

Under the above assumptions, for $1\le t\le n-1$, it holds $c_{t}\le {\mathcal {F}}_{t}(d)$ where ${\mathcal {F}}_{t}(d)\in {\mathbb {Q}}[d]$ and $\deg ({\mathcal {F}}_{t})=2^{n-t-1}$.

Proof

The proof proceeds by an induction on t. By the above arguments, the assertion holds for $n-4\le t\le n-1$. Assume that the claim is true for any $j+1< t\le n-4$ and we want to proof it for $j+1$. Using Equality (5), we have:

$$\begin{aligned} c_{j+1}= & {} -2 l (-d+n-j-1,n-j-1)+2+\dfrac{a_{j+2}^{2}+b_{j+2}^{2}}{2}+\dfrac{-a_{j+2} -b_{j+2}}{2}\\&+\sum _{i=j+3}^{n-1}\left[ l (-a_{i}+i-j-1,i-j)+ l (-b_{i}+i-j-1,i-j)\right] \\\le & {} -2 l (-d+n-j-1,n-j-1)+2+\dfrac{c_{j+2}^{2}}{2}-d\\&+\sum _{i=j+3}^{n-1}\left[ l (-a_{i}+i-j-1,i-j)+ l (-b_{i}+i-j-1,i-j)\right] . \end{aligned}$$

Note that to prove the last inequality, we used the fact that $-a_{j+2}-b_{j+2}\le -a_{n-1}-b_{n-1}=-2d$. By applying the inductive assumptions, we know that the polynomial ${\mathcal {F}}_{j+2}(d)\in {\mathbb {Q}}[d]$ exists such that $c_{j+2}\le {\mathcal {F}}_{j+2} (d)$ and $\deg ({\mathcal {F}}_{j+2})=2^{n-j-3}$. Hence $(c_{j+2})^{2}\le ({\mathcal {F}}_{j+2} (d))^{2}$ and $\deg (({\mathcal {F}}_{j+2})^{2})=2^{n-j-2}$. On the other hand, from $\deg ( l (-d+n-j-1,n-j-1))=n-j-1$ and $j+1< n-4$, it yields that $2^{n-j-2}>n-j-1$. Therefore, to prove the assertion, we must show that $\sum _{i=j+3}^{n-1}\left[ l (-a_{i}+i-j-1,i-j)+ l (-b_{i}+i-j-1,i-j)\right]$ is less than a polynomial in terms of d of degree less than $2^{n-j-2}$. We have

$$\begin{aligned}&l (-a_{i}+i-j-1,i-j)+ l (-b_{i}+i-j-1,i-j)\\&\quad =\dfrac{(-a_{i}+i-j-1)\cdots (-a_{i})}{(i-j)!}+\dfrac{(-b_{i}+i-j-1)\cdots (-b_{i})}{(i-j)!}\\&\quad =\dfrac{1}{(i-j)!}\sum _{t=1}^{i-j}q_{t}(a_{i}^{t}+b_{i}^{t}), \,\,\mathrm{with}\,\, q_{t}\in {\mathbb {Z}} \end{aligned}$$

Now, if $q_{t}>0$ then $q_{t}(a_{i}^{t}+b_{i}^{t})\le q_{t}c_{i}^{t}$ and if $q_{t}<0$ then $q_{t} (a_{i}^{t}+b_{i}^{t})\le q_{t}2d^{t}$. By the induction hypotheses, it follows that

$$\begin{aligned} l (-a_{i}+i-j-1,i-j)+ l (-b_{i}+i-j-1,i-j)\le \dfrac{1}{(i-j)!}\big [\sum _{q_{t}>0,t=1}^{i-j}q_{t}({\mathcal {F}}_{i}(d))^{t} +\sum _{q_{t}<0,t=1}^{i-j}q_{t}2d^{t}\big ]. \end{aligned}$$

For simplicity, define the polynomial $G_{i}(d)=\dfrac{1}{(i-j)!}[\sum _{q_{t}>0,t=1}^{i-j}q_{t}({\mathcal {F}}_{i} (d))^{t}+\sum _{q_{t}<0,t=1}^{i-j}q_{t}2d^{t}]$. It is easy to check that $\deg (G_{i})\le (i-j)(2^{n-i-1})$. From $j+3\le i\le n-1$, we have $i-j\ge 3$ and in turn $i-j<2^{i-j-1}$. This implies that $(2^{n-i-1})(i-j)<2^{n-j-2}$, which completes the proof. $\square$

Dubé in [6, Lemma 8.1] showed that for $1\le j\le n-2$, $c_{j}\le D_j:=2(\dfrac{d^{2}}{2}+d)^{2^{n-j-1}}$. However, the bound that we presented here has the property $\deg ({\mathcal {F}}_{j}(d))=2^{n-j-1}<\deg (D_j)=2^{n-j}$. In addition, in loc. cit., it was shown that an upper bound for $c_1$ remains a degree upper bound for the Gröbner basis of the initial ideal. We summarize the above discussion in the following theorem.

Theorem 4.3

Let $n\ge 2$ and ${\mathcal {I}}\subset {\mathcal {R}}$ be an ideal generated by a set of homogeneous polynomials of degree at most d. Then, the maximum degree of the polynomials in any reduced Gröbner basis of ${\mathcal {I}}$ is bounded above by ${\mathcal {F}}_{1}(d)\sim O(1)d^{2^{n-2}}$ where O(1) is meant for fixed n and growing d.

Based on the above discussion, the construction of ${\mathcal {F}}_i(d)$ for any i is inductive¹. In the following table, we give an explicit representation of ${\mathcal {F}}_1(d)$ for some values of n.

Number of variables	${\mathcal {F}}_1(d)$
$n=1$	d
$n=2$	2d
$n=3$	$d^{2}+2d$
$n=4$	$\dfrac{1}{2}d^{4}+2d^{3}+2d^{2}+2d$
$n=5$	$\dfrac{1}{8}d^{8}+d^{7}+3d^{6}+5d^{5}+\dfrac{85}{12}d^{4}+ 6d^{3}+\dfrac{35}{12}d^{2}+2d.$

We continue this section by extending Theorem 4.3 to non necessary homogeneous ideals. It is well-known that by considering a new variable $x_{n+1}$, we can transform a given finite set of polynomials into a homogeneous one. In addition, to compute a Gröbner basis of an ideal ${\mathcal {I}}\subset {\mathcal {R}}$, we can arrange first a new monomial ordering in the extended polynomial ring and the desired Gröbner basis of ${\mathcal {I}}$ is obtained directly from the Gröbner basis of the homogenized ideal. We shall note that, the homogenization process does not change the maximum degree of the initial generating set, see [7] for more details on this subject. Based on this observation, we can state the next theorem.

Theorem 4.4

Let $n\ge 1$ and ${\mathcal {I}}\subset {\mathcal {R}}$ be an ideal generated by a set of non necessary homogeneous polynomials of degree at most d. Then, the maximum degree of the polynomials in any reduced Gröbner basis of ${\mathcal {I}}$ is bounded above by $O(1)d^{2^{n-1}}$ where O(1) is meant for fixed n and growing d.

Remark 4.5

It is worth noting that in [14, 18], new dimension and depth depending upper bounds for the degrees of the elements of reduced Gröbner bases has been exhibited. However, since the approaches proposed in these papers are different from the original method given in [6], then we can expect only a depth depending variant of the bound presented in Theorems 4.3 and 4.4

Remark 4.6

Dubé in [6, page 771] claims that

$$\begin{aligned} 2+(-1)^{n-j}\left[ 2{\left( {\begin{array}{c}d-1\\ n-j-1\end{array}}\right) }-\left( {\begin{array}{c}a_{n-1}\\ n-j-1\end{array}}\right) -\left( {\begin{array}{c}b_{n-1}\\ n-j-1\end{array}}\right) \right] \le {\left( {\begin{array}{c}c_{n-1}\\ n-j-1\end{array}}\right) } \end{aligned}$$

However, unfortunately, this inequality is not in general true. For example if $n-j-1>c_{n-1}$ then all the binomial coefficients appeared above are zero and in turn the inequality does not hold. Moreover, as already mentioned, Dubé in [6, Lemma 8.1] proved that $c_{j}\le D_j:=2(\dfrac{d^{2}}{2}+d)^{2^{n-j-1}}$ for $1\le j\le n-2$. In his proof, he claimed that the sum $1/2-\sum ^{n-1}_{i=j+3}{2^{i-j}/(i-j+1)!}$ is positive. However, this holds only for $n\le 5$ and for each $n>5$ this sum is negative (it is less than $-0.23$). In the next theorem, we derive a correct version of Dubé’s bound.

Theorem 4.7

Let ${\mathcal {I}}\subset {\mathcal {R}}$ be an ideal generated by a set of homogeneous polynomials of degree at most d. Then, the maximum degree of the polynomials in any reduced Gröbner basis of ${\mathcal {I}}$ is bounded above by $(d+1)^{2^{n-2}}$ if $n>2$. If $n=1,2$, then the upper bound becomes d, 2d, respectively.

Proof

The bounds the corresponding to $n=1,2,3$ have been already proved above. Now, let us assume that $n>4$. Keeping the above notations, we claim (by induction on j) that $c_{j}\le E_j:=(d+1)^{2^{n-j-1}}$. For $j=n-2,n-3,n-4$, we showed, respectively that $c_{n-2}\le d^2+2d\le (d+1)^{2^{n-(n-2)-1}}$, $c_{n-3}\le d^{4}/2+2d^{3}+2d^{2}+2d\le (d+1)^{2^{n-(n-3)-1}}$ and $c_{n-4}\le \dfrac{1}{8}d^{8}+d^{7}+3d^{6}+5d^{5}+\dfrac{85}{12}d^{4}+ 6d^{3}+\dfrac{35}{12}d^{2}+2d\le (d+1)^{2^{n-(n-4)-1}}$, proving the claim in these cases. Now, assume inductively that the claim is true for each i with $j<i\le n-4$. Now, we are willing to prove the claim for j. Recall that

$$\begin{aligned} c_{j}\le & {} -2 l (-d+n-j,n-j)+2+\dfrac{c_{j+1}^{2}}{2}-\dfrac{c_{j+1}}{2}\\&+\sum _{i=j+2}^{n-1}\left[ l (-a_{i}+i-j,i-j+1)+ l (-b_{i}+i-j,i-j+1)\right] . \end{aligned}$$

Since $d\ge 1$, $a_{i}\ge d$ and $b_{i}\ge 0$ then $l (-d+n-j,n-j)=(-1)^{n-j}{d-1\atopwithdelims ()n-j}$, $l (-a_{i}+i-j,i-j+1)=(-1)^{i-j+1}{a_{i}\atopwithdelims ()i-j+1}$ and $l (-b_{i}+i-j,i-j+1)=(-1)^{i-j+1}{b_{i}\atopwithdelims ()i-j+1}$. Thus, by substituting these relations, we obtain

$$\begin{aligned} c_{j}\le 2(-1)^{n-j+1}{d-1\atopwithdelims ()n-j}+2+{c_{j+1}\atopwithdelims ()2}+\sum _{i=j+2}^{n-1}(-1)^{i-j+1}\left[ {a_{i}\atopwithdelims ()i-j+1}+{b_{i}\atopwithdelims ()i-j+1}\right] . \end{aligned}$$

Now two cases may arise: If $2\vert n-j+1$ then from $a_{n-1}\ge d$ we have ${d-1\atopwithdelims ()n-j}\le {a_{n-1}\atopwithdelims ()n-j}$ and so

$$\begin{aligned} c_{j}\le & {} 2{d-1\atopwithdelims ()n-j}+2+{c_{j+1}\atopwithdelims ()2}-{a_{n-1}\atopwithdelims ()n-j}-{b_{n-1}\atopwithdelims ()n-j}\\&+\sum _{i=j+2}^{n-2}(-1)^{i-j+1}\left[ {a_{i}\atopwithdelims ()i-j+1}+{b_{i}\atopwithdelims ()i-j+1}\right] \\\le & {} {d-1\atopwithdelims ()n-j}+2+{c_{j+1}\atopwithdelims ()2}+\sum _{\begin{array}{c} i=j+2\\ 2\vert i-j+1 \end{array}}^{n-2}\left[ {a_{i}\atopwithdelims ()i-j+1}+{b_{i}\atopwithdelims ()i-j+1}\right] \\\le & {} {d-1\atopwithdelims ()n-j}+2+{c_{j+1}\atopwithdelims ()2}+\sum _{\begin{array}{c} i=j+2\\ 2\vert i-j+1 \end{array}}^{n-2}{c_{i}\atopwithdelims ()i-j+1}. \end{aligned}$$

Otherwise, if $2\not \mid n-j+1$ then

$$\begin{aligned} c_{j}\le & {} -2{d-1\atopwithdelims ()n-j}+2+{c_{j+1}\atopwithdelims ()2}+\sum _{i=j+2}^{n-1}(-1)^{i-j+1}\left[ {a_{i}\atopwithdelims ()i-j+1}+{b_{i}\atopwithdelims ()i-j+1}\right] \\\le & {} 2+{c_{j+1}\atopwithdelims ()2}+\sum _{\begin{array}{c} i=j+2\\ 2\vert i-j+1 \end{array}}^{n-1}\left[ {a_{i}\atopwithdelims ()i-j+1}+{b_{i}\atopwithdelims ()i-j+1}\right] \\\le & {} 2+{c_{j+1}\atopwithdelims ()2}+\sum _{\begin{array}{c} i=j+2\\ 2\vert i-j+1 \end{array}}^{n-1}{c_{i}\atopwithdelims ()i-j+1}. \end{aligned}$$

To bound $c_j$, we shall need some more inequalities. For each $j+3\le i\le n-2$, $i-j+1\le 2^{i-j-1}$ and therefore

$$\begin{aligned} \left( {\begin{array}{c}E_i\\ i-j+1\end{array}}\right) \le \frac{E_i^{i-j+1}}{(i-j+1)!}\le \frac{E_i^{2^{i-j-1}}}{(i-j+1)!}\le \frac{E_{j+1}}{(i-j+1)!}. \end{aligned}$$

Note that for $i=n-1$, these inequalities hold, as well. Indeed, we have

$$\begin{aligned} \left( {\begin{array}{c}2d\\ n-1-j+1\end{array}}\right) \le \frac{(2d)^{n-j}}{(n-j)!}\le \frac{((d+1)^2)^{{n-j}}}{(n-j)!}\le \frac{E_{j+1}}{(n-j)!}. \end{aligned}$$

Let us consider again the case $2\vert n-j+1$. Using these inequalities, we can write

$$\begin{aligned} c_j\le & {} 2+{d-1\atopwithdelims ()n-j}+\left( {\begin{array}{c}E_{j+1}\\ 2\end{array}}\right) +\sum ^{n-2}_{\begin{array}{c} i=j+2\\ 2\vert i-j+1 \end{array}}{\left( {\begin{array}{c}E_{i}\\ i-j+1\end{array}}\right) } \\\le & {} 2+\dfrac{(d-1)^{n-j}}{(n-j)!}+\left( {\begin{array}{c}E_{j+1}\\ 2\end{array}}\right) +\sum ^{n-2}_{\begin{array}{c} i=j+2\\ 2\vert i-j+1 \end{array}}{\left( {\begin{array}{c}E_{i}\\ i-j+1\end{array}}\right) } \\\le & {} 2+\dfrac{(d-1)^{n-j}}{(n-j)!}+\frac{E_{j+1}^2-E_{j+1}}{2}+\sum ^{n-2}_{\begin{array}{c} i=j+2\\ 2\vert i-j+1 \end{array}}{\frac{E_{j+1}}{(i-j+1)!}}\\\le & {} 2+\dfrac{(d-1)^{n-j}}{(n-j)!}+\frac{E_{j+1}^2-E_{j+1}}{2}+E_{j+1}\sum ^{\infty }_{\begin{array}{c} i=j+2\\ 2\vert i-j+1 \end{array}}{\frac{1}{(i-j+1)!}}\\= & {} 2+\dfrac{(d-1)^{n-j}}{(n-j)!}+\frac{E_{j+1}^2-E_{j+1}}{2}+E_{j+1}\left( -\dfrac{3}{2}+\cosh (1)\right) \\\le & {} 2+\dfrac{(d-1)^{n-j}}{(n-j)!}-\frac{45}{100}E_{j+1}+E_{j+1}^{2}\le E_{j+1}^{2}. \end{aligned}$$

Indeed, to get the last inequality, we shall show that $\dfrac{45}{100}E_{j+1}\ge 2+\dfrac{(d-1)^{n-j}}{(n-j)!}$. Since $n-j\ge 5$ and $d\ge 1$ then we can write $\dfrac{45}{100}E_{j+1} = \dfrac{45}{100}(d+1)^{2^{n-j-2}}\ge \dfrac{45}{100}[(d-1)^{2^{n-j-2}}+2^{2^{n-j-2}}]$. In addition, from $n-j\ge 5$, it follows that $(n-j)!\ge 5!=120$ and $2^{n-j-2}\ge n-j$. These arguments imply that $\dfrac{45}{100}(d-1)^{2^{n-j-2}}\ge \dfrac{(d-1)^{n-j}}{(n-j)!}$ and $\dfrac{45}{100}2^{2^{n-j-2}}\ge 2$, proving the claim. A similar argument works in the case $2\not \mid n-j+1$. All in all, we conclude that $c_{j}\le E_{j+1}^{2}$ which ends the proof. $\square$

Note that the results analogous to those in Theorem 4.4 are obtained if ${\mathcal {I}}$ is not necessary homogeneous.

Remark 4.8

In the above proof, we removed negative terms from ${\mathcal {F}}_{j}$ to get an upper bound for $c_j$, and this shows that ${\mathcal {F}}_{j}<E_{j}$. Indeed, one observes that $\mathrm{LT}(E_{j})=d^{2^{n-j-1}}$, however $\mathrm{LT}({\mathcal {F}}_{j})=2(d^{2}/2)^{2^{n-j-2}}$.

Remark 4.9

We shall notice that in general the bound $2(1/2(d^{n-D}+d))^{2^{D-1}}$ due to Mayr and Ritscher [18] is sharper than the bound $(d+1)^{2^{n-2}}$ presented in Theorem 4.7. For example, if $D=n-2$ then it is easily verified that in general $(d+1)^2>1/\sqrt{2}(d^2+d)$ and this shows that Mayr-Ritscher’s bound is sharper than the bound given in Theorem 4.7. However, for the special case of $D=n-1$ it is seen that for $n=3,4,5$ if we take $d>11$ then the bound obtained in Theorem 4.7 is sharper than their bound.

5 Degree Upper Bounds for Pommaret Bases

In this section, show that the degree bounds that we discussed in Section 4 hold for Pommaret bases as well. Here our attention is focused on the Split algorithm and on the conditions under which this algorithm returns a Janet basis. More precisely, if $F\subset {\mathcal {R}}$ is a finite set of monomials and $(P,Q)=$ Split(1, X, F), we look for the conditions so that P is a Janet basis for the monomial ideal $\langle F \rangle$.

Below, when we refer to the Split algorithm, we shall address a variant of this algorithm as follows: In the lines 9 and 10, we select $x_j$ so that between all maximal subsets $s\subset u$ with $F\cap {\mathcal {K}}[s]=\emptyset$ and $x_j\in u\setminus s$, j has the minimum index.

Corollary 5.1

Let the finite set $U\subset {\mathcal {R}}$ be a monomial Janet basis for the monomial ideal ${\mathcal {I}}$. Then set $E=\{ C(h,u)\ | \ h\in U, u=M_{{\mathcal {J}}}(h,U) \}$ is a cone decomposition for ${\mathcal {I}}$.

Proof

Since U is a Janet basis for ${\mathcal {I}}$, then from definition we have ${\mathcal {I}}=\sum _{C(h,u)\in E}C(h,u)$. Now assume that there exists $v\in {\mathcal {I}}$ such that $v\in C(h_{1},u_{1})\cap C(h_{2},u_{2})$ with $C(h_{i},u_{i})\in E$. Then according to Definition 2.1, either $h_{1}\in C(h_{2},u_{2})$ or $h_{2}\in C(h_{1},u_{1})$. It follows that either $C(h_{1},u_{1})\subset C(h_{2},u_{2})$ or $C(h_{2},u_{2})\subset C(h_{1},u_{1})$ which is impossible for a monomial Janet basis, and this implies that ${\mathcal {I}}=\bigoplus _{C(h,u)\in E}C(h,u)$. $\square$

We describe below a variant of the Split algorithm which returns a pair of decompositions so that one of the decompositions is a Janet decomposition for its input ideal.

Proposition 5.2

The JanetDecomposition algorithm terminates in finitely many steps and is correct.

Proof

The termination of the algorithm is guaranteed by the lines 10 and 12. Indeed, since in the line 10, we consider $u \setminus \{x_{j}\}$ then by each recursive call to the algorithm in this line, we reduce by one the number of the variables. On the other hand, since the chosen variable $x_j$ appears in F, then $\langle F \rangle \subset \langle F' \rangle$, and from nœtherianity of ${\mathcal {R}}$ we conclude that the total number of recursive call to the algorithm should be finite. The correctness proof is similar to the proof of [6, Lemma 4.4].$\square$

Remark 5.3

In contrary to the Split algorithm, to choose $x_{j}$, we do not consider the maximal independent set $s\subset u$, and this yields that Q is not generally a $\deg (h)$-standard cone decomposition.

Theorem 5.4

Let $F\subset {\mathcal {M}}$ be a minimal monomial basis for ${\mathcal {I}}$. If $(P,Q)=$ is the output of JanetDecomposition(1, X, F) then P is a Janet basis for ${\mathcal {I}}$.

Proof

We must show that $U=\{h\mid C(h,u)\in P\}$ is a Janet basis for ${\mathcal {I}}$. Since P generates ${\mathcal {I}}$, then it is enough to show that for any cone $C(h,u)\in P$, $M_{{\mathcal {J}}}(h,U)=u$. Assume that, for some $h=x_1^{\alpha _1}\cdots x_{n}^{\alpha _{n}}$, $x_j\in M_{{\mathcal {J}}}(h,U)$ and it does not belong to u. Let $m=x_1^{\alpha _1}\cdots x_{j}^{\alpha _{j}}$. This shows that at one stage, $x_j$ has been selected and two branches JanetDecomposition$(m,u' \setminus \{x_{j}\},F)$ and JanetDecomposition$(x_{j}m,u',F')$ are produced. Now, let us consider the second branch. Since in this branch, $F'$ is a monomial basis for ${\mathcal {I}}:x_jm$, then at the end by multiplying $x_im$ by some variables, a cone is added into P. It should be noted that, due the selection strategy in the line 10, we are sure that $x_jm$ is multiplied by some variables with indices higher than j. Therefore, this implies that $x_j$ is not Janet multiplicative for h, leading to a contradiction. Conversely, suppose that $x_j\in u$. We must show that $x_j\in M_{{\mathcal {J}}}(h,U)$. Using the above notations and by reductio ad absurdum, suppose that there exists a monomial $f\in U$ so that $f\in [\deg _1(h), \ldots ,\deg _{j-1}(h)]$ and $\deg _{j}(f)>\deg _{j}(h)$. We know that $x_1^{\alpha _1}\cdots x_{j-1}^{\alpha _{j-1}}\in [\deg _1(h), \ldots ,\deg _{j-1}(h)]$. Then, due to the structure of the algorithm, at one step of the algorithm, we reach the branch JanetDecomposition$(m,u',F')$ with $\langle F' \rangle ={\mathcal {I}}:m$ and $u\subset u'$. From $x_j\notin M_{{\mathcal {J}}}(h,U)$, we deduce that $F'$ contains a monomial involving $x_j$ and in consequence in the construction of C(h, u), $x_j$ is excluded from u, giving rise to a contradiction. $\square$

Example 5.5

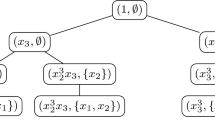
JanetDecomposition$(1,\{x_{1},x_{2}\},\{x_{1}^{2}x_{2},x_{1}x_{2}^{2},x_{2}^{3} \})$ returns (P, Q) with

$$\begin{aligned} P= & {} \big \{C(x_{2}^{3},\{x_{2}\}),C(x_{1}x_{2}^{2},\{x_{2}\}),C(x_{1}^{2} x_{2},\{x_{1},x_{2}\}) \big \} \nonumber \\ Q= & {} \big \{C(1,\emptyset ),C(x_{2},\emptyset ),C(x_{1},\emptyset ),C(x_{2}^{2} ,\emptyset ),C(x_{1}x_{2},\emptyset ),C(x_{1}^{2},\{x_{1}\})\big \}. \end{aligned}$$

(6)

Lemma 5.6

If $\langle F \rangle$ is quasi stable and F is a minimal monomial basis for this ideal, then both Split(1, X, F) and JanetDecomposition(1, X, F) output the same result.

Proof

Since ${\mathcal {I}}=\langle F \rangle$ is quasi stable then F consists of pure powers of the variables $\{ x_{1},\dots ,x_{n-D}\}$ where $D=\dim ({\mathcal {I}})$, see [23, Proposition 4.4]. Thus, at any intermediate stage of both the algorithms, when we encounter the triple $(h,u,F')$, two cases may happen: If $\{ x_{1},\dots ,x_{n-D}\}\cap u\ne \emptyset$ then both the algorithms must choose the same variable. Otherwise, $\{ x_{1},\dots ,x_{n-D}\}\cap u= \emptyset$. We may assume that $u\ne \emptyset$, $F'\cap {\mathcal {K}}[u]\ne \emptyset$ and $x_t\in u$ has the minimum index. We claim that a pure power of $x_t$ belongs to $F'$, and therefore both the algorithms will select $x_t$. To prove the claim, note that from $F'\cap {\mathcal {K}}[u]\ne \emptyset$, we conclude that there exists a monomial m in this intersection. In addition, we know that $\langle F' \rangle ={\mathcal {I}}:h$ and in turn, $mh\in {\mathcal {I}}$. Since $m\in {\mathcal {K}}[x_{n-D+1},\ldots ,x_n]$ and $mh\in {\mathcal {I}}$ then from quasi stability of ${\mathcal {I}}$, it follows that $x_t^\alpha h\in {\mathcal {I}}$ for some integer $\alpha$. This shows that $x_t^\alpha \in F'$ which ends the proof. $\square$

According to [23, Proposition 4.4], we know that every quasi stable monomial ideal has a finite Pommaret basis. Then, it follows immediately from the above lemma that both the algorithms return a finite Janet basis for its input ideal. In the next proposition, we show that this basis is also a Pommaret basis.

Proposition 5.7

Let ${\mathcal {I}}=\langle F\rangle$ be a quasi stable monomial ideal. Furthermore, assume that $(P,Q)=$

JanetDecomposition(1, X, F). Then, P forms a finite Pommaret basis for ${\mathcal {I}}$.

Proof

We shall show that for each $C(h,u)\in P$ we have $u=\{x_{t}\ | \ t\ge {{\,\mathrm{cls}\,}}(h)\}$. From the proof of Lemma 5.6, one observes that at each step of the algorithm, when we consider the triple $(h,u,F')$ then $x_j\in u$ with the minimum index, is chosen and this implies that u is of the form $\{x_{\ell },\ldots ,x_n\}$. Therefore, it remains only to prove that $\ell ={{\,\mathrm{cls}\,}}(h)$. Assume that $h=x_{1}^{\alpha _{1}}\cdots x_{{{\,\mathrm{cls}\,}}(u)}^{\alpha _{{{\,\mathrm{cls}\,}}(u)}}$. Since by the construction of the JanetDecomposition algorithm, each multiplied variable in h, comes from the line 12 of the algorithm then it is clear to see that $x_{{{\,\mathrm{cls}\,}}(u)}$ appears in u. Moreover, since at this stage, $x_{{{\,\mathrm{cls}\,}}(u)}$ is selected, then by the selection strategy in the Split algorithm (see Lemma 5.6), ${{\,\mathrm{cls}\,}}(u)$ should be the minimum index in u, and this completes the proof. $\square$

Corollary 5.8

If $\langle F \rangle$ is quasi stable and $(P,Q)=$ Split(1, X, F). Then, P represents the minimal Janet basis for ${\mathcal {I}}$. The same holds for the JanetDecomposition algorithm.

Proof

From Proposition 5.7, we know that set P is a Pommaret basis and a Janet basis. Then, the assertion follows from the fact that any finite Pormmaret basis is a minimal Janet basis, [8, Corollary 3]. $\square$

Remark 5.9

Let ${\mathcal {I}}=\langle F \rangle$ be a monomial ideal. In [12, Theorem 5.7], it was shown that ${\mathcal {I}}$ is quasi stable ideal iff $N_{{\mathcal {I}}}$ has a Rees decomposition, see loc. cit. for more information on Rees decomposition. Now, if (P, Q)=Split(1, X, F) then, from the proof of Lemma 5.6, Q is a Rees decomposition for $N_{{\mathcal {I}}}$.

Below, we state a generalization of [6, Lemma 7.2]. The next lemma allows us to deduce that if $b_0,\ldots ,b_{n+1}$ are the Macaulay constants for $N_{{\mathcal {I}}}$ then any upper bound for $b_0$ remains an upper bound for any basis constructed by the Dubé’s approach. It should be noticed that in the previous section, we found an upper bound for $c_1$ and by [6, page 773], any bound for $c_1$ is a bound for $b_0$.

Lemma 5.10

Let F be a finite set of monomials and $(P,Q)=$ Split(1, X, F). Then for every $C(f,u)\in P$, Q contains a cone C(h, v) with $\deg (f)=\deg (h)-1$.

Proof

Let ${\mathcal {I}}=\langle F \rangle \subset {\mathcal {R}}$. Since ${\mathcal {I}}\ne {\mathcal {R}}$, then $\deg (f)>1$. From the membership $C(f,u)\in P$, we conclude that Split$(f,u,F')=(\{C(f,u)\},\emptyset )$ where ${\mathcal {I}}:f=\langle F'\rangle$ and $1\in F'$. Therefore, $f=x_jh$ for some monomial h and some variable $x_j$. At the same time that we construct the branch Split$(f,u,F')$, we produce the branch Split$(h,u\setminus \{x_j\} ,F'')$ for some set $F''$. Thus, we can see easily that after some recursive calls of the algorithm, we arrive at Split$(h,u' ,F'')$ with $u'\subset u\setminus \{x_j\}$ and in turn the cone $C(h,u')$ is added into Q, thereby ending the proof. $\square$

As a consequence of Theorem 4.7, Proposition 5.7 and Lemma 5.10, we state the main result of this section.

Theorem 5.11

Let ${\mathcal {I}}\subset {\mathcal {R}}$ be an ideal generated by a set of homogeneous polynomials of degree at most d. Assume that ${\mathcal {I}}$ is in quasi stable position. Then, the maximum degree of the polynomials in the Pommaret basis of ${\mathcal {I}}$ is bounded above by $(d+1)^{2^{n-2}}$ if $n>2$. If $n=1,2$, then the upper bound becomes d, 2d, respectively.

Proof

Let $(P,Q)=$ Split$(1,X,\mathrm{LM}(F))$ where F is a Gröbner basis of ${\mathcal {I}}$. Since ${\mathcal {I}}$ is in quasi stable position then $\mathrm{LM}({\mathcal {I}})$ is quasi stable. Then, from Lemma 5.6 and Proposition 5.7, it follows that P is a Pommaret basis for $\mathrm{LM}({\mathcal {I}})$. In addition, the elements of P form the leading monomials of the elements of the Pommaret basis of ${\mathcal {I}}$. Therefore, from Lemma 5.10, we conclude that an upper bound for the degrees of the elements of P remains an upper bound for the maximum degree of the elements of the Pommaret basis of ${\mathcal {I}}$. Finally, the assertion is proved by Theorem 4.7. $\square$

Remark 5.12

From [23, Theorem 9.2], it follows that the maximum degree of the elements of the Pommaret basis of an ideal in quasi stable position is the Castelnuovo-Mumford regularity. Therefore, the bound presented in Theorem 5.11 remains an upper bound for the Castelnuovo-Mumford regularity of ${\mathcal {I}}$. On the other hand, Bayer and Stillman [2, Corollary 2.5] proved that in generic position the degree of the reduced Gröbner basis of a homogeneous ideal w.r.t. $\prec$ is bounded by the Castelnuovo-Mumford regularity of the ideal. Finally, in generic position, the Pommaret basis coincides with the reduced Gröbner basis [17, Theorem  2.15]. All these together gives an alternative proof to Theorem 5.11.

6 J-stable Ideals

From the proof of [10, Proposition 4.5], we conclude that $n(d+1)^{2^{n-2}}$ is a degree upper bound for Janet bases of homogeneous ideals. In this section, we introduce a new generic position in which the bound $(d+1)^{2^{n-2}}$ presented in Theorem 4.7 remains a degree upper bound for Janet bases.

Definition 6.1

A monomial ideal ${\mathcal {I}}\subset {\mathcal {R}}$ is J(anet)-stable if for any monomial $m\in {\mathcal {I}}$ and all positive integers i, j, s with $1 \le j< i< n$, if $x^{s}_{i}\mid m$, there exists an integer $t \ge 0$ such that $x^{t}_{j} (m/x^{s}_{i})\in {\mathcal {I}}$. An ideal ${\mathcal {I}}\subset {\mathcal {R}}$ is in J-stable position if $\mathrm{LM}({\mathcal {I}})$ w.r.t. $\prec$ is J-stable.

We shall emphasize that the difference between this definition and Definition 2.9 is that here we consider $i<n$ instead of $i\le n$. It is clear that any ideal in quasi stable position is in J-stable position, however, the converse does not hold in general, see Example 6.6.

Theorem 6.2

Let ${\mathcal {I}}=\langle F \rangle \subset {\mathcal {R}}$ be J-stable where F is a finite set of monomials. Furthermore, let $(P,Q)=$ Split(1, X, F). Then P is a Janet basis for ${\mathcal {I}}$.

Proof

We first show that in the construction of a cone $C(h,u)\in P$, the variables $\{x_1,\ldots ,x_{n-1}\}$ are selected in the order $x_1,\ldots ,x_{n-1}$. Note that in this claim, we ignore the last variable. Assume that in the course of the construction of this cone the variable $x_t$ has been selected. Therefore, there exists a maximal independent set $s\subset u'$ such that $F' \cap {\mathcal {K}}[s]=\emptyset$ and $x_{t}\in u'\setminus s$. Note that $u\subset u'$ and $\langle F \rangle \subset \langle F' \rangle$. Now, assume in contrary that later on, and in the course of the construction of $C(h,u)\in P$, the variable $x_\ell$ with $\ell <t$ is selected. Let $u'\setminus s=\{x_{t},x_{t_{1}},\dots ,x_{t_{k}}\}$ where $t<t_{1}<\cdots <t_{k}$. We claim that ${\text{ indet }}(m)\cap \{x_{t_{1}},\dots ,x_{t_{k}}\}\ne \emptyset$ for any $m\in F'$. For any $m\in F'$, two cases may happen: If $x_{t}\not \mid m$ then ${\text{ indet }}(m)\cap \{x_{t_{1}},\dots ,x_{t_{k}}\}\ne \emptyset$. Otherwise, $x_{t}\vert m$. Since ${\mathcal {I}}$ is J-stable and $t>l$ then there exists an integer $\alpha \ge 0$ such that $x_{l}^{\alpha }m/x_{t}^{\beta } \in \langle F\rangle$ where $\beta =\deg _{t}(m)$. From these arguments, we conclude that ${\text{ indet }}(m)\cap \{x_{t_{1}},\dots ,x_{t_{k}}\}\ne \emptyset$ and this proves the claim. This implies that $F'\cap {\mathcal {K}}[s\cup \{x_{t}\}]=\emptyset$, leading to a contradiction with the maximality of s. To complete the proof, we shall show that $x_n\in u$. From the structure of the algorithm, $u\ne \emptyset$. Assume in contrary that $x_n\notin u$. Since we start with X, then at one stage of the algorithm, $x_n$ would be selected. On the other hand, by the selection strategy, a variable with the minimum index is chosen. Therefore, $u' \setminus s =\{x_n\}$ for some $u'$ and s. In this case, we make two calls Split$(h',u'\setminus \{x_n\},F')$ and Split$(x_nh',u',F')$. The first call adds an element into Q and we do not consider it. In the second call, $x_n\in u'$ and therefore $x_n$ remains in u. In turn we do not need to consider $x_n$ in our discussion. Thus, the proof is ended by using an argument similar to the proof of Theorem 5.4. $\square$

Example 6.3

Let ${\mathcal {I}}=\langle F\rangle \subset {\mathcal {R}}$ where $F=\{x_{1}^{2},x_{2}^{2},\dots ,x_{n-2}^{2},x_{n-1}x_{n}\}$. Then, it is easy to see that ${\mathcal {I}}$ is J-stable. However, since $x_{n-1}^{\alpha }\notin {\mathcal {I}}$ for any $\alpha \ge 0$, then ${\mathcal {I}}$ is not quasi stable. Let $(P,Q)=$ Split(1, X, F). Then, we have

$$\begin{aligned} P= & {} \big \{ C(vx_{t}^{2},\{x_{t},\dots ,x_{n}\})\mid 1\le t\le n-2, v=x_{1}^{\alpha _{1}}\cdots x_{t-1}^{\alpha _{t-1}},0\le \alpha _{i}\le 1\big \},\\&\bigcup \big \{C(vx_{n-1}x_{n},\{x_{n-1},x_{n}\})\mid v=x_{1}^{\alpha _{1}}\cdots x_{n-2}^{\alpha _{n-2}},0\le \alpha _{i}\le 1\big \}.\\ Q= & {} \big \{C(v,\{x_{n}\}) \mid v=x_{1}^{\alpha _{1}}\cdots x_{n-2} ^{\alpha _{n-2}},0\le \alpha _{i}\le 1 \big \}\\&\bigcup \{C(vx_{n-1},\{x_{n-1}\}) \mid v=x_{1}^{\alpha _{1}}\cdots x_{n-2}^{\alpha _{n-2}},0\le \alpha _{i}\le 1 \big \}. \end{aligned}$$

From Theorem 6.2, it follows that P is a Janet basis for ${\mathcal {I}}$.

Based on Theorems 4.7 and  6.2 and Lemma 5.10, we present the main result of this section.

Theorem 6.4

Let ${\mathcal {I}}\subset {\mathcal {R}}$ be an ideal generated by a set of homogeneous polynomials of degree at most d. Assume that ${\mathcal {I}}$ is in J-stable position. Then, the maximum degree of the polynomials in the Janet basis of ${\mathcal {I}}$ is bounded above by $(d+1)^{2^{n-2}}$ if $n>2$. If $n=1,2$, then the upper bound becomes d, 2d, respectively.

Proof

Assume that $(P,Q)=$ Split$(1,X,\mathrm{LM}(F))$ where F is a Gröbner basis of ${\mathcal {I}}$. Since ${\mathcal {I}}$ is in J-stable position then $\mathrm{LM}({\mathcal {I}})$ is J-stable and from Theorem 6.2, it follows that P is a Janet basis for $\mathrm{LM}({\mathcal {I}})$. Further, the elements of P form the leading monomials of the elements of the Janet basis of ${\mathcal {I}}$. Thus, from Lemma 5.10, we conclude that an upper bound for the degrees of the elements of P remains an upper bound for the maximum degree of the elements of the Janet basis of ${\mathcal {I}}$. So, the assertion is proved by Theorem 4.7. $\square$

Now the main questions that we address at the end of this section are: How can we test whether or not a given monomial ideal is J-stable? If a given ideal is not in such a position, how can we transform it into this position? The next algorithm answers the first question.

Theorem 6.5

The JStableTest algorithm terminates in finitely many steps and is correct.

Proof

The finite termination of the algorithm is trivial. Let us deal with its correctness. If ${\mathcal {I}}=\langle F \rangle$ is J-stable then it is clear the algorithm returns true. Conversely, assume that the algorithm returns true. We must show that if $x_i\mid u$ then $x_{j}^{q}u/x_{i}^{\deg _{i}(u)} \in \langle F \rangle$ when $j<i<n$. Since the output is true, we conclude that $x_{k-1}^{q}u/x_{k}^{\deg _{k}(u)} \in {\mathcal {I}}$ where $k<n$ is the largest index of the variables dividing u. Using an induction we can show that $x_{j}^{q}u/(x_{j+1}^{\alpha _{j+1}}\cdots x_{k}^{\alpha _n}) \in {\mathcal {I}}$ . This shows the desired claim and so ${\mathcal {I}}$ is J-stable. $\square$

By applying this algorithm and using the method presented in [23] (to find deterministically a linear change of variables to transform an ideal into quasi stable position), we are able to present a deterministic and effective approach to transform a given ideal into J-stable. We have implemented this algorithm in Maple, and in the next example we apply this algorithm to a simple ideal.

Example 6.6

Let ${\mathcal {I}}_{1}=\langle x_{1}x_{3}^{2},x_{2}^{2} \rangle \subset {\mathcal {K}}[x_{1},x_{2},x_{3}]$ and $x_3\prec _{drl} x_2 \prec _{drl} x_1$. Then, one sees readily that JStableTest(F) returns $(false,x_{2},x_{1})$ where $F=\{ x_{1}x_{3}^{2},x_{2}^{2} \}$. By applying the linear change $[x_{2}=x_{2}+x_{1}]$ on ${\mathcal {I}}_1$, we get the ideal ${\mathcal {I}}_{2}=\langle x_{1}x_{3}^{2},(x_{2}+x_{1})^{2}\rangle$. Computing the reduced Gröbner basis $G=\{ x_{1}^{2}+2x_{1}x_{2}+x_{2}^{2},x_{1}x_{3}^{2}, x_{2}^{2}x_{3}^{2}\}$ for ${\mathcal {I}}_{2}$, we obtain $\mathrm{LM}(G)=\{x_{1}^{2},x_{1}x_{3}^{2},x_{2}^{2}x_{3}^{2}\}$. Since JStableTest$(\mathrm{LM}(G))$ outputs true then ${\mathcal {I}}_{2}$ is J-stable.

7 Ideals in Prime Position

In this section, we introduce a new notion of genericity and show that the degree of the minimal Janet basis of an ideal in this position is bounded above by the degree bounds that we presented in Sect. 4. Below, we define inductively the notion of prime position.

Definition 7.1

Let ${\mathcal {I}}\subset {\mathcal {R}}$ be a monomial ideal and F be its minimal monomial generating set. If either ${\mathcal {I}}=\{0\}$ or ${\mathcal {I}}={\mathcal {R}}$ then ${\mathcal {I}}$ is in prime position. Otherwise, ${\mathcal {I}}$ is called in prime position if the following conditions hold:

• 1. The variable $x_j$ with the minimum index in ${\text{ indet }}(F)$ appears in one of the minimal prime ideals of ${\mathcal {I}}$ having dimension $\dim ({\mathcal {I}})$.

• 2. both the ideals ${\mathcal {I}}:x_{j}$ and ${\mathcal {I}}\vert _{x_{j}=0}$ are in prime position.

A polynomial ideal ${\mathcal {I}}\subset {\mathcal {R}}$ is called in prime position if $\mathrm{LM}({\mathcal {I}})$ w.r.t. $\prec$ is in this position.

Example 7.2

We see readily that the ideal ${\mathcal {I}}=\langle x_{1}x_{2},x_{1}x_{3} \rangle = \langle x_1 \rangle \cap \langle x_2,x_3\rangle \subset {\mathcal {K}}[x_1,x_2,x_3]$ is in prime position. However, the ideal ${\mathcal {I}}=\langle x_{1}^{2},x_{2}x_{3}, x_{3}^{2} \rangle$ is not in prime position, because ideal ${\mathcal {I}}\vert _{x_{1}=0}=\langle x_{2}x_{3}, x_{3}^{2} \rangle$ has only the minimal prime ${\mathcal {P}}=\langle x_{3} \rangle$ which does not contain $x_{2}$.

Example 7.3

The ideal ${\mathcal {I}}=\langle x_{1}^{2},x_{1}x_{2}\cdots x_{n}\rangle \subset {\mathcal {R}}$ is in prime position, however, it is not J-stable. Indeed, we observe that $x_{2}^{\alpha }x_{1}x_{2}\cdots x_{n}/x_{3} \notin {\mathcal {I}}$ for all $\alpha \in {\mathbb {N}}$. On the other hand, the ideal ${\mathcal {I}}=\langle x_{1}^{2}x_{n},x_{2}^{2}x_{n},\dots ,x_{n-2}^{2}x_{n},x_{n-1}x_{n} \rangle \subset {\mathcal {R}}$ is J-stable, however it is not in prime position. We note that the minimal prime of ${\mathcal {I}}$ with dimension $n-1$ is $\langle x_n \rangle$ which does not contain $x_{1}$.

Lemma 7.4

Every ideal in quasi stable position is in prime position.

Proof

Assume that ${\mathcal {I}}$ is a monomial ideal in quasi stable position. Then, from [23, Proposition 4.4], every minimal prime of ${\mathcal {I}}$ is of the form $\langle x_1,\ldots ,x_i\rangle$ for some integer $i\ge n-\dim ({\mathcal {I}})$. This shows that $x_1$ appears in any minimal prime ideal of ${\mathcal {I}}$ with the dimension $\dim ({\mathcal {I}})$. On the other hand, one observes that ${\mathcal {I}}:x_1$ and ${\mathcal {I}}|_{x_1=0}$ remain quasi stable and using an induction, we can conclude the assertion. $\square$

Example 7.2 shows that there exists an ideal in prime position which is not quasi stable. Further, from this lemma, we infer that, given an ideal, any generic linear change of the variables transforms it into prime position. To prove the main result of this section, we shall need the next lemma.

Lemma 7.5

Suppose that ${\mathcal {I}}=\langle F\rangle$ and $F\subset {\mathcal {M}}$. Then for any maximal independent set $s\subset X$ with $F\cap {\mathcal {K}}[s]=\emptyset$, ${\mathcal {P}}=\langle X\setminus s\rangle$ is a minimal prime of ${\mathcal {I}}$ with $\dim ({\mathcal {I}})=\dim ({\mathcal {P}})$, and vice versa.

Proof

First we shall note that any prime of ${\mathcal {I}}$ is of the form $\langle x_{i_{1}},\dots ,x_{i_{k}}\rangle$. Now, let s be a maximal independent set. Then, ${\text{ indet }}(f)\cap (X\setminus s)\ne \emptyset$ for each $f\in F$. So ${\mathcal {I}}$ is contained in ${\mathcal {P}}$ and ${\mathcal {P}}$ is a prime ideal. Now, according to the maximality of $X\setminus s$, ${\mathcal {P}}$ is a minimal prime of ${\mathcal {I}}$. Clearly the converse implication holds. $\square$

Note that in the line 11 of the Split algorithm and in the line 10 of the JanetDecomposition algorithm, we can replace F by $F|_{x_j=0}$. We establish now the main result of this section

Theorem 7.6

Let ${\mathcal {I}}\subset {\mathcal {R}}$ be an ideal generated by a set of homogeneous polynomials of degree at most d. Assume that ${\mathcal {I}}$ is in prime position. Then, the maximum degree of the polynomials in the Janet basis of ${\mathcal {I}}$ is bounded above by $(d+1)^{2^{n-2}}$ if $n>2$. If $n=1,2$, then the upper bound becomes d, 2d, respectively.

Proof

From Lemma 7.5, it follows that the behaviour of both the algorithms Split and JanetDecomposition is similar. Considering this along with Theorems 4.7 and  5.4, the assertion is proved. $\square$

We continue this section by giving an example (which is a generalization of an example from [1] to an arbitrary number of variables) to illustrate that the maximum degree of a Janet basis may be higher than the Castelnuovo-Mumford regularity of the ideal it generates.

Example 7.7

Let d be a positive integer. Let us define the monomial ideal ${\mathcal {I}}^{(d)}=\langle F\rangle \subset {\mathcal {R}}$ where $F=B_{1}\cup B_{2}$ with

$$\begin{aligned} B_{1}= & {} \big \{x_{n-1}^{\alpha }x_{n}^{\beta }\mid \alpha \ge 0,\,\, \beta \ge 0,\,\, \alpha +\beta =d \big \},\\ B_{2}= & {} \big \{x_{1}^{\alpha _{1}}\cdots x_{n}^{\alpha _{n}}\ | \ \alpha _{n}> 0,\,\, \alpha _{1}+\cdots +\alpha _{n-2}\ne 0,\,\, \alpha _{1}+\cdots +\alpha _{n}=d \big \}. \end{aligned}$$

This ideal is a lex segement ideal which is interesting in combinatorial commutative algebra, see [19, Section 2.4] for more details. The set $H^{(d)}$ is the minimal Janet basis for ${\mathcal {I}}^{(d)}$ where $H^{(d)}=B_{1}\cup B_{2}\cup L_{1}\cup L_{2}$ with

$$\begin{aligned} L_{1}= & {} \big \{x_{1}^{\alpha _{1}}\cdots x_{n-2}^{\alpha _{n-2}}x_{n-1}^{d}\mid 1\le \alpha _{i}\le d-1 \big \},\\ L_{2}= & {} \big \{ vx_{n-1}^{\lambda }\mid v\in B_{2},\,\,\lambda >0,\,\,\deg _{n-1}(v)+\lambda <d \big \}. \end{aligned}$$

The maximum degree of this basis is $(n-1)d-(n-2)$. On the other hand, considering the ordering $x_{1}\prec \cdots \prec x_{n}$, this ideal is quasi stable and F is the minimal Pommaret and Janet basis for ${\mathcal {I}}^{(d)}$. This shows that the Castelnuovo-Mumford regularity of ${\mathcal {I}}^{(d)}$ is d, see [23, Theorem 9.2] (it should be noticed that the Castelnuovo-Mumford regularity of an ideal remains stable after any change of the variables). Let $(P,Q)=$ Split(1, X, F) where in the line 10 of the Split algorithm, we select $x_j$ with the maximum index j. Then Q is a 0-standard cone decomposition for $N_{{\mathcal {I}}^{(d)}}$. Let us consider Q as the union $Q=Q_{1}\cup Q_{2}$ where

$$\begin{aligned} Q_{1}= & {} \big \{C(x_{n-1}^{t},\{x_{1},\dots ,x_{n-2}\})\mid 0\le t\le d-1 \big \},\\ Q_{2}= & {} \big \{C(u,\emptyset )\mid x_{n}\vert u,\,\, u\notin {\mathcal {I}}^{(d)} \big \}. \end{aligned}$$

Since $Q_{1}$ is a 0-exact cone decomposition, then Q is also a 0-exact cone decomposition. Due to the definition, we have $b_{0}=1+\max \{\deg (h)\mid \exists u\subset X,\,\, C(h,u)\in Q\}$ and in consequence $b_{0}=d$. Summarizing, for the ideal ${\mathcal {I}}^{(d)}$, the maximum degree of the minimal Janet basis may become arbitrarily larger than its Castelnuovo-Mumford regularity. For instance, if $n=d=3$ we have:

$$\begin{aligned} {\mathcal {I}}^{(3)}= & {} \big \{x_{1}^{2}x_{3},x_{1}x_{3}^{2},x_{1}x_{2}x_{3}, x_{2}^{2}x_{3},x_{2}x_{3}^{2}, x_{2}^{3},x_{3}^{3} \big \},\\ H^{(3)}= & {} \big \{x_{3}^{3},x_{1}^{2}x_{3},x_{2}x_{3}^{2},x_{2}^{2}x_{3},x_{3}^{2}x_{1}, x_{1}x_{3}x_{2},x_{2}^{3},x_{2}^{3}x_{1},x_{3}x_{1}x_{2}^{2}, x_{2}^{3}x_{1}^{2},x_{3}x_{1}^{2}x_{2}, x_{3} x_{2}^{2} x_{1}^{2}\big \},\\ P= & {} \big \{C(x_{2}^{3},\{x_{1},x_{2}\}), C(x_{1}^{2}x_{3},\{x_{1}\}),C(x_{1}x_{2}x_{3}, \{x_{1}\}),C(x_{2}^{2}x_{3},\{x_{1},x_{2}\})\big \}\\&\bigcup \big \{C(x_{1}x_{3}^{2}\{x_{1}\}),C(x_{2}x_{3}^{2},\{x_{1},x_{2}\}) ,C(x_{3}^{3},\{x_{1},x_{2},x_{3}\}) \big \},\\ Q= & {} \big \{C(1,\{x_{1}\}),C(x_{2},\{ x_{1}\}),C(x_{2}^{2},\{x_{1}\}),C(x_{3},\emptyset ),C(x_{1}x_{3}, \emptyset ),C(x_{2}x_{3},\emptyset ),C(x_{3}^{2},\emptyset ) \big \}. \end{aligned}$$

Furthermore, it should be remarked that for this example the difference between the degree of the Janet basis and the Castelnuovo-Mumford regularity is O(nd) and thus gets larger for both increasing d and increasing n.

We conclude the paper by studying how we can test whether or not a given monomial ideal is in prime position. In addition, if the ideal is not in such a position, how we can transform it into this position. Let us first deal with the first problem. We shall note that in the next algorithm, we shall need the computation of minimal primes of a monomial ideal which can be done relatively simply via Alexander duality, see [19, Chapter 5].

To prove the termination of the PrimePosition algorithm, we shall need the next lemma.

Lemma 7.8

If PrimePositionTest(F) returns $(false,x_{j_{2}},x_{j_{1}})$, then $u\in F$ exists with $\beta =\deg _{j_{2}}(u)$ such that $\beta \ne 0$ and for every $\alpha \ge 0$, $x_{j_{1}}^{\alpha } u/x_{j_{2}}^{\beta } \notin \langle F \rangle$.

Proof

According to the structure of the PrimePositionTest algorithm, we have $x_{j_{1}}\ne x_{j_{2}}$ where $j_{1}:=\min \{ i \mid x_{i}\in {\text{ indet }}(F) \}$ and $j_{2}:=\min \{ i \mid x_{i}\in {\mathcal {P}}\ \text {where} \ {\mathcal {P}}\ \text {is a prime of} \ \langle F \rangle , \dim (\langle F \rangle )=\dim ({\mathcal {P}}) \}$. Assume that ${\mathcal {P}}$ is a prime of $\langle F \rangle$ so that ${\mathcal {P}}=\langle x_{j_{2}},x_{j_{3}},\dots ,x_{j_{t}}\rangle$ and $j_{2}<j_{3}<\cdots <j_{t}$. Assume in contrary that for every $u\in F$ that $x_{j_{2}}\vert u$ with $\beta =\deg _{j_{2}}(u)$, there is $\alpha \ge 0$ with $x_{j_{1}}^{\alpha }u/x_{j_{2}}^{\beta } \in \langle F \rangle$. We claim that the prime ideal ${\mathcal {P}}'=\langle x_{j_{3}},\dots ,x_{j_{t}}\rangle$ contains ${\mathcal {I}}$, leading to a contradiction. For every monomial $m\in F$, if $x_{j_{2}}\not \mid m$, ${\text{ indet }}(v)\cap \{x_{j_{3}},\dots ,x_{j_{t}}\}\ne \emptyset$ and we are done. Otherwise, assume that for a monomial $m\in F$ we have $x_{j_{2}}\vert m$ and $\lambda =\deg _{j_{2}}(m)$. Since $x_{j_{1}}\in {\text{ indet }}(F)$ then an integer $\alpha \ge 0$ exists such that $x_{j_{1}}^{\alpha } m/x_{j_{2}}^{\lambda } \in \langle F \rangle$ then ${\text{ indet }}(x_{j_{1}}^{\alpha } m/x_{j_{2}}^{\lambda } )\cap \{x_{j_{3}}, \dots ,x_{j_{t}}\}\ne \emptyset$. It follows that ${\text{ indet }}(m)\cap \{x_{j_{3}}, \dots ,x_{j_{t}}\}\ne \emptyset$ and this shows that ${\mathcal {P}}'$ includes a minimal prime ideal of ${\mathcal {I}}$. $\square$

Theorem 7.9

The PrimePosition algorithm terminates in finitely many steps and is correct.

Proof

Lemma 7.8 shows that if PrimePositionTest(F) returns $(false,x_{j_{2}},x_{j_{1}})$ then we find an obstruction to quasi stability of the ideal generated by F. On the other hand, the third author in [23] described a deterministic to find an elementary linear change of variables to find and solve an obstruction to quasi stability of the givn ideal. Thus the construction of the linear change to transform an ideal into the prime position is partially similar to the transformation which is needed for the quasi stability. This shows both the correctness and finite termination of the algorithm. $\square$

Remark 7.10

If in the PrimePosition algorithm we choose $c=1$, then the algorithm becomes deterministic, see [13, 23]. Note that in the case that the characteristic of ${\mathcal {K}}$ is positive, then by [13, Section 6] the algorithm terminates as well, and returns the correct output.

Example 7.11

We illustrate the steps of the algorithm by an example. Let ${\mathcal {I}}_{1}=\langle x_{1}x_{2}^{2},x_{2}^{3},x_{3}^{3} \rangle \subset {\mathcal {K}}[x_{1},x_{2},x_{3}]$ and $x_3\prec _{drl} x_2 \prec _{drl} x_1$. Let $B_{1}=\{ x_{1}x_{2}^{2},x_{2}^{3},x_{3}^{3} \}$. Then PrimePositionTest$(B_{1})$ returns $(false,x_{2},x_{1})$. We perform the linear change $[x_{2}=x_{2}+x_{1}]$. By applying this change on ${\mathcal {I}}_1$, we get the ideal ${\mathcal {I}}_{2}=\langle x_{1}(x_{2}+x_{1})^{2},(x_{2}+x_{1})^{3},x_{3}^{3} \rangle$. Computing the reduced Gröbner basis $B_{2}=\{ x_{3}^{3}, x_{1}^{2}x_{2}+2x_{1}x_{2}^{2}+x_{2}^{3}, x_{1}^{3}-3x_{1}x_{2}^{2}-2x_{2}^{3}\}$ for ${\mathcal {I}}_{2}$, we obtain $\mathrm{LM}(B_{2})=\{x_{1}^{3},x_{1}^{2}x_{2},x_{3}^{3}\}$. Then PrimePositionTest$(\mathrm{LM}(B_{2}))=true$ and in turn ${\mathcal {I}}_{2}$ is in prime position.

We end this section by comparing the performance of our proposed algorithms to transform a given ideal into J-stable and prime positions. We have implemented both these algorithms in Maple 18². In the following tables, we compare only the number of the performed elementary linear changes for some well-known examples from computer algebra literature³. All computations were done over the field of the rational numbers using the degree reverse lexicographical ordering.

Name	PrimePosition	JStable	Name	PrimePosition	JStable
Liu	1	6	Noon	0	6
Bermejo and Gimenez	0	0	Gerdt2	1	1
Weispfenning94	3	2	Cyclic 5	3	3
Sturmfels and Eisenbud	13	21	Cyclic 6	5	6
Lichtblau	1	0	Seiler	1	1
Green	2	1	Vermeer	5	4
Eco7	3	5	Katsura5	0	0
Eco8	3	6	Katsura6	0	0

As a simple observation, one sees that the PrimePosition algorithm needs less transformations than the JStable algorithm. Finally, we shall remark that the 0 entry in the PrimePosition column indicates that the corresponding ideal is already in this position. The same holds for the JStable column.