The Number and Location of Eigenvalues for the Two-Particle Schrödinger Operators on Lattices

Abstract

We study the Schrödinger operators $H_{\gamma \lambda \mu }(K)$, $K\in \mathbb {T}$ being a fixed (quasi)momentum of the particles pair, associated with a system of two identical bosons on the one-dimensional lattice ${\mathbb {Z}}$, where the real quantities $\gamma$, $\lambda$ and $\mu$ describe the interactions between pairs of particles on one site, two nearest neighboring sites and next two neighboring sites, respectively. We found a partition of the three-dimensional space $(\gamma , \lambda ,\mu )$ of interaction parameters into connected components and the exact number of eigenvalues of this operator that lie below and above the essential spectrum, in each component. Moreover, we show that for any $K\in \mathbb {T}$ the number of eigenvalues of $H_{\gamma \lambda \mu }(K)$ is not less than the corresponding number of eigenvalues of $H_{\gamma \lambda \mu }(0)$.

1 Introduction

Lattice models of physical systems are one of the widely used mathematical models in mathematical physics. Few-body Hamiltonians [29], among such models may be viewed as the simplest version of the corresponding Bose-Hubbard model involving a finite number of particles of a certain type. The few-body lattice Hamiltonians have been intensively studied over the past several decades [2,3,4,5, 10, 11, 17, 19,20,21,22,23, 25, 27, 30].

Another reason for studying the discrete Hamiltonians is that they can provide a natural approximation for their continuous counterparts [9], which allows studying few-body systems. It is well known that the Efimov effect [8] was originally attributed to the three-body systems moving in the three-dimensional continuous space ${\mathbb {R}}^3$. A rigorous mathematical proof of the Efimov effect has been given in [32, 35, 36, 39]. The celebrated Efimov’s phenomenon to take place also in lattice three-particle systems [2, 4, 7, 19]. Discrete Schrödinger operators also represent a simple model for description of few-body systems formed by particles traveling through periodic structures, such as ultracold atoms injected into optical crystals created by the interference of counter-propagating laser beams [6, 38]. The study of ultracold few-atom systems in optical lattices have became popular in the last years due to availability of controllable parameters, such as temperature, particle masses, interaction potentials etc. (see e.g., [6, 13, 14, 28] and references therein). These possibilities give an opportunity to experimentally observe stable repulsively bound pairs of ultracold atoms ( [31, 38], which is not the case for the traditional condensed matter systems, where stable composite objects are formed by means attractive forces. Lattice Hamiltonians are of particular interest in fusion physics too. For example, in [30], a one-dimensional one-particle lattice Hamiltonian has been successfully employed to show that certain class of molecules in lattice structures may enhance nuclear fusion probability.

In the continuous case, the center-of-mass motion can be separated, which is not the case for lattice few-body problems. However, for the lattice Hamiltonian $\textrm{H}$ acting in the functional Hilbert space $\mathbb {T}$ we have a von Neumann direct integral decomposition

$$\begin{aligned} \textrm{H}\simeq \int \limits _{K\in \mathbb {T}} ^\oplus H(K)\,d K, \end{aligned}$$

(1.1)

where $\mathbb {T}$ is the one-dimensional torus. The so called fiber Hamiltonians H(K) acting on the Hilbert space $\mathbb {T}$ nontrivially depends on the quasimomentum $K\in \mathbb {T}$ (see e.g., [2, 3, 33]). This decomposition allows us to reduce the problem to studying the operators H(K).

In this work, we study the spectral properties of the fiber Hamiltonians $H(K),\,K\in \mathbb {T}$ acting in the Hilbert space $L^{2,e}(\mathbb {T})$ as

$$\begin{aligned} H_{\gamma \lambda \mu }(K):=H_0(K) + V_{\gamma \lambda \mu }, \end{aligned}$$

(1.2)

where $H_0(K)$ is the fiber kinetic-energy operator,

$$\begin{aligned} \bigl (H_0(K)f\bigr )(p)={{\mathcal {E}}}_K(p)f(p), \end{aligned}$$

with

$$\begin{aligned} {{\mathcal {E}}}_K(p):= 2(1-\cos \tfrac{K}{2}\,\cos p) \end{aligned}$$

(1.3)

and $V_{\gamma \lambda \mu }$ is the combined interaction potential. The parameters $\gamma$, $\lambda$ and $\mu$, called coupling constants, describe interactions between the particles which are located on one site, on the nearest neighboring sites of the lattice and in the next nearest neighboring sites, respectively.

Within this new model, we find both the exact number of eigenvalues and their locations of the operator $H_{\gamma \lambda \mu }(0)$. We describe the mechanisms of emission and absorption of the eigenvalues of $H_{\gamma \lambda \mu }(0)$ at the thresholds of its essential (continuous) spectrum depending on the interaction parameters. Furthermore, we establish sharp lower bounds for the number of isolated eigenvalues $H_{\gamma \lambda \mu }(K)$ depending on the quasimomentum $K\in \mathbb {T}$, which lie both below the essential spectrum and above that.

For this, we apply the results obtained for the operator $H_{\gamma \lambda \mu }(0)$ and the nontrivial dependence of the dispersion relation ${{\mathcal {E}}}_K$ on the (quasi)momentum $K\in \mathbb {T}$. We recall that the two-particle Schrödinger operator ${H}_{\mu }(K)=-\Delta +\mu {V},\,\mu >0$ on the lattice $\mathbb {Z}^d$ associated to a system of two bosons with zero-range repulsive interactions $\mu >0$ has been considered as a theoretical basis for explanation of the experimental results obtained in [31, 38].

Note that the continuous counterpart of the two-particle Schrödinger operators on lattices, which associated with a system of two quantum-mechanical particles on $\mathbb {R}^d$ interacting via short-range potential v(x) has isolated eigenvalues lying only below the essential spectrum fulfilling the semi-axis $[0, + \infty )$ and hence this model is well adapted to describe systems of two-particles with attractive interactions.

To study the eigenvalues of the discrete Schrödinger operator $H_{\gamma \lambda \mu }(K)$, we apply analytic function theory, namely, we investigate the corresponding Fredholm determinant $\Delta _{\gamma \lambda \mu }(K,z)$, as there is a one-to-one mapping between the sets of eigenvalues of the operator $H_{\gamma \lambda \mu }(K)$ and the zeros of $\Delta _{\gamma \lambda \mu }(K,z)$ (see [23]). Correspondingly, the change in the number of zeros of Fredholm determinant $\Delta _{\gamma \lambda \mu }(0,z)$ results in the change of the number of isolated eigenvalues of Schrödinger operator $H_{\gamma \lambda \mu }(0)$.

Our main finding is that the number of zeros of the determinant $\Delta _{\gamma \lambda \mu }(0,z)$ located below (resp. above) the essential spectrum changes if and only if the principal term $C^{-}(\gamma ,\lambda , \mu )$ (resp. $C^{+} (\gamma , \lambda , \mu )$) of the asymptotics of the Fredholm determinant $\Delta _{\gamma \lambda \mu } (0,z)$ vanishes as z approaches the lower (resp. upper) threshold of the essential spectrum (see Lemma 4.3).

Using this property, we establish a partition of the three-dimensional $(\gamma , \lambda ,\mu )$-space into four disjoint connected components by means of surfaces $C^{-}(\gamma ,\lambda , \mu )=0$ or $C^{+}(\gamma ,\lambda ,\mu )=0$. This allows us to prove that the number of zeros of the Fredholm determinant is constant in each connected component.

In [23, 25], it was studied the Schrödinger operators on the lattice $\mathbb {Z}^d,\,d=1,2$, associated to a system of two bosons with the zero-range on one site interaction ($\lambda \in \mathbb {R}$) and interactions on the nearest neighboring sites ($\mu \in \mathbb {R}$) of the d- dimensional lattice $\mathbb {Z}^d$. We emphasize that, our results is an extension of [23, 25]. The authors of [23] consider the Schrödinger operators $H_{\lambda \mu }(K)$ on two-dimensional lattice $\mathbb {Z}^2$. The operator $H_{\lambda \mu }(K)$ can have one or two eigenvalues, lying as below the essential spectrum, as well as above it. The connected components, which split the two-dimensional plane $\mathbb {R}^2$ of interaction parameters are described by means of a second order elementary curves (hyperbolas). Similar results for the number of eigenvalues of one-particle Schrödinger operators in $\mathbb {Z}^d,\,d\ge 1$ have been obtained, for instance in [22] with attractive interactions and $d=3$ and also with attractive and repulsive interaction cases in [11] for all $d\ge 1$ considering only negative eigenvalues.

In the present work, the connected components are described by implicit functions (third-order polynomials) of three variables defined on $\mathbb {R}^3$, and therefore we have find an algorithm for describing the connected components given by third-order polynomials (see, Section Main results).

The discrete two-particle Schrödinger operator ${H}_{\mu }(k)$ associated to a system of one and two quantum-mechanical particles on $\mathbb {Z}^d$ interacting via short-range potentials have been studied in recent years [3, 5, 18, 20, 30].

Note that some results such as the existence of eigenvalues and their finiteness can be received for a large class of Schrödinger type operators (see e.g., [15, 16, 18, 24]). However, our results show that the study of a qualitative change in the number of eigenvalues of $H_{\gamma \mu \lambda }(K),$ even for $K=0,$ is very delicate: There is ball, with arbitrarily small radius, in the three-dimensional $(\gamma ,\lambda , \mu )$-space in which the number of eigenvalues has a jump (see Theorem 3.6).

The paper is organized as follows: The Sect. 1 is introduction. In Sect. 2, we introduce the two-particle Hamiltonian $\mathbb {H}_{\gamma \lambda \mu }$ of a system of two bosons in the position and momentum space representations and also the Schrödinger operator $H_{\gamma \lambda \mu }(K)$ associated to the Hamiltonian $\mathbb {H}_{\gamma \lambda \mu }$. The main results of the paper are stated in Sect. 3 and their proofs are contained in Sect. 4.

2 The Two-Particle Hamiltonian

2.1 The Position-Space Representation

Let $\mathbb {Z}$ be the one-dimensional lattice and $\mathbb {Z}\times \mathbb {Z}$ be cartesian square of $\mathbb {Z}$. Let $\ell ^{2,s}(\mathbb {Z}\times \mathbb {Z})$ be the Hilbert space of square-summable symmetric functions on $\mathbb {Z}\times \mathbb {Z}$.

The free Hamiltonian ${\hat{\mathbb {H}}}_0$ of a system of two identical particles (bosons), in the position space representation, is usually associated with the following self-adjoint (bounded) Toeplitz-type operator on the Hilbert space $\ell ^{2,s}(\mathbb {Z}\times \mathbb {Z})$:

$$\begin{aligned} ({\hat{\mathbb {H}}}_0 {\hat{f}})(x_1,x_2){} & {} = \sum _{s_1\in \mathbb {Z}} \hat{\epsilon }(x_1-s_1){\hat{f}}(s_1,x_2) \\{} & {} \quad +\sum _{s_2\in \mathbb {Z}}\hat{\epsilon }(x_2-s_2) {\hat{f}}(x_1,s_2), \,\, {\hat{f}} \in \ell ^{2,s}(\mathbb {Z}\times \mathbb {Z}) \end{aligned}$$

where

$$\begin{aligned} {\hat{\epsilon }}(s) = {\left\{ \begin{array}{ll} 2 &{} \hbox { if}\ |s|=0,\\ -\frac{1}{2} &{} \hbox { if}\ |s|=1,\\ 0 &{} \hbox { if}\ |s|>1. \end{array}\right. } \end{aligned}$$

(2.1)

The interaction operator ${\hat{\mathbb {V}}}_{\gamma \lambda \mu }$, in the position space representation, is the multiplication operator by the function ${\hat{v}} \in \ell ^{1}(\mathbb {Z}), i.e.,$

$$\begin{aligned} {\hat{\mathbb {V}}}_{\gamma \lambda \mu } {\hat{f}} (x,y) = {\hat{v}}_{\gamma \lambda \mu }(x-y) {\hat{f}}(x,y),\,\,{\hat{f}} \in \ell ^{2,s}(\mathbb {Z}\times \mathbb {Z}), \end{aligned}$$

where

$$\begin{aligned} {\hat{v}}_{\gamma \lambda \mu }(s)= {\left\{ \begin{array}{ll} 2\gamma &{} \hbox { if}\ |s|=0,\\ \lambda &{} \hbox { if}\ |s|=1,\\ \mu &{} \hbox { if}\ |s|=2,\\ 0 &{} \hbox { if}\ |s|>2. \end{array}\right. } \end{aligned}$$

(2.2)

The total Hamiltonian ${\hat{\mathbb {H}}}_{\gamma \lambda \mu }$ of a system of two identical particles is described as a bounded self-adjoint operator on $\ell ^{2,s}(\mathbb {Z}\times \mathbb {Z})$:

$$\begin{aligned} {\hat{\mathbb {H}}}_{\gamma \lambda \mu }={\hat{\mathbb {H}}}_0 + {\hat{\mathbb {V}}}_{\gamma \lambda \mu }, \,\, \gamma ,\lambda ,\mu \in \mathbb {R}. \end{aligned}$$

2.2 The Two-Particle Hamiltonian: The (quasi)Momentum-Space Representation

Let $\mathbb {T}= \mathbb {R}/2\pi \mathbb {Z}\equiv (-\pi ,\pi ]$ be the one-dimensional torus, the Pontryagin dual group of $\mathbb {Z}$. Let $L^{2}(\mathbb {T})$ be the Hilbert space of square-integrable functions on $\mathbb {T}$ and let

$$\begin{aligned} {{\mathcal {F}}}:\ell ^2(\mathbb {Z})\rightarrow L^2(\mathbb {T}), \,\, {{\mathcal {F}}}{\hat{f}}(p)=\frac{1}{2\pi } \sum _{x\in \mathbb {Z}} {\hat{f}}(x) e^{ip x}. \end{aligned}$$

is the standard Fourier transform with the inverse

$$\begin{aligned} {{\mathcal {F}}}^*: L^2(\mathbb {T}) \rightarrow \ell ^2(\mathbb {Z}), \,\, {{\mathcal {F}}}^* f(p)=\frac{1}{2\pi } \int _{\mathbb {T}} f(x) e^{ip x}dx. \end{aligned}$$

The free Hamiltonian $\mathbb {H}_0=({{\mathcal {F}}}\otimes {{\mathcal {F}}}){\hat{\mathbb {H}}}_0 ({{\mathcal {F}}}^{*} \otimes {{\mathcal {F}}}^{*})$ of a system of two identical particles,in the momentum space representation, is the multiplication operator by the function $\epsilon (p) + \epsilon (q)$ in the Hilbert space $L^{2,s}(\mathbb {T}\times \mathbb {T})$ of symmetric functions on the cartesian square $\mathbb {T}\times \mathbb {T}$ of the torus $\mathbb {T}$:

$$\begin{aligned} \mathbb {H}_0 f(p,q) = [\epsilon (p) + \epsilon (q)]f(p,q), \end{aligned}$$

where the continuous function (dispersion relation) $\epsilon$ is given by

$$\begin{aligned} \epsilon (p) =[{{\mathcal {F}}}{\hat{\epsilon }}](p)= 1-\cos p,\quad p\in \mathbb {T}. \end{aligned}$$

The interaction operator $\mathbb {V}_{\gamma \lambda \mu }=({{\mathcal {F}}}\otimes {{\mathcal {F}}}){\hat{\mathbb {V}}}_{\gamma \lambda \mu } ({{\mathcal {F}}}^{*} \otimes {{\mathcal {F}}}^{*})$ is the integral operator of convolution type acting in $L^{2,s}(\mathbb {T}\times \mathbb {T})$ as

$$\begin{aligned} (\mathbb {V}_{\gamma \lambda \mu } f)(p,q) = \frac{1}{2\pi }\int _{\mathbb {T}} v_{\gamma \lambda \mu }(p-u) f(u,p+q-u)\textrm{d}u, \end{aligned}$$

where the kernel function $v_{\gamma \lambda \mu }(\cdot )$ is given by

$$\begin{aligned} v_{\gamma \lambda \mu }(p){} & {} =[{{\mathcal {F}}}{\hat{v}}_{\gamma \lambda \mu }] (p)=\frac{1}{2\pi }\sum _{x\in \mathbb {Z}} {\hat{v}}_{\gamma \lambda \mu }(x) e^{ip x} \\{} & {} = \frac{1}{\pi } (\gamma +\lambda \cos p+\mu \cos 2p),\quad p\in \mathbb {T}. \end{aligned}$$

The total two-particle Hamiltonian $\mathbb {H}_{\gamma \lambda \mu }$ of a system of two identical quantum-mechanical particles interacting via a finite range attractive potentials ${\hat{v}}_{\gamma \lambda \mu }$, in the momentum space representation, is the bounded self-adjoint operator acting in $L^{2,s}(\mathbb {T}\times \mathbb {T})$ as

$$\begin{aligned} \mathbb {H}_{\gamma \lambda \mu }:=({{\mathcal {F}}}\otimes {{\mathcal {F}}}) {\hat{\mathbb {H}}}_{\gamma \lambda \mu }({{\mathcal {F}}}\otimes {{\mathcal {F}}})^*=\mathbb {H}_0 + \mathbb {V}_{\gamma \lambda \mu }. \end{aligned}$$

2.3 The Floquet-Bloch Decomposition of $\mathbb {H}_{\gamma \lambda \mu }$ and Discrete Schrödinger Operators

Since the operator ${\widehat{H}}_{\gamma \lambda \mu }$ commutes with the shift operators on the lattice $\mathbb {Z}\times \mathbb {Z}$, we can decompose the space $L^{2,s}(\mathbb {T}\times \mathbb {T})$ and Hamiltonian $\mathbb {H}_{\gamma \lambda \mu }$ into the von Neumann direct integrals as

$$\begin{aligned} L^{2,s}(\mathbb {T}\times \mathbb {T})\simeq \int \limits _{K\in \mathbb {T}} ^\oplus L^{2,e}(\mathbb {T})\,\textrm{d}K \quad \text {and} \quad \mathbb {H}_{\gamma \lambda \mu } \simeq \int \limits _{K\in \mathbb {T}} ^\oplus H_{\gamma \lambda \mu }(K)\,\textrm{d}K, \end{aligned}$$

(2.3)

respectively, where $L^{2,e}(\mathbb {T})$ is the Hilbert space of square-integrable even functions on $\mathbb {T}$ (see, e.g., [3]).

The fiber operator $H_{\gamma \lambda \mu }(K),$ $K\in \mathbb {T}$ is a self-adjoint operator defined in $L^{2,e}(\mathbb {T})$ as

$$\begin{aligned} H_{\gamma \lambda \mu }(K):= H_0(K) + V_{\gamma \lambda \mu }, \end{aligned}$$

where the unperturbed operator $H_0(K)$ is the multiplication operator by the function

$$\begin{aligned} {{\mathcal {E}}}_K(p):= 2 (1-\cos \tfrac{K}{2}\,\cos p) \end{aligned}$$

and the perturbation $V_{\gamma \lambda \mu }$ is defined as

$$\begin{aligned} V_{\gamma \lambda \mu } f(p)= \frac{1}{\pi }\int _{\mathbb {T}} (\gamma +\lambda \cos p\cos q+\mu \cos 2p\cos 2q) f(q)\textrm{d}q. \end{aligned}$$

In some literature, the parameter K is called quasimomentum and the fiber $H_{\gamma \lambda \mu }(K)$ is called discrete Schrödinger operator associated to the two-particle Hamiltonian $\mathbb {H}_{\gamma \lambda \mu }$.

2.4 The Essential Spectrum of Discrete Schrödinger Operators

Since $V_{\gamma \lambda \mu }$ is a finite rank operator, by well known Weyl’s Theorem (see [34, Theorem XIII.14]) for any $K\in \mathbb {T}$ the essential spectrum $\sigma _{\textrm{ess}}(H_{\gamma \lambda \mu }(K))$ of $H_{\gamma \lambda \mu }$ coincides with the spectrum of $H_0(K),$ i.e.,

$$\begin{aligned} \sigma _{\textrm{ess}}(H_{\gamma \lambda \mu }(K))=\sigma (H_0(K)) = [{{\mathcal {E}}}_{\min }(K),{{\mathcal {E}}}_{\max }(K)], \end{aligned}$$

(2.4)

where

$$\begin{aligned} {{\mathcal {E}}}_{\min }(K):=&\min _{p\in \mathbb {T}}\,{{\mathcal {E}}}_K(p) = 2(1-\cos \tfrac{K}{2})\ge 0={{\mathcal {E}}}_{\min }(0),\\ {{\mathcal {E}}}_{\max }(K):=&\max _{p\in \mathbb {T}}\,{{\mathcal {E}}}_K(p) = 2(1+\cos \tfrac{K}{2})\le 4={{\mathcal {E}}}_{\max }(0). \end{aligned}$$

3 Main Results

Let $K\in \mathbb {T}$ and $n_+({H}_{\gamma \lambda \mu }(K))$ resp. $n_-({H}_{\gamma \lambda \mu }(K))$ be the number of eigenvalues of the operator ${H}_{\gamma \lambda \mu }(K)$ above resp. below its essential spectrum.

Our first main result is a generalization of Theorem 2 in [3].

Theorem 3.1

Suppose that ${H}_{\gamma \lambda \mu }(0)$ has n eigenvalues below resp. above the essential spectrum for some $\gamma ,\lambda ,\mu \in \mathbb {R}.$ Then for each $K\in \mathbb {T}$ the operator ${H}_{\gamma \lambda \mu }(K)$ has at least n eigenvalues below resp. above its essential spectrum. In other words,

$$\begin{aligned} n_-({H}_{\gamma \lambda \mu }(K))\ge n_-({H}_{\gamma \lambda \mu }(0)) \end{aligned}$$

and

$$\begin{aligned} n_+({H}_{\gamma \lambda \mu }(K))\ge n_+({H}_{\gamma \lambda \mu }(0)). \end{aligned}$$

Let us consider the cubic polynomial $C^{\pm }$ of three-variable defined by

$$\begin{aligned} C^{\pm }(\gamma ,\lambda ,\mu ):=\mp (\gamma +\lambda +\mu +\gamma \lambda \mu )+\gamma \lambda +2\gamma \mu +\lambda \mu . \end{aligned}$$

(3.1)

Lemma 3.2

The set of points ${\mathbb {R}}^3$ satisfying the equation $C^{\pm }(\gamma ,\lambda ,\mu ) = 0$ coincides with the graph of function

$$\begin{aligned}&\gamma ^{\pm }(\lambda ,\mu )=-\frac{Q^{\pm }_{0}(\lambda ,\mu )}{Q^{\pm }_{1}(\lambda ,\mu )}, \end{aligned}$$

(3.2)

where $Q^{\pm }_{0}(\lambda ,\mu )$ and $Q^{\pm }_{1}(\lambda ,\mu )$ are defined as

$$\begin{aligned}&Q^{\pm }_{0}(\lambda ,\mu )=\mp (\lambda +\mu )+\lambda \mu ,\nonumber \\&Q^{\pm }_{1}(\lambda ,\mu )=\mp (\lambda +2\mu )+1+\lambda \mu . \end{aligned}$$

(3.3)

Proof

We observe that $C^{\pm }$ can be decomposed by means $Q^{\pm }_{0}$ and $Q^{\pm }_{1}$ as follows:

$$\begin{aligned} C^{\pm }(\gamma ,\lambda ,\mu )=Q^{\pm }_{0}(\lambda ,\mu )+\gamma Q^{\pm }_{1}(\lambda ,\mu ). \end{aligned}$$

(3.4)

Now we prove that the equality $C^{\pm }(\gamma ,\lambda ,\mu )= 0$ implies the inequality $Q^{\pm }_{1}(\lambda ,\mu )\ne 0,$ i.e., the following system of equations has no solutions

$$\begin{aligned} {\left\{ \begin{array}{ll} Q^{\pm }_{1}(\lambda ,\mu )=0\\ C^{\pm }(\gamma ,\lambda ,\mu )= 0. \end{array}\right. } \end{aligned}$$

(3.5)

Indeed. The system (3.5) yields

$$\begin{aligned} {\left\{ \begin{array}{ll} Q^{\pm }_{1}(\lambda ,\mu )=0\\ Q^{\pm }_{0}(\lambda ,\mu )=0. \end{array}\right. } \end{aligned}$$

(3.6)

This implies the system

$$\begin{aligned} {\left\{ \begin{array}{ll} \mu =0\\ \mu =\pm 1, \end{array}\right. } \end{aligned}$$

(3.7)

which is impossible.

Thus, the equality $C^{\pm }(\gamma ,\lambda ,\mu )=0$ yields the inequality $Q^{\pm }_{1}(\lambda ,\mu )\ne 0,$ which implies the representation (3.2) and vice versa. $\square$

Lemma 3.3

The set of points of ${\mathbb {R}}^2$ satisfying the equation $Q^{\pm }_{1}(\lambda ,\mu )= 0$ coincides with the graph of the function

$$\begin{aligned} \lambda ^{\pm }(\mu )=-\frac{2\mu \mp 1}{1\mp \mu }. \end{aligned}$$

(3.8)

Proof

Lemma 3.3 can be proved as Lemma 3.2. $\square$

The straight lines $\mu =-1$ and $\mu =1$ separate the graph of the functions $\lambda ^{-}(\cdot )$ and $\lambda ^{+}(\cdot )$ on the $(\lambda ,\mu )$-plane into two (different) continuous curves $\{\tau ^{-}_1, \tau ^{-}_2\}$ and $\{\tau ^{+}_1, \tau ^{+}_2\}$:

$$\begin{aligned}&\tau ^{-}_1=\{(\lambda ,\mu )\in \mathbb {R}^2: \lambda =-\frac{1+ 2\mu }{1+ \mu },\,\,\mu >-1\},\\&\tau ^{-}_2=\{(\lambda ,\mu )\in \mathbb {R}^2:\lambda =-\frac{1+ 2\mu }{1+\mu },\,\,\mu <-1\} \end{aligned}$$

and

$$\begin{aligned}&\tau ^{+}_1=\{(\lambda ,\mu )\in \mathbb {R}^2: \lambda =\frac{1- 2\mu }{1- \mu },\,\,\mu <1\},\\&\tau ^{+}_2=\{(\lambda ,\mu )\in \mathbb {R}^2:\lambda =\frac{1- 2\mu }{1-\mu },\,\,\mu >1\}. \end{aligned}$$

The curves $\{\tau ^{-}_1,\tau ^{-}_2\}$ and $\{\tau ^{+}_1,\tau ^{+}_2\}$ divide the $(\lambda ,\mu )$- plane into the domains $D^{-}_{1},D^{-}_{2},D^{-}_{3}$ and $D^{+}_{1},D^{+}_{2},D^{+}_{3}$ of the functions $\lambda ^{-}(\cdot )$ and $\lambda ^{+}(\cdot )$, respectively:

$$\begin{aligned}&D^{-}_1=\{(\lambda ,\mu )\in \mathbb {R}^2: Q^{-}_{1}(\lambda ,\mu )>0,\,\, \mu>-1\},\nonumber \\&D^{-}_2 =\{(\lambda ,\mu )\in \mathbb {R}^2: Q^{-}_{1}(\lambda ,\mu )<0\},\nonumber \\ {}&D^{-}_3= \{(\lambda ,\mu )\in \mathbb {R}^2: Q^{-}_{1}(\lambda ,\mu )>0,\,\,\mu <-1\} \end{aligned}$$

(3.9)

and

$$\begin{aligned}&D^{+}_1=\{(\lambda ,\mu )\in \mathbb {R}^2: Q^{+}_{1}(\lambda ,\mu )>0,\,\, \mu<1\},\nonumber \\&D^{+}_2 =\{(\lambda ,\mu )\in \mathbb {R}^2: Q^{+}_{1}(\lambda ,\mu )<0\},\nonumber \\ {}&D^{+}_3= \{(\lambda ,\mu )\in \mathbb {R}^2: Q^{+}_{1}(\lambda ,\mu )>0,\,\,\mu >1\}. \end{aligned}$$

(3.10)

Fig. 1

The domains $D^{\pm }_{\alpha }, \alpha =1,2,3$ of the principle functions $\gamma ^{\pm }$ in the $(\lambda ,\mu )$-plane of the parameters $\lambda ,\mu \in \mathbb {R}$

The following lemma summarizes the locations of the domains $D^{\pm }_{\alpha }, \alpha =1,2,3$ defined in (3.9) and (3.10) and also their relations.

Lemma 3.4

The followings are true:

• (i) $D^{-}_3 \subseteq D^{+}_1$,

• (ii) $D^{+}_3 \subseteq D^{-}_1$,

• (iii) $D^{-}_3 \cap D^{+}_3=\emptyset$,

• (iv) For any $\alpha =1,2,3$ the regions $D^{-}_\alpha$ and $D^{+}_\alpha$ are symmetric with respect to origin.

Proof

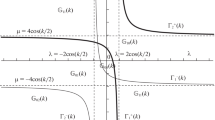
The definitions of $D^{\pm }_{\alpha }, \alpha =1,2,3$ yield the proofs of items (i)–(iii) of Lemma 3.4 and the equality $Q^{+}_{1}(\lambda ,\mu )=Q^{-}_{1}(-\lambda ,-\mu )$ yields (iv) (see Fig. 1). $\square$

Recall that, the domain of the function $\gamma ^{\pm }(\cdot ,\cdot )$ is an open set

$$\begin{aligned} \mathbb {R}^2\setminus (\tau ^{\pm }_1 \cup \tau ^{\pm }_2)=D^{\pm }_{1} \cup D^{\pm }_{2} \cup D^{\pm }_{3}. \end{aligned}$$

The curves $\tau ^{\pm }_1$ and $\tau ^{\pm }_2$ in $\mathbb {R}^2$ are define the corresponding surfaces $\Upsilon ^{\pm }_j\subset \mathbb {R}^3,\,j=1,2$

Further, the surfaces $\Upsilon ^{\pm }_1$ and $\Upsilon ^{\pm }_2$ will separate the graph of the function $\gamma ^{\pm }(\cdot ,\cdot )$ into three different continuous (connected) surfaces $\Gamma ^{\pm }_{1}$, $\Gamma ^{\pm }_{2}$ and $\Gamma ^{\pm }_{3}$ in $\mathbb {R}^3$:

$$\begin{aligned} \Gamma ^{\pm }_{j}=\{(\gamma ,\lambda ,\mu )\in \mathbb {R}^3:\gamma = -\frac{Q^{\pm }_{0}(\lambda ,\mu )}{Q^{\pm }_{1}(\lambda ,\mu )},\,\, (\lambda ,\mu )\in D^{\pm }_j\}, j=1,2,3. \end{aligned}$$

The surfaces $\Gamma ^{-}_{1},\Gamma ^{-}_{2},\Gamma ^{-}_{3}$ and $\Gamma ^{+}_{1},\Gamma ^{+}_{2},\Gamma ^{+}_{3}$ divides the three dimensional space $\mathbb {R}^3$ into four separated connected components ${\mathbb {G}}^{-}_{0}$, ${\mathbb {G}}^{-}_{1}$, ${\mathbb {G}}^{-}_{2}$, ${\mathbb {G}}^{-}_{3}$ and ${\mathbb {G}}^{+}_{0}$, ${\mathbb {G}}^{+}_{1}$, ${\mathbb {G}}^{+}_{2}$, ${\mathbb {G}}^{+}_{3}$ respectively:

$$\begin{aligned}&{\mathbb {G}}^{-}_{0}:=\{(\gamma ,\lambda ,\mu )\in \mathbb {R}^3:\,C^{-}(\gamma ,\lambda ,\mu )>0, \,\,(\lambda ,\mu )\in D^{-}_1\},\nonumber \\&{\mathbb {G}}^{-}_{1}:=\{(\gamma ,\lambda ,\mu )\in \mathbb {R}^3:\,C^{-}(\gamma ,\lambda ,\mu \}<0,\,\,(\lambda ,\mu )\in \overline{D^{-}_1}\cup D^{-}_2\},\nonumber \\&{\mathbb {G}}^{-}_{2}:=\{(\gamma ,\lambda ,\mu )\in \mathbb {R}^3:\,C^{-}(\gamma ,\lambda ,\mu )>0, \,\,(\lambda ,\mu )\in \overline{D^{-}_2}\cup D^{-}_3\},\nonumber \\&{\mathbb {G}}^{-}_{3}:=\{(\gamma ,\lambda ,\mu )\in \mathbb {R}^3:\,C^{-}(\gamma ,\lambda ,\mu )<0, \,\,(\lambda ,\mu )\in D^{-}_3\} \end{aligned}$$

(3.11)

and

$$\begin{aligned}&{\mathbb {G}}^{+}_{0}:=\{(\gamma ,\lambda ,\mu )\in \mathbb {R}^3:\,C^{+}(\gamma ,\lambda ,\mu )>0, \,\,(\lambda ,\mu )\in D^{+}_1\},\nonumber \\&{\mathbb {G}}^{+}_{1}:=\{(\gamma ,\lambda ,\mu )\in \mathbb {R}^3:\,C^{+}(\gamma ,\lambda ,\mu \}<0,\,\,(\lambda ,\mu )\in \overline{D^{+}_1}\cup D^{+}_2\},\nonumber \\&{\mathbb {G}}^{+}_{2}:=\{(\gamma ,\lambda ,\mu )\in \mathbb {R}^3:\,C^{+}(\gamma ,\lambda ,\mu )>0, \,\,(\lambda ,\mu )\in \overline{D^{+}_2}\cup D^{+}_3\},\nonumber \\&{\mathbb {G}}^{+}_{3}:=\{(\gamma ,\lambda ,\mu )\in \mathbb {R}^3:\,C^{+}(\gamma ,\lambda ,\mu )<0, \,\,(\lambda ,\mu )\in D^{+}_3\}. \end{aligned}$$

(3.12)

Theorem 3.5

Let ${{\mathcal {C}}}^-$ be one of the above connected components ${\mathbb {G}}^-_\alpha$, $\alpha =0,1,2,3$, of the partition of the $(\gamma ,\lambda ,\mu )$-space. Then for any $(\gamma ,\lambda ,\mu )\in {{\mathcal {C}}}^-$ the number $n_-({H}_{\gamma \lambda \mu }(0))$ of eigenvalues of ${H}_{\gamma \lambda \mu }(0)$ lying below the essential spectrum $\sigma _\textrm{ess}\bigl ({H}_{\gamma \lambda \mu }(0)\bigr )$ remains constant.

Analogously, let ${{\mathcal {C}}}^+$ be one of the above connected components ${\mathbb {G}}^+_\alpha$, $\alpha =0,1,2,3$, of the partition of the $(\gamma ,\lambda ,\mu )$-space. Then for any $(\gamma ,\lambda ,\mu )\in {{\mathcal {C}}}^+$ the number $n_+({H}_{\gamma \lambda \mu }(0))$ of eigenvalues of ${H}_{\gamma \lambda \mu }(0)$ lying above $\sigma _\textrm{ess}\bigl ({H}_{\gamma \lambda \mu }(0)\bigr )$ remains constant.

Now we study the number of eigenvalues of $H_{\gamma \lambda \mu }(0)$ in $(-\infty ,0)$ and $(4,+\infty )$ depending on the potential parameters $\gamma$, $\lambda$ and $\mu$.

Theorem 3.6

For any $\alpha =0,1,2,3$ the following statements are true:

• (i) if $(\gamma ,\lambda ,\mu )\in {\mathbb {G}}^{-}_{\alpha }$, then $n_-({H}_{\gamma \lambda \mu }(0))=\alpha$;

• (ii) if $(\gamma ,\lambda ,\mu )\in {\mathbb {G}}^{+}_{\alpha }$, then $n_+({H}_{\gamma \lambda \mu }(0))=\alpha$.

We set

$$\begin{aligned} {{\mathcal {C}}}_{\alpha \beta }={\mathbb {G}}_{\alpha }^{-}\cap {\mathbb {G}}_{\beta }^{+}, \,\, \alpha ,\beta =0,1,2,3. \end{aligned}$$

Recall that by the min-max principle $H_{\gamma \lambda \mu }(K)$ can have at most three eigenvalues outside its essential spectrum. The following theorem provides the sharp lower bound for the number of eigenvalues lying outside the essential spectrum of $H_{\gamma \lambda \mu }(K)$ depending only on $\gamma$, $\lambda$ and $\mu$.

Theorem 3.7

Let $K\in \mathbb {T}$ and $(\gamma ,\lambda ,\mu )\in \mathbb {R}^3.$ For all $\alpha ,\beta =0,1,2,3$ satisfying the condition $\alpha +\beta \le 3$ the following relations are true:

• (i) $\text {if} \quad (\gamma ,\lambda ,\mu )\in {{\mathcal {C}}}_{\alpha \beta } \quad \text {and} \quad \alpha +\beta <3,$ $\text {then} \,\, n_{-}(H_{\gamma \lambda \mu }(K)) \ge \alpha ,\,\, n_{+}(H_{\gamma \lambda \mu }(K)) \ge \beta$;

• (ii) $\text {if} \quad (\gamma ,\lambda ,\mu )\in {{\mathcal {C}}}_{\alpha \beta } \quad \text {and} \quad \alpha +\beta =3,$ then    $n_{-}(H_{\gamma \lambda \mu }(K)) = \alpha ,\,\, n_{+}(H_{\gamma \lambda \mu }(K)) = \beta .$

4 Proof of the Main Results

4.1 The Discrete Spectrum of $H_{\gamma \lambda \mu }(0)$

In the case of $K=0$, the Fredholm determinant $\Delta _{\gamma \lambda \mu }(0,z)$ is easier to study. Note that the essential spectrum of Hamiltonian $H_{\gamma \lambda \mu }(0)$ coincides with the segment [0, 4].

We try to find an (implicit) equation for the discrete eigenvalues of $H_{\gamma \lambda \mu }(0)$, i.e., for the non-zero solutions of equation

$$\begin{aligned} H_{\gamma \lambda \mu }(0)f=zf \end{aligned}$$

in $z\in \mathbb {R}\setminus [0,4]$.

We apply the Fredholm’s determinants method to study the number and location of eigenvalues (see, e.g., [1, 26]). The Fredholm determinant associated to $H_{\gamma \lambda \mu }(0)$ can be written as

$$\begin{aligned} \Delta _{\gamma \lambda \mu }(0;z)= \left| \begin{array}{cc} 1+\gamma a(z)\quad \lambda b(z)\quad \quad \mu c(z)\quad \\ \quad \gamma b(z)\quad 1+\lambda d(z)\quad \mu e(z)\quad \\ \quad \quad \gamma c(z)\quad \lambda e(z)\quad 1+\mu f(z)\quad \\ \end{array}\right| , \end{aligned}$$

(4.1)

where

$$\begin{aligned}&a(z):=\int \limits _{\mathbb {T}}\frac{2dt}{\varepsilon (t)-z},&b(z):=\int \limits _{\mathbb {T}}\frac{2\cos tdt}{\varepsilon (t)-z},\nonumber \\&c(z):=\int \limits _{\mathbb {T}}\frac{2\cos 2tdt}{\varepsilon (t)-z},&d(z):=\int \limits _{\mathbb {T}}\frac{2\cos ^2 tdt}{\varepsilon (t)-z}, \nonumber \\&e(z):=\int \limits _{\mathbb {T}}\frac{2\cos t\cos 2tdt}{\varepsilon (t)-z},&f(z):=\int \limits _{\mathbb {T}}\frac{2\cos ^2 {2t}dt}{\varepsilon (t)-z}. \end{aligned}$$

(4.2)

Functions $a(\cdot )$, $d(\cdot )$ and $f(\cdot )$ are analytic in $\mathbb {R}\backslash [0,4]$, strictly decreasing in $\mathbb {R}\backslash [0,\,4]$, positive in the interval $(-\infty ,0)$ and negative in $(4,+\infty )$. The functions $b(\cdot )$, $c(\cdot )$ and $e(\cdot )$ are analytic in $\mathbb {R}\backslash [0,4]$ too. Their behaviour near $z=0$ and $z=4$ are described in the following proposition.

Proposition 4.1

The functions defined in (4.2) have the following asymptotics

$$\begin{aligned}&a(z)={\left\{ \begin{array}{ll} \frac{1}{(-z)^{\frac{1}{2}}}+O((-z)^{\frac{1}{2}}), \,\, as \,\, z\nearrow 0 \\ -\frac{1}{(z-4)^{\frac{1}{2}}}+O((z-4)^{\frac{1}{2}}), \,\, as \,\, z\searrow 4 \end{array}\right. },\\&b(z)={\left\{ \begin{array}{ll} \frac{1}{(-z)^{\frac{1}{2}}}-1+O((-z)^{\frac{1}{2}}),\,\, as \,\, z\nearrow 0 \\ -\frac{1}{(z-4)^{\frac{1}{2}}}+1+O((z-4)^{\frac{1}{2}}),\,\, as \,\, z\searrow 4 \end{array}\right. }, \\&c(z)={\left\{ \begin{array}{ll} \frac{1}{(-z)^{\frac{1}{2}}}-2+O((-z)^{\frac{1}{2}}),\,\, as \,\, z\nearrow 0 \\ -\frac{1}{(z-4)^{\frac{1}{2}}}+2+O((z-4)^{\frac{1}{2}}),\,\, as \,\, z\searrow 4 \end{array}\right. }, \\&d(z)={\left\{ \begin{array}{ll} \frac{1}{(-z)^{\frac{1}{2}}}-1+O((-z)^{\frac{1}{2}}),\,\, as \,\, z\nearrow 0 \\ -\frac{1}{(z-4)^{\frac{1}{2}}}+1+O((z-4)^{\frac{1}{2}}),\,\, as \,\, z\searrow 4 \end{array}\right. }, \\&e(z)={\left\{ \begin{array}{ll} \frac{1}{(-z)^{\frac{1}{2}}}-2+O((-z)^{\frac{1}{2}}), \,\, as \,\, z\nearrow 0 \\ -\frac{1}{(z-4)^{\frac{1}{2}}}+2+O((z-4)^{\frac{1}{2}}), \,\, as \,\, z\searrow 4 \end{array}\right. }, \\&f(z)={\left\{ \begin{array}{ll} \frac{1}{(-z)^{\frac{1}{2}}}-2+O((-z)^{\frac{1}{2}}), \,\, as \,\, z\nearrow 0 \\ -\frac{1}{(z-4)^{\frac{1}{2}}}+2+O((z-4)^{\frac{1}{2}}), \,\, as \,\, z\searrow 4 \end{array}\right. }. \end{aligned}$$

Here $(-z)^{\frac{1}{2}}$ and $(z-4)^{\frac{1}{2}}$ are denote those branches of analytic functions that are positive for $-z>0$ and $z-4>0$.

Proposition 4.1 can be proved as [21, Proposition 4].

Lemma 4.2

For all $\gamma ,\lambda ,\mu \in {\mathbb {R}}$ the determinant $\Delta _{\gamma \lambda \mu }(0;z)$ has asymptotics

$$\begin{aligned}&\Delta _{\gamma \lambda \mu }(0;z)={\left\{ \begin{array}{ll} C^{-}(\gamma ,\lambda ,\mu )(-z)^{-\frac{1}{2}}+D^{-}(\gamma ,\lambda ,\mu )+O((-z)^{\frac{1}{2}}),\,\, as \,\, z\nearrow 0, \\ C^{+}(\gamma ,\lambda ,\mu )(z-4)^{-\frac{1}{2}}+D^{+}(\gamma ,\lambda ,\mu )+O((z-4)^{\frac{1}{2}}),\,\, as \,\, z\searrow 4, \end{array}\right. } \end{aligned}$$

(4.3)

where $C^{\pm }$ is defined in (3.1) and

$$\begin{aligned} D^{\pm }(\gamma ,\lambda ,\mu )=1-(\gamma \lambda +2\lambda \mu +4\gamma \mu )\mp (\lambda +\mu +\gamma \lambda \mu ). \end{aligned}$$

The proof of Lemma 4.2 can be derived by using the asymptotics of functions $a(\cdot ), b(\cdot ),c(\cdot ),d(\cdot ),e(\cdot )$ and $f(\cdot )$ in Proposition 4.1.

Corollary 4.3

For all $(\gamma ,\lambda ,\mu )\in {\mathbb {R}}^3$ the relations

• (i). $\lim \limits _{z\rightarrow {-\infty }}\Delta _{\gamma \lambda \mu }(0;z)=1,$

• (ii). $\lim \limits _{z\nearrow 0}\sqrt{-z}\Delta _{\gamma \lambda \mu }(0;z)=C^{-}(\gamma ,\lambda ,\mu ),$

• (iii). $\lim \limits _{z\searrow 4}\sqrt{z-4}\Delta _{\gamma \lambda \mu }(0;z)=C^{+}(\gamma ,\lambda ,\mu )$

hold.

Proof of Corollary 4.3

The first item follows from the Lebesgue dominated convergence theorem. Lemma 4.2 yields the proof of other items. $\square$

The next lemma describes a one-to-one correspondence between the eigenvalues of the operator $H_{\gamma \lambda \mu }(0)$ and the zeros of the Fredholm determinant $\Delta _{\gamma \lambda \mu }(0;z)$.

Lemma 4.4

The number $z\in \mathbb {R}\setminus [0,4]$ is an eigenvalue of $H_{\gamma \lambda \mu }(0)$ if and only if it is a zero of $\Delta _{\gamma \lambda \mu }(0;\cdot ).$ Moreover, in $\mathbb {R}{\setminus } [0,4]$ the function $\Delta _{\gamma \lambda \mu }(0;\cdot )$ has at most three zeros.

Proof

The first assertion follows from the theory of Fredholm determinants (see, for example, [1]). Since the operator $H_{\gamma \lambda \mu }(0)$ has rank at most three, by the min-max principle it has at most three eigenvalues outside the essential spectrum. So, according to the first part of the proposition, $\Delta _{\gamma \lambda \mu }(0;\cdot )$ has at most three zeros in $\mathbb {R}\setminus [0,4].$ $\square$

The following lemma determine the number and arrangement of eigenvalues of the operator $H_{\gamma \lambda 0}(0)$ that lie below the essential spectrum.

Lemma 4.5

Let $(\gamma ,\lambda )\in {\mathbb {R}}^2$, then the following relations hold.

(i):

If $\gamma +\lambda +\gamma \lambda >0$ and $\gamma +1>0$, then $H_{\gamma \lambda 0}(0)$ has no eigenvalues in $(-\infty ,0)$.

(ii):

If $\gamma +\lambda +\gamma \lambda <0$ or $\gamma +\lambda +\gamma \lambda =0$ and $\gamma +1>0$, then $H_{\gamma \lambda 0}(0)$ has one eigenvalue in $(-\infty ,0)$.

(iii):

If $\gamma +\lambda +\gamma \lambda \ge 0$ and $\gamma +1\le 0$, then $H_{\gamma \lambda 0}(0)$ has two eigenvalues in $(-\infty ,0)$.

The following lemma provides the dependence of the number of eigenvalues of the operator $H_{\gamma \lambda 0}(0)$ in $(4,+\infty )$ on $\gamma$ and $\lambda$:

Lemma 4.6

Let $(\gamma ,\lambda )\in {\mathbb {R}}^2$, then the following relations hold.

(i):

If $-\gamma -\lambda +\gamma \lambda >0$ and $\gamma -1<0$, then $H_{\gamma \lambda 0}(0)$ has no eigenvalues in $(4,+\infty )$.

(ii):

If $-\gamma -\lambda +\gamma \lambda <0$ or $-\gamma -\lambda +\gamma \lambda =0$ and $\gamma -1<0$, then $H_{\gamma \lambda 0}(0)$ has one eigenvalue in $(4,+\infty )$.

(iii):

If $-\gamma -\lambda +\gamma \lambda \ge 0$ and $\gamma -1\ge 0$, then $H_{\gamma \lambda 0}(0)$ has two eigenvalues in $(4,+\infty )$.

Lemmas 4.5 and 4.6 can be proved as in [25, Theorem 5.5].

Proof of Theorem 3.5

Let us assume, without loss of generality, that $C^{-}(\gamma ,\lambda ,\mu )<0$ for all $(\gamma ,\lambda ,\mu )\in {{\mathcal {C}}}$. The definition of determinant and Lemma 4.3 yield

$$\begin{aligned} \lim \limits _{z\rightarrow -\infty } \Delta _{\gamma \lambda \mu }(0,z) =1, \, \lim \limits _{z\nearrow 0} \Delta _{\gamma \lambda \mu }(0,z)<0. \end{aligned}$$

(4.4)

Since for any $(\gamma ,\lambda ,\mu )\in {{\mathcal {C}}}$ the equalities (4.4) are hold and the determinant $\Delta _{\gamma \lambda \mu }(z)$ is real analytic function in $(-\infty ,0)$, there exist such negative numbers $B_1<B_2<0$ that all roots of $\Delta _{\gamma \lambda \mu }(z)$ lay in $(B_1,B_2)$.

Let $(\gamma _0,\lambda _0,\mu _0)\in {{\mathcal {C}}}$ be a point of ${{\mathcal {C}}}$ and $z_0<0$ be a zero of the function $\Delta _{\gamma _0\lambda _0\mu _0}(z)$ of multiplicity $m\ge 1$. For each fixed $z<0$ the determinant $\Delta _{\gamma \lambda \mu }(z)$ is a real analytic function in $(\gamma ,\lambda ,\mu )\in {{\mathcal {C}}}$ and for each fixed $\gamma ,\lambda ,\mu \in \mathbb {R}$ the function $\Delta _{\gamma \lambda \mu }(z)$ is real analytic in $z\in (-\infty ,0)$. Hence, for each $\varepsilon >0$ there are numbers $\delta >0$, $\eta > 0$ and an open neighborhood $W_{\eta }(z_0)$ of $z_0$ with radius $\eta$ such that for all $z\in \overline{W_{\eta }(z_0)}$ and $(\gamma ,\lambda ,\mu )\in {{\mathcal {C}}}$ obeying the conditions $|z-z_0|=\eta$ and $||(\gamma ,\lambda ,\mu )-(\gamma _0,\lambda _0,\mu _0)||<\delta$ the following two inequalities $|\Delta _{\gamma _0\lambda _0\mu _0}(z)|>\eta$ and $|\Delta _{\gamma \lambda \mu }(z)-\Delta _{\gamma _0\lambda _0\mu _0}(z)|<\epsilon$ hold. Then by Rouché’s theorem the number of zeros of the function $\Delta _{\gamma \lambda \mu }(z)$ in ${W_{\eta }(z_0)}$ remains constant for all $(\gamma ,\lambda ,\mu )\in {{\mathcal {C}}}$ satisfying the inequality $||(\gamma ,\lambda ,\mu )-(\gamma _0,\lambda _0,\mu _0)||<\delta$. Since the root $z_0<0$ of the function $\Delta _{\gamma \lambda \mu }(z)$ is arbitrary in $(B_1,B_2)$ we conclude that the number of its zeros remains constant in $(B_1,B_2)$ for all $(\gamma ,\lambda ,\mu )\in {{\mathcal {C}}}$ satisfying $||(\gamma ,\lambda ,\mu )-(\gamma _0,\lambda _0,\mu _0)||<\delta$.

Further each Jordan curve $\Gamma \subset {{\mathcal {C}}}$ connecting any two points of ${{\mathcal {C}}}$ is a compact set, so the number of zeros of the function $\Delta _{\gamma \lambda \mu }(z)$ lying below the bottom of the essential spectrum for any $(\gamma ,\lambda ,\mu )\in \Gamma$ remains constant. Therefore, Lemma 4.4 yields that the number of eigenvalues $n_-\bigl (H_{\gamma \lambda \mu }(0)\bigr )$ of the operator ${H}_{\gamma \lambda \mu }(0)$ below the essential spectrum is constant.

The proof in the case of $n_+\bigl (H_{\gamma \lambda \mu }(0)\bigr )$ is done in the same way. $\square$

Proof of Theorem 3.6

Let us prove Theorem 3.6 in the cases $\alpha =0,1,2,3$ successively. According to (3.11) and (3.1) we have $(0,0,1)\in {\mathbb {G}}^{-}_{0}$.The representation (4.1) of the determinant $\Delta _{\gamma \lambda \mu }(0;z)$ yields that

$$\begin{aligned} \Delta _{001}(0;z)=1+f(z). \end{aligned}$$

By definition (4.2) of f(z), for all $z\in (-\infty ,0)$ the inequalities $f(z)>0$ and $\Delta _{001}(0;z)>0$ hold, i.e., the determinant $\Delta _{001}(0;z)$ has no negative zeros in $z\in (-\infty ,0)$. Lemma 4.4 yields that the operator $H_{001}(0)$ has no eigenvalues below the essential spectrum. Theorem 3.5 gives that the operator $H_{\gamma \lambda \mu }(0)$ has no eigenvalues below the essential spectrum for all $(\gamma ,\lambda ,\mu )\in {\mathbb {G}}^{-}_{0}$.

Due to (3.11) we have $(0,-1,0)\in {\mathbb {G}}^{-}_{1}$. Lemma 4.5 gives that the operator $H_{0(-1)0}(0)$ has exactly one eigenvalue. Theorem 3.5 yields that for any $(\gamma ,\lambda ,\mu )\in {\mathbb {G}}^{-}_{1}$, the operator $H_{\gamma \lambda \mu }(0)$ has exactly one eigenvalue below the essential spectrum.

We note $(-3,-3,0)\in {\mathbb {G}}^{-}_{2}$. According to (iii) of Lemma 4.5 the operator $H_{(-3)(-3)0}(0)$ has two eigenvalues. Theorem 3.5 yields that for any $(\gamma ,\lambda ,\mu )\in {\mathbb {G}}^{-}_{2}$ the operator $H_{\gamma \lambda \mu }(0)$ has two eigenvalues below the essential spectrum.

Now assume that $(\gamma ,\lambda ,\mu )\in {\mathbb {G}}^{-}_{3}$.

Due to (3.11) we have

$$\begin{aligned} C^{-}(\gamma ,\lambda ,\mu )<0, \,\,(\lambda ,\mu )\in D^{-}_3. \end{aligned}$$

Definition 3.9 and inclusion $(\lambda ,\mu )\in D^{-}_3$ give

$$\begin{aligned} \mu <-1, \,\, Q_1^{-}(\lambda ,\mu )>0. \end{aligned}$$

(4.5)

Inequalities (4.5) and $C^{-}(\gamma ,\lambda ,\mu )<0$ guarantee that

$$\begin{aligned} \gamma<-\frac{Q_0^{-}(\lambda ,\mu )}{Q_1^{-}(\lambda ,\mu )}=\frac{\mu +1}{Q_1^{-}(\lambda ,\mu )}-1<0. \end{aligned}$$

(4.6)

According to negativity of $\gamma$ the function $\Delta _{\gamma 00}(0;z)=1+\gamma a(z)$ is continuous and monotone decreasing in $(-\infty ,0)$.

By (3.1) and (4.6) we have that $C^{-}(\gamma ,0,0)=\gamma <0.$ Corollary 4.3 yields that

$$\begin{aligned} \quad \lim \limits _{z\rightarrow -\infty }\Delta _{\gamma 00}(0;z)=1 \quad \text {and} \lim \limits _{z\nearrow 0}\Delta _{\gamma 00}(0;z)=-\infty . \end{aligned}$$

(4.7)

Since the function $\Delta _{\gamma 00}(0;z)$ is continuous and monotone decreasing in the interval $(-\infty ,0)$ it has exactly one zero $z_{11}$ below the essential spectrum. Obviously

$$\begin{aligned} \begin{aligned}&\Delta _{\gamma 00}(0;z )=1+\gamma a(z )>0 \quad \text {if} \quad z<z_{11},\\&\Delta _{\gamma 00}(0;z )=1+\gamma a(z )<0 \quad \text {if} \quad z>z_{11}. \end{aligned} \end{aligned}$$

(4.8)

Observe

$$\begin{aligned} \Delta _{\gamma \lambda 0}(0;z_{11})=(1+\gamma a(z_{11}))(1+\lambda d(z_{11}))-\gamma \lambda (b(z_{11}))^2=-\gamma \lambda (b(z_{11}))^2<0.\nonumber \\ \end{aligned}$$

(4.9)

According to inequalities (4.5) we have

$$\begin{aligned} C^{-}(\gamma ,\lambda ,0)=\gamma +\lambda +\gamma \lambda =Q_1(\lambda ,\mu )-(\mu +1)>0. \end{aligned}$$

Corollary 4.3 and inequality (4.9) give

$$\begin{aligned} \lim \limits _{z\rightarrow -\infty }\Delta _{\gamma \lambda 0}(0;z)=1, \quad \Delta _{\gamma \lambda 0}(0;z_{11})<0 \quad \text {and} \quad \lim \limits _{z\nearrow 0}\Delta _{\gamma \lambda 0}(0;z)=+\infty . \end{aligned}$$

Thus, the continuous function $\Delta _{\gamma \lambda 0}(0;z)$ has at least one zero in each intervals $(-\infty ,z_{11})$ and $(z_{11},0)$. Therefore there exists real numbers satisfying the inequalities

$$\begin{aligned} z_{21}<z_{11}<z_{22}<0 \end{aligned}$$

(4.10)

such that the following equalities hold:

$$\begin{aligned} \Delta _{\gamma \lambda 0}(0;z_{21})=\Delta _{\gamma \lambda 0}(0;z_{22})=0. \end{aligned}$$

Lemma 4.4 and the min-max principle yield that $H_{\gamma \lambda 0}(0)$ has at least two eigenvalues below the essential spectrum. Hence the determinant $\Delta _{\gamma \lambda 0}(0;z)$ has exactly two zeros $z_{21}$ and $z_{22}$ in $(-\infty ,0)$, which yields

$$\begin{aligned} \begin{aligned}&(1+\gamma a(z_{21}))(1+\lambda d(z_{21}))=\gamma \lambda (b(z_{21}))^2>0, \\&(1+\gamma a(z_{22}))(1+\lambda d(z_{22}))=\gamma \lambda (b(z_{22}))^2>0. \end{aligned} \end{aligned}$$

(4.11)

The relations (4.8), (4.10) and (4.11) yield

$$\begin{aligned}&1+\gamma a(z_{21})>0 \quad \text {and} \quad 1+\lambda d(z_{21})>0 , \\&1+\gamma a(z_{22})<0 \quad \text {and} \quad 1+\lambda d(z_{22})<0. \end{aligned}$$

We note that $(\gamma ,\lambda ,\mu )\in {\mathbb {G}}^{-}_{3}$ and so $C^{-}(\gamma ,\lambda ,\mu )>0$. Applying Corollary 4.3 we have that

$$\begin{aligned} \lim \limits _{z\rightarrow -\infty }\Delta _{\gamma \lambda \mu }(0;z)=1 \quad \text {and} \quad \lim \limits _{z\nearrow 0}\Delta _{\gamma \lambda \mu }(0;z)=-\infty . \end{aligned}$$

Observe that

$$\begin{aligned} \Delta _{\gamma \lambda \mu }(0;z_{21})=&\, \Delta _{\gamma \lambda 0}(0;z_{21})[1+\mu f(z_{21})]+2\gamma \lambda \mu b(z_{21})c(z_{21})e(z_{21})\\&- \gamma \mu [1+\lambda d(z_{21})]c^2(z_{21})-\lambda \mu [1+\gamma a(z_{21})](e(z_{21}))^2\\ =&\, \mu \big [\sqrt{-\gamma [1+\lambda d(z_{21})]}c(z_{21})+\sqrt{-\lambda [1+\gamma a(z_{21})]}e(z_{21})\big ]^2<0. \end{aligned}$$

Similarly can be shown

$$\begin{aligned}&\Delta _{\gamma \lambda \mu }(0;z_{22})=-\mu \big [\sqrt{\gamma [1+\lambda d(z_{22})]}c(z_{22})+\sqrt{\lambda [1+\gamma a(z_{22})]}e(z_{22})\big ]^2>0. \end{aligned}$$

Then the relations

$$\begin{aligned}{} & {} \lim \limits _{z\rightarrow -\infty }\Delta _{\gamma \lambda \mu }(0;z)=1, \quad \Delta _{\gamma \lambda \mu }(0;z_{21})<0, \quad \Delta _{\gamma \lambda \mu }(0;z_{22})>0, \quad \\{} & {} \lim \limits _{z\nearrow 0}\Delta _{\gamma \lambda \mu }(0;z)=-\infty \end{aligned}$$

yield the existence of zeros $z_{31}$, $z_{32}$ and $z_{33}$ of function $\Delta _{\gamma \lambda \mu }(0;z)$ satisfying the inequalities $z_{31}<z_{21}<z_{32}<z_{22}<z_{33}<0$, i.e

$$\begin{aligned} \Delta _{\gamma \lambda \mu }(0;z_{31})=\Delta _{\gamma \lambda \mu }(0;z_{32})=\Delta _{\gamma \lambda \mu }(0;z_{33})=0. \end{aligned}$$

Hence the function $\Delta _{\gamma \lambda \mu }(0;z)$ has three single zeros less than 0. Lemma 4.4 gives that the operator $H_{\gamma \lambda \mu }(0)$ has three eigenvalues below the essential spectrum.

The proof of item (ii) of the theorem is carried out similarly to the proof of item (i). $\square$

4.2 The Discrete Spectrum of $H_{\gamma \lambda \mu }(K)$

For every $n\ge 1$ define

$$\begin{aligned} e_n(K;\gamma ,\lambda ,\mu ):= \sup \limits _{\phi _1,\ldots ,\phi _{n-1}\in L^{2}(\mathbb {T})}\,\,\inf \limits _{{\psi } \in [\phi _1,\ldots ,\phi _{n-1}]^\perp ,\,\Vert {\psi }\Vert =1} ({H}_{\gamma \lambda \mu }(K){\psi },{\psi }) \nonumber \\ \end{aligned}$$

(4.12)

and

$$\begin{aligned} E_n(K; \gamma ,\lambda ,\mu ):= \inf \limits _{\phi _1,\ldots ,\phi _{n-1}\in L^{2}(\mathbb {T})}\,\,\sup \limits _{{\psi } \in [\phi _1,\ldots ,\phi _{n-1}]^\perp ,\,\Vert {\psi }\Vert =1} ({H}_{\gamma \lambda \mu }(K){\psi },{\psi }). \nonumber \\ \end{aligned}$$

(4.13)

By the minimax principle, $e_n(K;\gamma ,\lambda ,\mu )\le {{\mathcal {E}}}_{\min }(K)$ and $E_n(K;\gamma ,\lambda ,\mu )\ge {{\mathcal {E}}}_{\max }(K).$ Since, the rank of $V_{\gamma \lambda \mu }$ does not exceed three, by choosing $\phi _1\equiv 1,$ $\phi _2(p)=\cos p$ and $\phi _3(p)=\cos 2p$ we immediately see that $e_n(K;\gamma ,\lambda ,\mu ) = {{\mathcal {E}}}_{\min }(K)$ and $E_n(K;\gamma ,\lambda ,\mu ) = {{\mathcal {E}}}_{\max }(K)$ for all $n\ge 4.$

Lemma 4.7

Let $n\ge 1$. Then the maps

$$\begin{aligned} K\in \mathbb {T}\mapsto {{\mathcal {E}}}_{\min }(K) - e_n(K;\gamma ,\lambda ,\mu ) \end{aligned}$$

and

$$\begin{aligned} K\in \mathbb {T}\mapsto E_n(K;\gamma ,\lambda ,\mu )-{{\mathcal {E}}}_{\max }(K) \end{aligned}$$

is non-increasing in $(-\pi ,0]$ and non-decreasing in $[0,\pi ]$.

Proof

For $\psi \in L^2(\mathbb {T})$, we consider

$$\begin{aligned} ((H_0(K) - {{\mathcal {E}}}_{\min }(K))\psi ,\psi )=\int _{\mathbb {T}} 2\cos \tfrac{K}{2}\,\big (1-\cos q\big )|\psi (q)|^2\,\textrm{d}q. \end{aligned}$$

Then, the map $K\in \mathbb {T}\mapsto ((H_0(K) - {{\mathcal {E}}}_{\min }(K))\psi ,\psi )$ is non-decreasing in $(-\pi ,0]$ and is non-increasing in $[0,\pi ].$ Since $V_{\gamma \lambda \mu }$ is independent of K,  from the definition of $e_n(K;\gamma ,\lambda ,\mu )$, the map $K\in \mathbb {T}\mapsto e_n(K;\gamma ,\lambda ,\mu ) - {{\mathcal {E}}}_{\min }(K)$ is non-decreasing in $(-\pi ,0]$ and is non-increasing in $[0,\pi ].$ $\square$

Proof of Theorem 3.1

For any $K\in \mathbb {T}$ and $m\ge 1$ Lemma 4.7 gives

$$\begin{aligned}&0\le {{\mathcal {E}}}_{\min }(0) - e_m(0;\gamma ,\lambda ,\mu ) \le {{\mathcal {E}}}_{\min }(K)-e_m(K;\gamma ,\lambda ,\mu ),\end{aligned}$$

(4.14)

$$\begin{aligned} \text {and} \nonumber \\&0\le E_m(0;\gamma ,\lambda ,\mu )- {{\mathcal {E}}}_{\max }(0) \le E_m(K;\gamma ,\lambda ,\mu ) - {{\mathcal {E}}}_{\max }(K). \end{aligned}$$

(4.15)

By assumption $e_n(0;\gamma ,\lambda ,\mu )$ is an discrete eigenvalue of $H_{\gamma \lambda \mu }(0)$ lying below the bottom ${{\mathcal {E}}}_{\min }(K)$. So ${{\mathcal {E}}}_{\min }(0) - e_n(0;\gamma ,\lambda ,\mu )>0$ and hence, by (4.14) and (2.4), $e_n(K;\gamma ,\lambda ,\mu )$ is a discrete eigenvalue of $H_{\gamma \lambda \mu }(K)$ for any $K\in \mathbb {T}.$ Since $e_1(K;\gamma ,\lambda ,\mu )\le \ldots \le e_n(K;\gamma ,\lambda ,\mu )<{{\mathcal {E}}}_{\min }(K),$ it follows that $H_{\gamma \lambda \mu }(K)$ has at least n eigenvalue below the essential spectrum. The case of $E_n(K;\gamma ,\lambda ,\mu )$ is similar. $\square$

Proof of Theorem 3.7

is obtained by combining Theorem 3.1 and Theorem 3.6. $\square$