Abstract
We study the Hamiltonian for a system of N identical bosons interacting with an impurity, i.e., a different particle, via zero-range forces in dimension three. It is well known that, following the standard approach, one obtains the Ter-Martirosyan Skornyakov Hamiltonian which is unbounded from below. In order to avoid such instability problem, we introduce a three-body force acting at short distances. The effect of this force is to reduce to zero the strength of the zero-range interaction between two particles, i.e., the impurity and a boson, when another boson approaches the common position of the first two particles. We show that the Hamiltonian defined with such regularized interaction is self-adjoint and bounded from below if the strength of the three-body force is sufficiently large. The method of the proof is based on a careful analysis of the corresponding quadratic form.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Hamiltonians with zero-range interactions are often used in Quantum Mechanics as toy models to describe the low energy behavior of a particle system. The advantage is that zero-range interactions are structurally simple, allow in many cases to make explicit computations and, at least formally, are characterized by a single physical parameter known as two-body scattering length. The mathematical construction of such Hamiltonians as self-adjoint (s.a.) and, possibly, lower bounded operators in a proper Hilbert space requires some care. In the one-body case a complete theory is available [3], while in the n-body case the situation depends on the space dimensions. In dimension one perturbation theory applies and the model is well understood (see, e.g., [4, 16] for recent contributions). In dimension two, using the same kind of boundary condition used in the one-body case, the s.a. and bounded from below Hamiltonian can be constructed [10, 11] and analysed in detail (see, e.g., [15]). On the other hand, in dimension three for \(n=3\) it is known ([18], see also [19]) that the same procedure leads to a symmetric but non s.a. operator. In order to restore self-adjointness one has to specify the behaviour of the wave function close to the triple coincidence point, i.e., where the positions of the three particles coincide. This means that a further three-body boundary condition is required, corresponding to a sort of three-body force acting between the particles. The three-body boundary condition introduced in [18] (see also the recent papers [13, 17] and the references therein) leads to a Hamiltonian unbounded from below which is unsatisfactory from the physical point of view. Such instability property is known as Thomas effect and it is due to the fact that the interaction becomes too singular when all the three particles are close to each other (we just recall that the situation is rather different for systems made of two species of fermions, see, e.g., [8, 9, 20,21,22]).
Following a suggestion contained in [18] (see also [2]), it has been recently proposed ([12, 5, 17, section 9], [13, section 6]) a regularized version of the Hamiltonian for the three-boson system with a different type of three-body boundary condition. Roughly speaking, such boundary condition corresponds to the introduction of an effective scattering length which decreases to zero when the position of two particles coincides and the third particle is close to the common position of the first two. In this sense, one introduces a three-body interaction that reduces to zero the strength of the interaction between two particles when the third particle approaches the common position of the first two.
In this paper we exploit the same idea to construct the Hamiltonian in dimension three for a gas of bosons interacting with an impurity. More precisely, we consider a quantum system of N identical spinless bosons of mass m and we assume that the bosons interact only with an impurity, i.e. a different particle of mass \(m_0\), via a zero-range, two-body interaction. Let us denote by

the Hilbert space of the system. At a formal level, the Hamiltonian reads
where \(\nu \) is a coupling constant and the free Hamiltonian is given by

We want to define a rigorous counterpart of the formal operator (1.2) as a s.a. and bounded from below operator \({\mathcal {H}}\) in  . By definition, such an operator must be a proper singular perturbation of \({\mathcal {H}}_0\) supported on the coincidence hyperplanes
. By definition, such an operator must be a proper singular perturbation of \({\mathcal {H}}_0\) supported on the coincidence hyperplanes

In particular, this means that \({\mathcal {H}}\) must satisfy the property
Motivated by this observation, we define the operator

which is symmetric and closed according to the graph norm of \({\mathcal {H}}_0\). Our goal is to find the Hamiltonian \({\mathcal {H}}\) as a s.a. and bounded from below extension of \(\dot{{\mathcal {H}}}_0\).
A typical class of extensions is obtained by requiring that an element \(\psi \) of the domain of \({\mathcal {H}}\) satisfies the following boundary condition on each hyperplane \(\pi _i\)
for some  , where \(\alpha _0\) is a real parameter and the notation \(\check{{\varvec{x}}}_i\) denotes the omission of the variable \({\varvec{x}}_i\). The boundary condition (1.7) is a natural generalization of the boundary condition satisfied in the one-body case ([3]). The two-body scattering length between the impurity and a boson \({\mathfrak {a}}\) is related to the parameter \(\alpha _0\) via the relation
, where \(\alpha _0\) is a real parameter and the notation \(\check{{\varvec{x}}}_i\) denotes the omission of the variable \({\varvec{x}}_i\). The boundary condition (1.7) is a natural generalization of the boundary condition satisfied in the one-body case ([3]). The two-body scattering length between the impurity and a boson \({\mathfrak {a}}\) is related to the parameter \(\alpha _0\) via the relation
Clearly, the strength of the point interaction between the impurity and a boson goes to zero as  .
.
The s.a. extensions obtained by requiring the boundary condition (1.7) are the same kind of lower-unbounded Hamiltonian studied in [18]. As already mentioned, in order to obtain an energetically stable system, we introduce a suitable regularization in (1.7) meant to handle the singularity associated with the triple-coincidence point. More precisely, we replace the parameter \(\alpha _0\) by a new position dependent coupling constant on each coincidence plane \(\pi _i\)
where the function  is given by
is given by
with \(\gamma >0\) and  an essentially bounded function satisfying
an essentially bounded function satisfying
We observe that assumption (1.10) implies that \(\theta \) is positive in a neighborhood of the origin and it is continuous at zero, with \(\theta (0)=1\). Simple choices for the function \(\theta \) are represented for instance by: the identically constant function \(\theta \equiv 1\); the characteristic function  of the ball of radius b centered at the origin; the decaying exponential function \(\theta (r)=e^{-\frac{r}{b}}\).
of the ball of radius b centered at the origin; the decaying exponential function \(\theta (r)=e^{-\frac{r}{b}}\).
With the above replacement, we define the modified boundary condition
where \(\Gamma ^{i}_{\!\textrm{reg}}\) acts as follows
In analogy with (1.7), the boundary condition (1.11) characterizes the point interaction between the impurity and the i-th boson. The function \(\alpha ({\varvec{x}}_0,{\varvec{x}}_1,\ldots \check{{\varvec{x}}}_i\ldots ,{\varvec{x}}_N)\) diverges if \({\varvec{x}}_j \!\longrightarrow {\varvec{x}}_0\), for any \(j \ne i\) and this means that the strength of the point interaction between the impurity and the i-th boson decreases to zero when a third particle, in our case another boson, approaches the common position of the first two particles. In other words, as already pointed out, we are introducing a three-body interaction meant to regularize the ultraviolet singular behavior occurring when the positions of more than two particles coincide. We also stress that if \(\textrm{supp}\,\theta \) is chosen to be a compact, the usual two-body point interaction between the impurity and the i-th boson is restored when the other particles are far enough.
The aim of this paper is to show that the modified boundary condition (1.11) allows to give a rigorous construction of a s.a. and bounded from below Hamiltonian \({\mathcal {H}}\).
The approach is based on the theory of quadratic forms. More precisely, the starting point of our analysis is a quadratic form in  (see (2.6)) associated to the expectation value of the energy of our system. Such a quadratic form is obtained by exploiting the formal Hamiltonian (1.2) and by imposing the boundary condition (1.11) (the derivation of the quadratic form can be done following the same line of [8]).
(see (2.6)) associated to the expectation value of the energy of our system. Such a quadratic form is obtained by exploiting the formal Hamiltonian (1.2) and by imposing the boundary condition (1.11) (the derivation of the quadratic form can be done following the same line of [8]).
Our main result is the proof that for any \(\gamma \) larger than a threshold value \(\gamma _c\), the quadratic form is closed and bounded from below and therefore uniquely defines a s.a. and bounded from below operator \({\mathcal {H}}\). Furthermore, domain and action of the operator \({\mathcal {H}}\) are explicitly characterized. Such operator, by definition, is our Hamiltonian for the boson gas interacting with an impurity via regularized zero-range interactions.
Let us stress two main points of our analysis. We show that the three-body boundary condition expressed in (1.11) is sufficient to obtain a lower bounded Hamiltonian and no further n-body, \(n>3\), boundary condition is required. Moreover, the threshold value \(\gamma _c\) is explicitly given (see (2.9)) and it is uniformly bounded both in the number of bosons N and the mass ratio \(\frac{m_0}{m}\).
Finally, let us briefly comment on a different method for the construction of lower-bounded n-body Hamiltonians based on the theory of Dirichlet forms ([1]). The method is relatively simple and allows one to define a class of Hamiltonians that are s.a. extensions of the free Hamiltonian restricted to smooth functions vanishing on coincidence hyperplanes. In this sense one surely defines n-body Hamiltonians with (regularized) contact interactions. It can also be shown that the infimum of the spectrum is a preassigned non-positive value. An intrinsic limitation of the method is the fact that the two-body scattering length (i.e., when all the other particles are far enough) must be non-negative. This fact is intuitively clear by analogy with the simple case of a particle subject to a point interaction placed at the origin. But the main point is that the construction of the Hamiltonian is rather implicit and it is not clear which boundary condition the elements of the operator domain satisfy on the coincidence hyperplanes. In other words, the domain of the Hamiltonian is not explicitly characterized and therefore it is not evident what kind of s.a. extension is being constructed.
As a further remark, we observe that the Hamiltonian defined via Dirichlet forms is identified by the choice of a single, non-negative free parameter, whereas our Hamiltonian is determined by the choice of the free parameters \(\alpha \in \mathbb {R}\), \(\gamma >\gamma _c\) and of the specific form of the cut-off function \(\theta \). In this sense, we are dealing with a much wider family of s.a. extensions with respect to [1].
We plan to discuss in detail the comparison between our approach and the one based on Dirichlet forms in a further work.
For the convenience of the reader, we collect here some of the notation used in the paper.
– Given the Euclidean space \((\mathbb {R}^n,\cdot )\), \({\varvec{x}}\) is a vector in \(\mathbb {R}^n\) and \(x=|{\varvec{x}}|\).
– \({\mathcal {S}}(\mathbb {R}^n)\) denotes the space of Schwartz functions.
–  is the Fourier transform of \(\psi \).
is the Fourier transform of \(\psi \).
– For any \(p\ge 1\) and \(\Omega \) open set in \(\mathbb {R}^n\),  is the Banach space of p-integrable functions with respect to the Borel measure \(\mu \). We use
is the Banach space of p-integrable functions with respect to the Borel measure \(\mu \). We use  in case \(\mu \) is the Lebesgue measure and we denote
in case \(\mu \) is the Lebesgue measure and we denote  .
.
– If  is a complex Hilbert space, we denote by
is a complex Hilbert space, we denote by  ,
,  the inner product and the induced norm.
the inner product and the induced norm.
– if  , we simply denote by
, we simply denote by  , \(\Vert \cdot \Vert \) the inner product and the norm.
, \(\Vert \cdot \Vert \) the inner product and the norm.
– \(H^s(\mathbb {R}^n)\) is the standard Sobolev space of order \(s>0\) in \(\mathbb {R}^n\).
– \(f|_{\pi }\in H^s(\mathbb {R}^{dn})\) is the trace of \(f\in H^{s+\frac{d}{2}}(\mathbb {R}^{d(n+1)})\) on the hyperplane \(\pi \) of codimension d.
– \(\mathscr {B}\left( X,Y\right) \) is the Banach space of the linear bounded operators from X to Y, where X and Y are Hilbert spaces, and  .
.
2 Main Results and Strategy of the Proof
In this section we introduce some definitions and we formulate our main results.
Let us define the bounded operator  whose Fourier representation is given by
whose Fourier representation is given by

where \(\lambda >0\) and

denotes the reduced mass of the two-particle subsystem composed of a boson and the impurity. We shall refer to \(G^{\lambda } \xi \) as the potential produced by the charge \(\xi \) distributed on \(\pi \). A more detailed discussion on the properties of the potential is postponed to the appendix (Sect. A.2). Here we only mention that \(G^\lambda \) is injective and  (see Remarks A.2, A.3).
(see Remarks A.2, A.3).
Then we define the following hermitian quadratic form in 

where



We point out that the singularity is contained within the term \(\Phi _{\textrm{off}}\) whereas the regularization is brought by \(\Phi _{\alpha }\). Moreover, consider the following decomposition
with


and
Notice that assumption (1.10) is equivalent to the choice  and therefore the quadratic form \(\Phi _0\) is bounded in
and therefore the quadratic form \(\Phi _0\) is bounded in  . This means that \(\Phi _0\) cannot play any role in compensating the ultraviolet singularity.
. This means that \(\Phi _0\) cannot play any role in compensating the ultraviolet singularity.
We are now in position to define the main object of our analysis, i.e., the quadratic form in  given by
given by

where

We observe that \(\mathscr {D}(Q)\) is an extension of the form domain of \({\mathcal {H}}_0\), since  is a proper subset of \(\mathscr {D}(Q)\) and
is a proper subset of \(\mathscr {D}(Q)\) and

This is due to the injectivity of \(G^\lambda \) that implies \(\psi \in \mathscr {D}(Q) \cap H^1(\mathbb {R}^{3(N+1)})\) if and only if \(\xi \equiv 0\).
Moreover, for any fixed  and \(N\!\ge 2\), we introduce the critical parameter
and \(N\!\ge 2\), we introduce the critical parameter

It is easy to see that \(\gamma _c\) is positive and
In particular, our main results shall hold for any \(\gamma >\gamma _c\). In the special case \(\varsigma =1\), \(N=2\) we have \(\gamma _c(2,1)= \frac{2}{3} - \frac{\sqrt{3}}{\pi } \simeq 0.115\), while in the case of three interacting bosons (discussed in [5]) a larger critical value \(\gamma _c^{\textrm{3 bos}}\! = \frac{4}{3} - \frac{\sqrt{3}}{\pi } \simeq 0.782\) is found. The difference is due to the fact that, in our case, the two bosons are non-interacting and therefore the singular negative contribution to be compensated, given by (2.4b), is smaller by a factor 2. Moreover, we observe that the Born-Oppenheimer regime is achieved when \(\varsigma \) is chosen small enough, since the positions of the N bosons would be approximately fixed with respect to the impurity which would play the role of a light particle. In particular one would have 
Our first result concerns the quadratic form \(\Phi ^{\lambda }\) and it is formulated in the next proposition.
Proposition 2.1
-
i)
For any \(\gamma >0\) and \(\lambda >0\) one has
$$\begin{aligned} \Phi ^{\lambda }[\xi ] \,\le \, C_1 \, \Phi ^\lambda _{\textrm{diag}} [\xi ], \qquad \xi \in H^{\frac{1}{2}}(\mathbb {R}^{3N}) \end{aligned}$$(2.10)where \(C_1\) is a positive constant.
-
ii)
Let us assume \(\gamma >\gamma _c\). Then, there exists \(\lambda _0>0\) s.t. for any \(\lambda >\lambda _0\) one has
$$\begin{aligned} C_2\, \Phi ^\lambda _{\textrm{diag}}[\xi ] \, \le \, \Phi ^{\lambda }[\xi ], \qquad \xi \in H^{\frac{1}{2}}(\mathbb {R}^{3N}) \end{aligned}$$(2.11)where \(C_2\) is a positive constant. In particular, the quadratic form \(\Phi ^{\lambda }\), \(\mathscr {D}(\Phi ^{\lambda })\) in
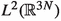 is closed and bounded from below by a positive constant.
is closed and bounded from below by a positive constant.
Proposition 2.1 implies that \(\Phi ^\lambda \) uniquely defines a s.a. and invertible operator \(\Gamma ^\lambda \) in  for any \(\lambda >\lambda _0\), as long as \(\gamma >\gamma _c\).
for any \(\lambda >\lambda _0\), as long as \(\gamma >\gamma _c\).
Using the above proposition, we can prove our main result.
Theorem 2.2
Let us assume \(\gamma >\gamma _c\). Then, the quadratic form Q, \(\mathscr {D}(Q)\) in  is closed and bounded from below. In particular, \(Q>-\lambda _0\). Moreover, the self-adjoint and bounded from below operator \({\mathcal {H}}\), \(\mathscr {D}({\mathcal {H}})\) uniquely defined by Q, \(\mathscr {D}(Q)\) is characterized as follows
is closed and bounded from below. In particular, \(Q>-\lambda _0\). Moreover, the self-adjoint and bounded from below operator \({\mathcal {H}}\), \(\mathscr {D}({\mathcal {H}})\) uniquely defined by Q, \(\mathscr {D}(Q)\) is characterized as follows
The resolvent  is given by
is given by

where  ,
,  and \(\xi \in \mathscr {D}(\Gamma ^\lambda )\) solves the equation
and \(\xi \in \mathscr {D}(\Gamma ^\lambda )\) solves the equation

Some comments are in order.
For any \(\psi \in \mathscr {D}({\mathcal {H}})\) vanishing in a neighborhood of the hyperplanes \(\pi \) we have \(\xi \equiv 0\) and then the action of \({\mathcal {H}}\) reduces to the action of the free Hamiltonian.
Moreover, one can verify that any \(\psi =w^\lambda +G^\lambda \xi \!\in \mathscr {D}({\mathcal {H}})\) satisfies the boundary condition (1.11) at least in the weak sense. Indeed, let us denote \({\varvec{r}}= {\varvec{x}}_N- {\varvec{x}}_0\), \({\varvec{R}}= \tfrac{m{\varvec{x}}_N + m_0{\varvec{x}}_0}{m+m_0}\) and fix any \(g \in {\mathcal {S}}(\mathbb {R}^{3N})\). Then we have

where we have used the equation \(w^{\lambda }|_{\pi _N}\!=\tfrac{\mu }{2\pi N} \Gamma ^\lambda \xi \) required in \(\mathscr {D}({\mathcal {H}})\), the expansion of the potential (A.21) and the explicit expression of the bilinear form  in terms of \(\,\Gamma _{\!\textrm{diag}}^{N,\lambda }\) and \(\Gamma _{\!\textrm{off}}^{N,\lambda }\) (see equations (A.18),(A.20)).
in terms of \(\,\Gamma _{\!\textrm{diag}}^{N,\lambda }\) and \(\Gamma _{\!\textrm{off}}^{N,\lambda }\) (see equations (A.18),(A.20)).
The above considerations show that the Hamiltonian constructed in the theorem is a rigorous version of the formal Hamiltonian discussed in the introduction.
Concerning the lower bound \(-\lambda _0\) of the quadratic form Q (and then of the infimum of the spectrum of \({\mathcal {H}}\)), in the proof of proposition 2.1 we explicitly find (see Sect. 6)
where

We notice that \(\Lambda _\gamma \longrightarrow 1\) for \(\gamma \longrightarrow \gamma _c^+\) for any choice of \(N\ge 2\) and \(\varsigma >0\) and therefore we have \(-\lambda _0 \longrightarrow {\scriptstyle -}\infty \) for \(\gamma \longrightarrow \gamma _c^+\).
Let us describe the strategy of the proof. We stress that the main technical point is the estimate from below of \(\Phi ^{\lambda }\) (see proposition 2.1) which is obtained through various steps.
In Sect. 3 we rewrite the quadratic form \(\Phi ^{\lambda }\) in  in terms of the quadratic form \(\Theta ^{\zeta }\) in
in terms of the quadratic form \(\Theta ^{\zeta }\) in  (see (3.5), (3.6) and (3.7)), that is of the type studied in [5, section 3] for the three-particle case. Then we expand the quadratic form \(\Theta ^{\zeta }\) in partial waves and recall some known results on the terms of the expansion \(F_\ell ^{\,\zeta }\), \(\ell \in \mathbb {N}_0\).
(see (3.5), (3.6) and (3.7)), that is of the type studied in [5, section 3] for the three-particle case. Then we expand the quadratic form \(\Theta ^{\zeta }\) in partial waves and recall some known results on the terms of the expansion \(F_\ell ^{\,\zeta }\), \(\ell \in \mathbb {N}_0\).
In Sect. 4 we prove some key estimates useful to control \(F_\ell ^{\,\zeta }\). We stress that we perform a careful analysis for each value of \(\ell \in \mathbb {N}_0\) that leads to a detailed control of the lower bound. In particular, the result of lemma 4.1 allows us to prove proposition 2.1 by introducing the threshold value \(\gamma _c\) that is uniformly bounded in \(\varsigma >0\) and \(N\ge 2\).
It is worth to mention that an analogous control is required in the three-boson case ([5, lemma 3.5]) in which case it is sufficient to study only the case \(\ell =0\) and to control higher momenta in terms of the \(\ell =2\) contribution. Such a strategy is not sufficient in the present case since it would force us to assume a further ad hoc constraint on \(\varsigma \) (depending on N). Owing to the new techniques developed in Sect. 4 we are able to avoid this problem and to remove such a technical constraint.
In Sect. 5 we use the above results to obtain the estimate from below of \(\Theta ^{\zeta }\) (see (5.1)).
In Sect. 6 we conclude the proof of proposition 2.1 and, following a standard procedure, we also prove theorem 2.2.
In the appendix we collect some useful technical results.
3 Reduction to a Three-Body Problem and Partial Wave Decomposition
We start the study of \(\Phi ^\lambda \), defined by (2.3), introducing suitable changes of variables that reduce the analysis to a quadratic form of the type studied in [5, section 3] for the three-particle case. In the end we shall prove that \(\mathscr {D}(\Phi ^{\lambda })=H^{\frac{1}{2}}(\mathbb {R}^{3N})\).
Let \(\eta \) be the modified reduced mass of the system

and set \(\tilde{{\varvec{k}}} = ({\varvec{k}}_1,\ldots ,{\varvec{k}}_{N-1})\). Then, we denote for short

In the next lemma we rewrite \(\Phi ^{\lambda }\) in terms of  .
.
Lemma 3.1
For any \(\xi \in H^{\frac{1}{2}}(\mathbb {R}^{3N})\) and  given by (3.2) one has
given by (3.2) one has

The proof is easily obtained by the change of coordinates dictated by definition (3.2), once the regularizing term has been written in its Fourier representation via the identity

Formula (3.3) suggests to define the hermitian quadratic form \(\Theta ^{\zeta }\), for \(\zeta \ge 0\), with

where, for a given \(\varphi \in H^{\frac{1}{2}}(\mathbb {R}^3)\),



Observe that

where \(\phi \) is given by (3.2). Equation (3.7) shows that the analysis of \(\Phi ^{\lambda }\) in  can be reduced to the analysis of \(\Theta ^{\zeta }\) in
can be reduced to the analysis of \(\Theta ^{\zeta }\) in  .
.
The following estimate from above of \(\Theta ^{\zeta }\) is proved in [5, proposition 3.1].
Proposition 3.2
Given \(\varphi \in H^{\frac{1}{2}}(\mathbb {R}^{3})\), \(\gamma >0\) and \(\zeta \ge 0\), there exists \(C>0\) such that
Taking into account (3.7) and the above proposition, it is easy to obtain the upper bound for \(\Phi ^{\lambda }\) and therefore the proof of point i) of proposition 2.1.
From now on we shall concentrate on the lower bound for \(\Theta ^{\zeta }\) and then for \(\Phi ^{\lambda }\).
In order to establish a lower bound for \(\Theta ^{\zeta }\), it is convenient to study the quadratic form decomposed in partial waves. Given  , one has
, one has

Here,  denotes the Spherical Harmonic of order \(\ell , \textrm{m}\), while \((p, \hat{{\varvec{\omega }}})\in \mathbb {R}_{+}\!\times {\mathbb {S}}^2\) represents \({\varvec{p}}\in \mathbb {R}^3\) in spherical coordinates and
denotes the Spherical Harmonic of order \(\ell , \textrm{m}\), while \((p, \hat{{\varvec{\omega }}})\in \mathbb {R}_{+}\!\times {\mathbb {S}}^2\) represents \({\varvec{p}}\in \mathbb {R}^3\) in spherical coordinates and  are the Fourier coefficients of
are the Fourier coefficients of  . We shall also denote by \(P_\ell (y)=\frac{1}{2^\ell \ell !}\frac{\textrm{d}^\ell }{\textrm{d}y^\ell }(y^2-1)^\ell \) the Legendre polynomial of degree \(\ell \in \mathbb {N}_0\). Accordingly, we decompose the quadratic form \(\Theta ^{\zeta }\) for any \(\zeta \ge 0\)
. We shall also denote by \(P_\ell (y)=\frac{1}{2^\ell \ell !}\frac{\textrm{d}^\ell }{\textrm{d}y^\ell }(y^2-1)^\ell \) the Legendre polynomial of degree \(\ell \in \mathbb {N}_0\). Accordingly, we decompose the quadratic form \(\Theta ^{\zeta }\) for any \(\zeta \ge 0\)


As usual, we consider the three-components

each of which is described in the following lemma, proved in [8, lemma 3.1].
Lemma 3.3
For any  , taking into account decomposition (3.10) and definition (3.12), we have the following expressions for any \(\zeta \ge 0,\, \ell \in \mathbb {N}_0\)
, taking into account decomposition (3.10) and definition (3.12), we have the following expressions for any \(\zeta \ge 0,\, \ell \in \mathbb {N}_0\)



In the following, we recall some known results concerning \(F^{\,\zeta }_\ell \). The first one characterizes the sign of \(F^{\,\zeta }_{\textrm{off};\,\ell }\) (see [8, lemma 3.3])
Moreover, the same procedure can be adapted to obtain \(F_{\textrm{reg};\,\ell }\ge 0\) for all \(\ell \in \mathbb {N}_0\).
Notice that, thanks to the previous estimates, for the sake of a lower bound, we can neglect \(F^{\,\zeta }_{\textrm{off};\,\ell }\) with \(\ell \) odd and focus on \(F^{0}_{\textrm{off};\,\ell }\) that represents a lower estimates for \(F^{\,\zeta }_{\textrm{off};\,\ell }\) in case \(\ell \) is even. A further useful result concerns the diagonalization of \(F^{0}_\ell \) (see [8, lemma 3.4] and [5, lemma 3.4]). Given  , let
, let  be defined by
be defined by

Then, considering the quantities computed in lemma 3.3, one has



where


Moreover,
and
4 A Key Estimate
In the following, we obtain an estimate useful to control \(F^{\,\zeta }_{\ell }\). To this end, let us introduce some further notation. For any \(a\in \mathbb {C}\) and \(n\in \mathbb {N}_0\), let \((a)_n\) be the Pochhammer symbol, also known as rising factorial, given by

It is easy to see that for any \(n\in \mathbb {N}_0\)
In particular, notice that if \(a\in -\mathbb {N}_0\), then \((a)_n=0\) for all \(n>|a|\). Next, we recall the definition of the Gauss hypergeometric function
Representation (4.2) is well defined for \(a,b\in \mathbb {C}\), \(c\in \mathbb {C}\smallsetminus -\mathbb {N}_0\) and its radius of convergence is 1. However, if a or b is a non-positive integer, then the Gauss hypergeometric function reduces to a polynomial in z. In this case, c can also assume non-positive integer values, provided that \(|c|\) is greater than or equal to the degree of the polynomial. We also remind the Gauss’ summation theorem
In the following lemma we give the explicit computation of the integrals appearing in \( S_{\textrm{off};\,\ell }\) and \( S_{\textrm{reg};\,\ell }\) for \(\ell \) even (see (3.17a), (3.17b)).
Now, let \(\Xi ^{\,\zeta }_{\ell ,\,s_\ell }\) be a sequence of auxiliary quadratic forms defined on  for any given \(\ell \in \mathbb {N}_0\) and for some parameter \(s_\ell \in (0,1)\) as follows
for any given \(\ell \in \mathbb {N}_0\) and for some parameter \(s_\ell \in (0,1)\) as follows

These quadratic forms will be useful to obtain a lower bound for \(F^{\,\zeta }_\ell \).
The next lemma is the key technical ingredient for the proof of proposition 2.1.
Lemma 4.1
Let  and \(\gamma _c\) given by (2.9). Then, for \(\gamma >\gamma _c\,\), there exists \(\{s^*_\ell \}_{\ell \in \mathbb {N}_0}\! \subset \!(0,1)\) such that each quadratic form \(\Xi ^{\,\zeta }_{\ell ,\,s^*_\ell }\) defined by (4.4), is non-negative for any \(\zeta \ge 0\) and \(\ell \in \mathbb {N}_0\).
and \(\gamma _c\) given by (2.9). Then, for \(\gamma >\gamma _c\,\), there exists \(\{s^*_\ell \}_{\ell \in \mathbb {N}_0}\! \subset \!(0,1)\) such that each quadratic form \(\Xi ^{\,\zeta }_{\ell ,\,s^*_\ell }\) defined by (4.4), is non-negative for any \(\zeta \ge 0\) and \(\ell \in \mathbb {N}_0\).
Proof
Taking into account the diagonalization given in (3.16), one has

The lemma is proved if we show that for each order \(\ell \), there exists \(s_\ell \in (0,1)\) such that the function \(f^N_{\ell ,\,s_\ell }\) is non-negative uniformly in \(N\ge 2\). Notice that this is actually the case for \(\ell \) odd, in light of (3.18), so from now on we focus on the case \(\ell \) even.
Moreover we have

We notice that \(S_{\textrm{off};\,\ell }\) and \(S_{\textrm{reg};\,\ell }\), and then \( f^{N}_{\ell ,\,s_\ell }\), are written in terms of the Gauss hypergeometric function \({}_{2}F_1\) (see (3.17a), (3.17b) and proposition A.1) and therefore the main point is a careful control of such a function.
The proof will be constructed in two steps: first we show that \(f^N_{\ell ,\,s_\ell }\) evaluated at zero is positive uniformly in \(N\ge 2\) for a proper choice of \(\{s_\ell \}_{\ell \in \mathbb {N}_0}\subset (0,1)\), then we prove that \(f^N_{\ell ,\,s_\ell }\) is bounded from below by a monotonic function \(h^N_{\ell ,\,s_\ell }\) that shares the same values with \(f^N_{\ell ,\,s_\ell }\) at zero and infinity. Once these statements are proven, we will have \(f^N_{\ell ,\,s_\ell }\ge h^N_{\ell ,\,s_\ell }>0\) as long as \(s_\ell \) is such that \(f^N_{\ell ,\,s_\ell }(0)>0\) for all \(\ell \in \mathbb {N}_0\) and uniformly in \(N\ge 2\).
Step 1. We observe that \(f^N_{\ell ,\,s_\ell }(0)\) is positive if and only if

The requirement \(s_\ell \in (0,1)\) implies a constraint for the parameter \(\gamma \), since we need the right hand side of (4.5) to be strictly less than 1. Therefore

Let us show that
Taking into account equations (A.10) and (A.11), condition (4.6) reads
with


We observe that \(\gamma ^\ell _{\varsigma ,2}\) is increasing in \(\ell \), since
Therefore
Let us consider \(\gamma ^\ell _{\varsigma ,1}\). Using the Euler’s integral representation of the Gauss hypergeometric function

one has for any \(x\in [0,1]\)

Exploiting the trivial inequality \(1-u^2\le 1-x^2u^2\), we obtain an estimate from above

where equality holds if \(\ell =0 \vee x=1\). From (4.12) one gets

where equality holds if \(\ell =0\vee \varsigma =0\). Hence, in particular we know that
In the following computations we set \(x=\frac{1}{\varsigma +1}\) for the sake of notation. Let us prove that \(\left\{ {\bar{\gamma }}^\ell _\varsigma \right\} _{\ell \in 2\mathbb {N}_0}\) is a decreasing sequence for all fixed \(\varsigma >0\). We have

Our goal is to show that the last integral is positive for any given \(x\in (0,1)\) and \(\ell \) even, so that \({\bar{\gamma }}^{\ell +2}_\varsigma \!<{\bar{\gamma }}^\ell _\varsigma \). To this end, we first point out that the integral is manifestly positive at \(x=0\), whereas the evaluation of the integral at \(x=1\) yields

We observe that, in order to obtain \(\inf \!\left\{ {\bar{\gamma }}^\ell _\varsigma -{\bar{\gamma }}^{\ell +2}_\varsigma \,|\;\varsigma >0\right\} \!\ge 0\) for any \(\ell \) even, it is sufficient to prove that the integral is a monotonic decreasing function in x. In other words, we want to show

By the Leibniz integral rule, the derivative with respect to x can be computed inside the integral. Therefore, for any \(x\in (0,1), u\in [0,1]\) and \(\ell \) even, one has
Since the integral of a negative function obviously yields a negative quantity, (4.15) is proven. This means that \(\left\{ {\bar{\gamma }}^\ell _\varsigma \right\} _{\ell \in 2\mathbb {N}_0}\!\) is decreasing for any fixed \(\varsigma >0\). Thus, taking into account (4.13) and (4.14), we finally get
Hence, thanks to (4.10), equation (4.7) is proved.
Step 2. Let us define the following function
where \(\gamma ^\ell _{\varsigma ,1}\) has been defined in (4.8). We shall prove that \(h^N_{\ell ,\,s_\ell }\) satisfies




Starting with (4.17a), we take into account proposition A.1 and equation (A.8) to obtain an explicit expression for \(f^N_{\ell ,\,s_\ell }\)
where we have introduced, for the sake of notation, the function
To achieve the result, consider the Euler’s transformation formula
and the inequality
Indeed, one can write
where we have used inequality (4.21), according to which
Using again (4.20) to the right hand side, one obtains
Making use of identity (A.7) in the previous inequality, one has
Exploiting this lower bound in (4.18), one finds out that \(h^N_{\ell ,\,s_\ell }\) satisfies condition (4.17a). Furthermore, we stress that we have obtained this estimate by using only inequality (4.21), according to which the equality sign holds in case \(p=0\). In other words, we have also proved (4.17b).
Next, we show (4.17c). Since \(\frac{p^2+(2k-1)^2}{p^2+4k^2}<1\) for all k,
where the right hand side vanishes as p goes to infinity. Therefore,

It remains to prove the monotonicity of \(h^N_{\ell ,\,s_\ell }\) in \(\mathbb {R}_{+}\). In particular, it suffices to show that the function
is decreasing in \(\mathbb {R}_{+}\). Let us remind the product representation of the hyperbolic tangent
Denoting \(z=\frac{\pi }{2}p\), one has
In order to prove that the function (4.23) is decreasing, we consider
We notice that for \(p>0\)
Hence, (4.25) is decreasing in \(p>0\) since it is a sum of decreasing functions. Therefore, also (4.23) is decreasing and (4.17d) is proven.
In conclusion, we know that whenever \(\gamma >\gamma _c\), there exists \(s^*_\ell \in (0,1)\) for any \(\ell \in \mathbb {N}_0\), such that \(f^N_{\ell ,\,s^*_\ell }(0)> 0\) uniformly in \(N\ge 2\). Since we also know that \(f^N_{\ell ,\,s_\ell }\) is eventually positive, conditions (4.17) imply that \(f^N_{\ell ,\,s^*_\ell }\ge h^N_{\ell ,\,s^*_\ell }\!> 0\) and the proof is completed. \(\square \)
Remark 4.1
In lemma 4.1, we have shown that, if \(\gamma \ge \gamma ^\ell _{\varsigma ,1}\), any \(s^*_\ell \in (0,1)\) is such that \(f^N_{\ell ,\,s^*_\ell }\ge 0\), whereas in case \(\gamma \in \!\left( \gamma _c,\,\gamma ^\ell _{\varsigma ,1}\right) \!,\) the function \(f^N_{\ell ,\,s^*_\ell }\) is still non negative for all \(s^*_\ell \) s.t.
Notice that the lower bound is non-increasing in \(\ell \), hence the sequence \(\{s^*_\ell \}\) that makes \(\Xi ^{\,\zeta }_{\ell ,\,s^*_\ell }\) non-negative for all \(\zeta \ge 0\) and \(\ell \in \mathbb {N}_0\) can be chosen within an interval that does not depend on \(\ell \), namely
5 Lower Bound for \(\,\Theta ^{\zeta }\)
Collecting the results obtained in the previous two sections, we can now establish detailed estimates for \(\Theta ^{\zeta }\). Indeed, in the next proposition we prove a lower bound, which is the crucial ingredient for the proof of our main results.
Proposition 5.1
Given \(\varphi \in H^{\frac{1}{2}}(\mathbb {R}^{3})\) and \(\zeta \ge 0\), we have
where \(\Lambda _\gamma \) is defined in (2.16).
Proof
Let \(\varphi \!\in \! H^{\frac{1}{2}}(\mathbb {R}^{3})\) and consider decomposition (3.10) and estimates (3.14). Then,

Taking account of definition (4.4), for any choice of \(\{s_\ell \}_{\ell \in \mathbb {N}_0}\!\subset \!(0,1)\), the previous inequality reads

According to lemma 4.1, there exists a sequence \(\{s^*_\ell \}_{\ell \in \mathbb {N}_0}\!\subset \! (0,1)\) such that \(\Xi ^{\,\zeta }_{\ell ,\,s^*_\ell }\ge 0\), hence

where, according to remark 4.1, each \(s^*_k\) can be arbitrarily chosen within an interval in (0, 1) that does not shrink as k varies. Exploiting this fact, we can optimize the inequality by choosing
so that \(\Theta ^{\zeta }[\varphi ]\ge (1-\Lambda _\gamma )\,\Theta ^{\zeta }_{\textrm{diag}}[\varphi ]\). \(\square \)
6 Proof of the Main Result
In this section we complete the proof of the results stated in Sect. 2.
Proof of point ii) of proposition 2.1
Let us recall that, for any charge \(\xi \in H^{\frac{1}{2}}(\mathbb {R}^{3N})\), we have defined a rescaled charge \(\phi \in H^{\frac{1}{2}}(\mathbb {R}^{3N})\) given by (3.2). According to equations (3.7) and (5.1), we can deduce a lower bound for the quadratic form \(\Phi ^\lambda \)

Recalling definition (2.4e) and assumption (1.10) (which implies \(\beta \) essentially bounded), we have

Collecting the results obtained so far, we get
The last expression is positive if \(\lambda \) is large enough, i.e. if \(\lambda >\lambda _0\), with

\(\square \)
The estimate (6.1) guarantee that \(\Phi ^\lambda \) is closed and bounded from below by a positive constant whenever \(\lambda >\lambda _0\). Then, if \(\gamma >\gamma _c\), the quadratic form \(\Phi ^\lambda \) uniquely defines a s.a. and positive operator \(\Gamma ^\lambda \) in  for all \(\lambda >\lambda _0 \). Such operator is characterized as follows
for all \(\lambda >\lambda _0 \). Such operator is characterized as follows

where \(\Phi ^\lambda [\cdot , \cdot ]\) is the sesquilinear form associated to \(\Phi ^\lambda [ \cdot ]\) via the polarization identity. Moreover, \(\Gamma ^\lambda \) is invertible for all \(\lambda >\lambda _0\).
We are now in position to conclude the proof of theorem 2.2.
Proof of theorem 2.2
Taking into account proposition 2.1, Q is bounded from below, since for any \(\psi \in \mathscr {D}(Q)\), one has

Now, let us fix \(\lambda >\lambda _0\). By construction Q is hermitian, hence, the associated sesquilinear form \(Q[ \cdot ,\cdot ]\) is symmetric. In particular, this means that the sesquilinear form \(s[ \cdot ,\cdot ]\) given by

defines a scalar product in  . Therefore, we equip
. Therefore, we equip  with the norm
with the norm

We prove that Q is closed by showing the completeness of \(\mathscr {D}(Q)\) with respect to  . To this end, let \(\{\psi _n\}\subset \mathscr {D}(Q)\) and
. To this end, let \(\{\psi _n\}\subset \mathscr {D}(Q)\) and  be respectively a sequence and a vector s.t.
be respectively a sequence and a vector s.t.  as n, m go to infinity and
as n, m go to infinity and  . By (6.3), we have
. By (6.3), we have
and, since both \({\mathscr {F}}_\lambda \) and \(\Phi ^\lambda \) are closed and positive, (6.4) means

Hence, \(\{w^\lambda _n\}\) and \(\{\xi _n\}\) are Cauchy sequences in  and
and  , respectively. Thus, there exist
, respectively. Thus, there exist  and
and  such that
such that

Furthermore, since \(G^\lambda \) defined in (2.1) is bounded for all \(\lambda >0\), one has that \(\psi _n=w^\lambda _n+G^\lambda \xi _n\) converges in  to the vector \(w^\lambda +G^\lambda \xi \). By uniqueness of the limit, \(\psi =w^\lambda +G^\lambda \xi \) and thus, \(\psi \in \mathscr {D}(Q)\). We have shown that
to the vector \(w^\lambda +G^\lambda \xi \). By uniqueness of the limit, \(\psi =w^\lambda +G^\lambda \xi \) and thus, \(\psi \in \mathscr {D}(Q)\). We have shown that  is a Banach space, hence Q is closed.
is a Banach space, hence Q is closed.
The quadratic form Q uniquely defines a s.a. and bounded from below Hamiltonian \({\mathcal {H}}\), \(\mathscr {D}({\mathcal {H}})\) in the Hilbert space  . In order to characterize domain and action of \({\mathcal {H}}\), let us assume that \(\psi =w^\lambda +G^\lambda \xi \in \mathscr {D}({\mathcal {H}})\), with \(\lambda >\lambda _0\). Then, there exists
. In order to characterize domain and action of \({\mathcal {H}}\), let us assume that \(\psi =w^\lambda +G^\lambda \xi \in \mathscr {D}({\mathcal {H}})\), with \(\lambda >\lambda _0\). Then, there exists  such that the sesquilinear form \(Q[\cdot ,\cdot ]\) associated to \(Q[\cdot ]\) via the polarization identity satisfies
such that the sesquilinear form \(Q[\cdot ,\cdot ]\) associated to \(Q[\cdot ]\) via the polarization identity satisfies

where  . By definition one has
. By definition one has

Let us consider  , so that \(\xi _v\equiv 0\) by injectivity of \(G^\lambda \). Then
, so that \(\xi _v\equiv 0\) by injectivity of \(G^\lambda \). Then

Hence,  and
and
which is equivalent to
Now, let \(v\in \mathscr {D}(Q)\). Taking account of (6.7), we have

On the other hand, recalling (6.5) and (6.6),

hence,

where we have used (A.13) in the last step. Therefore, we conclude that \(\xi \in \mathscr {D}(\Gamma ^\lambda )\) and the boundary condition \(\Gamma ^\lambda \xi =\frac{2\pi N}{\mu } \,w^\lambda \big |_{\pi _N}\) holds.
Concerning the resolvent, given  , one has
, one has  since, by definition,
since, by definition,  with
with  and \(\xi \) satisfies (2.14). Therefore, by an explicit application of the Hamiltonian one has
and \(\xi \) satisfies (2.14). Therefore, by an explicit application of the Hamiltonian one has

On the other hand, let \(\psi =w^\lambda +G^\lambda \xi \in \mathscr {D}({\mathcal {H}})\). One has

with  satisfying
satisfying

Since \(\xi \) satisfies the same equation and, for any \(\lambda >\lambda _0\) the operator \(\Gamma ^\lambda \) is invertible, we have found \(\chi =\xi \). Hence  . \(\square \)
. \(\square \)
We conclude this section observing that the proof of theorem 2.2, and then the construction of the Hamiltonian, has been obtained following an approach which, in our opinion, is concrete and intuitive. Nevertheless, we mention that an equivalent more abstract approach could be adopted to construct the Hamiltonian, given the result of proposition 2.1. Indeed, according to [23] (see also [7, theorem 2.19]) one can prove that any s.a. extension of \(\dot{{\mathcal {H}}}_0\) is characterized by

provided \(\textrm{Im}\,z=0\,\vee \, \phi _z\!\perp G^{-z}\xi \), for any linear map  such that
such that  is a densely defined operator for any z and satisfies
is a densely defined operator for any z and satisfies



Moreover, demanding the lower semi-boundedness of \({\mathcal {H}}_\Gamma \) means requiring an additional condition on the map \(\Gamma \). More precisely, a sufficient condition is \(\Gamma (\textrm{x})>0\) for all \(\textrm{x}<\textrm{x}_0<0\) that implies \({\mathcal {H}}_\Gamma \ge \textrm{x}_0\). Clearly, in this framework the goal is to determine the proper choice of the map \(\Gamma \) that encodes the regularization described in the introduction. In our case we have
More details involving this abstract setting are discussed in [6].
Data Availability
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
References
Albeverio, S., Høegh-Krohn, R., Streit, L.: Energy forms, Hamiltonians, and distorted Brownian paths. J. Math. Phys. 18, 907–917 (1977)
Albeverio, S., Høegh-Krohn, R., Wu, T.T.: A class of exactly solvable three-body quantum mechanical problems and the universal low energy behavior. Phys. Lett. 83A(3), 105–109 (1981)
Albeverio, S., Gesztesy, F., Høegh-Krohn, R., Holden, H.: Solvable Models in Quantum Mechanics - 2nd edition. AMS Chelsea Publishing, (2005)
Basti, G., Cacciapuoti, C., Finco, D., Teta, A.: The three-body problem in dimension one: from short-range to contact interactions. J. Math. Phys. 59, 072104 (2018)
Basti, G., Cacciapuoti, C., Finco, D., Teta, A.: Three-body Hamiltonian with regularized zero-range interactions in dimension three. Ann. Henri Poincarè. 24, 223–276 (2023)
Behrndt, J., Hassi, S., de Snoo, H.: Boundary Value Problems, Weyl Functions, and Differential Operators. Birkhäuser Switzerland Springer (2020)
Cacciapuoti, C., Fermi, D., Posilicano, A.: On inverses of Kreĭn’s \({\mathscr {Q}}\)-functions. Rend. Mat. Appl. 39, 229–240 (2018)
Correggi, M., Dell’Antonio, G., Finco, D., Michelangeli, A., Teta, A.: Stability for a system of N fermions plus a different particle with zero-range interactions. Rev. Math. Phys. 24, 1250017 (2012)
Correggi, M., Dell’Antonio, G., Finco, D., Michelangeli, A., Teta, A.: A Class of Hamiltonians for a Three-Particle Fermionic System at Unitarity. Math. Phys., Anal. and Geom., 18, 32, (2015)
Dell’Antonio, G. F., Figari, R., Teta, A.: Hamiltonians for systems of N particles interacting through point interactions. Ann. Inst. H. Poincare, Phys. Theor., 60, 253–290, (1994)
Dimock, J., Rajeev, S.G.: Multi-particle Schrödinger operators with point interactions in the plane. J. Phys. A 37, 9157–9173 (2004)
Figari, R., Teta, A.: On the Hamiltonian for three bosons with point interactions. In: Hilbert, A., Mastrogiacomo, E., Mazzucchi, S., Rudiger, B., Ugolini, S. (eds.) Quantum and Stochastic Mathematical Physics. Sergio Albeverio, Adventures of a Mathematician, vol. 377, p. 141–159. Springer Proceedings in Mathematics & Statistics, Springer (2023)
Gallone, M., Michelangeli, A.: Self-adjoint extension schemes and modern applications to quantum Hamiltonians. arXiv:2201.10205 [math-ph] Cited 25 Jan (2022)
Gradshteyn, I. S., Ryzhik, I. M.: Table of Integrals, Series, and Products - 7th edition. Academic Press, (2007)
Griesemer, M., Hofacker, M.: From Short-Range to Contact Interactions in Two-dimensional Many-Body System. Ann. Henri Poincare 23(8), 2769–2818 (2022)
Griesemer, M., Hofacker, M., Linden, U.: From short-range to contact interactions in the 1d Bose gas. Math. Phys., Anal. Geom., 23, 19, (2020)
Michelangeli, A.: Models of zero-range interaction for the bosonic trimer at unitarity. Rev. Math. Phys. 33, 2150010 (2021)
Minlos, R.A., Faddeev, L.: On the point interaction for a three-particle system in Quantum Mechanics. Soviet Phys. Dokl. 6, 1072–1074 (1962)
Minlos, R.A., Faddeev, L.: Comment on the problem of three particles with point interactions. Soviet Phys. Jetp. 14, 1315–1316 (1962)
Moser, T., Seiringer, R.: Triviality of a model of particles with point interactions in the thermodynamic limit. Lett. Math. Phys. 107, 533–552 (2017)
Moser, T., Seiringer, R.: Stability of a fermionic N + 1 particle system with point interactions. Comm. Math. Phys. 356, 329–355 (2017)
Moser, T., Seiringer, R.: Stability of the 2 + 2 fermionic system with point interactions. Math. Phys., Anal. Geom., 21, 19, (2018)
Posilicano, A.: A Krein-like formula for singular perturbations of self-adjoint operators and applications. J. Funct. Anal. 183, 109–147 (2001)
Funding
Open access funding provided by Università degli Studi di Roma La Sapienza within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Contributions
The contribution of the two authors to the elaboration and writing of the manuscript is equal
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no competing interests.
Additional information
Communicated by Petr Siegl
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The authors acknowledge the support of the GNFM Gruppo Nazionale per la Fisica Matematica—INdAM.
This article is part of the topical collection “Spectral Theory and Operators in Mathematical Physics” edited by Jussi Behrndt, Fabrizio Colombo and Sergey Naboko.
Appendix A
Appendix A
1.1 Some Useful Identities
Proposition A.1
For any \(x\in [0,1], p\in \mathbb {R}\) and \(\ell \) even we have

Proof
First let \(z\in (-1,1)\) and take into account [14, p. 1007, 9.121.32], so that
where the last identity is given by the following simple computations
Notice that (A.3) is a particular case of the Legendre’s duplication formula
Using the Rodrigues’ formula for \(P_\ell \) and integrating by parts \(\ell \) times, one gets

By (A.1), the function \(y\longmapsto \frac{\cosh [p\arcsin (xy)]}{\sqrt{1-x^2y^2}}\) is analytic in \((-1,1)\) for all \(x\in [0,1]\) and \(p\in \mathbb {R}\), thus one can compute the \(\ell \)-th derivative:
where we have set \(a_k(p^2):=\prod _{n=1}^k [p^2\!+ (2n-1)^2]\) for the sake of notation. Using Tonelli’s theorem to interchange the integral with the summation, one obtains

The last integral can be explicitly computed, namely

where in the last equality we have used (A.4). Therefore,

Using (A.3) and (A.2), the last expression can be rewritten in terms of the Pochhammer symbols

By definition (4.1a), one has
hence

Using again (A.2), (A.3) and definition (4.2) one concludes the proof. \(\square \)
Remark A.1
We point out that the integral evaluated in proposition A.1 considerably simplifies in case \(x=1\) or \(p=0\). Indeed, making use of (4.3) and (A.3), one gets in case \(x=1\)

Now, exploiting the identity
one obtains

Let us consider the case \(p=0\). Taking into account that
where \((\cdot )!!\) denotes the double factorial, i.e.

one obtains

In the special case \(x=1\) and \(p=0\), one has

where we have used (4.3) and (A.3).
1.2 Properties of the Potential
Denote by  the “charge” associated to \(\pi _i\). Since the particles interacting with the impurity are all indistinguishable with each other, all the charges must be equal, namely \(\xi _i({\varvec{x}}_0,{\varvec{x}}_1,\ldots \check{{\varvec{x}}}_i\ldots ,{\varvec{x}}_N)=\xi ({\varvec{x}}_0,{\varvec{x}}_1,\ldots \check{{\varvec{x}}}_i\ldots ,{\varvec{x}}_N)\), for all i and the total potential \(G^\lambda \), defined in (2.1), can be decomposed as follows
the “charge” associated to \(\pi _i\). Since the particles interacting with the impurity are all indistinguishable with each other, all the charges must be equal, namely \(\xi _i({\varvec{x}}_0,{\varvec{x}}_1,\ldots \check{{\varvec{x}}}_i\ldots ,{\varvec{x}}_N)=\xi ({\varvec{x}}_0,{\varvec{x}}_1,\ldots \check{{\varvec{x}}}_i\ldots ,{\varvec{x}}_N)\), for all i and the total potential \(G^\lambda \), defined in (2.1), can be decomposed as follows
with  the potential generated by the i-th charge. More precisely we have
the potential generated by the i-th charge. More precisely we have

Remark A.2
We stress that \(G^\lambda \) satisfies  and \(\ker (G^\lambda )=\{0\}\). Indeed, one can verify that its adjoint is given by
and \(\ker (G^\lambda )=\{0\}\). Indeed, one can verify that its adjoint is given by

and its image is clearly dense in  .
.
Remark A.3
From (2.1), one can verify that \(\textrm{ran}(G^\lambda )\cap H^1(\mathbb {R}^{3(N+1)})\!=\!\{0\}\). This fact is remarkable in defining the quadratic form Q in (2.6).
Next, we extract the asymptotic behaviour of the potential in a neighborhood of the coincidence hyperplanes, in the position representation. We compute such asymptotic behavior for a regular charge \(\xi \in {\mathcal {S}}(\mathbb {R}^{3N})\). From (A.12), we get

where a change of variables of Jacobian \(\left( \tfrac{\sqrt{m_0m}}{m_0+m}\right) ^{\!3}\) has occurred in the last step, where
The last integral in \(d{\varvec{\kappa }}\) is well known, since, given \(a>0\), one has

Hence,

From the last equation, notice that the term \(G^\lambda _j\xi \) is regular in \(\mathbb {R}^{3(N+1)}\smallsetminus \pi _j\). Furthermore, since we are working with  , with a Taylor expansion of the exponential, we can easily expand in terms of powers of \(|{\varvec{x}}_j-{\varvec{x}}_0|\):
, with a Taylor expansion of the exponential, we can easily expand in terms of powers of \(|{\varvec{x}}_j-{\varvec{x}}_0|\):

Therefore, one obtains an explicit behavior of the potential near \(\pi _j\)
where

A similar asymptotic expansion holds for \(G^\lambda \) in a neighborhood of \(\pi _j\)
with \(\Gamma _{\!\textrm{off}}^{j,\lambda }\) representing the contribution of all other potentials \(\{G^\lambda _i\}_{i\ne j}\) evaluated on \(\pi _j\), i.e.

Let us fix for notational simplicity \(j=N\) and define \({\varvec{r}}= {\varvec{x}}_N- {\varvec{x}}_0\), \({\varvec{R}}= \tfrac{m{\varvec{x}}_N + m_0 {\varvec{x}}_0}{m+m_0}\). Then for any \(g \in {\mathcal {S}}(\mathbb {R}^{3N})\) from (A.19) we have

Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ferretti, D., Teta, A. Zero-Range Hamiltonian for a Bose Gas with an Impurity. Complex Anal. Oper. Theory 17, 55 (2023). https://doi.org/10.1007/s11785-023-01358-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11785-023-01358-4



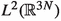 is closed and bounded from below by a positive constant.
is closed and bounded from below by a positive constant.