Optimal harvesting and sensing durations for multi-antenna cognitive radio networks using intelligent reflecting surfaces

Abstract

In this paper, we suggest to optimize harvesting and sensing duration for cognitive radio networks (CRN) using intelligent reflecting surfaces (IRS). The secondary source $S_S$ harvests energy using the signal of node A. Then, $S_S$ performs spectrum sensing to detect primary source $P_S$ activity. When $P_S$ activity is not detected, $S_S$ transmits a packet to secondary destination $S_D$. IRS reflects the signals from the secondary source so that all reflections are in phase at secondary destination. We show that the use of N=8,16,32,64,128, 256,512 reflectors offers 19, 25, 31, 37, 43, 49, 56 dB gain when compared to the absence of IRS [20]. We also propose to add a second IRS between node A and $S_S$ to increase the harvested energy since $S_S$ harvests energy using the reflected signals on the first IRS. The use of two IRS with $N_1=8$ reflectors in the first IRS and $N_2=8$ reflectors in the second IRS offers 12 dB and 30 dB gain when compared to a single IRS $N=8$ and the absence of IRS [20]. The use of two IRS with $N_1=16$ and $N_2=8$ offers 21 dB and 39 dB gain when compared to a single IRS $N=8$ and the absence of IRS [20].

1 Introduction

In CRN, primary and secondary users (PU and SU) share the same spectrum. In interweave CRN, secondary source transmits when primary source is idle. In underlay CRN, secondary source transmits with an adaptive transmit power to generate low interference at secondary destination. In overlay CRN, secondary source dedicates a part of its power to help the secondary destination in decoding its packet. In this paper, we optimize harvesting and sensing durations for interweave CRN using intelligent reflecting surfaces (IRSs). IRSs allow an increase in the throughput of wireless networks since the reflected signals are in phase at the destination [1,2,3,4,5]. IRS is placed between the source and the destination with optimized phase shifts so that all reflections are in phase at the destination [6, 7]. IRS has been suggested for wireless networks as well as non- orthogonal multiple access (NOMA) [8, 9]. IRSs have been used to increase the throughput of optical communications as well as millimeter wave communications [10,11,12]. IRS with finite phase shifts has been suggested in [13]. Asymptotic performance analysis of wireless communications using IRS was provided in [14]. Antenna design, simulations and measurements of wireless communication using IRS were discussed in [15,16,17]. Machine and deep learning algorithms were used to optimize IRS implementation [18, 19]. IRSs are nearly passive devices, made of electromagnetic material that can be deployed in primary or secondary networks of CRN on several structures, including but not limited to building facades, indoor walls, aerial platforms, roadside billboards, vehicle windows, etc.

In this article, we optimize harvesting and sensing duration for CRN using IRS. The secondary source $S_S$ harvests energy using the signal of node A. Then, $S_S$ performs spectrum sensing to detect the activity of $P_S$. When $P_S$ activity is not detected, $S_S$ transmits a packet to secondary destination $S_D$. The transmitted signal by $S_S$ is reflected by N reflectors of IRS so that all reflections are in phase at $S_D$. We show that the use of $N=8,16,32,64,128,256,512$ reflectors offers 19, 25, 31, 37, 43, 49, 56 dB gain when compared to the absence of IRS [20]. We also propose to add a second IRS between node A and $S_S$ to increase the harvested energy since $S_S$ harvests energy using the reflected signals on the first IRS. The use of two IRS with $N_1=8$ reflectors in the first IRS and $N_2=8$ reflectors in the second IRS offers 12 dB and 30 dB gain when compared to a single IRS $N=8$ and the absence of IRS [20]. The use of two IRS with $N_1=16$ and $N_2=8$ offers 21 dB and 39 dB gain when compared to a single IRS $N=8$ and the absence of IRS [20]. IRS with adaptive transmit power was studied in [21].

Next section derives the throughput when there is a single IRS. Section 3 proposes to add a second IRS to increase the harvested energy. Section 4 shows the throughput enhancement using a single or two IRS. Conclusions and perspectives are presented in Sect. 5.

2 CRN with one IRS

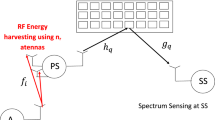
Figure 1 depicts the system model with a secondary source ($S_S$) equipped with $n_r$ receive antennas used to harvest energy over aT seconds using the signal of node A. $0<a<1$ is the harvesting percentage and T is the frame duration. $S_S$ performs spectrum sensing to detect primary source $P_S$ activity during $(1-a)bT$ seconds where $0<b<1$ provides the sensing duration. When $P_s$ activity is not detected, $S_S$ transmits data to secondary destination $S_D$ over $(1-b)(1-a)T$ seconds. The transmitter signal is reflected on IRS equipped with N reflectors so that all reflections are in phase at $S_D$. A Rayleigh fading channel is used during the simulations.

Fig. 1

CRN using a single IRS

The harvested energy at $S_S$ is expressed as

$$\begin{aligned} E=\mu a T P_A\sum _{l=1}^{n_r} |f_l|^2=\mu a L_0 E_A \sum _{l=1}^{n_r} |f_l|^2, \end{aligned}$$

(1)

where $\mu$ is the efficiency of energy conversion, $P_A=\frac{E_A}{T_s}$ is the power of A, $T_s$ is the symbol period, $L_0=\frac{T}{T_s}$. The average power of channel gain $f_l$ between A and l-th antenna of $S_S$ is $E(|f_l|^2)=\frac{1}{D_1^{ple}}$ where E(X) is the expectation of X, $D_1$ is the distance between A and $S_S$, and ple is the path loss exponent.

The symbol energy of $S_S$ is computed as

$$\begin{aligned} E_{S_S}=\frac{E}{L_0(1-a)(1-b)}=\frac{\mu a E_A}{(1-a)(1-b)}\sum _{l=1}^{n_r} |f_l|^2. \end{aligned}$$

(2)

Let $h_q$ be the channel gain between $S_S$ and q-th reflector of IRS. Let $g_q$ be the channel gain between q-th reflector of IRS and $S_D$. $h_q$ follows a zero mean Gaussian distribution with $E(|h_q|^2)=\frac{1}{D_2^{ple}}$ where $D_2$ is the distance between $S_S$ and IRS. $g_q$ follows a zero-mean Gaussian distribution with $E(|g_q|^2)=\frac{1}{D_3^{ple}}$ where $D_3$ is the distance between IRS and $S_D$.

We have $h_q=a_qe^{-jb_q}$ where $a_q=|h_q|$ and $b_q$ is the phase of $h_q$ such that $E(a_q)=\frac{\sqrt{\pi }}{2\sqrt{D_2^{ple}}}$ and $E(a_q^2)=E(|h_q|^2)=\frac{1}{D_2^{ple}}$ [25]. We have $g_q=c_qe^{-jd_q}$ such that $E(c_q)=\frac{\sqrt{\pi }}{2\sqrt{D_3^{ple}}}$ and $E(c_q^2)=E(|g_q|^2)=\frac{1}{D_3^{ple}}$.

The phase of q-th reflector is [1]

$$\begin{aligned} \phi _q=b_q+d_q. \end{aligned}$$

(3)

The received signal $S_D$ is written as

$$\begin{aligned} r_p=s_p\sqrt{E_{BS}}\sum _{q=1}^N h_qg_qe^{j\phi _q}+n_p. \end{aligned}$$

(4)

where $s_p$ is the p-th transmitted symbol and $n_p$ is a Gaussian noise of variance $N_0$.

Using (3), we obtain

$$\begin{aligned} r_p=s_p\sqrt{E_{S_S}}\sum _{q=1}^N a_qc_q+n_p. \end{aligned}$$

(5)

The signal-to-noise ratio (SNR) at $S_D$ is written as [1]

$$\begin{aligned} \gamma ^{S_D}=\frac{E_{S_S}}{N_0}[\sum _{q=1}^N a_qc_q]^2, \end{aligned}$$

(6)

Using (2), we obtain

$$\begin{aligned} \gamma ^{S_D}=\frac{\mu a E_A}{(1-a)(1-b)N_0}\sum _{l=1}^{n_r} |f_l|^2[\sum _{q=1}^N a_qc_q]^2, \end{aligned}$$

(7)

For a large number of reflectors, i.e., $N\ge 8$, $\sum _{q=1}^N a_qc_q$ follows a Gaussian distribution with mean $m=\frac{N \pi }{4\sqrt{D_2^{ple}D_3^{ple}}}$ and variance $\sigma ^2=\frac{N}{D_2^{ple}D_3^{ple}}[1-\frac{\pi ^2}{16}]$. As $[\sum _{q=1}^N a_qc_q]^2$ is non-central Chi-square r.v. and $\sum _{l=1}^{n_r} |f_l|^2$ is a central chi-square r.v, the probability density function (PDF) of $\gamma ^{S_D}$ is written as [22]

$$\begin{aligned} p_{\gamma ^{S_D}}(x)= & {} \frac{N_0(1-a)(1-b)e^{-0.5(\frac{m}{\sigma })^2}D_1^{ple}}{\mu a E_A\varGamma (n_r)} \nonumber \\&\times \sum _{q=0}^{+\infty }\frac{(\frac{m}{\sigma })^{2q}2^{\frac{-3q-n_r+1.5}{2}}}{q!\varGamma (q+0.5)} \nonumber \\&\times K_{q-n_r+0.5}(\sqrt{\frac{2xD_1^{ple}N_0(1-a)(1-b)}{a \mu E_A}})\nonumber \\&\times (\frac{xD_1^{ple}N_0(1-a)(1-b)}{\mu a E_A})^{\frac{q+n_r-1.5}{2}} \end{aligned}$$

(8)

We use [23]

$$\begin{aligned}&\int _0^{y}\frac{2(CD)^{0.5C+0.5D}}{\varGamma (C)\varGamma (D)} x^{0.5C+0.5D-1}K_{C-D}(2\sqrt{CDx})dx \nonumber \\&\quad =\frac{1}{\varGamma (C)\varGamma (D)}G_{1,3}^{2,1}\left( CDy|\begin{array}{ccc} 1 &{} &{} \\ C, &{} D, &{} 0 \end{array} \right) \end{aligned}$$

(9)

to obtain

$$\begin{aligned} \int _0^{\sqrt{x}}w^{C-1}K_D(w)dw=2^{C-2}G_{1,3}^{2,1}\left( \frac{x}{4}|\begin{array}{ccc} 1 &{} &{} \\ \frac{C+D}{2}, &{} \frac{C-D}{2}, &{} 0 \end{array} \right) \nonumber \\ \end{aligned}$$

(10)

where $G_{n,m}^{p,l}(x)$ is the Meijer G-function.

We deduce the cumulative distribution function (CDF) of $\gamma ^{S_D}$:

$$\begin{aligned}&P_{\gamma ^{S_D}}(x)\nonumber \\&\quad =\frac{e^{-(\frac{m}{\sqrt{2}\sigma })^2}}{\varGamma (n_r)} \sum _{p=0}^{+\infty }\frac{(\frac{m}{\sigma })^{2p} 2^{-p}}{p!\varGamma (p+0.5)}\nonumber \\&\qquad \times G_{1,3}^{2,1}\left( \frac{N_0(1-a)(1-b)xD_1^{ple}}{2\mu a E_A}|\begin{array}{ccc} 1 &{} &{} \\ p+0.5, &{} n_r, &{} 0 \end{array} \right) \nonumber \\ \end{aligned}$$

(11)

The packet error probability (PEP) at $S_D$ can be computed as [24]

$$\begin{aligned} PEP(a,b)<P_{\gamma ^{S_D}}(W_0) \end{aligned}$$

(12)

where $W_0$ is defined as [24]

$$\begin{aligned} W_0=\int _0^{+\infty }pep(v)dv \end{aligned}$$

(13)

pep(v) is the PEP for for Q-QAM modulation [25]

$$\begin{aligned}&pep(v)\nonumber \\&\quad =1-\left[ 1-2\left( 1-\frac{1}{\sqrt{Q}}\right) erfc\left( \sqrt{v\frac{3\log _2(Q)}{2(Q-1)}}\right) \right] ^{PL}\nonumber \\ \end{aligned}$$

(14)

and PL is packet length in symbols.

The throughput at $S_D$ is computed as

$$\begin{aligned} Thr(a,b)= & {} \frac{(1-b)(1-a)L_0log_2(Q)}{L_0T_sB}\nonumber \\&\times (1-PEP(a,b))P_{idle}(1-P_f(a,b))\nonumber \\= & {} (1-b)(1-a)log_2(Q)\nonumber \\&\times (1-PEP(a,b))P_{idle}(1-P_f(a,b)) \end{aligned}$$

(15)

where B is the used bandwidth, $P_f(a,b)$ is the false alarm probability written as

$$\begin{aligned} P_{f}(a,b) =\frac{\varGamma (\lfloor (1-a)b L_0\rfloor ,\frac{\zeta }{2})}{\varGamma (\lfloor (1-a)b L_0\rfloor )} \end{aligned}$$

(16)

$\zeta$ is the energy detector threshold, $\lfloor (1-a)b L_0\rfloor$ is the number of samples employed by the energy detector, and $\lfloor x \rfloor$ is the integer part of x,

$$\begin{aligned} \varGamma (N,u)=\int _{u}^{+\infty }x^{N-1}e^{-x}dx. \end{aligned}$$

(17)

Harvesting duration a and sensing duration b are optimized to maximize the throughput:

$$\begin{aligned} (a_{opt},b_{opt})=argmax_{a,b} Thr(a,b) \end{aligned}$$

(18)

3 CRN using two IRS

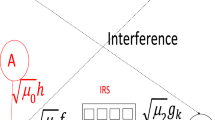
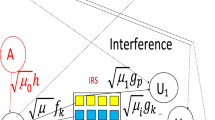
Figure 2 depicts a system model containing two IRS: $IRS_1$ is used for increase the harvested energy with $N_1$ reflectors . $IRS_1$ is between A and $S_S$ to increase the harvested energy. $IRS_2$ is located between $S_S$ and $S_D$; it contains $N_2$ reflectors to increase the SNR at $S_D$.

Fig. 2

IRS using in energy harvesting

When $IRS_1$ is used, the harvested energy is equal to

$$\begin{aligned} E=\mu a L_0 E_A[\sum _{l=1}^{N_1}\delta _l\eta _l]^2, \end{aligned}$$

(19)

$\delta _l=|u_l|$, where $u_l$ is channel gain between A and l-th reflector of $IRS_1$, and $\eta _l=|v_l|$ where $v_l$ is the channel gain between l-th reflector of $IRS_1$ and $S_S$.

For large values of $N_1\ge 8$, $[\sum _{l=1}^{N_1}\delta _l\eta _l]$ follows a Gaussian distribution with mean $m_2=\frac{N_1\pi }{4\sqrt{D_4^{ple}D_5^{ple}}}$ and variance $\sigma _2^2=\frac{N_1}{D_4^{ple}D_5^{ple}}$. $D_4$ is the distance between A and $IRS_1$, and $D_5$ is the distance between $IRS_1$ and $S_S$.

We can write

$$\begin{aligned} E_{S_D}=\frac{E}{L_0(1-a)(1-b)}=\frac{\mu a E_A [\sum _{l=1}^{N_1}\delta _l\eta _l]^2}{(1-a)(1-b)} \end{aligned}$$

(20)

The SNR at $S_D$ is equal to

$$\begin{aligned} \gamma ^{S_D}= & {} \frac{E_{S_S}[\sum _{q=1}^{N_2} a_qc_q]^2}{N_0}\nonumber \\= & {} \frac{\mu a E_A}{N_0(1-a)(1-b)}[\sum _{l=1}^{N_1}\delta _l\eta _l]^2[\sum _{q=1}^{N_2} a_qc_q]^2. \end{aligned}$$

(21)

where $a_q$, $c_q$ were defined in Sect. 2 and $N_2$ is the number of reflectors of $IRS_2$.

As $[\sum _{l=1}^{N_1}\delta _l\eta _l]^2$ and $[\sum _{q=1}^{N_2} a_qc_q]^2$ are two non-Chi-square r.v., the PDF of $\gamma ^{S_D}$ is written as [22]

$$\begin{aligned} f_{\gamma ^{S_D}}(z)= & {} e^{-\frac{m_2^2}{2\sigma _2^2}-\frac{m_4^2}{2\sigma _3^2}}\sum _{n=0}^{+\infty }\sum _{p=0}^{+\infty }\frac{2^{-2n-2p}(\frac{m_2}{\sigma _2})^{2p} (\frac{m_4}{\sigma _3})^{2n}}{n!p!\varGamma (n+0.5)\varGamma (p+0.5)}\nonumber \\&\times \frac{N_0(1-a)(1-b)}{\mu a E_A}K_{p-n}(\sqrt{\frac{N_0(1-a)z}{\mu a E_A}})\nonumber \\&\times (z\frac{N_0(1-a)(1-b)}{\mu a E_A})^{\frac{p+n-1}{2}} \end{aligned}$$

(22)

Using (10), the CDF of $\gamma ^{S_D}$ is equal to

$$\begin{aligned} P_{\gamma ^{S_D}}(z)= & {} e^{-\frac{m_2^2}{2\sigma _2^2} -\frac{m_3^2}{2\sigma _3^2}}\sum _{n=0}^{+\infty }\sum _{p=0}^{+\infty } \frac{2^{-n-p}(\frac{m_2}{2\sigma _2})^{2p} (\frac{m_3}{2\sigma _3})^{2n}}{n!p!\varGamma (n+0.5)\varGamma (p+0.5)}\nonumber \\&\times G_{1,3}^{2,1}\left( \frac{N_0(1-a)(1-b)z}{\mu a E_A4}|\begin{array}{ccc} 1 &{} &{} \\ p+0.5, &{} n+0.5, &{} 0 \end{array} \right) \nonumber \\ \end{aligned}$$

(23)

where $m_3=\frac{N_2^2 \pi }{4\sqrt{D_2^{ple}D_3^{ple}}}$, $\sigma _3^2=\frac{N_2^2}{D_2^{ple}D_3^{ple}}[1-\frac{\pi ^2}{16}]$.

The throughput is computed and optimized using (12-18).

4 Numerical results

Figures 3, 4 and 5 depicts the throughput for QPSK, 16 and 64 QAM modulation in the presence of one IRS with $M=8$ reflectors for $\zeta =1$, $D_1=1$, $D_2=1.3$, $D_3=1.4$, $E_A=1$. We notice that the optimization of harvesting and sensing duration offers the largest throughput when compared to $a=1/3$, $b=1/2$, optimal a, $b=1/2$ and optimal b with $a=1/3$.

Fig. 3

Throughput for QPSK and one IRS

Fig. 4

Throughput for 16QAM and one IRS

Fig. 5

Throughput for 64QAM and one IRS

For the same parameters as Figs. 3, 4 and 5, Figures 6 and 7 show the throughput for 16 and 64 QAM modulations and different number of reflectors $N=8,16,32,64,128,256,512$. The use of $N=8,16,32,64,128,256,512$ reflectors offers 19, 25, 31, 37, 43, 49, 56 dB gain when compared to the absence of IRS [20]. In Fig. 6-7, we used an optimal value of a and b.

Fig. 6

Throughput for 16QAM with different number of IRS reflectors

Fig. 7

Throughput for 64QAM and different number of reflectors

Figure 8 shows the effect of number of harvesting antennas $n_r=1,2,3$ on secondary throughput for QPSK modulation, $N=8$ reflectors and the same parameters as Fig. 3. We notice that $n_r=3$ harvesting antennas offers 2 dB and 7 dB gain when compared to $n_r=2,1$.

Fig. 8

Throughput for QPSK and different number of harvesting antennas

Figure 9 depict the throughput for QPSK modulation when there are two IRS with $D_4=1.1$ and $D_5=1.2$. The other parameters are the same as Fig. 3. The use of two IRS with $N_1=8$ reflectors in the first IRS and $N_2=8$ reflectors in the second IRS offers 12 dB and 30 dB gain when compared to a single IRS $N=8$ and the absence of IRS [20]. The use of two IRS with $N_1=16$ and $N_2=8$ offers 21 dB and 39 dB gain when compared to a single IRS $N=8$ and the absence of IRS [20].

Fig. 9

Throughput for QPSK with two IRS

5 Conclusion and perspectives

In this article, we optimized harvesting and sensing duration for CRN using intelligent reflecting surfaces (IRS). IRS reflects signals from secondary source so that all reflections are in phase at secondary destination. The use of $N=8,16,32,64,128,256,512$ reflectors offers 19, 25, 31, 37, 43, 49, 56 dB gain when compared to the absence of IRS [20]. We also proposed to add a second IRS to increase the harvested energy where the secondary source harvests energy using the reflected signals on the first IRS. The use of two IRS with $N_1=8$ reflectors in the first IRS and $N_2=8$ reflectors in the second IRS offers 12 dB and 30 dB gain when compared to a single IRS $N=8$ and the absence of IRS [20]. The use of two IRS with $N_1=16$ and $N_2=8$ offers 21 dB and 39 dB gain when compared to a single IRS $N=8$ and the absence of IRS [20]. As a perspective, we may extend the system model to NOMA systems.