1 Introduction

Adaptive filter algorithms can be classified into two main groups: gradient based and least squares based. The well-known gradient-based adaptive algorithms are the least-mean-squares (LMS) algorithm [1], the normalized LMS (NLMS) algorithm [2], and the affine projection algorithm (APA) [3]. These algorithms are widely used in practical implementations because of their relatively low computational complexity. The major limitations of the gradient-based algorithms are their relatively slow convergence rates and sensitivity to the eigenvalue spread of the input correlation matrix. The other type of adaptive algorithm is based on the least squares, and the most widely used one is the recursive least-squares (RLS) algorithm. The RLS algorithm has a faster convergence rate than the gradient-based algorithms, although the computational complexity is greater [4, 5].

There is a clear difference between gradient-based algorithms and the RLS algorithm in terms of the convergence rate and computational complexity [4, 5]. However, a recursive algorithm based on the solution of the time-averaged normal equation using a single-step Gauss–Seidel iteration between two consecutive data samples has been proposed as an intermediate method [6]. The Gauss–Seidel algorithm has also been used as an optimization algorithm called the Euclidean direction search (EDS) algorithm [7–13]. An accelerated version of the EDS algorithm is also presented in [14]. As an alternative to the Gauss–Seidel iterations, the one-step Jacobi iteration is used in [15]. A recursive implementation of the Gauss–Seidel algorithm (RGS) is also used to adjust self-tuning adaptive controller parameters directly in [16]. The main advantage of the RGS algorithm as an intermediate method is a faster convergence rate than gradient-based algorithms and a lower computational complexity than the RLS algorithm. Similar to the RGS algorithm, the recursive successive over-relaxation (RSOR) algorithm is proposed for adaptive FIR filtering based on the use of a one-step successive over-relaxation (SOR) iteration between two data samples [17].

The aim of this paper is to present a steady-state convergence analysis of the parameter error vector which is performed in the mean sense and mean-square sense. Also, the convergence performance of the RSOR algorithm is examined using computer simulations and compared with the well-known gradient-based algorithms and the RLS algorithm.

The paper is organized as follows: in Sect. 2, the use of the RSOR algorithm for adaptive filtering is presented. Stochastic convergence analysis of the RSOR algorithm is presented in Sect. 3. Computer simulations using a system identification example are presented in Sect. 4. Concluding remarks are given in Sect. 5.

2 Review of the RSOR algorithm

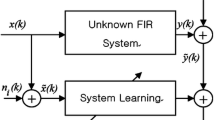
An adaptive filter is a digital filter whose parameters \({\hat{\mathbf{w}}}(n)\) are adjusted by an adaptive algorithm. The output signal y(n) can be obtained by the following adaptive FIR filter model

$$\begin{aligned} y(n)=\mathbf{x}^{\mathrm{T}}(n){\hat{\mathbf{w}}}(n) \end{aligned}$$
(1)

where the input vector \(\mathbf{x}(n)\) and the parameter vector \({\hat{\mathbf{w}}}(n)\) can be defined as follows:

$$\begin{aligned} \mathbf{x}(n)= & {} [{\begin{array}{cccc} {x(n)}&{} {x(n-1)}&{} \ldots &{} {x(n-M+1)} \\ \end{array} }]^{\mathrm{T}} \end{aligned}$$
(2)
$$\begin{aligned} {\hat{\mathbf{w}}}(n)= & {} [{\begin{array}{cccc} {\hat{{w}}_0 (n)}&{} {\hat{{w}}_1 (n)}&{} \ldots &{} {\hat{{w}}_{M-1} (n)} \\ \end{array} }]^{\mathrm{T}} \end{aligned}$$
(3)

where x(n) is the input signal of the filter and M is filter length. An error signal e(n) is defined by comparing the desired signal d(n) and the output signal y(n) as follows:

$$\begin{aligned} e(n)=d(n)-\mathbf{x}^{\mathrm{T}}(n){\hat{\mathbf{w}}}(n). \end{aligned}$$
(4)

Least-squares-based algorithms use the following cost function

$$\begin{aligned} \hbox {V}(n,\mathbf{w})=\sum _{i=1}^n {\lambda ^{n-i}e^{2}(i)} \end{aligned}$$
(5)

where \(\lambda \) is the forgetting factor, \(0<\lambda \le 1\). The estimated parameter vector \({\hat{\mathbf{w}}}(n)\), which minimizes least-squares error function (5) for n-step data, can be computed by

$$\begin{aligned} {\hat{\mathbf{w}}}(n)=\mathbf{R}^{-1}(n)\mathbf{p}(n) \end{aligned}$$
(6)

where \({\hat{\mathbf{w}}}(n)\) can also be obtained by solving the following time-averaged normal equation:

$$\begin{aligned} \mathbf{R}(n){\hat{\mathbf{w}}}(n)=\mathbf{p}(n) \end{aligned}$$
(7)

where \(\mathbf{R}(n)\) denotes an estimate of the \(M\times M\)- dimensional autocorrelation matrix of the input vector \(\mathbf{x}(n)\), \(\mathbf{p}(n)\) denotes an estimate of the \(M\times 1\)-dimensional cross-correlation vector between \(\mathbf{x}(n)\) and the desired signal d(n), and \({\hat{\mathbf{w}}}(n)\) is an estimate of the \(M\times 1\)- dimensional parameter vector (3). The estimated values \(\mathbf{R}(n)\) and \(\mathbf{p}(n)\) are computed at time step n as follows, respectively:

$$\begin{aligned} \mathbf{R}(n)= & {} \sum _{i=1}^n {\lambda ^{n-i}{} \mathbf{x}(i)\mathbf{x}^{\mathrm{T}}(i)} \end{aligned}$$
(8)
$$\begin{aligned} \mathbf{p}(n)= & {} \sum _{i=1}^n {\lambda ^{n-i}{} \mathbf{x}(i)d(i)}. \end{aligned}$$
(9)

In practical applications, the values of \(\mathbf{R}(n)\) and \(\mathbf{p}(n)\) are updated as follows:

$$\begin{aligned} \mathbf{R}(n)= & {} \lambda \mathbf{R}(n-1)+\mathbf{x}(n)\mathbf{x}^{\mathrm{T}}(n) \end{aligned}$$
(10)
$$\begin{aligned} \mathbf{p}(n)= & {} \lambda \mathbf{p}(n-1)+\mathbf{x}(n)d(n). \end{aligned}$$
(11)

By using a strategy similar to that of the RGS algorithm [16], the recursive implementation of the SOR (RSOR) algorithm to minimize the least-squares error function (5) can be given as

$$\begin{aligned}&\hat{{w}}_i (n+1)=\left[ p_i (n)-\sum _{j=1}^{i-1} {R_{ij} (n)\hat{{w}}_j (n+1)}\right. \nonumber \\&\quad \left. -\sum _{j=i+1}^M {R_{ij} (n)\hat{{w}}_j (n)} \right] \frac{\omega }{R_{ii} (n)}+(1-\omega )\hat{{w}}_i (n)\nonumber \\&\quad \quad i=1, 2, \ldots ,M, \quad (0<\omega <2) \end{aligned}$$
(12)

where \(\omega \) is known as the relaxation parameter, \(\hat{{w}}_i (n)\) is the ith element of the estimated parameter vector \({\hat{\mathbf{w}}}(n)\), \(p_i (n)\) is the ith element of the estimated cross-correlation vector \(\mathbf{p}(n)\), and \(R_{ij} (n)\) indicates the ith row and jth column of the estimated autocorrelation matrix \(\mathbf{R}(n)\). Equations (10)–(12) are used to implement the RSOR algorithm. In the RSOR algorithm, the discrete-time index n is used as the iteration index. Thus, the RSOR algorithm is implemented using a one-cycle SOR iteration between two consecutive data samples. When \(\omega =1\), the SOR iterations are equal to the Gauss–Seidel iterations [18]. By taking \(\omega >1\), the RSOR algorithm can be used to obtain faster convergence than the RGS algorithm [17].

3 Stochastic convergence analysis

In this section, the asymptotic convergence, i.e., the steady-state behavior, of the RSOR parameter estimation vector is analyzed in the mean sense and mean-square sense. The analysis is similar to that in [19, 20].

The parameter convergence of the RSOR algorithm is based on the positive definiteness of the autocorrelation matrix \(\mathbf{R}(n)\). In the analysis, the following assumption is used:

Assumption

The excitation signal x(n) is persistently exciting, i.e., there exist \(\alpha >0\) and \(\beta >0\) satisfying

$$\begin{aligned} 0<\alpha \mathbf{I}\le \frac{1}{n}\sum _{i=1}^n {\mathbf{x}(i)\mathbf{x}^{\mathrm{T}}(i)} \le \beta \mathbf{I}<\infty \end{aligned}$$
(13)

over a set of n consecutive data samples for all i. This assumption means that the minimum and maximum eigenvalues of the sum in (13) are bounded by \(\alpha \) and \(\beta \) [21].

3.1 Mean convergence analysis

The estimated autocorrelation matrix \(\mathbf{R}(n)\) can be decomposed as the sum of its lower triangular matrix, diagonal matrix, and upper triangular matrix as

$$\begin{aligned} \mathbf{R}(n)=\mathbf{R}_{\mathrm{L}} (n)+\mathbf{R}_{\mathrm{D}} (n)+\mathbf{R}_{\mathrm{U}} (n). \end{aligned}$$
(14)

Given the classical SOR method in [18], the splitting of \(\mathbf{R}(n)\) can be written as

$$\begin{aligned} \omega \mathbf{R}(n)= & {} [\mathbf{R}_{\mathrm{D}} (n)+\omega \mathbf{R}_{\mathrm{L}} (n)]\nonumber \\&-\,[(1-\omega )\mathbf{R}_{\mathrm{D}} (n)-\omega \mathbf{R}_{\mathrm{U}} (n)]. \end{aligned}$$
(15)

Based on the splitting in (15) and using (14), the corresponding RSOR algorithm (12) for the solution of (7) is rewritten as recursion

$$\begin{aligned}&[\mathbf{R}_{\mathrm{D}} (n)+\omega \mathbf{R}_{\mathrm{L}} (n)]{\hat{\mathbf{w}}}(n+1)=\{[\mathbf{R}_{\mathrm{D}} (n)+\omega \mathbf{R}_{\mathrm{L}} (n)]\nonumber \\&\quad -\,\omega \mathbf{R}(n)\} {\hat{\mathbf{w}}}(n)+\omega \mathbf{p}(n). \end{aligned}$$
(16)

Let us define

$$\begin{aligned}&{} \mathbf{x}(i)\mathbf{x}^{\mathrm{T}}(i)={\bar{\mathbf{R}}}+{\tilde{\mathbf{R}}}(i) \end{aligned}$$
(17)
$$\begin{aligned}&{} \mathbf{x}(i)d(i)={\bar{\mathbf{p}}}+{\tilde{\mathbf{p}}}(i) \end{aligned}$$
(18)

where \({\tilde{\mathbf{R}}}(i)\) denotes the random part of the autocorrelation matrix, \({\tilde{{\mathbf{p}}}}(i)\) denotes the random part of the cross-correlation vector, \({\bar{\mathbf{R}}}=E\{\mathbf{x}(i)\mathbf{x}^{\mathrm{T}}(i)\}\), \({\bar{\mathbf{p}}}=E\{\mathbf{x}(i)d(i)\}\), and \(E\{\cdot \}\) is the statistical expectation operator. Similar to (14), \({\bar{\mathbf{R}}}\) and \({\tilde{\mathbf{R}}}(i)\) can also be decomposed as

$$\begin{aligned}&{\bar{\mathbf{R}}}={\bar{\mathbf{R}}}_{\mathrm{L}} +{\bar{\mathbf{R}}}_{\mathrm{D}} +{\bar{\mathbf{R}}}_{\mathrm{U}} \end{aligned}$$
(19)
$$\begin{aligned}&{\tilde{\mathbf{R}}}(i)={\tilde{\mathbf{R}}}_{\mathrm{L}} (i)+{\tilde{\mathbf{R}}}_\mathrm{D} (i)+{\tilde{\mathbf{R}}}_{\mathrm{U}} (i). \end{aligned}$$
(20)

By substituting (17) into (8) and (18) into (9), the following equations are, respectively, written as

$$\begin{aligned}&{} \mathbf{R}(n)=\sum _{i=1}^n {\lambda ^{n-i}{\bar{\mathbf{R}}}} +\sum _{i=1}^n {\lambda ^{n-i}{\tilde{\mathbf{R}}}(i)} \end{aligned}$$
(21)
$$\begin{aligned}&{} \mathbf{p}(n)=\sum _{i=1}^n {\lambda ^{n-i}{\bar{\mathbf{p}}}} +\sum _{i=1}^n {\lambda ^{n-i}{\tilde{\mathbf{p}}}(i)}. \end{aligned}$$
(22)

With (14), (19), and (20), the autocorrelation matrix in (21) can be written as

$$\begin{aligned}&{} \mathbf{R}_{\mathrm{L}} (n)+\mathbf{R}_{\mathrm{D}} (n)+\mathbf{R}_{\mathrm{U}} (n)=\sum _{i=1}^n {\lambda ^{n-i}\left( {\bar{\mathbf{R}}}_{\mathrm{L}} +{\bar{\mathbf{R}}}_{\mathrm{D}} +{\bar{\mathbf{R}}}_{\mathrm{U}} \right) }\nonumber \\&\quad +\sum _{i=1}^n {\lambda ^{n-i}\left[ {\tilde{\mathbf{R}}}_{\mathrm{L}} (i)+{\tilde{\mathbf{R}}}_{\mathrm{D}} (i)+{\tilde{\mathbf{R}}}_{\mathrm{U}} (i)\right] } \end{aligned}$$
(23)

which can be decomposed into its lower triangular, diagonal, and upper triangular parts as

$$\begin{aligned} \mathbf{R}_{\mathrm{L}} (n)= & {} \sum _{i=1}^n {\lambda ^{n-i}{\bar{\mathbf{R}}}_\mathrm{L} } +\sum _{i=1}^n {\lambda ^{n-i}{\tilde{\mathbf{R}}}_{\mathrm{L}} (i)} \end{aligned}$$
(24)
$$\begin{aligned} \mathbf{R}_{\mathrm{D}} (n)= & {} \sum _{i=1}^n {\lambda ^{n-i}{\bar{\mathbf{R}}}_\mathrm{D} } +\sum _{i=1}^n {\lambda ^{n-i}{\tilde{\mathbf{R}}}_{\mathrm{D}} (i)} \end{aligned}$$
(25)
$$\begin{aligned} \mathbf{R}_{\mathrm{U}} (n)= & {} \sum _{i=1}^n {\lambda ^{n-i}{\bar{\mathbf{R}}}_\mathrm{U} } +\sum _{i=1}^n {\lambda ^{n-i}{\tilde{\mathbf{R}}}_{\mathrm{U}} (i)}. \end{aligned}$$
(26)

Using the Eqs. (21), (24), and (25), the following equations can be formed.

$$\begin{aligned}&{} \mathbf{R}_{\mathrm{D}} (n)+\omega \mathbf{R}_{\mathrm{L}} (n)=\sum _{i=1}^n {\lambda ^{n-i}({\bar{\mathbf{R}}}_{\mathrm{D}} +\omega {\bar{\mathbf{R}}}_{\mathrm{L}} )}\nonumber \\&\quad +\sum _{i=1}^n {\lambda ^{n-i}\left[ {\tilde{\mathbf{R}}}_{\mathrm{D}} (i)+\omega {\tilde{\mathbf{R}}}_{\mathrm{L}} (i)\right] } \end{aligned}$$
(27)
$$\begin{aligned}&{} \mathbf{R}_{\mathrm{D}} (n){+}\omega \mathbf{R}_{\mathrm{L}} (n)-\omega \mathbf{R}(n){=}\sum _{i=1}^n {\lambda ^{n-i}({\bar{\mathbf{R}}}_{\mathrm{D}} {+}\omega {\bar{\mathbf{R}}}_{\mathrm{L}} -\omega {\bar{\mathbf{R}}})}\nonumber \\&\quad +\sum _{i=1}^n {\lambda ^{n-i}\left[ {\tilde{\mathbf{R}}}_{\mathrm{D}} (i)+\omega {\tilde{\mathbf{R}}}_{\mathrm{L}} (i)-\omega {\tilde{\mathbf{R}}}(i)\right] } \end{aligned}$$
(28)

Let us define

$$\begin{aligned} {\hat{\mathbf{w}}}(n)={\bar{\mathbf{w}}}(n)+{\tilde{\mathbf{w}}}(n) \end{aligned}$$
(29)

where \({\bar{\mathbf{w}}}(n)=E\{{\hat{\mathbf{w}}}(n)\}\) and \({\tilde{\mathbf{w}}}(n)\) is the stochastic part of \({\hat{\mathbf{w}}}(n)\). Substituting (22), (27), (28), and (29) into the RSOR algorithm (16) gives

$$\begin{aligned}&\left\{ \sum _{i=1}^n {\lambda ^{n-i}({\bar{\mathbf{R}}}_{\mathrm{D}} +\omega {\bar{\mathbf{R}}}_{\mathrm{L}} )}\right. \nonumber \\&\qquad \left. +\sum _{i=1}^n {\lambda ^{n-i}\left[ {\tilde{\mathbf{R}}}_{\mathrm{D}} (i){+}\omega {\tilde{\mathbf{R}}}_{\mathrm{L}} (i)\right] } \right\} \left[ {{\bar{\mathbf{w}}}(n{+}1)+{\tilde{\mathbf{w}}}(n+1)} \right] \nonumber \\&\quad =\left\{ \sum _{i=1}^n {\lambda ^{n-i}({\bar{\mathbf{R}}}_{\mathrm{D}} +\omega {\bar{\mathbf{R}}}_{\mathrm{L}} -\omega {\bar{\mathbf{R}}})}\right. \nonumber \\&\qquad \left. {+}\sum _{i=1}^n {\lambda ^{n-i}\left[ {\tilde{\mathbf{R}}}_{\mathrm{D}} (i){+}\omega {\tilde{\mathbf{R}}}_{\mathrm{L}} (i){-}\omega {\tilde{\mathbf{R}}}(i)\right] } \right\} \left[ {{\bar{\mathbf{w}}}(n){+}{\tilde{\mathbf{w}}}(n)} \right] \nonumber \\&\qquad +\,\omega \sum _{i=1}^n {\lambda ^{n-i}{\bar{\mathbf{p}}}} +\omega \sum _{i=1}^n {\lambda ^{n-i}{\tilde{\mathbf{p}}}(i)}. \end{aligned}$$
(30)

The deterministic part of (30) is written as

$$\begin{aligned}&\left\{ {\sum _{i=1}^n {\lambda ^{n-i}({\bar{\mathbf{R}}}_{\mathrm{D}} +\omega {\bar{\mathbf{R}}}_{\mathrm{L}} )} } \right\} {\bar{\mathbf{w}}}(n+1)\nonumber \\&\quad =\left\{ {\sum _{i=1}^n {\lambda ^{n-i}({\bar{\mathbf{R}}}_\mathrm{D} +\omega {\bar{\mathbf{R}}}_{\mathrm{L}} -\omega {\bar{\mathbf{R}}})} } \right\} {\bar{\mathbf{w}}}(n)\nonumber \\&\qquad +\,\omega \sum _{i=1}^n {\lambda ^{n-i}{\bar{\mathbf{p}}}} \end{aligned}$$
(31)

which is independent of the sums. Therefore, (31) can be reduced to

$$\begin{aligned} ({\bar{\mathbf{R}}}_{\mathrm{D}} +\omega {\bar{\mathbf{R}}}_{\mathrm{L}} ) {\bar{\mathbf{w}}}(n+1)=({\bar{\mathbf{R}}}_{\mathrm{D}} +\omega {\bar{\mathbf{R}}}_{\mathrm{L}} -\omega {\bar{\mathbf{R}}}) {\bar{\mathbf{w}}}(n)+\omega {\bar{\mathbf{p}}}.\nonumber \\ \end{aligned}$$
(32)

Now, let us define

$$\begin{aligned} {\bar{\mathbf{w}}}(n)=\mathbf{w}_{\mathrm{o}} +\Delta \mathbf{w}(n) \end{aligned}$$
(33)

where \(\mathbf{w}_{\mathrm{o}} \) is the optimum solution of the normal equation. Writing the normal equation as

$$\begin{aligned} {\bar{\mathbf{R}}{} \mathbf{w}}_{\mathrm{o}} ={\bar{\mathbf{p}}} \end{aligned}$$
(34)

and using (33) and (34) in (32), we can write

$$\begin{aligned}&({\bar{\mathbf{R}}}_{\mathrm{D}} +\omega {\bar{\mathbf{R}}}_{\mathrm{L}} ) [\mathbf{w}_{\mathrm{o}} +\Delta \mathbf{w}(n+1)]\nonumber \\&\quad =({\bar{\mathbf{R}}}_{\mathrm{D}} +\omega {\bar{\mathbf{R}}}_{\mathrm{L}} -\omega {\bar{\mathbf{R}}}) [\mathbf{w}_{\mathrm{o}} +\Delta \mathbf{w}(n)]+\omega {\bar{\mathbf{R}}{} \mathbf{w}}_{\mathrm{o}}. \end{aligned}$$
(35)

By multiplying both sides of (35) from the left by \(({\bar{\mathbf{R}}}_{\mathrm{D}} +\omega {\bar{\mathbf{R}}}_{\mathrm{L}} )^{-1}\), we obtained after some rearrangement

$$\begin{aligned} \Delta \mathbf{w}(n+1)=\left[ \mathbf{I}-\omega ({\bar{\mathbf{R}}}_{\mathrm{D}} +\omega {\bar{\mathbf{R}}}_{\mathrm{L}} )^{-1}{\bar{\mathbf{R}}}\right] \Delta \mathbf{w}(n). \end{aligned}$$
(36)

The result in (36) is a time-invariant equation with a system matrix \([\mathbf{I}-\omega ({\bar{\mathbf{R}}}_{\mathrm{D}} +\omega {\bar{\mathbf{R}}}_{\mathrm{L}} )^{-1}{\bar{\mathbf{R}}}]\), and its solution is

$$\begin{aligned} \Delta \mathbf{w}(n+1)=\left[ \mathbf{I}-\omega ({\bar{\mathbf{R}}}_{\mathrm{D}} +\omega {\bar{\mathbf{R}}}_{\mathrm{L}} )^{-1}{\bar{\mathbf{R}}}\right] ^{n+1} \Delta \mathbf{w}(0). \end{aligned}$$
(37)

According to the solution (37), if the maximum eigenvalue of the system matrix satisfies \(\left| { \lambda _{\max } [\mathbf{I}-\omega ({\bar{\mathbf{R}}}_{\mathrm{D}} +\omega {\bar{\mathbf{R}}}_{\mathrm{L}} )^{-1}{\bar{\mathbf{R}}}] } \right| <1\), then \([\mathbf{I}-\omega ({\bar{\mathbf{R}}}_{\mathrm{D}} +\omega {\bar{\mathbf{R}}}_{\mathrm{L}} )^{-1}{\bar{\mathbf{R}}}]^{n+1}\rightarrow \mathbf{0}_{M\times M} \) for \(0<\omega <2\), ensuring that \(\Delta \mathbf{w}(n)\rightarrow \mathbf{0}_{M\times 1} \) as \(n\rightarrow \infty \). Therefore, the definition (33) shows that the expected value of the filter weight vector converges to its optimum value as

$$\begin{aligned} {\bar{\mathbf{w}}}(n)=\mathbf{w}_{\mathrm{o}}. \end{aligned}$$
(38)

Thus, the RSOR algorithm is an unbiased parameter estimator for the optimal Wiener solution of the normal equation in the mean sense.

3.2 Mean-square convergence analysis

The stochastic part of (30) can be written as

$$\begin{aligned}&\left\{ {\sum _{i=1}^n {\lambda ^{n-i}\left[ {\tilde{\mathbf{R}}}_{\mathrm{D}} (i)+\omega {\tilde{\mathbf{R}}}_{\mathrm{L}} (i)\right] } } \right\} {\bar{\mathbf{w}}}(n+1)\nonumber \\&\qquad +\left\{ \sum _{i=1}^n {\lambda ^{n-i}({\bar{\mathbf{R}}}_{\mathrm{D}} +\omega {\bar{\mathbf{R}}}_{\mathrm{L}} )}\right. \nonumber \\&\qquad \left. +\sum _{i=1}^n {\lambda ^{n-i}\left[ {\tilde{\mathbf{R}}}_{\mathrm{D}} (i)+\omega {\tilde{\mathbf{R}}}_{\mathrm{L}} (i)\right] } \right\} {\tilde{\mathbf{w}}}(n+1) \nonumber \\&\quad =\left\{ {\sum _{i=1}^n {\lambda ^{n-i}({\bar{\mathbf{R}}}_{\mathrm{D}} +\omega {\bar{\mathbf{R}}}_{\mathrm{L}} -\omega {\bar{\mathbf{R}}})} } \right\} {\bar{\mathbf{w}}}(n) \nonumber \\&\qquad +\left\{ \sum _{i=1}^n {\lambda ^{n-i}({\bar{\mathbf{R}}}_{\mathrm{D}} +\omega {\bar{\mathbf{R}}}_{\mathrm{L}} -\omega {\bar{\mathbf{R}}})}\right. \nonumber \\&\qquad \left. +\sum _{i=1}^n {\lambda ^{n-i}\left[ {\tilde{\mathbf{R}}}_{\mathrm{D}} (i)+\omega {\tilde{\mathbf{R}}}_{\mathrm{L}} (i)-\omega {\tilde{\mathbf{R}}}(i)\right] } \right\} {\tilde{\mathbf{w}}}(n) \nonumber \\&\qquad +\,\omega \sum _{i=1}^n {\lambda ^{n-i}{\tilde{\mathbf{p}}}(i)}. \end{aligned}$$
(39)

Using definition (29), (39) can be rearranged as

$$\begin{aligned}&\left\{ {\sum _{i=1}^n {\lambda ^{n-i}({\bar{\mathbf{R}}}_{\mathrm{D}} +\omega {\bar{\mathbf{R}}}_{\mathrm{L}} )} } \right\} {\tilde{\mathbf{w}}}(n+1)\nonumber \\&\quad =\left\{ {\sum _{i=1}^n {\lambda ^{n-i}({\bar{\mathbf{R}}}_{\mathrm{D}} +\omega {\bar{\mathbf{R}}}_{\mathrm{L}} -\omega {\bar{\mathbf{R}}})} } \right\} {\tilde{\mathbf{w}}}(n) \nonumber \\&\qquad -\left\{ {\sum _{i=1}^n {\lambda ^{n-i}\left[ {\tilde{\mathbf{R}}}_{\mathrm{D}} (i)+\omega {\tilde{\mathbf{R}}}_{\mathrm{L}} (i)\right] } } \right\} {\hat{\mathbf{w}}}(n+1) \nonumber \\&\qquad +\left\{ {\sum _{i=1}^n {\lambda ^{n-i}\left[ {\tilde{\mathbf{R}}}_{\mathrm{D}} (i)+\omega {\tilde{\mathbf{R}}}_{\mathrm{L}} (i)-\omega {\tilde{\mathbf{R}}}(i)\right] } } \right\} {\hat{\mathbf{w}}}(n) \nonumber \\&\qquad +\omega \sum _{i=1}^n {\lambda ^{n-i}{\tilde{\mathbf{p}}}(i)}. \end{aligned}$$
(40)

Using (29) and (33), we can write the following equations

$$\begin{aligned}&{\hat{\mathbf{w}}}(n+1)=\mathbf{w}_{\mathrm{o}} +\Delta \mathbf{w}(n+1)+{\tilde{\mathbf{w}}}(n+1) \end{aligned}$$
(41)
$$\begin{aligned}&{\hat{\mathbf{w}}}(n)=\mathbf{w}_{\mathrm{o}} +\Delta \mathbf{w}(n)+{\tilde{\mathbf{w}}}(n). \end{aligned}$$
(42)

If (41) and (42) are used in (40), then the last three terms on the right-hand side of (40) become

$$\begin{aligned}&-\left\{ {\sum _{i=1}^n {\lambda ^{n-i}\left[ {\tilde{\mathbf{R}}}_{\mathrm{D}} (i)+\omega {\tilde{\mathbf{R}}}_{\mathrm{L}} (i)\right] } } \right\} [\Delta \mathbf{w}(n+1)+{\tilde{\mathbf{w}}}(n+1)] \nonumber \\&\quad {+}\left\{ {\sum _{i=1}^n {\lambda ^{n-i}\left[ {\tilde{\mathbf{R}}}_{\mathrm{D}} (i){+}\omega {\tilde{\mathbf{R}}}_{\mathrm{L}} (i){-}\omega {\tilde{\mathbf{R}}}(i)\right] } } \right\} [\Delta \mathbf{w}(n){+}{\tilde{\mathbf{w}}}(n)] \nonumber \\&\quad +\,\omega \sum _{i=1}^n {\lambda ^{n-i}{\tilde{\mathbf{p}}}(i)} -\omega \sum _{i=1}^n {\lambda ^{n-i}{\tilde{\mathbf{R}}}(i)\mathbf{w}_{\mathrm{o}}}. \end{aligned}$$
(43)

Using (17), (18), and (34), the last term of (43) can be reduced as follows

$$\begin{aligned}&\omega \sum _{i=1}^n {\lambda ^{n-i}{\tilde{\mathbf{p}}}(i)} -\omega \sum _{i=1}^n {\lambda ^{n-i}{\tilde{\mathbf{R}}}(i)\mathbf{w}_{\mathrm{o}} }\nonumber \\&\quad =\omega \sum _{i=1}^n {\lambda ^{n-i}\left[ \mathbf{x}(i)d(i)-{\bar{\mathbf{p}}}\right] }\nonumber \\&\qquad -\,\omega \sum _{i=1}^n {\lambda ^{n-i}\left[ \mathbf{x}(i)\mathbf{x}^{\mathrm{T}}(i)-{\bar{\mathbf{R}}}\right] \mathbf{w}_{\mathrm{o}} } \nonumber \\&=\omega \sum _{i=1}^n {\lambda ^{n-i}{} \mathbf{x}(i)\left[ d(i)-\mathbf{x}^{\mathrm{T}}(i)\mathbf{w}_{\mathrm{o}} \right] }\nonumber \\&\qquad -\,\omega \sum _{i=1}^n {\lambda ^{n-i}{\bar{\mathbf{p}}}} +\omega \sum _{i=1}^n {\lambda ^{n-i}{\bar{\mathbf{R}}{} \mathbf{w}}_{\mathrm{o}} } \nonumber \\&\quad =\omega \sum _{i=1}^n {\lambda ^{n-i}{} \mathbf{x}(i)\left[ d(i)-\mathbf{x}^{\mathrm{T}}(i)\mathbf{w}_{\mathrm{o}} \right] }. \end{aligned}$$
(44)

If we define the error as

$$\begin{aligned} e_{\mathrm{o}} (i)=d(i)-\mathbf{x}^{\mathrm{T}}(i)\mathbf{w}_{\mathrm{o}} \end{aligned}$$
(45)

and consider the orthogonality between \(\mathbf{x}(n)\) and \(e_{\mathrm{o}} (n)\) [4], then the last term of (43) converges to the zero vector as

$$\begin{aligned} \omega \sum _{i=1}^n {\lambda ^{n-i}{} \mathbf{x}(i)e_{\mathrm{o}} (i)} \rightarrow \mathbf{0}_{M\times 1}. \end{aligned}$$
(46)

In addition, the first two terms in (43) can be considered as the weighted time averages of an ergodic process, and they are equal to their expected values by the ergodicity assumption. Based on the assumption of statistical independence between the \(\mathbf{x}(n)\) and \({\hat{\mathbf{w}}}(n)\), which is used in the analysis of the LMS algorithm [4], the first two terms in (43) can be considered zero vectors. Consequently, the last three terms on the right-hand side of (40) converge to zero vectors, and therefore, according to (40), the stochastic part of (30) can be reduced to

$$\begin{aligned}&\left\{ {\sum _{i=1}^n {\lambda ^{n-i}({\bar{\mathbf{R}}}_{\mathrm{D}} +\omega {\bar{\mathbf{R}}}_{\mathrm{L}} )} } \right\} {\tilde{\mathbf{w}}}(n+1)\nonumber \\&\quad =\left\{ {\sum _{i=1}^n {\lambda ^{n-i}({\bar{\mathbf{R}}}_\mathrm{D} +\omega {\bar{\mathbf{R}}}_{\mathrm{L}} -\omega {\bar{\mathbf{R}}})} } \right\} {\tilde{\mathbf{w}}}(n). \end{aligned}$$
(47)

Removing the deterministic quantities in (47), it can be reduced to

$$\begin{aligned} \left( {\bar{\mathbf{R}}}_{\mathrm{D}} +\omega {\bar{\mathbf{R}}}_{\mathrm{L}} \right) {\tilde{\mathbf{w}}}(n+1)=({\bar{\mathbf{R}}}_{\mathrm{D}} +\omega {\bar{\mathbf{R}}}_{\mathrm{L}} -\omega {\bar{\mathbf{R}}}) {\tilde{\mathbf{w}}}(n). \end{aligned}$$
(48)

The following result is obtained by multiplying both sides of (48) by \(({\bar{\mathbf{R}}}_{\mathrm{D}} +\omega {\bar{\mathbf{R}}}_{\mathrm{L}} )^{-1}\)

$$\begin{aligned} {\tilde{\mathbf{w}}}(n+1)=[\mathbf{I}-\omega ({\bar{\mathbf{R}}}_{\mathrm{D}} +\omega {\bar{\mathbf{R}}}_{\mathrm{L}} )^{-1}{\bar{\mathbf{R}}}] {\tilde{\mathbf{w}}}(n). \end{aligned}$$
(49)

To obtain the covariance matrix of the weight error vector, the equation in (49) is multiplied by its transpose:

$$\begin{aligned}&{\tilde{\mathbf{w}}}(n+1){\tilde{\mathbf{w}}}^{\mathrm{T}}(n+1)\nonumber \\&\quad =[\mathbf{I}-\omega ({\bar{\mathbf{R}}}_{\mathrm{D}} +\omega {\bar{\mathbf{R}}}_{\mathrm{L}} )^{-1}{\bar{\mathbf{R}}}] {\tilde{\mathbf{w}}}(n){\tilde{\mathbf{w}}}^{\mathrm{T}}(n)[\mathbf{I}\nonumber \\&\qquad -\,\omega ({\bar{\mathbf{R}}}_{\mathrm{D}} +\omega {\bar{\mathbf{R}}}_{\mathrm{L}} )^{-1}{\bar{\mathbf{R}}}] ^{\mathrm{T}}. \end{aligned}$$
(50)

Defining \(\mathbf{K}(n)=E\{{\tilde{\mathbf{w}}}(n){\tilde{\mathbf{w}}}^{\mathrm{T}}(n)\}\) and by taking the statistical expectation of both sides of (50), the following result is obtained:

$$\begin{aligned} \mathbf{K}(n+1)= & {} [\mathbf{I}-\omega ({\bar{\mathbf{R}}}_{\mathrm{D}} +\omega {\bar{\mathbf{R}}}_{\mathrm{L}} )^{-1}{\bar{\mathbf{R}}}] \mathbf{K}(n) [\mathbf{I}\nonumber \\&-\,\omega ({\bar{\mathbf{R}}}_{\mathrm{D}} +\omega {\bar{\mathbf{R}}}_{\mathrm{L}} )^{-1}{\bar{\mathbf{R}}}] ^{\mathrm{T}}. \end{aligned}$$
(51)

Similar to (36), the solution of (51) can be written as

$$\begin{aligned} \mathbf{K}(n+1)= & {} [\mathbf{I}-\omega ({\bar{\mathbf{R}}}_{\mathrm{D}} +\omega {\bar{\mathbf{R}}}_{\mathrm{L}} )^{-1}{\bar{\mathbf{R}}}]^{n+1} \mathbf{K}(0) \{[\mathbf{I}\nonumber \\&\qquad -\omega ({\bar{\mathbf{R}}}_{\mathrm{D}} +\omega {\bar{\mathbf{R}}}_{\mathrm{L}} )^{-1}{\bar{\mathbf{R}}}] ^{\mathrm{T}}\}^{n+1}. \end{aligned}$$
(52)

According to the solution given in (52), if the maximum eigenvalue of the system matrix satisfies \(\left| { \lambda _{\max } [\mathbf{I}-\omega ({\bar{\mathbf{R}}}_{\mathrm{D}} +\omega {\bar{\mathbf{R}}}_{\mathrm{L}} )^{-1}{\bar{\mathbf{R}}}] } \right| <1\), then \([\mathbf{I}-\omega ({\bar{\mathbf{R}}}_{\mathrm{D}} +\omega {\bar{\mathbf{R}}}_{\mathrm{L}} )^{-1}{\bar{\mathbf{R}}}]^{n+1}\rightarrow \mathbf{0}_{M\times M} \) for \(0<\omega <2\), ensuring that \(\mathbf{K}(n)\rightarrow \mathbf{0}_{M\times M} \) as \(n\rightarrow \infty \) in the mean-square sense. In addition, by using both (37) and (52), we can see that the covariance matrix of the weight error vector, \(\mathbf{K}(n)\), converges to the zero matrix much faster than the weight error vector in (37).

3.3 Excess of mean-square error and misadjustment

Considering the filter output error \(e(n)=d(n)-y(n)\) as defined in (4), let us denote the mean-squared error as \(J(n)=E[e^{2}(n)]\). The MSE produced by an algorithm can be written as [4]

$$\begin{aligned} J(n)=J_{\min } +E\left\{ \tilde{\mathbf{w}}^{\mathrm{T}}(n)\mathbf{x}(n)\mathbf{x}^\mathrm{T}(n)\tilde{\mathbf{w}}(n)\right\} , \end{aligned}$$
(53)

where \(J_{\min } \) is the minimum MSE produced by the optimum Wiener filter given as \(J_{\min } =\sigma _d^2 -\bar{{\mathbf{p}}}^{\mathrm{T}}{} \mathbf{w}_{\mathrm{o}} \) in which \(\sigma _d^2 \) is the variance of the desired signal d(n), and the excess of MSE defined by \(J_{\mathrm{exc}} (n)=J(n)-J_{\min } \) [4] can be written for the RSOR algorithm to have the form

$$\begin{aligned} J_{\mathrm{exc}} (n)=\hbox {trace}\{\bar{{\mathbf{R}}} \mathbf{K}(n) \}. \end{aligned}$$
(54)

It is seen from (52) and (54) that \(J_\mathrm{exc} (n)\), and therefore the misadjustment, which is defined by \({{\mathrm{M}}=J_\mathrm{exc} (\infty )}/{J_{\min } }\), converges to zero as \(n\rightarrow \infty \). Thus, similar to the RLS algorithm, the RSOR algorithm converges to zero excess of MSE value and zero misadjustment value.

3.4 Choice of filter parameters

According to (10)–(12), there are two initial parameters for the RSOR algorithm, \(\omega \) and \(\delta \), whereas the RGS algorithm has one initial parameter, \(\delta \) [16]. Typical values of the \(\delta \) parameter are \(\delta =1, 0.1, 0.01, \ldots \), and it is an initialized the autocorrelation as \(\mathbf{R}(0)=\delta \mathbf{I}_{M\times M} \). Similar to the RGS algorithm, \(\delta \) can be used to control the convergence speed of the parameter estimation vector in the initial steps of the RSOR algorithm. The second parameter \(\omega \) is known as the relaxation parameter, and it can also be used to control the convergence speed of the RSOR algorithm. The initial parameters \(\omega \) and \(\delta \) both affect the convergence speed of the RSOR algorithm, and they must be chosen carefully in the initial steps of the algorithm. According to the analysis of the iteration matrix of the RSOR algorithm in (36), a more suitable condition for convergence can be established easily for uncorrelated input signals. When the autocorrelation matrix is decomposed as \({\bar{\mathbf{R}}}=\mathbf{Q}{\varvec{\Lambda }} \mathbf{Q}^\mathrm{T}\), where the columns of \(\mathbf{Q}\) contain the eigenvectors of \({\bar{\mathbf{R}}}\) and the diagonal matrix \({{\varvec{\Lambda }}}\) contains the eigenvectors of \({\bar{\mathbf{R}}}\), the iteration in (36) is written as

$$\begin{aligned} \Delta \mathbf{w}(n+1)=\left[ \mathbf{I}-\omega ({\bar{\mathbf{R}}}_{\mathrm{D}} +\omega {\bar{\mathbf{R}}}_{\mathrm{L}} )^{-1}{} \mathbf{Q}{\varvec{\Lambda }} \mathbf{Q}^\mathrm{T}\right] \Delta \mathbf{w}(n). \end{aligned}$$
(55)

If the input signal \(\mathbf{x}(n)\) is uncorrelated and zero mean, the correlation matrix becomes \({\bar{\mathbf{R}}}=\sigma _x^2 \mathbf{I}_{M\times M} \) and thus, (55) reduces to

$$\begin{aligned} \Delta \mathbf{{w}'}(n+1)=[\mathbf{I}-\omega (\sigma _x^2 )^{-1}\mathbf{\varLambda }] \Delta \mathbf{{w}'}(n) \end{aligned}$$
(56)

where \(\Delta \mathbf{{w}'}(n)=\mathbf{Q}^\mathrm{T}\Delta \mathbf{w}(n)\) is the rotated weight error vector [5]. For the iteration (56) to converge, the absolute values of the diagonal elements of the iteration matrix must be less than 1:

$$\begin{aligned} \left| { 1-\omega (\sigma _x^2 )^{-1}\lambda _i } \right| <1 \quad \hbox { for } i=1,\ldots , M. \end{aligned}$$
(57)

Thus, the following result, which is the same as that for the accelerated EDS algorithm [14], is obtained from the above inequality for uncorrelated Gaussian input signals:

$$\begin{aligned} 0<\omega <\frac{2\sigma _x^2 }{\lambda _{\max } } \end{aligned}$$
(58)

where \(\lambda _{\max } \) is the maximum eigenvalue of \({\bar{\mathbf{R}}}\). The result in (58) is valid when an uncorrelated input signal is used, but can also be a guide for highly correlated input signals.

4 Simulation results: system identification example

By ensemble-averaged computer simulations, the performance of the RSOR algorithm is examined and compared to that of the NLMS algorithm, the APA, the recursive inverse (RI) algorithm [19], the RGS algorithm [16], and the RLS algorithm. The simulation studies are performed using a system identification problem described in [5]. The following optimum parameter vector is used for the unknown system impulse response

$$\begin{aligned} \mathbf{w}_{\mathrm{o}} =[{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} { 1.0}&{} {0.9}&{} {0.1}&{} {0.2} \\ \end{array} }]^\mathrm{T}. \end{aligned}$$
(59)

The filter length of algorithm is \(M=4\) taps, which is equal to the length of the unknown system.

In the first simulation study for the system identification example, the excitation signal of the unknown system was generated using the following AR process:

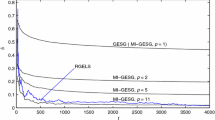
$$\begin{aligned} x(n)=-1.20x(n-1)-0.81x(n-2)+v(n) \end{aligned}$$
(60)

where v(n) is zero-mean white Gaussian noise sequence with variance \(\sigma _v^2 =1\). Thus, the system is excited with a zero-mean correlated input signal with variance \(\sigma _x^2 =5.863\). The eigenvalue spread of the autocorrelation matrix was computed as 58.38. The system response is corrupted by an additive white Gaussian signal, which is uncorrelated with the input signal x(n). The SNR at the output of the system is 36 dB. The following initial parameters are used in the simulations. For the NLMS algorithm and the APA, the step size parameter \(\mu =0.3\). For the RI algorithm, \(\mu _0 =0.00033\), \(\mu (n)={\mu _0 }/{(1-\lambda ^{n})}\), \(\mathbf{R}(0)=\mathbf{0}_{M\times M} \), and \(\mathbf{p}(0)=\mathbf{0}_{M\times 1} \). For the RGS algorithm, \(\delta =1\), \(\mathbf{R}(0)=\delta \mathbf{I}_{M\times M} \), and \(\mathbf{p}(0)=\mathbf{0}_{M\times 1} \). For the RSOR algorithm, \(\omega =1.5\), \(\delta =1\), \(\mathbf{R}(0)=\delta \mathbf{I}_{M\times M} \), and \(\mathbf{p}(0)=\mathbf{0}_{M\times 1} \). For the RLS algorithm, \(\mathbf{R}^{-1}(0)=10 \mathbf{I}_{M\times M} \). The forgetting factor is \(\lambda =0.995\) in the RI, RGS, RLS, and RSOR algorithms. The initial value of the parameter estimation vector is the zero vector in all cases. All simulation results were obtained by averaging 800 simulations of all algorithms. Figure 1 shows the MSE curves for the algorithms used. Figure 2 shows the ensemble-averaged normalized values of the parameter error vector norms, defined as

$$\begin{aligned} \varDelta ={\left\| {{\hat{\mathbf{w}}}(n)-\mathbf{w}_{\mathrm{o}} } \right\| }/{ \left\| {\mathbf{w}_{\mathrm{o}} } \right\| } \end{aligned}$$
(61)

where the vector norm is computed as \(\left\| \mathbf{w} \right\| =\sqrt{\mathbf{w}^\mathrm{T}{} \mathbf{w}}\).

Fig. 1
figure 1

Comparison of the MSE curves of the NLMS, APA, RI, RGS, RLS, and RSOR algorithms (\(\omega = 1.5\))

Full size image
Fig. 2
figure 2

Comparison of the normalized parameter error vector norms of the NLMS, APA, RI, RGS, RLS, and RSOR algorithms (\(\omega = 1.5\))

Full size image

The second simulation is performed to show the effect of the \(\omega \) parameter for the constant \(\delta =1\). The MSE curves of the algorithms for different \(\omega \) values are shown in Fig. 3. The third simulation study shows the effect of the \(\delta \) parameter for the constant \(\omega =1.4\). The MSE curves of the algorithms for different \(\delta \) values are shown in Fig. 4. The initial parameter values for the second and third simulations are the same as those for the first simulation.

Fig. 3
figure 3

Comparison of the MSE curves for different \(\omega \) values of the RSOR algorithm and the other algorithms (\(\delta = 1\))

Full size image
Fig. 4
figure 4

Comparison of the MSE curves for different \(\delta \) values of the RSOR algorithm and the other algorithms (\(\omega = 1.4\))

Full size image

The ensemble-averaged simulation results in Figs. 1 and 2 show that the RSOR algorithm produces results that are very close to the RLS results and better results than the results obtained by the gradient-based algorithms. The RSOR algorithm has a slightly better convergence rate than the RGS algorithm for \(\omega >1\). Figure 2 also shows that the normalized parameter error vector of the RSOR algorithm converges to zero vector, i.e., the parameter estimation vector converges to its optimum value. Also, the ensemble-averaged simulation results in Figs. 1, 3, and 4 show that the RSOR algorithm approaches the same minimum MSE value with the RLS algorithm, i.e., zero excess of MSE and misadjustment value.

5 Conclusion

In this paper, as a useful indication of performance, a stochastic convergence analysis of parameter estimation vector obtained by the RSOR algorithm was presented in the mean and mean-square sense. It is shown that the RSOR algorithm gives an unbiased estimate to optimum Wiener solution of normal equation, and the obtained parameter estimations are convergent in the mean and mean-square sense with zero excess of MSE and zero misadjustment. The convergence analysis results were verified by ensemble-averaged computer simulations. The simulation results showed that the RSOR algorithm has better convergence performance than the gradient-based methods, a slightly better convergence rate for \(\omega >1\) with a slightly higher computational complexity than the RGS algorithm, and comparable results obtained by the RLS algorithm.