Multipartition model for multiple change point identification

Abstract

The product partition model (PPM) is widely used for detecting multiple change points. Because changes in different parameters may occur at different times, the PPM fails to identify which parameters experienced the changes. To solve this limitation, we introduce a multipartition model to detect multiple change points occurring in several parameters. It assumes that changes experienced by each parameter generate a different random partition along the time axis, which facilitates identifying those parameters that changed and the time when they do so. We apply our model to detect multiple change points in Normal means and variances. Simulations and data illustrations show that the proposed model is competitive and enriches the analysis of change point problems.

1 Introduction

Change point identification is not a new problem; it plays an important role in many different fields, including finance, genetics, public health, and historical environmental measurements. It serves a range of purposes such as improving forecasts or identifying events that produced the changes, thus guiding future decisions and policies definition. The main goals when addressing multiple change point problems are to estimate number and positions of the changes. Estimation of structural parameters within clusters is also typically of interest.

Classical methods to identify change points include sequential hypothesis tests, threshold and hidden Markov models, supervised and unsupervised algorithms among others. Discussions about classical methods for this analysis can be found in Chen and Gupta (2000), Horváth and Rice (2014), Niu et al. (2016), Aminikhanghahi and Cook (2017), Tartakovsky et al. (2020), Truong et al. (2020), Yu and Cheng (2022), Chen et al. (2021), Ogunniran et al. (2021), and in references therein. These works provide a survey of some classic results in the area, also including some recent methodologies. Nevertheless, our focus is on Bayesian approaches for change point detection.

There is a wide range of Bayesian models to handle identification of multiple change points. Because this task is a particular case of cluster analysis where only contiguous clusters are possible, approaching this problem by way of the product partition model (PPM), introduced by Hartigan (1990), is appealing. The PPM was first applied in this context by Barry and Hartigan (1992), who consider that change points define a random partition $\rho$. They also explored theoretical aspects of PPMs under this setting. Barry and Hartigan (1993) applied PPMs to the mean of a sequence of Normal variables with unknown constant variance. Simulation-based methods for inference in these models are developed in, e.g., Barry and Hartigan (1993). PPM extensions to detect changes in several parameters are found in Loschi and Cruz (2005).

Multiple change point problems have been addressed through many different methodologies. Chib (1998) formulated these in terms of a latent discrete state variable that evolves according to a discrete-time Markov process and indicates the regime of each particular observation. Fearnhead (2006) presents efficient recursions to calculate the posterior probabilities of different numbers of change points and the posterior mean of the structural parameters, obtaining exact solutions. Fearnhead and Liu (2007) proposed an on-line algorithm for the exact filtering of multiple change point problems. Fearnhead and Rigaill (2019) presented a penalized cost approach that exhibits robustness to the presence of outliers under a bi-weight loss function. Martínez and Mena (2014) proposed a new prior model to $\rho$, assuming cohesion functions given by a suitable modification of an exchangeable partition probability function derived from Pitman’s sampling formula. García and Gutiérrez-Peña (2019) proposed a nonparametric PPM extension that assumes a random measure to model data within each cluster. This flexible approach for the sampling distribution also allows for correlation within regime observations. Correlated observations within clusters are also considered by Monteiro et al. (2011) and Wyse et al. (2011). A dependence structure among the regimes is considered in the models introduced by Fearnhead and Liu (2011) and Ferreira et al. (2014) where the across-cluster correlation is introduced through the prior for structural parameters. The case of multivariate sequences was studied in Nyamundanda et al. (2015), Jin et al. (2022) and Quinlan et al. (2022).

One advantage of PPM is that it allows inferring the change point positions in a probabilistic way, avoiding ad-hoc alternatives such as an analysis via sequential hypothesis test comparing the structural parameters of contiguous clusters. Despite being a competitive model, if applied to sampling models involving two or more parameters, the PPM fails to identify the parameter or subset of parameters associated to the change. In financial data, for instance, despite the long list of works linking volatility and mean return, the analysis presented in Loschi and Cruz (2005) shows that some events may produce changes in volatility but not in its mean return. The usual PPM would be capable of detecting that a change occurred but determining which of volatility and/or mean return was responsible for the change requires extra effort. A similar situation would be observed in cases where interest is on identifying multiple changes in multiparametric models as well as in multivariate ones. Under the PPM structure, we only obtain the posterior distribution of the random partition, that indicates when the structural changes occurred. However, one or more parameters may experience changes, and changes in different parameters may occur asynchronously. This is a long-standing limitation of the PPM. Recently, Peluso et al. (2019) proposed a semiparametric model for the case of several structural parameters. Extending the Chib (1998) model, they assume a specific latent Markovian discrete state variable for each structural parameter, allowing to identify which parameter experienced the change. One challenge when implementing this method is the need to precisely specify a priori the maximum number of changes to be experienced by each parameter. This requires precise prior knowledge about all events that may produce those changes and the specific parameter(s) being correspondingly affected. This is no simple task in general. Although innovative, the inferences for structural parameters obtained from fitting this model are indeed influenced by different specifications for the maximum number of change points.

To overcome this problem, we propose a model where the maximum number of changes in each parameter has no prior constraints. Our approach for tackling this problem differs from that in Peluso et al. (2019) in the prior construction. Our main contribution is the introduction of a multipartition model to detect multiple changes in sequential data (Sect. 2). We refer to it as the Bayesian multipartition change point model (BMCP). The proposed model assumes that different parameters may change at different and unknown times and also experience an unknown number of change points. BMCP is a natural generalization of Barry and Hartigan (1992)’s PPM, assuming different and independent random partitions for each structural parameter in the model. Changes in different parameters are independently driven by different Markovian processes imposing different product distributions for each partition. The posterior distributions for these partitions allow us to identify the instants when changes occurred and the parameter(s) involved. As the random partition is not an Euclidean vector, a great challenge in random partition models is to explore the corresponding posterior distributions. Another contribution of this work is thus the derivation of a computationally efficient algorithm to sample from the joint posterior of parameters and partitions (Sect. 2.1). In Sect. 3 we offer a detailed discussion for the special case of change points in means and/or variances in normal data, extending Barry and Hartigan (1993) and Loschi and Cruz (2005). To evaluate the BMCP performance, we carried out a Monte Carlo simulation study (Sect. 3.2). BMCP is compared to the models introduced by Barry and Hartigan (1993), Loschi and Cruz (2005) and Peluso et al. (2019). We apply BMCP to the analysis of a data set in finance (Sect. 4) and another in genetics (Sect. S.5 of the online supplementary material). Additional comparisons between BMCP and other models are provided in the online supplementary material. A final discussion is presented in Sect. 5.

2 Model definition

The original PPM (Barry and Hartigan 1992, 1993) for the identification of multiple change points is constructed following two main premises: (i) the behavior of the series experiences changes occurring at random instants that partition the time axis accordingly, and (ii) conditional on the positions of these changes and on structural parameters, observations belonging to different clusters are independent and those inside the same cluster are independent and identically distributed (iid). These ideas were previously applied to identify changes in multiple parameters (mean and variance, for instance) assuming they change synchronously. In the following, we extend this idea to identify changes in multiple parameters that may be asynchronous. In our proposal, separate partitions of the time axis are considered, one for each parameter.

Consider a sequence of n random variables $\varvec{X}=\left( X_1,\dots ,X_n\right)$. Let $\varvec{\theta }_1,\dots ,\varvec{\theta }_d$ be sequences of d unknown structural parameters where the sequence related to the kth parameter is $\varvec{\theta }_k=(\theta _{k,1},\dots ,\theta _{k,n})$ for $k=1,\dots ,d$. Let $f(X_i\vert \theta _{1,i},\dots ,\theta _{d,i})$ represent the sampling distribution of $X_i$, parametrized by $\theta _{1,i},\dots ,\theta _{d,i}$, for $i=1,\dots ,n$, and assume that $X_1,\dots ,X_n$ are conditionally independent given $\varvec{\theta }_1,\dots ,\varvec{\theta }_d$. Suppose that each $\varvec{\theta }_k$, $k=1,\dots ,d$, is affected by an unknown number $N_k$ of changes, that occur at unknown positions of the sequence. Let $\rho _k$ represent the random partition that splits the set of indexes $I=\{1,\dots ,n\}$ of $\varvec{\theta }_k$ into contiguous clusters induced by those changes. Consequently, the values in $\varvec{\theta }_k$ are divided into ${B_k=N_k+1}$ unknown contiguous clusters. Partition $\rho _k$ may be defined by $\rho _k = \{\tau _{k,0},\tau _{k,1},\dots ,\tau _{k,b_k}\}$, where $0=\tau _{k,0}<\tau _{k,1}<\dots <\tau _{k,b_k}=n$, denote the contiguous clusters endpoints of ${S_{k,j_k}=\{\tau _{k,j_{k-1}}+1,\dots ,\tau _{k,j_k}\}}$, $j_k=1,\dots ,b_k$, $k=1,\dots ,d$. Each partition $\rho _k$ is alternatively defined by its corresponding set of clusters $\{S_{k,1},\dots ,S_{k,b_k}\}$. The first element of each cluster $S_{k,j_k}$ is called a change point of $\varvec{\theta }_k$.

Given $\rho _k=\{S_{k,1},\dots ,S_{k,b_k}\}$, we assume that all observations belonging to cluster $S_{k,j_k}$ share the same value for the kth structural parameter. Let $\theta ^{\star }_{k,1},\dots ,\theta ^{\star }_{k,b_k}$ represent the cluster-specific parameters related to partition $\rho _k$, such that ${\theta _{k,i} = \theta ^{\star }_{k,j_k}}$ for all $i\in S_{k,j_k}$. We assume a priori that changes in different parameters occur independently, so that the d random partitions $\rho _1,\dots ,\rho _d$ are independent. To simplify notation, we may consider $S_{j_k}$ and $\theta ^{\star }_{j_k}$ to be reduced representations of $S_{k,j_k}$ and $\theta ^{\star }_{k,j_k}$, respectively, since index k is already specified in the index $j_k$. Based on the previous definitions, the vector $\varvec{\theta }_k$ can be written as ${\varvec{\theta }_k = \sum _{j_k=1}^{b_k}\left( \theta ^{\star }_{j_k}{\varvec{1}}\{1\in S_{j_k}\}, \dots , \theta ^{\star }_{j_k}\varvec{1}\{n\in S_{j_k}\} \right) }$, where $\mathbf{{1}}\{A\}$ denotes the indicator function of event A.

Figure 1 graphically depicts the relationships between the random objects in the proposed model when $d = 2$. The conditional dependence between objects is represented by arrows that link them.

Fig. 1

Graphical representation of the proposed model with two structural parameters. Alternative representations for the partitions are given by $\rho _1\!=\!\{S_{1,1}, S_{1,2},S_{1,3}\}\!=\!\{\{1,\dots ,4\},\{5,\dots ,12\}, \{13,\dots ,16\}\}$, $\rho _2\!=\!\{S_{2,1}, S_{2,2}\}\!=\!\{\{1,\dots ,8\}, \{9,\dots ,16\}\}$ and $\rho ^\star \!=\!\{S_1^\star ,S_2^\star ,S_3^\star ,S_4^\star \}\!=\!\{\{1,\dots ,4\},\{5,\dots ,8\},\{9,\dots ,12\},\{13,\dots ,16\}\}$

The combined partition $\rho ^\star$ is defined below in (4). In this example, we have $b_1=3$, $b_2=2$ and the resulting number of clusters in the combined partition $\rho ^\star$ is $b^\star =4$. All parameters inside the continuous-line box have the same value corresponding to the related cluster-specific parameter, for example, $\theta _{1,1}=\theta _{1,2}=\theta _{1,3}=\theta _{1,4}=\theta ^\star _{1,1}$, where $\theta ^\star _{1,1}$ represents the parameter related to cluster $j_1=1$ of partition $\rho _1$. We also have the objects $\varvec{\Theta }^\star _1$, $\varvec{\Theta }^\star _2$, $\varvec{\Theta }^\star _3$ and $\varvec{\Theta }^\star _4$ representing the pairs of cluster-specific parameters $\varvec{\Theta }^\star _1=(\theta ^\star _{1,1},\theta ^\star _{2,1})$, $\varvec{\Theta }^\star _2=(\theta ^\star _{1,2},\theta ^\star _{2,1})$, $\varvec{\Theta }^\star _3=(\theta ^\star _{1,2},\theta ^\star _{2,2})$ and $\varvec{\Theta }^\star _4=(\theta ^\star _{1,3},\theta ^\star _{2,2})$.

By the independence assumption among the random partitions, we have

$$\begin{aligned} P(\rho _1\!\!=\!\{S_{1,1},\dots ,S_{1,b_1}\!\},\ldots , \rho _d\!\!=\!\{S_{d,1},\dots ,S_{d,b_d}\!\}) \!=\!\!\prod _{k=1}^{d}\!P(\rho _k\!\!=\!\{S_{k,1},\dots ,S_{k,b_k}\!\}). \end{aligned}$$

(1)

Following Hartigan (1990), for each $\rho _k$ we assume the product distribution

$$\begin{aligned} P(\rho _k=\{S_{k,1},\dots ,S_{k,b_k}\})=\displaystyle \prod _{j_k=1}^{b_k}c(S_{j_k}) \left[ \displaystyle \sum \limits _{\rho _k\in \mathcal {P}}\;\,\prod _{S_{\ell _k}\in \rho _k}\!\!\!\!\!c(S_{\ell _k})\right] ^{-1}, \end{aligned}$$

(2)

where $\mathcal {P}$ represents the set of all possible partitions of I into contiguous blocks and the cohesions $c(S_{j_k})$ are positive numbers measuring how strongly we believe the components of $\varvec{\theta }_k$ in $S_{j_k}$ are to co-cluster a priori.

It is important to point out that the product form for the prior on $\rho _k$ arises naturally under a Markovian structure assumption for the sequence of change points occurring in $\varvec{\theta }_k$ (Barry and Hartigan 1992). Indeed, if the sequence of endpoints $\tau _{k,0},\dots ,\tau _{k,b_k}$ at the kth structural parameter is a realization of a Markov chain $\{Z_{\ell },\,\ell \in {\mathbb {N}} \}$ in which $Z_{\ell }=\tau _{k,0}=0$ if $\ell =0$ and, for $\ell >0$, $Z_{\ell }$ assumes values in the set $\{Z_{\ell -1}+1, \ldots ,n\}$ if $Z_{\ell -1}\ne n$ and $Z_\ell =\tau _{k,b_k}=n$ if $Z_{\ell -1}=n$, then the prior for $\rho _k$ is given by

$$\begin{aligned} \small { P(\rho _k\!=\!\{\tau _{k,0},\dots ,\tau _{k,b_k}\!\}) \!=\! P(Z_{b_k}\!=\!\tau _{k,b_k}\vert Z_{b_k-1}\!=\!\tau _{k,b_k-1}) \cdots P(Z_{1}\!=\!\tau _{k,1}\vert Z_{0}\!=\!\tau _{k,0}) }, \end{aligned}$$

considering that $P(Z_{0}=\tau _{k,0})=1$. In this case, the cohesions define the one-step transition probabilities on such a Markov chain. However, model (2) is more general and may accommodate different dependence structures among change points, as determined by the choice of $c(S_{j_k})$.

Given $\rho _1,\dots ,\rho _d$, we assume that (i) the d sequences of structural parameters $\varvec{\theta }_1,\dots ,\varvec{\theta }_d$ are independent and (ii) the cluster-specific parameters $\theta ^{\star }_{k,1},\dots ,\theta ^{\star }_{k,b_k}$ related to each sequence $k=1,\dots ,d$ are independent. Under these assumptions, the joint prior distribution of $\varvec{\theta }_1,\dots ,\varvec{\theta }_d$ given $\rho _1,\dots ,\rho _d$ is

$$\begin{aligned} f(\varvec{\theta }_1,\dots ,\varvec{\theta }_d\mid \rho _1,\dots ,\rho _d) =\prod _{k=1}^{d}\prod _{j_k=1}^{b_k}f(\theta ^{\star }_{j_k}), \end{aligned}$$

(3)

where $f(\theta ^{\star }_{j_k})$ is the prior distribution for the cluster-specific parameter $\theta ^{\star }_{j_k}$.

In the PPM by Barry and Hartigan (1992), the partition indirectly induces the clusterization of the sequence of variables $\varvec{X}=\left( X_1,\dots ,X_n\right)$ by imposing that observations with indexes belonging to the same cluster are identically distributed. It also assumes independence across clusters. In the proposed model, as the change points in the sequences of parameters $\varvec{\theta }_1,\dots ,\varvec{\theta }_d$ are realizations of independent processes, the corresponding random partitions do not necessarily induce the same number of clusters, and even if such numbers coincide, the clusters may be distinct across the various parameters. However, the partitions $\rho _1,\dots ,\rho _d$ will induce a unique combined partition $\rho ^\star$ in $\varvec{X}=\left( X_1,\dots ,X_n\right)$. By combining the ordered sequence of endpoints from of all d partitions, we will obtain an ordered sequence of endpoints $0=\tau ^\star _{0}<\tau ^\star _{1}<\dots <\tau ^\star _{b^\star }=n$ belonging to I that splits $\varvec{X}$ into contiguous sets of iid variables. Thus, the combined partition $\rho ^\star$ is defined as

$$\begin{aligned} \rho ^\star = \{\tau ^\star _{0},\tau ^\star _{1},\dots ,\tau ^\star _{b^\star }\} = \cup _{k=1}^{d}\;\rho _k, \;\;\;\; 0 = \tau ^\star _{0}< \tau ^\star _{1}< \dots < \tau ^\star _{b^\star } = n. \end{aligned}$$

(4)

Alternatively, $\rho ^\star$ may be represented by the clusters ${\{S^\star _{1},\dots ,S^\star _{b^\star }\}}$, where ${S^\star _{j}=\{\tau ^\star _{j-1}+1,\dots ,\tau ^\star _{j}\}}$, $j=1,\dots ,b^\star$. Then, given $\rho _1,\dots ,\rho _d$, each nonempty subset ${S_{j_1}\cap \dots \cap S_{j_d}}$, for ${j_k=1,\dots ,b_k}$ and ${k=1,\dots ,d}$, specifies one of the clusters $S^\star _j\in \rho ^\star$, such that $S^\star _j={S_{j_1}\cap \dots \cap S_{j_d}}$. Thus the observations whose indexes belong to $S^\star _{j}$ share the same structural parameters.

Denote by $\varvec{X}_{S^\star _j}$ the subsequence of observations indexed by $S^\star _j$. Assume that, given $(\varvec{\theta },\varvec{\rho })=(\varvec{\theta _1},\dots ,\varvec{\theta _d},\rho _1,\dots ,\rho _d)$, $\varvec{X}_{S^\star _1},\dots ,\varvec{X}_{S^\star _{b^\star }}$ are independent and that, for all $i\in S^\star _j$, $X_i$ are iid variables with conditional marginal density $f(X_i\vert \theta ^{\star }_{j_1},\dots ,\theta ^{\star }_{j_d})$, where ${j_1,\dots ,j_d}$ are the indexes defining $S^\star _j$. The likelihood function is then given by

$$\begin{aligned} f(\varvec{X}\vert \varvec{\theta },\varvec{\rho })\, = \prod _{j=1}^{b^\star }\;\prod _{i\in S^\star _j} f(X_i\mid \theta ^{\star }_{j_1},\dots ,\theta ^{\star }_{j_d}). \end{aligned}$$

(5)

Considering likelihood (5) and prior specifications (3) and (2), the joint posterior distribution for $(\varvec{\theta },\varvec{\rho })$ is given by

$$\begin{aligned} f(\varvec{\theta },\varvec{\rho } \,\vert \, \varvec{X}) \;\propto \; f(\varvec{X}\vert \varvec{\theta },\varvec{\rho })\; \prod _{k=1}^{d}\prod _{j_k=1}^{b_k}f(\theta ^{\star }_{j_k})c(S_{j_k}). \end{aligned}$$

(6)

Note that the model defined by the likelihood (5) and prior (3) and (2) assumes the following dependence structure on $\varvec{X}$. Given $\rho _1,\dots ,\rho _d$, the prior for $\varvec{\theta }_1,\dots ,\varvec{\theta }_d$ imposes (i) a conditional dependence structure among observations belonging to clusters with at least one cluster parameter in common; and (ii) as in the PPM by Barry and Hartigan (1992), conditional independence among observations belonging to clusters having no common parameters.

To the best of our knowledge, the only model that allows for separate identification of change points in different structural parameters is that introduced by Peluso et al. (2019). Next we briefly discuss the main differences between both approaches.

Our proposed model rests on separate partition processes for each parameter component, while Peluso et al. (2019) extend Chib (1998)’s approach, constructing a prior that allows indirect determination of change point locations. Concretely, they introduce a specific latent Markovian discrete state variable for each structural parameter, allowing them to detect which one experienced the change. They also requires that the maximum number of change points in each parameter is a priori a known value ${m_k}$, $k=1,\dots ,d$, that may equal the maximum number of possible changes $n-1$. To model uncertainty about the change points in the kth parameter, a random discrete vector of states $E_k=(\epsilon _{k,1},\dots ,\epsilon _{k,n})$ is defined such that $\epsilon _{k,i}=\ell$, $\ell =1,\dots ,{m_k}+1$, if the structural parameter k at time i belongs to the $\ell$th cluster. An uni-directional Markov process then models the uncertainty about state variables $\epsilon _{k,1},\dots ,\epsilon _{k,n}$. Change point positions are thus obtained by identifying cluster components. Fixing the maximum number of changes at a known value ${m_k\le n-1}$ implies assuming a null probability for realizations of the process with more than ${m_k}$ change points, which requires that reliable prior information about ${m_k}$ should be available. Instead our proposal (2) does not require such a pre-specified maximum. Another important issue is that the results from the model by Peluso et al. (2019) turn out to be very sensitive to the choice of ${m_k}$ (see Sect. S.4 in the online supplementary material).

2.1 Sampling from the posteriors in the proposed model

The posterior distribution in (6) is intractable and some computational procedures must be used to approximate it. We propose a partially collapsed Gibbs sampler (Van Dyk and Park 2008) based on a blocking strategy to sample from the joint posterior distribution of partitions $\varvec{\rho }=\{\rho _1,\dots ,\rho _d \}$ and parameters $\varvec{\theta }=\{\varvec{\theta }_1,\dots ,\varvec{\theta }_d\}$. In a more general context, let $\varvec{\delta }$ be the set of hyperparameters indexing the prior distribution of $(\varvec{\theta },\varvec{\rho })$. Denote by $\varvec{\theta }_{(-\ell )}$ the set $\varvec{\theta }$ without vector $\varvec{\theta }_\ell$ and $\varvec{\rho }_{(-\ell )}$ the set $\varvec{\rho }$ without partition $\rho _\ell$, and let the vector $\varvec{\theta }_{k,(-i)}=(\theta _{k,1},\dots ,\theta _{k,i-1},\theta _{k,i+1},\dots ,\theta _{k,n})$, i.e. $\varvec{\theta }_{k}$ without coordinate i. Assuming that the proposed model holds, and also that given a partition $\rho _k$, $\theta _{k,i}$ belongs to cluster $S_{k,J}$, the full conditional posterior distributions for $\rho _k$, $\varvec{\theta }_k$ and $\varvec{\delta }$ are, respectively,

$$\begin{aligned}&P(\rho _k=\{S_{k,1},\dots ,S_{k,b_k}\} \vert \varvec{\rho }_{(-k)},\varvec{\theta },\varvec{\delta },\varvec{X}) \;\propto \; f(\varvec{X}\vert \varvec{\theta },\varvec{\rho }) \displaystyle \prod _{j_k=1}^{b_k}f(\theta ^{\star }_{j_k})c(S_{j_k});\\&{f(\theta _{k,i}\vert \varvec{\rho },\varvec{\theta }_{(-k)},\varvec{\theta }_{k,(-i)}, \varvec{\delta },\varvec{X}) \;\propto \; f(\theta ^{\star }_{k,J})f(\varvec{X}\vert \varvec{\theta },\varvec{\rho })}; \\&f(\varvec{\delta } \vert \varvec{\rho },\varvec{\theta },\varvec{X}) \;\propto \; f(\varvec{\delta })\displaystyle \prod _{k=1}^{d}\prod _{j_k=1}^{b_k} f(\theta ^{\star }_{j_k})c(S_{j_k}). \end{aligned}$$

Because $\rho _1,\dots ,\rho _d$ are supported on discrete spaces, a major challenge in the proposed multipartition model is to handle their posterior distributions. To sample from the full conditional distributions of $\rho _1,\dots ,\rho _d$, we adapt the method in Barry and Hartigan (1993) to our multipartition model. Each random partition $\rho _k$ is represented by a fixed dimension random vector $\varvec{U}_k=(U_{k,1},\dots ,U_{k,n-1})$ where each coordinate $U_{k,i}$ indicates whether or not a change point occurred at position $i+1$ of the parameter vector $\varvec{\theta }_k$, that is, ${U_{k,i}=1}$ if ${\theta _{k,i}=\theta _{k,i+1}}$ and ${U_{k,i}=0}$, otherwise. The pseudo-code to sample from the joint posterior distribution $f(\varvec{\theta },\varvec{\rho },\varvec{\delta }\vert \varvec{X})$ is given in Algorithm 1, where ${\varvec{\theta }}_{(-k)}^{(t)}=(\varvec{\theta }_{1}^{(t)},\dots ,\varvec{\theta }_{k-1}^{(t)}, \varvec{\theta }_{k+1}^{(t-1)},\dots ,\varvec{\theta }_{d}^{(t-1)})$ denotes the imputed values of the parameter vectors $\{\varvec{\theta }_1,\dots ,\varvec{\theta }_d\}$ at iteration t without the parameter vector $\varvec{\theta }_{k}$ and $\varvec{U}^{(t)}_{k,(-i)}=(U^{(t)}_{k,1},\dots ,U^{(t)}_{k,i-1},U^{(t-1)}_{k,i+1},\dots ,U^{(t-1)}_{k,n-1})$ denotes the imputed value of $\varvec{U}_{k}$ at iteration t with the ith coordinate removed.

Samples from the posterior distribution of each partition $\rho _k$, $k=1,\dots ,d$, are obtained by sampling from the full conditional distribution of $\varvec{U}_{k}$. In the tth iteration, these samples are obtained considering the following ratio:

$$\begin{aligned} R^{(t)}_{k,i} = \frac{P(U_{k,i}=1 \mid \varvec{U}^{(t)}_{k,(-i)},\varvec{\theta }^{(t)}_{(-k)},\varvec{\delta },\varvec{X})}{P(U_{k,i}=0 \mid \varvec{U}^{(t)}_{k,(-i)},\varvec{\theta }^{(t)}_{(-k)},\varvec{\delta },\varvec{X})}. \end{aligned}$$

(7)

The partitions in the numerator and denominator of (7) only differ at position i. Assume that the partition in the numerator is $(U_{k,1},\dots ,U_{k,i-1},U_{k,i}=1,U_{k,i+1},\dots ,U_{k,n-1})$ and that a cluster $S_{k,J}$ contains the ith element of I. The partition in the denominator splits $S_{k,J}$ creating two new clusters. Although all the other clusters are shared by both partitions, these two partitions induce a different number of distinct $\varvec{\theta }_k$ coordinates in the numerator and denominator of (7). In fact, for one of these terms the number of distinct parameter values $\theta _{k,i}$ in $\varvec{\theta }_k$ differs from the configuration in $\varvec{\theta }^{(t-1)}_{k}$. Thus, sampling from the posterior of each $\rho _k$ requires that all components ${\theta }_{k,i}$ must be integrated out in (7), so that both probabilities in the numerator and denominator are not conditional to $\varvec{\theta }_k$. Conjugacy facilitates obtaining such integrals analytically; otherwise additional procedures such as numerical integration are needed.

Under the proposed model assumptions, the probabilities in (7) are

$$\begin{aligned} p(U_{k,i} \mid \varvec{U}_{k,(-i)},\varvec{\theta }_{(-k)},\varvec{\delta },\varvec{X}) \;\propto \; \displaystyle \prod _{j_k=1}^{b_k} f(\varvec{X}_{S_{j_k}}\vert \varvec{\theta }_{(-k)}) c(S_{j_k}), \end{aligned}$$

(8)

where the likelihood function restricted to cluster $S_{j_k}$ is given by

$$\begin{aligned} f(\varvec{X}_{S_{j_k}}\vert \varvec{\theta }_{(-k)}) = \displaystyle \int \Bigg ( \prod _{i\in S_{j_k}}\!\! f(\varvec{X}_{S_{j_k}}\vert \theta ^{\star }_{j_k},\varvec{\theta }_{(-k),i}) \Bigg ) f(\theta ^{\star }_{j_k})\,d\theta ^{\star }_{j_k}, \end{aligned}$$

(9)

and $\varvec{\theta }_{(-k),i}$ represents $\{\theta _{1,i},\dots ,\theta _{d,i}\}$ with $\theta _{k,i}$ removed. Parameter $\theta _{k,i}$ is represented in (9) by $\theta ^{\star }_{j_k}$ since by definition $\theta _{k,i}=\theta ^{\star }_{j_k}$ for all $i\in S_{j_k}$. For all $i\in S_{j_k}$, the new sample value for coordinate $U_{k,i}$ is ${U^{(t)}_{k,i}=\textbf{1}\left\{ \frac{u}{1-u}\le R^{(t)}_{k,i}\right\} }$, where u is a draw from the uniform distribution in (0,1) and

$$\begin{aligned} R^{(t)}_{k,i}= \frac{f(\varvec{X}_{S_{j_k}}\mid \varvec{\theta }_{(-k)})c(S_{j_k})}{f(\varvec{X}_{S^{(1)}_{j_k}}\mid \varvec{\theta }_{(-k)})c(S^{(1)}_{j_k})\; f(\varvec{X}_{S^{(2)}_{j_k}}\mid \varvec{\theta }_{(-k)})c(S^{(2)}_{j_k})}, \end{aligned}$$

(10)

where $S^{(1)}_{j_k}\!=\!\{\tau _{k,j_k-1}+1,\tau _{k,j_k-1}+2,\dots ,i-1,i\}$ and $S^{(2)}_{j_k}\!=\!\{i+1,i+2,\dots ,\tau _{k,j_k}-1,\tau _{k,j_k}\}$ are the two clusters generated by dividing cluster $S_{j_k}$ in the case of $U_{k,i}=0$.

3 The BMCP model for normal data

The model developed in the previous section is now applied to identify change points in the means and variances of normally distributed data. Consider the sequence of random variables $\varvec{X}=(X_1,\dots ,X_n)$ and the sequences of unknown structural parameters $\varvec{\mu }=(\mu _1,\dots ,\mu _n)$ and $\varvec{\sigma }=(\sigma ^2_1,\dots ,\sigma ^2_n)$. Following the general discussion in Sect. 2 we assume that $X_i\vert \varvec{\mu },\varvec{\sigma }\overset{ind}{\sim }N(\mu _i,\sigma ^2_i)$, $i=1,\dots ,n$. In addition, change points in $\varvec{\mu }$ and $\varvec{\sigma }$ are assumed to occur independently, at unknown and possibly different instants. Let $\rho _1$ and $\rho _2$ be the random partitions of I that induce contiguous clusters in $\varvec{\mu }$ and $\varvec{\sigma }$, respectively. Denote by $\mu ^{\star }_{j_1}$ the common mean into the cluster $S_{j_1}$, $j_1=1,\dots ,b_1$, and let $\sigma ^{2\star }_{j_2}$ be the common variance for observations into the cluster $S_{j_2}$, $j_2=1,\dots ,b_2$. Let $n_{j_k}\!=\#S_{j_k}$ for $k=1,2$ and $n^\star _j\!=\#S^\star _j$ where $S^\star _{j}=S_{j_1}\cap S_{j_2}$. Also, let $\overline{X}_{S^\star _j}\!=\textstyle \sum _{i\in S^\star _j}\!X_i/n^\star _j$, for $j=1,\dots ,b^\star$.

Given $\rho _1$ and $\rho _2$, assume that (i) the observations $X_i$ for ${i\in S^\star _{j}=S_{j_1}\cap S_{j_2}}$ are iid with $X_i\vert \mu ^{\star }_{j_1},\sigma ^{2\star }_{j_2} \overset{iid}{\sim } N(\mu ^{\star }_{j_1},\sigma ^{2\star }_{j_2})$ and (ii) observations in different clusters are independent. Under these assumptions, the likelihood function is given by

$$\begin{aligned} f(\varvec{X}\vert \varvec{\mu },\varvec{\sigma },\rho _1,\rho _2)= \prod _{j_1=1}^{b_1}\; \prod _{\{j_2\mid S^\star _{j}\ne \emptyset \}}\! \left( \frac{1}{2\pi \sigma ^{2\star }_{j_2}}\right) ^{n^\star _{j}/2}\!\!\!\!\!\!\!\! \exp \left\{ -\!\!\!\sum _{i\in S^\star _{j}}\!\!\! \frac{(X_i-\mu ^{\star }_{j_1})^2}{2\sigma ^{2\star }_{j_2}}\right\} , \end{aligned}$$

(11)

where $\{j_2\mid S^\star _{j}\ne \emptyset \}$ denotes the set of values $j_2$ for which ${S^\star _{j}\ne \emptyset }$. The double product in (11) is equivalent to the single product $\prod _{j=1}^{b^\star }$ over $\rho ^\star$ in (5) when $d=2$ or to its permuted form ${\prod _{j_2=1}^{b_2}\;\prod _{j_1\mid S^\star _{j}\ne \emptyset }}$. In fact, the likelihood function in (11) is the product of n Normal densities in which the means $\mu _i$ and the variances $\sigma _i^2$ are piecewise constant within the intervals defined by the partitions $\rho _1$ and $\rho _2$, respectively.

Given $\rho _1$ and $\rho _2$, we assume independence of $\varvec{\mu }$ and $\varvec{\sigma }$, and that the parameters in different clusters are also independent, with prior distributions

$$\begin{aligned} \begin{aligned} \mu ^{\star }_{j_1} \!\overset{iid}{\sim }\! N(\mu _0,\sigma ^2_0),\, j_1\!=\!1,\!...,b_1,&\;\;\;\text {and}\;\;\; \sigma ^{2\star }_{j_2} \!\overset{iid}{\sim }\! IG(a/2,d/2),\ j_2\!=\!1,\!...,b_2. \end{aligned} \end{aligned}$$

(12)

For the random partitions $\rho _1$ and $\rho _2$, we assume the independent product partition distributions given in (2). The cohesion proposed by Yao (1984) is considered to quantify how strongly we believe the components of $\varvec{\mu }$ and $\varvec{\sigma }$ are to co-cluster a priori. The Yao’s cohesion is indexed by a parameter that represents the probability of a change in the structural parameter to occur at any instant. In addition to allowing for the possibility that $\varvec{\mu }$ and $\varvec{\sigma }$ change at different times, our prior construction permits these parameters to have different numbers of changes. This is achieved by considering separate probabilities $p_1$ and $p_2$ of a change in the mean and variance, respectively. By assuming $p_1$ and $p_2$ to be independent and continuously distributed, as formalized in (15) below, we are not restricting the model to link positions or number of change points in mean and variance. In fact, it immediately follows that the prior probability that $p_1$ differs from $p_2$ is 1. Thus, to model prior uncertainty about $\rho _k$, $k=1,2$, we assume the cohesions

$$\begin{aligned} c(S_{j_k})={\left\{ \begin{array}{ll} (1-p_k)^{n_{j_k}-1}p_k \text {if} j_k=1,2,\dots ,b_k-1,\\ (1-p_k)^{n_{j_k}-1} \text {if} j_k=b_k. \end{array}\right. } \end{aligned}$$

(13)

Therefore, given $p_k$, the prior distribution for $\rho _k$ will depend only on the number of clusters $b_k$ in the partition $\rho _k$ and it is given by

$$\begin{aligned} P(\rho _k=\{\tau _{k,0},\tau _{k,1},\dots ,\tau _{k,b_k}\}\mid p_k) = (p_k)^{b_k-1}(1-p_k)^{n-b_k}. \end{aligned}$$

(14)

To complete the model specification, we assume a priori that

$$\begin{aligned} p_k\overset{ind}{\sim }\ Beta(\alpha _k,\beta _k),\quad k=1,2. \end{aligned}$$

(15)

The joint posterior and the full conditionals of the parameters of the BMCP model for Normal data, to be considered in Algorithm 1, are described in Sect. S.1 of the online supplementary material.

3.1 On the prior for the number of change points

Assuming the prior distributions for $\rho _k$ are defined as given by (14) and (15), the number $N_k$ of change points in the kth parameter, related to $\rho _k$, has an induced $Beta\text {-}Binomial(n-1,\alpha _k,\beta _k)$ prior distribution

$$\begin{aligned} \begin{aligned} P(N_k=\nu )&= \genfrac(){0.0pt}0{n-1}{\nu } \frac{\Gamma (\alpha _k+\beta _k)\Gamma (\alpha _k+\nu )\Gamma (n-1+\beta _k-\nu )}{\Gamma (\alpha _k)\Gamma (\beta _k)\Gamma (\alpha _k+\beta _k+n-1)},\;\; \end{aligned} \end{aligned}$$

for $\nu =0,1,\dots ,n-1.$ Thus, mean and variance are given, respectively, by

$$\begin{aligned} E(N_k) = (n-1)\frac{\alpha _k}{\alpha _k+\beta _k} \;\;\;\;\textrm{and} \;\;\;\; Var(N_k)=(n-1)\frac{\alpha _k\beta _k(\alpha _k+\beta _k+n-1)}{(\alpha _k+\beta _k)^2(\alpha _k+\beta _k+1)}. \end{aligned}$$

If $\alpha _k=\beta _k$, we assume a priori that around $50\%$ of the observations experienced a change. Considering $\alpha _k=\beta _k=1$ implies the prior assumption that ${N_k\sim U\{0,1,\dots ,n-1\}}$. If $\alpha _k \rightarrow 0$ and $\beta _k \rightarrow 0$ then the Beta-Binomial distribution assigns significant probability mass to the extreme values $N_k=0$ and $N_k =(n-1)$ and negligible probability to the other values. Although this prior choice for $N_k$ is highly informative, favoring the extremes of the interval [0, 1], it behaves very much like Jeffreys’ non-informative prior for Binomial models.

In practice, the prior information available about events that may produce change points is rather weak. Thus, a convenient strategy is to consider the moments of $N_k$ instead of specifying a prior for $p_k$. Noting that assuming $E(N_k)=\nu$ implies that $\beta _k=\alpha _k Q$, where $Q=(n-1-\nu )/\nu$, we get

$$\begin{aligned} \begin{aligned} Var(N_k)&= \nu \left( \frac{Q}{1+Q}\right) \left( \frac{\alpha _k(1+Q)+n-1}{\alpha _k(1+Q)+1}\right) . \end{aligned} \end{aligned}$$

The derivative of $Var(N_k)$ w.r.t $\alpha _k$ is given by $[{\nu }Q(2-n)][\alpha _k(1+Q)+1]^{-2}$, that is negative for $n\ge 3$, and $\lim _{\alpha _k\rightarrow \infty }Var(N_k)=\nu (n-1-\nu )/(n-1)$. These results are useful to guide our prior choices for $\alpha _k$ and $\beta _k$. Indeed, we obtain prior distributions for $N_k$ with large variances by eliciting lower values for $\alpha _k$.

Conditional to $p_1$ and $p_2$, the number of changes $N^\star$ in $\rho ^\star$ has a ${Binomial(n-1,\;p^\star )}$ distribution, where $p^\star =1-\prod _{k=1}^{2}(1-p_k)$. Therefore, the expectation and the variance of $N^\star$, respectively, are

$$\begin{aligned} \begin{aligned} E(N^\star )&= (n-1)\left( 1-\prod _{k=1}^{2}\frac{\beta _k}{\alpha _k+\beta _k}\right) ,\\ Var(N^\star )&= (n-1)\prod _{k=1}^{2}\frac{\beta _k}{\alpha _k+\beta _k} - (n-1)^2\prod _{k=1}^{2}\left( \frac{\beta _k}{\alpha _k+\beta _k}\right) ^2\\&+ (n^2-3n+2)\prod _{k=1}^{2}\left( \left( \frac{\beta _k}{\alpha _k+\beta _k}\right) ^2 + \frac{\alpha _k\beta _k}{(\alpha _k+\beta _k)^2(\alpha _k+\beta _k+1)}\right) .\\ \end{aligned} \end{aligned}$$

3.2 Monte Carlo simulation study

We ran a Monte Carlo simulation study to evaluate the performance of the proposed BMCP model when identifying multiple change points in Normal means and variances. We compare (Sect. 3.2.1) the proposed BMCP with the models DPM19 (Peluso et al. 2019), LCIA05 (Loschi and Cruz 2005) and BH93 (Barry and Hartigan 1993). Simulation studies for different scenarios can be found in Sect. S.2 of the online supplementary material. We also provide a sensitivity analysis of BMCP to prior choices for $\rho _1$ and $\rho _2$ (Sect. 3.2.2).

3.2.1 Comparing BMCP with models DPM19, LCIA05 and BH93

For normally distributed data applications, the DPM19 model identifies changes in $\varvec{\mu }$ and $\varvec{\sigma }$ separately through two random discrete state vectors indicating the regime of each parameter at every instant. We refer to these state vectors by $E_1$ and $E_2$, respectively. We consider the DPM19 prior specifications exactly as proposed by Peluso et al. (2019): a Beta(1, 1) prior distribution for the time-dependent probability of regime change; for the regime parameters, we assume Dirichlet process prior distributions with concentration parameters $M_1\overset{D}{=}M_2\sim Ga(0.05,0.0001)$ and base distributions $N(\mu _0,\sigma _0^2)$ for the regime means and IG(a, d) for the regime variances, where $(\mu _0,\sigma _0^2,a,d)=(0,1,1,1)$. Also following Peluso et al. (2019), we fix the maximum number of changes $m_1$ and $m_2$ as the true number of changes in $\varvec{\mu }$ and $\varvec{\sigma }$, respectively. This is a highly informative choice as discussed in Sect. 2.

BH93 and LCIA05 models consider a single partition $\rho$ to identify the changes. BH93 is proposed to identify changes only in the mean, under constant variance. It assumes that ${X_i\vert \mu _i,\sigma ^2\overset{ind}{\sim }N(\mu _i,\sigma ^2)}$, $i=1,\dots ,n$, and that, a priori, ${\mu ^{\star }_j\overset{iid}{\sim }N(\mu _0,\sigma _0^2/n_j)}$, where $n_j=\#S_j$, $j=1,\dots ,b$. We consider the same prior specifications proposed in Barry and Hartigan (1993) for $\sigma ^2$, $\mu _0$ and $\sigma _0^2$. LCIA05 identifies changes in $\varvec{\mu }$ or $\varvec{\sigma }$, but does not specify which parameter has changed. To analyze the data using LCIA05 the following prior distributions for the cluster parameters are assumed: ${\mu ^{\star }_j\vert \sigma ^{2\star }_j\overset{iid}{\sim }N(m,v\sigma ^{2\star }_j)}$ and ${\sigma ^{2\star }_j\overset{iid}{\sim }IG(a/2,d/2)}$ with ${(m,v,a,d)=(0,2,0.1,2.1)}$. In the simulation study, the changes estimated by the LCIA05 and BH93 models should be compared to the true $\rho ^\star$ and $\rho _1$ of the proposed model, respectively.

For the BMCP model, we assume the prior distributions given in (12), with hyperparameters $(\mu _0,\sigma ^2_0,a,d)=(0,100,0.1,2.1)$, which is a reasonably flat prior for both $\mu ^{\star }_{j_1}$ and $\sigma ^{2\star }_{j_2}$. For all the partition models (BH93, LCIA05 and BMCP), we consider the Yao’s cohesion to model the prior uncertainty about the random partitions. The Beta(1, 1) is assumed as the prior distributions for parameters $p_1$ and $p_2$ in BMCP and for parameter p in the LCIA05. In BH93, we assume $p\sim U(0,0.05)$.

We consider 400 data sequences of size $n=300$, in which four changes in the mean and one change in the variance occur at different times, inducing a total of six clusters. Changes in the mean and variance are given by the partitions $\rho _1=\{0,60,120,180,240,300\}$ and $\rho _2=\{0,150,300\}$, respectively, and the cluster parameters are $\varvec{\mu }^\star =(0,2,4,2,0)$ and $\varvec{\sigma }^\star =(1,4)$. For each data set, samples of the posterior distribution are obtained through the proposed MCMC scheme. In the case of the BMCP, LCIA05 and BH93 models, 20, 000 samples were generated after a warm-up period of 30, 000 iterations. These models were implemented in C++ language and integrated to R through the Rcpp package (Eddelbuettel 2013). For the DPM19 model, 2, 000 samples were generated after a warm-up period of 3, 000 iterations. Algorithm convergence is assessed by resorting to standard diagnostics, such as those discussed in Gelman and Rubin (1992). The specification of small values for $m_1$ and $m_2$ considerably reduces the parameter spaces of the DPM19 model, when compared to the parameter space of the PPM-based models. Therefore, a small number of iterations is required for the DPM19 sampling procedure. The R code of BMCP and DPM19 models are available at https://github.com/rcpedroso/bmcp and https://github.com/stefanopel/DPM-change-point, respectively.

Figure 2 shows the average of the 400 posterior means (product estimates) for the $\mu _i$’s (Fig. 2a–d) and the $\sigma _i^2$’s (Fig. 2e–h) and the $5\%$ and $95\%$ quantiles of such estimates at each instant $i=1,\dots ,300$ for all models. The simulation truth is indicated by gray solid lines, while the black dots represent the posterior means. The four models provide reasonable estimates for the means. These estimates are more biased around the true changes and it is more evident after instant 150, when the variance experiences an increase. For all the models the estimates for the means become less accurate after the change in the variance. However, in the LCIA05 and BH93 models the loss of accuracy is more severe. The BMCP model provides the most accurate estimates for the means (Fig. 2a) and for the variances (Fig. 2e).

Fig. 2

Average of the product estimates (black dots) for the means (a–d) and variances (e–h) in each instant and the $5\%$ and $95\%$ quantiles of such estimates based on the Monte Carlo replications, under BMCP, DPM19, LCIA05 and BH93. The solid gray horizontal lines indicate the true mean and variance. The vertical gray dotted and dashed lines are the true endpoints in $\varvec{\mu }$ and $\varvec{\sigma }$, respectively

As shown in Fig. 2g, the product estimates for the variance provided by model LCIA05 are clearly affected by changes in the mean. For example, the product estimates for the variance present a noticeable change at position 120, indicating the presence of a change point in this parameter and position, but such change does not truly exist. A similar but less evident bias can be seen in Fig. 2f. BMCP and DPM19 have similar performance but DPM19 produced more biased estimates in the third cluster for the means and for the variance between observations 100 and 150.

Regarding inference for means and variances, it is important to mention that, for all models, the posterior distributions for means (resp., variances) tend to be symmetric (resp., asymmetric) and unimodal for those time points inside (i.e. not at the border of) clusters. See examples of this in Fig. 3. However, the boundary effect for both parameters can be clearly seen at change point times or at positions close to these. In those cases, the corresponding posterior distributions exhibit bimodal behavior, as also illustrated in Fig. 3a and b. Specifically, Fig. 3a and b, respectively, show the posterior densities of the mean and variance at positions 150, the true endpoint of the variance, and 240, one of the true endpoints of the mean, under the BMCP model for one data set randomly selected among the 400 we generated. Also, Fig. 3c shows the estimated posterior densities of $p_1$ and $p_2$ disclosing that $p_1$ is higher than $p_2$. The differences between these posterior distributions were to be expected due to more changes in the mean than in the variance.

Fig. 3

Estimated posterior densities for parameters $\mu _{150}$ and $\mu _{250}$ (a), $\sigma ^2_{150}$ and $\sigma ^2_{250}$ (b) and $p_1$ and $p_2$ (c) under the BMCP model, for one simulated data set

Table 1 shows the partitions that were more frequently pointed out as the most probable ones among the 400 posterior modes obtained from the repeated simulations, for both structural parameters. Table 1 shows competitive performances between the BMCP and DPM19 models to identify the true partitions in the data. The LCIA05 model does not identify the variance change in the reported partitions. Under the LCIA05 model the most likely partitions under the posteriori, in the sense of being most frequently selected in our Monte Carlo study, indicate the occurrence of only the four changes in the mean. Under the BMCP and DPM19 models, the estimated partitions that differ from the true $\rho _1$ or $\rho _2$ are very close to the true ones, in the sense that differences occur only by one or two elements or positions. Assuming the BMCP and DPM19, for the majority of the data sets, the most likely partitions for the variance correctly indicate the existence of one change point. Not all of these partitions precisely identify its correct position, but even so, they indicate an instant that is not far from the true change point. For instance, by fitting the BMCP, the partition was correctly estimated for $22\%$ of the samples and the estimated partition indicates that a change occurred one instant (resp., two instants) after the true change point for $14.5\%$ ($10.25\%$) of the samples.

Table 1 Top posterior modes of $\rho _1$ and $\rho _2$ (BMCP), $E_1$ and $E_2$ (DPM19) and $\rho$ (LCIA05, BH93) estimated for each of the 400 data sets

Due to the high dimension of the space of random partitions ($2^{n-1}$ different elements), the posterior distribution tends to be too flat in many situations. This complicates inference related to the exact location of change points. In this context, the method proposed by Loschi and Cruz (2005) is a good auxiliary tool to this effect. For each parameter k, we obtain this probability for instant i, by summing the posterior probability in (2) for all partitions $\rho _k$ that identified i as a change. Figure 4 displays the average of the 400 posterior probabilities obtained for instant $i=1, \dots , 300$ for each model.

Fig. 4

Average of the posterior probabilities of each instant to be an endpoint (black dots) for each partition and the $5\%$ and $95\%$ quantiles range of such probabilities based on the Monte Carlo replications, for BMCP, DPM19, LCIA05 and BH93

Fig. 5

Counts distribution of the posterior modes of the number of changes, estimated in each of the 400 replications, for BMCP, LCIA05, DPM19 and BH93

These probabilities at the true change points are, on average, greater than at other instants. BMCP and DPM19 models indicate, with similar accuracy, the instants at which the changes took place for both, mean and variance. Unlike what is observed under the other models, the BH93 model probabilities tend to be greater than zero for all instants after the change in the variance.

Figure 5 shows the frequency at which a value $b=1, \dots , n$, was estimated as the number of changes in each structural parameter, for all models. We estimate the number of changes as the corresponding posterior mode. Figure 5 shows that for more than $85\%$ of the data sets, both BMCP and DPM19 models correctly estimate the number of changes in the mean as well as in the variance. LCIA05 underestimated the true number of changes (N=5) by one in most of the data sets (Fig. 5c). BH93 overestimated the number of mean changes for almost all data sets, reflecting the expected poor performance of this model due to its constant variance assumption (Fig. 5f).

In summary, the results of this study show that BMCP achieves the goal of identifying changes in the mean and variance separately, providing better results than LCIA05 and BH93. When compared to DPM19, BMCP provides highly competitive results. Considering that DPM19 requires the maximum number of change points in each parameter to be previously specified, which is not required by BMCP, together with the fact that we favor DPM19 by setting these values equal to the true number of changes, our results show that BMCP is a competitive model for change point analysis. BMCP provides very accurate estimates for the structural parameters as well as for the number and positions of the change points, effectively overcoming the DMP19 performance. Additional simulation study results evaluating different change positions and the sensitivity of the BMCP and DPM19 models to hyperparameter specifications can be found in the accompanying online supplementary material.

3.2.2 Sensitivity analysis to the priors of $\rho _1$ and $\rho _2$

Our goal in this section is to evaluate the effect of different prior specifications for the random partitions $\rho _1$ and $\rho _2$ in the posterior inference obtained by fitting the BMCP. Two flat priors for $\rho _k$ are elicited choosing $\alpha _k =\beta _k$ close to zero for $k=1,2$, a priori, overestimating the number of change points in both structural parameters. Two other prior distributions are considered, setting $\alpha _k$ and $\beta _k$ such that the expected number of changes is a priori equal to the true one, following the theoretical framework discussed in Sect. 3.1. These prior specifications are presented in Table 2.

Table 2 Hyperparameters for the prior distributions of $p_1$ and $p_2$

Using the same prior specifications for the structural parameters $\mu ^\star _{j_1}$ and $\sigma ^\star _{j_2}$ considered in Sect. 3.2.1, we estimate BMCP for the same 400 data sets considered in that section (Scenario 1) and also for 400 replications of a modified scenario in which the changes occurred at the same positions but the cluster-specific means and variances in different clusters are closer, given by $\varvec{\mu }^\star =(0,1,2,1,0)$ and $\varvec{\sigma }^\star =(1,2)$ (Scenario 2).

Our results indicate no remarkable difference in the posterior inferences for the Scenario 1. A slightly different posterior inference is observed only for the number of clusters in both the mean and the variance as shown in Fig. 6.

Fig. 6

Count distributions of the posterior modes for the number of changes in the mean $N_1$ (a–d) and in the variance $N_2$ (e–h), estimated for each of the 400 replications in Scenario 1 for all four prior specifications for $\rho _1$ and $\rho _2$

Figure 6 shows the frequency at which a value b, $b=1, \dots , n$, was estimated as the posterior mode of $N_1$ and $N_2$ under Scenario 1, considering the prior specifications for $p_1$ and $p_2$ given in Table 2. In this scenario, we found the prior specifications for $p_1$ and $p_2$ to have no effect on the posterior probabilities of each instant to be an endpoint for both mean and variance. The same conclusions are obtained when analyzing the case of $\varvec{\mu }$ and $\varvec{\sigma }$. These results are similar to those reported in Sect. 3.2.1, when adopting a uniform prior on both $p_1$ and $p_2$. Figure 7 displays these results for the case of the prior specification B1. Results for the prior specification B2, B3 and B4 are similar.

Fig. 7

Average of the product estimates (a and b, black dots) in each instant and for the posterior probabilities of each instant to be an endpoint (c and d, black dots) for the means (a and c) and variances (b and d) and the $5\%$ and $95\%$ quantiles of such estimates based on the 400 Monte Carlo replications, Scenario 1 and Model B1. The true means (a) and variances (b) are indicated by the solid gray horizontal lines. The vertical gray dotted and dashed lines indicate the true endpoints in $\rho _1$ and $\rho _2$, respectively

For Scenario 1, the sensitivity analysis empirically shows that our proposed BMCP was robust to different prior specifications for $p_1$ and $p_2$. However, it is important to mention that for this scenario, the means and variances are substantially different across clusters, favoring the correct identification of such changes. When the cluster-specific parameters have closer values (Scenario 2), the prior distributions for $\rho _1$ and $\rho _2$ play a more important role in the posterior inference obtained by fitting BMCP. Figure 8 shows that BMCP has better performance when more informative priors for $\rho _1$ and $\rho _2$ are assumed. The selected prior distributions have shown higher influence over the posterior inferences related to the variance (see Fig. 9). For instance, the number $N_2$ of changes in the variance is more precisely estimated if Model B4 is fitted, and the product estimates for the variance are less precise when Model B1 is assumed. Posterior inference about the means were less sensitive to these different prior specifications.

Fig. 8

Count distributions of the posterior modes for the number of changes in the mean $N_1$ (a–d) and in the variance $N_2$ (e–h), estimated for each of the 400 replications in Scenario 2 for all four prior specifications for $\rho _1$ and $\rho _2$

Fig. 9

Average of the product estimates (a and b, black dots) in each instant and for the posterior probabilities of each instant to be an endpoint (c and d, black dots) for the means (left) and variances (right) and the $5\%$ and $95\%$ quantiles of such estimates based on the 400 Monte Carlo replications, Scenario 2 and Models B1 -B4. The true means (a) and variances (b) are indicated by the solid gray horizontal lines. The vertical gray dotted and dashed lines indicate the true endpoints in $\rho _1$ and $\rho _2$, respectively

Although our sensitivity analysis has shown a relative robustness of BMCP to the prior specifications, this statement may not be valid for other simulated scenarios or even for real data applications. In practical situations, this type of analysis may be useful to evaluate how sensitive the results are to small variations of hyperparameters around those values that reflect our true prior knowledge about parameters. We should take more care about the prior specification if, for our data, the model shows great sensitivity to the prior choice. A discussion about this topic in the context of the original PPM may be found in Loschi et al. (2005) and Loschi and Cruz (2005). The impact of (hyper)parameter choices in several other change point models was also recently discussed by Van den Burg and Williams (2020).

4 Case study: US ex-post real interest rate

We now illustrate our BMCP by analyzing a financial dataset; the case of a genetic dataset can be found in Sect. S.5 of the online supplementary material.

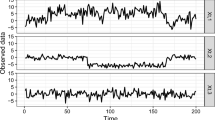
We apply BMCP, DPM19, LCIA05 and BH93 to analyze the time series of US ex-post real interest rates, available in the R package bcp (Erdman and Emerson 2007). The data, displayed in Fig. 10, correspond to the sequence of $n=103$ quarterly treasury bill rates deflated by the Consumer Price Index (CPI) inflation rate, denoted by $\varvec{X}$, from the first quarter of 1961 to the third quarter of 1986. The presence of regime changes in this data was previously analyzed by Garcia and Perron (1996) and Bai and Perron (2003).

We assume that at quarterly i, $X_i\vert \mu _i,\sigma _i^2 \sim N(\mu _i,\sigma _i^2)$, $i=1,\dots ,103$. For all models, the prior specifications are those considered in the simulation study. To fit DPM19 we fixed the maximum number of changes for both parameters in $m_1=m_2=10$. This number was motivated by results reported in Garcia and Perron (1996) and Bai and Perron (2003), which indicate up to three changes in the mean and one change in the variance. Different $m_1$ and $m_2$ choices were analyzed, showing that DPM19 is truly sensitive to such specifications (see Sect. S.4 of the online supplementary material). For this dataset, assuming $m_1$ and $m_2$ around the time series size, DPM19 showed to be ineffective for identifying possible changes, pointing out most of the instants as change points with high probability. The MCMC runs took 26, 715, 11 and 14 seconds to run 50, 000 iterations under BMCP, DPM19, LCIA05 and BH93, respectively. We discarded the first 30, 000 iterations as warm-up period.

Figure 10 shows parameter estimates for means and variances along time. The vertical lines indicate the posterior modes of $\rho _1$ (dotted line) and $\rho _2$ (dashed line) under BMCP. All models provided similar point estimates for the means, except DPM19 for which posterior means after instant 79 were below the data. Besides, under DPM19, there is more posterior uncertainty about the means as the HPD intervals have a broad range. All models indicate strong changes in the mean occurring around quarters 47 and 79. The product estimates for the means under BH93 are less smooth after quarter 51, the instant at which both models, BMCP and DPM19 detected a change point in the variance. A similar behavior for the mean estimates under BH93 was observed in clusters with higher variance in our simulation study. The estimates for the variance under BMCP, DPM19 and LCIA05 indicate a change around quarter 51. The LCIA05 model also indicates that the variance changes after the second mean change. Under this model, the product estimates for the variance are affected by the two changes in the mean, similar to what is observed in the simulation study (Sect. 3.2), where the mean and the variance change at different times. As for the posterior estimates of the means, DPM19 also presents the highest posterior uncertainty for the variance estimates. The posterior modes of the number of changes (Fig. 11) under BMCP and DPM19 indicated two changes in the mean. For the variance, these models provided strongly different estimates. While BMCP indicated only one change in the variance, DPM19 detected ten changes, which is the maximum number of changes assumed a priori to fit this model. The BMCP and DPM19 indicate quarters 47, 76 and 79 as change points in the mean (Fig. 12a and d) and quarter 51 as a change point in the variance (Fig. 12b and e), with posterior probabilities much higher than other quarters.

Fig. 10

Parameter estimates (black dots) and $90\%$ highest posterior density intervals (dashed lines) for the means (a–d) and variances (e–h) under BMCP, DPM19, LCIA05 and BH93, US ex-post Real Interest Rate dataset. The black solid lines represent the observed data (a–d) and the moving sample variance calculated over ranges of length 5 (e–h). The vertical dotted and dashed lines are the changes in $\varvec{\mu }$ and $\varvec{\sigma }$, respectively, according to the most likely partitions $\rho _1$ and $\rho _2$ as estimated by the BMCP model

Fig. 11

Posterior distribution for the number of changes, BMCP (a, b), LCIA05 (c), DPM19 (d, e) and BH93 (f), for the case study

Although not identical, the posterior inference results for partitions are similar; see Table 3. Under BMCP, the posterior most likely partitions for the mean and variance are $\rho _1=\{0,47,79,103\}$ and $\rho _2=\{0,51,103\}$, respectively. With higher posterior probabilities, quarters 47, 76 and 79 are also pointed out as change points by LCIA05 (Fig. 12c) and quarters 47, 76 and 82 are indicated as change points in the mean by BH93 (Fig. 12f). The posterior for $\rho$ under LCIA05 model only detects the changes that the proposed model indicates as change points in the mean (see Table 3 and Fig. 12c).

Fig. 12

Posterior probabilities that each instant is an endpoint (black bullets) under BMCP (a, b), LCIA05 (c), DPM19 (d, e), and BH93 (f), for the case study. The vertical dotted and dashed lines are the changes in $\varvec{\mu }$ and $\varvec{\sigma }$, respectively, given by the most likely partitions $\rho _1$ and $\rho _2$ estimated by the BMCP

Table 3 Top most likely $\rho _1$ and $\rho _2$ (BMCP), $E_1$ and $E_2$ (DPM19) and $\rho$ (LCIA05, BH93) based on the posterior probabilities, for the case study

Garcia and Perron (1996) analyzed these data by fitting an autoregressive time series model, coupled with a sequential test strategy to infer about the number of change points. Their null hypothesis, which assumes that the number of changes is a predetermined value B, is compared with the alternative hypothesis of a higher number $B+1$ of changes for, successively, $B=0, 1, \dots$. Although BMCP and DPM19 consider a simpler dependence model inside clusters, estimates provided by both models are similar to those reported in Garcia and Perron (1996), without the need to resort to any kind of sequential process. Considering a Markov switching model, Garcia and Perron (1996) concluded that a better fit for these data is obtained if three different means and two different variances are considered. Changes in the mean were identified in 1972/3 and 1980/1, that is, quarters 47 and 77, and the means of the three corresponding clusters were estimated as 1.4, $-1.8$ and 5.5. These estimates are comparable to those obtained with BMCP. The median squared difference between estimates provided by these two models is 0.016.

The estimates for the two different variances were not reported by Garcia and Perron (1996), but they also found that the 2nd and 3rd clusters share the same variance, which is different from that in the 1st cluster. This finding agrees with results obtained fitting BMCP and DPM19 which pointed to a unique change in the variance right after the first change in the mean. Results presented by Bai and Perron (2003) differ from those by BMCP and Garcia and Perron (1996), who detected one more change point in the mean at quarter 24. Notice that BMCP (Fig. 12a) and DPM19 (Fig. 12d) also point out instant 24 as a change point with higher probability (0.065 for BMCP and 0.081 for DPM19) than its neighboring instants.

5 Conclusions

One of the greatest limitations of traditional PPMs when used to deal with multiple change point identification is its inability to determine which structural parameter experienced each change. We proposed a multipartition model, BMCP, that provides a reasonable answer to this issue, allowing us to identify the positions and number of changes that occurred, as well as which parameters have changed along the observed data sequence. We illustrated the applicability of BMCP by considering the case of means and variances of Normal data. In random partition models, it is usually challenging to sample from the posterior distribution of partitions. We proposed for BMCP an efficient partially collapsed Gibbs sampler based on a blocking strategy, which facilitates simulation from the joint posterior distribution of parameters and partitions.

The simulation studies showed that BMCP is an efficient approach to identify when and which parameters changed along the sequence. Its performance is as good as that of the original PPM (Barry and Hartigan 1993) when only the mean changes over the time. BMCP is also competitive when compared to the model by Peluso et al. (2019), providing better or similar results even considering less prior information about the true number of changes.

Despite its good performance, some aspects of the proposed model require deeper analysis. Firstly, we need to evaluate the computational effort in more complex models. Although we do not consider conjugate prior distributions for structural parameters, our prior choice (12) produced known closed form distributions that facilitate computational aspects of our model. Other prior specifications can lead to unknown distributions for cluster structural parameters, which may increase the posterior simulation cost. Other point that needs a deeper study is that the proposed model assumes independence among the partitions, which may be unrealistic in many practical situations. To obtain a more general model some type of correlation among partitions should be considered. These are both interesting topics for future research.