1 Introduction

Although mean regression is still a traditional benchmark in regression studies, the quantile approach is receiving increasing attention, because it allows a more complete description of the conditional distribution of the response given the covariate, and it is more robust to deviations from error normality.

The quantile regression model could be stated as

$$\begin{aligned} Y=q_{\tau }(X)+\varepsilon \end{aligned}$$

where Y is the response variable of interest, X is the covariate, \(q_{\tau }\) is the quantile regression function of order \(\tau \) and \(\varepsilon \) represents the error. Then, the conditional \(\tau \)-quantile of \(\varepsilon \) given X will be zero, that is, \({\mathbb {P}}(\varepsilon \le 0|X)=\tau \) almost surely.

Estimation of the quantile regression model exploits the fact that the conditional quantile, \(q_\tau (x)\), is the value a that minimizes the expectation

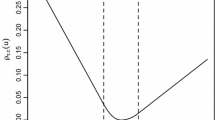
$$\begin{aligned} {\mathbb {E}}[\rho _{\tau }(Y-a)|X=x], \end{aligned}$$

where \(\rho _{\tau }(u)=u(\tau -{\mathbb {I}}(u<0))\) and \({\mathbb {I}}(\cdot )\) is the indicator function of an event. Koenker and Bassett (1978) can be considered a seminal work in estimating conditional quantiles in a parametric setup following this idea.

Along this work, we will focus on the univariate regression context, that is, the covariate X is assumed to be one-dimensional. Yu and Jones (1998) studied a local linear estimator of the quantile regression in a nonparametric framework. To this end, a random sample of independent observations \((X_{1},Y_{1}),\ldots ,(X_{n},Y_{n})\) of the pair (X, Y) is supposed to be available. Then, the estimator will be \({\widehat{q}}_{\tau ,h}(x)={\widehat{a}}\), where \({{\widehat{a}}}\) and \({{\widehat{b}}}\) are the minimizers of

$$\begin{aligned} \sum _{i=1}^{n}\rho _{\tau }\left( Y_{i}-a-b(X_{i}-x)\right) K\left( \frac{X_{i}-x}{h_\tau }\right) , \end{aligned}$$

where K is a kernel function and \(h_\tau \) is a bandwidth parameter.

Several authors have addressed the problem of bandwidth selection as Yu and Jones (1998), Abberger (1998), Yu and Lu (2004), Ghouch and Genton (2012) or Abberger (2002). In this work, a plug-in rule is designed to choose the bandwidth parameter, \(h_\tau \). The plug-in technique consists of minimizing the dominant terms of the mean integrated squared error (MISE) of the estimator. For the local linear quantile regression, it can be written as [see Fan et al. (1994) and Yu and Jones (1998)]

$$\begin{aligned}&\text{ MISE } \; ({\widehat{q}}_{\tau ,h_\tau })= {\mathbb {E}}\int {\left( {\widehat{q}}_{\tau ,h_\tau }(x)-q_{\tau }(x)\right) ^2g(x)\,\hbox {d}x} \nonumber \\&\quad \cong \frac{1}{4}h_\tau ^{4}\mu _{2}(K)^{2}\int {q^{(2)}_{\tau }(x)^{2}g(x)\,\hbox {d}x}+ \frac{R(K)\tau (1-\tau )}{nh_\tau } \int {\frac{1}{f(q_{\tau }(x)|x)^{2}}\,\hbox {d}x} \end{aligned}$$
(1)

where g is the density of X, \(f(q_{\tau }(x)|x)\) is the conditional density of Y at \(q_\tau (x)\) given \(X=x\), \(q^{(2)}_{\tau }\) is the second derivative of \(q_{\tau }\), \(\mu _{2}(K)=\int u^{2}K(u)\,\hbox {d}u\) and \(R(K)=\int K^{2}(u)\,\hbox {d}u\).

An asymptotically optimal bandwidth can be derived as

$$\begin{aligned} h_{\text{ AMISE },\tau }=\left[ \frac{R(K) \; \tau (1-\tau )}{n \; \mu _{2}(K)^{2} \; \int {q_{\tau }^{(2)}(x)^{2} \; g(x)\;\hbox {d}x}} \; \int {\frac{1}{f(q_{\tau }(x)|x)^{2}}\;\hbox {d}x}\right] ^{1/5} \end{aligned}$$
(2)

Note that \(\mu _2(K)\) and R(K) are obtained from the kernel function, while the two integrals in (2) are unknown and have to be estimated. Expression (2) is quite similar to the plug-in rule for mean regression. The curvature (integrated squared second derivative) is now calculated for the quantile regression function instead of the mean regression, while the integrated squared sparsity (where “sparsity” means the inverse of the conditional density) replaces the integrated conditional variance that appeared in mean regression. See Ruppert et al. (1995) where a plug-in rule is given for local linear mean regression.

Because of these similarities with mean regression, Yu and Jones (1998) proposed to use Ruppert et al. (1995) bandwidth with some simple transformations based on the assumptions of homoscedasticity and error normality. Homoscedasticity is useful to have the same curvature for any \(\tau \) as in mean regression, while normality allows to estimate the sparsity from the conditional variance.

The purpose of this work is to provide a plug-in bandwidth for local linear quantile regression without imposing restrictions on the conditional variability and the error distribution. Instead, nonparametric estimations of the curvature at the given quantile \(\tau \) will be used, as well as nonparametric estimations of the sparsity.

Other proposals in the literature for bandwidth selection in nonparametric quantile regression were given, based on cross-validation techniques. In particular, Abberger (1998) proposed to minimize in h the cross-validation function given by:

$$\begin{aligned} \hbox {CV} (h) =\sum _{i=1}^{n} \rho _{\tau }\biggl (Y_{i}-{\widehat{q}}_{\tau ,h}^{-i}(X_{i})\biggr ) \end{aligned}$$
(3)

where \({\widehat{q}}_{\tau ,h}^{-i}(X_{i})\) is the estimator of the \(\tau \)-quantile function obtained from a sample without the ith individual.

In Sect. 2, a preliminary rule of thumb is obtained, and afterwards, the proposed plug-in rule is derived. In Sect. 3, a simulation study is given to explore the virtues of the new bandwidth selectors in comparison with Yu and Jones (1998) and Abberger (1998) proposals. Section 4 contains the main conclusions. In “Appendix”, mean squared errors of curvature and sparsity estimators are derived.

2 Proposed selectors

As any plug-in rule, the crucial ingredients of our proposed selectors will be the estimators of unknown quantities, which in our case are the curvature and the sparsity. Our first proposal will consist of a rule of thumb, where the estimators are defined on a simple partition of the sample in blocks.

2.1 Rule of thumb

Following the ideas in Ruppert et al. (1995), a rule of thumb can be constructed by doing the next steps:

  1. 1.

    Partition the range of X into N blocks with the same number of observations. The original sample \(\{(X_{1},Y_{1}),\ldots ,(X_{n},Y_{n})\}\) is subsequently split into the N blocks. A polynomial of order 4 is adjusted at each block, thus providing N polynomials that will be denoted by \({\widehat{q}}_{\tau ,j}\) with \(j=1,\ldots ,N\). The number of blocks will be chosen as \({\widehat{N}}\) following the Mallows’s \(C_p\) criterion [see Mallows (1973)] adapted to the quantile frameworks, that is, \({\widehat{N}}\) will minimize

    $$\begin{aligned} C_{p}(N)=\frac{\text{ RSQ }(N)}{\text{ RSQ }(N_{\text{ max }})/(n-5N_{\text{ max }})}-(n-10N) \end{aligned}$$

    where \(\text{ RSQ }(N)\) is the residual sum of quantile losses given by \(\rho _{\tau }\) and summed over each blocked quartic fit, when the number of blocks is N, \(N_{\text{ max }}=\max \{ \min ([n/20],N^{*}),1 \}\) and \(N^{*}=5\). Here \([\cdot ]\) denotes the integer part of a number.

Remark 1

Following the ideas of Ruppert et al. (1995) in mean regression, we have considered polynomials of order 4 because it is the lowest degree that a polynomial admits estimates of the quantity \(\vartheta _{24}=\int {q_{\tau }^{(2)}(x) \, q_{\tau }^{(4)}(x) \, g(x)} \, \hbox {d}x\) other than zero. This integral \(\vartheta _{24}\) will be involved in the mean squared error of curvature estimator, see equation (4).

  1. 2.

    Estimate the curvature as:

    $$\begin{aligned} {\widehat{\vartheta }}_{\mathrm {B}}=\frac{1}{n} \; \sum _{i=1}^{n}\sum _{j=1}^{{\widehat{N}}}{\widehat{q}}_{\tau ,j}^{(2)}(X_{i})^2 \; I\; (X_{i} \in \text{ Block }\ j). \end{aligned}$$

    Observe that we are using the notation \(\vartheta =\int q^{(2)}_{\tau }(x)^2\,g(x)\;\hbox {d}x\).

  2. 3.

    Estimate the sparsity at each block j by means of

    $$\begin{aligned} {\widehat{s}}_j(\tau )=\frac{r_{[\tau +d_j]}-r_{[\tau -d_j]}}{2\,d_j} \end{aligned}$$

    where \(r_{[\tau -d_j]}\) and \(r_{[\tau +d_j]}\) are the sample quantiles of orders \((\tau -d_j)\) and \((\tau +d_j)\), respectively, of the residuals from the quartic fit at block j. This type of sparsity estimator was suggested by Siddiqui (1960) and studied by Bloch and Gastwirth (1968). For the parameter \(d_j\), the selector proposed by Bofinger (1975) will be used here. Finally, the integrated squared sparsity will be estimated by

    $$\begin{aligned} {\widehat{s}}_{\text{ B }}^2=\sum _{j=1}^{{{\widehat{N}}}} {\widehat{s}}_{j}^2\, l_j \end{aligned}$$

    where \(l_j\) denotes the length of block j.

  3. 4.

    Finally, the selector from the rule of thumb will be obtained as:

    $$\begin{aligned} {\widehat{h}}_{\tau ,\text{ RT }}=\left( \frac{R(K) \; \tau (1-\tau ) \; {\widehat{s}}_{\text{ B }}^2 }{n\; \mu _{2}(K)^{2} \; {\widehat{\vartheta }}_{\text{ B }}} \right) ^{1/5}. \end{aligned}$$

2.2 Plug-in rule

The plug-in rule will come from a more elaborated estimation of the curvature and the sparsity.

2.2.1 Curvature estimation

Now the second derivative of the regression will be nonparametrically estimated at each sample observation. In order to do this, a local polynomial of order 3 will be adjusted. Let us call \({\widetilde{q}}_{\tau ,h_\mathrm{c}}^{(2)}(X_i)\) to its second derivative at \(X_i\), for \(i=1,\ldots ,n\). Then, we can consider the following curvature estimator:

$$\begin{aligned} {\widehat{\vartheta }}_{h_\mathrm{c}}=\frac{1}{n} \sum _{i=1}^{n}{\widetilde{q}}^{(2)}_{\tau ,h_\mathrm{c}}(X_{i})^2 \end{aligned}$$

At this point, a pilot bandwidth \(h_\mathrm{c}\) for curvature estimation should be selected. The criterion for selecting \(h_\mathrm{c}\) will be the mean squared error of the curvature estimator. As in the case of classical mean regression, see Ruppert et al. (1995), the asymptotic mean squared error coincides, up to terms not depending on the bandwidth and negligible terms, with the asymptotic squared bias, which is given by

$$\begin{aligned} \begin{aligned} \text{ MSE } \left( {\widehat{\vartheta }}_{h_\mathrm{c}}\right)&\cong \left[ \delta _1 \; h_\mathrm{c}^2 \; \int {q_{\tau }^{(2)}(x)q_{\tau }^{(4)}(x)g(x)}\hbox {d}x\right. \\&\quad \left. +\,\delta _2 \; \tau (1-\tau ) \; \frac{1}{nh_\mathrm{c}^5} \; \int {\frac{1}{f(q_{\tau }(x)|x)^2}\hbox {d}x} \right] ^2 \end{aligned} \end{aligned}$$
(4)

where

$$\begin{aligned}&\delta _1=\frac{1}{6}(\alpha _{31} \mu _4(K)+\alpha _{33} \mu _6(K))\\&\delta _2=4\left( \alpha _{31}^2\int {K^2(v)\hbox {d}v}+\alpha _{33}^2\int {v^4K^2(v)\hbox {d}v}+ 2\alpha _{31}\alpha _{33}\int {v^2K^2(v)\hbox {d}v}\right) \\&\mu _i(K)=\int {v^iK(v)\hbox {d}v} \\&\alpha _{31}=\frac{-\mu _2(K)^2\mu _6(K)+\mu _2(K)\mu _4(K)^2}{\mu _2(K)\mu _4(K)\mu _6(K)-\mu _4(K)^3-\mu _2(K)^3\mu _6(K)+\mu _2(K)^2\mu _4(K)^2}\\&\alpha _{33}=\frac{\mu _2(K)\mu _6(K)-\mu _4(K)^2}{\mu _2(K)\mu _4(K)\mu _6(K)-\mu _4(K)^3-\mu _2(K)^3\mu _6(K)+\mu _2(K)^2\mu _4(K)^2} \end{aligned}$$

Minimizing the last expression, the asymptotically optimal pilot bandwidth will be

$$\begin{aligned} {\tilde{h}}_\mathrm{c}=C(K) \; \left( \frac{\tau (1-\tau )\int {1/f(q_{\tau }(x)|x)^2\hbox {d}x}}{ | \int {q_{\tau }^{(2)}(x)q_{\tau }^{(4)}(x)g(x)}\hbox {d}x | \;n} \right) ^{1/7} \end{aligned}$$

where

$$\begin{aligned} C(K)={\left\{ \begin{array}{ll} C^{I}=\left( \frac{5\delta _2}{2\delta _1}\right) ^{1/7} &{} \hbox { if}\ \int {q_{\tau }^{(2)}(x)q_{\tau }^{(4)}(x)g(x)\hbox {d}x}>0\\ C^{II}=\left( \frac{\delta _2}{\delta _1}\right) ^{1/7} &{} \hbox { if}\ \int {q_{\tau }^{(2)}(x)q_{\tau }^{(4)}(x)\hbox {d}x}<0 \end{array}\right. } \end{aligned}$$

To compute this pilot bandwidth, preliminary estimations of the integrated squared sparsity and the integral \(\vartheta _{24}=\int {q_{\tau }^{(2)}(x)q_{\tau }^{(4)}(x)g(x)}\hbox {d}x\) are required. They will be obtained from blocked estimators as those considered for the rule of thumb. They can be denoted by \({\widehat{s}}_{\text{ B }}^2\) and \({\widehat{\vartheta }}_{24,\text{ B }}\). The resulting estimated pilot bandwidth will be

$$\begin{aligned} {{\widehat{h}}}_\mathrm{c}=C(K) \; \left( \frac{\tau (1-\tau )\;{\widehat{s}}_{\text{ B }}^2}{| {\widehat{\vartheta }}_{24,\text{ B }}| \;n} \right) ^{1/7}. \end{aligned}$$

Finally, the curvature estimator will be given by

$$\begin{aligned} {\widehat{\vartheta }}_{{\widehat{h}}_\mathrm{c}}^{\alpha }=\frac{1}{n} \; \sum _{i=1}^{n} {\widetilde{q}}_{\tau ,{\widehat{h}}_\mathrm{c}}^{(2)}(X_{i})^2 \; {\mathbb {I}} \left( (1-\alpha )a+\alpha b<X_i<\alpha a+(1-\alpha ) b\right) \end{aligned}$$

where the sample was trimmed at each border a and b, by a small proportion \(\alpha \in [0,1]\), assuming that the covariate is supported in the interval [a, b]. This strategy was already used by Ruppert et al. (1995) in their estimation of similar quantities for mean regression. It is intended to prevent from the variability of local polynomial kernel estimates of high derivatives near the boundaries. Following their suggestion, we will take \(\alpha =0.05\).

2.2.2 Sparsity estimation

Since the sparsity, denoted by \(s_\tau (x)\), is the derivative of the quantile regression function, \(q_\tau (x)\), with respect to \(\tau \), we propose an estimate of this kind:

$$\begin{aligned} {\widehat{s}}_{\tau ,d_\mathrm{s},h_\mathrm{s}}(x)=\frac{{\widehat{q}}_{\tau +d_\mathrm{s},h_\mathrm{s}}(x)-{\widehat{q}}_{\tau -d_\mathrm{s},h_\mathrm{s}}(x)}{2\,d_\mathrm{s}} \end{aligned}$$

where \({\widehat{q}}_{\tau +d_\mathrm{s},h_\mathrm{s}}\) and \({\widehat{q}}_{\tau -d_\mathrm{s},h_\mathrm{s}}\) are local linear quantile regression estimates at the quantile orders \((\tau +d_\mathrm{s})\) and \((\tau -d_\mathrm{s})\), respectively, and \(h_\mathrm{s}\) denotes their bandwidth.

Note that we need two pilot bandwidths, \(d_\mathrm{s}\) and \(h_\mathrm{s}\). The bandwidth \(d_\mathrm{s}\) is placed in the Y-axis and plays a similar role to that of the bandwidth \(d_j\) in the rule of thumb. The bandwidth \(h_\mathrm{s}\) is necessary to compute the nonparametric estimations of the regression functions.

The choice of the two pilot bandwidths will be based on the asymptotic mean squared error, which comes from the asymptotic squared bias and variance:

$$\begin{aligned} \text{ MSE } \left( \int {{\widehat{s}}^2_{\tau , d_\mathrm{s},h_\mathrm{s}}(x)\,\hbox {d}x}\right)&\cong \left[ \frac{1}{nd_\mathrm{s} h_\mathrm{s}}\int {a(x)\,\hbox {d}x}+d_\mathrm{s}^2\int {b(x)\,\hbox {d}x}+h_\mathrm{s}^2\int {c(x)\,\hbox {d}x}\right] ^2 \nonumber \\&\quad +\, \frac{1}{nd_\mathrm{s}} \int d(x) \; \hbox {d}x +\frac{1}{n^2 d_\mathrm{s}^2 h_\mathrm{s}} \; \int e(x) \; \hbox {d}x \end{aligned}$$
(5)

where

$$\begin{aligned} \begin{aligned}&a(x)=\frac{1}{2}\frac{R(K) \; s_{\tau }(x)^2}{g(x)} \\&b(x)=\frac{1}{3} s_\tau (x) \; s^{(2,\tau )}_{\tau }(x)\\&c(x)=\mu _2(K) \; s_\tau (x)\; \frac{\partial q_{\tau }^{(2)}(x)}{\partial \tau } \end{aligned} \qquad \begin{aligned}&d(x)=2 \; \frac{s_{\tau }(x)^4}{g(x)} \\&e(x)= \left( \frac{1}{2} R(K*K)-R(K)\right) \; \frac{s_{\tau }(x)^4}{g(x)^2} \end{aligned} \end{aligned}$$
(6)

where \(*\) represents the convolution and \(s^{(2,\tau )}_{\tau }(x)=\frac{\partial ^2 }{\partial \tau ^2}s_{\tau }(x)\).

Minimization with respect to \(d_\mathrm{s}\) and \(h_\mathrm{s}\) can be carried out by means of optimization algorithms as Newton–Raphson or Nelder and Mead (1965)’s method. Estimation of the six integrals in expression (5) is done by blocks. The resulting pilot bandwidths will be denoted by \({\widehat{d}}_\mathrm{s}\) and \({\widehat{h}}_\mathrm{s}\) and the estimation of the integrated squared sparsity by \({\widehat{s}}_{\tau ,{\widehat{d}}_\mathrm{s},{\widehat{h}}_\mathrm{s}}^2\). Now details are given on how to estimate the unknown integrals.

  • Estimation of \(\mathbf {\int {a(x)\,\hbox {d}x}}\) Note that \(a(x)=(1/2)\, R(K) \, s_{\tau }(x)^2\,(g(x))^{-1}\). We will make use of the sparsity estimation at each block, \({{\widehat{s}}}_j\), together with a simple estimation of covariate density at that block, which could be given by \(n_j/(nl_j)\), where \(n_j\) is the number of observations at block j. Then, this integral can be estimated by:

    $$\begin{aligned} \widehat{\int {a(x)\,\hbox {d}x}}=\frac{1}{2}R(K) \sum _{j=1}^{{\widehat{N}}} {\widehat{s}}_j^2\left( \frac{n\,l_j}{n_j}\right) l_j. \end{aligned}$$

  • Estimation of \(\mathbf {\int {b(x)\,\hbox {d}x}}\) Recall that \(b(x)=(1/3) \; s_\tau (x)\; s^{(2,\tau )}_{\tau }(x)\), where \(s^{(2,\tau )}_{\tau }(x)\) is the second derivative of \(s_\tau (x)\) with respect to \(\tau \). The problem of estimating the second derivative of the sparsity without covariates was considered by Bofinger (1975). We apply her proposal to the residuals at each block

    $$\begin{aligned} {\widehat{s}}_j^{(2,\tau )}=\frac{1}{2\delta ^{3}} \; \left( r_{([n\tau ]+2m)}-2\,r_{([n\tau ]+m)}+2\,r_{([n\tau ]-m)}-r_{([n\tau ]-2m)}\right) \end{aligned}$$

    where the value of m is taken as \(m=[n\delta ]=[cn^{8/9}]\) with \(c=0.25\), following Sheather and Maritz (1983) proposal. Then, the considered integral is estimated as

    $$\begin{aligned} \widehat{\int {b(x)\,\hbox {d}x}}=\frac{1}{3}\sum _{j=1}^{{\widehat{N}}} {\widehat{s}}_{j} \; {\widehat{s}}_j^{(2,\tau )} l_j. \end{aligned}$$

  • Estimation of \(\mathbf {\int {c(x)\,\hbox {d}x}}\) The novel ingredient in c(x) is \(\partial q_{\tau }^{(2)}(x)/\partial \tau \). Since this is a derivative with respect to \(\tau \), it can be estimated by

    $$\begin{aligned} \widehat{\frac{\partial q_{\tau }^{(2)}(x)}{\partial \tau }}= \frac{q_{\tau +d_\mathrm{c}}^{(2)}(x)-q_{\tau -d_\mathrm{c}}^{(2)}(x)}{2d_\mathrm{c}} \end{aligned}$$

    In order to choose the pilot bandwidth \(d_\mathrm{c}\), a location and scale model, given by \(Y=q_{\tau }(X)+\sigma (X)\varepsilon \), is assumed. Here, \(\varepsilon \) is assumed independent of X and with a zero \(\tau \)th quantile. Note that under this model, for each \(\tau _1,\tau _2\in (0,1)\), \(q_{\tau _2}(x)-q_{\tau _1}(x)=\sigma (x)(c_{\tau _2}-c_{\tau _1})\), where \(c_{\tau _1}\) and \(c_{\tau _2}\) are \(\tau _1\) and \(\tau _2\) quantiles of \(\varepsilon \), respectively. Thus,

    $$\begin{aligned} \frac{\partial q_{\tau }^{(2)}(x)}{\partial \tau }=\sigma ^{(2)}(x) s_{\tau }(x). \end{aligned}$$

    This expression leads to consider for \(d_\mathrm{c}\) the same selector proposed by Bofinger (1975) to estimate the sparsity without covariates. This selector will also be based on the assumption of normality for \(\varepsilon \). Finally, we arrive at the following estimator at block j

    $$\begin{aligned} \widehat{\left( \frac{\partial q_{\tau }^{(2)}}{\partial \tau }\right) }_{j}= \frac{1}{n_j} \; \sum _{i=1}^{n} \frac{{\widehat{q}}_{\tau +{\widehat{d}}_\mathrm{c},j}^{(2)}(X_{i})-{\widehat{q}}_{\tau -{\widehat{d}}_\mathrm{c},j}^{(2)}(X_{i})}{2\,{\widehat{d}}_\mathrm{c}} \; {\mathbb {I}} \; (X_{i} \in \hbox { Block}\ j), \end{aligned}$$

    and the subsequent estimation of the integral

    $$\begin{aligned} \widehat{\int {c(x)\,\hbox {d}x}}=\mu _2(K) \; \sum _{j=1}^{{{\widehat{N}}}} {\widehat{s}}_{j} \; \widehat{\left( \frac{\partial q_{\tau }^{(2)}}{\partial \tau }\right) }_{j} l_j \end{aligned}$$

  • Estimation of \(\mathbf {\int {d(x)\,\hbox {d}x}}\) and \(\mathbf {\int {e(x)\,\hbox {d}x}}\) Note that \(d(x)=2\, s_{\tau }(x)^4\,(g(x))^{-1}\) and \(e(x)=\left( 0.5 R(K*K)-R(K)\right) \, s_{\tau }(x)^4 \, g(x)^{-2}\). Similarly to the previous integrals, these integrals can be estimated by

    $$\begin{aligned}&\widehat{\int {d(x)\,\hbox {d}x}}=2 \sum _{j=1}^{{\widehat{N}}} {\widehat{s}}_j^4\left( \frac{n\,l_j}{n_j}\right) l_j \\&\widehat{\int {e(x)\,\hbox {d}x}}= \left( \frac{1}{2} R(K*K)-R(K)\right) \; \sum _{j=1}^{{\widehat{N}}} {\widehat{s}}_j^4\left( \frac{n\,l_j}{n_j}\right) ^2 l_j . \end{aligned}$$

Finally, the plug-in bandwidth selector is obtained as

$$\begin{aligned} {\widehat{h}}_{\tau ,\text{ PI }}=\left( \frac{R(K) \; \tau (1-\tau ) \; {\widehat{s}}_{\tau ,{\widehat{d}}_\mathrm{s},{\widehat{h}}_\mathrm{s}}^2 }{n\; \mu _{2}(K)^{2} \; {\widehat{\vartheta }}_{{\widehat{h}}_\mathrm{c}} }\right) ^{1/5}. \end{aligned}$$

Remark 2

In the framework of local linear smoothing quantile regression, Yu and Jones (1998) presented a different approach based on inverting a local linear conditional distribution estimator that is called double-kernel estimator. Later, Jones and Yu (2007) proposed an improvement of their previous double-kernel estimator. Both estimators need bandwidth selectors. The choice of the main bandwidth (\(h_1\) in their notation) could be done by the plug-in rule proposed here. A small experiment is given at the end of the simulation study to show the performance of the new plug-in rule in double-kernel estimators.

2.3 Theoretical performance

The selector from the rule of thumb includes inconsistent estimators of curvature and sparsity. Thus, consistency properties cannot be derived for this selector. Meanwhile, convergence of the plug-in bandwidth selector to the optimal bandwidth relies on the asymptotic properties of curvature and sparsity estimators, \({\widehat{\vartheta }}_{{{\widehat{h}}}_\mathrm{c}}\) and \({\widehat{s}}_{\tau ,{\widehat{d}}_\mathrm{s},{\widehat{h}}_\mathrm{s}}^2\), respectively. The same arguments given in Ruppert et al. (1995) in the case of local linear mean regression can be followed here. The main difference comes from the sparsity estimator, which replaces the conditional variance in AMISE representation.

From expression (5), it can be obtained that for sequences of pilot bandwidths \(d_\mathrm{s}=D_\mathrm{s} n^{-1/5}\) and \(h_\mathrm{s}=H_\mathrm{s}n^{-1/5}\), where \(D_\mathrm{s}>0\) and \(H_\mathrm{s}>0\) are constants, \({\widehat{s}}_{\tau ,d_\mathrm{s},h_\mathrm{s}}^2-\int s_\tau ^2(x)\,\hbox {d}x=O_P(n^{-2/5})\). Even though this rate of convergence is slower than root-n, it is enough to achieve that the relative rate of the plug-in bandwidth selector is dominated by curvature estimation, that is,

$$\begin{aligned} ({\widehat{h}}_{\tau ,\text{ PI }}-h_\mathrm{MISE})/h_\mathrm{MISE}=-\frac{1}{5}({\widehat{\vartheta }}_{h_\mathrm{c}}-\vartheta )/\vartheta +O_P(n^{-2/5}) \end{aligned}$$

where \(\vartheta =\int {q_{\tau }^{(2)}(x)g(x)}\,\hbox {d}x\) is the true curvature.

Now, from expression (4), and for a sequence of pilot bandwidths \(h_\mathrm{c}=H_cn^{-1/7}\), with \(H_\mathrm{c}>0\) a certain constant, we have that, conditionally on \(X_1,\ldots ,X_n\),

$$\begin{aligned} ({\widehat{h}}_{\tau ,\text{ PI }}-h_\mathrm{MISE})/h_\mathrm{MISE}{\mathop {\longrightarrow }\limits ^{p}} L \end{aligned}$$
(7)

where \(L{=}-\frac{1}{5}\vartheta ^{-1}\left\{ \delta _1 \; \int {q_{\tau }^{(2)}(x)q_{\tau }^{(4)}(x)g(x)}\hbox {d}x\; H_\mathrm{c}^2 +\delta _2 \; \tau (1-\tau ) \; \int s_\tau ^2(x)\,\hbox {d}x\; H_\mathrm{c}^{-5}\right\} \).

A detailed proof of (7) would follow the steps given in Sánchez-Sellero et al. (1999). Expression (7) shows that the relative rate of convergence of \({\widehat{h}}_{\tau ,\text{ PI }}\) is \(O_p(n^{-2/7})\) for any choice of \(H_\mathrm{c}\). Observe now that the asymptotically optimal pilot bandwidth \({\tilde{h}}_\mathrm{c}\) allows to make L equal to zero, thanks to an ideal choice of \(H_\mathrm{c}\). This pilot bandwidth would lead to an improved \(O_p(n^{-5/14})\) relative rate of convergence for the plug-in bandwidth selector. To obtain this in practice, consistent estimators of the unknown quantities in \({\tilde{h}}_\mathrm{c}\) would be needed, which could be quite complicated. Our proposed estimated pilot bandwidth, \({\hat{h}}_\mathrm{c}\), is based on rule-of-thumb estimates of the unknown quantities, which are simple to implement although they do not guarantee consistency, neither improved rate of convergence. The theoretical performance of the plug-in bandwidth selector is then similar to that of Ruppert et al. (1995) bandwidth selector for mean regression. The only difference was found in the sparsity estimation, which replaces the conditional variance estimation. We can conclude that the slower rate of convergence of the sparsity estimation does not have an effect on the rate of convergence of the plug-in selector.

3 Simulation study

In this section, a simulation study is presented to analyse the behaviour of the new bandwidth selectors in comparison with already existing selectors. The natural competitors would be Yu and Jones (1998)’s bandwidth and Abberger (1998)’s cross-validation bandwidth. As regards Yu and Jones (1998)’s bandwidth, some theoretical considerations are useful as an orientation to a meaningful comparison. Recall the expression given in (2) for the asymptotically optimal bandwidth

$$\begin{aligned} h_{\text{ AMISE },\tau }=\left[ \frac{R(K) \; \tau (1-\tau )}{n \; \mu _{2}(K)^{2} \; \int {q_{\tau }^{(2)}(x)^{2} \; g(x)\;\hbox {d}x}} \; \int {\frac{1}{f(q_{\tau }(x)|x)^{2}}\;\hbox {d}x}\right] ^{1/5}. \end{aligned}$$

Observing that the same type of bandwidth for mean regression is given by

$$\begin{aligned} h_{\text{ AMISE },\text{ MEAN }}=\left[ \frac{R(K)}{n \; \mu _{2}(K)^{2} \; \int {m^{(2)}(x)^{2} \; g(x)\;\hbox {d}x}} \; \int {\sigma ^{2}(x)\;\hbox {d}x}\right] ^{1/5}, \end{aligned}$$

where m is the mean regression and \(\sigma ^2\) is the conditional variance, Yu and Jones (1998) proposed to use the following selector:

$$\begin{aligned} {\widehat{h}}_{\text{ YJ },\tau }={\widehat{h}}_{\text{ RSW }}\left[ \frac{\tau (1-\tau )}{\phi (\varPhi ^{-1}(\tau ))^2}\right] ^{1/5} \end{aligned}$$

where \({\widehat{h}}_{\text{ RSW }}\) is the Ruppert et al. (1995)’s plug-in selector for local linear mean regression and the last factor is a correction for quantile regression. Yu and Jones (1998)’s selector is based on assuming that quantile and mean regression have the same curvature and the error distribution is normal. The last factor then relates the conditional sparsity with the conditional variance under normality.

Since \({\widehat{h}}_{\text{ RSW }}\) converges to \(h_{\text{ AMISE },\text{ MEAN }}\), \({\widehat{h}}_{\text{ YJ }}\) converges to

$$\begin{aligned} h_{\text{ AMISE }, \text{ YJ },\tau }=h_{\text{ AMISE },\text{ MEAN }} \left[ \frac{\tau (1-\tau )}{\phi (\varPhi ^{-1}(\tau ))^2}\right] ^{1/5} \end{aligned}$$

which is generally different from the asymptotically optimal bandwidth for quantile regression, \(h_{\text{ AMISE },\tau }\). Meanwhile, the proposed plug-in selector \({\widehat{h}}_{\text{ NP }}\) converges to \(h_{\text{ AMISE },\tau }\). Then, for a sample size large enough, the new bandwidth is expected to outperform Yu and Jones (1998)’s selector, the latter selector being generally inconsistent. This simulation study will help to assess the consequences of these facts from smaller to larger sample sizes, and in models where the difference between \(h_{\text{ AMISE },\text{ YJ },\tau }\) and \(h_{\text{ AMISE },\tau }\) can be controlled.

In particular, for any homoscedastic quantile regression model \(Y=q_{\tau }(X)+\varepsilon \), where the model error \(\varepsilon \) has \(\tau \)-quantile zero and is assumed independent of X, the curvatures of mean and quantile regression coincide, and then, the quotient between \(h_{\text{ AMISE,YJ },\tau }\) and \(h_{\text{ AMISE },\tau }\) will be

$$\begin{aligned} \text{ Ratio }=\frac{h_{\text{ AMISE,YJ },\tau }}{h_{\text{ AMISE },\tau }}=\root 5 \of {\frac{\sigma ^2 \; f_{\varepsilon }(F_{\varepsilon }^{-1}(\tau ))^2}{\phi (\varPhi ^{-1}(\tau ))^2}} \end{aligned}$$
(8)

where \(f_{\varepsilon }\) and \(F_{\varepsilon }\) are the density and distribution functions of \(\varepsilon \) and \(\sigma ^2\) denotes the variance of \(\varepsilon \). Then, the ratio between both AMISE bandwidths only depends on the error distribution for any homoscedastic regression model. Some calculations lead to the following ratio between asymptotic mean integrated squared errors of the two bandwidths:

$$\begin{aligned} \frac{\text{ AMISE }(h_{\text{ AMISE,YJ },\tau })}{\text{ AMISE }(h_{\text{ AMISE },\tau })}= \frac{1}{5} \text{ Ratio }^{4} + \frac{4}{5} \text{ Ratio }^{-1} \end{aligned}$$
(9)

where Ratio is defined in (8). Note that, by construction, the ratio between AMISEs is always larger or equal to one. Part (a) of Fig. 1 shows the values taken by the ratio defined in (8) as a function of the quantile order \(\tau \) and for three error distributions: exponential with expectation one, uniform on the interval (0, 1) and beta with parameters 5 and 1. Part (b) of Fig. 1 shows the values taken by the ratio defined in (9) as a function of \(\tau \) and for the same three error distributions.

Fig. 1
figure 1

Representations of the ratios between the AMISE bandwidths [detailed in (8)] and the MISE values [detailed in (9)] as a function of the quantile order \(\tau \) and for three error distributions. The dashed line represents the uniform distribution, the dotted line represents the beta distribution, and the dashed and dotted line represents the exponential distribution

Full size image

As shown in Fig. 1, we observe that the differences between both AMISE bandwidths will be bigger as long as the error distribution differs from the Gaussian distribution. Furthermore, if we fix an error distribution, the compared behaviour of both optimal bandwidths will depend on the quantile of interest.

Our first simulated model is given by

$$\begin{aligned} \text{ Model } \text{1: } \qquad Y=10(X^4+X^2-X)+\varepsilon , \end{aligned}$$

where X follows a uniform distribution on the interval (0, 1) and \(\varepsilon \) is the unknown error, which is drawn independently of X. Note that in this case, \(q_{\tau }(X)=10(X^4+X^2-X)+c_{\tau }\) where \(c_{\tau }\) represents the \(\tau \)-quantile of the error distribution. This notation is common for all the homoscedastic models that will be considered. In this model, the error follows an exponential distribution with expectation 1, which is one of the distributions represented in Fig. 1. Part (a) of Fig. 2 shows a scatterplot of one sample of size 200 drawn from this model, together with three quantile functions, for \(\tau =0.1, 0.25, 0.5\).

Fig. 2
figure 2

Scatterplots of a sample of size 200, together with five quantile regression functions: \(\tau =0.1\) (dotted line), \(\tau =0.25\) (dashed line), \(\tau =0.5\) (solid line), \(\tau =0.75\) (dashed line) and \(\tau =0.9\) (dotted line), corresponding to Model 1 in (a) and Model 2 in (b)

Full size image
Fig. 3
figure 3

Boxplot representations of Yu and Jones (1998)’s selector (YJ), the new rule of thumb (RT), the new plug-in selector (NP) and the cross-validation selector (CV), from 1000 replications of Model 1 for different values of \(\tau \) and the sample size, n. The dashed line represents the MISE bandwidth, the dotted line represents the Yu and Jones (1998)’s AMISE bandwidth, and the dashed and dotted line represents the AMISE bandwidth

Full size image

Figure 3 represents the boxplots corresponding to the four bandwidth selectors: the plug-in selector proposed by Yu and Jones (1998), the selector based on the new rule of thumb, the new plug-in selector and the cross-validation selector. They are denoted by YJ, RT, NP and CV, respectively. The boxplots were obtained from 1000 replications of Model 1 for different values of \(\tau \), and sample sizes \(n=100, 500\). Three horizontal lines are added to the plots, representing the optimal bandwidths with three criteria: MISE (dashed line), Yu and Jones (1998)’s AMISE (dotted line) and AMISE (dashed and dotted line). The best of these bandwidths would be the one optimizing the MISE, so the performance of each selector is related to its approximation to this bandwidth. The AMISE bandwidth is an approximation to the MISE bandwidth. In fact, both lines approach to each other for increasing sample size. Meanwhile, Yu and Jones (1998)’s AMISE (YJ-AMISE) bandwidth do not approximate to MISE bandwidth even for a very large sample size. This is the cause for inconsistency of Yu and Jones (1998)’s selector. However, for a small sample size, the errors of approximation between the three bandwidths can be confounded. As regards the value of \(\tau \), Fig. 3 shows that for \(\tau =0.5\) the three bandwidths are quite similar, while for \(\tau =0.1\) they are far apart.

Yu and Jones (1998)’s selector estimates YJ-AMISE bandwidth, while the new selectors estimate AMISE bandwidth. For sample size \(n=500\), this leads to a clearer better performance of the new bandwidths, while for small sample size \(n=100\), the errors between optimal bandwidths are still confounded. The cross-validation bandwidth is generally centred to the MISE bandwidth, but its variability is clearly larger.

Now we are going to evaluate the performance of each selector in terms of the observed integrated squared error (OISE) in one thousand simulated samples. Following Jones (1991), for each sample the OISE will be computed for the local linear fit with the considered bandwidth selectors, that is,

$$\begin{aligned} \hbox {OISE}({{\widehat{h}}}_{\tau })=\frac{1}{n}\sum _{i=1}^{n}\left( {\widehat{q}}_{\tau ,{{\widehat{h}}}_\tau }(X_i)-q_{\tau }(X_i)\right) ^2, \end{aligned}$$

where \({{\widehat{h}}}_{\tau }\) plays the role of some bandwidth selector. Then, the sample means of the OISEs (denoted by SMISE) over the simulated samples will be employed for comparison.

To complete the presentation, a new model is included, again homoscedastic but with a larger curvature:

$$\begin{aligned} \text{ Model } \text{2: } \qquad Y=1-48X+218X^2-315X^3+145X^4 +\varepsilon , \end{aligned}$$

where X follows a uniform distribution on the interval (0, 1) and \(\varepsilon \) follows an exponential distribution with expectation 1 and is drawn independently of X. Part (b) of Fig. 2 shows a scatterplot and three quantile functions, for \(\tau =0.1, 0.25, 0.5\), corresponding to Model 2.

Table 1 contains the sample mean of the integrated squared error for the considered bandwidth selectors for several samples sizes and values of \(\tau \). We can observe that the new plug-in rule shows a better performance in terms of SMISE than the plug-in selector proposed by Yu and Jones (1998), for almost all sample sizes for \(\tau =0.10\) and 0.25. For \(\tau =0.50\), the SMISE associated with both plug-in rules is quite similar. Note that in this case the ratio described in (8) is near to 1 as shown in Fig. 2. That is, for \(\tau =0.5\) the two AMISE bandwidths are almost equal.

On the other hand, the results associated with quantiles \(\tau =0.75\) and 0.90 are better for the selector presented by Yu and Jones (1998). These results are consequence of the proximity of the ratio (9) to 1 (see Fig. 1) and a low density of the error distribution at these high quantiles. A ratio (9) close to 1 means that inconsistency of Yu and Jones (1998)’s selector has not a severe effect for small sample sizes. A low density of the error distribution at the considered quantile makes curvature and sparsity estimation more difficult. In a sense, we are in ideal conditions for Yu and Jones (1998)’s selector versus the new plug-in selector: being curvature and sparsity similar to their analogues in mean regression, and easier to estimate in mean regression.

Table 1 Sample mean of the integrated squared error (given values were multiplied by \(10^3\)) associated with the considered bandwidth selectors, from 1000 replications of Model 1 and Model 2, with several sample sizes n and values of \(\tau \)
Full size table

In any case, it should observed that due to inconsistency of Yu and Jones (1998)’s selector, for a sample size large enough SMISE will be better for the plug-in selector proposed here. Table 2 shows this behaviour. Table 2 does not include results for the cross-validation selector because of its computational cost for large sample sizes.

It is interesting to emphasize the good behaviour of the rule of thumb, despite its simplicity. For a fair interpretation, we should note that the considered models are homoscedastic and contain polynomial quantile regression functions of order 4, these being ideal conditions for the rule of thumb. The cross-validation bandwidth shows a generally worst SMISE in the considered scenarios.

Table 2 Sample mean of the integrated squared error (given values were multiplied by \(10^4\)) associated with the considered bandwidth selectors, from 1000 replications of Model 1 and Model 2, with several sample sizes n and values of \(\tau \)
Full size table

Now, we will analyse how the performance of the considered bandwidth selectors depends on the error distribution. To do this, we will generate samples from these two models:

$$\begin{aligned}&\text{ Model } \text{3: } \ \ Y=1-48X+218X^2-315X^3+145X^4 +\varepsilon \\&\text{ Model } \text{4: } \ \ Y=\sin (5\pi X)+\varepsilon \end{aligned}$$

where X follows a uniform distribution on the interval (0, 1) and \(\varepsilon \) is independent of X and follows one of these distributions: standard normal, uniform on the interval \((-3,3)\), Student’s t with two degrees of freedom and standard log normal. Quantile function in Model 3 coincides with that of Model 2, while the error distribution now takes different shapes. Model 4 is represented in Part (a) of Fig. 4, with a standard normal distribution.

Fig. 4
figure 4

Scatterplots of a sample of size 200 drawn from Model 4 and Model 5, where the error follows a standard normal distribution. The lines are quantile functions for \(\tau =0.25\) (dashed line), \(\tau =0.5\) (solid line) and \(\tau =0.75\) (dashed and dotted line)

Full size image

Table 3 shows the sample mean of the integrated squared errors for the compared bandwidth selectors, under Model 3 and Model 4. In all cases, the quantile function is estimated for \(\tau =0.5\). The new plug-in rule outperforms the other three selectors. Yu and Jones (1998)’s selector shows a good performance for the standard normal error distribution, where its assumptions are completely satisfied. However, the new plug-in rule has similar results to Yu and Jones (1998)’s selector, even under these conditions, which shows that in this case quantile estimations of curvature and sparsity are not much less efficient than its estimations under mean regression. For distributions far from normality, as Student’s t distribution or log normal, the new plug-in rule shows a clearly better behaviour. All these results are to be attributed to sparsity estimation, which is inconsistently biased in Yu and Jones (1998)’s method. Note that the simulated models are homoscedastic, and then, quantile curvature coincides with mean curvature.

The rule of thumb is slightly worse than the plug-in rule, although the difference is moderate in many cases. In particular, rule of thumb results are better under Model 3 than under Model 4, because the quantile function under Model 3 is better suited for blocked polynomial estimations carried out in the rule of thumb method. The cross-validation selector is generally worse than plug-in methods, and particularly worse than the new plug-in rule.

Table 3 Sample mean of the integrated squared error (given values were multiplied by \(10^2\)) associated with the considered bandwidth selectors, from 1000 replications of Model 3 and Model 4 with \(\tau =0.5\), and several error distributions and sample sizes
Full size table

Moreover, we are going to consider the following heteroscedastic quantile regression model:

$$\begin{aligned} \text{ Model } \text{5: }\ \ Y = \sin (5\pi X)+(\sin (5\pi X)+2) \varepsilon \end{aligned}$$

where X follows a uniform distribution on the interval (0, 1) and \(\varepsilon \) is independent of X. Note that in this case \(q_\tau (X)=\sin (5\pi X)+(\sin (5\pi X)+2) c_{\tau }\) where \(c_{\tau }\) denotes the \(\tau \)-quantile of the error distribution. Firstly, \(\varepsilon \) is drawn from the standard normal distribution. Then, the main deviation of Model 5 from Yu and Jones (1998)’s assumptions is the fact that curvature depends on the quantile order, \(\tau \), and then, it is not equal to the curvature of mean regression function. Part (b) of Fig. 4 shows a representation of Model 5. A scatterplot together with three quantile functions (for \(\tau = 0.25, 0.5, 0.75\)) is shown. It can be seen how heteroscedasticity leads to different curvatures of the quantile regression function for different values of \(\tau \). Secondly, we will suppose that the error follows a Student t distribution with three degrees of freedom. In this second situation, neither of the assumptions considered by Yu and Jones (1998) are verified.

In Table 4, the sample mean of the integrated squared error from each of the bandwidth selectors is given for several samples sizes and values of \(\tau \). The new plug-in method provides better results than its competitors. Note that for \(\tau =0.5\) and Gaussian error distribution quantile regression coincides with mean regression, so this setup would be quite favourable for Yu and Jones (1998)’s selector. In this case, both plug-in selectors shows similar results. For quantile orders far from the median, advantages of the new plug-in rule are more noticeable. Furthermore, the differences between the sample mean of the integrated squared error associated with both plug-in methods are bigger when we suppose that the error follows a Student t distribution, as it was expected.

Table 4 Sample mean of the integrated squared error (given values were multiplied by \(10^2\)) associated with the compared bandwidth selectors, from 1000 replications of Model 5 and for several values of \(\tau \) and the sample size n
Full size table

Now, we are going to check the robustness of the new method to deviations from some smoothness conditions assumed for the quantile regression model. In particular, we are going to generate values from a model that is not differentiable:

$$\begin{aligned} \text{ Model } \text{6: }\ \ Y = 5|X|+ \sigma (X) \, \varepsilon \end{aligned}$$

where X follows a uniform distribution on the interval \((-1,1)\) and \(\varepsilon \) is independent of X. Two possible error distributions will be considered: a \(\chi \)-squared distribution with two degrees of freedom and a Student’s t distribution with two degrees of freedom. Note that in this case \(q_\tau (X)=5|X|+ \sigma (X) \, c_{\tau }\) where \(c_{\tau }\) denotes the \(\tau \)-quantile of the error distribution. Two different options will be considered for the function \(\sigma (X)\): \(\sigma (X)=1\) (homoscedastic model) and \(\sigma (X)=(|X|+2)\) (heteroscedastic model). Figure 5 shows a representation of Model 6.

Fig. 5
figure 5

Scatterplots of samples of size 200 drawn from Model 6, where the error follows a \(\chi \)-squared distribution with two degrees of freedom. The lines represent the median regression function

Full size image

Table 5 shows the sample mean of the integrated squared error when estimating the median regression with each of the bandwidth selectors. The new rule-of-thumb and plug-in methods provide better results than the other selectors in most of the considered scenarios. No relevant anomalies were observed in the performance of the selectors when smoothness conditions are not satisfied.

Table 5 Sample mean of the integrated squared error (given values were multiplied by \(10^2\)) associated with the compared bandwidth selectors, from 1000 replications of Model 6 and for several sample sizes, n
Full size table

In a last experiment, we carried out some simulations to show the usefulness of the new plug-in selector for double-kernel methodology. In each of the two double-kernel estimators, one proposed by Yu and Jones (1998) and the other proposed by Jones and Yu (2007), two bandwidths are required. One of these bandwidths (\(h_1\) in their notation) plays a more relevant role and behaves as a classical bandwidth for local linear quantile regression. In both works, the authors proposed to use the selector proposed by Yu and Jones (1998) for this main bandwidth. Then, we are going to compare the plug-in rule and Yu and Jones (1998)’s rule, when applied to the selection of this bandwidth \(h_1\) for double-kernel estimators. The second and less relevant bandwidth will be chosen following the authors’ advices. Data will be drawn from Model 3 used previously that is given by

$$\begin{aligned}&\text{ Model } \text{3: } \ \ Y=1-48X+218X^2-315X^3+145X^4 +\varepsilon \end{aligned}$$

where X follows an uniform distribution on the interval (0, 1) and \(\varepsilon \) is independent of X and follows one of these two distributions: Student’s t with two degrees of freedom and standard log normal.

Table 6 contains the sample mean of the integrated squared error (SMISE) obtained from 1000 Monte Carlo replications, for different estimators: ordinary local linear estimator, double-kernel estimator proposed by Yu and Jones (1998) (denoted by DK YJ) and double-kernel estimator proposed by Jones and Yu (2007) (denoted by DK JY). Furthermore, the different bandwidth selectors used along this simulation study will be considered: YJ, RT, NP and CV. To simplify the comparison, for double-kernel estimator only YJ and NP selectors will be considered.

Table 6 Sample mean of the integrated squared error (given values were multiplied by \(10^2\)) associated with the considered estimators: ordinary local linear estimator, double-kernel estimator presented by Yu and Jones (1998) (DK YJ) and double-kernel estimator presented by Jones and Yu (2007) (DK JY), from 1000 replications of Model 3, for two error distributions, three values of \(\tau \) and two sample sizes. Four bandwidth selectors were considered: the plug-in selector proposed by Yu and Jones (1998) (YJ), the selector based on the new rule of thumb (RT), the new plug-in selector (denoted by NP) and the cross-validation selector (CV)
Full size table

According to the results shown in Table 6, we can conclude that the new plug-in rule improves the performance of both double-kernel estimators. Only for a Student’s t distribution with two degrees of freedom, \(\tau =0.75\) and \(n=100\), Yu and Jones (1998)’ bandwidth leads to a better performance. Note also that ordinary local linear estimator and the double-kernel estimator presented by Jones and Yu (2007) behave similarly when the new plug-in selector is used.

4 Real data application

The data set Mammals, included in the R package quantreg, contains 107 observations on the maximal running speed of mammal species and their body mass. Figure 6 represents the scatterplot of these two variables, together with local linear quantile fits for \(\tau =0.25\), 0.5 and 0.75. Koenker (2005) uses this data set to illustrate how sensitive the least-squares fitting procedure is to outlying observations (see pp. 232–234). Here, we only consider local linear quantile fits, and we will compare bandwidth selectors. Note that the proposed plug-in bandwidth selector is based on quantile techniques, while Yu and Jones (1998)’s selector is based on classical estimates of curvature and conditional variance and then could be sensitive to outliers. It can also be observed that the chosen data set shows asymmetry of the response (the maximal running speed) conditionally to the explanatory variable (the body weight), with more conditional density around high quantiles and lower density around low quantiles.

Solid lines in Fig. 6 represent local linear quantile fits with the new plug-in bandwidth selector, while dotted lines are obtained with Yu and Jones (1998)’s rule. For \(\tau =0.5\), both fits are quite similar. In this case, the proposed plug-in bandwidth takes the value 1.36, while Yu and Jones (1998)’s bandwidth takes the value 1.16. As a consequence, the dotted line seems slightly more wiggly, maybe due to the effect of outliers on curvature and conditional variance estimation. For \(\tau =0.25\), the bandwidths are 1.59 for the new rule and 1.20 for Yu and Jones (1998)’s rule. Then, the dotted line is even more wiggly than the solid line, showing spurious fluctuation. Note that the density of the response around the 0.25 conditional quantile is low. This fact is taken into account by the new plug-in rule, but not by Yu and Jones (1998)’s rule. On the contrary, the density of the response around the 0.75 conditional quantile is high. The selected bandwidths are 0.97 for the new rule and 1.20 for Yu and Jones (1998)’s rule. Thus, the dotted line is over-smoothed and hides relevant features in the data. In particular, the change in slope around 1 Kg of weight is not detected by the dotted line. It can also be observed that Yu and Jones (1998)’s rule selects the same bandwidth for 0.25 and 0.75 quantiles. This is a general behaviour of this rule, which takes the same value for \(\tau \) and \((1-\tau )\) conditional quantiles, as a consequence of assuming that the conditional distribution of the response is Gaussian. Then, it does not take into account possible asymmetries in the conditional distribution, as it is the case in this real data situation.

Fig. 6
figure 6

Local linear quantile regression fits for Mammals data set with \(\tau =0.25\), 0.5 and 0.75. Solid lines are obtained with bandwidths selected by the new plug-in rule. Dotted lines result from bandwidths selected by Yu and Jones (1998)’s rule

Full size image

5 Conclusions and extensions

We have proposed a new plug-in bandwidth selector for local linear quantile regression based on a nonparametric approach. This new method involves nonparametric estimation of the curvature of the quantile regression function and the integrated squared sparsity. Convergence of the new rule to the optimal bandwidth is shown, with the same rate as for mean regression selectors.

Thanks to a Monte Carlo simulation study, we have shown that the new proposal shows a good behaviour in terms of the sample mean of the integrated squared error compared with its natural competitors in both homoscedastic and heteroscedastic scenarios. Moreover, we have presented a simple rule of thumb that shows a quite good performance on a wide range of situations.

An R package called BwQuant has been developed to enable any user to apply the techniques proposed in this paper: rule of thumb and plug-in rule. The natural competitors, cross-validation and Yu and Jones (1998)’s bandwidths, were also implemented. Moreover, we have included a function that estimates the quantile regression function using local linear kernel regression.

The developed methodology can be used in the double-kernel estimator proposed by Yu and Jones (1998) and Jones and Yu (2007), as it was illustrated in a last experiment at the end of the simulation study. Moreover, the proposed techniques can be extended to the case of a multidimensional covariate, particularly to nonparametric additive models in a quantile regression context as those considered by Yu and Lu (2004). Similarly to Yu and Jones (1998), Yu and Lu (2004) proposed a heuristic rule for selecting the smoothing parameter, using Opsomer and Ruppert (1998)’s bandwidth for mean regression with some transformation based on assumptions such as homoscedasticity and error normality. A plug-in rule specifically designed for additive quantile regression would be more appropriate when these assumptions are not satisfied. This plug-in rule would benefit from the ideas given in this paper.