Inference with progressively censored k-out-of-n system lifetime data

Abstract

A system with n independent components which works if and only if a least k of its n components work is called a k-out-of-n system. For exponentially distributed component lifetimes, we obtain point and interval estimators for the scale parameter of the component lifetime distribution of a k-out-of-n system when the system failure time is observed only. In particular, we prove that the maximum likelihood estimator (MLE) of the scale parameter based on progressively Type-II censored system lifetimes is unique. Further, we propose a fixed-point iteration procedure to compute the MLE for k-out-of-n systems data. In addition, we illustrate that the Newton–Raphson method does not converge for any initial value. Finally, exact confidence intervals for the scale parameter are constructed based on progressively Type-II censored system lifetimes.

1 Introduction

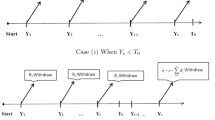
Terminating of a lifetime test before all objects have failed is a common practice. In a Type-II censoring process, the monitoring of failures continues up to a prefixed number of failures so that only v observations of a random sample of size w are available ($v, w\in {\mathbb {N}}=\{1, 2, 3,\dots \}$, $1\le v\le w$). Progressive Type-II censoring is a generalization due to Cohen (1963) which works as follows. Consider an experiment where w identical objects are put on a lifetime test. The number of observed failure times v and the censoring plan $(R_1,\dots , R_v)$ with $\sum _{i=1}^v R_i=w-v$ are prefixed before the beginning of the lifetest. After observing the first failure time $Y_{1:v:w}$, $R_1\in {\mathbb {N}}_0=\{0, 1, 2,\dots \}$ objects are randomly removed from the remaining $w-1$ (still functioning) objects. At the second failure time $Y_{2:v:w}$, $R_2\in {\mathbb {N}}_0$ objects are withdrawn from the remaining $w-2-R_1$ objects. Continuing this censoring process, $R_i\in {\mathbb {N}}_0$ objects are randomly removed at the i-th failure time $Y_{i:v:w}$ from the remaining $w-i-\sum _{j=1}^{i-1}R_j$ objects. At the v-th failure time $Y_{v:v:w}$, all remaining $R_v=w-v-\sum _{j=1}^{v-1}R_j$ objects are censored. For details, see Balakrishnan and Cramer (2014). For a censoring plan $(R_1,\dots ,R_v)$, the joint probability density function (pdf) of progressively Type-II censored order statistics $Y_{1:v:w},\dots ,Y_{v:v:w}$ based on a cumulative distribution function (cdf) F with pdf f is given by

$$\begin{aligned} f_{\mathbf {Y}}({\mathbf {y}})&=\prod _{i=1}^v\left( \gamma _i f(y_i)(1-F(y_i))^{R_i}\right) ,\quad y_1<\dots <y_v, \end{aligned}$$

(1)

where, for brevity, ${\mathbf {Y}}=(Y_{1:v:w},\dots , Y_{v:v:w})$, ${\mathbf {y}}=(y_1\dots , y_v)$, and $\gamma _i=\sum _{j=i}^v(R_j+1)$, $i=1,\dots ,v$, represents the number of surviving objects before the i-th failure (see Balakrishnan and Cramer (2014), p. 22). Many authors have discussed progressive Type-II censoring for different lifetime distributions and related inference (see Balakrishnan and Cramer (2014), Balakrishnan (2007), Balakrishnan and Aggarwala (2000)). In particular, likelihood inference is widely used in the context of progressively Type-II censoring (see Balakrishnan and Kateri (2008), Pradhan and Kundu (2009)). In this paper, parametric inference for the component lifetime distribution based on k-out-of-n system lifetime data is addressed when

• 1. The $n\in {\mathbb {N}}$ components of the k-out-of-n system are supposed to have independent and identically distributed lifetimes,

• 2. The system lifetimes $Y_1, \dots , Y_w$ of w independent k-out-of-n systems are available only, and

• 3. The sample $Y_1, \dots , Y_w$ of w k-out-of-n system lifetimes is subject to progressive Type-II censoring with censoring plan $(R_1,\dots , R_v)$ resulting in v observed failure times $Y_{1:v:w}, \dots , Y_{v:v:w}$.

Notice that, for $w=1$, inference is based on a single order statistic $X_{n-k+1:n}$ with $k\in \{1,\dots , n\}$. This problem has been discussed computationally in Glen (2010) for an exponential and Rayleigh distribution, respectively. For exponential populations, best linear unbiased estimators based on a single order statistic have been discussed in Harter (1961) (see also Kulldorff (1963)). It should be mentioned that this inferential problem has already been discussed when all component failures of each system have been observed, i.e., $X_{1:n,i},\dots , X_{n-k+1:n,i}$, $1\le i \le w$ (see, e.g., Cramer and Kamps (1996), Balakrishnan et al. (2001), Balakrishnan and Cramer (2014)). Notice that this scenario corresponds to multiple Type-II right censored samples whereas we consider a progressively sample of the maxima $X_{n-k+1:n,i}$, $1\le i \le w$.

A k-out-of-n system works when at least k of its components work. It fails when the $(n-k+1)$-th component failure occurs. Thus, supposing $X_1,\ldots , X_n$ to be the component lifetimes of a k-out-of-n system, the lifetime of the k-out-of-n system is given by the $(n-k+1)$-th order statistic $X_{n-k+1,n}$. Thus, the cdf F and pdf f of the system lifetime with known parameter $k,n\in \mathbb {N}$ and component lifetime cdf G are given by

$$\begin{aligned} F(t)&= \sum _{i=n-k+1}^n\left( {\begin{array}{c}n\\ i\end{array}}\right) \left( G(t)\right) ^{i}\left( 1-G(t)\right) ^{n-i}, \quad t\ge 0, \end{aligned}$$

(2)

$$\begin{aligned} f(t)&= (n-k+1)\left( {\begin{array}{c}n\\ n-k+1\end{array}}\right) g(t)\left( G(t)\right) ^{n-k}\left( 1-G(t)\right) ^{k-1}, \quad t\ge 0. \end{aligned}$$

(3)

Therefore, we have a progressively Type-II censored sample $Y_{1:v:w},\dots ,Y_{v:v:w}$ generated from an i.i.d. sample $Y_1,\dots , Y_w$ with $Y_j\sim F$, $1\le j\le w$. Thus, we can interpret the data as a progressively Type-II censored sample of independent order statistics. It is clear that our results can be applied to test situations without censoring ($R_1=\cdots =R_v=0$), that is, the data consists of w independent order statistics $X_{k:n,1},\dots , X_{k:n,w}$.

In the following, we are interested in inferential procedures for the component lifetime distribution G. Notice that the failure times of the components in each system are not available and that the cdf of $Y_i$ is a function of G. In the literature, two cases of this setting have been discussed so far. For $k=n$, we have series systems data. Several authors have discussed progressively Type-II censored series system lifetime data which is also called first failure progressive Type-II censoring (see Balakrishnan and Cramer 2014, Section 25.4). This model has been introduced by Wu and Kus (2009) who discussed likelihood inference in the case of series system lifetime data with Weibull distributed component lifetimes. Further references for other lifetime distributions are provided in Balakrishnan and Cramer (2014, p. 529). Balakrishnan and Cramer (2014) showed that progressively Type-II censored order statistics of series system lifetimes have the same distribution as progressively Type-II censored order statistics from the component lifetime distribution with a different censoring plan. Therefore, progressively censored series system data can be handled as standard progressively censored data with a modified censoring plan. For $k=1$, parallel systems data is given. Progressively Type-II censored parallel system lifetimes have been studied first by Pradhan (2007) who considered maximum likelihood estimation of the scale parameter in case of parallel systems with exponentially distributed component lifetimes. Continuing this work, Hermanns and Cramer (2017) proved that the MLE is unique and that it can be calculated by a fixed-point iteration procedure. As a generalization, this article focuses on inference for the lifetime distribution of the more general k-out-of-n structure with exponentially distributed component lifetimes. A k-out-of-n system with exponentially distributed component lifetimes has been discussed by Pham (2010) who considered the uniformly minimum variance unbiased estimator and the MLE based on both non-censored data and Type-II censored data. In addition, we prove that the MLE of the scale parameter based on progressively Type-II censored systems data is unique and can be determined by a modified fixed-point iteration procedure. Further, it turns out that the Newton–Raphson procedure does not converge when the initial value is not close enough to the solution of the likelihood equation. We illustrate by simulations that the percentage of non-converging situations may be rather large (see Sect. 2.2). Hence, our fixed-point iteration is a suitable choice to calculate the MLE. Furthermore, we derive exact confidence intervals for the scale parameter in Sect. 2.3. Proofs of the theorems and lemmas can be found in “Appendix”.

2 Exponential component lifetimes

In this section, let $G_\lambda (y)=1-\exp (-\,\lambda y)$, $y\ge 0$, be the cdf of an exponential distribution with scale parameter $\lambda >0$. For the case $k=1$ (parallel system), Hermanns and Cramer (2017) showed that the MLE uniquely exists. Further, they established a fixed-point iteration procedure to compute the MLE. For $k=n$, we can use the connection between series system lifetimes and component lifetimes according to Balakrishnan and Cramer (2014). Hence, we assume $1<k<n$ in the following.

2.1 Likelihood inference

Suppose the system lifetimes of w k-out-of-n systems with exponentially distributed component lifetimes are progressively Type-II censored with a prefixed censoring plan $R_1,\ldots ,R_v$. Let $G_{n-k+1:n;\lambda }$ be the cdf of the $n-k+1$-th order statistic based the population cdf $G_\lambda$. Using (1), for $\lambda >0$ and $0<y_1<\cdots <y_v$, the log-likelihood function is given by

$$\begin{aligned} l_{\mathbf {Y}}({\mathbf {y}};\lambda )=&\ln (C)+v\ln (\lambda )-\lambda k\sum _{i=1}^vy_i(n-k)\sum _{i=1}^v\ln \left( 1-\exp (-y_i\lambda \right) )\nonumber \\&+\sum _{i=1}^vR_i\ln (H(y_i,\lambda )), \end{aligned}$$

(4)

where

$$\begin{aligned} H(y,\lambda )&=\sum _{j=0}^{n-k}\left( {\begin{array}{c}n\\ j\end{array}}\right) \big (1-\exp (-y\lambda ))^j\left( \exp (-y\lambda \right) \big )^{n-j}\nonumber \\&=1-G_{n-k+1:n;\lambda }(y), \quad \lambda ,y>0, \end{aligned}$$

(5)

and $C=\ln \left( \prod _{i=1}^v\gamma _i\right) +v\ln \big ((n-k+1)\left( {\begin{array}{c}n\\ n-k+1\end{array}}\right) \big )$ is independent of the parameter $\lambda$. For the derivative of the log-likelihood function, we need the partial derivative of H with respect to (w.r.t.) $\lambda$, that is,

$$\begin{aligned} \frac{\partial }{\partial \lambda } H(y,\lambda )&=-\frac{\partial }{\partial \lambda } G_{n-k+1:n;\lambda }(y) \nonumber \\&=-k\left( {\begin{array}{c}n\\ n-k\end{array}}\right) \left( G_\lambda (y)\right) ^{n-k}\left( 1-G_\lambda (y)\right) ^{k-1}\frac{\partial }{\partial \lambda }G_\lambda (y) \nonumber \\&=-k\left( {\begin{array}{c}n\\ n-k\end{array}}\right) y\left( G_\lambda (y)\right) ^{n-k}\left( 1-G_\lambda (y)\right) ^{k}, \quad \lambda ,y>0. \end{aligned}$$

(6)

Here, we have used $\partial G_\lambda (y)/\partial \lambda =yG_\lambda (y)$, $y>0$, and the representation of the pdf of the $n-k+1$-th order statistic based on $G_\lambda$. For $0<y_1<\dots <y_v$, the likelihood equation can be written as

$$\begin{aligned} \frac{\partial l_{\mathbf {Y}}}{\partial \lambda }({\mathbf {y}};\lambda )=&\,\frac{v}{\lambda }-k\sum _{i=1}^v y_i+(n-k)\sum _{i=1}^v\frac{y_i\exp (-y_i\lambda )}{1-\exp (-y_i\lambda )}\nonumber \\&-k\left( {\begin{array}{c}n\\ n-k\end{array}}\right) \sum _{i=1}^vR_iy_i\frac{(G_\lambda (y_i))^{n-k}(1-G_\lambda (y_i))^{k}}{\sum _{j=0}^{n-k}\left( {\begin{array}{c}n\\ j\end{array}}\right) \left( G_\lambda (y_i)\right) ^{j}\left( 1-G_\lambda (y_i)\right) ^{n-j}} \nonumber \\ =&\,\frac{v}{\lambda }-n\sum _{i=1}^vy_i+(n-k)\sum _{i=1}^vy_i(1-\exp (-y_i\lambda ))^{-1} \nonumber \\&-k\left( {\begin{array}{c}n\\ n-k\end{array}}\right) \sum _{i=1}^vR_iy_i\left( \,\sum _{j=-(n-k)}^0\left( {\begin{array}{c}n\\ j+n-k\end{array}}\right) (\exp (y_i\lambda )-1)^j\right) ^{-1}=0. \end{aligned}$$

(7)

Obviously, the likelihood equation $\frac{\partial l_{\mathbf {Y}}}{\partial \lambda }({\mathbf {y}};\lambda )=0$ can not be solved explicitly for $\lambda >0$ so that numerical methods have to be applied. Of course, the second partial derivative of the log-likelihood function should be negative for the solution $\widehat{\lambda }$. To get an expression for the second derivative of $l_{\mathbf {Y}}$, we need the following identity

$$\begin{aligned} \partial&\Bigg (\sum _{j=-(n-k)}^0\left( {\begin{array}{c}n\\ j+n-k\end{array}}\right) (\exp (y_i\lambda )-1)^j\Bigg )\biggl /\partial \lambda \\&=\sum _{j=-(n-k)}^{-1}j\left( {\begin{array}{c}n\\ j+n-k\end{array}}\right) (\exp (y_i\lambda )-1)^{j-1}\exp (y_i\lambda )y_i<0, \quad \lambda >0, \end{aligned}$$

which yields

$$\begin{aligned} \frac{\partial ^2l_{\mathbf {Y}}}{\partial \lambda ^2}({\mathbf {y}};\lambda )&=-\frac{v}{\lambda ^2}-(n-k)\sum _{i=1}^vy_i^2\frac{\exp (-y_i\lambda )}{(1-\exp (-y_i\lambda ))^2}\nonumber \\&\quad +\,k\left( {\begin{array}{c}n\\ n\!-k\end{array}}\right) \sum _{i=1}^vR_iy_i^2\frac{\sum _{j=-(n-k)}^{-1}j\left( {\begin{array}{c}n\\ j+n-k\end{array}}\right) (\exp (y_i\lambda )\!-\!1)^{j-1}\exp (y_i\lambda )}{\left( \sum _{j=-(n-k)}^0\left( {\begin{array}{c}n\\ j+n-k\end{array}}\right) (\exp (y_i\lambda )-1)^j\right) ^2} \nonumber \\&<0, \quad \lambda >0. \end{aligned}$$

(8)

Notice that the sum in the denominator is always negative since $j\in \{-\,(n-k),\dots , -\,1\}$. Furthermore, all weights are positive. This proves that the log-likelihood function $l_{\mathbf {Y}}$ is strictly concave. Hence, a local maximum at an inner point $(0,\infty )$ yields the global maximum of $l_{\mathbf {Y}}$ on $(0, \infty )$. Theorem 1 shows that the likelihood equation has exactly one solution so that the MLE $\widehat{\lambda }_{\mathrm{ML}}$ is unique. The proof is given in “Appendix”. An illustration is depicted in Fig. 1.

Theorem 1

The likelihood given in Eq. (7) has an unique solution $\widehat{\lambda }_{\mathrm{ML}}>0$ showing that the MLE of $\lambda$ is unique.

Fig. 1

Log-likelihood function $l_{\mathbf {Y}}({\mathbf {y}};\cdot )$ (solid blue line), see (4), and partial derivative $\partial l_{\mathbf {Y}}/\partial \lambda ({\mathbf {y}};\cdot )$ (dashed red line), see (7), for a simulated sample of 2-out-of-4 system lifetimes with $\textsf {Exp}(2)$-distributed component lifetimes and censoring plan (1, 2, 0, 0, 2)

Numerical methods have to be applied to obtain the MLE $\widehat{\lambda }_{\mathrm{ML}}$. The fixed-point iteration proposed in Theorem 2 converges for every initial value $\lambda _0>0$ to the MLE $\widehat{\lambda }_{\mathrm{ML}}$. The same idea has previously been successfully applied in Hermanns and Cramer (2017) for the simpler setting of parallel systems. However, for general k and n, the situation is more involved. First, we need the following lemma.

Lemma 1

For $1<k<n$, the function $\phi :(0,\infty )\rightarrow \mathbb {R}$ defined by

$$\begin{aligned} \phi (x)=\frac{\sum _{j=-(n-k)}^0\left( {\begin{array}{c}n\\ j+n-k\end{array}}\right) \left( e^x-1\right) ^{j-1}\left( jxe^x-e^x+1\right) }{\left( \sum _{j=-(n-k)}^0\left( {\begin{array}{c}n\\ j+n-k\end{array}}\right) \left( e^x-1\right) ^{j}\right) ^2}, \quad x\in (0,\infty ), \end{aligned}$$

(9)

attains a global minimum $\phi _{\mathrm{min}}\le 0$ on $(0, \infty )$. Further, $\phi$ is bounded from below by

$$\begin{aligned} \phi ^*=&\min \Bigg (-\frac{1+(n-k)e}{\sum _{j=0}^{n-k}\left( {\begin{array}{c}n\\ n-k-j\end{array}}\right) \left( e-1\right) ^{-j}},\nonumber \\&\qquad \qquad -\frac{\sum _{j=0}^{n-k} \left( {\begin{array}{c}n\\ n-k-j\end{array}}\right) (e-1)^{-j}\left( 1+je(e-1)^{-1}\right) }{\left( \left( {\begin{array}{c}n\\ n-k\end{array}}\right) \right) ^2}\Bigg ). \end{aligned}$$

(10)

Furthermore, we have $\lim _{x\rightarrow 0+} \phi (x)=0$ and $\lim _{x\rightarrow \infty } \phi (x)=-1/\left( {\begin{array}{c}n\\ k\end{array}}\right)$.

In particular, $-1/\left( {\begin{array}{c}n\\ k\end{array}}\right) \ge \phi _{\mathrm{min}} \ge \phi ^*$.

Theorem 2

Suppose $1<k<n$ and $0<y_1<\cdots <y_v$ is an observation of the sample $Y_{1:v:w},\ldots ,Y_{v:v:w}$. Let

$$\begin{aligned} a&=\max \left( \frac{n+k}{2k},\frac{n\sum _{i=1}^vy_i-\phi ^*k\left( {\begin{array}{c}n\\ n-k\end{array}}\right) \sum _{i=1}^vR_iy_i}{k\sum _{i=1}^v(R_i+1)y_i}\right) , \end{aligned}$$

(11)

where $\phi ^*$ is the lower bound of the function $\phi$ given in (10). Then, the function

$$\begin{aligned} \xi :(0,\infty )\rightarrow (0,\infty ),\quad \lambda \mapsto \frac{\lambda }{k\sum _{i=1}^v(R_i+1)y_i}\left( \frac{1}{a}\frac{\partial l_{\mathbf {Y}}}{\partial \lambda }({\mathbf {y}};\lambda )+k\sum _{i=1}^v(R_i+1)y_i\right) \end{aligned}$$

has an unique fixed-point, i.e., the MLE $\widehat{\lambda }_{\mathrm{ML}}$ of $\lambda$. Hence, the sequence $(\lambda _h)_{h\in \mathbb {N}_0}$ defined recursively by $\lambda _{h+1}=\xi (\lambda _{h})$, $h\in {\mathbb {N}}_0=\{0, 1, 2,\dots \}$, converges for every $\lambda _0\in (0, \infty )$ to the MLE $\widehat{\lambda }_{\mathrm{ML}}$.

Remark 1

An alternative fixed-point procedure can be defined by replacing the lower bound $\phi ^*$ of the function $\phi$ by its global minimum $\phi _{\mathrm{min}}$ in the definition of a in (11). Then, the fixed-point iteration still converges to the MLE $\widehat{\lambda }_{\mathrm{ML}}$ for every $\lambda _0\in (0, \infty )$. The proof proceeds along the same lines as that one provided in “Appendix” for Theorem 2. Notice that, for given values k and n, $\phi _{\mathrm{min}}$ has to be computed numerically only once (some selected values are given in Table 1). However, the fixed-point iteration defined via $\phi _{\mathrm{min}}$ might converge faster in certain situations (cf. Sect. 2.2).

Notice that the function $\phi$ does not depend on the data but, as can be easily seen from (11), the parameter a in the fixed-point iteration does in most cases.

We have calculated the minimum $\phi _{\mathrm{min}}$ using the Newton–Raphson method. To ensure that the fixed-point iteration with $\phi _{\mathrm{min}}$ still works, we rounded the absolute values of the computed minimum $\phi _{\mathrm{min}}$ of $\phi$ for given k and n. Some selected results are provided in Table 1. Further, we provide the lower bound $\phi ^*$ for the different combinations of k and n. Some plots of $\phi$ are depicted in Fig. 2.

Fig. 2

Graphs of the function $\phi$ on (0, 10), with $k=2,n=4$ (long dashed red line), $k=3,n=5$ (space dashed blue line), $k=2,n=7$ (dashed green line) and $k=3,n=10$ (solid orange line)

Table 1 Absolute values of the minimum $\phi _{\mathrm{min}}$ and of the lower bound $\phi ^*$ of the function $\phi$ defined in (9)

Remark 2

It should be mentioned that the preceding results for the exponential distribution can also be applied to distributions with proportional hazard rates, i.e., $1-F_\lambda =(1-F_0)^\lambda$, where the parameter $\lambda >0$ is unknown and $F_0$ is a known distribution. This includes, e.g., Weibull distribution with known shape parameter, particular Burr XII-distributions, and Pareto distributions. The application can be done by a transformation of a given sample $X_1,\ldots ,X_n$ based on the cdf $1-F_\lambda$ to a sample $Z_1,\ldots ,Z_n$ of exponentially distributed lifetimes. The transformation is given by $Z_i=-\ln (1-F_0(X_i))\sim \textsf {Exp}(\lambda )$ for $i=1,\ldots ,n$.

Remark 3

In a test situation without censoring, that is $R_1=\cdots =R_v=0$, the data are given by a sample $X_{k:n,1},\dots , X_{k:n,w}$ of independent order statistics. Then, the results of Theorems 1 and 2 simplify. The likelihood equation is given by

$$\begin{aligned} \frac{\partial l_{\mathbf {Y}}}{\partial \lambda }({\mathbf {y}};\lambda )&=\frac{v}{\lambda }-n\sum _{i=1}^vy_i+(n-k)\sum _{i=1}^vy_i\left( 1-\exp (-y_i\lambda )\right) ^{-1}=0. \end{aligned}$$

In particular, we get $a=\max ((n+k)/(2k),n/k)=n/k$ which is independent of the data. Then, the fixed-point function is given by

$$\begin{aligned} \xi :(0,\infty )\rightarrow (0,\infty ),\quad \lambda \mapsto \frac{\lambda }{n\sum _{i=1}^vy_i}\frac{\partial l_{\mathbf {Y}}}{\partial \lambda }({\mathbf {y}};\lambda )+\lambda . \end{aligned}$$

2.2 Simulation results and comparison of Newton–Raphson and fixed-point iteration procedures

The proposed fixed-point iteration procedure converges for every initial parameter $\lambda _0\in (0,\infty )$ according to the Banach fixed-point theorem. In the context of system lifetime data or progressive censoring, the Newton–Raphson method is widely used to compute the MLE (see, e.g., Pradhan (2007) or Potdar and Shirke (2014)). Hermanns and Cramer (2017) showed by a detailed simulation study that the Newton–Raphson procedure converges only for some initial parameters based on parallel systems data. They recommended to use the fixed-point iteration when one has no reasonable guess about the solution of the likelihood equation. As a further alternative to the Newton–Raphson method, they introduced a ’mixed’ procedure where the first step is performed as a fixed-point iteration and the Newton–Raphson method is used afterward. Of course, this idea of a ’mixed’ procedure can be applied to k-out-of-n systems data, too. In order to compare the three methods, we generated samples $y_1,\dots , y_v$ of progressively Type-II censored order statistics $Y_{1:v:w},\dots , Y_{v:v:w}$ using the algorithm presented in Balakrishnan and Cramer (2014, p. 194). Since the quantile function $F^{-1}$ is not available in closed form, we inverted the cdf computationally. The simulation study has been performed for 12 different censoring plans $(R_1,\dots ,R_v)$. These plans are specified in Table 2.

Table 2 12 progressive censoring plans considered in the simulation study

Table 3 Average MLEs ($\overline{\widehat{\lambda }}_{\mathrm{ML}}$) for true value $\lambda =0.5$, sample standard error (SSE), percentage of convergence (p), average number of iterations ($\overline{i}$) and average computation time ($\overline{t}$) for 2-out-of-4 systems, initial value $\lambda _0$ and censoring plans given in Table 2

Table 4 Average MLEs ($\overline{\widehat{\lambda }}_{\mathrm{ML}}$) for true value $\lambda =0.5$, sample standard error (SSE), percentage of convergence (p), average number of iterations ($\overline{i}$) and average computation time ($\overline{t}$) for 2-out-of-4 systems, initial value $\lambda _0$ and censoring plans given in Table 2

The results in Tables 3, 4, 5 and 6 are the average of $N=10,000$ simulated samples using Maple 2016. Table 3 shows the results for the fixed-point iteration procedure based on $\phi ^*$, and Table 4 shows the results for the fixed-point iteration with $\phi _{\mathrm{min}}$. The first two columns in Tables 3 and 4 give the censoring plan R and the initial value $\lambda _0>0$, respectively. Columns 3, 8, and 12 contain the mean of the MLEs $\widehat{\lambda }_{\mathrm{ML}}$ computed by the Newton–Raphson method, the fixed-point iteration and the ’mixed’ procedure, respectively. In columns 4, 9, and 13, the corresponding sample standard error (SSE) of $\widehat{\lambda }_{\mathrm{ML}}$ with

$$\begin{aligned} \text {SSE}\left( \widehat{x}\right)&=\sqrt{\frac{1}{N^*-1}\sum _{i=1}^{N^*}\left( \widehat{x}_i-\overline{\widehat{x}}\right) ^2} \end{aligned}$$

(12)

is given. For the Newton-Raphson procedure, the sample standard error is based on these cases only where the procedure converges. $N^*$ denotes the total number of these cases. In column 5 and 14, the percentage of converging sequences of the simulated samples p is shown. Further, we add the average number of iteration steps $\overline{i}$ in columns 6, 10 and 15, and the average computation time $\overline{t}$ in columns 7, 11 and 16. As a stopping criterion, we used the absolute difference between two iteration steps with a tolerance of 0.0001. To show the non-convergence of the Newton–Raphson method and the ’mixed’ procedure with an initial value far away from the maximum likelihood estimate, we compare the percentage of converging sequences for larger initial values for the Newton–Raphson method and the ’mixed’ procedure in Table 5. Further, we present some results for other ’mixed’ procedures with two and three steps performed by the fixed-point iteration.

From Tables 3 and 4, we conclude for 2-out-of-4 systems:

• All five methods yield the same average estimate and the same SSE of $\widehat{\lambda }_{\mathrm{ML}}$ (provided that the generated sequence of estimates converges). When the Newton–Raphson method converges, it yields the same estimate as the fixed-point methods.

• The Newton–Raphson procedure does not converge for all initial values $\lambda _0\in [0.2,0.8]$ (the percentage of converging sequences p is given in column 5).

• The ’mixed’ procedures seem to converge for nearly all initial values $\lambda _0\in [0.2,0.8]$. The percentage p of converging sequences is below 100% only for the initial value $\lambda _0=0.8$.

• The ’mixed’ procedures need less iteration steps $\overline{i}$ and less computation time $\overline{t}$ than the Newton–Raphson method.

• The fixed-point iterations seem to converge faster than the Newton–Raphson method (see average computation time $\overline{t}$). However, as is shown by the results for the ’mixed’ procedures, the Newton–Raphson method seems to converge faster when the iterate is close to the solution of the equation (cf. average computation time $\overline{t}$ in column 11 and 16 for censoring plans [4], [5], [6], [7], [9] and [12]). This underlines the usefulness of ’mixed’ procedures in accelerating the computation. However, in some cases the price to pay may be that the iteration does not converge (see Table 5).

• The two fixed-point iteration methods have no significant difference in the average computation time $\overline{t}$. The fixed-point iteration based on $\phi ^*$ is faster for censoring plans [4], [5], [6], [7], [9] and [12], while the fixed-point iteration defined via $\phi _{\mathrm{min}}$ is faster for censoring plans [1], [2], [8] and [11].

Table 5 Percentage of convergence of Newton–Raphson method and ’mixed’ procedures for 2-out-of-4 and 3-out-of-10 systems for true value $\lambda =0.5$, initial value $\lambda _0$ and censoring plans as given in Table 2

From Table 5, we conclude that

• The Newton–Raphson procedure and the ’mixed’ procedures converge only in a small neighborhood of the MLE.

• More iteration steps of the fixed-point iteration in a ’mixed’ procedure lead to a higher percentage of convergence.

The procedures that include the Newton–Raphson method are sensitive to the initial value. One has to increase the steps of the fixed-point iteration with the number of components to get a converging sequence. Hence, if one has no guess about the value of the MLE it is recommended to use the fixed-point iterations.

Remark 4

Of course, it is possible to apply other numerical methods to compute the MLE. For example, the Nelder–Mead simplex algorithm converges for a strictly concave function on $\mathbb {R}$ with bounded level sets (see Lagarias et al. (1998)). Further simulations show that our introduced fixed-point iteration procedures converge faster (cf. average computation time in Table 6). Notice that the simulated samples used to establish the results in Table 6 are not the same as those used to compute Tables 3 and 4. Furthermore, it is worth mentioning that other initial values as those used in Table 6 deliver similar results.

Table 6 Average MLEs ($\overline{\widehat{\lambda }}_{\mathrm{ML}}$) for true value $\lambda =0.5$ and average computation time $(\overline{t})$ for 2-out-of-4 systems, initial value $\lambda _0=0.5$ ($\lambda _0=0.5$, $\lambda _1=1$ for Nelder–Mead simplex) and censoring plans as given in Table 2

2.3 Exact confidence intervals

To obtain exact confidence intervals of the parameter $\lambda$, we use an approach described by Wu and Kus (2009) or Wu (2002) to construct exact confidence intervals for the distribution parameter by a transformation to the exponential distribution using normalized spacings. We need a strictly increasing continuous transformation $\psi$ of the random variables $Y_1,\dots ,Y_w$ to $\textsf {Exp}(1)$-distributed random variables, i.e., $Z_i=\psi (Y_i)\sim \textsf {Exp}(1)$ for $i=1,\dots ,w$. For k-out-of-n systems with i.i.d. lifetimes $Y_1,\dots ,Y_w$ and $\textsf {Exp}(\lambda )$-distributed component lifetimes, these transformed random variables are given by

$$\begin{aligned} Z_i&=-\ln (1-F(Y_i))=-\ln \Bigg (1-\sum _{j=n-k+1}^n\left( {\begin{array}{c}n\\ j\end{array}}\right) \left( G_\lambda (Y_i)\right) ^{j}\left( 1-G_\lambda (Y_i)\right) ^{n-j}\Bigg ) \\&=-\ln \Bigg (1-\sum _{j=n-k+1}^n\left( {\begin{array}{c}n\\ j\end{array}}\right) \left( 1-\exp (-Y_i\lambda )\right) ^{j}\left( \exp (-Y_i\lambda )\right) ^{n-j}\Bigg ), \quad i=1,\ldots ,w. \end{aligned}$$

The progressively Type-II censored order statistics have the following representation, for $i=1,\ldots ,v$:

$$\begin{aligned} Z_{i:v:w}&=-\ln \Bigg (1-\sum _{j=n-k+1}^n\left( {\begin{array}{c}n\\ j\end{array}}\right) \left( 1-\exp (-Y_{i:v:w}\lambda )\right) ^{j}\left( \exp (-Y_{i:v:w}\lambda )\right) ^{n-j}\Bigg ) \end{aligned}$$

The construction of exact confidence intervals for the parameter $\lambda$ is based on this representation and the pivot

$$\begin{aligned} \eta&=2\sum _{i=1}^v(R_i+1)Z_{i:v:w} \\&=\!-\,2\sum _{i=1}^v(R_i\!+\!1)\ln \Bigg (1\!-\!\!\!\sum _{j=n-k+1}^n\left( {\begin{array}{c}n\\ j\end{array}}\right) \left( 1\!-\exp (-Y_{i:v:w}\lambda )\right) ^{j}\left( \exp (-Y_{i:v:w}\lambda )\right) ^{n-j}\Bigg ), \end{aligned}$$

where $\eta \sim \chi _{2v}^2$ according to Wu and Kus (2009, p. 3663). Further, we have to show that $\eta$, as a function of $\lambda >0$, is strictly increasing.

Lemma 2

Suppose $0<y_1<\cdots <y_m$ is a sample of $Y_{1:v:w},\ldots ,Y_{v:v:w}$ and

$$\begin{aligned} \eta (\lambda )&=-\,2\sum _{i=1}^v(R_i+1)\ln \Bigg (1-\sum _{j=n-k+1}^n\left( {\begin{array}{c}n\\ j\end{array}}\right) \left( 1-\exp (-y_i\lambda )\right) ^{j}\left( \exp (-y_i\lambda )\right) ^{n-j}\Bigg ). \end{aligned}$$

(13)

The function $\eta$ is strictly increasing on $(0, \infty )$ and the equation $\eta (\lambda )=t$ has an unique solution for every $t>0$.

Therefore, it is possible to obtain exact confidence intervals for the parameter $\lambda >0$.

Theorem 3

Let $Y_{1:v:w},\ldots ,Y_{v:v:w}$ be progressively Type-II censored order statistics from k-out-of-n system lifetimes, where the component lifetimes are exponentially distributed with parameter $\lambda >0$. Let $(R_1,\ldots , R_v)$ be the censoring plan and $\chi ^2_{2v}(\beta )$ be the $\beta$-quantile of the $\chi ^2$-distribution with 2v degrees of freedom. For any $\alpha \in (0,1)$, a $(1-\alpha )$-confidence interval for $\lambda$ is given by

$$\begin{aligned} \left( \eta \left[ {\mathbf {Y}},\chi _{2v}^2(\alpha /2)\right] ,\eta \left[ {\mathbf {Y}},\chi _{2v}^2(1-\alpha /2)\right] \right) , \end{aligned}$$

where $\eta \left[ {\mathbf {Y}},t\right]$ is the unique solution for $\lambda$ of the equation

$$\begin{aligned} -2\sum _{i=1}^v(R_i+1)\ln \Bigg (1-\sum _{j=n-k+1}^n\left( {\begin{array}{c}n\\ j\end{array}}\right) \left( 1-\exp (-Y_{i:v:w}\lambda )\right) ^{j} \left( \exp (-Y_{i:v:w}\lambda )\right) ^{n-j}\Bigg )=t. \end{aligned}$$

In Table 7, the average lower and upper limits $\overline{\lambda }_l$ and $\overline{\lambda }_r$ of the exact confidence intervals are simulated for 2-out-of-4 system lifetimes and 3-out-of-10 system lifetimes when $\lambda =0.5$. The results in Table 7 are the average of $N=10,000$ simulated samples. Notice that these results are based on different simulated samples than those used in the simulation study summarized in Tables 3 and 4. Moreover, we have added the standard error (SSE) of $\lambda _l$ and $\lambda _r$ (see (12)) and the coverage probabilities $p_c$ of the proposed confidence intervals. The MLE of $\lambda$ has been computed by the introduced fixed-point iteration procedures with an initial value $\lambda _0=0.5$ and a tolerance of 0.0001.

Table 7 Average MLEs and 95%-confidence intervals for true value $\lambda =0.5$ based on simulated samples of 2-out-of-4 system lifetimes and 3-out-of-10 system lifetimes (average lower limit $\overline{\lambda }_l$, average upper limit $\overline{\lambda }_r$, standard errors (SSE), and coverage probability $p_c$)

3 Conclusion and discussion

In the present paper, we propose a modified fixed-point procedure to compute the maximum likelihood estimate when the data is given by progressively Type-II censored k-out-of-n systems data with exponentially distributed component lifetimes. We have shown that the maximum likelihood estimator uniquely exists. Further simulations show that the fixed-point procedure is more suitable than the widely used Newton–Raphson method because the Newton–Raphson method does not converge when the initial value is too far away from the solution of the likelihood equation (see Tables 3, 4 and 5). Moreover, we propose ’mixed’ procedures which combine both methods. First, the fixed-point method is used to compute a suitable estimate of the MLE. Then, we switch to the (locally faster) Newton–Raphson procedure. However, further simulations in Table 5 illustrate that this does not overcome the problem of non-convergence in any case but may lead to some improvement. Therefore, if one has no reasonable guess about the solution of the likelihood equations it is recommended to use the fixed-point method.

Appendix

Proof

(Theorem 1) We consider the limits of $\frac{\partial l_{\mathbf {Y}}}{\partial \lambda }({\mathbf {y}};\lambda )$ for $\lambda \rightarrow 0$ and $\lambda \rightarrow \infty$,

$$\begin{aligned} \lim _{\lambda \rightarrow 0}\frac{\partial l_{\mathbf {Y}}}{\partial \lambda }({\mathbf {y}};\lambda )&=-\,n\sum _{i=1}^vy_i+\lim _{\lambda \rightarrow 0}\bigg (\frac{v}{\lambda }+(n-k)\sum _{i=1}^vy_i(1-\exp (-y_i\lambda ))^{-1}\bigg ) \\&=\infty >0,\\ \lim _{\lambda \rightarrow \infty }\frac{\partial l_{\mathbf {Y}}}{\partial \lambda }({\mathbf {y}};\lambda )&=-\,n\sum _{i=1}^vy_i+(n-k)\sum _{i=1}^vy_i-k\left( {\begin{array}{c}n\\ n-k\end{array}}\right) \sum _{i=1}^vR_iy_i\left( \left( {\begin{array}{c}n\\ n-k\end{array}}\right) \right) ^{-1} \\&=-\,k\sum _{i=1}^v(R_i+1)y_i<0. \end{aligned}$$

As a consequence the function $\frac{\partial l_{\mathbf {Y}}}{\partial \lambda }({\mathbf {y}};\lambda )$ has to be zero for some $\widehat{\lambda }>0$ since it is a continuous function. Thus, $\widehat{\lambda }$ is a solution of the likelihood equation. The first derivative $\frac{\partial l_{\mathbf {Y}}}{\partial \lambda }({\mathbf {y}};\lambda )$ is strictly decreasing since $\frac{\partial ^2l_{\mathbf {Y}}}{\partial \lambda ^2}({\mathbf {y}};\lambda )<0$ for $\lambda >0$, see (8). Therefore, $\widehat{\lambda }$ is the unique solution of the equation $\frac{\partial l_{\mathbf {Y}}}{\partial \lambda }({\mathbf {y}};\lambda )=0$, $\lambda >0$. Then, $\widehat{\lambda }$ is the global maximum of $l_{\mathbf {Y}}$ and the MLE of $\lambda$ since $l_{\mathbf {Y}}$ is a strictly concave function on $(0, \infty )$. $\square$

Proof

(Lemma 1) First, we rewrite $\phi (x)$ for $x\in (0,\infty )$:

$$\begin{aligned} \phi (x)&=\frac{\sum _{j=-(n-k)}^0\left( {\begin{array}{c}n\\ j+n-k\end{array}}\right) \left( e^x-1\right) ^{j-1}\left( jxe^x-e^x+1\right) }{\left( \sum _{j=-(n-k)}^0\left( {\begin{array}{c}n\\ j+n-k\end{array}}\right) \left( e^x-1\right) ^{j}\right) ^2} \\&=-\frac{\sum _{j=0}^{n-k}\left( {\begin{array}{c}n\\ n-k-j\end{array}}\right) \left( e^x-1\right) ^{-j}\left( 1+\frac{jxe^x}{e^x-1}\right) }{\left( \sum _{j=0}^{n-k}\left( {\begin{array}{c}n\\ n-k-j\end{array}}\right) \left( e^x-1\right) ^{-j}\right) ^2}. \end{aligned}$$

Let $x\in (0,1]$. Then, a lower bound results from the inequalities

$$\begin{aligned} \phi (x)\ge -\frac{1+(n-k)\frac{xe^x}{e^x-1}}{\sum _{j=0}^{n-k}\left( {\begin{array}{c}n\\ n-k-j\end{array}}\right) \left( e^x-1\right) ^{-j}}\overset{(*)}{\ge }-\frac{1+(n-k)e}{\sum _{j=0}^{n-k}\left( {\begin{array}{c}n\\ n-k-j\end{array}}\right) \left( e-1\right) ^{-j}}, \end{aligned}$$

where we used the inequality $e^x-1\ge x$, $x\in [0,\infty )$, in $(*)$. For $x\in [1,\infty )$ and $j\in \mathbb {N}_0$, we obtain

$$\begin{aligned} (e^x-1)^{-1}\left( 1+\frac{jxe^x}{e^x-1}\right) =\frac{1}{e^x-1}+\frac{jxe^x}{(e^x-1)^2}\le \frac{1}{e-1}+\frac{je}{(e-1)^2}. \end{aligned}$$

In the last inequality, we used that $\frac{xe^x}{(e^x-1)^2}$ is strictly decreasing on $[1,\infty )$. As a direct consequence, we find

$$\begin{aligned} \phi (x)&\ge -\frac{\sum _{j=0}^{n-k}\left( {\begin{array}{c}n\\ n-k-j\end{array}}\right) \left( e-1\right) ^{1-j}\left( \frac{1}{e-1}+\frac{je}{(e-1)^2}\right) }{\left( \sum _{j=0}^{n-k}\left( {\begin{array}{c}n\\ n-k-j\end{array}}\right) \left( e^x-1\right) ^{-j}\right) ^2} \\&\ge -\frac{\sum _{j=0}^{n-k}\left( {\begin{array}{c}n\\ n-k-j\end{array}}\right) (e-1)^{-j}\left( 1+je(e-1)^{-1}\right) }{\left( \left( {\begin{array}{c}n\\ n-k\end{array}}\right) \right) ^2}, \quad x\in [1,\infty ). \end{aligned}$$

Hence, the function $\phi$ is bounded and continuous on $(0,\infty )$. Then, the function $\phi$ has a global minimum $\phi _{\mathrm{min}}$ on the interval $(0, \infty )$. Obviously, $\phi (x)\le 0$, $x\in (0, \infty )$. The limits for $x\rightarrow 0+$ and $x\rightarrow \infty$ are easily obtained by standard calculations.

Proof

(Theorem 2) The proof uses the Banach fixed-point theorem (cf. Papageorgiou and Kyritsi-Yiallourou 2009, p. 226) for the continuous continuation of $\xi$ on $[0, \infty )$. For the definition of the continuous continuation of $\xi$ on $[0,\infty )$, we need the following limit

$$\begin{aligned}&\lim _{\lambda \rightarrow 0}\lambda \frac{\partial l_{\mathbf {Y}}}{\partial \lambda }({\mathbf {y}};\lambda )=v+(n-k)\sum _{i=1}^vy_i\times \lim _{\lambda \rightarrow 0}\frac{\lambda }{1-e^{-y_i\lambda }}\\&\quad =v+(n-k)v=(n-k+1)v, \end{aligned}$$

where we have used l’Hôspital’s rule to get $\lim _{\lambda \rightarrow 0}\frac{\lambda }{1-e^{-y_i\lambda }}=\lim _{\lambda \rightarrow 0}\frac{1}{y_ie^{-y_i\lambda }}=\frac{1}{y_i}$ for $i=1,\ldots ,v$. Then, the limit of $\xi$ for $\lambda \rightarrow 0$ is given by

$$\begin{aligned} \lim _{\lambda \rightarrow 0}\xi (\lambda )=\frac{1}{a}\frac{(n-k+1)v}{k\sum _{i=1}^v(R_i+1)y_i}>0. \end{aligned}$$

Therefore, the continuous continuation of $\xi$ on $[0,\infty )$ is defined as follows

$$\begin{aligned} \widetilde{\xi }:[0,\infty )\rightarrow [0,\infty ), \quad \lambda \mapsto {\left\{ \begin{array}{ll} \xi (\lambda ), &{}\quad \lambda \in (0,\infty ), \\ \displaystyle \lim _{\lambda \rightarrow 0}\xi (\lambda ), &{}\quad \lambda =0. \end{array}\right. } \end{aligned}$$

Since $\widetilde{\xi }(0)>0$ we conclude that $\lambda =0$ can not be a fixed-point of $\widetilde{\xi }$ on $[0,\infty )$. Hence, a fixed-point of $\widetilde{\xi }$ must be a fixed-point of $\xi$, too. Notice that we need the continuous continuation of $\widetilde{\xi }$ on $[0, \infty )$ for formal reasons in order to get a complete metric space. Now, according to the Banach fixed-point theorem, we have to show

• (I) $\widetilde{\xi }[0,\infty )\subseteq [0,\infty )$ and

• (II) $\widetilde{\xi }$ is Lipschitz continuous with Lipschitz constant $K\in [0,1)$.

Due to $\widetilde{\xi }(0)>0$, it is sufficient to show $\xi (0,\infty )\subseteq (0,\infty )$ to ensure $\widetilde{\xi }[0,\infty )\subseteq [0,\infty )$. According to Eq. (8), the first derivative of the log-likelihood function $\frac{\partial l_{\mathbf {Y}}}{\partial \lambda }({\mathbf {y}};\lambda )$ is strictly decreasing and the limit for $\lambda \rightarrow \infty$ is given by $-k\sum _{i=1}^v(R_i+1)y_i$. Then, $\frac{\partial l_{\mathbf {Y}}}{\partial \lambda }({\mathbf {y}};\lambda )>-k\sum _{i=1}^v(R_i+1)y_i$ for $\lambda \in (0,\infty )$. It follows $\xi (\lambda )>0$ for $\lambda \in (0,\infty )$ since $a\ge \frac{n+k}{2k}>1$. Therefore, condition (I) is satisfied.

The functions $\xi$ and $\widetilde{\xi }$ are differentiable on $(0,\infty )$ and have the same derivative. To ensure condition (II), it is sufficient to show that the derivative is bounded in the interval $[-K, K]$ with $K=\sup _\lambda |\frac{d}{\mathrm{d}\lambda }\xi (\lambda )|\in [0, 1)$ (see Arikawa and Furukawa 1999, p. 176). We define

$$\begin{aligned} A_{ij}:=\left( {\begin{array}{c}n\\ j+n-k\end{array}}\right) \left( e^{y_i\lambda }-1\right) ^{j-1}, \quad i=1,\ldots ,v \text{ and } j=-(n-k),\ldots ,0. \end{aligned}$$

Then, we get

$$\begin{aligned}&\frac{\partial l_{\mathbf {Y}}}{\partial \lambda }({\mathbf {y}};\lambda )+\lambda \frac{\partial ^2 l_{\mathbf {Y}}}{\partial \lambda ^2}({\mathbf {y}};\lambda )\\&\quad =-\,n\sum _{i=1}^vy_i+(n-k)\sum _{i=1}^v\frac{y_i}{G_\lambda (y_i)}-k\left( {\begin{array}{c}n\\ n-k\end{array}}\right) \sum _{i=1}^v\frac{R_iy_i}{\sum _{j=-(n-k)}^0A_{ij}\left( e^{y_i\lambda }-1\right) } \\&\qquad -(n\!-\!k)\lambda \sum _{i=1}^vy_i^2\frac{1\!-G_\lambda (y_i)}{(G_\lambda (y_i))^2}\!+\!k\left( {\begin{array}{c}n\\ n-k\end{array}}\right) \sum _{i=1}^v R_iy_i\frac{\lambda \sum _{j=-(n-k)}^0A_{ij}je^{y_i\lambda }}{\left( \sum _{j=-(n\!-\!k)}^0A_{ij}\left( e^{y_i\lambda }-1\right) \right) ^2} \\&\quad =-\,n\sum _{i=1}^vy_i+(n-k)\sum _{i=1}^vy_i\frac{G_\lambda (y_i)-\lambda y_i(1-G_\lambda (y_i))}{(G_\lambda (y_i))^2}\\&\qquad +k\left( {\begin{array}{c}n\\ n-k\end{array}}\right) \sum _{i=1}^vR_iy_i\phi (y_i\lambda ), \quad \lambda >0. \end{aligned}$$

Using $x>1-e^{-x}$ and $e^x>x+1$ for $x>0$, we have

$$\begin{aligned} 0<&\frac{1-e^{-x}-xe^{-x}}{\left( 1-e^{-x}\right) ^2}< \frac{1-e^{-x}-\left( 1-e^{-x}\right) e^{-x}}{\left( 1-e^{-x}\right) ^2}=1, \quad x>0. \end{aligned}$$

Substituting $x=\lambda y_i>0$, we get

$$\begin{aligned} 0<\sum _{i=1}^v y_i\frac{G_\lambda (y_i)-\lambda y_i(1-G_\lambda (y_i))}{(G_\lambda (y_i))^2}<\sum _{i=1}^vy_i=v\overline{y}, \end{aligned}$$

(14)

where $\overline{y}=\frac{1}{v}\sum _{i=1}^vy_i$. Applying Lemma 1, this yields

$$\begin{aligned} \frac{\partial l_{\mathbf {Y}}}{\partial \lambda }({\mathbf {y}};\lambda )+\lambda \frac{\partial ^2 l_{\mathbf {Y}}}{\partial \lambda ^2}({\mathbf {y}};\lambda )&<-n\sum _{i=1}^vy_i+(n-k)\sum _{i=1}^vy_i=-k\sum _{i=1}^vy_i \quad \text{ and } \\ \frac{\partial l_{\mathbf {Y}}}{\partial \lambda }({\mathbf {y}};\lambda )+\lambda \frac{\partial ^2 l_{\mathbf {Y}}}{\partial \lambda ^2}({\mathbf {y}};\lambda )&>-n\sum _{i=1}^vy_i+k\left( {\begin{array}{c}n\\ n-k\end{array}}\right) \sum _{i=1}^vR_iy_i\phi ^*. \end{aligned}$$

Using

$$\begin{aligned} \frac{d}{\mathrm{d}\lambda }\xi (\lambda )&=\frac{1/a}{k\sum _{i=1}^v(R_i+1)y_i}\left( \frac{\partial l_{\mathbf {Y}}}{\partial \lambda }({\mathbf {y}};\lambda )+\lambda \frac{\partial ^2 l_{\mathbf {Y}}}{\partial \lambda ^2}({\mathbf {y}};\lambda )\right) , \quad \lambda >0, \end{aligned}$$

we get

$$\begin{aligned} \frac{d}{\mathrm{d}\lambda }\xi (\lambda )&<-\frac{1}{a}\frac{\sum _{i=1}^vy_i}{\sum _{i=1}^v(R_i+1)y_i}<1 \quad \text {and} \\ \frac{d}{\mathrm{d}\lambda }\xi (\lambda )&>-\frac{1}{a}\frac{n\sum _{i=1}^vy_i-k\left( {\begin{array}{c}n\\ n-k\end{array}}\right) \sum _{i=1}^vR_iy_i\phi ^*}{k\sum _{i=1}^v(R_i+1)y_i}>-1. \end{aligned}$$

Thus, we know $\frac{d}{\mathrm{d}\lambda }\xi (\lambda )\in (-1,1)$ for $\lambda \in (0,\infty )$. To ensure $\sup _\lambda |\frac{d}{\mathrm{d}\lambda }\xi (\lambda )|\in [0,1)$, it is sufficient to show that $\lim _{\lambda \rightarrow 0}\frac{d}{\mathrm{d}\lambda }\xi (\lambda ),\lim _{\lambda \rightarrow \infty }\frac{d}{\mathrm{d}\lambda }\xi (\lambda )\in (-1,1)$. Using $\lim _{\lambda \rightarrow 0}G_\lambda (y_i)=0$, $\lim _{\lambda \rightarrow \infty }G_\lambda (y_i)=\infty$ for $i=1,\ldots ,v$ and l’Hôspital’s rule in $(*)$, we get

$$\begin{aligned} \lim _{\lambda \rightarrow 0}\frac{G_\lambda (y_i)-\lambda y_i\left( 1-G_\lambda (y_i)\right) }{\left( G_\lambda (y_i)\right) ^2}&{\mathop {=}\limits ^{(*)}}\lim _{\lambda \rightarrow 0}\frac{y_i\lambda }{2G_\lambda (y_i)}{\mathop {=}\limits ^{(*)}}\lim _{\lambda \rightarrow 0}\frac{1}{2e^{-y_i\lambda }}=\frac{1}{2} \quad \text{ and } \\ \lim _{\lambda \rightarrow \infty }\frac{G_\lambda (y_i)-\lambda y_i\left( 1-G_\lambda (y_i)\right) }{\left( G_\lambda (y_i)\right) ^2}&=\lim _{\lambda \rightarrow \infty }\frac{G_\lambda (y_i)-\lambda y_ie^{-y_i\lambda }}{\left( G_\lambda (y_i)\right) ^2}=1. \end{aligned}$$

Then, we arrive at

$$\begin{aligned} \lim _{\lambda \rightarrow 0}\left( \frac{\partial l_{\mathbf {Y}}}{\partial \lambda }({\mathbf {y}};\lambda )+\lambda \frac{\partial ^2 l_{\mathbf {Y}}}{\partial \lambda ^2}({\mathbf {y}};\lambda )\right)&=-n\sum _{i=1}^vy_i\!+\frac{n\!-\!k}{2}\sum _{i=1}^vy_i\!=-\frac{n\!+\!k}{2}\sum _{i=1}^vy_i\,\, \text{ and } \\ \lim _{\lambda \rightarrow \infty }\left( \frac{\partial l_{\mathbf {Y}}}{\partial \lambda }({\mathbf {y}};\lambda )+\lambda \frac{\partial ^2 l_{\mathbf {Y}}}{\partial \lambda ^2}({\mathbf {y}};\lambda )\right)&=-n\sum _{i=1}^vy_i+(n-k)\sum _{i=1}^vy_i-k\sum _{i=1}^vR_iy_i\\&=-k\sum _{i=1}^v(R_i+1)y_i, \end{aligned}$$

where we used the limits of $\phi$. Then, the limits of $\frac{d}{\mathrm{d}\lambda }\xi$ are given by

$$\begin{aligned} \lim _{\lambda \rightarrow 0}\frac{d}{\mathrm{d}\lambda }\xi (\lambda )&=\frac{1/a}{k\sum _{i=1}^v(R_i+1)y_i}\biggl (-\frac{n+k}{2}\sum _{i=1}^vy_i\biggr ){\mathop {>}\limits ^{(**)}} -\frac{1}{a}\cdot \frac{n+k}{2k}\ge -1 \quad \text{ and } \end{aligned}$$

(15)

$$\begin{aligned} \lim _{\lambda \rightarrow \infty }\frac{d}{\mathrm{d}\lambda }\xi (\lambda )&=\frac{1/a}{k\sum _{i=1}^v(R_i+1)y_i}\biggl (-k\sum _{i=1}^v(R_i+1)y_i\biggr )=-\frac{1}{a}\ge -\frac{2k}{n+k}>-1. \end{aligned}$$

(16)

The inequality $(**)$ is only strict for censored data, i.e., $(R_1,\ldots ,R_v)\ne (0,\ldots ,0)$. For the non-censored case, we have $a=\max \left( \frac{n+k}{2k},\frac{n}{k}\right) =\frac{n}{k}$, because $k<n$. Then, we get $\lim _{\lambda \rightarrow 0}\frac{d}{\mathrm{d}\lambda }\xi (\lambda )=-\frac{1}{a}\cdot \frac{n+k}{2k}>-1$. Hence, we have $\lim _{\lambda \rightarrow 0}\frac{d}{\mathrm{d}\lambda }\xi (\lambda ),\lim _{\lambda \rightarrow \infty }\frac{d}{\mathrm{d}\lambda }\xi (\lambda )\in (-1,0)$. Therefore, condition (II) is satisfied. Using Banach’s fixed-point theorem, we know that a fixed-point $\widehat{\lambda }$ of $\widetilde{\xi }$ exists, which is a fixed-point of $\xi$, too. Then, $\frac{\partial l_{\mathbf {Y}}}{\partial \lambda }({\mathbf {y}};\widehat{\lambda })=0$ and $\widehat{\lambda }$ is the MLE of $\lambda$. Furthermore, the Banach fixed-point theorem yields that the sequence $\lambda _{h+1}=\widetilde{\xi }(\lambda _h)=\xi (\lambda _h)$ converges to $\widehat{\lambda }$ for every $\lambda _0\in (0,\infty )$. $\square$

Proof

(Lemma 2) For $i=1,\ldots ,v$, the inner part of the logarithm in (13) can be rewritten as

$$\begin{aligned}&1-\sum _{j=n-k+1}^n\left( {\begin{array}{c}n\\ j\end{array}}\right) \left( 1-\exp (-y_i\lambda )\right) ^{j}\left( \exp (-y_i\lambda )\right) ^{n-j}\\&\quad =\sum _{j=0}^{n-k}\left( {\begin{array}{c}n\\ j\end{array}}\right) \left( G_\lambda (y_i)\right) ^{j}\left( 1-G_\lambda (y_i)\right) ^{n-j}= H(y_i,\lambda ). \end{aligned}$$

According to (6), the derivative of H w.r.t. $\lambda$ is given by

$$\begin{aligned} \frac{\partial H}{\partial \lambda }(y_i,\lambda )=-k\left( {\begin{array}{c}n\\ n-k\end{array}}\right) y_i\left( G_\lambda (y_i)\right) ^{n-k}\left( 1-G_\lambda (y_i)\right) ^{k}, \end{aligned}$$

and thus negative. Hence, the inner part of the logarithm is strictly decreasing in $\lambda$ so that $\eta (\lambda )$ strictly increases in $\lambda$. The limits of $\eta (\lambda )$ for $\lambda \rightarrow 0$ and $\lambda \rightarrow \infty$ are

$$\begin{aligned} \lim _{\lambda \rightarrow 0}\eta (\lambda )&=-2\sum _{i=1}^v(R_i+1)\ln (1)=0 \quad \text{ and } \\ \lim _{\lambda \rightarrow \infty }\eta (\lambda )&=\lim _{x\rightarrow 0}-2\sum _{i=1}^v(R_i+1)\ln (x)=\infty . \end{aligned}$$

Hence, the function $\eta :(0,\infty )\rightarrow (0,\infty )$ is strictly increasing and continuous so that the equation $\eta (\lambda )=t$ has an unique solution for $t>0$. $\square$

Proof

(Theorem 3) From Lemma 2, the solutions $\eta \left[ {\mathbf {Y}},\chi _{2v}^2(\alpha /2)\right]$ and $\eta \left[ {\mathbf {Y}},\chi _{2v}^2(1-\alpha /2)\right]$ exist. Using $\eta \sim \chi _{2v}^2$, we have

$$\begin{aligned} P&\left( \eta \left[ {\mathbf {Y}},\chi _{2v}^2(\alpha /2)\right]<\lambda<\eta \left[ {\mathbf {Y}},\chi _{2v}^2(1-\alpha /2)\right] \right) \\&=P\left( \chi _{2v}^2(\alpha /2)<\eta <\chi _{2v}^2(1-\alpha /2)\right) \\&=(1-\alpha /2)-\alpha /2=1-\alpha . \end{aligned}$$

Notice that, according to Lemma 2, $\eta$ is strictly increasing in $\lambda$ so that the direction of the inequalities does not change. $\square$