Introduction

Morphology is a key source of information for the study of biological organisms. This type of data combines insights into the geometrical properties of an organism or element in order to understand and classify evolutionary traits. The integration of morphological analyses has thus played a particular role in the field of human evolution. Nevertheless, this branch of science has seen a long evolution itself, with multiple innovations and debates about the optimal means of capturing morphological patterns (Bookstein, 1989, 2023, 2024; Durrleman, 2010; Mitteroecker et al., 2020; Rohlf, 1986; Rohlf & Bookstein, 2003; Rohlf & Corti, 2000).

Currently, landmark-based approaches, particularly from the perspective of the Procrustes analysis of landmark data, are the most widely used techniques for these types of analyses (Adams et al., 2004). The Procrustes analysis of landmark data in geometric morphometrics (GMMs) describes shape and form through the digitisation of a set of anatomically, mathematically, or geometrically distributed homologous points (Bookstein, 1991, 1997; Dryden & Mardia, 1998). The relative positions of landmarks are quantified by their 2D or 3D Cartesian coordinates, which are then projected onto a common coordinate system. This process involves the superimposition of landmarks through a series of procedures, including scaling, rotation and translation (Sneath, 1967), known as Generalised Procrustes Analyses (GPA) (Gower, 1975; Rohlf & Slice, 1990). GPA is thus a useful tool which can then be used for the direct comparison and visualisation of landmark configurations, highlighting their differences and similarities (Bookstein, 1989).

An additional advantage of superimposed landmarks is the ability to calculate multivariate statistical data regarding their overall position within the configuration. A popular technique for analysing this type of data consists in the eigendecomposition of the covariance matrix of superimposed landmark coordinates (Klingenberg & Monteiro, 2005; Rohlf, 1996, 2000). In this context, principal component analysis (PCA) is used to describe the major trends of sample variation in “as few statistically orthogonal dimensions as possible” (Rohlf, 1996). A PCA is a linear combination of the original variables, with each component maximising the total sample variance in a new set of uncorrelated dimensions. From this perspective, combinations of components can be used to describe the displacements in coordinate values along the x, y, and when 3D landmarks are used, z axes. The present study hypothesises that this approach to Dimensionality Reduction (DR) can be improved.

The present study intends to propose a new means of performing DR on landmark data by adapting graph theory for a more structurally aware visual representation of landmark data. Here we show that a Graph-based GMM approach is able to represent a higher degree of morphological variability in fewer dimensions. As a means of experimenting with this mathematical model, we present a number of theoretical applications, as well as two real-life case studies analysed with Graph-based GMM.

The GraphGMM R Library

All of the methods described in the present paper have been implemented in the R programming language, compatible with R v.3.0 and R v.4.0, and are available from the corresponding author’s GitHub page (https://github.com/LACourtenay/GraphGMM). A detailed description of the library, alongside instructions and a guide to its installation and usage, have also been provided as supplementary materials (Sup. Files 1 and 2).

Mathematical Model: Graph-Based Geometric Morphometrics

The mathematical model described in this study proposes a means of embedding landmark configurations into a new geometrically and structurally-meaningful feature space, prior to dimensionality reduction. The goal of information embedding is to map data into a new ℝn’ feature space, with n’ being the number of dimensions, such that landmarks that are similar are positioned closer together in the new space (Grover & Leskovec, 2016; Hamilton et al., 2018; Hoff et al., 2012; Leskovec, 2019). For this purpose, we use a message passing mechanism for neighbourhood aggregation. This process consists in representing each landmark as a mathematical function of itself and the spatial properties of its neighbours (Fig. 1). In the context of GMM, this can be adapted as a means of mapping landmarks into a new feature space, such that similarity in the embedded feature space approximates similarity in biological and geometrical structure. This proximity in the new feature space can be considered a means of revealing landmark homophily, i.e., the spatial similarity of landmarks (Fortunato, 2010; Yang & Leskovec, 2014), as well as structural equivalence (Henderson et al., 2012), in the global context of the entire configuration.

Fig. 1
figure 1

Graphic visualisation of the message passing mechanism after three convolutions across a set of landmarks placed on the proximal epiphysis of a chimpanzee radius. Landmark 13 (LM13) can thus be represented as a function of itself, and its neighbours (u)

Full size image

Let each set of landmarks (LM) be represented as a series of vertices LMv ∈ V, with neighbours LMu, connected by a series of undirected edges in a computational graph G. LMs should also be connected through a self-looping edge. Each configuration of G can thus be represented as an adjacency matrix A ∈ ℝp×p, with feature matrix X ∈ ℝp×k of Procrustes superimposed landmark coordinates, where p is the number of landmarks, and k is the number of dimensions. Landmarks can then be embedded using a message-passing mechanism (Eq. 1), similar to those proposed by Kipf and Welling (2017);

$$v_{i}^{(m)} = \left( {v_{i}^{(m - 1)} ,F_{j \in N(i)} \left( {v_{i}^{(m - 1)} ,v_{j}^{(m - 1)} ,e_{j,i} } \right)} \right)$$
(1)

where \(v_{i}^{(m - 1)}\) ∈ ℝX are the node features of node i in layer (m − 1), with each node j and i ∈ G being connected by an edge ej,i ∈ ℝK.

The definition of ej,i can be computed in a number of ways, either by the use of biological data with the domain-informed linking of landmark pairs (e.g. Adams, 1999), or using vertex spatial distributions (see “Case studies” section and Supplementary File 1). The spatial attributes of a given landmark in layer m can thus be redefined by aggregating the spatial attributes of neighbouring landmarks in layer m − 1, with the landmark’s own spatial attributes, and N being the neighbourhood of landmarks (Fig. 1). F (Eq. 1) is a differentiable, permutation invariant function that convolves freely over G (Kipf & Welling, 2017; Wang et al., 2019). In this application, let F be (Eq. 2);

$$v_{j}^{(m)} = \sum\limits_{{j \in N(i) \cup \{ i\} }} {\frac{1}{{\sqrt {\deg (i)} \cdot \sqrt {\deg (j)} }} \cdot v_{j}^{(m - 1)} }$$
(2)

which can be simplified using adjacency matrix A, identity matrix IN of A, feature matrix X, and the landmark degree centrality D ∀ v ∈ G, to embed landmarks X’ into a new feature space (Eqs. 3–5);

$$\tilde{A} = A + I_{N}$$
(3)
$$\tilde{D} = I_{N} \cdot D$$
(4)
$$X^{\prime} = \left( {\sqrt D \cdot \tilde{A} \cdot \sqrt D } \right) \cdot X$$
(5)

Through this, the neighbourhood of a node (v) is used to normalise the effect of highly central landmarks in the context of G (Kipf & Welling, 2017).

The convolutional operation across G is calculated by (Eqs. 6–8);

$$h_{v}^{0} = x_{v}$$
(6)
$$h_{v}^{(m)} = \left( {\sum\limits_{u \in N(v)} {\frac{{h_{u}^{(m - 1)} }}{{\left| {N(v)} \right|}} + h_{v}^{(m - 1)} } } \right),\,\,\forall \,\,m \in \left\{ {1,\,\,...\,,\,\,M} \right\}$$
(7)
$$z_{v} = h_{v}^{M}$$
(8)

where z is the output of each prior embedding in layer h (sensu Bruna et al., 2014), with LMi’ ∈ G now being represented by feature matrices X’ in a new ℝk feature space. From this perspective, the attributes of neighbouring landmarks can be passed through the computational graph in a series of steps, or “convolutions” (Fig. 1). With a single pass, LMi’ is now a function and representation of its own attributes, as well as the attributes of neighbouring vertices.

Once projected into the new feature space, landmark configurations can be represented in two different ways using the raw embedded landmark coordinates. These can then be processed using eigendecomposition to visualise patterns in a similar way to traditional GMM approaches, with the new PCA feature space presenting the added advantage of preserving more geometrical and structurally meaningful data from the feature matrix. The resulting representations can then be flattened into vectors equal in size to those used in traditional GMMs, i.e. x ∈ ℝp×k.

Theoretical and Technical Considerations

In contrast with representation and geometric learning applications, where achieving generalizability for the described formulae (Eqs. 1, 2, 6–8) requires some additional complexity (Bronstein & Kokkinos, 2010; Bronstein et al., 2017; Bruna et al., 2014; Henaff et al., 2015; Kipf & Welling, 2017; Murphy et al., 2019; Wang et al., 2019; Xu et al., 2019), the use of Procrustes-based feature matrices as input simplifies the message passing mechanism in a number of ways. Firstly, the laws behind the number of landmarks and their correspondence ensures a standardised topological structure across graphs, while graph size also remains constant (Bookstein, 1990, 1991; Dryden & Mardia, 1998; Rohlf, 1996). Secondly, Procrustes superimposition procedures eliminate the need for F to be invariant to vertex rotation and relative position, as GPA already ensures this. Finally, due to points 1 and 2, dataset sizes are no longer as large an issue, as no learnable parameters are needed to optimise graph embeddings.

It is also crucial to emphasize that the depth of convolutions across graphs differs from the concept of “depth” in computational sciences such as computer vision (Henaff et al., 2015). While graph- and image-based convolutions are similar in how their receptive field captures neighbouring nodes or pixels, the depth of a graph convolution is dependent on the total number of nodes in the graph (i.e., the diameter of G). From this perspective, a single convolution represents the neighbours of a vertex as well as the vertex itself. A second convolution will then represent the neighbours of the neighbouring vertices, along with the vertex itself (Fig. 1). As we increase the number of convolutions, the embedded feature space will capture more information from vertices further across the graph, which may not be relevant to the vertex itself. Consequently, graph-based convolutions are typically restricted to a few convolutions (typically between two and five), as convolving beyond the natural diameter of the graph is theoretically superfluous.

Finally, Supplementary File 3 presents two additional theorems on the advantages of using graph-embeddings for the analysis and representation of Geometric Morphometric data.

Theoretical Proof of Concept

Theorem 1

Landmark embeddings capture the geometric features of morphological variability even before Procrustes superimposition is performed.

For the proof of this theorem, we can define a simple geometry based on an irregular pentagon, presenting two adjacent right angles, one acute, and two obtuse angles, as well as two parallel edges. This shape can be defined by five landmarks marking each corner. To add complexity to later stages of this proof, we will add an additional landmark that can be used to condition the directionality of the deformation that will be imposed.

LMs 4 through to 5 are defined by fixed coordinates that do not change at any point during this set of proofs. They are defined as having 2D coordinates of (− 1, 1), (1, 1), (− 1, − 1) and (1, − 1), respectively. Both LM5 and LM6 have a fixed x coordinate of 0, while the y coordinate will alternate. For y coordinates, values were sampled from a uniform distribution between 1 and 4, to produce changes in the position of LM5, and between − 1 and − 4, to produce changes in LM6. 30 examples were simulated for variations in LM5 (here referred to as Group-5), and 30 examples were simulated for variations in LM6 (Group-6).

For the purpose of computing graph embeddings, a landmark graph was manually defined connecting each of the corners with LM5 and LM6 so as to observe how the movement of these landmarks will affect the overall representation of shape variation in graph embeddings (Fig. 2).

Fig. 2
figure 2

The theoretical model used in proof of Theorems 1 and 2

Full size image

PCA performed on Group-5 raw coordinates produces a feature space with 12 dimensions (Fig. 3), with a single PC score explaining 100% of morphological variance (described by changes only in Y value coordinates of either LM5 or LM6). Procrustes superimposition of this data produces a PCA with 100% of morphological variance being captured in the first 2 PC scores. Bi-plots in Fig. 3 show how PCA now captures variations in the x and y coordinates of other landmarks (even though they have not theoretically moved—a concept that will be explained more in the proof of Theorem 2). Please note our use of PCA bi-plots is only for the purpose of visualising and describing how PC scores are being constructed mathematically and algebraically, and should not be misconstrued as an attempt or a means in which landmark coordinates should be analysed, as rightly pointed out by Cardini and Marco (2022). Here we use bi-plots as a tool of understanding the weight landmark displacements have on the distribution of these purely theoretical points, and ‘per-landmark’ analyses should be refrained from in all applications of both traditional and Graph-based GMM.

Fig. 3
figure 3

(Left panel) PCA feature space computed on the raw coordinates of Group5. (Right panel) PCA performed on the superimposed Procrustes coordinates of Group5. Thin Plate Splines are represented on the extremities of each PC score

Full size image

Proof 1

Embeddings capture the overall trend in geometric deformation prior to Procrustes superimposition.

PCA performed on embedded coordinates, without the use of any Procrustes based superimposition procedures, produces an almost identical version of the original PCA (Fig. 4), prior to any pre-processing of the raw coordinates. This is seen in the first PC score representing 100% of variance and PC1 being described by change in the y coordinate of LM5. Nevertheless, while this PCA may appear to be identical to the original PCA, there is in fact a slight variation in y coordinates, represented mostly by residuals;

$$x = \left( {0.94,\,\,\,0,\,\,\,0,\,\,\,0,\,\,\,...,\,\,\,0} \right) \in {\mathbf{R}}^{12}$$
$$x^{\prime} = \left( {0.28,\,\,\,7.2 \times 10^{ - 17} ,\,\,\,5.1 \times 10^{ - 18} ,\,\,\,3.0 \times 10^{ - 17} ,\,\,\,...,\,\,\,0} \right) \in {\mathbf{R}}^{12}$$

where x is an example of a single individual’s PC coordinates, and x’ is an example of this same individual’s PC coordinates after embedding. In the embedded PCA, PC scores 2 to 10 contain residual data, with scores 11 and 12 being filled with 0 values. Additionally, embedded coordinates after a single embedding reveal LM1-LM4 to have cancelled each other out (Fig. 5), due to a lack of movement, while LM5 and LM6 are drawn together in the embedded space. This symbolises the trend in morphological variation, without any Procrustes superimposition procedures.

Fig. 4
figure 4

PCA performed on the superimposed embedded coordinates of Group5. Thin Plate Splines are represented on the extremities of each PC score

Full size image
Fig. 5
figure 5

Original (Left) and embedded (Right) landmark coordinates, with the graph edges indicated in red

Full size image

PCAs performed on both Group-5 and Group-6 produce similar patterns, with the added complexity of a second changing variable (Fig. 6). The original data without any superimposition procedures or graph embeddings preserves 100% of morphological variance in 2 PC scores. Procrustes superimposed data only represents 99.18% of variance in the same number of PC scores, with the influence of other landmarks in the configuration increasing. As before, graph embedded landmark data represents 100% in the first PC scores. Notably, graph embeddings capture much more information in the first PC score than in any of the other analyses, presenting very similar patterns to those from the original PCA (Fig. 6), while efficiently concentrating the encoded morphological information into a single dimension. Finally, Thin Plate Splines (TPS) derived from graph embeddings (Fig. 6, lower panels) show how, even without Procrustes superimposition, calculations are able to capture important morphological information. This is further proof on the effectiveness message passing mechanisms have on the processing and capturing of the geometrical properties of coordinate data.

Fig. 6
figure 6

(Upper panels) Three PCA bi-plots describing the comparison of two groups of landmarks, using (1) raw coordinate data, (2) Procrustes data, and (3) graph embeddings of the original raw data (no Procrustes superimposition). (Lower Panels) Thin Plate Splines describing the morphological variation captured by PCAs of graph embeddings of the original raw data

Full size image

Proof 2

Embeddings increase the degree of morphological variability reflected in reduced dimensions beyond those patterns already captured by Procrustes transformations.

As has already been demonstrated, graph embeddings, even without the use of Procrustes data, is able to encode the geometrical properties of morphological data efficiently. It has also been shown how Procrustes superimposed data is also efficient, however does not reach the same degree of efficiency in dimensionality reduction. When combining both Procrustes based methods and graph embeddings (Fig. 7), PCA results reach 99.86% variance in the present toy case study. This is due to how (1) Procrustes methods are powerful tools in describing morphological data, however, lose some critical information during the dimensionality reduction stage which (2) graph embeddings are able to recover. This will also be discussed and is the basis of Theorem 2.

Fig. 7
figure 7

Principal Component Analysis of Graph Embedded Procrustes Coordinates

Full size image

Theorem 2

Although Generalised Procrustes Analyses (GPA) are able to capture the influence one landmark’s coordinates may have on the entire configuration, and thus describe the relationship between landmarks in the global context of the configuration, original PCA approaches then lose sight of this relationship in the final representation of feature space. Graph-based methods are therefore able to reintroduce this information into the final feature space.

Proof 3

The Pinocchio effect is proof that GPA captures general information regarding the entire configuration.

As has been seen in the proofs provided for Theorem 1, the displacement of a single landmark along one axis is enough to create a shift in patterns in the corresponding shape feature space. This can slightly be perceived in the Thin Plate Splines presented in Fig. 3, however, is most evident in the PCAs described by Figs. 4, 6 and 7. Considering how in the original data LM1 to LM4 remain in a fixed position, PCA biplots still highlight them to be conditioning factors in the feature space dispersal patterns. This is due to the Pinocchio effect.

The Pinocchio effect describes how variation in a single landmark can have an effect on the entire configuration (Chapman, 1990; Hallgrímsson et al., 2015; Klingenberg, 2021; Walker, 2000). This can be easily visualised by considering how, as in the present case, variations in the position of LM5 will thus condition not just the distance of LM5 to the centroid, but will also condition the position of the centroid itself (especially if the centroid is calculated using the mean; see Additional Theoretical Notes in Supplementary File 3). Changes in centroid position implicate changes in general to the entire Procrustes superimposition procedure, as all three steps (translation, rotation and scaling) are dependent on this precise coordinate (Bookstein, 1986; Goodall, 1991; Gower, 1975; Kendall, 1984; Klingenberg, 2021; Rohlf & Slice, 1990). This is the easiest way to explain variation described by Thin Plate Splines, as well as the changes observed in most figures in the proof of Theorem 1, described by variables Y1, Y2 and Y3, even though their original coordinates never moved. This can be extended theoretically to visualise the Pinocchio effect when modifying two variables as well (Fig. 8).

Fig. 8
figure 8

(Upper panels) examples of the (left) original coordinates of two geometric icons prior to (right) Procrustes superimposition. (Lower panels) Examples of the superimposition of Group-5 and Group-6 icons

Full size image

From this perspective, it can be argued that in an original PCA (Fig. 6) information from all landmarks is captured, as the Kendall coordinates derived from Procrustes superimposition are dependent on the configuration as a whole, not just a single landmark (Cardini & Marco, 2022). Nevertheless, while this is true for Procrustes analyses, for dimensionality reduction we still lose some of the information regarding the entire configuration, and consequently lose some information in the final PCA.

The objective of using graph embeddings on Procrustes data is to remove the need for weighted parameters that make the message passing mechanism invariant to position and rotation. However, we can also see how, as presented throughout this set of theorems, graph embeddings are also able to capture morphological variation (Bronstein et al., 2017), even without the use of orthogonally projected Kendall coordinates. Bookstein coordinates (Bookstein, 1986, 1989), for example, would also produce similar results. Nevertheless, considering that Kendall coordinates create a change in the data represented in PCAs, graph embeddings seem to re-highlight the features that are important considering the neighbourhood of each landmark, putting weight on more global features, and resulting in a more complete representation of shape variation in just a few PC scores.

Simulating More Complex Geometries and Observing Patterns in Eigenvalues

The demonstrations presented in “Theoretical Proof of Concept” all consisted in observing the effects of Graph-based morphological analyses when only a single landmark changes. While useful to demonstrate some of the core algebraic concepts of Graph-based GMM, this model can be considered overly simplistic, while breaking one of the primary rules of modern morphometrics, where single landmark observations are to be avoided (Cardini & Marco, 2022). Theoretical research in GMM often uses simplistic geometric icons, such as triangles, in order to demonstrate the mechanisms behind most mathematical operations. From the perspective of Graph-based calculations, however, three landmarks do not provide much leeway with which to experiment. Here we show analyses of morphological patterns by considering the shearing of much more complex geometric icons, following the experimental and theoretic protocols outlined by Courtenay (2023).

For an initial demonstration, we simulate a set of 90 octagons produced by rotating a point with x and y coordinates around a centroid, of a fixed unit-less Centroid Size (CS = 3), considering the rotation operations (Eq. 9);

$$\left[ {\begin{array}{*{20}c} {\cos \theta } & { - \sin \theta } \\ {\sin \theta } & {\cos \theta } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x_{i} } \\ {y_{i} } \\ \end{array} } \right]\,\,\,\forall \,\,\,i \in p\,\,\,:\,\,\,\theta = {0}{\text{.7853982,}}\,\,\,p = 8$$
(9)

Centred on each of the points, we introduce a perturbation of (σ = 1) a total of 90 times. Once generated, 30 random icons were sampled and sheared by magnitudes of ϵ = 0.2 and another 30 with ϵ = − 0.2, through (Eq. 10);

$$\left[ {\begin{array}{*{20}c} {x^{\prime}_{i} } \\ {y^{\prime}_{i} } \\ \end{array} } \right] = \left[ {\frac{{x_{i} }}{{y_{i} }}} \right] + \left[ {\begin{array}{*{20}c} {\varepsilon y_{i} } \\ {\varepsilon x_{i} } \\ \end{array} } \right]\,\,\,\forall \,\,\,i \in p\,$$
(10)

So as to introduce a slight torsion that can be assessed through GMM means. Icons were then superimposed using GPA in shape space. Using this dataset, PCA calculated on the superimposed coordinates result in a feature space where the first two dimensions represent 32.88% of morphological information (Fig. 9), with > 90% of variation being captured by up to 10 PC scores.

Fig. 9
figure 9

PCA scatter plots computed on an 8-landmark theoretical geometric model, including the calculation of PC scores using the original superimposed Procrustes coordinates (left panel), and the embedded Procrustes coordinates (right panel)

Full size image

Considering how this simulation is, in essence, a stochastic process, we can repeat the generation of data 1000 times, and bootstrap the summary statistics, to calculate that in general the first two PC scores represent 33.14 ∈ [33.03, 33.26]% of information. In general, 95.4% of the simulations revealed > 90% of variation to be captured by up to 9 PC scores.

Constructing a completely geometric and theoretical graph, where each landmark is connected to its adjacent neighbours, we can establish a network of interconnected segments in the form of an octagon. Additional edges are then extended from each point, skipping one landmark, in a consistent pattern. This iterative process of establishing links creates a visually striking motif characterized by radial symmetry and connections between vertices, culminating in the form of an 8-point star within an octagon. Performing PCA on the calculated embeddings of this configuration results in a feature space representing 90.6% of the variation. This already captures the same amount of data as 10 PC scores using traditional PCA approaches in GMM. In this case, 10 PC scores represent 99.95% of the variation. Running the simulation 1000 times with a bootstrapped calculation of summary statistics reveals the first 2 PC scores to typically yield 90.31 ∈ [90.24, 90.37]% of the morphological information.

If we observe eigenvalue (λ) distributions produced by these two analyses (Fig. 10), it is immediately clear how Graph-based approaches compress information into much fewer dimensions much faster than traditional PCA. The Graph-based approach appears to produce a normalisation or regularisation effect to the corresponding λ values, producing a more “L” shaped curve with a marked elbow, as opposed to traditional techniques, where the curve presents a much smoother decrease towards zero.

Fig. 10
figure 10

Distribution of Eigenvalues across each PC score when analysing GMM datasets consisting of 8 and 100 landmarks, using both traditional and Graph-based GMM approaches

Full size image

To test the effect of the number of variables on these results, we can modify the experiment to simulate a set of centagons, by adjusting the above model with values of θ = 0.0628, p = 100, σ = 0.1, and ϵ = [− 0.002, 0, 0.002]. In order to avoid sample-size issues and the influence they may have on λ distribution properties (Bookstein, 2017a, 2019), we simulated 250 icons to ensure the variable to individual ratio stays at an acceptable value of 0.8.

Similar to previous experiments, it can be noted that Graph-based GMM captures more information in much fewer dimensions than traditional PCA. Traditional PCA was found to generate PC scores where the first two PCs represent 3.65 ∈ [3.65, 3.66]% of the morphological variance, while 81.8% of simulations found 106 PC scores necessary to describe up to 90%. On the other hand, the first two PC scores obtained through Graph-based GMM capture 7.91 ∈ [7.82, 8.00]% of the information, while requiring 101 PC scores to capture up to 90%. In this case, the λ distributions show another clear case of a sharper “L” shaped curve for Graph-based GMM, while traditional approaches require more PC scores to capture the same amount of information.

While in some of these cases the percentage of represented variance is considerably lower than what is typically observed in real case studies, this is due to how the data crafted here is “purely theoretical and of geometrical significance, with absolutely no biological value” (Courtenay, 2023).

Case Studies

Moving beyond the realm of theoretical simulations, we present two case studies for the application of Graph-based analyses on data derived from biological specimens. The first case-study consists in a 24-landmark model in 3-dimensions, consisting of fixed landmarks collected on the cortical surface of adult human brains described by Free et al. (2001), openly available as part of the “brain” dataset in the shapes R library (Dryden, 2023). The objectives of analysing this dataset are to assess the quality of Graph-based results on actual data, focusing primarily on a dataset that does not present extreme contrasts of scale in order to focus on morphological variance in shape. The second case-study consists in the analysis of 200 landmarks in 3D, consisting of both fixed and semi-landmarks, extracted from modern great-ape radii. This case study originates from the study by Aramendi (2021), a complete description of which is additionally provided in Supplementary File 3. The purpose of this case-study is to assess whether the Graph-based GMM model is able to reduce the dimensionality of datasets that present distinct patterns between samples, and preserve these structural patterns during the more extreme compression of information.

An Analysis of Adult Human Brains

This dataset consists of 58 individuals, landmarked using 24 fixed anatomical landmarks on both the left and the right hemisphere of the cortical surface of the brain, obtained using MRI images. The original publication of this dataset assessed the orientation and relative position of frontal lobe sulci and the possible differences between hemispheres by additionally considering patterns in functional asymmetry (Free et al., 2001). These authors considered, therefore, the relationship shape variables have with size, gender (27 females, 31 males), age (median = 30.5 years old), and handedness (15 left, 43 right handed individuals). Here we evaluate the same variables by first superimposing all the landmarks via GPA in shape space, and then testing the correlation between PC scores, constructed using both traditional and Graph-based approaches, with each of the sample variables. This was then repeated after reflecting the left hemisphere onto the right hemisphere along the midsagittal plane, so as to assess patterns between hemispheres. The graph to perform embeddings was constructed by establishing the connections between landmarks as detailed through wireframes by Free et al., (2001, p. 808).

PCA on the original landmarks produce a feature space where the first two dimensions represent up to 19.76% of the morphological variance (Fig. 11), and 25 PC scores are required to obtain > 90% of morphological information. Graph-based PCA on the other hand captures the same amount of information in just 10 PC scores, while the first 2 PC scores represent more than twice the amount of morphological variance, with a total of 54.11%. When considering the distribution of λ values (Fig. 11), we confirm our original observations from theoretical experiments by showing Graph-based PCA to produce a much more pronounced “L” shape, while the original PCA presents a relatively sharp decrease in λ values, which then levels off over approximately 30 PC scores. As for statistical analyses, taking into consideration the entire brain, our results using Graph-based analyses reveal similar patterns to the original PCA (Table 1), with a lack of correlation between PC scores and either of the possible conditioning variables to brain morphology. In general, the main differences between analyses are a slightly more pronounced presence or lack of correlations between variables as opposed to traditional PCA, generally indicating that this method has captured slightly more information to compare with.

Fig. 11
figure 11

Extreme morphological changes, PCA scatter plots, and λ distributions for the (upper) traditional and (lower) Graph-based analysis of brain morphology

Full size image
Table 1 Correlation coefficients, test statistics, and p-values, between each of the computed PC scores, using both traditional and Graph-based GMM, and the variables described in Free et al. (2001)
Full size table

With regards to the represented changes in morphology across feature spaces, it can be seen through wireframes that the two approaches highlight slightly different morphological trajectories, with the original PCA representing marked patterns in the position of the precentral sulcus’ intersection with the superior frontal sulcus, as well as the configuration of the central sulcus to the midline across both PC1 and PC2. Graph-based approaches highlight similar patterns, however PC1 is also slightly conditioned by relative variability in structural asymmetry with a slightly more anterior position of the termination of the cingulate sulcus at the midline, while PC2 presents a marked difference in the width of the midsagittal plane. This generally demonstrates that the Graph-based approach may be capturing slightly more changes to the overall configuration, reflected and conditioned by the larger amount of variability captured.

When reflecting landmarks across the midsagittal plane, traditional PCA now captures 90% in the first 18 PC scores (Fig. 12), with PC1 and PC2 capturing 24.3% of the information, while Graph-based PCA captures 47.1% of morphological variation in the first two dimensions (Fig. 12), and a total of 90% across just 8 PCs. Once again, λ distributions reflect our original observations on theoretical data (Fig. 12), while correlation results (Table 1) are similar between the two approaches, with Graph-based PCA revealing slightly more pronounced correlations. When considering the statistical differences or similarities between hemispheres, and thus assessing structural asymmetry in the brain, both original (Residuals = 261.4, F = 28.66, p = 4.5 × 10–07) and Graph-based (Residuals = 11.48, F = 24.1, p = 3.0 × 10–06) approaches reveal notable patterns of variation, with the Graph-based approach displaying a considerably lower number of squared residuals.

Fig. 12
figure 12

Extreme morphological changes, PCA scatter plots, and λ distributions for the (upper) traditional and (lower) Graph-based analysis of brain morphology after reflecting the left hemisphere across the midsagittal plane

Full size image

Visualisation of extreme morphological information across the PC scores once again reveal generally similar patterns. Both approaches highlight across PC1 the position of the intersection between the precentral sulcus and the Sylvian fissure, as well as rehighlighting the precentral sulcus’ intersection with the superior frontal sulcus (more so in the traditional than the Graph-based analysis). PC2 on the other hand marks the general position of the preoccipital notch in relation to the Parieto-occipital sulcus’ intersection with the calcarine, however, in the Graph-based approach we now see an additional pattern emerge towards the midsagittal plane and insertions of the parieto-occipital, central and cingulate sulcus. While the configuration of these landmarks varies slightly across PC2 in the traditional approach, the Graph-based analysis stresses this pattern more.

An Analysis of Modern Great Ape Radii

For this case study, landmarks extracted from 84 radii of chimpanzees (n = 20), gorillas (n = 17), orangutans (n = 17), and Anatomically Modern Humans (AMH, n = 30), were superimposed using full GPA in shape space. This dataset consists of 200 landmarks, of both a fixed anatomical, and sliding semi-landmark type, fully described in Supplementary File 3. The landmark graph was constructed using algorithms based on the spatial distribution of landmarks. For this purpose, we used a pivot ball triangulation algorithm (radius ρ = 25.5: Bernardini et al., 1999) on the median shape configuration. Graphs were then embedded using two convolutions, and then used for analysis. Here we evaluate the biological and biomechanical signal present across these radii using both approaches to assess whether Graph-based PCA not only performs more efficient dimensionality reduction, but also serves as a means to aid in the discrimination of given groups.

Initial observations of PCA distributions reveal sample scattering among the different approaches to present more pronounced differences in the amount of information represented in just the first PC score. Sample distributions, however, are relatively congruent across reduction techniques in shape space, including degrees of overlapping among groups, and the established variational relationships among groups. From this perspective, chimpanzees and gorillas slightly overlap in all analyses, while AMH and orangutans constitute their own independent clusters. AMH and orangutans only present a slight tendency to approximate each other in feature space in Graph-based PCA (Fig. 13). Despite certain differences in general robusticity and straightness of radii, the majority of morphological changes expressed by PC1 tend to be relatively congruent, with all types of PCA representing similar traits.

Fig. 13
figure 13

Examples of the three different Dimensionality Reduction results in shape space using traditional Principal Component Analyses in Geometric Morphometrics, as well as Graph-based Principal Component Analyses to analyse the radius morphology in great apes using anatomical landmarks and sliding semilandmarks. Changes in shape are visualised across the extremities of PC1. AMH anatomically modern human, C chimpanzee, G gorilla, O orangutan

Full size image

The largest differences among analyses, however, can be observed in dimensionality reduction performance. The original PCA-based method explains slightly more than 50% of the total variance along the first two PCs, whereas the Graph-based technique on the embedded data (64.1%) is able to increase the amount of variance contained in the first two components, with the original PCA reaching the same percentage of variance explained in the Graph-based versions of the PCA in the first three PCs. The most notable improvement, however, remains to be the considerably larger amount of information preserved in just the first PC score.

Differences in the morphological variance expressed by PC1 are more pronounced in the Graph-based PCA, where the slenderness and straightness of the radius is more marked towards the positive extremity of PC1, as opposed to a more robust radius towards the negative extremities, where AMH are located (Fig. 3). Nevertheless, both approaches similarly highlight a tendency towards a slightly more curved, less slender midshaft portion, and a more angled-positioned distal epiphysis towards the positive PC1 axis end.

Pairwise comparisons of great ape groups based on mesh warpings (Figs. 14, S3 in Sup. File 3), also indicate that the Graph-based approach provides more marked differences among the sample as a result of a more effective compression of information. Most differences are assembled on the proximal and distal portions of the bone, especially in the head and neck of the radius, the radial tuberosity, the sigmoid notch, the scaphoid, and the styloid process. Many of the differences are not only related to changes in relative proportions (e.g., distance between the head and the radial tuberosity), but also in the orientation and location of certain osseous landmarks (e.g., the angle of the sigmoid notch relative to the bone’s longitudinal axis, the position of the radial tuberosity relative to the interosseous crest). Although the diaphysis presents less abrupt changes, important differences in curvature and width are observed among groups. Morphological differences along the shaft are variably marked based on the PCA approach, though in general terms midshaft curvature degree along the posterior view presents the most notable changes on the diaphysis. In certain cases, however, important differences are also observed in the distal diaphyseal portion (e.g., when comparing orangutan versus gorilla).

Fig. 14
figure 14

Calculations of the differences between mesh warpings when predicting median shape changes using traditional Geometric Morphometrics (Upper) and Graph-based analyses (Lower). Heat maps indicate areas where mesh warpings differ from the original Thin Plate Spline prediction (red = positive deformations, blue = negative deformations). AMH anatomically modern human, C chimpanzee, G gorilla, O orangutan

Full size image

When the morphology of the radii in different great ape groups is only analysed by means of ‘fixed’ anatomical landmarks (most of them situated on the proximal and distal epiphyses), more strongly marked changes in shape space can be observed depending on the dimensionality reduction technique (Fig. S4, Supplementary File 3). The traditional GMM approach results in a plot that does not resemble those seen in Fig. 13, but instead presents different clustering patterns, with AMH clearly separated from nonhuman great apes, and orangutans and gorillas overlapping with chimpanzees, which fall right in between the former groups. On the other hand, Graph-based PCAs show a sample distribution that resembles those seen in Fig. 13 across all PCAs, with four distinct clusters slightly overlapping in pairs formed by AMH and orangutans, on one side, and chimpanzees and gorillas, on the other side.

Regarding the interpretability of such results, the generalised division among modern great apes based on the preferential use of the landscape (terrestrial versus arboreal), and the main modes of locomotion (e.g., bipedalism, suspension, quadrupedal walking), is well-reflected in the results obtained here. All types of PCA and their derived extreme shape warpings, reflect the existing morphological separation between humans and the rest of living great apes, as well as the distinction of orangutans from gorillas and chimpanzees. However, anatomical differences along the diaphysis of the great ape radius are not only perceptible in overall curvature degrees, but also in the relative position and orientation of specific osseous landmarks linked to the attachment of soft tissues (e.g., the radial tuberosity).

Some Final Remarks on the Interpretability of Graph-Based Results

While the objectives of DR in data science is primarily to represent information in as few dimensions as possible, so as to provide a more efficient means of detecting patterns and analysing this information, a fundamental component of GMM remains to be the interpretability of the results in terms of biological and anatomical structure and variation. From this perspective, while the increase in represented morphological variation is important in a PCA, an assessment of the relationship these patterns have with the original information is equally important. For this purpose, we carried out an additional analysis was used to evaluate the amount of signal captured by the Graph-based approach, in relation with those obtained using traditional methods.

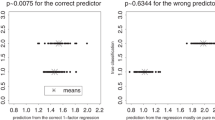
To perform this, we used the first 2 PC scores from each feature space derived from the radii dataset to predict the landmarks corresponding to each individual using linearly constructed relationships. These predictions were then evaluated using the Square-Root of the Mean Squared Error (RMSE) between the predicted landmarks and the original landmarks, so as to gauge the amount of residuals present. reliability and preservation of biological signal are very similar in shape space (Fig. 15), with the Graph-Based approach producing slightly less residuals (RMSE = 2.86), than the traditional PCA (RMSE = 2.96) in shape, as well as in Form (RMSE Original = 3.28, Graph RMSE = 3.09). Nevertheless, Analyses of Variance (ANOVA) between these two sets of residuals find a complete lack of differences (Shape F = 1.01, p = 0.32).

Fig. 15
figure 15

Distribution density plots comparing the residuals in shape produced when using the first 2 PC scores from original and graph-based PCAs to predict the morphology of a given individual

Full size image

Finally, we performed a small set of additional experiments adjusting the number of convolutions (Fig. S5, Supplementary File 3), which demonstrates how adjusting this parameter can fine tune the visualisation of regional or global structural features as convolutions increase. In the case of the present study, just 2 convolutions are sufficient in capturing a large percentage of morphological variance, however other studies may wish to weight their feature spaces according to the research questions at hand.

Discussion

Dimensionality reduction (DR) techniques are an extremely useful tool in data science for a more efficient representation of information. They are additionally frequently used as a means and basis of pattern recognition (Bishop, 2006). PCA is an essential means of performing DR in GMM, as it extracts vectors from a large set of variables, that allow for the compression of information into fewer dimensions. This additionally maintains the Procrustes distances between the different specimens, accounting for as much of the original variation as possible. The objective of DR in GMM should therefore be to compress information into as little and as meaningful dimensions as possible, presenting a more manageable dataset that can be used to describe morphological, structural, biomechanical or evolutionary patterns, as well as providing a direct means of testing hypotheses regarding this data.

Eigendecomposition reduces matrices into constituent parts which successively explain decreasing proportions of the total variance. In most cases, this technique is used to extract the most relevant information from a dataset in the form of the first few PC scores of PCA, thus removing any residual noise that may impede more complex analyses. Nevertheless, the elimination of the “least important” PC scores often raises concerns, as no unique accepted rule exists for this selection (Jolliffe, 2002). In many types of analyses, the first few PC scores may not explain all of the necessary variance to capture true or meaningful morphological patterns, while in many cases variables of biological significance can be found in latter PC scores as opposed to the first two—a good example of this would be the original publication of the brain dataset by Free et al. (2001). The only exception to this is if a strong distinctive feature is existent, such as the variable size. However, in these cases, form feature spaces are mostly biased, with the first PC being explained almost exclusively by size, with little explanatory power in terms of shape.

Other popular ordination techniques for the reduction of variables into smaller feature spaces have been proposed and debated over the decades, including (but not exclusive to) canonical variate analyses (CVA) and between-group PCA (bgPCA) (Bookstein, 2017a, 2019; Cardini et al., 2019; Klingenberg & Monteiro, 2005; Mitteroecker & Bookstein, 2011; Rao, 1948; Rohlf, 2021; Yendle & MacFie, 1989). Both of these approaches use calculations that are based on sample-labels to compress information into g-1 dimensions, where g is the number of groups within the dataset. For the present primate radii dataset this would result in a 3-dimensional feature space representing 100% of the information, appearing to be a much more “powerful” means of performing DR than either PCA or Graph-based PCA. Nevertheless, a very important issue that is often overlooked with these types of analyses is how reliant they are on the sample labels provided. As one of the present authors has recently pointed out (Courtenay, 2023), the objectives of DR are for pattern recognition and exploration, and should not be dependent on prior-knowledge about the structural organization of our data. This can be seen in how we may not always have reliable information about an individual’s association to certain groups, or debate may exist regarding the definition of the group in general. Likewise, detecting patterns based purely on the underlying mathematical properties of the data is much more informative and reliable than conditioning these properties to exist.

Beyond this, bgPCA and CVA have been noted to present a number of undesirable statistical properties, conditioned primarily by sample size (Bookstein, 2017a, 2019; Cardini et al., 2019; Rohlf, 2021, inter alia), but also by skew in sample sizes across the groups (Courtenay, 2023). In each of these cases, both types of analyses have been shown to force groups apart if the number of variables far exceeds the number of individuals in the sample, regardless of whether between-group separation should exist or not. PCA has since been shown to produce the most stable results (Courtenay 2023), despite its possible susceptibility to these issues as well (Bookstein, 2017a). Considering how the approach proposed here relies on a message passing system with no learnable parameters (see Sects. “Mathematical Model: Graph-Based Geometric Morphometrics” and “Theoretical and Technical Considerations”), while the final visualisation is also based on PCA, graph-based methods maintain the stability identified by previous authors when confronted with samples of varying sample sizes, or variable to individual ratios. It is also important to point out that the objective here is not to force possible group differences, yet instead try and enhance the information that is present in a smaller number of dimensions so as to visualise multivariate patterns more efficiently.

The advantage of using a Graph-based approach can additionally be found in the mathematical ability to describe landmark configurations according to the relationship landmarks have with their neighbours, as opposed to only the landmark’s position itself. While the displacement of even a single landmark, no matter how small, will have a consequent effect on the entire configuration during superimposition procedures (Chapman, 1990; Hallgrimson et al., 2015; Klingenberg, 2021; Walker, 2000; see Sect. “Theoretical Proof of Concept” of the present document as well), it can be argued that variations in morphological patterns cannot (and should not) be ascribed to an individual landmark, but more to the relationship between the landmarks (Cardini & Marco, 2022; Klingenberg, 2021). While the objective of any multivariate analysis is the evaluation of multiple variables, and no single PC score alone, the embedding procedures described here are more likely to encode and enhance inter-landmark and global relationships prior to PCA (see Sect. “Theoretical Proof of Concept”). From this perspective, Graph-based PCA captures information in a slightly different light to traditional PCA approaches used in GMMs, while additionally representing as much information in as few dimensions as possible.

In a number of examples presented by the current case studies it has been seen that Graph-based PCAs, apart from achieving a more comprehensive two-dimensional graphical representation of morphological variance, tend to be more congruent regardless of the data used as input. This can be seen in how Graph-based methods based on semi-landmarks and landmarks alone in the primate radii dataset (Fig. S5, Supplementary File 3) were able to reveal similar relationships between individuals, while traditional GMM PCAs are less congruent and more dependent upon the availability of morphological information. When we compare the warped surfaces of both methods, differences are most noticeable in the way these methods capture changes in the diaphyseal portions of radii. Likewise, residual analyses derived from TPS results in Fig. 7 show that Graph-based approaches are equally reliable in representing morphological patterns across feature spaces, and thus preserve the biological signal in this more compressed version of feature space.

The application of alternative DR techniques, as the ones presented here, can thus be seen important in exploring intra and interspecific variability in skeletal elements, which, in turn, might be an interesting way of revealing morphological patterns that are significant in group characterisation, as well as the description of morphological trajectories in analyses in general.

Here we have shown empirically and theoretically that a Graph-based approach enhances the amount of information represented in a fewer number of dimensions—whether this is applicable to all case studies is something only the test of time will tell. The biggest issue with an approach such as this one is the definition of the graph, as, of course, different means of defining the relationship between landmarks will lead to different results. This requires the user to have a certain degree of domain knowledge to give biological or geometric significance to the graph, as this is essentially what we use to project landmarks into the new embedded coordinate space. For this reason, we have also presented the possibility of empirically calculating graph edges, given the spatial distribution of points. This can at least serve as a starting point, which can later be refined depending on each application.

As a final remark, however, it is important to point out that we are far from the first to highlight potential issues with PCA in GMM analyses, with authors such as Bookstein (2017b) also providing alternative methods after a detailed description of the mathematical theory and history of such types of ordination analyses (see also Bookstein, 2016, 2017a, 2023). These discussions often centre on the limitations of decomposing data into series of linear combinations of variables, arguing that these types of analyses should not replace biological reasoning. In addition, it is worth noting that not all phenomena display strictly linear patterns or relationships, opening up a debate on the potential need to explore other non-parametric alternatives, and whether or not they can be used to portray meaningful biological processes.

Here it is also important to note, and perhaps rectify or clarify, our use of the term “feature space” at multiple points within this paper (primarily Sect. “The GraphGMM R Library”). Here we refer to a “feature space” in the sense of its use in the field of data science, whereby we simply convey the concept that a “feature” is a measurable property of an element being studied. From this perspective, we define a “feature space” as a set of constructed dimensions corresponding to a particular combination or derivation of “features” or “attributes”, that we may be able to correlate with real-life processes. However, as noted by Gould (1967), beyond the first PC score, subsequent scores are orthogonal to the first dimension, leading us to view the resulting eigenvalues and eigenvectors as 'mathematical abstractions’ lacking inherent biological meaning. From an epistemological perspective, it may be prudent to conceptualize these spaces as morphological coordinate spaces instead, focusing on the fundamental properties of landmarks as points in a Cartesian coordinate system, devoid of biological meaning beyond that which we assign them ourselves.

In the present study, we attempt to provide at least geometric meaning to constructed shape coordinate spaces by establishing the relationship between, and subsequently visualising, the morphological icons that are associated with either side of each PC’s extremities. As illustrated in Fig. 15, constructing these icons using PC scores derived from embedded landmarks yields results comparable to those derived from the original Procrustes superimposed landmarks. This at least allows us to establish a geometric correspondence between the dispersal of points in reduced dimensions and configurations of landmark coordinates. PCA additionally enables us to visualise a large amount of information in a reduced number of dimensions, while attempting to preserve important patterns about where individuals fall relative to each other (Howells, 1984). If we can then establish a relative correspondence between those distributions and morphological variation, this enables us to infer a relative relationship between these distributions and morphological variation. While this approach aids in interpreting such patterns, it is not exhaustive and may require additional heuristics and domain knowledge for imposing biological meaning onto these 'mathematical abstractions'.