1 Introduction

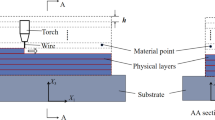
Directed energy deposition (DED) is an additive manufacturing (AM) process comprising of a laser or electron beam heat source that is coaxial with wire or blown powder feedstock, including processes such as direct metal deposition (DMD) and Laser Engineered Net Shaping (LENS) (Ref 1). Metal-based additive manufacturing (MBAM) parts with significant porosity or thermally induced residual stresses can exhibit a decrease in mechanical properties, excessive distortion, reduced part quality, and poor fatigue life (Ref 2, 3). Residual stress formation is often problematic in MBAM parts because tensile residual stresses tend to form at surfaces, which can lead to decreased strength and reduced fatigue life (Ref 4). Therefore, mitigation of residual stresses during the deposition process is vital to prevent premature failure (Ref 5). Implementation of baseplate heating, prescribed interpass temperature or dwell time, and varying deposition strategies can all be used as in situ residual stress mitigation strategies while heat treatment and hot isostatic pressing are viable post-processing methods (Ref 6, 7, 8). Furthermore, the formation of unwanted residual stresses and distortion actively hinders current DED process qualification and part certification efforts (Ref 9).

Residual stresses and distortion within as-built parts are driven by the thermal history of the AM process with increased heating and cooling rates driving higher levels of distortion and residual stresses (Ref 10). Similar to welding, residual stresses are formed during the cyclic heating and subsequent cooling phases of the MBAM process (Ref 11). Previous research discussed the temperature gradient mechanism for the formation of residual stresses during MBAM processes (Ref 12). In the time that the material is heated, the feedstock rapidly expands; however, the thermal expansion is restricted by the solid previously deposited surrounding material that is at a much lower temperature. As a result, a compressive stress state is created in the deposition. As the material contracts during cooling, the material is again restricted by the plastic strain formed at the interface with the surrounding material and tensile residual stresses are formed. Thus, thermal expansion of the newly deposited layer leads to hardening and formation of residual stresses, while static recovery relieves residual stresses.

Unlike microscale or mesoscale mechanical models that include the effects of powder/wire interaction (Ref 13), porosity (Ref 14), and fluid flow in the melt pool (Ref 15), macroscale finite element-based MBAM mechanical models focus on how the temperature history drives residual stresses and distortion (Ref 16). Thus, the primary boundary conditions for finite element-based mechanical modeling are the temperature history of the build, the clamping mechanism, and the element activation scheme (Ref 17). Varying levels of macroscale mechanical model complexity have been applied to predict the distortion and residual stresses on the part scale using the FEM: (i) inherent strain (Ref 18), (ii) J2 plasticity (Ref 19), (iii) Johnson–Cook (Ref 20), (iv) novel MBAM methods (Ref 21, 22), and (v) internal state variable (ISV) plasticity (Ref 23, 24).

The inherent strain method has been applied to various walled Ti-6Al-4V parts and found that larger, more geometrically complex parts showed more of an impact to the mechanical behavior compared to small simple structures, indicating a limitation of the inherent strain method (Ref 25). The elastic–perfectly plastic (EPP) model is a J2 approximation with an artificial stress relaxation and has been used to model the thermomechanical response of DED specimens (Ref 26). To account for the Ti-6Al-4V solid-state phase transformation strain, a stress relaxation temperature was implemented, which led to agreeance with experimental distortion measurements; this finding indicated a need to develop a microstructurally motivated high-temperature constitutive model rather than relying on an aphysical stress relaxation temperature to capture the effects of static recovery and temperature-induced stress relaxation. The effects of different versions of the Johnson–Cook plasticity model on the formation of plastic strain during the laser powder bed fusion (L-PBF) of Ti-6Al-4V have been studied (Ref 20). The primary conclusion suggested that strain-rate-dependent hardening is significant in the 700-1300 °C range for L-PBF processes, and the presence of rate hardening should not be ignored when predicting the formation of residual stresses or distortion. Inspired by previous computational welding mechanics work performed by Goldak et al. (Ref 27), Ganeriwala et al. (Ref 21) implemented a material model capable of capturing the strain-rate-dependent and annealing behavior observed in MBAM with the intention of minimizing the number of constitutive parameters. This approach was novel in that the annealing effects are captured as a consequence of the viscoplasticity model that causes the stress to relax as a function of plastic strain. Furthermore, the viscoelastic model results in full stress and plastic strain relaxation while retaining the thermal strains. Their findings suggested that the proposed modeling approach could capture the residual stresses well, but were limited by not fully capturing the temperature history of the part using a lumped layer heating approach.

Physics-based ISV plasticity models that consider the effects of microstructural evolution, dislocation motion, etc., have not often been used for the prediction of residual stress and distortion associated with MBAM despite the level of mechanical accuracy they can provide in the context of rate- and temperature-dependent loading. However, researchers have used ISV models to predict the formation of residual stresses for L-PBF and the LENS process (Ref 23, 24). Promoppatum et al. furthered their work with different implementations of Johnson–Cook along with the mechanical threshold stress (MTS) ISV model to examine how sensitive the prediction of residual stresses is to the choice of material model; the overall conclusion of the work was that either model could be used to predict the formation of residual stresses, but the MTS model better captured the development phase of plastic strains due to its more physically based nature. To further the notion that ISV models are better geared to capture the history and evolution of the material during processing, the Bammann–Chiesa–Johnson model (Ref 28) was implemented to track the mechanical history of a LENS build (Ref 29). Similar to Promoppatum et al., they concluded that an ISV model can more accurately predict the evolution and resultant final residual stresses and strains compared to other modeling methodologies, emphasizing that a physically motivated model is necessary for such predictions. Furthermore, Stender et al.’s conclusions are supported by measured residual strains and dislocation densities.

The purpose of this work is to present a novel ISV-based mechanical model that is equipped for capturing MBAM residual stresses and distortion. The thermal model is calibrated using with dual wave pyrometer images taken of the melt pool during the build. The rate- and temperature-dependent ISV mechanical model is calibrated using hot compression test data taken at multiple strain rates and temperatures (Ref 30). Research has demonstrated that ISV models can be used for the prediction of temperature- and strain-rate-dependent behavior in metals; thus, the results of this study can then be used to aid process parameter development to accelerate design for DED processes (Ref 31). Due to the wide range of temperatures and the rapid heating and cooling rates (106 K/s) observed in MBAM that result in strain rates up to approximately 4 s−1, a temperature- and rate-dependent ISV model was used to gain a better insight into the evolution of distortion, plastic strain, and residual stresses during a MBAM build.

2 Mechanical Model Background

2.1 The Evolving Microstructural Model of Inelasticity

The mechanical model selected for the prediction of thermally induced residual stresses and distortion of an as-built part is the evolving microstructural model of inelasticity (EMMI) (Ref 32). EMMI was developed for the prediction of the mechanical response of metals at high strain rates and temperatures. EMMI is a physically based ISV model with parameters derived from dislocation mechanics and is the successor to the Bammann–Chiesa–Johnson (BCJ) model (Ref 28). EMMI is a modification of the BCJ model with changes to the formulation of rate effects and recovery mechanisms to improve its physical basis by updating the plasticity equations to better represent dislocation mechanics. Previously, BCJ has been used to predict weld solidification cracking along with residual stresses associated with LENS™ (Ref 24, 29, 33). Although parts fabricated with MBAM do not experience the high strain rates that EMMI was intended for, the large fluctuations in temperature and thermal cycling along with resultant plastic distortion and residual stresses make EMMI an ideal candidate to model the process due to the its temperature dependence and ability to capture the evolution of hardening. Typically, strain rates of up to 4 s−1 are observed in the MBAM process. The primary features of EMMI used in this work are: (i) temperature-dependent elastic modulus and yield strength; (ii) plasticity is described by isotropic and kinematic hardening variables; and (iii) hardening and recovery mechanisms that characterize dislocations and cell structures formed during deformation.

The finite strain deformation gradient, \(F\), is multiplicatively decomposed into four parts for EMMI: (i) the thermal deformation gradient, \(F_{\theta }\), is associated with thermal expansion, (ii) the deviatoric plastic deformation gradient, \(F_{p}\), is associated with dislocation movement, (iii) the volumetric deformation gradient, \(F_{d}\), is associated with damage, and (iv) the elastic recoverable deformation gradient, \(F_{e}\), is associated with lattice rotation and stretch (Ref 32). Thus, the total deformation gradient is shown in Eq 1. Damage is neglected in this implementation due to the small strain nature of MBAM.

$$F = F^{e} F^{d} F^{p} F^{\theta }$$
(1)

The EMMI model is comprised of five configurations:

  1. (1)

    Undeformed, \(B_{0}\)

  2. (2)

    Deformed (current),\(B\)

  3. (3)

    First intermediate, defined by \(F^{\theta }\), denoted as \(\tilde{B}\)

  4. (4)

    Second intermediate, defined by \(F^{p} F^{\theta }\), denoted as \(\overline{B}\)

  5. (5)

    Third intermediate, defined by \(F^{d} F^{p} F^{\theta }\), denoted as \(\hat{B}\)

Since the components of the deformation gradient have been defined, five stretch tensors, also known as Cauchy–Green deformation tensors, can be defined in Eq 2, 3, 4, 5, and 6:

$$C = F^{T} F$$
(2)
$$\tilde{C}^{p} = F^{pT} F^{p}$$
(3)
$$C^{\theta } = F^{\theta T} F^{\theta }$$
(4)
$$\overline{C}^{e} = F^{eT} F^{e}$$
(5)
$$C^{*} = F^{*T} F^{*}$$
(6)

From there, the Green–Lagrange strain tensors can be defined in Eq 7, 8, 9, 10, and 11:

$$E = \frac{1}{2} (C - 1)$$
(7)
$$\tilde{E}^{p} = \frac{1}{2}(\tilde{C}^{p} - \tilde{1})$$
(8)
$$E^{\theta } = \frac{1}{2}(C^{\theta } - 1)$$
(9)
$$\overline{E}^{e} = \frac{1}{2}(\overline{C}^{e} - \overline{1})$$
(10)
$$E^{*} = \frac{1}{2}(C^{*} - 1)$$
(11)

The total strain can then be decomposed:

$$\overline{E} = \overline{E}^{e} + \overline{E}^{p} + \overline{E}^{\theta }$$
(12)

Using the additive property associated with the strain tensor, the relationship between the rate of deformation tensors (velocity gradient) in configurations \(\overline{B}\) and \(B\) can be defined. The velocity gradient, \(l\), in configuration \(B\) can be computed:

$$l = \dot{F}F^{ - 1} = \dot{F}^{e} F^{e - 1} + F^{e} \overline{L}^{*} F^{e - 1}$$
(13)
$$\overline{L}^{*} = \dot{F}^{*} F^{* - 1} = \dot{F}^{p} F^{p - 1} + F^{p} \dot{F}^{\theta } F^{\theta - 1} F^{p - 1}$$
(14)
$$l = l^{e} + l^{*}$$
(15)
$$l^{*} = F^{e} \overline{L}^{*} F^{e - 1} = l^{p} + l^{\theta }$$
(16)

where:

$$l^{e} = \dot{F}^{e} F^{e - 1}$$
(17)
$$l^{p} = F^{e} \overline{L}^{p} F^{e - 1}$$
(18)
$$\overline{L}^{p} = \dot{F}^{p} F^{p - 1}$$
(19)
$$l^{\theta } = F^{e} \overline{L}^{\theta } F^{e - 1} = F^{e} F^{p} \tilde{L}^{\theta } F^{p - 1} F^{e - 1}$$
(20)
$$\tilde{L}^{\theta } = \dot{F}^{\theta } F^{\theta - 1} = \frac{{\dot{F}_{\theta } }}{{F_{\theta } }}\tilde{1}$$
(21)
$$\overline{L}^{\theta } = \frac{{\dot{F}_{\theta } }}{{F_{\theta } }}\overline{1}$$
(22)

All of the previously listed velocity gradients can be decomposed into symmetric and skew parts in their respective configuration as follows. Finally, the deformation gradient can be visualized in Fig. 1.

$$l = d + w$$
(23)
$$d = {\text{sym}}(l)$$
(24)
$$w = {\text{skew}}(l)$$
(25)
Fig. 1
figure 1

The multiplicative decomposition of the deformation gradient used in EMMI

Full size image

The evolution of plastic strain in EMMI is represented by three primary equations: (i) the inelastic flow rule, (ii) isotropic hardening, and (iii) kinematic hardening. The inelastic flow rule is shown in Eq 26, where \(\overline{\sigma }_{{{\text{eq}}}}\) is the equivalent stress, \(\overline{\kappa }_{s}\) is internal stress field due to isotropic hardening, \(Y(\theta )\) is temperature-dependent yield function, \(f(\theta )\) is a temperature-dependent material parameter, and \(\theta\) is the current temperature divided by the melt temperature. Isotropic hardening in denominator represents probability that dislocations are gliding, resulting in a smoother plastic flow. The rate of strain evolution due to isotropic hardening, \(\dot{\overline{\varepsilon }}_{s}\), is shown in Eq 27, where \(H\) is a hardening material constant, \(R_{D} (\theta )\) is a dynamic recovery constant, and \(R_{s} (\theta )\) and \(Q_{s} (\theta )\) are temperature-dependent static recovery constants. The rate of strain evolution due to kinematic hardening, \(\dot{\overline{\beta }}\), is shown in Eq 28, where \(h\) is a hardening material constant, \(r_{d} (\theta )\) is a temperature-dependent dynamic recovery constant, and \(\overline{\beta }\) is isotropic hardening. The evolution of hardening is related to dislocation storage, the recovery term is based on dislocation cross slip, while the thermal (static) recovery term is based on dislocation climb via diffusion. Furthermore, the non-dimensional yield function, \(Y(\theta )\), is shown in Eq 29, 30, and 31, where terms \(m_{1}\) through \(m_{5}\) are fit parameters. Calibration for EMMI for this implementation requires the fitting of sixteen material constants that are determined by fitting the stress response with experimental stress–strain data taken from tension tests. Calibration can be extended to other mechanical testing methods such as creep and cyclic tests. Further documentation for EMMI can be found in Marin et al. (Ref 32).

$$\dot{\overline{\varepsilon }}^{p} = f(\theta )\left[ {\sinh \left( {\left\langle {\frac{{\overline{\sigma }_{{{\text{eq}}}} }}{{\overline{\kappa }_{s} + Y(\theta )}} - 1} \right\rangle } \right)} \right]^{n}$$
(26)
$$\dot{\overline{\varepsilon }}_{s} = [H - R_{D} (\theta )\overline{\varepsilon }_{s} ]\dot{\overline{\varepsilon }}^{p} - R_{s} (\theta )\overline{\varepsilon }_{s} \sinh [Q_{s} (\theta )\overline{\varepsilon }_{s} ]$$
(27)
$$\dot{\overline{\beta }} = hF^{eT} d^{p} F^{e} - r_{d} (\theta )\dot{\overline{\varepsilon }}\sqrt {\frac{2}{3}} \left\| {\overline{\beta }} \right\|\overline{\beta }$$
(28)
$$Y(\theta ) = \frac{{Y_{1} }}{{Y_{2} }}$$
(29)
$$Y_{1} = m_{1} \left[ {1 - \tanh (m_{4} (m_{5} - \theta ))} \right]$$
(30)
$$Y_{2} = \left[ {1 + m_{2} \exp \left( {\frac{{ - m_{3} }}{\theta }} \right)} \right]^{ - 1}$$
(31)

EMMI had to be modified to account for material behavior at elevated temperatures for application specific to MBAM. Modifications include the relaxation of deviatoric stresses, hardening state variables, and plastic strains once the element temperature exceeds 80% of the melt temperature. This assumption is based on the increased dislocation motion that occurs above this temperature causing the annihilation of work hardening, which is the result of the metal acting as a linear viscous material (Ref 34).

2.2 The Elastic–Perfectly Plastic (EPP) Mechanical Model

The EPP model was chosen as a comparative baseline against the EMMI model because of its use in the literature and contrast in features. EPP is based on the governing mechanical stress, \(\sigma\) equation in Eq 32, the mechanical constitutive law in Eq 33, and the total strain in Eq 34. \(C\) represents the fourth-order material stiffness tensor, \(\varepsilon\) is the total strain, \(\varepsilon_{e}\) is the elastic strain, \(\varepsilon_{p}\) is the plastic strain, and \(\varepsilon_{t}\) is the thermal strain. Phase transformation strain and an artificial stress relaxation temperature were neglected in this implementation. However, the initial temperature of the activated elements was set to the melting temperature to ensure that they were in a stress-free state before following the prescribed temperature history from the thermal analysis. The required mechanical inputs to run the EPP model in this formulation are temperature-dependent: elastic modulus, yield strength, and coefficient of thermal expansion.

$$\nabla \cdot \sigma = 0$$
(32)
$$\sigma = C\varepsilon_{e}$$
(33)
$$\varepsilon = \varepsilon_{e} + \varepsilon_{p} + \varepsilon_{t}$$
(34)

3 Thermomechanical Modeling Methodology

3.1 Thermomechanical Modeling Framework

A sequentially coupled thermomechanical modeling approach was used to model the AM process and resultant mechanical response. The EMMI model was implemented in a Fortran user material subroutine (UMAT) and read into ABAQUS, while the EPP model used the built-in ABAQUS implementation. The thermal analysis was run in its entirety and the temperature at each node was passed into the mechanical analysis at each time increment. At the beginning of each time increment, the deformation gradient is passed from ABAQUS to the UMAT, where it is decomposed into three parts: thermal, elastic, and plastic. Then, the multiplicatively decomposed deformation gradient is used to determine the stresses and strains. Finally, the internal state variables are updated. Lastly, ABAQUS performs a check to ensure that equilibrium is maintained before proceeding to the next increment; if equilibrium is not met in a user defined number of iterations, the analysis stops.

The finite element mesh used to model the double-track thin wall is visualized in Fig. 2. A total of 433,440 continuum hexahedral (C3D8/DC3D8) elements were used to model the thin wall, while a combined total of 39,862 continuum hexahedral and continuum tetrahedral were used to model the substrate. In the thin wall, the element size was 0.083 × 0.083 × 0.083 mm with an aspect ratio of 1. Other than the temperature history from the thermal model, the only boundary condition applied to the mechanical model is the fixing of the nodes on the bottom of the substrate in each direction to account for the clamping mechanism in the LENS process.

Fig. 2
figure 2

Representative finite element analysis mesh of the double-track thin wall

Full size image

3.2 Thermal Modeling Methodology

The parameters from the validated thermal model in previous work are used in the formulation of the double-track thin wall thermal model (Ref 35). The process parameters used for the build are listed in Table 1. Two different thermal histories were generated with a unidirectional and a bidirectional scanning strategy. To showcase the differences in thermal history, the temperature at a node at the end of the first deposition track is plotted in Fig. 3. The initial temperature for these simulations was 25 °C. The nodal coordinates are (50.25, 62.00, 3.675 mm) relative to the origin shown in Fig. 2. Although the observed temperatures are the same at the first two peaks above 800 °C, they begin to deviate due to the differing scanning strategies. This difference will contribute to differing thermal expansion at this node.

Table 1 Thin wall builds machine process parameters
Full size table
Fig. 3
figure 3

Temperature history at node of interest. The node of interest is located at the end of the first deposition track on layer one. After this point, the deposition strategy changes, as shown in the schematic

Full size image

3.3 Mechanical Model Calibration

To calibrate EMMI for Ti-6Al-4V, a single-point simulator was used to iterate model parameters and compare the response to experimentally gathered data. For this study, the model parameters were calibrated to hot compression data digitized from Babu et al. (Ref 36). The range of temperatures used in the calibration process varied from 20 to 800 °C, while the strain rates range from 0.001 to 1.0 s−1. Physical mechanical properties of Ti-6Al-4V used as inputs in the EMMI model are shown in Table 2. The initial step of the calibration procedure involves the fitting of the temperature-dependent yield function at quasi-static strain rate; results of this fitting procedure are shown in Fig. 4 and Table 3. The predicted temperature-dependent yield strength follows the overall trend of the experimental, although there is slight deviation around 20% and 40% of the melt temperature. The next step in the material parameter calibration process involved the fitting of non-dimensional terms relating to material hardening and recovery variables, which are shown in Table 4.

Table 2 Ti-6Al-4V material parameters (Ref 40,41,42)
Full size table
Fig. 4
figure 4

EMMI temperature-dependent normalized yield function compared to experimental data (Ref 30)

Full size image
Table 3 Ti-6Al-4V temperature-dependent EMMI yield function parameters
Full size table
Table 4 Ti-6Al-4V EMMI parameters
Full size table

The predicted mechanical response of both the calibrated EMMI and EPP models is compared with the experimental calibration data in Fig. 5. A significant drawback of the calibration process is that EPP is rate independent, and strain rates up to 4/s are observed in the DED process which could lead to significant error. However, EPP exhibits a good fit in the elastic region along with temperature-dependent the yield strength. In particular, EPP shows a more accurate fit than EMMI to the yield strength at 600 °C. Furthermore, none of the hardening behavior is captured in the EPP model, which could lead to a source of error if the associated DED processing parameters produce a part that has significant plastic deformation. For the EMMI model, the predicted stress–strain behavior captures the observed strain-rate and temperature dependency well. The hardening behavior is slightly under predicted at room temperature and over predicted at elevated temperatures, but due to the small residual strain behavior of MBAM, this set of parameters is acceptable for the prediction of residual stresses and distortion.

Fig. 5
figure 5

Simulated EMMI and EPP compression response compared with experimental data (Ref 30)

Full size image

4 Results and Discussion

The first result of interest is simulated as-built von Mises stress. Figure 6 compares the von Mises stress in the as-built double-track thin walls for both scanning strategies and mechanical models. Despite the differing scanning strategies, the von Mises stress profile is nearly identical for both cases, with more stresses observed in the upper middle section and the lower left section of the unidirectional wall for each model. Furthermore, the location of the maximum stress occurs in the same node at the bottom outer edge of the wall for each case. The maximum observed stresses were approximately 100 MPa above the quasi-static room temperature yield strength of Ti-6Al-4V, indicating a small amount of plastic deformation near the substrate, but these maximum residual stresses would not result in fracture of the material. Although the results using the same mechanical model are consistent, the difference in buildup of residual stresses between the two models is significant. The EMMI simulations predict a low amount of residual stress throughout the wall with a small concentration in the outer corners. On the other hand, the EPP model predicts significant residual stresses throughout the bulk of the wall at approximately half of the room temperature yield stress.

Fig. 6
figure 6

von Mises stress contours for the (a) EMMI unidirectional; (b) EMMI bidirectional; (c) EPP unidirectional; (d) EPP bidirectional

Full size image

Contour plots detailing stresses in the build direction are shown in Figs. 7 and 8. Compared to the similar von Mises stress profiles, the build direction stresses are where the stress contours begin to deviate for each model. The unidirectional scanning strategy resulted in higher magnitudes of compressive and tensile stresses compared to the bidirectional scanning strategy. Both scanning strategies resulted in tensile residual stresses at the outer free surfaces, particularly at the interface between the thin wall and the substrate, which is expected using Mercelis and Kruth’s temperature gradient mechanism for the formation of residual stresses in MBAM (Ref 12). The primary differences in build direction stresses observed in Fig. 7 are the gradual buildup of residual stresses using the EMMI model, while there is a steep gradient of residual stresses observed in the EPP model. For both models, bidirectional wall shows a higher buildup of tensile residual stress at the bottom of the wall, and the unidirectional wall shows more of a compressive stress concentration in the upper middle third of the wall. The differences in build direction residual stresses for the EMMI simulations are more evident in Fig. 8, with the majority of tensile residual stresses accumulated on one half of the bidirectional wall and a more uniform buildup in the unidirectional wall.

Fig. 7
figure 7

Cross section at the middle of the thin wall showing build direction residual stresses for the: (a) EMMI unidirectional; (b) EMMI bidirectional; (c) EPP unidirectional; (d) EPP bidirectional

Full size image
Fig. 8
figure 8

Cross section at the middle of the thin wall showing build direction residual stress comparison for the (a) EMMI unidirectional and (b) EMMI bidirectional thin wall

Full size image

The longitudinal stress contour for both scanning strategies is shown in Fig. 9. The primary differences in the contours occur near the outer edges of the build, where the difference in temperature history is greatest. The bulk of each wall shows a small buildup of tensile residual stresses, with compressive stresses just under zero for the bidirectional and closer to − 100 MPa for the unidirectional scanning strategy. The predicted contour of 0 to 200 MPa near the interface between the thin wall and the substrate is in agreement with the profile and magnitude observed in measurements by Denlinger et al. (Ref 37), meaning that EMMI has captured the evolution of longitudinal stresses in the thin walls.

Fig. 9
figure 9

Longitudinal stress profile for the (a) EMMI unidirectional; (b) EMMI bidirectional; (c) EPP unidirectional; (d) EPP bidirectional thin walls

Full size image

The evolution of longitudinal, build direction, and von Mises stress at the node of interest from Fig. 3 is shown in Figs. 10 and 11. For each case, the build direction stress is the dominant component to the stress tensor, with the von Mises stress mirroring its contour. Significant stress formation above 100 MPa does not occur until the temperature falls below 400 °C. This is significant for two reasons: (i) this indicates that overpredicting the hardening at elevated temperatures is not significantly contributing to the prediction of residual stresses because stresses at these temperatures are elastic and (ii) the majority of residual stress formation is actually occurring in a lower temperature region, due to the diminished stiffness and strength observed at higher temperatures. This conclusion is supported by the experimental dataset that the model was calibrated to. Furthermore, the fluctuations in predicted von Mises and build direction stresses are much greater for the EPP prediction of both scanning strategies, indicating that the same amount of thermal expansion resulted in a stiffer response compared to the EMMI model.

Fig. 10
figure 10

Temperature and stress evolution at the node of interest for the unidirectional scanning strategy model

Full size image
Fig. 11
figure 11

Temperature and stress evolution at the node of interest for the bidirectional scanning strategy model prediction

Full size image

Despite the general trend of the build direction stress dominating the stress tensor during the simulation, there are some exceptions, particularly in the EPP prediction of the unidirectional scanning strategy. The longitudinal stress hovers around 200 MPa for the majority of the build, and then falls just below zero at the end of the build. This trend is not replicated in the EPP bidirectional prediction, which raises some concern on the reliability of an EPP model to capture the evolution of stresses during the build. However, the end result for each model is similar in numerical value for their respective scanning strategy for the longitudinal stresses, while the von Mises and build direction stresses varied by 300-350 MPa, which is approximately one-third of the Ti-6Al-4V room temperature yield stress.

Tables 5 and 6 list the maximum von Mises stress, build direction stress, longitudinal stress, transverse stress, and distortion for each scanning strategy and mechanical model. For each component of the stress tensor other than the calculated von Mises stress, the percentage difference was greater between the EPP and EMMI model for each stress component and distortion for the unidirectional scanning strategy. The observed differences between each mechanical model and scanning strategy can be attributed to the increased stiffness of the EPP model due to the lack of static recovery compared to EMMI.

Table 5 Comparison of overall maximum stresses and distortion for the unidirectional scanning strategy with the EMMI and EPP models
Full size table
Table 6 Comparison of overall maximum stresses and distortion for the bidirectional scanning strategy with the EMMI and EPP models
Full size table

Figure 12 shows the evolution of the stress components at the location of maximum von Mises stress for the bidirectional build strategy for both the EMMI and EPP models. The locations for the maximum von Mises stress for each model were within 0.5 mm of each other at the interface between the outer surface of the wall deposit and the top of substrate. In contrast to the previous node of interest at the top of layer one, the build direction stress did not have the highest magnitude of stress in the stress tensor at the location of maximum von Mises stress for the EPP and EMMI simulations. Rather, the longitudinal stress was the highest magnitude component in the stress tensor. Furthermore, the shear stress component does not contribute much to the overall stress in the EMMI simulation until the node begins to cool under 100 °C. This is likely due to the constraint imposed by the substrate due to the location of maximum von Mises stress occurring at the interface between the substrate and the part. The increase in stress at the end could also be an artifact of the mechanical boundary conditions imposed on the bottom of the substrate, which fixed all of the bottom surface nodes in place. Such a constraint could artificially inflate the stress prediction at the interface between the wall and the substrate.

Fig. 12
figure 12

Comparison of stress evolution at location of maximum von Mises stress for the: (a) EMMI and (b) EPP models for the bidirectional scanning strategy

Full size image

5 Conclusions

A sequentially coupled finite element thermomechanical model for the LENS process to compare the thermally induced residual stresses and distortion for as-built Ti-6Al-4V double-track thin walls using the EMMI and EPP models has been presented. Notable conclusions drawn from this work can be summarized as follows:

  • When considering the calibration of the mechanical model for Ti-6Al-4V for the prediction of residual stresses and distortion, it is important to first focus on the temperature region from room temperature to 600 °C and lower, because a majority of residual stress formation occurs in this region.

  • For a simple thin wall geometry, the EMMI model was able to predict different results based on scanning strategy. The unidirectional specimen was hypothesized to demonstrate higher distortion and residual stresses compared to the bidirectional scanning strategy, which it did due to the varying thermal history at the ends of the wall.

  • The build direction stresses, the longitudinal stresses, and transverse stresses for the EPP model were much higher than the EMMI model. Additionally, the EMMI model better reflected the magnitude of the measured longitudinal residual stresses by Denlinger et al. (Ref 37); however, the EPP model followed the same contour shape with a higher magnitude. The stress profile at the end of the wall was likely different because the geometry in the literature was a single-track deposition.

  • The general trend of the stress profile prediction, tension on the outer surfaces, and the build direction stresses dominating the stress tensor due to the thermal gradient, falls in line with trends in the literature (Ref 38).

  • The predicted location of maximum stresses and distortion for each scanning strategy was the same for both the EPP and EMMI models. This is significant because if this type of thermomechanical modeling methodology is applied strictly with the intention of identifying critical stress or distortion concentrations, then a quick answer could be obtained with an EPP model.

  • The difference between the maximum predicted von Mises stress between the EMMI and EPP models is within 2% for each scanning strategy. However, this maximum for the EMMI model lies at a single node for each case, indicating that further mesh refinement may be needed. The EPP model indicates a much larger area of plastic stresses at the same area compared to the EMMI model. Furthermore, the overall buildup of von Mises stresses for the EPP model is much higher than indicated by the EMMI model. This is perhaps due to the lack of recovery mechanisms present in the EPP model.

  • The EPP model resulted in a much larger predicted final distortion than the EMMI model, but like the aforementioned stress contours, the patterns were the same despite the large difference in magnitude.

  • The results presented in this study strengthen the notion that an EPP model produces much larger residual stresses and distortion compared to a higher fidelity model that captures ISV evolution. These differences would likely be more drastic if the chosen DED process parameters produced a part with more distortion, as examined in other work (Ref 39).

  • Ti-6Al-4V does not have a significant strain rate dependency in the strain rates relevant to powder DED (quasi-static to 4/s). Applying this comparison framework to materials with a higher strain rate dependency could yield further conclusions regarding the differences between the two modeling strategies.

  • Furthermore, to better assess the differences between EMMI and EPP, more complex geometries need to be analyzed so that insight can be gained in more complex modes of conduction heat transfer.

  • Finally, the difference in the runtime between the two modeling methodologies was about 2 hours, as the EMMI model ran for a total of ~ 8 hours on 60 cores, while the EPP model ran for about 10 hours on 60 cores. This difference would likely be more significant on a larger part with more elements.