N and C Interstitial Diffusion and Thermodynamic Interactions in $\varepsilon$-Iron Carbonitride

Abstract

The simultaneous diffusion of N and C over the interstitial sites of the Fe-sublattice of $\varepsilon$-iron carbonitride was studied. To this end, gas nitrocarburizing experiments of pure Fe and Fe-C alloys were performed at 853 K (580 °C), leading to two different types of microstructures containing $\varepsilon$ (sub)layers. These microstructures were investigated by light microscopy, electron probe microanalysis, and X-ray diffraction in order to evaluate the components of the (N and C) diffusivity matrix. The off-diagonal components of the diffusivity matrix were shown to have significant, non-negligible values. These results provided insight into the thermodynamics of the Fe-N-C system.

1 Introduction

Nitriding and nitrocarburizing are common thermo-chemical heat treatment processes used in order to improve, e.g., the corrosion, wear, and fatigue resistances of iron-based alloys.[1] In view of nitriding and nitrocarburizing being widely applied in industry, there is a surprising lack of knowledge regarding the constitution of the ternary system Fe-N-C, whereas such knowledge is a prerequisite to arrive at fundamental understanding of the effects of nitriding and nitrocarburizing of steels (normally containing carbon).

For predictions of the growth of compound layers forming upon nitriding and nitrocarburizing of iron and steel, it is necessary to understand the simultaneous diffusion of the interstitially dissolved components N and C in the resulting phases. For an overview of the phases considered, see Table I. In the following, these phases will be abbreviated by the small Greek letters defined in Table I.

Table I Characteristics of the Fe-N-C Phases Relevant for the Present Work

Diffusion of N and C, separately, in Fe and the corresponding nitrides and carbides has been studied thoroughly in the past.[2–16] However, either upon nitriding or upon nitrocarburizing, as soon as the system contains C, which may already originate from the substrate (e.g., steel) and/or from the treatment medium (in case of nitrocarburizing), the role of this additional interstitially diffusing component C, next to the interstitially diffusing component N, has to be taken into account.

Diffusion of each of multiple components can be described by Fick’s first law,

$$\begin{aligned} j_i=-D_{ij}\nabla c_j. \end{aligned}$$

(1)

For the case of interstitial diffusion, the components of the diffusivity matrix, $D_{ij}$, read

$$\begin{aligned} D_{ij}=D^*_i\frac{c_i}{RT}\frac{\partial \mu _i}{\partial c_j}=D^*_i\vartheta _{ij}, \end{aligned}$$

(2)

with the self diffusion coefficient $D^*_i$, the concentrations of the diffusing components $i$ and $j$, $c_i$ and $c_j$, the gas constant $R$, the temperature $T$, the chemical potential of component $i$, $\mu _i$, and the so-called thermodynamic factor $\vartheta _{ij}$, relating the intrinsic diffusion coefficients to thermodynamics.[17,18] The cross(off-diagonal)-terms of this diffusivity matrix express the influence of the concentration gradient of one diffusing species on the flux of another one. The thermodynamic factors can be calculated if a thermodynamic description is available. In literature, several of these (partially incompatible) descriptions for the system Fe-N-C exist.[19–22]

A first theoretical treatment of simultaneous diffusion of N and C in an $\varepsilon$/$\gamma ^\prime$ double layer system offered an analytical solution of Fick’s second law by assuming concentration-independent diffusion coefficients.[23] However, the occurrence of a large solubility range of both N and C in $\varepsilon$-iron carbonitride, leading to large concentration variations in compound layers formed upon nitriding or nitrocarburizing of iron or steel, already indicates that the assumption of concentration-independent diffusivities of N and C is unacceptable. By avoiding a such affected, analytical solution of Fick’s second law in a later work and only using Fick’s first law, the first experimental analysis of simultaneous interstitial diffusion of N and C in $\varepsilon$-iron carbonitride was made possible:[24] the diffusivity matrix of N and C was evaluated at 823 K (550 °C) for $\varepsilon$/$\gamma ^\prime$ double layers growing upon nitriding and nitrocarburizing of pure Fe using a linear fit for the concentration-depth profiles of N and C.

The present work is devoted to the evaluation of the diffusivity matrix of N and C in $\varepsilon$-iron carbonitride at 853 K (580 °C) on the basis of an approach provided in Reference 24. It will be demonstrated that the proposed method can be applied to a variety of microstructures, essentially different from those examined in Reference 24. Thus, the kinetics of growth of $\theta /\varepsilon$ double layers and of pure $\varepsilon$ layers, containing considerably less N and considerably more C than in Reference 24, have been investigated. Further, the method has been expanded to incorporate the curved nature of the concentration-depth profiles occurring in some of these (sub)layers. Moreover, a graphical evaluation method is proposed for determining the values of the components of the diffusivity matrix, giving direct information about the accuracy of the measurements. The data obtained on the thermodynamic factors have been compared with thermodynamic descriptions of the Fe-N-C system to obtain decisive information about the thermodynamic interaction of N and C in the $\varepsilon$ phase.

2 Evaluation Method

The applied method is based on the following assumptions for interstitial diffusion in the Fe-N-C systems at constant temperature and pressure. The only mobile species considered here are N and C. Fe is immobile and forms a lattice with a volume that is taken to be independent of the amount of interstitials dissolved. The interfaces between the phases formed upon diffusion are planar. The shape of the concentration-depth profiles remains constant with increasing treatment time, i.e., the concentration-depth profile normalized with respect to the (sub)layer thickness is time-independent, which implies that the concentrations at the (sub)layer interfaces are constant over time. The surface concentration is constant as determined by the treatment atmosphere. Local equilibrium is adopted at the solid–solid interfaces.

Fick’s first law written explicitly for two diffusing components N and C reads

$$\begin{aligned} j_{\text{N}}=-D_{\text{NN}}\frac{{\text{d}}c_{\text{N}}}{{\text{d}}x}-D_{{\text{NC}}}\frac{{\text{d}}c_{\text{C}}}{{\text{d}}x};\nonumber \\ j_{\text{C}}=-D_{\text{CN}}\frac{{\text{d}}c_{\text{N}}}{{\text{d}}x}-D_{\text{CC}}\frac{{\text{d}}c_{\text{C}}}{{\text{d}}x}, \end{aligned}$$

(3)

which can also be written as

$$\begin{aligned} D_{\text{NC}}=-D_{\text{NN}}\frac{{\text{d}}c_{\text{N}}}{{\text{d}}x}\cdot \frac{{\text{d}}x}{{\text{d}}c_{\text{C}}}-j_{\text{N}}\cdot \frac{{\text{d}}x}{{\text{d}}c_{\text{C}}};\nonumber \\ D_{\text{CN}}=-D_{\text{CC}}\frac{{\text{d}}c_{\text{C}}}{{\text{d}}x}\cdot \frac{{\text{d}}x}{{\text{d}}c_{\text{N}}}-j_{\text{C}}\cdot \frac{{\text{d}}x}{{\text{d}}c_{\text{N}}}. \end{aligned}$$

(4)

Hence, for known fluxes ($j_{\text{N}}$ and $j_{\text{C}}$) and known concentration gradients (${\text{d}}c_{\text{N}}/{\text{d}}x$ and ${\text{d}}c_{\text{C}}/{\text{d}}x$), all mathematically (not necessarily physically) possible solutions of $D_{\text{NC}}$ ($D_{\text{CN}}$) are linearly dependent on $D_{\text{NN}}$ ($D_{\text{CC}}$). These solutions can be represented by straight lines in a plot of $D_{\text{NC}}$ vs $D_{\text{NN}}$ and in a plot of $D_{\text{CN}}$ vs $D_{\text{CC}}$. The fluxes and the concentration gradients needed for the proposed evaluation method can be determined experimentally by measuring concentration-depth profiles in the considered (sub)layers and their corresponding thicknesses. This is explained in Section III.

It is obvious that for values of the fluxes and concentration gradients of N and C measured at one specific set of conditions as defined by the employed gas atmosphere, treatment temperature, and time (and the constant, atmospheric pressure), the solution of Eq. [4] is not possible, but straight lines ($D_{\text{NC}}$ ($D_{\text{CN}}$) as a function of $D_{\text{NN}}$ ($D_{\text{CC}}$)) can be constructed in the above-mentioned plots. At the same temperature and pressure, but for a different treatment time and gas atmosphere, different values of the fluxes and concentration gradients of N and C will be found. The corresponding straight lines in the above-mentioned plots intersect the first mentioned straight lines. The intersection points define the solution of Eq. [4] for the four components of the diffusivity matrix. Adding the results of a third set of conditions, the additional straight lines in both plots should ideally have the same intersection points with the earlier two sets of straight lines. In reality, this need not occur: the values of the components of the diffusivity matrix represent effective diffusivities, i.e., a mean value of the diffusivities over the concentration range that is covered by the concentration-depth profile in the considered (sub)layer. Since the N and C concentration-depth profiles for each set of conditions are different, the resulting, corresponding effective diffusivities for the various sets of experimental conditions are (somewhat) different. Furthermore, all experimentally determined values and, therefore, also the parameters of the straight lines are prone to experimental errors. Hence, the intersection points of the straight lines in each of the plots of $D_{\text{NC}}$ vs $D_{\text{NN}}$ and $D_{\text{CN}}$ vs $D_{\text{CC}}$ for three different sets of conditions enclose a triangle. The coordinates of the geometric centers of both triangles then represent a solution of Eq. [4] that is approximately valid for all three cases. The area covered by the triangles indicates the ranges of possible values for the components of the diffusivity matrix, i.e., provides corresponding error estimates.

Data obtained from experiments at (even) more sets of experimental conditions can be added. This leads to an increase of intersection points of the straight lines in the plots of $D_{\text{NC}}$ vs $D_{\text{NN}}$ and $D_{\text{CN}}$ vs $D_{\text{CC}}$. These intersection points may also occur in areas that do not have a physical meaning (i.e., correspond to negative values for $D_{\text{NN}}$ or $D_{\text{CC}}$). Then, the area for the possible solutions of Eq. [4] must be limited to the physically meaningful intersection points. The centroid of this area then gives the (at this stage) most likely solution of Eq. [4]. The extent of the area of physically meaningful intersection points in the plots indicates the ranges of possible values for the components of the diffusivity matrix, i.e., provides corresponding error estimates. In a second step, this solution found for the values of the diffusivity matrix can be refined by minimizing the differences between the experimentally determined fluxes and those calculated from Fick’s first law.

3 Modeling of Interstitial Diffusion

Consider a double layer (cf. Figure 1) with an upper sublayer of phase III and a lower sublayer of phase II growing into a substrate of phase I at the time $t_1=t$ and at the time $t_2=t+{\text{d}}{t}$ between which the sublayer boundaries at the positions $x_1^{\text{III/II}}$ and $x_1^{\text{II/I}}$ at the time $t_1$ move by the amounts $v^{\text{III/II}}{\text{d}}{t}$ and $v^{\text{II/I}}{\text{d}}{t}$ to the positions $x_2^{\text{III/II}}$ and $x_2^{\text{II/I}}$ at the time $t_2$. Here, $v^{\text{III/II}}={\text{d}}x^{\text{III/II}}/{\text{d}}t$ and $v^{\text{II/I}}={\text{d}}x^{\text{II/I}}/{\text{d}}t$ describe the velocities of the positions of the sublayer boundaries. The flux difference of component $i$ at the layer boundary between the phases III and II is given by

$$\begin{aligned} \left( j_i^{\text{III/II}}-j_i^{\text{II/III}}\right) (t_2-t_1)=\left( c_i^{\text{III/II}}-c_i^{\text{II/III}}\right) \left(x_2^{\text{III/II}}-x_1^{\text{III/II}}\right), \end{aligned}$$

(5)

corresponding to the shaded area labeled 1 in Figure 1. The flux difference of component $i$ at the layer boundary between the phases II and I complies with

$$\begin{aligned} \left( j_i^{\text{II/I}}-j_i^{\text{I/II}}\right) (t_2-t_1)=\left( c_i^{\text{II/I}}-c_i^{\text{I/II}}\right) \left(x_2^{\text{II/I}}-x_1^{\text{II/I}}\right), \end{aligned}$$

(6)

corresponding to the shaded area labeled 3 in Figure 1. For the fluxes $j_i$ and the concentrations $c_i$, the superscript I/II denotes a quantity in phase I at the boundary between I and II, etc.

Fig. 1

Schematic concentration-depth profile of component $i$ in a III/II double layer growing into a substrate I at the time $t_1$ (solid lines) with the interfaces $x_1^{\text{III/II}}$ and $x_1^{\text{II/I}}$ and at the time $t_2=t_1+{\text{d}}{t}$ (dashed lines) with the interfaces $x_2^{\text{III/II}}$ and $x_2^{\text{II/I}}$. The shaded areas labeled with 1, 2 and 3 correspond to equations [5], [7], and [6]

The flux difference between the upper and lower boundaries of layer II can be calculated by

$$\begin{aligned} \left( j_i^{\text{II/III}}-j_i^{\text{II/I}}\right) (t_2-t_1)=\int _{x_2^{\text{II/I}}}^{x_2^{\text{III/II}}}c_i(x,t_2){\text{d}} x-\int _{x_1^{\text{II/I}}}^{x_1^{\text{III/II}}}c_i(x,t_1){\text{d}} x, \end{aligned}$$

(7)

corresponding with the shaded area labeled 2 in Figure 1. Note that these equations are valid regardless of the shape of the concentration-depth profile.

In case of a linear concentration-depth profile in layer II

$$\begin{aligned} c_i(x,t)=c_i^{\text{II/III}}-(c_i^{\text{II/III}}-c_i^{\text{II/I}})\frac{x-S^{\text{III}}(t)}{S^{\text{II}}(t)}, \end{aligned}$$

(8)

with $S^{\text{III}}$ and $S^{\text{II}}$ denoting the layer thicknesses of layers III and II, it follows from Eq. [7]

$$\begin{aligned} j_i^{\text{II/III}}-j_i^{\text{II/I}}=\frac{1}{2}(c_i^{\text{II/III}}-c_i^{\text{II/I}})(v^{\text{III/II}}+v^{\text{II/I}}). \end{aligned}$$

(9)

In case of an arbitrary error-function-shaped profile in layer II

$$\begin{aligned} c_i(x,t)=c_i^{\text{II/III}}-\frac{c_i^{\text{II/III}}-c_i^{\text{II/I}}}{{{{\text{erf}}}}w_i}{{{\text{erf}}}}\left( w_i\frac{x-S^{\text{III}}(t)}{S^{\text{II}}(t)}\right) , \end{aligned}$$

(10)

with $w_i$ as fitting parameter, it follows from Eq. [7]

$$\begin{aligned} j_i^{\text{II/III}}-j_i^{\text{II/I}}=\left[ v^{\text{III/II}}+\frac{1}{\sqrt{\pi }}\frac{1-\exp (-w_i^2)}{w_i {{{\text{erf}}}}w_i}(v^{\text{II/I}}-v^{\text{III/II}})\right] (c_i^{\text{II/III}}-c_i^{\text{II/I}}). \end{aligned}$$

(11)

By replacing III by the surface S and setting $v^{\text{II/S}}=0$ , the above treatment directly provides similar expressions for the flux difference between the upper and lower interfaces of the surface layer.

Now, by assuming certain fluxes (of N and C) into the substrate, the above-indicated flux difference equations for layers II and III can be used to straightforwardly calculate the flux of each component in each phase at each layer boundary. In the present work, two different approaches for such calculations will be used, depending on the microstructure of the substrate. In the first case, the flux of N and C into the substrate is assumed to be zero, which holds if the substrate is already saturated before the beginning of the experiment. In the second case, the following numerical approximation is adopted for the flux of N into the substrate I of thickness $2L$ at the boundary with layer II at the time $t,$[8,13]

$$\begin{aligned} j_{\text{N}}^{\text{I/II}}=D_{\text{N}}^{\text{I}}\frac{2(c_{\text{N}}^{\text{I/II}}-c_{\text{N}}^{\text{I,0}})}{L}\cdot \sum \limits _{n=1}^{\infty }\exp \left( -\frac{(2n-1)^2\pi ^2 D_{\text{N}}^{\text{I}}\cdot t}{4L^2}\right) \end{aligned}$$

(12)

with $c_{\text{N}}^{\text{I,0}}$ denoting the concentration of N in the center of the specimen. The intrinsic diffusion coefficient $D_{\text{N}}^{\text{I}}$ of N in phase I is taken from the literature. As in the first case, the flux of C into the substrate can be neglected.

The difference of flux equations [5] through [7] considered here are independent of the diffusion mechanism (i.e., interstitial or substitutional) in the considered phases. However, the values for the concentrations, i.e., the amount of atoms of a component considered per volume unit, in contrast with values for the (e.g., molar) fractions, are not easily accessible by experiments. By assuming constant volume of a substitutional solid solution, the concentration variable $c_i$ is directly proportional to the molar fraction $x_i=n_i/n$ (with the amount of atoms of component $i$, $n_i$, and the total amount of atoms $n=\sum _i n_i$). However, by similarly assuming the volume of an interstitial solid-solution phase, as $\varepsilon$-iron carbonitride, to be independent of the amount of interstitials (i.e., the (hcp) Fe-sublattice without interstitially dissolved atoms has the same volume as the fully occupied lattice), the concentration variable $c_i$ now is proportional to the so-called $u$-fraction

$$\begin{aligned} u_i=\frac{n_i}{n_{\text{host}}} \end{aligned}$$

(13)

with $n_{\text{host}}$ denoting the amount of the atoms forming the host lattice for the interstitially dissolved atoms.[25] If Fe, N, and C are the only components of the solid solution, the $u$-fraction can be calculated from the molar fractions by

$$\begin{aligned} u_i=\frac{x_i}{1-x_{\text{N}}-x_{\text{C}}}. \end{aligned}$$

(14)

Then, the proportionality constant in order to obtain $c_i$ from $u_i$ is the inverse volume of one mole Fe atoms in the corresponding crystal structure, $V_{\text{m,Fe}}$, i.e.,

$$\begin{aligned} c_i=\frac{u_i}{V_{\text{m,Fe}}} \end{aligned}$$

(15)

Table I lists the phases considered in the present work and the corresponding volumes of one mole Fe atoms, $V_{\text{m,Fe}}$, as calculated from the lattice-parameter data given in References 26 through 29.

The velocities of the sublayer boundaries are obtained by adopting a parabolic growth law (experimentally verified; see Section V–A) for the position, $x$, of the sublayer boundary,

$$\begin{aligned} x^2(t)=k\cdot t, \end{aligned}$$

(16)

and subsequently solving for $x$ and taking the derivative. Note that, in an ideal case of such parabolic growth, the growth constant $k$ contains a combination of the components of the diffusivity matrix, see Reference 23. This, however, requires that the Boltzmann transformation[17,18] is applicable which is not necessarily the case in the present work. Thus, here the growth constant $k$ is considered as a model parameter without that a physical interpretation is given.

It is possible to extend the kinetic model, especially for incubation effects in the early stage of the layer-growth process, by introducing a hypothetical initial squared layer thickness $S_0^2$, like in Reference 24, i.e.,

$$\begin{aligned} x^2(t)=k\cdot t + S_0^2. \end{aligned}$$

(17)

For reasons discussed in Section VI–A, the latter approach was avoided in the present work.

4 Experimental

Two different types of substrates were used, one consisting of an Fe-N alloy and one consisting of an Fe-C alloy.

For preparing the Fe-N specimens, a pure iron (Alfa Aesar, 99.98 wt pct) ingot of ${80}\,{\text{mm}}\,\times {30}\,{\text{mm}}\,\times {10}\,{\text{mm}}$ was cold-rolled to a thickness of about 1 mm and cut into plates with a size of ${20}\,{\text{mm}}\,\times {12}\,{\text{mm}}$. The plates were then ground and polished (down to 1 $\mu$m diamond suspension) to a final thickness of 0.5 mm. The specimens were then recrystallized in pure H$_2$ at 973 K (700 °C) for 2 hours, polished again, and presaturated with N over night (approx. 18 hours) at 853 K (580 °C) in an atmosphere containing 10.6 vol pct NH$_3$ and 89.4 vol pct H$_2$ (corresponding to a N activity of 69 relative to pure N$_2$ gas, i.e., a nitriding potential $r_{\text{N}}$ of 3.93 × 10⁻⁴ Pa$^{-1/2}$ (0.125 atm$^{-1/2}$)). This results in pure $\alpha$-iron, verified by X-ray diffraction, with a N content between 0.36 and 0.38 at. pct, determined gravimetrically. These N contents are very close to the maximum solubility of N in $\alpha$-iron in equilibrium with $\gamma ^\prime$-Fe$_4$N.[21,30,31] For recrystallization and N presaturation, the same furnace as for the nitrocarburizing experiments described below was used.

The Fe-C substrates were prepared by casting an Fe-C alloy with nominal composition corresponding to the composition in the binary system Fe-C,[32] into an ingot of the same dimensions as indicated above for the Fe-N specimens. The real C content of the Fe-C ingot was determined by chemical analysis as 0.63 wt pct (2.86 at. pct), smaller than the eutectoid composition of approx. 0.8 wt pct, due to loss of C during casting. Cold-rolling, cutting, grinding, and polishing were performed similar as for the preparation of the Fe-N substrates and as described above. The substrates were then fused in quartz vials containing 2 × 10⁴ Pa Ar at room temperature to prevent oxidation. The specimens were treated at 1273 K (1000 °C) and afterwards cooled by putting the quartz vial on a metallic surface in air at room temperature, resulting in a very fine pearlitic microstructure.

The nitriding (upon preparing the Fe-N substrates) and nitrocarburizing treatments were performed in a quartz-tube furnace at atmospheric pressure. This furnace is equipped with supplies for H$_2$, NH$_3$, CO, CO$_2$, CH$_4$ (not used in the present work), H$_2$O, and N$_2$ (as an inert filler gas). The partial pressures of these gases can be controlled by mass-flow controllers. By using a high flow rate of 500 ml min$^{-1}$ (determined at room temperature) in the furnace, the equilibria in the gas phase can be controlled. In an ideal case, equilibrium at the surface of the specimen or at least a steady state[31,33] leading to constant N (and C) concentration(s) in the substrate at the surface can, therefore, be achieved. The equilibria are thermodynamically characterized by the N and C activities or in technical terms the nitriding and carburizing potentials which are proportional to the activities.[34,35]

The N-saturated iron specimens were treated in a so-called uncontrolled nitrocarburizing atmosphere, i.e., a certain amount of CO gas was added to a nitriding (NH$_3$/H$_2$) atmosphere. In this way, the N activity is well-defined, whereas the C activity cannot be defined.[36] This type of atmospheres is known to produce pure cementite ($\theta$) layers on pure iron[36] and, at the N activities also applied in the present work, $\theta /\varepsilon$ double layers on N-saturated $\alpha$-iron.[33] The concentration variation in these double layers complies with the schematic diffusion path¹ labeled N in Figure 2 (drawn in a phase diagram calculated with data from Reference 22): starting at the surface with $\theta$ and proceeding to larger depths, i.e., skipping the $\varepsilon +\theta$ two-phase field along a tie line, progressing steeply through the $\varepsilon$ single phase field and skipping the $\alpha$+$\varepsilon$ two-phase field along a tie line to arrive at the $\alpha$ substrate. The atmospheres used for these experiments and the resulting N activities are shown in Table II. The parameters for each experiment (N1 to N4) have been gathered in Table III.

Fig. 2

Schematic diffusion paths for the N and C experimental series and the $\varepsilon$/$\gamma ^\prime$/$\varepsilon$ layer discussed in Section VI–C drawn in the phase diagram of the system Fe-N-C at 853 K (580 °C). Dashed lines indicate skipping of a two-phase or three-phase field. The phase diagram was calculated using the model described in Ref. [22]

Table II Gas Atmospheres Used for Nitrocarburizing of the Fe-N and Fe-C Specimens at 853 K (580 °C)

Table III Overview of Experimental Parameters of the Nitrocarburizing Experiments at 853 K (580 °C) of the N and C Series

The Fe-C specimens were treated in controlled nitrocarburizing atmospheres in which all relevant nitriding and nitrocarburizing equilibria are adjusted such that the C activities pertaining to the Boudouard reaction

$$\begin{aligned} 2{\text{CO}} \rightleftharpoons {\text{CO}}_2 +[{\text{C}}] \end{aligned}$$

(18)

and the heterogeneous water–gas reaction

$$\begin{aligned} {\text{CO}} +{\text{H}}_2 \rightleftharpoons [{\text{C}}] +{\text{H}}_2{{\text{O}}} \end{aligned}$$

(19)

(with [C] denoting C dissolved into iron) are all (forced to be) equal.[34,35] This treatment results in thick, almost pure $\varepsilon$ layers growing evenly into the substrate at the N and C activities used in the present work. The schematic diffusion path (labeled C in Figure 2) starts in the $\varepsilon$ single phase field and progresses through it until reaching the corner of the $\alpha$+$\varepsilon +\theta$ three-phase field. At the specific temperature concerned, 853 K (580 °C), only at this single point in an isothermal section of the ternary Fe-N-C phase diagram, defining the N and C concentrations in the $\varepsilon$ phase, the three-phase equilibrium of the $\varepsilon$ layer with the $\alpha +\theta$ substrate is possible. Thus, if $\varepsilon$ is in equilibrium with the $\alpha +\theta$ substrate, the diffusion path must pass through this point (at a single depth in the specimen; the $\alpha +\varepsilon +\theta$ equilibrium is non-variant at constant pressure and temperature) before skipping over the three-phase field to reach the $\alpha +\theta$ two-phase field at the (original) bulk composition of the substrate. The atmospheres used for these experiments and the corresponding N and C activities are also shown in Table II. The parameters for each experiment (labeled C1 to C5) have been gathered in Table III.

Qualitative phase analysis of the specimens was performed by XRD, Bragg–Brentano $\theta -\theta$ geometry, employing a Philips X’Pert MPD equipped with a Co tube and a secondary monochromator, selecting the Co $K_\alpha$ radiation. The resulting diffractograms were analyzed by Rietveld refinement using structure models for all considered phases (see Table I). This was done in favor of using peak-position databases because of the strongly varying (composition-dependent) values of the lattice parameters of the $\varepsilon$ phase.

For light microscopic analysis of the nitrocarburized specimens, a part cut from each specimen was electrolytically coated with Ni in a Watt’s bath, to produce a ductile protective layer on top of the brittle compound layer, embedded in resin, ground and polished (final stage 1$\mu$m diamond suspension), and finally etched with 1 pct Nital containing some HCl according to References 40 and 41. Some specimens were also treated with Groesbeck solution, i.e., an alkaline KMnO$_4$ solution which stains C-rich phases.[42] Thereby, the distinction of $\theta$, $\varepsilon$ , and $\gamma^\prime$ (in decreasing order of C content) is facilitated. From the micrographs, the positions of the (sub)layer boundaries, corresponding to the difference of flux Eqs. [5] through [7], were measured following a procedure provided by the software Olympus Stream. This measurement process involved manual selection of the surface and the sublayer boundaries. About 100 laterally equidistant measurements of these boundary positions (relative to the defined surface) were made on each micrograph. For each specimen, at least three micrographs were used in this process, resulting in at least 300 single measurements for the determination of each averaged sublayer-boundary position value.

For EPMA measurements, the same cross-sectional specimens as used for the light microscopic analysis were used but the etching steps were left out. The instrument used was a Cameca SX 100 equipped with five WDS spectrometers. The three elements Fe, N, and C were determined simultaneously, using pure $\alpha$-Fe, a $\gamma ^\prime$-Fe$_4$N layer, and a $\theta$-Fe$_3$C layer as standards. Inclusions of small, single $\gamma ^\prime$ grains in the $\varepsilon$ (sub)layer, visible in the SEM image taken from the cross-section prior to the EPMA measurement, were avoided during the measurement. In order to reduce the C contamination from decomposition of organic molecules in the residual gas by the electron beam, an oxygen jet was applied to the cross-sectional specimen surface for 40 seconds before each point measurement and a cold plate was present in the specimen chamber.[43] Even with these decontamination methods, the amount of C determined by EPMA is still too high and has to be corrected. The correction factor is determined by measuring the apparent C concentration on the C-free center of the N-saturated $\alpha$-Fe specimens and on the pure Fe standard for the Fe-C specimens. From the ratios of the intensities of the characteristic X-ray lines of the considered elements (corrected by a background measurement) and the corresponding intensities measured from the standards (pure Fe for Fe, $\gamma ^\prime$-Fe$_4$N for N, and $\theta$-Fe$_3$C for C), the mass fractions of Fe, N, and C were calculated using the $\Phi (\rho z)$ approach.[44] The step size of the scans perpendicular to the original surface of the specimen was chosen from 1 to 2 $\mu$m, depending on the thickness of the layers. For every specimen, at least three concentration-depth profiles for Fe, N, and C, each, were measured.

5 Results

5.1 Microstructure, Layer Thickness, and Kinetics

Exemplary micrographs of cross-sections of the compound layers resulting from nitrocarburizing treatments of both types of substrates are presented in Figure 3. For the N series, the resulting microstructure consisted of a $\theta$/$\varepsilon$ double layer in direct contact with the N-saturated $\alpha$-iron substrate. For the C series, the resulting microstructure consisted of a pure $\varepsilon$ layer in contact with the pearlitic $\alpha$+$\theta$ substrate; sometimes inclusions of tiny $\gamma ^\prime$ grains occurred in the middle of the compound layer, which were neglected in the evaluation. A variation of treatment parameters of the C series (increase of $a_{\text{C}}$, decrease of $a_{\text{N}}$) led to decomposition of the $\varepsilon$-iron carbonitride especially in the surface-adjacent regions and a porous carbide (mainly $\theta$) sublayer emerged close to the surface of the specimen (cf. Reference 45). These specimens were not included in the evaluation.

Fig. 3

Light microscopical micrographs of cross-sections of compounds layers resulting from the nitrocarburizing treatments in the present work, after etching with Groesbeck’s reagent. (a) N series. The compound layer consists of a $\theta$ sublayer on top of an $\varepsilon$ sublayer in direct contact with the N-saturated $\alpha$-iron substrate. (b) C series. The compound layer solely consists of an $\varepsilon$ layer in contact with the fine pearlitic ($\alpha$+$\theta$) substrate. In some cases, a few tiny $\gamma ^\prime$ grains had formed in the middle of the compound layer

The values determined for the positions (depths) of the sublayer boundaries have been gathered in Table IV. By solving Eq. [16] for $k$ and inserting the determined corresponding values of treatment times and layer-boundary positions, the (parabolic) growth constants were determined. This last procedure was also performed for the experiments N1 to N3 to sensitively account for a possible change in the conditions between the experiments although a common parabolic growth constant was found to provide an acceptable fit to the experimental data by a straight line in Figure 4. Hence, the velocities of the layer boundaries, at the treatment times of the (sub)layer-depth measurements, could then be determined by differentiating Eq. [16]. These kinetic data are also shown in Table IV.

Fig. 4

Plot of the squared positions of the $\theta$/$\varepsilon$ and $\varepsilon$/$\alpha$ interfaces $(x^{\theta /\varepsilon })^2$ and $(x^{\theta /\varepsilon })^2$, as measured from specimens N1 to N3, vs the treatment time $t$. Note the different scale for $(x^{\theta /\varepsilon })^2$ and $(x^{\theta /\varepsilon })^2$. The solid lines represent a fit of the data according to a parabolic growth law (cf. Eq. [16]); the dashed lines describe the experimental data according to a modified parabolic growth law (cf. Eq. [17])

Table IV Interface Positions $x^{\theta /\varepsilon }$ and $x^{\varepsilon /\alpha }$ as Determined for the N and C series Experiments, Parabolic Growth Constants $k$ (Assuming $x^2=k\cdot t$, cf. Eq. [16]), and Boundary Velocities $v={\text{d}}x/{\text{d}}x$ at the Time of the End of the Experiments

5.2 Concentration-Depth Profiles in the $\varepsilon$ (Sub)layers

From the mass fractions of Fe, N, and C determined by EPMA as function of depth in the $\varepsilon$ (sub)layer, the molar fractions were calculated by assuming that the only constituents of the examined layer material are Fe, N, and C. From these values, the C correction, typically around 1.6 at. pct, was subtracted (cf. Section IV).² After normalizing the values again to 100 at. pct, the $u$-fractions were calculated (cf. Eq. [14]) and plotted.

The (sub)layer boundaries are represented by steps in the $u$-fraction-depth profiles of both N and C. Thus, by inspection of the plots of the $u$-fraction-depth profiles, the positions of the (sub)layer boundaries can be defined. Additionally, for determining the position of the surface, the sum of the mass fractions of the determined elements Fe, N, and C can be taken as an indicator, being below 100 wt pct in the protective Ni layer.

For the (at least) three plots of the $u$-fraction-depth profiles of N and C, these layer-boundary positions may differ somewhat as the layer boundaries are not truly flat (see Figure 3). To handle this problem, the depth coordinate of each single $u$-fraction-depth profile of N and C was normalized with respect to the local layer thickness.

Typical $u$-fraction-depth profiles for the N and the C series are shown in Figure 5. For the N series, the $u$-fraction of N is almost constant over the whole layer. The $u$-fraction of C decreases with increasing depth. The profiles of both elements depend linearly on depth, allowing application of Eq. [9].

Fig. 5

Typical $u$-fraction-depth profiles of N and C in the $\varepsilon$ (sub)layer calculated (cf. Eq. [14]) from the mass-fraction-depth profiles as measured by EPMA. The full lines drawn through the experimental data points are the plots of the (linear or error) functions which were fitted to the experimental data. The depth coordinate was normalized with respect to the local layer thickness. (a) N series. The N and C contents depend linearly on depth. (b) C series. The N profile depends linearly on the depth; the C profile shows strong curvature. The N and C $u$-fraction-depth profiles show pronouncedly negative depth gradients

For the C series, the $u$-fraction-depth profiles of both elements show a distinct, negative depth gradient. This is remarkable recognizing that the substrate initially is already (relatively) rich in C. For the fit of the $u$-fraction-depth profile of N, in all cases a linear function could be fitted justifiably, allowing application of Eq. [9]. The $u$-fraction-depth profile of C shows a strong curvature in some cases. Therefore, the error function with curvature parameter $w_{\text{C}}$ (cf. Eq. [10]) was fitted in these cases, allowing application of Eq. [11].

Values derived from the fits to the $u$-fraction-depth profiles of the $\varepsilon$ (sub)layers have been gathered in Table III. For the N series, this includes the $u$-fractions of N and C in $\varepsilon$ at the $\theta$/$\varepsilon$ interface and at the $\varepsilon$/$\alpha$ interface; for the C series, the $u$-fractions of N and C in $\varepsilon$ at the specimen surface and at the $\varepsilon$/$\alpha$+$\theta$ interface, and, if applicable, the curvature parameter $w_{\text{C}}$ of the C $u$-fraction-depth profile has been determined.

5.3 Fluxes at Upper and Lower Boundaries of the $\varepsilon$ (Sub)layers

By using the difference of flux equations [5], [6], [9], and [11] given in Section III and the measured data for the concentrations of N and C at both boundaries of the $\varepsilon$ (sub)layer, (if applicable) for the curvature parameter $w_{\text{C}}$, and for the interface velocities, the flux differences at and between the upper and the lower boundary of the $\varepsilon$ (sub)layer can be calculated for each specimen/experiment. Then, from these data, the fluxes of N and C in $\varepsilon$ at the upper and lower (sub)layer boundaries can be determined by departing from the flux into the substrate (see what follows directly below) and subsequently adding up the previously calculated flux differences.

For the N series, the flux of N into the substrate is zero because the substrate was already initially saturated with N; the flux of C into the substrate can be assumed to be zero in all cases because of the very small C solubility in $\alpha$-iron. For the N concentration in the substrate, the maximum solubility of N in the binary Fe-N system in equilibrium with $\gamma ^\prime$ as calculated with data from Reference 21 was used ($x_{\text{N}}=0.0036$ at 853 K (580 °C) and 101,325 Pa (1 atm)), being closer to the gravimetrically determined N contents of the substrate than the value for the phase boundary $\alpha$/$\alpha$+$\gamma ^\prime$ in Reference 31.

For the C series, the C concentration in the substrate was assumed to remain constant at the initial value, i.e., at $x_{\text{C}}=0.0286$, implying zero flux of C into/out of the substrate. The N flux into the substrate was calculated using Eq. [12] adopting a value for the diffusion coefficient of N in $\alpha$-iron according to Reference 5. Hereby, the reduction of the diffusion cross-section due to the volume fraction of $\theta$ in the substrate (approx. 10 pct) was ignored and the volume per mole Fe of the $\alpha$+$\theta$ substrate (used for calculating the concentrations after Eq. [15]) was assumed to be equal to the volume per mole Fe of pure $\alpha$-iron.

The thus obtained values for the fluxes at the upper and lower layer boundaries of the $\varepsilon$ (sub)layers (pertaining to the finishing time of the corresponding experiment) for both the N and C series experiments have been listed in Table V.

Table V The Fluxes of N and C at the Top and the Bottom Interfaces of the $\varepsilon$ layer ($j={\theta }$ for N1 to N4, $j={\text{S}}$ for C1 to C5) as Determined for the N and C Series Experiments in $10^{-6}\,{\text{mol}}\,{\text{m}}^{-2}\,{\text{s}}^{-1}$ and Average Molar Fractions of N and C in the Corresponding $\varepsilon$ (Sub)layers

5.4 Diffusivity Matrix

With the calculated fluxes for each specimen at the $\varepsilon$ (sub)layer interfaces and the corresponding concentration gradients (determined by differentiation of either Eqs. [8] or [10]), the coefficients of the straight lines as defined by Eq. [4] can be calculated. Then the graphical evaluation as described in Section II can be performed. Such results for the upper interface of the $\varepsilon$ (sub)layer, i.e., the $\theta$/$\varepsilon$ interface for the N series and the surface for the C series, are presented in Figure 6.

Fig. 6

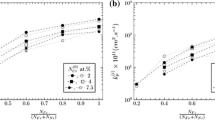
Plots of $D_{\text{NC}}$ vs $D_{\text{NN}}$ and $D_{\text{CN}}$ vs $D_{\text{CC}}$. The straight lines represent relationships (cf. Eq. [4]) as determined for all experiments of the N and C experimental series, following the evaluation method as proposed in Section II. The evaluation was performed at the upper boundary of the $\varepsilon$ (sub)layer, i.e., the boundary with the $\theta$ sublayer for the N series and the surface of the specimen for the C series. The likely possible values for the components of the diffusivity matrix pertaining to the concentration range covered by all experiments of the N and C series have been indicated by the dashed encircling lines. In a second stage, these components were refined, starting with values of the components given as the centroids of the encircled areas, see Section V–D. The final values for the components of the diffusivity matrix have been indicated with circles

Looking at the plots of $D_{\text{NC}}$ vs $D_{\text{NN}}$ and $D_{\text{CN}}$ vs $D_{\text{CC}}$ in Figure 6, containing one straight line for each experiment of both the N and the C series, there appears no single well-defined solution for all four components of the diffusivity matrix owing to the strong concentration dependence of the effective values of the components of the diffusivity matrix and also the experimental errors accumulating over the process of the evaluation (see Section II). However, as also made clear in Section II, it is possible to define a point in each plot that represents approximate values for the corresponding components of the diffusivity matrix, valid for the concentration range comprised by all experiments. Thus, the area of most probable possible solutions, i.e., the area in which most of the (physically meaningful) intersection points of the straight lines accumulate, has been indicated with dashed encircling lines in each of the two plots in Figure 6. The coordinates of the centroids of these areas have been taken as the most likely values of the components of the diffusivity matrix. Note that in Figure 6(a), all intersection points with a negative value of $D_{\text{NC}}$ have been excluded. This is due to a physical restriction: since $D_{\text{CN}}$ is clearly positive (cf. Figure 6(b)), the mathematical sign of $D_{\text{NC}}$ must also be positive due to the equality of mixed partial derivatives, cf. Eq. [2]. This is discussed in detail in Section VI–B.

In a second step, the preliminary values of the components of the diffusivity matrix were further refined by iteratively minimizing the difference of (i) the fluxes calculated, using Fick’s first law, with the (to be refined) components of the diffusivity matrix and the experimentally determined concentration-depth gradients of N and C and (ii) the fluxes calculated using the equations given in Section III and the experimentally determined boundary concentrations, and, if applicable, the curvature parameter of the C concentration-depth profiles and growth constants. The thus determined final values for the diffusivity matrix, as given by

$$\begin{aligned} D(853\,{\text{K}})&=\left(\begin{array}{ll} D_{{\text{NN}}}&D_{{\text{NC}}}\\ D_{{\text{CN}}}&D_{{\text{CC}}} \end{array}\right)\\ &=\left( \begin{array}{ll}50&4.9\\ 4.9&5.5\end{array}\right) \, \times \, 10^{-15}\,{{\text{m}}}^{2}\,{{\text{s}}}^{-1}, \end{aligned}$$

(20)

have been indicated in Figure 6.

A similar evaluation for the lower boundary of the $\varepsilon$ layer, i.e., the interface with the substrate for both experimental series, did not lead to well-defined results. This is due to the very small concentration gradient of C at the lower boundary for the profiles which were described with an error function (cf. Eq. [10]), leading to extremely steep slopes of the straight lines in the plot of $D_{\text{NC}}$ vs $D_{\text{NN}}$ and extremely flat slopes of the straight lines in the plot of $D_{\text{CN}}$ vs $D_{\text{CC}}$.

The graphical evaluation method used in the present work is mathematically equivalent to numerical solution of the system of linear equations defined by Eq. [4] with $D_{\text{NN}}$, $D_{\text{NC}}$, $D_{\text{CN}}$ and $D_{\text{CC}}$ as the unknown, independent variables. The advantage of the proposed graphical evaluation is the simplicity of performing a test for the validity of the assumptions and a corresponding estimation of the error in the obtained values. This error estimation can be done in (at least) two ways: (i) By introducing variations of the parameters in Eq. [4], the straight line of possible solutions for each set of conditions becomes a set of straight lines comprising an area of possible solutions. (ii) Already the area of accumulation of intersection points, as indicated in both plots in Figure 6, as a result of experimental over-determination (more than two sets of experimental conditions subject to the same values of the intrinsic diffusion coefficients), allows error estimation from the size of these accumulation areas.

Thus, following approach (ii), looking at the indicated areas in Figure 6, for $D_{\text{NN}}$ and $D_{\text{CC}}$, an error of approx. 20 pct can be estimated, leading to $D_{\text{NN}}=(50\pm 10)\, \times \, 10^{-15}\,{\text{m}}^{2}\,{\text{s}}^{-1}$ and $D_{\text{CC}}=(5.5\pm 1.0)\, \times \, 10^{-15}\,{\text{m}}^{2}\,{\text{s}}^{-1}$. For $D_{\text{CN}}$, the error can be estimated at approx. 20 pct or less, leading to $D_{\text{CN}}=(4.9\pm 1.0)\, \times \, 10^{-15}\,{\text{m}}^{2}\,{\text{s}}^{-1}$. Figure 6 indicates that $D_{\text{CN}}$ has the most well-defined solution; $D_{\text{NC}}$ is the least well-defined component in the present evaluation (note the scales of the coordinates of Figure 6).

6 Discussion

6.1 Merits and Limitations of the Model and the Evaluation Method

The concentration-depth profiles especially in the thick pure $\varepsilon$ layers growing into the pearlitic substrates (C series) show relatively large gradients in both the N and C content at the surface (e.g., see Figure 5). The strong curvature in the C concentration-depth profiles of the C series is a consequence of the high C content of the substrates used for the C series: This high C content results in a small C concentration difference at the $\varepsilon$/$\alpha$+$\theta$ interface, leading to a small C flux difference/total flux in $\varepsilon$ at the $\varepsilon$/$\alpha$+$\theta$ interface. Thus, the total flux in $\varepsilon$ at the surface of the specimen is mainly controlled by the flux difference between the upper and lower boundary of the $\varepsilon$ layer. Fick’s first law relates these significantly different fluxes in $\varepsilon$ at the surface and at the $\varepsilon$/$\alpha$+$\theta$ interface to significantly different depth gradients of the C concentration-depth profile in $\varepsilon$ at both interfaces. The thus resulting large difference of the concentration gradients in $\varepsilon$ at the surface and at the $\varepsilon$/$\alpha$+$\theta$ interface implies a significant curvature of the C concentration-depth profile. This curvature was well described in the present work by an error-function-shaped profile with only one profile-shape, fit parameter $w_{\text{C}}$. On this basis, the concentration-depth profiles in case of diffusion in the $\varepsilon$ phase of high C, low N contents were evaluated, whereas until now, only the $\varepsilon$ phase of high-N content (and variable C content) could be analyzed;[24] see also below.

In the present work, parabolic growth with $S_0^2=0$ (cf. Eqs. [16] and [17]) was adopted to describe the (macroscopic) layer-growth kinetics. Then the possible occurrence of, e.g., an incubation time (i.e., $S_0^2<0$), would be a cause of error. The conditions used for the experiments N1 to N3, cf. Table III, are identical except for the treatment time. The squared values of the $\theta$/$\varepsilon$ and $\varepsilon$/$\alpha$ sublayer-boundary positions measured for these specimens (cf. Section IV) are shown in Figure 4. The error bars shown were calculated from the standard deviation of the single measurement points. If a parabolic growth law holds for this series N1 to N3, the experimental data can be represented by straight lines through the origin in a plot of $x^2$ vs $t$ (cf. Eq. [16]), which holds for the experiments N1 to N3 within the accuracy of the measurements: see the solid straight lines in Figure 4. A modified parabolic growth law, i.e., fitting the experimental data according to Eq. [17], does not increase the quality of the fit significantly: cf. the dashed and solid lines in Figure 4. This indicates that also for experiment N4 with similar conditions and the same substrate as used for experiments N1 to N3, a parabolic growth law holds. Additional experiments not shown here with the same conditions as used for the experiment C4 but for different treatment time led to a similar result, indicating that also for the conditions of experiments C1 to C3 and C5, the description of the layer-growth kinetics by a parabolic growth law is justified. The validity of the ideal parabolic growth has two advantages. Firstly, it is possible to use every specimen investigated by EPMA in the evaluation without the need to collect additional kinetic data (e.g., to determine $S_0^2$). Secondly and more importantly, a single experiment suffices to determine the velocities of the migrating interfaces between sublayers and between (sub)layer and substrate, thereby avoiding the problems caused by irreproducible surface conditions: The gas–solid equilibrium at the specimen surface (if established at all, cf. References 1, 31, and 33) is found to be rather labile as compared to the solid–solid equilibria established at interfaces within the solid, leading to the formation of different phases (e.g., cementite, Hägg carbide) upon decomposition of interstitial-rich $\varepsilon$ close to the surface of the specimen; see also Reference 45.

Growth kinetics could also be affected by the formation of pores, nucleating at the grain boundaries in the region of the compound layer that is close to the surface and eventually forming channels through which N and C can be taken up from the gas atmosphere.[45] Figure 3(b) indicates that such pores have formed during the nitrocarburizing treatment. However, own experiments and literature data[46] show that severe pore formation in C-rich $\varepsilon$ is always connected with formation of Fe carbides, e.g., $\theta$ or Hägg carbide. There has been no indication in XRD for the formation of such phases. Furthermore, due to etching, the porosity appears much more pronounced than it actually is. Therefore, the effect of porosity on the nitrocarburizing kinetics can be neglected.

The interface, of the (sub)layer considered, for which the evaluation is performed, is determining for the results of the evaluation (i.e., the components of the diffusivity matrix). It has been made clear in Reference 13 that the diffusivities obtained from (the growth rates of) layers with concentration-depth gradients are always effective diffusivities. Performing the evaluation at another interface (in the present work, the top interface of the $\varepsilon$ (sub)layer was chosen in a considerate manner; cf. Section V–D) implies that other effective diffusivities are determined, i.e., the way the mean value of the diffusivities is defined changes then, cf. Eq. [3b] in Reference 13. Therefore, the values of the components of the diffusivity matrix determined at the top interface/surface and those determined at the bottom interface are principally different.

6.2 N and C Diffusion in the $\varepsilon$ Phase: Comparison with Literature Data

Various temperature dependencies for the effective diffusion coefficient of N in binary $\varepsilon$-iron nitride have been summarized in Reference 14 using data from References 4, 7, 11, and 12. Using these data, for the diffusion coefficient of N in pure $\varepsilon$-iron nitride at 853 K (580 °C), values are obtained between $21\times 10^{-15}\,{\text{m}}^{2}\,{\text{s}}^{-1}$ and $52\times 10^{-15}\,{\text{m}}^{2}\,{\text{s}}^{-1}$. The experimentally determined value at 853 K (580 °C) equals $39.8\times 10^{-15}\,{\text{m}}^{2}\,{\text{s}}^{-1}$ as determined in Reference 14. The here-determined value for $D_{\text{NN}}$ is at the high end of this range.

Values for the diffusivities at 823 K (550 °C) had been presented in Reference 24:

$$\begin{aligned} D(823\,{\text{K}})=\left( \begin{array}{ll} 21.2&19.6\\ 3.6&0.9 \end{array}\right)\, \times \, 10^{-15}\,{\text{m}}^{2}\,{\text{s}}^{-1}. \end{aligned}$$

(21)

The values of the diagonal components of the diffusivity matrix as determined in the present work at 853 K (580 °C) are larger than those at 823 K (550 °C) (cf. Eqs. [20] and [21]), which is in accordance with the expected Arrhenius-type temperature dependence of diffusion coefficients. The difference of the off-diagonal elements at 823 K (550 °C) and 853 K (580 °C), however, cannot be understood on the basis of the temperature difference, 823 K (550 °C) vs 853 K (580 °C); note the decrease of $D_{\text{NC}}$ upon going from 823 K to 853 K (550 °C to 580 °C). This phenomenon can be understood looking at the concentration range covered by the experiments in the present work and in Reference 24. The average molar fractions of N and C in each $\varepsilon$ (sub)layer were determined from the fit of the measured $u$-fraction-depth profiles, as shown in Figure 5, and applying Eq. [14] solved for $x_i$. The results have been listed in Table V for each profile incorporated in the evaluation. The molar fraction range of N and that of C covered by all these $u$-fraction-depth profiles together and the molar fractions of N and C averaged over all these $u$-fraction-depth profiles are shown in Table VI. The diffusivities at 853 K (580 °C) presented in Section V–D pertain to these molar fraction (range) values. The concentration range covered in the experiments considered in Reference 24 extends to much larger N contents and to smaller C contents than as in the present work (see the data in Table VI): a comparison of the concentration ranges investigated in the present work and in Reference 24 is provided by Figure 7, where these concentration ranges have been superimposed on the phase diagrams of the system Fe-N-C at 853 K (580 °C) calculated with data from either Reference 21 or 22.

Fig. 7

Comparison of the N and C concentration ranges for which the diffusivity matrix was determined in the present work and in Ref. [24], superimposed on the Fe-N-C phase diagrams at 853 K (580 °C) and at 101,325 Pa (1 atm) using the model described in Ref. [21] (dotted lines) and as calculated using the model described in Ref. [22] (solid lines). Note that the data from Ref. [24] were determined at 823 K (550 °C). The $\varepsilon$+$\gamma ^\prime$, two-phase area, however, has a very similar shape at both temperatures

Table VI Approximate Concentration Ranges (cf. Figure 7) and Average Concentrations Corresponding to the N and C Series Experiments Performed in the Present Work, and Those Pertaining to the Experiments in Ref. [24]

Both the results obtained in the present work and those obtained in Reference 24, prove that the N (C) flux caused by the concentration-depth gradient of C (N) significantly contributes to the total flux of N (C), indicating strong interactions of N and C in $\varepsilon$-iron carbonitride. Actually, such interactions are already the consequence of only ideal mixing entropy of the interstitially dissolved components, as shown in Reference 24. Thus, for interstitial diffusion of N and C in Fe, the off-diagonal values of the diffusivity matrix cannot be neglected.

Another approach was used in Reference 47. There, the thermodynamic interactions of N and C during interstitial diffusion in $\gamma$-Fe-based alloys (expanded austenite) in technical steels were expressed by introducing effective concentrations, i.e., the hypothetical N (C) concentration that would lead to the same chemical potential of N (C) in a solution of only N (C) in the material as occurring in reality for the real solution of both elements in the material. This enabled the authors of Reference 47 to apply a model[48] that describes the concentration dependence of the diffusion coefficient of C in $\gamma$ to ternary diffusion of both N and C in $\gamma$. However, this requires the assumption of a thermodynamic model for the Fe-N-C phase considered. The main conclusion drawn in Reference 47 is compatible with that of a preceding work[24] and the present rigorous approach: the chemical potentials of each N and C and thus the diffusivities of each interstitially dissolved component are largely influenced by the other element, originating mainly from entropic[24] interactions. Ternary diffusion in the system Fe-N-C cannot be described neglecting these interactions.

Values for the thermodynamic factors connecting the here-determined diffusivities to the self diffusion coefficients of N and C in $\varepsilon$-iron carbonitride (cf. Eq. [2]) can be calculated, using e.g., Thermo-Calc,[49] adopting a concentration-dependent thermodynamic description for the $\varepsilon$ phase in the Fe-N-C system as given in Reference 21 or 22. The values of the thermodynamic factors calculated using the average N and C concentrations pertaining to this study and as listed in Table VI are shown in Table VII. From the data obtained in the present work, it is not possible to directly obtain experimental values of the thermodynamic factors, owing to $D^*_{\text{N}}$ and $D^*_{\text{C}}$ being unknown. However, experimental values for the ratios of the average thermodynamic factors can be calculated by (cf. Eq. [2]):

$$\begin{aligned} \frac{\vartheta _{\text{NC}}}{\vartheta _{\text{NN}}}=\frac{D_{\text{NC}}}{D_{\text{NN}}}\nonumber \\ \frac{\vartheta _{\text{CN}}}{\vartheta _{\text{CC}}}=\frac{D_{\text{CN}}}{D_{\text{CC}}}. \end{aligned}$$

(22)

The experimental values for these ratios have also been given in Table VII. Evidently, the experimental results support the thermodynamic model for the $\varepsilon$ phase as presented in Reference 22. The description in Reference 21 leads to even negative values of the off-diagonal components of the diffusivity matrix, which is not at all compatible with the results obtained here. This important conclusion regarding the thermodynamics of $\varepsilon$-iron carbonitride is consistent with the results presented in Reference 24. Moreover, as follows from Figure 7, if the Fe-N-C phase diagram as calculated on the basis of Reference 21 is adopted, the experimentally determined concentration-depth profiles in the $\varepsilon$ phase would overlap with the $\alpha$+$\varepsilon$+$\theta$ three-phase field, which is physically impossible. Hence, the thermodynamic description of the $\varepsilon$ phase according to Reference 22 is the physically more realistic one.

Table VII Thermodynamic Factors, $\vartheta _{ij}$, and Their Corresponding Ratios, as Calculated Adopting the Model Description of Either Ref. [21] or [22] for the Average Concentrations $\bar{u}_{\text{N}}=0.197$ and $\bar{u}_{\text{C}}=0.062$

On the basis of Figure 6(a), one might argue that the value of $D_{\text{NC}}$ could have a negative sign. However, as briefly mentioned in Section V–D, since $D_{\text{CN}}$ is evidently positive, the mathematical sign of $D_{\text{NC}}$ also must be positive, as follows upon inspection of Eq. [2]: Since all other quantities ($D_i^*$, $c_i$) are necessarily positive, the mathematical sign of $D_{ij}$ is defined by $\partial \mu _i/\partial c_j$. This quantity represents is a second derivative of the Gibbs energy and therefore the equality of mixed partial derivatives holds, immediately leading to the important restriction of equal mathematical signs for the off-diagonal components of the diffusivity matrix.

The ratio of the off-diagonal entries of the diffusivity matrix only contains the ratio of the self diffusion coefficients of both N and C and the (known) ratio of the N and C concentrations (as $\partial \mu _{\text{N}}/\partial c_{\text{C}}=\partial \mu _{\text{C}}/\partial c_{\text{N}}$; see above):

$$\begin{aligned} \frac{D_{\text{NC}}}{D_{\text{CN}}}=\frac{D_{\text{N}}^*}{D_{\text{C}}^*}\frac{c_{\text{N}}}{c_{\text{C}}}. \end{aligned}$$

(23)

As a first approximation, the self diffusion coefficients of N and C in $\varepsilon$-iron carbonitride can be taken to be equal. Then, the ratio of the off-diagonal values of the diffusivity matrix $D_{\text{NC}}/D_{\text{CN}}$ equals the ratio of the average $u$-fractions (or concentrations) $u_{\text{N}}/u_{\text{C}}\approx 3$ (cf. Table VI). The experimental value for $D_{\text{NC}}/D_{\text{CN}}$ is 1. However, considering the experimental error in $D_{\text{NC}}$ and $D_{\text{CN}}$ , the range of experimental values for this ratio is compatible with the above theoretical prediction. Note that an (about) equality of the off-diagonal values of the diffusivity matrix, as determined above, is only by chance; it does not result from physical requirements.

6.3 Application to Other Microstructures

Upon pure nitriding at conditions characterized with $a_{\text{N}}=831$, $a_{\text{C}}=0$ (cf. Table II) of the same Fe-C alloy as used for the experiments of the C series, an $\varepsilon$/$\gamma ^\prime$/$\varepsilon$ triple layer was found to grow into the $\alpha$+$\theta$ substrate. In the following, the $\varepsilon$ sublayer adjacent to the surface will be designated as $\varepsilon _1$, whereas the $\varepsilon$ sublayer adjacent to the substrate will be designated as $\varepsilon _2$. A micrograph of a cross-section through this layer structure is shown in Figure 8. The corresponding N and C $u$-fraction-depth profiles, as measured by EPMA, are shown in Figure 9. In principle, these $u$-fraction-depth profiles and the additionally measured distances of the layer boundaries to the surface of the specimens can be used to calculate the fluxes of N and C at the layer boundaries of the $\varepsilon$ sublayers, applying the procedure described in Section III. The results are shown in Table VIII.³ This specimen was not used for the evaluation of the diffusivity matrix because of the high porosity of the $\varepsilon _1$ layer, leading to inaccurate concentration measurements by EPMA. Also, due to the formation of channels[45] due to pores that open during the nitriding treatment, N uptake can be influenced. The layer-growth kinetics was found to be less regular than those pertaining to the experiments of the N and C series. However, the data obtained from this specimen can be used to look for consistency with the values of the diffusivity matrix presented in Section V–D, as determined from the N and C series of experiments.

Fig. 8

Light microscopical micrograph (after Groesbeck staining) of a cross-section through the $\varepsilon$/$\gamma ^\prime$/$\varepsilon$ triple layer growing into the $\alpha$+$\theta$ substrate upon pure nitriding. In order to distinguish the upper and lower $\varepsilon$ sublayer, they have been labeled $\varepsilon _1$ and $\varepsilon _2$

Fig. 9

N and C $u$-fraction-depth profiles as measured by EPMA on a cross-section of the $\varepsilon$/$\gamma ^\prime$/$\varepsilon$ triple layer specimen produced by pure nitriding ($a_{\text{N}}=831$; $a_{\text{C}}=0$) of pearlitic Fe-C substrates identical to those used for the C series of experiments. As in Figure 8, the upper and lower $\varepsilon$ sublayer have been labeled $\varepsilon _1$ and $\varepsilon _2$. The $x$ coordinate, i.e., the total local layer thickness, was scaled with respect to the average total compound layer thickness as measured by light microscopy. The vertical lines have been drawn at the average position of the corresponding interfaces between the sublayers

Table VIII N and C Fluxes in $10^{-6}\,{\text{mol}}^{-6}\,{\text{m}}^{-2}\,{\text{s}}^{-1}$ in the Upper ($\varepsilon _1$) and Lower ($\varepsilon _2$) $\varepsilon$ Sublayer of the $\varepsilon$/$\gamma ^\prime$/$\varepsilon$ Triple Layer Growing into a Pearlitic Fe-C Substrate Upon Pure Nitriding

The N and C concentration-depth profiles of the lower $\varepsilon$ layer, labeled $\varepsilon _2$ in Figure 9, depend linearly on depth within experimental accuracy. Recognizing that the purely nitriding atmosphere applied in this experiment has a strong decarburizing character, due to its H$_2$ content (formation of CH$_4$), the occurrence of a negative gradient for also the component C is surprising. This phenomenon can be explained as a consequence of the rejection of C by the $\gamma ^\prime$ sublayer growing on top of the $\varepsilon _2$ sublayer as the solubility of C in $\gamma ^\prime$ is very low (max. 0.63 at. pct at 853 K (580 °C) as calculated using the model in Reference 21; the model given in Reference 22 assumes that C cannot be dissolved in $\gamma ^\prime$). This effect is also revealed by the positive value of the flux of C in this lower sublayer, see Table VIII.

The fluxes (i) as calculated from the experimental data for the $\varepsilon _1$/$\gamma$/$\varepsilon _2$ specimen using the flux equations from Section III, and those (ii) as calculated by Fick’s first law, using the N and C concentration-depth gradients pertaining to the $\varepsilon _2$ sublayer and the values for the diffusivity matrix as determined in the present work from experiments of the N and C series, can be compared in Table VIII. It follows that the both sets of flux values are comparable for the lower, $\varepsilon _2$ sublayer. The average N and C concentrations in this $\varepsilon _2$ sublayer ($x_{\text{N}}={14.4}\,{{\text{at.}}\,{\rm pct}}$ and $x_{\text{C}}={4.7}\,{{\text{at.}}\,{\rm pct}}$) are close to the average concentrations in the $\varepsilon$ layers of the N and C series, so that it can be expected that the diffusivities of Eq. [20] are good approximations for also those of the $\varepsilon _2$ sublayer (cf. discussion on effective diffusion coefficient in Section VI–B).

In the upper $\varepsilon$ sublayer, labeled $\varepsilon _1$ in Figure 9, the N content is very high and the C content is very low (on average $x_{\text{N}}={23.7}\,{{\text{at.}}\,{\rm pct}}$ and $x_{\text{C}}={0.3}\,{{\text{at.}}\,{\rm pct}}$). The depth gradient of the C content is positive, i.e., the C content increases from the surface to the substrate. This corresponds with a negative flux of C as derived from the experimental data of the $\varepsilon _1$/$\gamma ^\prime$/$\varepsilon _2$ specimen (see flux data in Table VIII). The fluxes calculated by application of Fick’s first law, using the N and C concentration-depth gradients pertaining to the $\varepsilon _1$ sublayer and the values for the diffusivity matrix as determined in the present work from the experiments of the N and C series, now largely deviate from the fluxes calculated from the experimental data for the $\varepsilon _1$/$\gamma ^\prime$/$\varepsilon _2$ specimen using the flux equations from Section III. This is an obvious consequence of the average N and C concentrations in this $\varepsilon _1$ sublayer being incompatible with the concentration ranges pertaining to the values compatible with the diffusivity matrix (cf. Table VI). For such low values of C concentration as in the $\varepsilon _1$ sublayer, the component $D_{\text{CN}}$ should be close to zero (see Eq. [2]). Hence, the flux of C in the $\varepsilon _1$ sublayer is predominated by the C concentration-depth gradient and not the N concentration-depth gradient, explaining the negative sign of the C flux.

On the other hand, in the $\varepsilon _1$ sublayer, the flux of N as calculated using Fick’s first law is much higher than the flux of N as calculated using the flux equations, see Table VIII. At such low C concentrations, the component $D_{\text{NC}}$ of the diffusivity matrix is expected to reach a value so high that already the small positive gradient present in the C concentration-depth profile significantly decreases the flux of N. This interpretation is supported by the magnitude of the value of $D_{\text{NC}}$ as determined in Reference 24 (cf. Eq. [21]) resulting from an analysis of $\varepsilon$ layers containing much less C than the $\varepsilon$ layers examined in the present work: in that case, $D_{\text{NC}}$ was nearly as large as $D_{\text{NN}}$ in Reference 24.

7 Conclusions

• 1. A straightforward, graphical procedure to determine the four intrinsic diffusion coefficients governing the simultaneous diffusion of N and C in a host lattice is possible utilizing experimentally determined concentration-depth profiles of N and C (e.g., measured by EPMA) and (parabolic) layer-growth constants (e.g., determined by light microscopy).

• 2. The diffusivity matrix thus determined for the diffusion of N and C in $\varepsilon$-iron carbonitride, for N contents of approx. $14\ldots {17}\,{{\text{at.}}\,{\rm pct}}$ and C contents of $4\ldots {6}\,{{\text{at.}}\,{\rm pct}}$, at 853 K (580 °C) and at 101,325 Pa (1 atm) is given by $D_{\text{NN}}=50\, \times \,10^{-15}\,{\text{m}}^{2}\,{\text{s}}^{-1}$, $D_{\text{NC}}=4.9\, \times \,10^{-15}\,{\text{m}}^{2}\,{\text{s}}^{-1}$, $D_{\text{CN}}=4.9\, \times \,10^{-15}\,{\text{m}}^{2}\,{\text{s}}^{-1}$ , and $D_{\text{CC}}=5.5\, \times \,10^{-15}\,{\text{m}}^{2}\,{\text{s}}^{-1}$.

• 3. The here-determined values of the off-diagonal components of the diffusivity matrix imply a pronounced influence of the N (C) concentration-depth profile on the C (N) flux: the off-diagonal values of the diffusivity matrix cannot be neglected at all for diffusional calculations, e.g., simulations of layer-growth kinetics.

• 4. Analysis of (ratios of) thermodynamic factors derived from the components of the diffusivity matrix indicates that the thermodynamic interaction of N and C on the same sublattice for the Fe-N-C system is better described by the thermodynamic model of Reference 22 than that of Reference 21.