1 Introduction

Functionally graded materials (FGMs), which have been developed widely in recent decades, can help researchers overcome the shortcomings of composite materials with jumps in material properties.[1] In this area, functionally graded steels (FGSs) are a special group of FGMs with elastic-plastic behavior. Some researchers have studied the fracture characteristics of specimens with this kind of material distribution.[2] For example, Bezensek and Hancock obtained the fracture toughness and the Charpy impact resistance of FGSs produced by the laser welding process.[3] Aghazadeh and Shahossini produced another type of FGSs from austenitic stainless and ferritic steels by means of the electroslag remelting (ESR) process.[4]

During the past decades, FGSs with different configurations have been produced and their tensile behavior has been experimentally studied and simulated considering the Vickers microhardness profile of over the material variation direction.[5] Recently, the Vickers microhardness profile of αβγ FGSs was predicted using the theory of mechanism-based strain gradient plasticity (MSG).[6] In this regard, the dislocation density of each layer in the graded region is related to the Vickers microhardness of the layers. Afterward, the tensile strength,[7] Charpy impact energy,[8] fracture toughness,[9] and behavior of notched structures[10] made of functionally graded steels were analytically obtained by MSG theory. Nevertheless, limited work was done to investigate the hot working characteristic of FGSs. Only in Reference 11 is the mean flow stress of FGSs under hot compression assessed based on a combination of constitutive equations and a mixtures rule based model. This work was related to the parameter of the compression strain to the strains of each individual layer of FGSs considering the variation of volume fractions at each layer. Even though this assumption was justified for αβγ and γMγ FGSs, the results were limited to a compressive strain of 0.5.[11]

Hot deformation behavior of metals and their alloys has major importance in the proper design of instrumentations for large deformation processes such as hot rolling, forging, and extrusion. Recently, the finite element method was widely used to study the material forming process. This numerical simulation may be reliable when proper stress-strain relationships are used to model the forging process of mechanical elements under appropriated loading conditions.[12,13] It must be noted that the forming temperature and strain rate change the hardening and softening mechanisms during the process. In general, higher strain rates and lower temperatures increase the resistance of plastic deformation and make the flow stress higher. Accordingly, the effects of these parameters are usually studied simultaneously. Therefore, much effort has been put into predicting good constitutive equations based on metallurgical factors to describe the plastic deformation of materials during hot deformation processes. This is always developed based on the deformation parameters including the strain, the strain rate, and the temperature.[14–17]

In this work, we tried to investigate the influence of strain, strain rate, and temperature on the compressive hot working behavior of FGSs with different grading compositions. For this, an empirical model is presented to obtain the flow stress of αβγMγ FGSs that considers the strain compensation. In addition, a theoretical model is presented to assess the flow stress of FGSs under hot compression based on the Zener–Hollomon (Z-H) constitutive model and the mixtures rule. The given data for the flow stress of αβγMγ steels from both methods are verified with the experimental results of other references.

2 Problem Statement

In dealing with hot compression modeling of an isotropic material, some integrated constitutive equations were developed that relate the plastic stress to working parameters such as the strain, strain rate, and temperature.[15,18] The constitutive empirical equations as semianalytical relations require a number of constants, which are basically derived from fitting of experimental data in a single equation to obtain a general unique equation for the stress-strain curve of materials in large strain domains. Because the experiments are difficult to conduct and test instruments are not precise in some cases, a wide range of theoretical results have been obtained based on different constitutive equations even for alloy materials.[19] Therefore, establishing appropriate theoretical models for estimating the flow stress of advanced materials such as FGS in hot deformation conditions regardless of empirical results is very necessary in the design of advanced engineering materials and structures for which the cost of relevant experiments is considerable. In this study, well common Z-H constitutive equations are employed to establish appropriate empirical and analytical models for FGS.

In the fabrication process of FGS by means of ESR, the diffusion of alloy ingredients such as chromium, nickel, and carbon atoms that occurs during the remelting stage controls the distribution profile of the final gradient material and leads to the production of alternating regions with different transformation characteristics. Consequently, the diffusing atoms in this process produce ferritic α and austenitic γ graded regions together with different phases such as bainite β and martensite M within the interface of the initial electrode configuration.[4]

Beside the generalized framework developed in this work, which is applicable for any type of FGSs under hot deformation with a wide range of numerical results, a special attempt is made for αβγMγ FGSs as a case study with complicated configuration. This helps to demonstrate the validity of the developed empirical and analytical methods. Distribution of graded regions together with bainitic and martensitic layers in the mentioned composite under compression test loading is schematically illustrated in the sketch in Figure 1(a). Also, Figure 1(b) illustrates the hardness profile along the height of αβγMγ specimens that is reported in a previous study.[4] From this figure, it is seen that the intermediate austenitic γ′ layer has a different hardness than the primary austenitic γ layer, which must not be overlooked in the analyses.

Fig. 1
figure 1

Configuration of αβγMγ graded specimens: (a) the specimen under compression, (b) hardness profile along the specimen height, and (c) layer’s distribution

Full size image

In Section III, regarding the relationship between the layers’ strain rates and considering the uniform compressive stress distribution along the specimens (Figure 1(c)), the stress-strain curve for each arbitrary hot compression loading condition is obtained by empirical and analytical methods.

3 Constitutive Equations

A good constitutive relation between the strain rate, the flow stress, and the temperature for the high-temperature condition is the well-known Arrhenius equation. In addition, the effects of the temperatures and strain rate on the corresponding deformation behaviors can be described by the Z-H expression introduced as follows[20]:

$$ Z = \dot{\varepsilon }^{\frac{Q}{RT}} $$
(1)

in which \( \dot{\varepsilon } \), Q, T, and R are strain rate, deformation process activation energy (J/mol), absolute temperature (K), and the universal gas constant (8.314 J·mol−1·K−1), respectively. It should be noted that Z is a parameter relating to temperature interactions and strain rate, which is constant for constant temperatures and strain rates. The term exp(Q/RT) specifies the heat activation process and Q shows the speed of atomic mechanism control. On the other hand, some relations have been used to describe the Z parameter as follows[21–25]:

$$ \left\{ \begin{aligned} Z_{1} &= A^{\prime}\sigma^{n} ; \hfill \\ Z_{2} &= A^{\prime\prime}\text{e}^{\beta \sigma } ; \hfill \\ Z_{3} &= A\sinh^{n} (\alpha \sigma ) \hfill \\ \end{aligned} \right. $$
(2)

in which n, A, A′, A″, α, and β are material constants and α = β/n. The first of these relations is suitable for expressing the low stress condition (ασ < 0.8), since in this relation n does not depend on the temperature. The exponential function is suitable for high stress loadings (ασ > 1.2), while the third case in Eq. [2] represents an appropriate description of flow stress in hot deformation loading conditions with high strain rates and also can take into account the creep in low strain rates as a basic concept. It should be noted that the stress-strain exponent in the constitutive equation, n, has an inverse relation to the sensitivity of the problem to the strain rate. The introduced hyperbolic sine function in Eq. [2] is shown to give better results, which are in good agreement with the experimental ones. Therefore, substituting from Eq. [2], Eq. [1] is reduced to the following well-known form for the Z-H expression:

$$ Z = \dot{\varepsilon }\text{e}^{{{\raise0.7ex\hbox{$Q$} \!\mathord{\left/ {\vphantom {Q {{{R}}T}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${{{R}}T}$}}}} = A\sinh^{n} (\alpha \sigma ) $$
(3)

Note that this equation will be used later to characterize the hot working behavior for FGSs.

4 Development of Empirical Expression for αβγMγ FGS

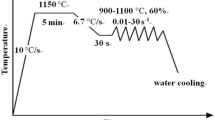
First, it should be noted that in spite of the strain rate, the effect of strain on the stress is not covered in Eq. [3]. In this study, the effect of strain on the material constants of constitutive equations is investigated also as a strain compensation concept. In former investigations, a compression test was carried out on the specimens for αβγMγ FGSs in the temperature range of 1273 K to 1473 K (1000 °C to 1200 °C) and strain rates of 0.01, 0.1, and 1.0 s−1,[26] and we used these data to establish the constitutive equation. The regression analysis of data leads to the determination of Z-H equation constants from the following equation, which is a simplified form of Eq. [3]:

$$ \ln \dot{\varepsilon } = \ln A - \frac{Q}{{{{R}}T}} + n\ln \left( {\sinh (\alpha \sigma )} \right) $$
(4)

Applying linear regression to the empirical data, the slope of ln\( \dot{\varepsilon } -\text{ln}(\text{sinh}(\alpha \sigma))\) curves as representative strain rate–stress curves from Eq. [4] gives the value of n at a constant temperature (Figure 2(a)), which must be determined for characterization of the materials. On the other hand, by applying a simple optimization procedure, the amount of α is calculated so that the empirical lines become parallel, as shown in Figure 2(b). In addition, as another required parameter in Eq. [4], the activation energy Q can be simply obtained at a constant strain rate condition from the following relation:

Fig. 2
figure 2

Variation of flow stress for αβγMγ graded steels obtained from empirical constitutive modeling vs (a) strain rate and (b) temperature

Full size image
$$ Q = n{{R}}\left. {\frac{{\partial \ln \left[ {\sinh (\alpha \sigma )} \right]}}{{\partial T^{ - 1} }}} \right|_{{\dot{\varepsilon }}} $$
(5)

By plotting lnsinh(ασ) vs the inverse of temperature, the average slope of the corresponding curves gives the value of Q/nR. From another viewpoint, the intercept of ln Z-lnsinh(ασ) lines gives the values of ln A. Finally, according to Eq. [3], the flow stress σ can be written as a function of Z parameter:

$$ \sigma = \frac{1}{\alpha }\left\{ {\ln \left( \frac{Z}{A} \right)^{\frac{1}{n}} + \left[ {\left( \frac{Z}{A} \right)^{\frac{2}{n}} + 1} \right]^{1/2} } \right\} $$
(6)

4.1 Compensation of Strain Effect

In order to give a precise prediction with consideration of the influences of compressive strain, here, the material parameters Q, A, α, and n included in the constitutive equations are calculated for different values of strains within the range of 0.05 to 0.5 with increments of 0.05. The values of flow stresses, corresponding strain rates, and the temperatures are substituted into Eqs. [4] and [5] for the strains of 0.1, 0.3, and 0.5 as examples to introduce the solution method for determination of other material constants included in the constitutive model. Finally, the relation between ln\( \dot{\varepsilon } \) and lnsinh(ασ) at constant temperature condition and between lnsinh(ασ) and 1/T at constant strain rate condition is obtained for αβγMγ FGSs, as shown in Figures 2(a) and (b), respectively.

In Figure 2, it is seen that the slopes of the lines vary slightly, and this illustrates that the values of n and Q are not approximately dependent on the magnitude of test temperatures and strain rate. This allows control of the deformation mechanisms of αβγMγ FGSs in real situations relatively similar to the experimental condition. In addition, the corresponding material constants from the developed model are sorted in Table I.

Table I Material Constants Calculated for αβγMγ Composites Under Different Strains
Full size table

On the other hand, from the results, a good correlation is obtained from calculation of Z for the aforementioned strains with the empirical data so that the correlation coefficient is approximately equal to 0.988, as shown in Figure 3. From this figure, it is observed that the experimental data for flow stress at different hot compression conditions are fitted to the hyperbolic sine function satisfactorily.

Fig. 3
figure 3

Regression analysis of experimental data for αβγMγ FGSs considering the Z-H equation of hyperbolic sine function between flow stress and Z parameter for different strains

Full size image

Furthermore, the parameters Q, n, α, and ln A can be related to the true strain of αβγMγ steels by conventional polynomial functions by compensation of the strain, as stated in Eq. [7a, 7b, 7c, 7d]. Next, the results of such polynomial fitting are given in Table II.

Table II Coefficients of Polynomial Fit for Z Equation Parameters of αβγMγ FGS
Full size table
$$ Q = C_{10} + C_{11} \varepsilon + C_{12} \varepsilon^{2} + C_{13} \varepsilon^{3} + C_{14} \varepsilon^{4} + C_{15} \varepsilon^{5} $$
(7a)
$$ n = C_{20} + C_{21} \varepsilon + C_{22} \varepsilon^{2} + C_{23} \varepsilon^{3} + C_{24} \varepsilon^{4} + C_{25} \varepsilon^{5} $$
(7b)
$$ \alpha = C_{30} + C_{31} \varepsilon + C_{32} \varepsilon^{2} + C_{33} \varepsilon^{3} + C_{34} \varepsilon^{4} + C_{35} \varepsilon^{5} $$
(7c)
$$ \ln A = C_{40} + C_{41} \varepsilon + C_{42} \varepsilon^{2} + C_{43} \varepsilon^{3} + C_{44} \varepsilon^{4} + C_{45} \varepsilon^{5} $$
(7d)

From further numerical analysis, the plots of Figure 4 show the value of the mentioned constants vs true strain of the specimens. Form this figure as an early general conclusion; the decrease in Q at higher strains relates to the fact that in this case, the stress increases to overcome the hot deformation resistance of the material while n increases to compensate the reduction of flow stress that returns to the dynamic softening.

Fig. 4
figure 4

Variation of material constants of αβγMγ composites including (a) n, (b) Q, (c) α, and (d) A vs true strain using polynomial curve fitting

Full size image

5 Generalized Constitutive-Based Theoretical Model

The primary objective of this section is to develop a general framework for determination of the stress-strain curve of FGSs under hot compression through an analytical method. In this section, Z-H constitutive equations and the rule of mixtures are employed to establish an appropriate analytical model.

For this purpose, a FGS specimen is divided into many layers in the material grading direction so that each layer with finite thickness is considered as an isotropic homogenous slice. On the other hand, it must be noted that the stress is uniformly distributed along the specimen under compression. The slice’s thickness is chosen so that does not violate 5 units rise or fall in the Vickers hardness along its height. The mean value of Vickers hardness of each slice will be calculated from the following relation where i indicates the layer number:

$$ {\text{VH}}^{(i)} = \frac {1}{2}[{\text{VH}}(x_i)+{\text{VH}}(x_{i-1})]$$
(8)

Here, it is assumed that the strain follows the Reuss expression of the phase mixtures rule for FGSs as follows:

$$ \varepsilon = \sum\limits_{i = 1}^{I} {\varepsilon_{i} f_{vi} } $$
(9)

in which f vi is the volume fractions of the included constituents in the ith layer. The time derivative of this equation for calculation of the strain rate is given as follows:

$$ \dot{\varepsilon } = \sum\limits_{i = 1}^{I} {(\dot{\varepsilon }_{i} f_{vi} + \varepsilon_{i} \dot{f}_{vi} )} $$
(10)

in which \( \dot{\varepsilon } \), \( \dot{\varepsilon }_{i} \), and \( \dot{f}_{vi} \) are the stain rate of the whole specimen, strain rate of the ith layer, and volume fraction variation rate, respectively. Here, it must be noted that most of the researchers have neglected the volume fraction variations in hot deformation processes, which are a physically tangible concept also. Therefore, the second term in each Σ would vanish in Eq. [10]. However, here in the case of FGSs, as demonstrated by Abolghasemzadeh et al. especially because of the presence of a martensitic layer adjacent to the ferritic and austenitic layers, the volume fraction variations along the axial direction must not be neglected. Assuming that the variation of the strain rate and the volume fraction corresponding to each layer is constant during the described hot deformation, a suitable expression for\( \dot{f}_{vi} \) according to the initial volume fraction is stated by the following relation[11]:

$$ \dot{f}_{vi} = \frac{{\dot{\varepsilon }_{i} - \dot{\varepsilon }}}{1 + \varepsilon }f_{vi} = \chi \left( {\dot{\varepsilon }_{i} - \dot{\varepsilon }} \right)f_{vi} \quad \chi = \frac{1}{1 + \varepsilon } $$
(11)

in which χ is a constraint factor that depends only on the specimen total true strain under compressive loadings. By substituting from Eq. [11] in Eq. [10] and reformulating the relations with respect to the strain rate, the following equation is obtained:

$$ \dot{\varepsilon } = \frac{{\sum_{i = 1}^{I} {f_{vi} \dot{\varepsilon }_{i} \left( {1 + \chi \varepsilon_{i} } \right)} }}{{1 + \chi \sum_{i = 1}^{I} {f_{vi} \varepsilon_{i} } }} $$
(12)

The strain ε i corresponding to the ith layer can now be obtained from the Hollomon relation for plastic deformation and Hook’s law for elastic deformation for the relating stress-strain curves[5,7]:

$$ \varepsilon_{i} = \varepsilon_{yi} \left( {\frac{{\sigma_{i} }}{{\sigma_{yi} }}} \right)^{{n^{\prime}_{i} }} = \frac{{\sigma_{yi} }}{E}\left( {\frac{{\sigma_{i} }}{{\sigma_{yi} }}} \right)^{{n^{\prime}_{i} }} $$
(13)

where σ i , σ yi , ε yi , and \( n_{i}^{\prime} \) are the ith layer’s true stress, yield strength, yield strain, and strain hardening exponent, respectively, where E is the Young’s modulus that is assumed constant along the graded direction of FGSs equal to 210 GPa. In the theoretical models for FGMs, it is seen that the material properties such as elastic modules are assumed to vary along the grading direction by exponential, power, or linear functions.[27] Here, in this work, according to the physics of the problem and for proper description of the material grading, the strain hardening exponent n′ is considered to vary exponentially with respect to the layer positions by the following characteristic law in which the subscripts i, 1, and 2 correspond to the ith, first, and last layers of region, respectively[5,7]:

$$ n^{\prime}_{i} = \frac{1}{{x_{2} - x_{1} }}e^{{\frac{{x_{i} - x_{1} }}{{x_{2} - x_{1} }}\ln \frac{{n_{2} }}{{n_{1} }}}} \ln \frac{{n_{2} }}{{n_{1} }} $$
(14)

In the previous study,[11] in order to determine the yield strength distribution along the graded region of FGSs, it is assumed that the yield strength is proportional to Vickers hardness and varies exponentially with the layer position. Next, in the latter works, it is shown that the yield strength σ y of each layer is related to the density of dislocations ρ S of that layer regarding the MSG theory by the following relation[7]:

$$ \sigma_{y}^{i} = \sqrt 3 G\alpha {\mathbf{b}}\sqrt {\rho_{S}^{i} } $$
(15)

where G is the elastic shear modulus, which is taken equal to 80 GPa. In addition, α is an empirical coefficient between 0.2 and 0.5, which is considered equal to 0.3 in this section. Finally, b is the Burger’s vector with a constant value of 0.707a 0 for fcc crystals such as austenitic steels and 0.866a 0 for bcc crystals such as ferritic steels, which are the minimum values of the corresponding Burger’s vector. In these parameters, a 0 is the crystal lattice parameter equal to 2.828R for fcc crystals and 2.309R for bcc crystals, where R is the atomic radius, which is equal to 1.27 Å and for iron. Now, by assuming the exponential characteristic law in the graded region for ρ s , the yield strength of each layer can be determined from the following equation[7]:

$$ \sigma_{y}^{i} = \sqrt 3 \alpha G{\mathbf{b}}\sqrt {\frac{1}{{x_{2} - x_{1} }}e^{{\frac{{x_{i} - x_{1} }}{{x_{2} - x_{1} }}\ln \frac{{\rho_{S}^{2} }}{{\rho_{S}^{1} }}}} \ln \frac{{\rho_{S}^{2} }}{{\rho_{S}^{1} }}} $$
(16)

Next, the density of statistically stored dislocations corresponding to the first and last layers, i.e., \( \rho_{S}^{1} \) and \( \rho_{S}^{2} \), can be obtained simply from Eq. [15] as follows:

$$ \rho_{S}^{j} = \left( {\frac{{\sigma_{y}^{j} }}{{\sqrt 3 G\alpha {\mathbf{b}}}}} \right)^{2} \quad j = 1,2 $$
(17)

The superiority of this approach (Eq. [16]) in comparison with previous ones[17] is that the hardness profile is not required for determination of the yield strength variation in the graded region.

On the other hand, the parameters of the Z-H equation are assumed as a function of layer positions that are defined from the material gradient. The previously introduced parameter, i.e., distribution of ln A, sensitivity of strain rate, and activation energy are evaluated according to the exponential law similar to the description given for the strain hardening exponent (Eq. [14]). In addition, the value of the stress coefficient α is assumed to be constantly equal to 0.01, while its variation is neglected. Therefore, this parameter is considered the same with the ferritic phase α α for all the layers within the ferritic region (i.e. α-β region) and with the austenitic phase α γ for all the austenitic regions (i.e., β-γ and M-γ regions) of FGS specimens in the same manner as Reference 11.

It is worthy to note that the corresponding parameters of the boundary layers must be chosen according to Eq. [7a, 7b, 7c, 7d]. The values of these parameters are determined for α-β and M-γ regions in similar ways, whereas they are known for boundary layers. In contrast, the determination of the parameter for the β-M region that consists of graded austenitic phase γ′ between martensitic and bainitic layers must be treated in a different manner. For the considered configuration of αβγMγ FGSs, the hardness distribution curve in β-γ′ and M-γ′ regions is taken similar to β-γ and M-γ regions, respectively, as given in the following relation:

$$ P_{\beta - M} (x) = \left\{ \begin{array}{ll} P_{\beta - \gamma} , & x < x_{\gamma^{\prime}} \hfill \\ P_{\gamma - M} , & x > x_{{\gamma^{\prime}}} \\ \end{array} \right. $$
(18)

Here, P β-M , P β-γ , and P γ-M represent the distribution function of parameter P in β-M, β-γ, and M-γ regions, respectively. As will be discussed later, this assumption (Eq. [18]) is justified with excellent agreement with experiments and demonstrates that in FGS structures, mechanical property variation follows the pattern of hardness variation precisely. In the next step, after determining the parameters of the Z-H equation for each layer and considering Eq. [3], the strain rate of every layer can be expressed as a function of its corresponding temperature and flow stress from the following relation:

$$ \dot{\varepsilon }_{i} = A_{i} \sinh^{{n_{i} }} (\alpha_{i} \sigma )\text{e}^{{ - {\raise0.7ex\hbox{${Q_{i} }$} \!\mathord{\left/ {\vphantom {{Q_{i} } {{{R}}T}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${{{R}}T}$}}}} $$
(19)

By substituting Eqs. [13] and [19] into Eq. [12], an equation with a single unknown is written for the applied temperature T ap , strain rate \( \dot{\varepsilon }_{ap}, \) and given composite strain ε com as follows, which will be evaluated for calculation of the flow stress for FGSs under general material, loading, and environmental conditions:

$$ \dot{\varepsilon }_{ap} = h(\sigma ,\varepsilon_{\text{com}} ,T_{ap} ) $$
(20)

A wide range of numerical results for the developed method are given in the next section for different types of FGSs with satisfactory discussion about verification of the method for a complicated system.

6 Results and Verifications

6.1 Results for αβγMγ FGSs

As another important numerical example, the results of the theoretical model for the flow stress σ M of αβγMγ are obtained by solving Eq. [20] for various temperatures and strain rates at three different strains, the results of which are given in Figure 5. In addition, Eq. [8] is evaluated for calculation of σ M from empirical constitutive modeling. From this figure, good agreement is observed between the experimental data with the presented numerical results, as shown in Figure 5.

Fig. 5
figure 5

Flow stress for αβγMγ graded steels obtained from constitutive model (σ Z ), theoretical model (σ M ) and experiment at different strain rates and temperatures

Full size image

In this case, the average errors corresponding to empirical and theoretical models are obtained as less than 4 and 9 pct, respectively. In addition, since the interfaces of FGSs fabricated from the same primary electrodes save the material properties,[4] this model can be generalized to other kinds of FGSs such as αβγ and γMγ composites and can give a good prediction of flow stress without having the required empirical results for constitutive modeling. Here, the results are presented for other commonly used configurations of FGS under hot compression to give a general viewpoint on their mechanical and material behavior in severe conditions.

6.2 Results for αβγ and γMγ FGSs

In this section, some examples are given for prediction of the flow stress of FGSs from the developed analytical method. As special cases, αβγ and γMγ three-phase steels are chosen. A similar procedure for calculation of flow stress for αβγMγ is used. For more information, comparison of the results for these examples can give a general viewpoint for calculation of flow stress for αβγMγ and verify the results by those of Section VI–A. Figure 6 gives the variation of the flow stress vs the true strain for αβγ and γMγ steels for different thermal conditions.

Fig. 6
figure 6

Predicted values of flow stress vs the true strain obtained from the analytical model for αβγ and γMγ FGSs for different strain rates and working temperatures: (a) 1273 K (1000 °C), (b) 1372 K (1100 °C), and (c) 1473 K (1200 °C)

Full size image

From this figure, it is seen that we have the maximum value of flow stress at lower values of strain rates for any applied temperature. As another conclusion, it is seen that in general the flow stress is decreased at higher temperatures. In this case, it should be noted that even strain rates equal to unity predict some controversial results, but in a manner, they can predict the impact resistance of FGSs. In addition, from comparison of the results in each plot for αβγ steels (solid lines) and γMγ (dashed lines), it is seen that the first case is lower sensitive to temperature than the latter one. This indicates a different behavior of FGSs at higher temperature that must not be neglected in engineering design purposes.

From figure 6, it is seen that, in general, a higher level of stresses is obtained for γMγ steels in comparison with αβγ ones, which is related to the higher strength of martensite phase in the former case. As an interesting result, even if the martensite phase is brittle with low failure strains, the γMγ steels undertake high level strains that are comparable with those of steel phases. Therefore, providing graded steel phases without step changes in material distribution gives the opportunity to design high strength specimens with higher values of failure strains. In addition, since the αβγMγ steels contain martensite and bainite layers, their compressive strength is obtained between those of γMγ and αβγ steels. In this regard, it is shown that changing the arrangement and thickness of the primary steel phases used to set up the electrodes and heat treatment cycles gives the desirable opportunity to control the material gradient and thickness of the emerging phases during the ESR process and to design an optimal specimen with the required values of strength and yield strain.[4] This is also achievable by changing the length of each grading layer and using the appropriate combination of their material properties.

7 Summary and Conclusions

In summary, the hot compression behavior of FGSs is investigated from both empirical and theoretical models at various prevalent thermal and loading rate conditions. Using experimental stress-strain data for αβγMγ FGSs, the empirical constitutive model is presented so that it includes the temperature and strain rate effects. As a generalized application, this model is established based on strain compensation to describe the plastic flow stress of FGSs. The developed theoretical model considers the boundary layer characteristics and the strain contribution without using the empirical data as an advantage. This model is applicable for any configuration of FGSs produced from the same electrodes. Here, the results are given for αβγ, γMγ, and αβγMγ FGSs at different strains. In order to rely on the presented models, the theoretical and empirical results are verified with experiments of other references with excellent agreement.