Experimental and Numerical Modeling of Segregation in Metallic Alloys

Abstract

Electromagnetic levitation (EML) has been used as an experimental technique for investigating the effect of the nucleation and cooling rate on segregation and structure formation in metallic alloys. The technique has been applied to aluminum-copper alloys. For all samples, the primary phase nucleation has been triggered by the contact of the levitated droplet with an alumina plate at a given undercooling. Based on the recorded temperature curves, the heat extraction rate and the nucleation undercooling for the primary dendritic and the secondary eutectic structures have been determined. Metallurgical characterizations have consisted of composition measurements using a scanning electron microscope (SEM) equipped with energy dispersive X-ray spectrometry and the analysis of SEM images. The distribution maps drawn for the composition, the volume fraction of the eutectic structure, and the dendrite arm spacing (DAS) reveal strong correlations. Analysis of the measurements with the help of a cellular-automaton (CA)–finite-element (FE) model is also proposed. The model involves a new coupling scheme between the CA and FE methods and a segregation model accounting for diffusion in the solid and liquid phases. Extensive validation of the model has been carried out on a typical equiaxed grain configuration, i.e., considering the free growth of a mushy zone in an undercooled melt. It demonstrates its capability of dealing with mass exchange inside and outside the envelope of a growing primary dendritic structure. The model has been applied to predict the temperature curve, the segregation, and the eutectic volume fraction obtained upon single-grain nucleation and growth from the south pole of a spherical domain with and without triggering of the nucleation of the primary solid phase, thus simulating the solidification of a levitated droplet. Predictions permit a direct interpretation of the measurements.

1 Introduction

In the last two decades, the numerical modeling of the solidification of metallic alloys has received great interest.[1] One of the main objectives is to achieve maximum control of the structure and segregation formed upon the solidification processes. Confrontation of such models with measurements is yet rarely completed due to the difficulty of defining model experiments in metallic alloys. Containerless techniques offer an advanced control, because various degrees of nucleation undercooling can be achieved.[2] In addition, the cooling rate, the system geometry and shape (generally spherical), the limited temperature gradient, and the low variation of the heat extraction rate throughout the entire surface of the system within the solidification interval define a suitable experimental model for equiaxed solidification. In the recent past, the atomization process was first proposed by Heringer et al. as an experimental model for the study of segregation induced by equiaxed growth.[3] Prasad et al. extracted a data set from several atomization runs of aluminum (Al)-copper (Cu) alloys consisting of X-ray tomography, neutron diffraction, and stereology.[4,5] However, measurements of the nucleation undercooling of the primary dendritic and secondary eutectic structures were not directly available and had to be estimated from measurements using levitated droplets.[6] Electromagnetic levitation (EML) is indeed a containerless technique that can be seen as a model experiment of equiaxed solidification. Thanks to its combination with in-situ temperature measurements, it can be used to collect information such as the cooling rate prior to and during solidification and the nucleation undercooling of the structures.[2] An analytical segregation model for the prediction of the primary dendritic and secondary eutectic growth was also developed and applied to solidification during EML.[6] Good agreements were found between the measurements and the simulations for the temperature evolution and the final amount of the eutectic structure in Al-Cu alloys processed by EML, thus identifying the role of the eutectic recalescence. Similarly, Kasperovich et al. applied different solidification techniques to study segregation in an Al-4 wt pct-Cu alloy, including EML.[7]

Analytical and numerical models for segregation have been developed.[1] Based on work by Rappaz and Thévoz,[8] Wang and Beckermann developed an analytical multiphase multiscale segregation model for both columnar and equiaxed solidification.[9] They succeeded in predicting the effect of back diffusion in the solid at a low cooling rate and the effect of dendrite tip undercooling at a high cooling rate. A simplified version of this model was used by Martorano et al.[10] to study the columnar-to-equiaxed transition based on a solutal interaction mechanism between the two grain structures. The growth kinetics of the dendrite tips being a function of the local supersaturation of the extradendritic liquid, the velocity of the columnar structure was found to vanish upon growth of the equiaxed grains. Tourret and Gandin extended the segregation model by taking into account the nucleation and growth of the peritectic structures[11] while removing the assumption of a uniform composition of the interdendritic liquid, i.e., the liquid located inside the grain envelope that defines the mushy zone. The diffusion length in the extradendritic liquid (located outside the grain envelope) was approximated by an analytical formulation based upon a steady-state assumption. Heringer et al. developed a numerical model for equiaxed growth in which both heat and solute diffusions were numerically calculated.[3] However, back diffusion in the solid was neglected and the growth kinetics was only taken as a function of the nominal composition of the alloy. The latter means that the extradendritic liquid composition had no direct influence on the supersaturation of the dendrite tip, an effect which is accounted for in the analytical models[6,8–11] and sometimes referred to as solutal interaction. The model presented in this article integrates the effect of back diffusion in the solid and solutal interaction with a nonisothermal model.

Variation in composition at the scale of the casting, referred to as macrosegregation, is mainly due to the relative transport of phases by convection and sedimentation. Comparison of predicted segregation maps with experiments thus also requires dealing with phase distribution in the casting. The simultaneous measurement of the distribution of species and phases is not common because it requires heavy characterization efforts. In addition, numerical models have not been so far benchmarked, a recent effort in that direction just being released.[12] A more sophisticated approach based on a cellular-automaton (CA)–finite-element (FE) model[13–15] was recently proposed for the prediction of the grain structure and segregation formed during ingot solidification. The heat and solute mass transfers at the scale of the ingot were modeled using the FE method to solve volume-averaged conservation equations. Coupling with the CA method permitted the integrations over the time and space of the physical phenomena that govern solidification, such as the nucleation and growth of the primary dendritic solid phase and the grain movements. This was done at the scale of cells defined by a regular square lattice (or CA grid) superimposed onto the static FE mesh. When coupling with segregation induced by natural convection, application was limited by the use of a simple lever rule approximation for the mass balance applied at each cell. Some agreement could yet be reached with an in-situ observation of the development of a single grain formed in a gallium-5 wt pct indium alloy.[16,17]

Other confrontations between measurements and simulations deal with the segregation taking place at the scale of a few dendrite arms. Such a system is close with respect to mass transfer. The distribution of species is then referred to as microsegregation. These studies are very common in the literature since the work of Flemings.[18] One can cite characterization by electron probe microanalyses on samples solidified in well-controlled conditions, e.g., using directional solidification and quenching.[19–22] Because the fraction of the phases can also be measured as a function of the temperature or local composition, it is then possible to conduct a comparison with predictions. Not only could the combined interpretation of such experimental and modeling analyses explain the effect of solid diffusion, but it was also used to identify the effect of the nucleation undercooling of a second phase.[23,24] This effect was expected due to the work of Sarreal and Abbaschian.[25] It was also modeled by Voller and Sundarraj.[26] The work by Gandin et al.[6] can be seen as an extension using EML as the experimental technique, with the advantage of accessing a direct estimation of the nucleation undercooling of the eutectic through measurement. The main objective of this work is to achieve a comparison between the solidification experiments and the numerical simulation of the distribution of structures and species. It can be seen as an extension of the microsegregation analysis developed in Reference 6 to analyze the macrosegregation induced by diffusion in the extradendritic liquid. The EML is still the experimental technique used hereafter to study the effect of the nucleation of the primary dendritic and the secondary eutectic structures on the solidification of Al-Cu alloys. Metallurgical characterizations are performed to construct the distribution maps of the average composition of copper, the volume fraction of the eutectic structure, and the dendrite arm spacing (DAS). Regarding numerical modeling, the development of a CAFE model is considered with an advanced microsegregation model. A parametric study is achieved that demonstrates the model capabilities compared to previous approaches to model solidification while accounting for the mass exchange with an extradendritic liquid. The model is then applied to the solidification of the Al-Cu samples with spontaneous[6] and triggered nucleation.

2 Experimental

A detailed description of the EML technique developed at the Deutsches Zentrum für Luft-und Raumfahrt e.V. (DLR) (Köln, Germany) can be found in References 2 and 27. It consists of an induction coil with a conical geometry designed to create an alternating radio-frequency electromagnetic field. Samples, with typically 0.2 g in mass, were prepared from pure Al (99.9999 pct) and Cu (99.999 pct). The compositions were selected as 4, 14, and 24 wt pct Cu for later comparison with previous published work.[6] The magnetic field was used to levitate and melt the sample under a low gas pressure of approximately 40 to 50 mbar He that was maintained during the whole solidification process. The levitated sample was then cooled down by reducing the power of the magnetic field. For some samples, nucleation occurred spontaneously at a certain degree of undercooling that was not controlled but could be measured by optical pyrometry. The corresponding experimental results are presented in Reference 6. For other samples, solidification was triggered by bringing an alumina plate into contact with the bottom surface of the droplet. Once solidified, the metal consisted of an approximately spherical volume with a diameter close to 5.3 mm. During the experiments, temperature histories were recorded using a pyrometer located at the top of the levitated droplet, i.e., opposite the triggering device with respect to the droplet. Precision with such a pyrometer is within ±5 K and the temperature signal is affected by a noise that could be attributed to the translations and rotations of the levitated samples as well as to the pyrometer sensitivity. More details on the experimental procedure are given elsewhere.[2]

3 Modeling

The two-dimensional (2-D) FE method is used to solve the conservation equations for energy and solute mass averaged over a representative elementary volume containing a mushy zone, i.e., a mixture of the solid and liquid phases.[28,29] It is coupled with a CA method for the modeling of the solidification structure, as originally proposed by Gandin et al.[13–15] In this section, only extensions are presented, consisting of the use of a mesh adaptation technique to compute the heat and solute diffusion at the scale of the FE mesh, a microsegregation model for the cells of the CA grid, and a coupling scheme between the CA and FE methods.

3.1 Macroscopic Heat and Solute Flows

The solid and liquid phases are assumed to have constant and equal densities. Hence, in a pure diffusion regime, the average energy conservation can be written as follows:

$$ {\frac{\partial \left\langle H \right\rangle }{\partial t}} - \nabla{\cdot}\left( {\left\langle \kappa \right\rangle \nabla T} \right) = 0 $$

(1)

where $\left\langle H \right\rangle$ is the average enthalpy per unit volume, T is the temperature, and t is the time. The average thermal conductivity $\left\langle \kappa \right\rangle$ is taken as a constant in the following. Further, assuming constant and equal values of the specific heat for the liquid and solid phases C _p , one can write $\left\langle H \right\rangle = C_{p} T + g^{f} L,$ where L denotes the latent heat of fusion per unit volume and g ^f is the volume fraction of the liquid phase. The average enthalpy is chosen as the primary unknown in Eq. [1]. The solution of this nonlinear equation is obtained by using a Newton–Raphson procedure, which necessitates calculating the derivative ∂H _n /∂T _n at each node n of the FE mesh.[29]

With a fixed solid and no liquid convection, the average conservation equation of a solute element is written:[28]

$$ {\frac{\partial \left\langle w \right\rangle }{\partial t}} - \nabla{\cdot}\left( {g^{f} D^{l} \nabla \left\langle {w^{f} } \right\rangle^{f} } \right) = 0 $$

(2)

where $\left\langle w \right\rangle$ is the average composition of solute and $\left\langle {w^{f} } \right\rangle^{f}$ is the average composition of the solute in the entire liquid phase. The ratio of the diffusion coefficient of Cu in the primary solid Al-rich phase D ^s over the diffusion coefficient of Cu in the liquid phase D ^l shows that diffusion in the solid phase can be neglected at the scale of the FE mesh. The primary unknown considered in Eq. [2] is the average composition of the solute $\left\langle w \right\rangle .$ The average composition of the liquid phase $\left\langle {w^{f} } \right\rangle^{f}$ is eliminated following the work of Prakash and Voller, who introduced a split operator technique with an Euler backward scheme.[30]

3.2 Mesh Adaptation

The FE mesh adaptation approach initially proposed by Fortin[31] and developed by Alauzet and Frey[32] has been integrated into the FE method. It consists of a minimization method that evaluates the mesh size required to access a given error for a chosen field of the FE solution. The main idea is that the mesh size can be controlled by a directional error estimator based on the recovery of the second derivatives of the FE solution of the selected scalar field.[31–33] This strategy is known as the Hessian strategy. The Hessian, which is the tensor of the second spatial derivatives, can be computed for any scalar component of the FE solution. As shown in the previous references, this directional information can be converted into a mesh metric field that prescribes the desired element size and orientation to satisfy a given objective error level. The implementation of this technique can be found in Reference 33. For the present application, this approach is used to track the solute field. The average composition of solute is thus used as the scalar field to generate the objective metric. This is first useful in the extradendritic liquid because of the necessity of capturing the diffusion flux of the solute ahead of the growing mushy-zone–liquid boundaries. The mesh size then needs to be smaller than the corresponding characteristic diffusion length. However, the criterion based on the average composition also permits tracking of the segregation pattern within the mushy zone and after completion of the solidification. The Gruau and Coupez[34] unstructured and anisotropic mesh generator with adaptation has been used to generate the FE mesh.

3.3 Solidification Path

Figure 1(a) gives a schematic presentation of the coupled CAFE model. The continuous domain is divided into an FE mesh using coarse triangles F defined by nodes n ^F _i  (i = [1, 3]) to solve the average conservation equations at the macroscopic scale. A regular lattice of fine squares defining the cells of the CA grid is superimposed onto the FE mesh. Each cell ν located in an element F is uniquely defined by the coordinates of its center C _v . Linear interpolation coefficients $c_{v}^{{n_{i}^{F} }}$ are defined between each node n ^F _i  and the cell ν. A variable defined at the nodes, such as the average enthalpy $\left\langle {H_{n} } \right\rangle$ or the average composition $\left\langle {w_{n} } \right\rangle ,$ can thus be used to calculate an interpolated value at a given cell ν, either$\left\langle {H_{v} } \right\rangle$ or $\left\langle {w_{v} } \right\rangle ,$ respectively. Similarly, information computed onto the CA grid can be projected onto the FE mesh.[15] Nucleation and growth algorithms previously designed to track the development of the grain envelopes are used hereafter.[15] Upon cooling, when the nucleation undercooling prescribed in a cell ν is reached, an equilateral quadrangular surface is defined, with its center G _v located at cell center C _v . An orientation θ with respect to the (x, y) frame of coordinates is then assigned to the cell that defines the main growth directions of the dendritic structure, i.e., the $\left\langle {10} \right\rangle$ crystallographic directions for cubic metals. An illustration of the square growth shape is presented in Figure 1(b). The cell is then in a mushy state, i.e., formed by a mixture of the primary dendritic solid phase s, the interdendritic liquid phase d, and the extradendritic liquid phase l. A mushy zone volume fraction assigned to each cell v, g ^m _v , is defined as the volume fraction of the solid phase s, g ^s _v , plus the interdendritic liquid phase d, g ^d _v : g ^m _v  = g ^s _v  + g ^d _v . It is estimated by the half-diagonal of the equilateral quadrangle R ^e _v divided by its maximum extension R ^f _v : g ^m _v  = (R ^e _v /R ^f _v )². The final radius associated with cell ν, R ^f _v , is defined as the spatial limit for the growth of the equilateral quadrangle, which is of the order of several secondary arm spacings. In the case of a columnar dendritic structure, this limit is chosen proportional to the primary DAS, R ^f _v  = λ ₁/2. In the case of equiaxed dendritic grains, such a definition can still apply. Indeed, equiaxed dendritic growth first proceeds with the development of six perpendicular dendritic trunks in cubic metals. From each primary trunk (e.g., [100] _p ), secondary branches develop (e.g., [010] _s ) that are parallel to one of the other primary trunks (e.g., [010] _p ). Providing sufficient development of the equiaxed grain takes place, some selected secondary dendrite arms can develop freely from its primary trunk and contribute to the definition of the grain envelope. It then naturally forms a primary DAS, with the primary trunk growing in the same direction. The distance R ^f _v depends on the local cooling rate and can fluctuate during the solidification process. For the present study, it is yet assumed constant and the same strategy is chosen for columnar and equiaxed grains. The average enthalpy $\left\langle {H_{n} } \right\rangle$ and solute composition $\left\langle {w_{n} } \right\rangle$ at the FE node n being deduced from the solution of Eqs. [1] and [2], conversions are required into a temperature T _n and a fraction of solid g ^s _n . Instead of directly applying a solidification path at the FE nodes,[28,29] the conversions are first carried out for each CA cell ν to compute the temperature T _v and a fraction of solid g ^s _v from the interpolated enthalpy $\left\langle {H_{v} } \right\rangle$ and average composition $\left\langle {w_{v} } \right\rangle .$ The fields at the CA cells are finally projected back to the FE nodes.[15] Assuming equal and constant densities in all phases, one can write: g ^s _v  + g ^f _v  = 1, with g ^f _v  = g ^d _v  + g ^l _v and $\left\langle {w_{v} } \right\rangle = g_{v}^{s} \left\langle {w_{v}^{s} } \right\rangle^{s} + g_{v}^{d} \left\langle {w_{v}^{d} } \right\rangle^{d} + g_{v}^{l} \left\langle {w_{v}^{l} } \right\rangle^{l} .$ A microsegregation model is required to model the time evolution of the average volume fraction and composition of the solid phase s, $g_{v}^{s} \left\langle {w_{v}^{s} } \right\rangle^{s} ,$ the interdendritic liquid phase d, $g_{v}^{d} \left\langle {w_{v}^{d} } \right\rangle^{d}$ and the extradendritic liquid phase l, $g_{v}^{l} \left\langle {w_{v}^{l} } \right\rangle^{l} .$ The corresponding mass balances are derived as an extension of the Wang and Beckermann (WB) analysis.[9] Mass exchanges are considered between the solid phase and the interdendritic liquid phase through the interfacial area concentration S ^sd _v , as well as between the extradendritic liquid phase and the interdendritic liquid phase through the interfacial area concentration S ^ld _v , while the mass exchange between the solid phase and the extradendritic liquid phase is neglected:

$$ {\frac{\partial }{\partial t}}\left( {g_{v}^{s} \left\langle {w_{v}^{s} } \right\rangle^{s} } \right) = w_{v}^{sd} S_{v}^{sd} v_{v}^{sd} + S_{v}^{sd} {\frac{{D^{s} }}{{l_{v}^{sd} }}}\left( {w_{v}^{sd} - \left\langle {w^{s} } \right\rangle_{v}^{s} } \right) $$

(3)

$$ {\frac{\partial }{\partial t}}\left( {g_{v}^{d} \left\langle {w_{v}^{d} } \right\rangle^{d} } \right) = - w_{v}^{sd} S_{v}^{sd} v_{v}^{sd} - w_{v}^{ld} S_{v}^{ld} v_{v}^{ld} - S_{v}^{sd} {\frac{{D^{s} }}{{l_{v}^{sd} }}}\left( {w_{v}^{sd} - \left\langle {w^{s} } \right\rangle_{v}^{s} } \right) - S_{v}^{ld} {\frac{{D^{l} }}{{l_{v}^{ld} }}}\left( {w_{v}^{ld} - \left\langle {w^{l} } \right\rangle_{v}^{l} } \right) + g_{v}^{d} \dot{\varphi }_{v}^{d} $$

(4)

$$ {\frac{\partial }{\partial t}}\left( {g_{v}^{l} \left\langle {w_{v}^{l} } \right\rangle^{l} } \right) = w_{v}^{ld} S_{v}^{ld} v_{v}^{ld} + S_{v}^{ld} {\frac{{D^{l} }}{{l_{v}^{ld} }}}\left( {w_{v}^{ld} - \left\langle {w^{l} } \right\rangle_{v}^{l} } \right) + g_{v}^{l} \dot{\varphi }_{v}^{l} $$

(5)

where w ^sd _v is the average composition of the solid phase at the sd interface and w ^ld _v is the average composition of the liquid phases at the ld interface. Solute profiles are assumed in the solid phase and in the extradendritic liquid phase characterized by the diffusion lengths l ^sd _v and l ^ld _v , respectively. The expressions for the interfacial area concentrations and the diffusion lengths, derived with the same assumptions as in the appendices of References 9 and 10, are provided in Table I. Complete mixing of the interdendritic liquid composition and continuity of the composition at interface ld is assumed, $w_{v}^{ld} = \left\langle {w_{v}^{d} } \right\rangle^{d} ,$ together with equilibrium at the sd interface. Thus, at temperature T _v , readings of the liquidus and solidus curves of the equilibrium phase diagram give $\left\langle {w_{v}^{d} } \right\rangle^{d}$ and w ^sd _v , respectively. With k the partition ratio, one can also write $w_{v}^{sd} = k\left\langle {w_{v}^{d} } \right\rangle^{d}$.

Fig. 1

Schematic view of the CAFE model with an illustration of (a) topological coupling between the tessellation made of the square cells ν, defined by their center C _v in the CA grid and the triangles of the FE mesh F, defined by the nodes n ^F _i (i = [1, 3]) and (b) simplified spatial representation of the growing dendritic microstructure in a cell ν using a square centered in G _ν with a half-diagonal R ^e _ν and an orientation θ with respect to the x-axis. The cells painted in gray are mushy, i.e., made of a mixture of the solid phase s, an interdendritic liquid phase d, and an extradendritic liquid phase l, the fraction of which is provided by a microsegregation model. While the dendritic microstructure schematized is not directly simulated, its primary and secondary DAS, λ ₁ and λ ₂, respectively, are used by the microsegregation model

Table I Mathematical Expressions Used for Diffusion Lengths l ^sd _v and l ^ld _v and Interfacial Area Concentrations S ^sd _v and S ^ld _v Entering Equations [3], [4], and [5]

The time derivative of the volume fraction of the solid phase s, ∂g ^s _v /∂t, can be written as a function of its interfacial area concentration S ^sd _v , and the normal velocity of the sd interface v ^sd _v as S ^sd _v v ^sd _v  = ∂g ^s _v /∂t = ∂g ^m _v /∂t − ∂g ^d _v /∂t. Similarly, one can write S ^ld _v v ^ld _v  = ∂g ^l _v /∂t = −∂g ^m _v /∂t. The volume fraction of the interdendritic liquid phase and the external liquid phase are defined and computed as g ^d _v  = g ^m _v  − g ^s _v and g ^l _v  = 1 − g ^m _v , respectively. The growth rate of the mushy zone ∂g ^m _v /∂t is calculated with the growth rates of the half-diagonal of the rhombus surface v ^e _v  = ∂R ^e _v /∂t. This is done assuming a dendrite tip growth kinetics model:[35]

$$ v_{v}^{e} = {\frac{{\partial R_{v}^{e} }}{\partial t}} = {\frac{{4\sigma^{*} D^{l} m_{L} \left( {k - 1} \right)w_{v}^{ls} }}{\Upgamma }}\left( {{\text{Iv}}^{ - 1} \left( {\Upomega_{v} } \right)} \right)^{2} $$

(6)

$$ \Upomega_{v} = {\frac{{w_{v}^{ls} - w_{v}^{l,\infty } }}{{w_{v}^{ls} \left( {1 - k} \right)}}} $$

(7)

where Γ is the Gibbs–Thomson coefficient, Iv⁻¹ is the inverse of the Ivantsov function,[36] σ* is a constant taken equal to 1/(4π ²),[35] m _L is the liquidus slope of the phase diagram, and Ω _v is the local supersaturation defined at the tip of a growing dendrite located at the growth front, i.e., at the boundary between the mushy zone and the extradendritic liquid. The local supersaturation in Eq. [7] is defined as the deviation of the liquid composition at the dendrite tip w ^ls _v from the composition far away from the dendrite tip w ^l,∞ _v , i.e., in the extradendritic liquid, normalized by the composition jump between the liquid phase and the solid phase w ^ls _v (1 − k). The curvature undercooling is inversely proportional to the dendrite tip radius. It is taken into account by adding its contribution 2Γ/r to the solutal undercooling. Local equilibrium is assumed at the dendrite tip via the relation T = T _M  − m _L w ^ls _v  − 2Γ/r.[15] For this purpose, an iterative procedure is developed, a detailed description of which is provided in Reference 37. Dendrite tip models assume the steady-state growth of the microstructure in an undercooled liquid with an initial uniform composition taken equal to the nominal alloy composition w ^l,∞ _v  = w ₀. However, in order to account for the solutal interactions between grain boundaries, Wang and Beckermann and Martorano et al. choose to use the value of the liquid composition averaged over the extradendritic domain that remains in a predefined grain envelop, later denoted $\left\langle {w^{l} } \right\rangle_{\text{CAFE}}^{l}$ in this article.[9,10] Three strategies will be tested later for the determination of w ^l,∞ _v , one of which consists of a direct numerical estimation of $\left\langle {w^{l} } \right\rangle_{\text{CAFE}}^{l}$.

The source terms in Eqs. [4] and [5], $\dot{\varphi }_{v}^{d}$ and $\dot{\varphi }_{v}^{l}$, account for the solute mass exchange of the cell ν with its surrounding. According to the solute mass conservation written at the macroscopic scale (Eq. [2]), solute exchange between cells is only based on diffusion in the liquid f, i.e., through the interdendritic liquid phase d and the extradendritic liquid phase l. By summing up $g_{v}^{d} \dot{\varphi }_{v}^{d}$ and $g_{v}^{l} \dot{\varphi }_{v}^{l} ,$ we obtain the equivalent terms at the scale of the CA model of the solute diffusion term $\nabla{\cdot}\left( {g^{f} D^{l} \nabla \left\langle {w^{f} } \right\rangle^{f} } \right)$ computed by the FE model and interpolated at cell ν. The relative portions $\dot{\varphi }_{v}^{l}$ and $\dot{\varphi }_{v}^{d}$ can be quantified by introducing a partition ratio for the diffusion in the liquid, $\varepsilon_{{D^{l} }} = {{\dot{\varphi }_{v}^{l} } \mathord{\left/ {\vphantom {{\dot{\varphi }_{v}^{l} } {\dot{\varphi }_{v}^{d} }}} \right. \kern-\nulldelimiterspace} {\dot{\varphi }_{v}^{d} }}$. The following correlation is proposed as a function of the volume fraction of the interdendritic liquid phase and the extradendritic liquid phase: $\varepsilon_{{D^{l} }} = {{g_{v}^{l} } \mathord{\left/ {\vphantom {{g_{v}^{l} } {\left( {g_{v}^{l} + g_{v}^{d} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {g_{v}^{l} + g_{v}^{d} } \right)}}$ Hence, the terms $g_{v}^{d} \dot{\varphi }_{v}^{d}$ and $g_{v}^{l} \dot{\varphi }_{v}^{l}$ can be evaluated from the solution of Eq. [2].

Finally, the microsegregation model requires a local heat balance for cell ν:

$$ {\frac{{\partial \left\langle {H_{v} } \right\rangle }}{\partial t}} = C_{p} {\frac{{\partial T_{v} }}{\partial t}} - {\text{L}}{\frac{{\partial g_{v}^{s} }}{\partial t}} $$

(8)

Equations [3] through [5] and [8] constitute a complete system of differential equations with the four main unknowns, $\left\langle {w_{v}^{s} } \right\rangle^{s}$, g ^s _v , $\left\langle {w_{v}^{l} } \right\rangle^{l}$, and T _v . A splitting scheme is applied to the differential equations together with a first-order Taylor series. An iterative algorithm is implemented to calculate the solution. Once the prescribed growth temperature of the eutectic structure is reached, a simple isothermal transformation is assumed in order to transform the remaining liquid phase (1 – g ^s _v ) into a volume fraction of eutectic g ^E _v . Only Eq. [8] is then solved, considering no temperature variation over time and simply adjusting the total fraction of solid with the variation of enthalpy up to completion of the solidification.[3,15]

3.4 CAFE Coupling Scheme

The main steps of the implemented coupling scheme within time-stepping procedures are as follows.

• (1) s1: FE mesh and CA grid initializations. While the CA grid is fixed, the FE mesh is adapted as explained earlier. Based on the current FE tessellation, each cell ν is located inside a unique triangular element F defined by its nodes n ^F _i  (i = [1, 3]). This is done based on the position of the cell center C _v . Subsequently, the linear interpolation coefficients $c_{v}^{{n_{i}^{F} }}$ are evaluated. All fields computed at the CA cells ν, $\left\langle {\xi_{v} } \right\rangle ,$ are then projected to the FE nodes n, $\left\langle {\xi_{n} } \right\rangle$.[15] This procedure is equivalent to a transport from the old mesh to the new one, but with the advantages of giving more accuracy and keeping consistency between the fields at the level of the CA and FE tessellations.

• (2) s2: FE solution. Eqs. [1] and [2] are solved, giving access to the fields at the FE nodes n for the average enthalpy $\left\langle {H_{n} } \right\rangle$ and composition $\left\langle {w_{n} } \right\rangle$.

• (3) s3: interpolation onto the CA grid. This step permits the interpolation on the CA grid of the fields computed on the FE mesh, thus accessing to $\left\langle {H_{v} } \right\rangle$ and $\left\langle {w_{v} } \right\rangle$. A micro time step is required to subdivide the macro time step used by the implicit FE method. The quantities $\left\langle {H_{v} } \right\rangle$ and $\left\langle {w_{v} } \right\rangle$ are thus also interpolated at a micro time within the macro time step, as presented in Reference 15.

• (4) s4: CA calculations. The nucleation, growth, and microsegregation of a dendritic mushy zone are simulated using Eqs. [3] through [8] to compute fields at the CA cells ν, such as the average composition in the solid $\left\langle {w_{v}^{s} } \right\rangle^{s}$, the volume fraction of the solid g ^s _v , the average composition of the extradendritic liquid $\left\langle {w_{v}^{l} } \right\rangle^{l}$, and the temperature T _v . The derivative ${{\partial \left\langle {H_{v} } \right\rangle } \mathord{\left/ {\vphantom {{\partial \left\langle {H_{v} } \right\rangle } {\partial T_{v} }}} \right. \kern-\nulldelimiterspace} {\partial T_{v} }}$ is also computed.

• (5) s5: loop on micro time steps. Achieved by going back to s3.

• (6) s6: projection onto the FE mesh. All fields at the CA cells are projected back onto the FE mesh.

• (7) s7: loop on macro time steps. Achieved by going back to s1.

3.5 Comparison with Literature

This section presents simulations for Al-4 wt pct-Cu and Al-10 wt pct-Cu alloys with the objective of conducting a comparison with the previous model developed for equiaxed solidification. The following approximations are considered.

• (1) a1: geometry and nucleation. Simulations are carried out on a quarter-disk geometry of radius R with axisymmetrical conditions with respect to its two perpendicular rectilinear edges. The location for nucleation of the primary solid structure is imposed at the corner of the simulation domain, where the two perpendicular rectilinear edges intersect.

• (2) a2: heat transfer. The heat exchange on the spherical boundary of the droplet follows a global heat balance defined by an extraction rate $\dot{q}_{\text{ext}}$. A Fourier boundary condition is assumed, defined by constant values for the heat transfer coefficient $h_{\text{ext}}$ and for the temperature $T_{\text{ext}}$ such that $\dot{q}_{\text{ext}} = h_{\text{ext}} \left( {T - T_{\text{ext}} } \right)$.

• (3) a3: alloy. Linear monovariant lines of the phase diagram are assumed that delimit the equilibrium domains of the mushy zone from the fully liquid and fully solid ones. The phase diagram is thus defined by the liquidus slope m _L , the segregation coefficient k, the eutectic temperature T _E , the eutectic composition w _E , and the liquidus temperature of the alloys T _L , for each alloy composition w ₀.

• (4) a4: nucleation undercooling. The nucleation undercooling of the primary solid structure ΔT ^s _N and the eutectic structure ΔT ^E _N are prescribed with respect to the liquidus temperature of the alloy T _L and the eutectic temperature T _E , respectively.

• (5) a5: growth. The grain is assumed to be spherical in shape. The growth rate is calculated as a function of the supersaturation, using Eqs. [6] and [7]. In the following, w ^l,∞ _v will be taken equal to the average composition of the external liquid phase[9,10] $\left\langle {w^{l} } \right\rangle_{\text{CAFE}}^{l}$, the nominal composition of the alloy[3] w ₀, or the average composition of the cell[15] $\left\langle {w_{v} } \right\rangle$.

The first test case follows the study by Heringer et al.[3] The simulation is carried out for a 250-μm-diameter droplet produced by the impulse atomization of an Al-10 wt pct-Cu alloy. Primary solidification is assumed to start 30 K below the liquidus temperature. The goal of the test is to compare the predicted composition profiles within the droplet. The mushy zone growth rate is thus computed with a supersaturation defined by the initial alloy composition w ^l,∞ _v  = w ₀, as was the case in Reference 3. A summary of the physical and numerical simulation parameters is listed in Table II. Figure 2 shows the model predictions when the volume fraction of the mushy zone in the droplet reaches 0.64. The triangular elements are displayed in Figure 2(a), while the volume fraction of the solid, the average solute composition, and the temperature are displayed in Figures 2(b) through (d), respectively. The location at which the fraction of solid drops to zero is made accessible in Figure 2(b). It compares favorably with the position of the thick black line drawn on top of the FE mesh in Figure 2(a), the latter being deduced from the CA simulation by drawing the boundary between the growing mushy cells and the liquid cells. Figure 2(c) reveals the sudden increase in the average composition in the vicinity of the grain envelope, due to the solute pileup in the liquid ahead of the growth front. A comparison of Figure 2(a) with Figure 2(c) thus gives an illustration of the use of the second spatial derivatives of the average composition in adapting the FE mesh size. Figure 2(d) also gives access to the temperature field inside the droplet. While the maximum temperature variation only reaches a few degrees during the propagation of the mushy zone, it is also localized at the growing interface. This is due to the release of the latent heat at the grain envelope. The mushy zone is actually remelting due to the recalescence taking place at its boundary.[3] Finally, as shown in Figure 2(e), the present model retrieves well the final segregation profile predicted by Heringer et al.[3] Further validations of the present CAFE model with respect to Heringer et al.,[38] as well as with a front tracking model, are presented elsewhere,[39,40] in addition to other illustrations of the mesh adaptation.[40]

Table II Simulation Data and Parameters

Fig. 2

Simulation results of CAFE model applied to the solidification of an atomized Al-10 wt pct-Cu droplet showing (a) FE triangular mesh and CA growth front corresponding to the grain envelope (thick black line), (b) volume fraction of the solid phase g ^s, (c) average composition 〈w〉, (d) temperature T, and (e) radial profile of the average composition 〈w〉 after completion of solidification compared with prediction by Heringer et al.[3] A single nucleation event is assumed at the center of the spherical domain with 30-K undercooling. Simulation is carried out for a quarter-disk in axisymmetric coordinates with a radius equal to 125 μm. All simulation data are listed in Table II. Maps (a) through (d) are drawn when the volume fraction of the grain (volume ratio of the grain envelope over the simulation domain) reaches 0.64

The second test case is chosen to compare the model predictions with respect to simulations performed with a semianalytical model for a different final grain radius.[10] These simulations intend to illustrate the capabilities of the CAFE model in dealing with mass exchange outside the grain envelope, as well as to study the effect of the solutal interaction as a function of the composition w ^l,∞ _v , entering the definition of the growth front supersaturation in Eq. [7]. The effect of the final radius associated with cell ν, R ^f _v , the control of which is provided by λ _l , is also studied as a model parameter. The results are presented in Figures 3 through 5.

Fig. 3

Predictions of the evolution of the volume fraction of the mushy zone g ^m and the volume fraction of the solid phase inside the mushy zone g ^sm = g ^s/g ^m, for three equiaxed grains with radius equal to (r1) R = 0.1 mm, (r2) R = 1 mm, and (r3) R = 10 mm. Predictions of the present CAFE simulations g ^sm_CAFE (plain black curves) and g ^sm_CAFE (dashed black curves) are compared to the semianalytical WB model,[9] g ^m (plain gray curves) and g ^sm (dashed gray curves). While λ ₁ = λ ₂, w ^l,∞ _ν entering Εq. [7] for the definition of the supersaturation is computed using (c1) the average composition of the extradendritic liquid phase 〈w ^l〉 ^l_CAFE , and (c2) the average composition of the growing cells ν of the CA grid at the boundary between the mushy zone and the extradendritic liquid $\langle w_{v} \rangle$ (Fig. 1). The solidification times t _s used for normalization are (r1) t _s  = 3 s, (r2) t _s  = 40 s, and (r3) t _s  = 300 s. All simulation data are reported in Table II

Figure 3 shows the time evolution of the mushy zone volume fraction of the grain g ^m_CAFE and the average internal volume fraction of the solid in the envelope of the grain, g ^sm_CAFE  = g ^s_CAFE /g ^m_CAFE , predicted by the CAFE model, compared with the evolution using the semianalytical model.[9,10] Because the CAFE predictions lead to nonuniform fields, an averaging procedure is performed over the FE mesh to obtain information g ^m_CAFE and g ^sm_CAFE to be compared with the quantities g ^m and g ^sm, respectively, predicted by the semianalytical model. The time scale has been normalized for all simulations using the solidification time. This representation permits comparison between systems of various sizes. In Figure 3(c1), $w_{v}^{l,\infty } = \left\langle {w^{l} } \right\rangle_{\text{CAFE}}^{l}$ and λ ₁ = λ ₂, while the grain size is progressively increased from (r1) 0.1 mm to (r2) 1 mm and finally to (r3) 10 mm. Composition $\left\langle {w^{l} } \right\rangle_{\text{CAFE}}^{l}$ is also calculated at a given time by a space integration of the average composition at each FE node over the extradendritic liquid region and can thus be compared with the prediction of the semianalytical model $\left\langle {w^{l} } \right\rangle^{l}$. For all calculations, no diffusion in the solid is considered and nucleation takes place at the liquidus temperature (no nucleation undercooling). When considering only Figure 3((c1r1) through (c1r3)), one can observe a general agreement between the predictions of the semianalytical model and the present numerical CAFE model. This is due to the use by the CAFE model of the average composition of the extradendritic liquid $\left\langle {w^{l} } \right\rangle_{\text{CAFE}}^{l}$ for calculation of the supersaturation. However, while the deviation in Figure 3(c1r3) is found small for R = 10 mm, it does increase in Figure 3(c1r1) for R = 0.1 mm. In fact, for a smaller grain size, the interaction of the solute buildup ahead of the growing mushy zone with the boundary of the spherical domain starts very soon after nucleation, leading to a slower development of the mushy zone. The reason is due to the approximations of the semianalytical model for solute mass exchange between the interdendritic liquid and the extradendritic liquid, i.e., steady-state regime for the evaluation of the diffusion length l ^ld and uniform composition of the interdendritic liquid $\left\langle {w^{d} } \right\rangle^{d}$.[9,10] The present model does not need such approximations because diffusion is explicitly computed onto the FE mesh, outside and inside the mushy zone. Transient regimes are thus captured and predictions are improved compared to the semianalytical model. In Figure 3(c1r1), the semianalytical model overestimates the solute mass exchange between the mushy zone and the extradendritic liquid, leading to a higher internal fraction of solid g ^sm and a lower growth kinetics g ^m compared to the CAFE prediction. This is also shown by comparing g ^m_CAFE in Figure 3((c1r1) and (c1r3)) as well as by the time evolution of $\left\langle {w^{l} } \right\rangle_{\text{CAFE}}^{l}$ drawn in Figure 5(c1r1). For the intermediate grain size, in Figure 3(c1r2), the solutal interaction takes place almost at the same time for the two simulations. However, the mushy zone predicted by the semianalytical model never reaches unity. The CAFE model also systematically shows a different nonmonotonic behavior of g ^sm_CAFE . The semianalytical model first predicts a decrease followed by an increase in g ^sm, thus leading to a single minimum, while the CAFE model predicts two minima. The first minimum takes place just after nucleation and the second minimum almost corresponds in time and intensity to that predicted by the semianalytical model. Similar behavior is found in Reference 3. This difference is due to the isothermal approximation of the semianalytical model, preventing the prediction of the first minimum.

The use of $w_{v}^{l,\infty } = \left\langle {w^{l} } \right\rangle_{\text{CAFE}}^{l}$ is not convenient for the evaluation of the supersaturation with the CAFE model. Indeed, it requires integrating over space the average composition at each FE node over a fully liquid zone the shape and size of which needs to be arbitrarily evaluated with time. For this reason, Guillemot et al. proposed to evaluate the supersaturation using $w_{v}^{l,\infty } = \left\langle {w_{v} } \right\rangle$.[15] The simulations corresponding to this practice are presented in Figures 3(c2) and 5(c2r1), in which the same results of the semianalytical simulations are appended for comparison. Similar deviations are found with respect to the semianalytical simulations. However, one can observe that the second minimum on g ^sm_CAFE only remains for the 10-mm grain radius and is suppressed for the two others. It is to be remembered that the interpretation of this minimum was recently given as a global remelting taking place inside the grain envelope upon its development.[3] Thus, the present CAFE calculations show that for a given grain size, such a global remelting also depends on the growth kinetics computed for the grain envelope. The remelting does not systematically take place as explained earlier, depending not only on the nucleation undercooling but also on the grain size and the corresponding mass exchange with the extradendritic liquid.

Calculations have finally been made to study the effect of the additional parameter introduced in the CAFE microsegregation model, i.e., the maximum extension of the mushy zone associated with a cell R ^f _v evaluated as the half of the primary DAS, λ _l /2. For that purpose, the primary DAS has arbitrarily been changed to 4λ ₂ in Figures 4 and 5(r2), while still using (c1) $w_{v}^{l,\infty } = \left\langle {w^{l} } \right\rangle_{\text{CAFE}}^{l}$ and (c2) $w_{v}^{l,\infty } = \left\langle {w_{v} } \right\rangle$. As for Figure 3, a comparison with the semianalytical model is made accessible. The main observation when comparing Figures 3(c1r2) and 4(c1r2) is on the role of R ^f _v with respect to the solutal interaction with the limit of the domain for the intermediate grain size. The mushy zone volume fraction reaches unity more quickly. This is linked to the composition of the extradendritic liquid w ^l,∞ _v , which does increase later for a larger value of R ^f _v . The reason for using this second length-scale parameter R ^f _v thus appears meaningful when considering the solutal interaction within the equiaxed dendritic microstructure. While between secondary dendrite arms a uniform composition field can be assumed, it is not the case between active secondary dendrite arms, i.e., between dendrite arms the tips of which are located at the limit of the grain envelope. A second length scale defining this distance is thus required, which permits the control of the solutal interaction with the extradendritic liquid located outside the grain envelope. In fact, such a limited solutal interaction is nothing but that modeled upon columnar growth by Wang and Beckermann,[9] in which the primary DAS indeed plays the same role. Finally, comparing Figure 4(c2) with Figure 3(c2) and also with Figure 4(c1), one can observe that an intermediate behavior is found when increasing R ^f _v and using $w_{v}^{l,\infty } = \left\langle {w_{v} } \right\rangle$. At this stage, in-situ experimental measurements on single equiaxed growth while tracking the development of the solute buildup outside the grain envelope are missing; these are needed to evaluate further the validity of the parameters proposed. In the following, all simulations are consequently conducted with parameters λ ₁ = 5λ ₂ and $w_{v}^{l,\infty } = \left\langle {w_{v} } \right\rangle$.

Fig. 4

Same as Fig. 3, with the analysis of the effect of the primary DAS on the predictions of the CAFE model: black curves, compared to the WB[9] model, gray curves, (c1) $w_{\nu }^{l,\infty } = \left\langle {w^{l} } \right\rangle_{\text{CAFE}}^{l}$, and (c2) $w_{\nu }^{l,\infty } = \left\langle {w_{v} } \right\rangle$

Fig. 5

Predictions of the evolution of the average extradendritic liquid composition as a function of (c1) and (c2), the composition used for the calculation of the supersaturation in Eq. [7], w ^l,∞ _ν , and (r1) and (r2) the primary DAS, λ ₁. Predictions with the present CAFE model (black curves) and the WB model[9] (gray curves) are compared for grain sizes 0.1, 1, and 10 mm. Curves are interrupted when the volume fraction of the mushy zone reaches unity. The simulations are the same as those in Figs. 3 and 4

4 Results

4.1 Experimental

The thick gray curves in Figure 6 present the recorded cooling histories for the Al-Cu samples solidified under EML while triggering nucleation with an alumina plate. In the liquid state, i.e., for the first part of the recorded curves above the liquidus temperature T _L , cooling is controlled by convection of the He gas in the vicinity of the droplet surface. The alumina plate entered into contact with the droplet plays the role of a heat sink and extracts heat by conduction. The first significant change in the cooling rate is observed at the time at which the alumina plate is put in contact with the sample. This time is identified as the nucleation event of the primary structure, t ^s _N . However, while the nucleation event is observed very close to the liquidus temperature for the Al-4 wt pct-Cu and Al-14 wt pct-Cu samples, a large nucleation undercooling is measured for the Al-24 wt pct-Cu sample. The reason for the delayed nucleation is only due to the fact that the triggering device was brought to the levitated droplet later, while the heat exchange by convection of the He gas had already undercooled the liquid.

Fig. 6

Measured temperature (thick gray curves) for the (a) Al-4 wt pct-Cu, (b) Al-14 wt pct-Cu, and (c) Al-24 wt pct-Cu droplets with triggered nucleation together with the predicted averaged system temperature T _CAFE, by the CAFE model (black curves). The predicted temperature at the south pole (SP), T _SP ( ), and north pole (NP), T _NP ( ), of the simulation domain are also drawn. Measurements have been achieved using an optical pyrometer at the top of the system

The small plateaus below the eutectic temperature T _E observed in Figures 6(b) and (c) are the marker of a heat release, typical of the growth of the eutectic structure. The nucleation and growth of the eutectic structure compensate the extraction of energy from the system. This is also verified by the duration of the plateau, which increases with the initial copper composition w ₀. It is indeed proportional to the amount of eutectic measured in the solidified state g ^E _D that is reported in Table IV. For the Al-4 wt pct-Cu sample, no plateau is found in Figure 6(a) below T _E , because the fraction of eutectic is too small. The times for the beginnings of these plateaus are labeled t ^E _N in Figure 6. Therefore, the temperatures measured at times t ^s _N and t ^E _N (T ^s _N and T ^E _N , respectively) also correspond to the nucleation temperature of the dendritic and eutectic structures. Additional information is extracted from the cooling curves and is listed in Table III, such as the nucleation undercooling for the primary dendritic and eutectic structures (ΔT ^s _N  = T _L – T ^s _N and ΔT ^E _N  = T _E – T ^E _N , respectively). Note that because of the low precision of the measurement, the nucleation undercoolings for the Al-4 wt pct-Cu and Al-14 wt pct-Cu samples are set to zero in Table III. The times at which nucleation took place, t ^s _N and t ^E _N , and the end of solidification t _end could be estimated from Figure 6 as the characteristic times at which a significant slope change is observed in the cooling curve. For the Al-4 wt pct-Cu, the end of the solidification is defined as the time at which the recorded temperature is below the equilibrium eutectic temperature T _E , because the small fraction of eutectic prevents a clear signal on the cooling curve and thus a slope change. Other measurements on each curve are the cooling rates just before and after solidification, $\dot{T}\left( {t < t_{N}^{s} } \right)$ and $\dot{T}\left( {t > t_{\text{end}}^{s} } \right)$, respectively, listed in Table III.

Table III Summary of Measurements Deduced from Recorded Cooling Curves for Six Al-Cu Samples Processed by EML*

For all samples, the first nucleation event is followed by a temperature increase. While the same trend is observed for samples solidified upon spontaneous nucleation, the magnitude and shape are very different. Indeed, experimental data reported earlier for the same alloys but with no triggering lead to larger nucleation undercooling and sudden recalescences measured for both the primary dendritic and the secondary eutectic microstructures.[6] The reason is linked to the absence of a heat sink when no triggering device is used, thus permitting the system to adopt an almost uniform temperature and to have an extraction rate defined only by convection of the He gas. The growth of the microstructure is accompanied by a rapid increase in the temperature measured by the pyrometer, which corresponds to a global recalescence of the system. All parameters listed in Table III are also provided for the samples solidified under spontaneous nucleation.[6] Hence, in the case of triggered nucleation, two conditions of heat extraction jointly coexist after the contact with the alumina plate, which are linked to the convection of the gas at almost the entire surface of the droplet and conduction through the small surface of the triggering device into contact with the droplet. Further interpretation of the cooling curves thus requires a modeling of the heat flow in the entire droplet, which is presented later in this section.

Experimental measurements also consist of the distribution of copper on the meridian cross section of the droplets. Analyses were conducted on images produced by a scanning electron microscope (SEM)[6,41] in order to reveal the distribution of the eutectic volume fraction and the DAS in the same cross sections. Global averaging over the entire measurements for each sample leads to the values listed in Table IV for the copper content w _D , the eutectic volume fraction g ^E _D , and the DAS _D , respectively. The average copper content w _D shows a deviation from the nominal composition ${{\left( {w_{D} - w_{0} } \right)} \mathord{\left/ {\vphantom {{\left( {w_{D} - w_{0} } \right)} {w_{0} }}} \right. \kern-\nulldelimiterspace} {w_{0} }}$ that varies from –8.37 pct for the 24 wt pct Cu to +9.25 pct for the 4 wt pct Cu. As explained previously, these deviations are expected to result from a nonsymmetric growth of the dendritic structure within the analyzed central meridian cross sections.[6] The average eutectic volume fraction over the entire section plane g ^E _D is closer to the prediction of the Gulliver–Scheil model g ^E_GS for the triggered samples. This could be partly explained by the shorter solidification times for the triggered samples as compared to the spontaneous samples. Hence, solute diffusion in the solid is not expected to influence the final amount of eutectic structure for such short solidification times. In addition, no recalescence has been measured for the eutectic structure that would have led to an increase in the eutectic fraction by partial remelting of the already existing dendritic structure, as was shown for spontaneous nucleation.[6]

Table IV Summary of Measurements for Average over Sample Sections of Cu Composition w _D , DAS _D , and Volume Fraction of Eutectic g ^E _D , Compared with Predictions Using the Present CAFE Model g ^E _CAFE , a Semianalytical Model g ^E_[6] ,[6] and the Gulliver–Scheil Prediction g ^E _GS

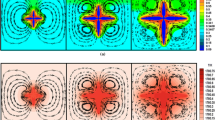
Figure 7(c1) presents the results of the normalized distribution maps of the average Cu content $\left\langle w \right\rangle$ for measurements conducted on a regular square lattice of 120·10⁻⁶ m × 150·10⁻⁶ m local surfaces. Normalization is achieved with respect to the initial composition using ${{\left( {\left\langle w \right\rangle - w_{0} } \right)} \mathord{\left/ {\vphantom {{\left( {\left\langle w \right\rangle - w_{0} } \right)} {w_{0} }}} \right. \kern-\nulldelimiterspace} {w_{0} }}$. Macrosegregations at the scale of the analyzed surfaces are thus identified by regions with negative or positive deviations with respect to the nominal composition w ₀. The normalized distribution maps drawn for the average volume fraction of the eutectic structure deduced from image analyses g ^E are shown in Figure 7(c2). Normalization is achieved following the work of Sarreal and Abbaschian,[25] i.e., using the value of the volume fraction of the eutectic structure predicted by the Gulliver–Scheil approximation for each alloy g ^E_GS listed in Table IV. Finally, the distributions of the average DAS, $\left\langle {DAS} \right\rangle$, are given in Figure 7(c3). Measurements are conducted using the same images and averaging surfaces as for the average fraction of eutectic. Similar to that previously reported for spontaneous nucleation,[6] a strong correlation is found for the Al-4 wt pct-Cu alloy. To a positive deviation of the average composition in Figure 7(c1r1) corresponds a positive deviation of the average fraction of eutectic in Figure 7(c2r1) and a finer microstructure in Figure 7(c3r1). This general trend was also found for the Al-14 wt pct-Cu and Al-24 wt pct-Cu alloys solidified upon spontaneous nucleation. However, while such a dependence is not as clear for the Al-14 wt pct-Cu sample presented in Figure 7(r2), it is not any more valid when increasing the alloy composition and considering the Al-24 wt pct-Cu sample in Figure 7(r3). While the positive deviation in the average fraction of eutectic in Figure 7(c2r3) corresponds to a finer microstructure in Figure 7(c3r3) close to the nucleation area, a negative macrosegregation is found in Figure 7(c1r3). Further interpretations are now given based on direct simulations of the solidification experiments.

Fig. 7

Characterization of a central meridian cross section of aluminum-copper samples processed by EML with triggered nucleation for Al-Cu alloys with (r1) 4 wt pct Cu, (r2) 14 wt pct Cu, and (r3) 24 wt pct Cu. Distributions are presented for (c1) the normalized average mass fraction of copper ${{\left( { \langle w \rangle - w_{0} } \right)} \mathord{\left/ {\vphantom {{\left( { \langle w \rangle - w_{0} } \right)} {w_{0} }}} \right. \kern-\nulldelimiterspace} {w_{0} }}$, (c2) the normalized average volume fraction of eutectic, (g ^E − g ^E_GS )/g ^E_GS , and (c3) the DAS, <DAS> (μm). Approximate system diameter: 5.3 mm. (1) Measurements of the copper content, 〈w〉, are averaged over 120·10⁻⁶ m × 150·10⁻⁶ m surface areas. (2) Measurements of the volume fraction of the eutectic structure, g ^E, are averaged over 150·10⁻⁶ m × 150·10⁻⁶ m surface areas

4.2 Simulations

With respect to previous simulations, approximations are modified as follows, a3 and a4 being kept unchanged.

• (1) a1: geometry and nucleation. Simulations are carried out on the half-disk geometry of radius R with an axisymmetrical condition with respect to the rectilinear edge of length 2R. The location for nucleation is imposed at the bottom of the simulation domain, i.e., at the south pole, labeled SP in Figure 8(r1).

  Fig. 8

  

  Present CAFE model predictions for (c1) the normalized average copper content ${{\left( { \langle w \rangle - w_{0} } \right)} \mathord{\left/ {\vphantom {{\left( { \langle w \rangle - w_{0} } \right)} {w_{0} }}} \right. \kern-\nulldelimiterspace} {w_{0} }}$, and (c2) the normalized eutectic volume fraction (g ^E − g ^E_GS )/g ^E_GS , with g ^E_GS the volume fraction of the eutectic structure predicted by the Gulliver–Scheil model for the nominal composition w ₀. The contact area of the alumina plate with the south pole of the droplet (SP), is simulated by the model using surface A′ (thick black line). Heat is also extracted through the droplet-free surface A (thick gray line). Approximate system diameter: 5.3 mm

• (2) a2: heat transfer. In order to model the heat exchange for triggered samples, the total boundary of the domain is divided into two parts, A and A′, in which distinct time-dependent heat transfer conditions are applied. The A′ is nothing but the contact area between the droplet and the alumina plate, while A represents the rest of the droplet surface. The configuration is applied for all calculations and is schematized in Figure 8(r1). Fourier boundary conditions are assumed, defined by two values of the heat transfer coefficients related to the A and A′ external boundaries h ^A_ext (t) and $h_{\text{ext}}^{A^{\prime}} \left( t \right)$and temperature T _ext such that $\dot{q}_{\text{ext}} = h_{\text{ext}}^{A} \left( {T|_{A} - T_{\text{ext}} } \right) + h_{\text{ext}}^{A^{\prime} } \left( t \right)\left( {T|_{A^{\prime} } - T_{\text{ext}} } \right)$ with $T|_{A}$ and $T|_{A^{\prime} }$, the temperature fields at the various location of the boundaries, defined by A and A′. Prior to the nucleation of the primary phase, $h_{\text{ext}}^{A^{\prime} } \left( t \right)$ is taken equal to h ^A_ext and the boundary condition is thus similar to that used for spontaneous nucleation. Its adjustment is based on the cooling rates measured prior to the primary phase nucleation, $\dot{T}\left( {t < t_{N}^{s} } \right)$.[6] While h ^A_ext is maintained constant after nucleation, the heat transfer coefficient between the alumina plate and the fully solid droplet is adjusted by assuming that $h_{\text{ext}}^{A^{\prime} } \left( {t > t_{\text{end}} } \right)$ is representative of the heat flow from the time of nucleation, $h_{\text{ext}}^{A^{\prime} } \left( {t > t_{N}^{s} } \right) = h_{\text{ext}}^{A^{\prime} } \left( {t > t_{\text{end}} } \right)$. A single value is used for the simulation of all droplets. After nucleation, $h_{\text{ext}}^{A^{\prime} } \left( t \right)$ is thus abruptly increased from $h_{\text{ext}}^{A^{\prime} } \left( {t < t_{N}^{s} } \right)$ to $h_{\text{ext}}^{A^{\prime} } \left( {t > t_{N}^{s} } \right)$. The fitted values h ^A_ext , $h_{\text{ext}}^{A^{\prime} } \left( {t < t_{N}^{s} } \right)$, and $h_{\text{ext}}^{A^{\prime} } \left( {t > t_{N}^{s} } \right)$ are listed in Table II.

• (3) a5: growth. The standard growth algorithm of the CA model is used,[15] thus not considering an arbitrarily spherical shape for the grain envelope. The growth rate is calculated as a function of the supersaturation using Eqs. [6] and [7] with $w_{v}^{l,\infty } = \left\langle {w_{v} } \right\rangle$.

All data for the simulations are listed in Tables II and III. The present model has first been applied to the solidification experiments with spontaneous nucleation, yet assuming no nucleation undercooling for the eutectic structure and using parameters for the Fourier boundary condition reported in Reference 6. Only the results in terms of the final global amount of eutectic are reported in Table IV as g ^E_CAFE  = 6.8 pct for the Al-4 wt pct-Cu, g ^E_CAFE  = 33.48 pct for the Al-14 wt pct-Cu, and g ^E_CAFE  = 67 pct for the Al-24 wt pct-Cu. These predictions are very close to the results of the simulations presented earlier with the semianalytical model when an isothermal transformation is assumed to occur at the eutectic temperature (values in c2l2, c2l6, and c2l10 in Table VI of Reference 6 are provided in the normalized fraction of eutectic ${{g^{e} } \mathord{\left/ {\vphantom {{g^{e} } {g_{\text{GS}}^{e} }}} \right. \kern-\nulldelimiterspace} {g_{\text{GS}}^{e} }}$ equivalent to ${{g^{E} } \mathord{\left/ {\vphantom {{g^{E} } {g_{\text{GS}}^{E} }}} \right. \kern-\nulldelimiterspace} {g_{\text{GS}}^{E} }}$ with the notations of the present contribution): ${{g^{e} } \mathord{\left/ {\vphantom {{g^{e} } {g_{\text{GS}}^{e} }}} \right. \kern-\nulldelimiterspace} {g_{\text{GS}}^{e} }} = 0. 7 2$ for the Al-4 wt pct-Cu, ${{g^{e} } \mathord{\left/ {\vphantom {{g^{e} } {g_{\text{GS}}^{e} }}} \right. \kern-\nulldelimiterspace} {g_{\text{GS}}^{e} }} = 0. 8 1$ for the Al-14 wt pct-Cu, and ${{g^{e} } \mathord{\left/ {\vphantom {{g^{e} } {g_{\text{GS}}^{e} }}} \right. \kern-\nulldelimiterspace} {g_{\text{GS}}^{e} }} = 0. 7 1$ for the Al-24 wt pct Cu. But these predictions deviate from the measurements also given in Table IV, g ^E _D . These deviations were explained by the role of the nucleation undercooling and recalescence associated with the eutectic microstructure, which cannot be neglected for the prediction of the final as-solidified state.[6] The present CAFE simulations thus provide a new validation of the numerical model compared with a semianalytical model,[6] but at the same time clearly identify its limitation for the prediction of the phase fractions when nucleation undercooling and the possible recalescence of secondary phases occur. Implementation of the nucleation and growth of secondary microstructures forming mainly in an interdendritic liquid but also possibly in the extradendritic liquid would thus be justified in order to improve the present CAFE model.

Figure 6 compares the predicted cooling to the measurements for the three Al-Cu triggered samples. The black, plain curves correspond to the temperature averaged over the entire simulation domain T _CAFE, while the black curves with upward triangles and downward triangles are the temperature at the north and south poles of the simulation domain, T _NP and T _SP , respectively. During the initial cooling in the liquid state (t < t ^s _N ), the predicted cooling rate is almost constant and reproduces well the recorded temperature histories. This is due to the adjustment of the same parameters of the Fourier boundary condition applied to A and A′ before t ^s _N . At the time at which the nucleation undercooling is reached, sharp changes in the predicted cooling rate starts at the nucleation point, as is clearly revealed by T _SP . Again, the increase in the cooling rate is due to the adjustment of the parameters on A′, thus simulating the contact of the triggering device on the droplet. Very soon after this nucleation event at the south pole, a temperature increase is computed at the north pole, T _NP . This evolution is comparable with the temperature evolution recorded by the pyrometer seeing the top surface of the droplet. Consideration of the three simulated temperatures for each sample also shows nonuniform cooling due to the role of the triggering device that almost serves as a chill. The effect is also very clear when considering the systematic increase in the DAS from the south pole to the north pole displayed in Figure 7(c3). Also of interest is the large deviation in the average predicted temperature T _CAFE from the recorded cooling history. The present nonisothermal CAFE model is thus found very useful for interpreting the experimental cooling curve. The situation is different for spontaneous nucleation because, in the absence of a heat sink, the entire system experiences a recalescence.[3,6] The temperature gradient is then limited and is localized in the liquid surrounding the mushy zone soon after the onset of the spontaneous nucleation event. The assumption of a uniform temperature field can thus be justified for spontaneous nucleation but not for triggered nucleation. A eutectic plateau is predicted by the model on the cooling curves in Figures 6(b) and (c). The length of the plateau increases with the alloy composition. This result is in line with the experimental observations. The predicted average eutectic volume fractions g ^E_CAFE are listed in Table IV together with the measured values g ^E _D . These values are close to the Gulliver–Scheil model predictions g ^E_GS . Again, this can be explained by the short solidification time and the high heat extraction rate through the trigger, leading to a small effect of solid diffusion. However, for the Al-24 wt pct-Cu sample, the final amount of eutectic can only be retrieved if one account for the measured undercooling prior to the nucleation ΔT ^E _N  = 20 K (Table III), leading to the value g ^E_CAFE  = 65 pct, i.e., close to the measured value g ^E _D  = 61.62 pct. The model prediction increases up to g ^E_CAFE  = 81.4 pct when the simulation is run with an isothermal eutectic transformation at the eutectic temperature T _E , i.e., with no nucleation undercooling.

For a given alloy composition, consideration of microsegregation modeling accounting only for diffusion in the solid phase and complete mixing in the liquid predicts more eutectic in a location in which the Fourier number for the solid phase is smaller. With a Fourier number equal to zero, such a microsegregation approach retrieves the result of the Gulliver–Scheil approximation. The Fourier number is proportional to the diffusion in the solid phase and the solidification time and inversely proportional to the square of the characteristic DAS. A higher fraction of eutectic is thus expected at the south pole, at which the solidification time is the lowest and the DAS the smallest. This is for the instance observed on the Al-24 wt pct-Cu sample. However, the solute diffusion in the solid phase is not sufficient for the interpretation of the present results. It is not only the average composition of the alloy that is not constant, as shown in Figure 7(c1); in addition, no sign of the eutectic transformation is present on T _SP , as shown in Figure 6(c). Evaluation of the magnitude of the Fourier number for such a high cooling rate also reveals that solid diffusion is very unlikely to play a significant role. This comment demonstrates that interpretation of the experimental results is only possible using a numerical approach such as the one provided by the CAFE model.

Figure 8 summarizes the model predictions for the normalized average copper composition, ${{\left( {\left\langle w \right\rangle - w_{0} } \right)} \mathord{\left/ {\vphantom {{\left( {\left\langle w \right\rangle - w_{0} } \right)} {w_{0} }}} \right. \kern-\nulldelimiterspace} {w_{0} }}$, and the eutectic volume fraction, (g ^E – g ^E_GS )/g ^E_GS . No map is provided for the DAS because the CAFE model is still limited by the use of a uniform value over the simulation domain. For the simulations of Figure 8, the average values listed in Table III measured over the entire experimental cross sections, DAS _D , are used. It should be recalled that a direct comparison with the experimental results in Figure 7 is not possible because there is no attempt to exactly reproduce the dendritic grain structure (as was the case, for example, in Reference 15). The overall variations of the distributions are yet retrieved by the model and can thus be used hereafter.

The first observation is that the magnitude of the segregation is less than the measured one for each alloy. For the triggered Al-4 pct wt-Cu sample, the correlation between the distribution map of copper and the eutectic fraction found in Figure 7(r1) is retrieved on the simulated maps presented in Figure 8(r1). Because the eutectic transformation is modeled with no eutectic undercooling, the remaining liquid at T _E that transforms into eutectic only depends on the average local composition and the effect of diffusion in the solid. But the latter effect is small for the triggered samples, as explained earlier. Consequently, less eutectic is found in the region of lower average copper content, typical of the result known from classical microsegregation analyses when decreasing the alloy composition. The lower average composition at the south pole is explained by the diffusion of species from the mushy zone toward the extradendritic liquid as well as inside the mushy zone, due to the temperature gradient that creates a gradient of the interdendritic liquid composition. Thus, diffusion in the liquid is a key phenomenon to account for in order to give an adequate interpretation of the present observations.

The case of Al-24 wt pct-Cu is not as straightforward. As mentioned previously, more eutectic is found at the bottom of the sample, where the average composition is only slightly lower than elsewhere in the sample (Figure 7(r3)), which is thus opposite to the observation for the Al-4 wt pct-Cu. The simulation in Figure 8(r3) shows a trend similar to the experimental observations and can thus be analyzed in more detail. While diffusion of Cu outside the mushy zone is still accounted for, it does only slightly change the amount of solute at the bottom of the sample. In fact, a quenching mechanism is observed. As shown in Figure 6(c), the bottom part of the sample becomes fully solid (its temperature decreases below T _E – ΔT _E ) in only a fraction of second after primary nucleation of the dendritic phase. Because a large nucleation undercooling was used for the primary solid, a small fraction of solid was formed prior to nucleation and growth of the eutectic structure in the interdendritic liquid. In other words, the bottom part of the sample underwent phase transformations with a large deviation from the initial and final temperatures defined by the equilibrium solidification interval. Such a quenching of the interdendritic liquid into a eutectic structure is not observed in the Al-4 wt pct-Cu sample for several reasons. At first, solidification started close to the liquidus temperature and the solidification interval is larger as compared to Al-24 wt pct-Cu. As a consequence, the release of latent heat prevents fast cooling of the bottom part of the system below the temperature at which the eutectic transformation takes place. The intermediate situation found with the Al-14 wt pct-Cu sample is interesting to analyze. With a nucleation event also close to the liquidus temperature of the alloy, the solidification interval is smaller and, hence, solidification takes place in less than 1 second. Small variations of the eutectic fraction are found in the distribution maps of Figures 7(c2r2) and 8(c2r2). However, while small variations of the Cu distribution are simulated in Figure 8(c1r2), the measurements reveal a significant gradient of the average composition, from high content at the bottom to low content at the top. It is believed that inverse segregation thus also plays a role,[42] revealed when no large nucleation undercooling is achieved and the solidification interface is sufficiently large. Although the present model is capable of dealing with the macrosegregation influenced by fluid flow, as shown elsewhere,[40] it is not yet coupled with a general thermomechanical analysis.[43,44] To account for these phenomena, a variation in the density of the alloy with the fraction of the phases is required. Even with a fixed solid, considering a constant density of the solid phase and potentially no thermomechanical deformation, the total volume of the simulation domain must be adapted by tracking the interface between the liquid and the gas, which is not yet possible with the present CAFE model.

5 Conclusions

The findings of the experimental and numerical studies are summarized as follows.

• 1. The Al-Cu alloy systems have been solidified using the EML technique developed at the DLR with compositions of 4, 14, and 24 wt pct Cu. Samples are approximately spherical in shape with a radius of 2.65·10⁻³ m. The nucleation of the primary phase has been initiated using an alumina plate at the lower surface for each sample. Nonequilibrium temperature histories have been recorded using an optical pyrometer. Significant heat loss is found to take place through the trigger from the south pole of the droplets. The local Cu content together with the eutectic volume fraction and the DAS have been measured. The normalized distribution maps reveal macrosegregation at the scale of the droplet and monotonic increase of the DAS from the south pole to the north pole. These data, averaged over the entire metallographic cross sections, give values that can be compared with those previously obtained for spontaneously solidified samples.[6]

• 2. An advanced microsegregation model has been embedded in a 2-D CAFE model together with a mesh adaptation technique. The new model could be seen as an extension of the previous CAFE modeling in two main directions, as follows.

  • a. The CA model accounts for diffusion in the solid and liquid phases together with the nucleation and growth undercooling of the primary solid phase.

  • b. The FE method solves the solute diffusion in the liquid in front of the mush/liquid boundary over an adaptive mesh the size of which depends on the local solute profile. Extensive validations of the model have been conducted showing its capability of dealing with solute diffusion inside and outside a growing mushy zone.

• 3. Applications of the CAFE model to the solidification of the processed Al-Cu droplet have been achieved. The predicted temperature curves give a coherent explanation of the measured temperature evolutions (Figure 6). Although the magnitudes of the simulated average composition and eutectic maps (Figure 8) show a deviation from the measurements, the model is successfully used to interpret the experimental observations. Diffusion in the solid is identified to have a minor effect compared to diffusion in the liquid. As for spontaneously solidified samples, the nucleation undercooling of the secondary eutectic structure is found to play a major role.

• 4. Limitations of the CAFE model are also found, such as the absence of a coarsening model to be embedded in the CA microsegregation model, and the possibility of accounting for the nucleation and growth of secondary microstructures, such as eutectics. Similarly, laboratory-scale experiments are required in order to quantify the solutal interaction between grains. This would ideally benefit from in-situ measurements using a synchrotron radiation facility.