1 Introduction

Macrosegregation refers to variations in composition that arise in alloy castings or ingots and range in scale from several millimeters to centimeters or even meters. These compositional variations detrimentally affect the subsequent processing behavior and properties of cast materials and can lead to rejection of cast components or processed products.[1] Therefore, it is important to study macrosegregation and its formation mechanism experimentally[2,3] or via simulation methods,[4,5,6,7] such studies are of great significance for applying appropriate technological means to eliminate these defects. The typical segregation pattern in the ingot is a positive segregation in the upper region, a negative segregation in the lower region, V-segregation along the centerline, and A-segregations in the middle-radius region between the outer surface of the casting and the centerline.[8,9]

A-segregation is a kind of channel segregation caused by the enrichment of solute in a local area during ingot solidification. Researchers have been investigating the formation mechanism of A-segregation for decades, and many mechanisms have been proposed,[10] including flow due to solidification shrinkage, thermal and solutal natural convection of the liquid, motion of free equiaxed grains, and deformation of the solid skeleton in the mushy zone. According to the most accepted theory, the main factor is the flow instability of the solidification front, which is controlled by the solute and temperature conditions during solidification.[11]

Bennon and Incropera[12] were among the first to predict A-segregation in solidification from the side of an H2O-30 wt pct NH4Cl solution in a rectangular cavity. Mehrabian et al.[13] studied the combined effect of shrinkage and natural convection in the liquid phase. They showed that the macrosegregation pattern strongly depends on the orientation of the variation in the density of the interdendritic liquid and the solid fraction. They also proposed the hypothesis that A-segregations develop due to flow instability, which occurs at a critical flow condition. Combeau et al.[14] used the volume-averaging method, which takes into account the motion and the morphology of equiaxed grains, to predict A-segregation in a large, 3.3-ton ingot. They showed that many A-segregations formed at the top of the ingot. They also investigated the role of inertia of flow through the dendritic mushy zone in channel segregations.[15] Wu and co-workers[11] used the three-phase columnar–equiaxed mixed model to simulate macrosegregation in a 2.45-ton ingot. The results showed that equiaxed grains are not necessary to producing A-segregation. However, both the appearance of equiaxed grains and their interaction with the growing columnar dendrite tips strengthen A-segregation. They also showed that with increasing flow intensity, the deflection angle of A-segregations toward the top of ingot increases gradually. In 2017, they proposed a four-phase volume-averaging model,[16] which included the gas phase; the results showed that the motion of the equiaxed grains and their interaction with the melt flow in the vicinity of the growing columnar caused A-segregation. Zaloznik and Combeau[10] studied the effects of the thermosolutal flow in steel ingots on A-segregation using a multiscale solidification model. The difference between A-segregation and V-segregation was found to be determined by the flow direction, namely, A-segregation was caused by upward flow and V-segregation by downward flow. Medina et al.[17] investigated the effects of alternating magnetic fields on channel segregation; they changed the flow direction of the melt using a magnetic field and obtained channel segregation in different directions. Ge and co-workers investigated the effects of secondary dendrite arm spacing[18] and ingot size[19] on macrosegregation. The results showed that the flow channel, remelting, and sedimentation of equiaxed grains are not the necessary conditions for the formation of A-segregation.

In the study of the formation mechanism of A-segregation, the morphology is recognized to be an important and indispensable factor. Therefore, in recently established numerical models,[11,14] the simplified morphology of columnar and equiaxed grains was taken into account to study A-segregation. However, these numerical models all preset the standard shape and growth direction of the columnar and simplified the equiaxed grains as an outline crystal surrounded by an envelope, neglecting the wall equiaxed grains.

In this paper, a cellular automaton–lattice Boltzmann method (CA–LBM) coupling model is established, and the mechanism of A-segregation of Fe-0.34 wt pct C alloy ingot is investigated on the basis of microstructural morphology. In addition, compared with the continuum model and the volume-averaging method, the CA–LBM model is far simpler, with a simplified programming process and high computational efficiency.

2 Model Description

The CA–LBM coupling model[20,21,22,23] is used to simulate the solidification process of a Fe-0.34 wt pct C ingot. The solute diffusion model in the CA method is used to capture the solid/liquid interface, while the LBM is used to calculate the transport phenomena.

2.1 LBM Model

In contrast with the traditional computational fluid dynamics models, the LBM abstracts the fluid into a large collection of virtual particles, which collide and migrate on a discrete lattice in a certain manner to form the macroscale fluid flow phenomenon. The advantages of this method are simple calculation, good stability, and complex boundaries that are essentially parallel and easy to deal with.[24]

In this paper, a single-relaxation-time LBGK (lattice Bhatnagar–Gross–Krook) D2Q9 model[25] is used. The evolution of the distribution function, considering the force term, can be written as

$$ f_{i} \left( {\varvec{x} + \varvec{e}_{i} \Delta t,\;t + \Delta t} \right) - f_{i} (\varvec{x},\;t) = 1/\tau_{\text{f}} \left[ {f_{i}^{\text{eq}} (\varvec{x},\;t) - f_{i} (\varvec{x},\;t)} \right] + F_{i} (\varvec{x},\;t), $$
(1)
$$ h_{i} \left( {\varvec{x} + \varvec{e}_{i} \Delta t,\;t + \Delta t} \right) - h_{i} (\varvec{x},\;t) = 1/\tau_{\text{h}} \left[ {h_{i}^{\text{eq}} (\varvec{x},\;t) - h_{i} (\varvec{x},\;t)} \right] + H_{i} (\varvec{x},\;t), $$
(2)
$$ g_{i} \left( {\varvec{x} + \varvec{e}_{i} \Delta t,\;t + \Delta t} \right) - g_{i} (\varvec{x},\;t) = 1/\tau_{\text{g}} \left[ {g_{i}^{\text{eq}} (\varvec{x},\;t) - g_{i} (\varvec{x},\;t)} \right] + G_{i} (\varvec{x},\;t), $$
(3)

where x and t are the space and time of the particles, respectively, Δt is the time step, and f i (x, t), h i (x, t), and gi(x, t) are the distribution functions of fluid flow, thermal transport, and the solute transport, respectively, indicating that a particle at time t appears in the probability of position x, and the discrete velocity of the particle in the i direction can be expressed as (4)

$$ \varvec{e}_{i} = \left\{ {\begin{array}{ll} {(0,\;0)} &\quad {i = 0}, \\ {c(\cos [(i - 1)\pi /2],\;\sin [(i - 1)\pi /2])} &\quad {i = 1,\;2,\;3,\;4}, \\ {\sqrt 2 c(\cos [(2i - 1)\pi /4],\;\sin [(2i - 1)\pi /4])} &\quad {i = 5,\;6,\;7,\;8}. \\ \end{array} } \right. $$
(4)

\( f_{i}^{\text{eq}} (\varvec{x},\;t),\;h_{i}^{\text{eq}} (\varvec{x},\;t), \) and \( g_{i}^{\text{eq}} (\varvec{x},\;t) \) are the equilibrium distribution functions for the fluid flow, thermal transport and solute transport field, respectively; they can be written as (5) through (7)

$$ f_{i}^{\text{eq}} (\varvec{x},\;t) = \omega_{i} \rho \left[ {1 + 3\varvec{e}_{i} \cdot \varvec{u}/c^{2} + 9\left( {\varvec{e}_{i} \cdot \varvec{u}} \right)^{2} /2c^{4} - 3(\varvec{u} \cdot \varvec{u})/2c^{2} } \right], $$
(5)
$$ h_{i}^{\text{eq}} (\varvec{x},\;t) = \omega_{i} T\left[ {1 + 3\varvec{e}_{i} \cdot \varvec{u}/c^{2} + 9\left( {\varvec{e}_{i} \cdot \varvec{u}} \right)^{2} /2c^{4} - 3(\varvec{u} \cdot \varvec{u})/2c^{2} } \right], $$
(6)
$$ g_{i}^{\text{eq}} (\varvec{x},\;t) = \omega_{i} C\left[ {1 + 3\varvec{e}_{i} \cdot \varvec{u}/c^{2} + 9\left( {\varvec{e}_{i} \cdot \varvec{u}} \right)^{2} /2c^{4} - 3(\varvec{u} \cdot \varvec{u})/2c^{2} } \right], $$
(7)

where ω i is the weighting coefficient for each direction, namely, ω0 = 4/9, ω1-4 = 1/9, ω5-8 = 1/36, and c is the lattice speed.

τf, τh, and τg are the relaxation times for fluid flow, thermal transport, and solute transport, respectively. According to the Chapman–Enskog analysis, the kinematic viscosity, ν, thermal diffusivity, α, and solutal diffusivity, D, are related to τf, τh, and τg, respectively,

$$ \nu = c^{2} \Delta t\left( {\tau_{\text{f}} - 1/2} \right)/3\quad \alpha = c^{2} \Delta t\left( {\tau_{\text{h}} - 1/2} \right)/3\quad D = c^{2} \Delta t\left( {\tau_{\text{g}} - 1/2} \right)/3. $$
(8)

F i (x, t) is the force term caused by natural convection,

$$ F_{i} (\varvec{x},\;t) = \left( {1 - 1/2\tau_{\text{f}} } \right)\omega_{i} \left[ {3\left( {\varvec{e}_{i} - \varvec{u}} \right)/c^{2} + 9\left( {\varvec{e}_{i} \cdot \varvec{u}} \right)\varvec{e}_{i} /c^{4} } \right] \cdot \varvec{F}\Delta t, $$
(9)

where F is the buoyancy term; according to the Boussinesq approximation,[21] F can be written as (10)

$$ \varvec{F} = - g\rho_{0} \beta_{\text{T}} \left( {T - T_{0} } \right) - g\rho_{0} \beta_{\text{C}} \left( {C_{\text{l}} - C_{0} } \right), $$
(10)

where βT and βC are the expansion coefficients for the temperature and composition, respectively:

$$ \beta_{\text{T}} = - \partial \rho /\rho_{0} \cdot \partial T\quad \beta_{\text{C}} = - \partial \rho /\rho_{0} \cdot \partial C. $$
(11)

H i (x, t) and G i (x, t) are the source terms for the latent heat and solute diffusion, respectively:

$$ H_{i} (\varvec{x},\;t) = \omega_{i} \Delta f_{\text{s}} \Delta H/C_{\text{P}} \quad G_{i} (\varvec{x},\;t) = \omega_{i} \Delta f_{\text{s}} C_{\text{l}} (1 - k), $$
(12)

where Δfs is the increased solid fraction, ΔH is the latent heat, Cp is the specific heat capacity, and k is the equilibrium distribution coefficient.

The macroscopic variables such as the fluid density, ρ, velocity, u, composition, Cl, and temperature, T, can be obtained by the corresponding distribution function:

$$ \rho = \sum\limits_{i = 0}^{8} {f_{i} } \quad \rho \varvec{u} = \sum\limits_{i = 0}^{8} {f_{i} \varvec{e}_{i} + F\Delta t/2} \quad C_{\text{l}} = \sum\limits_{i = 0}^{8} {g_{i} } \quad T = \sum\limits_{i = 0}^{8} {h_{i} } . $$
(13)

2.2 CA Model

2.2.1 Nucleation model

In this paper, we use the continuous nucleation model based on the Gaussian distribution proposed by Rappaz. For the specific steps, please refer to Reference 26.

2.2.2 Growth model

The cells in the domain are divided into three states: solid, liquid, and interface. Initially, all cells are set as liquid, and assigned a temperature, concentration, velocity, and solid fraction. Nucleation is simulated by the continuous nucleation model. Once a certain cell reaches the nucleation condition, it begins to nucleate and transform the cell into the interface state. The increased solid fraction is calculated using the solute diffusion model.[27] When the solid fraction of the interface cells reaches one, the cells are transformed into a solid. The difference between the equilibrium solute concentration of the solid/liquid interface and the actual solute concentration of the liquid phase constitutes the driving force of the dendrite growth. From the thermodynamic conditions, the interface equilibrium composition can be written as (14)

$$ C_{\text{L}}^{\text{eq}} = C_{0} + \left( {T_{\text{L}}^{ * } - T_{\text{L}}^{\text{eq}} } \right)/m, $$
(14)

where C0 is the initial composition, the interface temperature \( T_{\text{L}}^{*} \) can be calculated by LBM, \( T_{\text{L}}^{\text{eq}} \) is the equilibrium liquidus temperature at the initial composition, and m is the liquidus slope of the phase diagram.

The increased solid fraction of the interface cells can be expressed as (15)

$$ \Delta f_{\text{s}} = \left( {C_{\text{l}}^{\text{eq}} - C_{\text{l}} } \right)/\left[ {C_{\text{l}}^{\text{eq}} (1 - k)} \right]. $$
(15)

2.3 CA–LBM Coupling Model

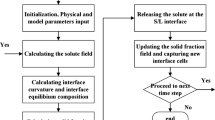
The calculation steps of the CA–LBM coupling model during the solidification process are as follows:

  1. (1)

    Initializing the composition, temperature, velocity, and solid fraction of each cell.

  2. (2)

    Calculating the flow, temperature, and solutal field by solving Eqs. [1] through [13] for each cell; the macroscopic physical variables (such as velocity, temperature, and composition) can be obtained using Eq. [13].

  3. (3)

    Calculating the increased solid fraction of interface cells according to Eqs. [14] and [15].

  4. (4)

    Adding the latent heat and rejected solute to the distribution function of the same interface cell according to Eq. [12]; if the solute concentration of the interface cell is higher than its equilibrium composition, then the excess solute is added to the surrounding neighbor interface or liquid cells according to concentration gradient. If the interface cells are solidified, then the neighboring liquid cells are captured as interface cells by the eight-neighbor capture method,[22] and the rejected solute is added to these cells.

  5. (5)

    Repeating steps (2) through (4) until the end of the solidification.

3 Model Verification

To verify the accuracy of the CA–LBM coupling model for dendrite growth, the growth of a single dendrite under natural convection is simulated. The region is divided into 200 × 200 grids, each with a grid size of 0.5 μm. The initial supercooling is 1 K, and the initial component is Fe-0.34 wt pct C.

The supercooling of dendritic growth is composed mainly of three parts, ignoring the kinetic effect. The total supercooling can be expressed as thermal, solutal, and capillary supercooling:

$$ \Delta T = H\Omega_{\text{T}} /C_{\text{P}} + |m|C_{0} (k - 1)\Omega_{\text{C}} /\left[ {1 - (1 - k)\Omega_{\text{C}} } \right] + 2\Gamma /R, $$
(16)

where H is the latent heat, Cp is the specific heat capacity, Γ is the Gibbs–Thomson coefficient, and R is the tip radius. According to the two-dimensional modified Ivantsov solutions mentioned in the literature,[28] we obtain the dimensionless temperature saturation ΩT and the dimensionless composition saturation ΩC under natural convection:

$$ \Omega_{\text{T}} = \sqrt {\pi P_{\text{T}} } e^{{P_{\text{T}} }} \left( {{\text{erfc}}\left( {\sqrt {P_{\text{T}} } } \right)} \right) - {\text{erfc}}\left( {\sqrt {P_{\text{T}} \left( {1 + 2\delta_{\text{T}} /R} \right)} } \right), $$
(17)
$$ \Omega_{\text{C}} = \sqrt {\pi P_{\text{C}} } e^{{P_{\text{C}} }} \left( {{\text{erfc}}\left( {\sqrt {P_{\text{C}} } } \right)} \right) - {\text{erfc}}\left( {\sqrt {P_{\text{C}} \left( {1 + 2\delta_{\text{C}} /R} \right)} } \right), $$
(18)

where δT and δC are the thicknesses of the temperature and composition boundary layers, respectively, and PT and PC are the temperature and the composition Peclet numbers, respectively, which can be expressed as

$$ \delta_{\text{T}} /R = \lambda Ra_{\text{T}}^{ - 1/4} (1 + N/\sqrt {Le} )^{ - 1/4} \quad \delta_{\text{C}} /R = \lambda Ra_{\text{C}}^{ - 1/4} (1 + \sqrt {Le} /N)^{ - 1/4} , $$
(19)
$$ P_{T} \equiv VR/ 2\alpha \quad P_{C} \equiv VR/ 2D ,$$
(20)

where Le is the Lewis number, and the coefficient λ is set to be 2.2.[29] N is the buoyancy parameter:

$$ Le \equiv \alpha /D\quad N = \beta_{\text{C}} \left( {C_{i} - C_{0} } \right)/\beta_{\text{T}} \left( {T_{i} - T_{0} } \right), $$
(21)

where RaT and RaC are the thermal and solutal Rayleigh numbers, respectively, and can be written as

$$ Ra_{\text{T}} = g\beta_{\text{T}} L^{3} \left( {T_{i} - T_{0} } \right)/\alpha \nu \quad Ra_{\text{C}} = g\beta_{\text{C}} L^{3} \left( {C_{i} - C_{0} } \right)/D\nu . $$
(22)

The single-dendrite growth morphology of Fe-0.34 wt pct C alloy under natural convection is shown in Figure 1. Evidently, the dendrite is asymmetric, and the growth of the upstream arm is promoted, whereas that of the downstream arm is suppressed.

Fig. 1
figure 1

Simulated single-dendrite growth of Fe-0.34 wt pct C under natural convection in the supercooled melt. (a) Composition field and (b) temperature field

Full size image

The steady-state growth velocity of the upstream tip is 4.012 × 10−6 m s−1, according to the above LGK model. The steady-state growth velocity of the upstream, downstream, and horizontal tips according to the CA–LBM coupling model is shown in Figure 2. The dendritic growth time step is taken as 5 × 10−5 seconds. The steady-state growth velocity of the upstream tip is 3.94 × 10−6 m s−1, which is consistent with the LGK analytical solution. This agreement verifies that the coupling model accurately calculates the dendritic growth.

Fig. 2
figure 2

Evolution of the tip growth velocity under natural convection

Full size image

4 Research Program

To understand the formation mechanism of A-segregation, researchers have conducted many studies. Prescott and Incropera[30] argued that A-segregation is caused by the fusing of secondary dendrites of columnar, which means that segregation should occur in the columnar region. In contrast, Lesoult[31] found that A-segregation occurs in the equiaxed region; thus, the fusing of the secondary dendrites of columnar is unnecessary for the formation of A-segregation. To address this issue, the research program of this paper is as follows:

  1. (1)

    In calculating the solidification process of the ingot using the CA–LBM model, set the limit conditions so that the columnar merely appear in the ingot. In other words, in addition to the wall of the equiaxed grain area, the other areas of the ingot consist of columnar dendrites. Calculate whether A-segregation occurs in this case and determine the reasons.

  2. (2)

    Set the limit conditions, so that the columnar–equiaxed transition (CET) occurs in the ingot. Calculate whether A-segregation occurs in this case and determine the reasons.

  3. (3)

    Set the limit conditions in which the equiaxed region can only appear in the ingot. Calculate whether A-segregation occurs in this case and determine the reasons.

  4. (4)

    Summarize the above situations, and analyze the formation mechanisms of A-segregation.

5 Simulation Results

5.1 Two-Dimensional Global Columnar Solidification Process

The CA–LBM coupling model was used to simulate the solidification process of the two-dimensional global columnar region. The formation of macrosegregation was analyzed to determine whether A-segregation occurred in the ingot.

5.1.1 Calculation conditions

A typical Fe-0.34 wt pct C ingot is simulated; the calculation conditions are set as follows:

(1) The size is 32 mm × 85 mm, the initial composition is Fe-0.34 wt pct C, the temperature is 1785 K, and the ambient temperature is constant at 300 K. The upper boundary is adiabatic, wherein the heat transfer coefficients between the other three boundaries and the environment are 700 W m−2 K−1, and gravity is 9.8 m s−2.

(2) Solute diffusion exists only in the liquid phase, and the diffusion of the solute in the solid phase is neglected.

(3) The internal equiaxed nucleation density is set to zero, so that only the wall equiaxed and columnar regions coexist in the ingot.

(4) The remelting phenomenon is overlooked during solidification.

5.1.2 Boundary conditions

When calculating the flow field, we use the non-slip boundary condition[22] for the regional and solid/liquid boundaries. For the temperature field, the thermal conductivity of the solid and liquid phases is approximately equal, and the non-equilibrium extrapolation scheme[32] is used for the regional boundaries. For the solutal field calculation, the solute diffusion in the solid is neglected, the zero-flux boundary condition is used for the regional boundaries, and the bound-back scheme[33] is used for the solid/liquid boundaries.

5.1.3 Alloy thermo-physical parameters

The thermo-physical parameters of Fe-0.34 wt pct C are shown in Table I.

Table I Thermo-physical Parameters of Fe-0.34 Wt Pct C
Full size table

5.1.4 Evolution of the flow field and temperature field of global columnar solidification

The columnar morphology and the flow field of the melt calculated by the CA–LBM model are shown in Figure 3. The corresponding temperature field is shown in Figure 4. Half of the area of the ingot is considered for analysis. Figure 3 shows that due to the chilling effect of the wall, the thin equiaxed region formed in the three cooling boundaries, and the direction of heat dissipation caused the equiaxed regions to competitively grow into columnar regions. At the same time, the excess solute discharged to the interface front enriched this region with the solute. Because carbon is less dense than iron, its solutal buoyancy force is upward. On the other side, the melt temperature near the wall is lower than that of the internal melt because of the heat dissipation of the wall, and its thermal buoyancy force is downward. Thus, two opposite movements exist in the melt in front of the interface.

Fig. 3
figure 3

Predicted morphology and flow direction of the melt during global columnar solidification. (a) 30 s, (b) 60 s, (c) 90 s, (d) 120 s, and (e) 200 s

Full size image
Fig. 4
figure 4

Evolution of temperature during global columnar solidification. (a) 30 s, (b) 60 s, (c) 90 s, (d) 120 s, and (e) 200 s

Full size image

According to the literature,[10] the intensities of the two opposite trends are compared with the ratio of N (solutal buoyancy to thermal buoyancy):

$$ N = \beta_{\text{C}} \Delta C/\beta_{\text{T}} \Delta T = \beta_{\text{C}} /m_{\text{L}} \beta_{\text{T}} , $$
(23)

where ΔC and ΔT are the characteristic concentration and temperature differences, respectively, and mL is the liquidus slope. When we enter the data into the above formula, we find that |mLβT| < |βC|, i.e., the solutal buoyancy effect dominates over the thermal buoyancy effect, causing the melt at the interface to flow upward and the internal melt to flow downward, thus forming a counter-clockwise vortex. As the solidification proceeds, the columnar dendrites continue to move forward; however, because they are tightly connected, with no gaps between them, the melt does not infiltrate into the columnar dendrites.

The phase diagram shows that the actual crystallization temperature is lower than the theoretical crystallization temperature in the liquid due to the change in concentration in a certain range front of the solid/liquid interface, forming a concentration supercooling zone. However, a critical condition exists:

$$ G/R = mC_{0} \left( {1 - k_{0} } \right)/Dk_{0} , $$
(24)

where G is the actual temperature gradient in the liquid front of the solid/liquid interface, R is the crystallization rate (the advancing velocity of the interface toward the liquid), m is the liquidus slope, D is the solute diffusion coefficient in liquid, and k0 is the solute partition coefficient. Only G/R < mC0(1 − k0)/Dk0 corresponds to the concentration of supercooling; however, because G/R > mC0(1 − k0)/Dk0 in this paper, the growth rate of the dendrites is determined by the heat dissipation, and the columnar will grow continuously in a planar manner.

The progress of the temperature field in Figure 4 is consistent with the principle of heat conduction. Notably, at the bottom-right corner, the columnar dendrites grow fastest (Figure 3) due to the faster cooling rate in this region than in the other regions.

5.1.5 A-segregation analysis during global columnar solidification

The evolution of the segregation is shown in Figure 5. At the initial stage of solidification, two high-concentration areas exist at the interface, one at the top (Figure 5, Zone-1) and the other at the bottom (Figure 5, Zone-2). During solidification, the top area gradually expands and eventually forms the top positive segregation. Moreover, the bottom area moves upward as the vortex moves, and a positive A-segregation forms in the middle-radius region between the surface of the ingot wall and the centerline. The number of such high-concentration melt regions varies depending on the rate of solidification and the strength of the flow, thus forming different numbers of A-segregation bands. Two A-segregation bands were found in this study.

Fig. 5
figure 5

Evolution of segregation during global columnar solidification. (a) 30 s, (b) 60 s, (c) 90 s, (d) 120 s, and (e) 200 s

Full size image

To analyze the A-segregation that appeared in Figure 5, the segregation values on the three straight lines [y = 20, 40, and 60 mm (Figure 6)] in the Y direction in Figure 5(e) are compared. In Figure 7, x = 0 mm is the center, and x = 16 mm is the wall of the ingot. The degree of segregation at x = 0 mm is the highest because the central axis is the final solidified area. As the value of x increases, the degree of segregation decreases, with some fluctuations. In particular, two peaks exist between the centerline and the wall, where the area of A-segregations appears. The three curves demonstrate that the values of A-segregation on the respective curves are not uniform, and the value near the upper curve is higher.

Fig. 6
figure 6

Configuration of the ingot

Full size image
Fig. 7
figure 7

The segregation ratio at y = 60 mm, y = 40 mm, and y = 20 mm

Full size image

To further explain the formation mechanism of A-segregation, we analyze Zone-3 (Figure 5). In the early state of solidification, the upward flow of the melt at the interface promotes the flow of the solute, resulting in the accumulation of the solute at the upstream position, thereby forming a high-concentration melt [Figure 8(a)] and a vortex [Figure 8(b)]. As the solid/liquid interface advances, the columnar regions solidify at this concentration, resulting in a higher concentration than that of the other regions. The high-concentration melt moves in two directions: one is the upward movement with the melt, and the other is the internal movement with the advance of the interface. Next, A-segregation [Figure 8(a)] is formed. Figure 8(c) shows the picture after the superposition of the columnar morphology and segregation. Clearly, segregation occurs through the columnar boundaries rather than at the columnar boundaries.

Fig. 8
figure 8

Formation of segregation in Zone-3 (marked in Fig. 5). (a) Segregation ratio. (b) Morphology of columnar dendrites and the streamlines. (c) Segregation mixed the morphology of columnar dendrites

Full size image

The flow instability of the melt results in the formation of the high-concentration melt, and the movement of the high-concentration melt results in A-segregation. Therefore, the flow state of the high-concentration melt will definitely affect the morphology of A-segregation. Next, we apply the three different heat dissipation coefficients of K1 = 800 W m−2 K−1, K2 = 700 W m−2 K−1, and K3 = 600 W m−2 K−1 to the simulation and compare the segregation values for y = 20 mm of the three results. As shown in Figure 9, with the increase in the heat dissipation coefficient, the A-segregation gradually moves toward the inside of the ingot, i.e., the deflection angle to the centerline of the A-segregation increases because the increase in the coefficient accelerates the velocity of the advancing interface.

Fig. 9
figure 9

Segregation ratio at y = 20 mm for three different coefficients of heat transfer. K1 = 800 W m−2 K−1, K2 = 700 W m−2 K−1, and K3 = 600 W m−2 K−1

Full size image

5.2 Two-Dimensional Global Columnar Solidification Process Without Natural Convection

To explore the effect of natural convection on the formation of A-segregation, the Fe-0.34 wt pct C solidification without natural convection is simulated. The calculation conditions and boundary conditions of the ingot are consistent with the conditions above. The morphology of the ingot is shown in Figure 10, and the corresponding segregation formation is shown in Figure 11.

Fig. 10
figure 10

Morphology of the ingot without natural convection. (a) 20 s, (b) 60 s, (c) 100 s, (d) 140 s, and (e) 200 s

Full size image
Fig. 11
figure 11

Predicted macrosegregation without natural convection. (a) 20 s, (b) 60 s, (c) 100 s, (d) 140 s, and (e) 200 s

Full size image

Comparing Figures 5 and 11 reveals that the presence of natural convection significantly affects the segregation patterns. With natural convection, the top positive segregation and A-segregation occur in the final ingot. In contrast, only positive segregation occurs at the centerline and the bottom corner, and no A-segregation occurs when the effect of convection is ignored.

At the beginning of solidification, the columnar region near the bottom-right corner will discharge excess solute, resulting in the liquid concentration being significantly higher than that at the other locations [Figure 11(a)]. At the same time, the temperature decline of this position is also the fastest. These two trends will offset each other, making the solid/liquid interface approach right-angle growth. As the solidification proceeds, the high-concentration region gradually expands and moves toward the inside, eventually forming a positive segregation band at the bottom-right corner. Moreover, the columnar region at the right side will discharge the excess solute into the solid/liquid interface because without natural convection, no concentration disturbance will occur to form the high-concentration melt and vortexes. Thus, these enriched melt areas gradually expand and extend inside, forming the large positive segregation zone.

We can thus conclude that the natural convection caused by thermosolutal flow is an important factor causing A-segregation. By changing the intensity of natural convection, A-segregations can be reduced effectively.

5.3 Two-Dimensional CET Solidification Process

No definite conclusion is drawn regarding the position of A-segregation. A study by Wu and co-workers[34] in a Sn-Pb laboratory casting revealed that channel segregation can originate and develop during pure columnar solidification, in which no equiaxed regions exist. Lesoult[31] found that the A-segregation can occur in the equiaxed region by studying 65-ton steel ingots. In this section, we analyze the CET process to discuss the position of the A-segregation.

5.3.1 Calculation conditions of CET

The calculation conditions and boundary conditions of the ingot are consistent with those in Section V–A. The only difference is that we must set the nucleation parameters of the internal equiaxed grains; the nucleation base density of internal equiaxed nmax is set to 3.6 × 108, and the mean value of nucleation supercooling ΔTV is set to 5 K.

5.3.2 Evolution of the flow and temperature field of CET

The evolution of the morphology and flow field is shown in Figure 12, and the temperature field is shown in Figure 13.

Fig. 12
figure 12

Predicted morphology and the flow direction of CET. (a) 20 s, (b) 60 s, (c) 100 s, and (d) 180 s

Full size image
Fig. 13
figure 13

Evolution of the temperature of CET. (a) 20 s, (b) 60 s, (c) 100 s, and (d) 180 s

Full size image

Figure 12 shows that, before the nucleation of equiaxed grains, the flow in front of interface is relatively stable, and two vortexes with opposite directions are formed inside the melt [Figure 12(a)]. With the solidification, the cooling effect of the wall reduces the melt temperature front of the columnar dendrites. When the melt temperature is lower than the equilibrium liquid temperature and meets the nucleation conditions, the equiaxed grains begin to nucleate and grow. The growth of the equiaxed grains intensifies the instability of fluid flow and forms multiple vortexes [Figure 12(b)]. When the growth of the equiaxed grains prevents the columnar from extending into the liquid, the transformation of columnar to equiaxed (i.e., CET) occurs [Figure 12(c)].

The trend of the temperature field is similar to that in Figure 4; however, when the equiaxed grains appear, the temperature field front of the interface will fluctuate significantly, which is related to the presence of multiple vortexes in front of the solidification.

5.3.3 A-segregation analysis of CET

The evolution of segregation of CET is shown in Figure 14. Evidently, the appearance of the equiaxed grains leads to the formation of multiple high-concentration melt masses in front of solid/liquid interface. The movements of the high-concentration melt masses form the final A-segregations [Figure 14(d)].

Fig. 14
figure 14

Predicted A-segregation formation of CET. (a) 20 s, (b) 60 s, (c) 100 s, and (d) 180 s

Full size image

To further analyze the A-segregation of CET, we analyze Zone-1 [Figure 14(c)]. The segregation degree and morphology and the mixed morphology and segregation are shown in Figure 15. With the upward movement of the melt, a high-concentration melt appears in front of the equiaxed region [Figure 15(a)], and the counter-clockwise vortex is simultaneously formed [Figure 15(b)]. The high-concentration melt also moves in two directions, eventually resulting in A-segregation. Figure 15(c) shows the picture after the superposition of the morphology and segregation. The A-segregation passes through the equiaxed grains rather than at the grain boundaries; this mechanism is similar to that of the global columnar solidification.

Fig. 15
figure 15

Formation of segregation in Zone-1 [marked in Fig. 14(c)]. (a) Segregation ratio. (b) Morphology of equiaxed and the streamlines. (c) Segregation in the mixed morphology

Full size image

5.4 Study of Global Equiaxed Solidification

After analyzing the above simulation, A-segregation bands were found in the global columnar solidification and CET processes. At the same time, the upward movement of the high-concentration melt front of the crystals is found to be the main factor influencing the formation of A-segregation. To explore the formation of A-segregation during global equiaxed solidification process, the following studies are carried out.

5.4.1 Calculation conditions of global equiaxed solidification

The calculation conditions and boundary conditions of the ingot are consistent with those in Section V–A. The only difference is that we must set the nucleation parameters of internal equiaxed crystals, the nucleation base density of internal equiaxed nmax is set to 3.6 × 1010, and the mean value of nucleation supercooling ΔTV is set to 2 K.

5.4.2 Evolution of the flow and temperature field during global equiaxed solidification

The evolution process of equiaxed grains and flow field of global equiaxed solidification is shown in Figure 16. Because of the large number of nucleation sites for equiaxed grains, the flow field at the dendrite front is more disordered than that of the CET process. Despite the many vortexes, they interact with each other; thus, the vortexes in front of the equiaxed crystals will not be able to complete a steady upward flow.

Fig. 16
figure 16

Morphology of equiaxed crystals and the flow direction of global equiaxed solidification. (a) 20 s, (b) 40 s, (c) 60 s, (d) 80 s, and (e) 140 s

Full size image

The temperature field is shown in Figure 17. The process of variation is similar to that of the CET process.

Fig. 17
figure 17

Temperature field of global equiaxed solidification. (a) 20 s, (b) 40 s, (c) 60 s, (d) 80 s, and (e) 140 s

Full size image

5.4.3 Analysis of the segregation during global equiaxed solidification

The segregation diagram of the ingot is shown in Figure 18. No A-segregation was apparent, and only positive segregation appeared at the centerline of the ingot. Figure 16 shows that the flow front of the crystals is more disturbing than the CET process because no columnar dendrites exist. Thus, no high-concentration melts are formed in front of the equiaxed crystals (Figure 18). From the previous simulation results, we conclude that the upward movement of the high-concentration melt front of the solid/liquid interface is the key to forming A-segregation. Thus, no A-segregation occurs during the global equiaxed solidification process.

Fig. 18
figure 18

Segregation diagram of the global equiaxed solidification. (a) 20 s, (b) 40 s, (c) 60 s, (d) 80 s, and (e) 140 s

Full size image

6 Discussion

The most important feature of this paper is that A-segregation was simulated based on the microstructure. A-segregation is mainly caused by the upward movement of the high-concentration melt. The dependence of the orientation of A-segregation on the flow direction was also observed in other studies[10,17]; by using the volume-averaging method, they found that A-segregation occurred for upward flow, and V-segregation occurred for downward flow. The other important finding is that the deflection angle of the segregation is influenced by the heat dissipation of the wall surface; with increasing heat dissipation, the angle to the centerline increases. Wu and co-workers[11] concluded that the deflection angle increases with the intensity of the interdendritic flow. Zaloznik and Combeau[10] demonstrated that the deflection angle appears to result from the most favorable condition to continue the initial instability that triggers the onset of the mesosegregate. Until now, the mechanisms underlying the deflection angle were not well known and were not fully explained.

No A-segregation was found during the global equiaxed solidification process; this observation is inextricably linked to the vortexes in front of the solid/liquid interface, which cannot achieve stable upward movement. Therefore, in industrial production, adding a nucleating agent to increase the number of equiaxed grains and increasing the disorder of the flow field by mechanical vibration and stirring are effective ways to reduce A-segregation.

7 Conclusion

A CA–LBM model was established to simulate the A-segregation in a Fe-0.34 wt pct C alloy ingot. The simulation results were analyzed, leading to the following conclusions:

  1. (1)

    In front of the solid/liquid surface, the upward movement of the high-concentration melt caused by natural convection is the key to forming A-segregation. Remelting is not necessary to form A-segregation.

  2. (2)

    The deflection angle of the A-segregation can be affected by the heat dissipation rate of the wall. With the increasing heat dissipation rate, the deflection angle to the centerline of the ingot increases.

  3. (3)

    The position of the A-segregation is not fixed, and it can appear in the columnar or equiaxed region, which is mainly determined by the position of the high-concentration melt. However, these high-concentration melts must be able to move steadily upward. The segregation crosses through the grains rather than occurring at the grain boundaries. The equiaxed is not a necessary condition for the formation of A-segregation, but the appearance of the equiaxed accelerates the formation of the high-concentration melt; thus, many A-segregation bands can form during CET solidification.

  4. (4)

    In the global equiaxed solidification, because the vortexes in front of the solid/liquid interface are unable to move steadily upward, no A-segregation can be found in the final results.