Using Bagging to improve clustering methods in the context of three-dimensional shapes

Abstract

Cluster Analysis techniques are a common approach to classifying objects within a dataset into distinct clusters. The clustering of geometric shapes of objects holds significant importance in various fields of study. To analyze the geometric shapes of objects, researchers often employ Statistical Shape Analysis methods, which retain crucial information after accounting for scaling, locating, and rotating an object. Consequently, several researchers have focused on adapting clustering algorithms for shape analysis. Recently, three-dimensional (3D) shape clustering has become crucial for analyzing, interpreting, and effectively utilizing 3D data across diverse industries, including medicine, robotics, civil engineering, and paleontology. In this study, we adapt the K-means, CLARANS and Hill Climbing methods using an approach based on the Bagging procedure to achieve enhanced clustering accuracy. We conduct simulation experiments for both isotropy and anisotropy scenarios, considering various dispersion variations. Furthermore, we apply the proposed approach to real datasets from relevant literature. We evaluate the obtained clusters using cluster validation measures, specifically the Rand Index and the Fowlkes-Mallows Index. Our results demonstrate substantial improvements in clustering quality when implementing the Bagging approach in conjunction with the K-means, CLARANS and Hill Climbing methods. The combination of the Bagging method and clustering algorithms provided substantial gains in the quality of the clusters.

1 Introduction

In many everyday situations, it is relevant to classify individuals from a dataset into groups, either to help understand the phenomenon studied or to organize data. Cluster Analysis is a set of techniques that aims to create clusters so that each element is similar, but the clusters are different. Clustering methods differ in several ways, Everitt et al. (2011) comment that the two main methods are hierarchical and partitional. The methods of interest in the present work are the partitioning ones, which form groups from an initial partition and the pre-defined number $K$ of clusters. Initially, there is an initial partition, and, according to the algorithm process, the elements change from cluster to cluster until their formats reach a final version (final clustering) (Friedman and Rubin 1967).

The K-means method, proposed over 50 years ago, is based on the sum of squares, also known as the “Within-cluster Sum of Squares” (WSS). It aims to minimize the sum of the squared distances between data points and the centroids of their respective clusters (Hastie et al. 2009; Jain 2010). Another well-known method is CLARANS (Clustering Algorithm based on Randomized Search), introduced by Ng and Han (2002), which utilizes a representative object called the medoid, positioned closer to the center of the cluster. The medoid reduces the search space, enhances robustness against outliers, and allows for identifying complex cluster structures. Additionally, the Hill Climbing method, proposed by Friedman and Rubin (1967), aims to iteratively find the cluster with the optimal value of a given clustering criterion, such as WSS or the “Between-cluster Sum of Squares” (BSS).

Geometric representations and images of objects play a vital role in studies and research across various fields and applications, including Biology, Medicine, Neuroscience, Archaeology, and, with the advancement of technological resources, Logic, Computer Vision, and Pattern Recognition (Adams and Otárola-Castillo 2013; Srivastava et al. 2005; Baxter 2015; Srivastava and Klassen 2016; Guo et al. 2023; King and Eckersley 2019). Statistical Analysis of Shapes is a branch of statistics used to work with geometric representations and shapes of objects. In the geometric approach to shape analysis, the central idea is to utilize the representation of the object itself. Certain mathematical operations remove the effects of location, scale, and rotation, encapsulating all the information in the shape. Some related practical applications involve comparing the shapes of the brain cortex in patients with and without schizophrenia in a neuroscientific study based on brain magnetic resonance (Brignell et al. 2010).

Studying summary measures and comparisons between shapes is necessary in several areas of knowledge to gain a deeper and more comprehensive understanding of objects and phenomena in various research and application fields. Developing different statistical techniques in the context of shapes provides a systematic and quantitative approach for applications and theoretical development. Bookstein et al. (1986) and Kendall (1984) proposed the fundamental concepts of statistical analysis of shapes. In several situations, it is necessary to classify data sets of shapes that belong to non-Euclidean spaces into clusters. In this context, several authors have adapted algorithms for this purpose. For two-dimensional shapes (2D), there is the work by Amaral et al. (2010), who adapted the K-means algorithm proposed by Hartigan and Wong (1979) for an application in Oceanography. In their study, they needed to classify species of fish based on their shapes.

One of the main advantages of working with three-dimensional data is the ability to analyze the surface area and volume of objects of interest and their shapes. Although there are many applications of three-dimensional data in science and technology, there are relatively few studies related to 3D shapes in the literature. Moving from 2D shapes to 3D is not simply the addition of a new dimension, as the 3D shape space is part of a stratified space that contains some singularities¹ These singularities can make the analysis more complex and computationally costly, unlike the 2D shape space, a Riemannian manifold (Bhattacharya and Bhattacharya 2012).

Few works involving adaptations of clustering methods address three-dimensional (3D) shapes. One of the most significant works in this area, developed by Vinué et al. (2014), presents adaptations of the K-means (Lloyd 1982) and trimmed K-means (García-Escudero and Gordaliza 1999) versions for clustering three-dimensional shapes. Despite the scarcity of these methods, the present work also aims to adapt the CLARANS (Ng and Han 2002) and Hill Climbing (Friedman and Rubin 1967) methods to the context of three-dimensional shapes.

Clustering methods can benefit from leveraging the strengths of other algorithms. The Bagging method has been applied in conjunction with clustering algorithms to enhance their performance by incorporating new training sets formed through bootstrap samples into the cluster analysis framework. An example of clustering ensembles is the bagged clustering method introduced by Leisch (1999), which combines hierarchical and partitioning methods in cluster analysis to improve stability. Additionally, to improve the clustering performance of partitioning algorithms based on medoids, such as PAM (Rousseeuw and Kaufman 1990), Dudoit and Fridlyand (2003) utilized the Bagging method for data analysis and stabilize the results. The method provides robustness against outliers, consistency, and lower sensitivity to the dimensionality of the data.

Regarding the use of clustering ensemble techniques in the context of shape analysis, the work by Assis et al. (2021) introduces the Bagging method, proposed by Breiman (1996), in conjunction with the K-means algorithm, proposed by MacQueen (1967), to enhance the quality of clustering results for 2D shapes. The method is more resistant to random fluctuations in the data.

Motivated by all these works, this paper aims to leverage the Bagging method, specifically BagClust1 proposed by Dudoit and Fridlyand (2003), to enhance the quality of clustering results for three-dimensional shapes obtained using the adapted versions of K-means, CLARANS and Hill Climbing algorithms in the context of 3D shapes. By incorporating the Bagging method, we seek to improve the clustering outcomes’ robustness and resistance to fluctuations. To evaluate the clustering quality of these methods, the Rand Index (Rand 1971) and the Fowlkes-Mallows Index (Fowlkes and Mallows 1983) are used as performance measures. To validate the results of the metrics obtained via simulations, we used the paired Wilcoxon test (Wilcoxon 1992).

This paper is organized as follows. Section 2 deals with the basic concepts of statistical analysis of shapes. In Sect. 3, we present how the algorithms under study can be adapted for statistical shape analysis in three-dimensional space. A simulation study and applications on real datasets are presented in Sect. 4. Finally, the conclusions are discussed in Sect. 5.

2 Background

According to Kendall (1977), the geometric information of an object that remains when the effects of location, scale, and rotation are removed is referred to as shape. Additionally, the book by Dryden and Mardia (2016) synthesizes the main concepts of shape analysis and provides a overview of the necessary definitions for statistical shape analysis to establish the notation used throughout this paper. One way to characterize the shape of an object is to detect a finite set of points around its silhouette, which are called landmarks.

A configuration is a collection of landmarks in a given object, mathematically represented by a matrix $\textbf{X}$ of dimension $k \times m$, where k is the number of landmarks and m is the number of dimensions (Cartesian coordinates) for each landmark. The space of all possible coordinates of the landmarks is called the configuration space. In this work, we will study the shapes of objects in three dimensions, i.e., the cases where $m = 3.$ Next, we present some definitions for statistical shape analysis according to Dryden and Mardia (2016).

Definition 1

The shape space is the space of all shapes. It is the set of equivalence classes of the configuration matrices under the action of Euclidean similarity transformations (location, rotation, and scale).

The shape space admits a Riemannian manifold structure, meaning standard statistical methods cannot be directly applied. The complexity of working with this structure depends on the values of k and m. When $m=2$, the shape space is a complex projective space (Goodall and Mardia 1999). However, for dimensions $m \ge 3$, the shape space is not a Riemannian manifold but a stratified space (Dryden and Mardia 2016). This space contains singularities and is less familiar than a Riemannian manifold. Nevertheless, in practical applications, it is generally assumed that we are far from these singularities and confined to a restricted variation within the shape space.

However, the configuration matrix $\textbf{X}$ does not adequately describe an object, as it is not invariant under Euclidean similarity transformations, i.e., location, scale, and rotation. The location and rotation effects of $\textbf{X}$ are removed one at a time. Initially, the Kendall coordinates (Kendall 1984) will be used to remove the location effect, employing the Helmert submatrix. The location effect is removed by multiplying $\textbf{X}$ by the Helmert submatrix $\textbf{H}$ (see Dryden and Mardia (2016), p. 49). The Helmert matrix $\textbf{H}^{F}$ is an orthogonal matrix of dimension $k \times k$, where all the elements of the first row are equal to $1/\sqrt{k}$, and the j-th row has $(j-1)$ elements equal to $-{j(j+1)}^{\frac{1}{2}}$, followed by an element equal to $(j-1)*{(j(j+1))}^{\frac{1}{2}}$, and $(k-j)$ zeros.

In order to eliminate the scaling effect, the Helmertized configuration must be divided by its norm, as follows:

$$\begin{aligned} \textbf{Z}=\frac{\mathbf {X_H} }{ || \mathbf {X_H}|| } = \frac{\textbf{HX}}{ || \textbf{HX}|| } = \frac{\textbf{HX}}{\sqrt{ \textrm{tr}((\textbf{HX})^{T}(\textbf{HX}})) } , \end{aligned}$$

(1)

where $\textbf{Z}$ is called the pre-shape of the configuration matrix $\textbf{X}$. It is important to realize that, in the pre-shape, the rotation effects remain.

Definition 2

The pre-shape space $S_{m}^{k}$ is the set of all possible pre-shapes.

It can be mathematically represented as:

$$\begin{aligned} S_{m}^{k} = \left\{ \textbf{Z} = \frac{\textbf{HX}}{||\textbf{HX}||} \ \bigg | \ \textbf{X} \in \mathbb {R}^{k \times m} \right\} \end{aligned}$$

where $\textbf{Z}$ is the pre-shape of the configuration matrix $\textbf{X}$, $\textbf{X} \in \mathbb {R}^{k \times m}$ represents the matrix of Cartesian coordinates of k landmarks in m dimensions. The space $S_{m}^{k}$ contains all possible configurations after removing the scaling effect from the original shape space.

Definition 3

The shape of a configuration matrix is all the geometric information that remains after removing the effects of location, scale, and rotation. The shape can be represented by:

$$\begin{aligned} \mathbf {[Z]}= \{\textbf{Z}{\boldsymbol {\Gamma } }\ : \ {\boldsymbol {\Gamma } }\in SO(m)\}, \end{aligned}$$

(2)

where $\boldsymbol{\Gamma }$ is a rotation matrix, $\textbf{Z}$ is the pre-shape, and SO(m) is the orthogonal group of rotations.

According to Vinué et al. (2014), $S_{m}^{k}$ is a hypersphere of unit radius in $\mathbb {R}^{(k-1)m}$, a Riemannian submanifold that is widely studied and known. However, for $m>2$, $\Sigma _{m}^{k}$ is not a usual space. As $\Sigma _{m}^{k}$ is considered a quotient space of $S_{m}^{k}$ under rotations, it is easier and more intuitive to work in this space, given that it is a Riemannian submanifold.

In practice, comparing and measuring objects is of constant interest to understand their variations, similarities, and dissimilarities. Procrustes analysis is a widely used technique for statistical shape analysis. It deals with the comparison and alignment of shapes by removing the effects of translation, rotation, and scaling. The method aims to fit shapes onto a standard template by minimizing the distance between corresponding points on the shapes through rigid transformations.

In this context, defining distance concepts aimed at shape analysis is essential. Consider two configuration matrices of k landmarks in m dimensions, denoted by $\mathbf {X_1}$ and $\mathbf {X_2}$, with pre-shapes equal to $\mathbf {Z_1}$ and $\mathbf {Z_2}$, respectively. Next, a distance measure focused on the analysis of shapes is defined.

Definition 4

The Riemannian distance $\rho (\mathbf {X_1}, \mathbf {X_2})$ is the nearest great circle distance (over rotations) between $\mathbf {Z_1}$ and $\mathbf {Z_2}$ in the pre-shape hypersphere $S_{m}^{k}$.

The Riemannian distance is intrinsic, as it is defined in the space of the form $\Sigma _{m}^{k}$. For more comprehensive details, see Dryden and Mardia (2016). Yet,

Definition 5

The full Procrustes distance between $\mathbf {X_1}$ and $\mathbf {X_2}$ is:

$$d_{F}( \mathbf {X_1}, \mathbf {X_2}) = \inf _{\Gamma \in SO(m), \ \beta \in \mathbb {R}^{+}} || \mathbf {Z_2} - \beta \mathbf {Z_1} \Gamma ||,$$

where $\beta$ is a scalar.

The full Procrustes distance and the Riemannian distance have the following relationship: $d_F=\sin (\rho )$. Another important concept that needs to be defined is the mean shape. In statistical shape analysis, the definition of the mean shape plays a crucial role in data analysis. However, in non-Euclidean spaces, no concept of mean is equivalent to the commonly known arithmetic mean. To address this, we will employ a Fréchet-type mean (Fréchet 1948), a type of mean or average that minimizes the sum of squared distances to any shape.

Consider $\mathbf {X_1}, \dots , \mathbf {X_n}$ as a set of configuration matrices representing the coordinates of landmark points on shapes.

Definition 6

The full Procustes mean shape in shape space is given by

$$\begin{aligned}{}[\hat{\mu }] = \arg \inf _{\mu } \sum _{i=1}^{n} {d_{F}}^{2} (\mathbf {X_i}, \mu ), \end{aligned}$$

(3)

where $d_F$ represents the full Procrustes distance of Definition 5.

For two-dimensional data, where $m=2$, Kent (1994) presents an eigenvector solution for the optimization problem in Definition 6 to find a mean shape. However, an iterative process becomes necessary for dimensions where $m \ge 3$ since the matching procedure cannot be expressed as a linear expression. The iterative process is outlined in Algorithm 1 [see pp. 138 in (Dryden and Mardia 2016) for more details].

Algorithm 1

Algorithm for calculating the mean shape of Procrustes $[\hat{\mu }]$.

3 Clustering three-dimensional shapes

The classification problem in shape analysis is to separate the objects in a dataset into groups based on their shapes. In this paper, the clustering methods discussed in the context of 3D shapes are the version of K-means adapted by Vinué et al. (2014), and our adaptations of the CLARANS and Hill Climbing methods. In principle, we consider $\mathbf {X^*} = \{ \mathbf {X_i}, i = 1, \cdots , n \}$ as a set of n objects, where each of them is a configuration matrix, as defined in Sect. 2. The algorithms will form these objects into a set $G = (G_r, r = 1, \cdots , K)$ of K clusters.

3.1 K-means clustering algorithm for three-dimensional shapes

The K-means clustering algorithm, introduced by Lloyd (1982), was adopted and built a new version Vinué et al. (2014) to work with three-dimensional shape data. The Riemannian distance, presented in Definition 4, replaced the Euclidean distance used in the original algorithm.

The K-means optimization problem, in the context of shape analysis, aims to minimize the following criterion:

$$\begin{aligned} W = \sum _{r=1}^{K} \sum _{i \in G_r} Dist^2(\mathbf {X_i},{{\boldsymbol{\mu}} _{\mathbf {r}}}), \end{aligned}$$

(4)

here, $G_r, r=1, \cdots , K$, represents the formed groups that contain each of the $\mathbf {X_i}, i=1, \cdots , n$, observations in the dataset. Note that a configuration matrix is a collection of landmarks of a given geometric object. The Dist function is a measure of distance. In this case, it is the Riemannian distance as defined in Definition 4, and ${{\boldsymbol{\mu}} _{\mathbf {r}}}$ represents the mean shape (centroid) obtained using Algorithm 1. The K-means clustering algorithm for three-dimensional shapes follows the steps below.

Algorithm 2

K-means algorithm for three-dimensional shapes.

The clusters formed by Algorithm 2 depend on an initial partition (randomly defined) representing the centroids, which can lead to convergence to a local optimum. It is necessary to run the algorithm multiple times with different initial partitions and then select the execution that yields the best value of the clustering criterion to mitigate this issue. The K-means method is primarily limited by its sensitivity to outliers in the dataset because it uses the sample mean to calculate the centroids of the clusters, allowing outliers to influence the resulting clusters significantly. Outliers can pull the centroids away from the central cluster, leading to suboptimal cluster assignments. Algorithm 2 updates centroids (means of groups) only after assigning all elements to a cluster. The algorithm performs a two-step process. First, it assigns all elements to the closest cluster centroid based on the distance criterion, and then it recalculates the centroids based on the newly formed clusters.

3.2 CLARANS clustering algorithm for three-dimensional shapes

Ng and Han (2002) proposed the CLARANS (Clustering Algorithm based on Randomized Search) algorithm as an extension of the PAM (Partitioning Around Medoids) algorithm. In PAM, the cluster representatives are called medoids. A medoid is the data point within a cluster with the lowest average dissimilarity (distance) to all other points in the cluster, which makes PAM less sensitive to outliers compared to K-means, as the medoids are actual data points, whereas K-means uses the mean of the cluster to represent its center.

The CLARANS forms clusters based on a random search approach, and the groups are generated by searches over the entire dataset, which is treated as a graph. Let $G_{n, K}$ be the graph, where nodes are defined as sets of medoids, and each node results in different clusterings. Each of these nodes has $K(n-K)$ neighbors, where K represents the number of clusters, and n is the number of individuals in the dataset. Two nodes are considered neighbors if they differ by only one object. Consequently, it is possible to have different groups depending on the selected medoid set. A cost is assigned to each node, defined as the total dissimilarity between every object and the medoid of its group. Overall, the CLARANS searches for the optimal node in the complete graph, applying the PAM for a sample of neighbors.

The CLARANS algorithm has two main parameters: maxneighbor, which represents the maximum number of neighbors to be examined, and numlocal, which represents the number of search iterations for a minimal node. If the value of maxneighbor is very close to or equal to $K(n-K)$, the quality of the groups formed by CLARANS will be closer to those generated by PAM, and the search for a minimal node will take longer (Ng and Han 2002). Algorithm 3 presents the steps for adapting CLARANS to the context of 3D shapes, which is one of the proposals of the present work.

Algorithm 3

CLARANS algorithm for three-dimensional shapes.

In general, CLARANS searches for the optimal node in the entire graph by applying PAM in a sample of neighbors. These algorithms examine the notions of proximity between the partitions examined during the iterative process. By examining multiple neighboring partitions and considering the quality of their clustering solutions, CLARANS tries to overcome the limitations of traditional methods like PAM or K-means, mainly when dealing with noisy or large datasets. The iterative exploration of the search space through proximity-based evaluations enhances the effectiveness of CLARANS in forming meaningful and robust clusters (Ng and Han 2002).

3.3 Hill Climbing clustering algorithm for three-dimensional shapes

The Hill Climbing algorithm was initially proposed by Friedman and Rubin (1967). Such an algorithm motivated the development of algorithms designed to seek the optimal value of a clustering criterion, restructuring existing partitions and maintaining the new partition only if it provides improvements. This algorithm can also be called Hill Descending in cases where criteria minimization is required (Everitt et al. 2011). The Hill Climbing method is considered a search algorithm and aims to find the solution to a given problem by exploring a series of possible paths. The Hill Climbing algorithm is a loop that repeats itself continuously in search of an optimal value of the clustering criterion. In this paper, this method was adapted to group three-dimensional shapes.

The clustering criterion that we used for the Hill Climbing method, according to Rousseeuw and Kaufman (1990), has the following equation, which can be used as a criterion to measure the quality of the groups:

$$\begin{aligned} TD= \sum _{r=1}^{K} \sum _{i \in G_r}d(\mathbf {X_i}, m_r). \end{aligned}$$

(5)

Here, $G_r, r=1, \cdots , K,$ represents the groups formed containing each of the observations $\mathbf {X_i}, i=1, \cdots , n,$ from the data set. The TD criterion represents total dissimilarity, a quality measure used to evaluate how well the data points within each cluster are represented by their respective $m_r$ medoids. The lower the value of Eq. (5), the better the clustering. The steps of the Hill Climbing method for three-dimensional shapes are presented in Algorithm 4. Note that the update of $m_r$ takes place in steps 4 and 5.

Algorithm 4

Hill Climbing algorithm for three-dimensional shapes.

In his book, Everitt et al. (2011) described the Hill Climbing algorithm and the clustering criteria used. Hill Climbing represents a simple and effective method for optimization problems with small search spaces. However, it can be susceptible to getting stuck in local optima and only sometimes finding the global optimum for complex problems. Various enhancements and variations, such as Simulated Annealing and Genetic Algorithms, can be adopted to overcome these limitations and improve the search capabilities of the algorithm in future research. However, it is a motivation to improve the algorithm via the Bagging procedure, as proposed in the following sections.

3.4 Bagging algorithm

Combining clustering algorithms with ensemble techniques is known as “clustering ensembles”. The algorithms used in clustering ensembles have two stages and aim to improve the performance of clustering algorithms by focusing on finding a global optimal result. In the first stage, the results generated by individual clustering algorithms are stored. In the second stage, a consensus function is applied to combine the stored results and define a final clustering solution. In summary, ensemble techniques are used to solve problems by combining several models or algorithms, whether for classification or regression tasks, through adapted versions of the data and unifying their outputs (Flach 2012). Clustering ensembles leverage this approach to enhance the clustering process and achieve more robust and accurate results. Ensemble techniques are not limited to clustering and can be applied in various machine learning domains to improve model performance and generalization. Ensemble techniques can mitigate overfitting and enhance overall predictive power by harnessing the collective knowledge of multiple algorithms.

We used ensemble techniques to improve the quality of the clusters obtained by the presented algorithm, specifically the Bagging method. The reason for applying this method in cluster analysis is to reduce the variability of the results obtained from partitioning algorithms. For example, it can stabilize the results of the CLARANS method. The Bagging method, which stands for Bootstrap Aggregating (Breiman 1996), involves training multiple instances of the same algorithm on different subsets of the data and then combining their outputs to create a more robust and stable final result. By reducing the variance and mitigating the impact of random fluctuations, Bagging can improve clustering performance and enhance the reliability of the obtained clusters (Bühlmann 2012).

The Bagging method used in the present work, initially proposed by Dudoit and Fridlyand (2003) to reduce the possible variability of the clusters formed by the PAM, is called BagClust1. In short, this algorithm applies the PAM multiple times for each bootstrap sample obtained from the data set, and the final cluster is then formed based on the labels that obtained the most votes for each observation. Assis et al. (2021) used the Bagging method, inspired by the work of Breiman (1996), to improve statistical analysis data clustering in two-dimensional shapes partitioning different subsets of the original data and using the voting approach as a consensus function to find the best partition generated by clustering algorithms.

In this paper, we have used the Bagging method to improve the clustering of data-oriented methods for statistical analysis of three-dimensional shapes. In this article, the K-means, CLARANS or Hill Climbing methods are applied multiple times for each bootstrap sample obtained from the data set of three-dimensional shapes, and the final cluster is then formed based on the labels that receive the most votes for each observation. The steps of the Bagging method are presented in Algorithm 5.

Algorithm 5

Bagging algorithm adapted for the analysis of three-dimensional shapes.

Note that $\tau$ represents the permutations between the clustering labels of the set bootstrap and $\tau ^{b}$ represents the permutation that maximizes the condition from step 6. Algorithm 5 uses b-th bootstrap samples as input data for the clustering algorithms. The process is then repeated B times to obtain different sets of cluster labels for each sample used as three-dimensional shape data. At the end of the repetitions, it is verified which cluster label was most attributed to each object, and the label that received the most votes is then chosen as the final one. Therefore, the final clustering is formed by the winning labels for each object. In case of a tie, the label is chosen at random. For this algorithm class, $B=20$ was originally used, which can substantially improve clustering accuracy when applying Bagging for cluster analysis, as demonstrated in the experiment conducted by Dudoit and Fridlyand (2003). However, in our experiments, we chose to use $B=100$.

Applying Bagging to cluster analysis aims to reduce variability in dataset partitioning results and improve the robustness of clustering results. It achieves this by averaging the effects of different bootstrap samples, which helps stabilize the clustering process and reduce the impact of random fluctuations Dudoit and Fridlyand (2003).

However, it is essential to acknowledge that the Bagging method may have a higher computational cost, especially when dealing with large data sets, when training multiple instances of the same clustering algorithm on different bootstrap samples. To address this issue in future research, one can use parallel computing or distributed processing techniques (Lazarevic and Obradovic 2002) to speed up the execution of the Bagging method or explore ensemble techniques that may offer similar advantages with potentially lower computational costs, such as Random Subspace Method (García-Pedrajas and Ortiz-Boyer 2008) or Random Patches Method (Louppe and Geurts 2012).

4 Numerical evaluation

Next, the methods K-means, CLARANS, and Hill Climbing for three-dimensional shape clustering were compared to their Bagging versions. We conducted experiments on simulated datasets. Additionally, two real datasets were analyzed. The Riemannian distance given in Definition 4 was used as an appropriate dissimilarity measure for the shape space. The analyzed algorithms were implemented in the R programming language (R Core Team 2024). The experiments were conducted on an Aspire A315-41 laptop, with a Ryzen 3 2200U processor, 2.50 GHz, 18GB of RAM, 64-bit system, and Windows 10 Home platform, using R version 4.4.0.

As for the values of the parameters used by the adapted algorithms, we decided to use the values proposed/used by the authors in their original applications for each application. We set the stop criterion for K-means to 0.0001, meaning that observations will no longer switch groups once the criterion in Eq. (4) reaches the value 0.0001. We also fixed the number of initializations and steps per initialization at 10. The number of steps per initialization (iteration steps) searches for the best value of the objective function, while number of initializations represents the number of random initializations in each of these iteration steps. For CLARANS, numlocal was considered equal to 2, and maxneighbor was set to $1.25\%$ of $K(N-K)$, where N is the size of the dataset, and K is the number of groups. The algorithm’s search process, Hill Climbing, ends when it reaches the loop size. We chose these parameter settings to ensure consistency and comparability with the original algorithms’ applications. In our studies, the number of groups K is known priori for both the simulated and real data sets. We use K as preprocessing in the context of partitional clustering. However, when we do not know the predefined number K of groups, we can use hierarchical clustering to find K (Everitt et al. 2001).

To compare the efficiency of the algorithms proposed in this article, we used the Rand Index (RI) (Rand 1971) and Fowlkes-Mallows Index (FMI) (Fowlkes and Mallows 1983) validation measures. These indexes measure the similarity between a cluster provided by a clustering method and true clusters known a priori. They assume values in the [0, 1] range, where 1 indicates perfect agreement between the clusters generated by the algorithm and the known true clusters, while values close to 0 correspond to an agreement found by chance. We opted not to explore other more complex procedures, such as the Adjusted Rand Index (Hubert and Arabie 1985) or the Silhouette Index (Rousseeuw 1987), as they produce measurements with negative output. This limitation could pose a significant disadvantage to the procedures we adopted for analyzing the data in our work.

Based on the RI and FMI results, we use the paired Wilcoxon test for simulation experiments to evaluate whether the methods improve with the Bagging approach. The null hypothesis was that there is no difference between the results of the indexes without and with Bagging, and the alternative hypothesis was that the results of the indexes without Bagging are inferior to the results with Bagging. In short, we want to evaluate whether there was an improvement in the clusterings generated by the methods combined with Bagging. A p-value less than or equal to the $5\%$ significance level is statistically significant. We chose $B=100$ because the test results were consistent across all algorithms for this value. The value of $B=100$ is also commonly used in the literature and in experiments that use resampling bootstrap, as is the case with the work of Assis et al. (2021) which also uses the Bagging approach in clustering context and form analysis.

We calculate the Rand Index and the Fowlkes-Mallows Index for the best result of each clustering algorithm, that is, for the best partition found by each clustering algorithm. For each algorithm, $B=100$ bootstrap replicas were generated and combined to form the labels. These labels went through the voting process to generate the best partition. The objective is to demonstrate the efficiency of using the Bagging method in combination with clustering algorithms compared to their standalone versions without it. Applying the Bagging, method can reduce the variability in the labeling processes’ clustering results and make the final clustering more robust and stable (Dudoit and Fridlyand 2003).

In experiments with simulated data, the methods were evaluated through different artificial data configurations using Monte Carlo experiments; more specifically, 50 replications were performed. Each method was run for each replication with different random partitions until convergence, and the best result according to the objective function was selected. We chose to work with 50 Monte Carlo replicas to balance time and precision because, for our experiments, we considered this number of replicas sufficient to have adequate variability in the generated data.

We carried out a single execution of the methods to analyze the algorithms on real data sets and subsequently calculated the results of interest based on this execution. We also use a Relative Gain measure to evaluate the results of applying the methods to real data sets and the validation indexes. We use this measure to compare the effectiveness of clustering methods with and without Bagging, based on the values of the clusters validation measures. The gain relative to the use of Bagging is defined by:

$$Relative \ Gain = 100 * \dfrac{\textrm{Validation} \,\textrm{Index}_\textrm{Bagging} - \textrm{Validation} \,\textrm{Index}}{\mathrm{Validation \,Index}},$$

where ${\mathrm{Validation \,Index}_\textrm{Bagging}}$ is the value of the RI or FMI when the algorithm uses the Bagging method and $\mathrm{Validation \,Index}$ is the value for the RI or FMI when the algorithm acts alone. This measure aims to verify whether there was a gain when using the proposed algorithms combined with the Bagging method on real data sets.

Our comparison of the performance of the Bagging-based clustering algorithms with their standalone counterparts will not only reveal any improvements in clustering accuracy and quality but also underscore the effectiveness of the Bagging technique in enhancing clustering performance. This analysis will further highlight the benefits of combining Bagging with various clustering algorithms, instilling confidence in our approach.

4.1 Simulation study results

Experiments were conducted in the landmark space based on the data simulated by Vinué et al. (2014) to illustrate the performance of the algorithms. To represent the average configurations, the experiments utilized two predefined geometric figures, a cube, and a parallelepiped. The number of landmarks for each object was set to $k = 8$.

Then, $n_1$ objects corresponding to one cluster and $n_2$ objects corresponding to another cluster were simulated. The clusters 1 and 2 were defined by a multivariate normal distribution with a three-dimensional mean vector of dimension 3k, represented by the predefined cube for the cluster 1 and predefined parallelepiped for the cluster 2. And additionally, a covariance matrix ${\boldsymbol{\Sigma}} _{\mathbf {i}}, i=1,2$ of dimension $3k \times 3k$.

The orientation of the cubes and parallelepipeds was defined arbitrarily. A rotation was applied about the axis z according to a random angle generated by the function rvm from the R package CircStats (Agostinelli and Agostinelli 2018). This function generates pseudo-random numbers from a von Mises distribution. The Von Mises distribution probability function density has the form

$$f (\theta ;\mu , \kappa ) = \dfrac{1}{2\pi I_0(\kappa )} \exp \left\{ \kappa \cos (\theta - \mu )\right\} ,$$

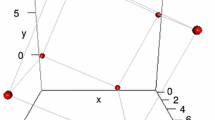
where: $I_0(\kappa )$ is the modified Bessel function of order 0, $\mu$ is the mean direction and $\kappa$ measures the concentration of the angles around the mean direction (Best and Fisher 1979). In Fig. 1, the predefined cube and parallelepiped shapes are shown for the landmark size $k=8$. In Fig. 2, the parallelepiped is displayed after being rotated according to a random angle generated by the rvm function. Different sample sizes and dispersion scenarios were considered, including isotropy (similar dispersion in all directions) and anisotropy (different dispersion in different directions).

Fig. 1

Parallelepiped and cube formed by 8 landmarks

Fig. 2

Parallelepiped formed by 8 landmarks rotated by a random angle

In the isotropy scenario, the landmarks have approximately the same variability. The covariance matrix ${\boldsymbol{\Sigma }}$ is a multiple of the identity matrix $\textbf{I}$, i.e., ${\boldsymbol{\Sigma}}_{\mathbf {i}}=\sigma _i^2 \mathbf {I_{3k \times 3k}}$ with different values for $\sigma _i, \ i=1,2$. The values for $\sigma _1$ and $\sigma _2$ were chosen so that the data have low $(\sigma _i=3)$, average $(\sigma _i=6)$, and high $(\sigma _i=9)$ dispersion, respectively, in each case. In the anisotropy scenario, the landmarks do not have approximately the same variability. The covariance matrix in this case is represented by the result of the Kronecker product between two operations involving the identity matrix, as follows:

$${\boldsymbol{\Sigma}}_{\mathbf{i}}=\frac{\sigma _i^{2}}{\gamma ^{2}} \left( \mathbf {1_k} \mathbf {1_k}^{T} + (\gamma -1) \mathbf {I_{k \times k}} \right) \otimes \left( \mathbf {1_m} \mathbf {1_m}^{T} + (\gamma -1) \mathbf {I_{m \times m}}\right) , \quad i=1,2$$

where m represents the dimension. The values for $\sigma _1$ and $\sigma _2$ are the same as in the isotropy scenario, and $\gamma$ equals 4.

Each simulated dataset consists of N objects divided into two groups: one containing cubes and the other containing parallelepipeds. We considered sample sizes of $N=100$. The values of $n_1$ and $n_2$ were $n_1=50$ and $n_2=50$, respectively. We choose these sample sizes to manage computational costs when applying Bagging on large samples of 3D shapes. The landmarks were generated following a multivariate normal distribution and transformed into configuration matrices to form the objects of each cluster. Tables 1, 2 and 3 show the RI and FMI values obtained for the simulated isotropy data, while Tables 4, 5 and 6 present the results of the simulated anisotropy data. In all Tables, the symbols $\bar{x}$ and sd represent the mean and standard deviations, respectively, calculated for applying the algorithms to 50 Monte Carlo replicas, where each replica represents a set of distinct 3D shape data containing $N=100$ objects.

4.2 Results in the isotropy scenario

In Tables 1, 2, and 3, the results of applying the methods to data sets simulated under isotropy for $N=100$ are presented. Table 1 shows the results obtained for the K-means and K-means Bagging methods. The combined use of the Bagging method with the K-means method resulted in an improvement in the estimates of the results measured by the indexes, according to the significance of the paired Wilcoxon test for the significance level of $5\%$, only for the Fowlkes-Mallows in cases with high dispersion. Furthermore, the results show no significance of Bagging for low and medium dispersion cases.

Table 1 Results for the algorithms K-means and K-means Bagging applied to simulated data of cubes and parallelepipeds represented by $k=8$ landmarks, under isotropy

Table 2 presents the results obtained for the CLARANS and CLARANS Bagging methods. It is observed that the application of the Bagging method in the CLARANS algorithm led to an improvement in the method clusterings according to the estimates of both validation indexes and in all dispersion scenarios, according to the significance of the paired Wilcoxon test at the $5\%$ significance level. Table 3 presents the results obtained for the Hill Climbing and Hill Climbing Bagging methods. According to the Wilcoxon test, it is evident that there was an improvement in the quality of the clusters with the Bagging approach, according to the estimates of both indexes, in all dispersion scenarios considered.

Table 2 Results for the algorithms CLARANS and CLARANS Bagging applied to simulated data of cubes and parallelepipeds represented by $k=8$ landmarks, under isotropy

Table 3 Results for the algorithms Hill Climbing and Hill Climbing Bagging applied to simulated data of cubes and parallelepipeds represented by $k=8$ landmarks, under isotropy

Figure 3 presents the violin plots of the pairwise differences of the results between Bagging and the original algorithm for the simulated isotropy data. The Fig 3a, c, and d show the results for the Rand Index. As we can see in item (a), Bagging did not provide major improvements to the K-means method. However, we can see improvements in the results of items (b) CLARANS and (c) Hill Climbing, especially under medium or high dispersion. We can see a similar interpretation in the results for the Fowlkes-Mallows Index presented in the Fig. 3b, e and f. Furthermore, note that there were cases in which we obtained sd=0 for both validation measures, which seems to be a characteristic of these simulated data. We can observe similar situations in the experiments of the work Vinué et al. (2014), especially when $\sigma$ is small.

As expected, in cases of isotropy, the Bagging approach showed significant improvements in clustering, except for some scenarios with low dispersion. In the context of isotropic landmarks, the algorithms that benefited most from the use of Bagging were CLARANS and Hill Climbing. Furthermore, as expected, as the dispersion between the landmarks grew, the IR and FMI values decreased, given that the landmarks show a large variability between them. This behavior was observed consistently across all methods and scenarios analyzed in the experiments.

4.3 Results in the anisotropy scenario

In Tables 4, 5 and 6, we present the results obtained for the methods K-means, CLARANS and Hill Climbing, respectively, along with their Bagging versions, applied to the simulated anisotropy data. Table 4 shows the results obtained for the K-means and K-means Bagging methods. Based on the significance of the paired Wilcoxon test at the $5\%$ significance level, it is evident that the combination of Bagging did not improve the clusters generated.

For the case of anisotropy, Table 5 presents the results obtained for the methods CLARANS and CLARANS Bagging and Table 6 presents the results obtained for the Hill Climbing and Hill Climbing Bagging methods. Both tables show that applying the Bagging method along with the algorithms improves the quality of the clusters generated in most dispersion scenarios, based on the significance of the Wilcoxon test at a $5\%$ significance level. However, we observed that the results did not show significance for cases with low dispersion.

Fig. 3

Paired violin plots of the results comparing bagging and the original algorithm for the simulated isotropy data

Table 4 Results for the algorithms K-means and K-means Bagging applied to simulated data of cubes and parallelepipeds represented by $k=8$ landmarks, under anisotropy

Table 5 Results for the algorithms CLARANS and CLARANS Bagging applied to simulated data of cubes and parallelepipeds represented by $k=8$ landmarks, under anisotropy

Table 6 Results for the algorithms Hill Climbing and Hill Climbing Bagging applied to simulated data of cubes and parallelepipeds represented by $k=8$ landmarks, under anisotropy

Figure 4 presents violin plots of the pairwise differences of the results between Bagging and the original algorithm for the simulated anisotropy data. The Fig. 4a, c and e show the Rand Index results. As we can see in item (a), Bagging did not provide improvements to the K-means method, as occurred in the isotropy scenario. However, we can observe improvements in the results of items (b) CLARANS and (c) Hill Climbing, especially under medium or high dispersion. We can see a similar interpretation in the results of the Fowlkes-Mallows Index presented in Fig. 4b, d, and f.

Furthermore, note that in this scenario, there are also cases where we obtain sd=0 for both validation measures. Note that, as in the case of isotropy, the methods did not benefit from using Bagging in low-dispersion scenarios. The Bagging method did not benefit K-means, while the other two algorithms benefited from the Bagging approach.

The supplemental material includes hypothesis tests concerning the results from simulations under various isotropy and anisotropy dispersion scenarios. These experiments consider different values of B.

Fig. 4

Paired violin plots of the results comparing bagging and the original algorithm for the simulated anisotropy data

4.4 Macaques skull

In a study to evaluate the existence of differences in size and shape between the skulls of male and female Macaca fascicularis, a sample of 18 individuals was obtained by Paul O’Higgins (Hall York Medical School). This data set is composed of $K=2$ groups, one group being made up of 9 male macaques and the other group being made up of 9 females. A subset of $k = 7$ anatomical landmarks were selected from a total of $k = 26$ representing each skull (Dryden and Mardia 2016). The selected landmark names are 1-prosthion, 2-nasion, 3-bregma, 4-opisthion, 5-asterion, 6-interfrontomalare, and 7-midpoint. An artist’s impression of a 3D representation of a skull with projections of anatomical landmarks can be seen in Fig. 5. More details about the data are given by Dryden and Mardia (1993).

Fig. 5

3D representation of a macaque skull of the species Macaca fascicularis: a side view; b front view; and c bottom view

Table 7 presents the results for clustering algorithms applied to the Macaques Skull dataset. From these values, we can observe that using the Bagging method improves the clustering quality for the Hill Climbing algorithm, considering both validation indexes. The CLARANS algorithm shows an improvement in clustering according to the FMI. However, the K-means algorithm does not exhibit performance gains, even when the Bagging method is used for this dataset. This data set has only $N=18$ objects; in this sense, it is easy for the clustering algorithms to find the best formation of groups according to the dissimilarities between the objects, even when the Bagging method is not used. The relative gains presented show that the joint operation of the algorithms with the Bagging method can provide more efficiency in the quality of the clusters, except for the K-means method. Figure 6 displays the labels clustering the Macaques Skull dataset into two clusters using the proposed methods. The axes of the plot are the Principal Components (PCs). Each point on the plot represents the shape of a single analysis object. According to Vinué et al. (2014), the closer two objects are, the more similar they are in shape.

Table 7 Results for the Macaque Skull dataset

Fig. 6

Clusterings scatter plot for Macaques Skull dataset

4.5 Brains

In an investigation to verify the difference between the shapes of adult human brains, anatomical landmarks distributed across the surface of the cerebral cortex of healthy adults were collected. The data set can be divided into $K=2$ distinct groups: 43 right-handed adults and 15 left-handed adults. $k=12$ anatomical landmarks were identified in each brain hemisphere, accounting for $k=24$ landmarks per individual. Figure 7 presents three views of an individual’s left hemisphere indicating the approximate locations of anatomical landmarks, totaling 12. More details about the dataset can be found in Free et al. (2001).

Fig. 7

Visualization of the locations of $k=12$ anatomical landmarks of an individual’s left hemisphere

Continuing with the applications of our approaches to different datasets already present in the literature, we evaluate the effectiveness of our methods by applying them directly to the Brains dataset and calculating the results of the Rand and Fowlkes-Mallows indexes and the Relative Gain. Table 8 presents the results for the Brains dataset. From these values, we can observe that using the Bagging method improves the clustering quality for all algorithms. In all cases, the relative gain was greater than $10\%$. In this sense, there is a benefit to using the Bagging approach. Figure 8 displays the labels clustering the Brains dataset into two clusters using the proposed methods. The plot axes are the principal components (PCs), and each point on the plot represents the shape of a single object. The use of PCs to generate this type of plot is widespread in cluster analysis.

Table 8 Results for the Brains dataset

Fig. 8

Clusterings scatter plot for Brains dataset

5 Conclusions

The discussion about adapting new methods in Statistical Shape Analysis is essential for the scientific community. This paper introduced the K-means, CLARANS, and Hill Climbing methods for clustering three-dimensional shapes and applied a Bagging procedure to improve their performances. Experimental results with different datasets demonstrated the effectiveness of the Bagging approach in this context, in some cases. Unlike typical cluster analysis studies that only show the best result when running the algorithm, we perform repeated applications of the algorithms with Monte Carlo simulations. We calculated the mean and standard deviation for two cluster validation measures: Rand Index (RI) and Fowlkes-Mallows Index (FMI). We also used the paired Wilcoxon test to validate the effectiveness of the methods using the Bagging approach in simulation experiments.

The findings indicate that the Bagging approach consistently improves clustering quality, with the RI estimates exhibiting values and variability close to the FMI estimates. We evaluate the algorithms with and without Bagging, considering $B=100$ replicas of bootstrap.

By applying Bagging to improve the clustering of algorithms on simulated datasets, we found different scenarios for each algorithm. Based on the results obtained by the paired Wilcoxon test, we observed that the use of Bagging did not significantly impact the metric estimates for small values of $\sigma _i$ in our simulated datasets.

For K-means, the use of Bagging resulted in group quality improvements only for some cases, indicating that the benefits of Bagging for K-means can be limited and may not provide consistent improvements across all data sets.

On the other hand, for CLARANS, using Bagging was generally advantageous as it led to improved validation measure estimate values in most cases. This improvement is probably due to the small value used for the maxneighbor parameter, which, although recommended by the authors, may limit the algorithm’s ability to explore the solution space effectively. However, high values for maxneighbor would significantly increase computational costs.

For Hill Climbing, Bagging also improved the metric estimates for the cases under medium and high dispersion, suggesting that Hill Climbing can also benefit from the diversity introduced by Bagging.

The results for the real data set depended on each data set’s specific characteristics. Based on RI and FMI measurements, the real datasets’ clustering results suggest that both algorithms have similar clustering effectiveness in some cases. The interpretation of the results based on the Relative Gain measure suggests that the proposed methods improved the quality of the clusters generated, especially for the Brains dataset.

Our work includes a comparative study of three different clustering methods in the context of three-dimensional shapes, as only some studies of this type are present in the literature. In summary, the impact of Bagging varies between algorithms and datasets. While CLARANS and Hill Climbing tend to benefit from Bagging, K-means may show limited improvements. The BagClust1 method was initially proposed to improve the clustering of the PAM method. For this reason, we think that the CLARANS method, precisely because it is a variation of PAM, was the one that benefited most from this Bagging approach as well as Hill Climbing , which in the approach of the present work focused on the clusters classifications formed by the same clustering criteria used in the PAM algorithm.

In conclusion, the Bagging method applied to the proposed clustering algorithms showed significant improvements in the precision and quality of the generated clusters, particularly in cases of medium to high dispersion between landmarks. As a future direction for this research, we suggest exploring other ensemble clustering methods, such as Boosting, and comparing their performance with the results obtained using Bagging when applied with clustering methods. Ultimately, we believe our paper can serve as a valuable guide for further use of Bagging methods in shape clustering. Applying ensemble techniques to shape analysis can pave the way for more accurate and robust clustering results, benefiting various fields of study that rely on shape data.