Dimension reduction for model-based clustering via mixtures of multivariate $t$-distributions

Abstract

We introduce a dimension reduction method for model-based clustering obtained from a finite mixture of $t$-distributions. This approach is based on existing work on reducing dimensionality in the case of finite Gaussian mixtures. The method relies on identifying a reduced subspace of the data by considering the extent to which group means and group covariances vary. This subspace contains linear combinations of the original data, which are ordered by importance via the associated eigenvalues. Observations can be projected onto the subspace and the resulting set of variables captures most of the clustering structure available in the data. The approach is illustrated using simulated and real data, where it outperforms its Gaussian analogue.

1 Introduction

In this paper, we introduce a dimension reduction method for model-based clustering via $t$-mixtures, which is analogous to the approach of Scrucca (2010) for Gaussian mixtures. Dimension reduction methods summarize the information available in a set of variables through a reduced subset of features derived from the original variables. At the same time, using multivariate $t$-distributions to model data can be advantageous because it provides robustness to outliers (cf. Peel and McLachlan 2000). Our aim is to estimate a subspace which captures most of the clustering structure contained in the data. Following the work of Li (1991, 2000), the dimension reduction subspace is found by looking at the variation in both group means and group covariances. This subspace contains linear combinations of the original data, which are ordered by importance via the associated eigenvalues. Observations can be projected onto the subspace and the resulting set of variables captures most of the clustering structure available in the data.

The remainder of the paper is outlined as follows. Background material is presented in Sect. 2. In Sect. 3, we outline our dimension reduction clustering method and highlight an algorithm for selecting a subset of the variables while retaining most of the clustering information contained within the data. We apply the algorithm to simulated and real data sets, including comparison of the performance of our method with its Gaussian analogue and five other dimension reduction techniques (Sect. 4). The paper concludes with discussion and suggestions for future work (Sect. 5). All the computational work in this paper was carried out within R (R Development Core Team 2012).

2 Background

Clustering algorithms based on probability models are a popular choice for exploring structures in modern data sets, which continue to grow in size and complexity. The model-based approach assumes that the data are generated by a finite mixture of probability distributions. A $p$-dimensional random vector $\varvec{X}$ is said to arise from a parametric finite mixture distribution if $f(\varvec{x} |\varvec{\vartheta })=\sum _{g=1}^G\pi _g\, f_g(\varvec{x}| \varvec{\theta }_g)$, where $G$ is the number of components, $\pi _g$ are mixing proportions, so that $\sum _{g=1}^G\pi _g=1$ and $\pi _g>0$, and $\varvec{\vartheta }=(\pi _1, \ldots , \pi _G, \varvec{\theta }_1,\ldots , \varvec{\theta }_G)$ is the parameter vector. The $f_g(\varvec{x}| \varvec{\theta }_g)$ are called component densities and $f(\varvec{x} |\varvec{\vartheta })$ is formally referred to as a $G$-component parametric finite mixture distribution.

For Gaussian mixtures, Banfield and Raftery (1993) developed a model-based framework for clustering by using the following eigenvalue decomposition of the covariance matrix

$$\begin{aligned} \varvec{\Sigma }_g=\lambda _g\varvec{D}_g\varvec{A}_g\varvec{D}_g^{\top }\,, \end{aligned}$$

(1)

where $\varvec{D}_g$ is the orthogonal matrix of eigenvectors of $\varvec{\Sigma }_g, \varvec{A}_g$ is a diagonal matrix with elements proportional to the eigenvalues of $\varvec{\Sigma }_g$, and $\lambda _g$ is a scalar. Here, $\varvec{D}_g$ determines the orientation of the principal components of $\varvec{\Sigma }_g, \varvec{A}_g$ determines the shape of the density contours, and $\lambda _g$ specifies the volume of the corresponding ellipsoid.

By imposing constraints on the elements of (1), a family of Gaussian parsimonious clustering models (GPCM) is obtained and discussed by Celeux and Govaert (1995). A description of a subset of these models appears in Table 1.

Table 1 Nomenclature for a subset of models in the MCLUST family which appear in this paper: ‘E’ indicates that a constraint is imposed, ‘V’ indicates that a constraint is not imposed (Fraley and Raftery 1999)

Recent work on model-based clustering using the multivariate $t$-distribution has been contributed by Peel and McLachlan (2000), McLachlan et al (2007), Greselin and Ingrassia (2010a, b), Andrews et al. (2011), Baek and McLachlan (2011), Andrews and McNicholas (2011a, b), Andrews and McNicholas (2012a), Steane et al. (2012), McNicholas and Subedi (2012), and McNicholas (2013). In particular, Andrews and McNicholas (2012a) used the decomposition (1) of the multivariate $t$-distribution scale matrix to build a family of 20 mixture models which are called the $t$EIGEN family (a selection is shown in Table 2). The $t$EIGEN family uses the ten MCLUST covariance structures as well as two of the other GPCM structures and also includes constraints on the degrees of freedom (cf. Andrews and McNicholas 2012a).

Table 2 Nomenclature for a subset of models in the $t$EIGEN family which appear in this paper: ‘C’ indicates that a constraint is imposed, ‘U’ indicates that a constraint is not imposed (Andrews and McNicholas 2012a)

Parameter estimation for the $t$EIGEN family is carried out via the expectation-conditional maximization algorithm (ECM; Meng and Rubin 1993), an iterative procedure for finding maximum likelihood estimates when data are incomplete or treated as being incomplete. Extensive details on the ECM algorithm are given by McLachlan and Krishnan (2008). The ECM algorithm replaces the M-step in the expectation-maximization (EM) algorithm (Dempster et al. 1977) with a number of conditional maximization steps that can be more computationally efficient.

Model selection for the $t$EIGEN family is carried out using the Bayesian information criterion (BIC; Schwarz 1978):

$$\begin{aligned} \text{ BIC }=2 l(\varvec{x}, \varvec{\hat{\vartheta }})-r\log n\,, \end{aligned}$$

where $l(\varvec{x}, \varvec{\hat{\vartheta }})$ is the maximized log-likelihood, $\varvec{\hat{\vartheta }}$ is the maximum likelihood estimate of $\varvec{\vartheta }, r$ is the estimated number of free parameters, and $n$ is the number of observations. While alternatives to the BIC exist, the authors feel safe contending that it remains the most popular mixture model selection criterion within the literature. Note that the $t$EIGEN family is implemented within the teigen package (Andrews and McNicholas 2012b) for R; we use teigen in our analyses (Sect. 4).

Recently, Scrucca (2010) proposed a new method of dimension reduction for model-based clustering in the Gaussian framework, called GMMDR. Given a $G$-component Gaussian mixture model (GMM) of the form

$$\begin{aligned} f(\varvec{x}|\varvec{\vartheta })=\sum _{g=1}^G \pi _g f_{\text{ N }}(\varvec{x}| \varvec{\mu }_g, \varvec{\Sigma }_g), \end{aligned}$$

the procedure finds the smallest subspace that captures the clustering information contained within the data. The core of the method is to identify those directions where the cluster means $\varvec{\mu }_g$ and the cluster covariances $\varvec{\Sigma }_g$ vary as much as possible, provided that each direction is $\varvec{\Sigma }$-orthogonal to the others. The variations in cluster means and cluster covariances are captured by the matrices $\varvec{M}_\text{ I }$ and $\varvec{M}_\text{ II }$, respectively, as given below. Identifying these directions is achieved via the generalized eigen-decomposition of the kernel matrix $\varvec{M}$, defined by Scrucca (2010) as

$$\begin{aligned} \varvec{M} \varvec{v}_i=l_i\varvec{\Sigma }\varvec{v}_i, \end{aligned}$$

(2)

where $l_1\ge l_2\ge \cdots \ge l_d > 0$ and $\varvec{v}_i^{\top }\varvec{\Sigma }\varvec{v}_j={\left\{ \begin{array}{ll} 1 &{} \text{ if }\,\,\, i=j, \,\,\text{ and } \\ 0 &{}\text{ otherwise. } \end{array}\right. }$

Here,

$$\begin{aligned} \varvec{M}&= \varvec{M}_\mathrm{I }\varvec{\Sigma }^{-1}\varvec{M}_\mathrm{I } +\varvec{M}_\mathrm{II },\\ \varvec{M}_\mathrm{I }&= \sum _{g=1}^G \pi _g (\varvec{\mu }_g-\varvec{\mu })(\varvec{\mu }_g-\varvec{\mu })^{\top },\\ \varvec{M}_\mathrm{II }&= \sum _{g=1}^G \pi _g(\varvec{\Sigma }_g-\bar{\varvec{\Sigma }})\varvec{\Sigma }^{-1}(\varvec{\Sigma }_g-\bar{\varvec{\Sigma }})^{\top }. \end{aligned}$$

Also, $\varvec{\mu }=\sum _{g=1}^G\pi _g\varvec{\mu }_g$ is the global mean, $\varvec{\Sigma }=\frac{1}{n}\sum _{i=1}^n(\varvec{x}_i-\varvec{\mu })(\varvec{x}_i-\varvec{\mu })^{\top }$ is the covariance matrix and $\bar{\varvec{\Sigma }}=\sum _{g=1}^G\pi _g\varvec{\Sigma }_g$ is the pooled within-cluster covariance matrix.

3 Mehodology

The dimension reduction approach of Scrucca (2010) is extended herein through development of a $t$-analogue. The density of a multivariate $t$-mixture model ($t$MM) is given by

$$\begin{aligned} f(\varvec{x}|\varvec{\vartheta })=\sum _{g=1}^G\pi _g\, f_t(\varvec{x}|\varvec{\mu }_g, \varvec{\Sigma }_g, \nu _g)\,, \end{aligned}$$

(3)

where $\pi _g$ are the mixing proportions and

$$\begin{aligned} f_t(\varvec{x} | \varvec{\mu }_g, \varvec{\Sigma }_g, \nu _g)= \displaystyle \frac{\Gamma (\frac{\nu _g+p}{2}) | \varvec{\Sigma }_g |^{-\frac{1}{2}}}{(\pi \nu _g)^{\frac{p}{2}}\Gamma (\frac{\nu _g}{2})(1+\frac{\delta (\varvec{x}, \varvec{\mu }_g|\varvec{\Sigma }_g)}{\nu _g})^{\frac{\nu _g+p}{2}}} \,, \end{aligned}$$

(4)

is the density of a multivariate t-distribution with mean $\varvec{\mu }_g$, scale matrix $\varvec{\Sigma }_g$, and $\nu _g$ degrees of freedom, and $\delta (\varvec{x}, \varvec{\mu }_g | \varvec{\Sigma }_g)=(\varvec{x}-\varvec{\mu }_g)^{\top }\varvec{\Sigma }_g^{-1}(\varvec{x}-\varvec{\mu }_g)$ is the squared Mahalanobis distance between $\varvec{x}$ and $\varvec{\mu }_g$.

Note that, although $\varvec{\Sigma }_g$ is a covariance matrix, it is not the covariance matrix of the random variable $\varvec{X}$ with the density in (4). The covariance matrix of $\varvec{X}$ is $\tilde{\varvec{\Sigma }}_g={\nu _g /(\nu _g - 2) \varvec{\Sigma }_g}$, for $\nu _g > 2$. Thus, we obtain a modified version of the kernel matrix $\varvec{M}_t$ (cf. 2), where $\varvec{M}_\mathrm{II } = \sum _{g=1}^G \pi _g(\tilde{\varvec{\Sigma }}_g-\bar{\varvec{\Sigma }})\varvec{\Sigma }^{-1}(\tilde{\varvec{\Sigma }_g}-\bar{\varvec{\Sigma }})^{\top }$.

Given a $t$MM (3), we wish to find a subspace, ${\fancyscript{S}}({\varvec{\beta }})$, where the cluster means and cluster covariances vary the most. As outlined in Sect. 2, this is achieved through the eigen-decomposition of the modified kernel matrix $\varvec{M}_t$.

Definition 3.1

The $t$MMDR directions are the eigenvectors $[\varvec{v}_1, \ldots , \varvec{v}_d]\equiv \varvec{\beta }$ which form the basis of the dimension reduction subspace $\fancyscript{S}(\varvec{\beta })$.

Suppose $\fancyscript{S}(\varvec{\beta })$ is the subspace spanned by the $t$MMDR directions obtained from the eigen-decompostion of $\varvec{M}_t$, and that $\varvec{\mu }_g$ and $\tilde{\varvec{\Sigma }_g}$ are the mean and covariance matrix, respectively, for the $g$th component. Then the projections of the parameters onto $\fancyscript{S}(\varvec{\beta })$ are given by $\varvec{\beta }^{\top } \varvec{\mu }_g$ and $\varvec{\beta }^{\top }\tilde{\varvec{\Sigma }}_g\varvec{\beta }$, respectively. For an $n\times p$ sample data matrix $\varvec{X}$, the sample version $\hat{\varvec{M}_t}$ of the kernel $\varvec{M}_t$ is obtained using the corresponding estimates from the fit of a $t$-mixture model via the ECM algorithm. Then the $t$MMDR directions are calculated from the generalized eigen-decomposition of $\hat{\varvec{M}_t}$ with respect to $\hat{\varvec{\Sigma }}$. The $t$MMDR directions are ordered based on eigenvalues; this means that directions associated with approximately zero eigenvalues can be discarded in practice because clusters will overlap substantially along these directions. Also, their contribution to the overall location of the sample points in an eigenvector expansion is approximately zero and so they provide little positional information.

Definition 3.2

The $t$MMDR variables, $\varvec{Z}$, are the projections of the $n\times p$ data matrix $\varvec{X}$ onto the subspace $\fancyscript{S}(\varvec{\beta })$ and can be computed as $\varvec{Z}=\varvec{X}\varvec{\beta }$.

As in the case of GMMDR, the estimation of the $t$MMDR variables can be viewed as a form of feature extraction where the components are reduced through a set of linear combinations of the original variables. This set of features may contain estimated $t$MMDR variables that provide no clustering information but require parameter estimation. Thus, the next step in the process of model-based clustering is to detect and remove these unnecessary $t$MMDR variables.

Scrucca (2010) used the subset selection method of Raftery and Dean (2006) to prune the subset of GMMDR features. We will also use this approach to select the most appropriate $t$MMDR features. We compare two subsets of features, $s$ and $s^{\prime }=\{ s{\setminus } i\}\subset s$, using the BIC difference

$$\begin{aligned} \text{ BIC }_{\text{ diff }}(Z_{i\in s})&= \text{ BIC }_{\text{ clust }}(Z_{ s})-\text{ BIC }_{\text{ not } \text{ clust }}(Z_{s})\,\nonumber \\&= \text{ BIC }_{\text{ clust }}(Z_{ s})-[\text{ BIC }_{\text{ clust }}(Z_{ s^{\prime }})+\text{ BIC }_{\text{ reg }}(Z_i | Z_{ s^{\prime }})]\,, \end{aligned}$$

(5)

where $\text{ BIC }_{\text{ clust }}(Z_{ s})$ is the BIC value for the best clustering model fitted using features in $s$, $\text{ BIC }_{\text{ clust }}(Z_{ s^{\prime }})$ is the BIC value for the best clustering model fitted using features in $s^{\prime }$, and $\text{ BIC }_{\text{ reg }}(Z_i | Z_{ s^{\prime }})$ is the BIC value for the regression of the $i$th feature on the remaining features in $s^{\prime }$.

Now, the space of all possible subsets contains $2^d-1$ elements and an exhaustive search is not feasible. To bypass this issue, we employ the greedy search algorithm of Scrucca (2010) to find a local optimum in the model space, which is based on the forward-backward search algorithm of Raftery and Dean (2006). The greedy search from Scrucca (2010) is a forward-only procedure; a backward step is not necessary because the $t$MMDR variables are $\varvec{\Sigma }$-orthogonal. Because a backward step is not needed, computing time is decreased.

• 1. Select the first feature to be the one which maximizes the BIC difference in (5) between the best clustering model and the model which assumes no clustering, i.e., a single component.

• 2. Select the next feature amongst those not previously included, to be the one which maximizes the BIC difference in (5).

• 3. Iterate the previous step until all the BIC differences for the inclusion of a variable become negative.

At each step, the search over the model space is performed with respect to the model parametrization and the number of clusters. A summary of our new method of dimension reduction for model-based clustering via $t$-mixtures, $t$MMDR, appears below.

4 Applications

4.1 Simulated data

We ran the $t$MMDR algorithm on the data simulation schemes outlined in Scrucca (2010) and compared its performance to that of the GMMDR procedure. Data were generated from the Gaussian distribution and the following models (corresponding to family members) were considered: three overlapping clusters with common covariance, three overlapping clusters with common shape, and three overlapping clusters with unconstrained covariance. For each model we ran three scenarios, namely:

• I. No noise variables: generated three variables from a multivariate normal distribution.

• II. Noise variables: started with scenario one and added seven noise variables generated from independent standard normal variables.

• III. Redundant and noise variables: started with scenario one and added three variables correlated with each clustering variable (with correlation coefficients equal to 0.9, 0.7, 0.5, respectively) as well as four independent standard normal variables.

For the full details on developing the synthetic data see Scrucca (2010). To ascertain the performance of the clustering methods under varying data dimensions, each scenario was run for three data sets consisting of 100, 300, and 1,000 data points, respectively, generated according to the schemes described earlier. Every run comprised 1,000 simulations. We evaluated the clustering results by computing the adjusted Rand index (ARI; Hubert and Arabie 1985) for each scenario: higher values of ARI correspond to better performance, with the value $1$ reflecting perfect class agreement.

We chose to generate only 10 variables in the latter two simulation scenarios so that we could provide a direct comparison between our results for $t$MMDR and the results for GMMDR from Scrucca (2010); results are given in Table 3. When no noise or redundant variables are present, the performance of the two methods is quite similar. However, for the scenarios which include noise and redundant variables, $t$MMDR exhibits ARI values which are higher than those for GMMDR, particularly for small sample sizes. This occurs consistently for all models as well as for varying data dimensions.

Table 3 Average ARIs, with standard errors in brackets, for all three scenarios, based on 1,000 simulations

Next, we simulated data with higher dimensions using the R package cluster

Generation (Qiu and Joe 2006). With this procedure, we chose to generate five clusters with equal numbers of observations by setting the degree of separation between them to 0.4 (with 1 representing the most separation), and choosing arbitrary positive definite covariance matrices. We generated four data sets, each comprising 300 observations, with dimensions 10, 30, 50, and 100, respectively.

Figure 1 depicts the scatterplot of five random variables from the data which indicate the underlying structure. The clustering results (Table 4) show that the number of features selected and the computing time increases with the dimensionality of the data. These simulations were performed on a computer with 128 GB of RAM utilizing one core of an Intel$^{\textregistered }$ Xeon$^{\textregistered }$ E7-8837 CPU running at 2.67 GHz. Note that the computing times for our approach will decrease with any future improvements in the efficiency of the teigen package.

Fig. 1

Scatterplot of five variables from the higher dimensional simulation indicating the five clusters present in the data (colour figure online)

Table 4 Computing time for the $t$MMDR procedure applied to simulated data, based on five runs

4.2 Real data

For the analyses in this section, we ran the GMMDR and $t$MMDR algorithms on the scaled version of each data set. We used the MCLUST hierarchical agglomerative procedure for initialization (cf. Fraley and Raftery 1999). In order to gauge the performance of our algorithm, we compared our results with five other dimension reduction procedures, outlined briefly below.

• 1. Robust PCA algorithm (Hubert et al. 2005) paired with $t$-mixtures via the $t$EIGEN family: principal components analysis resistant to outliers, with robust loadings computed by using projection-pursuit techniques and the minimum covariance determinant method. We used the R package rrcov (Todorov and Filzmoser 2009) for the ROBPCA computations as well as the teigen package.

• 2. Mixtures of $t$-factor analyzers (MM$t$FA; Andrews and McNicholas 2011a, b) extend the mixtures of multivariate $t$-factor analyzers model to include constraints on the degrees of freedom, the factor loadings, and the error variance matrices. These models are essentially a $t$-analogue of the Gaussian family developed by McNicholas and Murphy (2008, 2010). For the MM$t$FA results, the algorithms were initialized using a hierarchical agglomerative clustering and they were run for a range of $1$–$5$ components and $1$–$4$ factors. The BIC was used to select the number of components and the number of factors. The numbers of components and factors do not need to be specified a priori but when we write about the number of features, note that we are referring to the number of latent factors $q$, where each component requires $q$ factors.

• 3. FisherEM algorithm (Bouveyron and Brunet 2012): a subspace clustering method based on Gaussian mixtures where the EM-like algorithm estimates both the discriminative subspace and the parameters of the model. This procedure requires the number of clusters to be specified. We used the R package FisherEM (Bouveyron and Brunet 2012) in our analyses.

• 4. Clustvarsel algorithm (Raftery and Dean 2006) paired with Gaussian mixtures via the MCLUST family: a greedy procedure to find the (locally) optimal subset of variables in a dataset. We employed the R package clustvarsel (Dean and Raftery 2009) in our analyses.

• 5. SelvarClust algorithm (Maugis et al 2009): a greedy algorithm for variable selection in model-based clustering via Gaussian mixtures which modifies the method of Raftery and Dean (2006) by allowing data where individuals are described by quantitative block variables. We used the software available at http://www.math.univ-toulouse.fr/~maugis/SelvarClustHomepage.html for our analyses.

4.2.1 Wine data

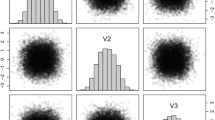
Forina et al (1986) recorded several chemical and physical properties for three types of Italian wines: Barolo, Grignolino, and Barbera. For our analysis, we used the data set comprising $13$ variables and $178$ observations which is available from the gclus package (Hurley 2004) in R. The resulting classifications (Table 5) and algorithm comparisons (Table 6) show that the MM$t$FA with $2$ factors produces the best results $(\text{ ARI }=0.96)$. Also, the $t$MMDR and FisherEM procedures (both with $\text{ ARI }=0.93$) outperform the GMMDR method $(\text{ ARI }=0.85)$, while using less features in the process. Figure 2 illustrates a scatterplot of the estimated $t$MMDR directions corresponding to the three clusters found by the procedure. The separation between the varieties of wine is clear in the plots of direction 1 against directions 2 and 3.

Table 5 A classification table for the best $t$MMDR model fitted to the wine data

Table 6 Summary of results for the best models fitted to the wine data

Fig. 2

Plots of estimated $t$MMDR directions for the wine data. The labels of the observations indicate their true cluster classification and the colour gives their estimated $t$MMDR cluster allocation (colour figure online)

4.2.2 Crabs data

Campbell and Mahon (1974) recorded five measurements for specimens of Leptograpsus crabs found in Australia. Crabs were classified according to their colour (blue or orange) and their gender. This data set, which consists of $200$ observations, is available through the R package MASS (Venables and Ripley 2002). The known classification of the crabs data by colour and gender has four groups: $50$ blue/orange males and $50$ blue/orange females. The $t$MMDR method $(\text{ ARI }=0.86)$ produces a better clustering than the GMMDR method $(\text{ ARI }=0.82)$ on the crabs data but it requires one more feature than GMMDR. The resulting classification is presented in Table 7, while the procedure comparison appearing in Table 8 shows that $t$MMDR outperforms all other algorithms.

Table 7 A classification table for the best $t$MMDR model fitted to the crabs data

Table 8 Summary of results for the best models fitted to the crabs data

Figure 3 illustrates a scatterplot of the estimated $t$MMDR directions corresponding to the four clusters found by the procedure. The separation between the crabs species is most clear in the plots of direction 1 against direction 3. As the number of clusters increases, it becomes more difficult to visualize their separation as evidenced in the plots of direction 2 against directions 3 and 4. Looking at Fig. 3, it is interesting to compute the ARI for each set of directions and compare the values to those obtained by GMMDR. Using $t$MMDR, direction $1$ has $\text{ ARI }=0.1394$, directions $1$ and $2$ have $\text{ ARI }=0.4507$, directions $1$–$3$ have $\text{ ARI }=0.5556$, and directions $1$–$4$ have $\text{ ARI }=0.8617$. By comparison, using GMMDR, direction $1$ has $\text{ ARI }=0.5342$, directions $1$ and $2$ have $\text{ ARI }=0.7738$, and directions $1$–$3$ have $\text{ ARI }=0.8195$. We observe that, for up to three directions, the ARI for $t$MMDR is less than those directions computed for GMMDR, but when the 4th direction is used for $t$MMDR, the ARI gets larger. Thus, adding this ‘extra’ direction improves accuracy.

Fig. 3

Plots of estimated $t$MMDR directions for the crabs data. The labels of the observations indicate their true cluster classification and the colour gives their estimated $t$MMDR cluster allocation (colour figure online)

4.2.3 Diabetes data

Reaven and Miller (1979) examined the relationship between five measures of blood plasma glucose and insulin in order to classify people as normal, overt diabetic, or chemical diabetic. This data set consists of observations from $145$ adult patients at the Stanford Clinical Research Centre and is available through the R package locfit (Loader 2012). There are $76$ normal patients, $36$ chemical diabetics, and $33$ overt diabetics; their $t$MMDR classifications are given in Table 9. Table 10 indicates that the selvarclust algorithm $(\text{ ARI }=0.81)$ outperforms both the $t$MMDR $(\text{ ARI }=0.70)$ and GMMDR methods $(\text{ ARI }=0.65)$, while the rest of the procedures do not do particularly well on these data.

Table 9 A classification table for the best $t$MMDR model fitted to the diabetes data

Table 10 Summary of results for the best models fitted to the diabetes data

Figure 4 illustrates the overlap between the predicted groups. In particular, the chemical group is sometimes classified into the normal or overt group, but normal is never wrongly classified as overt or vice-versa. The average uncertainty associated with each identified cluster is as follows: $0.0106$ for overt, $0.0524$ for chemical, and $0.0158$ for normal. The modest ARI is likely due to the nature of chemical diabetes.

Fig. 4

Plots of estimated $t$MMDR directions for the diabetes data. The letters of the observations indicate their true cluster classification and the colour gives their estimated $t$MMDR cluster allocation (colour figure online)

4.2.4 SRBCT data

Khan et al. (2001) used microarray experiments of small round blue cell tumours (SRBCT) to classify childhood cancer. Their data contained $2308$ genes and $83$ tissue samples which were used to measure gene expressions in four types of tumours, namely Ewing sarcoma (EWS), Burkitt lymphoma (BL), neuroblastoma (NB), and rhabdomyosarcoma (RMS). The SRBCTs of childhood are given this collective name because of their similar appearance on routine histology. These data are available via the R package plsgenomics (Boulesteix et al. 2011).

One of the main challenges in clustering these data is the large number of gene expression levels compared with the small number of cancer samples. As is the case with microarrays in general, there may be many non-informative genes which could hinder the clustering of the cancer clusters. Thus, gene filtering is very important for dimensionality reduction and further analysis. Khan et al. (2001) identified $96$ genes which were useful in the classification of tissue samples, while Tibshirani et al (2002) isolated $43$ such genes. We used gene-filtering based on $t$-tests and identified $36$ differentially expressed genes which were then analyzed via our dimension reduction procedure.

The resulting classification (Table 11) and algorithm comparisons (Table 12) show that the tMMDR and FisherEM procedures (both with $\text{ ARI } = 0.96$) outperform the GMMDR method $(\text{ ARI } = 0.8)$, which does not identify the correct number of clusters. Figure 5 depicts a scatterplot of the estimated $t$MMDR directions corresponding to the four clusters found by the procedure. The separation between the tumour classes is clear in the plots of directions 2 and 3 against the others, as they clearly reveal the underlying structure.

Table 11 A classification table for the best $t$MMDR model fitted to the SRBCT data

Table 12 Summary of results for the best models fitted to the SRBCT data

Fig. 5

Plots of the estimated $t$MMDR directions for the SRBCT data. The labels of the observations indicate their true cluster classification and the colour gives their estimated $t$MMDR cluster allocation (colour figure online)

4.2.5 Summary

The results of our real data analyses are summarized in Table 13. Clearly, the $t$MMDR approach has outperformed the GMMDR method on these data. The $t$MMDR approach also performed very well when benchmarked against other well established dimension reduction procedures.

Table 13 Summary results for the $t$MMDR and GMMDR approaches on all five real data sets

5 Conclusion

This paper introduced an effective dimension reduction technique for model-based clustering within the multivariate $t$-distribution framework. Our method, known as $t$MMDR, focused on identifying the smallest subspace of the data that captured the inherent cluster structure. The $t$MMDR approach was illustrated using simulated and real data, where it performed favourably compared to its Gaussian analogue (GMMDR; Scrucca 2010), as well as five other dimension reduction methods (ROBPCA with $t$-mixtures, mixtures of $t$-factor analyzers, clustvarsel with Gaussian mixtures, selvarclust, and FisherEM).

Future work will focus on dimension reduction using distributions that account for skewness (e.g., Karlis and Santourian 2009; Lin 2010; Vrbik and McNicholas 2012; Franczak et al. 2012; Lee and McLachlan 2013). However, it is not clear that the resulting methods would necessarily outperform the $t$MMDR method introduced herein.