Introduction

Carbonate reservoirs have complex structures, and challenged research community, such as petroleum engineers, geologists, fluid mechanics, and water resource researches (Gua and Chalaturnyk 2010; Jazayeri Noushabadi et al. 2011; Popov et al. 2009). Each reservoir is composed of different combinations of matrix, fracture, and vug systems, and thus, it has various properties of porosity, permeability, and fluid transport behavior. The flow problem of fluids through a reservoir is a complicated inverse problem. Therefore, a task for researchers is to establish various test models for the industry to evaluate the properties of these reservoirs.

The flow problem for vertical well production in carbonate reservoirs is well known. Bourdet and Gringarten (1980) used type curve analysis to analyze fissure volume and block size in fractured reservoirs. Camacho-Velázquez et al. (2005) studied an oil transient flow modeling in naturally fractured-vuggy reservoirs and analyzed its pressure transient behaviors. Corbett et al. (2010) studied the numerical well test modeling of fractured carbonate reservoirs, and discovered that numerical well testing has its limitations. Izadi and Yildiz (2007) examined transient flow in discretely fractured porous media, and Jalali and Ershaghi (1987) investigated pressure transient analysis of heterogeneous naturally fractured reservoirs. In addition, Leveinen (2000) established a composite model with fractional flow for well test analysis in fractured reservoirs, Wu et al. (2004, 2007, 2011) investigated a triple-continuum pressure transient model for a naturally fractured-vuggy reservoir, and Pulido et al. (2006) established a well-test pressure theory of analysis for naturally fractured reservoirs, considering transient interporosity matrix, micro fractures, vugs, and fractures flow, Cai and Jia (2007) investigated dynamic analysis for pressure in limit conductivity vertical fracture wells of triple-porosity reservoir, Nie et al. (2011, 2012) investigated a flow model for triple-porosity carbonate reservoirs by conceptualizing vugs as spherical shapes, Wang et al. (2013) studied pressure transient analysis of horizontal wells with positive/negative skin in triple-porosity reservoirs, Jiang et al. (2014) studied rate transient analysis for multistage fractured horizontal well in tight oil reservoirs considering stimulated reservoir volume, Su et al. (2015) investigated performance analysis of a composite dual-porosity model in multi-scale fractured shale reservoir, Zhang et al. (2015a, b) investigated triple-continuum modeling of shale gas reservoirs considering the effect of kerogen, Guo et al. (2015) investigated transient pressure behavior for a horizontal well with multiple finite-conductivity fractures in tight reservoirs, Zhang et al. (2015a, b) studied the production performance of multistage fractured horizontal well in shale gas reservoir, Wu et al. (2016) investigated a practical method for production data analysis from multistage fractured horizontal wells in shale gas reservoirs, Wei et al. (2016) studied pressure transient analysis for finite-conductivity multi-staged fractured horizontal well in fractured-vug carbonate reservoirs, Wu et al. (2017) investigated numerical analysis for promoting uniform development of simultaneous multiple-fracture propagation in horizontal wells, Ma and Liu (2016), and Ma et al. (2017) studied the oil production using the novel multivariate nonlinear model based on Arps decline model and kernel method, and Wang and Yi (2017) investigated transient pressure behavior of a fractured vertical well with a finite-conductivity fracture in triple media carbonate reservoir.

However, to the best of our knowledge, little has been done on modeling the nonlinear oil–water two-phase flow behavior for a horizontal well in triple media carbonate reservoir by conceptualizing vugs as spherical shapes. The main purpose of this article is to study the nonlinear oil–water two-phase flow behavior for a horizontal well in triple media carbonate reservoir.

The outline of this article is as follows. In Sect. 2, a physical model is introduced, which is of horizontal well in triple media carbonate reservoir by conceptualizing vugs as spherical shapes. In Sect. 3, some key source functions are obtained. In Sect. 4, a mathematic model is developed, which is of the horizontal well in triple media carbonate reservoir. In Sect. 5, we selected a set of the oil and water relative permeability for the matrix, fracture, and vug systems, respectively, which can provide the necessary base data for the theoretical analysis and calculation of oil–water two-phase well test. In Sect. 6, pressure behavior analyses are done. Section 7 gives some conclusions.

Physical model of a horizontal well in triple media carbonate reservoir

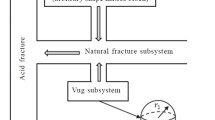
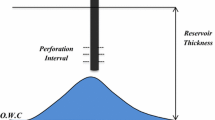
The practical reservoir may be triple media for most carbonate reservoirs, and the fractured-vuggy triple media reservoir scheme and its flow scheme are shown in Figs. 1 and 2.

Fig. 1
figure 1

Triple media carbonate reservoir flow scheme

Full size image
Fig. 2
figure 2

Schematic of a horizontal well in triple media carbonate reservoir

Full size image

Physical model assumptions are as follows:

  1. 1.

    A horizontal well production at constant rate in fractured-vuggy triple media reservoir, and the upper and lower boundaries of the reservoir are both closed, while the external boundary of the reservoir is infinite.

  2. 2.

    Oil–water two-phase flow with constant oil and water saturation at a certain moment in the early production period.

  3. 3.

    The shape of all the vugs is spherical, the radius of the vugs is equal and equals to \( r_{1} \), the distribution of pressure in the vug is spherically symmetric, and the shape of matrix block is arbitrary; both vug and matrix connect individually to fractures.

  4. 4.

    The fracture subsystem is the main flow pathway, and the interporosity flow between matrix and vug subsystems is ignored; the interporosity flow manner of matrix to fracture is pseudo-steady, and the interporosity flow manner of vug to fracture is unsteady.

  5. 5.

    Total compressibility is a constant.

  6. 6.

    Fluid flow in reservoir is isothermal and Darcy flow, and the gravity and capillary effect are ignored.

  7. 7.

    At the initial time, pressure is uniformly distributed in reservoir, equals to the initial pressure \( p_{i} \).

Basic solutions of governing flow equations in triple media carbonate reservoir

The governing equations in triple media carbonate reservoir

By Darcy’s law, the oil flow velocity at spherical surface of vug is

$$ v_{o} = \left. { - \frac{{k_{v} k_{\text{vro}} }}{{\mu_{o} }}\left( {\frac{{\partial p{}_{v}}}{{\partial r_{v} }}} \right)} \right|_{{r_{v} = r_{\;1} }} . $$
(1)

The water flow velocity at spherical surface of vug is

$$ v_{w} = \left. { - \frac{{k_{v} k_{\text{vrw}} }}{{\mu_{w} }}\left( {\frac{{\partial p{}_{v}}}{{\partial r_{v} }}} \right)} \right|_{{r_{v} = r_{\;1} }} . $$
(2)

Because the outflow oil and water volume in unit time from the unit volume vug is \( q_{\text{vo}} \) and \( q_{\text{vw}} \), the velocity at the spherical surface equals the result that the surface area of a spherical vug divides the outflow volume of fluid from a vug in unit time, that is

$$ v_{o} = \frac{1}{3}r_{1} q_{\text{vo}} $$
(3)

and

$$ v_{w} = \frac{1}{3}r_{1} q_{\text{vw}} . $$
(4)

Combining Eqs. (1)–(4), the connecting condition of interporosity flow between vug and fracture can be obtained from the following equation:

$$ q_{\text{vo}} = \left. { - \frac{3}{{r_{1} }}\frac{{k_{v} k_{\text{vro}} }}{{\mu_{o} }}\left( {\frac{{\partial p_{v} }}{{\partial r_{v} }}} \right)} \right|_{{r_{v} = r_{\;1} }} $$
(5)

and

$$ q_{\text{vw}} = \left. { - \frac{3}{{r_{1} }}\frac{{k_{v} k_{\text{vrw}} }}{{\mu_{w} }}\left( {\frac{{\partial p_{v} }}{{\partial r_{v} }}} \right)} \right|_{{r_{v} = r_{\;1} }} , $$
(6)

where \( r_{1} \) is the radius of vug; \( v_{\text{o}} \) is the oil flow velocity, m/s; \( v_{w} \) is the water flow velocity, m/s; \( q_{\text{vo}} \) is the outflow oil volume in unit time from the unit volume vug, m3/(m3 \( \cdot \)s); \( q_{\text{vw}} \) is the outflow water volume in unit time from the unit volume vug, m3/(m3 \( \cdot \)s).

The oil flow governing differential equations of vug system in radial spherical coordinate system is as follows:

$$ \frac{{k_{v} k_{\text{vro}} }}{{\mu_{o} }}\frac{{\partial^{2} p_{v} }}{{\partial r_{v}^{2} }} + \frac{{k_{v} k_{\text{vro}} }}{{\mu_{o} }}\frac{2}{{r_{v} }}\frac{{\partial p_{v} }}{{\partial r_{v} }} = S_{\text{vo}} \phi_{v} c_{\text{vto}} \frac{{\partial p_{v} }}{\partial t}\;\;\;\;(0 < r_{v} < r_{1} ). $$
(7)

The water flow governing differential equations of vug system in radial spherical coordinate system is as follows:

$$ \frac{{k_{v} k_{\text{vrw}} }}{{\mu_{w} }}\frac{{\partial^{2} p_{v} }}{{\partial r_{v}^{2} }} + \frac{{k_{v} k_{\text{vrw}} }}{{\mu_{w} }}\frac{2}{{r_{v} }}\frac{{\partial p_{v} }}{{\partial r_{v} }} = S_{\text{vw}} \phi_{v} c_{\text{vtw}} \frac{{\partial p_{v} }}{\partial t}\;\;\;\;(0 < r_{v} < r_{1} ). $$
(8)

Combining Eqs. (7) and (8), we have

$$ k_{v} \left( {\frac{{k_{\text{vro}} }}{{\mu_{o} }} + \frac{{k_{\text{vrw}} }}{{\mu_{w} }}} \right)\frac{{\partial^{2} p_{v} }}{{\partial r_{v}^{2} }} + k_{v} \left( {\frac{{k_{\text{vro}} }}{{\mu_{o} }} + \frac{{k_{\text{vrw}} }}{{\mu_{w} }}} \right)\frac{2}{{r_{v} }}\frac{{\partial p_{v} }}{{\partial r_{v} }} = \phi_{v} c_{vt} \frac{{\partial p_{v} }}{\partial t}\;\;\;\;(0 < r_{v} < r_{1} ), $$
(9)

where \( c_{\text{vt}} = c_{v} + S_{vo} c_{\text{Lo}} + S_{\text{vw}} c_{\text{Lw}} \) is the compressibility of oil–water two-phase flow in vug system, 1/Pa.

Initial conditions:

$$ p_{v} \left| {_{t = 0} = p_{i} } \right.. $$
(10)

At the center point of vugs:

$$ \left. {\frac{{\partial p_{v} }}{{\partial r_{v} }}} \right|_{{r_{v} = 0}} = 0. $$
(11)

At the spherical surface of vugs, the vugs pressure is equal to the fracture pressure:

$$ p_{v} (r_{v} ,t)\left| {_{{r_{v} = r_{\;1} }} } \right. = p_{f} . $$
(12)

The oil flow governing differential equation of fracture system in Cartesian coordinate system is as follows:

$$ \begin{aligned} \frac{\partial }{\partial x}\left( {\frac{{k_{\text{fh}} k_{\text{fro}} }}{{\mu_{o} }}\frac{{\partial p_{f} }}{\partial x}} \right) + \frac{\partial }{\partial y}\left( {\frac{{k_{\text{fh}} k_{\text{fro}} }}{{\mu_{o} }}\frac{{\partial p_{f} }}{\partial y}} \right) + \frac{\partial }{\partial z}\left( {\frac{{k_{\text{fv}} k_{\text{fro}} }}{{\mu_{o} }}\frac{{\partial p_{f} }}{\partial z}} \right) + \hfill \\ \alpha_{m} \frac{{k_{m} k_{\text{mro}} }}{{\mu_{o} }}\left( {p_{m} - p_{f} } \right) + q_{\text{vo}} = S_{\text{fo}} \phi_{f} c_{\text{fto}} \frac{{\partial p_{f} }}{\partial t}. \hfill \\ \end{aligned} $$
(13)

The water flow governing differential equation of fracture system in Cartesian coordinate system is as follows:

$$ \begin{aligned} \frac{\partial }{\partial x}\left( {\frac{{k_{\text{fh}} k_{\text{frw}} }}{{\mu_{w} }}\frac{{\partial p_{f} }}{\partial x}} \right) + \frac{\partial }{\partial y}\left( {\frac{{k_{\text{fh}} k_{\text{frw}} }}{{\mu_{w} }}\frac{{\partial p_{f} }}{\partial y}} \right) + \frac{\partial }{\partial z}\left( {\frac{{k_{\text{fv}} k_{{{\text{fr}}w}} }}{{\mu_{w} }}\frac{{\partial p_{f} }}{\partial z}} \right) + \hfill \\ \alpha_{m} \frac{{k_{m} k_{\text{mrw}} }}{{\mu_{w} }}\left( {p_{m} - p_{f} } \right) + q_{\text{vw}} = S_{\text{fw}} \phi_{f} c_{\text{ftw}} \frac{{\partial p_{f} }}{\partial t} \hfill \\ \end{aligned} $$
(14)

Combining Eqs. (13) and (14), we have

$$ \begin{aligned} &k_{\text{fh}} \left( {\frac{{k_{\text{fro}} }}{{\mu_{o} }} + \frac{{k_{\text{frw}} }}{{\mu_{w} }}} \right)\frac{{\partial^{2} p_{f} }}{{\partial x^{2} }} + k_{\text{fh}} \left( {\frac{{k_{\text{fro}} }}{{\mu_{o} }} + \frac{{k_{\text{frw}} }}{{\mu_{w} }}} \right)\frac{{\partial^{2} p_{f} }}{{\partial y^{2} }} + k_{\text{fv}} \left( {\frac{{k_{\text{fro}} }}{{\mu_{o} }} + \frac{{k_{\text{frw}} }}{{\mu_{w} }}} \right)\frac{{\partial^{2} p_{f} }}{{\partial z^{2} }} \hfill \\ &\quad+ \alpha_{m} k_{m} \left( {\frac{{k_{\text{mro}} }}{{\mu_{o} }} + \frac{{k_{\text{mrw}} }}{{\mu_{w} }}} \right)\left( {p_{m} - p_{f} } \right) + q_{\text{vo}} + q_{\text{vw}} = \left( {S_{\text{fo}} c_{\text{fto}} + S_{{f{\text{w}}}} c_{\text{ftw}} } \right)\phi_{f} \frac{{\partial p_{f} }}{\partial t}. \hfill \\ \end{aligned} $$
(15)

The oil flow governing differential equation of matrix system is as follows:

$$ \alpha_{m} \frac{{k_{m} k_{\text{mro}} }}{{\mu_{o} }}\left( {p_{m} - p_{f} } \right) + S_{\text{mo}} \phi_{m} c_{\text{mto}} \frac{{\partial p_{m} }}{\partial t} = 0. $$
(16)

The water flow governing differential equation of matrix system is as follows:

$$ \alpha_{m} \frac{{k_{m} k_{\text{mrw}} }}{{\mu_{w} }}\left( {p_{m} - p_{f} } \right) + S_{\text{mw}} \phi_{m} c_{\text{mtw}} \frac{{\partial p_{m} }}{\partial t} = 0. $$
(17)

Combining Eqs. (16) and (17), we have

$$ \alpha_{m} k_{m} \left( {\frac{{k_{\text{mro}} }}{{\mu_{o} }} + \frac{{k_{\text{mrw}} }}{{\mu_{w} }}} \right)\left( {p_{m} - p_{f} } \right) + \phi_{m} c_{\text{mt}} \frac{{\partial p_{m} }}{\partial t} = 0. $$
(18)

Initial condition:

$$ p_{f} \left| {_{t = 0} = } \right.p_{m} \left| {_{t = 0} = p_{i} } \right.. $$
(19)

External boundary condition:

$$ \mathop {\lim }\limits_{{r_{f} \to \infty }} p_{f} = p_{i} \; \left( {\text{infinite}} \right). $$
(20)

Cube geometric shape factor (Warren and Root 1963; Al-Ghamdi and Ershaghi 1996):

$$ \alpha_{m} = 16/L^{2} . $$
(21)

Spherical geometric shape factor (De Swaan 1976; Rangel-German and Kovscek 2005):

$$ \alpha_{v} = 15/r_{1}^{2} . $$
(22)

Interporosity flow factor of vug subsystem to fracture subsystem is as follows

$$ \lambda_{v} = \alpha_{v} r_{w}^{2} \frac{{k_{v} }}{{k_{f} }} = 15\left( {\frac{{r_{w} }}{{r_{1} }}} \right)^{2} \frac{{k_{v} }}{{k_{f} }}. $$
(23)

Interporosity flow factor of matrix subsystem to fracture subsystem is as follows:

$$ \lambda_{m} = 16\left( {\frac{{r_{w} }}{L}} \right)^{2} \frac{{k_{m} }}{{k_{f} }}. $$
(24)

Capacitance coefficient:

$$ \omega_{j} = \phi_{j} c_{\text{jt}} /(\phi_{f} c_{\text{ft}} + \phi_{m} c_{\text{mt}} + \phi_{v} c_{\text{vt}} ),\;\;\;(j = f,m,v). $$
(25)

The dimensionless governing equations in triple media carbonate reservoir

For simplification, the mathematical model is derived and solved in dimensionless form. Table 1 lists some dimensionless variables used in the mathematical model presented in this article. The dimensionless models are as follows:

Table 1 Definitions of dimensionless variables
Full size table

The governing differential equations of vug system in radial spherical coordinate system are as follows:

$$ \frac{{\partial^{2} p_{\text{vD}} }}{{\partial r^{2}_{\text{vD}} }} + \frac{2}{{r_{\text{vD}} }}\frac{{\partial p_{\text{vD}} }}{{\partial r_{\text{vD}} }} = \frac{{15\omega_{v} }}{{\varOmega_{3} \lambda_{v} }}\frac{{\partial p_{\text{vD}} }}{{\partial t_{\text{D}} }}\;\;\;\;(0 < r_{\text{vD}} < 1), $$
(26)

where \( \varOmega_{3} = \frac{{\mu_{o} }}{{k_{\text{fro}} }}\left( {\frac{{k_{\text{vro}} }}{{\mu_{o} }} + \frac{{k_{\text{vrw}} }}{{\mu_{w} }}} \right). \)

Initial conditions:

$$ p_{\text{vD}} \left| {_{{t_{\text{D}} = 0}} = 0} \right.. $$
(27)

At the center point of vugs:

$$ \left. {\frac{{\partial p_{\text{vD}} }}{{\partial r_{\text{vD}} }}} \right|_{{_{{r_{\text{vD}} = 0}} }} = 0. $$
(28)

At the spherical surface of vugs, the vugs’ pressure is equal to the fracture pressure:

$$ p_{\text{vD}} (r_{\text{vD}} ,t_{\text{D}} )\left| {_{{r_{\text{vD}} = 1}} } \right. = p_{{f{\text{D}}}} . $$
(29)

The governing differential equations of fracture system in radial cylindrical system are as follows:

$$ \begin{aligned} \varOmega_{1} \frac{{\partial^{2} p_{\text{fD}} }}{{\partial r_{\text{fD}}^{2} }} + \varOmega_{1} \frac{2}{{r_{\text{fD}} }}\frac{{\partial p_{\text{fD}} }}{{\partial r_{\text{fD}} }} + \varOmega_{2} \lambda_{m} (p_{{m{\text{D}}}} - p_{\text{fD}} ) - \hfill \\ \varOmega_{3} \frac{{\lambda_{v} }}{5}\left. {\left( {\frac{{\partial p_{\text{vD}} }}{{\partial r_{\text{vD}} }}\;} \right)} \right|_{{r_{\text{vD}} = 1}} = \omega_{f} \frac{{\partial p_{\text{fD}} }}{{\partial t_{\text{D}} }}, \hfill \\ \end{aligned} $$
(30)

where \( \varOmega_{1} = \frac{{\mu_{o} }}{{k_{\text{fro}} }}\left( {\frac{{k_{\text{fro}} }}{{\mu_{o} }} + \frac{{k_{\text{frw}} }}{{\mu_{w} }}} \right) \), \( \varOmega_{2} = \frac{{\mu_{o} }}{{k_{\text{fro}} }}\left( {\frac{{k_{\text{mro}} }}{{\mu_{o} }} + \frac{{k_{\text{mrw}} }}{{\mu_{w} }}} \right) \), and \( \varOmega_{3} = \frac{{\mu_{o} }}{{k_{\text{fro}} }}\left( {\frac{{k_{\text{vro}} }}{{\mu_{o} }} + \frac{{k_{\text{vrw}} }}{{\mu_{w} }}} \right) \)

The matrix system:

$$ \varOmega_{2} \lambda_{m} (p_{\text{fD}} - p_{{m{\text{D}}}} ) = \omega_{m} \frac{{\partial p_{{m{\text{D}}}} }}{{\partial t_{\text{D}} }}. $$
(31)

Initial condition:

$$ p_{\text{fD}} \left| {_{{t_{\text{D}} = 0}} = 0} \right.. $$
(32)

External boundary condition:

$$ \mathop {\lim }\limits_{{r_{\text{fD}} \to \infty }} p_{{f{\text{D}}}} = 0 \;\left( {\text{infinite}} \right). $$
(33)

Laplace transformation of dimensionless governing equations

Introduce the Laplace transformation based on \( t_{\text{D}} \), that is

$$ L[p_{\text{D}} (r_{\text{D}} ,t_{\text{D}} )] = \bar{p}_{\text{D}} (r_{\text{D}} ,u) = \int_{0}^{\infty } {p_{\text{D}} (r_{\text{D}} ,t_{\text{D}} )e^{{ - ut_{\text{D}} }} {\text{d}}} t_{\text{D}} , $$
(34)

where \( p_{\text{D}} \) is the dimensionless pressure in real space; \( \bar{p}_{\text{D}} \) is the dimensionless pressure in Laplace space; \( t_{\text{D}} \) is the dimensionless time in real space; \( u \) is the Laplace transformation variable.

Now making the Laplace transformation to Eqs. (26)–(33), then they become as follows.

The governing differential equations of vug system in radial spherical coordinate system are as follows:

$$ \frac{{\partial^{2} \bar{p}_{\text{vD}} }}{{\partial r_{\text{vD}}^{2} }} + \frac{2}{{r_{\text{vD}} }}\frac{{\partial \bar{p}_{\text{vD}} }}{{\partial r_{\text{vD}} }} = \frac{{15u\omega_{v} }}{{\varOmega_{3} \lambda_{v} }}\bar{p}_{\text{vD}} \;\;\;(0 < r_{\text{vD}} < 1). $$
(35)

Initial conditions:

$$ \bar{p}_{\text{vD}} \left| {_{{t_{\text{D}} = 0}} = 0} \right.. $$
(36)

At the center point of vugs:

$$ \left. {\frac{{\partial \bar{p}_{\text{vD}} }}{{\partial r_{\text{vD}} }}} \right|_{{r_{\text{vD}} = 0}} = 0. $$
(37)

At the spherical surface of vugs, the vugs’ pressure is equal to the fracture pressure:

$$ \bar{p}_{\text{vD}} (r_{{v{\text{D}}}} ,t_{\text{D}} )\left| {_{{r_{\text{vD}} = 1}} } \right. = \bar{p}_{\text{fD}} . $$
(38)

The governing differential equations of fracture system in radial cylindrical system are as follows:

$$ \varOmega_{1} \frac{{\partial^{2} \bar{p}_{\text{fD}} }}{{\partial r_{\text{fD}}^{2} }} + \varOmega_{1} \frac{2}{{r_{\text{fD}} }}\frac{{\partial \bar{p}_{\text{vD}} }}{{\partial r_{\text{vD}} }} + \varOmega_{2} \lambda_{m} (\bar{p}_{{m{\text{D}}}} - \bar{p}_{\text{fD}} ) - \varOmega_{3} \frac{{\lambda_{v} }}{5}\left. {\left( {\frac{{\partial \bar{p}_{\text{vD}} }}{{\partial r_{\text{vD}} }}\;} \right)} \right|_{{r_{\text{vD}} = 1}} = u\omega_{f} \bar{p}_{\text{fD}} . $$
(39)

The matrix system:

$$ \varOmega_{2} \lambda_{m} (\bar{p}_{\text{fD}} - \bar{p}_{{m{\text{D}}}} ) = u\omega_{m} \bar{p}_{{m{\text{D}}}} \;. $$
(40)

Initial condition:

$$ \bar{p}_{\text{fD}} \left| {_{{t_{\text{D}} = 0}} = 0} \right.. $$
(41)

External boundary condition:

$$ \mathop {\lim }\limits_{{r_{\text{fD}} \to \infty }} \bar{p}_{\text{fD}} = 0\; \left( {\text{infinite}} \right). $$
(42)

The general solution of Eq. (35) is as follows:

$$ \bar{p}_{\text{vD}} = (A_{v} e^{{\sigma_{v} r_{\text{vD}} }} + B_{v} e^{{ - \sigma_{v} r_{\text{vD}} }} )/r_{\text{vD}} $$
(43)
$$ \sigma_{v} = \sqrt {15u\omega_{v} /\varOmega_{3} \lambda_{v} } . $$
(44)

Substitute Eq. (43) into Eqs. (36) and (37), we then obtain

$$ A_{v} = \frac{1}{{e^{{\sigma_{v} }} - e^{{ - \sigma_{v} }} }}\bar{p}_{\text{fD}} $$
(45)
$$ B_{v} = - \frac{1}{{e^{{\sigma_{v} }} - e^{{ - \sigma_{v} }} }}\bar{p}_{\text{fD}} . $$
(46)

Then, the solution of Eq. (35) in Laplace space is as follows:

$$ \bar{p}_{\text{vD}} = \frac{{\bar{p}_{\text{fD}} }}{{r_{\text{vD}} }}\frac{{e^{{\sigma_{v} r_{\text{vD}} }} - e^{{ - \sigma_{v} r_{\text{vD}} }} }}{{e^{{\sigma_{v} }} - e^{{ - \sigma_{v} }} }}. $$
(47)

Through the derivative calculation to \( r_{\text{vD}} \) of Eq. (47), we have

$$ \left. {\frac{{{\text{d}}\bar{p}_{\text{vD}} }}{{{\text{d}}r_{\text{vD}} }}} \right|_{{_{{r_{\text{vD}} = 1}} }} = [\sigma_{v} cth(\sigma_{v} ) - 1]\bar{p}_{\text{fD}} , $$
(48)

where hyperbolic cotangent function \( cth(\sigma_{v} ) = (e^{{\sigma_{v} }} + e^{{ - \sigma_{v} }} )/(e^{{\sigma_{v} }} - e^{{ - \sigma_{v} }} ) \).

Substitute Eqs. (40) and (48) into Eq. (39), the governing equation of fracture system in radial spherical coordinate system is as follows:

$$ \frac{{\partial^{2} \bar{p}_{\text{fD}} }}{{\partial r^{2}_{\text{fD}} }} + \frac{2}{{r_{\text{fD}} }}\frac{{\partial \bar{p}_{\text{fD}} }}{{\partial r_{\text{fD}} }} = f(u)\bar{p}_{\text{fD}} $$
(49)
$$ f(u) = \frac{{\varOmega_{2} }}{{\varOmega_{1} }}\frac{{u\omega_{m} \lambda_{m} }}{{u\omega_{m} + \varOmega_{2} \lambda_{m} }} + \frac{{\varOmega_{3} }}{{\varOmega_{1} }}\frac{{\lambda_{v} }}{5}[\sigma_{v} cth(\sigma_{v} ) - 1] + \frac{{u\omega_{f} }}{{\varOmega_{1} }}. $$
(50)

Point-source function in triple media carbonate reservoir

The boundary condition at the surface of a vanishingly small sphere corresponding to the instantaneous withdrawal of an amount of oil fluid \( \tilde{q}_{o} \) and water fluid \( \tilde{q}_{w} \) at \( t = 0 \) can be expressed by the following:

$$ \mathop {\lim }\limits_{{\xi_{\text{D}} \to 0^{ + } }} \left. {\left[ {4\pi r_{w} r_{\text{fD}}^{2} k_{f} \frac{{k_{\text{fro}} }}{{\mu_{o} }}\frac{{\partial \Delta p_{f} }}{{\partial r_{\text{fD}} }}} \right]} \right|_{{r_{\text{fD}} = \xi_{\text{D}} }} = - B_{o} \tilde{q}_{o} \delta (t) $$
(51)

and

$$ \mathop {\lim }\limits_{{\xi_{\text{D}} \to 0^{ + } }} \left. {\left[ {4\pi r_{w} r_{\text{fD}}^{2} k_{f} \frac{{k_{\text{frw}} }}{{\mu_{w} }}\frac{{\partial \Delta p_{f} }}{{\partial r_{\text{fD}} }}} \right]} \right|_{{r_{\text{fD}} = \xi_{\text{D}} }} = - B_{w} \tilde{q}_{w} \delta (t), $$
(52)

where \( \delta (t) \) is the Dirac Delta function.

Combining Eqs. (51) and (52), we have

$$ \mathop {\lim }\limits_{{\xi_{\text{D}} \to 0^{ + } }} \left. {\left[ {4\pi r_{w} r_{\text{fD}}^{2} k_{f} \left( {\frac{{k_{\text{fro}} }}{{\mu_{o} }} + \frac{{k_{\text{frw}} }}{{\mu_{w} }}} \right)\frac{{\partial \Delta p_{f} }}{{\partial r_{fD} }}} \right]} \right|_{{r_{\text{fD}} = \xi_{\text{D}} }} = - \left( {B_{o} \tilde{q}_{o} + B_{w} \tilde{q}_{w} } \right)\delta (t). $$
(53)

Because it assumes that only natural fracturing systems in the carbonate reservoir are connected to the wellbore, the water cut of well can be expressed by the following:

$$ f_{w} = \frac{{\tilde{q}_{w} }}{{\tilde{q}_{o} + \tilde{q}_{w} }}. $$
(54)

Substitute Eqs. (54) into Eq. (53), we get

$$ \mathop {\lim }\limits_{{\xi_{\text{D}} \to 0^{ + } }} \left. {\left[ {4\pi r_{w} r_{\text{fD}}^{2} \frac{{k_{f} k_{\text{fro}} }}{{\mu_{o} }}\frac{{\partial \Delta p_{f} }}{{\partial r_{\text{fD}} }}} \right]} \right|_{{r_{\text{fD}} = \xi_{\text{D}} }} = - \frac{{\varOmega_{0} B_{o} \tilde{q}_{o} \delta (t)}}{{\varOmega_{1} }}, $$
(55)

where \( \varOmega_{0} = 1 + \frac{{B_{w} f_{w} }}{{B_{o} (1 - f_{w} )}} \) and \( \varOmega_{1} = \frac{{\mu_{o} }}{{k_{\text{fro}} }}\left( {\frac{{k_{\text{fro}} }}{{\mu_{o} }} + \frac{{k_{\text{frw}} }}{{\mu_{w} }}} \right) \).

Taking Laplace transformation for \( t \) with Eq. (55) and setting the source strength to unity, and then combining with Eq. (49), the instantaneous point-source solution can be obtained (Raghavan 1993; Ozkan and Raghavan 1992). Using the image-well technique and the superposition method, the continuous point-source solution in laterally infinite triple media carbonate reservoir with impermeable top and bottom boundaries in Laplace domain is given as follows:

$$ \begin{aligned} \Delta \bar{p}_{f} &= \frac{{\varOmega_{0} \tilde{q}_{o} B_{o} \mu_{o} }}{{2\pi \varOmega_{1} k_{f} k_{\text{fro}} r_{w} uh_{\text{D}} }}\left[ {K_{0} (r_{\text{fD}} \sqrt {f(u)} ) } \right. \hfill \\ &\quad \left.+ {2\sum\limits_{n = 1}^{\infty } {K_{0} } \left( {r_{\text{fD}} \sqrt {f(u) + \frac{{n^{2} \pi^{2} }}{{h_{D}^{2} }}} } \right)\cos n\pi \frac{{z_{\text{D}} }}{{h_{\text{D}} }}\cos n\pi \frac{{z_{{w{\text{D}}}} }}{{h_{\text{D}} }}} \right], \hfill \\ \end{aligned} $$
(56)

where \( K_{0} (x) \) is the modified Bessel function of second kind, zero order.

Flow model of horizontal well in triple media carbonate reservoir

According to the superposition principle, we can get the pressure response in triple media carbonate reservoir caused by horizontal well by integrating the point-source solution obtained in the previous section along the horizontal well, that is

$$ \begin{aligned} \Delta \bar{p}_{f} = \frac{{\varOmega_{0} \tilde{q}B_{o} \mu_{o} }}{{2\pi \varOmega_{1} k_{f} k_{\text{fro}} r_{w} uh_{\text{D}} }}\int_{{ - L_{h} /2}}^{{L_{h} /2}} {\left[ {K_{0} (r_{\text{fD}} \sqrt {f(u)} ) + } \right.} \hfill \\ \left. {2\sum\limits_{n = 1}^{\infty } {K_{0} } \left( {r_{\text{fD}} \sqrt {f(u) + \frac{{n^{2} \pi^{2} }}{{h_{\text{D}}^{2} }}} } \right)\cos n\pi \frac{{z_{D} }}{{h_{D} }}\cos n\pi \frac{{z_{{w{\text{D}}}} }}{{h_{D} }}} \right]{\text{d}}x_{w} , \hfill \\ \end{aligned} $$
(57)

where \( \varOmega_{0} = 1 + \frac{{B_{w} f_{w} }}{{B_{o} (1 - f_{w} )}} \), \( \varOmega_{1} = \frac{{\mu_{o} }}{{k_{\text{fro}} }}\left( {\frac{{k_{\text{fro}} }}{{\mu_{o} }} + \frac{{k_{{f{\text{rw}}}} }}{{\mu_{w} }}} \right) \), and \( r_{\text{fD}} = \sqrt {(x_{\text{D}} - x_{\text{wD}} )^{2} + (y_{\text{D}} - y_{\text{wD}} )^{2} } \).

For a horizontal well, the assumption of constant flow rate can yield the following equation:

$$ q_{\text{sc}} = \tilde{q}L_{h} . $$
(58)

Combining Eqs. (57) and (58), we have

$$ \begin{aligned} \Delta \bar{p}_{f} &= \frac{{\varOmega_{0} q_{\text{sc}} B_{o} \mu_{o} }}{{2\pi \varOmega_{1} k_{f} k_{\text{fro}} r_{w} uh_{\text{D}} L_{h} }}\int_{{ - L_{h} /2}}^{{L_{h} /2}} {\left[ {K_{0} (r_{\text{fD}} \sqrt {f(u)} ) } \right.} \hfill \\ & \quad \left.+{2\sum\limits_{n = 1}^{\infty } {K_{0} } \left( {r_{\text{fD}} \sqrt {f(u) + \frac{{n^{2} \pi^{2} }}{{h_{\text{D}}^{ 2} }}} } \right)\cos n\pi \frac{{z_{\text{D}} }}{{h_{\text{D}} }}\cos n\pi \frac{{z_{{w{\text{D}}}} }}{{h_{\text{D}} }}} \right]{\text{d}}x_{w} . \hfill \\ \end{aligned} $$
(59)

Substitute \( r_{\text{fD}} = \sqrt {(x_{\text{D}} - x_{\text{wD}} )^{2} + (y_{\text{D}} - y_{\text{wD}} )^{2} } \) into Eq. (59) and together with \( y_{\text{wD}} = 0 \), then we can get the dimensionless as follows:

$$ \begin{aligned} \bar{p}_{\text{fD}} &= \frac{{\varOmega_{0} }}{{u\varOmega_{1} L_{\text{hD}} }}\int_{{ - L_{\text{hD}} /2}}^{{L_{\text{hD}} /2}} {\left[ {K_{0} (\sqrt {(x_{\text{D}} - x_{\text{wD}} )^{2} + y_{\text{D}}^{ 2} } \sqrt {f(u)} ) } \right.} \hfill \\ &\quad\left. +{2\sum\limits_{n = 1}^{\infty } {K_{0} } \left( {\sqrt {(x_{\text{D}} - x_{\text{wD}} )^{2} + y_{\text{D}}^{ 2} } \sqrt {f(u) + \frac{{n^{2} \pi^{2} }}{{h_{\text{D}}^{2} }}} } \right)\cos n\pi \frac{{z_{\text{D}} }}{{h_{\text{D}} }}\cos n\pi \frac{{z_{{w{\text{D}}}} }}{{h_{\text{D}} }}} \right]{\text{d}}x_{\text{wD}} . \hfill \\ \end{aligned} $$
(60)

According to Ozkan’s conclusion (Ozkan 1988), the equivalent pressure point for the horizontal well bottom pressure in the top-bottomed reservoir is as follows:

$$ \left\{ \begin{aligned} &x_{\text{D}} = \frac{{0.732L_{\text{hD}} }}{2} \hfill \\ &y_{\text{D}} = 0 \hfill \\ &z_{\text{D}} = z_{\text{wD}} + 1 \hfill \\ \end{aligned} \right.. $$
(61)

Substitute Eq. (61) into Eq. (60), we can get the bottom hole pressure of the horizontal well in triple media carbonate reservoir:

$$ \begin{aligned} \bar{p}_{\text{wD}} & = \frac{{\Omega _{0} }}{{u\Omega _{1} L_{\text{hD}} }}\int_{{ - L_{\text{hD}} /2}}^{{L_{\text{hD}} /2}} {\left[ {K_{0} \left( {\left| {\frac{{0.732L_{\text{hD}} }}{2} - x_{\text{wD}} } \right|\sqrt {f(u)} } \right)} \right.} \\ & \quad + \left. {2\sum\limits_{{n = 1}}^{\infty } {K_{0} } \left( {\left| {\frac{{0.732L_{\text{hD}} }}{2} - x_{\text{wD}} } \right|\sqrt {f(u) + \frac{{n^{2} \pi ^{2} }}{{h_{\text{D}}^{2} }}} } \right)\cos n\pi \frac{{z_{\text{wD}} + 1}}{{h_{\text{D}} }}\cos n\pi \frac{{z_{\text{wD}} }}{{h_{\text{D}} }}} \right]{\text{d}}x_{\text{wD}} . \\ \end{aligned} $$
(62)

Following Van-Everdingen (1953) and Kucuk and Ayestaran (1985), the wellbore storage (\( C_{\text{D}} \)) and skin (\( S \)) can be incorporated in the above solution by the following:

$$\bar{p}_{{{\text{wD}}}} = \frac{{u\bar{p}_{{{\text{wD}}}}^{*} + S}}{{u + C_{D} u^{2} (u\bar{p}_{{{\text{wD}}}}^{*} + S)}},$$
(63)

where the dimensionless pressure solution \( \bar{p}_{{_{\text{wD}} }}^{*} \) at the bottom hole of a horizontal well without considering the wellbore storage and skin can be obtained from the solution of Eq. (62).

With the numerical inversion algorithm proposed by Stehfest (1970), we can get the real dimensionless bottom hole pressure of the horizontal well, \( p_{\text{wD}} \), in real-time space with consideration the wellbore storage and skin in the triple media carbonate reservoir. Subsequently, the transient pressure behavior of a horizontal well will be analyzed, and the type curves will also be shown.

Oil and water relative permeability of triple media carbonate reservoir

According to the research results of the oil and water relative permeability for the matrix, fracture, and vug systems of the triple media carbonate reservoir (Lian et al. 2011, 2013), we selected a set of the oil and water relative permeability for the matrix, fracture, and vug systems, respectively, which can provide the necessary base data for the theoretical analysis and calculation of oil–water two-phase well test. The detailed data are shown in Tables 2, 3, 4 and Figs. 3, 4, 5. The field measured oil and water relative permeability data should be used when the results of this article are applied to the field.

Table 2 Oil and water relative permeability of matrix system (Lian et al. 2011)
Full size table
Table 3 Oil and water relative permeability of fracture system (Lian et al. 2011)
Full size table
Table 4 Oil and water relative permeability of vug system (Li et al. 2013)
Full size table
Fig. 3
figure 3

Oil and water relative permeability of matrix system (Lian et al. 2011)

Full size image
Fig. 4
figure 4

Oil and water relative permeability of fracture system (Lian et al. 2011)

Full size image
Fig. 5
figure 5

Oil and water relative permeability of vug system (Li et al. 2013)

Full size image

Pressure behavior analyses

Flowing periods

Figure 6 shows the whole transient flow process of a horizontal well in triple media carbonate reservoir; it can be divided into seven flow stages:

Fig. 6
figure 6

Dimensionless pressure and pressure derivative responses of a horizontal well in triple media carbonate reservoir

Full size image

Stage 1: The pure wellbore storage stage; the pressure and pressure derivative assume unit slope;

Stage 2: The skin effect stage; the shape of the derivative curve is just like a ‘hump’ due to the wellbore storage effect and the skin effect;

Stage 3: Early, or first, radial flow regime (Fig. 7a). Slope of the pressure derivative curve is zero. Duration of the regime is very short, because formation thickness is usually less than 100 m. Radial flow regime will stop when pressure wave spreads to the closed boundary on top or bottom. This regime would be hardly observed for a small thickness.

Fig. 7
figure 7

a Early radial flow. b Linear flow. c Late pseudo-radial flow

Full size image

Stage 4: Linear flow regime (see Fig. 7b). The pressure derivative curve is a line with a slope of 0.5.

Stage 5: The interporosity flow stage of the vug system to fracture system; because the permeability of vug is better than that of the matrix, the interporosity flow of the vug system to fracture system takes place first, and the pressure derivative is V-shaped, which is the reflection of the interporosity flow of vug to fracture;

Stage 6: The interporosity flow stage of the matrix system to fracture system; the interporosity flow of the vug system to fracture system has already been completed, and in this stage, the manner of pseudo-steady interporosity flow of matrix system to fracture system takes place;

Stage 7: The whole radial flow stage of fracture system, vug system, and matrix system (see Fig. 7c); the interporosity flow of matrix to fracture has already been completed, and the pressures between matrix and vug and fracture have come up to a state of dynamic balance.

Effect of water saturation of matrix system

Figure 8 shows the effect of water saturation of matrix system on pressure and pressure derivative of a horizontal well in triple media carbonate reservoir. It can be seen that the parameter \( S_{\text{mw}} \) represents the starting time of interporosity flow of matrix subsystem to fracture subsystem; the time of interporosity will be earlier if the parameter \( S_{\text{mw}} \) is smaller, since the flow resistance of oil phase in the matrix is also smaller.

Fig. 8
figure 8

Effect of water saturation of matrix system on pressure transient responses

Full size image

Effect of water saturation of vug system

Figure 9 shows the effect of water saturation of vug system on pressure and pressure derivative of a horizontal well in triple media carbonate reservoir. It can be seen that the parameter \( S_{\text{vw}} \) represents the starting time of interporosity flow of vug subsystem to fracture subsystem; the time of interporosity will be earlier if the parameter \( S_{\text{vw}} \) is smaller, since the flow resistance of oil phase in the matrix is also smaller.

Fig. 9
figure 9

Effect of water saturation of vug system on pressure transient responses

Full size image

Effect of water saturation of fracture system

Figure 10 shows the effect of water saturation of fracture system on pressure and pressure derivative of a horizontal well in triple media carbonate reservoir. Figure 1 indicates that only the fracture system supplies fluid to the wellbore in the model of this article. Hence, the pressure and pressure derivative will be smaller if the parameter \( S_{\text{fw}} \) is smaller, since the flow resistance of oil phase in the fracture is also smaller.

Fig. 10
figure 10

Effect of water saturation of fracture system on pressure transient responses

Full size image

Effect of horizontal section length in a horizontal well

Figure 11 shows the effect of horizontal section length in a horizontal well on pressure and pressure derivative of a horizontal well in triple media carbonate reservoir. It can be seen that the pressure and pressure derivative of the early radial flow and the linear flow stage will be smaller if the horizontal section length in a horizontal well is longer.

Fig. 11
figure 11

Effect of horizontal section length in a horizontal well on pressure transient responses

Full size image

Effect of horizontal well position

Figure 12 shows the effect of horizontal well position on pressure and pressure derivative of a horizontal well in triple media carbonate reservoir. It can be seen that the pressure and pressure derivative of the early radial flow and the linear flow stage will be smaller if the horizontal well position is closer to the middle of the reservoir.

Fig. 12
figure 12

Effect of horizontal section length in a horizontal well on pressure transient responses

Full size image

Conclusions

The main purpose of this work is to provide a mathematical model to analyze oil–water two-phase flow transient pressure for a horizontal well in triple media carbonate reservoir. The following conclusions can be obtained

  1. 1.

    A solution is obtained in the Laplace space. With the Stehfest numerical inversion algorithm, transient pressure in the real-time space can be obtained.

  2. 2.

    Seven flow periods can be identified for a horizontal well in triple media carbonate reservoir.

  3. 3.

    Parametric analysis indicates that parameters pertinent to horizontal well, such as water saturation of matrix, vug, and fracture system, horizontal section length, and horizontal well position, have obvious influence on dimensionless pressure and pressure derivative curves of a horizontal well in triple media carbonate reservoir.

  4. 4.

    The model can be applied to interpret actual transient pressure responses for horizontal well in triple media carbonate reservoir.

  5. 5.

    Comparing the method of this paper with the well-known commercial software Saphir (Ecrin v4.12.03), developed by the French company Kappa, we can see that the software Saphir did not contain the oil–water two-phase well test model of triple media carbonate reservoir; hence, our model is new, and our method improved the current well test interpretation theory. The method of this paper may be used if the sort of field well test data is like Fig. 6.