A lexicographic optimization approach to the deviation-flow refueling station location problem on a general network

Abstract

The problem of setting up an Alternative Fuel (AF) refueling infrastructure along traffic networks is gaining more interest as AF powered vehicles are becoming more popular due to environmental and economic reasons. This study addresses the refueling station location problem with allowed deviations on a general network. The primary objective is to maximize the amount of flow covered by a given number of stations. Unlike the common practice of having a predetermined set of candidate station locations that may not necessarily hold an optimal solution, this study considers the characteristics of the traffic network and vehicle driving range to discretize the continuous version of the problem and select a finite set of candidate locations that guarantees optimality. This is done by finding the greatest common divisor, g, of the lengths of all edges in the network and half of the vehicle driving range. We prove that there is always an optimal solution where all refueling stations are located at distances that are integer multiples of g from network vertices. This result is used to define refueling sets along the network. The endpoints of these sets are then considered as candidate locations. A secondary objective is introduced to minimize the total travel distance of covered flows. This bi-objective approach does not only optimize the utility of available resources by maximizing covered flows, but also improves convenience, lowers travel cost, and reduces greenhouse gas emissions by minimizing the total travel distance. Finally, a numerical example is provided to illustrate the proposed methods.

1 Introduction

In recent decades, science and technology have progressed very rapidly. This progress positively affected the quality of our lives, boosted the economy, and introduced significant changes to the society. Many of these developments relied on fossil fuel as the main source of energy. This energy source has brought great benefits for large-scale economic activities, mass production, and global transportation. However, the consumption of fossil fuel generates large quantities of Greenhouse Gas (GHG) emissions. Recent studies show that GHG emissions from human activities play a major role in climate change [3, 9]. These emissions prevent heat from escaping earth’s atmosphere causing extraordinary weather conditions including severe storms, floods, droughts, etc. According to the US Environmental Protection Agency [24], the transportation sector contributed by about 28% of total GHG emissions in the US in 2018. The dangerous consequences of climate change and high GHG emissions produced from transportation activities directed many governments around the world to incentivize their citizens to use vehicles powered by Alternative Fuels (AFs) [22, 27]. In addition to environmental benefits, there are many direct economic benefits from transitioning to AFs. Although significant investments are needed to develop AF refueling infrastructure, Ventura et al. [26] showed that the lower operating costs and positive economic impact from improving air quality on health, agriculture, etc., outweigh the initial investment needed. It is also important to note that a significant portion of the conventional fossil fuel used in the US is imported from foreign sources. This could be a national security concern and a potential risk for economic growth if the supply chain were interrupted.

Despite the significant benefits of transitioning to AF powered vehicles, the major challenge remains in the development of the refueling infrastructure that is necessary to support the transition. In addition, the limited driving range of vehicles powered by certain types of AFs adds to the challenge and increases the need to improve the current underdeveloped infrastructure [17]. Even with recent technological advancements that have improved the driving range of AF powered vehicles, these vehicles eventually need to refuel. Given the underdeveloped infrastructure, it is likely that some of these vehicles will need to deviate from their shortest paths to refuel. This may discourage new drivers from making the transition to AF powered vehicles and keep current drivers under a certain level of range anxiety [8]. These challenges have encouraged many researchers to develop mathematical models and algorithms to locate refueling stations in traffic networks taking into consideration the limitations of AF powered vehicles.

Hodgson [10], and Berman, Larson, and Fouska [5] proposed path-based flow-capturing models where flows are considered to be captured if they pass through a node where a refueling station is located. This was a different approach from the common practice of considering demand as vertex weights in the network. The Flow-Capturing Location Model (FCLM) proposed by Hodgson [10] was solved using a simple greedy algorithm. To enable more flexibility in the refueling station location problem, Berman, Bertsimas, and Larson [4] allowed vehicles to deviate from their original paths. Averbakh and Berman [2] considered a network where the demand is affected by the number of encountered facilities. Nicholas and Ogden [21] used the p-median model, to locate refueling stations in a way that minimizes the weighted sum of driving time to the closest refueling station.

The Flow Refueling Location Model (FRLM) proposed by Kuby and Lim [16] extends the FCLM by considering the vehicle driving range. This is important for AF powered vehicles since they tend to have shorter driving ranges compared to conventional fossil fuel vehicles. In addition, the underdeveloped AF refueling infrastructure puts additional requirements in considering the driving range when planning for long trips. Their study proposed an algorithm that determines all possible combinations of vertices needed to serve a certain round trip and used a mixed-integer programming model to maximize the total flow covered by a predetermined number of stations. The FRLM performed better than the p-median model [23]. The FRLM model is computationally expensive due to the need to determine all combinations of vertices that cover round trips. Therefore, Capar and Kuby [6] presented a new formulation for the FRLM to eliminate the need to generate all combinations. This made the model more applicable for realistic sized networks. Kim and Kuby [13, 14] proposed the Deviation-Flow Refueling Location Model (DFRLM) which extend the FRLM by allowing deviations from preplanned paths. The model was then solved using two heuristic algorithms. Hwang, Kweon, and Ventura [11] proposed a model to locate AF refueling stations on a directed network with stations that can only serve vehicles on one side of the road. Ko, Gim, and Guensler [15] provided a comprehensive review of the proposed models and applications for locating AF refueling infrastructure.

Most of the literature reviewed consider the discrete approach to the problem with a predetermined set of candidate locations, usually at network vertices. Kuby and Lim [17] considered adding candidate locations on the edges of the network to expand the set of candidate locations beyond network vertices. The first study to consider the continuous approach with an infinite number of candidate locations was proposed by Ventura, Hwang, and Kweon [25]. The study considered a tree network with the objective to maximize the amount of covered flow by a single refueling station. The problem was then extended by Kweon, Hwang, and Ventura [18] to consider deviations from the shortest path. Abbaas and Ventura [1] proposed a polynomial time algorithm, called the Edge Scanning (ES), for the Continuous Deviation-Flow Refueling Station Location (CDFRSL) problem. The study first considered the continuous approach on a general network starting with the problem of locating a single refueling station. Then they extended the methodology to locate multiple refueling stations considering a limit on the deviation distance from the original shortest path.

As can be seen above, studies that examine the refueling station location problem take one of two broad approaches; the first approach considers a predetermined set of candidate locations. This set could be network vertices, a set of existing facilities in the network such as service plazas [26], or locations selected based on factors not necessarily related to the problem. The objective here is to find the best combination of these locations to serve the maximum amount of traffic flow. The discrete approach may lead to sub-optimal solutions since it only considers a subset of possible refueling station locations. The second approach, called the continuous version of the problem, considers all points in the network as candidate locations. The continuous approach guarantees optimality because it examines all possible locations, but it may be computationally expensive for a large-scale network. Global optimality is important due to the significant investment required to build a new AF refueling station.

The goal of setting up an AF refueling infrastructure could be either locating a predetermined number of refueling stations that maximizes the covered flow or finding the minimum number of refueling stations that is necessary to cover all flows in the network. In both cases, finding a global optimal solution is important. In particular, when it is necessary to cover all flows, the global optimal solution may reduce the required number of refueling stations, which will have significant cost savings. Since finding a global optimal solution using the continuous approach may be computationally expensive. An approach that guarantees global optimality with a reduced search space is needed.

In this study we combine the best of the two approaches. The proposed methodology does not start with a predetermined set of candidate locations like in the discrete approach; rather, it uses the network characteristics and vehicle driving range to discretize the problem by selecting a finite set of candidate locations that guarantees global optimality. Thus, a finite search space is established like in the discrete approach, and global optimality is guaranteed like in the continuous approach. After that, the finite set of candidate locations is used in a set covering model to solve the problem. In addition, to the best of our knowledge, this is the first study that combines global coverage optimality on a general network with the secondary objective of minimizing the total travel distance to reach a refueling station. Here, the information from the optimal solution regarding the primary objective is used in a set covering model to minimize travel distance. This is important in practice as it improves convenience, reduces fuel and maintenance cost for vehicles, and most importantly reduces GHG emissions.

The proposed methodology assumes that any point in the network is a candidate location. This premise is realistic in rural and underdeveloped areas where any piece of land can be considered as a candidate location. However, in developed areas this conjecture may not be realistic due to budget constraints or existing infrastructure. In this case, the proposed approach can be used to find an upper bound for the total flow that can be covered. If the gap between the upper bound coverage and the discrete approach coverage is large enough, we may decide to expand the set of candidate locations. Finally, large sized networks will contain both developed areas with a predetermined set of candidate locations and underdeveloped areas with more flexibility for candidate locations.

The rest of the paper is organized as follows. In Sect. 2 the problem statement, assumptions, and preliminary concepts are discussed. The proposed method is introduced in Sect. 3, starting with network discretization, then the Discrete Edge Scanning (DES) algorithm is presented. In Sect. 4, the secondary objective of minimizing the total travel distance for covered flows is discussed. In Sect. 5 we solve a simple numerical example to illustrate the proposed procedure. Finally, conclusions and suggestions for future research are presented in Sect 6.

2 Problem Statement

In this study, the problem of locating refueling stations on a symmetric (undirected) and connected network $G \left( {V,E} \right)$ is examined, where $V$ is the set of vertices, $\left| V \right| = n$, $n \ge 2$, and $E$ is the set of edges, $\left| E \right| = e$, $e \ge 1$. All trips in $G\left( {V,E} \right)$ are assumed to be round trips that go from an origin vertex $v_{i} \in V$ to a destination vertex $v_{j} \in V$ in what is called the original trip, then return from $v_{j}$ to $v_{i}$ in what is called the return trip. An origin–destination (O-D) pair is denoted by $q\left( {v_{i} ,v_{j} } \right)$, $v_{i} ,v_{j} \in V$. Average traffic flow between an O-D pair $q\left( {v_{i} ,v_{j} } \right)$ (in roundtrips per time unit) is referred to as by $f\left( {v_{i} ,v_{j} } \right)$. $q\left( {v_{i} ,v_{j} } \right)$ and $f\left( {v_{i} ,v_{j} } \right)$ are only defined for $i < j$, meaning that both the flows that start from $v_{i}$ or $v_{j}$ in their original trips are included in $f\left( {v_{i} ,v_{j} } \right)$. The shortest distance between any two points in the network $x_{1} ,x_{2} \in G\left( {V,E} \right)$ is denoted by $d\left( {x_{1} ,x_{2} } \right)$. Network edges are identified by their endpoints, an edge connecting two adjacent vertices $v_{i} ,v_{j} \in V$ is denoted by $\left( {v_{i} ,v_{j} } \right) \in E$. Let $x_{1} ,x_{2} \in G\left( {V,E} \right)$ be two points on the same edge in $E$, the closed line segment connecting $x_{1}$ and $x_{2}$ is referred to as $C\left( {x_{1} ,x_{2} } \right)$, while the open line segment is denoted by ${\text{int}} C\left( {x_{1} ,x_{2} } \right)$. The length of this line segment is denoted by $l\left( {x_{1} ,x_{2} } \right)$.

The proposed methodology utilizes the network characteristics and vehicle driving range to reduce the search space while maintaining guaranteed optimality. The set of candidate refueling station locations is not restricted to network vertices or artificially added candidate points in the interior of network edges. Nonetheless, under certain conditions, the network can be discretized and only a subset of points needs to be considered to find an optimal solution. This subset of candidate locations is then used in a set covering model to maximize the amount of flow that can be served by a predetermined number of refueling stations, $p$. This is the primary objective. The secondary objective is to minimize the total travel distance for the flows covered in the solution.

Figure 1 shows a high-level flow chart to the proposed methodology along with an illustrative network example. From left to right, we start with a network that contains an infinite number of candidate locations. Then, the network is discretized to find a finite set of candidate locations. These locations are called common divisor points and are represented by empty circles in Fig. 1b. A subset of the set of common divisor points, called the set of endpoints, is then created. This subset is guaranteed to contain an optimal solution to the primary and secondary objectives. The set of endpoints is represented by solid circles in Fig. 1c. The set of endpoints is then used in a set covering model to find an optimal solution that maximizes the amount of covered flow. The endpoints that are optimal are represented by diamonds in Fig. 1d. Then, using the set of optimal endpoints found by the set covering model, the complete set of optimal solutions regarding the primary objective can be found. This set can be finite or infinite since it may include line segments connecting two endpoints that can serve in the optimal solution, as shown in Fig. 1d. Finally, the complete set of optimal solutions for the primary objective is used to find the subset of points that minimize the total travel distance for the covered flows. The optimal endpoints regarding the primary and secondary objectives are represented by the stars in Fig. 1e. The detailed steps and the supporting theorems and lemmas are presented in the following sections.

Fig. 1

Flow chart of the proposed approach

Following is the set of assumptions used to formulate and solve this problem. Except for the integrality assumptions (viii) and (ix), these assumptions are consistent with related literature [16, 25].

Assumptions:

• i. Refueling stations can serve vehicles driving in both sides of the road with no capacity limit.

• ii. Vehicles travel along the network between their O-D pairs, $q\left( {v_{i} ,v_{j} } \right)$, $v_{i} ,v_{j} \in V$, in round trips.

• iii. Deviations from the shortest path between an O-D pair are allowed for refueling purposes. Vehicles take the shortest path that includes a refueling station in their one-way trips in both directions.

• iv. Distances in the network are symmetric, i.e., $x_{1} , x_{2} \in G\left( {V,E} \right)$, $d\left( {x_{1} ,x_{2} } \right) = d\left( {x_{2} ,x_{1} } \right)$.

• v. The driving range with a full fuel tank for all vehicles is fixed and denoted by $R$.

• vi. Vehicles are assumed to start their trips at the origin and destination vertices with a half full fuel tank. That is, vehicles can drive a distance $R/2$ starting from their origin and destination vertices before running out of fuel.

• vii. Vehicles refuel once in each one-way trip.

• viii. The distance $R/2$ is a positive integer quantity, $R/2 \in {\mathbb{Z}}^{ + }$.

• ix. All edges in the network have positive integer lengths that are less than or equal to $R$, $l\left( {v_{i} ,v_{j} } \right) \in {\mathbb{Z}}^{ + }$, $l\left( {v_{i} ,v_{j} } \right) \le R$, for all $\left( {v_{i} ,v_{j} } \right) \in E$.

Assumption (iii) allows vehicles to deviate from their shortest path to refuel. Assumptions (i) and (iv) assure that vehicles will follow the same path in opposite directions in their original and return trips. The sixth assumption is common in the literature [16] and gives vehicles the flexibility to refuel away from their origin and destination vertices. The seventh assumption means that, although the proposed method can be used to locate multiple refueling stations in the network, the flow between any O-D pair performs only one refueling operation in each one-way trip. This assumption simplifies the analysis and restricts the length of a round trip to 2R. However, it allows a wide range of applications both in urban areas and intercity transportation. The integrality assumptions (viii) and (ix) facilitate the derivation of the results in this study. These assumptions are not far from practice since the driving range and edge lengths, if not integer, can be easily rounded to the closest integer values. Note that, the symbol ${\mathbb{Z}}^{ + }$ is used to denote the set of positive integer numbers excluding the zero, while the symbol ${\mathbb{Z}}^{0 + }$ will be used later to denote the set of non-negative integer numbers including the zero.

Based on assumptions (vi) and (vii), a refueling station location $x \in G\left( {V,E} \right)$ can serve an O-D pair $q\left( {v_{i} ,v_{j} } \right)$, $v_{i} ,v_{j} \in V$ only if point $x$ falls within $R/2$ from both origin and destination vertices. In this case, we say O-D pair $q\left( {v_{i} ,v_{j} } \right)$ is covered by point $x$. Let $S\left( x \right)$ be the set of O-D pairs covered by a point $x \in G\left( {V,E} \right)$, $S\left( x \right)$ is defined as follows:

$$ S\left( x \right) = \left\{ {q\left( {v_{i} ,v_{j} } \right) | x \in G\left( {V,E} \right),d\left( {v_{i} ,x} \right) \le R/2,{ }} \right. \left. {d\left( {x,v_{j} } \right) \le R/2, v_{i} ,v_{j} \in V,{\text{ and}}\; i < j{ }} \right\} .$$

(1)

Note that, the distance between the vertices of any O-D pair $q\left( {v_{i} ,v_{j} } \right)$ covered by a point $x \in G\left( {V,E} \right)$ can be at most $R$. Therefore, if an O-D pair $q\left( {v_{i} ,v_{j} } \right)$ is separated by a distance greater than $R$, it cannot be covered by a single refueling station as required by assumption (vii). Also, if flow $f\left( {v_{i} ,v_{j} } \right) = 0$, covering $q\left( {v_{i} , v_{j} } \right)$ does not improve the quality of the solution. Based on that, let $Q$ be the set of O-D pairs that needs to be considered when looking for potential refueling station locations. Mathematically, $Q$ is defined as follows:

$$Q = \left\{ {q\left( {{v_i},{v_j}} \right)|d\left( {{v_i},{v_j}} \right) \le R,\;f\left( {{v_i},{v_j}} \right) > 0,\;{v_i},{v_j} \in V,{\rm{and}}\;i < j} \right\}.$$

(2)

The total flow covered by a point $x \in G\left( {V,E} \right)$, can be calculated by adding the flows in $S\left( x \right)$ as follows:

$$ F\left( x \right) = \mathop \sum \limits_{{q\left( {v_{i} ,v_{j} } \right) \in S\left( x \right)}} f\left( {v_{i} ,v_{j} } \right). $$

(3)

3 Discrete edge scanning (DES) algorithm

In this section we introduce a method to reduce the size of the search space in the Single Refueling Deviation-Flow Station Allocation (SRDFSA) problem while maintaining guaranteed optimality. The method uses integrality assumptions (viii) and (ix) to reduce the network by representing distances as integer multiples of a Basic Distance Unit (BDU). To achieve the maximum reduction of the search space, the BDU will be set equal to the Greatest Common Divisor (GCD), denoted by $g$, of the lengths of all edges in the network and the initial driving range $R/2$. A point at a distance $mg$, $m \in {\mathbb{Z}}^{0 + }$, from any network vertex will be referred to as a common divisor point. The set of common divisor points is denoted by $C$ and can be defined as follows:

$$ C = \left\{ {x | x \in G\left( {V,E} \right), d\left( {v_{i} ,x} \right) = mg,m \in {\mathbb{Z}}^{0 + } , v_{i} \in V} \right\}. $$

(4)

Given that the lengths of all edges in $E$ and $R/2$ are positive integer distances, $g$ is a positive integer, $g \in {\mathbb{Z}}^{ + }$, with a minimum value of $1$. However, $m$ is a non-negative integer, i.e., $m \in {\mathbb{Z}}^{0 + }$. Clearly, network vertices fit the definition of common divisor points with $m = 0$, i.e., $V \subseteq C$.

After discussing network discretization and reduction, we review an algorithm that finds a subset of $C$ that is guaranteed to include an optimal solution. Next, this subset is used in a set covering model to find an optimal solution. This solution can then be used to find the complete set of optimal solutions.

3.1 Network discretization

Given that the length of any edge in $E$ is an integer multiple of $g$, the length of any path connecting two different vertices in $V$ must also be an integer multiple of $g$. Therefore, if a point is at a distance $mg$, $m \in {\mathbb{Z}}^{0 + }$, from a vertex, it is also at an integer multiple of $g$ distance from any other vertex in the network.

Deviation from the shortest path between an O-D pair $q\left( {v_{i} ,v_{j} } \right) \in Q$ is necessary when the refueling station is located on an edge $\left( {v_{a} ,v_{b} } \right) \in E$ that does not belong to the shortest path between $v_{i}$ and $v_{j}$. Generally, there are two types of trips that drivers of an O-D pair $q\left( {v_{i} ,v_{j} } \right) \in Q$ can follow in both the original and return trips when the refueling station is located on an edge $\left( {v_{a} ,v_{b} } \right) \in E$ [1]. In type 1 trips, drivers travel through edge $\left( {v_{a} ,v_{b} } \right)$ using one vertex as an entry point and the other vertex as an exit point. If vertex $v_{a}$ is used to enter the edge in the original trip, this trip is said to be of type 1 case (a). However, if vertex $v_{b}$ is used to enter edge $\left( {v_{a} ,v_{b} } \right)$ in the original trip, this trip is said to be of type 1 case (b). In type 2 trips, drivers of O-D pair $q\left( {v_{i} ,v_{j} } \right)$ enter edge $\left( {v_{a} ,v_{b} } \right)$ using one vertex, reach the refueling station location, then go back to the same vertex and leave edge $\left( {v_{a} ,v_{b} } \right)$. If vertex $v_{a}$ is used to enter and leave edge $\left( {v_{a} , v_{b} } \right)$, this trip is said to be of type 2 case (a). Otherwise, if vertex $v_{b}$ is used, then this trip is said to be of type 2 case (b). These types and cases are shown in Fig. 2, dashed arrows represent the routes followed by vehicles in each trip type and case. Let points $w_{1}$, $w_{2}$ in the figure be located such that $d\left( {v_{i} ,w_{1} } \right) = R/2$ and $d\left( {v_{j} ,w_{2} } \right) = R/2$. If the two paths from $v_{i}$ to $w_{1}$ and from $v_{j}$ to $w_{2}$ intersect on edge $\left( {v_{a} ,v_{b} } \right)$ in some trip types and cases, then any point in the intersection line segment falls within $R/2$ from both $v_{i}$ and $v_{j}$ and can cover the O-D pair $q\left( {v_{i} ,v_{j} } \right)$. This intersection line segment is called a refueling segment. Given that the lengths of all edges in the network and $R/2$ are integer multiples of $g$, the endpoints of all refueling segments must be common divisor points. The set of common divisor points in a refueling segment is called a refueling set.

Fig. 2

Types and cases of trips between an O-D pair

To find the refueling set of O-D pair $q\left( {v_{i} ,v_{j} } \right) \in Q$ associated with type 1 case ($r$) trips, $r = a,b$, on edge $\left( {v_{a} ,v_{b} } \right) \in E$, calculate the remaining driving distance to refuel for a vehicle travelling between O-D pair $q\left( {v_{i} ,v_{j} } \right)$ when it reaches the vertices of edge $\left( {v_{a} ,v_{b} } \right)$ as follows:

$$ \gamma \left( {v_{k} ;v_{r} ,v_{c} } \right) = \min \left\{ {R/2 - d\left( {v_{k} ,v_{r} } \right),l\left( {v_{a} ,v_{b} } \right)} \right\},\;k = i,j;\,r = a,b;\,c = a,b;\,c \ne r. $$

(5)

Note that, a negative $\gamma \left( {v_{k} ;v_{r} ,v_{c} } \right)$ means that a vehicle starting its trip from $v_{k}$ cannot reach vertex $v_{r}$ before running out of fuel. Therefore, if $\gamma \left( {v_{k} ;v_{r} ,v_{c} } \right) \ge 0$, type 1 case $\left( r \right)$ refueling set is defined as follows:

$$ \begin{gathered} RS_{1}^{\left( r \right)} \left( {v_{i} ,v_{j} ;v_{a} ,v_{b} } \right) = \left\{ {x \in \left( {v_{a} ,v_{b} } \right) | x \in C,l\left( {v_{r} ,x} \right) \le \gamma \left( {v_{i} ;v_{r} ,v_{c} } \right), {\text{and}}\,\, l\left( {v_{c} ,x} \right) \le \gamma \left( {v_{j} ;v_{c} ,v_{r} } \right)} \right\},\; \hfill \\ r = a,b;\;c = a,b;\;c \ne r. \hfill \\ \end{gathered} $$

(6)

Using a similar logic for type 2, case $\left( r \right)$ trips, $r = a,b$, the remining driving distances and refueling sets are defined as follows:

$$ \delta^{\left( r \right)} \left( {v_{i} ,v_{j} ;v_{a} ,v_{b} } \right) = \min \left\{ {R/2 - {\text{max }}\left\{ {d\left( {v_{i} ,v_{r} } \right), d\left( {v_{j} ,v_{r} } \right)} \right\},l\left( {v_{a} ,v_{b} } \right)} \right\},\;r = a,b, $$

(7)

$$ RS_{2}^{\left( r \right)} \left( {v_{i} ,v_{j} ;v_{a} ,v_{b} } \right) = \left\{ {x \in \left( {v_{a} ,v_{b} } \right) | x \in C,l\left( {v_{r} ,x} \right) \le \delta^{\left( r \right)} \left( {v_{i} ,v_{j} ;v_{a} ,v_{b} } \right)} \right\},\;r = a,b. $$

(8)

The combined refueling set for an O-D pair $q\left( {v_{i} ,v_{j} } \right)$ on edge $\left( {v_{a} ,v_{b} } \right) \in E$ is denoted by $RS\left( {v_{i} ,v_{j} ;v_{a} ,v_{b} } \right)$. Also, the set of all common divisor points capable of covering O-D pair $q\left( {v_{i} ,v_{j} } \right)$ in $G\left( {V,E} \right)$ is denoted by $RS\left( {v_{i} ,v_{j} } \right)$. These sets are defined as follows:

$$ RS\left( {v_{i} ,v_{j} ;v_{a} ,v_{b} } \right) = RS_{1}^{\left( a \right)} \left( {v_{i} ,v_{j} ;v_{a} ,v_{b} } \right) \cup RS_{1}^{\left( b \right)} \left( {v_{i} ,v_{j} ;v_{a} ,v_{b} } \right) \cup RS_{2}^{\left( a \right)} \left( {v_{i} ,v_{j} ;v_{a} ,v_{b} } \right) \cup RS_{2}^{\left( b \right)} \left( {v_{i} ,v_{j} ;v_{a} ,v_{b} } \right), $$

(9)

$$ RS\left( {v_{i} ,v_{j} } \right) = \cup_{{\left( {v_{a} ,v_{b} } \right) \in E}} RS\left( {v_{i} ,v_{j} ;v_{a} ,v_{b} } \right). $$

(10)

The set $RS\left( {v_{i} ,v_{j} } \right)$ contains all common divisor points, including endpoints, in the refueling segments associated with O-D pair $q\left( {v_{i} ,v_{j} } \right) \in Q$. Keep in mind, that $RS\left( {v_{i} ,v_{j} } \right)$ might include endpoints of refueling segments associated with other O-D pairs in the network. Each refueling segment of an O-D pair $q\left( {v_{i} ,v_{j} } \right) \in Q$ on an edge $\left( {v_{a} ,v_{b} } \right) \in E$ associated with a trip type and case can have up to two endpoints; hence, $RS\left( {v_{i} ,v_{j} ;v_{a} ,v_{b} } \right)$ can have up to eight endpoints denoted by $w_{{v_{i} ,v_{j} ;v_{a} ,v_{b} }}^{k}$, $k = 1, \ldots ,{ }8$. The different refueling segments of $q\left( {v_{i} ,v_{j} } \right)$ on the same edge may overlap and form a connected line segment that can cover $q\left( {v_{i} ,v_{j} } \right)$. In this case, the endpoints inside the connected line segment are ignored. The rest of the endpoints are stored in $EP\left( {v_{i} ,v_{j} ;v_{a} ,v_{b} } \right)$. The overall set of endpoints in the network is denoted by $EP$. These sets are defined as follows:

$$ EP\left( {v_{i} ,v_{j} ;v_{a} ,v_{b} } \right) = \left\{ {w_{{v_{i} ,v_{j} ;v_{a} ,v_{b} }}^{k} |} \right.w_{{v_{i} ,v_{j} ;v_{a} ,v_{b} }}^{k} , k = 1, \ldots ,{ }8,{\text{ are endpoints of }}\;\left. {RS\left( {v_{i} ,v_{j} ;v_{a} ,v_{b} } \right)} \right\}, $$

(11)

$$ EP = \cup_{{\left( {v_{a} ,v_{b} } \right) \in E}} \cup_{{q\left( {v_{i} ,v_{j} } \right) \in Q}} EP\left( {v_{i} ,v_{j} ;v_{a} ,v_{b} } \right). $$

(12)

Lemma 1.

Let $w_{1} ,w_{2} \in C\left( {v_{a} ,v_{b} } \right)$, $\left( {v_{a} ,v_{b} } \right) \in E$ be two adjacent points in $EP$. Then, all points in ${\text{int}} C\left( {w_{1} ,w_{2} } \right)$ cover the same set of O-D pairs. Additionally, let $x$ be an interior point of $C\left( {w_{1} ,w_{2} } \right)$, $x \in {\text{int}} C\left( {w_{1} ,w_{2} } \right)$, $x \notin EP$. The set of O-D pairs covered by $x$ must also be covered by points $w_{1}$ and $w_{2}$, $S\left( x \right) \subseteq S\left( {w_{1} } \right) \cap S\left( {w_{2} } \right)$.

Proof.

Given that $w_{1} ,w_{2}$ are two adjacent points in $EP$, no refueling segment ends in ${\text{int}} C\left( {w_{1} ,w_{2} } \right)$. Hence, a refueling segment cannot include an interior point $x \in {\text{int}} C\left( {w_{1} ,w_{2} } \right)$, without including the two adjacent endpoints that surround it. Therefore, all interior points of $C\left( {w_{1} ,w_{2} } \right)$ must cover the same set of O-D pairs, and any O-D pair covered by a point $x \in {\text{int}} C\left( {w_{1} ,w_{2} } \right)$ must also be covered by its surrounding adjacent endpoints from $EP$, namely $w_{1}$ and $w_{2}.$$\square$

Theorem 1.

Let $G\left( {V,E} \right)$ be a network with the lengths of all edges in $E$ and the initial driving distance $R/2$ can be represented as integer multiples of $g$. There is always an optimal solution $W^{*}$ to the SRDFSA problem where all refueling stations are located at common divisor endpoints, $W^{*} \subseteq EP$.

Proof.

Let $X^{*}$ be an optimal solution to the SRDFSA problem where one or more refueling stations are located at points that do not belong to $EP$, let $x \in G\left( {V,E} \right)$, $x \notin EP$ be one of these points. By definition, any point that covers a non-empty set of O-D pairs must belong to a refueling segment. Given that $x \notin EP$, then $x$ must be an interior point of a refueling segment surrounded by two adjacent endpoints, $w_{1} ,w_{2} \in EP$. By Lemma 1 the set of O-D pairs covered by $x$, must also be covered by $w_{1}$ and $w_{2}$, $S\left( x \right) \subseteq S\left( {w_{1} } \right) \cap S\left( {w_{2} } \right)$. Therefore, any refueling station located at a point that does not belong to $EP$ can be moved to a point in $EP$ that covers at least the same set of O-D pairs. Moving all refueling stations to points in $EP$ will produce a solution, $W^{*}$, that covers at least the same set of O-D pairs as $X^{*}$. Given that $X^{*}$ is optimal, then $W^{*}$ is also an optimal solution. $\square$

It is interesting to note that, both Lemma 1 and Theorem 1 and their proofs remain correct if the set of endpoints $EP$ is replaced by the larger set of common divisor points $C$. Theorem 1 enables us to only consider the set of endpoints as candidate locations when looking for an optimal solution to the SRDFSA problem. In addition, using Lemma 1, we can find the complete set of points capable of covering any flow in the network. To do that, for each pair of adjacent endpoints $w_{1} ,w_{2} \in EP$, we pick a random point $x \in {\text{int}} C\left( {w_{1} ,w_{2} } \right)$ and find the set of O-D pairs covered by $x$, $S\left( x \right)$. All points in ${\text{int}} C\left( {w_{1} ,w_{2} } \right)$ cover the same set of O-D pairs as $x$. Any point $x \notin EP$ that does not belong to a line segment connecting two adjacent endpoints in $EP$ on the same edge, cannot cover any flow since it does not belong to any refueling segment.

The set of endpoints can be used in a set covering model to find an optimal solution. To reduce the size of the set covering problem, rather than considering all points in $EP$ as candidate locations, we consider only the points that cover unique sets of O-D pairs. Let us denote this set by $EP^{\prime}$. Following is the model proposed by Hodgson [10] to maximize the amount of flow covered by a predetermined number of refueling stations. First, let us define the necessary notation:

• $EP^{\prime}$: Set of candidate locations, $EP^{\prime} \subseteq EP$, that cover unique sets of O-D pairs. $\left| {EP^{\prime}} \right| = s.$

• $Q$: Set of O-D pairs, $\left| Q \right| = h$.

• $A$: ($s \times h)$ binary matrix where element $a_{{w,q\left( {v_{i} ,v_{j} } \right)}} = 1$, if O-D pair $q\left( {v_{i} ,v_{j} } \right) \in Q$ can be covered by a refueling station located at endpoint $w \in EP^{\prime}$; $a_{{w,q\left( {v_{i} ,v_{j} } \right)}} = 0$, otherwise.

• $p$: Number of refueling stations to be located.

• $x$: $\left( s \right)$-vector of binary decision variables. $x_{w} = \left\{ \begin{gathered} 1,\; {\text{if}}\; {\text{a}}\, {\text{station is located at}}\, w \in EP^{\prime}, \hfill \\ 0, \;{\text{otherwise}}. \hfill \\ \end{gathered} \right.$

• $y$: $\left( h \right)$-vector of binary decision variables. $y_{{q\left( {v_{i} ,v_{j} } \right)}} = \left\{ \begin{gathered} 1, \;{\text{if}}\, q\left( {v_{i} ,v_{j} } \right) \in Q\; {\text{is}}\;{\text{ covered}}, \hfill \\ 0,\; {\text{otherwise}}. \hfill \\ \end{gathered} \right.$

Set covering model:

$$ {\text{Maximize}}:F_{p}^{*} = \mathop \sum \limits_{{q\left( {v_{i} ,v_{j} } \right) \in Q}} f\left( {v_{i} ,v_{j} } \right)y_{{q\left( {v_{i} ,v_{j} } \right)}} , $$

(13)

subject to:

$$ \mathop \sum \limits_{{w \in EP^{\prime}}} a_{{w,q\left( {v_{i} v_{j} } \right)}} x_{w} \ge y_{{q\left( {v_{i} ,v_{j} } \right)}} ,\;\;q\left( {v_{i} ,v_{j} } \right) \in Q, $$

(14)

$$ \mathop \sum \limits_{{w \in EP^{\prime}}} x_{w} = p, $$

(15)

$$ x_{w} ,\;y_{{q\left( {v_{i} ,v_{j} } \right)}} \in \left\{ {0,1} \right\},\;w \in EP^{\prime},\;q\left( {v_{i} ,v_{j} } \right) \in Q. $$

(16)

An iterative approach can be used to determine the set of all optimal solutions where refueling stations are located at endpoints in $EP^{\prime}$. Let us define $W_{p}^{\left( u \right)}$ as the optimal solution from iteration $u$, $u = 1,2,3,...$, given that the number of stations to be located is $p$. $W_{p}^{\left( u \right)}$ is defined as follows:

$$ W_{p}^{\left( u \right)} = \{ w {|} w \in EP^{\prime}, x_{w} = 1\, {\text{in the optimal solution found in iteration }}u\} . $$

(17)

Now, to find a new optimal solution in iteration $u + 1$, the following set of constraints can be added to prevent the prior $u$ solutions from being regenerated:

$$ \mathop \sum \limits_{{w \in W_{p}^{\left( k \right)} }} x_{w} \le p - 1,\;k = 1, \ldots ,u. $$

(18)

The set covering algorithm terminates when the maximum flow covered by the new solution is less than the maximum flow covered in prior solutions.

After solving the set covering model, if a point $w \in EP^{\prime}$ is selected in the optimal solution, any point $x \in G\left( {V,E} \right)$, such that $S\left( w \right) \subseteq S\left( x \right)$, can replace point $w$ in the optimal solution.

3.2 Exact algorithm for the primary objective

In this subsection, an exact polynomial-time algorithm is proposed to find the optimal solution to the SRDFSA problem. First, the set of O-D pairs $Q$ is generated. Then, for each edge $\left( {v_{a} ,v_{b} } \right) \in E$, the algorithm considers each O-D pair $q\left( {v_{i} ,v_{j} } \right) \in Q$ and finds the set of endpoints for all refueling segments on this edge. All endpoints belong to the set of common divisor points $C$. The set of endpoints is then used in a set covering model to find an optimal solution.

DES Algorithm

• Step 1: Establish the set of O-D pairs and the set of common divisor points:

  $$ Q = \left\{ {q\left( {v_{i} ,v_{j} } \right) \big| { d\left( {v_{i} ,v_{j} } \right) \le R, f\left( {v_{i} ,v_{j} } \right) } > 0, v_{i} ,v_{j} \in V,{\text{and}}\,i < j} \right\}, $$
  $$ C = \left\{ {x | x \in G\left( {V,E} \right), d\left( {v_{i} ,x} \right) = mg,m \in {\mathbb{Z}}^{0 + } , \forall v_{i} \in V} \right\}. $$

• Step 2: For each edge in the network $\left( {v_{a} ,v_{b} } \right) \in E$, examine each O-D pair $q\left( {v_{i} ,v_{j} } \right) \in Q$ to find the corresponding refueling sets and sets of endpoints.

  • Sub-step 2.1: Find the refueling set corresponding to type 1 case $\left( r \right)$, $r = a,b$, trips using:

    $$ \gamma \left( {v_{k} ;v_{r} ,v_{c} } \right) = \min \left\{ {R/2 - d\left( {v_{k} ,v_{r} } \right),l\left( {v_{a} ,v_{b} } \right)} \right\},\;\;k = i,j;\,r = a,b;\,c = a,b;\,c \ne r, $$
    $$ RS_{1}^{\left( r \right)} \left( {v_{i} ,v_{j} ;v_{a} ,v_{b} } \right) = \left\{ {x \in \left( {v_{a} ,v_{b} } \right) | x \in C,l\left( {v_{r} ,x} \right) \le \gamma \left( {v_{i} ;v_{r} ,v_{c} } \right), {\text{and}}\, l\left( {v_{c} ,x} \right) \le \gamma \left( {v_{j} ;v_{c} ,v_{r} } \right)} \right\},\;r = a,b;\;c = a,b;\;c \ne r. $$

  • Sub-step 2.2: Find the refueling set corresponding to type 2 case $\left( r \right)$, $r = a,b$, trips using:

    $$ \delta^{\left( r \right)} \left( {v_{i} ,v_{j} ;v_{a} ,v_{b} } \right) = \min \left\{ {R/2 - {\text{max }}\left\{ {d\left( {v_{i} ,v_{r} } \right), d\left( {v_{j} ,v_{r} } \right)} \right\},l\left( {v_{a} ,v_{b} } \right)} \right\},\;r = a,b, $$
    $$ RS_{2}^{\left( r \right)} \left( {v_{i} ,v_{j} ;v_{a} ,v_{b} } \right) = \left\{ {x \in \left( {v_{a} ,v_{b} } \right) | x \in C,l\left( {v_{r} ,x} \right) \le \delta^{\left( r \right)} \left( {v_{i} ,v_{j} ;v_{a} ,v_{b} } \right)} \right\},\;r = a,b. $$

  • Sub-step 2.3: Determine the refueling set and the set of endpoints for O-D pair $q\left( {v_{i} ,v_{j} } \right)$ on edge $\left( {v_{a} ,v_{b} } \right)$ using:

    $$ RS\left( {v_{i} ,v_{j} ;v_{a} ,v_{b} } \right) = RS_{1}^{\left( a \right)} \left( {v_{i} ,v_{j} ;v_{a} ,v_{b} } \right) \cup RS_{1}^{\left( b \right)} \left( {v_{i} ,v_{j} ;v_{a} ,v_{b} } \right) \cup RS_{2}^{\left( a \right)} \left( {v_{i} ,v_{j} ;v_{a} ,v_{b} } \right) \cup RS_{2}^{\left( b \right)} \left( {v_{i} ,v_{j} ;v_{a} ,v_{b} } \right), $$
    $$ EP\left( {v_{i} ,v_{j} ;v_{a} ,v_{b} } \right) = \left\{ {w_{{v_{i} ,v_{j} ;v_{a} ,v_{b} }}^{k} |} \right.w_{{v_{i} ,v_{j} ;v_{a} ,v_{b} }}^{k} , k = 1, \ldots ,{ }8,{\text{ are endpoints of }}\left. {RS\left( {v_{i} ,v_{j} ;v_{a} ,v_{b} } \right)} \right\}. $$

• Step 3: Combine the refueling sets of each O-D pair $q\left( {v_{i} ,v_{j} } \right) \in Q$ to establish the set $RS\left( {v_{i} ,v_{j} } \right)$ using:

  $\qquad RS\left( {v_{i} ,v_{j} } \right) = \cup_{{\left( {v_{a} ,v_{b} } \right) \in E}} RS\left( {v_{i} ,v_{j} ;v_{a} ,v_{b} } \right)$.

• Step 4: Determine the set of all endpoints in the network using:

  $\qquad EP = \cup_{{\left( {v_{a} ,v_{b} } \right) \in E}} \cup_{{q\left( {v_{i} ,v_{j} } \right) \in Q}} EP\left( {v_{i} ,v_{j} ;v_{a} ,v_{b} } \right)$.

• Step 5: Determine the set of O-D pairs and total flow covered by each endpoint $w \in EP$.

  • Sub-step 5.1: For each refueling set $RS\left( {v_{i} ,v_{j} } \right)$ of an O-D pair $q\left( {v_{i} ,v_{j} } \right) \in Q$ only keep the points that belong to the set of endpoints.

    $\qquad RS\left( {v_{i} ,v_{j} } \right) \leftarrow RS\left( {v_{i} ,v_{j} } \right) \cap EP$.

  • Sub-step 5.2: Let $S\left( w \right) = \emptyset$ for each endpoint $w \in EP$.

  • Sub-step 5.3: Consider all sets $RS\left( {v_{i} ,v_{j} } \right)$, $q\left( {v_{i} ,v_{j} } \right) \in Q$. For each point $w \in RS\left( {v_{i} ,v_{j} } \right)$, let

    $\qquad S\left( w \right) \leftarrow S\left( w \right) \cup q\left( {v_{i} ,v_{j} } \right)$.

• Step 6: Use the set of endpoints that cover unique sets of O-D pairs, $EP^{\prime}$, and coverage information for each endpoint in the set covering model, Eqs. (13)–(18), to find an optimal refueling station location solution.

Theorem 2.

The computational complexity of the DES algorithm is $O\left( {en^{2} } \right)$, where $e = \left| E \right|$ and $n = \left| V \right|$.

Proof.

In the preprocessing step, the distances between all pairs of vertices in $V$ are found using Johnson’s algorithm in $O\left( {n^{2} log n + ne} \right)$ [12]. Step 1 constructs sets $Q$ and $C$. Set $Q$ has at most $n\left( {n - 1} \right)$ O-D pairs. Set $C$ requires finding the GCD between the lengths of all edges in $E$ and $R/2$. Since the maximum length of an edge in the network is $R$, finding $g$ takes $O\left( {elog^{3} \left( R \right)} \right)$ [20]. There are at most $eR$ points in $C$. In Step 2, for each edge $\left( {v_{a} ,v_{b} } \right) \in E,$ all O-D pairs in $Q$ are considered. A constant number of operations is performed to find the refueling sets and the sets of endpoints associated with the different trip types and cases; this takes $O\left( {en^{2} } \right)$, $e$ for the number of edges, and $n^{2}$ for the number of O-D pairs in $Q$. Steps 3 and 4 combine the refueling sets and the sets of endpoints, they take at most $en^{2}$ union operations. The longest sub-step in Step 5 is Sub-step 5.3, each set $RS\left( {v_{i} ,v_{j} } \right)$ can have up to $8e$ endpoints, and there can be up to $n\left( {n - 1} \right)$ sets. Therefore, this sub-step takes $O\left( {en^{2} } \right)$. After that the set covering model is solved separately using an efficient algorithm like the one proposed in [19].$\square$

Although we are not discussing limiting the allowed deviation distance from the shortest path between an O-D pair in this study. This could be easily done by modifying Eqs. (5) and (7) to include an upper limit on deviation distance. The rest of the algorithm remains the same.

4 Lexicographic Optimization

The primary objective of our algorithm is to maximize traffic flow (in roundtrips per time unit) covered by a predetermined number of refueling stations $p$. However, to further improve the solution, a secondary objective can be introduced to minimize the total travel distance for all flows covered by the optimal solution.

We can utilize the properties of flow types discussed in Sect. 3 to find the optimal solution regarding the secondary objective. Assume that all points in a line segment $C\left( {w_{1} ,w_{2} } \right)$ on edge $\left( {v_{a} ,v_{b} } \right) \in E$, where $w_{1}$, $w_{2} \in EP$, cover the same non-empty set of O-D pairs. Recall that, flows covered by the line segment $C\left( {w_{1} ,w_{2} } \right)$ that make type 1 trips go naturally through edge $\left( {v_{a} ,v_{b} } \right)$ from one endpoint to the other. Therefore, the specific station location within the line segment makes no difference regarding travel distance for flows making type 1 trips to reach all points in $C\left( {w_{1} ,w_{2} } \right)$. Figure 3a shows an example of type 1 flow with two candidate locations for a refueling station $x_{1}$ and $x_{2}$.

Fig. 3

Effect of trip type on total travel distance

On the other hand, a type 2 trip uses one vertex to enter edge $\left( {v_{a} ,v_{b} } \right)$, reaches the refueling station location, then makes a U-turn and leaves the edge using the same entry vertex. Therefore, the further the refueling station location is from the entry vertex, the more distance this flow has to travel within edge $\left( {v_{a} ,v_{b} } \right)$ as shown in Fig. 3b, bent arrows represent the distance to reach points $x_{1}$ and $x_{2}$ from vertex $v_{a}$.

Given the assumption that drivers take the shortest path that includes a refueling station between an O-D pair, some flows may change their trip type or case to reach different points within the same line segment. We will call these flows type 3 flows. Figure 4 shows an example of a type 3 flow. In this example, if a refueling station is located near $w_{1}$, $f\left( {v_{i} ,v_{j} } \right)$ will make type 2 case (a) trips. However, if the refueling station is located near $w_{2}$ then $f\left( {v_{i} ,v_{j} } \right)$ will make type 2 case (b) trips. Finally, if the refueling station is located exactly at the middle point of $C\left( {w_{1} ,w_{2} } \right)$, $f\left( {v_{i} ,v_{j} } \right)$ will travel the same distance regardless of the trip type and case.

Fig. 4

Type 3 flow example

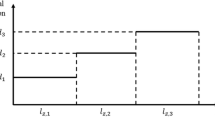
Note that, if the refueling station location is shifted from one endpoint toward the other, the travel distance for $f\left( {v_{i} ,v_{j} } \right)$ would increase linearly until it reaches a maximum value at the middle point, then it would decrease as the refueling station location gets closer to the other endpoint. The middle point of $C\left( {w_{1} ,w_{2} } \right)$ in this example is called the switching point since the flow changes its trip type and/or case at this point. This change in travel distance is shown in Fig. 5a. Figure 5b shows another example where there is no path between $v_{i}$ and $v_{b}$ that does not go through $v_{a}$. In this case, if we shift the refueling station location from $w_{1}$ toward $w_{2}$, $f\left( {v_{i} ,v_{j} } \right)$ will make type 2 case (a) trips at the beginning, then at the middle point the flow will switch to type 1 trips for the rest of the refueling segment. Therefore, the travel distance for $f\left( {v_{i} ,v_{j} } \right)$ increases linearly from $w_{1}$ to the middle point, then remains constant from the middle point to $w_{2}$.

Fig. 5

Changing flow examples

Based on this discussion, we have the following four situations. Situation (1): if all flows covered by a line segment $C\left( {w_{1} ,w_{2} } \right)$ make type 1 trips regardless of the specific refueling station location in $C\left( {w_{1} ,w_{2} } \right)$, then the total travel distance required to reach any point in this refueling segment is the same. Situation (2): if there are type 2 flows covered by $C\left( {w_{1} ,w_{2} } \right)$ but there are no type 3 flows and the amount of flow making type 2 case (a) trips is equivalent to that making type 2 case (b) trips, then the total travel distance required to reach any point in this refueling segment is the same. This is because, if the refueling station location is shifted within $C\left( {w_{1} ,w_{2} } \right)$, the increase/decrease in travel distance for type 2 case (a) flows will be equivalent to the decrease/increase in travel distance for type 2 case (b) flows. In this situation, flows are said to be balanced for the refueling segment $C\left( {w_{1} ,w_{2} } \right)$. Situation (3) is similar to situation (2); however, the amount of flow making type 2 case (a) trips is not equivalent to that making type 2 case (b) trips. Here, only one of the endpoints minimizes the total travel distance within $C\left( {w_{1} ,w_{2} } \right)$. An example of situations (2) and (3) is shown in Fig. 6. In this example, there are two O-D pairs, $Q = \left\{ {q\left( {v_{i} ,v_{j} } \right), q\left( {v_{k} ,v_{l} } \right)} \right\}$, covered by line segment $C\left( {w_{1} ,w_{2} } \right)$. The flow between O-D pair $q\left( {v_{i} ,v_{j} } \right)$ makes type 2 case (a) trips, while the flow between O-D pair $q\left( {v_{k} ,v_{l} } \right)$ makes type 2 case (b) trips. If $f\left( {v_{i} ,v_{j} } \right) = f\left( {v_{k} ,v_{l} } \right)$, then this example represents situation (2), and the total travel distance to any point in line segment $C\left( {w_{1} ,w_{2} } \right)$ is the same. However, if $f\left( {v_{i} ,v_{j} } \right) \ne f\left( {v_{k} ,v_{l} } \right)$, then this example represents situation (3), and the total travel distance can be minimized by locating the refueling station at one of the endpoints. If $f\left( {v_{i} ,v_{j} } \right) > f\left( {v_{k} ,v_{l} } \right)$, then the total travel distance can be minimized by locating the refueling station at endpoint $w_{1}$; on the other hand, if $f\left( {v_{i} ,v_{j} } \right) < f\left( {v_{k} ,v_{l} } \right)$, then locating the refueling station at endpoint $w_{2}$ minimizes the total travel distance. Situation (4) happens when there are type 3 flows covered by $C\left( {w_{1} ,w_{2} } \right)$. Here, only endpoints can minimize the total travel distance within $C\left( {w_{1} ,w_{2} } \right)$. These results will be formally introduced and proven later in this section.

Fig. 6

Situations (2) and (3) example

Consider a line segment $C\left( {w_{a} ,w_{b} } \right) \subseteq C\left( {v_{a} ,v_{b} } \right)$, $\left( {v_{a} ,v_{b} } \right) \in E$, all points in $C\left( {w_{a} ,w_{b} } \right)$ cover the same non-empty set of O-D pairs. $w_{a} ,w_{b} \in EP$, where $w_{a}$ is the endpoint closer to $v_{a}$ and $w_{b}$ is the endpoint closer to $v_{b}$. Let $d\left( {v_{i} ,v_{j} ;x} \right)$ be the total travel distance for the flow between O-D pair $q\left( {v_{i} ,v_{j} } \right)$ assuming the flow is covered by a station located at some point $x \in C\left( {w_{a} ,w_{b} } \right)$. In addition, let $D\left( x \right)$ denote the total travel distance for all covered flows by a station located at $x \in C\left( {w_{a} ,w_{b} } \right)$. These distances can be calculated as follows:

$$ d\left( {v_{i} ,v_{j} ;x} \right) = 2 \times f\left( {v_{i} ,v_{j} } \right) \times \left[ {{\text{min }}\left\{ {d\left( {v_{i} ,v_{a} } \right) + d\left( {v_{a} ,x} \right),d\left( {v_{i} ,v_{b} } \right) + d\left( {v_{b} ,x} \right)} \right\} + {\text{min }}\left\{ {d\left( {x,v_{a} } \right) + d\left( {v_{a} ,v_{j} } \right),d\left( {x,v_{b} } \right) + d\left( {v_{b} ,v_{j} } \right)} \right\}} \right], $$

(19)

$$ D\left( x \right) = \mathop \sum \limits_{{q\left( {v_{i} ,v_{j} } \right) \in S\left( x \right)}} d\left( {v_{i} ,v_{j} ;x} \right). $$

(20)

The shortest distances between all pairs of vertices are found in the preprocessing step of the DES algorithm, and the remaining distances between $v_{a}$, $x$, and $v_{b}$ are easy to find.

Since drivers take the shortest refuellable path, the total travel distance for the different trip types and cases for each O-D pair is needed in order to know which trip type and case will be used by the flow between a given O-D pair. The one-way travel distance for the flow between O-D pair $q\left( {v_{i} ,v_{j} } \right)$ to reach any point in the line segment $C\left( {w_{a} ,w_{b} } \right)$ using type 1 trips will be denoted by $d_{1} \left( {v_{i} ,v_{j} ;w_{a} ,w_{b} } \right)$ and is defined as follows:

$$ d_{1} \left( {v_{i} ,v_{j} ;w_{a} ,w_{b} } \right) = {\text{min}}\left\{ {d\left( {v_{i} ,v_{a} } \right) + d\left( {v_{a} ,v_{b} } \right) + d\left( {v_{b} ,v_{j} } \right), d\left( {v_{i} ,v_{b} } \right) + d\left( {v_{b} ,v_{a} } \right) + d\left( {v_{a} ,v_{j} } \right)} \right\} $$

(21)

For type 2 flows, since the total travel distance depends on the specific location within the line segment, we define the maximum and minimum travel distances for a flow making type 2 case (a) or (b) trips. The maximum and minimum one-way travel distances for the flow between O-D pair $q\left( {v_{i} ,v_{j} } \right)$ using type 2 case (a) path are denoted by $d_{{2, {\text{max}}}}^{\left( a \right)} \left( {v_{i} ,v_{j} ;w_{a} ,w_{b} } \right)$ and $d_{{2,{\text{min}}}}^{\left( a \right)} \left( {v_{i} ,v_{j} ;w_{a} ,w_{b} } \right)$ are respectively defined as follows:

$$ d_{{2, {\text{max}}}}^{\left( a \right)} \left( {v_{i} ,v_{j} ;w_{a} ,w_{b} } \right) = d\left( {v_{i} ,v_{a} } \right) + 2 \times d\left( {v_{a} ,w_{b} } \right) + d\left( {v_{a} ,v_{j} } \right), $$

(22)

$$ d_{{2,{\text{min}}}}^{\left( a \right)} \left( {v_{i} ,v_{j} ;w_{a} ,w_{b} } \right) = d\left( {v_{i} ,v_{a} } \right) + 2 \times d\left( {v_{a} ,w_{a} } \right) + d\left( {v_{a} ,v_{j} } \right). $$

(23)

Similarly, the one way maximum and minimum travel distances for type 2 case (b) trips $d_{{2, {\text{max}}}}^{\left( b \right)} \left( {v_{i} ,v_{j} ;w_{a} ,w_{b} } \right)$ and $d_{{2,{\text{min}}}}^{\left( b \right)} \left( {v_{i} ,v_{j} ;w_{a} ,w_{b} } \right)$ are respectively defined.

Now, we can define the sets of O-D pairs with flows that follow each trip type to reach segment $C\left( {w_{a} ,w_{b} } \right)$. Let $S_{1} \left( {C\left( {w_{a} ,w_{b} } \right)} \right)$ be the set of O-D pairs with positive traffic flows covered by line segment $C\left( {w_{a} ,w_{b} } \right)$ that perform type 1 trips to reach any point in $C\left( {w_{a} ,w_{b} } \right)$. $S_{1} \left( {C\left( {w_{a} ,w_{b} } \right)} \right)$ is defined as follows:

$$ \begin{aligned} S_{1} \left( {C\left( {w_{a} ,w_{b} } \right)} \right) &= \{ q\left( {v_{i} ,v_{j} } \right) {|} q\left( {v_{i} ,v_{j} } \right) \in S\left( {w_{a} } \right), C\left( {w_{a} ,w_{b} } \right) \subseteq C\left( {v_{a} ,v_{b} } \right),\left( {v_{a} ,v_{b} } \right) \in \\ & E,d_{1} \left( {v_{i} ,v_{j} ;w_{a} ,w_{b} } \right) \le {\text{min }}\left\{ {d_{{2,{\text{min}}}}^{\left( a \right)} \left( {v_{i} ,v_{j} ;w_{a} ,w_{b} } \right), d_{{2,{\text{min}}}}^{\left( b \right)} \left( {v_{i} ,v_{j} ;w_{a} ,w_{b} } \right)} \right\},v_{i} ,v_{j} \in V, {\text{and}}\, i < j\}. \end{aligned} $$

(24)

Also, let $S_{2}^{\left( a \right)} \left( {C\left( {w_{a} ,w_{b} } \right)} \right)$ be the set of O-D pairs with positive traffic flows covered by line segment $C\left( {w_{a} ,w_{b} } \right)$ that perform type 2 case (a) trips to reach any point in $C\left( {w_{a} ,w_{b} } \right)$. This set is defined as follows:

$$\begin{aligned}S_2^{\left( a \right)}\left( {C\left( {{w_a},{w_b}} \right)} \right) &= \{ q\left( {{v_i},{v_j}} \right)|q\left( {{v_i},{v_j}} \right) \in S\left( {{w_a}} \right),\;C\left( {{w_a},{w_b}} \right) \subseteq C\left( {{v_a},{v_b}} \right),\left( {{v_a},{v_b}} \right) \in \\& E,d_{2,\;\;\max }^{\left( a \right)}\left( {{v_i},{v_j};{w_a},{w_b}} \right) < \min \;\{ {d_1}\left( {{v_i},{v_j};{w_a},{w_b}} \right),\;d_{2,\min }^{\left( b \right)}\left( {{v_i},{v_j};{w_a},{w_b}} \right)\} ,{v_i},{v_j} \in V,\;{\rm{and}}\;i < j\} \end{aligned}$$

(25)

Set $S_{2}^{\left( b \right)} \left( {C\left( {w_{a} ,w_{b} } \right)} \right)$ is defined in a similar manner. Finally, the set of type 3 flows is defined as follows:

$$ \begin{aligned} S_{3} \left( {C\left( {w_{a} ,w_{b} } \right)} \right) & = \{ q\left( {v_{i} ,v_{j} } \right) {|} q\left( {v_{i} ,v_{j} } \right) \in S\left( {w_{a} } \right),q\left( {v_{i} ,v_{j} } \right) \notin \left( {S_{1} \left( {C\left( {w_{a} ,w_{b} } \right)} \right) \cup S_{2}^{\left( a \right)} \left( {C\left( {w_{a} ,w_{b} } \right)} \right) \cup S_{2}^{\left( b \right)} \left( {C\left( {w_{a} ,w_{b} } \right)} \right)} \right),C\left( {w_{a} ,w_{b} } \right) \subseteq \\ & C\left( {v_{a} ,v_{b} } \right),\left( {v_{a} ,v_{b} } \right) \in E,v_{i} ,v_{j} \in V,{\text{and }}i < j{ }\} . \\ \end{aligned} $$

(26)

Note that each O-D pair with positive flow that can reach a station located anywhere in $C\left( {w_{a} ,w_{b} } \right)$ is assigned to only one of these sets depending on the total travel distance.

Now, we can define flow balance using these sets. Let $F_{2}^{\left( r \right)} \left( {C\left( {w_{a} ,w_{b} } \right)} \right)$ denote the total flow for O-D pairs in $S_{2}^{\left( r \right)} \left( {C\left( {w_{a} ,w_{b} } \right)} \right)$, $r = a,b$.

$$ F_{2}^{\left( r \right)} \left( {C\left( {w_{a} ,w_{b} } \right)} \right) = \mathop \sum \limits_{{q\left( {v_{i} ,v_{j} } \right) \in S_{2}^{\left( r \right)} \left( {C\left( {w_{a} ,w_{b} } \right)} \right)}} f\left( {v_{i} ,v_{j} } \right),\;r = a,b. $$

(27)

The flows covered by $C\left( {w_{a} ,w_{b} } \right)$ are said to be balanced if $S_{3} \left( {C\left( {w_{a}^{*} ,w_{b}^{*} } \right)} \right) = \emptyset$ and $F_{2}^{\left( a \right)} \left( {C\left( {w_{a} ,w_{b} } \right)} \right) = F_{2}^{\left( b \right)} \left( {C\left( {w_{a} ,w_{b} } \right)} \right)$.

Lemma 2.

Let $C\left( {w_{a} ,w_{b} } \right) \subseteq C\left( {v_{a} ,v_{b} } \right)$, $w_{a} ,w_{b} \in EP$, $\left( {v_{a} ,v_{b} } \right) \in E$ be a line segment, such that all of its points cover the same non-empty set of O-D pairs. Then, all points in $C\left( {w_{a} ,w_{b} } \right)$ have the same total travel distance if and only if the flows covered by $C\left( {w_{a} ,w_{b} } \right)$ are balanced.

Proof.

($\Rightarrow$) (By contradiction) Let us assume that all points in $C\left( {w_{a} ,w_{b} } \right)$ have the same total travel distance but the flows covered by $C\left( {w_{a} ,w_{b} } \right)$ are not balanced. Take points $x$, $y \in C\left( {w_{a} ,w_{b} } \right)$, $x \ne y$. If there is no balance because the amount of flows strictly making type 2 case (a) trips is not equivalent to that strictly making type 2 case (b) trips to reach points $x$ and $y$, then $D\left( x \right) - D\left( y \right) = 2 \times \left( {F_{2}^{\left( a \right)} \left( {C\left( {w_{a} ,w_{b} } \right)} \right) - F_{2}^{\left( b \right)} \left( {C\left( {w_{a} ,w_{b} } \right)} \right)} \right) \times d\left( {x,y} \right)$. Note that, $D\left( x \right) - D\left( y \right) = 0$ only if $F_{2}^{\left( a \right)} \left( {C\left( {w_{a} ,w_{b} } \right)} \right) = F_{2}^{\left( b \right)} \left( {C\left( {w_{a} ,w_{b} } \right)} \right)$ or $d\left( {x,y} \right) = 0$. This contradicts the assumptions $x \ne y$ and $F_{2}^{\left( a \right)} \left( {C\left( {w_{a} ,w_{b} } \right)} \right) \ne F_{2}^{\left( b \right)} \left( {C\left( {w_{a} ,w_{b} } \right)} \right)$. On the other hand, if there is no balance because $S_{3} \left( {C\left( {w_{a} ,w_{b} } \right)} \right) \ne \emptyset$, then when we shift the refueling station location starting from $w_{a}$ to $w_{b}$, initially the total travel distance for all type 3 flows will change with constant rates that are $\ge 0$. Once we reach the switching point for any type 3 flow, its total travel distance will change with a constant rate that is $\le 0$. As we get very close to $w_{b}$, the total travel distance for all type 3 flows will be changing with constant rates that are $\le 0$. The change rate cannot be exactly 0 for any type 3 flow for the entire line segment $C\left( {w_{a} ,w_{b} } \right)$, because otherwise it will not change its trip type or case. This contradicts the assumption that all points in $C\left( {w_{a} ,w_{b} } \right)$ have the same total travel distance.

($\Leftarrow$) Since the flow is balanced then $S_{3} \left( {C\left( {w_{a} ,w_{b} } \right)} \right) = \emptyset$. Let $x$, $y$ be two points in $C\left( {w_{a} ,w_{b} } \right)$, such that $d\left( {v_{a} ,y} \right) = d\left( {v_{a} ,x} \right) + d\left( {x,y} \right)$, and $d\left( {v_{b} ,y} \right) = d\left( {v_{b} ,x} \right) - d\left( {x,y} \right)$. In addition, let $D\left( x \right)$ and $D\left( y \right)$ be the total travel distances to points $x$ and $y$, respectively. Then,

$\begin{aligned} D\left( r \right) &= 2 \times \mathop \sum \limits_{{q\left( {v_{i} ,v_{j} } \right) \in S_{1} \left( {C\left( {w_{a} ,w_{b} } \right)} \right)}} \left( {f\left( {v_{i} ,v_{j} } \right) \times d_{1} \left( {v_{i} ,v_{j} ;w_{a} ,w_{b} } \right)} \right) \\& + \mathop \sum \limits_{{q\left( {v_{i} ,v_{j} } \right) \in S_{2}^{\left( a \right)} \left( {C\left( {w_{a} ,w_{b} } \right)} \right)}} d\left( {v_{i} ,v_{j} ;r} \right) + \mathop \sum \limits_{{q\left( {v_{i} ,v_{j} } \right) \in S_{2}^{\left( b \right)} \left( {C\left( {w_{a} ,w_{b} } \right)} \right)}} d\left( {v_{i} ,v_{j} ;r} \right). \end{aligned}$

The total distance travelled by vehicles making type 1 trips is the same for both points $x$ and $y$; that is, $2 \times \sum_{{q\left( {v_{i} ,v_{j} } \right) \in S_{1} \left( {C\left( {w_{a} ,w_{b} } \right)} \right)}} \left( {f\left( {v_{i} ,v_{j} } \right) \times d_{1} \left( {v_{i} ,v_{j} ;w_{a} ,w_{b} } \right)} \right)$. However, the total travel distance for the flows between O-D pair $q\left( {v_{i} ,v_{j} } \right)$ that make type 2 case (a) trips when a refueling station is located at point $y$ is:

$d\left( {v_{i} ,v_{j} ;y} \right) = 2 \times f\left( {v_{i} ,v_{j} } \right) \times \left( {d\left( {v_{i} ,v_{a} } \right) + 2 \times d\left( {v_{a} ,y} \right) + d\left( {v_{a} ,v_{j} } \right)} \right)$.

Since $d\left( {v_{a} ,y} \right) = d\left( {v_{a} ,x} \right) + d\left( {x,y} \right)$ we can rewrite $d\left( {v_{i} ,v_{j} ;y} \right)$ as follows:

$$ d\left( {v_{i} ,v_{j} ;y} \right) = 2 \times f\left( {v_{i} ,v_{j} } \right) \times \left( {d\left( {v_{i} ,v_{a} } \right) + 2 \times \left( {d\left( {v_{a} ,x} \right) + d\left( {x,y} \right)} \right) + d\left( {v_{a} ,v_{j} } \right)} \right), $$

$d\left( {v_{i} ,v_{j} ;y} \right) = d\left( {v_{i} ,v_{j} ;x} \right) + 4 \times f\left( {v_{i} ,v_{j} } \right) \times d\left( {x,y} \right).$

Similarly, the total travel distance for the flows between O-D pair $q\left( {v_{i} ,v_{j} } \right)$ that make type 2 case (b) trips when a refueling station is located at point $y$ can be represented in terms of $d\left( {v_{i} ,v_{j} ;x} \right)$ using the relation $d\left( {v_{b} ,y} \right) = d\left( {v_{b} ,x} \right) - d\left( {x,y} \right)$. Hence, the total travel distance for point $y$ becomes:

$$ \begin{aligned} D\left( y \right) & = 2 \times \mathop \sum \limits_{{q\left( {v_{i} ,v_{j} } \right) \in S_{1} \left( {C\left( {w_{a} ,w_{b} } \right)} \right)}} \left( {f\left( {v_{i} ,v_{j} } \right) \times d_{1} \left( {v_{i} ,v_{j} ;w_{a} ,w_{b} } \right)} \right) \hfill \\ &+ \mathop \sum \limits_{{q\left( {v_{i} ,v_{j} } \right) \in S_{2}^{\left( a \right)} \left( {C\left( {w_{a} ,w_{b} } \right)} \right)}} d\left( {v_{i} ,v_{j} ;x} \right) + \mathop \sum \limits_{{q\left( {v_{i} ,v_{j} } \right) \in S_{2}^{\left( b \right)} \left( {C\left( {w_{a} ,w_{b} } \right)} \right)}} d\left( {v_{i} ,v_{j} ;x} \right) \hfill \\& + 4 \times F_{2}^{\left( a \right)} \left( {C\left( {w_{a} ,w_{b} } \right)} \right) \times d\left( {x,y} \right) - 4 \times F_{2}^{\left( b \right)} \left( {C\left( {w_{a} ,w_{b} } \right)} \right) \times d\left( {x,y} \right). \hfill \\ \end{aligned} $$

Given that flows are balanced $F_{2}^{\left( a \right)} \left( {C\left( {w_{a} ,w_{b} } \right)} \right) = F_{2}^{\left( b \right)} \left( {C\left( {w_{a} ,w_{b} } \right)} \right)$, then $D\left( x \right) = D\left( y \right).$$\square$

Lemma 2 implies that, if the flows covered by $C\left( {w_{a} ,w_{b} } \right)$ are balanced and we are able to find one point in $C\left( {w_{a} ,w_{b} } \right)$ that minimizes the total travel distance for the flows covered by $C\left( {w_{a} ,w_{b} } \right)$, then any point in line segment $C\left( {w_{a} ,w_{b} } \right)$ also minimizes the total travel distance for the flows covered by $C\left( {w_{a} ,w_{b} } \right)$.

Lemma 3.

Let $C\left( {w_{a} ,w_{b} } \right) \subseteq C\left( {v_{a} ,v_{b} } \right)$, $w_{a} ,w_{b} \in EP$, $\left( {v_{a} ,v_{b} } \right) \in E$ be a line segment, such that all of its points cover the same non-empty set of O-D pairs. Then, for any point $x \in {\text{int}} C\left( {w_{a} ,w_{b} } \right)$, there is always a point $w \in \left\{ {w_{a} ,w_{b} } \right\}$ where $D\left( w \right) \le D\left( x \right)$.

Proof.

By definition of type 1 trips $d\left( {v_{i} ,v_{j} ;w_{a} } \right) = d\left( {v_{i} ,v_{j} ;w_{b} } \right) = d\left( {v_{i} ,v_{j} ;x} \right)$, for all $x \in {\text{int}} C\left( {w_{a} ,w_{b} } \right)$, $q\left( {v_{i} ,v_{j} } \right) \in S_{1} \left( {C\left( {w_{a} ,w_{b} } \right)} \right)$. On the other hand, flows covered by $C\left( {w_{a} ,w_{b} } \right)$ that make type 2 trips case ($r$), $r = a,b$, travel a distance $2 \times d\left( {v_{r} ,x} \right)$ in edge $\left( {v_{a} ,v_{b} } \right)$ to use a refueling station located at $x \in {\text{int}} C\left( {w_{a} ,w_{b} } \right)$. Since $x \in {\text{int}} C\left( {w_{a} ,w_{b} } \right)$, vehicles of type 2 flow have to pass by one of the endpoints $\left\{ {w_{a} ,w_{b} } \right\}$ before reaching $x$. Therefore $d\left( {v_{i} ,v_{j} ;w_{r} } \right) \le d\left( {v_{i} ,v_{j} ;x} \right)$, for all $x \in {\text{int}} C\left( {w_{a} ,w_{b} } \right)$, $q\left( {v_{i} ,v_{j} } \right) \in S_{2}^{\left( r \right)} \left( {C\left( {w_{a} ,w_{b} } \right)} \right)$. If the flows covered by $C\left( {w_{a} ,w_{b} } \right)$ are not balanced, the endpoint closer to the entry vertex with higher type 2 flow volume will have minimum total travel distance. Otherwise, by Lemma 2, if the flows covered by $C\left( {w_{a} ,w_{b} } \right)$ are balanced, then all points in $C\left( {w_{a} ,w_{b} } \right)$ have the same total travel distance. Hence, there is always $w \in \left\{ {w_{a} ,w_{b} } \right\}$ where $D\left( w \right) \le D\left( x \right).$ $\square$

Since all points that cover any O-D pairs are either endpoints in $EP$ or belong to line segments surrounded by endpoints in $EP$, then by Theorem 1 and Lemma 3, there is always an optimal solution regarding both the primary and secondary objectives that belongs to the set of endpoints $EP$.

Solving the problem regarding the primary objective gives us the maximum amount of flow that can be covered by $p$ stations, $F_{p}^{*}$. This information with the complete set of endpoints $EP$ can then be used in the set covering model below to minimize the total travel distance. First, let us define some additional notation:

• $EP$: Set of refueling segments endpoints, $\left| {EP} \right| = s$.

• $D$: ($s \times h)$ distance matrix where $d_{{w,q\left( {v_{i} ,v_{j} } \right)}} = d\left( {v_{i} ,w} \right) + d\left( {w,v_{j} } \right)$, for a trip between O-D pair $q\left( {v_{i} ,v_{j} } \right) \in Q$ going through a refueling station located at endpoint $w \in EP$.

• $x$: $\left( s \right)$-vector of binary decision variables. $x_{w} = \left\{ {\begin{array}{*{20}c} {1, \,\,\text{if a station is located at}\, w \in EP,} \\ {0,\,\, \text{otherwise}. } \\ \end{array} } \right.$

• $z$: $\left( {s \times h} \right)$-matrix of binary decision variables. $z_{{w,q\left( {v_{i} ,v_{j} } \right)}} = \left\{ {\begin{array}{*{20}c} {1, \, \text{if}\, q\left( {v_{i} ,v_{j} } \right) \in Q \, \text{is covered by a refueling station located at}\,w \in EP,} \\ {0, \, \text{otherwise}. } \\ \end{array} } \right.$

• 
  

  Set covering model:

  $$ {\text{Minimize}}:D_{p}^{*} = \mathop \sum \limits_{{q\left( {v_{i} ,v_{j} } \right) \in Q}} \mathop \sum \limits_{w \in EP} d_{{w,q\left( {v_{i} ,v_{j} } \right)}} f\left( {v_{i} ,v_{j} } \right)z_{{w,q\left( {v_{i} ,v_{j} } \right)}} , $$

  (28)

• subject to:

  $$ \mathop \sum \limits_{w \in EP} x_{w} = p, $$

  (29)
  $$ \mathop \sum \limits_{w \in EP} a_{{w,q\left( {v_{i} ,v_{j} } \right)}} z_{{w,q\left( {v_{i} ,v_{j} } \right)}} = y_{{q\left( {v_{i} ,v_{j} } \right)}} ,\;q\left( {v_{i} ,v_{j} } \right) \in Q, $$

  (30)
  $$ \mathop \sum \limits_{{q\left( {v_{i} ,v_{j} } \right) \in Q}} z_{{w,q\left( {v_{i} ,v_{j} } \right)}} \le hx_{w} ,\;w \in EP, $$

  (31)
  $$ \mathop \sum \limits_{{q\left( {v_{i} ,v_{j} } \right) \in Q}} f\left( {v_{i} ,v_{j} } \right)y_{{q\left( {v_{i} ,v_{j} } \right)}} = F_{p}^{*} , $$

  (32)
  $$ x_{w} ,y_{{q\left( {v_{i} ,v_{j} } \right)}} ,z_{{w,q\left( {v_{i} ,v_{j} } \right)}} \in \left\{ {0,1} \right\},\;w \in EP,\;q\left( {v_{i} ,v_{j} } \right) \in Q. $$

  (33)

The model above minimizes the total travel distance given the inputs from the primary optimal solution. If a point ${w}_{1}\in EP$ is selected in an optimal solution $W^{*}$ regarding the secondary objective, let the set of O-D pairs assigned to be covered by $w_{1}$ in this particular solution be $S_{{W^{*} }} \left( {w_{1} } \right)$. Now, if there exists a point $w_{2} \in EP$ that does not belong to $W^{*}$, $S_{{W^{*} }} \left( {w_{1} } \right) \subseteq S\left( {w_{2} } \right)$, and the total travel distance for the flows between O-D pairs in $S_{{W^{*} }} \left( {w_{1} } \right)$ to refuel at point $w_{2}$ is the same as the distance for point $w_{1}$, then $w_{1}$ in the solution can be replaced by $w_{2}$. Moreover, if there are two adjacent points $w_{2} ,w_{3} \in EP$ that can cover the set of O-D pairs $S_{{W^{*} }} \left( {w_{1} } \right)$, the total travel distance for the flows between O-D pairs in $S_{{W^{*} }} \left( {w_{1} } \right)$ to refuel at points $w_{1}$, $w_{2}$, and $w_{3}$ is the same, and the flows are balanced in the line segment $C\left( {w_{2} ,w_{3} } \right)$, then any point in $C\left( {w_{2} ,w_{3} } \right)$ can replace $w_{1}$ in the optimal solution. Note that, $S_{{W^{*} }} \left( {w_{1} } \right)$ is not necessarily equal to $S\left( {w_{1} } \right)$, $S\left( {w_{2} } \right)$, or $S\left( {w_{3} } \right)$.

5 Numerical example

In this section, a simple numerical example is solved to illustrate the concepts discussed in this paper. Figure 7 shows a traffic network that consists of 8 nodes.These nodes could be different intersections, zones, or neighborhoods within a city. The edges represent the roads connecting these nodes. Average daily flows, $f({v}_{i},{v}_{j})$, for each O-D pair $q({v}_{i},{v}_{j})$, $i < j$, are shown in Table 1. The vehicle driving range is set to $R = 96$ distance units. The primary objective is to locate a number, $p$, of AF refueling stations in the network in a way that maximizes total covered flow. We will solve the problem with different values of $p$ and compare the results. Then we will use the results from the solutions regarding the primary objective to minimize the total travel distance for all covered flows.

Fig. 7

Numerical example network

Table 1 Average daily flow between O-D pairs

In Step 1 of the DES algorithm, the set of O-D pairs that needs to be considered, $Q$, is constructed. Note that, some of the O-D pairs in Fig. 7 cannot be in $Q$. For example, $d\left( {v_{3} ,v_{7} } \right) = 108$ which is more than $R = 96$; therefore, $q\left( {v_{3} ,v_{7} } \right) \notin Q$. Also, $f\left( {v_{1} ,v_{5} } \right) = 0$; therefore, $q\left( {v_{1} ,v_{5} } \right) \notin Q$. Set $Q = \left\{ {q\left( {v_{1} ,v_{2} } \right),q\left( {v_{1} ,v_{4} } \right),q\left( {v_{1} ,v_{7} } \right),q\left( {v_{2} ,v_{3} } \right),q\left( {v_{2} ,v_{4} } \right),q\left( {v_{2} ,v_{5} } \right),q\left( {v_{2} ,v_{7} } \right),q\left( {v_{3} ,v_{6} } \right),q\left( {v_{3} ,v_{8} } \right),q\left( {v_{4} ,v_{5} } \right), q\left( {v_{5} ,v_{6} } \right),q\left( {v_{5} ,v_{7} } \right),q\left( {v_{6} ,v_{7} } \right),q\left( {v_{6} ,v_{8} } \right),q\left( {v_{7} ,v_{8} } \right)} \right\}$. The GCD here is $g = 12$. The set of common divisor points is shown in Fig. 8.

Fig. 8

Common divisor points

In Step 2, each edge in $E$ is scanned to find refueling sets for all O-D pairs in $Q$. For example, the refueling set of O-D pair $q\left( {v_{2} ,v_{3} } \right)$ on edge $\left( {v_{5} ,v_{6} } \right)$ can be found as follows: for type 1 case (a) we find the remaining driving distances to refuel when a vehicle starts its trip from vertices $v_{2}$ and $v_{3}$ with a half full fuel tank and reaches vertices $v_{5}$ and $v_{6}$, respectively.

$\gamma \left( {v_{2} ;v_{5} ,v_{6} } \right) = \min \left\{ {R/2 - d\left( {v_{2} ,v_{5} } \right),l\left( {v_{5} ,v_{6} } \right)} \right\} = \min \left\{ {48 - 24, 36} \right\} = 24$,

$\gamma \left( {v_{3} ;v_{6} ,v_{5} } \right) = \min \left\{ {R/2 - d\left( {v_{3} ,v_{6} } \right),l\left( {v_{5} ,v_{6} } \right)} \right\} = \min \left\{ {48 - 24, 36} \right\} = 24$,

Note that these two line segments overlap in the line segment connecting $w_{20}$ and $w_{21}$, as shown in Fig. 9; therefore, $RS_{1}^{\left( 5 \right)} \left( {v_{2} ,v_{3} ;v_{5} ,v_{6} } \right) = \{ w_{20} ,w_{21} \}$. However, for type 1 case (b), $d\left( {v_{2} ,v_{6} } \right) = 60 > R/2$; hence, a vehicle starting from vertex $v_{2}$ cannot reach vertex $v_{6}$ before refueling, $\gamma \left( {v_{2} ;v_{6} ,v_{5} } \right) = - 12$. Next, we find the refueling sets corresponding to type 2 cases (a) and (b).

$$\begin{aligned} & \delta^{\left( 5 \right)} \left( {v_{2} ,v_{3} ;v_{5} ,v_{6} } \right) = \min \left\{ {R/2 - \max \left\{ {d\left( {v_{2} ,v_{5} } \right), d\left( {v_{3} ,v_{5} } \right)} \right\},l\left( {v_{5} ,v_{6} } \right)} \right\} = \min \left\{ {48 - \max \left\{ {24, 60} \right\},36} \right\} = - 12,\\& RS_{2}^{\left( 5 \right)} \left( {v_{2} ,v_{3} ;v_{5} ,v_{6} } \right) = \emptyset \end{aligned}, $$

$$\begin{aligned} & \delta^{\left( 6 \right)} \left( {v_{2} ,v_{3} ;v_{5} ,v_{6} } \right) = \min \left\{ {R/2 - \max \left\{ {d\left( {v_{2} ,v_{6} } \right), d\left( {v_{3} ,v_{6} } \right)} \right\},l\left( {v_{5} ,v_{6} } \right)} \right\} = \min \left\{ {48 - \max \left\{ {60, 24} \right\},36} \right\} = - 12, \\&RS_{2}^{\left( 6 \right)} \left( {v_{2} ,v_{3} ;v_{5} ,v_{6} } \right) = \emptyset \end{aligned} . $$

Fig. 9

Type 1 case (a) refueling set for O-D pair $q\left( {v_{2} ,v_{3} } \right)$ on edge $\left( {v_{5} ,v_{6} } \right)$

Based on that, the refueling set of O-D pair $q\left( {v_{2} ,v_{3} } \right)$ on edge $\left( {v_{5} ,v_{6} } \right)$, $RS\left( {v_{2} ,v_{3} ;v_{5} ,v_{6} } \right) = \left\{ {w_{20} ,w_{21} } \right\}$ and $EP\left( {v_{2} ,v_{3} ;v_{5} ,v_{6} } \right) = \left\{ {w_{20} ,w_{21} } \right\}$. Tables 2 and 3 list all refueling sets and the set of O-D pairs covered by each endpoint, respectively. Figure 10 shows the set of endpoints in the network.

Table 2 Refueling sets

Table 3 Set of endpoints and their covered O-D pairs

Table 4 Solution to the set covering model with different values of $p$

Table 5 Distance minimization solution

Table 6 Total one-way travel distance comparison between optimal solutions regarding the primary objective

Fig. 10

Set of endpoints

Next, endpoints that cover unique sets of O-D pairs can be used in Hodgson’s model to maximize the amount of flow covered by a certain number of refueling stations. Table 4 shows optimal solutions regarding the primary objective with different values of p.

After solving the set covering model, we can look for other optimal solutions in the network. For instance, consider the solutions with $p = 2$, note that endpoint $w_{15}$ covers the same set of O-D pairs as point $w_{16}$. Furthermore, pick any point $x \in {\text{int}} C\left( {w_{15} ,w_{16} } \right)$, point $x$ covers the same set of O-D pairs as points $w_{15}$ and $w_{16}$; hence, by Lemma 1 the entire line segment $C\left( {w_{15} ,w_{16} } \right)$ covers the same set of O-D pairs and any point from $C\left( {w_{15} ,w_{16} } \right)$ can replace $w_{16}$ in the optimal solution regarding the primary objective. Furthermore, note that $S\left( {w_{20} } \right) \ne S\left( {w_{21} } \right)$; however, the set of O-D pairs covered in $\left( {S\left( {w_{20} } \right) \cap S\left( {w_{21} } \right)} \right) \cup S\left( {w_{16} } \right) = S\left( {w_{20} } \right) \cup S\left( {w_{16} } \right)$. Therefore, $w_{20}$ can be replaced by $w_{21}$ without changing the set of covered flows. Furthermore, pick any point $x \in {\text{int}} C\left( {w_{20} ,w_{21} } \right)$, $S\left( x \right) = S\left( {w_{20} } \right) \cap S\left( {w_{21} } \right)$, and by Lemma 1, all points in ${\text{int}} C\left( {w_{20} ,w_{21} } \right)$ cover the same set of O-D pairs. Therefore, any point in $C\left( {w_{20} ,w_{21} } \right)$ can replace $w_{20}$ in the optimal solution.

Now, let us consider the secondary objective for the case with $p = 3$, $F_{p}^{*} = 1140$. Model (28)–(33) is solved and the results are shown in Table 5. Comparing this solution with the third solution in Table 4, we see that the solution in Table 5 selected endpoints $w_{15}$ instead of $w_{16}$, $w_{20}$, and $w_{27}$ instead of $w_{26}$. Let us consider each one of these selections; $w_{15}$ and $w_{16}$ cover the same set of O-D pairs. Of those pairs $q\left( {w_{1} ,w_{7} } \right)$, $q\left( {w_{2} ,w_{7} } \right)$, and $q\left( {w_{5} ,w_{7} } \right)$ make type 1 trips, so they have the same total travel distance for both endpoints. However, the rest of the flows covered by these two endpoints make type 2 trips, entering edge $\left( {v_{4} ,v_{7} } \right)$ using $v_{4}$; therefore, the flows covered by $C\left( {w_{15} ,w_{16} } \right)$ are not balanced. By Lemma 2, the total travel distance to different points in $C\left( {w_{15} ,w_{16} } \right)$ is not the same; additionally, by Lemma 3, we know that one of the two endpoints must minimize the total travel distance for the flows covered by this line segment, this endpoint is $w_{15}$. Next, consider points $w_{20}$ and $w_{21}$; in this solution, all flows assigned to be covered by point $w_{20}$ can also be covered by point $w_{21}$ and any point in ${\text{int}} C\left( {w_{20} ,w_{21} } \right)$. Note that, the amounts of flows making type 2 trips cases (a) and (b) to reach a refueling station in line segment $C\left( {w_{20} ,w_{21} } \right)$ are equal, $f\left( {v_{2} ,v_{5} } \right) = f\left( {v_{3} ,v_{6} } \right) + f\left( {v_{3} ,v_{8} } \right)$. The rest of the covered flows make type 1 trips. Therefore, the flows covered by $C\left( {w_{20} ,w_{21} } \right)$ in this solution are balanced, and any point in $C\left( {w_{20} ,w_{21} } \right)$ can replace $w_{20}$ in the optimal solution. Finally, $w_{26}$ and $w_{27}$ cover the same set of O-D pairs. Given, that $q\left( {v_{6} ,v_{8} } \right)$ makes type 2 trips using $v_{8}$ to enter edge $\left( {v_{7} ,v_{8} } \right)$ and that $q\left( {v_{6} ,v_{7} } \right)$ and $q\left( {v_{7} ,v_{8} } \right)$ make type 1 trips. The flows covered by $C\left( {w_{26} ,w_{27} } \right)$ are not balanced and $w_{27}$ minimizes the total travel distance for these flows.

Table 6 and Fig. 11 present a comparison between total one-way travel distances using the primary objective alone versus the lexicographic bi-objective approach. Although, this is a simple example, the variation in total travel distance among optimal solutions regarding the primary objective is obvious. In real life networks with many O-D pairs and high volumes of flow, any small difference makes a significant impact on the total travel distance and consequently on convenience, operating cost of vehicles like fuel and maintenance, and most importantly GHG emissions.

Fig. 11

Total one-way travel distance comparison between optimal solutions regarding the primary objective

6 Conclusions and future research

In this paper, we have proposed an algorithm for the SRDFSA problem on a general (symmetric) network. Our approach takes advantage of the characteristics of the traffic network and vehicle driving range to discretize the network and reduce the size of the search space while maintaining guaranteed optimality as in the continuous approach. The algorithm starts with finding the GCD $g$ of all edge lengths and the initial driving range $R/2$ starting from the origin and destination vertices. Distances in the network can be represented as integer multiples of $g$. Common divisor points are used to define a refueling set for each O-D pair that can be covered in the network. In this study, we prove that there is always an optimal solution to the problem where all refueling stations are located at endpoints of refueling sets. Next, a set covering model is used to maximize the amount of flow covered by a predetermined number of refueling stations. Using this solution, the complete set of optimal solutions can be found. After that, a secondary objective to minimize the total travel distance for the covered flows is discussed. Again, we prove that there is always an optimal solution regarding both objectives where all refueling stations are located at endpoints of refueling sets. Therefore, the set of endpoints and the results from the optimal solution regarding the primary objective are used in a second set covering model to minimize the total travel distance. A numerical example is solved to illustrate the proposed methods. These two objectives are important for the overall objective of reducing GHG emissions and negative environmental impact of transportation activities.

The results of this study can be easily generalized. Although assumptions about network symmetry and integrality may seem not realistic, the dominating design of traffic networks in the US uses two-way roads. One-way roads are regularly used in urban downtown areas where the distances are relatively short, and the difference in lengths between the two one-way trips for each O-D pair can be neglected [7]. Also, in traffic networks, rounding a distance to the nearest integer value is not a significant adjustment when compared to the driving range of vehicles. Realistically, drivers tend to underestimate their vehicles driving range to allow for a safety buffer, so they do not run out of fuel. Therefore, integrality assumptions are not far from being realistic. The obtained global optimal solution from the model can be used directly to locate AF refueling stations in the network, or to define an upper bound on the amount of flow that can be covered by a certain number of AF refueling stations. This upper bound can be used to justify the additional investment to acquire the recommended locations. Also, if the gap between the global optimal solution and a solution based on a predetermined set of candidate locations is not large, then it may be acceptable to follow the sub-optimal solution. Either way, a global optimal solution will help the stakeholders to make an informed decision.

Suggested future research topics include relaxing the assumption of one refueling operation per one-way trip. This allows for longer trips and generalizes the results in this study. Also, having multiple types of vehicles with different driving ranges is more realistic than a fixed driving range for all vehicles.