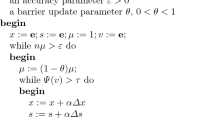An efficient parameterized logarithmic kernel function for linear optimization

Abstract

The introduction of kernel function in primal-dual interior point methods represents not only a measure of the distance between the iterate and the central path, but also plays an important role in the amelioration of the computational complexity of an interior point algorithm. In this work, we present a primal-dual interior point method for linear optimization problems based on a new kernel function with an efficient logarithmic barrier term. We derive the complexity bounds for large and small-update methods respectively. We obtain the best known complexity bound for large-update given by Peng et al., which improves significantly the so far obtained complexity results based on a logarithmic kernel function given by El Ghami et al. The results obtained in this paper are the first with respect to the kernel function with a logarithmic barrier term.

1 Introduction

In 1984, Karmarkar [1] proposed a new polynomial method for solving linear optimization problems $\text{(LO) }$. This method, and its variants that were developed subsequently, are now called interior-point methods $\text{(IPMs) }$. For a survey, we refer to recent books on the subject [2,3,4]. In order to describe the idea of this paper, we need to recall some ideas underlying new primal-dual $\text{ IPMs }$. Recently, Peng et al. [2] introduced the so-called self-regular barrier functions for primal-dual $\text{ IPMs }$ for linear optimization. Each such barrier function is determined by its univariate self regular kernel function.

Most of $\text{ IPMs }$ for $\text{ LO }$ are based on the logarithmic barrier function [3, 5]. In 2001, Peng et al. [6] proposed new variants of $\text{ IPMs }$ based on a new nonlogarithmic kernel functions. Such a function is strongly convex and smooth coercive on its domain: the positive real axis. They obtained the best known complexity results for large and small-update methods.

In 2004, Bai et al. [7] proposed new kernel function with an exponential barrier term, and introduced the first new kernel function with a trigonometric barrier term.

In 2008, El Ghami et al. [8] proposed parameterized kernel function with a logarithmic barrier term. This function generalized the kernel functions given in [3, 5]. In the same year, Bai et al. [9] proposed parameterized kernel function which is not a logarithmic barrier term in the general case. This function generalized the kernel functions given in [2, 3, 5, 8, 10].

In 2012, El Ghami et al. [11] evaluated the first new kernel function with a trigonometric barrier term given by Bai et al. [7]. Since then, research on giving new kernel function with a trigonometric barrier term continued for improving the complexity bound obtained by El Ghami et al. [11].

In 2016, Bouafia et al. [12, 13] proposed two parameterized kernel function for primal-dual $\text{ IPMs }$ for $\text{ LO }$. They obtained the best known complexity results for large and small-update methods. The first function in [12] generalizes the kernel function given by Bai et al. [7], whereas the second in [13] is the first kernel function with trigonometric barrier term primal-dual $\text{ IPMs }$ for $\text{ LO }$. This last function generalized and improved the complexity bound based on a new kernel function with trigonometric barrier term obtained in [11, 14,15,16,17,18]. The objective of this work is to generalize and improve the complexity bound based on a new kernel function with logarithmic barrier term.

The paper is organized as follows. In Sect. 2, we start with some notations and preliminaries. In Sect. 3, we present some properties of the new kernel function, as well as several properties and the growth behavior of the barrier function based on this kernel function. The estimate of the step size and the decrease behavior of the new barrier function are discussed in Sect. 4 where we present the inner iteration bound as well as the iteration bound of the algorithm. In Sect. 5, we offer a compared results of the algorithm given by El Ghami et al. [8] and the results of our algorithm. Finally, concluding remarks are given in the last section.

2 Notations and preliminaries

2.1 Notations

Let $\mathbb {R}^{n}$ be the n-dimensional Euclidean space with the inner product $\langle .,.\rangle$ and $\left\| {.}\right\|$ be 2-norm. $\mathbb {R}_{+}^{n}$ and $\mathbb {R}_{++}^{n}$ denote the set of n-dimensional nonnegative vectors and positive vectors respectively. For $x,\ s\in \mathbb {R}^{n}$, $x_{\min }$ and xs denote the smallest component of the vector x and the componentwise product of the vector x and s respectively. We denote by $X=diag(x)$ the $n\times n$ diagonal matrix with components of the vector $x\in \mathbb {R}^{n}$ are the diagonal entries. Finally, e denotes the n-dimensional vector of ones. For $f\left( x\right) ,\ g\left( x\right) :$ $\mathbb {R}_{++}^{n}\rightarrow \mathbb {R}_{++}^{n},$ $f\left( x\right) =\mathbf {O}\left( g\left( x\right) \right)$ if $f\left( x\right) \le C_{1}g\left( x\right)$ for some positive constant $C_{1}$and $f\left( x\right) ={\varvec{\Theta }}\left( g\left( x\right) \right)$ if $C_{2}g\left( x\right)$ $\le f\left( x\right) \le C_{3}g\left( x\right)$ for some positive constant $C_{2}$ and $C_{3}$.

2.2 Preliminaries

In this paper, we deal with primal-dual methods for solving the standard $\text{ LO }$:

where $A\in \mathbb {R}^{m\times n}$, $rank(A)=m$, $b\in \mathbb {R}^{m}$ and $c\in \mathbb {R}^{n}$, and its dual problem

In 1984, Karmarkar [1] proposed a new polynomial-time method for solving $\text{ LO }$. This method and its variants that were developed subsequently are now called $\text{ IPMs }$. For a survey, we refer to recent books on the subject as Peng et al. [2], Roos et al. [3], Ye [4] and Bai et al. [19]. Without loss of generality, we assume that (P) and (D) satisfy the interior-point condition $\text{(IPC), }$ i.e. there exist $(x^{0}$,$y^{0}$,$s^{0})$ such that

$$\begin{aligned} Ax^{0}=b, x^{0}>0, A^{T}y^{0}+s^{0}=c, s^{0}>0. \end{aligned}$$

(1)

It is well known that finding an optimal solution of (P) and (D) is equivalent to solving the following system

$$\begin{aligned} Ax=b, x\ge 0, A^{T}y+s=c, s\ge 0, xs=0. \end{aligned}$$

(2)

The basic idea of primal-dual $\text{ IPMs }$ is to replace the third equation in (2), the so-called complementarity condition for (P) and (D), by the parameterized equation $xs=\mu e,$ with $\mu >0$. Thus we consider the system

$$\begin{aligned} Ax=b, x\ge 0, A^{T}y+s=c, s\ge 0, xs=\mu e. \end{aligned}$$

(3)

Surprisingly enough, if the $\text{ IPC }$ is satisfied, then there exists a solution for each $\mu >0$, and this solution is unique. It is denoted as $(x(\mu ),y(\mu ),s(\mu ))$, and we call $x(\mu )$ the $\mu$-center of (P) and $(y(\mu ),s(\mu ))$ the $\mu$-center of (D). The set of $\mu$-centers (with $\mu$ running through all positive real numbers) gives a homotype path, which is called the central path of (P) and (D). The relevance of the central path for $\text{ LO }$ was recognized first by Megiddo [20] and Sonnevend [21]. If $\mu \rightarrow 0$, then the limit of the central path exists, and since the limit points satisfy the complementarity condition, the limit yields optimal solutions for (P) and (D). From a theoretical point of view, the $\text{ IPC }$ can be assumed without loss of generality. In fact we may, and will, assume that $x^{0}=s^{0}=e$. In practice, this can be realized by embedding the given problems (P) and (D) into a homogeneous self-dual problem, which has two additional variables and two additional constraints. For this and the other properties mentioned above, see [3]. The $\text{ IPMs }$ follow the central path approximately. We describe briefly the usual approach. Without loss of generality, we assume that $(x(\mu ),y(\mu ),s(\mu ))$ is known for some positive $\mu$. For example, due to the above assumption, we may assume this for $\mu =1$, with $x(1)=s(1)=e$. We then decrease $\mu$ to $(1-\theta )\mu$ for some fixed $\theta \in ] 0,1[$, and we solve the following Newton system:

$$\begin{aligned} A\varDelta x=0, A^{T}\varDelta y+\varDelta s=0, s\varDelta x+x\varDelta s=\mu e-xs. \end{aligned}$$

(4)

This system defines uniquely a search direction $(\varDelta x,\varDelta y,\varDelta s)$. By taking a step along the search direction, with the step size defined by some line search rules, we construct a new triple (x, y, s). If necessary, we repeat the procedure until we find iterates that are “close” to $(x(\mu ),y(\mu ),s(\mu ))$. Then $\mu$ is again reduced by the factor $1-\theta$, and we apply Newton’s method targeting the new $\mu -$centers, and so on. This process is repeated until $\mu$ is small enough, say until $n\mu \le \epsilon$; at this stage we have found an $\epsilon -$solution of problems (P) and (D). The result of a Newton step with step size $\alpha$ is denoted as

$$\begin{aligned} \begin{array}{ccc} x_{+}=x+\alpha \varDelta x,&s_{+}=s+\alpha \varDelta s,&y_{+}=y+\alpha \varDelta y. \end{array} \end{aligned}$$

(5)

where the step size $\alpha$ satisfies $0<\alpha \le 1$. Now, we introduce the scaled vector v and the scaled search directions $d_{x}$ and $d_{s}$ as follows:

$$\begin{aligned} \begin{array}{ccc} v=\sqrt{\frac{xs}{\mu }},&d_{x}=\frac{v\varDelta x}{x},&d_{s}=\frac{v\varDelta s}{s}. \end{array} \end{aligned}$$

(6)

System (4) can be rewritten as follows:

$$\begin{aligned} \overline{A}d_{x}=0, \overline{A}^{T}\varDelta y+d_{s}=0, d_{x}+d_{s}=v^{-1}-v, \end{aligned}$$

(7)

where $\overline{A}=\frac{1}{\mu }AV^{-1}X,$ $V=diag(v),$ $X=diag(x)$. Note that the right-hand side of the third equation in (7) is equal to the negative gradient of the logarithmic barrier function ${\varvec{\Phi }}_{L}\left( v\right)$ , i.e., $d_{x}+d_{s}=-\nabla {\varvec{\Phi }}_{L}\left( v\right)$, system (7) can be rewritten as follows:

$$\begin{aligned} \overline{A}d_{x}=0, \overline{A}^{T}\varDelta y+d_{s}=0, d_{x}+d_{s}=-\nabla {\varvec{\Phi }}_{L}\left( v\right) , \end{aligned}$$

(8)

where the barrier function ${\varvec{\Phi }}_{L}(v):\ \mathbb {R}_{++}^{n}\rightarrow \mathbb {R}_{+}$ is defined as follows:

$$\begin{aligned} {\varvec{\Phi }}_{L}\left( v\right)= & {} {\varvec{\Phi }}_{L}\left( x,s;\mu \right) = \sum _{i=1}^{n}\psi _{L} \left( v_{i}\right) , \end{aligned}$$

(9)

$$\begin{aligned} \psi _{L} \left( v_{i}\right)= & {} \frac{v_{i}^{2}-1}{2}-\log v_{i}. \end{aligned}$$

(10)

We use ${\varvec{\Phi }}_{L}\left( v\right)$ as the proximity function to measure the distance between the current iterate and the $\mu -$center for given $\mu >0$. We also define the norm-based proximity measure, $\delta (v)$ $:\ \mathbb {R}_{++}^{n}\rightarrow \mathbb {R}_{+}$, as follows

$$\begin{aligned} \delta \left( v\right) =\frac{1}{2}\left\| \nabla {\varvec{\Phi }}_{L}\left( v\right) \right\| =\frac{1}{2}\left\| d_{x}+d_{s}\right\| . \end{aligned}$$

(11)

We call $\psi \left( t\right)$ the kernel function of the logarithmic barrier function ${\varvec{\Phi }}\left( v\right)$. In this paper, we replace $\psi \left( t\right)$ by a new kernel function $\psi _{LB}\left( t\right)$ and ${\varvec{\Phi }}\left( v\right)$ by a new barrier function ${\varvec{\Phi }}_{LB}\left( v\right)$, which will be defined in Sect. 3. Note that the pair (x, s) coincides with the $\mu -$center $(x(\mu ),s(\mu ))$ if and only if $v=e$. It is clear from the above description that the closeness of (x, s) to $\left( x(\mu ),s(\mu )\right)$ is measured by the value of ${\varvec{\Phi }}_{LB}\left( v\right)$ with $\tau >0$ as a threshold value. If ${\varvec{\Phi }}_{LB}\left( v\right) \le \tau$, then we start a new outer iteration by performing a $\mu -$update; otherwise, we enter an inner iteration by computing the search directions at the current iterates with respect to the current value of $\mu$ and apply (5) to get new iterates. If necessary, we repeat the procedure until we find iterates that are in the neighborhood of $(x(\mu ),s(\mu )).$ Then $\mu$ is again reduced by the factor $1-\theta$ with $0<\theta <1$, and we apply Newton’s method targeting the new $\mu -$centers, and so on. This process is repeated until $\mu$ is small enough, say until $n\mu <\epsilon$; at this stage we have found an $\epsilon -$approximate solution of $\text{ LO }$. The parameters $\tau ,\theta$ and the step size $\alpha$ should be chosen in such a way that the algorithm is optimized in the sense that the number of iterations required by the algorithm is as small as possible. The choice of the so-called barrier update parameter $\theta$ plays an important role in both theory and practice of $\text{ IPMs }$ . Usually, if $\theta$ is a constant independent of the dimension n of the problem, for instance, $\theta = 1/2$, then we call the algorithm a large-update (or long-step) method. If $\theta$ depends on the dimension of the problem, such as $\theta =1/n$ , then the algorithm is called a small-update (or short-step) method. The generic form of the algorithm is shown in Fig. 1.

Fig. 1

Generic algorithm

In most cases, the best complexity result obtained for small-update IPMs is $\mathbf {O}( \sqrt{n}\log \frac{n}{\epsilon })$. For large-update methods the best obtained bound is $\mathbf {O}( \sqrt{n}\log n\log \frac{n}{\epsilon })$, which until now has been the best known bound for such methods [6, 7].

In this paper, we define a new kernel function with logarithmic barrier term and propose primal–dual interior point methods which improve all the results of the complexity bound for large-update methods based on a logarithmic kernel function for $\text{ LO }$. More precisely, based on the proposed kernel function, we prove that the correspondent algorithm has $\mathbf {O}\left( qn^{\frac{q+1}{2q}}\log \frac{n}{\epsilon }\right)$ complexity bound for large-update method and $\mathbf {O}\left( q^{2}\sqrt{n}\log \frac{n}{\epsilon }\right)$ for small-update method. Another interesting choice is q dependent with n, which minimizes the iteration complexity bound. In fact, if we take $q=\frac{\log n}{2}$, we obtain the best known complexity bound for large-update methods namely $\mathbf {O}\left( \sqrt{n}\log n\log \frac{n}{\epsilon }\right)$. This bound improves the so far obtained complexity results for large-update methods based on a logarithmic kernel function given by El Ghami et al. [8].

3 Properties of the kernel function and the barrier function

3.1 Properties of the new kernel function

In this section, we investigate some properties of the new kernel function with a logarithmic barrier term which are essential to our complexity analysis. We call $\psi \left( t\right)$: $\mathbb {R}_{++}\rightarrow \mathbb {R}_{+}$ a kernel function if $\psi$ is twice differentiable and satisfies the following conditions:

$$\begin{aligned} \psi ^{\prime }(1)=\psi (1)=0, \psi ^{\prime \prime }(t)>0, \lim \limits _{t\downarrow 0^{+}} \psi \left( t\right) =\lim \limits _{t\rightarrow +\infty } \psi \left( t\right) =+\infty . \end{aligned}$$

Now, we define a new function $\psi _{LB}\left( t\right)$ as follows:

$$\begin{aligned} \psi _{LB}\left( t\right) =\frac{t^{2}-1-\log t}{2}+\frac{t^{1-q}-1}{2\left( q-1\right) }, \ \ \ q>1. \end{aligned}$$

(12)

For convenience of reference, we give the first three derivatives with respect to t as follows:

$$\begin{aligned} \begin{array}{l} \psi _{LB}^{\prime }(t)=t-\frac{1}{2t}-\frac{1}{2}t^{-q}, \\ \psi _{LB}^{\prime \prime }\left( t\right) =1+\frac{1}{2t^{2}}+\frac{q}{2} t^{-q-1}, \\ \psi _{LB}^{\prime \prime \prime }\left( t\right) =-\frac{1}{t^{3}}-\frac{ q\left( q+1\right) }{2}t^{-q-2}. \end{array} \end{aligned}$$

(13)

Obviously, $\psi _{LB}\left( t\right)$ is a kernel function and

$$\begin{aligned} \psi _{LB}^{\prime \prime }\left( t\right) >1 \end{aligned}$$

(14)

In this paper, we replace the function ${\varvec{\Phi }}\left( v\right)$ in (8) with the function ${\varvec{\Phi }}_{LB}\left( v\right)$ as follows:

$$\begin{aligned} d_{x}+d_{s}=-\nabla {\varvec{\Phi }}_{LB}\left( v\right) , \end{aligned}$$

(15)

where

$$\begin{aligned} {\varvec{\Phi }}_{LB}\left( v\right) =\sum _{i=1}^{n}\psi _{LB} \left( v_{i}\right) , \end{aligned}$$

(16)

and $\psi _{LB}\left( t\right)$ is defined in (12). Hence, the new search direction $(\varDelta x,\varDelta y,\varDelta s)$ is obtained by solving the following modified Newton system:

$$\begin{aligned} \begin{array}{l} \overline{A}d_{x}=0, \\ \overline{A}^{t}\varDelta y+d_{s}=0, \\ d_{x}+d_{s}=-\nabla {\varvec{\Phi }}_{LB}\left( v\right) . \end{array} \end{aligned}$$

(17)

Note that $d_{x}$ and $d_{s}$ are orthogonal because the vector $d_{x}$ belongs to null space and vector $d_{s}$ to the row space of the matrix $\overline{A}$.

Since $d_{x}$ and $d_{s}$ are orthogonal, we have

$$\begin{aligned} d_{x}=d_{s}=0&\Longleftrightarrow \nabla {\varvec{\Phi }}_{LB}\left( v\right) =0 \\&\Longleftrightarrow v=e \\&\Longleftrightarrow {\varvec{\Phi }}_{LB}\left( v\right) =0 \\&\Longleftrightarrow x=x( \mu ),s=s( \mu ). \end{aligned}$$

We use ${\varvec{\Phi }}_{LB}\left( v\right)$ as the proximity function to measure the distance between the current iterate and the $\mu -$center for given $\mu >0$. We also define the norm-based proximity measure, $\delta (v)$: $\mathbb {R}_{++}\rightarrow \mathbb {R}_{+}$, as follows:

$$\begin{aligned} \begin{array}{c} \delta (v)=\frac{1}{2}\left\| \nabla {\varvec{\Phi }}_{LB}\left( v\right) \right\| =\frac{1}{2}\left\| d_{x}+d_{s}\right\| . \end{array} \end{aligned}$$

(18)

Lemma 3.1

For $\psi _{LB}\left( t\right)$, we have the following.

$\psi _{LB}\left( t\right)$ is exponentially convex for all $t>0$; that is,

Proof

For (a), using (13), we have

$$\begin{aligned} t\psi _{LB}^{\prime \prime }\left( t\right) +\psi _{LB}^{\prime }\left( t\right)= & {} t\left( 1+\frac{1}{2t^{2}}+\frac{q}{2}t^{-q-1}\right) \nonumber \\&+\left( t- \frac{1}{2t}-\frac{1}{2}t^{-q}\right)>0\ for\ all\ t>0. \end{aligned}$$

And by Lemma 2.1.2 in [2], we have the result.

For (b), using (13), we have $\psi _{LB}^{\prime \prime \prime }\left( t\right) <0$, so we have the result.

For (c), using (13), we have

$$\begin{aligned} t\psi _{LB}^{\prime \prime }\left( t\right) -\psi _{LB}^{\prime }\left( t\right)= & {} t\left( 1+\frac{1}{2t^{2}}+\frac{q}{2}t^{-q-1}\right) -\left( t- \frac{1}{2t}\right. \nonumber \\&\left. -\frac{1}{2}t^{-q}\right)>0\ for\ all\ t>0. \end{aligned}$$

For (d), using Lemma 2.4 in [7], (b) and (c), we have the result. This completes the proof. $\square$

Lemma 3.2

For $\psi _{LB}\left( t\right)$, we have

$$\begin{aligned} \frac{1}{2}\left( t-1\right) ^{2}\le & {} \psi _{LB}\left( t\right) \le \frac{1}{ 2}\left[ \psi _{LB}^{\prime }\left( t\right) \right] ^{2},\ \ \ t>0. \end{aligned}$$

(19)

$$\begin{aligned} \psi _{LB}\left( t\right)\le & {} \frac{q+3}{4}\left( t-1\right) ^{2},\ \ \ \ \ t>1. \end{aligned}$$

(20)

Proof

For (19), using (14), we have

$$\begin{aligned} \psi _{LB}\left( t\right)&=\int \limits _{1}^{t}\int \limits _{1}^{x}\psi _{LB}^{\prime \prime }\left( y\right) dydx\ge \int \limits _{1}^{t}\int \limits _{1}^{x}1dydx=\frac{1}{2}\left( t-1\right) ^{2}\\ \psi _{LB}\left( t\right)&=\int \limits _{1}^{t}\int \limits _{1}^{x}\psi _{LB}^{\prime \prime }\left( y\right) dydx \\&\le \int \limits _{1}^{t}\int \limits _{1}^{x}\psi _{LB}^{\prime \prime }\left( y\right) \psi _{LB}^{\prime \prime }\left( x\right) dydx \\&=\int \limits _{1}^{t}\psi _{LB}^{\prime \prime }\left( x\right) \psi _{LB}^{\prime }\left( x\right) dx \\&=\int \limits _{1}^{t}\psi _{LB}^{\prime }\left( x\right) d\psi _{LB}^{\prime }\left( x\right) \\&=\frac{1}{2}\left[ \psi _{LB}^{\prime }\left( t\right) \right] ^{2}. \end{aligned}$$

For (20), since $\psi _{LB}\left( 1\right) =\psi _{LB}^{\prime }\left( 1\right) =0,\psi _{LB}^{\prime \prime \prime }\left( t\right) <0,$ $\psi _{LB}^{\prime \prime }\left( 1\right) =\frac{q+3}{2},$ and by using Taylor’s Theorem, we have

$$\begin{aligned} \psi _{LB}\left( t\right)&=\psi _{LB}\left( 1\right) +\psi _{LB}^{\prime }\left( 1\right) \left( t-1\right) +\frac{1}{2}\psi _{LB}^{\prime \prime }\left( 1\right) \left( t-1\right) ^{2}+\frac{1}{6}\psi _{LB}^{\prime \prime \prime }\left( \xi \right) \left( t -1\right) ^{3} \\&=\frac{1}{2}\psi _{LB}^{\prime \prime }\left( 1\right) \left( t-1\right) ^{2}+\frac{1}{6}\psi _{LB}^{\prime \prime \prime }\left( \xi \right) \left( t -1\right) ^{3} \\&\le \frac{1}{2}\psi _{LB}^{\prime \prime }\left( 1\right) \left( t-1\right) ^{2} \\&=\frac{q+3}{4}\left( t-1\right) ^{2}. \end{aligned}$$

for some $\xi ,$ $1\le \xi \le t.$ This completes the proof. $\square$

Let $\sigma : [ 0,+\infty [ \rightarrow [ 1,+\infty [$ be the inverse function of $\psi _{LB}\left( t\right)$ for $t\ge 1$ and $\rho :\left[ 0,+\infty \left[ \rightarrow \right] 0,1\right]$ be the inverse function of $\frac{-1}{2}\psi _{LB}^{\prime }\left( t\right)$ for all $t\in ] 0,1]$. Then we have the following lemma.

Lemma 3.3

For $\psi _{LB}\left( t\right)$, we have

$$\begin{aligned} 1+\sqrt{\frac{4}{q+3}s}\le & {} \sigma \left( s\right) \le 1+\sqrt{2s}, \ \ s\ge 0.\end{aligned}$$

(21)

$$\begin{aligned} \rho \left( z\right)> & {} \frac{1}{\left( 4z+2\right) ^{\frac{1}{q}}},\ \ \ z\ge 0. \end{aligned}$$

(22)

Proof

For (21), let

$$\begin{aligned} s=\psi _{LB}\left( t\right) ,t\ge 1\ ,i.e.\ \sigma \left( s\right) =t, \ \ \ t\ge 1. \end{aligned}$$

By (19), we have

$$\begin{aligned} \psi _{LB}\left( t\right) \ge \frac{1}{2}\left( t-1\right) ^{2}. \end{aligned}$$

then

$$\begin{aligned} s\ge \frac{1}{2}\left( t-1\right) ^{2},t\ge 1. \end{aligned}$$

which implies that

$$\begin{aligned} t=\sigma \left( s\right) \le 1+\sqrt{2s}. \end{aligned}$$

By (20), we have

$$\begin{aligned} s=\psi _{LB}\left( t\right) \le \frac{q+3}{4}\left( t-1\right) ^{2}, \end{aligned}$$

so

$$\begin{aligned} t=\sigma \left( s\right) \ge 1+\sqrt{\frac{4}{q+3}s}. \end{aligned}$$

For (22), let

$$\begin{aligned} \left. \left. z=\frac{-1}{2}\psi _{LB}^{\prime }\left( t\right) ,t\in \right] 0,1\right] . \end{aligned}$$

By the definition of:

$$\begin{aligned} \left. \left. \rho :\rho \left( z\right) =t,t\in \right] 0,1\right] . \end{aligned}$$

and by the definition of $\psi _{LB}\left( t\right)$, we have

$$\begin{aligned} \begin{array}{ll} z &{} =-\frac{1}{2}\left( t-\frac{1}{2t}-\frac{1}{2}t^{-q}\right) \\ &{}>\frac{1}{4}\left( t^{-q}-2t\right) >\frac{1}{4}\left( t^{-q}-2\right) , \end{array} \end{aligned}$$

which implies that

$$\begin{aligned} t=\rho \left( z\right) >\frac{1}{\left( 4z+2\right) ^{\frac{1}{q}}}. \end{aligned}$$

This completes the proof. $\square$

Lemma 3.4

Let $\sigma : [ 0,+\infty [ \rightarrow [ 1,+\infty [$ be the inverse function of $\psi _{LB}\left( t\right)$ for $t\ge 1$. Then we have

$$\begin{aligned} {\varvec{\Phi }}_{LB}\left( \beta v\right) \le n\psi _{LB}\left( \beta \sigma \left( \frac{{\varvec{\Phi }}_{LB}\left( v\right) }{n}\right) \right) ,\ \ \ \ v\in \mathbb {R}_{++} ,\ \beta \ge 1. \end{aligned}$$

Proof

Using (d), and Theorem 3.2 in [7], we can get the result. This completes the proof. $\square$

Lemma 3.5

Let $0\le \theta <1$, $v_{+}=\frac{v}{\sqrt{1-\theta }},$ If $\ {\varvec{\Phi }}_{LB}\left( v\right) \le \tau ,$ then we have

$$\begin{aligned} {\varvec{\Phi }}_{LB}\left( v_{+}\right) \le \frac{\left( \theta n+2\tau +2 \sqrt{2\tau n}\right) }{2\left( 1-\theta \right) }. \end{aligned}$$

Proof

Since $\frac{1}{\sqrt{1-\theta }}\ge 1$ and $\sigma \left( \frac{{\varvec{\Phi }}_{LB}\left( v\right) }{n}\right) \ge 1$, then $\frac{\sigma \left( \frac{{\varvec{\Phi }}_{LB}\left( v\right) }{n}\right) }{\sqrt{1-\theta }}\ge 1$.

And for $t\ge 1,$ we have

$$\begin{aligned} \psi _{LB}\left( t\right) \le \frac{t^{2}-1}{2}. \end{aligned}$$

Using Lemma 3.4 with $\beta =\frac{1}{\sqrt{1-\theta }}$, (21), and ${\varvec{\Phi }}_{LB}\left( v\right) \le \tau ,$ we have

$$\begin{aligned} {\varvec{\Phi }}_{LB}\left( v_{+}\right)&\le n\psi _{LB}\left( \frac{1}{ \sqrt{1-\theta }}\sigma \left( \frac{{\varvec{\Phi }}_{LB}\left( v\right) }{n} \right) \right) \\&\le \frac{n}{2}\left( \left[ \frac{1}{\sqrt{1-\theta }}\sigma \left( \frac{{\varvec{\Phi }}_{LB}\left( v\right) }{n}\right) \right] ^{2}-1\right) \\&=\frac{n}{2\left( 1-\theta \right) }\left( \left[ \sigma \left( \frac{ {\varvec{\Phi }}_{LB}\left( v\right) }{n}\right) \right] ^{2}-(1-\theta ) \right) \\&\le \frac{n}{2\left( 1-\theta \right) }\left( \left[ 1+\sqrt{2\frac{ {\varvec{\Phi }}_{LB}\left( v\right) }{n}}\right] ^{2}-(1-\theta )\right) \\&=\frac{n}{2\left( 1-\theta \right) }\left( \left[ 1+2\frac{{\varvec{\Phi }} _{LB}\left( v\right) }{n}+2\sqrt{2\frac{{\varvec{\Phi }}_{LB}\left( v\right) }{n} }\right] -(1-\theta )\right) \\&\le \frac{n}{2\left( 1-\theta \right) }\left( \theta +2\frac{\tau }{n}+2\sqrt{2\frac{\tau }{n}}\right) \\&=\frac{\theta n+2\tau +2\sqrt{2\tau n}}{2\left( 1-\theta \right) }. \end{aligned}$$

This completes the proof. $\square$

Denote

$$\begin{aligned} \left( {\varvec{\Phi }}_{LB}\right) _{0}=\frac{\theta n+2\tau +2\sqrt{ 2\tau n} }{2\left( 1-\theta \right) }=L\left( n,\theta ,\tau \right) ; \end{aligned}$$

(23)

then $\left( {\varvec{\Phi }}_{LB}\right) _{0}$ is an upper bound for ${\varvec{\Phi }}_{LB}\left( v_{+}\right)$ during the process of the algorithm.

3.2 An estimation for the step size

In this section, we compute a default step size $\alpha$ and the resulting decrease of the barrier function. After a damped step we have

$$\begin{aligned} x_{+}=x+\alpha \varDelta x; y_{+}=y+\alpha \varDelta y; s_{+}=s+\alpha \varDelta s. \end{aligned}$$

Using (6), we have

$$\begin{aligned} \begin{array}{ll} x_{+}=x\left( e+\alpha \frac{\varDelta x}{x}\right) =x\left( e+\alpha \frac{ d_{x}}{v}\right) =\frac{x}{v}\left( v+\alpha d_{x}\right) ;&{}\\ s_{+}=s\left( e+\alpha \frac{\varDelta s}{s}\right) =s\left( e+\alpha \frac{ d_{s}}{v}\right) =\frac{s}{v}\left( v+\alpha d_{s}\right) . \end{array} \end{aligned}$$

So, we have $v_{+}=\sqrt{\frac{x_{+}s_{+}}{\mu }}=\sqrt{\left( v+\alpha d_{x}\right) \left( v+\alpha d_{s}\right) }.$

Define, for $\alpha >0$, $f\left( \alpha \right) ={\varvec{\Phi }}_{LB}\left( v_{+}\right) -{\varvec{\Phi }} _{LB}\left( v\right) .$

Then $f\left( \alpha \right)$ is the difference of proximities between a new iterate and a current iterate for fixed $\mu$. By (a), we have

$$\begin{aligned} {\varvec{\Phi }}_{LB}\left( v_{+}\right) ={\varvec{\Phi }}_{LB}\left( \sqrt{\left( v+\alpha d_{x}\right) \left( v+\alpha d_{s}\right) }\right) \le \frac{{\varvec{\Phi }}_{LB}\left( v+\alpha d_{x}\right) +{\varvec{\Phi }} _{LB}\left( v+\alpha d_{s}\right) }{2}. \end{aligned}$$

Therefore, we have $f\left( \alpha \right)$ $\le$ $f_{1}\left( \alpha \right)$, where

$$\begin{aligned} f_{1}\left( \alpha \right) =\frac{{\varvec{\Phi }}_{LB}\left( v+\alpha d_{x}\right) +{\varvec{\Phi }}_{LB}\left( v+\alpha d_{s}\right) }{2} -{\varvec{\Phi }}_{LB}\left( v\right) . \end{aligned}$$

(24)

Obviously, $f\left( 0\right) =$ $f_{1}\left( 0\right) =0$. Taking the first two derivatives of $f_{1}\left( \alpha \right)$ with respect to $\alpha$, we have

$$\begin{aligned} f_{1}^{\prime }\left( \alpha \right)= & {} \frac{1}{2}\sum _{i=1}^{n}\left( \psi _{LB}^{\prime }\left( v_{i}+\alpha d_{xi}\right) d_{xi}+\psi _{LB}^{\prime }\left( v_{i}+\alpha d_{si}\right) d_{si}\right) ,\\ f_{1}^{\prime \prime }\left( \alpha \right)= & {} \frac{1}{2}\sum _{i=1}^{n}\left( \psi _{LB}^{\prime \prime }\left( v_{i}+\alpha d_{xi}\right) d_{xi}^{2}+\psi _{LB}^{\prime \prime }\left( v_{i}+\alpha d_{si}\right) d_{si}^{2}\right) . \end{aligned}$$

Using (8) and (11), we have

$$\begin{aligned} f_{1}^{\prime }\left( 0\right) =\frac{1}{2}\langle \nabla {\varvec{\Phi }}_{LB}\left( v\right) ,\left( d_{x}+d_{s}\right) \rangle =-\frac{1}{2}\langle \nabla {\varvec{\Phi }} _{LB}\left( v\right) ,\nabla {\varvec{\Phi }}_{LB}\left( v\right) \rangle =-2\delta (v)^{2}. \end{aligned}$$

For convenience, we denote $v_{1}=\min \left( v\right) ,\ \delta =\delta (v),\ {\varvec{\Phi }}_{LB}= {\varvec{\Phi }}_{LB}\left( v\right)$.

Lemma 3.6

Let $\delta (v)$ be as defined in (11). Then we have

$$\begin{aligned} \delta (v)\ge \sqrt{\frac{1}{2}{\varvec{\Phi }}_{LB}\left( v\right) }. \end{aligned}$$

(25)

Proof

Using (19), we have

$$\begin{aligned} {\varvec{\Phi }}_{LB}\left( v\right) =\sum _{i=1}^{n}\psi _{LB}\left( v_{i}\right) \le \sum _{i=1}^{n}\frac{1}{2} \left( \psi _{LB}^{\prime }\left( v_{i}\right) \right) ^{2}=\frac{1}{2} \left\| \nabla {\varvec{\Phi }}_{LB}\left( v\right) \right\| ^{2}=2\delta (v)^{2}, \end{aligned}$$

so $\delta (v)\ge \sqrt{\frac{1}{2}{\varvec{\Phi }}_{LB}\left( v\right) }$. This completes the proof. $\square$

Remark 3.1

Throughout the paper, we assume that $\tau$ $\ge 1$. Using Lemma 3.6 and the assumption that ${\varvec{\Phi }}_{LB}\left( v\right) \ge \tau ,$ we have $\delta (v)\ge \sqrt{\frac{1}{2}}$.

From Lemmas 4.1–4.4 in [7], we have the following Lemmas 3.7–3.10, because $\psi _{LB}(t)$ is kernel function and $\psi _{LB}^{\prime \prime }(t)$ is monotonically decreasing.

Lemma 3.7

([7]) Let $f_{1}\left( \alpha \right)$ be as defined in (24) and $\delta (v)$ be as defined in (11). Then we have $f_{1}^{\prime \prime }\left( \alpha \right) \le 2\delta ^{2}\psi _{LB}^{\prime \prime }\left( v_{\min }-2\alpha \delta \right)$. Since $f_{1}\left( \alpha \right)$ is convex, we will have $f_{1}^{\prime }\left( \alpha \right) \le 0$ for all $\alpha$ less than or equal to the value where $f_{1}\left( \alpha \right)$ is minimal, and vice versa.

The previous Lemma leads to the following three Lemmas:

Lemma 3.8

([7]) $f_{1}^{\prime }\left( \alpha \right) \le 0$ certainly holds if $\alpha$ satisfies the inequality

$$\begin{aligned} \psi _{LB}^{\prime }\left( v_{\min }\right) -\psi _{LB}^{\prime }\left( v_{\min }-2\alpha \delta \right) \le 2\delta , \end{aligned}$$

(26)

Lemma 3.9

([7]) The largest step size $\overline{\alpha }$ holding (26) is given by $\overline{\alpha }=\frac{\rho \left( \delta \right) -\rho \left( 2\delta \right) }{2\delta }$.

Lemma 3.10

([7]) Let $\overline{\alpha }$ be as defined in Lemma 3.9. Then $\overline{\alpha }\ge \frac{1}{\psi _{LB}^{\prime \prime }\left( \rho \left( 2\delta \right) \right) }$.

Lemma 3.11

Let $\rho$ and $\overline{\alpha }$ be as defined in Lemma 3.10. If ${\varvec{\Phi }}_{LB}\left( v\right) \ge \tau \ge 1$, then we have $\overline{\alpha }\ge \frac{2}{2+\left( q+1\right) \left( 8\delta +2\right) ^{\frac{q+1}{q}}}$.

Proof

Using Lemma 3.10, (13) and (22) we have

$$\begin{aligned} \begin{array}{ll} \overline{\alpha } &{} \ge \frac{1}{\psi _{LB}^{\prime \prime }\left( \rho \left( 2\delta \right) \right) } \\ &{} =\frac{1}{1+\frac{1}{2\rho \left( 2\delta \right) ^{2}}+\frac{q}{2}\left( \rho \left( 2\delta \right) \right) ^{-\left( q+1\right) }} \\ &{} \ge \frac{1}{1+\frac{1}{2}\left( 4\left( 2\delta \right) +2\right) ^{ \frac{2}{q}}+\frac{q}{2}\left( 4\left( 2\delta \right) +2\right) ^{\frac{q+1 }{q}}} \\ &{} \ge \frac{2}{2+\left( q+1\right) \left( 8\delta +2\right) ^{\frac{q+1}{q}}} . \end{array} \end{aligned}$$

This completes the proof. $\square$

Denoting

$$\begin{aligned} \widetilde{\alpha }=\frac{2}{2+\left( q+1\right) \left( 8\delta +2\right) ^{\frac{q+1}{q}}}; \end{aligned}$$

(27)

we have that $\widetilde{\alpha }$ is the default step size and that $\widetilde{\alpha }\le \overline{\alpha }$.

Lemma 3.12

(Lemma 3.12 in [2]) Let h be a twice differentiable convex function with $h(0) = 0$, $h^{\prime }(0) < 0$, which attains its minimum at $t^{*}> 0$. If $h^{\prime \prime }$ is increasing for $t\in [0, t^{*}]$, then

$$\begin{aligned} h(t)\le \frac{th(0)}{2},\ \ 0\le t\le t^{*}. \end{aligned}$$

In this respect the next result is important.

Lemma 3.13

(Lemma 4.5 in [7]) If the step size $\alpha$ satisfies $\alpha$ $\le \overline{\alpha }$, then

$$\begin{aligned} f\left( \alpha \right) \le -\alpha \delta ^{2}. \end{aligned}$$

Lemma 3.14

Let $\widetilde{\alpha }$ be the default step size as defined in (27) and let

$$\begin{aligned} {\varvec{\Phi }}_{LB}\left( v\right) \ge 1. \end{aligned}$$

Then

$$\begin{aligned} f\left( \widetilde{\alpha }\right) \le -\frac{\sqrt{2}}{\left( q+1\right) 148}\left[ {\varvec{\Phi }}_{LB}\left( v\right) \right] ^{^{^{\frac{ q-1}{2q}}}}. \end{aligned}$$

(28)

Proof

Since ${\varvec{\Phi }}_{LB}\left( v\right) \ge 1$, then from (25), we have

$$\begin{aligned} \delta\ge & {} \sqrt{\frac{1}{2}{\varvec{\Phi }}_{LB}\left( v\right) }\ge \sqrt{ \frac{1}{2}}. \end{aligned}$$

Using Lemma 3.13 (4.5 in [7]) with $\alpha =\widetilde{\alpha }$ and (27), we have

$$\begin{aligned} f\left( \widetilde{\alpha }\right)&\le -\widetilde{\alpha } \delta ^{2} \\&=-\frac{2\delta ^{2}}{2+\left( q+1\right) \left( 8\delta +2\right) ^{ \frac{q+1}{q}}} \\&\le -\frac{2\delta ^{2}}{2\left( 2\delta \right) +\left( q+1\right) \left( 4\left( 2\delta \right) +2\left( 2\delta \right) \right) ^{\frac{q+1}{ q}}} \\&\le -\frac{2\delta ^{2}}{2\left( 2\delta \right) ^{^{\frac{q+1}{q} }}+\left( q+1\right) \left( 12\delta \right) ^{^{\frac{q+1}{q}}}} \\&=-\frac{2\delta ^{2}}{\left( 2\left( 2\right) ^{^{\frac{q+1}{q}}}+\left( q+1\right) \left( 12\right) ^{^{\frac{q+1}{q}}}\right) \left( \delta \right) ^{^{\frac{q+1}{q}}}} \\&\le -\frac{2\delta ^{^{2-\frac{q+1}{q}}}}{\left( 2\left( 2\right) ^{2}+\left( q+1\right) \left( 12\right) ^{^{2}}\right) } \\&\le -\frac{2\delta ^{^{\frac{q-1}{q}}}}{\left( q+1\right) 148} \\&\le -\frac{\sqrt{2}}{\left( q+1\right) 148}\left[ {\varvec{\Phi }} _{LB}\left( v\right) \right] ^{^{^{\frac{q-1}{2q}}}} \end{aligned}$$

This completes the proof. $\square$

4 Complexity of the algorithm

4.1 Inner iteration bound

After the update of $\mu$ to $\left( 1-\theta \right) \mu$, we have

$$\begin{aligned} {\varvec{\Phi }}_{LB}\left( v_{+}\right) \le \left( {\varvec{\Phi }}_{LB}\right) _{0}=\frac{\left( \theta n+2\tau +2\sqrt{2\tau n}\right) }{2\left( 1-\theta \right) }=L\left( n,\theta ,\tau \right) . \end{aligned}$$

We need to count how many inner iterations are required to return to the situation where ${\varvec{\Phi }}_{LB}\left( v\right) \le \tau$ . We denote the value of ${\varvec{\Phi }}_{LB}\left( v\right)$ after the $\mu$ update as $\left( {\varvec{\Phi }}_{LB}\right) _{0}$; the subsequent values in the same outer iteration are denoted by $\left( {\varvec{\Phi }}_{LB}\right) _{k}$, $k=1,2,...,K$, where K denotes the total number of inner iterations in the outer iteration. The decrease in each inner iteration is given by (28). In [7], we can find the appropriate values of $\kappa$ and $\gamma \in$ ]0, 1] :

$$\begin{aligned} \kappa =\frac{\sqrt{2}}{\left( q+1\right) 148}, \ \ \ \ \gamma =1-\frac{q-1}{2q}=\frac{q+1}{2q}. \end{aligned}$$

Lemma 4.1

Let K be the total number of inner iterations in the outer iteration. Then we have

$$\begin{aligned} K\le \left( 148\sqrt{2}q\right) \left[ \left( {\varvec{\Phi }}_{LB}\right) _{0} \right] ^{\frac{q+1}{2q}}. \end{aligned}$$

Proof

By Lemma 1.3.2 in [2], we have $K\le \frac{\left( {\varvec{\Phi }} _{LB}\right) _{0}^{\gamma }}{\kappa \gamma }=\left( 148\sqrt{2} q\right) \left[ \left( {\varvec{\Phi }}_{LB}\right) _{0}\right] ^{\frac{q+1}{2q} }$. This completes the proof. $\square$

4.2 Total iteration bound

The number of outer iterations is bounded above by $\frac{\log \frac{n}{ \epsilon }}{\theta }$ (see [3] Lemma $\mathbf {II}$.$\mathbf {17}$, page $\mathbf {116}$). By multiplying the number of outer iterations by the number of inner iterations, we get an upper bound for the total number of iterations, namely,

$$\begin{aligned} \left( 148\sqrt{2}q\right) \left[ \left( {\varvec{\Phi }}_{LB}\right) _{0} \right] ^{\frac{q+1}{2q}}\frac{\log \frac{n}{\epsilon }}{\theta }. \end{aligned}$$

(29)

For large-update methods with $\tau =\mathbf {O}\left( n\right)$ and $\theta ={\varvec{\Theta }}\left( 1\right)$, we have

$$\begin{aligned} \mathbf {O}\left( qn^{\frac{q+1}{2q}}\log \frac{n}{\epsilon }\right) \textit{iterations complexity}. \end{aligned}$$

In case of a small-update methods, we have $\tau =\mathbf {O}\left( 1\right)$ and $\theta ={\varvec{\Theta }}\left( \frac{1}{\sqrt{n}}\right)$. Substitution of these values into (28) does not give the best possible bound. A better bound is obtained as follows.

By (20), with

$$\begin{aligned} \psi _{LB}\left( t\right) \le \frac{q+3}{4}\left( t-1\right) ^{2},\ \ \ \ \ t>1, \end{aligned}$$

we have

$$\begin{aligned} {\varvec{\Phi }}_{LB}\left( v_{+}\right)&\le n\psi _{LB}\left( \frac{1}{ \sqrt{1-\theta }}\sigma \left( \frac{{\varvec{\Phi }}_{LB}\left( v\right) }{n} \right) \right) \\&\le \frac{n\left( q+3\right) }{4}\left( \frac{1}{\sqrt{1-\theta }}\sigma \left( \frac{{\varvec{\Phi }}_{LB}\left( v\right) }{n}\right) -1\right) ^{2}\\&=\frac{n\left( q+3\right) }{4\left( 1-\theta \right) }\left( \sigma \left( \frac{{\varvec{\Phi }}_{LB}\left( v\right) }{n}\right) -\sqrt{1-\theta } \right) ^{2} \end{aligned}$$

Using (21), we have

$$\begin{aligned}&\frac{n\left( q+3\right) }{4\left( 1-\theta \right) }\left( \sigma \left( \frac{{\varvec{\Phi }}_{LB}\left( v\right) }{n}\right) -\sqrt{1-\theta } \right) ^{2}\\&\quad \le \frac{n\left( q+3\right) }{4\left( 1-\theta \right) }\left( \left( 1+ \sqrt{2\frac{{\varvec{\Phi }}_{LB}\left( v\right) }{n}}\right) -\sqrt{1-\theta } \right) ^{2} \\&\quad =\frac{n\left( q+3\right) }{4\left( 1-\theta \right) }\left( \left( 1- \sqrt{1-\theta }\right) +\sqrt{2\frac{{\varvec{\Phi }}_{LB}\left( v\right) }{n}} \right) ^{2} \\&\quad \le \frac{n\left( q+3\right) }{4\left( 1-\theta \right) }\left( \theta + \sqrt{2\frac{\tau }{n}}\right) ^{2} \\&\quad =\frac{\left( q+3\right) }{4\left( 1-\theta \right) }\left( \theta \sqrt{n }+\sqrt{2\tau }\right) ^{2}=\left( {\varvec{\Phi }}_{LB}\right) _{0}. \end{aligned}$$

where we also used that $1-\sqrt{1-\theta }=\frac{\theta }{1+\sqrt{1-\theta } }\le \theta$ and ${\varvec{\Phi }}_{LB}(v) \le \tau$, using this upper bound for $\left( {\varvec{\Phi }}_{LB}\right) _{0}$, we get the following iteration bound:

$$\begin{aligned} \left( 148\sqrt{2}q\right) \left[ \left( {\varvec{\Phi }}_{LB}\right) _{0} \right] ^{\frac{q+1}{2q}}\frac{\log \frac{n}{\epsilon }}{\theta }. \end{aligned}$$

note now $\left( {\varvec{\Phi }}_{LB}\right) _{0}=\mathbf {O}\left( q\right)$, and the iteration bound becomes $\mathbf {O}\left( q^{2}\sqrt{n} \log \frac{n}{\epsilon }\right)$ iteration complexity.

Table 1 The conditions (a), (b) and (c)

Table 2 The estimated bound terms of the algorithm

Table 3 Complexity results for large- and small-update methods

5 Comparison of algorithms

To prove the effectiveness of our new kernel function and evaluate its effect on the behavior of the algorithm, we offer a comparison between the following two kernel functions with a logarithmic barrier term and the results of their correspondent $\text{ IPMs }$ algorithms.

• 1) The first kernel function, given by El Ghami et al. [8], is noted kernel function LE, defined by

  $$\begin{aligned} \psi _{LE}\left( t\right) =\frac{t^{1+p}-1}{1+p}-\log t, \ \ \ p\in [0,1], t>0. \end{aligned}$$

• 2) Our new kernel function is noted kernel function LB, defined in (12) by

  $$\begin{aligned} \psi _{LB}\left( t\right) =\frac{t^{2}-1-\log t}{2}+\frac{t^{1-q}-1}{2\left( q-1\right) }, \ \ \ q>1, t>0. \end{aligned}$$

  We summarize these results in the Tables 1, 2 and  3.

6 Conclusion

In this paper, our objective is to propose a new efficient parameterized logarithmic kernel function for developing a new descent direction and improve the algorithmic complexity of the interior-point method proposed. We have analyzed large-update and small-update versions of the primal-dual interior algorithm described in Fig. 1 which is based on the new kernel functions defined by (12). The results obtained in this paper represent important contributions to improve the convergence and the complexity analysis of primal-dual $\text{ IPMs }$ for $\text{ LO }$. So far, and to our knowledge, these results are the best known complexity bound for large-update with a logarithmic barrier term.