Searching for a cycle with maximum coverage in undirected graphs

Abstract

The present contribution considers the problem of identifying a simple cycle in an undirected graph such that the number of nodes in the cycle or adjacent to it, is maximum. This problem is denoted as the Maximum Covering Cycle Problem and it is shown to be NP-complete. We present an iterative procedure that, although it cannot be shown to be polynomial, yields (in practice) high-quality solutions within reasonable time on graphs of moderate density.

1 Introduction

Consider an undirected graph $G=(V,E)$; a covering cycle is a simple cycle C in G that covers all the nodes of the graph—a node $i\in V$ is said to be covered if it either lies on C or is adjacent to a node on C. This paper deals with the problem of finding a simple cycle $C^*$ that covers the largest number of nodes $f(C^*)$ in the graph (Maximum Covering Cycle Problem, MCCP). The problem arises in the design of communication networks when a closed backbone is needed and client nodes must connect directly to hubs. More generally, applications of such a problem can be found in situations where a closed line (for gas, water, power) is needed to serve different utilities that cannot be linked to a tree-based backbone.

To the authors’ knowledge there is no work in the literature dealing with the MCCP precisely as it is defined here. Nevertheless, the problem of detecting a connected subset of nodes satisfying some dominance or covering property is not at all new.

In [1] the problem of finding a minimum-size cycle covering all nodes is tackled for the special case of permutation graphs; the authors denote such a cycle a dominating cycle. In this work this term is deliberately avoided since it can be confused with a different graph-theoretic problem. From a computational point of view, one of the earliest formulations of a problem involving covering by cycles is due to Current and Schilling [2]. Their paper studies a so-called Covering Salesman Problem (CSP), where a cycle is required to pass within a certain distance from all nodes in the graph, and proposes a heuristic solution procedure. The authors of [2] motivated the problem definition in the context of health-care delivery or transportation systems. The same authors later investigated a (bicriteria) maximal covering tour problem, where a minimum-cost tour is drawn among at most $p<|V|$ nodes in order to cover as much of a demand specified at the nodes as possible. Gendreau et al. [5] considered a similar Covering Tour Problem where a tour must go through a given subset of nodes, and another set of nodes (not allowed to be on the tour) must be covered. They developed a branch-and-cut approach, possibly the first exact method for this kind of problems. More recently, Golden et al. [6] introduced a Generalized CSP, where each node can be required to be covered several times (for example for taking into account vehicle capacities) and a cost has to be payed for including a node in the cycle. They proposed and tested local search heuristics.

It should be noted that this paper’s approach to the MCCP is essentially computational; in contrast, a fair number of papers concerned with similar problems deliver mostly graph-theoretical studies. Related problems that aim to identify dominating or covering node sets exhibiting connectivity properties have already been studied by Lesniak-Foster and Williamson [10], and Veldman [13, 14], both giving sufficient conditions for the existence of spanning and dominating circuits. For the problem of determining a (minimum-size) connected dominating set, a naive enumeration scheme can solve it in time $O(2^n)$. Approximation algorithms—although with non constant ratio—are studied by Guha and Khuller [7]. The first exact algorithm with running time smaller than $O(2^n)$ is given by Fomin et al. [4].

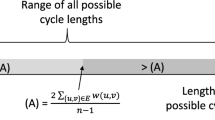
The complexity of the problem is easily established (we refer the reader to Fig. 1 for a rough idea of the proof).

Proposition 1

The decision version of MCCP is NP-complete.

In this paper, an ILP based solution procedure is developed that, although exact in nature can be used to produce high-quality heuristic solutions together with upper bounds that assess the solution quality (along the trends established by [3]). Computational experiments with this procedure are presented, showing that for graphs with small-to-medium density (from 1 up to 50 %) the problem can be solved efficiently.

The paper is organized as follows. In Sect. 2, an ILP model of the problem is described that naturally leads to a relaxed formulation. Although still involving integer variables, the relaxed formulation turns out (experimentally verified) to be easy to solve to optimality with the optimization software package CPLEX. In Sect. 3, a so-called Constraint Generation procedure is described in which constraints are iteratively added to the relaxed formulation until an optimal solution is found or a given time limit is exceeded. In order to speed up the procedure, a number of intensification and diversification techniques are added to this basic approach, which are discussed in Sect. 4. Finally, to assess the overall performance of the proposed approach, Sect. 5 reports on computational experiments performed on graphs of different sizes and densities.

Fig. 1

Reduction from Hamiltonian Cycle to Maximum Covering Cycle (sketch). In graph b all nodes can be covered iff graph a admits a Hamiltonian Cycle

2 ILP formulation and relaxation

In the following, an ILP formulation of the problem with binary variables is presented. Given an undirected graph $G=(V,E)$, let $u_i$ be the binary variables indicating if a node i is covered ($u_i=1$) or not (otherwise), and let $w_i$ be the binary variables indicating whether the node i is on the cycle or not. Let $x_{ij}=1$ if both nodes i and j are on the cycle, $x_{ij}=0$ otherwise. We specify variables $x_{ij}$ for each ordered pair (i, j) even if the problem is given for undirected graphs. This dummy orientation of arcs will be useful later on. The model is then as follows:

$$\begin{aligned} \text {maximize}&\quad \sum _{i\in V} u_i\end{aligned}$$

(1)

$$\begin{aligned} \text {subject to}&\quad x_{ij}+x_{ji}\le 1\qquad \qquad \qquad \qquad \qquad \;\quad \forall \,\{i,j\}\in E\end{aligned}$$

(2)

$$\begin{aligned}&\quad \sum _{j:\{i,j\} \in E}x_{ji}=\sum _{j:\{i,j\} \in E}x_{ij}=w_i\quad \forall \,i\in V\end{aligned}$$

(3)

$$\begin{aligned}&\quad w_i+\sum _{j:\{i,j\} \in E}w_j\ge u_i\qquad \qquad \;\qquad \forall \,i\in V\end{aligned}$$

(4)

$$\begin{aligned}&\quad \sum _{i \in S} \sum _{j \in V{\setminus } S} x_{ij} + \sum _{j \in S} \sum _{i \in V{\setminus } S} x_{ij}\ge 2(w_k+w_l-1) \nonumber \\&\quad \forall k,l,S:S\subset V,\ 2\le |S|\le |V|-2,\quad k\in S,\ l\in V{\setminus } S \end{aligned}$$

(5)

$$\begin{aligned}&\quad {x_{ij},x_{ji}\in \{0,1\}}\qquad \qquad \qquad \qquad \qquad \qquad \forall \,\{i,j\}\in E\end{aligned}$$

(6)

$$\begin{aligned}&\quad {w_i,u_i\in \{0,1\}}\qquad \qquad \;\qquad \qquad \qquad \;\qquad \forall \,i\in V. \end{aligned}$$

(7)

Constraints (2) provide an orientation for each edge belonging to the cycle. Constraints (3) ensure that exactly two edges are incident to each node of the cycle. Note that constraints (2) and (3) together force the solution to be a directed cycle. Constraints (4) enforce the covering property of the nodes belonging the cycle. Constraints (5) are subtour elimination constraints (SEC), as formulated in [6].

Given model (1)–(7), a straightforward relaxation of the problem is to exclude all the subtour elimination constraints (5). Although the remaining model still contains integer variables, the relaxed problem becomes much easier to solve in practice. The solution of this relaxation will be a collection of disjoint cycles maximally covering the graph, for which the coverage also serves as an upper bound on the optimal value of the original model.

Preliminary tests performed on random instances of various sizes show that CPLEX 12.5 is able to solve the relaxed model within 5 s, on average, for 1000 nodes instances. Increasing the number of nodes makes the relaxation harder to solve but still tractable. We were unable to solve instances larger than 5000 nodes due to memory limits.

3 Constraint generation approach

We present computational experience with an effective algorithm based on constraint generation for solving the MCCP. The optimal solution of the (integer) relaxed program (1)–(4), (6) and (7) generally consists of a finite set of disjoint cycles. The main idea is to iteratively introduce into the model constraints that exclude all disjoint cycles generated by the relaxation at the previous iteration, and solve again the relaxed model in order to refine the search. Meanwhile, we keep track of the best found cycle for future reference. Similar ideas can be found in [9] for example, or more recently in [12], although on different problems. Such constraints are not valid cuts in the sense of cutting planes theory, since they can exclude integer feasible solutions from the feasible set. Nevertheless, the resulting algorithm is provably optimal.

Algorithm 1 presents pseudocode for this approach. Without loss of generality, it is assumed that the instance is feasible; i.e. the graph contains at least a cycle (the forests being easily recognizable a priori). Also, from now on we denote by V(C) and E(C) the set of edges of cycle C.

It should be noted that the algorithm terminates in a finite (although possibly very large) number of iterations since the statement on line 17 can only be executed a finite number of times before the problem becomes infeasible, i.e. all cycles have been excluded. Three exit points are possible for the procedure:

• (i) Line 5: the problem has become infeasible, all possible cycles have been generated thus the optimal one is $C^*$.

• (ii) Line 7: the calculated bound is worse than the current best known solution thus certifying optimality of $C^*$.

• (iii) Line 12: the current problem is optimally solved by $C_1$ so the optimum is either $C_1$ or the best cycle known at the previous iteration.

The above discussion justifies the following proposition:

Proposition 2

Algorithm 1 returns the optimal solution in a finite number of iterations.

The performance of this basic constraint generation algorithm can be further improved. Two directions of improvement can be followed. On the one hand, it is worthwhile to increase the size of the set of generated cycles that will be forbidden in the following iterations; on the other hand it is important to increase the total coverage of each generated cycle. The latter will speed up recognition of high-quality solutions to be compared with generated bounds. In order to deal with those two directions, the heuristic methods described in the following section can be introduced within the basic framework of Algorithm 1.

4 Improving the pool of cycles

The pool of cycles S used by Algorithm 1 should be as rich and diverse as possible. Several heuristics can be devised in order to generate additional cycles apart from those provided by the solution of the relaxed problem. In this section we present four methods for improving the pool of cycles. Note that these methods can be combined in various ways; we will discuss in Sect. 5 the effectiveness of the possible combinations.

(a) Local improvement By this we mean, given a cycle $C\in S$, generating a new cycle with better coverage (or a shorter cycle with an equivalent coverage) by applying small perturbations, similarly to what would be done in a neighborhood search. We consider three such operators.

• Greedy Insert Increase (GII) This operator loops over all edges $\{i,j\}\in E(C)$ such that $\exists \ k\in V{\setminus } V(C)$ with $\{i,k\},\{j,k\}\in E$, and inserts node k between i and j. Considers the insertion giving the highest increase in coverage and returns the corresponding cycle $C'$.

• Greedy Swap Increase (GSI) This operator loops over all consecutive edge pairs $\{i,k\},\{k,j\}\in E(C)$ such that $\{i,v\},\{j,v\}\in E$ for some $v\in V{\setminus } V(C)$, and replaces node k with v in cycle C—i.e. swaps k and v. Determines the swap giving the highest increase in coverage and returns the corresponding cycle, or C itself if no swap increases the coverage.

• Decrease Cycle Length (DCL) This operator sequentially loops over all consecutive edge pairs $\{i,j\},\{j,k\}\in E(C)$ such that $\{i,k\}\in E$. If $\{i,j\},\{j,k\}$ can be replaced by $\{i,k\}$ (“bypassing” node j in the cycle) without decreasing the coverage, the substitution is performed.

These three operators are applied sequentially to the best cycle $C^*\in S$ i.e. we compute $C'=\mathbf {GII}(C^*)$, then $C''=\mathbf {GSI}(C')$, $C'''=\mathbf {DCL}(C'')$.

(b) Diversification 1: merging cycles Given a collection of cycles S, consider two disjoint cycles $C',C''\in S$ such that $C'=(A',i,B',j)$, $C''=(A'',k,B'',l)$ with $\{i,k\}, \{j,l\}\in E$.

We consider the four cycles obtained from combining $C'$ and $C''$ as follows.

$$\begin{aligned} C_1= & {} (A',i,k,A'',l,j)\quad C_3=(B',i,k,B'',l,j)\\ C_2= & {} (A',i,k,B'',l,j)\quad C_4=(B',i,k,A'',l,j) \end{aligned}$$

We compute $C_1,C_2,C_3,C_4$ for all pairs $C',C''\in S$; the cycle $\hat{C}$ with highest coverage $f(\hat{C})$ will replace in S the two cycles it was generated from. Given the ordered lists of nodes that make up the two cycles, the resulting $C_1,C_2,C_3,C_4$ can be computed quickly in $\mathcal O(|V(C')|+|V(C'')|)$.

Using the sketched procedure, we have the chance to improve a set of cycles S by replacing cycles by cycles with better coverage. We call this procedure MergePool. MergePool is repeated as long as cycles with higher coverage are found.

(c) Diversification by ILP: generating more cycles In addition to merging cycles, we can use the ILP model to generate more cycles, slightly modifying the relaxed formulation. Consider $C^*=\arg \max \{{f(C):C \in S} \}$. We consider two kinds of modified relaxations.

• (I) Solve the relaxed model where $C^*$ is forced to be part of the solution, i.e. solve the relaxed model with the additional constraint

  $$\begin{aligned} \sum _{(i,j) \in C} x_{ij} = |C^*|. \end{aligned}$$

  (8)

  The solution of the relaxed model will in general contain other cycles, different from $C^*$, that will be added to S.

• (II) Force the relaxed model to find a new set of cycles not containing $C^*$, by adding the constraint:

  $$\begin{aligned} \sum _{(i,j) \in C^*} (1-x_{ij}) = K \end{aligned}$$

  (9)

  where K is a constant indicating how many edges of C should not be present in the new set of cycles.

4.1 Final algorithm

We embed the operators described above in Algorithm 1. They are used to refine the pool of cycles S delivered by the solution of the relaxed model. The refinement takes place in two stages.

• 1. We first repeatedly apply the merge operator to the cycles in S; the new cycles are added to S and the merge procedure is iterated until no cycles with higher coverage can be generated. Then we apply the local improvement operator to the best cycle of the pool $C^*=\arg \max \{f(C):C\in S\}$. Finally, we generate more cycles applying the diversification by ILP, method (I).

  This whole stage is repeated until no more cycles with higher coverage emerge.

• 2. In the second stage, we use diversification by ILP, method (II). We start by the required distance $K=1$ and add the new cycles into S. We repeat the procedure increasing K by 1 as long as cycles with higher coverage emerge.

The above methods for improving the set of cycles are organized in the procedure ImprovePool reported in Algorithm 2. In the final algorithm, a call to ImprovePool(S) is inserted between lines 16 and 17 of Algorithm 1.

5 Computational results and discussion

Firstly, preliminary testing was performed in order to assess the validity of the constraint generation approach.

5.1 Multistart algorithm

In order to benchmark the presented approach against a baseline, a multistart heuristic method was also developed, in which the Local Improvement and MergePool operators can be naturally embedded. The multistart approach works as follows.

We randomly generate cycles from the graph G while building a partial spanning forest F. Starting from a randomly shuffled list L of the edges of G, set F to an empty forest and iterate as follows.

• 1. Extract an edge e from L;

• 2. Insert e in F;

• 3. If F contains a cycle C, delete all edges incident to C from L and F;

Four different configurations leading to multistart (MS) algorithms, combining the proposed operators in various ways, are considered.

• (MS0) Pure random search. Among the cycles generated by the above steps, the maximum covering cycle is selected. The search is performed over 100 trials.

• (MS1) Multistart plus MergePool. The complete set of cycles generated in a trial of the above steps is given as input to MergePool. The procedure is run to update the set of cycles until no further improving merge operations are possible. The cycle in the pool exhibiting the maximum coverage is returned as the final heuristic solution. Again, 100 trials of such a search are performed.

• (MS2) Multistart Local Improvement. After each trial of random search, the operators (GII, GSI, DCL) are applied, up to a local optimum.

• (MS3) Multistart MergePool + Local Improvement. A combination of (MS1) and (MS2): the best cycle in the pool is used as a starting solution for the Local Improvement operators.

5.2 Constraint generation algorithm

The ILP based constraint generation approach was tested in 6 different configurations:

• (ILP0) The basic constraint generation of Algorithm 1.

• (ILP1) Algorithm 1 equipped with MergePool for improving the set of generated cycles.

• (ILP2) Algorithm 1 equipped with the Local Improvement operators for improving the set of generated cycles.

• (ILP3) Algorithm 1 equipped with MergePool and diversification operators.

• (ILP4) Algorithm 1 equipped with the Local Improvement and diversification methods.

• (ILP5) Algorithm 1 equipped with the full set of operators.

5.3 Numerical results

For this test phase, we used both randomly generated graphs and graphs available from the literature on the Hamiltonian Cycle problem—such instances are interesting because they are guaranteed to have at least one optimal solution of value |V| due to the existence of a Hamiltonian Cycle. For the randomly generated graphs, we generated graphs with a number of nodes |V| equal to 50, 100, 200, 300 and 500, and density d (${=}\frac{2|E|}{|V|\times (|V|-1)}$) equal to 1, 2, 5, 10 %. For larger densities, we observed that such instances quickly become ‘easy’, because even small cycles can cover most of the nodes. These instances were produced by generating complete graphs of |V| nodes, and subsequently removing randomly (uniformly) selected edges from the graphs to meet the required density. For the instances from the literature we used the ‘DLV’ instances for the Hamiltonian Cycle problem from NP-Datalog [8]. Ultimately, this first dataset is made up of 120 instances.

Table 1 reports aggregated results of all different configurations of both methods. In column 2 the number of optimal solutions found is reported. Column 3 reports the average optimality gap ($(UB-LB)/UB$), which is either calculated as the relative gap from the optimal solution value (if found) or the best found upper bound (over all configurations). Column 4 reports the average CPU time; the time limit was set to 600 s for all instances. For all configurations, the different features enabled are also reported (as ON/OFF entries in columns 5–7).

Table 1 Global results, first dataset

In general, the overall percentage gap generated by every configuration of the algorithms is small; the worst case being configuration MS0 with a gap of 2.13 %. A more significant variability is observed on the average CPU time that never exceeds (roughly) 100 s for all configurations.

Concerning the multistart configurations, in terms of number of detected optima and average optimality gap, MS0 has the worst performance. Adding the Local Improvement operators (see configuration MS2) results in a slight improvement in the average optimality gap and number of optima, at the expense of a modest increase in the average CPU time. The MergePool operator enabled in MS1 turns out to be computationally intensive, but delivers a significant improvement in solution quality.

Configuration MS3 has the best performance among MS configurations in terms of solutions quality, at a computational cost comparable to that of MS1.

The constraint generation approach, in every configuration, outperforms the MS algorithms. The simple constraint generation approach based on the sole relaxation and cut generation is already quite effective (ILP0) compared to the MS configurations. On average, the optimality gap is 0.33 % and the configuration is able to find 111 optimal solutions over 120 instances. Adding the MergePool operator (ILP1) improves the obtained results, lowering the gap to 0.0 %. Again, the MergePool operator boosts solution quality, mixing well with the constraint generation approach, but allowing in this case also to save more than 50 % of CPU time. This confirms the effectiveness of the MergePool operator that allows to build large high quality cycles by combining the smaller ones extracted from the relaxed solutions. With configuration ILP2, the proposed Local Improvement operators achieve an improvement with respect to ILP0 in solution quality (in terms of optimality gap) but at the expense of a slight worsening of the CPU time.

Configurations ILP3, ILP4 and ILP5 also apply the diversification operators, but only ILP5 really delivers competitive performances, being only slightly worse than ILP1 in terms of solution quality. Thus we selected ILP1 and ILP5 (second best) as the most promising configurations and performed additional tests on a larger instance set.

For constructing the second, larger, dataset we added to the first set:

• 912 randomly generated instances with similar sizes and density up to 50 %;

• 336 randomly generated scale-free graphs (where the node degree distribution follows a power law), with up to 1000 nodes in size;

• 57 graphs from the graph coloring section in the ORLIB [11];

• a large instance (900 nodes) from [8], in the “structured 3-col” collection.

For this second experiment, a time limit of 600 s has also been set for solving each instance. According to Table 2, ILP5 offers an average optimality gap and a CPU time that are slightly better than those of ILP1. On the other hand the number of optima slightly favors ILP1. ILP5 outperforms ILP1 on the random instances while ILP1 performs best on the scale-free instances. The overall results confirm the observations reported in the preliminary testing on the first dataset. The hardest instances appear to be the scale free graphs, while the large figures for the “structured-3col” instances are entirely dependent upon the 900 nodes instance. On such an instance, ILP1 gets an objective value of 333 within the time limit, whereas ILP5 reaches a value of 880. Would this particular instance not be taken into account, the overall average gaps of ILP1 and ILP5 would be practically the same.

Table 2 Global results, second dataset

In view of the presented results we note that the design choice of embedding a ILP solver into the proposed constraint generation based approach wins over more naive combinations of the heuristic operators considered in the paper, offering the best trade-off between CPU time and solution quality. The two best performing configurations are the simpler ILP1 and the somehow more complex ILP5 where the full set of enhancing operators are enabled. Furthermore, from the presented result, ILP1 and ILP5 show a different behaviour on different classes of instances. While both configurations work extremely well on the HC-DLV instances, interestingly on the remaining classes the performances appear to be complementary.