Introduction

The complex dynamics in excitable neurons have attracted great interest in recent years (Wang et al. 2016, 2018; Xu et al. 2019a, 2020; Zhou et al. 2020). Numerous studies have found that weak signals can be processed and amplified by excitable neurons (Erkan et al. 2019; He et al. 2020; Yao et al. 2019a, b; Zhao et al. 2016). The system is best amplified and optimized for weak signals with the appropriate level of external stimuli. Noise plays an essential role in the dynamics of nonlinear systems such as stochastic resonance (SR) (Gammaitoni et al. 1998), which was first proposed in long-term atmospheric change research (Benzi et al. 1982). Generally, the characteristic of SR is to optimize the output signal-to-noise ratio (SNR) (Guo et al. 2017; Hu et al. 1993; LoCher et al. 1998) or Fourier coefficient (Volkov et al. 2003; Yao and He 2020; Yao and Ma 2018b; Yao et al. 2018a) in a nonlinear dynamic system after introducing a weak external signal. SR was observed in the mammalian brain (Mori and Kai 2002; Srebro and Malladi 1999; Stufflebeam et al. 2000) and neurobiological experiment on the caudal photoreceptors of crayfish (Bahar et al. 2002; Bahar and Moss 2004). In addition, there are many other resonance phenomena in the neuron system. Inverse stochastic resonance indicates that an appropriate noise intensity can suppress or even eliminate the firing of neurons. (Anatoly et al. 2016; Muhammet et al. 2017; Lu et al. 2020; Uzuntarla et al. 2017). When two periodic stimuli with different frequencies are input in a bistable system (Borromeo and Marchesoni 2005, 2007a), vibration resonance (Asir et al. 2019; Landa and Mcclintock 2000; Wang et al. 2021a; Wu et al. 2015; Yao et al. 2011) occurs. Delays have a strong moderating effect on nonlinear systems’ dynamic behavior (Borromeo et al. 2006; Borromeo and Marchesoni 2007b; Masoller 2002, 2003). If delay length is fine-turned to meet the forcing frequency, SR will appear at every multiple of the forcing frequency. (Gan et al. 2010; Hu et al. 2014; Wang et al. 2009, 2012).

Neurons are influenced by their internal and external environment. Previous studies have shown that natural and artificial neuronal networks can demonstrate the presence of chaotic regimes (Canavier et al. 1990; Jia et al. 2012; Rosanova and Timofeev 2005; Vanvreeswijk and Sompolinsky 1996). Thalamic and cortical neurons show chaotic dynamics during the transition period between sleep and waking (Paul et al. 2016). In the inferior olive neuronal network, appropriate electrical coupling produces chaotic firing and enhanced information transmission (Schweighofer et al. 2004). Some recent works have found that the system’s response to a weak signal can be amplified by chaotic activity, known as chaotic resonance (CR). The CR is triggered in two ways: the first one is CR can be induced by an external chaotic signal; (Baysal et al. 2019, 2021), and the other is it can be triggered by intrinsic chaotic activities. (Nobukawa et al. 2015).

In recent years, several studies have focused on detecting and transmitting weak signals in single neuron and neuronal networks. Yang et al. studied the VR in FitzHugh-Nagumo (FHN) system. They found that the VR of the excitable system is caused by the transition between different phase-locked modes (Yang et al. 2012). Baysal found that neurons can detect weak signals even in a chaotic state (Baysal et al. 2019). An optimal chaotic current intensity was found to ensure the optimal detection of weak signals of Hodgkin-Huxley neurons by CR. Furthermore, further research supports the above findings in the small-world network (Baysal et al. 2019, 2021). The collective behavior and signal transmission of the feed-forward feed-back FHN neuronal network were investigated (Ge et al. 2020a). By increasing the amplitude of high-frequency stimulation, the weak input signal of the system is synchronized with the output, and the information of the weak signal is amplified. Deng’s study of a three coupled FHN neuron system found that chemical coupling was more conducive to information transmission than electrical coupling for local signal input (Deng et al. 2009). The effects of electrical and chemical autapses on signal transmission were investigated in scale-free and small-world neuronal networks (Yao et al. 2019a, b). It was found that VR could significantly enhance weak signal transmission, but electrical and excitatory chemical autapses weaken the signal transmission. Our recent studies have found that synchronization modes between neurons can be modulated by synaptic delays (Yu et al. 2021). It is vital to study the effect of synaptic delay between coupled neurons on signal transmission.

Although there are extensive researches on transmission phenomena in neuronal systems (Ge et al. 2019, 2020b, 2021; Li et al. 2007; Lu et al. 2019a; Xu et al. 2019b), little attention has been devoted to the phenomenon of chaotic activity enhancing information transmission in FitzHugh-Nagumo (FHN) neuron and neuronal networks. In this paper, the effects of chaotic activity on signal transmission in a single neuron and the neuronal network are investigated. The structure of this paper is as follows: in “Model” section, the mathematical model of a single FHN neuron and a chain neuronal network are introduced. The main results are presented in “Results and discussions” section, while in “Conclusions” section we summarize and discuss the potential implications of our findings.

Model

The excitable FHN (Fitzhugh 1961) model is given as:

$$\left\{ \begin{gathered} \varepsilon \frac{{{\text{d}}x}}{{{\text{d}}t}} = x - x^{3} - y + A\cos (\omega t) + I_{{{\text{chaos}}}} , \hfill \\ \frac{{{\text{d}}y}}{{{\text{d}}t}} = 4x - y + 2.8,\quad \quad \quad \quad \quad \quad \quad \hfill \\ \end{gathered} \right.$$
(1)

where x is the fast variable of neuron membrane potential, y is the slow variable representing the effective membrane conductivity. The time scale of ε = 0.02 is chosen to make the dynamics of x much faster than the dynamics of y, which provides the necessary components for excitability. Acos(ωt) stands for an external signal, and ω = 2π /T. A and T are the amplitude and period of the signal, respectively. It should be noted that the parameter values of A and T were chosen in this paper to ensure that the signal is sub-threshold and cannot evoke large-amplitude excitation by itself.

In Eq. (1), Ichaos = M·u represents the chaotic current derived from the chaotic activity of environmental neurons. M is chaotic current intensity, and u is the external chaotic signal based on the Lorenz system, given by the following equation (Ma et al. 2005):

$$\left\{ \begin{gathered} \frac{{{\text{d}}u}}{{{\text{d}}t}} = \sigma \left( {v - u} \right),\quad \hfill \\ \frac{{{\text{d}}v}}{{{\text{d}}t}} = \rho u - v - uw, \hfill \\ \frac{{{\text{d}}w}}{{{\text{d}}t}} = uv - \beta w.\quad \hfill \\ \end{gathered} \right.$$
(2)

The external chaotic current is obtained from Eq. (2) with the chaotic system parameters of β = 8/3, σ = 10, ρ = 28. In order that the output of Lorentz system is chaotic, the initial value is set to: u0 = 20, v0 = 0, w0 = 0.

A chained neuronal network composed of N neurons is considered in this paper. The i-th (i = 1, 2, … N) node’s kinetics can be described by the dynamical evolution of the membrane potentials as:

$$\left\{ \begin{gathered} \varepsilon \frac{{{\text{d}}x_{i} }}{{{\text{d}}t}} = x{}_{i} - x_{i}^{3} - y_{i} + I_{{syn}} + I_{i} + I_{{i{\text{,chaos}}}} , \hfill \\ \frac{{{\text{d}}y_{i} }}{{{\text{d}}t}} = 4x_{i} - y_{i} + 2.8,\quad \quad \quad \quad \quad \quad \; \hfill \\ \end{gathered} \right.$$
(3)

The synaptic current Isyn = IE + IC. IC and IE are chemical synapses and electrical synapses, respectively. Their forms are as follows:

$$I_{E} = \left\{ \begin{gathered} g_{e,R} (x_{2}^{\tau } - x{}_{1}), \, i = 1 \hfill \\ g_{e,L} (x_{i - 1}^{\tau } - x{}_{i}) + g_{e,R} (x_{i + 1}^{\tau } - x{}_{i}), \, 1 < i < N \hfill \\ g_{e,L} (x_{N - 1}^{\tau } - x{}_{N}){, }i = N \hfill \\ \end{gathered} \right.$$
(4)

The ge,R and ge,L indicate the electrical coupling strength between adjacent neurons.

$$I_{C} = \left\{ \begin{gathered} f\left( {x_{1} ,x_{2}^{\tau } } \right), \, i = 1 \hfill \\ f\left( {x_{i} ,x_{i + 1}^{\tau } } \right) + f\left( {x_{i} ,x_{i - 1}^{\tau } } \right), \, 1 < i < N \hfill \\ f\left( {x_{N} ,x_{N - 1}^{\tau } } \right). \, i = N \hfill \\ \end{gathered} \right.$$
(5)

In this paper, the fast threshold modulation (FTM) scheme proposed by Somers and Kopell (Somers and Kopell 1993) is considered to illustrate the couple of systems, it is given by the following function:

$$f(x_{i} ,x_{i + 1}^{\tau } ) = - g_{c,R} (x_{i} - V_{s} )\frac{1}{{1 + \exp [ - K(x_{i + 1}^{\tau } - \theta_{s} )]}},$$
(6)
$$f(x_{i} ,x_{i - 1}^{\tau } ) = - g_{c,L} (x_{i} - V_{s} )\frac{1}{{1 + \exp [ - K(x_{i - 1}^{\tau } - \theta_{s} )]}},$$
(7)

with

$$x_{j}^{\tau } = x_{j} (t - \tau ),$$
(8)

and the i-th neuron at time t and j-th neuron at t–τ, in which gc,R and gc,L is the chemical coupling strength between adjacent neurons. Vs is the reversal potential. The difference between the synaptic reversal potential Vs and the synaptic potential x determines the type of coupling. The positive or negative sign of the difference corresponds to the excitatory or inhibitory effect of the synapse, respectively. The Vs is set as 1.0 for excitatory synapses. \(f(x_{i} ,x_{j}^{\tau } )\) exhibits an abrupt or more gradual threshold-like behavior, depending on the value of parameter K (Somers and Kopell 1993). The parameters are set as θs =−0.25, and K = 10. the chaotic current Ii,chaos = M·ui. ui is given by

$$\left\{ \begin{gathered} \frac{{{\text{d}}u_{i} }}{{{\text{d}}t}} = \sigma \left( {v_{i} - u_{i} } \right), \hfill \\ \frac{{{\text{d}}v_{i} }}{{{\text{d}}t}} = \rho u_{i} - v_{i} - u_{i} w_{i} , \hfill \\ \frac{{{\text{d}}w_{i} }}{{{\text{d}}t}} = u_{i} v_{i} - \beta w_{i} , \hfill \\ \end{gathered} \right.$$
(9)

The chaotic system parameters of β = 8/3, σ = 10, ρ = 28. The chaotic stimulus applied to each neuron is different. We set different initial values to obtain different chaotic sequences: u0 = 10 + αIn(i), v0 = 0, w0 = 0, α is set to random value (0 ~ 1).

In order to study the signal transmission in the neuronal network, the sub-threshold current is only added on the first node, i.e., I1 = Acos(ωt), else Ii = 0. The response of i-th node to external STS is estimated by computing the Fourier coefficient Q of i neuron for the input frequency ω, it is defined as follows (Landa and Mcclintock 2000):

$$\left\{ \begin{gathered} Q_{i} = \sqrt {Q_{\sin ,i}^{2} + Q_{\cos ,i}^{2} } , \hfill \\ Q_{\sin ,i} = \frac{\omega }{2\pi m}\int_{{T_{0} }}^{{T_{0} + 2\pi m/\omega }} {2x_{i} } \left( t \right)\sin (\omega t)dt, \hfill \\ Q_{\cos ,i} = \frac{\omega }{2\pi m}\int_{{T_{0} }}^{{T_{0} + 2\pi m/\omega }} {2x_{i} } \left( t \right)\cos (\omega t)dt, \hfill \\ \end{gathered} \right.$$
(10)

T0 is selected as a sufficiently large value to eliminate the influence of model initialization on the calculations, and in the whole numerical simulation, the number of the period is set to m = 500. In the neuronal system, the information is carried through large spikes instead of sub-threshold oscillations, and we are more interested in the frequency of spikes (Deng et al. 2010). Therefore, in the calculation, we set the threshold as xs = 0, and if x < xs, x is replaced by the value of the fixed point x =  − 1; otherwise, x remains the same. The Fourier coefficients more intuitively indicate the extent to which the neuron fires at a particular forcing frequency ω. The larger the Q, the more phase synchronization between the system output and the STS input, which means the more information the system transmits.

Results and discussions

Single FHN neurons system with chaotic current

The mode transition of neuronal electrical activity can be induced by external stimulus signals (Hou et al. 2021; Liu et al. 2019; Lu et al. 2019b; Xu et al. 2018a, 2018b). We obtained the characteristic curve (depicted with dash-dotted line) separating the sub-threshold (quiescent state) and supra-threshold (firing state) regimes in the amplitude-period parameters plane in Fig. 1. The periodic signal applied to the membrane potential is sub-threshold by selecting appropriate parameters.

Fig. 1
figure 1

The domain of amplitude A and period T in the parameter plane. The periodic signals in the red parameter region excite neurons to firing, while signals in the green region do not

Full size image

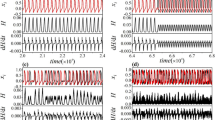
Figure 2 shows the temporal evolution of membrane potentials x for different chaotic current intensities. For comparison, the STS is plotted in Fig. 2, indexed by red lines. When the chaotic current is weak (M = 0.001 in Fig. 2(a)), the total output of the neuron is below the threshold and cannot carry STS information. When the chaotic current increases (M = 0.01 in Fig. 2(b)), the system’s output shows a burst discharge of period T, which is precisely the period of the STS. An optimum chaotic current intensity (M = 0.016 in Fig. 2(c)) allows the system to carry the STS information best. So the input and the output are well synchronized and the weak signal’s information is amplified remarkably. When the chaotic current is excessively strong (M = 0.03 in Fig. 2(d)), the spike is sparsely emerged, disrupting the neuron’s burst discharge. Increasing the chaotic current intensity further (M = 0.1 in Fig. 2(e)) leads to a very high-frequency spiking, and the weak signal’s information completely disappears from the system’s output. Thus, chaotic resonance (CR) is observed, which occurs due to chaotic currents.

Fig. 2
figure 2

Temporal evolution of membrane potentials x for different chaotic current intensities. a M = 0.001; b M = 0.01; c M = 0.016; d M = 0.03; e M = 0.1. Red and black lines represent STS and x respectively. The parameters are fixed at A = 0.5, T = 20. The rhythmic synchronization of neuronal firing with the signal is dependent on the strength of the chaotic current

Full size image

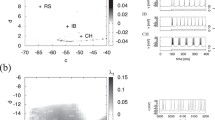
To study the effect of chaotic current and STS on the system output, the evolution of inter-spike interval (ISI) of x with the chaotic current intensity M and STS amplitude A are shown in Fig. 3. In Fig. 3(a), the neuron keeps in a quiescent state in the case of M < 0.0035, which means that the neurons cannot respond to STS under the influence of a weak chaotic current. In the case of 0.06 < M < 0.017, the ISI has values for different regions. ISI approximately at integer multiples of the period of the STS (T = 20) and the intrinsic neuronal oscillation period (approximately 1). This is because the neuron exhibits various time scales corresponding to the harmonics of the weak signal frequency under the influence of the weak chaotic current. The strong chaotic current puts the neuron in a high-frequency spiking state, while a large amplitude puts the neuron in a bursting state with the period of STS.

Fig. 3
figure 3

Bifurcation diagram associated with a chaotic current intensities M for A = 0.5; b STS amplitude A for M = 0.01. ISI denotes the inter-spike interval in membrane potential series. The parameters are fixed at T = 20. The neurons exhibit different time-scale firing states related to the signal period

Full size image

The response measure Q as a function of chaotic current intensities M for different A and T are shown in Fig. 4. The response measure Q shows a bell-shaped dependence on chaotic current intensities M. It is a characteristic curve of chaotic resonance phenomena. As the STS amplitude A increases in Fig. 4(a), the response measure’s switching point (where Q starts to change) shifts to smaller noise intensity. The neuron’s response performance to STS is enhanced. The larger amplitude puts the neuron in a more excited state, while the weaker chaotic current enables the neuron to discharge and respond to the signal. The larger amplitude and smaller STS period enable neurons to carry more information.

Fig. 4
figure 4

Dependencies of response measure Q on chaotic current intensities M for a different A, T = 20; b different T, A = 0.5. The response measure Q shows a bell-shaped dependence on chaotic current intensities M for different system parameters

Full size image

The contour plots of the response measure Q are drawn in Fig. 5. When the results in Fig. 5 are analyzed, it can be seen that there is a region (red area) where the system responds best to STS. In Figs. 5(a, b), the large amplitude and small period of the STS enhance the signal response phenomenon by the system. The dark red area on the upper left of Fig. 5(c) confirms the above conclusion. It is seen that the weak signal detection performance of the FHN neuron displays a resonance-like dependence on the chaotic current intensity for all values of A and T in Figs. 5(a, b). From this result, we can infer that CR is a robust phenomenon, which occurs independently of the parameter level of the signal.

Fig. 5
figure 5

The dependence of the weak signal detection performance of the neuron (Q) on a M and A in the presence of T = 20; b M and T in the presence of A = 0.5; c T and A in the presence of M = 0.01. The level of Q obeys the criterion given by the rightmost vertical bar

Full size image

Electrically and chemically coupled neuronal system with chaotic current

In this section, we consider a two-neuron system where the STS is applied to the first neuron and observe the response of the second neuron to the signal. The signal transmission performance between neurons can be detected by the response measure Q of the second neuron to the signal. We set the time delay τ = 0, and use the same scale for the contour plots drawn in Figs. 5, 6, 7, 8, and 9 (the rightmost vertical bar has the same setting level). Compared to Figs. 6, 7, 8, and 9 with Fig. 5, the response measure in Figs. 6, 7, 8, and 9 are significantly decreased. This suggests that regardless of whether the second neuron has a feed-back current to the first neuron, the signal transmission performance will decrease. Feed-forward coupling (Fig. 6) has advantages over bidirectional (Fig. 7) in signal transmission for electrical synapses.

Fig. 6
figure 6

The dependence of the weak signal transmission performance of the neuron (Q) on a M and A in the presence of T = 20; b M and T in the presence of A = 1.0; c T and A in the presence of M = 0.01. The coupling strength are fixed at ge,L = 0.2, gc,R = gc,L = ge,R = 0 to obtain a feed-forward electrical coupling connection

Full size image
Fig. 7
figure 7

The dependence of the weak signal transmission performance of the neuron (Q) on a M and A in the presence of T = 20; b M and T in the presence of A = 1.0; c T and A in the presence of M = 0.01. The coupling strength are fixed at ge,R = ge,L = 0.2, gc,R = gc,L = 0 to obtain a feed-forward chemical coupling connection

Full size image
Fig. 8
figure 8

The dependence of the weak signal transmission performance of the neuron (Q) on a M and A in the presence of T = 20; b M and T in the presence of A = 1.0; c T and A in the presence of M = 0.01. The coupling strength are fixed at gc,L = 0.2, gc,R = ge,R = ge,L = 0 to obtain a bi-directional electrical coupling connection

Full size image
Fig. 9
figure 9

The dependence of the weak signal transmission performance of the neuron (Q) on a M and A in the presence of T = 20; b M and T in the presence of A = 1.0; c T and A in the presence of M = 0.01. The coupling strength are fixed at gc,R = gc,L = 0.2, ge,R = ge,L = 0 to obtain a bi-directional chemical coupling connection

Full size image

On the other hand, for chemical synapses, feed-forward (Fig. 8) and bidirectional (Fig. 9) coupling have almost identical performances for signal transmission. Furthermore, Chemical synapses have an advantage over electrical synapses in terms of signal transmission. This is because chemical synapses only act when presynaptic neurons spike, whereas electrical coupling always connects neurons (Vanvreeswijk and Sompolinsky 1996). Chemical coupling separates sub-threshold oscillatory neurons from each other, giving them more firing opportunities. Once one spike is present, it stimulates others to spike synchronously. In contrast, with electrical coupling, robust synchronization between sub-threshold oscillatory neurons results in the decrease of oscillatory amplitude and thus the increase of the threshold for firing.

To investigate the effect of time delay on the information transmission of the chemically coupled neuronal system, the response measure Q of the second neuron as a function of time delay τ are shown in Fig. 10(a). It can be seen that response measure Q can achieve a certain maximum with increasing time delay, which means that multiple chaotic resonances occur. Further observations show that when g = 0.2–0.4, the Q value varies periodically with time delay. The special time delay τs = NT / 4 (where N is a positive integer and T = 20 denotes the period of STS) causes a unique phenomenon. More interestingly, it can be observed that the Q value is at a local maximum when N is odd, which indicates the occurrence of sub-harmonic chaotic resonance. When N is an even number, the value of Q is at a local minimum, which means that chaotic anti-resonance occurs. Hence, it is inferred that sub-harmonic chaotic resonance and chaotic anti-resonance alternatively appear as the time delay increases for the suitable chaotic currents levels. When the connection between two neurons is strong (g = 0.5, 0.7), there are some local maxima at τ = T/2, n = 1, 2… This means that the signal transmission is enhanced if the time delay is equal to a half-integer multiple of the STS period; otherwise, it is inhibited. For the electrically coupled neuronal system in Fig. 11, fine-tuning of time delays can also lead to multiple chaotic resonances. Nevertheless, the sub-harmonic chaotic resonance and chaotic anti-resonance phenomenon disappear.

Fig. 10
figure 10

a The dependence of the weak signal transmission performance of the neuron (Q) on time delay τ for different coupling strengths g. b The 3D plot of Q vs g and τ. The other parameters are fixed at A = 1.0, T = 20, M = 0.006, and the coupling strength are fixed at gc,R = gc,L = g, ge,R = ge,L = 0 to obtain a bi-directional chemical coupling connection. The signal transmission performance varies rhythmically with time delay. Such rhythmic variation is robust

Full size image
Fig. 11
figure 11

a The dependence of the weak signal transmission performance of the neuron (Q) on on time delay τ for different coupling strengths g. b The 3D plot of Q vs g and τ. The other parameters are fixed at A = 1.0, T = 20, M = 0.016, and the coupling strength are fixed at ge,R = ge,L = g, gc,R = gc,L = 0 to obtain a bi-directional electrical coupling connection

Full size image

To investigate the sub-harmonic chaotic resonance and chaotic anti-resonance phenomena induced by fine-tuning the time delay of chemically coupled neurons. The selection of particular points is shown in Fig. 12(a), and the corresponding temporal evolution are plotted in Fig. 12(b). In Fig. 12(b1), there are many disorderly spikes between burst discharges, representing the second neuron’s weak response to the STS. When the time delay is an odd multiple of T/4 in Fig. 12(b2), the disorderly spikes between burst discharges are reduced. The signal transmission performance of the system is enhanced. By further fine-tuning the time delay in Fig. 12(a), the signal transmission performance of the system is reduced. So the mechanism of the sub-harmonic chaotic resonance phenomenon is that the disorderly spikes between burst discharges are reduced when the time delay is an odd multiple of T/4. Further observations in Figs. 12(b3–5) show that the number of spikes in each burst differs. The number of spikes per burst is relatively small for τ = 10.0. So the mechanism of the chaotic anti-resonance phenomenon is that the number of spikes in the burst decreases when the time delay is an even multiple of T/4.

Fig. 12
figure 12

a The dependence of the weak signal transmission performance of the neuron (Q) on on time delay τ; b Temporal evolution of membrane potentials x2 for time delay: (b1) τ = 3.6, (b2) τ = 5.0, (b3) τ = 9.9, (b4) τ = 10.0, (b5) τ = 10.01. Red and black lines represent STS and x2 respectively. A = 1.0, T = 20, M = 0.006, and the coupling strength are fixed at gc,R = gc,L = 0.3, ge,R = ge,L = 0 to obtain a bi-directional chemical coupling connection. The periodicity of the neurons is enhanced in (b2), leading to sub-harmonic chaotic resonances. The number of spikes per burst is reduced in (b4), leading to chaotic anti-resonance

Full size image

The signal transmission performance is attenuated in the coupled neurons. To investigate the attenuation of signal transmission performance in larger size networks, we consider a chained network composed of 10 nodes. Larger networks have the same properties. In feed-forward electrical coupling networks in Fig. 13(a), when the coupling strength is constant, Qi decreases with the increase of i, indicating that the signal transmission attenuation always exists. In bi-directional electrical coupling networks in Fig. 13(b), the degree of attenuation becomes greater. However, in feed-forward chemical coupling networks in Fig. 13(c), Qi remains constant after i > 4. This suggests that signal transmission attenuation occurs just in the first few neurons and eventually reaches a steady state. In bi-directional chemical coupling networks in Fig. 13(d), signal transmission to the last neuron is attenuated because the last neuron only receives synaptic currents from the previous neuron. Basically, the bi-directional chemical coupling has the best signal transmission performance.

Fig. 13
figure 13

The dependence of the weak signal transmission performance of the i-th neuron (Qi) on g and i with different connections a feed-forward electrical coupling connection; b bi-directional electrical coupling connection; c feed-forward chemical coupling connection; d bi-directional chemical coupling connection. The other parameters are fixed at A = 1.0, T = 20, M = 0.016

Full size image

Conclusions

The signal detection and transmission phenomena of FHN chained networks with different types of coupling connections were discussed in this paper. Unlike previous studies (Baysal et al. 2019, 2021; Deng et al. 2009; Ge et al. 2020a; Yang et al. 2012; Yao et al. 2019a, b; Yu et al. 2021), neurons were driven by chaotic currents rather than high-frequency stimuli (Deng et al. 2009; Ge et al. 2020a; Yang et al. 2012;) and noise (Yao et al. 2019a, b). We investigated the phenomenon of signal transmission in chained networks, which is different from small-world networks (Baysal et al. 2019, 2021). In addition, previous work had not considered the effect of time delay on signal transmission (Baysal et al. 2019, 2021; Ge et al. 2020a; Yang et al. 2012; Yao et al. 2019a, b).

This paper indicated that the system responds best to STS at the appropriate level of chaotic activity. Fourier coefficient Q is chosen for quantitatively characterizing the efficiency of the signal detection and transmission. The larger Q is, the more information is transported through the system. The plot of response measure Q versus chaotic current strength M has a peak, which implies the presence of chaotic resonance. It is also found that both signal oscillation period and amplitude improve the detection of weak signals.

In the coupled neuronal system, the obtained results showed that chaotic currents could drive the transmission of STS at appropriate chaotic currents levels, so that the untransmitted signal can be successfully transmitted to the second neuron. A comparison of chemical synapses with electrical synapses shows that the former has better signal transmission performance.

The effects of coupling intensity on the signal transmission have been investigated by adjusting time delay. The signal transmission is enhanced intermittently by adjusting the length of the time delay, which implies multiple chaotic resonances can be observed. As time delay and oscillation period of STS are locked, the intermittent outlay emerges. In a bidirectional chemically coupled neuronal system, it can be observed that sub-harmonic chaotic resonance and chaotic anti-resonance can alternatively appear as the condition of the time delay is met. For the electrically coupled neuronal system, fine-tuning of time delays can also lead to multiple chaotic resonances. However, the sub-harmonic chaotic resonance and chaotic anti-resonance phenomenon disappear.

The signal may be attenuated during the transmission of the neural network. In a relatively larger size of electrical chain network, it was found that the signal was constantly attenuated. In contrast, the signal just attenuated in the first few neurons and eventually reached a steady state in a chemically coupled system, and neurons have better signal transmission performance in bidirectional chemical coupling.

In the present study, we have investigated the effect of chaotic activities on the sub-threshold signal transmission performance of coupled neurons and neuronal networks. In future studies, the transmission of STS can be considered for improved multi-layer neuronal systems (Ge et al. 2018; Lu et al. 2019c; Wang et al. 2021b), excitatory-inhibitory networks (Xue et al. 2014; Yu et al. 2020), and further extended to complex neuronal networks with different topologies.