Introduction

Spatiotemporal patterns of propagating electrical activity are prevalent in the cortex. These events include travelling waves in the motor (Rubino et al. 2006), visual (Zanos et al. 2015; Xu et al. 2007; Roland et al. 2006), and auditory cortices (Song et al. 2005; Reimer et al. 2010), as well as standing waves/synchronous firing alternating with travelling waves in the visual cortex (Benucci et al. 2007; Zanos et al. 2016), and rarer patterns such as ripples/wavelets (Patel et al. 2013), and spiral waves (Huang et al. 2004).

The detection of spatiotemporal patterns are instrument-independent, occurring in voltage-sensitive dyes, EEG and implanted multi-electrode array studies. Interestingly, they do not encode sensory stimuli in sensory areas (Chen et al. 2006; Jancke et al. 2004; Xu et al. 2007) nor movement parameters in motor areas (Rubino et al. 2006; Takahashi et al. 2011). Nevertheless, since they reflect a temporal variance in the firing rate of sub-populations (Jacobs et al. 2007; Jansen and Brandt 1991), they might be a mechanism to prioritize the processing of behaviourally relevant information (Ermentrout and Kleinfeld 2001). It suffices to say that the functional relevance, much less the computational role of cortical travelling waves, synchrony, and other activity, remains incompletely understood (for a recent review see Muller et al. 2018). Given the sheer quantity of neuroelectrophysiology data that is experimentally collected, it would be useful to compare spatiotemporal activity in the cortex with a common method. Our approach focuses on designing a simple yet accurate machine classification tool to qualitatively analyze a mathematical model of spatiotemporal pattern generation.

Until recently, previous methods have focused on coarse velocity information to analyze travelling waves. One can manually identify spatiotemporal patterns of interest, thereby producing a template, and then compute correlations with other events to find matches (Han et al. 2008; Takahashi et al. 2011). Tracking the center-of-mass of matched events then provides location and velocity information. Often, before this approach is applied, voltage measurements are first transformed into a phase representation through a Hilbert transform (Hahn 1996) or Morlet wavelets (Torrence and Compo 1998). Since waves can be defined as a phase offset that varies as a function of space, one can detect both standing and travelling waves with this method (Rubino et al. 2006; Muller et al. 2014).

In the last few years, studies have taken advantage of work in the field of machine vision to increase information yield from data. The so-called optical flow algorithms convert raw or phase-transformed data (Townsend et al. 2015) into a dense (individual-pixel scale) vector fields that encode the movement of activity patterns between time points (see Horn and Schunck (1981) for the canonical formulation of this problem). This allows the calculation of velocity much more accurately than in previous methods as well as the identification of geometric features such as spiral patterns, sources, and sinks (Mohajerani et al. 2013; Afrashteh et al. 2017; Townsend and Gong 2018). However, as in correlation methods, the focus has always been on the analysis of events of interest from experimental data, rather than classification of spatiotemporal patterns in neuronal activity.

To this end, we have trained a random forest (Breiman 2001) machine classifier to distinguish spatiotemporal activity patterns. We thoroughly consider many statistical 1D measures, and 2D measures (from the field of image analysis) to produce an optimal feature set with which to train the classifier. As training data, we use a simple spiking neuronal network model that produces a surprisingly large range of 2D patterns while varying a set of parameters.

Many of the cortical waves in the literature travel with speeds between 10 and 80 cm/s, which is consistent with conduction through unmyelinated horizontal fibres in cortical layer II/III (Girard et al. 2001; Sato et al. 2012) which may be part of a feedback loop with inhibitory interneurons of layer IV (Muller et al. 2018). This inhibitory/excitatory interplay can modelled by the “synaptic-footprint method” (Ermentrout and Kleinfeld 2001): a center-surround coupling method, consisting of short-range excitatory connections, and an annulus of longer-range inhibitory connections. This topology shows rapid switching between spatiotemporal patterns, at least in networks of phase oscillators (Heitmann et al. 2012, 2015).

Rebound firing in neuronal networks can generate oscillatory activity that propagates slowly, consistent with experimentally observed travelling waves (Golomb et al. 1996; Coombes and Doole 1996; Adhikari et al. 2012). Additionally, rebound firing has been hypothesized to have a role in coupling visual and oculomotor activity through travelling waves. When local inhibition is relieved after a saccade, a rebound effect may lead to the observed generation of waves that reorder the firing of neurons that are passed over (Zanos et al. 2015). Interestingly, the wave events appear suddenly, a “fast-switching” aspect we wish to recapitulate. The relationship between center-surround spatial topology and rebounding temporal responses has not been yet explored in a 2D spiking network model, making it a novel system that can be studied with our machine classification approach.

We chose the Izhikevich simple spiking model as our artificial neuron model to develop our spiking network (Izhikevich 2003). This model is very computationally efficient; it can produce nearly any spiking pattern of interest and is canonical to more biophysically realistic models such as the Hodgkin–Huxley model (Izhikevich 2004). When coupled with the synaptic footprint method, the network displays many spatiotemporal patterns. These include network wide travelling waves, localized wavelets, synchrony, and noise-induced network spiking (Eytan and Marom 2006). By manipulating the values of five parameters: level of inhibition, synaptic coupling strength, width of the kernel, order of the kernel, and noise, we demonstrate through the machine classifier that the network can switch between these activity regimes.

Since a mathematical analysis of this network is difficult, and since the number of possible parameter combinations is large, we have an ideal scenario to employ our automated approach. Using the classification algorithm, we are able to map eight spatiotemporal regimes across five primary parameters. Our results reveal that noise could spontaneously drive switching between synchrony and travelling waves, but in the absence of noise, switching can also be induced by varying coupling strength, level of inhibition and/or the width of the coupling kernel. Altogether, we present a machine learning scheme that rapidly and efficiently categorizes spatiotemporal patterns. Additionally, by applying a simple coupling scheme that mirrors putative wave generation mechanisms in the cortex, we can phenomenologically produce spatiotemporal patterns similar to those in the cortex.

Neuronal model

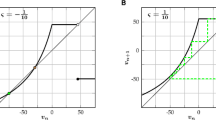
A dynamical depiction of the Izhikevich rebounding neuron model can be seen in Fig. 1a. The neuron is excitable, both through depolarizing and hyperpolarizing inputs, due to the shape of the nullclines. This means that activity initiated by an inhibitory stimulus is self-propagating, causing spikes generated by a rebounding neuron to induce depolarization in nearby neurons as seen in Fig. 1b.

Fig. 1
figure 1

Neuronal and network properties. a Nullclines of the Izhikevich neuronal model (as defined by the legend) governing the dynamics of post-inhibitory rebound exhibited by the model. A typical solution produced by the entire network (gray line) is superimposed onto the phase space. b A simulated trace of a particular rebounding neuron. An inhibitory stimulus (red bar) induces a rebounding spike. c Several profiles of the coupling kernel \(K_{1,2}\), defined by Eq. (5), for various levels of inhibition determined by the value of the level of inhibition parameter \(\omega\) specified in the legend. d A hypothesized wave generation mechanism. Distal brain areas activate local inhibitory interneurons in the cortex. These inhibit layers II/III pyramidal cells. When the suppression is relived, a rebound-generated travelling wave propagates across layers II/III

Full size image

These neurons are coupled together through a center-surround coupling kernel inspired by previous work that showed rapid switching of local field potential (LFP) dynamics in the motor cortex (Heitmann et al. 2012, 2015). Although this is the first time that this particular kernel has been given a thorough analysis in a spiking model. In this center-surround kernel a neuron has a strong, local, excitatory connectivity and sparse long range inhibitory connectivity (see Fig. 1c). It has been previously shown such a pattern is ubiquitous in the cortex and is able to produce waves and synchrony in neuronal models (Ermentrout 1998; Ermentrout and Terman 2010). This kernel is then convolved with the network at each node to produce the synaptic coupling. This network structure was constructed to mirror efferent inhibitory inputs from distal brain areas which triggers propagation of spatiotemporal events as described by Fig. 1d.

Model description

In the network model developed, we use Izhikevich spiking neurons, equally spaced (i, j) on a square lattice of size \(N \times N\). The simplicity of this model allows for fast simulation of networks even up to the scale of the cortex (\(2.0 \times 10^6\)), using an ordinary workstation. Even though the model is phenomenological in nature, it is capable of spiking and rebounding upon stimulation. Its dynamics is governed by the following pair of ordinary differential equations,

$$\begin{aligned} \frac{dv}{dt}&= 0.04v^2 + 5v + 140 + SI_{syn} + I_{app} + D\xi \end{aligned}$$
(1)
$$\begin{aligned} \frac{du}{dt}&= p_{1}(p_{2}v - u), \end{aligned}$$
(2)

combined with an auxiliary after spike resetting, given by

$$\begin{aligned} {{\text {if }}} v \ge 30 {{\text { mV}}}, {{\text { then }}} v \leftarrow p_{3} {{\text { and }}} u \leftarrow u + p_{4} . \end{aligned}$$
(3)

The parameters (\(p_1,\ p_2,\ p_3,\ p_4\)) are chosen to generate a network of rebound spiking neurons (Izhikevich 2004) (see Table 1). The applied current (\(I_{app}\)) is a strong hyperpolarizing input applied for 1 ms in a symmetrical disc-shaped domain (25 units in diameter) in the center of the network. For some trials, Gaussian white noise (\(\xi\)), with a scaled noise intensity D is added. The synaptic input (\(I_{syn}\)) at time \(t_{m}\) is a two-dimensional (zero-padded) convolution of the (\(N \times N\)) matrix \(\varvec{C }\) of spikes and the (\(p \times p\)) coupling kernel matrix \(\varvec{K}\). An element of the spike matrix, \(\varvec{c}_{i,j}\), is 1 if the neuron in position \((i,j) \!\) spikes at time \(t_{m-1}\), and zero otherwise. The synaptic input is scaled by a parameter S, representing synaptic coupling strength. The coupling kernel is a convex combination of a Gaussian function (\(G^{[0]}(x; b)\), where b is related to the full width at half maximum) and its scaled nth derivative (\(G^{[n]}(x; b)\)), with \(\omega\) as a weight parameter. Based on the above, the synaptic input and the coupling kernel can be described mathematically by

$$\begin{aligned} I_{syn}&= {{\varvec{C}}}_{t_{m-1}} \, * \, {{\varvec{K}}}_{i,j}(\bar{x};\; b, \omega ) \end{aligned}$$
(4)
$$\begin{aligned} {{\varvec{K}}}_{i,j}(\bar{x}; b, \omega )&= \omega \, G_i(\bar{x};b) + (1 - \omega ) \, G_j( \bar{x} ; b ), \end{aligned}$$
(5)

where

$$\begin{aligned} G_n( \bar{x};b) = (-1)^{ \left\lfloor {\frac{n}{2}} \right\rfloor } \ \frac{(\frac{n}{2})!}{n!} \ \frac{d^n}{d\bar{x}^n} e^{-b\bar{x}^2} \end{aligned}$$
(6)

and \(\bar{x} = |x - x'|\) and n is even.

Numerical simulations and parameter values

A fixed time-step 2nd order Runge–Kutta method is ideal for conducting the computations due to its efficiency and accuracy (Hopkins and Furber 2015). The time step is kept small at 0.1 ms, in order to reduce numerical errors. The spatiotemporal activity patterns formed from the simulations are stable over a wide range of network sizes. A standard network size of 100 \(\times\) 100 neurons is used for all simulations unless otherwise stated.

In order to quantify the effect of inhibitory and excitatory (I/E) connections, the ratio of signed volumes (\(D^- = \{x:G_n < 0 \}, D^+ = \{x:G_n > 0 \}\)) is calculated for various kernels, as follows

$$\begin{aligned} {{\text {I/E balance}}} = \frac{\iint _{{{{\mathbf {D}}}^-}}^{ }G_{n}( \bar{x} ; b) \, dx}{\iint _{{{{\mathbf {D}}}^+}}^{ }G_{n}( \bar{x} ; b)\, dx}. \end{aligned}$$
(7)

This I/E balance ratio is an important determinant of the types of spatiotemporal patterns that form.

Parameter values of the neuronal and network models are adapted from (Izhikevich 2003). For the whole list of parameter values, see Table 1.

Table 1 Neuronal and network parameters
Full size table

Spatiotemporal pattern classifier

We use a machine classification approach to tackle the problem of sorting and labelling large number of simulations. Several potential features are examined before selecting a subset of them (see Table 2 for a summary of all considered features). The details of feature selection are explained in the “Results” section.

Classification features and training data

First, we use common statistical measures such as the median and range computed across all time points and for every neuron in the network. These provide excellent coarse-grained information about the magnitude of activity present. Second, in order to take a measure of the temporal change in activity, a kymograph (Ghai 2012) is produced for each simulation. This is a plot comprised of concatenated 1-D slices from each \(N \times N\) frame, which, in effect, transposes moving fronts of activity into curves (see Fig. 2 as an example). For target waves, these curves follow a tight linear or quadratic form. The length of a curve indicates the distance the wave travels, while the curvature can be measured to determine wave speed. Finally, gaps in the kymographs indicate quiescent periods in the simulations. The total of these quiescent periods is the quiescence measure.

Fig. 2
figure 2

Kymographs of network simulations as the weight parameter (\(\omega\), shown above each kymograph) is varied from top-left to bottom-right in each panel. Each kymograph is N units tall, and consists of concatenated vertical cross-sections every millisecond for 200 ms. a In the presence of high synaptic strength (\(S = 15\)), spatiotemporal pattern varies from synchrony (solid yellow), to “granular” waves (mottled yellow), to travelling bumps (bumpy texture). Asterisk indicates pinning phenomenon, where quiescence occurs between the dashed lines. b In the presence of low synaptic strength (\(S = 5\)), the curvature in the kymographs increases, indicating that wave speed diminishes as \(\omega\) increases. At higher values of \(\omega\), waves do not make it to the edge of the network, or do not start at all. (Color figure online)

Full size image
Table 2 List of features to identify spatiotemporal patterns
Full size table

Third, we employ a common technique for summarizing 3D (i.e., x, y, t) data by computing the intensity projections of our simulations. For each neuron at location (i, j), we calculate the median value for all time points (see Table 2). The median intensity projection can then be thought of as a texture. This texture can be analyzed using Haralick features (Haralick et al. 1973), which were developed to give numerical values to intuitive aspects of an image. Haralick features are computed using the MATLAB graycomatrix, and graycoprops functions.

Before feeding the features into a classifier, it is trained on a set of manually categorized simulations. We have sorted 441 simulations (200 ms each) into eight categories of interest: (I) quiescence, where the network is not excited by a stimulus with lasting effect; (II) “slow” smooth waves, that propagate smoothly and have a wavefront in tens-of-millisecond timescale (comparable to real data); (III) “fast” smooth waves, that have few millisecond timescales; (IV) slow “granular” waves, that propagate in a lurching manner and have discontinuous wavefronts; (V) fast granular waves; (VI) “pinning”, where the network has intermittent quiescence; (VI) travelling wavelets (or “bumps”); and (VIII) whole network synchrony. Representative kymographs for these eight categories are shown in Fig. 2. The distinction between smooth and granular waves is clear when comparing the bottom row of Fig. 2a and the top row of Fig. 2b. This obvious qualitative difference leads us to consider these wave events as separate types.

In total, parameters representing synaptic strength, noise, kernel width, kernel order, and level of inhibition (denoted by S, D, b, n and \(\omega\), respectively) are varied in 200 ms simulations. An example of the parameter regimes associated with the eight categories identified when varying synaptic strength S and level of inhibition \(\omega\) are shown as intensity projections in Fig. 3. For each simulation, the selected features of Table 2 are extracted and input into the classifier.

Fig. 3
figure 3

Classification of spatiotemporal patterns. a level of inhibition (\(\omega\)) and synaptic strength (S) are varied on the abscissa and ordinate respectively. Each square represents a median intensity projection of the entire network for 200 ms of simulation time. Qualitatively different spatiotemporal patterns are present. b Categorization of activities seen in a: (I) no activity (purple), (II) slow smooth waves (blue), (III) slow granular waves (pink), (IV) fast smooth waves (yellow), (V) fast granular waves (teal), VI) pinning (orange), (VII) travelling bump field (lime green), and (VIII) synchrony (red). c Five examples of spatiotemporal patterns; from left to right, smooth target waves, granular target waves, synchrony, quiescence, and travelling bumps. All snapshots are taken at representative time points to showcase the qualitative patterns and are labelled with their parent category number. (Color figure online)

Full size image
Table 3 Parameter values for representative spatiotemporal patterns
Full size table

Classifier algorithm

We have chosen the random forest algorithm out of a panel of other methods (e.g., support vector machines, naive Bayes and simple decision trees) as it produces the lowest error rates during validation. The MATLAB treebagger function is used to create a random forest classifier as it performs automatic cross-validation (fivefold) and also reports an error for the overall classifier (i.e., “out-of-bag error” or OOB error). In short, for every decision tree in the forest (100 total), observations are partitioned based on threshold values for each feature. Each individual tree only consists of a subset of features, and is trained only on a subset of observations. This subset approach makes the random forest resistant to overfitting when compared to other classification algorithms (Breiman 2001).

The final set of selected features are shown in Table 2, and consist of six individual measures in four types: (1) summary statistics of the simulation across time; (2) a texture analysis feature (Haralick et al. 1973); (3) features based on the kymograph representation of the simulations; and (4) the number of independent clusters of activity (or “connected components”), quantified using the MATLAB bwconncomp function). Before computing the features, the network simulation is downsampled to a total of 80 total frames, for computational efficiency. The pixel values for each frame are normalized by the maximum from the entire set of frames. The classification process is blind to the type of simulated or experimental data given, as long as the data can be represented as magnitude values at discrete points on a lattice.

Software

The network model and classification algorithm are coded in MATLAB (MathWorks Inc., Massachusetts, USA) versions 2017(a,b) and 2018a. Software is run on a DELL Precision Tower 5810 (Intel Xeon CPU E5-1630 @ 3.7 GhZ, with 32 GB of RAM). The codes used for the classifier and producing the simulations can be obtained online (Oprea et al. 2019).

Results

Spatiotemporal patterns in the Izhikevich-based neuronal network

Snapshots of some of the spatiotemporal patterns produced with the model network are shown in Fig. 3c. In this case, a network of forty thousand Izhikevich neurons (\(200 \times 200\)) are simulated with several coupling parameters. In every panel, the same standard central hyperpolarizing stimulus is applied, and all other parameters are held constant except for the kernel parameters (\(\omega , S, b, n, {{\text {and}}} \ D\)). The important parameter values for each panel in Fig. 3c are shown in Table 3.

The network model in this framework produces 8 distinct spatiotemporal activities. Target waves are generated as rebound events in the excitable network (see Fig. 3c, II). An inhibitory input at the center of the network transiently produces a travelling wave of activity. Although, the stimulus is only for one millisecond at \({{\mathrm{t}}} = 0\), several wave-fronts are formed. Interestingly, when low amplitude Gaussian white noise is added, these waves are followed transiently by a long period of whole network synchrony (Fig. 4). What makes these fast transient transitions between target-wave activity to synchrony peculiar is that they spontaneously occur without stimulus.

Fig. 4
figure 4

Network spiking during spontaneous transition from wave to synchrony. a Time series of network spiking showing the action potential-like structure of the waveform transitioning to synchronous activity. After 500 ms, recovery from refractoriness allows for a greater peak amplitude in subsequent spikes. b Snapshots of the 2D network model with a central stimulus, inducing network spiking in the form of initially target wave (two left panels) followed by a whole network synchrony (two right panels), caused by noise-induced threshold crossing

Full size image

These network spikes are spontaneous, random synchronization events of a network of coupled neurons. They arise in networks that are otherwise homogeneous except for small differences in connectivity. The generator for each synchronous event changes over time as other sub-populations take on the role. The network spiking observed in the model presented here is due to the interaction of random noise with the slow recovery variable u. The slow return to baseline of the recovery variable prevents sub-populations that have had significant recent firing activity from firing again.

When considering the wave activity of this Izhikevich-based network model, we find that the speed of these waves depends on several parameters, particularly the scaling factor that represents the strength of synaptic coupling S and the level of synaptic noise D. Indeed, by selecting parameter regimes that correspond to target waves, the speed of the these waves can be increased arbitrarily by increasing the coupling strength. Depending on the coupling kernel used, spiral waves can be also produced with up to several rotors. A striking form of activity that can be seen, is the self-replicating travelling wavelets (“bumps”) produced using the 2nd order Gaussian derivative (a.k.a. “Mexican hat” or “Ricker”) kernel (Fig. 3c, VII). These are created from the rebounding effect of the network. Wavelets come into existence in areas that have recently been passed through by the inhibitory “tails” of another wavelet. These wavelets are reminiscent of travelling bumps obtained in neuronal field models (Pinto and Ermentrout 2001) where they have been hypothesized to play a role in working memory (Lu et al. 2011), and have been shown to appear in a variety of brain areas (Wu et al. 2008; Prechtl et al. 1997; Ermentrout and Kleinfeld 2001).

Feature selection and classifier error

We have designed a machine classification algorithm to automatically identify the various activities based on a set of features (see “Classification features and training data” Section). Features are selected from a larger bank of possible metrics: (1) common statistics which include: mean, sum, median, range, variance, skewness (asymmetry of distribution), and kurtosis (“peakedness” of the distribution). Each of these are applied to a vector of voltage values across time. (2) Measures of kymographs: that include fit to a quadratic (indicating curvature), slope of the fit (speed of the activity), and quiescent duration. (3) Firing time histograms: these provide mean and skewness measures of the temporal spiking activity. (4) The number of isolated areas of activity (connected components). (5) Haralick texture features: that includes entropy (randomness of the image), homogeneity (consistency across the recording), correlation (how correlated a pixel is to its neighborhood), energy (uniformity in the image) and contrast (intensity contrast between a pixel and its neighborhood) (Haralick et al. 1973).

In a random forest, prediction time increases with the number of features. We therefore wish to reduce the classifier input to as few predictors as possible. We are able to eliminate a large number of the initial feature set by removing instances of high correlation between features, as these do not convey any additional information (results not shown). Eleven features are considered for further evaluation (see Fig. 5a). Due to the relatively low number of feature combinations that need to be tested (\(2^{11}\)), all possible subsets are compared in a brute force search for the lowest classification error (see Fig. 5b). Additional feature selection techniques show similar results, such as forward selection, backward selection, and principal component analysis. The OOB error, is an error measure of the MATLAB function treebagger. As indicated by Fig. 5b, after 6 features, the marginal benefit of adding another feature to the classifier is low. A list of six features that occur most frequently in high performing subsets (see Fig. 5a) are chosen. They are quiescent duration, homogeneity, speed, median, range and connected components. With these six features, observations are classified at a rate of about 2200 observations per second at an average accuracy of 94.4%. Therefore even an increase in input size from 1000 to 10,000 observations would only take 4 seconds longer to fully classify.

Fig. 5
figure 5

Results of brute force feature selection obtained by constructing a random forest of every possible combination of the strongest 11 features. a Frequency of features in the best performing random forests. b The OOB error reported for each set of features (each circle represents one member of the power set of features). The dashed line shows the general decreasing trend of the OOB error upon the addition of more features. Notice that inserting additional features to a set of 6 existing ones marginally improves the OOB error

Full size image

Classifier allows rapid parameter regime exploration

The machine classifier is used to scan parameter space in order to find regimes where waves and synchrony (the two most prominent activity types seen in experimental recordings) are adjacent to each other and thus allow for fast transitions between the two. Fast switching between these activity types can be produced by perturbing the network through a stimulus Heitmann et al. (2012). If waves and synchrony regimes are adjacent in parameter space, it should only require a small perturbation to induce this effect. This is different from the spontaneous switching characterized earlier. The kernel width (b), the synaptic strength (S), the level of inhibition (\(\omega\)), and the kernel order (n) parameter values are scanned in parameter space to find such a domain. Each of the activity types shown in Fig. 3b can be recognized within the parameter ranges considered for the level of inhibition \(\omega\) and synaptic strength S, (see Fig. 6a). In the three kernel orders tested (\(n = 2, 4, 8\)) with kernel width \(b=0.025\), synchrony and waves dominate at low levels of inhibition, while quiescence and wavelets dominate at higher levels. Increasing the kernel order gradually expands the regimes associated with synchronous and smooth waves at the expense of the other categories. This indicates that inhibition decreases the spatial extent of spatiotemporal phenomena, as exemplified by travelling bumps at high values of omega.

Based on this, we limit our search to inhibitory levels below \(\omega = 0.60\), in order to focus on regimes where smooth waves and synchrony are present. The Gaussian derivative kernel is kept at the fourth order, \(n = 4\), due to the smaller quiescent regime. We find that wave and synchronous activities are all present for the entire range of synaptic input, with the quiescent regime gradually diminishing at higher width values until it eventually disappears (Fig. 6b). As before, increasing the width or order of the coupling kernel makes the wave and synchronous regimes dominate over other regimes of activities within the parameter space and allow them to become adjacent to each other. In particular, moderate levels of inhibition have the smooth slow wave and synchronous regimes closest at low coupling strength values. These results thus provide insights onto possible coupling topologies required to produce stimulus-induced fast switching between synchrony and travelling waves through post-inhibitory rebound. This type of stimulus-induced switching should be distinguished from that induced by noise in a spontaneous manner.

Fig. 6
figure 6

The regimes of spatiotemporal patterns obtained when various model parameters are varied, showing how these parameters affect model outcomes. The various regimes of behaviour obtained when varying a the coupling strength (S) and the level of inhibition (\(\omega\)) at different values of the order of the coupling kernel (n) specified on the top of each panel, and b the coupling strength (S) and width of the kernel (b), at different levels of inhibition (\(\omega\)) specified on the top of each panel. The width of the Gaussian kernel parameter is kept fixed at \(b=0.025\) in a while the order of the coupling kernel is kept fixed at \(n=4\) in b. The various activities produced by the model are color-coded according to the color-bar shown to the left of each panel. (Color figure online)

Full size image

Classifier outputs follow inhibitory/excitatory balance contours

As suggested before, the inhibitory components of the Gaussian kernel affect the spatiotemporal activities of the network model significantly. To investigate this further, we examine the effect of kernel order on the types of activity produced (recall that higher order coupling kernels possess smaller inhibitory contributions). Although center-surround patterns greater than that represented by the 4th order kernel (i.e., center—near surround—far surround) are less likely to be realistic topologies in vivo, the ease of parameter scanning with the classifier allows us to explore them. We use moderate coupling strength and kernel width values (i.e., \(S = 10\), and \(b = 0.025\)) in order to narrow the focus on wave behaviour. Our results reveal that kernel order has an intriguing nonlinear relationship with the level of inhibition (Fig. 7a). At low orders, less manipulation of \(\omega\) is required to transition between spatiotemporal states, even though smooth slow waves exist at all kernel orders.

Fig. 7
figure 7

The relationship between kernel order, level of inhibition, and spatiotemporal patterns. a The output of the classifier, identifying the spatiotemporal activities of the network model when kernel order (n) and the level of inhibition (\(\omega\)) are varied, with each pattern color-coded based on the color-bar to the right. Here, synaptic strength and kernel width are kept fixed at intermediate values. b The heatmap of the I/E balance, measured as the ratio of volumes under the surface of the coupling kernel, when the level of inhibition and kernel order are varied within the same ranges as in panel a. The heatmap is color-coded based on the color-bar to the right. Note the correspondence between the specific I/E values marked with white contours, and edges of spatiotemporal regimes in panel a. (Color figure online)

Full size image

In order to understand the nonlinear effects of kernel order and level of inhibition, we measure the I/E balance in the network, quantified as the signed ratio of the volumes under the surface of the coupling kernel (see Eq. 7). This can be thought of as the synaptic contributions that excitatory and inhibitory connections have on the network. Thus higher values of \(\omega\) implies inhibitory dominance. Figure 7b shows that both parameters effect the I/E balance, but the effect of kernel order saturates after \(n = 10\). Note that due to the rebounding nature of this network, we see activity even at high levels of inhibitory dominance. Comparing the two panels, when inhibition is dominant, granular and (especially) travelling bump patterns dominate. In fact, the transitions between spatiotemporal regimes occur at specific values of the I/E ratio, with all other parameters kept equal, as seen by the contour curves in Fig. 7b. For instance, smooth waves cease to occur when the inhibition is more than about half as strong as excitation. Also, fast smooth waves transition to slow smooth waves when inhibition becomes more than 10% as strong as excitation. These results suggest that the balance between synaptic inputs is a determining factor in the patterns produced by this spiking rebounding network.

Discussion

In this study, we designed a fast and simple automated method to classify spatiotemporal activities of the Izhikevich-based neuronal network (associated with the eight types of activities identified). We show that moderate levels of the inhibition and small values of coupling strength bring the synchronous and smooth slow wave regimes adjacent to each other. Simulations in which travelling waves and synchronous regimes are adjacent in parameter space represent the most physiologically interesting ones as they allow perturbations (induced by stimuli or noise) to cause fast switching between them. Millisecond time-scale switching between synchrony and waves have been found in LFP recordings in both the motor (Heitmann et al. 2012) and visual (Zanos et al. 2015) cortices. In both of these cases, neuronal firing was altered.

A theoretical interpretation is that this places the system in a bistable state, in which (at least) two forms of computation may be switched between as needed. Directionally polarized dendritic arbors have been suggested as a mechanism by which layer II/III pyramidal cells may detect travelling waves (Heitmann et al. 2015). Therefore, on a scale larger than monosynaptic connections, neurons in a small brain region may send signals that change the computational properties of their neighbours (Muller et al. 2018). Our results detected by the machine classifier reveal that strong local excitatory coupling along with weaker peripheral inhibitory coupling are best suited to produce regimes where synchrony and travelling waves are adjacent.

Interestingly, adjacent parameter regimes produce spatiotemporal patterns similar to those seen in other experimental data. Our fast travelling waves exhibit a rapid albeit “lurching” manner of propagation. This is similar to waves observed in thalamic preparations (Golomb et al. 1996; Destexhe et al. 1996). This is a likely consequence of the rebounding nature of our network, as other rebounding and inhibition heavy network architectures have produced similar waves in 1D networks (Rinzel et al. 1998).

We additionally observe transient and spontaneous switching in the presence of noise that is stimulus independent. This type of switching is due to the nature of Izhikevich model that allows action potentials to occur through both inhibitory and excitatory stimulation. This effect is similar to network spiking behaviour, seen in in vitro plated pyramidal cells (Eytan and Marom 2006; Orlandi et al. 2013). Intriguingly, it appears that wave-like pacemaking may be a default state for neuronal cultures in the absence of strong input.

Certainly a biophysically accurate model such as Hodgkin–Huxley could produce rebound behaviour (Hodgkin and Huxley 1952). However this would be computationally infeasible given the size of the network we wish to construct. Two modified versions of the simple integrate-and-fire model may potentially be appropriate; integrate-and-fire-or-burst (Smith et al. 2000) and resonate-and-fire (Izhikevich 2001) both produce rebounding for some parameter regimes. However their computational efficiency advantage to the Izhikevich simple spiking model is minimal to none, and they have overall smaller repertoire of spiking patterns (Izhikevich 2004). We therefore expect our novel Guassian kernel-coupled spiking Izhikevich network to represent a good model to further explore spatiotemporal patterns in cortex-like networks.

One exciting outcome of using this network analysis approach, is that the classifier seems to have zeroed-in on some intrinsic property of the network that delineates spatiotemporal regimes. The inhibitory/excitatory balance was not an explicit part of any of the data features we considered. However, different levels of I/E balance tracked boundaries in two-parameter space. We also saw that other pairwise combinations of parameters show redundancy (notice the synchrony/fast-wave/slow-wave tend to always appear adjacent in Fig. 6). This finding suggests a future model optimization approach; namely, map the spatiotemporal regimes by automated classification, find combinations of parameters that produce greatest variety of patterns, then remove or combine the remaining parameters. Of course, the variety quantification and parameter removal could be automated as well. In this manner a complex model may be simplified with little user input.

The classifier itself possesses several strengths. First it is computationally inexpensive, performing 2200 per second; even large data-sets can be quickly run through the classifier on an average computer. Second, the features are simple to understand; they represent intuitive aspects of the 2D simulation videos. Third, the classifier does not depend on the type of data, or the size of the data. This is because the features are dimensionless statistics computed in a frame-wise manner. Fourth, we can update the classifier with additional data, features, or spatiotemporal categories to broaden its applicability. For example, the addition of Fourier/wavelet (Johannesen et al. 2010), or fractal features (Maeda et al. 1998), the latter of which have been found to pair well with Haralick texture features (Korchiyne et al. 2014), can be incorporated into the classifier.

Compared to other supervised learning algorithms, the random forest has relatively few hyperparameters, and therefore requires less optimization. Random forests are also unlikely to overfit (Breiman 2001). Since they consist of many decision trees independently labelling input data, the majority vote of the forest evens out outliers, leading to more robust classification (Breiman 2001). In comparison, support vector machines require an appropriate choice of kernel (linear, polynomial, radial basis function, etc. ) (Andrew 2000). In addition, the hyperparameters must be well chosen (e.g., regularization penalty, regularization strength, polynomial degree, gamma etc.) (Andrew 2000). This amount of extra optimization seemed unnecessary given the already high accuracy of the random forest.

Although our focus was on classification, it would be useful to implement a multilevel approach, where a cursory labelling pass finds interesting simulations to explore in more depth. Ideally one could implement an optical flow methodology (Townsend and Gong 2018) which can extract frame-by-frame information about the spatiotemporal phenomena. Since optical flow is more computationally expensive, a selection criterion should be provided.

The natural next step for spatiotemporal pattern analysis would be leveraging the full force of deep learning (in particular, convolutional neural networks, CNNs) that have exploded in popularity in the past few years. They have been applied to cancer diagnoses (Fakoor et al. 2013), chest pathologies (Bar et al. 2015), and EEG pathologies (Schirrmeister et al. 2017) among many other things. Of course, the major hurdle to developing CNN classifiers is the need for a large pre-existing databank of images for training. These exist for pathologies, but the community of cortical wave researchers have yet to organize a similar initiative. One potential downside of CNNs is that they are black boxes, while our random forest approach uses human-intelligible features.

These results emphasize that a simple machine classification approach can be a powerful tool in analyzing a rebounding network of excitable Izhikevich neurons. While simple, the network produces many spatiotemporal patterns similar to those found in experimental data. Our results are particularly relevant for studies where the computational cost of running simulations is low, but the parameter space is large and not easily tractable through analytical methods. As a future avenue, the algorithm could be adapted to analyzing stochastic experimental recordings by additionally implementing de-noising techniques.