Introduction

The analysis of many brain signals ranging from the microscopic scale of single neurons (Celletti et al. 1999; Segundo 2003) to the mesoscale of large neuronal populations within, e.g., cortical columns (Stam 2005; Myers and Kozma 2018) has reinforced the hypothesis of a nonlinear source of complexity in brain dynamics (Korn and Faure 2003). Single neuron experimental recordings show that precise neuronal discharges can be arranged in sequences of spikes that appear much more often than expected by chance (Abeles and Gerstein 1988; Tetko and Villa 2001; Reinoso et al. 2016). The relationship between subsequent action potentials forms complex patterns typically associated with nontrivial dynamics and fractal dimensionality   (Longtin 1993; Iglesias et al. 2007; Fukushima et al. 2007; Iglesias and Villa 2010). At the scale of neuronal dynamics, it has been hypothesized that complex information can be transmitted through neural networks (Asai et al. 2008), even in the presence of noise (Asai and Villa 2008), thanks to their sensitivity to the temporal precision in sequences of spikes.

Following the general encoding principle that neurons that are more strongly depolarized are going to fire earlier than the neurons that are less optimally stimulated (von der Malsburg and Schneider 1986; Singer 1993; Fries et al. 2008), synchronized inputs received by selected cell assemblies are able to generate waves of depolarization following the complex dynamics (Makarenko and Llinás 1998; Gollo et al. 2010; Qu et al. 2014) introduced by the input. Thus, subcortical inputs may ignite the activity producing oscillatory activity in a wide range of frequencies that may propagate throughout the cerebral cortex (Nunez 1995; Buzsáki et al. 2012). Neuronal oscillations suggest that the synchronization relationships between brain signals may be a sign for computation and communication (Singer 1999; Brette 2012; Malagarriga et al. 2015a, b). Experimental observations in electroencephalography (EEG) and magnetoencephalography (MEG) have revealed that event-related oscillations can be robust to perturbations and fluctuations in wave amplitude becoming markers of cognitive processing (Rubino et al. 2006; Gross et al. 2013; Tal and Abeles 2018; Tewarie et al. 2018). These studies suggest that amplitude and latency modulation of oscillations may be coupled to functional connectivity because increased amplitude would necessarily mean increased synchrony in the depolarization of the cell assemblies. In this way, functional brain networks should be able to reorganize and coordinate cortical activity at a high temporal resolution (Tal and Abeles 2018).

We analyze here the phase-amplitude responses of a cortical column, simulated by a neural mass model (Jansen et al. 1993), receiving a discrete time series of pulsed inputs. Using a mean-field approach, we investigate to what extent precise temporal information, carried by deterministic nonlinear attractor mappings, is filtered and transformed into fluctuations in phase, frequency and amplitude of oscillatory brain activity. We explore the hypotheses that different classes of amplitude output wave peaks may form multiple point processes capable of transmitting dynamical features of the input time series and that amplitude threshold-filtering alone may also produce relevant point processes associated with the input dynamics. We show that the output activity produced by the neuronal mass model is highly dependent on the internal dynamics of the input point process and no same threshold or same amplitude criteria can be applied to the input dynamics. On the basis of our results, we suggest that local excitatory/inhibitory balance and excitability of cortical columns may contribute to set a fine tuning and gating of the ascending information in the cerebral cortex.

Methods

Neural mass model

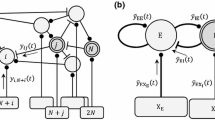
We consider here the Jansen-Rit model, a neural mass model (NMM) corresponding to a cortical column (Jansen et al. 1993; Jansen and Rit 1995). This model considers three interconnected neural populations formed by long projecting pyramidal neurons (population P), and two classes of local projecting neurons (interneurons) characterized by their excitatory (population E) and inhibitory (population I) feedback loops within the column. The E population projects to the P population, the I population projects to the P population, and in turn the P population sends projections to both E and I populations (Fig. 1). All values of the parameters chosen for the dynamical equations of this study are based on previous analyses (Malagarriga et al. 2014, 2015b).

The dynamics of a single NMM is based on a mean field approximation (Malagarriga et al. 2015b). Each excitatory coupling is described by a second-order differential operator \(L(y_{n}(t);a)\) transforming the mean input firing rate, \(p^j_m(t)\) from all j afferences, to a mean membrane potential \(y_n(t)\):

$$\begin{aligned} L(y_{n}(t);a) = \frac{d^2y_{n}}{dt^2} + 2a \frac{dy_{n}}{dt}+a^{2}y_{n} = Aa\left\{ \sum _j p_{m}^j(t)\right\} , \end{aligned}$$
(1)

where the subscript n refers to either excitatory populations P and E. Constant terms A and a are referred to excitatory couplings, with \(A=3.25\) mV corresponding to the maximum value of the excitatory postsynaptic potential and constant term \(a=100\,{\mathrm{s}}^{-1}\) associated with the membrane time constants and dendritic delays. The mean input firing rate \(p^j_m(t)\) is computed by a sigmoidal transfer function S of the net average membrane potential \(m^j(t)\) of all j afferences, that is \(p^j_m(t) = C_{i=1\ldots 4} S[m^j(t)]\). Coefficients \(C_1 = 133.5\), \(C_2 = 0.8C_1\), \(C_3 = 0.25C_1\) and \(C_4 = 0.25C_1\)) weight the synaptic efficiency. The sigmoidal transformation is such that

$$\begin{aligned} S[m^j(t)] =\frac{2e_{0}}{1+e^{r(\nu _{0} -m^j(t))}}, \end{aligned}$$
(2)

where \(e_0=2.5\,{\mathrm{s}}^{-1}\) is a value corresponding to the maximum firing rate of the neural population, \(\nu _0=6\) mV is a voltage reference associated with 50% of the firing rate, and \(r=0.56\,{\mathrm{mV}}^{-1}\) is the steepness of this sigmoidal transformation.

We can similarly define \(L(y_{n}(t);b)\), with subscript n referred to the population I of local inhibitory cells, and constant terms \(B=22\,{\mathrm{mV}}\) and \(b=50\,{\mathrm{s}}^{-1}\) referred to inhibitory couplings transforming the mean input firing rate \(p^k_m(t)\) to a mean membrane potential \(y_n(t)\):

$$\begin{aligned} L(y_{n}(t);b) = \frac{d^2y_{n}}{dt^2} + 2b \frac{dy_{n}}{dt}+b^{2}y_{n} = Bb\left\{ \sum _k p_{m}^k(t)\right\} , \end{aligned}$$
(3)

with \(p^k_m(t) = C_{i=1\ldots 4} S[m^k(t)]\) and \(m^k(t)\) the net average membrane potential of all k afferences to I.

In the absence of external inputs we consider that each column receives an excitatory input \({\bar{p}}=155\,{\mathrm{s}}^{-1}\) produced by a constant background mean firing rate. With all these elements, the equations of the model read:

$$\begin{aligned} \frac{d^2y_{P}}{dt^2} + 2a \frac{dy_{P}}{dt}+a^{2}y_{P}= & {} Aa\{S[y_E-y_I]\}, \end{aligned}$$
(4)
$$\begin{aligned} \frac{d^2y_{E}}{dt^2} + 2a \frac{dy_{E}}{dt}+a^{2}y_{E}= \,& {} Aa\{C_2S[C_1y_P]+{\bar{p}}\}, \end{aligned}$$
(5)
$$\begin{aligned} \frac{d^2y_{I}}{dt^2} + 2b \frac{dy_{I}}{dt}+b^{2}y_{I}= \,& {} Bb\{C_4S[C_3y_P]\} \end{aligned}$$
(6)

This model produces an internal oscillatory activity in the NMM centered on 10.8 Hz, which is a frequency that fits the alpha range of the EEG and LFP.

External inputs

In order to test the capacity of transmitting precise complex temporal information through cortical columns modeled by NMM, we have considered time series \(x_n\) of external pulses generated by the Chen and Ueta, Hénon, and Zaslavsky dynamical systems calculated in addition to the constant background frequency input. These dynamical systems were chosen on the basis of our previous studies at the neuronal scale dynamics (Asai and Villa 2008).

The Chen and Ueta (referred to as ChenUeta) system equations (Chen and Ueta 1999) can be writen as:

$$\begin{aligned} \frac{dx}{dt}= \,& {} a_{CU}(y-x) \nonumber \\ \frac{dy}{dt}= \,& {} (c_{CU}-a_{CU})x -xz + c_{CU}y \\ \frac{dz}{dt}= \,& {} xy - b_{CU}z, \nonumber \end{aligned}$$
(7)

where \(a_{CU}=35.0\), \(b_{CU} =3.0\) and \(c_{CU}=28.0\) and with initial conditions \(x(0)=3.0\) and \(y(0)=3.0\). We considered the Poincaré map defined by \(dz/dt =0\), with a tracking of x(t), whose discrete form provides the time series \({x_n}\).

The Hénon mapping (Hénon 1976) is defined by:

$$\begin{aligned} x_{n+1}= \,& {} 1 - a_{H}x_n^2 + y_n \nonumber \\ y_{n+1}= \,& {} b_{H}x_n, \end{aligned}$$
(8)

where \(a_{H}=1.15\) and \(b_{H}=0.3\). Iterations of the map allow to obtain the values of the point processes, corresponding to discrete time series \({x_n}\).

The equations for the Zaslavsky map (Zaslavsky 1978) are:

$$\begin{aligned} x_{n+1}= \,& {} x_n + v(1 + \mu y_n) + \epsilon v \mu \cos (x_n )\quad (mod. 2\pi ), \nonumber \\ y_{n+1}= \,& {} e^{-\gamma }(y_n + \epsilon \cos (x_n)-n), \end{aligned}$$
(9)

where \(x,y \in {\mathbb {R}}\), \(\mu = \frac{1-e^{-\gamma }}{\gamma }\), \(v = 400/3\), \(\gamma = 3.0\) and \(\epsilon = 0.1\). The initial conditions are \(x_0 = 0.3\) and \(y_0 = 0.3\). Iterations of the map allow to obtain the values of the discrete time series \({x_n}\).

For each dynamical system, we transform the information contained in the Poincaré sections (Parker and Chua 1989) defined by the 2D projection of the points \(x_n\), \(x_{n+1}\) of the dynamical systems into a new time series \(\omega _n\) derived to avoid negative values, as follows:

$$\begin{aligned} \omega _n = x_{n+1} - x_n + K, \end{aligned}$$
(10)

where K is a constant to make all values positive, i.e., \(K = min{(x_{n+1} - x_n)} + 0.1\). The time series \(\omega _n\) corresponds to the Inter-Pulse Interval (IPI) of the external input. Hence, from \(\omega _n\) we derive the time series \(t_k\), corresponding to the absolute times of occurrence of the external pulses. The time series \(t_k\) is used to transform the external input into the series of Gaussian-shaped pulses, Each cortical column receives a time dependent excitatory input \(I(t) = {\bar{p}} + p_{T}(t)\), where \({\bar{p}}\) is the mean background activity and \(p_{T}(t)\) is a mean spike density of Gaussian-shaped pulses described by

$$\begin{aligned} p_{T}(t) = \sum _k\xi \, e^{\left( \frac{t-t_k}{2\delta }\right) ^2 }, \end{aligned}$$
(11)

where \(\xi = 2\) Hz is a constant frequency, \(\delta =500\) ms is a time constant, and \(t_k\) corresponding to the timing of a specific train of external input pulses. The LFP generated by the NMM is \(y = y_E(t) - y_I(t)\), which is the signal that is analyzed further throughout this study (Fig. 1).

Fig. 1
figure 1

Representation of a cortical column (modeled as a NMM) receiving an input I(t) formed by a pulsed background input \({\bar{p}}\) and an external train of pulsed stimuli \(p_T(t)\) carrying temporal information. The integration of these inputs with the intra-columnar dynamics produces an output signal y(t), representing a mean Local Field Potential

Full size image

Computational analysis

The external input time series were generated with a time step resolution of 0.1 ms. All events falling within the interval 0–1 ms were ignored. The simulation of the model had an integration time step of 1 ms. We used Heun’s method to integrate the NMM model equations (García-Ojalvo and Sancho 1999) and a general purpose tool, called XPPAUT, for numerically solving and analyzing dynamical systems (Ermentrout 2002, 2012) to extract the Poincaré maps. Delay embeddings were constructed with a time delay of \(\tau =10\) ms. Different initial conditions were randomly set when performing multiple runs of the simulation. An initial period of 60 s was omitted, unless stated otherwise, to obtain stationary data and avoid any transient effect appearing at the begining of the simulation. Coding-related material and scripts may be requested via email to to “daniel.malagarriga@gmail.com”. The version used here uses several libraries publicly available and it is necessary to set carefully the operating system dependent environment.

Results

We consider the hypothesis that the LFP generated by the NMM filters external contributions and the output activity has wiped out much of the temporal information carried by the external inputs. Firstly, we examine some features of the external input pulse trains and the dependence on the phase delay with respect to intrinsic NMM dynamics. Secondly, we analyze the features of the distribution of the amplitudes of LFP peaks and the dynamics of the corresponding point processes. Thirdly, we analyze the dynamics of the output point processes generated by the sequences of LFP peaks filtered according to an amplitude thresholding operation.

Frequency and phase-related filtering

The three different dynamical systems were tuned in order to generate pulse trains with approximately the same pulse density. Input frequencies were computed over all inter-pulse intervals lasting at least 40 ms (i.e., corresponding to an instantaneous input frequency of 25 pulses/s) as shown in Fig. 2. The actual average (median) external input frequencies were equal to 4.09 (4.24), 4.74 (3.32), and 4.03 (2.53) pulses/s for ChenUeta, Hénon, and Zaslavsky maps, respectively.

Fig. 2
figure 2

Histograms of the input frequencies calculated over inter-pulse intervals lasting at least 40 ms for a Zaslavsky, \(n=14319\) intervals; b Hénon, \(n=15680\); and c ChenUeta, \(n=16835\), mappings

Full size image

The dynamics of the external Zaslavsky (Z.inp), Hénon (H.inp), and ChenUeta (C.inp) pulsed inputs are illustrated by the return maps in the interval 0–800 ms in Fig. 3a, c, e. These signals are processed and integrated with the internal dynamics of the NMM. The dynamics of the corresponding output signals, analog to LFPs, is shown by the delay embedding trajectories and selected Poincaré sections using a time delay of \(\tau =10\) ms (Fig. 3b, d, f). Notice the similarities in the Poincaré sections that suggest a strong filtering effect played by the intrinsic activity of the NMM, that is characterized by an oscillation at a frequency of 10.8 Hz.

Fig. 3
figure 3

Return map a of the external Zaslavsky pulsed input time series (Z.inp) fed to the NMM, in the interval 0–800 ms. The dynamics of the corresponding mean field LFP generated by the NMM b is illustrated by the time delay embeddings of the \(\tau =10\) ms and selected Poincaré section. Same graphics for Hénon (c, d) and ChenUeta (e, f) attractor maps. Notice that the intrinsic dynamics of the NMM determines the similarity between all Poincaré sections

Full size image

We investigate the effect of applying external pulses with respect to specific phase delays of the NMM oscillatory period (Fig. 4a). Two consecutive pulses were applied at characteristic phase delays (\(\pi /2\), \(\pi\), \(3\pi /2\), \(2\pi\), e.g. Fig. 4b, c). The output response was characterized by peaks with latencies translated into phase delays. Figure 4d shows the input–output phase difference for all combinations of first (IP1) and second (IP2) inter-pulse intervals. We observed that high amplitude peaks in the output signals were associated with pulsed inputs, whereas low amplitude peaks followed the internal dynamics of NMM. These results suggest that the output signals may peak at times that reliably follow the input dynamics, despite a filtering effect produced by the NMM internal dynamics.

Fig. 4
figure 4

a Pulsed inputs are introduced at specific phase delays with respect to intrinsic NMM oscillatory activity. For example, the first inter-pulse interval (IP1) at delay \(\pi /2\) and the second inter-pulse interval (IP2) at additional delay \(\pi\). b Example of two consecutive external pulses occurring at delays \(\pi /2\) and \(\pi /2\). c Example of two consecutive external pulses occurring at delays \(\pi\) and \(\pi\). d Input–output phase difference of the peaks corresponding to IP1 (solid line, red) and IP2 (dashed line, green) with all combinations of phase relations. (Color figure online)

Full size image

Distribution of LFP peak amplitudes

Fig. 5
figure 5

Amplitudes of the output LFP generated by a NMM after receiving an external input from temporally organized discrete time series generated from a Zaslavsky, b Hénon, and c ChenUeta attractor maps. Panel d shows the output of the NMM after receiving a Poisson generated time series with the same intensity. Each panel shows the peak amplitudes of the LFPs, between 600 and 4100 s from the begin of the simulation, and the corresponding probability density curves. The three highest peaks corresponding to the most representative amplitudes are marked by arrows in each panel

Full size image

We analyzed the peak amplitudes of the LFP signals generated by NMM and their distributions for the three dynamical system inputs and a control distribution represented by a Poissonian pulsed input train with a similar intensity of the other time series. Figure 5 shows that in all cases the internal dynamics of NMM generates a multimodal distribution of the LFP peaks. No LFP with amplitudes comprised between 4.75 and 7.25 mV were observed, irrespective of the external input time series. The three highest modes for each kind of pulse inputs, and their labels, are indicated on the probability density curves in Fig. 5, by Z1, Z2, Z3 for Zaslavky, and H1, H2 H3 for Hénon, and so on for ChenUeta and Poisson. All modes characterized by density higher than 0.07 in the probability density curves are presented in Table 1. In this Table it is interesting to notice that all most relevant modes (i.e. Z1, H1, C1 and P1) correspond to an LFP amplitude near 12.12 mV, irrespective of the dynamics of the external pulses. Notice that both modes Z2 and H2 correspond to the same amplitude near 11.12 mV (Fig. 5a, b). Modes C2 and C3 in ChenUeta and mode P2 in Poisson correspond to very low amplitudes of LFP, below 4 mV, in a range that is likely dominated by the background inputs rather than by external pulsed time series (Fig. 5c).

Table 1 Most relevant modes of the LFP amplitudes and corresponding density, computed on the probability density curves (Fig. 5)
Full size table

The finding that pulsed inputs from different time series were characterized by similar LFP amplitude modes raised the question whether those LFP waves were also characterized by a similar time distribution. Then, we have generated discrete point processes corresponding to the timings of all LFP waves having a peak amplitude falling within the interval \([\text {mode}-0.15, \text {mode}+0.15]\), which means three time series for the processes corresponding to modes Z1, Z2, Z3 and so on for the other input pulsed distributions. Figure 6 shows the superimposed autocorrelograms for such point processes. Processes Z1 and Z3 (Fig. 6a) show curves peaking at regularly spaced intervals corresponding to the average frequency of the input pulses (period \(\sim 250\) ms, i.e. \(\sim 4\) pulses/s, see Fig. 2). This pattern is very similar to the control condition represented by the Poissonian input pulse train (Fig. 6d) with all three P1, P2, and P3 point processes showing autocorrelogram peaks associated with the mean intensity of the process. Modes H1 and C1 were characterized by the same LFP amplitude of the other principal modes Z1 and P1. On the contrary to the expectations, their autocorrelogram showed limited (in case of H1) or almost no sign of period \(\sim 250\) ms, but periods of 374 and 380 ms in H1 (Fig. 6b) and \(\sim 385\) ms in C1 (Fig. 6c) were observed. It is also interesting to notice that modes Z2 and H2, although characterized by the same amplitude (Table 1), show a very different pattern of their autocorrelogram.

Fig. 6
figure 6

Autocorrelograms of the discrete point processes corresponding to the timings of the LFP peaks with amplitudes Z1–Z3, H1–H3, C1–C3, P1–P3 of Fig. 5. The vertical axis is scaled in rate units events/s following a Gaussian-shaped bin of 10 ms (Abeles 1982b). Notice that the scaling is different for each point process in order to facilitate the observation of peaking lags on the superimposed curves. the dashed grey curve corresponds to the main mode

Full size image

The differences among the various LFP modes is further illustrated by the return maps of the corresponding point processes in Fig. 7. The regular pattern observed for Poissonian inputs shows, in this case, that NMM filters out any time related information and retains only the mean intensity of the process. In the cases of Zaslavsky and ChenUeta pulsed inputs, the regular patterns appear to some extent in the return maps, in agreement with the observation made with the autocorrelograms. In case of Hénon input, even the point process derived from the principal mode of LFP shows less regularity. To this respect, it is interesting to compare the panels of the return maps corresponding to modes P1, Z1, H1, and C1 (Fig. 7 upper row) and observe the differences, despite the fact that these point processes correspond to LFPs characterized by the same amplitude. This analysis shows that selected LFPs according to the amplitudes carry different temporal information. The principal mode retains always an information associated with the mean intensity of the input process and additional information which is related to the time-dependent organization of the specific input pulsed train.

Fig. 7
figure 7

Return maps of the inter-pulse intervals (IPI) in the interval 0–3000 ms. For each panel, the black dots show the return map of the plain external input pulse train (P.inp, Z.inp, H.inp, C.inp). The red dots show the return map of the IPIs of the point process generated by the timings of the LFPs corresponding to the principal modes of amplitude (Fig. 5), noted in the legend of each panel. Notice that main modes P1, Z1, H1, and C1 are characterized by LFPs with the same amplitude, \(\sim 12.12\) mV

Full size image

LFP peak thresholding

Figure 5 has shown that the distributions of the LFP amplitudes show multimodal curves with commonalities and characteristic features for each input time series. We consider that an hypothetical threshold T may be set at the output channel of a NMM in order to filter the overall activity and transmit only selected output activity elsewhere in the brain. The thresholding operation is illustrated by Fig. 8. The outcome of this operation is a threshold-filtered point process (oft), labeled Z.oft, H.oft, C.oft and P.oft for Zaslavsky, Hénon, ChenUeta, and Poisson input pulsed trains. In order to determine whether the oft point processes retained temporal information of the corresponding input time series inp we generated a surrogate time series, as a control, by shuffling randomly the inter-pulse intervals of oft and producing a point process labeled sft, with the same first-order time statistics and totally scrambled higher-order timing relations.

Fig. 8
figure 8

Illustration of the procedure to obtain a threshold-filtered output point process and its corresponding surrogate time series, by shuffling inter-pulse intervals. In this example it is supposed that all mean field LFPs with an amplitude higher than a threshold T, here set \(T=18.5\) to exemplify, contribute to the output point process

Full size image

We analyzed the return maps of oft and sft output point processes as a function of increasing threshold values. In addition, we considered the output activity following the external input driven by the Poisson pulse train—i.e., P.oft—as a control point process for the nonlinear deterministic mappings. Each row of Fig. 9 shows the return maps, in the interval between 0 and 800 ms, of the point processes corresponding to the peaks of the output signals (big dots in red) filtered by the threshold value indicated on the left of the legend, for selected values of \(T \in [9.0, 11.0, 12.0, 12.5, 13.0, 15.0]\). The small black points for each panel of Fig. 9 correspond to the input point process, as indicated in the heading of the columns. If an output point process follows the dynamics of the input point process, the red dots should overlap, to a large extent, the black points. Notice that for threshold values up to \(T=12.0\) there is a majority of return intervals less than 400 ms for all time series, with little, if any, correspondence between input and output point processes. Threshold values from 12.0 to 13.0 show an increase in the overlap of the return maps between Z.inp versus Z.oft, H.inp versus H.oft, and C.inp versus C.oft.

Figure 9 shows also that the surrogate point processes Z.sft, H.sft, and C.sft show very limited with the corresponding input time series Z.inp, H.inp, and C.inp, but the overlap of several points suggest that 0-order time domain statistics might retain some information carried by the external pulses. The general picture offered by the return maps of the surrogate filtered point processes rather emphasizes the bias introduced by the internal dynamics of the NMM. The comparison between the Poisson output filtered point process P.oft and the nonlinear dynamical mappings Z.inp, H.inp, and C.inp shows that the overlap is almost null. On the contrary, Fig. 9 shows similarities between Z.sft, H.sft, C.sft with P.oft for threshold values \(T\ge 12.5\), as a consequence of the drive due to the internal dynamics of the NMM.

Fig. 9
figure 9

Return maps of the the inter-pulse intervals (IPI) in the interval 0–800 ms. For each panel, the black dots show the return map of the external input pulse train (P.inp, Z.inp, H.inp, C.inp) for Poisson, Zaslavsky, Hénon, and ChenUeta inputs, respectively. The red dots show the return map of the output generated point processes, labeled P.x, Z.x, H.x, and C.x with reference to Poisson, Zaslavsky, Hénon, and ChenUeta point processes, respectively. Labels x.oft, x.sft refer to output threshold-filtered (oft) and shuffled-filtered (sft) point processes (see Fig. 8). Each row shows the return maps for a specific value of the threshold T, from \(T=9.0\) (uppermost row) to \(T=15.0\) (lowermost row). For Zaslavsky, Hénon, and ChenUeta we show also a panel superimposing the return map of the inp IPIs and the corresponding Poisson triggered output threshold-filtered (P.oft) point process

Full size image

We introduce an index to measure the distance, within a delimited area in the return map space, between an output activity filtered point process and a reference input point process. Let us consider an input point process including \(N+1\) events and \(s_i\) denotes the time interval between the ith event and the \((i+1)\)th one. In a 2-dimensional Euclidean space we consider the return map formed by points \(S_i\) defined by coordinates \(s_i\) and \(s_{i+1}\), \(S_i = (s_i,s_{i+1})\). Let us consider the output activity point process X(T), filtered by threshold T and including \(K+1\) events. Let us denote \(x(T)_j\) the time interval between the jth event and the \((j+1)\)th one. The return map of the threshold-filtered output activity point process is formed by points \(X(T)_j = (x(T)_j, x(T)_{j+1})\). We compute the distance \(d_j^{X(T)}\) for any point j of the output activity map \(X(T)_j\) as its Euclidian distance to the closest point of the reference map \(S_i\), that is

$$\begin{aligned} d_j^{X(T)} = \min _{i=1}^{N} ( \root 2 \of {(x(T)_j - s_i)^2 + (x(T)_{j+1} - s_{i+1})^2} ). \end{aligned}$$
(12)

Then, we compute the distance

$$\begin{aligned} D_{X}^{T} = \displaystyle \sum _{j=1}^{K} d_j^{X(T)}. \end{aligned}$$
(13)

The distance of the threshold-filtered point process (oft) from the input point process should always be smaller than the distance computed for the corresponding shuffled-filtered point process (sft), if temporal information is retained in the interpulse intervals. Hence, for any threshold T a normalized index for the ChenUeta input point process is defined as \(\langle D_{C}^T \rangle = D_{C.sft}^T / D_{C.oft}^T\) and, in a similar way, the indexes \(\langle D_{H}^T \rangle\), \(\langle D_{Z}^T \rangle\) for Hénon and Zaslavsky input point processes, respectively. In addition, the distance computed for oft should also be smaller than the output activity if the input were triggered by a Poissonian process given the same threshold T, i.e. compared to P.oft. On this basis, we defined another distance index \(\langle {\tilde{D}}_{C}^T \rangle = D_{P.oft}^T / D_{C.oft}^T\) for the ChenUeta input point process, and indexes \(\langle {\tilde{D}}_{H}^T \rangle\), \(\langle {\tilde{D}}_{Z}^T \rangle\) for Hénon and Zaslavsky input point processes, respectively.

We have run the simulations in order to get 10 realizations of each output threshold-filtered point process (oft) and for each one we have produced 10 independent shuffled point processes (sft). For each value of T, between \(T=7\) and \(T=19\), by steps of 0.5, we have rerun the simulations and computed the average normalized distances \(\langle D_{X}^T \rangle\) and \(\langle {\tilde{D}}_{X}^T \rangle\). Then, we computed the distances for any point \(X(T)_j\) with coordinates \(x(T)_j \le 700\,\mathrm {ms}\) and \(x(T)_{j+1} \le 700\,\mathrm {ms}\). For each value of T we computed the confidence intervals of the mean distance and estimated independently whether \(\langle D_{X}^T \rangle < 1\) and \(\langle {\tilde{D}}_{X}^T \rangle < 1\). The rationale is that both normalized distance indexes should be significantly lower than 1 if the oft point process retains some initial time information and is closer to the input nonlinear dynamic mapping than the sft and Poissonian P.oft point processes, given the same value of threshold.

Figure 10 shows the curves of the normalized distance indexes for all input dynamics as a function of threshold T. It is interesting to notice that in case of Zaslavsky Z.oft tended to retain some temporal structure for values \(10 \le T \le 17.5\) (Fig. 10a). We considered three levels of significance for these curves. The highest level, labeled (***), is reached if \(prob(\langle D_{X}^T \rangle < 1) \ge 0.99\)and\(prob(\langle {\tilde{D}}_{X}^T \rangle < 1) \ge 0.99\). The second level, labeled (**), is reached if \(prob(\langle D_{X}^T \rangle < 1\)or\(\langle {\tilde{D}}_{X}^T \rangle < 1) \ge 0.99\)and\(prob(\langle D_{X}^T \rangle < 1\)or\(\langle {\tilde{D}}_{X}^T \rangle < 1) \ge 0.95\). The third level of significance is lower than the previous two and is labeled (*): this level is reached if \(prob(\langle D_{X}^T \rangle < 1) \ge 0.95\)and\(prob(\langle {\tilde{D}}_{X}^T \rangle < 1) \ge 0.95\). According to the above criterion we considered as critical threshold levels only those values of T with both normalized distance indexes being significantly below 1. In case of Hénon mapping the critical values of T were observed in the interval 15.5–17.5 mV (Fig. 10b) and only from 18 to 19 mV for ChenUeta (Fig. 10c). These results show that NMM internal dynamics filtered the temporal structure of the input point process in a selective way, such that different thresholds should be applied to different input point processes in order to recover the temporal structure of interpulse intervals (IPIs).

Fig. 10
figure 10

Normalized distance indexes as a function of threshold values for output point processes generated by a Zaslavsky, b Hénon, and c ChenUeta attractor maps (see Fig. 8). An index between 1 and 0 means that the output threshold-filtered point process X.oft is characterized by a return map closer to the X input point process of stimulation pulses than the corresponding shuffled-filtered point process X.sft, for index \(\langle D_{X}^T \rangle\) (continuos lines), and closer than the control Poisson threshold-filtered point process P.oft, for index \(\langle {\tilde{D}}_{X}^T \rangle\) (dashed lines). Indexes greater than 1 (shaded area) mean that surrogate provide better results than actual time series. See text for the definition of the normalized indexes and for the explanation regarding the levels of significance represented by (***), (**), (*)

Full size image

Discussion

In this study we show, for the first time, that time-coded information, in the form of input pulses associated with nonlinear deterministic time series generated by chaotic mappings, can be reliably transmitted through LFP dynamics despite a complex gating and filtering operated by a NMM of cortical column (Jansen and Rit 1995; Wennekers 2008). This NMM is characterized by rhythmic activity when there is a constant input onto the system and may exhibit quasi-periodic or low dimensional chaotic behavior in the presence of oscillatory (Malagarriga et al. 2015a, b) or pulse-like periodic inputs (Spiegler et al. 2010). The frequency of oscillations is determined by the kinetics of the ensuing population dynamics and it was shown that the whole spectrum of EEG/MEG signals can be reproduced within the oscillatory regime of the NMM by simply changing the population kinetics (David and Friston 2003). We purposely avoided gamma-band frequencies after observing that the studied NMM filtered high frequency bands and no information could be retrieved from its output. The intrinsic dynamics of the NMM influences its capacity to transmit time-coded information because of a resolution limit due to the internal oscillatory dynamics and the resonant interaction with the input. The response of the system becomes highly irregular and highly dependent on the input pulse frequency (Spiegler et al. 2010). Time scales, in the range of the millisecond, imply pulse frequencies of about 10 pulses/s, which is in the range of the NMM dynamics (\(\sim 10\,{\mathrm{Hz}}\)).

It has been shown that stochasticity or chaos in oscillatory elements may play an important role in helping the systems explore small basins of attractor in the vicinity of their local dynamics (Rabinovich and Varona 2011). EEG recordings of healthy volunteers also have shown evidences of chaotic dynamics (Theiler and Rapp 1996; Andrzejak et al. 2001; Gao et al. 2011) with larger complexity than patients with brain dysfunction, such as Alzheimer’s disease (Deng et al. 2017; Nobukawa et al. 2019) or individuals with altered states of consciousness (Mateos et al. 2018). Mean-field approaches to NMM dynamics allow to find conditions for the emergence of deterministic chaos, and relate it to the properties of lumped parameters (Malagarriga et al. 2015b; Montbrió et al. 2015). Nevertheless, the role of irregular, chaotic-like dynamics in the brain is not yet clarified. We raise the hypothesis that such dynamics may be ignited by a nonlinear deterministic series of subcortical inputs fed to cortical columns. Complex spatiotemporal firing patterns have been described experimentally (Abeles 1982a; Villa and Abeles 1990; Villa and Fuster 1992; Abeles et al. 1993; Tetko and Villa 2001; Tal and Abeles 2016) and it was demonstrated that they can propagate with high accuracy in feed-forward networks (Asai et al. 2008; Asai and Villa 2012). Here, we have shown that pulsed inputs associated with Chen and Ueta (Chen and Ueta 1999), Hénon, (Hénon 1976) and Zaslavsky (Zaslavsky 1978) dynamical systems can be processed by a Jansen and Rit oscillator (Jansen and Rit 1995) generating a LFP whose phase pattern and wave amplitude—i.e., the dynamic oscillation signature—carry information contained in the original time series of input pulses.

In some cases, we have observed that point processes associated with selected wave amplitudes could be mainly determined by the internal dynamics of the NMM. For instance, we observed that the most frequent wave amplitudes produced by the Zaslavsky input followed a time distribution very similar to a stochastic (Poissonian) input with the same frequency (see Z1 and P1 in Fig. 6a, d). This finding indicates that the process operated by the NMM may be dominated by the internal dynamics and the NMM acts as an active filter of the temporal information embedded in the sequence of pulsed inputs. However, despite being characterized by the same amplitude (see Table 1), the most frequent wave amplitudes produced by ChenUeta and Hénon inputs displayed a much more complex temporal pattern of distribution (Fig. 6b, c). The physiological interpretation of this finding could be associated with the effect of synaptic plasticity, given the assumption that wave amplitudes scale with the intensity of the depolarization of selected targeted cell assemblies. Studies on memory formation and synaptic plasticity have demonstrated the importance of precise timing relations between the firings of interconnected neurons for use dependent synaptic modifications (Markram et al. 1997; Vogt and Hofmann 2012). Then, the most frequent wave amplitudes would be the best candidate to reinforce synaptic links through spike-timing dependent plasticity mechanisms (Guyonneau et al. 2005; Feldman 2012).

Virtual microcircuits with asynchronous communication protocols can be encoded into symbolic expressions that may give rise to cognitive processes (Bonzon 2017). Accurate selective transmission of population-coded information can be achieved after switching from an asynchronous to an oscillatory state (Akam and Kullmann 2010; Qu et al. 2014). The information can be extracted by means of band-pass filtering implemented with sparsely synchronized network oscillations and temporal filtering by feed-forward inhibition. It is interesting that the facilitation by homeostatic mechanisms that can dynamically regulate the Excitatory/Inhibitory (E/I) balance of brain networks on the basis of inhibitory synaptic plasticity has recently been proposed as a possible explanation of robust information extraction over long timescales (Abeysuriya et al. 2018). This view is also in agreement with the gating hypothesis of multiple signals in cortical networks, where locally evoked inhibition would cancel incoming excitatory signals as a function of fine tuning of the E/I balance by modulating excitatory and inhibitory gains (Vogels and Abbott 2009; Vogt and Hofmann 2012). Indeed, several studies suggest that regulation of the activity and firing dynamics of inhibitory neurons expressing Calcium binding proteins—e.g., parvalbumin (PV), calretinin, calbindin—by monaminergic and cholinergic inputs, from the brainstem and basal forebrain, is likely to be the main source of regulation of the E/I balance (Parnavelas and Papadopoulos 1989; Benes et al. 2000; Caillard et al. 2000; Reynolds et al. 2004; Schwaller et al. 2004; Manseau et al. 2010; Cutsuridis 2012; Furth et al. 2013). In particular, the GABAergic (PV)-positive neurons play a key role in regulating synchronous activity observed in the thalamocortical circuit (Carlén et al. 2012; Albéri et al. 2013; Lintas et al. 2013; Gruart et al. 2016). Long-range projecting GABAergic PV-expressing neurons in the neocortex (Lee et al. 2014) and hypothalamus (Lintas 2014) further emphasize inhibitory synaptic plasticity as an attractive candidate mechanism for controlling the dynamic state of cortical networks involved in gating transitions of awareness and non-conscious perception.

These evidences can be reconciled with an another finding presented in this study, that is the gating obtained by band-pass threshold-filtering. The state of local networks could be changed by neuromodulatory inputs with sufficient spatial and cellular selectivity to operate a fine tuning of the E/I balance. Such gain modulation can be achieved by flexible routing of neural signals and network oscillations (Akam and Kullmann 2010; Zylberberg et al. 2010). We observed that Zaslavsky inputs processed by the NMM produced output waves with any amplitude roughly between 10 and 17 mV with a dynamics sufficiently close to the original input time series (Fig. 10a). Conversely, the output activity after the Hénon input could be reliably retrieved for wave amplitudes falling into a narrower range, i.e. 15.5–17.5 mV (Fig. 10b), and above 18 mV after ChenUeta input (Fig. 10c). A parallel channel for information transmission that is minimally affected by asynchronous distracting inputs occur if the pattern of firing rates is reproduced in the pattern of oscillation amplitudes (Akam and Kullmann 2010). We have already reported that the internal dynamics of the NMM produces a resonance phenomenon that does not wipe out the entire temporal information of the pulsed input dynamical system time series. This phenomenon, akin of spontaneous oscillations generated by interneuron networks (Brunel and Hakim 1999; Whittington and Traub 2003), may convey sensitivity to modulated input patterns such to switch to an asynchronous state following the level of noise or heterogeneity in the temporal pattern of the input signal (Brunel and Hansel 2006). Modulated threshold-filtering gating may offer as a form of multiplexing for neural codes, when multiple inputs are oscillating in different amplitude bands and filtering at the appropriate amplitude can be used to extract selected information from the input pattern.

The gating mechanism we have suggested might also be interpreted as a kind of temporal multiplexing because it can be used to encode and transmit multiple attributes of the input pattern at different timescales. In this way it appears conceptually similar to the multiplexing encoding mechanism described for frequency band filtering, where stimuli that vary relatively slowly relative to the oscillation frequency can route signals with high accuracy (Akam and Kullmann 2010). Temporal multiplexing was also suggested to play a key role to enable disambiguation of stimuli that cannot be discriminated at a single response timescale and to allow the transmission of information in a stable and reliable way in presence of noise and variability (Myers and Kozma 2018; Panzeri et al. 2010). An interrelation between EEG signals and neural firing beyond simple amplitude covariations in both signals provided evidence for a neural basis for stimulus selective and entrained EEG phase patterns (Ng et al. 2013). Motor output and behavioral expression would come up with a state-dependency of temporal multiplexing determined by local interactions and regulatory mechanisms driven by neuromodulatory pathways (Abeles 2014; Vogt and Hofmann 2012).

A further important question posed by our results is how a network of cortical columns, with externally fed driving pulses associated to precise temporal features, can shape complex oscillatory activity in the brain. Oscillations in brain dynamics can travel along brain networks at multiple scales, transiently modulating spiking and excitability as they pass (Schroeder and Lakatos 2009; Ozaki et al. 2012; Muller et al. 2018). Traveling waves may save processing time via distributed information processing through networks of interconnected NMMs and serve a variety of other functions ranging from memory consolidation to binding activity across distributed brain areas (Brama et al. 2015; Tal and Abeles 2016). This feature may result into a mechanism of dynamic network formation in mesoscopic neural populations, where extracted complex spatiotemporal patterns may be a sign for an oscillation based coding paradigm. The next step will consist to study how accurate can be the transmission of dynamical system generated point processes fed to a NMM and transmitted to various topologies of interconnected cortical columns.