Delay-decomposing approach to robust stability for switched interval networks with state-dependent switching

Abstract

This paper is concerned with a class of nonlinear uncertain switched networks with discrete time-varying delays . Based on the strictly complete property of the matrices system and the delay-decomposing approach, exploiting a new Lyapunov–Krasovskii functional decomposing the delays in integral terms, the switching rule depending on the state of the network is designed. Moreover, by piecewise delay method, discussing the Lyapunov functional in every different subintervals, some new delay-dependent robust stability criteria are derived in terms of linear matrix inequalities, which lead to much less conservative results than those in the existing references and improve previous results. Finally, an illustrative example is given to demonstrate the validity of the theoretical results.

Introduction

Recently, a class of hybrid systems (Ye et al. 1998) have attracted many researchers’ significant attentions as they can model several practical control problems that involve the integration of supervisory logic-based control schemes and feedback control algorithms. As a special class of hybrid systems, switched networks (Brown 1989; Liberzon 2003) consist of a set of individual subsystems and a switching rule, play an important role in research activities, since they have witnessed the successful applications in many different fields such as electrical and telecommunication systems, computer communities, control of mechanical, artificial intelligence and gene selection in a DNA microarray analysis and so on. Therefore, the stability issues of switched networks have been investigated (Huang et al. 2005; Li and Cao 2007; Lian and Zhang 2011; Zhang and Yu 2009; Niamsup and Phat 2010). By using common Lyapunov function method and linear matrix inequality (LMI) approach, authors considered the problem of global stability in switched recurrent neural networks with time-varying delay under arbitrary switching rule in (Li and Cao 2007). However, common Lyapunov function method requires all the subsystems of the switched system (Liu et al. 2009) to share a positive definite radially unbounded common Lyapunov function. Generally, this requirement is difficult to achieve. The average dwell time method is proposed to deal with the analysis and stability of switched networks, which is regarded as an important and attractive method to find a suitable switching signal to guarantee switched system stability or improve other performance, and has been widely applied to investigate the analysis and stability for switched system with or without time-delay. In (Lian and Zhang 2011), employing the average dwell time approach (ADT), novel multiple Lyapunov functions were employed to investigate the stability of the switched neural networks under the switching rule depending on time. Generally speaking, switching rule is a piecewise constant function dependent on the state or time, most of existing works focus on stability for switched networks with switching rule dependent on time. Perhaps it is limited by existing method and technique, to the best of our knowledge, there are few scholars to deal with the robust stability (He and Cao 2008; Xu et al. 2012) for switched uncertain networks under state-dependent switching rule (Thanha and Phat 2013; Ratchagit and Phat 2011), despite its potential and practical importance.

Due to the finite switching speed of amplifiers, time delay especially time-varying delay is inevitably encountered in many engineering applications and hardware implementations of networks, it is often the main cause for instability and poor performance of system. Consequently, the stability of networks with time-varying delay is a meaningful research topic (Liu and Chen 2007). What the most we concern is how to choose the appropriate Lyapunov–Krasovskii functional, derive the better stability criteria, which can be shown that the results has less conservativeness. To reduce the conservatism of the existing results, new analysis methods such as free weighting matrix method, matrix inequality method, input–output approach are proposed. However, it is impossible to derive a less conservative result by using the common Lyapunov–Krasovskii functional, the delay central-point (DCP) method was firstly proposed in (Yue 2004), to solve the problem for robust stabilization of uncertain systems with unknown input delay. In this approach, introducing the central point of variation of the delay, the variation interval of the delay is divided into two subintervals (Zhang et al. 2009) with equal length. The main advantage of the method is that more information on the variation interval of the delay is employed, and the idea of delay-decomposing (Zhang et al. 2010; Zeng et al. 2011; Wang et al. 2012; Hu and Wang 2011; Wang et al. 2008) has been successfully applied in investigating the $H_{\infty}$ control and the delay-dependent stability analysis for discrete-time or continuous-time systems with time-varying delay, which significantly reduced the conservativeness of the derived stability criteria. In (Zhang et al. 2010), the delay interval [0, d(t)] was divided into some variable subintervals by employing weighting delays, the stability results based on the weighting delay method were related to the number of subintervals, and the size of the variable subintervals or the position of the variable points. Authors considered the exponential stability analysis for a class of cellular neural networks, constructed a more general Lyapunov–Krasovskii functional by utilizing the central point of the lower and upper bounds of delay, since more information was involved and no useful item was ignored throughout the estimate of upper bound of the derivative of Lyapunov functional, the developed conditions were expected to be less conservative than the previous ones (Wang et al. 2012). Up to now, there no results have been proposed for the switched uncertain systems with discrete time-varying delay based on the delay-decomposing approach. Therefore, it is of great importance to study robust stability of switched uncertain networks with interval time-varying delay.

Motivated by the aforementioned discussions, the purpose of this paper is to deal with the robust asymptotic stability problem for switched interval networks with interval time-varying delays and general activation functions, the activation function can be unbounded and the lower bound of time-varying delay do not need to be zero. Inspired by the (DCP) method in (Yue 2004), constructing new Lyapunov–Krasovskii functional decomposing the delays in integral terms, based on the strictly complete property of the matrices system the delay-decomposing approach, some new delay-dependent robust stability criteria are derived in terms of LMIs, which can be efficiently solved by the interior point method (Boyd et al. 1994). The main novelty of this paper can be summarized as following: (1) switching signal in the paper depends on state of networks. (2) consider the parameters fluctuation, a new mathematical model of the switched networks with parameters in interval is established, it become much closer to the actual model. (3) introduce the delay-decomposing idea and piecewise delay method, analyzing the variation of the Lyapunov functional in every different subintervals, some new delay-dependent robust stability criteria are derived. Note that the delay-decomposing approach has proven to be effective in reducing the conservatism.

The rest of this paper is organized as follows: In “Switched networks model and preliminaries” section, the model formulation and some preliminaries are presented. In “Main results” section, some delay-dependent robust stability criteria for switched interval networks are obtained. An numerical example is given to demonstrate the validity of the proposed results in “An illustrative example” section. Some conclusions are drawn in “Conclusion” section.

Notations Throughout this paper, R denotes the set of real numbers, R ⁿ denotes the n-dimensional Euclidean space, R ^m × n denotes the set of all m × n real matrices. For any matrix A, A ^T denotes the transpose of A, A > 0 (A < 0) means that A is positive definite (negative definite), * represents the symmetric form of matrix. $\dot{x}(t)$ denotes the derivative of x(t). Matrices, if their dimensions not explicitly stated, are assumed to have compatible dimensions for algebraic operations.

Switched networks model and preliminaries

Consider the interval network model with discrete time-varying delay described by the following differential equation in the form:

$$ \left\{\begin{array}{ll} \dot{y}(t)=-Ay(t)+B_{1}g(y(t))+B_{2}g(y(t-\tau(t))+u,\\ A\in{A_{l}},\quad B_{k}\in{B_{l}^{(k)}},\quad k=1,2, \end{array}\right. $$

(1)

where $y(t)=\left(y_{1}(t),\ldots,y_{n}(t)\right)^{T}\in R^{n}$ denotes the state vector associated with n neurons; $g(y)=\left(g_{1}(y_{1}),\ldots,g_{n}(y_{n}\right))^{T}{:}R^{n}\rightarrow R^{n}$ is a vector-valued neuron activation function; $u=\left(u_{1},\ldots,u_{n}\right)^{T}$ is a constant external input vector. τ(t) denotes the discrete time-varying delay. $A=\hbox{diag}(a_{1},\ldots,a_{n})>0$ is an n × n constant diagonal matrix, denotes the rate with which the cell i resets its potential to the resting state when being isolated from other cells and inputs; $B_{k}=(b_{ij}^{(k)})\in R^{n\times n}, k=1,2$, represent the connection weight matrices, and $A_{l}=[\underline{A},\overline{A}]= \{A=\hbox{diag}(a_{i}){:}\,0<\underline{a}_{i}\leq a_{i}\leq \overline{a}_{i},i=1,2,\ldots,n\}\,B_{l}^{(k)}=\left[\underline{B}_{k},\overline{B}_{k}\right] =\{B_{k}=(b_{ij}^{(k)}){:} \underline{b}_{ij}^{(k)}\leq b_{ij}^{(k)}\leq \overline{b}_{ij}^{(k)},\,i, j=1,2,\ldots,n\}$ with $\underline{A} =\hbox{diag}(\underline{a}_{1},\underline{a}_{2},\ldots,\underline{a}_{n}), \overline{A}=\hbox{diag}(\overline{a}_{1},\overline{a}_{2}, \ldots,\overline{a}_{n}), \underline{B}_{k}=(\underline{b}_{ij}^{(k)})_{n\times n}, \overline{B}_{k}=(\overline{b}_{ij}^{(k)})_{n\times n}$.

Throughout this paper, the following assumptions are made on the activation functions $g_{j}(\bullet),j=1,\,2,\ldots,\,n$ and discrete time-varying delay τ(t):

$(\mathcal{H}_{1})$: There exist known constant scalars $\check{l}_{i}$ and $\hat{l}_{i}$, such that the activation function g _j (•) are continuous on R and satisfy:

$$ \check{l}_{i} \leq\frac{g_{j}(s_{1})-g_{j}(s_{2})}{s_{1}-s_{2}}\leq \hat{l}_{i}\quad \forall s_{1}\neq s_{2}\in R,\quad j=1,2\ldots n $$

$(\mathcal{H}_{2})$: The time-varying delay τ(t) is differentiable and bounded with constant delay-derivative bounds:: $\tau_n\leq \tau(t)\leq \tau_N, \,\dot{\tau}(t)\leq \mu<1$, where τ _n , τ _N ,  μ are positive constants.

$(\mathcal{H}_{3})$: The time-varying delay τ(t) satisfies: τ _n  ≤ τ(t) ≤ τ _N , where τ _n , τ _N are positive constants.

Remark 1

In assumption $(\mathcal{H}_{2})$, the time-varying delay τ(t) is differentiable with the derivative less than 1, it is called ’slow delay’; when removing the derivability, τ(t) maybe show a large rate of change, hence, we call it as ’fast delay’. In this paper, we will discuss interval network model with slow delay and fast delay respectively.

The initial value associated with (1) is assumed to be y(s) = ψ(s), ψ(s) is a continuous function on [ − τ _N , 0]. Similar with proof of Theorem 3.3 in (Balasubramaniam et al. 2011), we can show that system (1) has one equilibrium point $y^{\ast}$ under the above assumptions, the equilibrium $y^{\ast}$ will be always shifted to the origin by letting $x(t)=y(t)-y^{\ast}$, and the network system (1) can be represented as follows:

$$ \left\{\begin{array}{l} \dot{x}(t)=-Ax(t)+B_{1}f(x(t))+B_{2}f(x(t-\tau(t)),\\ A\in{A_{l}},\quad B_{k}\in{B_{l}^{(k)}},\quad k=1,2, \end{array}\right. $$

(2)

where $f_{j}(x_{j}(t))=g_{j}(x_{j}(t)+y_{j}^{\ast})-g_{j}(y_{j}^{\ast})$, and $f_{j}(0)=0,\,j=1,2,\ldots,n$.

The initial condition associated with (2) is given in the form $x(s)=y(s)-y^{\ast}=\varphi(s)=\psi(s)-y^*,\,s\in[-\tau_{N},0]$. It is easy to see f(x(t)) satisfy the assumption $(\mathcal{H}_1)$.

Based on some transformations, the system (2) can be written as an equivalent form:

$$ \dot{x}(t)=-[A_{0}+E_{A}\Upsigma_{A}F_{A}]x(t)+[B_{10}+E_{1} \Upsigma_{1}F_{1}]f(x(t))+[B_{20}+E_{2}\Upsigma_{2}F_{2}]f(x(t-\tau(t)), $$

(3)

where $\Upsigma_{A}\in \Upsigma,\,\Upsigma_{k}\in \Upsigma,\,k=1,2$.

$$ \begin{aligned} \Upsigma&= \left\{\hbox{diag}\left[\delta_{11},\ldots,\delta_{1n},\ldots,\delta_{n1},\ldots,\delta_{nn}\right]\in R^{n^{2}\times n^{2}}: |\delta_{ij}|\leq1,\quad i,j=1,2,\ldots,n\right\}. \\ A_{0}&=\frac{\overline{A}+\underline{A}}{2},\quad H_{A}=\left[\alpha_{ij}\right]_{n\times n}=\frac{\overline{A}-\underline{A}}{2}.\quad B_{k0}=\frac{\overline{B}_{k} +\underline{B}_{k}}{2}, \quad H_{B}^{(k)}=\left[\beta_{ij}\right]_{n\times n}=\frac{\overline{B}_{k}-\underline{B}_{k}}{2}. \\ E_{A}&=\left[\sqrt{\alpha_{11}}e_{1},\ldots,\sqrt{\alpha_{1n}}e_{1},\ldots, \sqrt{\alpha_{n1}}e_{n},\ldots,\sqrt{\alpha_{nn}}e_{n}\right]_{n\times n^{2}}, \\ F_{A}&=\left[\sqrt{\alpha_{11}}e_{1},\ldots,\sqrt{\alpha_{1n}}e_{n},\ldots, \sqrt{\alpha_{n1}}e_{1},\ldots,\sqrt{\alpha_{nn}}e_{n}\right]_{n^{2}\times n}^{T}, \\ E_{k}&=\left[\sqrt{\beta_{11}^{(k)}}e_{1},\ldots,\sqrt{\beta_{1n}^{(k)}}e_{1}, \ldots,\sqrt{\beta_{n1}^{(k)}}e_{n},\ldots,\sqrt{\beta_{nn}^{(k)}}e_{n}\right]_{n\times n^{2}}, \\ F_{k}&=\left[\sqrt{\beta_{11}^{(k)}}e_{1},\ldots,\sqrt{\beta_{1n}^{(k)}}e_{n}, \ldots,\sqrt{\beta_{n1}^{(k)}}e_{1},\ldots,\sqrt{\beta_{nn}^{(k)}}e_{n}\right]_{n^{2}\times n}^{T}, \end{aligned} $$

where $e_{i}\in R^{n}$ denotes the column vector with ith element to be 1 and others to be 0.

System (3) can be changed as

$$ \dot{x}(t)=-A_{0}x(t)+B_{10}f(x(t))+B_{20}f(x(t-\tau(t)))+E\Updelta(t) $$

(4)

where E = [E _A , E ₁, E ₂],

$$ \begin{aligned} \Updelta(t)&=\left[\begin{array}{c} -\Upsigma_{A}F_{A}x(t)\\ \Upsigma_{1}F_{1}f(x(t)) \\ \Upsigma_{2}F_{2}f(x(t-\tau))\end{array}\right]\\ &=\hbox{diag}\{\Upsigma_{A},\Upsigma_{1},\Upsigma_{2}\}\left[\begin{array}{c} -F_{A}x(t)\\ F_{1}f(x(t)) \\ F_{2}f(x(t-\tau(t))) \end{array}\right], \\ \end{aligned} $$

and $\Updelta(t)$ satisfies the following matrix quadratic inequality:

$$ \begin{array}{c} \Updelta^{T}(t)\Updelta(t)\leq \left[\begin{array}{c} x(t)\\ f(x(t)) \\ f(x(t-\tau(t))) \end{array}\right]^{T}\left[\begin{array}{c} F_{A}^{T}\\ F_{1}^{T}\\ F_{2}^{T} \end{array}\right]\left[\begin{array}{c} F_{A}^{T}\\ F_{1}^{T}\\ F_{2}^{T} \end{array}\right]^{T}\left[\begin{array}{c} x(t)\\ f(x(t)) \\ f(x(t-\tau(t))) \end{array}\right]. \end{array} \\ $$

In this paper, our main purpose is to study the switched interval networks, it consists of a set of interval network with discrete time-varying delays and a switching rule. Each of the interval networks regards as an individual subsystem. The operation mode of the switched networks is determined by the switching rule. According to (2), the switched interval network with discrete interval delay can be described as follows:

$$ \left\{\begin{array}{l}\dot{x}(t)=-A^{\sigma}x(t)+B_{1}^{\sigma}f(x(t)) +B_{2}^{\sigma}f(x(t-\tau(t)),\\ A^{\sigma}\in{A_{l_{\sigma}}},\quad B_{k}^{\sigma}\in{B_{l_{\sigma}}^{(k)}},\quad k=1,2, \end{array}\right. $$

(5)

where $A_{l_{\sigma}}=[\underline{A}^{\sigma},\overline{A}^{\sigma}]= \{A^{\sigma}=\hbox{diag}(a_{i_{\sigma}}){:}\,0<\underline{a}_{i_{\sigma}}\leq a_{i_{\sigma}}\leq \overline{a}_{i_{\sigma}},i=1,2,\ldots,n\}\,B_{l_{\sigma}}^{(k)}=[\underline{B}_{k}^{\sigma}, \overline{B}_{k}^{\sigma}]=\{B_{k}^{\sigma}=[b_{ij_{\sigma}}^{(k)}]{:} \,0<\underline{b}_{ij_{\sigma}}^{(k)}\leq b_{ij_{\sigma}}^{(k)}\leq \overline{b}_{ij_{\sigma}}^{(k)},\,i, j=1,2,\ldots,n\}$ with $\underline{A}^{\sigma}=\hbox{diag}(\underline{a}_{1_{\sigma}}, \underline{a}_{2_{\sigma}},\ldots,\underline{a}_{n_{\sigma}})\,\overline{A}^{\sigma}=\hbox{diag}(\overline{a}_{1_{\sigma}}, \overline{a}_{2_{\sigma}},\ldots,\overline{a}_{n_{\sigma}})\,\underline{B}_{k}^{\sigma}=[\underline{b}_{ij_{\sigma}}^{(k)}]_{n\times n},\,\overline{B}_{k}^{\sigma}=[\overline{b}_{ij_{\sigma}}^{(k)}]_{n\times n}$.

$$ \begin{aligned} A_{0}^{\sigma}&=\frac{\overline{A}^{\sigma}+\underline{A}^{\sigma}}{2}, \quad H_{A}^{\sigma}=\left[\alpha_{ij_{\sigma}}\right]_{n\times n}=\frac{\overline{A}^{\sigma}-\underline{A}^{\sigma}}{2}. \quad B_{k0}^{\sigma} =\frac{\overline{B}_{k}^{\sigma}+\underline{B}_{k}^{\sigma}}{2}, \quad H_{B_{\sigma}}^{(k)}=\left[\beta_{ij_{\sigma}}\right]_{n\times n}=\frac{\overline{B}_{k}^{\sigma}-\underline{B}_{k}^{\sigma}}{2}. \\ E_{A}^{\sigma}&=\left[\sqrt{\alpha_{11_{\sigma}}} e_{1},\ldots,\sqrt{\alpha_{1n_{\sigma}}} e_{1},\ldots,\sqrt{\alpha_{n1_{\sigma}}} e_{n},\ldots,\sqrt{\alpha_{nn_{\sigma}}}e_{n}\right]_{n\times n^{2}}. \\ F_{A}^{\sigma}&=\left[\sqrt{\alpha_{11_{\sigma}}} e_{1},\ldots,\sqrt{\alpha_{1n_{\sigma}}}e_{n},\ldots, \sqrt{\alpha_{n1_{\sigma}}} e_{1},\ldots,\sqrt{\alpha_{nn_{\sigma}}}e_{n}\right]_{n^{2}\times n}^{T}. \\ E_{k}^{\sigma}&=\left[\sqrt{\beta_{11_{\sigma}}^{(k)}} e_{1},\ldots,\sqrt{\beta_{1n_{\sigma}}^{(k)}}e_{1}, \ldots,\sqrt{\beta_{n1_{\sigma}}^{(k)}} e_{n},\ldots,\sqrt{\beta_{nn_{\sigma}}^{(k)}} e_{n}\right]_{n\times n^{2}}. \\ F_{k}^{\sigma}&=\left[\sqrt{\beta_{11_{\sigma}}^{(k)}} e_{1},\ldots,\sqrt{\beta_{1n_{\sigma}}^{(k)}}e_{n}, \ldots,\sqrt{\beta_{n1_{\sigma}}^{(k)}} e_{1},\ldots,\sqrt{\beta_{nn_{\sigma}}^{(k)}}e_{n}\right]_{n^{2}\times n}^{T}. \\ \end{aligned} $$

$\sigma{:}R^{n}\rightarrow \Upgamma=\{1, 2, \ldots,N\}$ is the switching signal, which is a piecewise constant function dependent on state x(t). For any $i\in \{1, 2, \ldots,N\}\,A^{i}=A_{0}^{i}+E_{A}^{i}\Upsigma_{A}^{i}F_{A}^{i}\,B_{k}^{i}=B_{k0}^{i}+E_{k}^{i}\Upsigma_{k}^{i}F_{k}^{i}$, and $\Upsigma_{A}^i\in \Upsigma,\,\Upsigma_{k}^i\in \Upsigma,\,k=1,2$. This means that the matrices (A ^σ, B ^σ₁ , B ^σ₂ ) are allowed to take values, at an arbitrary time, in the finite set $\{(A^{1},B_{1}^{1},B_{2}^{1}), (A^{2},B_{1}^{2},B_{2}^{2}), \ldots, (A^{N},B_{1}^{N},B_{2}^{N})\}$.

By (4), the system (5) can be written as

$$ \dot{x}(t)=-A_{0}^{\sigma}x(t)+B_{10}^{\sigma}f(x(t))+B_{20}^{\sigma}f(x(t-\tau(t)) +E^{\sigma}\Updelta^{\sigma}(t), $$

(6)

where E ^σ = [E ^σ _A , E ^σ₁ , E ^σ₂ ]and $\Updelta^{\sigma}(t)$ satisfies the following quadratic inequality:

$$ (\Updelta^{\sigma}(t))^{T}\Updelta^{\sigma}(t)\leq \left[\begin{array}{c} x(t)\\ f(x(t)) \\ f(x(t-\tau(t))) \end{array}\right]^{T}\left[\begin{array}{c} (F_{A}^{\sigma})^{T}\\ (F_{1}^{\sigma})^{T}\\ (F_{2}^{\sigma})^{T} \end{array}\right]\left[\begin{array}{c} (F_{A}^{\sigma})^{T}\\ (F_{1}^{\sigma})^{T}\\ (F_{2}^{\sigma})^{T} \end{array}\right]^{T}\left[\begin{array}{c} x(t)\\ f(x(t)) \\ f(x(t-\tau(t))) \end{array}\right]. $$

(7)

To derive the main results in the next section, the following definitions and lemmas are introduced.

Definition 2.1

The switched interval neural network model (5) is said to be globally robustly asymptotically stable if there exists a switching function $\sigma(\cdot)$ such that the neural network model (5) is globally asymptotically stable for any $A^{\sigma}\in{A_{l_{\sigma}}},\,B_{k}^{\sigma}\in{B_{l_{\sigma}}^{(k)}},\,k=1,2$.

Definition 2.2

The system of matrices $\{G_{i}\}quad i=1,2,\ldots,N$, is said to be strictly complete if for every $x\in R^{n} \backslash \{0\}$ there is $i\in\{1,2,\ldots,N\}$ such that x ^T G _i x < 0.

Let us define N regions

$$ \Upomega_{i}=\{x\in R^{n}: x^{T}G_{i}x < 0\},\quad i=1,\,2 \ldots,\,N. $$

where $\Upomega_{i}$ are open conic regions, obvious that the system {G _i } is strictly completely if and only if these open conic regions overlap and together cover R ⁿ \ {0}, that is

$$ \bigcup_{i=1}^{N}\Upomega_{i}=R^{n} \backslash \{0\}. $$

Proposition 2.1

(Uhlig 1979)The system $\{G_{i}\},\,i=1,\,2, \ldots,\,N$, is strictly complete if there exist $\lambda_{i} \geq 0,\,i=1,\,2,\ldots,\,N,\,\sum\limits_{i=1}^{N}\lambda_{i}=1$, such that

$$ \sum\limits_{i=1}^{N}\lambda_{i}G_{i}<0. $$

Lemma 2.1

(Han and Yue 2007) Given any real matrix M = M ^T > 0, for any t > 0, function τ(t) satisfies τ _n  ≤ τ(t) ≤ τ _N , and $\dot{x(t):[-\tau_{N},-\tau_{n}]}\longrightarrow R^{n}$, the following integration is well defined:

$$ -(\tau_{N}-\tau_{n})\int\limits_{t-\tau_{N}}^{t-\tau_{n}} \dot{x}^{T}(s)R\dot{x}(s)ds\leq \left[\begin{array}{c} x(t-\tau_{n})\\ x(t-\tau_{N}) \end{array}\right]^{T}\left[\begin{array}{cc} -M &M\\ M &-M \end{array}\right]\left[\begin{array}{c} x(t-\tau_{n})\\ x(t-\tau_{N}) \end{array}\right]. $$

Lemma 2.2

(Zhang et al. 2009) For any constant matrices ψ₁ and ψ₂ and $\Upomega$ of appropriate dimensions, function τ(t) satisfies τ _n  ≤ τ(t) ≤ τ _N , then

$$ (\tau(t)-\tau_{n})\psi_{1}+(\tau_{N}-\tau(t))\psi_{2}+\Upomega<0 $$

holds, if and only if

$$ (\tau_{N}-\tau_{n})\psi_{1}+\Upomega<0, (\tau_{N}-\tau_{n})\psi_{2}+\Upomega<0 $$

In the following section, we use the generalized the DCP method, partition the interval delay into m subintervals with equal length, be some scalars satisfying

$$ \tau_{n}=\tau_{0}\leq\tau_{1}\leq\tau_{2}\leq \ldots \,\tau_{m}=\tau_{N} $$

Obviously, $[\tau_{n},\tau_{N}]=\bigcup\limits_{j=1}^{m}[\tau_{j-1},\tau_{j}]$. For convenience, we denote the length of the subinterval δ = τ _j  − τ _j-1, therefor, for any t > 0, there should exist an integer k, such that $\tau(t)\in[\tau_{k-1},\tau_{k}]$.

Remark 2

In this paper, we consider the case when m = 3, interval delay is decomposed into three subintervals: [τ _n , τ₁], [τ₁, τ₂], and [τ₂,τ _N ]. Let $\mathcal{S}_{1}=\{t|t>0,\,\tau(t)\in[\tau_{n},\tau_{1}]\}\,\mathcal{S}_{2}=\{t|t>0,\,\tau(t)\in(\tau_{1},\tau_{2}]\}\,\mathcal{S}_{3}=\{t|t>0,\,\tau(t)\in(\tau_{2},\tau_{N}]\}$, in the proof of our main results, applying a piecewise analysis method (Zhang et al. 2009) to check the variation of derivative of the Lyapunov functional in S1 S2 and S3 respectively.

Main results

In this section, the global robust asymptotic stability of the proposed model (5) will be discussed. By delay fractioning approach, designing a effective switch rule and constructing a suitable Lyapunov functional, a new robust delay-dependent criterion for the global asymptotic stability of switched network system (5) is derived in terms of LMIs.

$$ \begin{aligned}\,\hbox{Set}\; G_{i}(A_{0}^{i},Q_{1},Q_{2},Q_{3}) &=-(A_{0}^{i})^{T}P-PA_{0}^{i}+Q_{1}+Q_{2}+Q_{3},\\ \Upomega_{i}&=\{x\in R^{n}:x^{T}(t)G_{i}(A_{0}^{i},Q_{1},Q_{2},Q_{3})x(t)<0\}, \\ \bar{\Upomega_{1}}&=\Upomega_{1},\quad \bar{\Upomega_{i}}=\Upomega_{i}\backslash \bigcup\limits_{j=1}^{i-1}\bar{\Upomega}_{j}, \quad i=2,3,\ldots,\,N. \\ L_{1}&=diag\{\check{l_{1}}\hat{l_{1}},\check{l_{2}} \hat{l_{2}},\ldots,\,\check{l_{n}}\hat{l_{n}}\}\\ L_{2}&=diag\{\check{l_{1}}+\hat{l_{1}},\check{l_{2}} +\hat{l_{2}},\ldots,\,\check{l_{n}}+\hat{l_{n}}\}\\ N&=[N_{1}\,N_{2}\,N_{3}\,N_{4}\,N_{5}\,N_{6}\,N_{7}\,N_{8}\,N_{9}]\\ M&=[M_{1}\,M_{2}\,M_{3}\,M_{4}\,M_{5}\,M_{6}\,M_{7}\,M_{8}\,M_{9}]\\ S&=[S_{1}\,S_{2}\,S_{3}\,S_{4}\,S_{5}\,S_{6}\,S_{7}\,S_{8}\,S_{9}]\\ Z&=[Z_{1}\,Z_{2}\,Z_{3}\,Z_{4}\,Z_{5}\,Z_{6}\,Z_{7}\,Z_{8}\,Z_{9}]\\ X&=[X_{1}\,X_{2}\,X_{3}\,X_{4}\,X_{5}\,X_{6}\,X_{7}\,X_{8}\,X_{9}]\\ Y&=[Y_{1}\,Y_{2}\,Y_{3}\,Y_{4}\,Y_{5}\,Y_{6}\,Y_{7}\,Y_{8}\,Y_{9}]\\ \delta&=\frac{1}{3}(\tau_{N}-\tau_{n}), \,\tau_{1}=\tau_{n}+\delta,\,\tau_{2}=\tau_{n}+2\delta \end{aligned} $$

Theorem 3.1

Under the assumption $(\mathcal{H}_1)$ and $(\mathcal{H}_2)$, if there exist matrices P > 0,  T ₁ > 0,  T ₂ > 0,  Q _j  > 0,  R _j  > 0 (j = 1,  2,  3,  4) and diagonal matrices $\gamma_{k}=diag\{\gamma_{k,1},\,\gamma_{k,2}, \ldots,\,\gamma_{k,n}\}>0\,(k=1,\,2,\,3)$, and matrices $N_{l},\,M_{l},\,Z_{l},\,S_{l}(l=1,\,2,\,\ldots,\,9)$ with appropriate dimensions such that for all m and n, the following conditions hold:

• (i) $\exists\,\xi^{i}\geq 0, \quad i=1,\,2,\,\ldots, N, \quad\sum_{i=1}^{N}\xi^{i}=1: \sum_{i=1}^{N}\xi^{i}$ G _i (A ⁱ₀ , Q ₁, Q ₂, Q ₃) < 0.

• (ii)
  $$ \left[\begin{array}{cc} \Uppi^{i}+\Uptheta_{m}^{i} &\ast \\ \Upupsilon_{mn}^{i} & -R_{m}^{i} \end{array} \right]<0,\quad m=1,\,2,\,3,\quad n=1,\,2 $$

  (8)

  where

  $$ \Uppi^{i}=\left[\begin{array}{ccccccccc} \Uppi_{11}^{i} & \ast & \ast & \ast & \ast & \ast & \ast & \ast & \ast\\ R_{4} & -Q_{1}-R_{4} & \ast & \ast & \ast & \ast & \ast & \ast & \ast\\ 0 & 0 & -Q_{2} & \ast & \ast & \ast & \ast & \ast & \ast \\ 0 & 0 & 0 & -Q_{3} & \ast & \ast & \ast & \ast & \ast \\ 0 & 0 & 0 & 0 & -Q_{4} & \ast & \ast & \ast & \ast \\ 0 & 0 & 0 & 0 & 0 & \Uppi_{66}^{i} & \ast & \ast & \ast \\ \Uppi_{71}^{i} & 0 & 0 & 0 & 0 & 0 & \Uppi_{77}^{i} & \ast & \ast \\ \Uppi_{81}^{i}& 0 & 0 & 0 & 0 & \gamma_{3}L_{2} & \Uppi_{87}^{i} & \Uppi_{88}^{i} & \ast \\ (E^{i})^{T}P-(E^{i})^{T}\phi A_{0}^{i} & 0 & 0 & 0 & 0 & 0 &\Uppi_{97}^{i} &\Uppi_{98}^{i} &\Uppi_{99}^{i} \end{array} \right]<0, $$

  where

  $$ \begin{aligned} \Uppi_{11}^{i}&=T_{1}+(A_{0}^{i})^{T}\phi A_{0}^{i}+Q_{4}-R_{4}-\gamma_{2}L_{1}-L_{1} \gamma_{2}+(F_{A}^{i})^{T}F_{A}^{i} \\ \Uppi_{66}^{i}&=-(1-\mu)T_{1}-\gamma_{3}L_{1}-L_{1}\gamma_{3} \\ \Uppi_{71}^{i}&=L_{2}\gamma_{2}+(B_{10}^{i})^{T} P-\gamma_{1}A_{0}^{i}-(B_{10}^{i})^{T}\phi A_{0}^{i}+(F_{A}^{i})^{T}F_{1}^{i} \\ \Uppi_{77}^{i}&=\gamma_{1}B_{10}^{i}+(B_{10}^{i})^{T}\gamma_{1} +T_{2}-\gamma_{2}-\gamma_{2}^{T}+(B_{10}^{i})^{T}\phi B_{10}^{i}+(F_{1}^{i})^{T}F_{1}^{i} \\ \Uppi_{81}^{i}&=(B_{20}^{i})^{T}P-(B_{20}^{i})^{T}\phi A_{0}^{i}+(F_{A}^{i})^{T}F_{2}^{i} \\ \Uppi_{87}^{i}&=(B_{20}^{i})^{T}\gamma_{1}+(B_{20}^{i})^{T}\phi B_{10}^{i}+(F_{1}^{i})^{T}F_{2}^{i} \\ \Uppi_{88}^{i}&=-(1-\mu)T_{2}-\gamma_{3}-\gamma_{3}^{T}+(B_{20}^{i})^{T}\phi B_{20}^{i}+(F_{2}^{i})^{T}F_{2}^{i} \\ \Uppi_{97}^{i}&=(E^{i})^{T}\gamma_{1}+(E^{i})^{T}\phi^{T}(B_{10}^{i})^{T} \\ \Uppi_{98}^{i}&=(E^{i})^{T}\phi^{T}(B_{20}^{i})^{T} \\ \Uppi_{99}^{i}&=(E^{i})^{T}\phi E^{i}-I \\ \end{aligned} $$
  $$ \Uptheta_{1}^{i}=\left[\begin{array}{ccccccccc} 0 &\ast & \ast & \ast & \ast & \ast & \ast & \ast & \ast\\ \delta N_{1}^{T} & \delta N_{2}^{T}+\delta N_{2}^{T} & \ast & \ast & \ast & \ast & \ast & \ast & \ast\\ -\delta M_{1}^{T} & \delta N_{3}^{T}-\delta M_{2}^{T} & \Uptheta_{1_{33}}^{i} & \ast & \ast & \ast & \ast & \ast & \ast \\ 0 & \delta N_{4}^{T} & R_{2}-\delta M_{4}^{T} & -R_{2}-R_{3} & \ast & \ast & \ast & \ast & \ast\\ 0 & \delta N_{5}^{T} & -\delta M_{5}^{T} & R_{3} & -R_{3} & \ast & \ast & \ast & \ast \\ \delta M_{1}^{T}-\delta N_{1}^{T} & \Uptheta_{1_{62}}^{i} & \Uptheta_{1_{63}}^{i} & -\delta N_{4}^{T}+\delta M_{4}^{T} & \Uptheta_{1_{65}}^{i} & \Uptheta_{1_{66}}^{i}& \ast & \ast & \ast \\ 0 & \delta N_{7}^{T} & -\delta M_{7}^{T} & 0 & 0 & -\delta N_{7}^{T}+\delta M_{7}^{T} & 0 & \ast & \ast \\ 0 & \delta N_{8}^{T} & -\delta M_{8}^{T} & 0 & 0 & -\delta N_{8}^{T}+\delta M_{8}^{T} & 0 & 0 & \ast \\ 0 & \delta N_{9}^{T} & -\delta M_{9}^{T} & 0 & 0 & -\delta N_{9}^{T}+\delta M_{9}^{T} & 0 & 0 & 0\\ \end{array} \right]<0, \\ $$
  $$ \begin{aligned} \Uptheta_{1_{33}}^{i}&=-R_{2}-\delta M_{3}^{T}-\delta M_{3} \\ \Uptheta_{1_{62}}^{i}&=\delta N_{6}^{T}-\delta N_{2}^{T}+\delta M_{2}^{T} \\ \Uptheta_{1_{63}}^{i}&=-\delta N_{3}^{T}+\delta M_{3}^{T}-\delta M_{6}^{T} \\ \Uptheta_{1_{65}}^{i}&=-\delta N_{5}^{T}+\delta M_{5}^{T} \\ \end{aligned} $$
  $$ \Uptheta_{2}^{i}=\left[\begin{array}{ccccccccc} 0 &\ast & \ast & \ast & \ast & \ast & \ast & \ast & \ast\\ 0 & -R_{1}& \ast & \ast & \ast & \ast & \ast & \ast & \ast\\ \delta Z_{1}^{T} & R_{1}+\delta Z_{2}^{T} & \Uptheta_{2_{33}}^{i} & \ast & \ast & \ast & \ast & \ast & \ast\\ -\delta S_{1}^{T} & -\delta S_{2}^{T} & \delta Z_{4}^{T}-\delta S_{3}^{T} & \Uptheta_{2_{44}}^{i} & \ast & \ast & \ast & \ast & \ast \\ 0 & 0 & \delta Z_{5}^{T} & R_{3}-\delta S_{5}^{T} & -R_{3} & \ast & \ast & \ast & \ast\\ -\delta Z_{1}^{T}+\delta S_{1}^{T} & -\delta Z_{2}^{T}+\delta S_{2}^{T} & \Uptheta_{2_{63}}^{i} & \Uptheta_{2_{64}}^{i} & \Uptheta_{2_{65}}^{i} & \Uptheta_{2_{66}}^{i} & \ast & \ast & \ast \\ 0 & 0 & \delta Z_{7}^{T} & -\delta S_{7}^{T} & 0 & -\delta Z_{7}^{T}+\delta S_{7}^{T} & 0 & \ast & \ast \\ 0 & 0 & \delta Z_{8}^{T} & -\delta S_{8}^{T} & 0 & -\delta Z_{8}^{T}+\delta S_{8}^{T} & 0 & 0 & \ast\\ 0 & 0 & \delta Z_{9}^{T} & -\delta S_{9}^{T} & 0 & -\delta Z_{9}^{T}+\delta S_{9}^{T} & 0 & 0 & 0 \end{array} \right]<0, \\ $$
  $$ \begin{aligned} \Uptheta_{2_{33}}^{i}&=-R_{1}+\delta Z_{3}+\delta Z_{3}^{T} \\ \Uptheta_{2_{44}}^{i}&=-R_{3}-\delta S_{4}^{T}-\delta S_{4} \\ \Uptheta_{2_{63}}^{i}&=\delta Z_{6}^{T}-\delta Z_{3}^{T}+\delta S_{3}^{T} \\ \Uptheta_{2_{64}}^{i}&=-\delta Z_{4}^{T}+\delta S_{4}^{T}-\delta S_{6}^{T} \\ \Uptheta_{2_{65}}^{i}&=-\delta Z_{5}+\delta S_{5} \\ \Uptheta_{2_{66}}^{i}&=-\delta Z_{6}-\delta Z_{6}^{T}+\delta S_{6}+\delta S_{6}^{T} \\ \end{aligned} $$
  $$ \Uptheta_{3}^{i}=\left[\begin{array}{ccccccccc} 0 &\ast & \ast & \ast & \ast & \ast & \ast & \ast & \ast\\ 0 & -R_{1}& \ast & \ast & \ast & \ast & \ast & \ast & \ast\\ 0 & R_{1} & -R_{1}-R_{2} & \ast & \ast & \ast & \ast & \ast & \ast\\ \delta X_{1}^{T} & \delta X_{2}^{T} & \delta X_{3}^{T}+R_{2} & \Uptheta_{3_{44}}^{i} & \ast & \ast & \ast & \ast & \ast \\ -\delta Y_{1}^{T} & -\delta Y_{2}^{T} & -\delta Y_{3}^{T} & \delta X_{5}^{T}-\delta Y_{4}^{T} & -\delta Y_{5}^{T}-\delta Y_{5} & \ast & \ast & \ast & \ast\\ -\delta X_{1}^{T}+\delta Y_{1}^{T} & -\delta X_{2}^{T}+\delta Y_{2}^{T} & \Uptheta_{3_{63}}^{i} & \Uptheta_{3_{64}}^{i} & \Uptheta_{3_{65}}^{i} &\Uptheta_{3_{66}}^{i} & \ast & \ast & \ast \\ 0 & 0 & 0 & \delta X_{7}^{T} & -\delta X_{7}^{T} & -\delta X_{7}^{T}+\delta Y_{7}^{T} & 0 & \ast & \ast \\ 0 & 0 & 0 & \delta X_{8}^{T} & -\delta Y_{8}^{T} & -\delta X_{8}^{T}+\delta Y_{8}^{T} & 0 & 0 & \ast\\ 0 & 0 & 0 & \delta X_{9}^{T} & -\delta Y_{9}^{T} & -\delta X_{9}^{T}+\delta Y_{9}^{T} & 0 & 0 & 0 \end{array} \right]<0, \\ $$
  $$ \begin{aligned} \Uptheta_{3_{44}}^{i}&=-R_{2}+\delta X_{4}^{T}+\delta X_{4} \\ \Uptheta_{3_{63}}^{i}&=-\delta X_{3}^{T}+\delta Y_{3}^{T} \\ \Uptheta_{3_{64}}^{i}&=\delta X_{6}^{T}-\delta X_{4}^{T}+\delta Y_{4}^{T} \\ \Uptheta_{3_{65}}^{i}&=-\delta X_{5}^{T}+\delta Y_{5}^{T}-\delta Y_{6}^{T} \\ \Uptheta_{3_{66}}^{i}&=-\delta X_{6}-\delta X_{6}^{T}+\delta Y_{6}^{T}+\delta Y_{6} \\ \phi&=\delta^{2}R_{1}+\delta^{2}R_{2}+\delta^{2}R_{3}+\tau_{n}^{2}R_{4} \\ \Upupsilon_{11}^{i}&=\delta N\,\Upupsilon_{12}^{i}=\delta M\,\Upupsilon_{21}^{i}=\delta S \,\Upupsilon_{22}^{i}=\delta Z\,\Upupsilon_{31}^{i}=\delta X \,\Upupsilon_{32}^{i}=\delta Y \end{aligned} $$

  then, switched interval network (5) is global robust asymptotic stable, the switching rule is chosen as σ(x(t)) = i whenever $x(t)\in \bar{\Upomega_{i}}$.

Proof

Consider the following Lyapunov–Krasovskii functional

$$ V(t,x_{t})=V_{1}(t,x_{t})+V_{2}(t,x_{t})+V_{3}(t,x_{t}) +V_{4}(t,x_{t})+V_{5}(t,x_{t}) $$

(9)

where

$$ \begin{aligned} V_{1}(t,x_{t})&=x^{T}(t)Px(t)+2\sum_{i=1}^{n}\gamma_{1,i} \int\limits_{0}^{x_{i}(t)}f_{i}(s)ds\\ V_{2}(t,x_{t})&=\int\limits_{t-\tau(t)}^{t}[x^{T}(s)T_{1}x(s)+f^{T} (x(s))T_{2}f(x(s))]ds\\ V_{3}(t,x_{t})&=\int\limits_{t-\tau_{n}}^{t}x^{T}(s)Q_{1}x(s)ds +\int\limits_{t-\tau_{1}}^{t}x^{T}(s)Q_{2}x(s)ds \\ &\quad +\int\limits_{t-\tau_{2}}^{t}x^{T}(s)Q_{3}x(s)ds +\int\limits_{t-\tau_{N}}^{t}x^{T}(s)Q_{4}x(s)ds\\ V_{4}(t,x_{t})&=\delta\int\limits_{t-\tau_{1}}^{t-\tau_{n}} \int\limits_{s}^{t}\dot{x}^{T}(\theta)R_{1}\dot{x}(\theta)d\theta ds +\delta\int\limits_{t-\tau_{2}}^{t-\tau_{1}}\int\limits_{s}^{t} \dot{x}^{T}(\theta)R_{2}\dot{x}(\theta)d\theta ds \\ &\quad +\delta\int\limits_{t-\tau_{N}}^{t-\tau_{2}}\int\limits_{s}^{t} \dot{x}^{T}(\theta)R_{3}\dot{x}(\theta)d\theta ds\\ V_{5}(t,x_{t})&=\tau_{n}\int\limits_{t-\tau_{n}}^{t}\int\limits_{s}^{t} \dot{x}^{T}(\theta)R_{4}\dot{x}(\theta)d\theta ds \\ \end{aligned} $$

Calculating the time derivative of V(t, x _t ) along the trajectory of (6), it can follow that

$$ \begin{aligned} \dot{V}_{1}(t,x_{t})&=2x^{T}(t)P\dot{x}(t)+2\sum_{i=1}^{n} \gamma_{1,i}f_{i}(x_{i}(t))\dot{x}_{i}(t)\\ &=2x^{T}(t)P[-A_{0}^{i}x(t)+B_{10}^{i}f(x(t))+B_{20}^{i}f(x(t-\tau(t)) +E^{i}\Updelta^{i}(t)]\\ &\quad +2f^{T}(x(t))\gamma_{1}[-A_{0}^{i}x(t)+B_{10}^{i}f(x(t)) +B_{20}^{i}f(x(t-\tau(t))+E^{i}\Updelta^{i}(t)]\\ &=-2x^{T}(t)(A_{0}^{i})^{T}Px(t)+2f^{T}(x(t))(B_{10}^{i})^{T}Px(t) +2f^{T}(x(t-\tau(t))(B_{20}^{i})^{T}Px(t)\\ &\quad +2(\Updelta^{i}(t))^{T}(E^{i})^{T}Px(t)-2f^{T}(x(t))\gamma_{1}A_{0}^{i}x(t) +2f^{T}(x(t))\gamma_{1}B_{10}^{i}f(x(t))\\ &\quad 2f^{T}(x(t))\gamma_{1}B_{20}^{i}f(x(t-\tau(t))) +2f^{T}(x(t))\gamma_{1}E^{i}\Updelta^{i}(t) \end{aligned} $$

(10)

$$ \begin{aligned} \dot{V}_{2}(t,x_{t})&=x^{T}(t)T_{1}x(t)-(1-\dot{\tau}(t))x^{T} (t-\tau(t))T_{1}x(t-\tau(t))+f^{T}(x(t))T_{2}f(x(t))\\ &\quad -(1-\dot{\tau}(t))f^{T}(x(t-\tau(t)))T_{2}f(x(t-\tau(t)))\\ &\quad \leq x^{T}(t)T_{1}x(t)+f^{T}(x(t))T_{2}f(x(t))-(1-\mu)x^{T} (t-\tau(t))T_{1}x(t-\tau(t))\\ &\quad -(1-\mu)f^{T}(x(t-\tau(t)))T_{2}f(x(t-\tau(t))) \end{aligned} $$

(11)

$$ \begin{aligned} \dot{V}_{3}(t,x_{t})&=x^{T}(t)(Q_{1}+Q_{2}+Q_{3} +Q_{4})x(t)-x^{T}(t-\tau_{n})Q_{1}x(t-\tau_{n})-x^{T}(t-\tau_{1})Q_{2}\\ &\quad x(t-\tau_{1})-x^{T}(t-\tau_{2})Q_{3}x(t-\tau_{2}) -x^{T}(t-\tau_{N})Q_{4}x(t-\tau_{N}) \end{aligned} $$

(12)

$$ \begin{aligned} \dot{V}_{4}(t,x_{t})&=\delta^{2}\dot{x}^{T}(t) R_{1}\dot{x}(t)-\delta\int\limits_{t-\tau_{1}}^{t-\tau_{n}} \dot{x}^{T}(s)R_{1}\dot{x}(s)ds +\delta^{2}\dot{x}^{T}(t)R_{2}\dot{x}(t)\\ &\quad-\delta\int\limits_{t-\tau_{2}}^{t-\tau_{1}}\dot{x}^{T}(s)R_{2}\dot{x}(s)ds +\delta^{2}\dot{x}^{T}(t)R_{3}\dot{x}(t)-\delta\int\limits_{t-\tau_{M}}^{t-\tau_{2}} \dot{x}^{T}(s)R_{3}\dot{x}(s)ds \end{aligned} $$

(13)

By applying Lemma 2.1, we have

$$ \begin{aligned} \dot{V}_{5}(t,x_{t})&=\tau^{2}_{n}\dot{x}^{T}(t)R_{4}\dot{x}(t) -\tau_{n}\int\limits_{t-\tau_{n}}^{t}\dot{x}^{T}(s)R_{4}\dot{x}(s)ds\\ &\leq\tau^{2}_{n}\dot{x}^{T}(t)R_{4}\dot{x}(t)+\left[\begin{array}{c} x(t)\\ x(t-\tau_{n}) \end{array}\right]^{T}\left[\begin{array}{cc} -R_{4} & R_{4}\\ R_{4} &-R_{4} \end{array}\right]\left[\begin{array}{c} x(t)\\ x(t-\tau_{n}) \end{array}\right] \end{aligned} $$

(14)

Based on (10)–(14), we can get

$$ \begin{aligned} \dot{V}(t,x_{t})&\leq x^{T}(t)[(A_{0}^{i})^{T}P-PA_{0}^{i}+T_{1}+Q_{1}+Q_{2}+Q_{3}+Q_{4}]x(t) +f^{T}(x(t))[\gamma_{1}B_{10}^{i}+B_{10}^{i}\gamma_{1}\\ &\quad+T_{2}]f(x(t))+2(\Updelta^{i}(t))^{T}(E^{i})^{T}Px(t) +2f^{T}(x(t-\tau(t)))(B_{20}^{i})^{T}Px(t)\\ &\quad+2f^{T}(x(t))\gamma_{1}B_{20}^{i}f(x(t-\tau(t)))-x^{T}(t-\tau_{n})Q_{1}x(t-\tau_{n}) +2f^{T}(x(t))\gamma_{1}E^{i}\Updelta^{i}(t)\\ &\quad+2f^{T}(x(t))[(B_{10}^{i})^{T}P-\gamma_{1}A_{0}^{i}]x(t) -(1-\mu)x^{T}(t-\tau(t))T_{1}x(t-\tau(t))\\ &\quad -x^{T}(t-\tau_{1})Q_{2}x(t-\tau_{1})-(1-\mu)f^{T}(x(t-\tau(t)))T_{2}f(x(t-\tau(t))) -x^{T}(t-\tau_{2})Q_{3}x(t-\tau_{2})\\ &\quad+\dot{x}^{T}(t)\phi\dot{x}(t)-x^{T}(t-\tau_{N})Q_{4}x(t-\tau_{N}) +\left[\begin{array}{c} x(t)\\ x(t-\tau_{n}) \end{array}\right]^{T}\left[\begin{array}{cc} -R_{4} & R_{4}\\ R_{4} &-R_{4} \end{array}\right]\left[\begin{array}{c} x(t)\\ x(t-\tau_{n}) \end{array}\right]\\ &\quad-\delta\int\limits_{t-\tau_{1}}^{t-\tau_{n}}\dot{x}^{T}(s)R_{1}\dot{x}(s)ds -\delta\int\limits_{t-\tau_{2}}^{t-\tau_{1}}\dot{x}^{T}(s)R_{2}\dot{x}(s)ds -\delta\int\limits_{t-\tau_{M}}^{t-\tau_{2}}\dot{x}^{T}(s)R_{3}\dot{x}(s)ds \end{aligned} $$

(15)

By the assumption $(\mathcal{H}_1)$, one has

$$ [f_{i}(x_{i}(t))-\check{l}_{_{i}}x_{i}(t)][f_{i}(x_{i}(t)) -\hat{l}_{_{i}}x_{i}(t)]\leq0 $$

(16)

$$ [f_{i}(x_{i}(t-\tau(t)))-\check{l}_{_{i}}x_{i}(t-\tau(t))] [f_{i}(x_{i}(t-\tau(t)))-\hat{l}_{_{i}}x_{i}(t-\tau(t))]\leq0 $$

(17)

It follows from (16) and (17) that

$$ \begin{aligned} &2\sum_{i=1}^{n}\gamma_{2,i}[f_{i}(x_{i}(t))-\check{l}_{_{i}}x_{i}(t)] [f_{i}(x_{i}(t))-\hat{l}_{_{i}}x_{i}(t)]\\ &\quad ={\sum_{i=1}^{n}\gamma_{2,i}\left[\begin{array}{c} x(t)\\ f(x(t)) \end{array}\right]^{T}\left[\begin{array}{cc} 2\check{l}_{_{i}}\hat{l}_{_{i}}e_{i}e_{i}^{T} & \ast\\ -(\check{l}_{_{i}}+\hat{l}_{_{i}})e_{i}^{T}e_{i} & 2e_{i}e_{i}^{T} \end{array}\right]\left[\begin{array}{c} x(t)\\ f(x(t)) \end{array}\right]}\\ &\quad ={\left[\begin{array}{c} x(t)\\ f(x(t)) \end{array}\right]^{T}\left[\begin{array}{cc} 2\gamma_{2}L_{1} & \ast\\ -\gamma_{2}L_{2} & 2\gamma_{2} \end{array}\right]\left[\begin{array}{c} x(t)\\ f(x(t)) \end{array}\right]} \leq0 \end{aligned} $$

(18)

$$ \begin{aligned} &2\sum_{i=1}^{n}\gamma_{3,i}[f_{i}(x_{i}(t-\tau(t))) -\check{l}_{_{i}}x_{i}(t-\tau(t))][f_{i}(x_{i}(t-\tau(t))) -\hat{l}_{_{i}}x_{i}(t-\tau(t))]\\ &\quad ={\left[\begin{array}{c} x(t-\tau(t))\\ f(x(t-\tau(t))) \end{array}\right]^{T}\left[\begin{array}{cc} 2\gamma_{3}L_{1} & \ast\\ -\gamma_{3}L_{2} & 2\gamma_{3} \end{array}\right] \left[\begin{array}{c} x(t-\tau(t))\\ f(x(t-\tau(t))) \end{array}\right]} \leq0 \end{aligned} $$

(19)

where e _i denotes the unit column vector with a “1′′ on its ith row and zeros elsewhere.

By substituting (7) and (18), (19) into (15), it yields

$$ \begin{aligned} \dot{V}(t,x_{t})&\leq x^{T}(t)G_{i}(A_{0}^{i},Q_{1},Q_{2},Q_{3})x(t)+ \eta^{T}(t)\Uppi^{i}\eta(t)-\delta\int\limits_{t-\tau_{1}}^{t-\tau_{n}} \dot{x}^{T}(s)R_{1}\dot{x}(s)ds\\ &\quad -\delta\int\limits_{t-\tau_{2}}^{t-\tau_{1}}\dot{x}^{T}(s)R_{2}\dot{x}(s)ds -\delta\int\limits_{t-\tau_{M}}^{t-\tau_{2}}\dot{x}^{T}(s)R_{3}\dot{x}(s)ds \end{aligned} $$

(20)

where

$$ \begin{aligned} \eta^{T}(t)&=\left[x^{T}(t)\,x^{T}(t-\tau_{n})\,x^{T}(t-\tau_{1})\,x^{T} (t-\tau_{2})\right.\\ &\left.\quad \times x^{T}(t -\tau_{N})\,x^{T}(t-\tau(t))\, f^{T}(x(t))\,f^{T}(x(t-\tau(t)))\,(\Updelta^{i}(t))^{T}\right] \end{aligned} $$

In the following, we will consider three cases: that is $t \in \mathcal{S}_{1},\,t \in \mathcal{S}_{2},\,t \in \mathcal{S}_{3}$.

Case 1: when $t \in \mathcal{S}_{1}$, i.e. $\tau(t)\in[\tau_{n},\tau_{1}]$.

By using Lemma 2.1, we have

$$ -\delta\int\limits_{t-\tau_{2}}^{t-\tau_{1}}\dot{x}^{T}(s)R_{2}\dot{x}(s)ds \leq\left[\begin{array}{c} x(t-\tau_{1})\\ x(t-\tau_{2}) \end{array}\right]^{T}\left[\begin{array}{cc} -R_{2} &R_{2}\\ R_{2} &-R_{2} \end{array}\right]\left[\begin{array}{c} x(t-\tau_{1})\\ x(t-\tau_{2}) \end{array}\right] $$

(21)

$$ -\delta\int\limits_{t-\tau_{N}}^{t-\tau_{2}}\dot{x}^{T}(s)R_{3}\dot{x}(s)ds \leq\left[\begin{array}{c} x(t-\tau_{2})\\ x(t-\tau_{N}) \end{array}\right]^{T}\left[\begin{array}{cc} -R_{3} & R_{3}\\ R_{3} &-R_{3} \end{array}\right]\left[\begin{array}{c} x(t-\tau_{2})\\ x(t-\tau_{N}) \end{array}\right]\\ $$

(22)

Combing (20)–(22), and applying Newton-Leibniz formula and adding the free weighting matrices N and M, it can be obtained

$$ \begin{aligned} \dot{V}(t,x_{t})&\leq x^{T}(t)G_{i}(A_{0}^{i},Q_{1},Q_{2},Q_{3})x(t) +\eta^{T}(t)\Uppi^{i}\eta(t)-\delta\int\limits_{t-\tau_{1}}^{t-\tau_{n}} \dot{x}^{T}(s)R_{1}\dot{x}(s)ds\\ &\quad {+\left[\begin{array}{c} x(t-\tau_{1})\\ x(t-\tau_{2}) \end{array}\right]^{T}\left[\begin{array}{cc} -R_{2} & R_{2}\\ R_{2} &-R_{2} \end{array}\right]\left[\begin{array}{c} x(t-\tau_{1})\\ x(t-\tau_{2}) \end{array}\right]}\\ &\quad{+\left[\begin{array}{c} x(t-\tau_{2})\\ x(t-\tau_{N}) \end{array}\right]^{T}\left[\begin{array}{cc} -R_{3} & R_{3}\\ R_{3} &-R_{3} \end{array}\right]\left[\begin{array}{c} x(t-\tau_{2})\\ x(t-\tau_{N}) \end{array}\right]}\\ &\quad+2\delta\eta^{T}(t)N\left[x(t-\tau_{n})-x(t-\tau(t)) -\int\limits_{t-\tau(t)}^{t-\tau_{n}}\dot{x}(s)ds\right]\\ &\quad +2\delta\eta^{T}(t)M\left[x(t-\tau(t))-x(t-\tau_{1}) -\int\limits_{t-\tau_{1}}^{t-\tau(t)}\dot{x}(s)ds\right] \end{aligned} $$

(23)

It is easy to deduce the following inequality:

$$ \begin{aligned} &-2\delta\eta^{T}(t)N\int\limits_{t-\tau(t)}^{t-\tau_{n}}\dot{x}(s)ds =\delta\int\limits_{t-\tau(t)}^{t-\tau_{n}}2\eta^{T}(t)(-N)\dot{x}(s)ds\\ &\quad\leq(\tau(t)-\tau_{n})\delta\eta^{T}(t)NR_{1}^{-1}N^{T}\eta(t) +\delta\int\limits_{t-\tau(t)}^{t-\tau_{n}}\dot{x}^{T}(s)R_{1}\dot{x}(s)ds \end{aligned} $$

(24)

$$ \begin{aligned} &-2\delta\eta^{T}(t)M\int\limits_{t-\tau_{1}}^{t-\tau(t)}\dot{x}(s)ds\\ &\quad\leq(\tau_{1}-\tau(t))\delta\eta^{T}(t)MR_{1}^{-1}M^{T}\eta(t) +\delta\int\limits_{t-\tau_{1}}^{t-\tau(t)}\dot{x}^{T}(s)R_{1}\dot{x}(s)ds \end{aligned} $$

(25)

By substituting (24)–(25) into (23), it follows that

$$ \begin{aligned} \dot{V}(x(t))&\leq x^{T}(t)G_{i}(A_{0}^{i},Q_{1},Q_{2},Q_{3})x(t) +\eta^{T}(t)[\Uppi^{i}+\Uptheta_{1}^{i}+ (\tau(t)-\tau_{n})\delta NR_{1}^{-1}N^{T}\\ &\quad +(\tau_{1}-\tau(t))\delta MR_{1}^{-1}M^{T}]\eta(t) \end{aligned} $$

(26)

when m = n = 1, using Schur complement, (8) is equivalent to

$$ \Uppi^{i}+\Uptheta_{1}^{i}+\delta^{2} NR_{1}^{-1}N^{T}<0\\ $$

(27)

Similarly, when m = 1 and n = 2, (8) is equivalent to

$$ \Uppi^{i}+\Uptheta_{1}^{i}+\delta^{2} MR_{1}^{-1}M^{T}<0 $$

(28)

From (27) and (28), by using Lemma 2.2, we can obtain

$$ \Uppi^{i}+\Uptheta_{1}^{i}+(\tau(t)-\tau_{n})\delta NR_{1}^{-1}N^{T}+(\tau_{1}-\tau(t))\delta MR_{1}^{-1}M^{T}<0 $$

(29)

Therefore, we finally obtain from (26) and (29) that

$$ \dot{V}(x(t))< x^{T}(t)G_{i}(A_{0}^{i},Q_{1},Q_{2},Q_{3})x(t),\quad \forall i=1,\,2, \ldots, N,\,t \in {\mathcal{S}}_{1} $$

(30)

Case 2: when $t \in \mathcal{S}_{2}$, i.e. $\tau(t)\in(\tau_{1},\tau_{2}]$.

Similar to case 1, we have

$$ -\delta\int\limits_{t-\tau_{1}}^{t-\tau_{n}}\dot{x}^{T}(s)R_{1}\dot{x}(s)ds \leq\left[\begin{array}{c} x(t-\tau_{n})\\ x(t-\tau_{1}) \end{array}\right]^{T}\left[\begin{array}{cc} -R_{1} &R_{1}\\ R_{1} &-R_{1} \end{array}\right]\left[\begin{array}{c} x(t-\tau_{n})\\ x(t-\tau_{1}) \end{array}\right] $$

(31)

$$ -\delta\int\limits_{t-\tau_{N}}^{t-\tau_{2}}\dot{x}^{T}(s)R_{3}\dot{x}(s)ds \leq\left[\begin{array}{c} x(t-\tau_{2})\\ x(t-\tau_{N}) \end{array}\right]^{T}\left[\begin{array}{cc} -R_{3}& R_{3}\\ R_{3} &-R_{3} \end{array}\right]\left[\begin{array}{c} x(t-\tau_{2})\\ x(t-\tau_{N}) \end{array}\right]\\ $$

(32)

Combing (20), (31), (32), and applying Newton-Leibniz formula and adding the free weighting matrices S and Z, it can be obtained

$$ \begin{aligned} \dot{V}(t,x_{t})&\leq x^{T}(t)G_{i}(A_{0}^{i},Q_{1},Q_{2},Q_{3})x(t)+ \eta^{T}(t)\Uppi^{i}\eta(t)-\delta\int\limits_{t-\tau_{2}}^{t-\tau_{1}} \dot{x}^{T}(s)R_{2}\dot{x}(s)ds\\ &\quad +\left[\begin{array}{c} x(t-\tau_{n})\\ x(t-\tau_{1}) \end{array}\right]^{T}\left[\begin{array}{cc} -R_{1} & R_{1}\\ R_{2} &-R_{1} \end{array}\right]\left[\begin{array}{c} x(t-\tau_{n})\\ x(t-\tau_{1}) \end{array}\right]\\ &\quad +\left[\begin{array}{c} x(t-\tau_{2})\\ x(t-\tau_{N}) \end{array}\right]^{T}\left[\begin{array}{cc} -R_{3} & R_{3}\\ R_{3} &-R_{3} \end{array}\right]\left[\begin{array}{c} x(t-\tau_{2})\\ x(t-\tau_{N}) \end{array}\right]\\ &\quad +2\delta\eta^{T}(t)S\left[x(t-\tau_{1})-x(t-\tau(t)) -\int\limits_{t-\tau(t)}^{t-\tau_{1}}\dot{x}(s)ds\right]\\ &\quad +2\delta\eta^{T}(t)Z\left[x(t-\tau(t))-x(t-\tau_{2}) -\int\limits_{t-\tau_{2}}^{t-\tau(t)}\dot{x}(s)ds\right] \end{aligned} $$

(33)

Then, according to a similar method in Case 1, we have

$$ \begin{aligned} \dot{V}(x(t))&\leq x^{T}(t)G_{i}(A_{0}^{i},Q_{1},Q_{2},Q_{3})x(t)+\eta^{T}(t)[\Uppi^{i}+\Uptheta_{2}^{i}+ (\tau(t)-\tau_{1})\delta SR_{2}^{-1}S^{T}\\ &\quad+(\tau_{2}-\tau(t))\delta ZR_{2}^{-1}Z^{T}]\eta(t) \end{aligned} $$

(34)

when m = 2, n = 1, using Schur complement, (8) is equivalent to

$$ \Uppi^{i}+\Uptheta_{2}^{i}+\delta^{2} SR_{2}^{-1}S^{T}<0 $$

(35)

Similarly, when m = 2 and n = 2, (8) is equivalent to

$$ \Uppi^{i}+\Uptheta_{2}^{i}+\delta^{2} ZR_{2}^{-1}Z^{T}<0 $$

(36)

From (35) and (36), by using Lemma 2.2, it yields

$$ \Uppi^{i}+\Uptheta_{2}^{i}+(\tau(t)-\tau_{1})\delta SR_{2}^{-1}S^{T}+(\tau_{2}-\tau(t))\delta ZR_{2}^{-1}Z^{T}<0 $$

(37)

Therefore, we finally obtain from (34) and (37) that

$$ \dot{V}(x(t))< x^{T}(t)G_{i}(A_{0}^{i},Q_{1},Q_{2},Q_{3})x(t),\,\forall i=1,\,2,\ldots, N, \quad t \in {\mathcal{S}}_{2} $$

(38)

Case 3: when $t \in \mathcal{S}_{3}$, i.e. $\tau(t)\in(\tau_{2},\tau_{N}]$.

From the above (21) and (31), we can get

$$ \begin{aligned} \dot{V}(t,x_{t})&\leq x^{T}(t)G_{i}(A_{0}^{i},Q_{1},Q_{2},Q_{3})x(t) + \eta^{T}(t)\Uppi^{i}\eta(t) -\delta\int\limits_{t-\tau_{N}}^{t-\tau_{2}}\dot{x}^{T}(s)R_{3}\dot{x}(s)ds\\ &\quad +\left[\begin{array}{c} x(t-\tau_{n})\\ x(t-\tau_{1}) \end{array}\right]^{T}\left[\begin{array}{cc} -R_{1} & R_{1}\\ R_{1} &-R_{1} \end{array}\right]\left[\begin{array}{c} x(t-\tau_{n})\\ x(t-\tau_{1}) \end{array}\right]\\ &\quad +\left[\begin{array}{c} x(t-\tau_{1})\\ x(t-\tau_{2}) \end{array}\right]^{T}\left[\begin{array}{cc} -R_{2} & R_{2}\\ R_{2} &-R_{2} \end{array}\right]\left[\begin{array}{c} x(t-\tau_{1})\\ x(t-\tau_{2}) \end{array}\right]\\ &\quad +2\delta\eta^{T}(t)X\left[x(t-\tau_{2})-x(t-\tau(t)) -\int\limits_{t-\tau(t)}^{t-\tau_{2}}\dot{x}(s)ds\right]\\ &\quad +2\delta\eta^{T}(t)Y\left[x(t-\tau(t))-x(t-\tau_{N}) -\int\limits_{t-\tau_{N}}^{t-\tau(t)}\dot{x}(s)ds\right] \end{aligned} $$

(39)

Similar to the analysis methods in case 1 and case 2, it can be obtained:

$$ \dot{V}(x(t))< x^{T}(t)G_{i}(A_{0}^{i},Q_{1},Q_{2},Q_{3})x(t), \quad \forall i=1,2,\ldots, N,\quad t \in {\mathcal{S}}_{3} $$

(40)

From the above discussions, for all t > 0, (8) with m = 1, 2, 3, n = 1 and 2, we can get the following equality:

$$ \dot{V}(x(t))< x^{T}(t)G_{i}(A_{0}^{i},Q_{1},Q_{2},Q_{3})x(t), \quad \forall i=1,2,\ldots, N,\quad t>0 $$

(41)

By the condition (i) and Proposition 2.1, the system of matrices G _i (A ⁱ₀ , Q ₁, Q ₂, Q ₃) is strictly complete. Then we have

$$ \bigcup\limits_{i=1}^{N}\bar{\Upomega_{i}}=R^{n} \backslash \{0\},\quad \,\bar{\Upomega_{i}}\bigcap\bar{\Upomega_{j}}=\phi,\quad i\neq j $$

(42)

Hence, for any $x(t)\in R ^{n}$, there exists $i\in\{1,\,2,\,\ldots,\,N\}$ such that $x(t)\in \bar{\Upomega_{i}}$. By choosing switching rule as σ(x) = i whenever $\sigma(x)\in \bar{\Upomega_{i}}$, from (41), it can derive

$$ \dot{V}(x(t))< x^{T}(t)G_{i}(A_{0}^{i},Q_{1},Q_{2},Q_{3})x(t)<0,\quad t>0 $$

(43)

According to Definition 2.1, the switched interval network (5) is global robust asymptotic stable. The proof is completed. □

Next, we will consider the situation when the time-varying delay τ(t) becomes the fast delay, by structuring the different Lyapunov–Krasovskii functional, it is easy to obtain the following corollary:

Corollary 3.1

Under the assumption $(\mathcal{H}_1)$ and $(\mathcal{H}_3)$, if there exist matrices P > 0,  Q _j  > 0,  R _j  > 0 (j = 1,  2,  3,  4), and diagonal matrices $\gamma_{k}=diag\{\gamma_{k,1},\,\gamma_{k,2},\,\ldots,\,\gamma_{k,n}\}>0 (k=1,\,2,\,3)$, and matrices $N_{l},\,M_{l},\,Z_{l},\,S_{l}\,(l=1,\,2,\,\ldots,\,9)$ with appropriate dimensions such that for all m and n, the following LMIs hold:

• (i) $\exists\,\xi^{i}\geq 0, i=1,\,2,\,\ldots,\,N, \sum_{i=1}^{N}\xi^{i}>0:\quad \sum_{i=1}^{N}\xi^{i}G_{i}(A_{0}^{i},Q_{1},Q_{2},Q_{3})<0$.

• (ii)
  $$ \left[\begin{array}{cc} \Uppi^{i}+\Uptheta_{m}^{i} &\ast \\ \Upupsilon_{mn}^{i} & -R_{m}^{i} \end{array} \right]<0,\quad \,m=1,\,2,\,3,\,n=1,\,2 $$

  (44)

  where

  $$ \Uppi^{i}=\left[\begin{array}{ccccccccc} \Uppi_{11}^{i} &\ast & \ast & \ast & \ast & \ast & \ast & \ast & \ast\\ R_{4} & -Q_{1}-R_{4} & \ast & \ast & \ast & \ast & \ast & \ast & \ast\\ 0 & 0 & -Q_{2} & \ast & \ast & \ast & \ast & \ast & \ast \\ 0 & 0 & 0 & -Q_{3} & \ast & \ast & \ast & \ast & \ast \\ 0 & 0 & 0 & 0 & -Q_{4} & \ast & \ast & \ast & \ast \\ 0 & 0 & 0 & 0 & 0 & \Uppi_{66}^{i} & \ast & \ast & \ast \\ \Uppi_{71}^{i} & 0 & 0 & 0 & 0 & 0 & \Uppi_{77}^{i} & \ast & \ast \\ \Uppi_{81}^{i}& 0 & 0 & 0 & 0 & \gamma_{3}L_{2} & \Uppi_{87}^{i} & \Uppi_{88}^{i} & \ast \\ (E^{i})^{T}P-(E^{i})^{T}\phi A_{0}^{i} & 0 & 0 & 0 & 0 & 0 &\Uppi_{97}^{i} &\Uppi_{98}^{i} &\Uppi_{99}^{i} \end{array} \right]<0, $$

  where

  $$ \begin{aligned} \Uppi_{11}^{i}&=(A_{0}^{i})^{T}\phi A_{0}^{i}+Q_{4}-R_{4}-\gamma_{2}L_{1}-L_{1}\gamma_{2}+(F_{A}^{i})^{T}F_{A}^{i} \\ \Uppi_{66}^{i}&=-\gamma_{3}L_{1}-L_{1}\gamma_{3} \\ \Uppi_{71}^{i}&=L_{2}\gamma_{2}+(B_{10}^{i})^{T}P -\gamma_{1}A_{0}^{i}-(B_{10}^{i})^{T}\phi A_{0}^{i}+(F_{A}^{i})^{T}F_{1}^{i} \\ \Uppi_{77}^{i}&=\gamma_{1}B_{10}^{i}+(B_{10}^{i})^{T}\gamma_{1} -\gamma_{2}-\gamma_{2}^{T}+(B_{10}^{i})^{T}\phi B_{10}^{i}+(F_{1}^{i})^{T}F_{1}^{i} \\ \Uppi_{81}^{i}&=(B_{20}^{i})^{T}P-(B_{20}^{i})^{T}\phi A_{0}^{i}+(F_{A}^{i})^{T}F_{2}^{i} \\ \Uppi_{87}^{i}&=(B_{20}^{i})^{T}\gamma_{1}+(B_{20}^{i})^{T}\phi B_{10}^{i}+(F_{1}^{i})^{T}F_{2}^{i} \\ \Uppi_{88}^{i}&=-\gamma_{3}-\gamma_{3}^{T}+(B_{20}^{i})^{T}\phi B_{20}^{i}+(F_{2}^{i})^{T}F_{2}^{i} \\ \Uppi_{97}^{i}&=(E^{i})^{T}\gamma_{1}+(E^{i})^{T}\phi^{T}(B_{10}^{i})^{T} \\ \Uppi_{98}^{i}&=(E^{i})^{T}\phi^{T}(B_{20}^{i})^{T} \\ \Uppi_{99}^{i}&=(E^{i})^{T}\phi E^{i}-I \\ \end{aligned} $$
  $$ \Uptheta_{1}^{i}=\left[\begin{array}{ccccccccc} 0 &\ast & \ast & \ast & \ast & \ast & \ast & \ast & \ast\\ \delta N_{1}^{T} & \delta N_{2}^{T}+\delta N_{2}^{T} & \ast & \ast & \ast & \ast & \ast & \ast & \ast\\ -\delta M_{1}^{T} & \delta N_{3}^{T}-\delta M_{2}^{T} & \Uptheta_{1_{33}}^{i} & \ast & \ast & \ast & \ast & \ast & \ast \\ 0 & \delta N_{4}^{T} & R_{2}-\delta M_{4}^{T} & -R_{2}-R_{3} & \ast & \ast & \ast & \ast & \ast\\ 0 & \delta N_{5}^{T} & -\delta M_{5}^{T} & R_{3} & -R_{3} & \ast & \ast & \ast & \ast \\ \delta M_{1}^{T}-\delta N_{1}^{T} & \Uptheta_{1_{62}}^{i} & \Uptheta_{1_{63}}^{i} & -\delta N_{4}^{T}+\delta M_{4}^{T} & \Uptheta_{1_{65}}^{i} & \Uptheta_{1_{66}}^{i}& \ast & \ast & \ast \\ 0 & \delta N_{7}^{T} & -\delta M_{7}^{T} & 0 & 0 & -\delta N_{7}^{T}+\delta M_{7}^{T} & 0 & \ast & \ast \\ 0 & \delta N_{8}^{T} & -\delta M_{8}^{T} & 0 & 0 & -\delta N_{8}^{T}+\delta M_{8}^{T} & 0 & 0 & \ast \\ 0 & \delta N_{9}^{T} & -\delta M_{9}^{T} & 0 & 0 & -\delta N_{9}^{T}+\delta M_{9}^{T} & 0 & 0 & 0\\ \end{array} \right]<0, \\ $$
  $$ \begin{aligned} \Uptheta_{1_{33}}^{i}&=-R_{2}-\delta M_{3}^{T}-\delta M_{3} \\ \Uptheta_{1_{62}}^{i}&=\delta N_{6}^{T}-\delta N_{2}^{T}+\delta M_{2}^{T} \\ \Uptheta_{1_{63}}^{i}&=-\delta N_{3}^{T}+\delta M_{3}^{T}-\delta M_{6}^{T} \\ \Uptheta_{1_{65}}^{i}&=-\delta N_{5}^{T}+\delta M_{5}^{T} \\ \end{aligned} $$
  $$ \Uptheta_{2}^{i}=\left[\begin{array}{ccccccccc} 0 & \ast & \ast & \ast & \ast & \ast & \ast & \ast & \ast\\ 0 & -R_{1}& \ast & \ast & \ast & \ast & \ast & \ast & \ast\\ \delta Z_{1}^{T} & R_{1}+\delta Z_{2}^{T} & \Uptheta_{2_{33}}^{i} & \ast & \ast & \ast & \ast & \ast & \ast\\ -\delta S_{1}^{T} & -\delta S_{2}^{T} & \delta Z_{4}^{T}-\delta S_{3}^{T} & \Uptheta_{2_{44}}^{i} & \ast & \ast & \ast & \ast & \ast \\ 0 & 0 & \delta Z_{5}^{T} & R_{3}-\delta S_{5}^{T} & -R_{3} & \ast & \ast & \ast & \ast\\ -\delta Z_{1}^{T}+\delta S_{1}^{T} & -\delta Z_{2}^{T}+\delta S_{2}^{T} & \Uptheta_{2_{63}}^{i} & \Uptheta_{2_{64}}^{i} & \Uptheta_{2_{65}}^{i} & \Uptheta_{2_{66}}^{i} & \ast & \ast & \ast \\ 0 & 0 & \delta Z_{7}^{T} & -\delta S_{7}^{T} & 0 & -\delta Z_{7}^{T}+\delta S_{7}^{T} & 0 & \ast & \ast \\ 0 & 0 & \delta Z_{8}^{T} & -\delta S_{8}^{T} & 0 & -\delta Z_{8}^{T}+\delta S_{8}^{T} & 0 & 0 & \ast\\ 0 & 0 & \delta Z_{9}^{T} & -\delta S_{9}^{T} & 0 & -\delta Z_{9}^{T}+\delta S_{9}^{T} & 0 & 0 & 0 \end{array} \right]<0, \\ $$
  $$ \begin{aligned} \Uptheta_{2_{33}}^{i}&=-R_{1}+\delta Z_{3}+\delta Z_{3}^{T} \\ \Uptheta_{2_{44}}^{i}&=-R_{3}-\delta S_{4}^{T}-\delta S_{4} \\ \Uptheta_{2_{63}}^{i}&=\delta Z_{6}^{T}-\delta Z_{3}^{T}+\delta S_{3}^{T} \\ \Uptheta_{2_{64}}^{i}&=-\delta Z_{4}^{T}+\delta S_{4}^{T}-\delta S_{6}^{T} \\ \Uptheta_{2_{65}}^{i}&=-\delta Z_{5}+\delta S_{5} \\ \Uptheta_{2_{66}}^{i}&=-\delta Z_{6}-\delta Z_{6}^{T}+\delta S_{6}+\delta S_{6}^{T} \\ \end{aligned} $$
  $$ \Uptheta_{3}^{i}=\left[\begin{array}{ccccccccc} 0 &\ast & \ast & \ast & \ast & \ast & \ast & \ast & \ast\\ 0 & -R_{1}& \ast & \ast & \ast & \ast & \ast & \ast & \ast\\ 0 & R_{1} & -R_{1}-R_{2} & \ast & \ast & \ast & \ast & \ast & \ast\\ \delta X_{1}^{T} & \delta X_{2}^{T} & \delta X_{3}^{T}+R_{2} & \Uptheta_{3_{44}}^{i} & \ast & \ast & \ast & \ast & \ast \\ -\delta Y_{1}^{T} & -\delta Y_{2}^{T} & -\delta Y_{3}^{T} & \delta X_{5}^{T}-\delta Y_{4}^{T} & -\delta Y_{5}^{T}-\delta Y_{5} & \ast & \ast & \ast & \ast\\ -\delta X_{1}^{T}+\delta Y_{1}^{T} & -\delta X_{2}^{T}+\delta Y_{2}^{T} & \Uptheta_{3_{63}}^{i} & \Uptheta_{3_{64}}^{i} & \Uptheta_{3_{65}}^{i} &\Uptheta_{3_{66}}^{i} & \ast & \ast & \ast \\ 0 & 0 & 0 & \delta X_{7}^{T} & -\delta X_{7}^{T} & -\delta X_{7}^{T}+\delta Y_{7}^{T} & 0 & \ast & \ast \\ 0 & 0 & 0 & \delta X_{8}^{T} & -\delta Y_{8}^{T} & -\delta X_{8}^{T}+\delta Y_{8}^{T} & 0 & 0 & \ast\\ 0 & 0 & 0 & \delta X_{9}^{T} & -\delta Y_{9}^{T} & -\delta X_{9}^{T}+\delta Y_{9}^{T} & 0 & 0 & 0 \end{array} \right]<0, \\ $$
  $$ \begin{aligned} \Uptheta_{3_{44}}^{i}&=-R_{2}+\delta X_{4}^{T}+\delta X_{4} \\ \Uptheta_{3_{63}}^{i}&=-\delta X_{3}^{T}+\delta Y_{3}^{T} \\ \Uptheta_{3_{64}}^{i}&=\delta X_{6}^{T}-\delta X_{4}^{T}+\delta Y_{4}^{T} \\ \Uptheta_{3_{65}}^{i}&=-\delta X_{5}^{T}+\delta Y_{5}^{T}-\delta Y_{6}^{T} \\ \Uptheta_{3_{66}}^{i}&=-\delta X_{6}-\delta X_{6}^{T}+\delta Y_{6}^{T}+\delta Y_{6} \\ \phi&=\delta^{2}R_{1}+\delta^{2}R_{2}+\delta^{2}R_{3}+\tau_{n}^{2}R_{4} \\ \Upupsilon_{11}^{i}&=\delta N\,\Upupsilon_{12}^{i}=\delta M\,\Upupsilon_{21}^{i}=\delta S \,\Upupsilon_{22}^{i}=\delta Z\,\Upupsilon_{31}^{i}=\delta X \,\Upupsilon_{32}^{i}=\delta Y \end{aligned} $$

  then, switched interval network (5) is global robust asymptotic stable, the switching rule is chosen as σ(x(t)) = i whenever $x(t)\in \bar{\Upomega_{i}}$.

Proof

By choosing the following Lyapunov–Krasovskii functional:

$$ V(t,x_{t})=V_{1}(t,x_{t})+V_{2}(t,x_{t})+V_{3}(t,x_{t}) +V_{4}(t,x_{t})+V_{5}(t,x_{t}) $$

where

$$ \begin{aligned} V_{1}(t,x_{t})&=x^{T}(t)Px(t)+2\sum_{i=1}^{n}\gamma_{1,i} \int\limits_{0}^{x_{i}(t)}f_{i}(s)ds \\ V_{2}(t,x_{t})&=\int\limits_{t-\tau_{n}}^{t}x^{T}(s)Q_{1}x(s)ds +\int\limits_{t-\tau_{1}}^{t}x^{T}(s)Q_{2}x(s)ds \\ &\quad +\int\limits_{t-\tau_{2}}^{t}x^{T}(s)Q_{3}x(s)ds +\int\limits_{t-\tau_{N}}^{t}x^{T}(s)Q_{4}x(s)ds \\ V_{3}(t,x_{t})&=\delta\int\limits_{t-\tau_{1}}^{t-\tau_{n}} \int\limits_{s}^{t}\dot{x}^{T}(\theta)R_{1}\dot{x}(\theta)d\theta ds +\delta\int\limits_{t-\tau_{2}}^{t-\tau_{1}} \int\limits_{s}^{t}\dot{x}^{T}(\theta)R_{2}\dot{x}(\theta)d\theta ds \\ &\quad +\delta\int\limits_{t-\tau_{N}}^{t-\tau_{2}}\int\limits_{s}^{t} \dot{x}^{T}(\theta)R_{3}\dot{x}(\theta)d\theta ds \\ V_{4}(t,x_{t})&=\tau_{n}\int\limits_{t-\tau_{n}}^{t} \int\limits_{s}^{t}\dot{x}^{T}(\theta)R_{4}\dot{x}(\theta)d\theta ds \\ \end{aligned} $$

the derivation process of Corollary 3.1 is similar to Theorem 3.1.

Remark 3

In (Zhang et al. 2009), author investigate the global asymptotic stability of a class of recurrent neural networks with interval time-varying delays via delay-decomposing approach, the variation interval of the time delay is divided into two subintervals with equal length by introducing its central point, several new stability criteria are derived in terms of LMIs. However, in this paper, we divide the interval time delay into three subintervals, as we all know, when the number of the divided subintervals increases, the corresponding criteria can be improved in results, hence, the proposed criteria expand and improve the results in the existing literatures. Moreover, when N = 1 and without regard to robustness in (5), the model in our paper is degenerated as the nonlinear functional differential equation (1) in (Zhang et al. 2009), so model studied in (Zhang et al. 2009; Shen and Cao 2011; Liu and Cao 2011; Phat and Trinh 2010) can be seen a special case of the model (5).

An illustrative example

In this section, an illustrative example will be given to check the validity and effectiveness of the proposed stability criterion obtained in Theorem 3.1.

Example

Consider the the following second-order switched interval networks with interval time-varying delay described by

$$ \left\{\begin{array}{l} \dot{x_{i}}(t)=-a_{i_{\sigma}}x_{i}(t) +\sum_{j=1}^{2}b^{(1)}_{ij_{\sigma}}f_{j}(x_{ij}(t))+ \sum_{j=1}^{2}b^{(2)}_{ij_{\sigma}}f_{j}(x_{ij}(t-\tau(t)))\\ a_{i_{\sigma}}\in{[\underline{a}_{i_{\sigma}}, \overline{a}_{i_{\sigma}}]},\quad b^{(k)}_{ij_{\sigma}} \in{[\underline{b}^{(k)}_{ij_{\sigma}}, \overline{b}^{(k)}_{ij_{\sigma}}]},\quad k=1,2,\end{array}\right. $$

(45)

where $\sigma(x(t)): R^{n}\rightarrow \{1,2\}$, and $\check{l}_{1}=0.1, \,\check{l}_{2}=0.2, \,\hat{l}_{1}=0.3, \,\hat{l}_{2}=0.6, \,\tau_{n}=0.5, \,\tau_{N}=2, \,\mu=\delta=0.5$, The networks system parameters are defined as

$$ \begin{aligned} \underline{A}_{1}&=\left(\begin{array}{cc}17.99&0\\ 0&14.99\end{array}\right), \quad\overline{A}_{1}=\left(\begin{array}{cc}18.01&0\\ 0&15.01\end{array}\right), \quad\underline{B}_{11}=\left(\begin{array}{cc}-0.17&0.1\\ 0.13&-0.14\end{array}\right), \\ \overline{B}_{11}&=\left(\begin{array}{cc}-0.15&0.12\\ 0.15&-0.12\end{array}\right), \underline{B}_{21}=\left(\begin{array}{cc}-0.47&0.13\\ 0.11&-0.54\end{array}\right), \overline{B}_{21}=\left(\begin{array}{cc}-0.45&0.15\\ 0.13&-0.52\end{array}\right), \\ \underline{A}_{2}&=\left(\begin{array}{cc}15.99&0\\ 0&16.99\end{array}\right), \quad\overline{A}_{2}=\left(\begin{array}{cc}16.01&0\\ 0&17.01\end{array}\right), \quad\underline{B}_{12}=\left(\begin{array}{cc}-0.208&0\\ 0&-0.208\end{array}\right), \\ \overline{B}_{12}&=\left(\begin{array}{cc}-0.188&0.02\\ 0.02&-0.188\end{array}\right), \quad\underline{B}_{22}=\left(\begin{array}{cc}-0.12&0.14\\ 0.05&-0.12\end{array}\right), \quad\overline{B}_{22}=\left(\begin{array}{cc}-0.09&0.16\\ 0.07&-0.09\end{array}\right), \end{aligned} $$

Solving the LMI in condition (ii) by using appropriate LMI solver in the Matlab, the feasible positive definite matrices P,  Q ₁,  Q ₂,  Q ₃, and diagonal matrices could be as

$$ \begin{aligned} P={\left(\begin{array}{cc}1.6853&0.0095\\ 0.0095&1.6431\end{array}\right), \quad \,Q_{1}=\left(\begin{array}{cc}17.6516&-0.0006\\ -0.0006&17.6480\end{array}\right),} \\ Q_{2}={\left(\begin{array}{cc}17.6708&-0.0000\\ -0.0000&17.6655\end{array}\right), \,Q_{3}=\left(\begin{array}{cc}17.6835&0.0000\\ 0.0000&17.6809\end{array}\right),} \end{aligned} $$

Let ξ₁ = 0.1,ξ₂ = 0.9, it can be shown that

$$ G_{1}(A_{0}^{1},Q_{1},Q_{2},Q_{3})=\left(\begin{array}{cc}-7.6637&-0.3142\\ -0.3142&3.7002\end{array}\right), G_{2}(A_{0}^{2},Q_{1},Q_{2},Q_{3})=\left(\begin{array}{cc}-0.9226&-0.3142\\ -0.3142&-2.8724\end{array}\right) $$

Moreover, the sum

$$ \xi_{1}G_{1}(A_{0}^{1},Q_{1},Q_{2},Q_{3}) +\xi_{2}G_{2}(A_{0}^{2},Q_{1},Q_{2},Q_{3})= \left(\begin{array}{cc}-1.5967 &-0.3142\\ -0.3142&-2.2152\end{array}\right)<0 $$

The sets $\Upomega_{1}$ and $\Upomega_{2}$ are given as

$$ \begin{aligned} \Upomega_{1}&=\{(x_{1},x_{2})\in R^{2}:-7.6637x_{1}^{2}-0.6284x_{1}x_{2}+3.7002x_{2}^{2}<0\}, \\ \Upomega_{2}&=\{(x_{1},x_{2})\in R^{2}:0.9226x_{1}^{2}+0.6284x_{1}x_{2}+2.8724x_{2}^{2}>0\}. \\ \end{aligned} $$

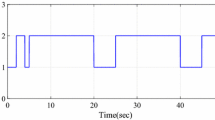
then, the switching regions (Figs. 1, 2) are defined as

$$ \begin{aligned} \bar{\Upomega_{1}}&=\{(x_{1},x_{2})\in R^{2}:-7.6637x_{1}^{2}-0.6284x_{1}x_{2}+3.7002x_{2}^{2}\leq0 \}, \\ \bar{\Upomega_{2}}&=\{(x_{1},x_{2})\in R^{2}:-7.6637x_{1}^{2}-0.6284x_{1}x_{2}+3.7002x_{2}^{2}\geq0 \}. \end{aligned} $$

Fig. 1

Regions $\bar{\Upomega}_{1}$

Fig. 2

Regions $\bar{\Upomega}_{2}$

The switching rule σ(x(t)) can be given by

$$ \sigma(t)= \left\{\begin{array}{ll}1, &if\,x(t)\in\bar{\Upomega_{1}},\\ 2, &if \,x(t)\in\bar{\Upomega_{2}}.\end{array}\right. $$

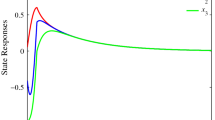
By Theorem 3.1, this switched interval network (45) is global robust asymptotic stable.

Conclusion

In this paper, we have proposed a new scheme of switched interval networks with interval time-varying delay and general activation functions. By introducing the delay fractioning approach, the variation interval of the time delay is divided into three subintervals, by checking the variation of the Lyapunov functional for the case when the value of the time delay is in every subinterval, the switching rule which depends on the state of the network is designed and some new delay-dependent robust stability criteria are derived in terms of LMIs. An illustrative example has been also provided to demonstrate the validity of the proposed robust asymptotic stability criteria for switched interval networks.