An excellent derivative-free multiple-zero finding numerical technique of optimal eighth order convergence

Abstract

A number of higher order Newton-like methods (i.e. the methods requiring both function and derivative evaluations) are available in literature for multiple zeros of a nonlinear function. However, higher order Traub-Steffensen-like methods (i.e. the methods requiring only function evaluations) for computing multiple zeros are rare in literature. Traub-Steffensen-like iterations are important in the circumstances when derivatives are complicated to evaluate or expensive to compute. Motivated by this fact, here we present an efficient and rapid-converging Traub-Steffensen-like algorithm to locate multiple zeros. The method achieves eighth order convergence by using only four function evaluations per iteration, therefore, this convergence rate is optimal. Performance is demonstrated by applying the method on different problems including some real life models. The computed results are compared with that of existing optimal eighth-order Newton-like techniques to reveal the computational efficiency of the new approach.

1 Introduction

Locating a zero of a nonlinear function is very significant problem in many areas such as Physics, Chemistry, Mathematical Biology and also in Engineering science to name a few [2, 3, 14, 20]. This is the case since problems from these areas are reduced to finding a zero. In general, closed form solutions can not be obtained so researchers use iterative methods for approximating the solution. In this work, we develop derivative-free methods to compute a multiple root (say, $t^*$) with multiplicity m, that means, $f^{(k)}(t^*) = 0, k = 0, 1, 2, . . . , m - 1$ and $f^{(m)}(t^*) \ne 0$, of the equation $f(t) = 0$.

A plethora of higher order methods, either independent or dependent on the Newton’s method [17]

$$\begin{aligned} t_{i+1}=t_i-m \frac{f(t_i)}{f'(t_i)}, \ \ \ i=0,\, 1,\, 2, \ldots \end{aligned}$$

(1)

have been proposed in literature, see [1, 4,5,6, 9, 11,12,13, 16, 19, 23, 24]. Such methods require the evaluation of derivatives of either first or first and second order both of the function f. However, higher order derivative-free methods to handle the case of multiple roots are yet to be investigated. The derivative-free methods are important in the situations when derivative $f'$ is complicated to evaluate or is expensive to obtain. The most basic derivative-free method is the well-known Traub-Steffensen method [20] which actually replaces $f'$ in the classical Newton’s method by a suitable approximation based on finite difference formula,

$$\begin{aligned} f'(t_i)\simeq \frac{f(t_i +\alpha f(t_i))-f(t_i)}{\alpha f(t_i)}= f^{\angle }(w_i,t_i), \end{aligned}$$

where $w_i= t_i +\alpha f(t_i)$ and $\alpha \in {\mathbb {R}}{\setminus }\{0\}$. In this way the modified Newton’s method (1) can be transformed to Traub-Steffensen iterative scheme

$$\begin{aligned} t_{i+1}= t_i-m \frac{f(t_i)}{f^{\angle }(w_i,t_i)}. \end{aligned}$$

(2)

The Traub-Steffensen iteration (2) is indeed a noticeable improvement of Newton’s iteration for the reason that it preserves the order of convergence without requiring any derivative computation.

Very recently, Sharma et al. in [18] have developed two-point derivative-free (Traub-Steffensen-like) methods of fourth order convergence to compute the multiple zeros. These methods require three function evaluations per iteration and, therefore, according to Kung-Traub hypothesis these possess optimal convergence [15]. According to this hypothesis multi-point methods without memory based on n function evaluations have optimal order $2^{n-1}$. Such methods are usually known as optimal methods. In this work our aim is to develop efficient higher order iterative method that satisfies Kung-Traub conjecture. Consequently, we introduce a derivative-free eighth order scheme that requires four new information of the function f per iteration, and hence the method has optimal convergence of eighth order in the sense of Kung-Traub hypothesis. The iterative scheme uses the Traub-Steffensen iteration (2) in the first step and Traub-Steffensen-like iterations in the second and third steps.

Rest of the paper is precisely as follows. In Sect. 2, the scheme of new iterative method is formulated and convergence properties for some particular cases are explored. In Sect. 3, the main result showing eighth order of convergence is presented. To test the applicability and efficiency of the method some numerical experiments are performed in Sect. 4. A comparison with the existing methods is also performed in this section. Finally, a conclusion of the main points is given in Sect. 5.

2 Formulation of scheme

Higher order Newton-like methods have been developed using various approaches by the researchers around the world. Some useful techniques are: Composition approach, Sampling approach, Interpolation approach, Geometrical approach, Adomian approach and Weight-function approach. Of these the Weight-function approach has been used extensively in recent times, see, for example [4,5,6, 11, 12, 23, 24] and references cited therein. In the present work of computing a multiple root with multiplicity $m > 1$, we also use this technique. Thus, consider the following three-step iterative scheme:

$$\begin{aligned} \left\{ \begin{array}{l} y_{i} = \ t_i-m \frac{f(t_i)}{f^{\angle }(w_i,t_i)}, \\ z_{i} = \ y_i - G(u_i,v_i) \frac{f(t_i)}{f^{\angle }(w_i,t_i)}, \\ t_{i+1} = \ z_i - s_i H(u_i,v_i,r_i) \frac{f(t_i)}{f^{\angle }(w_i,t_i)}, \end{array}\right. \end{aligned}$$

(3)

where the functions $G: {\mathbb {C}}^2\rightarrow {\mathbb {C}}$ and $H: {\mathbb {C}}^3\rightarrow {\mathbb {C}}$ are holomorphic in a neighborhood of (0, 0) and (0, 0, 0), respectively with $u_i =\root m \of {\frac{f(y_i)}{f(t_i)}}$, $v_i =\root m \of {\frac{f(w_i)}{f(t_i)}}$, $r_i =\root m \of {\frac{f(z_i)}{f(y_i)}}$, $s_i=\root m \of {\frac{f(z_i)}{f(t_i)}}$. Notice that this is a three-step scheme with first step as the Traub-Steffensen iteration (2) and next two steps as the Traub-Steffensen-like iterations. The second and third steps are weighted by the factors G and H. Hence, these steps are also called weighted Traub-Steffensen steps and the factors G and H are called weight factors or weight functions.

In what follows, we shall explore certain conditions under which the scheme (3) achieves convergence of order as high as possible. For simplicity the results are presented separately for different m. This strategy will also help us to construct the generalized iterative scheme. Firstly, for the case $m=2$ we prove the following theorem:

Theorem 1

Let $f: {\mathbb {C}}\rightarrow {\mathbb {C}}$ be an analytic function in a region enclosing a multiple zero $t^*$ with multiplicity 2. Assume that initial guess $t_0$ is sufficiently close to $t^*$, then the local order of convergence of scheme (3) is at least 8, provided that $G_{00} = 0$, $G_{10} = 3$, $G_{01} = 0$, $G_{20} = 8$, $G_{11} = -1$, $G_{02} = 0$, $H_{000} = 3$, $H_{100} = 4$, $H_{010} = -1$, $H_{110} = 1$, $H_{210} = 2-2H_{200}$, $H_{020} = 0$, $H_{120} = -2$, $H_{220} = 4+2H_{200}$, $H_{320} = -96-2H_{300}-2H_{310}$, $H_{011} = 5-2H_{001}$, $H_{021} = -6+2H_{001}$, $H_{121} = 16-2H_{101}-2H_{111}$, $\text {max} \ \{|H_{001}|,|H_{101}|,|H_{111}|,|H_{200}|,|H_{201}|,|H_{211}|,|H_{221}|,|H_{300}|,|H_{310}|\} < \infty$, where $G_{kj}=\frac{\partial ^{k+j}}{\partial {u^k}\partial {v^j}}G({u_i,v_i})|_{(u_i=0,v_i=0)}$, $0\le k,j\le 2$ and $H_{abc}=\frac{\partial ^{a+b+c}}{\partial {u^a}\partial {v^b}\partial {r^c}}H({u_i,v_i,r_i})|_{(u_i=0,v_i=0,r_i=0)}$, for $0\le a\le 3$, $0\le b\le 2$, $0\le c\le 1$.

Proof

Let the error at i-th iteration be $e_{i}=t_{i}-t^*$. Using the Taylor’s expansion of $f(t_i)$ about $t^*$ and taking into account that $f(t^*)=0$, $f'(t^*)=0$ and $f^{(2)}(t^*)\ne 0,$ we have

$$\begin{aligned} f(t_i) = \frac{f^{(2)}(t^*)}{2!}e_i^2 \big (1+ A_1 e_i+ A_2 e_i^2+A_3 e_i^3+A_4 e_i^4+A_5 e_i^5+A_6 e_i^6+A_7 e_i^7+A_8 e_i^8+\cdots \big ), \end{aligned}$$

(4)

where $A_n = \frac{2!}{(2+n)!}\frac{f^{(2+n)}(t^*)}{f^{(2)}(t^*)}$ for $n\in {\mathbb {N}}$.

Similarly we have the Taylor’s expansion of $f(w_i)$ about $t^*$

$$\begin{aligned} f(w_i) = \frac{f^{(2)}(t^*)}{2!}e_{w_i}^2 \big (1+ A_1 e_{w_i}+ A_2 e_{w_i}^2+A_3 e_{w_i}^3+A_4 e_{w_i}^4+A_5 e_{w_i}^5+A_6 e_{w_i}^6+\cdots \big ), \end{aligned}$$

(5)

where $e_{w_i}= w_{i}-t^* = e_i+ \frac{\alpha f^{(2)}(t^*)}{2!}e_i^2 \big (1+ A_1 e_i+ A_2 e_i^2+A_3 e_i^3+A_4 e_i^4+A_5 e_i^5+A_6 e_i^6+A_7 e_i^7+\cdots \big ).$

Then the first step of (3) yields

$$\begin{aligned} e_{y_i}&= \ y_i-t^* \nonumber \\&= \frac{1}{2}\Big (\frac{\alpha f^{(2)}(t^*)}{2}+A_1\Big )e_i^2-\frac{1}{16}\big ((\alpha f^{(2)}(t^*))^2-8 \alpha f^{(2)}(t^*) A_1\nonumber \\&\quad +12 A_1^2-16A_2\big )e_i^3 + \frac{1}{64}\big ((\alpha f^{(2)}(t^*))^3- 20 \alpha f^{(2)}(t^*) A_1^2 + 72 A_1^3 \nonumber \\&\quad + 64 \alpha f^{(2)}(t^*)A_2 -10 A_1 \big ((\alpha f^{(2)}(t^*))^2 + 16 A_2\big ) + 96 A_3\big )e_i^4 \nonumber \\&\quad +\frac{1}{256}\big (-(\alpha f^{(2)}(t^*))^4 + 144 \alpha f^{(2)}(t^*) A_1^3- 432 A_1^4 \nonumber \\&\quad - 48 A_1^2 \big ((\alpha f^{(2)}(t^*))^2 -28 A_2\big ) - 16 (\alpha f^{(2)}(t^*))^2 A_2- 512 A_2^2 \nonumber \\&\quad + 4 A_1 \big (3 (\alpha f^{(2)}(t^*))^3 - 96 \alpha f^{(2)}(t^*) A_2 - 224 A_3\big ) + 448 \alpha f^{(2)}(t^*) A_3 \nonumber \\&\quad + 512 A_4\big )e_i^5 +\sum _{n=1}^{3}\phi _n e_i^{n+5}+O(e_i^9), \end{aligned}$$

(6)

where $\phi _n = \phi _n (\alpha ,A_1,A_2,A_3,A_4,A_5,A_6,A_7)$, $n=1, 2, 3.$ Here, the expressions of $\phi _1$, $\phi _2$ and $\phi _3$ are not being produced explicitly since they are very lengthy.

Expanding $f(y_i)$ about $t^*$, it follows that

$$\begin{aligned} f(y_i) = \ \frac{f^{(2)}(t^*)}{2!}e_{y_i}^2 \big (1+A_1 e_{y_i}+A_2 e_{y_i}^2+A_3 e_{y_i}^3+A_4 e_{y_i}^4+A_5 e_{y_i}^5+\cdots \big ). \end{aligned}$$

(7)

Using (4), (5) and (7) in $u_i$ and $v_i$, some simple calculations yield

$$\begin{aligned} u_i =&\ \frac{1}{2}\Big (\frac{\alpha f^{(2)}(t^*)}{2}+A_1\Big )e_i-\frac{1}{16}\big ((\alpha f^{(2)}(t^*))^2- 6 \alpha f^{(2)}(t^*) A_1 +16( A_1^2 - A_2)\big )e_i^2 \nonumber \\&\ +\frac{1}{64}\big ( (\alpha f^{(2)}(t^*))^3 - 22 \alpha f^{(2)}(t^*) A_1^2 + 4\big (29 A_1^3 + 14 \alpha f^{(2)}(t^*) A_2\big )\nonumber \\&\ -2 A_1 \big (3 (\alpha f^{(2)}(t^*))^2 + 104 A_2\big ) + 96 A_3\big )e_i^3 \nonumber \\&\ +\frac{1}{256} \big (212 \alpha f^{(2)}(t^*) A_1^3 - 800 A_1^4 +2 A_1^2 (-7(\alpha f^{(2)}(t^*))^2 + 1040 A_2) \nonumber \\&\ +2 A_1 \big (3 (\alpha f^{(2)}(t^*))^3 - 232 \alpha f^{(2)}(t^*) A_2 \nonumber \\&\ - 576 A_3\big ) -\big ((\alpha f^{(2)}(t^*))^4 + 8 (\alpha f^{(2)}(t^*))^2 A_2 + 640 A_2^2 \nonumber \\&- 416 \alpha f^{(2)}(t^*) A_3 -502 A_4\big )\big )e_i^4 +\sum _{n=1}^{4}\psi _n e_i^{n+4}+O(e_i^9), \end{aligned}$$

(8)

and

$$\begin{aligned} v_i =&\ 1 + \frac{\alpha f^{(2)}(t^*)}{2} e_i\Big (1+\frac{3}{2}A_1 e_i+\frac{1}{4}(\alpha f^{(2)}(t^*) A_1 + 8 A_2) e_i^2\nonumber \\&\ + \frac{1}{16}\big (3 \alpha f^{(2)}(t^*) A_1^2 + 12 \alpha f^{(2)}(t^*) A_2 +40 A_3\big ) e_i^3 \nonumber \\&\ -\frac{1}{32}\big ((\alpha f^{(2)}(t^*))^2 A_1^2 - 24 \alpha f^{(2)}(t^*) A_1 A_2 -4 \big ((\alpha f^{(2)}(t^*))^2 A_2 \nonumber \\&\ + 12(\alpha f^{(2)}(t^*) A_3 +2 A_4)\big )\big )e_i^4 \nonumber \\&\ -\frac{1}{64}\big ((\alpha f^{(2)}(t^*))^2 A_1^3 - 4 \alpha f^{(2)}(t^*) A_1 (\alpha f^{(2)}(t^*) A_2 + 22 A_3) \nonumber \\&\ -8 \big (\alpha f^{(2)}(t^*) A_2^2 + (\alpha f^{(2)}(t^*))^2 A_3 \nonumber \\&\ + 5 \alpha f^{(2)}(t^*) A_4 +7 A_5\big )\big )e_i^5+O(e_i^6)\Big ). \end{aligned}$$

(9)

where $\psi _n = \psi _n (\alpha ,A_1,A_2,A_3,A_4,A_5,A_6,A_7)$, $n=1, 2, 3, 4$.

Developing $G(u_i,v_i)$ by Taylor formula in the neighborhood of origin (0, 0)

$$\begin{aligned} G(u_i,v_i) \approx G_{00} + u_i G_{10}+v_i G_{01} + \frac{1}{2} u_i^2 G_{20}+u_i v_i G_{11}+\frac{1}{2}v_i^2 G_{02}. \end{aligned}$$

(10)

By using (4)-(10) in the second step of (3), we obtain that

$$\begin{aligned} e_{z_i} =&\ z_i - t^* \nonumber \\ =&\ -\frac{1}{4}(G_{02}+2 G_{00} +2 G_{01})e_i+\frac{1}{16} \big (\alpha f^{(2)}(t^*) \nonumber \\&(4 + 2 G_{00} - 2 G_{01} - 3 G_{02} - 2 G_{10} - 2 G_{11}) \nonumber \\&+ 2(4 + 2 G_{00} + 2 G_{01} + G_{02} - 2 G_{10} - 2 G_{11}) A_1\big )e_i^2\nonumber \\&-\frac{1}{64}\big ((\alpha f^{(2)}(t^*))^2 (4 + 2 G_{00} - 2 G_{01} + G_{02}- 4 G_{10} \nonumber \\&+ G_{20})+ 4 \alpha f^{(2)}(t^*) (-8 - 4 G_{00} + 2 G_{02} + G_{10} + 3 G_{11} + G_{20}) A_1 \nonumber \\&+ 4(12 + 6 G_{00} + 6 G_{01}+ 3 G_{02} - 10 G_{10} \nonumber \\&- 10 G_{11} + G_{20}) A_1^2- 16 (4 + 2 G_{00} + 2 G_{01} + G_{02} - 2 G_{10} - 2 G_{11}) A_2\big )e_i^3\nonumber \\&+\sum _{n=1}^{5} \delta _n e_i^{n+3}+O(e_i^9), \end{aligned}$$

(11)

where $\delta _n = \delta _n (\alpha ,A_1,A_2,A_3,A_4,A_5,A_6,A_7,G_{00},G_{10},G_{01},G_{20},G_{11},G_{02})$, $n=1, 2, 3, 4, 5.$

It is clear from the above equation (11) that we will obtain at least fourth order convergence if we set coefficients of $e_i$, $e_i^2$ and $e_i^3$ simultaneously equal to zero. Then solving the resulting equations, one gets

$$\begin{aligned} G_{00} = 0, \ \ G_{10} = 3, \ \ G_{01} = 0, \ \ G_{20}= 8, \ \ G_{11}= -1, \ \ G_{02}= 0. \end{aligned}$$

(12)

By using (12), the error equation (11) is given by

$$\begin{aligned} e_{z_{i}}&= \frac{1}{16}\Big (\frac{\alpha f^{(2)}(t^*)}{2} + A_1\Big )\big ((\alpha f^{(2)}(t^*))^2 + 3 \alpha f^{(2)}(t^*) A_1 + 11 A_1^2 - 4 A_2 \big )e_i^4\nonumber \\ {}&\quad +\sum _{n=1}^{4}\xi _n e_i^{n+4}+O(e_i^9), \end{aligned}$$

(13)

where $\xi _n = \xi _n (\alpha ,A_1,A_2,A_3,A_4,A_5,A_6)$, $n=1, 2, 3, 4.$ Expansion of $f(z_i)$ about $t^*$ leads us to the expression

$$\begin{aligned} f(z_i) = \frac{f^{(2)}(t^*)}{2!}e_{z_i}^2 \big (1+A_1 e_{z_i}+A_2 e_{z_i}^2+A_3 e_{z_i}^3+A_4 e_{z_i}^4+\cdots \big ). \end{aligned}$$

(14)

Using (4), (7) and (14), we obtain

$$\begin{aligned} r_i&= \frac{1}{8}\big ((\alpha f^{(2)}(t^*))^2 + 3 \alpha f^{(2)}(t^*) A_1 +11 A_1^2 - 4 A_2\big )e_i^2\nonumber \\&\quad \mathbf{}-\frac{1}{32} \big (2(\alpha f^{(2)}(t^*))^3 +4 \alpha f^{(2)}(t^*) A_1^2 + 148 A_1^3 \nonumber \\&\quad - 16 \alpha f^{(2)}(t^*) A_2 - A_1 \big (5(\alpha f^{(2)}(t^*))^2 + 176 A_2\big ) + 32 A_3\big )e_i^3\nonumber \\&\quad +\sum _{n=1}^{5}\zeta _n e_i^{n+3}+O(e_i^9), \end{aligned}$$

(15)

where $\zeta _n = \zeta _n (\alpha ,A_1,A_2,A_3,A_4,A_5,A_6,A_7)$, $n=1, 2, 3, 4, 5$

and

$$\begin{aligned} s_i =&\ \frac{1}{16}\Big (\frac{\alpha f^{(2)}(t^*)}{2} + A_1\Big ) \big ((\alpha f^{(2)}(t^*))^2 + 3 \alpha f^{(2)}(t^*) A_1 +11 A_1^2 - 4 A_2\big )e_i^3 \nonumber \\&\ +\sum _{n=1}^{5}\chi _n e_i^{n+3}+O(e_i^9), \end{aligned}$$

(16)

where $\chi _n = \chi _n (\alpha ,A_1,A_2,A_3,A_4,A_5,A_6)$, $n=1, 2, 3, 4, 5$.

Developing by Taylor formula the weight function $H(u_i,v_i,r_i)$ in the neighborhood of origin (0, 0, 0), we have

$$\begin{aligned}&H(u_i,v_i,r_i) \nonumber \\&\quad = H_{000} + u_i H_{100} + \frac{1}{2} u_i^2 H_{200} + \frac{1}{6} u_i^3 H_{300}\nonumber \\&\qquad + v_i \Big (H_{010} + u_i H_{110} + \frac{1}{2} u_i^2 H_{210} + \frac{1}{6} u_i^3 H_{310}\Big ) \nonumber \\&\qquad + v_i^2 \Big (\frac{1}{2} H_{020} + \frac{1}{2} u_i H_{120} + \frac{1}{4} u_i^2 H_{220} + \frac{1}{12} u_i^3 H_{320}\Big )\nonumber \\&\qquad + r_i \Big (H_{001} + u_i H_{101} + \frac{1}{2} u_i^2 H_{201}\nonumber \\&\qquad + v_i \Big (H_{011} + u_i H_{111} + \frac{1}{2} u_i^2 H_{211}\Big ) + v_i^2 \Big (\frac{1}{2} H_{021} + \frac{1}{2} u_i H_{121} + \frac{1}{4} u_i^2 H_{221}\Big )\Big ). \end{aligned}$$

(17)

By using (4)-(17) in third step of (3), we have

$$\begin{aligned} e_{i+1} =&\ t_{i+1} - t^* \nonumber \\ =&\ \frac{1}{64}\Big (\frac{\alpha f^{(2)}(t^*)}{2} + A_1\Big ) \big ( (\alpha f^{(2)}(t^*))^2 + 3 \alpha f^{(2)}(t^*) A_1 + 11 A_1^2 - 4 A_2\big )\nonumber \\&\ (4 \ - 2 H_{000} - 2 H_{010} - H_{020}) e_i^4 +\sum _{n=1}^{4}\eta _n e_i^{n+4} +O(e_i^9), \end{aligned}$$

(18)

where $\eta _n = \eta _n(\alpha ,A_1,A_2,A_3,A_4,A_5,A_6,H_{abc})$, $n=1,2,3$ and $0\le a\le 3$, $0\le b\le 2$, $0\le c\le 1$.

It is clear from the above equation (18) that we will obtain at least eighth order convergence if we set coefficients of $e_i^4$, $e_i^5$, $e_i^6$ and $e_i^7$ simultaneously equal to zero. Then solving the resulting equations, we get

$$\begin{aligned}&\ H_{000} = 3, \, H_{100} = 4, \, H_{010} = -1, \, H_{110} = 1,\nonumber \\&\quad H_{210} = 2-2H_{200}, \, H_{020} = 0, \, H_{120} = -2, \, H_{220} = 4+2H_{200}, \nonumber \\&\ H_{320} = -96-2H_{300}-2H_{310}, \, H_{011} = 5-2H_{001},\nonumber \\&\quad H_{021} = -6+2H_{001}, \, H_{121} = 16-2H_{101}-2H_{111}. \end{aligned}$$

(19)

As a result the error equation is given by

$$\begin{aligned} e_{i+1} =&\ -\frac{1}{49152}\Big (\frac{\alpha f^{(2)}(t^*)}{2} + A_1\Big ) \big ((\alpha f^{(2)}(t^*))^2 +3 \alpha f^{(2)}(t^*) A_1 + 11 A_1^2 -4 A_2 \big ) \\&\ \times \Big (8\alpha f^{(2)}(t^*) (48 - 132 H_{101} - 66 H_{111} + 42 H_{201} + 42 H_{211} \\&\ + 21 H_{221} - 4 H_{300} - 2 H_{310}) A_1^3 \\&\ + 12 (-884 + 22 H_{201} + 22 H_{211} + 11 H_{221}) A_1^4 + 3 A_1^2 ((\alpha f^{(2)}(t^*))^2 \\&\ (176 + 176 H_{001} -272 H_{101} - 136 H_{111}\\&\ + 16 H_{200} + 54 H_{201} + 54 H_{211} + 27 H_{221} - 16 H_{300} - 8 H_{310}) \\&\ - 16 (-168 + 2 H_{201} + 2 H_{211} + H_{221}) A_2)\\&\ + 3 A_1 ((\alpha f^{(2)}(t^*))^3 (-8 + 48 H_{001} - 80 H_{101} - 40 H_{111} \\&\ + 16 H_{200} + 14 H_{201} + 14 H_{211} + 7 H_{221} - 8 H_{300} \\&\ - 4 H_{310})+ 16 \alpha f^{(2)}(t^*) (8 H_{101} + 4 H_{111} - 2 H_{201}- 2 H_{211}\\&\ - H_{221}) A_2 - 256 A_3)+ ((\alpha f^{(2)}(t^*))^4 (48 H_{001} \\&\ - 48 H_{101}- 24 H_{111} + 12 H_{200} + 6 H_{201} + 6 H_{211}+ 3 H_{221}\\&\ - 4 H_{300} - 2 H_{310}) - 3 (\alpha f^{(2)}(t^*))^2 (48 \\&\ + 16 H_{001} - 16 H_{101} - 8 H_{111}+ 2 H_{201} + 2 H_{211} + H_{221}) A_2- 192 A_2^2 \\&\ - 96 \alpha f^{(2)}(t^*) A_3)\Big )e_i^8+O(e_i^9). \end{aligned}$$

Thus, the theorem is proved. $\square$

Theorem 2

Using the assumption and notation of Theorem 1, the convergence order of (3) for the case $m = 3$ is at least 8, if $G_{00} = 0$, $G_{01} = 0$, $G_{20}= 12$, $G_{11}= 3-G_{10}$, $G_{02}= 0$, $H_{010} = 3+G_{10}-2H_{000}$, $H_{110} = 3+ 2G_{10}-2H_{100}$, $H_{020} = 2H_{000}-2G_{10}$, $H_{120} = 6-4G_{10}+2H_{100}$, $H_{220} = 12-2 H_{200}-2H_{210}$, $H_{320} = -144-2 H_{300}-2H_{310}$, $H_{021} = 6-2 H_{001}-2H_{011}$, $H_{121} = 24-2 H_{101}-2H_{111}$, wherein $\text {max} \ \{|G_{10}|,|H_{000}|,|H_{001}|,|H_{011}|,|H_{200}|,|H_{201}|,|H_{210}|,|H_{211}|,|H_{221}|\} < \infty$.

Proof

By Taylor’s expansion of $f(t_i)$ about $t^*$ taking into account that $f(t^*)=0$, $f'(t^*)=0$, $f^{(2)}(t^*)=0$ and $f^{(3)}(t^*)\ne 0,$ we have

$$\begin{aligned} f(t_i) = \frac{f^{(3)}(t^*)}{3!}e_i^3 \big (1+ B_1 e_i+ B_2 e_i^2+B_3 e_i^3+B_4 e_i^4+ B_5 e_i^5+B_6 e_i^6+B_7 e_i^7+B_8 e_i^8+\cdots \big ), \end{aligned}$$

(20)

where $B_n = \frac{3!}{(3+n)!}\frac{f^{(3+n)}(t^*)}{f^{(3)}(t^*)}$ for $n\in {\mathbb {N}}$.

Also Taylor’s expansion of $f(w_k)$ about $t^*$ yields

$$\begin{aligned} f(w_i) = \frac{f^{(3)}(t^*)}{3!}e_{w_i}^3 \big (1+ B_1 e_{w_i}+ B_2 e_{w_i}^2+B_3 e_{w_i}^3+B_4 e_{w_i}^4+ B_5 e_{w_i}^5+B_6 e_{w_i}^6+\cdots \big ), \end{aligned}$$

(21)

where $e_{w_i}= w_{i}-t^* = e_i + \frac{\alpha f^{(3)}(t^*)}{3!}e_i^3 \big (1+ B_1 e_i+ B_2 e_i^2+B_3 e_i^3+B_4 e_i^4+ B_5 e_i^5+B_6 e_i^6+B_7 e_i^7+\cdots \big ).$

Then the first step of (3) yields

$$\begin{aligned} e_{y_i} =&\ y_i-t^* \nonumber \\ =&\ \frac{B_1}{3}e_i^2 +\frac{1}{18} \big (3\alpha f^{(3)}(t^*)- 8 B_1^2 + 12 B_2\big )e_i^3 \nonumber \\&\ + \frac{1}{27} \big (16 B_1^3 +3 B_1 \big (2\alpha f^{(3)}(t^*)- 13 B_2\big ) + 27 B_3\big )e_i^4 \nonumber \\&\ -\frac{1}{162}\big (128 B_1^4 +9B_1^2(\alpha f^{(3)}(t^*)-48 B_2)+324 B_1 B_2+3\big ((\alpha f^{(3)}(t^*))^2 \nonumber \\&\ -18 \alpha f^{(3)}(t^*) B_2+60 B_2^2-72 B_4\big )\big )e_i^5\nonumber \\&\ +\frac{1}{486}\Big (512 B_1^5 + 6 B_1^3(7 \alpha f^{(3)}(t^*) -368 B_2) + 1728 B_1^2 B_3 \nonumber \\&\ -3 B_1 \big (7 (\alpha f^{(3)}(t^*))^2 + 42 \alpha f^{(3)}(t^*) B_2 \nonumber \\&\ - 630 B_2^2 + 414 B_4\big ) +81 \big (3 (\alpha f^{(3)}(t^*) - 6 B_2) B_3 + 10 B_5\big )\Big )e_i^6\nonumber \\&\ +\sum _{n=1}^{2}\phi '_n e_i^{n+6} +O(e_i^9), \end{aligned}$$

(22)

where $\phi '_n = \phi '_n (\alpha ,B_1,B_2,B_3,B_4,B_5,B_6,B_7)$, $n=1, 2.$ Also the expansion of $f(y_i)$ about $t^*$ is

$$\begin{aligned} f(y_i) = \frac{f^{(3)}(t^*)}{3!}e_{y_i}^3 \big (1+B_1 e_{y_i}+B_2 e_{y_i}^2+B_3 e_{y_i}^3+B_4 e_{y_i}^4+B_5 e_{y_i}^5+\cdots \big ). \end{aligned}$$

(23)

Then from (20), (21) and (23), it follows that

$$\begin{aligned} u_i =&\ \frac{B_1}{3}e_i +\frac{1}{18} \big (3\alpha f^{(3)}(t^*) -10 B_1^2 + 12 B_2\big )e_i^2 + \frac{1}{27}\nonumber \\&\ \big (23 B_1^3+ \frac{3}{2} B_1\big (3 f^{(3)}(t^*) \alpha -32 B_2\big ) + 27 B_3\big )e_i^3 \nonumber \\&\ -\frac{1}{486} \Big (610 B_1^4 + B_1^2 (27 f^{(3)}(t^*) \alpha - 1818 B_2) +1188 B_1 B_3 \nonumber \\&\ +9 \big ((f^{(3)}(t^*) \alpha )^2 - 15 f^{(3)}(t^*) \alpha B_2 \nonumber \\&\ + 72 B_2^2 - 72 B_4\big )\Big )e_i^4 +\sum _{n=1}^{4}\psi '_n e_i^{n+4} +O(e_i^9), \end{aligned}$$

(24)

where $\psi '_n = \psi '_n (\alpha ,B_1,B_2,B_3,B_4,B_5,B_6,B_7)$, $n=1, 2, 3, 4$

and

$$\begin{aligned} v_i =&1 + \frac{\alpha f^{(3)}(t^*)}{3!} e_i^2\Big (1+\frac{4}{3}B_1 e_i+\frac{5}{3}B_2 e_i^2+\frac{1}{18}(\alpha f^{(3)}(t^*) B_1+ 36 B_3)e_i^3\nonumber \\&+\frac{1}{54}\big (2 \alpha f^{(3)}(t^*) B_1^2+9\alpha f^{(3)}(t^*) B_2 +126 B_4\big )e_i^4\nonumber \\&+\frac{2}{54}\big (4 \alpha f^{(3)}(t^*) B_1 B_2 +9\alpha f^{(3)}(t^*) B_3+72 B_5\big )e_i^5 +O(e_i^6)\Big ). \end{aligned}$$

(25)

The Taylor formula of $G(u_i,v_i)$ in the neighborhood of origin (0, 0) is given by

$$\begin{aligned} G(u_i,v_i) \approx G_{00} + u_i G_{10}+v_i G_{01} + \frac{1}{2} u_i^2 G_{20}+u_i v_i G_{11}+\frac{1}{2}v_i^2 G_{02}. \end{aligned}$$

(26)

By using (20)–(26) in the second step of (3), we obtain

$$\begin{aligned} e_{z_i} =&\ z_i - t^* \nonumber \\ =&\ -\frac{1}{6} (2 G_{00} +2 G_{01} + G_{02}) e_i+\frac{1}{18}\big (6 + 2 G_{00} + 2 G_{01} \nonumber \\&\ + G_{02} - 2 G_{10} - 2 G_{11}\big )B_1 e_i^2 -\frac{1}{108}\big (2(24 + 8 G_{00} + 8 G_{01} \nonumber \\&\ + 4 G_{02} - 12 G_{10} - 12 G_{11} + G_{20}) B_1^2 - 3 \big (\alpha f^{(3)}(t^*) (2 G_{00} - G_{02} \nonumber \\&\ - 2 (-3 + G_{10} + G_{11})) + 4 (6 + 2 G_{00} + 2 G_{01} + G_{02} - 2 G_{10}- 2 G_{11}) B_2\big )\big )e_i^3 \nonumber \\&\ +\sum _{n=1}^{5} \delta '_n e_i^{n+3}+O(e_i^9), \end{aligned}$$

(27)

where $\delta '_n = \delta '_n (\alpha ,B_1,B_2,B_3,B_4,B_5,B_6,B_7,G_{00},G_{10},G_{01},G_{20},G_{11},G_{02})$, $n=1, 2, 3, 4, 5.$

It is clear from the above equation (27) that we will obtain at least fourth order convergence if we set coefficients of $e_i$, $e_i^2$ and $e_i^3$ simultaneously equal to zero. Then solving the resulting equations, one gets

$$\begin{aligned} G_{01} = -2 G_{00}, \ \ G_{20}= 12, \ \ G_{11}= 3-G_{10}, \ \ G_{02}= 2 G_{00}. \end{aligned}$$

(28)

By using (28), the error Eq. (27) is given by

$$\begin{aligned} e_{z_{i}} =&\ \frac{B_1}{54}\big ((G_{10} - 6)\alpha f^{(3)}(t^*)+ 12 B_1^2-6B_2\big )e_i^4 \nonumber \\&\ -\frac{1}{972}\Big (880 B_1^4 + 12 B_1^2 \big (\alpha f^{(3)}(t^*) (-21 + G_{10}) - 120 B_2\big ) \nonumber \\&\ + 3 (3(\alpha f^{(3)}(t^*))^2 (6 + G_{00}-G_{10}) + 6 \alpha f^{(3)}(t^*)(15-2G_{10}) B_2+72 B_2^2) \nonumber \\&\ + 216 B_1 B_3 \Big ) e_i^5 +\sum _{n=1}^{3}\xi '_n e_i^{n+5}+O(e_i^9), \end{aligned}$$

(29)

where $\xi '_n = \xi '_n (\alpha ,B_1,B_2,B_3,B_4,B_5,B_6,G_{00},G_{10})$, $n=1, 2, 3.$ Expansion of $f(z_i)$ about $t^*$ leads us to the expression

$$\begin{aligned} f(z_i) = \frac{f^{(3)}(t^*)}{3!}e_{z_i}^2 \big (1+B_1 e_{z_i}+B_2 e_{z_i}^2+B_3 e_{z_i}^3+B_4 e_{z_i}^4+B_5 e_{z_i}^5+\cdots \big ). \end{aligned}$$

(30)

Using (20), (23) and (30), we obtain

$$\begin{aligned} r_i =&\ \frac{1}{18}\big ((G_{10}- 6)\alpha f^{(3)}(t^*)+ 12 B_1^2-6B_2\big )e_i^2 \nonumber \\&\ -\Big (\frac{(\alpha f^{(3)}(t^*))^2 G_{00}}{36 B_1}+\frac{148}{81}B_1^3 -\frac{2}{54}B_1(\alpha f^{(3)}(t^*) G_{10} +72 B_2) +\frac{2}{3}B_3\Big )e_i^3\nonumber \\&\ +\sum _{n=1}^{5}\zeta '_n e_i^{n+3}+O(e_i^9), \end{aligned}$$

(31)

where $\zeta '_n = \zeta '_n (\alpha ,B_1,B_2,B_3,B_4,B_5,B_6,B_7,G_{00},G_{10})$, $n=1, 2, 3, 4, 5.$

$$\begin{aligned} s_i =&\ \frac{B_1}{54}\big ((G_{10}- 6)\alpha f^{(3)}(t^*)+ 12 B_1^2-6B_2\big )e_i^3\nonumber \\&\ -\frac{1}{243}\Big (238 B_1^4 + \frac{9}{2} B_1^2 (\alpha f^{(3)}(t^*) (-16 + G_{10}) - 82 B_2) \nonumber \\&\ + \frac{9}{4} ( (\alpha f^{(3)}(t^*))^2 (6 + G_{00} - G_{10}) + 2 \alpha f^{(3)}(t^*)\nonumber \\&\quad \times (15 - 2 G_{10}) B_2 + 24 B_2^2) + 54 B_1 B_3 \Big )e_i^4 \nonumber \\&\ +\sum _{n=1}^{4}\chi '_n e_i^{n+4} +O(e_i^9), \end{aligned}$$

(32)

where $\chi '_n = \chi '_n (\alpha ,B_1,B_2,B_3,B_4,B_5,B_6,G_{00},G_{10})$, $n=1, 2, 3, 4$.

Writing the Taylor expansion of weight function $H(u_i,v_i,r_i)$ in the neighborhood of origin (0, 0, 0), we have

$$\begin{aligned} H(u_i,v_i,r_i) =&\ H_{000} + u_i H_{100} + \frac{1}{2} u_i^2 H_{200} + \frac{1}{6} u_i^3 H_{300} + v_i \nonumber \\&\ \Big (H_{010} + u_i H_{110} + \frac{1}{2} u_i^2 H_{210} + \frac{1}{6} u_i^3 H_{310}\Big ) \nonumber \\&\ + v_i^2 \Big (\frac{1}{2} H_{020} + \frac{1}{2} u_i H_{120} + \frac{1}{4} u_i^2 H_{220} + \frac{1}{12} u_i^3 H_{320}\Big ) \nonumber \\&\ + r_i \Big (H_{001} + u_i H_{101} + \frac{1}{2} u_i^2 H_{201} \nonumber \\&\ + v_i \Big (H_{011} + u_i H_{111} + \frac{1}{2} u_i^2 H_{211}\Big ) \nonumber \\&\ + v_i^2 \Big (\frac{1}{2} H_{021} + \frac{1}{2} u_i H_{121} + \frac{1}{4} u_i^2 H_{221}\Big )\Big ). \end{aligned}$$

(33)

By using (20)-(33) in third step of (3), we have

$$\begin{aligned} e_{i+1} =&\ t_{i+1} - t^* \nonumber \\ =&\ \frac{B_1}{324} \big (\alpha f^{(3)}(t^*)(G_{100}-6) + 12 B_1^2 - 6 B_2\big )\nonumber \\&\ (6 - 2 H_{000} - 2 H_{010} - H_{020})e_i^4 +\sum _{n=1}^{4}\eta '_n e_i^{n+4} +O(e_i^9), \end{aligned}$$

(34)

where $\eta '_n = \eta '_n(\alpha ,B_1,B_2,B_3,B_4,B_5,B_6,G_{00},G_{10},H_{abc})$, $n=1,2,3,4.$ and $0\le a\le 3$, $0\le b\le 2$, $0 \le c \le 1$.

It is clear from the above equation (34) that we will obtain at least eighth order convergence if we set coefficients of $e_i^4$, $e_i^5$, $e_i^6$ and $e_i^7$ simultaneously equal to zero. Then solving the resulting equations, we get

$$\begin{aligned}&\ G_{00} =0 , \ H_{010} = 3+G_{10}-2H_{000}, \ H_{110} = 3+ 2 G_{10}-2H_{100},\nonumber \\&\ H_{020} = 2H_{000}-2G_{10}, \ H_{120} = 6-4G_{10}+2H_{100},\nonumber \\&\ H_{220} = 12-2 H_{200}-2H_{210},\ H_{320} = -144-2 H_{300}-2H_{310}, \nonumber \\&\ H_{021} = 6-2 H_{001}-2H_{011}, H_{121} = 24-2 H_{101}-2H_{111}. \end{aligned}$$

(35)

As a result the error equation is given by

$$\begin{aligned} e_{i+1} =&\ \frac{B_1}{8748}\Big (\big (\alpha f^{(3)}(t^*)(-6 + G_{10}) + 12 B_1^2 - 6B_2\big )\nonumber \\&\times \big (-2 ( 6 H_{201} + 6 H_{211} + 3 H_{221}-400) B_1^4 \\&\ + \frac{1}{2} B_1^2 (\alpha f^{(3)}(t^*) (G_{10} (120 - 2 H_{201} - 2 H_{211} - H_{221}) +6 ( 24 H_{001} + 12 H_{011} \\&\ + 2 H_{200} + 2 H_{201} + H_{210} + 2 H_{211} + H_{221}-228 )) + 6(-276+ 2 H_{201}\\&\ + 2 H_{211} + H_{221}) B_2) + 3((\alpha f^{(3)}(t^*))^2{10} (-6 + 2 H_{001} + H_{011}) - 3 (H_{000}\\&\ + 2 (-9 + 2 H_{001} + H_{011}))) - 6\alpha f^{(3)}(t^*)(-15 + G_{10} + 2 H_{001} + H_{011}) B_2 +36_2^2)\\&\ +108 B_1 B_3\big )\Big )e_i^8 +O(e_i^9). \end{aligned}$$

Thus, the theorem is proved. $\square$

Below we state the theorems (without proof ) for the cases $m = 4, 5, 6$ as the proof is similar to the above proved theorems.

Theorem 3

Using the assumption and notation of Theorem 1, the convergence order of (3) for the case $m = 4$ is at least 8, if $G_{01} = -G_{00}$, $G_{20}= 16$, $G_{11} = 4-G_{10}$, $G_{02} = 0$, $H_{010} = 4+G_{10}-2H_{000}$, $H_{020} = 2H_{000}-2G_{10}$, $H_{120} = 16-2H_{100}-2H_{110}$, $H_{220} = 16-2 H_{200}-2H_{210}$, $H_{320} = -192-2 H_{300}-2H_{310}$, $H_{021} = 8-2 H_{001}-2H_{011}$, $H_{121} = 32-2 H_{101}-2H_{111}$. Moreover, the method satisfies the error equation

$$\begin{aligned} e_{i+1}=&\frac{1}{1048576}C_1(13 C_1^2 - 8 C_2)\Big ((2536-26 H_{201} - 26 H_{211} - 13 H_{221}) C_1^4 \\&+ 8 (2 H_{201} + 2 H_{211} + H_{221}-400) C_1^2 C_2 + 512 C_2^2\\&- \frac{64}{3} C_1 (\alpha f^{(4)}(t^*) (2 + 2 G_{10} - 2 H_{100} - H_{110}) - 24C_3)\Big )e_i^8+O(e_i^9), \end{aligned}$$

where $\text {max} \ \{|G_{10}|,|H_{100}|,|H_{110}|, |H_{201}|,|H_{211}|,|H_{221}|\} < \infty$ and $C_n = \frac{4!}{(4+n)!}\frac{f^{(4+n)}(t^*)}{f^{(4)}(t^*)}$ for $n\in {\mathbb {N}}$.

Theorem 4

Using the assumption and notation of Theorem 1, the convergence order of (3) for the case $m = 5$ is at least 8, if $G_{01} = -2G_{00}$, $G_{20}= 20$, $G_{11} = 5-G_{10}$, $G_{02} = 2G_{00}$, $H_{020} = 10-2H_{000}-2H_{010}$, $H_{120} = 20-2H_{100}-2H_{110}$, $H_{220} = 20-2 H_{200}-2H_{210}$, $H_{320} = -240-2 H_{300}-2H_{310}$, $H_{021} = 10-2 H_{001}-2H_{011}$, $H_{121} = 40-2 H_{101}-2H_{111}$. The error equation for this case is given by

$$\begin{aligned} e_{i+1}=-&\ \frac{1}{1562500}\Big (D_1(7 D_1^2 - 5 D_2)\big ((-1860 + 14 H_{201} + 14 H_{211} + 7 H_{221}) D_1^4 \\&\ - 5 (-540 + 2 H_{201}+ 2 H_{211} + H_{221}) D_1^2 D_2 + \frac{125}{6} (\alpha f^{(5)}(t^*)(5 + G_{10} \\&- 2 H_{000} - H_{010}) - 24 D_2^2) - 500 D_1 D_3\big )\Big )e_i^8+O(e_i^9), \end{aligned}$$

where $\text {max} \ \{|G_{10}|,|H_{000}|,|H_{010}|, |H_{201}|,|H_{211}|,|H_{221}|\} < \infty$ and $D_n = \frac{5!}{(5+n)!}\frac{f^{(5+n)}(t^*)}{f^{(5)}(t^*)}$ for $n\in {\mathbb {N}}$.

Theorem 5

Using the assumption and notation of Theorem 1, the convergence order of (3) for the case $m = 6$ is at least 8, if $G_{20}= 24$, $G_{11} = 6-G_{10}$, $G_{02} = -2(G_{00}+G_{01})$, $H_{020} = 12-H_{000}-2H_{010}$, $H_{120} = 24-2H_{100}-2H_{110}$, $H_{220} = 24-2 H_{200}-2H_{210}$, $H_{320} = -288-2 H_{300}-2H_{310}$, $H_{021} = 12-2 H_{001}-2H_{011}$, $H_{121} = 48-2 H_{101}-2H_{111}$. Moreover, the method satisfies the error equation

$$\begin{aligned} e_{i+1}=&- \frac{1}{44789760}\Big ((5 E_1^2 - 4 E_2)\big ( 432 \alpha f^{(6)}(t^*) (2 G_{00} + G_{01}) + 25 (6 H_{201} \\&+ 6 H_{211} + 3 H_{221} -1036) E_1^5- 60 (-696 + 2 H_{201} + 2 H_{211}\\&+ H_{221}) E_1^3 E_2 - 8640 E_1 E_2^2 - 8640 E_1^2 E_3\big )\Big )e_i^8+O(e_i^9), \end{aligned}$$

where $\text {max} \ \{|G_{00}|,|G_{10}|, |H_{201}|,|H_{211}|,|H_{221}|\} < \infty$ and $E_n = \frac{6!}{(6+n)!}\frac{f^{(6+n)}(t^*)}{f^{(6)}(t^*)}$ for $n\in {\mathbb {N}}$.

Remark 1

In order to prove the eighth order convergence of the method (3) we can observe from the above results that the number of conditions on $G_{kj}$ and $H_{abc}$ are $6, \, 5,\, 4, \, 4, \, 3$ and $12, \, 8, \, 7, \, 6, \, 6$ respectively, corresponding to the cases $m=2,\,3,\, 4,\,5,\,6$. It has been seen that the conditions on $G_{kj}$ and $H_{abc}$ are always fixed (i.e. three and six, respectively) in number when $m\ge 6$. However, the error equations differ from each other in the sense that the terms containing the parameter $\alpha$ do not appear in the equations for $m\ge 7$. We shall prove this fact in next section.

3 Main result

For the multiplicity $m\ge 7$, we prove the order of convergence of scheme (3) by the following theorem:

Theorem 6

Let $f: {\mathbb {C}}\rightarrow {\mathbb {C}}$ be an analytic function in a region enclosing a zero $t^*$ with multiplicity $m\ge 7$. Further assume that initial guess $t_0$ is sufficiently close to $t^*$, then the local order of convergence of scheme (3) is at least 8, provided that $G_{20}= 4m$, $G_{11} = m-G_{10}$, $G_{02} = -2(G_{00}+G_{01})$, $H_{020} = 2m-2H_{000}-2H_{010}$, $H_{120} = 4m-2H_{100}-2H_{110}$, $H_{220} = 4m-2 H_{200}-2H_{210}$, $H_{320} = -48m-2 H_{300}-2H_{310}$, $H_{021} = 2m-2 H_{001}-2H_{011}$, $H_{121} = 8m-2 H_{101}-2H_{111}$, $\text {max} \ \{ |H_{201}|,|H_{211}|,|H_{221}|\} < \infty$. Moreover, error equation of the scheme is given by

$$\begin{aligned} e_{i+1} =&\ -\frac{1}{48 m^8}\Big (K_1\big ((9+m) K_1^2 - 2m K_2\big )\\&\ \big ((27 H_{221} - 862 m + 3 H_{221} m - 204 m^2 - 14 m^3 + 6 H_{201} (9 + m) \\&\ + 6 H_{211} (9 + m)) K_1^4 - 6 m (2 H_{201} + 2 H_{211} + H_{221} - 68 m - 8 m^2) K_1^2 K_2 \\&\ - 24 m^3 K_2^2 -24 m^3 K_1 K_3\big )\Big )e_i^8 +O(e_i^9), \end{aligned}$$

where $K_n = \frac{m!}{(m+n)!}\frac{f^{(m+n)}(t^*)}{f^{(m)}(t^*)}$ for $n\in {\mathbb {N}}$.

Proof

Taking into account that $f^{(j)}(t^*) = 0, j = 0, 1, 2, . . . , m - 1$ and $f^{(m)}(t^*)\ne 0,$ the Taylor’s expansion of $f(t_i)$ about $t^*$ is expressed as

$$\begin{aligned} f(t_i) = \frac{f^{(m)}(t^*)}{m!}e_i^m \big (1+ K_1 e_i+ K_2 e_i^2+K_3 e_i^3+K_4 e_i^4+K_5 e_i^5+K_6 e_i^6+K_7 e_i^7+\cdots \big ), \end{aligned}$$

(36)

where $K_n = \frac{m!}{(m+n)!}\frac{f^{(m+n)}(t^*)}{f^{(m)}(t^*)}$ for $n\in {\mathbb {N}}$.

Also the Taylor’s expansion of $f(w_i)$ about $t^*$ is

$$\begin{aligned} f(w_i) = \frac{f^{(m)}(t^*)}{m!}e_{w_i}^m \big (1+ K_1 e_{w_i}+ K_2 e_{w_i}^2+K_3 e_{w_i}^3+K_4 e_{w_i}^4+\cdots \big ), \end{aligned}$$

(37)

where $e_{w_i}= w_{i}-t^* = e_i +\frac{\alpha f^{(m)}(t^*)}{m!}e_i^m \big (1+ K_1 e_i+ K_2 e_i^2+K_3 e_i^3+K_4 e_i^4+K_5 e_i^5+K_6 e_i^6+\cdots \big ).$

From the first step of (3)

$$\begin{aligned} e_{y_i} =&\ y_i-t^* \nonumber \\ =&\ \frac{K_1}{m}e_i^2+\frac{-(1+m)K_1^2+2mK_2}{m^2}e_i^3 +\frac{1}{m^3}\big ((1+m)^2 K_1^3\nonumber \\&\ -m(4+3m)K_1 K_2 +3m^2 K_3\big )e_i^4-\frac{1}{m^4}\big ((1 + m)^3 K_1^4 \nonumber \\&\ - 2 m (3 + 5 m + 2 m^2) K_1^2 K_2 +2 m^2 (2 + m) K_2^2 +2 m^2 (3 + 2 m) K_1 K_3\big )e_i^5 \nonumber \\&\ +\sum _{n=1}^{3}\phi ''_n e_i^{n+5}+O(e_i^9), \end{aligned}$$

(38)

where $\phi ''_n = \phi ''_n (m,K_1,K_2,K_3,K_4,K_5,K_6,K_7)$, $n=1, 2, 3.$ Expand $f(y_i)$ about $t^*$, we have

$$\begin{aligned} f(y_i) = \frac{f^{(m)}(t^*)}{m!}e_{y_i}^2 \big (1+K_1 e_{y_i}+K_2 e_{y_i}^2+K_3 e_{y_i}^3+K_4 e_{y_i}^4+\cdots \big ). \end{aligned}$$

(39)

Using (36), (37) and (39) in the expressions of $u_i$ and $v_i$, we have that

$$\begin{aligned} u_i =&\ \frac{K_1}{m}e_i+\frac{-(2 + m) K_1^2+2 m K_2}{m^2}e_i^2+\frac{1}{2m^3}\nonumber \\&\ \big ((7+7 m+ 2m^2)K_1^3-2m(7+3 m)K_1 K_2 +6m^2K_3\big )e_i^3\nonumber \\&\ + \sum _{n=1}^{5}\psi ''_n e_i^{n+3}+O(e_i^9), \end{aligned}$$

(40)

where $\psi ''_n = \psi ''_n (m,K_1,K_2,K_3,K_4,K_5,K_6,K_7)$, $n=1, 2, 3, 4, 5$ and

$$\begin{aligned} v_i =&\ 1 + \frac{\alpha f^{(m)}(t^*)}{m!}e_i^{m-1} \Big (1+\frac{(m+1) K_1}{m}e_i+\frac{(m+2) K_2}{m}e_i^2+\frac{(m+3) K_3}{m}e_i^3\nonumber \\&\ +\sum _{n=1}^{5}\rho _n e_i^{n+3} +O(e_i^9)\Big ), \end{aligned}$$

(41)

where $\rho _n = \rho _n (m,K_1,K_2,K_3,K_4,K_5,K_6,K_7)$, $n=1, 2, 3, 4, 5.$

Expanding $G(u_i,v_i)$ by Taylor formula in the neighborhood of origin (0, 0)

$$\begin{aligned} G(u_i,v_i) \approx G_{00} + u_i G_{10}+v_i G_{01} + \frac{1}{2} u_i^2 G_{20}+u_i v_i G_{11}+\frac{1}{2}v_i^2 G_{02}. \end{aligned}$$

(42)

By inserting (36)–(42) in the second step of (3), we have

$$\begin{aligned} e_{z_{i}} =&z_{i}- t^* \nonumber \\ =&-\frac{1}{2m}(2 G_{00} + 2 G_{01} + G_{02})e_i\nonumber \\&\ +\frac{1}{2m^2} (2 G_{00} + 2 G_{01} + G_{02} -2 G_{10}-2 G_{11} + 2m)K_1e_i^2 \nonumber \\&\ -\frac{1}{2m^3}\big (( G_{02} - 6 G_{10} - 6 G_{11} + G_{20} + 2 m + m \ G_{02} - 2m \ G_{10} \nonumber \\&\ - 2m \ G_{11} +2 m^2 + 2(1 + m) \ G_{00}+ 2 (1 + m) G_{01} ) K_1^2 -2 m (2 G_{00} \nonumber \\&\ + 2 G_{01} + G_{02} - 2 G_{10} - 2 G_{11} + 2 m) K_2\big )e_i^3 +\sum _{n=1}^{5}\delta ''_n e_i^{n+3}+O(e_i^9), \end{aligned}$$

(43)

where $\delta ''_n = \delta ''_n (m,K_1,K_2,K_3,K_4,K_5,K_6,K_7,G_{00},G_{10},G_{01},G_{20},G_{11},G_{02})$, $n=1, 2,3,4,5.$

It is clear from the above Eq. (43) that we will obtain at least fourth order convergence if we set coefficients of $e_i$, $e_i^2$ and $e_i^3$ simultaneously equal to zero. Then solving the resulting equations, one gets

$$\begin{aligned} G_{20} = 4m, \ \ G_{11}= m- G_{10}, \ \ G_{02}=- 2(G_{00} + G_{01}). \end{aligned}$$

(44)

By using (44), the error equation (43) is given by

$$\begin{aligned} e_{z_{i}} =&\ \frac{1}{2m^3}\big ((9 + m) K_1^3 -2 m K_1 K_2\big )e_i^4-\frac{1}{6m^4}\big ((125 +84 m +7 m^2) K_1^4\nonumber \\&\ -24 m (7 + m)K_1^2 K_2 +12 m^2 K_2^2 \nonumber \\&\ +12 m^2 K_1 K_3 \big )e_i^5+\sum _{n=1}^{3}\xi ''_n e_i^{n+5}+O(e_i^9), \end{aligned}$$

(45)

where $\xi ''_n = \xi ''_n (m,K_1,K_2,K_3,K_4,K_5,K_6)$, $n=1, 2, 3.$ Expansion of $f(z_i)$ around $t^*$ yields

$$\begin{aligned} f(z_i) = \frac{f^{(m)}(t^*)}{m!}e_{z_i}^m \big (1+K_1 e_{z_i}+K_2 e_{z_i}^2+K_3 e_{z_i}^3+K_4 e_{z_i}^4+\cdots \big ). \end{aligned}$$

(46)

Using (36), (39) and (46), we obtain

$$\begin{aligned} r_i =&\ \frac{1}{2m^2}\big ((9 + m) K_1^2 -2 m K_2\big )e_i^2 -\frac{1}{3m^3}\big ((49 + 27 m + 2 m^2)K_1^3\nonumber \\&\ -6 m (9 + m)K_1 K_2 +6 m^2 K_3 \big )e_i^3 +\frac{1}{24m^4}\big ((899 + 1002 m + 313 m^2 \nonumber \\&\ + 18 m^3) K_1^4 -12 m (167 + 87 m + 6 m^2) K_1^2 K_2 + 24 m^2 (26 + 3 m) K_1 K_3 \nonumber \\&\ +12 m^2 ((35 + 3 m) K_2^2 + 2 m K_4)\big )e_i^4 +\sum _{n=1}^{4}\zeta ''_n e_i^{n+4}+O(e_i^9), \end{aligned}$$

(47)

where $\zeta ''_n = \zeta ''_n (m,K_1,K_2,K_3,K_4,K_5,K_6,K_7)$, $n=1, 2, 3, 4.$

$$\begin{aligned} s_i =&\ \frac{1}{2m^3}\big ((9 + m) K_1^3 -2 m K_1 K_2\big )e_i^3-\frac{1}{6m^4}\Big ((152 + 87 m +7 m^2)K_1^4\nonumber \\&\ -6 m (29 + 4 m)K_1^2 K_2 +12 m^2 K_2^2 +12 m^2 K_1 K_3\Big )e_i^4 \nonumber \\&\ +\frac{1}{24 m^5}\Big ((2061 + 2246 m + 711 m^2 + 46 m^3) K_1^5 - 4 m (1123 + 624 m \nonumber \\&\ + 53 m^2) K_1^3 K_2+12 m^2 (87 + 13 m) K_1^2 K_3 - 168 m^3 K_2 K_3 \nonumber \\&\ +12 m^2 K_1 ((121 + 17 m) K_2^2 + 2 m K_4)\Big )e_i^5+\sum _{n=1}^{3}\chi ''_n e_i^{n+5} +O(e_i^9), \end{aligned}$$

(48)

where $\chi ''_n = \chi ''_n (m,K_1,K_2,K_3,K_4,K_5,K_6)$, $n=1, 2, 3.$

Developing $H(u_i,v_i,r_i)$ by Taylor formula in the neighborhood of origin (0, 0, 0), we have

$$\begin{aligned} H(u_i,v_i,r_i) =&\ H_{000} + u_i H_{100} + \frac{1}{2} u_i^2 H_{200} + \frac{1}{6} u_i^3 H_{300} \nonumber \\&\ + v_i \Big (H_{010} + u_i H_{110} + \frac{1}{2} u_i^2 H_{210} + \frac{1}{6} u_i^3 H_{310}\Big ) \nonumber \\&\ + v_i^2 \Big (\frac{1}{2} H_{020} + \frac{1}{2} u_i H_{120} + \frac{1}{4} u_i^2 H_{220} + \frac{1}{12} u_i^3 H_{320}\Big )\nonumber \\&\ + r_i \Big (H_{001} + u_i H_{101} + \frac{1}{2} u_i^2 H_{201} + v_i \Big (H_{011} + u_i H_{111} \nonumber \\&\ + \frac{1}{2} u_i^2 H_{211}\Big ) + v_i^2 \Big (\frac{1}{2} H_{021} + \frac{1}{2} u_i H_{121} + \frac{1}{4} u_i^2 H_{221}\Big )\Big ). \end{aligned}$$

(49)

By using (36)–(49) in third step of (3), we have

$$\begin{aligned} e_{i+1} =&\ -\frac{1}{4 m^4}\big (K_1 ((9 + m) K_1^2 - 2 m K_2)(2 H_{000} + 2 H_{010} + H_{020} - 2 m)\big )e_i^4\nonumber \\&\ +\sum _{n=1}^{4}\eta ''_n e_i^{n+4}+O(e_i^9), \end{aligned}$$

(50)

where $\eta ''_n = \eta ''_n(m,K_1,K_2,K_3,K_4,K_5,K_6,H_{abc})$, $n=1,2,3,4$ and $0\le a\le 3$, $0\le b\le 2$, $0\le c\le 1$.

It is clear from the above Eq. (50) that we will obtain at least eighth order convergence if we set coefficients of $e_i^4$, $e_i^5$, $e_i^6$ and $e_i^7$ simultaneously equal to zero. Then solving the resulting equations, we get

$$\begin{aligned}&\ H_{020} = 2m-2H_{000}-2H_{010}, \, H_{120} = 4m-2H_{100}-2H_{110},\nonumber \\ {}&\ H_{220} = 4m-2 H_{200}-2H_{210}, \, H_{320} = -48m-2 H_{300}-2H_{310},\nonumber \\&\ H_{021} = 2m-2 H_{001}-2H_{011}\, H_{121} = 8m-2 H_{101}-2H_{111}. \end{aligned}$$

(51)

As a result the error equation is given by

$$\begin{aligned} e_{i+1} =&\ -\frac{1}{48 m^8}\Big (K_1\big ((9+m) K_1^2 - 2m K_2\big )\nonumber \\&\ \big ((27 H_{221} - 862 m + 3 H_{221} m - 204 m^2 - 14 m^3 + 6 H_{201} (9 + m) \nonumber \\&\ + 6 H_{211} (9 + m)) K_1^4 - 6 m (2 H_{201} + 2 H_{211} + H_{221} - 68 m\nonumber \\&\ - 8 m^2) K_1^2 K_2 - 24 m^3 K_2^2 -24 m^3 K_1 K_3\big )\Big )e_i^8 +O(e_i^9). \end{aligned}$$

(52)

Thus, the theorem is proved. $\square$

Many special cases of the family (3) can be generated satisfying the corresponding conditions on the functions $G(u_i,v_i)$ and $H(u_i,v_i,r_i)$ shown above in theorems 1–6 depending on the multiplicity m. However, we must generate a unified iterative scheme that may satisfy the conditions of theorems 1–6 simultaneously for all $m>1$. Moreover, we will restrict choices to consider the forms of low order polynomials. These choices should be such that the resulting methods may converge to the root with order eight for $m > 1$. Accordingly, the following simple forms are chosen:

$$\begin{aligned} G(u_i,v_i) =&\ \big (3 + 2 m u_i + (m-3) v_i\big )u_i, \end{aligned}$$

(53)

$$\begin{aligned} H(u_i,v_i,r_i) =&(1 - v_i) \big (3 + (5 r_i - 3 u_i-6) v_i \big ) +m \big (4 + (r_i-3) v_i \big )v_i \nonumber \\&+ 2 m \big (1 + v_i + (2 r_i-1) v_i^2 \big )u_i - m \Big (4 u_i v_i - \frac{1}{2} (1 + v_i)\Big )u_i^2 v_i. \end{aligned}$$

(54)

Combining Eqs. (3), (53) and (57), the eighth order method for $m > 1$ is expressed as

$$\begin{aligned} \left\{ \begin{array}{l} y_{i} = \ t_i-m \frac{f(t_i)}{f^{\angle }(w_i,t_i)}, \\ z_{i} = \ y_i - \big (3 + 2 m u_i + (m-3) v_i\big )u_i \frac{f(t_i)}{f^{\angle }(w_i,t_i)}, \\ t_{i+1} = z_i - s_i \big [(1 - v_i) \big (3 + (5 r_i - 3 u_i-6) v_i \big ) +m \big (4 + (r_i-3) v_i \big )v_i \\ \quad \quad \quad \quad + 2 m \big (1 + v_i+ (2 r_i-1) v_i^2 \big )u_i -m \big (4 u_i v_i - \frac{1}{2} (1 + v_i)\big )u_i^2 v_i \big ] \frac{f(t_i)}{f^{\angle }(w_i,t_i)}. \end{array}\right. \end{aligned}$$

(55)

For further reference the new method (55) is now denoted by NM.

Remark 2

It is important to note that parameter $\alpha$, which is used in $w_i$, appears only in the error equations of the cases $m= 2, \, 3, \, 4, \, 5, \, 6$ but not for $m \ge 7$ (see equation (52)). It has been observed that this parameter appears in the terms of $e_i^{9}$ and higher order. However, such terms are difficult to compute in general. Moreover, we do not need these in order to show the required eighth order convergence.

Remark 3

The new method (NM) reaches at eighth order of convergence under certain conditions on weight functions used. This convergence rate is achieved by using only four functional evaluations viz. $f(t_i)$, $f(w_i)$, $f(y_i)$ and $f(z_i)$ per iteration. Therefore, NM is optimal by the Kung-Traub hypothesis [15].

Remark 4

Besides the cases (53) and (54) of weight functions G(u, v) and H(u, v, r), respectively, some other forms satisfying the conditions can also be explored. For readers’ interest we provide the following forms:

$$\begin{aligned} G(u_i,v_i) =&\ \frac{1}{1+u_i+v_i}\big (2 m u_i^3 + u_i^5 v_i \nonumber \\&\ \ + u_i^2 ( 5 m + 3 v_i-3) + u_i ((3 + v_i)m + (3 - 2 m )v_i^2-3)\big ), \end{aligned}$$

(56)

$$\begin{aligned} G(u_i,v_i) =&\ \frac{1}{1+u_i^3}\big (2 m u_i^2 + u_i (3 m-3 + (3 - 2 m) v_i) \nonumber \\&\ \ + u_i^4 (3 m-3 + (3 - 2 m) v_i) + 2 u_i^5 (m + v_i^2)\big ), \end{aligned}$$

(57)

$$\begin{aligned} H(u_i,v_i,r_i) =&\ \frac{1}{2 (1 + r_i + u_i)} \Big (-8 m u_i^4 v_i^2 + m u_i^3 (1 - 7 v_i - 8 r_i v_i)v_i\nonumber \\&\ \ + u_i^2 (4 m + (5 m + m r_i-6) v_i + (6 - 3 m + 9 m r_i )v_i^2) \nonumber \\&\ \ + u_i (6 + 4 m + 4 m r_i +( 12 m + 4 r_i + 4 m r_i-24) v_i \nonumber \\&\ \ + (18 - 10 m - 4 r_i + 6 m r_i + 8 m r_i^2) v_i^2) + 2 (3 + 3 r_i \nonumber \\&\ \ +( 4 m - 4 r_i + 4 m r_i + 5 r_i^2 + r_i^4-9) v_i \nonumber \\&\ \ + (6 - 3 m + r_i - 2 m r_i - 5 r_i^2 + m r_i^2 + r_i^4 )v_i^2\Big ). \end{aligned}$$

(58)

However, being complicated expressions we will not consider these in our further work.

4 Numerical results

In this section, we consider some numerical problems to illustrate the convergence behavior and computational efficiency of the new method (NM). Performance is also compared with existing eighth order Newton-like methods requiring derivative evaluations in their formulae. For example, we consider the methods by Akram et al. [1], Behl et al. [4] and Zafar et al. [23]. For ready reference the methods are expressed as follows:

Method by Akram et al. (AM-1):

$$\begin{aligned} \left\{ \begin{array}{l} y_i = \ t_i -m \frac{f(t_i)}{f'(t_i)}, \\ z_i = \ y_i - m \, u_i (1 + 2u_i - u_i^2+ 6u_i^3)\frac{f(t_i)}{f'(t_i)}, \\ t_{i+1}= \ z_i -m \, u_i ( 2 s_i + 4 r_i \, s_i+r_i + r_i^2) \frac{f(t_i)}{f'(t_i)}. \end{array}\right. \end{aligned}$$

Method by Akram et al. (AM-2):

$$\begin{aligned} \left\{ \begin{array}{l} y_i = \ t_i -m \frac{f(t_i)}{f'(t_i)}, \\ z_i = \ y_i - m \, u_i \frac{5+18 u_i}{5+ 8 u_i-11 u_i^2}\frac{f(t_i)}{f'(t_i)}, \\ t_{i+1}= \ z_i -m \, u_i ( 2s_i + 4 r_i \, s_i+r_i + r_i^2) \frac{f(t_i)}{f'(t_i)}. \end{array}\right. \end{aligned}$$

Method by Behl et al. (BM-1):

$$\begin{aligned} \left\{ \begin{array}{l} y_i = \ t_i -m \frac{f(t_i)}{f'(t_i)}, \\ z_i = \ y_i -m u_i (1 + 2 u_i - u_i^2)\frac{f(t_i)}{f'(t_i)}, \\ t_{i+1}= \ z_i +m \frac{r_i u_i}{1-r_i} \Big [-1-2s_i-2u_i+6u_i^3 -\frac{1}{6}(85+21m+2m^2)u_i^4 \Big ]\frac{f(t_i)}{f'(t_i)}. \end{array}\right. \end{aligned}$$

Method by Behl et al. (BM-2):

$$\begin{aligned} \left\{ \begin{array}{l} y_i = \ t_i -m \frac{f(t_i)}{f'(t_i)}, \\ z_i = \ y_i -m u_i (1+2u_i)\frac{f(t_i)}{f'(t_i)}, \\ t_{i+1}= \ z_i -m \frac{r_i u_i}{1-r_i} \Big [\frac{1+2s_i+u_i(6+8s_i)+9u_i^2}{1+4u_i}\Big ]\frac{f(t_i)}{f'(t_i)}. \end{array}\right. \end{aligned}$$

Method by Zafar et al. (ZM-1):

$$\begin{aligned} \left\{ \begin{array}{l} y_i = \ t_i -m \frac{f(t_i)}{f'(t_i)}, \\ z_i = \ y_i -m u_i \Big [\frac{1-5u_i^2+8u_i^3}{1-2u_i}\Big ] \frac{f(t_i)}{f'(t_i)}, \\ t_{i+1}= \ z_i -m u_i r_i (1+2u_i)(1+r_i)(1+2s_i)\frac{f(t_i)}{f'(t_i)}. \end{array}\right. \end{aligned}$$

Method by Zafar et al. (ZM-2):

$$\begin{aligned} \left\{ \begin{array}{l} y_i = \ t_i -m \frac{f(t_i)}{f'(t_i)}, \\ z_i = \ y_i -m u_i \big (1+2u_i-u_i^2+6u_i^3\big ) \frac{f(t_i)}{f'(t_i)}, \\ t_{i+1}= \ z_i -m u_i r_i (1+2u_i)(1+r_i)(1+2s_i)\frac{f(t_i)}{f'(t_i)}, \end{array}\right. \end{aligned}$$

where $u_i=\Big (\frac{f(y_i)}{f(t_i)}\Big )^{\frac{1}{m}}$, $r_i=\Big (\frac{f(z_i)}{f(y_i)}\Big )^{\frac{1}{m}}$ and $s_i=\Big (\frac{f(z_i)}{f(t_i)}\Big )^{\frac{1}{m}}$.

Computational work is compiled in the programming package of Mathematica software [22] using multiple-precision arithmetic in a PC with Intel(R) Pentium(R) CPU B960 @ 2.20 GHz, 2.20 GHz (32-bit Operating System) Microsoft Windows 7 Professional and 4 GB RAM. Performance of the considered method is tested by choosing value 0.01 of the parameter $\alpha$. The tabulated results obtained by the methods for each problem include (i) number of iterations (i) required to obtain the solution using the stopping criterion $|t_{i+1} - t_i| + |f(t_i)| < 10^{-100}$, (ii) estimated error $|t_{i+1}-t_i|$ in the first three iterations, (iii) computational order of convergence (COC) and (iv) CPU time (CPU-time) in seconds utilized in execution of a program, which is computed by the command “TimeUsed[ ]”. The computational order of convergence (COC) is calculated by the formula (see [21])

$$\begin{aligned} \text {COC}= \frac{\ln |(t_{i+2}-t^*)/(t_{i+1}-t^*)|}{\ln |(t_{i+1}-t^*)/(t_{i}-t^*)|}. \end{aligned}$$

(59)

The following numerical examples are chosen for experimentation:

Example 1

Consider a standard test function which is defined as

$$\begin{aligned} f_1(t)= e^{t}-t-1. \end{aligned}$$

This function has multiple zero at $t^*= 0$ of multiplicity 2. We select initial approximation $t_0 = \frac{1}{2}$ to obtain zero of this function. Numerical results are exhibited in Table 1.

Example 2

Next, consider a problem of continuous stirred tank reactor. We observe a reaction scheme that develops in the chemical reactor (see [8] for more information), which is defined as follows:

$$\begin{aligned} W_1+T\rightarrow W_2 \nonumber \\ W_2+T\rightarrow W_3 \nonumber \\ W_3+T\rightarrow W_4 \nonumber \\ W_4+T\rightarrow W_5 \end{aligned}$$

(60)

The above model was studied in detail by Douglas [10] to find a simple system that can control feedback problem. Finally, he transferred the above model to the following mathematical equation:

$$\begin{aligned} t^4+11.50 t^3+47.49 t^2+83.06325 t+51.23266875=-2.98(t+2.25)K_H , \end{aligned}$$

(61)

where $K_H$ denotes the gaining proportional controller. The control system in Eq. (61) is balanced with the values of $K_H$. If we assume $K_H = 0$, we obtain the poles of the open-loop transferred function as the solutions of univariate equation

$$\begin{aligned} f_2(t) = t^4+11.50 t^3+47.49 t^2+83.06325 t+51.23266875 =0, \end{aligned}$$

(62)

given as: $t = -2.85, -2.85, -1.45, -4.35$. It is straightforward to say that we have one root $t^* = -2.85$, having multiplicity 2. We select initial approximation $t_0 = -2.7$ to obtain zero of this function. The computational results are displayed in Table 1.

Table 1 Numerical results of the methods.

Example 3

Van der Waals equation-of-state (see [6])

$$\begin{aligned} \Big ( P+ \frac{m_1 n^2}{V^2}\Big )(V-m_2 \,n )= n R T, \end{aligned}$$

is considered that describes the behavior of a real gas by presenting in the perfect gas equations two parameters, $m_1$ and $m_2$, particular for each gas. Finding the volume V of a real gas in terms of $m_1$, $m_2$, P, R and T, requires the solution of equation

$$\begin{aligned} P V^3-(n m_2 P+n R T)V^2+m_1 n^2 V-m_1 m_2 n^2 = 0. \end{aligned}$$

Given the constants $m_1$ and $m_2$ of a specific gas, one can find values for n, P and T, such that this equation has a three real zeros. By using the specific values, we get the nonlinear function

$$\begin{aligned} f_3(t)= t^3-5.22 \, t^2+ 9.0825 \, t-5.2675. \end{aligned}$$

The zeros of function $f_3$ are given by $t^* = 1.75, 1.75, 1.72.$ However, our desired zero is $t^* =1.75$ with multiplicity 2. We assumed initial guess $t_0= 2.5$ for this example. Numerical results are displayed in Table 1.

Example 4

The fourth example we consider is originated from the equation of L-C-R circuit in electrical engineering [7]. The equation governing the L-C-R circuit is given by

$$\begin{aligned} {L}\frac{d^2 {q}}{dt^2}+{R}\frac{d{q}}{dt}+\frac{{q}}{{C}}=0, \end{aligned}$$

whose solution q(t) is

$$\begin{aligned} {q}(t)={q}_0 e^{-{R}t/2{L}}\cos \left( \sqrt{\frac{1}{{L}{C}}-\left( \frac{{R}}{2{L}}\right) ^2} \ t\right) , \end{aligned}$$

where at $t=0,$ ${q}={q}_0.$

For a particular case study, the problem is given as: Assume that the charge must be dissipated to 1 percent of its original value $({q}/{q}_0=0.01)$ in $t=0.05$ seconds, with ${L}=5$ Henry and ${C}=10^{-4}$ Farad. Find proper value of R?

Using the numerical values, the problem reduces to

$$\begin{aligned} e^{-0.005t}\cos \Big (\sqrt{2000-0.01t^2}\,(0.05)\Big )-0.01=0, \end{aligned}$$

where $t={R}$.

We consider this case for five times and obtained the required nonlinear function

$$\begin{aligned} f_4(t)= \Big (e^{-0.005 t}\cos \big (\sqrt{2000-0.01 t^2}\,(0.05)\big )-0.01\Big )^5. \end{aligned}$$

The function $f_4$ has a multiple zero at $328.15142908514817\ldots$ of multiplicity 5. We choose the initial approximation $t_0 = 300$ for obtaining the zero of the function. Numerical results are displayed in Table 1.

Example 5

Next, we assume a nonlinear test function of the academic interest which is defined by

$$\begin{aligned} f_5(t) = t(t^2+1)(2e^{t^2+1}+t^2-1)\text {cosh}^4\Big (\frac{\pi t}{2}\Big ). \end{aligned}$$

This function has a imaginary zero $t^*=i$ with multiplicity 6. We choose the initial approximations $t_0 = 1.5 i$ for computing the zero. The obtained results are shown in Table 1.

Example 6

Lastly, we consider another standard test function which is defined as

$$\begin{aligned} f_6(t)&= \Big [\tan ^{-1}\Big (\frac{\sqrt{5}}{2}\Big )-\tan ^{-1}(\sqrt{t^2-1})\\&\quad +\sqrt{6}\Big (\tan ^{-1}\Big (\sqrt{\frac{t^2-1}{6}}\Big ) -\tan ^{-1}\Big (\frac{1}{2}\sqrt{\frac{5}{6}}\Big )\Big ) -\frac{11}{63}\Big ]^{10}. \end{aligned}$$

This function has multiple zero $t^*=1.84112940685019962\ldots$ of multiplicity 10. Let us choose the initial approximation $t_0 = 2$ to compute this zero. The computed results are displayed in Table 1.

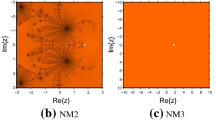
From the numerical results as shown in Table 1 we observe that the errors generated by the methods show the increasing accuracy in the successive approximations, which justifies the good convergence. In case of the existing eighth order methods, the performance is not uniformly consistent, see the results of example 5. The entry 0 for $|t_{i+1}-t_i|$ means that the stopping criterion $|t_{i+1}- t_i|+|f(t_i)| < 10^{-100}$ has been reached. Results of computational order of convergence shown in penultimate column in the table overwhelmingly support the theoretical eighth order of convergence. However, note that this is not true in case of existing eighth-order methods BM-1 and BM-2. Computational efficiency of the methods can be judged by observing the entries of CPU-time. Indeed, the NM is efficient in general, since CPU time consumed is less than that of the time taken by the existing ones in majority of the cases. The similar robust nature of the new method has been observed by implementing it on many other different numerical examples.

5 Conclusions

In the present work, we have derived a Traub-Steffensen-like derivative-free iterative scheme having eighth order convergence for computing multiple roots of nonlinear equations. The analysis of convergence has been studied in detail under standard hypotheses. The most important feature of the obtained scheme is its optimal eighth order convergence which is difficult to attain in derivative-free numerical algorithms. Performance has been examined by numerical testing on variety of problems including those that arise in real applications. Moreover, the comparison of performance of the methods with existing optimal eighth order methods has also been shown. It has been observed that unlike that of some of existing techniques the proposed technique has consistent convergence behavior. Comparison of estimated CPU-time has also proved the efficient and robust character of the new method. We conclude the work with a remark that Traub-Steffensen-like techniques are good options to Newton-type techniques in the problems where derivatives are costlier to compute or complicated to evaluate.