On the qualitative behaviour of solutions to certain second order nonlinear differential equation with delay

Abstract

This paper establishes explicit criteria in form of inequalities for all solutions to a class of second order nonlinear differential equations (with and without delay) to be bounded, ultimately bounded and globally asymptotically stable using Lyapunov second method. Obtained results are new and they complement existing results in the literature. Some examples are given to illustrate the main results.

1 Introduction

It is well known that stability and boundedness properties of solutions are fundamental in the theory and application of differential equations. The study of qualitative properties of solution to second order nonlinear differential equations has attracted the interest of many researchers. As a tool of investigation, the Lyapunov second method has been one of the most effective tool used and it is still playing a central role in studying the qualitative behaviour of solution of both linear and nonlinear differential equations.

Consider the second order nonlinear differential equations of the form

$$\begin{aligned} \ddot{x}+a(t)f(x,\dot{x})+ g(x)= & {} p(t, x, \dot{x}), \end{aligned}$$

(1.1)

$$\begin{aligned} \ddot{x}+a(t)f(x,\dot{x})+ g(x(t-\tau ))= & {} p(t, x, \dot{x}), \end{aligned}$$

(1.2)

where a, f, g and p are continuous functions that depend (at most) only on the arguments displayed explicitly and $\tau \in [0, h]$ ($\tau >0$). Here and elsewhere, all the solutions considered and all the functions which appear are supposed real. The dots indicate differentiation with respect to t. The continuity of these functions is sufficient for the existence of the solutions of Eqs. (1.1) and (1.2). Furthermore, it is assumed that the functions f, g and p satisfy a Lipschitz condition in their respective arguments which guarantee the uniqueness of solutions of Eqs. (1.1) and (1.2). The derivative of g also exists and is continuous. The dots denote differentiation with respect to the independent variable t.

Equations (1.1) and (1.2) are ordinary and delay differential equations with nonlinear terms respectively. Let us observe that when $f(x,\dot{x}) = \dot{x},~~g(x)= x$ and $\tau = 0$, Eqs. (1.1) and (1.2) reduce to

$$\begin{aligned} \ddot{x}+a(t)\dot{x}+x=p(t,x,\dot{x}), \end{aligned}$$

(1.3)

which has remained one of the oldest problems in differential equations for more than six decades. This equation appears in a number of physical models and it is important in describing fluid mechanical and nonlinear elastic mechanical phenomena [2]. Some notable contributions in the dynamical behaviour of this class of equation include but are not limited to Bilhari [7], Hatvani [12], Karsai [13, 14], Napoles [17], Napoles and Repilado [18], Pucci and Serrin [21, 22]. An immense body of relevant literature has been devoted to stability, boundedness, convergence and periodic solutions to equations of the form (1.1), we can mention in this regard the work of [25], Tunc and Ayhan [26], Tunc and Tunc [27] as well as the expositions in [5–24, 28] and references cited therein. With the aid of Lyapunov’s second method, Burton [8], Napoles [17] and Napoles and Repilado [18] discussed the boundedness of solutions. Burton and Hatvani [9], Murakami [16], Thurston and Wong [24] are further examples on the subject matter that employed the second method of Lyapunov to discuss stability (asymptotic) of solutions to the Eq. (1.1). In Napoles [17], ultimate boundedness of solutions of the equation (1.1) was considered for the autonomous case while Ogundare and Okecha [20] discussed the boundedness, periodicity and stability of solutions to certain class of the Eq. (1.1). Recently, Ogundare and Afuwape [19], discussed the boundedness and stability properties of solutions of

$$\begin{aligned} \ddot{x}+f(x)\dot{x}+g(x) = p(t; x, \dot{x}) \end{aligned}$$

(1.4)

via the Lyapunov second method. Also Ademola [1] as well as Alaba and Ogundare [3, 4] discussed boundedness and stability of solutions of non-autonomous equation of second order from where (1.4) was easily treated.

In [9], the authors considered (1.1) and (1.2) and developed a transformation which allowed the treatment of the two equations in a unified way using the Lyapunov second method.

The motivation for the current paper comes from the work of Burton and Hatvani [9] where the Lyapunov functions employed mainly were incomplete ones. In this work, a suitable complete Lyapunov function is used to discuss the stability and boundedness of (1.2). Conditions on the nonlinear terms that guarantee global asymptotic stability and boundedness of solutions of the Eq. (1.2) are obtained. Our results complement existing results on qualitative behaviour of solutions of second order nonlinear differential equations with and without delay.

The paper is organised in this order: basic assumptions are presented in Sect. 2 alongside with the main results. Section 3 is devoted to some preliminary results and in Sect. 4, the proofs of the main theorems are given while related examples are given to illustrate the main results in Sect. 5.

2 Formulation of results

An associated system to the Eq. (1.2) of interest to us is

$$\begin{aligned} \begin{aligned} \dot{x}&= y\\ \dot{y}&= -a(t)f(x, y)-g(x)+N(t) \end{aligned} \end{aligned}$$

(2.1)

where $N(t)=\int ^{0}_{-\tau }{g'(x(t+\theta ))y(t+\theta )}d\theta + p(t,x,y)$.

Let a(t) be continuous and non decreasing, in addition let $0 < a_{0}\le a(t)\le a_{1}$ with $a' \le \displaystyle \frac{1}{2}$; also let the functions f,   g and p be continuous with the following conditions:

• (i)
  $$\begin{aligned} \alpha _{0}\le \displaystyle \frac{f(x,y)-f(x,0)}{y}=\alpha \le \alpha _{1}, \quad y\ne 0; \end{aligned}$$
• (ii)
  $$\begin{aligned} \beta _{0}\le \displaystyle \frac{f(x,y)-f(0,y)}{x}=\beta \le \beta _{1}, \quad x\ne 0; \end{aligned}$$
• (iii)
  $$\begin{aligned} \gamma _{0}\le \displaystyle \frac{g(x)-g(0)}{x}=\gamma \le \gamma _{1}, \quad x\ne 0; \end{aligned}$$
• (iv)
  $$\begin{aligned} f(x,0) = f(0,y) =g(0) = 0, \end{aligned}$$

where $\alpha ,~\alpha _{0},~\alpha _{1},~\beta ,~\beta _{0},~\beta _{1},~\gamma ,~ \gamma _{0}~~\text{ and }~~\gamma _{1}$ are all positive constants belonging to a closed sub-interval of the Routh-Hurwitz interval $I_{0} = [0, \kappa ], \kappa =\max \{\alpha , \beta , \gamma \}$.

Next we state our main results.

Theorem 2.1

Suppose that conditions (i)–(iv) are satisfied with $p(t) \equiv 0$, then the trivial solution of the Eq. (1.2) is globally asymptotically stable.

Corollary 2.1

If $g(x(t-\tau ))=g(x)$, then the trivial solution of the Eq. (1.1) is globally asymptotically stable.

Theorem 2.2

In addition to conditions (i)–(iv), suppose that

• (v)    $|p(t,x,y)|\le M,$

for all $t\le 0$, then there exists a constant $\sigma , (0< \sigma < \infty )$ depending only on the constants $\alpha ,~\beta$ and $\gamma$ such that every solution of Eq. (1.2) satisfies

$$\begin{aligned} x^{2}(t)+\dot{x}^{2}(t)\le {e^{-\sigma t} \left\{ A_{1}+A_{2}\int ^{t}_{t_{0}}\left| p(s)\right| e^{\frac{1}{2}\sigma s}ds\right\} ^{2}} \end{aligned}$$

(2.2)

for all t $\ge t_{0}$, where the constant $A_{1}>0$, depends on $\alpha ,~\beta$ and $\gamma$ as well as on $t_{0}, x(t_{0}), \dot{x}(t_{0});$ and the constant $A_{2}>0$ depends on $\alpha ,~\beta$ and $\gamma$.

Corollary 2.2

If $g(x(t-\tau ))=g(x)$, then the inequality (1.2) holds for the Eq. (1.1).

Theorem 2.3

Suppose the conditions of the Theorem 2.2 are satisfied with condition (iv) replaced with

• (vi)    $|p(t, x, y)|\le (|x|+|y|)\phi (t),$

where $\phi (t)$ is a non negative and continuous function of t such that $\int ^{t}_{0}{\phi (s)ds}\le M < \infty$ is satisfied with a positive constant M. Then, there exists a constant $K_{0}$ which depends on $M, K_{1}, K_{2}$ and $t_{0}$ such that every solution x(t) of the Eqs. (1.1) and (1.2) satisfies

$$\begin{aligned} \left| x(t)\right| \le K_{0},\quad \left| \dot{x}(t)\right| \le K_{0} \end{aligned}$$

for sufficiently large t.

Corollary 2.3

If $g(x(t-\tau ))=g(x)$, then every solution of the Eq. (1.1) satisfies

$$\begin{aligned} \left| x(t)\right| \le K_{0},\qquad \left| \dot{x}(t)\right| \le K_{0} \end{aligned}$$

for sufficiently large t.

Remark

We wish to remark here that while the Theorem 2.1 is on the global asymptotic stability of the trivial solution, Theorems 2.2 and 2.3 deal with the boundedness and ultimate boundedness of the solutions respectively.

Notations

Throughout this paper $K, K_{0}, K_{1},\ldots K_{12}$ denote finite positive constants whose magnitudes depend only on the functions f, g and p as well as constants $\alpha ,~\beta ,~\gamma$ and $\delta$ but are independent of solutions of the Eqs. (1.1) and (1.2). $K_{i}'s$ are not necessarily the same for each time they occur, but each $K_{i}, i=1,2,\ldots$ retains its identity throughout. $V, V_{1}$ and $V_{2}$ denote Lyapunov functionals and $\dot{V}|_{(*)}=\frac{d}{dt}V|_{(*)}$ stands for the derivative of V with respect to t along the solution path of a system $(*)$ (say).

3 Preliminary results

We shall use as a tool to prove our main results a Lyapunov functional V(t; x, y) defined by

$$\begin{aligned} V(t;x,y) = V_{1} + V_{2} \end{aligned}$$

(3.1)

with

$$\begin{aligned} 2V_{1} = \displaystyle \frac{\delta }{a}\left\{ (a^{2}+2)x^{2}+ 2axy + 2y^{2}\right\} , \end{aligned}$$

where $\alpha , \beta$ and $\delta$ are positive real numbers, a is a continuous non-decreasing function with $a'\le 2$, and

$$\begin{aligned} V_{2} = \displaystyle \frac{2\mu }{\tau }\displaystyle \int _{-\tau }^{0}\left\{ \displaystyle \int ^{0}_{\theta _{1}}{(x^{2}(t+\theta )+y^{2}(t+\theta ))}d\theta \right\} d\theta _{1}.\end{aligned}$$

The following lemmas are needed to prove the Theorems 2.1, 2.2 and 2.3.

Lemma 3.1

Subject to the assumptions of Theorem 2.1 there exist positive constants $K_{i}= K_{i}(a~,\delta ), i = 1,2$ such that

$$\begin{aligned} K_{1}(x^{2}+y^{2}) \le V(t; x, y) \le K_{2}(x^{2}+y^{2}). \end{aligned}$$

(3.2)

Proof

First, it is clear from the Eq. (3.1) that $V(0; 0, 0)\equiv 0.$

We can re-arrange $V_{1}$ in Eq. (3.1) to have

$$\begin{aligned} 2V_{1} =\displaystyle \frac{2\delta }{a}\left( x+\frac{1}{2}ay\right) ^{2}+ \delta ax^{2}+\displaystyle \frac{\delta }{a}(4-a^{2})y^{2}, \end{aligned}$$

(3.3)

from which the estimate

$$\begin{aligned} 2V_{1}\ge \displaystyle \frac{\delta }{a}\left\{ a^{2}x^{2}+(4-a^{2})y^{2}\right\} . \end{aligned}$$

(3.4)

is obtained.

It follows from the above that there exists a constant $K_1$ such that

$$\begin{aligned} V \ge K_{1}(x^{2}+y^{2}) \end{aligned}$$

(3.5)

where

$$\begin{aligned} K_{1}= \displaystyle \frac{\delta }{a}\times \min \left\{ a^{2}, (4-a^{2})\right\} . \end{aligned}$$

On one hand, it is not difficult to establish that

$$\begin{aligned} V(t; x, y )\ge K_{1}(x^{2}+y^{2})+\displaystyle \frac{2\mu }{\tau }\displaystyle \int _{-\tau }^{0}\left\{ \displaystyle \int ^{0}_{\theta _{1}}{(x^{2}(t+\theta )+y^{2}(t+\theta ))}d\theta \right\} d\theta _{1} \end{aligned}$$

(3.6)

since $V_{2}$ is always positive, while on the other hand, on using the inequality $|xy|\le \displaystyle \frac{1}{2}(x^{2}+y^{2})$ in Eq. (3.1),

$$\begin{aligned} 2V_{1}\le \displaystyle \frac{\delta }{a}\left\{ (a^{2} + a + 2 )x^2 +(a+2)y^{2}\right\} . \end{aligned}$$

(3.7)

Consequently, from the inequality (3.7),

$$\begin{aligned} V_{1} \le K_{2}(x^{2}+ y^{2}) \end{aligned}$$

(3.8)

where

$$\begin{aligned} K_{2}=\displaystyle \frac{\delta }{a}\times \max \left\{ (a^{2} + a + 2 ),(a+2)\right\} . \end{aligned}$$

Furthermore,

$$\begin{aligned} V(t; x, y) \le K_{2}(x^{2}+ y^{2})+ \displaystyle \frac{2\mu }{\tau } \displaystyle \int _{-\tau }^{0}\left\{ \displaystyle \int ^{0}_{\theta _{1}}{(x^{2}(t+\theta )+y^{2}(t+\theta ))}d\theta \right\} d\theta _{1}. \end{aligned}$$

(3.9)

At last, combination of inequalities (3.6) and (3.9) give

$$\begin{aligned} \begin{array}{ll} &{}K_{1}(x^{2}+y^{2})+\displaystyle \frac{2\mu }{\tau } \displaystyle \int _{-\tau }^{0}\left\{ \displaystyle \int ^{0}_{\theta _{1}}{(x^{2}(t+\theta )+y^{2}(t+\theta ))}d\theta \right\} d\theta _{1}\le V(t; x, y)\\ &{}\quad \le K_{2}(x^{2}+y^{2})+\displaystyle \frac{2\mu }{\tau } \displaystyle \int _{-\tau }^{0}\left\{ \displaystyle \int ^{0}_{\theta _{1}}{(x^{2}(t+\theta )+y^{2}(t+\theta ))}d\theta \right\} d\theta _{1},\end{array} \end{aligned}$$

(3.10)

which is equivalent to

$$\begin{aligned} K_{1}(x^{2}+y^{2})\le V(t; x, y)\le K_{2}(x^{2}+y^{2}). \end{aligned}$$

(3.11)

$\square$

The Lemma 3.1 is established.

Lemma 3.2

In addition to the assumptions of the Theorem 2.1, let condition (v) of the Theorem 2.2 be satisfied. Then there are positive constants $K_{j}=K_{j}(a,~\alpha ,~\delta ,~\gamma ) (j=4,5)$ such that for any solution (x, y) of the system (2.1),

$$\begin{aligned} \dot{V}|_{(2.1)} \equiv \frac{d}{dt}V|_{(2.1)}(x, y) \le -K_{5}(x^{2}+y^{2})+ K_{4}(\left| x\right| +\left| y\right| ), \end{aligned}$$

(3.12)

where V is as given in Eq. (3.1).

Proof

Differentiating the Eq. (3.1) along the solution path of the system (2.1), we have

$$\begin{aligned} \dot{V}(t; x, y)|_{(2.1)} = \dot{V_{1}}+\dot{V_{2}}, \end{aligned}$$

(3.13)

where

$$\begin{aligned} \dot{V_{1}}&= \displaystyle \frac{\delta }{a^{2}(t)} \{a(t)[2a(t)a'(t)x^{2}+2a'(t)xy]-[(a^{2}(t)+2)x^{2}+2axy+2y^{2}]a'(t)\}\\&\quad +\displaystyle \frac{\delta }{a(t)}\{2(a^{2}(t)+2)xy + 2a(t)y^{2} + 2a^{2}(t)x[-a(t)f(x,y)-g(x)+N(t)]\\&\quad +4y[-a(t)f(x,y)-g(x)+N(t)]\} \end{aligned}$$

and

$$\begin{aligned} \dot{V_{2}} = \displaystyle \frac{2\mu }{\tau }\displaystyle \int ^{0}_{-\tau }{[x^{2}(t)+y^{2}(t)-x^{2}(t+\theta )-y^{2}(t+\theta )]}d\theta \end{aligned}$$

Next is to obtain an upper bound on $\dot{V_{1}}$. This shall be done using the hypotheses on the functions f and g. Thus we have

$$\begin{aligned} \dot{V_{1}}= & {} \displaystyle \frac{\delta }{a(t)}\displaystyle \left\{ (2a^{2}(t)a'(t)-a^{2}(t)-2)x^{2}-2a'(t)y^{2}\right\} + \displaystyle \frac{\delta }{a(t)}\left\{ -2a^{2}(t)(\gamma +\beta )\right. \\&\left. -(4a(t)\alpha )y^{2}-4\beta xy + 2(a^{2}(t)+2)xy + (2a^{2}(t)x+4y)N(t)\right\} . \end{aligned}$$

Further simplification yields

$$\begin{aligned} \dot{V_{1}}= & {} - \displaystyle \frac{\delta }{a^{2}(t)}\displaystyle \left\{ [2a^{3}(t)(\beta + \gamma )+ a^{2}(t) + 2 - 2a^{2}(t)a'(t)]x^{2}+ [4a^{2}(t)\alpha + 2a'(t)] y^{2}\right. \nonumber \\&\left. +\, a(t)[4\beta - 2(a^{2}(t)+2)]xy - [2a^{2}(t)x+4y]N(t)\right\} . \end{aligned}$$

(3.14)

On choosing $\beta = \frac{1}{2}(a^{2}(t)+2)$, Eq. (3.14) becomes

$$\begin{aligned} \dot{V_{1}}= & {} - \displaystyle \frac{\delta }{a^{2}(t)}\displaystyle \left\{ [a^{3}(t)(2\gamma +a^{2}(t)+2)+ a^{2}(t) + 2 - 2a^{2}(t)a'(t)]x^{2}\right. \\&\left. +\, 2[2a^{2}(t)\alpha + a'(t)] y^{2}- [2a^{3}(t)x+4a(t)y]N(t)\right\} . \end{aligned}$$

It is obvious that

$$\begin{aligned} \dot{V_{1}}\le & {} - \displaystyle \frac{\delta }{a^{2}_{1}}\displaystyle \left\{ [a^{3}_{1}(2\gamma _{1}+a^{2}_{1}+2)+ a^{2}_{1} + 2 - 2a^{2}_{1}a'_{1}]x^{2}+ 2[2a^{2}_{1}\alpha _{1} + a'_{1}] y^{2}\right. \nonumber \\&\quad \left. -\, [2a^{3}_{1}x +4a_{1}y] N(t) \right\} . \end{aligned}$$

(3.15)

From the inequality (3.15), it follows that

$$\begin{aligned} \dot{V_{1}}\le - K_{3}(x^{2}+y^{2})+K_{4}(|x|+|y|)N(t), \end{aligned}$$

(3.16)

where $K_{3} = \frac{\delta }{a^{2}_{1}}\times \max \left\{ a^{3}_{1}(2\gamma _{1}+a^{2}_{1}+2)+ a^{2}_{1} + 2 - 2a^{2}_{1}a'_{1}, 2[2a^{2}_{1}\alpha _{1} + a'_{1}]\right\}$

and $K_{4} = \frac{\delta }{a^{2}_{1}}\times \max \left\{ 2a_{1}^{3}, 4a_{1}\right\}$.

Similarly, on simplifying $\dot{V_{2}}$, we have

$$\begin{aligned} \dot{V_{2}}= & {} - 2\mu (x^{2}+y^{2})- \displaystyle \frac{2\mu }{\tau }\displaystyle \int ^{0}_{-\tau }{[x^{2}(t+\theta )+y^{2}(t+\theta )]}d\theta \end{aligned}$$

(3.17)

$$\begin{aligned} \dot{V_{2}}\le & {} - 2\mu (x^{2}+y^{2}). \end{aligned}$$

(3.18)

Combining estimates (3.16) and (3.18), yield

$$\begin{aligned} \dot{V}\le - K_{5}(x^{2}+y^{2})+K_{4}(|x|+|y|)N(t), \end{aligned}$$

(3.19)

where $K_{5} = K_{3}+2\mu$.

For the case when $p(t)\equiv 0$,

$$\begin{aligned} \dot{V}\le -K_{3}(x^{2}+y^{2}) \end{aligned}$$

Hence the proof of Lemma 3.2. $\square$

4 Proof of main results

We shall now give the proofs of the main results.

Proof of Theorem 2.1

The proof of the Theorem 2.1 follows from Lemmas 3.1 and 3.2 where it has been established that the trivial solution of the Eq. (1.1) is globally asymptotically stable. i.e every solution $(x(t),\dot{x}(t))$ of the system (2.1) satisfies $x^{2}(t)+\dot{x}^{2}(t)\longrightarrow 0 ~\text{ as }~ t\longrightarrow \infty$. $\square$

Proof of Theorem 2.2

Indeed, by using the inequality (3.19), it follows that

$$\begin{aligned} \frac{dV}{dt}\le -K_{5}(x^{2}+y^{2})+ K_{4} (x^{2}+y^{2})^\frac{1}{2}\left| p\right| . \end{aligned}$$

Again, it also follows from the inequality (3.8) that

$$\begin{aligned} (x^{2}+y^{2})^\frac{1}{2}\le \left( \frac{V}{K_{1}}\right) ^\frac{1}{2}. \end{aligned}$$

Thus, the inequality (3.19) becomes

$$\begin{aligned} \dot{V}\le -K_{6}V+K_{7}V^{\frac{1}{2}}\left| p\right| . \end{aligned}$$

(4.1)

It is noted that $K_{3}(x^{2}+y^{2})= K_{3}\cdot \frac{V}{K_{1}}$ and

$$\begin{aligned} \frac{dV}{dt}\le -K_{6}V+K_{7}V^\frac{1}{2}\left| p\right| , \end{aligned}$$

where $K_{6}=\frac{K_{5}}{K_{1}}$ and $K_{7}=\frac{K_{4}}{K_{2}^\frac{1}{2}}.$

Furthermore, from the above inequality we have

$$\begin{aligned} \dot{V}\le -2K_{8}V+K_{7}V^\frac{1}{2}\left| p\right| , \end{aligned}$$

where $K_{8}=\frac{1}{2}K_{6}.$

Therefore

$$\begin{aligned} \dot{V}+K_{8}V\le -K_{8}V+K_{7}V^\frac{1}{2}\left| p\right| . \end{aligned}$$

On choosing a constant $K_{9}$ such that $K_{9}= \frac{K_{8}}{K_{7}}$ gives

$$\begin{aligned} \dot{V}+K_{8}V\le K_{7}V^\frac{1}{2}\left\{ \left| p\right| -K_{9}V^{\frac{1}{2}}\right\} . \end{aligned}$$

(4.2)

Thus the inequality (4.2) becomes

$$\begin{aligned} \dot{V}+K_{8}V\le K_{7}V^{\frac{1}{2}}V^{*} \end{aligned}$$

where

$$\begin{aligned} V^{*}= & {} \left| p\right| -K_{9}V^{\frac{1}{2}}\\\le & {} V^{\frac{1}{2}}\left| p\right| \\\le & {} \left| p\right| . \end{aligned}$$

When $\left| p\right| \le K_{9}V^{\frac{1}{2}}$, then

$$\begin{aligned} V^{*}\le 0, \end{aligned}$$

and when $\left| p\right| \ge K_{9}V^{\frac{1}{2}}$, we have

$$\begin{aligned} V^{*} \le \left| p\right| \cdot {\frac{1}{K_{9}}}. \end{aligned}$$

(4.3)

On substituting the inequality (4.3) into the inequality (4.2), we have

$$\begin{aligned} \dot{V}+K_{8}V \le K_{10}V^{\frac{1}{2}}\left| p\right| , \end{aligned}$$

where

$$\begin{aligned} K_{10}=\frac{K_{7}}{K_{9}}. \end{aligned}$$

This implies that

$$\begin{aligned} V^{-\frac{1}{2}}{\dot{V}}+K_{8}V^{\frac{1}{2}} \le K_{10}\left| p\right| . \end{aligned}$$

(4.4)

Multiplying both sides of the inequality (4.4) by $e^{\frac{1}{2}K_{8}t}$, gives

$$\begin{aligned} e^{\frac{1}{2}K_{8}t}\left\{ V^{-\frac{1}{2}}{\dot{V}}+K_{8}V^{\frac{1}{2}}\right\} \le e^{\frac{1}{2}K_{10}t}K_{12}\left| p\right| , \end{aligned}$$

i.e

$$\begin{aligned} 2\frac{d}{dt}\left\{ V^{\frac{1}{2}}e^{\frac{1}{2}K_{8}t}\right\} \le e^{\frac{1}{2}K_{8}t}K_{12}\left| p\right| . \end{aligned}$$

(4.5)

Integrating both sides of inequality (4.5) from $t_{0}$ to t gives

$$\begin{aligned} \left\{ V^{\frac{1}{2}} e^{\frac{1}{2}K_{8}\gamma }\right\} ^{t}_{t{0}}\le \int ^{t}_{t{0}}\frac{1}{2}e^{\frac{1}{2}K_{8}s}K_{10}\left| p(s)ds\right| . \end{aligned}$$

Further simplifications give

$$\begin{aligned} \left\{ V^{\frac{1}{2}}(t)\right\} e^{\frac{1}{2}K_{8}t}\le V^{\frac{1}{2}}(t_{0})e^{\frac{1}{2}K_{8}t_{0}}+\frac{1}{2}K_{10}\int ^{t}_{t{0}}{\left| p(s)\right| e^{\frac{1}{2}K_{8}s}ds}, \end{aligned}$$

or

$$\begin{aligned} V^{\frac{1}{2}}(t)\le e^{-\frac{1}{2}K_{8}t}\left\{ V^{\frac{1}{2}}(t_{0})e^{\frac{1}{2}K_{8}t_{0}}+\frac{1}{2}K_{10}\int ^{t}_{t{0}}{\left| p(s)\right| e^{\frac{1}{2}K_{8}s}ds}\right\} . \end{aligned}$$

On utilizing inequalities (3.8) and (3.11), we have

$$\begin{aligned} K_{1}(x^{2}(t)+\dot{x}^{2}(t))&\le e^{-K_{8}t}\displaystyle \left\{ (K_{2}(x^{2}(t_{0}) + \dot{x}^{2}(t_{0})))^{\frac{1}{2}}e^{\frac{1}{2}K_{8}t_{0}}\right. \nonumber \\&\quad \left. +\frac{1}{2}K_{10}\displaystyle \int ^{t}_{t{0}}{\left| p(s)\right| e^{\frac{1}{2}K_{8}s}ds}\right\} ^{2}, \end{aligned}$$

(4.6)

for all $t \ge t_{0}.$

Thus,

$$\begin{aligned} x^{2}(t)+\dot{x}^{2}(t)&\le \frac{1}{K_{1}}\left\{ e^{-K_{8} t}\left\{ (K_{2}(x^{2}(t_{0})+\dot{x}^{2}(t_{0})))^{\frac{1}{2}}e^{\frac{1}{2}K_{8} t_{0}}\right. \right. \nonumber \\&\quad \left. \left. +\frac{1}{2}K_{10}\displaystyle \int ^{t}_{t{0}}{\left| p(s)\right| e^{\frac{1}{2}K_{8}s}ds}\right\} ^{2}\right\} \nonumber \\&\le \left\{ e^{-K_{8}t} \left\{ A_{1}+A_{2}\int ^{t}_{t{0}} {\left| p(s)\right| e^{\frac{1}{2}K_{8}s}ds}\right\} ^{2}\right\} , \end{aligned}$$

(4.7)

where $A_{1}$ and $A_{2}$ are constants depending on $\{K_{1},K_{2}, \ldots K_{10}$ and $(x^{2}(t_{0})+\dot{x}^{2}(t_{0}))$.

On substituting $K_{8}=\sigma$ in the inequality (4.7), we have

$$\begin{aligned} x^{2}(t)+\dot{x}^{2}(t)\le \left\{ e^{-\sigma t} \left\{ A_{1}+A_{2}\int ^{t}_{t{0}}{\left| p(s)\right| e^{\frac{1}{2}\sigma s}ds}\right\} ^{2}\right\} . \end{aligned}$$

This completes the proof. $\square$

Proof of Theorem 2.3

From the definition of function V and the conditions of the Theorem 2.3, the conclusion of Lemma 3.1 can be obtained as

$$\begin{aligned} V \ge K_{1}\left( x^{2}+y^{2}\right) , \end{aligned}$$

(4.8)

and since $p\ne 0$ we can revise the conclusion of the Lemma 3.2, i.e,

$$\begin{aligned} \dot{V}\le -K_{5}(x^{2}+y^{2})+K_{4}(\left| x\right| +\left| y\right| )\left| p\right| , \end{aligned}$$

to obtain

$$\begin{aligned} \dot{V}\le K_{4}(\left| x\right| +\left| y\right| )^{2}\theta (t) \end{aligned}$$

(4.9)

by using the condition (v) as stated in the Theorem 2.3. On employing the inequality $|xy|\le \displaystyle \frac{1}{2}(x^{2}+y^{2})$ on inequality (4.9), we have

$$\begin{aligned} \dot{V}\le K_{11}(x^{2}+y^{2})\theta (t), \end{aligned}$$

(4.10)

where $K_{11}=2K_{4}.$

From inequalities (4.8) and (4.10) we have,

$$\begin{aligned} \dot{V}\le K_{11}V\theta (t). \end{aligned}$$

(4.11)

Integrating inequality (4.11) from 0 to t gives

$$\begin{aligned} V(t)-V(0)\le K_{12}\int ^{t}_{0}V(s)\theta (s)ds, \end{aligned}$$

(4.12)

where $K_{12}=\frac{K_{11}}{K_{1}}=\frac{2K_{4}}{K_{1}}$. Thus,

$$\begin{aligned} V(t)\le V(0)+K_{12}\int ^{t}_{0}V(s)\theta (s)ds. \end{aligned}$$

(4.13)

At last on applying the Gronwall-Reid-Bellman theorem on the inequality (4.13), we have

$$\begin{aligned} V(t)\le V(0)exp\left( K_{12}\int ^{t}_{0}\theta (s)ds\right) . \end{aligned}$$

(4.14)

Hence the proof of Theorem 2.3. $\square$

Remark

The proofs of Corollaries 2.1, 2.2 and 2.3 follow respectively from the proofs of Theorems 2.1, 2.2 and 2.3 with appropriate modifications.

5 Examples

Example 5.1

We shall consider a second order delay differential equation given as

$$\begin{aligned} \ddot{x}+\frac{\dot{x}^{2}\sin t\sin x}{2(1+t^{2})(1+x^{2})}+2x(t-\tau )\bigg [1+\frac{1}{(1+x^{2}(t-\tau ))}\bigg ]=0, \end{aligned}$$

(5.1)

and its equivalent system of first order delay differential equations

$$\begin{aligned} \begin{aligned}&\dot{x} = y\\&\dot{y} = -\frac{y^{2}\sin t\sin x}{2(1+^{2})(1+x^{2})}-2x\bigg (1+\frac{1}{1+x^{2}}\bigg )+\int ^{0}_{-\tau }\bigg [2-\frac{2[x^{2}(t+\theta )-1]}{[x^{2}(t+\theta )+1]^{2}}\bigg ]d\theta . \end{aligned} \end{aligned}$$

(5.2)

Fig. 1

Functions a(t) and $a'(t)$

Comparing the system (2.1) with system (5.2) when $p(t,x,y)=0,$ we note that

• (i) $a(t):=\dfrac{\sin t}{2(1+t^{2})}.$ Furthermore,

  $$\begin{aligned} -\frac{3}{10}< \frac{\sin t}{2(1+t^{2})}<\frac{3}{10},\quad \forall ~t\ge 0. \end{aligned}$$

  It then follows that

  $$\begin{aligned} 0=a_0\le a(t)\le a_1=\frac{3}{10},\quad \forall ~t\ge 0, \end{aligned}$$

  and

  $$\begin{aligned} a'(t):=\frac{2(1+t^{2})\cos t-4t\sin t}{4(1+t^{2})^{2}}\le \frac{1}{2},\quad \forall ~t\ge 0. \end{aligned}$$

  The behaviour of a(t) and $a'(t)$ are shown in Fig. 1.

• (ii) $f(x,y):=\frac{y^{2}\sin x}{1+x^{2}}$. Clearly $f(x,0)=0.$ Let

  $$\begin{aligned} F_{11}(x,y):=\frac{f(x,y)-f(x,0)}{y}=\frac{y\sin x}{1+x^{2}},\quad \forall x,y\ne 0. \end{aligned}$$

  It follows that

  $$\begin{aligned} 0=\alpha _{0}\le F_{11}(x,y)=\alpha \le \alpha _{1}=\frac{4}{4+\pi ^{2}},\quad \forall ~x,y\ne 0. \end{aligned}$$

• (iii) Similarly

  $$\begin{aligned} 0=\beta _{0}\le F_{12}(x,y)\!:=\!\frac{f(x,y)-f(0,y)}{x}\!=\!\beta \le \beta _{1}=\frac{8}{\pi (\pi +4)^{2}},\quad \forall ~y,x\ne 0. \end{aligned}$$

  The behaviour of the functions $F_{11}(x,y)$ and $F_{12}(x,y)$ are shown respectively in Fig. 2.

• (iv) The function $g(x)=2x+\frac{2x}{1+x^{2}},$ from where we have $g(0)=0$ for all x. Let

  $$\begin{aligned} G_{1}(x):=\frac{g(x)-g(0)}{x}=2+\frac{2}{x^{2}+5},\quad \forall ~x\ne 0. \end{aligned}$$

  Then

  $$\begin{aligned} 0\le \frac{2}{x^{2}+5}\le 1\quad \forall ~x. \end{aligned}$$

  It follows that

  $$\begin{aligned} 2=\gamma _{0}\le G_{1}(x)=\gamma \le \gamma _{1}=3\quad \forall ~x\ne 0, \end{aligned}$$

  this is depicted by Fig. 3.

• (v) From (ii), (iii) and (iv) we have the assumption that

  $$\begin{aligned} f(x,0)=f(0,y)=g(0)=0,\quad \forall ~x,y. \end{aligned}$$

  Furthermore, since $\alpha ,\beta$ and $\gamma$ are non negative constants, it follows that $I_{0}=[0,2]$. We can see that hypotheses (i)–(v), of the Theorem 2.1 hold. Hence by the Theorem 2.1, the trivial solution of the Eq. (5.1) [or the system (5.2)] is globally asymptotically stable.

Fig. 2

The behaviour of the functions $F_{11}(x,y)$ and $F_{12}(x,y)$ respectively

Fig. 3

The inequalities $2=\gamma _{0}\le G_{1}(x)=\gamma \le \gamma _{1}=3$

Example 5.2

Consider the second order delay differential equation

$$\begin{aligned} \ddot{x}\bigg (1+\frac{t+2}{e^{t}+1}\bigg )\sin (x\dot{x})+\bigg [x(t-\tau ) +\frac{x(t-\tau )}{1+x^{2}(t-\tau )}\bigg ]=p(t,x,y) \end{aligned}$$

(5.3)

where

$$\begin{aligned} p(t,x,y)=\frac{(2t\cos t+(t^{2}+1)\sin t-2t)(\sin x+\cos \dot{x})}{(1+t^{2})^{2}}. \end{aligned}$$

The Eq. (5.3) is equivalent to system of first order delay differential equation

$$\begin{aligned} \dot{x}= & {} y\nonumber \\ \dot{y}= & {} -\bigg [1+\frac{t+2}{e^{t}+1}\bigg ]\sin xy-\bigg [1+\frac{1}{1+x^{2}}\bigg ]x+\int ^{0}_{-\tau }\bigg [1-\frac{x^{2}(t+\theta )-1}{(x^{2}(t+\theta )+1)^{2}}\bigg ] d\theta \nonumber \\&+\frac{(2t\cos t+(t^{2}+1)\sin t-2t)(\sin x+\cos y)}{(1+t^{2})^{2}}. \end{aligned}$$

(5.4)

It is easy to see, from the system of Eqs. (2.1) and (5.4), that

• (i) $a(t):=1+\frac{t+2}{(1+e^{t})^{2}}$ from where we obtain

  $$\begin{aligned} 0<1=a_{0}\le a(t)\le a_{1}=\frac{3}{2}, \end{aligned}$$

  for all $t\ge 0$ and

  $$\begin{aligned} a'(t)=\frac{1-(2t+3)e^{t}}{(1+e^{t})^{3}}\le \frac{3}{10}<\frac{1}{2}, \end{aligned}$$

  for all $t\ge 0.$ The bounds on the functions a(t) and $a'(t)$ are shown in Fig. 4.

• (ii) $f(x,y):=\sin (xy),$ with $f(x,0)=0.$ If we define

  $$\begin{aligned} F_{21}(x,y):=\frac{f(x,y)-f(x,0)}{y}=\frac{\sin (xy)}{y},\quad \forall ~x,y\ne 0. \end{aligned}$$

  It is not difficult to show that

  $$\begin{aligned} 0=\alpha _{0}\le F_{21}(x,y)=\alpha \le \alpha _{1}=1, \end{aligned}$$

  for all $x,y\ne 0.$

• (iii) $f(x,y):=\sin (xy),$ with $f(0,y)=0$ for all x, y. If we define

  $$\begin{aligned} F_{22}(x,y):=\frac{f(x,y)-f(0,y)}{x}=\frac{\sin (xy)}{x},\quad \forall ~y,x\ne 0. \end{aligned}$$

  We see that

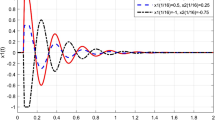
  $$\begin{aligned} 0=\beta _{0}\le F_{22}(x,y)=\beta \le \beta _{1}=1, \end{aligned}$$

  for all $y,x\ne 0$. Figure 5 shows the behaviour of functions $F_{21}(x,y)$ and $F_{22}(x,y).$

• (iv) Let $g(x):=x+\displaystyle \frac{x}{1+x^{2}},$ so that $g(0)=0$ and define

  $$\begin{aligned} G_{2}(x):=\frac{g(x)-g(0)}{x}=1+\frac{1}{1+x^{2}},\quad \forall ~x\ne 0. \end{aligned}$$

  It follows that

  $$\begin{aligned} 1=\gamma _{0}\le G_{2}(x)=\gamma \le \gamma _{1}=2, \end{aligned}$$

  for all $x\ne 0.$ The upper and lower bounds of the function $G_{2}$ are shown in Fig. 6.

• (v) From (ii), (iii) and (iv) we note that

  $$\begin{aligned} f(x,0)=f(0,y)=g(0)=0,\quad \forall ~x, y. \end{aligned}$$

  Also $I_{0}=[0,2]$. For the case $p(t,x,y)=0,$ all assumptions of the Theorem 2.1 hold. By Theorem 2.1 the trivial solution of the system (5.4) [or the Eq. (5.3)] is globally asymptotically stable.

• (vi) If p(t, x, y) in the system (2.1) is replaced by

  $$\begin{aligned} p(t):=\frac{2t}{3+5t^{2}},\quad \forall ~t\ge 0, \end{aligned}$$

  then, since

  $$\begin{aligned} 0\le \frac{2t}{3+5t^{2}}< \frac{3}{10}, \end{aligned}$$

  for all $t\ge 0,$ it follows that

  $$\begin{aligned} |p(t)|< 1=M<\infty . \end{aligned}$$

  The behaviour of p(t) is described by Fig. 7.

  At this point, assumptions (i)–(vi) of Theorem 2.2 hold and the conclusion is immediate.

• (vii) Finally, we shall consider the forcing term defined as

  $$\begin{aligned} p(t,x,y):=\frac{(2t\cos t+(t^{2}+1)\sin t-2t)(\sin x+\cos \dot{x})}{(1+t^{2})^{2}}. \end{aligned}$$

  This implies that

  $$\begin{aligned} |p(t,x,y)|\le (|\sin x|+|\cos y|)\phi (t) \end{aligned}$$

  for all x, y and $t\ge 0,$ where

  $$\begin{aligned} \phi (t):=\frac{2t\cos t+(1+t^{2})\sin t-2t}{(t^{2}+1)^{2}}. \end{aligned}$$

  Let

  $$\begin{aligned} \Phi (t)=\int ^{t}_{0}\phi (\mu )d\mu =\frac{1-\cos t}{t^{2}+1}<\frac{3}{10}<M,\quad \forall ~t\ge 0. \end{aligned}$$

  The bounds on $\Phi (t)$ are shown in Fig. 8.

All hypotheses of Theorem 2.3 are satisfied and the conclusion followed.

Fig. 4

Boundedness of the functions a(t) and $a'(t)$

Fig. 5

The behaviour of the functions $F_{21}(x,y)$ and $F_{22}(x,y)$ respectively

Fig. 6

Boundedness of the functions a(t) and $a'(t)$

Fig. 7

The functions p(t) for all $t\ge 0$

Fig. 8

The function $\Phi (t)$ for all $t\ge 0.$