Dynamics of Competitive Systems with Diffusion Between Source–Sink Patches

Abstract

This paper considers two-species competitive systems with one-species’ diffusion between patches. Each species can persist alone in the corresponding patch (a source), while the mobile species cannot survive in the other (a sink). Using the method of monotone dynamical systems, we give a rigorous analysis on persistence of the system, prove local/global stability of the equilibria and show new types of bi-stability. These results demonstrate that diffusion could lead to results reversing those without diffusion, which extend the principle of competitive exclusion: Diffusion could lead to persistence of the mobile competitor in the sink, make it reach total abundance larger than if non-diffusing and even exclude the opponent. The total abundance is shown to be a distorted function (surface) of diffusion rates, which extends both previous theory and experimental observations. A novel strategy of diffusion is deduced in which the mobile competitor could drive the opponent into extinction, and then approach the maximal abundance. Initial population density and diffusive asymmetry play a role in the competition. Our work has potential applications in biodiversity conservation and economic competition.

1 Introduction

With the uncontrolled land use by human, more and more habitats occupied by species are fragmented. The fragmentation forms a threat for viability of many endangered species (Andren 1994). One way to reduce the threat is to construct ecological corridors between fragmented patches, which would act as diffusion routes of individuals between different patches. Indeed, Gilbert et al. (1998) reported that the presence of ecological corridors increases the richness of species in a system of microarthropods inhabiting moss patches in stones. However, ecological corridors could also lead to movement of individuals from suitable to unsuitable patches with low reproduction rates. For instance, Aström and Pärt (2013) showed that the presence of ecological corridors could decrease total population abundance of oribatid mites in their laboratory experiments. Thus, it is significant to study whether or not diffusion is detrimental or beneficial for total population abundance of mobile species.

Holt (1985) studied single-species systems with diffusion. In the system, individuals of the species diffuse between a source and a sink patch. Here, a patch is called a source (resp. a sink) if the species can (resp. cannot) survive on it. By analyzing dynamics of the model, Holt showed that if diffusion from the source to sink is small and the growth rate in the source is higher than the death rate in the sink, the species would persist in both patches and the diffusion would make the species approach total abundance larger than if non-diffusing. Wu et al. (2020) considered a simplified form of Holt’s model. Based on complete analysis on the model, Wu et al. obtained explicit expression of the total abundance, which showed a mechanism by which diffusion can enhance the abundance. It is also shown that total abundance increases with a relatively small diffusion, then approaches a maximum and finally decreases. This is the so-called hump-shaped response observed by Zhang et al. (2015) in their laboratory experiments, in which they checked total abundances with four different diffusion rates, namely $0\%$, $6\%$, $10\%$ and $20\%$, and found that the maximum was attained at $6\%$.

Any real species is limited by resources and subject to competition with different coexisting populations. Thus, single-species models are oversimplified. Takeuchi (1990) considered a two-species competitive system, in which one of the species moves between two source patches. Rigorous analysis on the model showed that the system can be made persistent under appropriate diffusion conditions. Poggiale (1998) studied a competitive system, where two species can move rapidly between two source patches. Using aggregation method, Poggiale showed that migration could have positive or negative effect on coexistence of the competitors in the ecological system. Ruiz-Herrera and Torres (2018) studied competition/predation systems with small diffusion. In the two-species competition system, one of the species can move between two source patches. Theoretical analysis on the model proved precise thresholds which determine when diffusion is detrimental/beneficial for overall abundances of the competitors. Zhang et al. (2020) checked effects of diffusion between source–sink patches in their experiments. A wells in the experiments is a source for the consumer if the toxin is low, while it is a sink if the toxin is high such that the consumer cannot survive. It was observed that diffusion source–sink wells makes the consumer persist in both wells and approach total abundance larger than if non-diffusing. For additional relevant researches, we refer to Takeuchi (1986, 1989, 1992), Takeuchi and Lu (1995), Ruiz-Herrera (2018), Zhang et al. (2017), etc. While these works provided interesting predictions, the patches are assumed to be sources. Since endangered species often live in poor patches, it is necessary to study sinks and show whether or not diffusion from a source (e.g., a refuge) to sink can promote persistence of the species in the sink.

In this paper, we consider a two-species competitive system with one-species’ diffusion between patches. Each species can persist alone in the corresponding patch, while the mobile species cannot survive in the other. Using the method of monotone dynamical systems in Takeuchi (1990) and Gao and Liang (2007), we give a rigorous analysis on persistence of the system and show new types of bi-stability (see Theorem 3.6(iii–iv)). Then we prove local/global stability of equilibria (see Theorems 3.1, 3.5–3.8). These results demonstrate that diffusion could lead to results reversing those without diffusion, which extend the principle of competitive exclusion. Roughly speaking, while each competitor persists in the corresponding source without diffusion, competitive exclusion occurs in the presence of diffusion (see Sect. 4): When diffusion of the mobile competitor from the source to sink is large, it would go to extinction; when the diffusion is small, the mobile competitor would persist in both patches and could reach total abundance larger than if non-diffusing, while the opponent could be excluded; when the diffusion is intermediate, coexist of the species in the system is density-dependent, while the mobile competitor can approach total abundance larger than if non-diffusing. The total abundance is shown to be a distorted function (surface) of diffusion rates, which can be both hump-shaped and bowl-shaped. This finding extends both previous theory and experimental observations. A novel strategy of diffusion is deduced in which the mobile competitor could drive the opponent into extinction, and then approach the maximal abundance. Initial population density and diffusive asymmetry play a role in the competition. Meanwhile, the diffusion is not beneficial to growth of the non-mobile species. Numerical simulations illustrate and extend our results.

The paper is organized as follows. In the next section, we describe the model. Section 3 shows dynamics of the model, while principle of competitive exclusion is studied in Sect. 4. Discussion and application are given in Sect. 5.

2 Model

In this section, we present some notions in monotone dynamical systems theory and describe the model.

First, we give some notions. Let n be a positive integer. Denote

$$\begin{aligned} \mathbb {R}_+^n = \{ x \in \mathbb {R}^n: x_i \ge 0, 1\le i \le n \},~ \text {Int}\mathbb {R}_+^n = \{ x \in \mathbb {R}^n: x_i > 0, 1\le i \le n \}. \end{aligned}$$

Let K be an orthant of $\mathbb {R}^n$. For two points $x, y \in \mathbb {R}^n$, we say $x \le _K y$ if $y-x \in K$; $x <_K y$ if $y-x \in K$ and $y\ne x$; $x \ll _K y$ if $y-x \in \text {Int} K$. If $x <_K y$, we define $[x, y ]_K = \{ z \in \mathbb {R}^n: x \le _K z \le _K y \}$. If $x \ll _K y$, we define $(x, y )_K = \{ z \in \mathbb {R}^n: x \ll _K z \ll _K y \}$.

Consider differential equations $\dot{x} =f(x), x\in \mathbb {R}^n$. The semi-flow $\varphi$ generated by the equations is said to be type-K monotone if

$$\begin{aligned} \varphi _t(x) \le _K \varphi _t(y)~~ whenever ~~x \le _K y ~~and~~ t>0. \end{aligned}$$

$\varphi$ is said to be strongly type-K monotone if $\varphi _t(x) \ll _K \varphi _t(y)$ whenever $x <_K y$ and $t>0.$ The system is called type-K cooperative if the Jacobian matrix Df(x) has the form

$$\begin{aligned} \begin{pmatrix} J_1 &{} -J_2 \\ -J_3 &{} J_4 \end{pmatrix} \end{aligned}$$

where all entries of matrices $J_2$ and $J_3$ are nonnegative, and $J_1, J_4$ are cooperative square matrices, i.e., all off-diagonal entries are nonnegative.

Smith (1995) proved that the flow generated by a type-K monotone system is type-K monotone. Moreover, if Df(x) is irreducible in some open set $\Theta \in \mathbb {R}_+^n$, the flow is strongly type-K monotone in $\Theta$. An orbit $\varphi _t$ is said to be K-monotonic non-decreasing (resp. non-increasing) if $\varphi _{t_1}(x) \le _K \varphi _{t_2}(x)$ whenever $t_1 < t_2$ (resp. $t_1 > t_2$). Smith (1986, 1995) showed the following results.

Lemma 2.1

Let $\dot{x} =f(x)$ be type-K monotone on $\mathbb {R}_+^n$. If $f(x_0) \le _K 0$ (resp. $f(x_0) \ge _K 0$) for some $x_0 \in \mathbb {R}_+^n$, then the flow $\varphi _t (x_0)$ is type-K monotonic non-increasing (resp. monotonic non-decreasing) for $t>0$.

Lemma 2.2

Let $\dot{x} =f_m (x)$ be type-K monotone on $\mathbb {R}_+^n$ with flow $\varphi _t^m, m=1,2$. Assume that $f_1 (x) \le _K f_2 (x)$ for all $x \in \mathbb {R}_+^n$. If $x_* \le _K x^*$, then $\varphi _t^1(x_*) \le _K \varphi _t^2(x^*)$ for $t>0$.

Second, we describe the model. Let species u be the first competitor, which lives in patch 1 all the time. Let species v be the second competitor that can move between patch 1 and 2. Patch 1 is a sink for species v, while patch 2 is a source (e.g., a refuge). Then the competitive system with diffusion can be described by

$$\begin{aligned} \frac{\mathrm{d}U_1}{\mathrm{d}\tau }= & {} \bar{r}_1 U_1 \left( 1-\frac{U_1}{\bar{K}_1} - \bar{a}_{12} V_1 \right) , \end{aligned}$$

(1)

$$\begin{aligned} \frac{\mathrm{d}V_1}{\mathrm{d}\tau }= & {} -\bar{r}_2 V_1 - \bar{a}_{21} U_1 V_1 + \bar{D}_2 V_2 - \bar{D}_1 V_1,\end{aligned}$$

(2)

$$\begin{aligned} \frac{\mathrm{d}V_2}{\mathrm{d}\tau }= & {} \bar{r}_3 V_2 \left( 1-\frac{V_2}{\bar{K}_2}\right) + \bar{D}_1 V_1 - \bar{D}_2 V_2, \end{aligned}$$

(3)

where $U_1$ represents population density of the first competitor in patch 1 and $V_i$ is that of the second competitor in patch $i, i=1,2$. Parameter $\bar{r}_1$ represents the intrinsic growth rate of species u in patch 1, and $\bar{K}_1$ is the carrying capacity. $\bar{r}_3$ represents the intrinsic growth rate of species v in patch 2, and $\bar{K}_2$ is the carrying capacity. Parameter $\bar{r}_2$ represents the death rate of species v in patch 1. $\bar{a}_{12}$ and $\bar{a}_{21}$ represent the competition degrees in patch 1. Parameter $\bar{D}_1$ represents the diffusion rate of species v from patch 1 to 2, and $\bar{D}_2$ is that from patch 2 to 1.

To minimize the set of parameters, we take the following transformations:

$$\begin{aligned} u_1= & {} \frac{U_1}{\bar{K}_1} ,~v_1= V_1,~v_2= \frac{v_2}{\bar{K}_2} ,~ t= \bar{r}_2 \tau ,~ r_1= \frac{\bar{r}_1}{\bar{r}_2}, r_2= \frac{\bar{r}_3}{\bar{r}_2},\\ b_1= & {} \bar{a}_{12} ,~ b_2 = \frac{\bar{a}_{21}}{\bar{r}_2} \bar{K}_1,~ D_1 = \frac{\bar{D}_1 }{\bar{r}_2},~ D_2 = \frac{\bar{D}_2 \bar{K}_2 }{\bar{r}_2}. \end{aligned}$$

Then system (1) can be rewritten as

$$\begin{aligned} \frac{\mathrm{d}u_1}{\mathrm{d}t}= & {} r_1 u_1 (1-u_1 - b_1 v_1 ), \nonumber \\ \frac{\mathrm{d}v_1}{\mathrm{d}t}= & {} - v_1 - b_2 u_1 v_1 + D_2 v_2 - D_1 v_1,\nonumber \\ \frac{\mathrm{d}v_2}{\mathrm{d}t}= & {} r_2 v_2 (1-v_2) + D_1 v_1 - D_2 v_2. \end{aligned}$$

(4)

We consider solutions of system (4) with nonnegative initial values, i.e., $u_1(0)\ge 0, v_i(0)\ge 0$.

Since the Jacobian matrix of (4) is

$$\begin{aligned} J=\begin{pmatrix} r_1 (1- 2 u_1 - b_1 v_1 ) &{}-r_1 b_1 u_1 &{}0 \\ - b_2 v_1 &{}-1 - b_2 u_1 - D_1&{}D_2 \\ 0 &{}D_1 &{}r_2 (1-2 v_2) - D_2 \end{pmatrix}, \end{aligned}$$

(5)

system (4) is type-K cooperative with

$$\begin{aligned} K= \left\{ (u_1,v_1,v_2 ) \in \mathbb {R}_+^3: u_1\ge 0,v_1\le 0,v_2\le 0 \right\} . \end{aligned}$$

Let f represent the vector field defined by (4) and $\varphi$ the corresponding flow. Because matrix J is irreducible in Int$\mathbb {R}_+^3$, the flow $\varphi _t$ is type-K monotone in $\mathbb {R}_+^3$ and strongly type-K monotone in Int$\mathbb {R}_+^3$ by Smith (1995).

The Jacobian matrix J in (5) is tri-diagonal and system (4) is type-K cooperative. Since the result of Smillie (1984) for cooperative systems is still valid for type-K cooperative ones, we have the following result.

Lemma 2.3

For any $x\in \mathbb {R}_+^3$, the $\omega$-limit set of $\varphi _t(x)$ in system (4) is precisely one equilibrium.

Stability of boundary equilibria is as follows. There are three boundary equilibria in system (4), namely O(0, 0, 0), $P_1(1, 0, 0)$ and $P_{23}(0, v_1^+,v_2^+)$ with

$$\begin{aligned} v_1^+ = \frac{ D_2}{1 +D_1 } v_2^+,~~ v_2^+ = 1 - \frac{ D_2}{r_2 (1 +D_1) }. \end{aligned}$$

(6)

On the invariant $u_1$-axis, equilibrium $P_1$ is asymptotically stable. On the invariant plane $u_1=0$, system (4) becomes

$$\begin{aligned} \frac{\mathrm{d}v_1}{\mathrm{d}t}= & {} -v_1 + D_2v_2 -D_1v_1, \nonumber \\ \frac{\mathrm{d}v_2}{\mathrm{d}t}= & {} r_2 v_2 ( 1- v_2) +D_1v_1 - D_2v_2. \end{aligned}$$

(7)

Dynamics of system (7) are well known, which are shown as follows.

Lemma 2.4

(Wu et al. 2020) Let $D_2^+ = r_2 (1 +D_1)$.

• (i) If $D_2 \ge D_2^+,$ the boundary equilibrium O(0, 0) of system (7) is globally asymptotically stable in Int$\mathbb {R}_+^2$.

• (ii) If $D_2 < D_2^+$, there is a unique positive equilibrium $E_{23}(v_1^+,v_2^+)$ of system (7), which is globally asymptotically stable in Int$\mathbb {R}_+^2$. Total abundance $T_1^+ = v_1^+ + v_2^+$ of the species reaches the maximum $T_{1max}^+ = r_2 (1+D_1)/4$ at $D_2 = r_2 (1+D_1)/2$.

Since solutions $u_1(t)$ and $v_i(t)$ of system (4) represent population densities, they must be nonnegative. On the other hand, they should be bounded since it is impossible for a species to approach infinite density in nature. These properties are guaranteed by the following result.

Theorem 2.5

Solutions of system (4) are nonnegative and bounded.

Proof

Let $P= (u_1,v_1,v_2 ) \in \mathbb {R}_+^3$. Then $(0,v_1,v_2 ) \le _K (u_1,v_1,v_2 ) \le _K (u_1,0,0 )$. By monotonicity of system (4), there hold

$$\begin{aligned} \varphi _t(0,v_1,v_2 ) \le _K \varphi _t(u_1,v_1,v_2 ) \le _K \varphi _t(u_1,0,0 ),~~t>0. \end{aligned}$$

(8)

From stability of equilibria $O, P_1$ and $P_{23}$ on the boundary of $\mathbb {R}_+^3$, the set $[P_{23}, P_1]_K$ or $[O, P_1]_K$ attracts all solutions of (4), which means that solutions of system (4) are nonnegative and dissipative. $\square$

3 Persistence

In this section, we prove local/global stability of equilibria of system (4), give a rigorous analysis on persistence of the system and show new types of bi-stability in competitive systems.

First, we show stability of boundary equilibria O(0, 0, 0), $P_1(1,0,0)$ and $P_{23}(0,v_1^+,v_2^+)$. For simplicity, we focus on the generic case where the equilibria are hyperbolic. Denote

$$\begin{aligned} D_2^a=r_2 -(1+b_2+D_1 ),~ D_2^b=r_2+ \frac{r_2 D_1}{1+b_2}. \end{aligned}$$

Then $D_2^a < D_2^b$.

Theorem 3.1

• (i) Assume $D_2 \ge D_2^+$. Then $P_1$ is globally asymptotically stable in $\mathbb {R}_+^3 \backslash \{(u, v_1, v_2) : u = 0\}$.

• (ii) Assume $D_2 <D_2^+$.

  • (iia) O is a saddle point with $W^s(O) \cap \mathbb {R}_+^3 = \{O\}$.

  • (iib) $P_1$ is linearly stable if $D_2 >D_2^b$. $P_1$ is linearly unstable if $D_2 < D_2^b$, where $W^s(P_1) \cap \mathbb {R}_+^3 = \{(u_1,v_1,v_2) \in \mathbb {R}_+^3: u_1>0,v_1=0,v_2=0 \}$.

  • (iic) $P_{23}$ is linearly stable if $1- b_1 v_1^+ <0$. $P_{23}$ is linearly unstable if $1- b_1 v_1^+ >0$, where $W^s(P_{23}) \cap \mathbb {R}_+^3 = \{(u_1,v_1,v_2) \in \mathbb {R}_+^3: u_1=0,v_1\ge 0,v_2\ge 0, v_1+v_2>0 \}$.

  Here, $W^s(P)$ represents the strong stable manifold of an equilibrium P.

Proof

(i) By Theorem 2.5, solutions of system (4) are nonnegative. Denote

$$\begin{aligned} V(u_1,v_1,v_2 ) = \frac{D_2 -r_2}{D_2} v_1 + v_2. \end{aligned}$$

Let $(u_1(t),v_1(t),v_2(t))$ be a solution of (4) with initial condition $u_1(0)>0,v_1(0)\ge 0 ,v_2(0)\ge 0$. Then

$$\begin{aligned} \frac{\mathrm{d} V(u_1(t),v_1(t),v_2(t) )}{\mathrm{d}t}|_{(2.2)} = - \frac{D_2 -D_2^+}{D_2} v_1 - \frac{D_2 -r_2}{D_2} b_2 u_1 v_1 - r_2 v_2^2\le 0. \end{aligned}$$

Let $\dfrac{\mathrm{d} V}{dt }|_{(2.2) } =0$. Then $v_1 = v_2=0$, which means $\lim _{t\rightarrow \infty } u_1(t) = 1$ by the first equation of (1). By the LaSalle invariance principle (Hofbauer and Sigmund 1998), equilibrium $P_1$ is globally asymptotically stable in $\mathbb {R}_+^3 \backslash \{(u, v_1, v_2) : u = 0\}$.

(iia) By (5), the Jacobian matrix of (4) at equilibrium O is

$$\begin{aligned} J_0=\begin{pmatrix} r_1 &{}0 &{}0 \\ 0 &{}-1 - D_1&{}D_2 \\ 0 &{}D_1 &{}r_2 - D_2 \end{pmatrix}. \end{aligned}$$

(9)

Thus, equilibrium O has an eigenvalue $\lambda _1 = r_1>0$ and has the positive $u_1$-axis as its unstable manifold. The other eigenvalues satisfy

$$\begin{aligned} \lambda ^2+c_1\lambda + c_2=0,~ c_1= D_2-r_2 + 1+D_1,~ c_2= D_2-r_2(1+D_1). \end{aligned}$$

From $D_2 <D_2^+$, we have $c_2 <0$, which means that O is a saddle point with eigenvalues $\lambda _2 >0, \lambda _3<0$. Then $\lambda _3 = \frac{1}{2}(-c_1 -\sqrt{c_1^2-4 c_2 } ).$ Let $(x_1,y_1,y_2)$ be an eigenvector of $\lambda _3$. Then we can obtain $x_1=0, y_1 = -D_2 ,y_2= -1 - D_1 - \lambda _3$. Since

$$\begin{aligned} c_1^2-4 c_2 - (D_2-1-r_2-D_1)^2 = 4 D_1D_2>0, \end{aligned}$$

we have $y_2\ge 0$, which implies that the eigenvector of $\lambda _3$ does not direct toward Int$\mathbb {R}_+^3$. Thus, equilibrium O has no stable manifold in Int$\mathbb {R}_+^3$.

(iib) By (5), the Jacobian matrix of (4) at equilibrium $P_1$ is

$$\begin{aligned} J_1=\begin{pmatrix} -r_1 &{}-r_1 b_1 &{}0 \\ 0 &{}-1 - b_2 -D_1&{}D_2 \\ 0 &{}D_1 &{}r_2 - D_2 \end{pmatrix}. \end{aligned}$$

(10)

Thus, $P_1$ has an eigenvalue $\lambda _1 = -r_1<0$ and has the positive $u_1$-axis as its stable manifold. The other eigenvalues satisfy

$$\begin{aligned} \lambda ^2+\hat{c}_1\lambda + \hat{c}_2=0,~ \hat{c}_1= D_2-D_2^a,~ \hat{c}_2= (1+b_2) (D_2-D_2^b). \end{aligned}$$

(11)

Since $D_2^a <D_2^b$, $P_1$ is linearly stable if $D_2 >D_2^b$. A similar discussion can be given for the case where $P_1$ is linearly unstable.

(iic) By (5), the Jacobian matrix of (4) at equilibrium $P_{23}$ is

$$\begin{aligned} J_{23}=\begin{pmatrix} r_1 (1- b_1 v_1^+ ) &{}0 &{}0 \\ - b_2 v_1^+ &{}-1 -D_1&{}D_2 \\ 0 &{}D_1 &{}r_2 - D_2 - 2 r_2 v_2^+ \end{pmatrix}. \end{aligned}$$

Thus, $P_{23}$ has an eigenvalue $\lambda _1 = r_1 (1- b_1 v_1^+ )$. Since $\det J_{23} = r_1 r_2 (1+ D_1) (1- b_1 v_1^+ )$ and $P_{23}$ is globally asymptotically stable on the plane $u_1=0$, $P_{23}$ is linearly stable if $1- b_1 v_1^+ <0$. A similar discussion can be given for the case where $P_{23}$ is linearly unstable. $\square$

From Lemma 2.3 and Theorem 2.5, we obtain the following result.

Corollary 3.2

If system (4) has no positive equilibrium, either $P_1$ or $P_{23}$ is globally asymptotically stable.

Proof

If $D_2 \ge D_2^+$, then $P_1$ is globally asymptotically stable in $\mathbb {R}_+^3 \backslash \{(u, v_1, v_2) : u = 0\}$ by Theorem 3.1(i).

Assume $D_2 < D_2^+$. By (8), the set $[P_{23}, P_1]_K$ attracts all solutions of (4). Suppose that there are two different points $x_{0}$ and $\widetilde{x_{0}}$ such that $\omega (x_{0})=P_{1}$ and $\omega (\widetilde{x_{0}}) =P_{23}$. Let $B(P_{1})$ (resp. $B(P_{23})$) be the basin of attraction of $P_{1}$ (resp. $P_{23}$) in $[P_{23}, P_1]_K$. Since $\omega (x_{0})=P_{1}$ and $\omega (\widetilde{x_{0}}) =P_{23}$, the set $B(P_{1})$ (resp. $B(P_{23})$) is not empty and is an open set, e.g., including the set of $(x_{0}, P_1)_K$. Then the boundary $\bigodot$ of $B(P_{1})$ (resp. $B(P_{23})$) is a closed, bounded and invariant set in $[P_{23}, P_1]_K$. Since equilibrium O is a saddle point with $W^s(O) \cap \mathbb {R}_+^3 = \{O\}$ by Theorem 3.1(iia), there is at least one positive equilibrium in $\bigodot$, which forms contradiction. Thus, either $P_1$ or $P_{23}$ is globally asymptotically stable. $\square$

Second, we show stability of the positive equilibrium $P(u_1,v_1,v_2 )$. By the right-hand side of (4), P satisfies

$$\begin{aligned} \begin{aligned} 1-u_1 - b_1 v_1&=0, \\ - v_1 - b_2 u_1 v_1 + D_2 v_2 - D_1 v_1&=0,\\ r_2 v_2 (1-v_2) + D_1 v_1 - D_2 v_2&=0, \end{aligned} \end{aligned}$$

(12)

so that

$$\begin{aligned} u_1 = 1 - b_1 v_1,~~ v_2 = \frac{v_1}{D_2} (1 + b_2 + D_1 - b_1 b_2 v_1). \end{aligned}$$

$v_1$ satisfies

$$\begin{aligned} a_0 v_1^3 + a_1 v_1^2 + a_2 v_1 +a_3 =0 \end{aligned}$$

(13)

with

$$\begin{aligned} a_0= & {} \frac{r_2 b_1^2 b_2^2 }{D_2} ,~~ a_1 = -\frac{2 r_2 b_1 b_2 }{D_2} (1 + b_2 + D_1),~~ a_2 = \frac{r_2 }{D_2} (1 + b_2 + D_1)^2 + b_1 b_2 (r_2 - D_2),\\ a_3= & {} (1 + b_2 + D_1) (D_2 - r_2) -D_1 D_2. \end{aligned}$$

Lemma 3.3

System (4) has at most two positive equilibrium.

Proof

Let $P(u_1,v_1,v_2 )$ be a positive equilibrium of (4). Denote $w = v_1/v_2$. By the second and third equations of (12), we have

$$\begin{aligned} \begin{aligned} -1 - b_2 (1 - b_1 v_1) + D_2 w^{-1} - D_1&=0,\\ r_2 (1-v_2) + D_1 w - D_2&=0. \end{aligned} \end{aligned}$$

Then

$$\begin{aligned} v_1 = \frac{1}{b_1b_2} (1 + b_2 + D_1- D_2 w^{-1} ),~~ v_2 = \frac{1}{r_2} (r_2- D_2 + D_1 w ), \end{aligned}$$

so that

$$\begin{aligned} w^3 + \bar{c}_1 w^2 + \bar{c}_2 w + \bar{c}_3=0 \end{aligned}$$

(14)

with

$$\begin{aligned} \bar{c}_1 = \frac{D_2- r_2 }{D_1},~ \bar{c}_2 = \frac{r_2(1 + b_2 + D_1)}{b_1b_2 D_1},~ \bar{c}_3 = \frac{r_2 D_2}{b_1b_2 D_1}. \end{aligned}$$

Since $\bar{c}_3>0$, there is a negative root of equation (14), which means there are at most two positive roots of (14). $\square$

Lemma 3.4

• (i) If system (4) has a positive equilibrium P, then all eigenvalues of the Jacobian matrix J(P) are real.

• (ii) If system (4) has two positive equilibria $P_*$ and $P^*$, then the equilibria are totally strongly ordered with respect to $\ll _K$, i.e., $P_* \ll _K P^*$.

Proof

(i) Since matrix J(P) is tri-diagonal and quasi-symmetric (i.e., all nonzero off-diagonal entries $a_{ij}$ and $a_{ji}$ have the same sign), all eigenvalues of J(P) are real by Wilkinson (1965).

(ii) Let $P_*= (u_{1*},v_{1*},v_{1*} )$ and $P^*= (u_1^*,v_1^*,v_2^* )$. Without loss of generality, we assume $u_{1*} < u_1^*$. By $u_1 = 1- b_1 v_1$, we obtain $v_{1*} > v_1^*$. Suppose $v_{2*} \le v_2^*$. Then $\dfrac{v_{1*}}{v_{2*}} > \dfrac{v_1^* }{v_2^*}$. By the third equation of (4), we have

$$\begin{aligned} v_2= 1- \frac{D_2}{r_2} + \frac{D_1 v_1}{r_2 v_2}, \end{aligned}$$

which implies $v_{2*} > v_2^*$ and forms a contradiction. $\square$

Theorem 3.5

Let $P(u_1,v_1,v_2 )$ be a positive equilibrium of system (4). Then P is linearly stable if and only if

$$\begin{aligned} D_2 > \frac{b_1b_2 v_1^2 }{ v_2} (1 + D_1 \frac{v_1}{r_2 v_2^2}), \end{aligned}$$

where $u_1=u_1(D_2) ,v_1=v_1(D_2),v_2=v_2(D_2)$.

Proof

By (4), the Jacobian matrix J(P) of (4) at equilibrium P can be written as

$$\begin{aligned} J(P)=\begin{pmatrix} - r_1u_1 &{}- r_1b_1u_1 &{}0 \\ -b_2v_1 &{}-D_2 \frac{ v_2}{ v_1} &{}D_2 \\ 0 &{}D_1 &{}-r_2v_2 -D_1 \frac{ v_1}{ v_2} \end{pmatrix}. \end{aligned}$$

(15)

Then tr$J(P) = - r_1u_1 -D_2 \frac{ v_2}{ v_1} -r_2v_2 -D_1 \frac{ v_1}{ v_2} <0$.

Let $S(J)= \max \{Re \lambda : \lambda \in \sigma (J) \}$, where $\sigma (J)$ is the set of eigenvalues of J. In Theorem 2.7 by Smith (1988), for the type-K matrix J(P), $S(J(P))<0$ if and only if the following three inequalities hold

$$\begin{aligned}&(-1)(- r_1u_1)>0,\\&\quad (-1)^2 \begin{vmatrix} - r_1u_1&r_1b_1u_1 \\ b_2v_1&-D_2 \frac{ v_2}{ v_1} \end{vmatrix} = \frac{ v_2}{ v_1} \left( D_2 - \frac{b_1b_2 v_1^2 }{ v_2} \right)>0,\\&\quad (-1)^3 \begin{vmatrix} - r_1u_1&r_1b_1u_1&0 \\ b_2v_1&-D_2 \frac{ v_2}{ v_1}&D_2 \\ 0&D_1&-r_2v_2 -D_1 \frac{ v_1}{ v_2} \end{vmatrix}= \frac{r_2 v_2^2}{ v_1} \left[ D_2 - \frac{b_1b_2 v_1^2 }{ v_2} \left( 1 + D_1 \frac{v_1}{r_2 v_2^2} \right) \right] >0. \end{aligned}$$

Since the third inequality implies the second one, we obtain the result. $\square$

Theorem 3.6

Assume $D_2 < D_2^+$.

• (i) If equilibria $P_1$ and $P_{23}$ are linearly unstable, system (4) has a unique positive equilibrium $P^*$, which is globally asymptotically stable in $\{ (u_1,v_1,v_2 ) \in \mathbb {R}_+^3: u_1>0,v_1\ge 0,v_2\ge 0, v_1+v_2>0 \}$.

• (ii) If equilibria $P_1$ and $P_{23}$ are linearly stable, system (4) has a unique positive equilibrium $P_*$. The stable manifold of $P_*$ divides Int$\mathbb {R}_+^3$ into two regions: One is the basin of attraction of $P_1$, while the other is that of $P_{23}$.

• (iii) Assume that equilibrium $P_1$ is linearly stable but $P_{23}$ is linearly unstable.

  • (iiia) If system (4) has two hyperbolic positive equilibria $P_*$ and $P^*$ with $P_* \ll _K P^*$, then the stable manifold of $P^*$ divides Int$\mathbb {R}_+^3$ into two regions: One is the basin of attraction of $P_1$, while the other is that of $P_*$.

  • (iiib) If system (4) has no positive equilibrium, then equilibrium $P_1$ is globally asymptotically stable in $\{ (u_1,v_1,v_2 ) \in \mathbb {R}_+^3: u_1>0,v_1\ge 0,v_2\ge 0, v_1+v_2>0 \}$.

• (iv) Assume that equilibrium $P_1$ is linearly unstable but $P_{23}$ is linearly stable.

  • (iva) If system (4) has two hyperbolic positive equilibria $P_*$ and $P^*$ with $P_* \ll _K P^*$, then the stable manifold of $P_*$ divides Int$\mathbb {R}_+^3$ into two regions: One is the basin of attraction of $P_{23}$, while the other is that of $P^*$.

  • (ivb) If system (4) has no positive equilibrium, then equilibrium $P_{23}$ is globally asymptotically stable in $\{ (u_1,v_1,v_2 ) \in \mathbb {R}_+^3: v_1+v_2>0 \}$.

Proof

Since $D_2 < D_2^+$, equilibrium $P_{23}$ is a boundary equilibrium of (4) and is globally asymptotically stable on the $(v_1,v_2)$-plane.

(i) We argue by contradiction to show uniqueness of the positive equilibrium. Suppose that system (4) has two positive equilibria $P_*$ and $P^*$ at $b_2=b_{20}$. Without loss of generality, we assume $P_* \ll _K P^*$.

We show that $P_*$ and $P^*$ are non-hyperbolic as follows. If both of $P_*$ and $P^*$ are hyperbolic, they are linearly stable. By the result of connecting orbits in Perko (2001), there exists another positive equilibrium, which contradicts Lemma 3.3. Thus, one of the equilibria is non-hyperbolic. Suppose that $P_*$ is non-hyperbolic and $P^*$ is linearly stable, while a similar discussion can be given for the other case. Then there exists a small $\delta >0$ such that for $b_2= b_{20} - \delta$, system (4) has a linearly stable positive equilibrium $P^{* \delta }$ with $P_* \ll _K P^{* \delta }$. On the other hand, let $f=(f_1,f_2,f_3)^T$ be the right-hand side of (4). Then $f_i(P_*)=0$ when $b_2= b_{20}, i=1,2,3$. When $b_2= b_{20}- \delta$, we have $f_2(P_*)>0, f_1(P_*)=f_3(P_*)=0$. Then $0- f(P_*) \in K$, i.e., $f(P_*) <_K 0$. Since $f(P_*) <_K 0$ and $P_{23}$ is linearly unstable, $\varphi _t(P_*)$ decreases to a positive equilibrium $P_{*\delta }$ with $P_{*\delta } \ll _K P^{* \delta }$ by Lemma 2.1. Thus, both $P_{*\delta }$ and $P^{* \delta }$ are stable in $[P_{*\delta }, P^{* \delta }]_K$. By the result in Perko (2001), there exists another positive equilibrium, which contradicts Lemma 3.3.

Suppose that both of $P_*$ and $P^*$ are non-hyperbolic. Then we have $\det J(P_*) = \det J(P^*) = 0$, i.e.,

$$\begin{aligned} (1+ b_2 u_1- b_1 b_2 v_1) (r_2 - D_2 - 2 r_2 v_2) + D_1 (r_2 - 2 r_2 v_2)=0 \end{aligned}$$

so that

$$\begin{aligned} 4 a_0 v_1^3 + 3 a_1 v_1^2 + 2 a_2 v_1 +a_3 =0, \end{aligned}$$

(16)

where $a_i$ is defined in (13), $0\le i \le 3$. Then equation (16) has two positive roots.

By taking (13)$\times 4$ - (16), we obtain

$$\begin{aligned} a_1 v_1^2 + 2 a_2 v_1 + 3 a_3 =0. \end{aligned}$$

(17)

By taking (16)$\times 3$ - (17), we have

$$\begin{aligned} 3 a_0 v_1^2 + 2 a_1 v_1 + a_2 =0. \end{aligned}$$

(18)

By (17) and (18), we obtain

$$\begin{aligned} \frac{a_1 }{3 a_0} = \frac{a_2 }{ a_1} = \frac{3 a_3 }{ a_2} \end{aligned}$$

where $a_0a_1 a_2\ne 0$. Then $a_2^2 = 3 a_1 a_3$ and $(2a_2)^2 - 12 a_1 a_3 =0$, which means that equation (18) has a unique root. This forms a contradiction and shows uniqueness of the positive equilibrium $P^*$. Since every solution of system (4) converges to an equilibrium, $P^*$ is globally asymptotically stable in the region $\{ (u_1,v_1,v_2 ) \in \mathbb {R}_+^3: u_1>0,v_1\ge 0,v_2\ge 0, v_1+v_2>0 \}$.

(ii) By a proof similar to that for (i), we obtain the uniqueness of the positive equilibrium $P_*$: $P_{23}$ attracts all solutions in $(P_{23}, P_*)_K$, while $P_1$ attracts those in $(P_*, P_1)_K$. By continuity of the flow of system (4), the stable manifold of $P_*$ divides Int$\mathbb {R}_+^3$ into two regions: One is the basin of attraction of $P_{23}$, while the other is that of $P_1$.

(iii–iv) We focus on the proof for (iii), while a similar discussion can be given for (iv). Since equilibrium $P_1$ is linearly stable, it attracts all solutions in $(P^*, P_1)_K$. Similarly, equilibrium $P_*$ attracts all solutions in $(P_{23}, P_*)_K$. Since equilibria $P_*$ is hyperbolic, it is asymptotically stable and attracts all solutions in $(P_*, P^*)_K$. By continuity of the flow of system (4), the stable manifold of $P^*$ divides $(P_*, P_1)_K$ into two regions: One is the basin of attraction of $P_*$, while the other is that of $P_1$. Thus, this manifold divides Int$\mathbb {R}_+^3$ into two basins of attraction of $P_*$ and $P_1$. If system (4) has no positive equilibrium, then equilibrium $P_1$ is globally asymptotically stable by Corollary 3.2. $\square$

Remark 3.7

(I) Assume that equilibrium $P_1$ is linearly stable but $P_{23}$ is linearly unstable. If system (4) has one positive equilibrium $P^*$, numerical simulations show that $P^*$ is non-hyperbolic and the stable manifold of $P^*$ divides Int$\mathbb {R}_+^3$ into two regions: One is the basin of attraction of $P_1$, while the other is that of $P^*$.

Assume that equilibrium $P_1$ is linearly unstable but $P_{23}$ is linearly stable. If system (4) has one positive equilibrium $P_*$, numerical simulations show that $P_*$ is non-hyperbolic and the stable manifold of $P_*$ divides Int$\mathbb {R}_+^3$ into two regions: One is the basin of attraction of $P_{23}$, while the other is that of $P_*$.

(II) The condition for equilibrium $P_1$ (resp. $P_{23}$) to be linearly stable/unstable, is algebraically given in Theorem 3.1. By Lemma 3.4, the condition for a positive equilibrium P to be hyperbolic is algebraically given by $J(P)\ne 0$, where J(P) is defined in (15).

(III) The condition for existence of one/two positive equilibria is algebraically given by (20) and (13).

Finally, we show global stability of $P_1$ and $P_{23}$. Denote

$$\begin{aligned} \bar{v}_1^+ = \frac{(1+ b_2)(D_2- r_2)- D_1 r_2 }{b_1b_2(D_2- r_2)} \end{aligned}$$

when $D_2 > D_2^b$.

Theorem 3.8

Assume $D_2 < D_2^+$.

• (i) Let $D_2 > D_2^b$ and $v_1^+ < \bar{v}_1^+$. Then $P_1$ is globally asymptotically stable in $\{ (u_1,v_1,v_2 ) \in \mathbb {R}_+^3: u_1>0, v_1\ge 0, v_2\ge 0 \}$.

• (ii) Let $1-b_1 v_1^+<0$. Then for sufficiently small $b_2>0$, $P_{23}$ is globally asymptotically stable in $\{ (u_1,v_1,v_2 ) \in \mathbb {R}_+^3: v_1+v_2>0 \}$.

Proof

(i) Since $D_2 > D_2^b$, we have $\bar{v}_1^+ >0$ and $P_1$ is asymptotically stable in Int$\mathbb {R}_+^3$. Let

$$\begin{aligned} V(u_1,v_1,v_2 ) = w_1 (u_1 -1 -\ln u_1 ) +\sum _{i=1}^{2} w_{i+1} v_i, \end{aligned}$$

where coefficient $w_i >0$ need to be determined. Then

$$\begin{aligned} \dfrac{\mathrm{d} V}{dt }|_{(2.2) }= & {} -r_1 w_1 \left[ u_1 -1 + \frac{1}{2 } \left( b_1+ \frac{b_2 w_2}{r_1w_1 } \right) v_1\right] ^2 \nonumber \\&- v_1 \left[ w_2 (1+ b_2 + D_1) - D_1 w_3 - \frac{r_1 w_1}{4 } \left( b_1+ \frac{b_2 w_2}{r_1w_1 } \right) ^2 v_1\right] \nonumber \\&- v_2 [(D_2- r_2)w_3 - D_2w_2 ]- w_3r_2v_2^2. \end{aligned}$$

(19)

Let

$$\begin{aligned} \frac{w_3}{w_2 } = \frac{D_2}{D_2- r_2 },~ \frac{w_1}{w_2 } = \frac{b_2}{r_1b_1 }. \end{aligned}$$

The second term of (19) becomes

$$\begin{aligned} - \frac{1}{4 } \left( b_1+ \frac{b_2 w_2}{r_1w_1 } \right) ^2 v_1 [\bar{v}_1^+ - v_1]\le 0, \end{aligned}$$

since $\limsup _{t \rightarrow \infty } v_1(t) \le v_1^+ < \bar{v}_1^+$. Let $\dfrac{\mathrm{d} V}{dt }|_{(2.2) } =0$. Then $v_1 = v_2=0$, which means $\lim _{t\rightarrow \infty } u_1(t) = 1$ by the first equation of (1). By the LaSalle invariance principle, equilibrium $P_1$ is globally asymptotically stable in $\{ (u_1,v_1,v_2 ) \in \mathbb {R}_+^3: u_1>0, v_1\ge 0, v_2\ge 0 \}$.

(ii) Let $(u_1^*,v_1^*,v_2^* )$ be a solution of (13). By continuity of (13) on $b_2$, we have $\lim _{b_2\rightarrow 0+} v_1^*(b_2) = v_1^+$. By $1-b_1v_1^+<0$, there is $\bar{b}_2>0$ such that $1-b_1v_1^*<0$ if $b_2< \bar{b}_2$. Then there is no positive equilibrium in system (4) if $b_2< \bar{b}_2$.

We show that if $b_2< (D_2^+ - D_2) /D_2$, then $P_1$ is linearly unstable and has no stable manifold in Int$\mathbb {R}_+^3$. Indeed, from $b_2< (D_2^+ - D_2) /D_2$ and (11), we have $\hat{c}_2<0$, which means that $P_1$ is linearly unstable and has the second negative eigenvalue $\lambda _2= \frac{1}{2}(-\hat{c}_1 -\sqrt{\hat{c}_1^2-4\hat{c}_2 }) <0$. By (10), the corresponding eigenvector of $\lambda _2$ can be chosen as $X= (*, D_2, 1 + b_2 +D_1 + \lambda _2)$. We have $1 + b_2 +D_1 + \lambda _2 <0$ by

$$\begin{aligned} \hat{c}_1^2-4\hat{c}_2-[2 (1 + b_2 +D_1) - \hat{c}_1]^2 =D_1D_2>0. \end{aligned}$$

Thus, the eigenvector X does not direct toward Int$\mathbb {R}_+^3$, which means that $P_1$ has no stable manifold in it.

By $1-b_1v_1^+<0$, $P_{23}$ is linearly stable. Since every solution of (4) converges to an equilibrium, $P_{23}$ is globally asymptotically stable in $\{ (u_1,v_1,v_2 ) \in \mathbb {R}_+^3: v_1+v_2>0 \}$. $\square$

4 Principle of Competition Exclusion

In this section, we show that diffusion in system (4) could lead to results reversing those without diffusion, which extend the principle of competitive exclusion.

When there is no diffusion (i.e., $D_1= D_2= 0$), species u and v persist in patch 1 and 2, respectively, and reach their carrying capacity ($= 1$).

When there is diffusion, there are four possible results: (a) extinction of species v; (b) extinction of species u; (c) coexistence of two species; and (d) three types of bi-stability. These results reverse those without diffusion, which are described as follows.

Denote

$$\begin{aligned} \bar{D}_2^b= & {} r_2 + \frac{- \bar{b} + \sqrt{\bar{b}^2 + 4 b_1b_2r_2^2 D_1(1 + D_1)} }{2 b_1b_2} ,~ \bar{b}= r_2 (1 + D_1) (1 + b_2)-b_1b_2r_2D_1,\\ D_2^{c\pm }= & {} \frac{1}{2} (1 + D_1)\left[ b_1 \pm \sqrt{b_1\left( b_1-\frac{4}{r_2}\right) } \right] ~~~as~~b_1> \frac{4}{r_2}. \end{aligned}$$

Then $D_2 > \bar{D}_2^b$ is equivalent to $v_1^+ < \bar{v}_1^+$ when $D_2 > D_2^b$. If $b_1 <4/r_2$, we always have $1- b_1 v_1^+ >0$. If $b_1 >4/r_2$, then $1- b_1 v_1^+ >0$ when $D_2 < D_2^{c-}$ or $D_2 > D_2^{c+}$; $1- b_1 v_1^+ <0$ when $D_2^{c-}< D_2 < D_2^{c+}$.

(a) Extinction of species v. First, as shown in Theorem 3.6(i), when diffusion of species v from the source to sink is extremely large (i.e., $D_2 \ge D_2^+$), species v goes to extinction in both patches, while species u persists in patch 1 and reaches their carrying capacity. The reason is that with the extremely large diffusion, too many individuals of species v move to the sink to die, which leads to the extinction even in the absence of competitor u by Theorem 2.4. Second, as shown in Theorem 3.8(i), when the diffusion is large but its competition ability is weak (i.e., $D_2 > \bar{D}_2^b$, $b_1 < \bar{b}_1 = \frac{(1+ b_2)(D_2- r_2)- D_1 r_2 }{v_1^+ b_2(D_2- r_2)}$), species v goes to extinction. The reason is that with the large diffusion and weak competition ability, the loss of individuals of species v in patch 1 is large, which leads to its weak competitive ability with species u and results in its extinction. Since species v can persist in patch 2 in the absence of diffusion, it is the diffusion that leads to its extinction. Finally, in more general situations as shown in Corollary 3.2, species v goes to extinction if system (4) has no positive equilibrium and equilibrium $P_1$ is asymptotically stable.

(b) Extinction of species u. As shown in Theorem 3.8(ii), when diffusion of species v to the sink is relatively small (i.e., $D_2^{c-}< D_2 < D_2^{c+}$) and the competition ability of species u is extremely weak, species v would drive species u into extinction, and persist in both patches. The reason is that with the small diffusion and opponent’s weak competition, the loss of individuals of species v in the sink is compensated by those moving from the source, which leads to its persistence in the sink and extinction of species u. Since species u can persist in patch 1 in the absence of diffusion, it is the diffusion that leads to its extinction. More generally, as shown in Corollary 3.2, species u goes to extinction if system (4) has no positive equilibrium and equilibrium $P_{23}$ is asymptotically stable.

(c) Three types of bi-stability. (c1) Stability of $P_1$ and $P_{23}$. As shown in Theorem 3.8(ii), when diffusion of species v to the sink is relatively large (i.e., $\max \{D_2^{c-}, D_2^b \}< D_2 < D_2^{c+}$), the species with high initial population density will persist, while the other goes to extinction. (c2) Stability of $P_1$ and $P_*$. As shown in Theorem 3.8(iii), when diffusion of species v to the sink satisfies $D_2^b< D_2 < D_2^{c-}$ or $D_2 > \max \{D_2^{c+}, D_2^b \}$, species v with high initial density would coexist with species u. Otherwise, species v goes to extinction while species u reaches its carrying capacity. (c3) Stability of $P_{23}$ and $P^*$. As shown in Theorem 3.8(iv), when diffusion of species v to the sink satisfies $D_2^{c-} < \max \{D_2^{c+}, D_2^b \}$, species u with high initial density would coexist with species v. Otherwise, species u goes to extinction while species v persists in two patches.

(d) Coexistence of two species and increase of total abundance. First, as shown in Theorem 3.6(i), when diffusion of species v to the sink is intermediate (i.e., $D_2 < D_2^b$ if $b_1< 4/r_2$ ; $D_2 < \max \{D_2^b, D_2^{c-} \}$, or $D_2^{c+}< D_2 < D_2^b \}$ if $b_1>4/r_2$), species u and v coexist at a steady state $P^*$ in the system. The reason is that with the intermediate diffusion, the loss of individuals of species v in the sink is compensated by those moving from the source, which leads to its persistence in the sink and the coexistence of two species. Second, diffusion can make the mobile competitor approach total population abundance higher than if non-diffusing. Indeed, the roots of (13) can be explicitly given by Cardano formula as follows. Let $v_1 = x - \frac{a_1}{3a_0}$. Equation (13) becomes

$$\begin{aligned} x^3 + px +q =0,~ p= - \frac{a_1^2 }{3a_0^2 } + \frac{a_2}{a_0},~ q= \frac{2a_1^3 }{27a_0^3 } - \frac{a_1 a_2}{3 a_0^2 } + \frac{a_3}{a_0}. \end{aligned}$$

(20)

Then two possible positive roots of (13) are $v_1 = x - \frac{a_1}{3a_0}$ with

$$\begin{aligned} x= & {} x^*= \omega \root 3 \of {- \frac{q}{2} +\sqrt{ \left( \frac{q}{2}\right) ^2 + \left( \frac{p}{3}\right) ^3 } } + \omega ^2 \root 3 \of {- \frac{q}{2} - \sqrt{ \left( \frac{q}{2}\right) ^2 + \left( \frac{p}{3}\right) ^3 } },\\ x= & {} x_*= \omega ^2 \root 3 \of {- \frac{q}{2} +\sqrt{ \left( \frac{q}{2}\right) ^2 + \left( \frac{p}{3}\right) ^3 } } + \omega \root 3 \of {- \frac{q}{2} - \sqrt{ \left( \frac{q}{2}\right) ^2 + \left( \frac{p}{3}\right) ^3 } }, \end{aligned}$$

where $\omega = \frac{-1+ \sqrt{3}i}{2}$.

When there is no dispersal, system (1) becomes two logistic equations, and population abundances of the mobile competitor are the carrying capacity $T_0 =1$.

When there is dispersal and condition in Proposition 3.3 holds, system (4) has a stable positive equilibrium $P^*(u_1^*,v_1^*,v_2^*)$ given by (12) and (20). Total population abundance of the mobile competitor is $T_1(D_1, D_2)= v_1^*+v_2^*$. From boundedness of solutions and continuity of $T_1(D_1, D_2)$, there exist diffusions $D_1, D_2$ at which $T_1(D_1, D_2)$ reaches the maximal value. Because of complexity of the expression of $T_1(D_1, D_2)$, we show the increase of total abundance by numerical computations. Indeed, as shown in Fig. 1a, let $b_1=0.45, b_2=0.5, D_1=1$, $D_2= 2.591$. Then the species coexist at a steady state with $T_1 = 1.3637>1$. That is, diffusion can make species v reach total abundance larger than if non-diffusing, even though the competitive species u persists.

Asymmetry in diffusion plays a role in the increase of total abundance. For extremely large diffusion rates $D_1$ and $D_2$, i.e., there is little barrier between the patches with $D_1\rightarrow \infty , D_2\rightarrow \infty$, we consider a specific case of $D_1=D, D_2=sD$ with $D \rightarrow \infty$, where s represents the asymmetry to the sink. Then we have

$$\begin{aligned} D_3=\dfrac{D_2}{1 +D_1} =\dfrac{sD}{1 +D} \rightarrow s~~ \text {as} ~~D \rightarrow \infty . \end{aligned}$$

Denote

$$\begin{aligned} s^\pm = \frac{1 }{2} \left( r_2 \pm \sqrt{r_2^2 - 4\frac{r_2 }{b_1}} \right) ~~as ~~b_1>\frac{4 }{r_2}. \end{aligned}$$

Then $s^\pm < r_2$. Condition $D_2 <D_2^+$ can be written as $s < r_2$. Condition $1- b_1 v_1^+ >0$ can be written as $s < s^-$ or $s> s^+$ if $b_1>\frac{4 }{r_2}$, while we always have $1- b_1 v_1^+ >0$ if $b_1< \frac{4 }{r_2}$. Condition $D_2 <D_2^b$ can be written as $s < r_2$. By Theorem 3.6, existence and global stability of equilibrium $P^*$ can be guaranteed by $s < r_2$ if $b_1< \frac{4 }{r_2}$; $s < s^-$ or $s^+<s<r_2$ if $b_1>\frac{4 }{r_2}$. By (12), equilibrium $P^*(u_1,v_1,v_2 )$ can be written as

$$\begin{aligned} u_1=1 - b_1 v_1,~ v_2 = s^{-1}v_1,~ v_1= \frac{r_2 - (1+ b_2)s }{r_2 - b_1 b_2 s^2} s,~ \end{aligned}$$

so that

$$\begin{aligned} T_1= & {} v_1 + v_2 = \frac{r_2 - (1+ b_2)s }{r_2 - b_1 b_2 s^2} (1+ s),\\ T_1-1= & {} \frac{r_2 -1- b_2 - (1+ b_2 - b_1 b_2)s }{r_2 - b_1 b_2 s^2} . \end{aligned}$$

Therefore, we conclude the following result.

Theorem 4.1

Let $D_1=D, D_2=sD$ with $D \rightarrow \infty$. Assume $s < r_2$ if $b_1< \frac{4 }{r_2}$; $s < s^-$ or $s^+<s<r_2$ if $b_1>\frac{4 }{r_2}$. We have $T_1 >1$ if

$$\begin{aligned} (r_2 - b_1 b_2 s^2) [r_2 -1- b_2 - (1+ b_2 - b_1 b_2)s ]>0. \end{aligned}$$

Corollary 4.2

Let $D_1=D, D_2=sD$ with $D \rightarrow \infty$. Assume $b_1< \frac{4 }{r_2}$. We have $T_1 >1$ if $r_2 > 1+ b_2$ and $s \rightarrow 0$.

Corollary 4.2 makes sense biologically. When competition between the species is weak (i.e., $b_1< \frac{4 }{r_2}, b_2< r_2 - 1$), small asymmetry in diffusion to the sink leads to coexistence of the species, in which the mobile species reaches total abundance larger than if non-diffusing, even in the presence of the competitive species.

Fig. 1

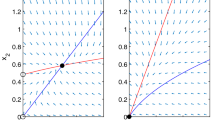
Let $r_1=1, r_2=4.2, D_1=1$. a–c Fix $b_1=0.45, b_2=0.5, D_1=1$ but let $D_2$ vary. When $D_2$ increases from 2.591, to 5 and to 8, the species change from coexistence at a steady state with $T_1 = 1.3637$, to that with $T_1 = 0.9901$, and to that with $T_1 = 0$, i.e., the extinction of species v. d Diffusion can drive species u into extinction and then make species v reach the maximal abundance in (4). Let $b_1=1.45, b_2=0.0001,D_2=3$. Then species u goes to extinction. After the extinction, diffusion $D_2= 4.2$ makes species v reach the maximal abundance $T_1 = 2.1$

Fig. 2

Comparison of $T_1(D_1,D_2)$ and $T_0$. The blue and red lines represent $T_1$ and $T_0$, respectively. Let $r_1=1, r_2=4.2, b_1=0.45, b_2=0.5$. a Fix $D_1=1$ but let $D_2$ vary. $T_1$ approaches its maximum $T_1=1.3637$ at $D_2=2.591$, and the curve is hump-shaped. We have $T_1>T_0$ if $D_2<4.911$; $T_1<T_0$ if $D_2>4.911$; $T_1=0$ if $D_2\ge 7$. b Fix $D_2=3$ but let $D_1$ vary. $T_1$ approaches its maximum $T_1=1.3632$ at $D_1=1.231$. The curve is hump-shaped if $D_1<2.911$ but is bowl-shaped if $D_1>2.911$. We have $T_1>T_0$ if $D_1>0.181$; $T_1<T_0$ if $D_1<0.181$

Fig. 3

Surface of $T_1(D_1,D_2)$ when both $D_1$ and $D_2$ vary. Let $r_1=1, r_2=4.2, b_1=0.45, b_2=0.5$. Then $T_1$ approaches its maximum $T_1=1.3637$ at $D_1=1, D_2=2.591$. This figure provides an intuition of $T_1=T_1(D_1,D_2)$, which is a combination of Fig. 2a, b, i.e., when $D_1$ is fixed, the surface becomes Fig. 2a; when $D_2$ is fixed, the surface becomes Fig. 2b

5 Discussion and Application

In this paper, we consider competitive systems with diffusion, in which one of the competitors can move between sink–source patches. Global dynamics of the model show that varying a diffusion rate could lead to transition of the interaction outcomes between coexistence at a steady state, extinction of one of the competitors, and three types of bi-stability in a smooth fashion. These results provide new insights in the principle of competition exclusion.

The diffusion could lead to new types of bi-stability in competitive systems. In Lotka–Volterra competitive systems with two species, bi-stability means that one of the competitors goes to extinction but the other persists, which depends on initial population density as shown in Theorem 3.6(ii). As shown in Theorem 3.6(iii–iv), two new types of bi-stability could occur in the diffusive competitive system. One type means either extinction of the mobile competitor, or coexistence of two species, which depends on initial population density; the other means either extinction of the non-mobile competitor or coexistence of two species. Moreover, the diffusion could lead to results reversing those without diffusion. When there is no diffusion, each competitor persists in its patch independently. However, when its diffusion to the other patch (a sink) is large, the mobile species goes to extinction in both patches. When the diffusion is intermediate, two species coexist at a steady state, in which the mobile species can reach total abundance larger than if non-diffusing, even in the presence of the opponent. When the diffusion is small, the mobile species could drive the other into extinction and persists in two patches. Meanwhile, there are three types of bi-stability as shown in Sect. 4. On the other hand, as shown in Theorems 3.1 and 3.6, there is a strategy for the mobile species to maximize the total abundance: It can exclude the non-mobile species by using a small diffusion; after the exclusion, it can reach the maximal abundance by the optimal diffusion in Lemma 2.4.

Numerical simulations show that there are three types of bi-stability in system (4), which illustrate and extend our results in Theorem 3.6(ii–iv). (a) When $P_{23}$ is linearly stable but $P_1$ is linearly unstable, there may exist two positive equilibria $P_*$ and $P^*$. Equilibrium $P_*$ is a saddle point and $P^*$ is a stable node. The two-dimensional stable manifold divides Int$\mathbb {R}_+^3$ into two regions: One is the basin of attraction of $P^*$, while the other is that of $P_*$. Indeed, let $r_1=r_2=D_1= D_2=1, b_1=5, b_2=4.5$. Then system (4) has a positive equilibrium $P_*(0.0711, 0.1858,0.4310)$ with eigenvalues $\lambda _1 =-2.9121, \lambda _2 =0.1339, \lambda _3 =-0.4747$. That is, $P_*$ is a saddle point with a two-dimensional stable manifold. System (4) has the other positive equilibrium $P^*(0.8534, 0.0293,0.1711)$ with eigenvalues $\lambda _1 =-6.1195, \lambda _2 =-0.7770, \lambda _3 =-0.1388$. That is, $P^*$ is a stable node. Since every solution of (4) converges to an equilibrium, we obtain the bi-stability.

(b) When both $P_1$ and $P_{23}$ are linearly stable, there exists a positive equilibrium $P^*$, which is unstable. The stable manifold of $P^*$ divides Int$\mathbb {R}_+^3$ into two regions: One is the basin of attraction of $P_1$, while the other is that of $P_{23}$. Indeed, let $r_1=D_1=1, r_2=0.5, D_2=0.8, b_1=13, b_2=4$. Then system (4) has a unique positive equilibrium $P^*(0.0042, 0.0766,0.1931)$ with eigenvalues $\lambda _1 =-2.4355, \lambda _2 =0.0285, \lambda _3 =-0.1071$. That is, $P^*$ is a saddle point with a two-dimensional stable manifold. Since every solution of (4) converges to an equilibrium, we obtain the bi-stability.

(c) When $P_{23}$ is linearly unstable but $P_1$ is linearly stable, there may exist two positive equilibria $P_*$ and $P^*$. Equilibrium $P_*$ is a stable node and $P^*$ is a saddle point. The stable manifold of $P^*$ divides Int$\mathbb {R}_+^3$ into two regions: One is the basin of attraction of $P_*$, while the other is that of $P_1$. Indeed, let $r_1=1, r_2=2, D_1=1, D_2=3, b_1=0.01, b_2=1.1$. Then system (4) has a positive equilibrium $P_*(0.9706, 2.9331,2.9993)$ with eigenvalues $\lambda _1 =-0.9513, \lambda _2 =-2.4294, \lambda _3 =-7.6342$. That is, $P_*$ is a stable node. System (4) has the other positive equilibrium $P^*(0.9729, 2.7033,2.7667)$ with eigenvalues $\lambda _1 =-2.3669, \lambda _2 =0.9546, \lambda _3 =-7.2321$. That is, $P^*$ is a saddle point with a two-dimensional stable manifold. Since every solution of (4) converges to an equilibrium, we obtain the bi-stability.

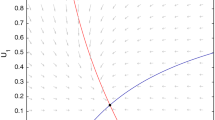
Numerical computations display that total abundance of the mobile species can be convex downward. Indeed, as shown in Fig. 2b, let $r_1=1, r_2=4.2, b_1=0.45, b_2=0.5, D_2=3$, but let $D_1$ vary. $T_1$ approaches its maximum $T_1=1.3632$ at $D_1=1.231$. The curve is hump-shaped if $D_1<2.911$ but is convex if $D_1>2.911$. This finding extends both previous theory and experimental observations (e.g., Zhang et al. 2017; Wu et al. 2020). Moreover, our results are different from those in previous works. While previous works focused on symmetric diffusion between source–source patches, we consider asymmetric diffusion between source–sink patches (Fig. 3). Theoretical analysis on the model shows that diffusion could make the mobile competitor persist in the sink, reach total abundance larger than its carrying capacity, and even exclude the opponent which can persist in the patch in the absence of diffusion. We also show effects of diffusion on total abundance and deduce an optimal diffusion strategy for the mobile competitor. Thus, for an endangered species, if its diffusion from a source (e.g., a refuge) to a sink (e.g., a poor fragmented patch) is well controlled through particular organisms (see Soulé and Gilpin 1991), the species can persist in the sink and approach total abundance larger than if non-diffusing. This would promote its persistence and viability. Similarly, for a competitor in a new market, appropriate diffusion from its original market (source) to the new one (sink) could make it survive and even win in the new market (Lopez and Sanjuan 2001).

While the sink–source competition model in this work is a simplification of real interactions, our study shows all properties in diffusion systems such as asymmetry, general diffusion rates and explicit expression of total abundances. These results may be helpful in understanding effects of diffusion on protection of endangered species and conservation of biodiversity.