Asymptotic State of a Two-Patch System with Infinite Diffusion

Abstract

Mathematical theory has predicted that populations diffusing in heterogeneous environments can reach larger total size than when not diffusing. This prediction was tested in a recent experiment, which leads to extension of the previous theory to consumer-resource systems with external resource input. This paper studies a two-patch model with diffusion that characterizes the experiment. Solutions of the model are shown to be nonnegative and bounded, and global dynamics of the subsystems are completely exhibited. It is shown that there exist stable positive equilibria as the diffusion rate is large, and the equilibria converge to a unique positive point as the diffusion tends to infinity. Rigorous analysis on the model demonstrates that homogeneously distributed resources support larger carrying capacity than heterogeneously distributed resources with or without diffusion, which coincides with experimental observations but refutes previous theory. It is shown that spatial diffusion increases total equilibrium population abundance in heterogeneous environments, which coincides with real data and previous theory while a new insight is exhibited. A novel prediction of this work is that these results hold even with source–sink populations and increasing diffusion rate of consumer could change its persistence to extinction in the same-resource environments.

1 Introduction

Carrying capacity of a homogeneous environment is defined as the steady-state upper limit on a population’s abundance. It is determined by resources in the environment such as light, water, nutrient. However, carrying capacity of a heterogeneous environment is ambiguous for populations in diffusion. Mathematical theory predicts that populations diffusing in a heterogeneous environment can approach larger total size than when not diffusing and can approach even larger size than in the corresponding homogeneous environment.

Freedman and Waltman (1977) studied a two-patch model with Pearl–Verhulst logistic growth $~\mathrm{{d}}x_i/\mathrm{{d}}t = r_i x_i (1 - \frac{x_i }{K_i}) ~$ with diffusion, $i=1,2$. It is shown that if there is a positive relationship between growth rate and carrying capacity, i.e.,

$$\begin{aligned} K_1> K_2,\quad \frac{r_1}{K_1} > \frac{r_2}{K_2}, \end{aligned}$$

(1)

the population’s abundance with high diffusion rate can approach larger size than with no diffusion (i.e., $~x_1^* +x_2^* > K_1 + K_2~$) and can approach even larger size than in the corresponding homogeneous environment (i.e., ${{\bar{r}}}_i=\frac{r_1 +r_2}{2},~ {{\bar{K}}}_i= \frac{K_1 + K_2}{2}$). Holt (1985) exhibited that this result also holds in source–sink systems, in which the sink patch is not self-sustaining (e.g, $r_2 \le 0$ and $K_2 = 0$). Lou (2006) demonstrated that this result even holds in continuous spatial systems by applying a reaction-diffusion model. For additional relevant works, we refer to Hutson et al. (2005), He and Ni (2013a, b), Zhang et al. (2015), DeAngelis et al. (2016a, b), Wang and DeAngelis (2018), etc.

The theoretical result is tested by Zhang et al. (2017) in laboratory experiments. In the experiments, the population is the heterotrophic budding yeast, Saccharomyces cerevesiae, and the resource is the amino acid tryptophan which is the single exploited and renewable nutrient. The yeast population is spatially distributed in a 96-well microtitre plate, and the wells are linearly arrayed and linked by nearest neighbor diffusion. In heterogeneous distribution of resource, the wells with even number have the same high nutrient input, while those with odd number have the same low nutrient input. Thus the wells can be regarded as two types of patches, which corresponds to a two-patch system. In homogeneous distribution, all wells have the same nutrient input, which is the average of the high and low inputs in the heterogeneous distribution. The experimental process was repeated over 9 days. First, the initial yeast had 24-h growth, followed by diffusion from the original plate (plate 1) to a new empty plate (plate 2), in which 3$\%$ volume in each well was transferred to the well on the left in plate 2 and another 3$\%$ to the right well of the plate. Then the remaining $94\%$ volume was transferred to the same well in plate 2. After the diffusion and transfer, old media in plate 2 were removed and fresh media were added, and the yeast population underwent another 24-h growth. Experimental observations displayed that (i) populations diffusing in heterogeneous environments can reach higher total size than if non-diffusing, in which the “extra individuals” were observed to reside in the low nutrient patches. (ii) The higher size in a heterogeneous environment with diffusion is associated with a positive relationship of growth rate and carrying capacity. (iii) Homogeneously distributed resources support higher total carrying capacity than heterogeneously distributed resources, even with species diffusion. Meanwhile, homogeneously distributed resources support the same carrying capacity with or without species diffusion.

In order to study mechanism by which the empirical observations occur, Zhang et al. (2017) proposed a pair of new equations to model the diffusion system. By assuming existence of stable positive equilibria in the equations, they confirmed the three observations by considering two special cases of the model. However, their confirmation on the second case is not a theoretically proof (see Remarks 4.2). Thus, it is necessary to study the equations in general cases, give a theoretical proof for the three observations, and provide new predictions.

In this paper, we consider the general two-patch model with diffusion that characterizes the experiment. Rigorous analysis on the model exhibits that solutions of the equations are nonnegative and bounded, and there exist stable positive equilibria. It is proven that homogeneously distributed resources support larger carrying capacity than heterogeneously distributed resources with or without diffusion, which coincides with experimental observations but refutes previous theory. It is also shown that spatial diffusion increases total equilibrium population abundance in heterogeneous environments, which coincides with real data and previous theory while a new insight is exhibited. A novel prediction of this work is that these results hold even with source–sink populations, while increasing diffusion rate of consumer could change its persistence to extinction in the same-resource environments.

The paper is organized as follows. In the next section, we characterize the equations in general cases with two patches, demonstrate nonnegativeness and boundedness of the solutions, and exhibit global dynamics of one-patch subsystems. Section 3 displays existence of stable positive equilibria, while proof of experimental observations and new predictions are exhibited in Sect. 4. Discussion is in Sect. 5.

2 Mechanistic Model

In this section, we describe the mechanistic model established by Zhang et al. (2017), which characterizes a population diffusing between two patches with external resource inputs. Then we exhibit nonnegativeness and boundedness of the solutions and demonstrate global dynamics of the subsystems.

The equations for diffusion systems with external resource input are (Zhang et al. 2017)

$$\begin{aligned} \begin{aligned} \frac{\partial u(x,t) }{\partial t}&= D \frac{\partial ^2 u(x,t) }{\partial x^2} + \frac{ r(x) n(x,t) u(x,t) }{k+n(x,t) } -m(x) u(x,t) -g(x) u(x,t)^2 \\ \frac{\mathrm{{d}} n(x,t) }{\mathrm{{d}}t}&= N_\mathrm{{input}}(x) - n(x,t) - \frac{ r(x) n(x,t) u(x,t) }{\gamma (k+n(x,t)) } \\ \end{aligned} \end{aligned}$$

where u(x, t) is the consumer population abundance, n(x, t) is the nutrient concentration, r(x) is the growth rate under infinite resources, k is the half saturation coefficient, m(x) is the mortality rate, g(x) is the density-dependent loss rate, $\gamma$ is the yield, or fraction of nutrient per unit biomass, D is the diffusion rate, and $N_\mathrm{{input}}(x)$ is the nutrient input.

The equations in a spatially discrete, or patch version, along one dimension are (Zhang et al. 2017)

$$\begin{aligned} \begin{aligned} \frac{\mathrm{{d}}U_i}{\mathrm{{d}}t}&= U_i \left( \frac{r_i N_i }{k+N_i} -m_i -g_i U_i \right) +D\left( \frac{1}{2}U_{i-1} +\frac{1}{2}U_{i+1} -U_i \right) \\ \frac{\mathrm{{d}}N_i}{\mathrm{{d}}t}&= N_{0i} -N_i - \frac{r_i N_i U_i}{\gamma \left( k+N_i\right) } \\ \end{aligned} \end{aligned}$$

where $N_{0i} (= N_\mathrm{{input},i})$ represents the nutrient input in patch $i, 1\le i \le n, i=i~ mod~ n$. Let

$$\begin{aligned} U_i := \frac{U_i }{k \gamma }, \ N_i := \frac{N_i}{k}, \ g_i := g_i k \gamma , \ N_{0i} := \frac{N_{0i}}{k} \end{aligned}$$

then the above equations for two patches become

$$\begin{aligned} \begin{aligned} \frac{\mathrm{{d}}U_1}{\mathrm{{d}}t}&= U_1 \left( \frac{r_1 N_1 }{1+N_1} -m_1 -g_1 U_1 \right) +D\left( U_2 -U_1 \right) \\ \frac{\mathrm{{d}}N_1}{\mathrm{{d}}t}&= N_{0i} -N_1 - \frac{r_1 N_1 U_1}{1+N_1} \\ \frac{\mathrm{{d}}U_2}{\mathrm{{d}}t}&= U_2 \left( \frac{r_2 N_2 }{1+N_2} -m_2 -g_2 U_2 \right) +D\left( U_1 -U_2 \right) \\ \frac{\mathrm{{d}}N_2}{\mathrm{{d}}t}&= N_{0i} -N_2 - \frac{r_2 N_2 U_2}{1+N_2}. \\ \end{aligned} \end{aligned}$$

(2)

We consider solutions of system (2) with nonnegative initial values, i.e., $U_i(0)\ge 0, N_i(0)\ge 0, i=1,2$.

Proposition 2.1

All solutions of system (2) are nonnegative and bounded with $\limsup _{t \rightarrow \infty } \sum _{i=1}^2(U_i(t)+N_i(t)) \le (N_{01} + N_{02}) /q, ~q =\min \{m_1, m_2,1 \}$.

Proof

On the boundary $N_1=0$, from the second equation of (2) we have $\mathrm{{d}}N_1/\mathrm{{d}}t = N_{01} >0$. Then $N_1(t)>0$ if $t>0$. Similarly, $N_2(t)>0$ if $t>0$.

On the boundary $U_1=0$, from the first equation of (2) we have $\mathrm{{d}}U_1/\mathrm{{d}}t = D U_2$. When $U_2>0$, then $\mathrm{{d}}U_1/\mathrm{{d}}t >0$, which implies that $U_1(t)$ is nonnegative if t increases. Assume $U_2=0$. Since $U_1=0$ is an invariant set of system (2) if $U_2=0$, no orbit could pass through the invariant set, which implies that $U_1(t)$ is nonnegative. Thus $U_1(t)\ge 0$ if $t>0$. Similarly, $U_2(t)\ge 0$ if $t>0$.

Boundedness of the solutions is shown as follows. From (2), we have

$$\begin{aligned} \begin{aligned} \frac{\mathrm{{d}}(U_1+N_1+U_2+N_2)}{\mathrm{{d}}t}&= N_{01} + N_{02} -(N_1 +N_2) - (m_1 U_1 +m_2 U_2+ g_1 U_1^2 +g_2 U_2^2)\\&\le N_{01} + N_{02} - q (U_1+N_1+U_2+N_2).\\ \end{aligned} \end{aligned}$$

From the comparison theorem (Hale 1969), we obtain $\limsup _{t \rightarrow \infty } \sum _{i=1}^2(U_i(t)+N_i(t)) \le (N_{01} + N_{02}) /q.$ Thus there are $\delta _0 >0$ and $T>0$ such that when $t>T$, we have $U_i(t) \le (N_{01} + N_{02}) /q + \delta _0, N_i(t) \le (N_{01} + N_{02}) /q + \delta _0, i=1,2.$ Therefore, solutions of (2) are bounded. $\square$

When there is no diffusion, system (2) becomes two independent subsystems. We consider subsystem 1, while a similar discussion can be given for subsystem 2. Now model (2) becomes

$$\begin{aligned} \begin{aligned} \frac{\mathrm{{d}}U_1}{\mathrm{{d}}t}&= U_1 \left( \frac{r_1 N_1 }{1+N_1} -m_1 -g_1 U_1 \right) \\ \frac{\mathrm{{d}}N_1}{\mathrm{{d}}t}&= N_{01} -N_1 - \frac{r_1 N_1 U_1}{1+N_1}. \\ \end{aligned} \end{aligned}$$

(3)

Then solutions of system (3) are nonnegative and bounded by Proposition 2.1.

If $r_1\le m_1$, then $\mathrm{{d}}U_1 /\mathrm{{d}}t <0$, which implies that $U_1 \rightarrow 0, N_1 \rightarrow N_{01}$. Thus we assume $r_1> m_1$ in the following discussion. Since $U_1 =0$ is a solution of (3), the $N_1$-axis is an invariant set of (3).

Proposition 2.2

  There is no periodic solution in system (3).

Proof

Let $F_1$ and $F_2$ be the right-hand side of (3). Let $B=1/U_1$. Then

$$\begin{aligned} \frac{\partial (BF_1)}{\partial U_1} + \frac{\partial (BF_2)}{\partial N_1} = - \frac{r_1}{(1+N_1)^2 } -g_1 -\frac{1}{U_1 } <0. \end{aligned}$$

By the Dulac’s Criterion, there is no periodic solution in (3). $\square$

Equilibria of (3) are considered as follows. Denote $H_1=1/(1+N_1)$. Then the Jacobian matrix of (3) is

$$\begin{aligned} J= \left( \begin{array}{lccr} r_1 N_1 H_1- m_1-2 g_1 U_1 &{} \quad r_1 U_1 H_1^2 \\ -r_1 N_1 H_1 &{}\quad -1- r_1 U_1 H_1^2 \end{array} \right) . \end{aligned}$$

There is one-boundary equilibrium of (3), namely, $E_1(0,N_{01} )$. $E_1$ has eigenvalues $\mu _1^{(1)} = -1,~~\mu _1^{(2)} = \frac{r_1 N_{01}}{1+N_{01}}-m_1.$

There is at most one positive equilibrium of (3). Indeed, system (3) has two isoclines:

$$\begin{aligned}&L_1:~ (r_1-m_1-g_1 U_1 ) (1 + N_1) =r_1~~~~~~~~~~\\&L_2:~ U_1 = f_2(N_1) = \frac{1}{r_1} (N_{01} -N_1) (1+ \frac{1}{N_1}). \end{aligned}$$

Then

$$\begin{aligned} f_2(N_{01}) = 0,~~ \lim _{N_1 \rightarrow 0+} f_2(N_1) = \infty ,~~ \frac{\mathrm{{d}} f_2}{\mathrm{{d}} N_1} = - \frac{1}{r_1} \left( 1+ \frac{N_{01}}{N_1^2}\right) <0. \end{aligned}$$

Thus isocline $L_2$ is monotonically decreasing and $(0,N_{01})\in L_2$, as shown in Fig. 1. Isocline $L_1$ is a hyperbola with asymptotes $U_1= (r_1-m_1)/g_1, N_1 =-1$ and $(0, m_1/(r_1-m_1 )), (-m_1/g_1, 0)\in L_1$. Thus system (3) has a positive equilibrium $E^+(U_1^+, N_1^+ )$ if and only if $N_{01} > m_1/(r_1-m_1 )$, i.e., $\mu _1^{(2)} >0$.

Fig. 1

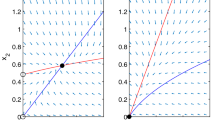
Phase-plane diagram of system (3). Stable and unstable equilibria are identified by solid and open circles, respectively. Vector fields are shown by gray arrows. Isoclines of $U_1,N_1$ are represented by blue and red lines, respectively. Let $r_1 = 2, m_1 =g_1 = 1, N_{01}=1.5$. All positive solutions of (3) converge to a positive equilibrium (Color figure online)

The Jacobian matrix of (3) at $E^+$ is

$$\begin{aligned} J^+= \left( \begin{array}{lccr} -g_1U_1 &{}\quad r_1 U_1 H_1^2 \\ -r_1 N_1 H_1 &{}\quad -1- r_1 U_1 H_1^2 \end{array} \right) . \end{aligned}$$

Then tr$J^+ = -g_1U_1 -1- r_1 U_1 H_1^2<0$ and $\det J^+ = (1+ r_1 U_1 H_1^2)g_1U_1 + r_1^2 N_1 U_1 H_1^3 >0$. Thus $E^+$ is asymptotically stable. By Proposition 2.2, $E^+$ is globally asymptotically stable. When $\mu _1^{(2)} \le 0$, there is no positive equilibrium in (3) and $E_1$ is globally asymptotically stable.

Therefore, global dynamics of system (3) are concluded as follows.

Theorem 2.3

• (i) Assume $r_1 >m_1$ and $N_{01} > m_1/(r_1-m_1 )$. System (3) has a unique positive equilibrium $E^+( U_1^+,N_1^+)$, which is globally asymptotically stable in int$R_+^2$ as shown in Fig. 1.

• (ii) Assume $r_1 \le m_1$, or $r_1 >m_1, N_{01} \le m_1/(r_1-m_1 )$. Equilibrium $E_1(0,N_{01} )$ is globally asymptotically stable in int$R_+^2$ in (3).

3 The Positive Equilibrium

Since the carrying capacity of system (2) is defined by stable positive equilibria, we demonstrate existence of the equilibria in this section by showing uniform persistence of the system. Denote

$$\begin{aligned} {{\bar{D}}} = \prod _{i=1}^2\left( \frac{r_iN_{0i} }{1+N_{0i} }-m_i\right) / \sum _{i=1}^2\left( \frac{r_iN_{0i} }{1+N_{0i} }-m_i\right) . \end{aligned}$$

Theorem 3.1

• (i) Let $r_i> m_i, N_{01} > \frac{m_1}{r_1-m_1}, N_{02} \le \frac{m_2}{r_2-m_2}, i=1,2.$ When $\sum _{i=1}^2 (\frac{r_iN_{0i} }{1+N_{0i} }-m_i)>0,$ system (2) is uniformly persistent. When $\sum _{i=1}^2 (\frac{r_iN_{0i} }{1+N_{0i} }-m_i)<0$, system (2) is uniformly persistent if $0<D<{{\bar{D}}}$ and is not persistent if $D>{{\bar{D}}}$.

• (ii) Let $r_i> m_i, N_{0i} > \frac{m_i}{r_i-m_i}, i=1,2.$ Then system (2) is uniformly persistent.

• (iii) Let $r_1> m_1, r_2\le m_2.$ When $\sum _{i=1}^2 (\frac{r_iN_{0i} }{1+N_{0i} }-m_i)>0,$ system (2) is uniformly persistent. When $N_{01} > \frac{m_1}{r_1-m_1}$ and $\sum _{i=1}^2 (\frac{r_iN_{0i} }{1+N_{0i} }-m_i)<0$, system (2) is uniformly persistent if $0<D<{{\bar{D}}}$ and is not persistent if $D>{{\bar{D}}}$.

• (iv) Let $r_i> m_i, N_{0i} < \frac{m_i}{r_i-m_i}, i=1,2$, or $r_i\le m_i, i=1,2$. Then system (2) is not persistent, and equilibrium $P_1(0,N_{01},0, N_{02})$ is globally asymptotically stable in int$R_+^4$.

Proof

(i) On the boundary $N_i=0$ for $i=1,2$, we have $\mathrm{{d}}N_i/\mathrm{{d}}t=N_{0i}>0$, which implies that no positive solutions of (2) would approach the boundary $N_i=0$.

On the boundary $U_1=0$, we have $\mathrm{{d}}U_1/\mathrm{{d}}t=DU_2 \ge 0$. If $U_2>0$, then $\mathrm{{d}}U_1/\mathrm{{d}}t>0$, which implies that no positive solutions of (2) would approach the boundary $U_1=0$. Assume $U_2=0$. On the $(N_1, N_2)$-plane, it is obvious that all solutions of (2) converge to equilibrium $P_1(0,N_{01},0, N_{02})$. $P_1$ has no stable manifold in int$R_+^4$, which is shown as follows. Let $H_i=1/(1+ N_i),i=1,2$. The Jacobian matrix of (2) at $P_1$ is

$$\begin{aligned} J= \left( \begin{array}{lccccr} J_{11} &{}\quad 0 &{}\quad D &{}\quad 0 \\ J_{21} &{}\quad -1 &{}\quad 0 &{}\quad 0 \\ D &{}\quad 0 &{}\quad J_{33} &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad J_{43} &{}\quad -1 \\ \end{array} \right) \end{aligned}$$

where $J_{11} = r_1 N_1 H_1-m_1-D,~J_{21} = -r_1 N_1 H_1, ~ J_{33} = r_2 N_2 H_2-m_2-D, ~J_{43} = -r_2 N_2 H_2.$ The characteristic equation of J is $(\mu +1)^2 [\mu ^2 +a \mu +b ]=0$ with

$$\begin{aligned} a = 2D- \sum _{i=1}^2\left( \frac{r_iN_{0i} }{1+N_{0i} }-m_i\right) , ~ b= \prod _{i=1}^2\left( \frac{r_iN_{0i} }{1+N_{0i} }-m_i\right) -D\sum _{i=1}^2\left( \frac{r_iN_{0i} }{1+N_{0i} }-m_i\right) . \end{aligned}$$

(4)

If $\sum _{i=1}^2\big (\frac{r_iN_{0i} }{1+N_{0i} }-m_i\big )>0$, then $b<0$ and $P_1$ is a saddle point. The matrix J has eigenvalues $\mu _{1,2}=-1$, which have eigenvectors $v_1=(0,1,0,0)$ and $v_2=(0,0,0,1)$, respectively. Its other eigenvalues and corresponding eigenvectors are

$$\begin{aligned} \mu _{3,4}= & {} \frac{1}{2} \left[ J_{11}+J_{33} \pm \sqrt{ (J_{11}+J_{33})^2 - 4 (J_{11}J_{33}-D^2) } \right] ~~ \text {with} ~~ \mu _4 <0\\ v_3= & {} (-D, 0, J_{11} - \mu _3,0 ),~~v_4 = (-D, 0, J_{11} - \mu _4,0 ) \end{aligned}$$

Since $J_{11} - \mu _4 = [J_{11}-J_{33} + \sqrt{ (J_{11}+J_{33})^2 - 4 (J_{11}J_{33}-D^2) } ]/2>0$, $v_4$ does not direct toward int$R_+^4$, which implies that $P_1$ has no stable manifold in int$R_+^4$. Therefore, no positive solutions of (2) would approach the boundary $U_1=0$. Similarly, no positive solutions of (2) would approach the boundary $U_2=0$. Since $P_1$ is the unique boundary equilibrium and cannot be in a heteroclinic cycle in $R_+^4$, we obtain uniform persistence of system (2) by the Acyclicity Theorem of Butler et al. (1986).

If $\sum _{i=1}^2\big (\frac{r_iN_{0i} }{1+N_{0i} }-m_i\big )<0$ and $0<D<\bar{D}$, then $b<0$ and $P_1$ is a saddle point. By a proof similar to the above one, we obtain that system (2) is uniformly persistent.

If $\sum _{i=1}^2\big (\frac{r_iN_{0i} }{1+N_{0i} }-m_i\big )<0$ and $D>\bar{D}$, then $a>0, b>0$ and $P_1$ is asymptotically stable. Thus system (2) is not persistent.

(ii) Denote $V= U_1+U_2$ and

$$\begin{aligned} {{\bar{N}}}_{0i}= & {} \frac{1}{2}\left( N_{0i}+ \frac{m_i}{r_i-m_i}\right) ,~ \delta _i = \frac{1}{2}\left( N_{0i}- \frac{m_i}{r_i-m_i}\right) ,~ \sigma _i = \frac{1}{g_i}\left( \frac{r_i \bar{N}_{0i} }{1+{{\bar{N}}}_{0i}} -m_i \right) \\ \Omega= & {} \{P\left( U_1,N_1,U_2,N_2\right) : 0< U_i< \sigma _i, 0<|N_i - N_{0i}|< \delta _i \},~~i=1,2. \end{aligned}$$

Then $\Omega$ is an open neighborhood of equilibrium $P_1(0,N_{01},0, N_{02})$ in int$R_+^4$. When $P\in \Omega$, we have

$$\begin{aligned} \frac{\mathrm{{d}} V}{\mathrm{{d}}t}|_{(2.1)} = \sum _{i=1}^2 U_i \left( \frac{r_i N_i }{1+N_i} -m_i- g_i U_i \right) >0 \end{aligned}$$

which implies that $P_1$ has no stable manifold in int$R_+^4$ by the Liapunov Theorem (Hofbauer and Sigmund 1998). Since $P_1$ is the unique boundary equilibrium of (2), $P_1$ cannot be in a heteroclinic cycle in $R_+^4$. Thus, we obtain uniform persistence of system (2) by the Acyclicity Theorem of Butler et al. (1986).

(iii) The proof is similar to that of (i).

(iv) We consider the case $r_i> m_i, N_{0i} < \frac{m_i}{r_i-m_i}, i=1,2$, while a similar proof can be given for $r_i\le m_i, i=1,2$.

From the second and fourth equations of (2), we have $\limsup _{t\rightarrow \infty } N_i(t) \le N_{0i}, i=1,2$. Let $\delta _0 = \frac{1}{2} \min _{i=1,2}\{ m_i/(r_i-m_i)-N_{0i} \}$. Then for a positive solution of (2), there exists $T>0$ such that when $t>T$, we have $0< N_i(t) \le N_{0i} + \delta _0, i=1,2$. Denote $V= U_1+U_2$. Then when $t>T$, we have $\frac{r_i N_i(t) }{1+N_i(t)} -m_i<0$ and

$$\begin{aligned} \frac{\mathrm{{d}} V}{\mathrm{{d}}t}|_{(2.1)} = U_1 \left( \frac{r_1 N_1 }{1+N_1} -m_1 - g_1 U_1\right) + U_2 \left( \frac{r_2 N_2 }{1+N_2} -m_2 - g_2 U_2\right) \le 0 \end{aligned}$$

which implies that $P_1$ is globally asymptotically stable in int$R_+^4$ by the Liapunov Theorem. $\square$

Theorem 3.1(i)(iii) exhibits the role of diffusion rates in persistence of consumer. When the growth rates are intermediate such that $\frac{r_1N_{01} }{1+N_{01} }-m_1>0$ and $\sum _{i=1}^2 (\frac{r_iN_{0i} }{1+N_{0i} }-m_i)<0$, the consumer survives in two patches when the diffusion rate is small ($0<D<{{\bar{D}}}$). However, it would go to extinction when the rate is large ($D>{{\bar{D}}}$) because $P_1(0,N_{01},0, N_{02})$ is asymptotically stable. The underlying reason is displayed in Sect. 5. Since the consumer persists in system (2) when $0\le D<{{\bar{D}}}$, it is the large diffusion rate that results in the extinction.

By Theorem 3.1, we conclude the following result.

Corollary 3.2

If $\sum _{i=1}^2 (\frac{r_iN_{0i} }{1+N_{0i} }-m_i)>0$, system (2) is uniformly persistent for $D\in (0,\infty )$.

When system (2) is uniformly persistent, its dissipativity by Proposition 2.1 guarantees that it has a positive equilibrium $P^*$ (Butler et al. 1986).

Theorem 3.3

Assume that $P^*$ is a positive equilibrium of system (2). Then $P^*$ is asymptotically stable when D is large.

Proof

Denote $H_i=1/(1+N_i),i=1,2$. The Jacobian matrix of (2) at $P^*$ is

$$\begin{aligned} {{\bar{J}}}^*= \left( \begin{array}{lccccr} {{\bar{J}}}_{11} &{}\quad {{\bar{J}}}_{12} &{}\quad D &{}\quad 0 \\ {{\bar{J}}}_{21} &{}\quad -1 - {{\bar{J}}}_{12} &{}\quad 0 &{}\quad 0 \\ D &{}\quad 0 &{}\quad {{\bar{J}}}_{33} &{}\quad {{\bar{J}}}_{34} \\ 0 &{}\quad 0 &{}\quad {{\bar{J}}}_{43} &{}\quad -1 - {{\bar{J}}}_{34} \\ \end{array} \right) \end{aligned}$$

where

$$\begin{aligned} {{\bar{J}}}_{11}= & {} -D \frac{U_2}{U_1} - g_1U_1<0, \ {{\bar{J}}}_{12} = r_1 U_1 H_1^2>0, \ {{\bar{J}}}_{21} = -r_1 N_1 H_1<0, \\ {{\bar{J}}}_{33}= & {} -D \frac{U_1}{U_2} - g_2U_2<0, \ {{\bar{J}}}_{34} = r_2 U_2 H_2^2>0, \ {{\bar{J}}}_{43} = -r_2 N_2 H_2<0 . \end{aligned}$$

Then the characteristic equation of ${{\bar{J}}}^*$ is $\mu ^4+ {{\bar{a}}}_1 \mu ^3+ {{\bar{a}}}_2\mu ^2+ {{\bar{a}}}_3\mu + {{\bar{a}}}_4=0.$ When $D \rightarrow \infty$, we have

$$\begin{aligned} \begin{aligned} {{\bar{a}}}_1&= 2+ {{\bar{J}}}_{12} + {{\bar{J}}}_{34} - {{\bar{J}}}_{11}- {{\bar{J}}}_{33} \propto D\left( \frac{U_1}{U_2}+\frac{U_2}{U_1}\right)>0\\ {{\bar{a}}}_2&= -D^2 - {{\bar{J}}}_{11} (1 + {{\bar{J}}}_{12}) - {{\bar{J}}}_{21} \bar{J}_{12} - {{\bar{J}}}_{33} (1 + {{\bar{J}}}_{34}) - {{\bar{J}}}_{43} {{\bar{J}}}_{34} + (1 + {{\bar{J}}}_{12}- {{\bar{J}}}_{11}) (1 + {{\bar{J}}}_{34} - {{\bar{J}}}_{33})\\&\propto D (2 + {{\bar{J}}}_{12}+ {{\bar{J}}}_{34}) \left( \frac{U_1}{U_2}+\frac{U_2}{U_1}\right) +D \Delta >0\\ \end{aligned} \end{aligned}$$

$$\begin{aligned} \begin{aligned} {{\bar{a}}}_3&= [- {{\bar{J}}}_{11} (1 + {{\bar{J}}}_{12}) - {{\bar{J}}}_{21} {{\bar{J}}}_{12}] (1 + {{\bar{J}}}_{34} - {{\bar{J}}}_{33})+ [- {{\bar{J}}}_{33} (1 + {{\bar{J}}}_{34}) - {{\bar{J}}}_{43} {{\bar{J}}}_{34}] (1 + {{\bar{J}}}_{12} - {{\bar{J}}}_{11})\\&~~- D^2 (2+ {{\bar{J}}}_{12} + {{\bar{J}}}_{34})\\&\propto D \left\{ \frac{U_2}{U_1} \left[ (1 + {{\bar{J}}}_{12}) (1 + {{\bar{J}}}_{34}) - {{\bar{J}}}_{43} {{\bar{J}}}_{34}\right] + \frac{U_1}{U_2} \left[ (1 + {{\bar{J}}}_{12}) (1 + {{\bar{J}}}_{34}) - {{\bar{J}}}_{21} {{\bar{J}}}_{12}\right] \right\} \\&~~~~+ D \Delta (2+ {{\bar{J}}}_{12} + {{\bar{J}}}_{34})>0 \\ {{\bar{a}}}_4&= [- {{\bar{J}}}_{11} (1 + {{\bar{J}}}_{12}) - {{\bar{J}}}_{21} \bar{J}_{12}] [- {{\bar{J}}}_{33} (1 + {{\bar{J}}}_{34}) - {{\bar{J}}}_{43} {{\bar{J}}}_{34}] - D^2 (1+ {{\bar{J}}}_{12})(1 + {{\bar{J}}}_{34})\\&\propto -D \left[ \frac{U_2}{U_1} (1 + {{\bar{J}}}_{12}) {{\bar{J}}}_{43} \bar{J}_{34}+ \frac{U_1}{U_2} (1 + {{\bar{J}}}_{34}) {{\bar{J}}}_{21} {{\bar{J}}}_{12} \right] + D \Delta (1 + {{\bar{J}}}_{12})(1 + {{\bar{J}}}_{34}) >0 \\ \end{aligned} \end{aligned}$$

where $\Delta = g_1 U_1^2 /U_2 + g_2 U_2^2 /U_1 >0$. Then we have

$$\begin{aligned} \left| \begin{array}{lccr} {{\bar{a}}}_1 &{}\quad 1 \\ {{\bar{a}}}_3 &{}\quad {{\bar{a}}}_2 \\ \end{array} \right| \propto D^2 (2 + {{\bar{J}}}_{12}+ {{\bar{J}}}_{34}) \left( \frac{U_1}{U_2}+\frac{U_2}{U_1}\right) ^2 + D^2 \Delta \left( \frac{U_1}{U_2}+\frac{U_2}{U_1}\right) >0,~~ \end{aligned}$$

$$\begin{aligned} \begin{aligned} \left| \begin{array}{lcccr} {{\bar{a}}}_1 &{}\quad 1 &{}\quad 0 \\ {{\bar{a}}}_3 &{}\quad {{\bar{a}}}_2 &{}\quad {{\bar{a}}}_1 \\ 0 &{}\quad {{\bar{a}}}_4 &{}\quad {{\bar{a}}}_3 \\ \end{array} \right|&\propto D^3 \left( \frac{U_1}{U_2}+\frac{U_2}{U_1}\right) ^2 \left[ \left( \frac{U_1}{U_2}+\frac{U_2}{U_1}\right) \left( 2 + {{\bar{J}}}_{12}+ {{\bar{J}}}_{34}\right) (1 + {{\bar{J}}}_{12})(1 + {{\bar{J}}}_{34}) \right. \\&\left. \quad -\,\frac{U_2}{U_1} (1 + {{\bar{J}}}_{34}) {{\bar{J}}}_{43} {{\bar{J}}}_{34} - \frac{U_1}{U_2}(1 + {{\bar{J}}}_{12}){{\bar{J}}}_{21} {{\bar{J}}}_{12} \right] + D^3 \Delta ^2 {{\bar{a}}}_3 \left( \frac{U_1}{U_2}+\frac{U_2}{U_1}\right) \\&\quad +\, D^3 \Delta \left( \frac{U_1}{U_2}+\frac{U_2}{U_1}\right) ^2 \left[ (1 + \bar{J}_{12})^2 + (1 + {{\bar{J}}}_{12})(1 + {{\bar{J}}}_{34}) +(1 + \bar{J}_{34})^2 \right] >0.\\ \end{aligned} \end{aligned}$$

By the Hurwitz Criterion, $P^*$ is asymptotically stable when D is large. $\square$

When there is diffusion and the diffusion rate approaches very large values (i.e., $D\rightarrow \infty$), that is, $D \gg U_i(\frac{r_i N_i}{1+N_i}-m_i-g_iU_i)$, the stable positive equilibrium $P^*( U_1,N_1, U_2,N_2 )$, in this limit, satisfies $U_1- U_2 \rightarrow 0$. This must be true because $U_i(\frac{r_i N_i}{1+N_i}-m_i-g_iU_i)$ is bounded to finite values by Proposition 2.1. That is, equilibrium $P^*( U_1,N_1, U_2,N_2 )$ of (2) satisfies $U_1\approx U_2\approx Z$. By Proposition 2.1, equilibria $P^*$ are bounded if $D\rightarrow \infty$. Thus the sequence $\{P^*: D\in (0,\infty )\}$ has convergent subsequences, whose limit points can be written as ${{\bar{P}}}(Z,N_1, Z,N_2 )$.

By summing the first and third equations of (2) and by the second and fourth equations of (2), we obtain the following equations that the limit point ${{\bar{P}}}(Z,N_1, Z,N_2 )$ satisfies:

$$\begin{aligned} \begin{aligned}&\frac{r_1 N_1 }{1+N_1} -m_1 -g_1 Z+ \frac{r_2 N_2 }{1+N_2} -m_2-g_2 Z=0 \\&N_{01} -N_1 - \frac{r_1 N_1 Z}{1+N_1}=0 ,\quad N_{02} -N_2 - \frac{r_2 N_2 Z}{1+N_2} =0.\\ \end{aligned} \end{aligned}$$

(5)

Therefore, we conclude the following result.

Theorem 3.4

Assume $\sum _{i=1}^2 (\frac{r_iN_{0i} }{1+N_{0i} }-m_i)>0$. Then Eq. (5) has a unique positive solution ${{\bar{P}}}$.

Proof

The point ${{\bar{P}}}$ is positive if $\sum _{i=1}^2 (\frac{r_iN_{0i} }{1+N_{0i} }-m_i)>0$. Indeed, suppose $Z=0$. Then $U_i\rightarrow 0$ if $D\rightarrow \infty$. From (2), we have $N_i \rightarrow N_{0i}$ if $D\rightarrow \infty$, which implies that $\sum _{i=1}^2 U_i ( \frac{r_i N_{0i} }{1+N_{0i}} -m_i -g_i U_i ) >0$ if $D\rightarrow \infty$. However, from (2), we always have $\sum _{i=1}^2 U_i ( \frac{r_i N_i }{1+N_i} -m_i -g_i U_i ) =0$ as $D\in (0, \infty )$, which forms a contradiction. Suppose $N_1=0$. From the second equation of (2), we have $dN_1/dt \rightarrow N_{0i} >0$ if $D\rightarrow \infty$, which contradicts with $N_1=0$. Thus $N_1>0$. Similarly, we have $N_2>0$.

The positive point ${{\bar{P}}}$ is unique. Indeed, let $F_i= F_i(\Theta , U_1,N_1, U_2,N_2)$ be the left hand of (5), where $\Theta = \{N_{0j}, r_j, m_j,g_j, j=1,2 \}$, $i=1,2,3$. The Jacobian matrix of $F_i$ at ${{\bar{P}}}$ satisfies

$$\begin{aligned} \begin{aligned}&\det \frac{D(F_1,F_2,F_3)}{D(Z, N_1,N_2)}|_{{{\bar{P}}}} = \det \left( \begin{array}{lcccr} - (g_1+g_2 ) &{}\quad r_1 H_1^2 &{}\quad r_2 H_2^2\\ - r_1 N_1 H_1 &{}\quad -1- r_1 H_1^2 Z &{}\quad 0\\ - r_2 N_2 H_2 &{}\quad 0 &{}\quad -1- r_2 H_2^2 Z \\ \end{array} \right) \\&\quad = - (g_1+g_2 ) \prod _{i=1}^2(1+ r_i H_i^2 Z) - r_2^2 N_2 H_2^3 (1+ r_1 H_1^2 Z) - r_1^2 N_1 H_1^3 (1+ r_2 H_2^2 Z)<0. \end{aligned} \end{aligned}$$

(6)

Let $\Theta _0 = \{N_{0j}=N_0, r_j=r, m_j=m, g_j=g, j=1,2 \}$. By symmetry in (5) and Theorem 2.2, Eq. (5) has a unique positive solution ${{\bar{P}}}_0$. By (6) and the Implicit Function Theorem, there is a small neighborhood of $\Theta _0$ in which equation (5) has a unique positive solution ${{\bar{P}}}$. Since (6) holds for all $\Theta$ and positive solution ${{\bar{P}}}$, the Implicit Function Theorem implies that the unique positive solution ${{\bar{P}}}$ derived from ${{\bar{P}}}_0$ can be extended to all $\Theta$ with $\sum _{i=1}^2 \big (\frac{r_iN_{0i} }{1+N_{0i} }-m_i\big )>0$. This completes the proof. $\square$

4 Asymptotic State

Total realized asymptotic population abundance (abbreviated TRAPA by Arditi et al. 2015) varies in heterogeneous/homogeneous resource distributions with/without consumer diffusion. For convenience, denote

$$\begin{aligned} T_0= & {} \mathrm{{TRAPA}}_\mathrm{{heterogeneous, ~no~ diffusion}}, ~~~~T_1 = \mathrm{{TRAPA_{heterogeneous,~ diffusion}}}\\ T_2= & {} \mathrm{{TRAPA}}_\mathrm{{homogeneous, ~no~ diffusion}},\quad T_3 = \mathrm{{TRAPA}}_\mathrm{{homogeneous, diffusion}} \end{aligned}$$

in which $T_1 = \mathrm{{TRAPA_{heterogeneous, ~diffusion}}}$ denotes TRAPA at equilibrium in heterogeneous environments with infinite diffusion, and similar explanations can be given for the others.

4.1 Source–Source Populations

This subsection considers source–source populations in which the species can persist in each patch without diffusion. We exhibit $T_1>T_0$ under conditions and show $T_3=T_2>T_1$. Let

$$\begin{aligned} N_{01}=N_0 + \epsilon , \ N_{02}=N_0 - \epsilon , ~r_i=r>m,~m_i=m,~g_i=g,~i=1,2 \end{aligned}$$

(7)

where $N_0 > \frac{m}{r-m}, |\epsilon |< {{\bar{\epsilon }}}, {{\bar{\epsilon }}} = N_0 - \frac{m}{r-m}$. Then resource inputs in two patches are homogeneous if $\epsilon =0$.

Theorem 4.1

Let (7) hold. Then

• (i) $T_3 = T_2 >T_1$.

• (ii) $T_2 >T_0$.

Proof

(i) When there is no diffusion (i.e., $D=0$), the positive equilibrium $P(u_1,n_1, u_2,n_2 )$ of (2) satisfies

$$\begin{aligned} \begin{aligned}&\frac{r n_1 }{1+n_1} -m -g u_1 =0, \quad \frac{r n_2 }{1+n_2} -m -g u_2 =0\\&N_0 + \epsilon -n_1 - \frac{r n_1 u_1}{1+n_1}=0, \quad N_0 - \epsilon -n_2 - \frac{r n_2 u_2}{1+n_2} =0\\ \end{aligned} \end{aligned}$$

(8)

where $T_0 = u_1(\epsilon )+u_2(\epsilon ), T_2 = u_1(0)+u_2(0)$. By differentiating each side of (8) on $\epsilon$, we obtain

$$\begin{aligned} \frac{\mathrm{{d}} n_1 }{\mathrm{{d}} \epsilon } = \frac{g }{r h_1^2} \frac{\mathrm{{d}} u_1 }{\mathrm{{d}} \epsilon },~ \frac{\mathrm{{d}} u_1 }{\mathrm{{d}} \epsilon } = \left[ r n_1 h_1 +(1+r h_1^2 u_1 ) \frac{g }{r h_1^2} \right] ^{-1} >0,~~ h_1=\frac{1 }{1 +n_1}. \end{aligned}$$

(9)

When there is diffusion (i.e., $D>0$), it follows from Corollary 3.2 and Theorem 3.3 that system (2) has a stable positive equilibrium $P^*$ if the diffusion rate D is large, and their accumulation point ${{\bar{P}}}$ is positive.

Assume $\epsilon =0$. Then $T_3 = 2Z$ where Z is defined by (5). From the symmetry in (5) and (8), we obtain $T_3 = T_2$ since the root is unique by Theorem 2.3.

Assume $\epsilon >0$. Then $T_1 = 2Z(\epsilon )$ where Z is defined by (5). From the analyticity of (5), components of ${{\bar{P}}}(N_1,Z,N_2,Z)$ are differentiable on $\epsilon$. Denote $H_i=1/(1+N_i), i=1,2.$ By subtracting the second and third equations of (5), we have $N_1-N_2 = \frac{2 \epsilon }{1+ r Z H_1H_2 } >0.$ By differentiating each side of (5) on $\epsilon$, we obtain

$$\begin{aligned} \begin{aligned}&r H_1^2 \frac{\mathrm{{d}}N_1}{\mathrm{{d}}\epsilon } + r H_2^2 \frac{\mathrm{{d}}N_2}{\mathrm{{d}}\epsilon } -2g \frac{\mathrm{{d}}Z}{\mathrm{{d}}\epsilon } =0\\&1- \frac{\mathrm{{d}}N_1}{\mathrm{{d}}\epsilon } - r H_1^2 \frac{\mathrm{{d}}N_1}{\mathrm{{d}}\epsilon } Z -r N_1 H_1 \frac{\mathrm{{d}}Z}{\mathrm{{d}}\epsilon } =0\\&-1- \frac{\mathrm{{d}}N_2}{\mathrm{{d}}\epsilon } - r H_2^2 \frac{\mathrm{{d}}N_2}{\mathrm{{d}}\epsilon } Z -r N_2 H_2 \frac{\mathrm{{d}}Z}{\mathrm{{d}}\epsilon } =0.\\ \end{aligned} \end{aligned}$$

From $N_1>N_2$, we have

$$\begin{aligned} \frac{\mathrm{{d}}Z}{\mathrm{{d}}\epsilon } = \frac{a}{b} ,~~ a= \frac{r H_1^2 }{1+ r H_1^2 Z } - \frac{r H_2^2 }{1+ r H_2^2 Z },~~ b= 2g+ \frac{r^2 N_1 H_1^3 }{1+ r H_1^2 Z} + \frac{r^2 N_2 H_2^3 }{1+ r H_2^2 Z}>0. \end{aligned}$$

Thus $\frac{\mathrm{{d}}Z}{\mathrm{{d}}\epsilon } <0$ if $\epsilon >0$, which means $T_2 >T_1$ because $T_3=T_2=T_1(0)$. A similar discussion could show that $\frac{\mathrm{{d}}Z}{\mathrm{{d}}\epsilon } >0$ if $\epsilon < 0$. Thus $T_2 >T_1$.

(ii) By Theorem 2.3, there is a unique positive solution $P(u_1,n_1, u_2,n_2)$ of (8), and $u_i = u_i(\epsilon ),n_i=n_i(\epsilon )$ are differentiable on $\epsilon$ by the analyticity of (8). By differentiating each side of (8) on $\epsilon$, we obtain

$$\begin{aligned} \begin{aligned} \frac{\mathrm{{d}}n_i}{\mathrm{{d}}\epsilon }&= \frac{g}{r h_i^2} \frac{\mathrm{{d}}u_i}{\mathrm{{d}}\epsilon },\quad \frac{\mathrm{{d}}u_i}{\mathrm{{d}}\epsilon } = (-1)^{i+1} [(1 + r h_i^2 u_i ) \frac{g}{r h_i^2} + r n_i h_i ]^{-1}\\ \frac{\mathrm{{d}}(u_1+u_2 ) }{d\epsilon }&= \left[ (1 + r h_1^2 u_1 ) \frac{g}{r h_1^2} + r n_1 h_1 \right] ^{-1} - \left[ (1 + r h_2^2 u_2 ) \frac{g}{r h_2^2} + r n_2 h_2 \right] ^{-1}.\\ \end{aligned} \end{aligned}$$

We focus on $\epsilon >0$, while a similar discussion can be given for $\epsilon <0$. Then we have $\frac{\mathrm{{d}}n_1}{\mathrm{{d}}\epsilon }>0, \frac{\mathrm{{d}}u_1}{\mathrm{{d}}\epsilon } >0$ and $n_1>n_2, u_1 >u_2$, which implies $\frac{\mathrm{{d}}(u_1+u_2) }{\mathrm{{d}}\epsilon } <0$. Thus, $\frac{\mathrm{{d}}(T_2-T_0) }{\mathrm{{d}}\epsilon } >0$ and $T_2 >T_0$. $\square$

Remark 4.2

• (i) Theorem 4.1 demonstrates that $T_3=T_2 >T_1$ and $T_3=T_2 >T_0$ for general heterogeneous/homogeneous distributions of resources. Indeed, for any nutrient inputs with $N_{01}> N_{02}> \frac{m }{r-m }$, we can rewrite them as $N_{01}= N_0 + \epsilon , N_{02}= N_0 - \epsilon$ with $N_0 = ( N_{01}+ N_{02})/2, \epsilon = ( N_{01}- N_{02})/2$.

• (ii) Zhang et al. (2017) displayed $T_2 >T_1$ in (2) if $g_i=0$, in which $T_1$ is obtained by letting $N_i = \frac{m_i}{r_i-m_i}$ (see (D19), Supporting Information Appendix D, Zhang et al. 2017). This is not appropriate because $N_1 > N_2$ as shown in the above proof.

Next we exhibit $T_1>T_0$ under conditions. Let

$$\begin{aligned} N_{01}=N_0+ \delta \epsilon , ~N_{02}=N_0- \delta \epsilon ,~ r_1 = r + \epsilon , r_2 = r - \epsilon ,~m_i=m,~g_i=g,~i=1,2 \end{aligned}$$

(10)

where $r>m, N_{0i} > \frac{m}{r-m}, \delta \ge 0$.

When there is no diffusion (i.e., $D=0$), the positive equilibrium $P(u_1,n_1, u_2,n_2 )$ of (2) satisfies

$$\begin{aligned} \begin{aligned}&\frac{(r + \epsilon ) n_1 }{1+n_1} -m -g u_1 =0 ,~~~~~~ \frac{(r - \epsilon ) n_2 }{1+n_2} -m -g u_2 =0\\&N_0+ \delta \epsilon -n_1 - \frac{(r + \epsilon ) n_1 u_1}{1+n_1}=0,~~~~ N_0- \delta \epsilon -n_2 - \frac{(r - \epsilon ) n_2 u_2}{1+n_2} =0\\ \end{aligned} \end{aligned}$$

(11)

where $u_i=u_i( \epsilon )$, $n_i=n_i( \epsilon ), i=1,2$. Then $T_0 = u_1( \epsilon )+u_2( \epsilon )$.

When there is diffusion (i.e., $D\rightarrow \infty$), the positive solution $P( Z,N_1, Z,N_2 )$ of (5) satisfies

$$\begin{aligned} \begin{aligned}&~~~~~~~~ \frac{(r + \epsilon ) N_1 }{1+N_1} + \frac{(r - \epsilon ) N_2 }{1+N_2} -2m -2g Z=0 \\&N_0+ \delta \epsilon -N_1 - \frac{(r + \epsilon ) N_1 Z}{1+N_1}=0 ,~~~~ N_0- \delta \epsilon -N_2 - \frac{(r - \epsilon ) N_2 Z}{1+N_2} =0\\ \end{aligned} \end{aligned}$$

(12)

where $N_i=N_i( \epsilon )$, $Z=Z( \epsilon ), i=1,2$. Then $T_1 = 2Z( \epsilon )$.

If $\epsilon =0$, symmetry of equations (11)–(12) implies

$$\begin{aligned} u_i( 0)=Z( 0), \ n_i( 0)=N_i( 0), \ i=1,2. \end{aligned}$$

(13)

Theorem 4.3

Let (10) hold. Let $\delta < \delta _0 =\frac{N_1^+ U_1^+}{1+N_1^+}$, where $(U_1^+, N_1^+)$ is the positive equilibrium of the corresponding subsystem (3) with $\epsilon =0$. Then there exists $\epsilon _0 >0$ such that if $0< |\epsilon | < \epsilon _0$, then $T_1(\epsilon ) >T_0(\epsilon )$, and $T_1(\epsilon ) - T_0(\epsilon )$ is a monotonically increasing function of $|\epsilon |$.

Proof

Let $f(\epsilon ) = T_1(\epsilon ) - T_0(\epsilon )= 2Z(\epsilon ) -u_1(\epsilon )-u_2(\epsilon ).$ From (13), we have $f(0) =0$.

We show $\frac{\mathrm{{d}}f}{\mathrm{{d}}\epsilon }(0) =0$ as follows. Denote $h_i=1/(1+n_i), i=1,2.$ From the analyticity of (11) and (14), $u_i(\epsilon ),n_i(\epsilon ),U_i(\epsilon )$ and $N_i(\epsilon )$ are differentiable on $\epsilon$ if $\epsilon$ is small. By differentiating each side of (11) on $\epsilon$, we obtain

$$\begin{aligned} \begin{aligned}&\delta - \frac{\mathrm{{d}}n_1}{\mathrm{{d}}\epsilon } -n_1 h_1 u_1 - (r + \epsilon ) h_1^2 u_1 \frac{\mathrm{{d}}n_1}{\mathrm{{d}}\epsilon } - (r + \epsilon ) n_1 h_1 \frac{\mathrm{{d}}u_1}{\mathrm{{d}}\epsilon }=0\\&-\delta - \frac{\mathrm{{d}}n_2}{\mathrm{{d}}\epsilon } +n_2 h_2 u_2 - (r - \epsilon ) h_2^2 u_2 \frac{\mathrm{{d}}n_2}{\mathrm{{d}}\epsilon } - (r - \epsilon ) n_2 h_2 \frac{\mathrm{{d}}u_2}{\mathrm{{d}}\epsilon }=0\\&n_1 h_1 + (r + \epsilon ) h_1^2 \frac{\mathrm{{d}}n_1}{\mathrm{{d}}\epsilon } - g \frac{\mathrm{{d}}u_1}{\mathrm{{d}}\epsilon }=0\\&-n_2 h_2 + (r - \epsilon ) h_2^2 \frac{\mathrm{{d}}n_2}{\mathrm{{d}}\epsilon } - g \frac{\mathrm{{d}}u_2}{\mathrm{{d}}\epsilon }=0.\\ \end{aligned} \end{aligned}$$

(14)

By summing the first two and last two equations of (14) and letting $\epsilon =0$, we have

$$\begin{aligned}&\left( \frac{\mathrm{{d}}n_1}{\mathrm{{d}}\epsilon } + \frac{\mathrm{{d}}n_2}{\mathrm{{d}}\epsilon }\right) |_{\epsilon =0} = - \frac{r n_1 h_1}{1+ r h_1^2 u_1} \left( \frac{\mathrm{{d}}u_1}{\mathrm{{d}}\epsilon } + \frac{\mathrm{{d}}u_2}{\mathrm{{d}}\epsilon }\right) |_{\epsilon =0}\\&\left( \frac{r n_1 h_1}{1+ r h_1^2 u_1} + \frac{g}{r h_1^2} \right) \left( \frac{\mathrm{{d}}u_1}{\mathrm{{d}}\epsilon } + \frac{\mathrm{{d}}u_2}{\mathrm{{d}}\epsilon }\right) |_{\epsilon =0} =0 \end{aligned}$$

which implies

$$\begin{aligned} \left( \frac{\mathrm{{d}}n_1}{\mathrm{{d}}\epsilon } + \frac{\mathrm{{d}}n_2}{\mathrm{{d}}\epsilon }\right) |_{\epsilon =0} = \left( \frac{\mathrm{{d}}u_1}{\mathrm{{d}}\epsilon } + \frac{\mathrm{{d}}u_2}{\mathrm{{d}}\epsilon }\right) |_{\epsilon =0}=0. \end{aligned}$$

(15)

Denote $H_i=1/(1+N_i), i=1,2.$ By differentiating each side of (12) on $\epsilon$, we obtain

$$\begin{aligned} \begin{aligned}&N_1 H_1 + (r + \epsilon ) H_1^2 \frac{\mathrm{{d}}N_1}{\mathrm{{d}}\epsilon } - 2 g \frac{\mathrm{{d}}Z}{\mathrm{{d}}\epsilon } - N_2 H_2 + (r - \epsilon ) H_2^2 \frac{\mathrm{{d}}N_2}{\mathrm{{d}}\epsilon } =0.\\&\delta - \frac{\mathrm{{d}}N_1}{\mathrm{{d}}\epsilon } -N_1 H_1 Z - (r + \epsilon ) H_1^2 Z \frac{\mathrm{{d}}N_1}{\mathrm{{d}}\epsilon } - (r + \epsilon ) N_1 H_1 \frac{\mathrm{{d}}Z}{\mathrm{{d}}\epsilon }=0\\&-\delta - \frac{\mathrm{{d}}N_2}{\mathrm{{d}}\epsilon } +N_2 H_2 Z - (r - \epsilon ) H_2^2 Z \frac{\mathrm{{d}}N_2}{\mathrm{{d}}\epsilon } - (r - \epsilon ) N_2 H_2 \frac{\mathrm{{d}}Z}{\mathrm{{d}}\epsilon }=0.\\ \end{aligned} \end{aligned}$$

(16)

Let $\epsilon =0$. From the first equation of (16), we obtain

$$\begin{aligned} \frac{\mathrm{{d}}N_1}{\mathrm{{d}}\epsilon } + \frac{\mathrm{{d}}N_2}{\mathrm{{d}}\epsilon } = \frac{2g}{r H_1^2} \frac{\mathrm{{d}}Z}{\mathrm{{d}}\epsilon }. \end{aligned}$$

By summing the second and third equations of (16), we have

$$\begin{aligned} \left[ 2r N_1 H_1 + \frac{2g(1+ r H_1^2Z )}{r H_1^2} \right] \frac{\mathrm{{d}}Z}{\mathrm{{d}}\epsilon }=0 \end{aligned}$$

which implies that

$$\begin{aligned} \frac{\mathrm{{d}}Z}{\mathrm{{d}}\epsilon }(0)=0, \ \frac{\mathrm{{d}}N_1}{\mathrm{{d}}\epsilon }(0)+ \frac{\mathrm{{d}}N_2}{\mathrm{{d}}\epsilon }(0) =0. \end{aligned}$$

Thus $\frac{\mathrm{{d}}f}{\mathrm{{d}}\epsilon }(0)=0$.

We show $\frac{\mathrm{{d}}^2f}{\mathrm{{d}}\epsilon ^2}(0) >0$ as follows. By differentiating each side of (14) on $\epsilon$ and letting $\epsilon =0$, we obtain

$$\begin{aligned} \begin{aligned}&- \frac{\mathrm{{d}}^2n_1}{\mathrm{{d}}\epsilon ^2} - 2 h_1^2 u_1 \frac{\mathrm{{d}}n_1}{\mathrm{{d}}\epsilon } - 2 n_1 h_1 \frac{\mathrm{{d}}u_1}{\mathrm{{d}}\epsilon } +2r h_1^3 u_1 \left( \frac{\mathrm{{d}} n_1}{\mathrm{{d}}\epsilon }\right) ^2 - r h_1^2 u_1 \frac{\mathrm{{d}}^2n_1}{\mathrm{{d}}\epsilon ^2} \\&\quad =2r h_1^2 \frac{\mathrm{{d}}n_1}{\mathrm{{d}}\epsilon } \frac{\mathrm{{d}}u_1}{\mathrm{{d}}\epsilon } + rn_1 h_1 \frac{\mathrm{{d}}^2u_1}{\mathrm{{d}}\epsilon ^2}\\&- \frac{\mathrm{{d}}^2n_2}{\mathrm{{d}}\epsilon ^2} + 2 h_2^2 u_2 \frac{\mathrm{{d}} n_2}{\mathrm{{d}}\epsilon } + 2 n_2 h_2 \frac{\mathrm{{d}}u_2}{\mathrm{{d}}\epsilon } +2r h_2^3 u_2 \left( \frac{\mathrm{{d}} n_2}{\mathrm{{d}}\epsilon }\right) ^2 - r h_2^2 u_2 \frac{\mathrm{{d}}^2n_2}{\mathrm{{d}}\epsilon ^2} \\&\quad =2r h_2^2 \frac{\mathrm{{d}} n_2}{\mathrm{{d}}\epsilon } \frac{\mathrm{{d}}u_2}{\mathrm{{d}}\epsilon } + rn_2 h_2 \frac{\mathrm{{d}}^2u_2}{\mathrm{{d}}\epsilon ^2} \\&2 h_1^2 \frac{\mathrm{{d}} n_1}{\mathrm{{d}}\epsilon } -2r h_1^3 \left( \frac{\mathrm{{d}} n_1}{\mathrm{{d}}\epsilon }\right) ^2 + r h_1^2 \frac{\mathrm{{d}}^2n_1}{\mathrm{{d}}\epsilon ^2} = g \frac{\mathrm{{d}}^2u_1}{\mathrm{{d}}\epsilon ^2}\\&-2 h_2^2 \frac{\mathrm{{d}} n_2}{\mathrm{{d}}\epsilon } -2r h_2^3 \left( \frac{\mathrm{{d}} n_2}{\mathrm{{d}}\epsilon }\right) ^2 + r h_2^2 \frac{\mathrm{{d}}^2n_2}{\mathrm{{d}}\epsilon ^2} = g \frac{\mathrm{{d}}^2u_2}{\mathrm{{d}}\epsilon ^2}.\\ \end{aligned} \end{aligned}$$

(17)

By summing the first two and last two equations of (17) respectively, we have

$$\begin{aligned} \begin{aligned}&\left( \frac{\mathrm{{d}}^2n_1}{\mathrm{{d}}\epsilon ^2}+\frac{\mathrm{{d}}^2n_2}{\mathrm{{d}}\epsilon ^2}\right) \left( 1+ r h_1^2 u_1 \right) + \left( \frac{\mathrm{{d}}^2u_1}{\mathrm{{d}}\epsilon ^2}+\frac{\mathrm{{d}}^2u_2}{\mathrm{{d}}\epsilon ^2}\right) r n_1 h_1\\&= -4 h_1^2 u_1 \frac{\mathrm{{d}}n_1}{\mathrm{{d}}\epsilon } -4 h_1 n_1 \frac{\mathrm{{d}}u_1}{\mathrm{{d}}\epsilon } +4r h_1^3 u_1 \left( \frac{\mathrm{{d}}n_1}{\mathrm{{d}}\epsilon }\right) ^2 -4r h_1^2 \frac{\mathrm{{d}}n_1}{\mathrm{{d}}\epsilon } \frac{\mathrm{{d}}u_1}{\mathrm{{d}}\epsilon }\\&\frac{\mathrm{{d}}^2n_1}{\mathrm{{d}}\epsilon ^2}+\frac{\mathrm{{d}}^2n_2}{\mathrm{{d}}\epsilon ^2} = \frac{g}{r h_1^2} \left( \frac{\mathrm{{d}}^2u_1}{\mathrm{{d}}\epsilon ^2}+\frac{\mathrm{{d}}^2u_2}{\mathrm{{d}}\epsilon ^2}\right) - \frac{4}{r} \left( 1- r h_1 \frac{\mathrm{{d}} n_1}{\mathrm{{d}}\epsilon } \right) \frac{\mathrm{{d}} n_1}{\mathrm{{d}}\epsilon }\\ \end{aligned} \end{aligned}$$

(18)

which implies

$$\begin{aligned} \begin{aligned}&\frac{\mathrm{{d}}^2u_1}{\mathrm{{d}}\epsilon ^2}+\frac{\mathrm{{d}}^2u_2}{\mathrm{{d}}\epsilon ^2} = \frac{1}{k_0} \left[ -4 h_1 \left( \frac{\mathrm{{d}} n_1}{\mathrm{{d}}\epsilon }\right) ^2 + \frac{4}{r} \frac{\mathrm{{d}} n_1}{\mathrm{{d}}\epsilon } -4 h_1 \left( n_1 +r h_1 \frac{\mathrm{{d}} n_1}{\mathrm{{d}}\epsilon } \right) \frac{\mathrm{{d}} u_1}{\mathrm{{d}}\epsilon }\right] \\&k_0 = \frac{g}{r h_1^2} (1+ r h_1^2 u_1) + r h_1 n_1>0.\\ \end{aligned} \end{aligned}$$

(19)

By differentiating each side of (15) on $\epsilon$ and letting $\epsilon =0$, we obtain

$$\begin{aligned} \begin{aligned}&\frac{\mathrm{{d}}^2N_1}{\mathrm{{d}}\epsilon ^2}+\frac{\mathrm{{d}}^2N_2}{\mathrm{{d}}\epsilon ^2} = \frac{2g }{r H_1^2} \frac{\mathrm{{d}}^2 Z}{\mathrm{{d}}\epsilon ^2} + +4 H_1 \left( \frac{\mathrm{{d}} N_1}{\mathrm{{d}}\epsilon }\right) ^2 - \frac{4}{r} \frac{\mathrm{{d}} N_1}{\mathrm{{d}}\epsilon } \\&- \frac{\mathrm{{d}}^2N_1}{\mathrm{{d}}\epsilon ^2} \left( 1+ r H_1^2 Z \right) -2 H_1^2 Z \frac{\mathrm{{d}} N_1}{\mathrm{{d}}\epsilon } +2r H_1^3 Z \left( \frac{\mathrm{{d}} N_1}{\mathrm{{d}}\epsilon }\right) ^2 -r H_1 N_1 \frac{\mathrm{{d}}^2 Z}{\mathrm{{d}}\epsilon ^2}=0\\&- \frac{\mathrm{{d}}^2N_2}{\mathrm{{d}}\epsilon ^2} \left( 1+ r H_2^2 Z \right) +2 H_2^2 Z \frac{\mathrm{{d}} N_2}{\mathrm{{d}}\epsilon } +2r H_2^3 Z \left( \frac{\mathrm{{d}} N_2}{\mathrm{{d}}\epsilon }\right) ^2 -r H_2 N_2 \frac{\mathrm{{d}}^2 Z}{\mathrm{{d}}\epsilon ^2}=0.\\ \end{aligned} \end{aligned}$$

(20)

By summing the second and third equations of (20), we obtain

$$\begin{aligned} -\left( \frac{\mathrm{{d}}^2N_1}{\mathrm{{d}}\epsilon ^2}+\frac{\mathrm{{d}}^2N_2}{\mathrm{{d}}\epsilon ^2}\right) \left( 1+ r H_1^2 Z\right) -4 H_1^2 Z \frac{\mathrm{{d}} N_1}{\mathrm{{d}}\epsilon } +4r H_1^3 Z \left( \frac{\mathrm{{d}} N_1}{\mathrm{{d}}\epsilon }\right) ^2 -2r H_1 N_1 \frac{\mathrm{{d}}^2Z}{d\epsilon ^2}=0.\nonumber \\ \end{aligned}$$

(21)

From the first equation of (20) and (21), we obtain

$$\begin{aligned} \frac{\mathrm{{d}}^2 (2Z)}{\mathrm{{d}}\epsilon ^2}= \frac{1}{k_0} \left[ -4 H_1 \left( \frac{\mathrm{{d}} N_1}{\mathrm{{d}}\epsilon }\right) ^2 + \frac{4}{r} \frac{\mathrm{{d}} N_1}{\mathrm{{d}}\epsilon }\right] . \end{aligned}$$

(22)

Let $\epsilon =0$. From (14), we have

$$\begin{aligned} \frac{\mathrm{{d}}u_1}{\mathrm{{d}}\epsilon } = \frac{\delta + n_1/(rh_1)}{r n_1 h_1 +(1+ r h_1^2 u_1) g/ (rh_1^2) }>0,~ n_1+ rh_1 \frac{\mathrm{{d}}n_1}{\mathrm{{d}}\epsilon } = \frac{g}{h_1 } \frac{\mathrm{{d}}u_1}{\mathrm{{d}}\epsilon } >0. \end{aligned}$$

From (14) and (16), we have

$$\begin{aligned} \frac{\mathrm{{d}}n_1}{\mathrm{{d}}\epsilon } = \frac{\delta - n_1 h_1 u_1 - r n_1 h_1 \frac{\mathrm{{d}}u_1}{\mathrm{{d}}\epsilon }}{1+ r h_1^2 u_1}<0,~~ \frac{\mathrm{{d}}N_1}{\mathrm{{d}}\epsilon } = \frac{\delta - N_1 H_1 Z }{1+ r H_1^2 Z }<0 \end{aligned}$$

which means $\mathrm{{d}}n_1/\mathrm{{d}}\epsilon< \mathrm{{d}}N_1/\mathrm{{d}}\epsilon <0$ by (13). Thus, from (13), (19) and (22), we obtain

$$\begin{aligned} \frac{\mathrm{{d}}^2 (2Z)}{\mathrm{{d}}\epsilon ^2} > \frac{\mathrm{{d}}^2u_1}{\mathrm{{d}}\epsilon ^2}+\frac{\mathrm{{d}}^2u_2}{\mathrm{{d}}\epsilon ^2} \end{aligned}$$

which implies $\frac{\mathrm{{d}}^2f}{\mathrm{{d}}\epsilon ^2}(0) >0.$

Since $f(0) =0, \frac{\mathrm{{d}}f}{\mathrm{{d}}\epsilon }(0) =0$ and $\frac{\mathrm{{d}}^2f}{\mathrm{{d}}\epsilon ^2}(0) >0,$ the function $f =f(\epsilon )$ is convex downward at $\epsilon =0$. Thus there exists $\epsilon _0 >0$ such that $f(\epsilon ) = T_1(\epsilon ) - T_0(\epsilon ) >0$ if $0< |\epsilon | < \epsilon _0$ and $T_1(\epsilon ) - T_0(\epsilon )$ is a monotonically increasing function of $|\epsilon |$. $\square$

Theorem 4.3 makes sense biologically. The result that $T_1(\epsilon ) - T_0(\epsilon )$ is a monotonically increasing function of $|\epsilon |$ means that the larger the difference between the growth rates, the higher the difference between $T_1$ and $T_0$, which is clearly observed in experiments (see Fig. 4 in Zhang et al. 2017).

4.2 Source–Sink Populations

This subsection considers source–sink populations in which the species cannot persist in one patch (the sink) without diffusion. We exhibit $T_1>T_0$ under conditions and show $T_3=T_2>T_1$. Let

$$\begin{aligned} r_i=r,~m_i=m,~g_i=g,\quad \sum _{i=1}^2 \left( \frac{rN_{0i} }{1+N_{0i} }-m\right) >0. \end{aligned}$$

(23)

Then a direct computation shows $\frac{ N_{01} + N_{02} }{2 }> \frac{m }{r-m }$. By Corollary 3.2 and a proof similar to that of Theorem 4.1 and Remark 4.2(i), we conclude the following result.

Theorem 4.4

Let (23) holds. Then $T_3 = T_2 >T_1$ and $T_2 >T_0$ in system (2) with source–sink populations.

Next we exhibit $T_1>T_0$ in source–sink populations. First, we demonstrate a threshold for $T_1>T_0$ under conditions (e.g., $N_{02} = \frac{m}{r-m}$). Let

$$\begin{aligned} N_{01} = N_0 + c \epsilon , \ N_{02} = N_0, \ r_1 = r+ \epsilon , \ r_2 = r, \ m_i=m,\ g_i=g, \ i=1,2 \end{aligned}$$

(24)

where $c>0, \epsilon \ge 0, N_0 = \frac{m}{r-m}.$

Note that $N_{01} > \frac{m}{r_1 -m}, N_{02} = \frac{m}{r_2 -m}.$ Assume $D=0$. By Theorem 2.3, patch 2 is a sink and patch 1 is a source with a steady-state $E^+( U_1^+, N_1^+)$ which satisfies

$$\begin{aligned} N_0 + c \epsilon -n_1 - \frac{(r + \epsilon ) n_1 u_1}{1 +n_1}=0,\quad \frac{(r + \epsilon ) n_1 }{1 +n_1} -m -g u_1 =0 \end{aligned}$$

(25)

where $n_1=n_1( \epsilon )$, $u_1=u_1( \epsilon )$.

Note that $\sum _{i=1}^2 (\frac{r_iN_{0i} }{1+N_{0i} }-m_i)>0$. By Corollary 3.2 and Theorems 3.3–3.4, system (2) has a stable positive equilibrium $P(U_1,N_1, U_2,N_2 )$, and the accumulation point ${{\bar{P}}}( Z,N_1, Z,N_2 )$ of the equilibria satisfies

$$\begin{aligned} \begin{aligned}&N_0 + c \epsilon -N_1 - \frac{(r + \epsilon ) N_1 Z}{1 +N_1}=0,\quad N_0 -N_2 - \frac{r N_2 Z}{1 +N_2} =0\\&\quad \frac{(r + \epsilon ) N_1 }{1 +N_1} + \frac{r N_2 }{1 +N_2} -2m -2g Z=0 \\ \end{aligned} \end{aligned}$$

(26)

where $N_i=N_i( \epsilon )$, $Z=Z( \epsilon )$ are differentiable on $\epsilon$ by the analyticity of (26), $i=1,2$. Then $T_1 = 2Z( \epsilon )$.

If $\epsilon = 0$, symmetry in Eqs. (25)–(26) implies

$$\begin{aligned} n_i( 0)=N_i( 0) =N_0, \ u_i( 0)=Z( 0)=0, \ i=1,2. \end{aligned}$$

(27)

If $\epsilon < 0$, then $N_0 + c \epsilon < m/(r+ \epsilon -m )$, which implies that $n_i( \epsilon )=N_i( \epsilon ) =N_0, u_i( \epsilon )=Z( \epsilon )=0, i=1,2$. Denote

$$\begin{aligned} c_0= \frac{N_1 (g+ r^2 N_1 H_1^3 + r^2 N_1^2 H_1^3 ) }{ r N_1 H_1 (2g + r^2 N_1 H_1^3)}|_{N_1=N_0}. \end{aligned}$$

Theorem 4.5

Let (24) hold. Then there exists $\epsilon _0 >0$ such that when $0< \epsilon < \epsilon _0$, we have $T_1 >T_0$ if $0< c <c_0$, and $T_1 < T_0$ if $c >c_0$.

Proof

Let $f(\epsilon ) = T_1(\epsilon ) - T_0(\epsilon )= 2Z(\epsilon ) -u_1(\epsilon ).$ From (27), we have $f(0) =0$.

We show $\frac{\mathrm{{d}}f}{\mathrm{{d}}\epsilon }(0) =0$ as follows. Denote $h_i=1/(1 +n_i), i=1,2.$ By differentiating each side of (25) on $\epsilon$, we obtain

$$\begin{aligned} \begin{aligned}&c - \frac{\mathrm{{d}}n_1}{\mathrm{{d}}\epsilon } - n_1 h_1 u_1 - (r + \epsilon ) h_1^2 u_1 \frac{\mathrm{{d}}n_1}{\mathrm{{d}}\epsilon } - (r + \epsilon ) n_1 h_1 \frac{\mathrm{{d}}u_1}{\mathrm{{d}}\epsilon }=0\\&n_1 h_1 + (r + \epsilon ) h_1^2 \frac{\mathrm{{d}}n_1}{\mathrm{{d}}\epsilon } - g \frac{\mathrm{{d}}u_1}{\mathrm{{d}}\epsilon }=0\\ \end{aligned} \end{aligned}$$

(28)

which implies

$$\begin{aligned} \frac{\mathrm{{d}}n_1}{\mathrm{{d}}\epsilon }(0) = c - r n_1 h_1 \frac{\mathrm{{d}}u_1}{\mathrm{{d}}\epsilon }(0), \ \frac{\mathrm{{d}}u_1}{\mathrm{{d}}\epsilon }(0) = \frac{ c r h_1^2 + h_1 n_1}{g + r^2 n_1 h_1^3 }|_{\epsilon =0} >0. \end{aligned}$$

(29)

Denote $H_i=1/(1 +N_i), i=1,2.$ By differentiating each side of (26) on $\epsilon$, we obtain

$$\begin{aligned} \begin{aligned}&c - \frac{\mathrm{{d}}N_1}{\mathrm{{d}}\epsilon } - N_1 H_1 U_1 - (r + \epsilon ) H_1^2 U_1 \frac{\mathrm{{d}}N_1}{\mathrm{{d}}\epsilon } - (r + \epsilon ) N_1 H_1 \frac{\mathrm{{d}}Z}{\mathrm{{d}}\epsilon }=0\\&- \frac{\mathrm{{d}}N_2}{\mathrm{{d}}\epsilon } - r H_2^2 U_2 \frac{\mathrm{{d}}N_2}{\mathrm{{d}}\epsilon } - r N_2 H_2 \frac{\mathrm{{d}}Z}{\mathrm{{d}}\epsilon }=0\\&N_1 H_1 + (r + \epsilon ) H_1^2 \frac{\mathrm{{d}}N_1}{\mathrm{{d}}\epsilon } + r H_2^2 \frac{\mathrm{{d}}N_2}{\mathrm{{d}}\epsilon } - 2g \frac{\mathrm{{d}}Z}{\mathrm{{d}}\epsilon }=0.\\ \end{aligned} \end{aligned}$$

(30)

Let $\epsilon =0$ in (30). Then we have

$$\begin{aligned} \begin{aligned}&\frac{\mathrm{{d}}N_1}{\mathrm{{d}}\epsilon }(0) = c- r N_1 H_1 \frac{\mathrm{{d}}Z}{\mathrm{{d}}\epsilon }(0), \ \frac{\mathrm{{d}}N_2}{\mathrm{{d}}\epsilon }(0) = - r N_1 H_1 \frac{\mathrm{{d}}Z}{\mathrm{{d}}\epsilon }(0)\\&\frac{\mathrm{{d}}(2Z)}{\mathrm{{d}}\epsilon }(0) = \frac{\mathrm{{d}}u_1}{\mathrm{{d}}\epsilon }(0) \end{aligned} \end{aligned}$$

(31)

which implies $\frac{\mathrm{{d}}f}{\mathrm{{d}}\epsilon }(0)=0$.

We show $\frac{\mathrm{{d}}^2f}{\mathrm{{d}}\epsilon ^2}(0+) >0$ as follows. By differentiating each side of (25) on $\epsilon$ and letting $\epsilon =0$, we obtain $u_1(0)=0$ and

$$\begin{aligned} \begin{aligned}&- \frac{\mathrm{{d}}^2n_1}{\mathrm{{d}}\epsilon ^2} - 2 n_1 h_1 \frac{\mathrm{{d}}u_1}{\mathrm{{d}}\epsilon } - 2 r h_1^2 \frac{\mathrm{{d}}n_1}{\mathrm{{d}}\epsilon } \frac{\mathrm{{d}}u_1}{\mathrm{{d}}\epsilon } - r n_1 h_1 \frac{\mathrm{{d}}^2u_1}{\mathrm{{d}}\epsilon ^2}=0 \\&2 h_1^2 \frac{\mathrm{{d}}n_1}{\mathrm{{d}}\epsilon } -2r h_1^3 \left( \frac{\mathrm{{d}} n_1}{\mathrm{{d}}\epsilon }\right) ^2 + r h_1^2 \frac{\mathrm{{d}}^2n_1}{\mathrm{{d}}\epsilon ^2} -g \frac{\mathrm{{d}}^2u_1}{\mathrm{{d}}\epsilon ^2} =0 \\ \end{aligned} \end{aligned}$$

so that

$$\begin{aligned} \begin{aligned} \frac{\mathrm{{d}}^2n_1}{\mathrm{{d}}\epsilon ^2}&= - 2 n_1 h_1 \frac{\mathrm{{d}}u_1}{\mathrm{{d}}\epsilon } - 2 r h_1^2 \frac{\mathrm{{d}}n_1}{\mathrm{{d}}\epsilon } \frac{\mathrm{{d}}u_1}{\mathrm{{d}}\epsilon } - r n_1 h_1 \frac{\mathrm{{d}}^2u_1}{\mathrm{{d}}\epsilon ^2} \\ \frac{\mathrm{{d}}^2u_1}{\mathrm{{d}}\epsilon ^2}&= \frac{1}{C} \left[ 2 h_1^2 \frac{\mathrm{{d}}n_1}{\mathrm{{d}}\epsilon } - 2r h_1^3 \left( \frac{\mathrm{{d}} n_1}{\mathrm{{d}}\epsilon }\right) ^2 - 2r h_1^3 \left( n_1 +r h_1 \frac{\mathrm{{d}}n_1}{\mathrm{{d}}\epsilon } \right) \frac{\mathrm{{d}}u_1}{\mathrm{{d}}\epsilon } \right] \end{aligned} \end{aligned}$$

where $C = g + r^2 n_1 h_1^3$.

By differentiating each side of (26) on $\epsilon$ and letting $\epsilon =0$, we obtain

$$\begin{aligned} \begin{aligned}&- \frac{\mathrm{{d}}^2N_1}{\mathrm{{d}}\epsilon ^2} - 2 N_1 H_1 \frac{\mathrm{{d}}Z}{\mathrm{{d}}\epsilon } - 2 r H_1^2 \frac{\mathrm{{d}}N_1}{\mathrm{{d}}\epsilon } \frac{\mathrm{{d}}Z}{\mathrm{{d}}\epsilon } - r N_1 H_1 \frac{\mathrm{{d}}^2Z}{\mathrm{{d}}\epsilon ^2} =0\\&- \frac{\mathrm{{d}}^2N_2}{\mathrm{{d}}\epsilon ^2} - 2 r H_2^2 \frac{\mathrm{{d}}N_2}{\mathrm{{d}}\epsilon } \frac{\mathrm{{d}}Z}{\mathrm{{d}}\epsilon } - r N_2 H_2 \frac{\mathrm{{d}}^2Z}{\mathrm{{d}}\epsilon ^2} =0\\&2 H_1^2 \frac{\mathrm{{d}}N_1}{\mathrm{{d}}\epsilon } - 2r H_1^3 \left[ \left( \frac{\mathrm{{d}} N_1}{\mathrm{{d}}\epsilon }\right) ^2 + \left( \frac{\mathrm{{d}} N_2}{\mathrm{{d}}\epsilon }\right) ^2 \right] + r H_1^2 \left[ \frac{\mathrm{{d}}^2N_1}{\mathrm{{d}}\epsilon ^2} +\frac{\mathrm{{d}}^2N_2}{\mathrm{{d}}\epsilon ^2}\right] -2g \frac{\mathrm{{d}}^2Z}{\mathrm{{d}}\epsilon ^2} =0\\ \end{aligned} \end{aligned}$$

(32)

so that

$$\begin{aligned} \begin{aligned} \frac{\mathrm{{d}}^2N_1}{\mathrm{{d}}\epsilon ^2} +\frac{\mathrm{{d}}^2N_2}{\mathrm{{d}}\epsilon ^2}&= - 2 r N_1 H_1 \frac{\mathrm{{d}}^2Z}{\mathrm{{d}}\epsilon ^2} - 2 N_1 H_1 \frac{\mathrm{{d}}Z}{\mathrm{{d}}\epsilon } - 2 r H_1^2 \frac{\mathrm{{d}}Z}{\mathrm{{d}}\epsilon } \left( \frac{\mathrm{{d}}N_1}{\mathrm{{d}}\epsilon } +\frac{\mathrm{{d}}N_2}{\mathrm{{d}}\epsilon }\right) \\ \frac{\mathrm{{d}}^2\left( 2Z\right) }{\mathrm{{d}}\epsilon ^2}&= \frac{1}{C} \left\{ 2 H_1^2 \frac{\mathrm{{d}}N_1}{\mathrm{{d}}\epsilon } - 2r H_1^3 \left[ \left( \frac{\mathrm{{d}} N_1}{\mathrm{{d}}\epsilon }\right) ^2 + \left( \frac{\mathrm{{d}} N_2}{\mathrm{{d}}\epsilon }\right) ^2\right] \right. \\&\quad \left. -\, 2r H_1^3 \left[ N_1 +r H_1 \left( \frac{\mathrm{{d}}N_1}{\mathrm{{d}}\epsilon } +\frac{\mathrm{{d}}N_2}{\mathrm{{d}}\epsilon }\right) \right] \frac{\mathrm{{d}}Z}{\mathrm{{d}}\epsilon } \right\} . \end{aligned} \end{aligned}$$

(33)

From (31), we have

$$\begin{aligned} \frac{\mathrm{{d}}N_1}{\mathrm{{d}}\epsilon } +\frac{\mathrm{{d}}N_2}{\mathrm{{d}}\epsilon } = c - 2r N_1 H_1 \frac{\mathrm{{d}}Z}{\mathrm{{d}}\epsilon } = c - r n_1 h_1 \frac{\mathrm{{d}}u_1}{\mathrm{{d}}\epsilon }. \end{aligned}$$

A direct computation shows that

$$\begin{aligned} \begin{aligned} \frac{\mathrm{{d}}^2f }{\mathrm{{d}}\epsilon ^2}(0+)&= \frac{\mathrm{{d}}^2(2Z)}{\mathrm{{d}}\epsilon ^2}(0+) - \frac{\mathrm{{d}}^2u_1}{\mathrm{{d}}\epsilon ^2}(0+)\\&= \frac{2 r^2 N_1 H_1^4 (2g + r^2 N_1 H_1^3) }{C} (c_0-c) \frac{\mathrm{{d}}Z}{\mathrm{{d}}\epsilon } |_{\epsilon =0},\\ \end{aligned} \end{aligned}$$

(34)

Since $f(0) =0, \frac{\mathrm{{d}}f}{\mathrm{{d}}\epsilon }(0) =0$ and $\frac{\mathrm{{d}}^2f}{\mathrm{{d}}\epsilon ^2}(0+) >0$ if $c<c_0$, the function $f =f(\epsilon )$ is convex downward if $\epsilon \ge 0$. Thus there exists $\epsilon _{01} >0$ such that $f(\epsilon ) = T_1(\epsilon ) - T_0(\epsilon ) >0$ if $0< \epsilon < \epsilon _{01}$.

Similarly, there exists $\epsilon _{02} >0$ such that $f(\epsilon ) = T_1(\epsilon ) - T_0(\epsilon ) <0$ if $0< \epsilon < \epsilon _{02} , c > c _0$, which implies $T_1 < T_0$. Let $\epsilon _0 =\min \{\epsilon _{01},\epsilon _{02} \}$, then the proof is completed. $\square$

Second, we exhibit $T_1>T_0$ under conditions (e.g., $N_{02} < \frac{m}{r-m}$). Let

$$\begin{aligned} N_{01}=N_0+ c \epsilon , \ N_{02}=N_0- c \epsilon , \ r_1 = r + \epsilon , \ r_2 = r - \epsilon , \ m_i=m, \ g_i=g, \ i=1,2 \end{aligned}$$

(35)

where $r>m, N_0 = \frac{m}{r-m}, c \ge 0$.

Theorem 4.6

Let (35) hold. Let $c < {{\bar{c}}}_0 =\frac{r N_0^2 H_1^2 }{2g + r^2 N_0 H_1^3}, H_1 =\frac{1}{1+ N_0}$. Then there exists $\epsilon _0 >0$ such that if $0< |\epsilon | < \epsilon _0$, then $T_1(\epsilon ) >T_0(\epsilon )$, and $T_1(\epsilon ) - T_0(\epsilon )$ is a monotonically increasing function of $|\epsilon |$.

Proof

When we regard c as $\delta$ in the proof of Theorem 4.3, we obtain the proof of $f(0) = \frac{\mathrm{{d}}f }{ \mathrm{{d}} \epsilon }(0)=0$. Recall $u_i(0) = Z(0)=0$ if $\epsilon =0$. A direct computation shows

$$\begin{aligned} \frac{\mathrm{{d}}u_1}{\mathrm{{d}}\epsilon } |_{\epsilon =0}= \frac{r c H_1^2 + N_0 H_1 }{g + r^2 N_0 H_1^3}. \end{aligned}$$

Then from $c < {{\bar{c}}}_0$, we obtain $\frac{\mathrm{{d}}^2f }{ \mathrm{{d}} \epsilon ^2 } (0)>0$ by a proof similar to that of Theorem 4.3. $\square$

5 Discussion

In this paper, we demonstrate existence of stable positive equilibria in a two-patch system with diffusion. Limit of the equilibrium exhibits that homogeneously distributed resources support higher carrying capacity ($T_3$ and $T_2$) than in heterogeneously distributed resources with diffusion ($T_1$), which can support higher carrying capacity than heterogeneously distributed resources without diffusion ($T_0$). These results coincide with experimental observations by Zhang et al. (2017) and extend previous theory to consumer-resource systems with external resource input.

The biological reason for $T_3=T_2$ is homogeneous environments. Indeed, in homogeneously distributed resources, there is no difference between the two patches, which implies that there is no difference between diffusion and non-diffusion, such that $T_3=T_2$ as shown in Theorem 4.1(i). The reason for $T_2>T_1$ in Theorem 4.1(i) is resource-wasting. Recall $N_{01}=N_0+\epsilon , N_{02} = N_0- \epsilon , r_1=r_2$ with $\epsilon >0$. Assume that the consumer approaches carrying capacities $U_i^+$ in each patch without diffusion. From (9), we have $U_2^+ < U_1^+$. Then assume that diffusion D occurs: $D U_2^+$ (resp. $D U_1^+$) individuals are transferred to patch 1 (resp. patch 2) with $D U_2^+ < D U_1^+$. Because $r_1 =r_2$, the larger resource $N_{01}$ in patch 1 is wasted since $D U_2^+ < D U_1^+$, such that $T_1<T_2$. Similar discussions can be given for $T_2>T_0$ in Theorem 4.1(ii) and $T_3=T_2>T_0$ in Corollary 4.4.

The result of $T_1>T_0$ in Theorem 4.5 holds if

$$\begin{aligned} N_{01}>N_{02}, ~~\frac{r_1-r_2}{N_{01} -N_{02}} >\frac{1}{c_0} \end{aligned}$$

(36)

which means that for one increased unit of nutrient input in patch 1 (i.e., $N_{01} -N_{02}=1$), the increased growth rate in the patch should be larger than a certain value (i.e., $r_1-r_2 >1/c_0$). Thus, condition (36) exhibits that there should be a positive relationship between nutrient input, $N_0$, and growth rate, r, for $T_1 > T_0$, which provides an insight different from that in (1) and may be useful in testing systems with resources.

If $r_1-r_2 < 1/c_0$, then $T_1<T_0$ by Theorem 4.5. On the other hand, the condition given by Freedman and Waltman (1977) can be written as

$$\begin{aligned} K_1>K_2, \quad \frac{r_1-r_2}{K_1 -K_2} > \frac{1}{{{\bar{c}}}_0} \end{aligned}$$

(37)

where ${{\bar{c}}}_0 = K_2/r_2$. Thus, both of (36) and (37) mean that the larger the nutrient input (resp. the carrying capacity) in a patch, the higher the growth rate should be. That is, there is a positive relationship between resource input and growth rate since carrying capacity in a homogeneous environment is determined by resource. However, since condition in (36) is different from (37) and is more testable, it provides new insight. The biological reason for $T_1>T_0$ in Theorem 4.5 is explained as follows. Recall $N_{01}=N_0+c \epsilon , N_{02} = N_0,$$r_1=r+ \epsilon , r_2=r$ with $\epsilon>0, c>0, N_0 =m/(r-m)$. Assume that the consumer approaches the carrying capacity $U_i^+$ in each patch without diffusion. From Theorem 2.3, we have $0=U_2^+ < U_1^+$. Then assume that diffusion D occurs: $D U_2^+$ (resp. $D U_1^+$) individuals are transferred to patch 1 (resp. patch 2) with $0=D U_2^+ < D U_1^+$. Since $r_1$ is high, subpopulation 1 rebounds quickly to diffusion losses and subpopulation 2 remains “overfilled,” such that $T_1>T_0$. This is confirmed by experimental observations that the “extra individuals” reside in the low nutrient wells. However, when $r_1$ is not high, the increase of $D U_2^+$ ($<D U_1^+$) in patch 1 cannot compensate the loss of $D U_1^+$ in patch 2 where $r_2$ is low, such that $T_1<T_0$. Similar discussions can be given for $T_1>T_0$ (resp. $T_1<T_0$) in source–sink populations in Theorem 4.3 and the extinction of consumer because of diffusion in Theorem 3.1(i)(iii).

Theorem 3.1 displays new prediction that increasing diffusion rate of consumer could change its persistence to extinction in the same-resource environment. As shown in Theorem 3.1(i)(iii), the consumer cannot persist in patch 2 with non-diffusing. If the growth rates are intermediate such that $r_i>m_i$ and $\sum _{i=1}^2 (\frac{r_iN_{0i} }{1+N_{0i} }-m_i)<0$, the consumer persists in both patches when the diffusion rate is small (i.e., $0<D<{{\bar{D}}}$), while it goes to extinction when the diffusion is large (i.e., $D>{{\bar{D}}}$). The reason is that when the diffusion rate is small, subpopulation 1 has sufficient time to rebound to diffusion losses, which results in the persistence. When the diffusion rate is large, the consumer goes to extinction because of the sink patch 2.

It is worth mentioning that the analysis method in this paper can be applied to the multiple-patch model though our analysis uses the simplest two-patch system. The comparison of carrying capacities in the n-patch model is left to be studied in the future.