A Mathematical Model of Fluid Transport in an Accurate Reconstruction of Parotid Acinar Cells

Abstract

Salivary gland acinar cells use the calcium (${\mathrm{Ca}}^{2+}$) ion as a signalling messenger to regulate a diverse range of intracellular processes, including the secretion of primary saliva. Although the underlying mechanisms responsible for saliva secretion are reasonably well understood, the precise role played by spatially heterogeneous intracellular ${\mathrm{Ca}}^{2+}$ signalling in these cells remains uncertain. In this study, we use a mathematical model, based on new and unpublished experimental data from parotid acinar cells (measured in excised lobules of mouse parotid gland), to investigate how the structure of the cell and the spatio-temporal properties of ${\mathrm{Ca}}^{2+}$ signalling influence the production of primary saliva. We combine a new ${\mathrm{Ca}}^{2+}$ signalling model [described in detail in a companion paper: Pages et al. in Bull Math Biol 2018, submitted] with an existing secretion model (Vera-Sigüenza et al. in Bull Math Biol 80:255–282, 2018. https://doi.org/10.1007/s11538-017-0370-6) and solve the resultant model in an anatomically accurate three-dimensional cell. Our study yields three principal results. Firstly, we show that spatial heterogeneities of ${\mathrm{Ca}}^{2+}$ concentration in either the apical or basal regions of the cell have no significant effect on the rate of primary saliva secretion. Secondly, in agreement with previous work (Palk et al., in J Theor Biol 305:45–53, 2012. https://doi.org/10.1016/j.jtbi.2012.04.009) we show that the frequency of ${\mathrm{Ca}}^{2+}$ oscillation has no significant effect on the rate of primary saliva secretion, which is determined almost entirely by the mean (over time) of the apical and basal $[{\mathrm{Ca}}^{2+}]$. Thirdly, it is possible to model the rate of primary saliva secretion as a quasi-steady-state function of the cytosolic $[{\mathrm{Ca}}^{2+}]$ averaged over the entire cell when modelling the flow rate is the only interest, thus ignoring all the dynamic complexity not only of the fluid secretion mechanism but also of the intracellular heterogeneity of $[{\mathrm{Ca}}^{2+}]_i$. Taken together, our results demonstrate that an accurate multiscale model of primary saliva secretion from a single acinar cell can be constructed by ignoring the vast majority of the spatial and temporal complexity of the underlying mechanisms.

1 Introduction

In most mammals, the majority of saliva is secreted by three principal pairs of exocrine glands: the parotid, the sub-mandibular, and the sub-lingual. Clusters of salivary epithelia, called acini, secrete a primary fluid into a collecting region called the acinar lumen. The collected secretion is low in potassium (${\mathrm{K}}^+$), but its sodium (${\mathrm{Na}}^+$) and chloride (${\mathrm{Cl}}^-$) concentrations are similar to those in plasma (Martin and Young 1971). Along with evidence regarding the inhomogeneous distribution of plasma membrane (PM) transporters, channels, and exchangers in water-transporting epithelia, these observations led to the construction of the currently accepted secretion model (Silva et al. 1977). In this model, basolateral PM mechanisms accumulate ${\mathrm{Cl}}^-$ to levels well above its electrochemical equilibrium. Following an increase in the intracellular concentration of calcium ($[{\mathrm{Ca}}^{2+}]_i$), a ${\mathrm{Cl}}^-$ efflux through apical ${\mathrm{Ca}}^{2+}$-dependent ${\mathrm{Cl}}^-$ channels generates a transepithelial osmotic gradient. Water follows this gradient by osmosis.

${\mathrm{Cl}}^-$ uptake via basolateral ${\mathrm{Na}}^+$-${\mathrm{K}}^+$-2${\mathrm{Cl}}^-$ cotransporters (Nkcc1) is the major driver of fluid secretion in acinar cells, and its inhibition causes an approximate 70$\%$ decrease in the rate of saliva secretion (Evans et al. 2000). The residual secretion is bicarbonate (${\mathrm{HCO}}_3^-$)-dependent and involves two ${\mathrm{Na}}^+$/H$^+$ (Nhe1) paired ${\mathrm{Cl}}^-$/${\mathrm{HCO}}_3^-$ anion exchangers: the anion exchanger 2 (Ae2) and the anion exchanger 4 (Ae4) (Melvin et al. 2005). However, recent studies by Peña-Münzenmayer et al. (2015) revealed that only the Ae4 is relevant in the secretory process. Experiments on Ae4 knockout mice exhibited a decreased gland fluid secretion ($\sim$ 30$\%$ of the control fluid flow rate), whereas mice lacking Ae2 expression displayed an unchanged secretion rate. Sigüenza et al. (2018) developed a mathematical model, based on Palk et al. (2010), that aimed to understand the mechanisms behind these results. The model supports the observations by Peña-Münzenmayer et al. (2015) and suggests that the Ae4’s cotransport of monovalent cations is likely to be important in establishing the osmotic gradient necessary for optimal transepithelial fluid movement.

The model of Sigüenza et al. (2018) assumes that $[{\mathrm{Ca}}^{2+}]_i$ is a given function of time (for example, a given constant), not a dependent variable. Although this simplifies the computations, there is a great deal of evidence that ${\mathrm{Ca}}^{2+}$ spatio-temporal phenomena are involved in water transport (Foskett 1990; Tanimura 2009; Palk et al. 2012). In particular, it is well known that ${\mathrm{Ca}}^{2+}$ travels in waves from apical to basolateral regions of the cell (Foskett and Melvin 1989; Foskett et al. 1991). These encode a large amount of signalling information that a constant, and homogeneous, $[{\mathrm{Ca}}^{2+}]_i$ does not. Variations in wave amplitude, mean concentration, frequency, and also wave speed serve as potential modifiers of saliva secretion.

In this study, we investigate how the three-dimensional structure of a salivary acinar cell and the spatio-temporal heterogeneities of ${\mathrm{Ca}}^{2+}$ signalling affect transepithelial water transport. To do so, we use a partial differential equation model of ${\mathrm{Ca}}^{2+}$ signalling to drive fluid secretion on seven anatomically accurate three-dimensional cells consisting of individual volumetric tetrahedral meshes. The details of the ${\mathrm{Ca}}^{2+}$ signalling model, and construction of the meshes, are presented in a companion paper by Pages et al. (2018). Here, we demonstrate that given physiologically accurate spatio-temporal ${\mathrm{Ca}}^{2+}$ responses to agonist-induced stimulation, each acinar cell will secrete primary saliva at the correct physiological rate. In addition, we show that the model reproduces critical experimental data, including the expected changes in cellular volume and the concentrations of the ionic species involved in fluid secretion such as ${\mathrm{Cl}}^-$, ${\mathrm{Na}}^+$, ${\mathrm{K}}^+$, ${\mathrm{HCO}}_3^-$ and H$^+$. We conclude with a brief discussion on how many of the complexities of a spatial ${\mathrm{Ca}}^{2+}$ signalling model are unnecessary in the modelling of primary secretion by these epithelia.

Fig. 1

A parotid acinar cell depicted by a tetrahedral mesh. Two images of the same cell are shown. The cell is rotated to exhibit the apical (red) and basal (blue) regions of the plasma membrane (PM). The non-coloured triangular faces represent its lateral portion. The image reflects the hallmark pyramidal shape seen in several water secreting epithelia. Details of the mesh construction can be found in Pages et al. (2018) (Color figure online)

2 Experimental Data and Cell Reconstruction

The model presented in this study uses a mesh constructed by Pages et al. (2018) and described in detail there. Briefly, it is based on 31 confocal microscopy images of parotid gland epithelia at 1024 by 1024 pixels, with a resolution of 0.069 $\upmu$m per pixel and a stack spacing of 0.8 $\upmu$m. These consist of fluorescent staining of the apical ${\mathrm{Ca}}^{2+}$-dependent ${\mathrm{Cl}}^-$ channels, (TMeM16a), and NaK-ATPases as a way to visualise apical and basolateral plasma membranes of acinar cells. Using these data, a mesh was created of a cluster of seven cells where every cell touches at least one or more other cells. Here, we present in detail the results of our model applied to one of these cells (Fig. 1). Refer to the supporting material for the results in all seven cells.

The ${\mathrm{Ca}}^{2+}$ dynamics model is based on previously unpublished data from excised parotid gland lobules stimulated by 300 nM Carbachol (CCh), as described in Pages et al. (2018) and in Sect. 3.3.

3 Secretion Model

3.1 Assumptions

We use the mathematical model of primary secretion developed by Sigüenza et al. (2018). Here, the interstitial and luminal compartments are modelled as constant volume sub-domains. In particular, the interstitial space is assumed to be an infinite ionic bath (i.e. all its ionic concentrations are constant). Furthermore, with the exception of $[{\mathrm{Ca}}^{2+}]_i$, the ionic species are assumed well-stirred at all times throughout the three compartments. This is because the intracellular diffusion of the ions involved in fluid secretion occurs relatively fast compared to the time scale in which water travels across the cell and its plasma membrane (from interstitium to lumen) (Swietach et al. 2003).

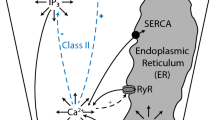
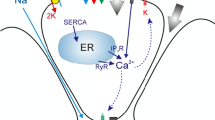
Saliva flow is initiated, from rest, by an agonist-induced $[{\mathrm{Ca}}^{2+}]_i$ increase that causes the opening of apical ${\mathrm{Ca}}^{2+}$-activated ${\mathrm{Cl}}^-$ channels (TMem16a) in order to establish a ${\mathrm{Cl}}^-$ efflux into the acinar lumen. This is maintained by a compensating ${\mathrm{K}}^+$ current through the basolateral ${\mathrm{Ca}}^{2+}$-activated ${\mathrm{K}}^+$ channels (BK/IK), along with a paracellular cation current. Consequently, an osmotic gradient from the interstitium, through the cell, to the lumen is created, enabling the flow of water in the secretory direction (see Fig. 2). In our model, the ${\mathrm{Ca}}^{2+}$-activated ${\mathrm{Cl}}^-$ channels are restricted to the apical PM (Young 1968), and the ${\mathrm{Ca}}^{2+}$-activated ${\mathrm{K}}^+$ channels are restricted to the basolateral PM. Although there is evidence for a limited number of ${\mathrm{Ca}}^{2+}$-activated ${\mathrm{K}}^+$ channels on the apical PM considerable uncertainty as to the relative distribution between apical and basolateral PM exists, so for simplicity we choose to avoid this question entirely (Almassy et al. 2012). This problem has been addressed in previous studies (Almássy et al. 2018; Palk et al. 2010). The distributions of all pumps, transporters, and exchangers in their respective PM portions are assumed to be homogeneous (see Fig. 2). As a consequence, the PM electric potentials, basolateral and apical alike, are also homogeneous. Finally, as a simplification, we do not include the basolateral anion exchanger 2 (Ae2). This is because the exchanger has been shown to be less important for fluid secretion (Peña-Münzenmayer et al. 2015; Sigüenza et al. 2018).

Fig. 2

Schematic diagram of the secretion model. Basolateral Nkcc1, NaK-ATPase, Ae4, Nhe1, and the ${\mathrm{Ca}}^{2+}$-activated ${\mathrm{K}}^+$ channels (K$_{\text {Ca}}$) are in charge of accumulating ${\mathrm{Cl}}^-$ in the cytoplasm. Opposite to these, the apical PM is equipped with ${\mathrm{Ca}}^{2+}$-activated ${\mathrm{Cl}}^-$ channels (Cl$_{\text {Ca}}$) whose task is to extrude the accumulated ${\mathrm{Cl}}^-$. Both apical and basolateral plasma membranes are permeable to water, which follows the osmotic gradient created by the transepithelial passage of ${\mathrm{Cl}}^-$ into the lumen. In this model, there are paracellular ${\mathrm{K}}^+$ and ${\mathrm{Na}}^+$ currents along with a paracellular water flow (Sigüenza et al. 2018) (Color figure online)

3.2 Equations

We introduce the subscripts, e, i, and l to denote, respectively, the interstitial, intracellular, and luminal compartments. The cellular PM fluxes are denoted by j, and each flux is represented by a sub-model based on experimental data (where possible) and/or previous models. To take the three-dimensional structure of the cell into account requires only a small modification from the previous model of Sigüenza et al. (2018). All the ions, with the exception of ${\mathrm{Ca}}^{2+}$, which is treated in detail in a companion paper (Pages et al. 2018) are assumed to be spatially homogeneous. Thus, conservation gives, for ${\mathrm{Cl}}^-$, say,

$$\begin{aligned} \frac{\text {d} ( [{\mathrm{Cl}}^-]_i\omega )}{\text {d}t} = \int _{\partial \varOmega _b} \Bigg ( 2j_{\text {Nkcc1}} + j_{\text {Ae4}} \Bigg ) dS - \int _{\partial \varOmega _a} j_{\text {Cl}} \ \text {d}S, \end{aligned}$$

where $j_{\text {Nkcc1}}$ and $j_{\text {Ae4}}$ are the molar fluxes of ${\mathrm{Cl}}^-$ (with units of amol/$\mu \text {m}^2$ s) through the basolateral PM ($\partial \varOmega _b$) and $j_{\text {Cl}}$ the molar flux through the apical PM ($\partial \varOmega _a$) ${\mathrm{Ca}}^{2+}$-activated ${\mathrm{Cl}}^-$ channels. Performing the surface integrals and using the product rule, we obtain:

$$\begin{aligned} \frac{\text {d} \Big ([{\mathrm{Cl}}^-]_i\Big )}{\text {d}t} = \frac{S_b}{\omega _i} \ 2 J_{\text {Nkcc1}} + \frac{S_b}{\omega _i} \ J_{\text {Ae4}} - \frac{1}{\omega _i} \int _{\partial \varOmega _a} j_{\text {Cl}} \ \text {d}S - \frac{\text {d}\omega _i}{\text {d}t} \frac{[{\mathrm{Cl}}^-]_i}{\omega _i}, \end{aligned}$$

(1)

where $S_b$ is the surface area of the basolateral PM. Note that the integral over the basolateral PM disappears, as these fluxes do not depend on ${\mathrm{Ca}}^{2+}$. However, the integral over the apical membrane cannot be similarly reduced. This is because the apical ${\mathrm{Cl}}^-$ flux term depends on ${\mathrm{Ca}}^{2+}$, which is spatially heterogeneous.

After performing the respective integrals, Eq. (1) describes how the intracellular ${\mathrm{Cl}}^-$ concentration changes over time (in units of mM/sec). The integral for the apical PM ${\mathrm{Cl}}^-$ flux term is described in more detail in Sect. 3.3. The volume’s ($\omega _i$) rate of change with respect to time is given by the difference between basolateral and apical PM water fluxes ($J^w$) through aquaporins (PM water-selective channels):

$$\begin{aligned} \frac{\text {d} \omega _i}{\text {d}t} = J_a^w - J_b^w. \end{aligned}$$

(2)

The luminal concentration equation is derived similarly. However, $\omega _l$ (the luminal volume) is kept constant, and using conservation laws the water flux out of the lumen is given by,

$$\begin{aligned} J^w_{\text {out}} = J^w_a + J^w_t \end{aligned}$$

(3)

where $J^w_t$ is the paracellular water flux through the tight junctions. Hence,

$$\begin{aligned} \frac{\text {d} \Big ([{\mathrm{Cl}}^-]_l\Big )}{\text {d}t} = \frac{1}{ \omega _l} \int _{\partial \varOmega _a} j_{\text {Cl}} \ \text {d}S - J^w_{\text {out}} \frac{[{\mathrm{Cl}}^-]_l}{\omega _l}. \end{aligned}$$

(4)

Following this approach, we obtain the following system of ordinary differential equations:

$$\begin{aligned}&\omega _l \frac{\text {d}[{\mathrm{Na}}^+]_l}{\text {d}t} = J^t_{Na} - J^w_{\text {out}} [{\mathrm{Na}}^+]_l, \end{aligned}$$

(5)

$$\begin{aligned}&\omega _l \frac{\text {d}[{\mathrm{K}}^+]_l}{\text {d}t} = J^t_{K} - J^w_{\text {out}} [{\mathrm{K}}^+]_l,\end{aligned}$$

(6)

$$\begin{aligned}&\omega _l \frac{\text {d}[{\mathrm{Cl}}^-]_l}{\text {d}t} = \int _{\partial \varOmega _a} j_{\text {Cl}} \ \text {d}S - J^w_{\text {out}} [{\mathrm{Cl}}^-]_l,\end{aligned}$$

(7)

$$\begin{aligned}&\frac{\text {d} \omega _i}{\text {d}t} = J^w_b - J^w_a,\end{aligned}$$

(8)

$$\begin{aligned}&\frac{ \text {d}\Big ([{\mathrm{Na}}^+]_i\omega _i\Big )}{\text {d}t} = S_b \Bigg ( J_{\text {Nkcc1}} - 3 J_{\text {NaK}} + J_{\text {Nhe1}} - J_{\text {Ae4}} \Bigg ),\end{aligned}$$

(9)

$$\begin{aligned}&\frac{\text {d}\Big ([{\mathrm{K}}^+]_i\omega _i \Big )}{\text {d}t} = S_b \Bigg ( J_{\text {Nkcc1}} + 2 J_{\text {NaK}} \Bigg ) -\int _{\partial \varOmega _b} \ j_{\text {K}} \ \text {d}S, \end{aligned}$$

(10)

$$\begin{aligned}&\frac{\text {d} \Big ([{\mathrm{Cl}}^-]_i\omega _i\Big )}{\text {d}t} = S_b \Bigg ( 2J_{\text {Nkcc1}} + J_{\text {Ae4}} \Bigg ) - \int _{\partial \varOmega _a} j_{\text {Cl}} \ \text {d}S,\end{aligned}$$

(11)

$$\begin{aligned}&\frac{\text {d} \Big ([{\mathrm{HCO}}_3^-]_i\omega _i\Big )}{\text {d}t} =\omega _i J_{\text {Buffer}} - S_b 2J_{\text {Ae4}}, \end{aligned}$$

(12)

$$\begin{aligned}&\frac{\text {d} \Big ([\text {H}^+]_i \omega _i\Big )}{\text {d}t} = \omega _i J_{\text {Buffer}} - S_b J_{\text {Nhe1}},\end{aligned}$$

(13)

$$\begin{aligned}&\Big ( \frac{C_m}{F}\Big ) \frac{\text {d}V_a}{\text {d}t} = \int _{\partial \varOmega _a} j_{\text {Cl}} \ \text {d}S - \Big (J^t_{\text {K}} + J^t_{\text {Na}}\Big ),\end{aligned}$$

(14)

$$\begin{aligned}&\Big ( \frac{C_m}{F}\Big ) \frac{\text {d}V_b}{\text {d}t} = - \int _{\partial \varOmega _b} j_{\text {K}} \ \text {d}S -S_b J_{\text {NaK}} + \Big (J^t_{\text {K}} + J^t_{\text {Na}}\Big ). \end{aligned}$$

(15)

$C_m$ and F are the PM capacitance and Faraday’s constant, respectively. The conductances and densities of the system were chosen such that the resting states of the system are physiologically accurate. The various expressions of the transporters, exchangers, and ion channels used in this model are briefly presented in the “Appendix”. The parameters used here can be found in Table 1 in the “Appendix”. For further details on the specific details of the flux models refer to Palk et al. (2010), Sigüenza et al. (2018) and the companion paper Pages et al. (2018).

3.3 ${\mathrm{Ca}}^{2+}$ Signalling

Full details of the ${\mathrm{Ca}}^{2+}$ signalling model are given in Pages et al. (2018). For convenience, some of the experimental data and a typical result from the ${\mathrm{Ca}}^{2+}$ dynamics model are reproduced in Fig. 3.

Fig. 3

a Cell-wide average cytosolic $[{\mathrm{Ca}}^{2+}]$ response to agonist. Our simulation is initiated such that $[{\mathrm{Ca}}^{2+}]_i$ remains at its resting state ($\sim$ 72nM) for a period of 60 s before introducing agonist. Soon thereafter, the concentration oscillates around a plateau with a mean of $\sim$200 nM. The result is presented and analysed in a companion paper (Pages et al. 2018). b Experimental cytosolic $[{\mathrm{Ca}}^{2+}]$, spatially averaged over the entire cell. Upon stimulation with the InsP$_3$-generating agonist ([CCh] = 300 nM), oscillatory changes in the intracellular $[{\mathrm{Ca}}^{2+}]$ of a parotid acinar cell can be observed (by means of the fluorescent ${\mathrm{Ca}}^{2+}$ indicator Fluo-4) for the duration of the agonist exposure

Water transport is driven by ${\mathrm{Ca}}^{2+}$ signalling with ${\mathrm{Ca}}^{2+}$-dependent ${\mathrm{Cl}}^-$ channels in the apical membrane, and ${\mathrm{Ca}}^{2+}$-dependent ${\mathrm{K}}^+$ channels in the basal membrane. Here, the channel flux is described by:

$$\begin{aligned} J_{c}= \frac{G_{c}}{F} \Bigg ( V_{a,b} - \frac{R T}{F z^{c}} \ln \Bigg [\frac{[c]_{\text {out}}}{[c]_{\text {inside}}} \Bigg ] \Bigg ), \end{aligned}$$

where [c] represents the total concentration of either ${\mathrm{K}}^+$ or ${\mathrm{Cl}}^-$ and the subscripts a apical, and b basolateral. The parameters R, T, F, and $z^{c}$ denote the universal gas constant, temperature in Kelvin, Faraday’s constant, and the valence of the ionic species (c), respectively. $G_c$ is the channel conductance (dependent on $[{\mathrm{Ca}}^{2+}]_i$) and is given by

$$\begin{aligned} G_{c}= \Bigg (\frac{g_c}{S_{a,b}} \Bigg )\int _{\partial \varOmega _{a,b}} \Bigg ( \frac{[{\mathrm{Ca}}^{2+}]_i^{\eta }}{K_{c}^{\eta }+ [{\mathrm{Ca}}^{2+}]_i^{\eta }} \Bigg ) \ dS, \end{aligned}$$

(16)

where $g_c$ is the whole cell maximum conductance, $K_{\text {c}}$ represents the half-maximal activation concentration, $\eta$ its Hill coefficient, $S_{a,b}$ the respective PM surface area, and $[{\mathrm{Ca}}^{2+}]_i$ the local ${\mathrm{Ca}}^{2+}$ concentration.

To compute Eq. (16), we note that each node of the tetrahedral mesh comprising the PM surface ($\partial \varOmega$) has a $[{\mathrm{Ca}}^{2+}]_i$ value associated with it (Pages et al. 2018). The current (either ${\mathrm{K}}^+$ or ${\mathrm{Cl}}^-$) across each triangular surface face of the tetrahedral mesh is computed by calculating the average $[{\mathrm{Ca}}^{2+}]$ on the surface triangle using the three values at the corners of the triangular face (i.e. the nodes of the mesh). This average $[{\mathrm{Ca}}^{2+}]_i$ ($\tilde{c}$) is then used in Eq. (16) to calculate the ${\mathrm{K}}^+$ or ${\mathrm{Cl}}^-$ current across that triangular face. Thus,

$$\begin{aligned} G_{c} = \Bigg (\frac{g_c}{S_{a,b}} \Bigg ) \sum _{k=1}^N \int _{\partial \varOmega _{a,b}^k } \Bigg (\frac{\tilde{c}_k^{\eta }}{K_{c}^{\eta }+ \tilde{c}_k^{\eta }}\Bigg ) \ dS_k . \end{aligned}$$

(17)

Here, k denotes the $k^{th}$ tetrahedral face comprising the respective PM surface ($\partial \varOmega _{a,b}$), and N is the total number of tetrahedral faces in $\partial \varOmega _{a,b}$. This procedure is repeated with every step of the numerical integration and incorporated into the equations for $[{\mathrm{Cl}}^-]_l$, $[{\mathrm{Cl}}^-]_i$, and $[{\mathrm{K}}^+]_i$, accordingly.

Fig. 4

Response of the intracellular ionic concentrations and intracellular pH to agonist-induced secretion. a An increase in cytosolic $[{\mathrm{Ca}}^{2+}]$ promotes an approximate 2.5-fold increase in the $[{\mathrm{Na}}^+]_i$. The result is an improvement from previous models and is consistent with observations by Soltoff et al. (1989). b A pronounced ${\mathrm{K}}^+$ efflux serves to hyperpolarise the membrane and sustain apical ${\mathrm{Cl}}^-$ efflux. Our model reproduces the behaviour reported by Poulsen and Bledsoe (1978). c, d The pH and $[{\mathrm{HCO}}_3^-]_i$ are seen varying relatively little, in agreement with Peña-Münzenmayer et al. (2015). e Upon secretion, the $[{\mathrm{Cl}}^-]_i$ decreases to $\sim$ 50$\%$ of its resting value during each oscillation. The result is the hallmark of water secreting epithelia (Silva et al. 1977)

4 Results

4.1 Ionic Concentrations, PM Potentials, Cellular Volume, and Fluid Flow Rate

In order to mimic the experimental procedure shown in Fig. 3b, we initiated our simulation by setting the cytosolic $[{\mathrm{Ca}}^{2+}]$ at rest (corresponding to the steady-state value of $\sim$72 nM) for a period of 60 s before introducing agonist. Upon maximal stimulation (corresponding to 300 nM of the agonist CCh, $t>60$ in Fig. 3), the cell-wide spatial average intracellular $[{\mathrm{Ca}}^{2+}]$ reaches an oscillatory plateau with an average value of $\sim$200 nM. The rest of the ionic concentrations, the PM potentials, and the cellular volume mirror the $[{\mathrm{Ca}}^{2+}]_i$ and oscillate with the same frequency around a plateau for the duration of the agonist exposure (Figs. 4, 5, 6, and 7). For instance, the $[{\mathrm{Na}}^+]_i$ oscillates with a relatively small amplitude around the mean value of 63.5 mM (Fig. 4a). This is consistent with the 2.5-fold increase, from rest, reported by Soltoff et al. (1989). The result reflects the complex interplay between the NaK-ATPases, the Ae4 exchangers (which, together with the NaK-ATPases, extrude a large quantity of ${\mathrm{Na}}^+$), and the electroneutral Nhe1 antiporters whose task includes the re-introduction of extracellular ${\mathrm{Na}}^+$ to promote an inwardly directed gradient whilst maintaining an adequate intracellular pH. The net ${\mathrm{Na}}^+$ transport serves to energise the electroneutral cotransport of ${\mathrm{Cl}}^-$ by the basolateral Nkcc1 cotransporters.

Fig. 5

Response of cellular PM potentials, to changes in $[{\mathrm{Ca}}^{2+}]_i$ upon agonist stimulation. a Apical potential and b basal potential. As [${\mathrm{Ca}}^{2+}$] in the apical region reaches its maximum value, the negatively outward directed current depolarises the entire plasma membrane, but soon thereafter (nearly instantaneously) the basolateral [${\mathrm{Ca}}^{2+}$] activates a ${\mathrm{K}}^+$ current that hyperpolarises the PM and sustains the apical ${\mathrm{Cl}}^-$ efflux

Fig. 6

Response of the cellular volume and fluid flow rate to changes in the cytosolic $[{\mathrm{Ca}}^{2+}]$ upon agonist stimulation. a During secretion, the fluid flow rate reaches an oscillating plateau with a mean value of $\sim$78 $\upmu$m$^3$/s above its resting value of 22 $\upmu$m$^3$/s. b Experimental observations in parotid epithelia demonstrate that the transcellular passage of water is responsible for an approximate 30$\%$ decrease in cellular volume (Melvin et al. 2005). Our model exhibits a volume decrease of approximately 27$\%$ of its resting value for the duration of the agonist exposure

Fig. 7

Luminal ionic response to changes in cytosolic [${\mathrm{Ca}}^{2+}$]. a, b At maximal stimulation, the $[{\mathrm{Na}}^+]_l$ and $[{\mathrm{K}}^+]_l$ reach an oscillating plateau $\sim$15$\%$ larger than their respective resting values. Note how the luminal concentration of ${\mathrm{Cl}}^-$ is higher than that of ${\mathrm{Na}}^+$. This is because the paracellular movement of ${\mathrm{Na}}^+$ and ${\mathrm{K}}^+$ ions through the tight junction into the lumen requires a lumen negative driving force. c The $[{\mathrm{K}}^+]_l$ in the lumen is relatively low, in agreement with Mangos et al. (1973)

The $[{\mathrm{K}}^+]_i$ can be seen decreasing by approximately 20$\%$ from its resting state of 120 mM to a mean value of $\sim$97 mM (Fig. 4b). This result is in agreement with Poulsen and Bledsoe (1978) who reported an increase in interstitial $[{\mathrm{K}}^+]$ increase of 2.2–18.7 meq/l corresponding to the loss of intracellular ${\mathrm{K}}^+$ after maximal cholinergic stimulation.

The cellular pH is consistent with Peña-Münzenmayer et al. (2015). The model indicates that the variation of $[{\mathrm{HCO}}_3^-]_i$ is relatively small and the intracellular pH is approximately constant (Fig. 4c, d). This suggests that the complex dynamics between the Ae4 and Nhe1, and their role as parallel ${\mathrm{Cl}}^-$ accumulation supporting mechanism, are within physiological agreement with what Sigüenza et al. (2018) reported.

Upon agonist stimulation, apically localised inositol 1,4,5-trisphosphate (InsP$_3$) receptors release ${\mathrm{Ca}}^{2+}$ from internal stores causing the activation of neighbouring apical ${\mathrm{Cl}}^-$ channels resulting in a drop in $[{\mathrm{Cl}}^-]_i$ to approximately 50$\%$ of its resting value (Fig. 4e). This causes a fast apical PM depolarisation (Fig. 5). Note that if this depolarisation were to continue, it would prevent the efflux of ${\mathrm{Cl}}^-$ and consequently stop water transport. To prevent this, a slightly delayed increase in basolateral $[{\mathrm{Ca}}^{2+}]_i$ causes rapid activation of the basolateral IK/BK1 channels allowing ${\mathrm{K}}^+$ to exit towards the interstitial compartment. The cation efflux decreases the basolateral and apical PM potentials, thus maintaining apical ${\mathrm{Cl}}^-$ efflux.

It is interesting to note that the responses of the apical and basolateral membrane potentials are not simple oscillations, but have a complicated structure. This is because any change in voltage at either membrane portion is mirrored in the other membrane section. For example, when apical ${\mathrm{Ca}}^{2+}$ increases this causes an immediate increase in the apical ${\mathrm{Cl}}^-$ current, and thus an immediate depolarisation of both the apical and basolateral plasma membranes. The subsequent increase in basal ${\mathrm{Ca}}^{2+}$ then increases the basal ${\mathrm{K}}^+$ current, which hyperpolarises the basolateral PM, but also reduces the potential of the apical PM. Thus, both $V_a$ and $V_b$ show complex responses with multiple peaks and troughs.

The salivary flow rate changes from a resting state of 22 to a $\sim$78 $\upmu$m$^3$/s mean upon agonist-induced $[{\mathrm{Ca}}^{2+}]_i$ increases (Fig. 6a). Fluid flow rate experiments in mouse parotid glands, demonstrated that cholinergic-induced secretion results in a gland secretory rate of approximately 11–16 $\upmu$L/min (Evans et al. 2000; Romanenko et al. 2010). Accordingly, our model estimates about 2.86 $\times 10^{6}$ cells in a typical mouse parotid gland. This is an improvement from previous mathematical models in which the flow did not attain a physiological rate (Gin et al. 2007; Palk et al. 2010; Sigüenza et al. 2018). Water transport causes a decrease in cellular volume of approximately 29$\%$ (Fig. 6b), in agreement with Foskett et al. (1991). The electrolyte concentration of primary saliva produced by the model has a relatively high concentration of ${\mathrm{Na}}^+{\mathrm{Cl}}^-$, whilst $[{\mathrm{K}}^+]_i$ is relatively low (Fig. 7), consistent with Mangos et al. (1973).

5 Effects of Calcium Signalling in Fluid Secretion

The following results correspond to a series of “in-silico” experiments with distinct variations of the model presented in Sect. 4. We define:

• Model 1 to be the model whose results are presented in Figs. 4, 5, 6, 7. It corresponds to the secretion model solved in conjunction with the spatially heterogeneous, and oscillating in time, ${\mathrm{Ca}}^{2+}$ signalling model (described in Pages et al. 2018).

• Model 2 is the secretion model driven by the mean apical and the mean basal $[{\mathrm{Ca}}^{2+}]$. Note that each of these spatial means will be oscillating in time.

• Model 3 is the secretion model driven by the mean apical and the mean basal $[{\mathrm{Ca}}^{2+}]$, where (as opposed to Model 2) the means are now taken in both space and time. Thus, water secretion in Model 3 is driven by a constant apical and a constant basal $[{\mathrm{Ca}}^{2+}]$.

• QSS Model is a quasi-steady-state (QSS) approximation of the fluid secretion model. Here, water secretion is assumed to be an algebraic function of the mean $[{\mathrm{Ca}}^{2+}]$, where the mean is now taken over the entire cell at each point in time. Thus, in this model, the mean $[{\mathrm{Ca}}^{2+}]$ is oscillating, but is the same in both the apical and basal regions.

5.1 Apical and Basolateral Heterogeneities

We analysed the distribution of ${\mathrm{Cl}}^-$ and ${\mathrm{K}}^+$ current densities given by Model 1. Figure 8a, b depict a spread of surface current density values across the tetrahedral faces that form the apical and basolateral plasma membranes of the cell, respectively. These correspond to the different values of peak $[{\mathrm{Ca}}^{2+}]_i$ during a period of the oscillation. Figure 8a shows that the majority of the apical ${\mathrm{Cl}}^-$ current ($\sim 76 \%$) peaks at approximately 140 $\text {pA}/\upmu$m$^2$. Similarly, Fig. 8b shows that the majority of the basal ${\mathrm{K}}^+$ current peaks at 220 pA/$\upmu$m$^2$. Given the large number of triangular faces in the PM with approximately similar surface current density, we hypothesised that only the spatial $[{\mathrm{Ca}}^{2+}]_i$ mean at the apical and basolateral regions of the cell may be needed to attain an appropriate secretion rate. To test this, we computed the fluid flow rate using the cytosolic $[{\mathrm{Ca}}^{2+}]$ spatial mean response to agonist stimulation at the apical and basolateral regions of the cell (Fig. 8c). The results, shown in Fig. 8d (denoted as Model 2), indicate that the spatial heterogeneities of the $[{\mathrm{Ca}}^{2+}]_i$ exhibited in Model 1 have little impact on the mean saliva secretion rate.

5.2 Effects of Oscillations on Fluid Flow

Palk et al. (2012) reported that using the spatio-temporal mean of an oscillating $[{\mathrm{Ca}}^{2+}]_i$ to drive water transport, in an earlier secretion model, resulted in an almost identical flow rate as when using its oscillating counterpart. Thus, they concluded, this was sufficient to drive secretion when the flow rate is the only modelling concern [as in Sigüenza et al. (2018)]. We thus simulated Model 3 the spatio-temporal mean of the apical and basolateral cytosolic $[{\mathrm{Ca}}^{2+}]$ response to agonist stimulation (see Fig. 9a). Results reveal that using the spatio-temporal mean $[{\mathrm{Ca}}^{2+}]_i$ to drive secretion generates a mean flow rate almost identical to the one given by Model 1 (Fig. 9b). Our result validates the findings of Palk et al. (2012), and indicates that the spatio-temporal patterns emerging from ${\mathrm{Ca}}^{2+}$ signalling are not an important determining factor when it comes to secretion. Interestingly, if saliva secretion is driven by a ${\mathrm{Ca}}^{2+}$ model that exhibits low-frequency baseline spiking, the oscillation period and shape has a large effect on saliva secretion (results not shown). Thus, we conclude that the insensitivity of saliva secretion to the frequency and shape of the oscillations is a result of the fact that the oscillations are of high frequency and on a raised baseline. In saliva secreting cells, $[{\mathrm{Ca}}^{2+}]_i$ oscillations are invariably of this type.

Fig. 8

a Distribution of the ${\mathrm{Cl}}^-$ surface current densities of Model 1 at maximal $[{\mathrm{Ca}}^{2+}]_i$, as a function of the percentage of tetrahedral faces that form the apical PM. The majority reach a maximal ${\mathrm{Cl}}^-$ current of approximately 140 pA/$\upmu$m$^2$. b Distribution of ${\mathrm{K}}^+$ surface current densities of Model 1 as a function of the percentage of triangular faces that form the basolateral PM at maximum $[{\mathrm{Ca}}^{2+}]_i$. The majority reach a maximal ${\mathrm{K}}^+$ current of approximately 220 pA/$\upmu$m$^2$. cModel 2. Spatial mean of the $[{\mathrm{Ca}}^{2+}]_i$ response to agonist stimulation at the apical (green) and basolateral (orange) cellular regions. d Mean fluid flow rate of Model 2 (red) compared to the mean fluid flow rate of Model 1 (black). Model 2 gives an 8$\%$ decrease in mean flow rate compared to Model 1. The result indicates that the signalling heterogeneities in the apical and basal regions, exhibited in Model 1, are not necessary to drive a physiological secretion rate (Color figure online)

Fig. 9

aModel 3. Spatio-temporal mean of the apical and the basolateral cytosolic $[{\mathrm{Ca}}^{2+}]$ responses to agonist stimulation. Here, both $[{\mathrm{Ca}}^{2+}]_i$, the apical (green) and the basolateral (orange), elevate from rest into a sustained non-oscillatory plateau upon agonist stimulation. b Mean flow rate of Model 3 compared to the mean flow rate given by Model 1. The mean rate generated by Model 3 is identical to the mean rate given by Model 1. The figure shows that only the $[{\mathrm{Ca}}^{2+}]_i$ spatio-temporal mean is needed to drive secretion to physiological levels. Our result supports a previous hypothesis by Palk et al. (2012) (Color figure online)

Fig. 10

aQSS Model. We fitted a Hill function (red) to the flow rate steady states of the secretion model. These were driven by the cell-wide spatio-temporal mean $[{\mathrm{Ca}}^{2+}]_i$ responses to different agonist concentrations (dotted black curve). b Single flow rate oscillation given by the QSS Model (red) driven by the cell-wide spatial $[{\mathrm{Ca}}^{2+}]_i$ mean, against the flow rate given by Model 1 (black). The QSS Model gives a reasonably accurate prediction of the mean flow rate (Color figure online)

5.3 Quasi-Steady-State Approximation

We next consider how the time scales involved in the various ionic currents and changes in cell volume affect saliva secretion. For a given fixed [Ca] (across the entire cell), the fluid flow can be calculated. When this is done for a range of fixed [Ca] we can then derive a relationship between steady state $[{\mathrm{Ca}}^{2+}]_i$ and fluid flow. This relationship is plotted in Fig. 10a. The functional relationship is given by,

$$\begin{aligned} f_\text {FR}([{\mathrm{Ca}}^{2+}]_i) = V \Bigg (\frac{[{\mathrm{Ca}}^{2+}]_i^{3.5}}{K+[{\mathrm{Ca}}^{2+}]_i^{3.5}}\Bigg ), \end{aligned}$$

where $V=91$ and $K=3\times 10^{-4}$.

In Fig. 10b, we present a comparison between the QSS Model (driven by the cell-wide spatial, but not temporal, mean $[{\mathrm{Ca}}^{2+}]$ see Fig. 3a) and Model 1 flow rates (Fig. 6a). Although the shape of the flow rate curves differs, the mean fluid secretion rate is almost identical. The result indicates that a quasi-steady-state approximation to the saliva secretion model gives a reasonably accurate prediction of the flow rate and if modelling the latter is the only goal, the QSS Model suffices. However, in doing so, all the dynamic complexity, not only of the fluid secretion mechanism but also of the intracellular heterogeneity of cytosolic $[{\mathrm{Ca}}^{2+}]$, is ignored.

This is a startling result, potentially of great importance for future attempts at model simplification. It shows that, although in our current model some of the time scales of the ionic currents (or those of volume change) affect total fluid flow, the entire model can be replaced by a QSS curve that algebraically relates spatially averaged $[{\mathrm{Ca}}^{2+}]_i$ to fluid flow. Thus, in a more complex multicellular setting, the entire fluid flow model (in each cell) could potentially be replaced by an algebraic relationship that could be computed separately (for each cell), leading to an enormous increase in simulation speed.

As yet we have performed no detailed analysis of this result (for example, to what extent does the volume affect the result?) and so it is not yet possible to say with certainty that the fluid flow model for any realistic parotid cell can always be reduced to a single algebraic relationship between saliva secretion and $[{\mathrm{Ca}}^{2+}]_i$. Nevertheless, the possibilities are intriguing.

5.4 Other Cells

Until now we have concentrated on discussing the results from a single cell. To demonstrate that our model works in any given cell, we solved Model 1 in seven different cells, each of which has a different shape and volume constructed from a z stack of confocal slices. The results can be found in the supplementary material. Here, we briefly present the results from one of the other cells. Figure 11 shows the cellular mesh created by Pages et al. (2018). From Figs. 12 and 13, we see that the model reproduces critical experimental data for this cell also, including the expected changes in cellular volume and the concentrations of the ionic species involved in fluid secretion.

Fig. 11

Tetrahedral mesh depicting a salivary gland acinar cell constructed by Pages et al. (2018). Two images of the same cell are shown, where the cell is rotated to exhibit the apical (red) and basal (blue) regions of the cellular plasma membrane. The non-coloured triangular faces represent the lateral portion (Color figure online)

Fig. 12

Intracellular concentrations, pH, and volume responses to agonist stimulation in the cell shown in Fig. 11 (Color figure online)

Fig. 13

Fluid flow and luminal concentrations upon agonist stimulation in the cell shown in Fig. 11 (Color figure online)

6 Discussion

${\mathrm{Ca}}^{2+}$ signalling plays a pivotal role in the process of water transport regulation by salivary epithelia. The second messenger modulates the activation of PM channels, providing the cell with a means of control for the efflux and influx of ${\mathrm{Cl}}^-$ and ultimately fluid secretion. Although secretion models that include ${\mathrm{Ca}}^{2+}$ signalling exist, up until now the majority have been based on highly simplified dynamics (Palk et al. 2010, 2012; Gin et al. 2007; Sigüenza et al. 2018). In this study, we used a physiologically accurate ${\mathrm{Ca}}^{2+}$ signalling model, solved on seven anatomically accurate domains, to drive fluid secretion. The ${\mathrm{Ca}}^{2+}$ model is described in detail in a companion paper (Pages et al. 2018). Our aim was to investigate how the structure of the cells and the heterogeneity of the ${\mathrm{Ca}}^{2+}$ dynamics affects saliva secretion.

We found that our model successfully reproduces the observed physiological responses of salivary epithelia upon agonist-induced stimulation, including the expected changes in cell volume and the relevant ionic concentrations involved in the transport of water (Figs. 4, 7). The addition of the spatio-temporal ${\mathrm{Ca}}^{2+}$-signalling model to drive fluid secretion resolves several problems encountered in previous models. For instance, the $[{\mathrm{Na}}^+]_i$ increases approximately 2.5 fold upon agonist stimulation, a result seen often in experimental settings (Fig. 4a). The result is an improvement from earlier models which display only an increase of 30$\%$ above the rest state (Palk et al. 2010; Sigüenza et al. 2018). Similarly, Foskett (1990) observed a decrease of approximately 50$\%$ in cytosolic $[{\mathrm{Cl}}^-]_i$ upon stimulation, and our model successfully reproduces their results. As a consequence, the cell volume decreases by approximately 29$\%$ (Nauntofte 1992). The mean fluid flow rate of the model upon agonist-induced stimulation is $\sim$78 $\upmu$m$^3$/sec or a $\sim$4 fold increase from rest (Fig. 6a). Although the figure seems low, given that Sigüenza et al. (2018) claim a 12-fold increase, this is because we based our model on experiments which use only 300 nM of CCh agonist to induce ${\mathrm{Ca}}^{2+}$ responses. In Peña-Münzenmayer et al. (2015), the study that Sigüenza et al. (2018) results are based on, they use 2 agonists, CCh and isoproterenol (IPR), to stimulate secretion. This results in a larger $[{\mathrm{Ca}}^{2+}]_i$, ultimately elevating the secretion rate to a 12-fold increase above rest. Nevertheless, our result is an improvement on previous models in which the fluid flow rate increases by only 2–2.5-fold from rest under similar conditions to our model (Palk et al. 2010; Gin et al. 2007). Furthermore, Evans et al. (2000) observed a volume of 400 $\upmu$L per 100 mg of parotid gland in 50 min. We estimated that an upper bound of approximately 2.86$\times 10^6$ acinar cells exists in 100 mg of parotid gland. According to this figure, our model’s results are consistent with experimental data.

Here, as in previous studies, the secretion model includes two coupled PM potentials to account for the polarised nature of acinar cells (Palk et al. 2010; Sigüenza et al. 2018). However, the corresponding responses (apical and basolateral) to the transmembrane movement of ions display complicated oscillatory structures previously unreported in primary saliva models (Fig. 5a, b). Our results show that following a $[{\mathrm{Ca}}^{2+}]_i$ increase in the apical region, an immediate depolarisation of both plasma membranes occurs. Shortly thereafter, as a consequence of the relay of ${\mathrm{Ca}}^{2+}$ signals towards the basolateral region, a delayed hyperpolarisation of the basolateral PM occurs, causing a reduction in the apical PM potential. The coupling of both membranes is evident here, as a change in voltage at either membrane portion is mirrored by the other.

Measuring the response of apical ${\mathrm{Cl}}^-$ and basolateral ${\mathrm{K}}^+$ currents revealed that the majority of the PM surface reaches a similar ${\mathrm{Cl}}^-$ and ${\mathrm{K}}^+$ current density (Fig. 8a, b). Interestingly, these correspond to the current densities given by the average apical and basolateral $[{\mathrm{Ca}}^{2+}]_i$ traces (Fig. 8c). The observation suggests that averaging the $[{\mathrm{Ca}}^{2+}]_i$ at each region (basolateral and apical) would yield the same fluid flow as would a heterogeneous distribution of $[{\mathrm{Ca}}^{2+}]_i$ in the cell. When this hypothesis is tested (Fig. 8d) we see that the fluid flow rate obtained by averaging the $[{\mathrm{Ca}}^{2+}]_i$ in each region produces the same result as its heterogeneous counterpart. We propose that heterogeneity of $[{\mathrm{Ca}}^{2+}]_i$ in the apical and basal regions is not an important mechanism in the secretion process. Thus, at least for modelling purposes, we claim that to predict and understand the acinar secretion, a three-dimensional model of ${\mathrm{Ca}}^{2+}$ signalling is, perhaps, not necessary. Instead, a simpler ordinary differential equation model describing the signalling phenomena that reproduces the appropriate ${\mathrm{Ca}}^{2+}$ responses at each end of the cell may be sufficient.

Perhaps one of the most important results, and a prediction of our study, stemmed from computing the fluid flow rate of the system using a spatio-temporal homogeneous distribution of apical and basolateral $[{\mathrm{Ca}}^{2+}]_i$ - denoted Model 3 in Sect. 5 (see Fig. 9a). The resultant non-oscillating mean flow rate was found to be nearly identical to its oscillating counterpart - given by Model 1 (see Fig. 9b). Palk et al. (2012) suggested that driving secretion using the spatio-temporal mean of a $[{\mathrm{Ca}}^{2+}]_i$ oscillation, results in an accurate flow rate. Our result supports their hypothesis. Although Palk et al. (2012) never tested this with an accurate ${\mathrm{Ca}}^{2+}$ model, it is evident now that because of the high-frequency $[{\mathrm{Ca}}^{2+}]_i$ oscillations, the only important factor determining secretion is the temporal mean $[{\mathrm{Ca}}^{2+}]_i$.

Our secretion model can possibly be simplified even further, as long as the only output of interest is the mean fluid flow. Equation 5 assumes a quasi-steady-state approximation to the rate of change in cellular volume and the associated ionic concentrations in order to compute the fluid flow rate as a function of $[{\mathrm{Ca}}^{2+}]_i$. Using the cell-wide cytosolic $[{\mathrm{Ca}}^{2+}]$ spatial mean, we compared the solution of Model 1 to the solution using this quasi-steady-state approximation (Fig. 9b), and found that mean saliva secretion was identical. Although we have not tested this result exhaustively, it raises the intriguing possibility that an accurate model of fluid flow may be constructed by assuming that all ionic flows and cell volume changes are at quasi-steady state, and thus that their dynamic responses have little effect on fluid secretion. One possible difficulty with this simplified approach is that our present model does not include an accurate model of bicarbonate buffering. It is possible that slower time scales involved in pH control and bicarbonate buffering will make a quasi-steady-state assumption inaccurate, but resolution of this question awaits further work.

Lastly, our simulations were performed using the Sigüenza et al. (2018) model for fluid secretion. However, we simplified their model by omitting the basolateral ${\mathrm{Cl}}^-$/${\mathrm{HCO}}_3^-$ Anion Exchanger 2, and assuming that [CO$_2$] is constant. It has been shown mathematically, and experimentally, that the Ae2 is not important for fluid secretion. Furthermore, Sigüenza et al. (2018) show that throughout stimulation and the rest phases of secretion [CO$_2$] is constant, as is pH. Thus, in our pursuit of computational simplicity we set [CO$_2$] to be constant. It is unclear how much of a difference this simplifying assumption makes. However, it remains possible that, for some cells and for some parameters, the dynamics of pH and bicarbonate buffering will introduce time scales that have a more significant impact on the rate of saliva secretion. This is a question that will be explored in further work.

In summary, the exact details of the cytosolic $[{\mathrm{Ca}}^{2+}]$ heterogeneity seem to matter little. Our study still does not resolve to what extent does the propagation of ${\mathrm{Ca}}^{2+}$ waves, from apical to basolateral affect the secretory process due to the high-frequency of $[{\mathrm{Ca}}^{2+}]_i$ oscillations. What we can infer from our results, however, is that these waves occur very fast, resulting in a near instantaneous ${\mathrm{Ca}}^{2+}$ response across the cell as reported by Giovannucci et al. (2002). But based on the results of our study, we claim that a partial differential equation model of ${\mathrm{Ca}}^{2+}$ signalling may not be necessary to attain a physiological secretion rate in this model. When combined with the fact that the dynamics of ion currents and cell volume control appear to be unimportant if the only modelling concern is flow rate, we conclude that an accurate model of saliva secretion could possibly be constructed by a small system of ODEs coupled with an algebraic function describing secretion as a function of $[{\mathrm{Ca}}^{2+}]_i$. Such an extreme simplification, if shown to be reliably accurate, would make multicellular and multiscale computations possible and efficient.

Appendices

Appendix

Fluxes of the Model

$$\begin{aligned} j_{\text {NaK}}&=\alpha _{\text {NaK}}\left( r \frac{[\text {K}^+]_e^2 [\text {Na}^+]_i^3}{[\text {K}^+]_e^2+\alpha [\text {Na}^+]_i^3} \right) , \end{aligned}$$

(18)

$$\begin{aligned} j_{\text {Nkcc1}}&=\alpha _{\text {Nkcc1}} \left( \frac{a_1-a_2 [\text {Na}^+]_i [\text {K}^+]_i [\text {Cl}^-]_i^2}{a_3+a_4 [\text {Na}^+]_i [\text {K}^+]_i [\text {Cl}^-]_i^2}\right) ,\end{aligned}$$

(19)

$$\begin{aligned} j_{\text {Nhe1}}&=G_{\text {Nhe1}} \Bigg (\frac{[\text {H}^+]_i}{[\text {H}^+]_i+K_\text {H}}\Bigg )^2 \Bigg (\frac{[{\mathrm{Na}}^+]_e}{[{\mathrm{Na}}^+]_e+K_{\text {Na}}} \Bigg ),\end{aligned}$$

(20)

$$\begin{aligned} J_{\text {Ae4}}&= G_{Ae4} \Bigg (\frac{[{\mathrm{Cl}}^-]_e}{[{\mathrm{Cl}}^-]_e + K_{\text {Cl}}}\Bigg ) \Bigg (\frac{[{\mathrm{Na}}^+]_i}{[{\mathrm{Na}}^+]_i+ K_{\text {Na}}}\Bigg ) \Bigg (\frac{[{\mathrm{HCO}}_3^-]_i}{[{\mathrm{HCO}}_3^-]_i+ K_{\text {B}}}\Bigg )^2,\end{aligned}$$

(21)

$$\begin{aligned} J_{\text {Buffer}}&=k_1[\text {CO}_2]_i-k_{-1}[\text {H}^+]_i[\text {HCO}_3^-]_i\end{aligned}$$

(22)

$$\begin{aligned} J^t_{{\mathrm{Na}}^+}&= \frac{G^t_{{\mathrm{Na}}^+}}{F z^{Na}} \Bigg [V_a - V_b - \frac{RT}{F} \ln \Bigg ( \frac{[{\mathrm{Na}}^+]_l}{[{\mathrm{Na}}^+]_e}\Bigg )\Bigg ],\end{aligned}$$

(23)

$$\begin{aligned} J^t_{{\mathrm{K}}^+}&= \frac{G^t_{{\mathrm{K}}^+}}{F z^{K}} \Bigg [V_a - V_b - \frac{RT}{F} \ln \Bigg ( \frac{[{\mathrm{K}}^+]_l}{[{\mathrm{K}}^+]_e}\Bigg )\Bigg ]. \end{aligned}$$

(24)

Water Fluxes

$$\begin{aligned} J^w_a&= P_a \Bigg ( \sum [c]_l + \varPsi _l - \sum [c]_i -\frac{x_i}{\omega _i}\Bigg ),\end{aligned}$$

(25)

$$\begin{aligned} J^w_b&= P_b \Bigg ( \sum [c]_i + \frac{x_i}{\omega _i} - \sum [c]_e \Bigg ),\end{aligned}$$

(26)

$$\begin{aligned} J^w_t&= P_t \Bigg ( \sum [c]_l + \varPsi _l - \sum [c]_e \Bigg ). \end{aligned}$$

(27)

Where,

$$\begin{aligned}&\sum [c]_e = [{\mathrm{K}}^+]_e + [{\mathrm{Na}}^+]_e + [{\mathrm{Cl}}^-]_e + [{\mathrm{HCO}}_3^-]_e + [\text {H}^+]_e + [\text {CO}_2]_e,\\&\sum [c]_i = [{\mathrm{K}}^+]_i+ [{\mathrm{Na}}^+]_i+ [{\mathrm{Cl}}^-]_i+ [{\mathrm{HCO}}_3^-]_i+ [\text {H}^+]_i + [{\mathrm{CO}}_2]_i,\\&\sum [c]_l = [{\mathrm{K}}^+]_l+ [{\mathrm{Na}}^+]_l+ [{\mathrm{Cl}}^-]_l+ [{\mathrm{HCO}}_3^-]_l + [\text {H}^+]_l. \end{aligned}$$

The parameter $x_i$ denotes the amount of negatively charged ions with valence $z = -1$impermeable to the cellular PM. Its value is determined by imposing electroneutrality in the cellular compartment. Note that all compartments of the model are assumed electroneutral at all times. The parameter $\varPsi _l$ in Eq. (26) represents the concentration of uncharged impermeable species present in the lumen, including (but not limited to) proteins such as amylase and big molecules like CO$_2$.

Parameters of the Model

See the Table 1.

Table 1 Table of parameters