A Mathematical Model of Forager Loss in Honeybee Colonies Infested with Varroa destructor and the Acute Bee Paralysis Virus

Abstract

We incorporate a mathematical model of Varroa destructor and the Acute Bee Paralysis Virus with an existing model for a honeybee colony, in which the bee population is divided into hive bees and forager bees based on tasks performed in the colony. The model is a system of five ordinary differential equations with dependent variables: uninfected hive bees, uninfected forager bees, infected hive bees, virus-free mites and virus-carrying mites. The interplay between forager loss and disease infestation is studied. We study the stability of the disease-free equilibrium of the bee-mite-virus model and observe that the disease cannot be fought off in the absence of varroacide treatment. However, the disease-free equilibrium can be stable if the treatment is strong enough and also if the virus-carrying mites become virus-free at a rate faster than the mite birth rate. The critical forager loss due to homing failure, above which the colony fails, is calculated using simulation experiments for disease-free, treated and untreated mite-infested, and treated virus-infested colonies. A virus-infested colony without varroacide treatment fails regardless of the forager mortality rate.

1 Introduction

A honeybee colony functions as an integrated whole, performing all of the basic physiological processes that support life. Like other social insects, a honeybee colony shows two types of division of labour: a division of labour between queen, drones and workers for reproduction, and a division of labour among workers for tasks related to colony growth and development (Robinson 1992). Reproductive division of labour between queen and workers is based on the differences in nutrition during larval development. The only role of drones is to mate with the queen. Division of labour between worker castes is based on the age of the individuals; young adults work within the hive and perform tasks related to hive management and brood care, and older workers switch to foraging tasks (Seeley 1982, 2009). The size of a colony and the life span of the bees vary greatly between seasons. The queen bee starts laying eggs slowly in Spring, then at an increasing rate in Summer and then at a lower rate in Fall; egg laying stops before Winter.

Honeybees play an outstanding role economically and ecologically. They are responsible for crops valuing more than $2 billion each year through their pollination services in Canada (Canadian Honey Council 2013a). One-third of the human diet comes from the food crops that are pollinated by honeybees (Canadian Honey Council 2013b). There have been dramatic losses of honeybee colonies in Canada, the USA and in Europe since 2006 (Kevan et al. 2007; Potts et al. 2010; Hayes et al. 2008). The symptoms are different in different parts of the world, and hence, losses are designated by different names. The syndrome was named colony collapse disorder (CCD) in the USA and wintering losses in Canada. The exact reasons for these colony losses are not clear yet; there could be a single reason or a combination of several. Possible causes include parasites, viruses, environmental factors and management practices (Becher et al. 2013; Staveley et al. 2014). It is suspected that a leading cause of honeybee losses is the parasitic mite Varroa destructor and the deadly viruses it carries (Le Conte et al. 2010; McMenamin and Genersch 2015; Stankus 2008). Any stressor that can affect the ability of the forager bees to return to the hive can also lead to colony failure (Henry et al. 2012; Perry et al. 2015; Sánchez-Bayo et al. 2016). These include

• Precocious Foraging Hive bees may accelerate their behavioural development and start foraging precociously at an early age. Precocious foragers are at high risk because they are weaker than the foragers that have adopted foraging at the normal age (Khoury et al. 2011).

• Use of Environmental Pesticides Honeybees are regularly exposed to pesticides because they rely heavily on common blooming crops, such as oilseed rape, maize or sunflower, that are now routinely treated against insect pests (Mullin et al. 2010). These pesticides contaminate nectar and pollen (Rortais et al. 2005). Foraging honeybees are therefore directly exposed, with possibly adverse effects on their memory, learning ability and navigational skills. Such disoriented bees might fail to return to the hive which is known as homing failure (Henry et al. 2012). The rest of the colony is also affected as the returning foragers store or exchange contaminated material with hive individuals (Krupke et al. 2012; Rortais et al. 2005). Exposure to pesticides also affects the bees’ immune system making them more vulnerable to parasites and pathogens (Brandt et al. 2016).

• Diseases The homing ability of honeybees depends mainly on their spatial memory and navigation which could be impaired by pathogens. For instance, it is observed that varroa mites affect the flight duration and homing ability of infested bees (Li et al. 2013). Nosema ceranae is another pathogen, a microsporidian gut parasite first found in the Eastern honeybee (Apis cerana) that later infested the Western honeybee (Apis mellifera). The presence of higher numbers of microsporidians causes dysentery and early ageing in adult workers. Nosema is found to have a huge impact on the homing performance and navigation abilities of foragers (Petric et al. 2016; Wolf et al. 2014).

Our objective is to study the interplay between a varroa–virus infestation and the loss of forager bees in the population dynamics of the hive.

Varroa destructor is an ectoparasitic mite that infests honeybee colonies. It is one of the haplotypes of Varroa jacobsoni, a parasite that infests the Eastern honeybee Apis cerana (Anderson and Trueman 2000). Varroa destructor is the species that parasitized Apis mellifera and spread rapidly in Western countries thereafter (Sumpter and Martin 2004). The mite not only feeds on the haemolymph of individual bees but also carries and transmits deadly viruses from bee to bee. Infestation thus results in a reduced bee life span and a decrease in survivorship. The life cycle of the varroa mite is tightly adapted to the development of honeybees. Mite reproduction takes place exclusively in the capped cells of developing bee pupae. A female mite enters the brood cell before the cell is capped and then feeds on the developing bee and also reproduces in the capped cell. When the host bee leaves the cell, the mother mite leaves the cell with its progeny. The adult female mite becomes attached to the adult bee and feeds on it by squeezing between the overlapping segments on the ventral side of the bee’s abdomen (Martin 2001a).

More than 20 bee viruses are known, 12 of which are carried and transmitted by varroa mites (Kevan et al. 2006; Ostiguy 2004). These viruses differ in pathogenesis, morphology, routes of transmission, virulence and in their interaction with the host. For instance, brood infected with Acute Bee Paralysis Virus (ABPV) do not develop into adult bees and die rapidly. On the other hand, Deformed Wing Virus (DWV) also infects the brood in the hive, but the brood usually survives to the adult stage which has a reduced life span as compared to healthy bees (Sumpter and Martin 2004). In this study, we focus on the Acute Bee Paralysis Virus (ABPV). It belongs to the family Dicistroviridae, which includes the Kashmir Bee Virus (KBV), Black Queen Cell Virus (BQCV) and the Israeli Acute Paralysis Virus (IAPV). ABPV is a common infective agent of honeybees that is frequently detected in apparently healthy colonies. This virus is distributed worldwide and appears to be the most common bee virus in Europe and South America (Antúnez et al. 2005; Ball and Allen 1988). Bees affected by this virus are unable to fly, lose the hair from the thorax and abdomen, and tremble uncontrollably. Infected pupae and adults infected with this virus suffer rapid death. ABPV has been implicated in honeybee colony failure when transmitted by varroa mites (Kevan et al. 2006). ABPV is transmitted to bees when mites feed on bees. A virus-free phoretic mite starts carrying virus when it feeds on an infected bee. When the virus-carrying mite attaches to an uninfected bee, it releases the virus into the bee’s haemolymph and the bee becomes infected (Bowen-Walker et al. 1997; Martin 2001a). The level of virus infestation in a honeybee colony depends on the mite population present in the colony. Varroa mites are a mechanical vector for the transmission of ABPV, i.e. unlike other honeybee viruses such as the Deformed Wing Virus (DWV) or the Israeli Acute Paralysis Virus (IAPV), ABPV does not replicate within the mites (Genersch and Aubert 2010; McMenamin and Genersch 2015; ZKBS 2012). Other transmission routes of ABPV have been suggested, but the literature is inconclusive and quantitative data that would allow a parameterization of a mathematical model are scarce. Evidence of vertical transmission has been found for five viruses including DWV, but there seems to be no evidence for ABPV that infection of the queen implies infection of her offspring (Chen et al. 2006). Another study detected ABPV in pollen but not in the bees and their glandular secretion, suggesting that the ingestion of food which contains virus might not lead to infection (Chen and Siede 2007). Moreover, they report that in colonies without varroa mites, ABPV, if it is present, is latent, whereas the presence of varroa triggers the disease, suggesting that ABPV virulence is directly related to varroa infestation, c.f. also Genersch and Aubert (2010), Moore et al. (2015) and ZKBS (2012).

Several mathematical models have been developed to study the disease dynamics of a honeybee colony infested with varroa mites and viruses (Eberl et al. 2010; Ratti et al. 2012, 2015; Sumpter and Martin 2004). In these models, the hive bees and forager bees are considered together in one class of worker bees. To study the effect of stressors on homing failure, it is necessary to distinguish between these two sub-classes. A model framework that is based on this division of labour was introduced in Khoury et al. (2011, 2013) and Kribs-Zaleta and Mitchell (2014), but does not consider diseases. It is important to combine the two causes (disease infestation and forager loss) and study the impact on the colony strength and survival, which is also suggested by Barron (2015). Since there does not exist any mathematical model in the literature that studies the interplay of the two factors (Becher et al. 2013), in this paper we take the first step by combining the disease model in Ratti et al. (2015) with the division of labour model in Khoury et al. (2011). The primary structure of the disease part of our model is based on Ratti et al. (2015) which, in turn, is based on Sumpter and Martin (2004) which presents a first model of the honeybee–mite–virus complex using the traditional SIR approach of infectious disease modelling. In Sumpter and Martin (2004), the authors consider two varroa transmitted bee viruses, DWV and ABPV, and formulate separate models for each. The model quantifies the critical mite population, which depends on model parameters, below which the colony survives. The total mite load in the colony is assumed to be constant, but the virus-carrying mite population is considered to be a dependent variable. The model for ABPV is extended in Eberl et al. (2010) by adding a brood maintenance term to take into account the fact that a sufficient number of healthy adult bees are required to care for the brood present in the colony. The addition of this brood maintenance term introduces an Allee effect with an unconditionally stable trivial equilibrium which is not present in the model of Sumpter and Martin (2004) because bee eclosion rate is considered to be constant.

Both Sumpter and Martin (2004) and Eberl et al. (2010) analyse the model with constant parameters. The model of Eberl et al. (2010) is extended in Ratti et al. (2012) by introducing a logistic growth model for the total mite population, with carrying capacity of the mites dependent on the total bee population. Since an explicit equation for the mite population is included, the model distinguishes natural death of bees and death due to mites. The model in Eberl et al. (2014) and Ratti et al. (2012) is studied numerically using computer simulations assuming piecewise constant parameters with discontinuous jumps between the seasons. In Ratti et al. (2015), the model is extended to study the seasonal effects on the mite and virus-infested colony by considering the coefficients to be periodic functions of time with a period of 1 year. Floquet theory is used to analyse the stability of virus-free periodic solutions. The model also includes the effect of varroacide application. The model presented in Kang et al. (2016) follows Sumpter and Martin (2004) and Ratti et al. (2015), but also take into account the fact that virus transmission occurs at different biological stages of varroa mites and honeybees. The model also follows Eberl et al. (2010) by including Allee effects in the honeybee population.

The division of labour aspect of our model is based on Khoury et al. (2011), where the authors present an ordinary differential equations (ODE) model in which the colony population is divided based on the tasks performed. The model is two-dimensional with hive bees and forager bees as dependent variables, and is studied using phase plane analysis.

The model in Henry et al. (2012) studies the forager mortality due to exposure to pesticides as a result of which the bees fail to return to the hive. The authors incorporate forager mortality into the model of Khoury et al. (2011) as an additional linear death term for the forager population. They also perform field experiments to determine lower and upper bounds for forager mortality due to homing failure. A comparison between the dynamics of colonies that are exposed to treated crops against unexposed colonies is carried out. The authors investigate how loss of foragers accelerates the precocious recruitment of hive bees to the forager class which in turn affects the survival of the colony. The authors observe that the exposed colonies show a marked decline and hardly recovers afterwards. Moreover, if natural death is also considered, the colonies are not able to recover at all.

In Kribs-Zaleta and Mitchell (2014), the model of Khoury et al. (2011) is extended to account for a hypothetical infection that is brought into the colony by the foragers and spreads in the hive via bee-to-bee transmission. This model is studied in detail both analytically and numerically. The disease dynamics assumed in this paper are rather general, and it is left open to what extent the results would apply to particular diseases such as ABPV and DWV, which require both a vector and a causative agent. In Petric et al. (2016), the model of Khoury et al. (2011) is coupled with a model of the nosemosis, and the combined effects of this microsporidian disease and of forager losses as in Henry et al. (2012) are studied. There are other studies which are not directly relevant for our particular study but are important to study forager loss using division of labour. For instance, in Khoury et al. (2013) the model of Khoury et al. (2011) is extended by adding two new equations, one for colony food stores and one for the brood population. The authors explore the interactions between food availability and forager mortality on colony fate. In Betti et al. (2014), a generic disease model similar to Kribs-Zaleta and Mitchell (2014) is studied. This model explicitly accounts for food storage as in Khoury et al. (2013) and assumes that the eclosion rate is limited by both the worker population and food availability. The resulting system of five ODEs is studied numerically through a sensitivity analysis, including an investigation of Wintering effects, by adjusting the growth rate, forager recruitment rate and food production rate. As in Kribs-Zaleta and Mitchell (2014), Betti et al. (2014) also assumes direct transmission between bees, without a vector. It is important to note that all of the hive-forager models discussed above study only the constant coefficient case. Russell et al. (2013) study the hive-forager model with food availability in Khoury et al. (2013) by taking into account seasonal variations and by temporally varying the egg laying rate of the queen bee. They observe the dynamics of the bee population over the period of 3 years and find that colony survival is influenced by forager mortality rates, food availability and factors that affect the age at which worker bees transition from hive bees to foragers.

In this paper, we present a mathematical model for the dynamics of a honeybee colony affected by varroa mites, ABPV and division of labour between hive and forager bees. The model is a combination of existing models that independently describe the varroa-ABPV (Ratti et al. 2015) and division of labour (Khoury et al. 2011) systems, with a provision for increased forager bee mortality due to homing failure (Henry et al. 2012); the combined system consists of five nonlinear ODEs. Using a combination of stability analysis and numerical simulations, we investigate (i) stability of equilibria in an autonomous and non-autonomous presentation of the model, and (ii) the effect of forager mortality parameters on the strength and survival of the colony under various varroacide treatment conditions in a non-autonomous (full) presentation of the model.

2 Mathematical Model

2.1 Model Assumptions

Our model is based on these assumptions:

• 1. Following Khoury et al. (2011), the healthy bee population is divided into hive bees and foragers. The base model is combined with the model in Ratti et al. (2015) to incorporate the effect of mites and virus. The resulting model is formulated in terms of the dependent variables: (i) uninfected hive bees, (ii) uninfected forager bees, (iii) infected hive bees, (iv) virus-carrying mites and (v) virus-free mites. Since the bees infected with ABPV are not able to fly and suffer rapid death, it is assumed that they are not recruited as foragers.

• 2. Unlike Ratti et al. (2012, 2015), where the mite population is categorized into virus-carrying mites and the total mite population, the mite population is categorized into virus-carrying mites and virus-free mites. This categorization allows us to study the virus-free mites as a separate class of individuals. We also assume that the maximum birth rate for virus-free and virus-carrying mites is the same.

• 3. Since a minimum number of healthy worker bees are required to take care of the brood, bee eclosion is dependent on the number of worker bees. We assume the number of workers to be the sum of the hive bees and foragers based on Khoury et al. (2011). Following Eberl et al. (2010), we formulate this assumption in the form of a sigmoidal Hill function, which introduces an Allee effect.

• 4. Following Betti et al. (2014), Eberl et al. (2010), Khoury et al. (2011), Kribs-Zaleta and Mitchell (2014), Petric et al. (2016), Ratti et al. (2012, 2015) and Sumpter and Martin (2004), we assume that the queen bee is not affected by the disease. This assumption implies that the egg laying rate of the queen is independent of the mites and virus.

• 5. We assume that the only route of virus transmission is horizontal transmission vectored by varroa mites. In accordance with (Genersch and Aubert 2010; Miranda et al. 2010; ZKBS 2012), the mites are treated as a mechanical vector.

• 6. In accordance with Martin (1998) and Moore et al. (2015), we assume that the pupae affected with ABPV die quickly before developing into adult bees and so all newly born bees are uninfected. To incorporate this assumption, we follow Sumpter and Martin (2004) and include a term that represents the decrease in bee eclosion rate due to virus-carrying mites.

• 7. Following Ratti et al. (2015), we account for varroacide treatment by introducing additional sink terms for the mites and bees depending on varroacide treatment. However, we assume that the varroacide has a much stronger effect on the mites than on the bees.

• 8. We assume that hive bees, forager bees and infected bees die due to both natural causes and due to mites feeding on them and/or mites transmitting viral infection. As in Ratti et al. (2012, 2015), the death term is divided into two components one that depends on mites and one that does not. Since the mite population was considered to be a constant in Eberl et al. (2010) and Sumpter and Martin (2004), it was unnecessary to explicitly include the effect of mites on the life span of bees. In the absence of more detailed information, we assume here that death terms of bees due to mites are in first-order approximation proportional to both, the number of bees and mites. While it would probably be more realistic to have some type of saturation effects, this seems the simplest assumption for now, in the absence of more detailed information. In the case of foragers, along with the natural death rate and death rate due to mites, the loss of foragers due to homing failure is considered as well, as a third factor. Here, we follow the approach of Henry et al. (2012). We further assume that the death rate of infected hive bees is higher than the death rates of uninfected hive bees.

• 9. Following Khoury et al. (2011, 2013), we assume that in the absence of foragers, hive bees are recruited to the foraging class at a maximum rate. As the number of foragers increases, the rate of recruitment of hive bees to foraging decreases following social inhibition. We formulate this process of social inhibition as a Holling type II functional response.

• 10. The mite population is dependent on the availability of brood in the hive. This leads to the fact that increases in the mite population are limited by colony strength [which is a measure of brood size, as in Ratti et al. (2012, 2015)]. We use a logistic model to describe the growth of the mite population. We assume that mites that carry the ABPV virus produce offspring that carries the virus, and mites that do not carry the virus produce virus-free offspring, and that mites that do and do not carry virus have the same logistic growth parameters. This is a simplifying assumption which we introduced for now, in the absence of more detailed information.

• 11. The dynamics of disease transmission for ABPV from mites to bees is described as originally worked out in Sumpter and Martin (2004) and later used in Eberl et al. (2010) and Ratti et al. (2012, 2015).

• 12. We assume that there is no flow of mites into and out of the colony via foragers. The only process through which mites leave the colony is through the varroacide treatment.

• 13. Biological parameters change with the seasons, to account for this we assume that all model parameters are periodic functions.

2.2 Model Equations

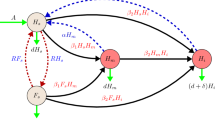
The resulting model reads

$$\begin{aligned} \frac{\mathrm{d}x_h}{\mathrm{d}t}= & {} \mu g(x_h+x_f)h(m)-\beta _1 m \frac{x_h}{x_h+y+x_f}-(d_1+\delta _1) x_h\nonumber \\&-\gamma _1 (m+n) x_h -x_hR(x_h,x_f), \end{aligned}$$

(1)

$$\begin{aligned} \frac{\mathrm{d}x_f}{\mathrm{d}t}= & {} x_hR(x_h,x_f)-\beta _1 m \frac{x_f}{x_h+y+x_f}-(p+d_2+\delta _2) x_f \nonumber \\&-\gamma _2 (m+n) x_f, \end{aligned}$$

(2)

$$\begin{aligned} \frac{\mathrm{d}y}{\mathrm{d}t}= & {} \beta _1 m \frac{x_h+x_f}{x_h+y+x_f}-(d_3+\delta _3) y-\gamma _3 (m+n)y, \end{aligned}$$

(3)

$$\begin{aligned} \frac{\mathrm{d}m}{\mathrm{d}t}= & {} rm\left( 1-\frac{m+n}{\alpha (x_h+y+x_f)}\right) +\beta _2 n\frac{y}{x_h+y+x_f}\nonumber \\&-\beta _3 m \frac{x_h+x_f}{x_h+y+x_f} -\delta _4 m, \end{aligned}$$

(4)

$$\begin{aligned} \frac{\mathrm{d}n}{\mathrm{d}t}= & {} rn\left( 1-\frac{m+n}{\alpha (x_h+y+x_f)}\right) -\beta _2 n \frac{y}{x_h+y+x_f}\nonumber \\&+\beta _3 m \frac{x_h+x_f}{x_h+y+x_f} -\delta _5 n, \end{aligned}$$

(5)

where

• $x_h$ is the number of uninfected hive bees,

• $x_f$ is the number of uninfected forager bees,

• y is the number of infected hive bees,

• m is the number of virus-carrying mites, and

• n is the number of virus-free mites.

The parameters are assumed to be non-negative and periodic functions of time with period T; in practice $T = 1$ year.

The parameter $\mu$ in (1) is the maximum eclosion rate, specified as the number of worker bees (i.e. hive bees) emerging per day.

The function $g(x_h+x_f)$ expresses that a sufficiently large number of healthy worker bees is required to care for the brood. We think of $g(x_h+x_f)$ as a switch function. If $x_h+x_f$ falls below a critical value, which may vary seasonally, essential work in the maintenance of the brood cannot be carried out anymore and no new bees are born. If $x_h+x_f$ is above this value, the eclosion of bees is not hampered. Thus $g(0,\cdot )=0$, $\frac{dg(0)}{\mathrm{d}x_h}\ge 0$, $\frac{dg(0)}{\mathrm{d}x_f}\ge 0$, $\lim _{x_h+x_f\rightarrow \infty } g(x_h+x_f)=1$. A convenient formulation of such switch like behaviour is given by the sigmoidal Hill function

$$\begin{aligned} g(x_h+x_f)=\frac{(x_h+x_f)^i}{K^i+(x_h+x_f)^i}, \end{aligned}$$

(6)

where the parameter K is the size of the bee colony at which the eclosion rate is half the maximum possible rate and the integer exponent $i>1$. If $K=0$ is chosen, then the bee eclosion term of the original model of Sumpter and Martin (2004) is recovered. Then the brood is always reared at maximum capacity, independent of the actual bee population size, because $g(x_h+x_f)\equiv 1$.

The function h(m) in (1) indicates that the eclosion rate is affected by the presence of virus-carrying mites in the hive. This modulation of the eclosion rate is particularly important for viruses like ABPV that kill infected pupae before they develop into adult bees. The function h(m) is assumed to decrease as m increases, $h(0)=1$, $\frac{\mathrm{d}h}{\mathrm{d}mm}(m)<0$ and $\lim _{m\rightarrow \infty } h(m)=0$; Sumpter and Martin (2004) suggests that this is an exponential function $h(m) \approx \mathrm{e}^{-m k}$, where k is non-negative. We will use this expression in computer simulations.

The parameter $\beta _2$ in (4) is the rate at which mites that do not carry the virus acquire it. The rate at which infected mites lose their virus to an uninfected host is $\beta _3$. The rate at which uninfected (hive and forager) bees become infected is $\beta _1$, in units of bees per virus-carrying mite and time. We assumed that the rate at which hive bees get infected (i.e. $\beta _1$) is the same as the rate at which foragers get infected (i.e. $\beta _2$). With this assumption, the first term in (3) becomes the rate at which total bees get infected.

Finally, $d_1$, $d_2$ and $d_3$ are the death rates for uninfected hive bees, uninfected foragers and infected hive bees. We can assume that infected bees live shorter lives than healthy bees, thus $d_3 > d_1$ and $d_3>d_2$.

The seasonal averages of the parameters $\beta _i(i=1,2,3), d_1,d_2,d_3,\mu , k$, $\alpha ,r,K,$ $\sigma _1,\sigma _2$ and $\gamma _i$ $(i=1,2,3)$ are given in Table 1. We assume that hive bees are not recruited as foragers in winter, i.e. the parameter $\sigma _1=0$ in Winter.

Table 1 Seasonal averages of some of the model parameters, derived from the data in Khoury et al. (2011), Martin (1998, 2001b), Ratti et al. (2012) and Sumpter and Martin (2004)

By r we denote the maximum mite birth rate. The carrying capacity for the mites changes with the host population size, and is characterized by the parameter $\alpha$, the average number of mites that can be sustained per bee.

The parameter p in Eq. (2) represents the rate at which foragers are lost, i.e. forager mortality due to homing failure.

Mites contribute to an increased mortality of bees. This factor is considered in (1), (2) and (3) by including death terms that depend on the total mite population ($m+n$); the parameters $\gamma _{1,2,3}$ are the rates at which mites kill bees. We assume that the mites kill the sick bees more quickly. Thus, $\gamma _3>\gamma _1$ and $\gamma _3>\gamma _2$.

As in Khoury et al. (2011), the term $R(x_h,x_f)$ in Eq. (1) represents the effect of social inhibition on the recruitment rate and is formulated as

$$\begin{aligned} R(x_h,x_f)=\sigma _1-\sigma _2\left( \frac{x_f}{x_h+x_f}\right) \end{aligned}$$

(7)

where the parameter $\sigma _1$ is the maximum rate at which hive bees are recruited as foragers when there are no foragers present in the colony. The term $\sigma _2 \frac{x_f}{x_h+x_f}$ represents social inhibition, that is, the process whereby a surplus of foragers causes the foragers to revert to being hive bees. We assume that social inhibition is directly proportional to the forager population present in the colony.

Remark 2.1

Our model (1)–(7) presents a general framework that encompasses the features of existing models in the literature (Khoury et al. 2011; Kribs-Zaleta and Mitchell 2014; Ratti et al. 2012) under particular assumptions. For instance, the model in Khoury et al. (2011) can be obtained if we study a honeybee colony without initial disease infestation (neither parasites nor viruses) (i.e. $y=m=n=0$ at $t=0$), eclosion rate of bees is modelled by Holling type II term (i.e. $i=1$) and the hive bees and forager bees do not die from natural (non-disease) causes ($d_1=d_2=0$).

The model in Kribs-Zaleta and Mitchell (2014) is a special case of our model obtained by assuming a hypothetical infection in which there is no vector involved in the disease transmission. It is also assumed that (i) the eclosion rate of bees depends only on the hive bees and not on the total bee population, i.e. $g(x_h+x_f)=g(x_h)$, and (ii) the hive bees do not die of natural causes, i.e. $d_1=0$; they are only recruited as foragers. The assumption regarding the brood maintenance term in Khoury et al. (2011) still holds in Kribs-Zaleta and Mitchell (2014).

The model in Ratti et al. (2012) can be obtained from our model by simply assuming that the total population is not divided into categories based on the division of tasks, i.e. if $x_h+x_f=x$.

3 Model with Constant Parameters

We first study the model with constant coefficients as in Eberl et al. (2010) and Ratti et al. (2012). This study will allow us to determine critical parameter ranges of the model, and guide the selection of simulation scenarios later on. In order to prepare for the analysis of the complete five-dimensional model (1)–(5), we start our investigation by studying smaller, more easily accessible sub-models. We begin by discussing the model for a healthy bee colony without mites and virus. In a second preliminary step, we will introduce mites into the system but not the virus. The complete model will be studied with the help of the results from these simpler special cases.

3.1 The Two-Dimensional Disease-Free Bee Model

In the absence of mites and viruses, the model becomes

$$\begin{aligned} \dot{x_h}= & {} \mu g(x_h+x_f)-d_1 x_h-x_h\left( \sigma _1-\sigma _2\frac{x_f}{x_h+x_f}\right) \end{aligned}$$

(8)

$$\begin{aligned} \dot{x_f}= & {} x_h\left( \sigma _1-\sigma _2\frac{x_f}{x_h+x_f}\right) -(p+d_2)x_f \end{aligned}$$

(9)

where $g(x_h+x_f)=\frac{(x_h+x_f)^i}{K^i+(x_h+x_f)^i}$. We assume that the parameters are positive. We study here the case for $i > 1$ and assume i to be an integer, whereas the case for $i=1$ was already studied in Khoury et al. (2011).

Proposition 3.1

(Existence of equilibria) We define

$$\begin{aligned} F:=\frac{1}{2}\left( \frac{\sigma _1-\sigma _2-p-d_2}{p+d_2}+ \sqrt{\left( \frac{\sigma _1-\sigma _2-p-d_2}{p+d_2}\right) ^2+\frac{4\sigma _1}{p+d_2}} \right) , \end{aligned}$$

(10)

and

$$\begin{aligned} a:= -\frac{\mu }{\frac{\sigma _2 F}{1+F}-d_1-\sigma _1}. \end{aligned}$$

The trivial equilibrium (0, 0) of the bee-only model (8)–(9) always exists. If

$$\begin{aligned} \frac{\sigma _2 F}{1+F}-d_1-\sigma _1>0, \end{aligned}$$

(11)

then it is the only equilibrium. If the inequality is reversed, then two positive equilibria $(x_{h_1}^*,x_{f_1}^*)$ and $(x_{h_2}^*,x_{f_2}^*)$ with $x_{f_1}^*= F x_{h_1}^*$ and $x_{f_2}^*= F x_{h_2}^*$ exist if furthermore

$$\begin{aligned} a>\frac{Ki}{1+F}(i-1)^{-(1+1/i)} \end{aligned}$$

Proof

That (0, 0) is always an equilibrium is immediate from (8), (9). From (9) it follows that positive equilibrium points $(x_h^*,x_f^*)$ need to satisfy

$$\begin{aligned} x_f^2+\left( \frac{\sigma _2+p+d_2-\sigma _1}{p+d_2}\right) x_hx_f-\sigma _1 x_h^2=0, \end{aligned}$$

(12)

which gives between $x_h^*$ and $x_f^*$ the relationship

$$\begin{aligned} x_f^*=Fx_h^* \end{aligned}$$

(13)

The values of $x_h^*$ can then be calculated from (1) as polynomial roots of

$$\begin{aligned} f(x_h):=x_h^{i}-ax_h^{i-1}+\left( \frac{K}{1+F}\right) ^i=0. \end{aligned}$$

(14)

With Descartes’ rule of signs, there are two positive roots if $a<0$ and none otherwise. We have $f(0)>0$ and, as $x_h \rightarrow +\infty$, $f(x_h)\rightarrow +\infty$. Therefore, for two positive roots of $f(x_h)$ to exist, it is required that there is an $\hat{x}_h>0$ s.t $f(\hat{x}_h)<0$. The minimum of f is attained for

$$\begin{aligned} x_h = a \left( \frac{i-1}{i}\right) \end{aligned}$$

(15)

and $f(x_h^*)<0$ if

$$\begin{aligned} a>\frac{Ki}{1+F}(i-1)^{-(1+1/i)}. \end{aligned}$$

(16)

$\square$

Proposition 3.2

(Stability of trivial equilibrium) The trivial equilibrium (0, 0) of the model (8)–(9) is asymptotically stable.

Proof

It follows from the tangent criterion that positive initial data lead to non-negative solutions. The stability of the trivial equilibrium is proved using differential inequalities. We note that for $x_h \ge 0$ and $x_f \ge 0$,

$$\begin{aligned} \dot{x_h}+\dot{x_f}&=\mu g(x_h+x_f)-d_1x_h-(p+d_2)x_f\\&\le \mu g(x_h+x_f)-\delta (x_h+x_f)\\&=: G(x_h+x_f). \end{aligned}$$

where $\delta :={\text {min}}\{d_1,d_2+p\}$. Let x be the solution of $\dot{x}=G(x)$. Then, for small enough x we have $G(x)<0$, and $x(t)\rightarrow 0$ as $t\rightarrow 0$. By the comparison theorem, we have $x(t) \ge x_h+x_f\ge 0$, i.e. $x_h+x_f \rightarrow 0$. $\square$

This result means that, in order to establish itself as a properly working colony, a sufficiently large healthy adult bee population is required to take care of the brood. If the number of healthy bees in the colony falls below this critical value, the colony will die off.

Proposition 3.3

(Stability of non-trivial equilibria) Let $(x_h^*,x_f^*)$ be a positive equilibrium as per Proposition 3.1. It is stable if

$$\begin{aligned} \frac{i\mu K^i (x_{h}^*)^{i-1}(1+F)^{i-1}}{[K^i+(x_{h}^*)^i(1+F)^i]^2}<\frac{d_1+(p+d_2)F}{(1+F)^2}. \end{aligned}$$

Proof

The Jacobian matrix $J(x_h^*, F x_h^*)$ of the system (8)–(9) in the equilibrium is

$$\begin{aligned} J(x_{h}^*, F x_{h}^*)=\left[ \begin{array}{ll} \mu \frac{\partial g}{\partial x_{h}^*}-d_1-\sigma _1+\frac{\sigma _2 F^2}{(1+F)^2}&{}\quad \mu \frac{\partial g}{\partial x_{f}^*}+\frac{\sigma _2}{(1+F)^2}\\ \sigma _1-\frac{\sigma _2 F^2}{(1+F)^2}&{}\quad -\frac{\sigma _2}{(1+F)^2}-(p+d_2) \end{array}\right] \end{aligned}$$

(17)

where

$$\begin{aligned} \frac{\partial g}{\partial x_{h}^*}=\frac{\partial g}{\partial x_{f}^*}=\frac{i K^i x_{h}^{*^{i-1}} (1+F)^{i-1}}{(K^i+x_{h}^{*^i}(1+F)^i)^2}. \end{aligned}$$

(18)

The determinant of the Jacobian matrix is obtained as

$$\begin{aligned} {\text {det}}&=-\frac{\sigma _2}{(1+F)^2}\left( \mu g^\prime (x_{h})+(p+d_2)F^2-d_1\right) \nonumber \\&\quad -(p+d_2)(\mu g^\prime (x_{h})-d_1) \nonumber \\&\quad -\sigma _1(\mu g^\prime (x_{h})-(p+d_2)). \end{aligned}$$

(19)

For $\sigma _1$ we find from (10)

$$\begin{aligned} \sigma _1=(p+d_2)F+\frac{\sigma _2 F}{1+F} \end{aligned}$$

(20)

Thus, the determinant is positive if

$$\begin{aligned} \frac{i\mu K^i x_{h}^{i-1}(1+F)^{i-1}}{[K^i+x_{h}^i(1+F)^i]^2}<\frac{d_1}{(1+F)^2}+\frac{(p+d_2)F}{(1+F)^2}. \end{aligned}$$

(21)

If inequality (21) holds, then the trace of the Jacobian is negative. Positive determinant and negative trace imply stability. $\square$

3.2 The Three Dimensional Bee-Mite Model

We now investigate how the stability of the equilibria A, B and C changes when virus-free mites infest the colony. To this end, we study the bee-mite subsystem of (1)–(5),

$$\begin{aligned} \dot{x_h}= & {} \mu g(x_h+x_f)-(d_1+\delta _1) x_h-\gamma _1 n x_h-x_h\left( \sigma _1-\sigma _2\frac{x_f}{x_h+x_f}\right) \end{aligned}$$

(22)

$$\begin{aligned} \dot{x_f}= & {} x_h\left( \sigma _1-\sigma _2\frac{x_f}{x_h+x_f}\right) -(p+d_2+\delta _2)x_f-\gamma _2 n x_f \end{aligned}$$

(23)

$$\begin{aligned} \dot{n}= & {} rn\left( 1-\frac{n}{\alpha (x_h+x_f)}\right) -\delta _5 n \end{aligned}$$

(24)

Proposition 3.4

(Stability of the trivial equilibrium) The trivial equilibrium (0, 0, 0) of the model (22)–(24) is asymptotically stable.

Proof

That (0, 0, 0) is an equilibrium follows immediately from (22), (23), (24). We use the same argument as in Proposition 3.3. From (22) to (23), it follows that for $x_h>0, x_f>0$

$$\begin{aligned} \dot{x_h}+\dot{x_f}&=\mu g(x_h+x_f)-(d_1+\delta _1)x_h-(p+d_2+\delta _2)x_f-(\gamma _1 x_h+\gamma _2 x_f)n\\&\le \mu g(x_h+x_f)-\delta (x_h+x_f)\\&=: G(x_h+x_f). \end{aligned}$$

where $\delta ={\text {min}}\{\tilde{d_1}, \tilde{d_2}\},$ $\tilde{d_1}=d_1+\delta _1$ an, $\tilde{d_2}=d_2+p+\delta _2.$ Let $x_h+x_f=x$ and let x be the solution of $\dot{x}=G(x)$. Then for small enough x we have $G(x)<0$, and $x(t)\rightarrow 0$ as $t\rightarrow 0$. By the comparison theorem, we have $x(t) \ge x_h+x_f>0$, i.e. $x_h+x_f \rightarrow 0$. Moreover, note that for $n>\alpha x$, due to (24) we have $\dot{n}<0$. For small enough $\tilde{x}$ and $\tilde{n}>\alpha \tilde{x}$, the set

$$\begin{aligned} Z_{\{\tilde{x}, \tilde{n}\}}=\{x,n: 0<x<\tilde{x},0<n<\tilde{n} \} \end{aligned}$$

is positively invariant with inward pointing flux. Every solution starting from a point in the set $Z_{\{\tilde{x},\tilde{n}\}}$ enters a positively invariant set. We have $\dot{x}<0$ for small enough $\tilde{x}$, wherefore all solutions converge to (0, 0, 0). $\square$

This result means that, in order to establish itself as a properly working colony, a sufficiently large number of healthy worker (hive and forager) bees is required to maintain the hive.

Proposition 3.5

(Stability of mite-free equilibria) Suppose $(x_{h}^*, x_{f}^*)$ is a non-trivial equilibrium of (8)–(9) as per Proposition 3.1. Then $(x_{h}^*, x_{f}^*,0)$ is an equilibrium of (22)–(24). If $r-\delta _5>0$ then it is unstable. If the inequality is reversed, then it inherits the stability or instability of $(x_{h}^*, x_{f}^*)$ under (8)–(9).

Proof

That $(x_h^*,x_f^*,0)$ is an equilibrium follows immediately from the model equations. The Jacobian matrix $J(x_h^*, Fx_h^*, 0)$ is obtained as

$$\begin{aligned}&J(x_h^*, Fx_h^*,0)\\&\quad =\left[ \begin{array}{lll} \mu \frac{\partial g}{\partial x_h}-d_1-\delta _1-\sigma _1+\frac{\sigma _2 F^2}{(1+F)^2}&{}\quad \mu \frac{\partial g}{\partial x_f^*}+\frac{\sigma _2}{(1+F)^2}&{}\quad -\gamma _1 x_h^*\\ \sigma _1-\frac{\sigma _2 {F}^2}{(1+F)^2}&{}\quad -\frac{\sigma _2 }{(1+F)^2}-(p+d_2+\delta _2)&{}\quad -\gamma _2 Fx_h^*\\ 0&{}\quad 0 &{}\quad r-\delta _5\\ \end{array}\right] \end{aligned}$$

One eigenvalue is $\lambda _1 = r-\delta _5$, the other two are the eigenvalues of the top left $2\times 2$ submatrix, i.e. the eigenvalues of (17). $\square$

This means that the mite-free equilibria are stable if Eq. (21) is satisfied and the maximum birth rate of mites is less than their death rate due to varroacide treatment. It is also observed that in the absence of varroacide treatment, it is not possible for the hive to fight off the mites. On the other hand, if the mite-free equilibrium is unstable, then it is not clear whether the system converges to the trivial equilibrium or an endemic equilibrium. We will use numerical simulations to investigate this behaviour. It is important to note that these results are in agreement with the results corresponding to the stability of the mite-free equilibrium in Ratti et al. (2015).

3.3 The Complete Bee-Mite-Virus Model

We investigate now whether or not a stable, mite-infested honeybee colony can fight off the virus. To this end, we consider the complete five-dimensional model (25)–(29)

$$\begin{aligned} \frac{\mathrm{d}x_h}{\mathrm{d}t}= & {} \mu g(x_h+x_f)h(m)-\beta _1 m \frac{x_h}{x_h+y+x_f}-(d_1+\delta _1) x_h\nonumber \\&-\gamma _1 (m+n)x_h -x_h\left( \sigma _1-\sigma _2\frac{x_f}{x_h+x_f}\right) \end{aligned}$$

(25)

$$\begin{aligned} \frac{\mathrm{d}x_f}{\mathrm{d}t}= & {} x_h\left( \sigma _1-\sigma _2\frac{x_f}{x_h+x_f}\right) -\beta _1 m \frac{x_f}{x_h+y+x_f}\nonumber \\&-(p+d_2+\delta _2) x_f-\gamma _2 (m+n) x_f \end{aligned}$$

(26)

$$\begin{aligned} \frac{\mathrm{d}y}{\mathrm{d}t}= & {} \beta _1 m \frac{x_h+x_f}{x_h+y+x_f}-(d_3+\delta _3) y-\gamma _3 (m+n)y \end{aligned}$$

(27)

$$\begin{aligned} \frac{\mathrm{d}mm}{\mathrm{d}t}= & {} rm\left( 1-\frac{m+n}{\alpha (x_h+y+x_f)}\right) +\beta _2 n\frac{y}{x_h+y+x_f}\nonumber \\&-\beta _3 m \frac{x_h+x_f}{x_h+y+x_f}-\delta _4 m \end{aligned}$$

(28)

$$\begin{aligned} \frac{\mathrm{d}n}{\mathrm{d}t}= & {} rn\left( 1-\frac{m+n}{\alpha (x_h+y+x_f)}\right) -\beta _2 n \frac{y}{x_h+y+x_f}\nonumber \\&+\beta _3 m \frac{x_h+x_f}{x_h+y+x_f}-\delta _5 n \end{aligned}$$

(29)

Proposition 3.6

(Stability of the disease-free equilibrium) Suppose $(x_h^*, x_f^*)$ is a non-trivial equilibrium of (8)–(9) as per Proposition 3.1. Then $(x_h^*, x_f^*,0,0,0)$ is an equilibrium of (25)–(29). If (i) $r-\beta _3-\delta _4<0$ and, (ii) $r-\delta _5<0$, then it inherits the stability or instability of $(x_h^*, x_f^*)$ under (8)–(9); if one of these two inequalities is reversed, then it is unstable.

Proof

That $(x_h^*,x_f^*,0,0,0)$ is an equilibrium follows immediately from the model equations. The Jacobian evaluated at this point is obtained as

$$\begin{aligned} J(x_h^*, F x_h^*,0, 0,0)=\left[ \begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} A+q(F) F^2&{}\mu \frac{\partial g}{\partial x_f}+q(F)&{} 0 &{} C &{} -\gamma _1 x_h\\ \sigma _1-q(F)F^2&{} -q(F)-D&{} 0&{}E&{} -\gamma _2 Fx_h^*\\ 0 &{} 0 &{} -d_3-\delta _3 &{} \beta _1 &{}0\\ 0 &{} 0 &{} 0 &{} r-\beta _3-\delta _4 &{} 0\\ 0&{}0 &{} 0 &{} \beta _3 &{} r-\delta _5\\ \end{array}\right] \end{aligned}$$

where

$$\begin{aligned} A= & {} \mu \frac{\partial g}{\partial x_h^*}-d_1-\delta _1-\sigma _1,\\ q(F)= & {} \frac{\sigma _2 }{(1+F)^2},\\ C= & {} \mu g(x_h^*+x_f^*)h^\prime (0)- \frac{\beta _1}{1+F}-\gamma _1 x_h,\\ D= & {} p+d_2+\delta _2,\\ E= & {} -\beta _1 \frac{F}{1+F}-\gamma _2 Fx_h^*\end{aligned}$$

Three of the eigenvalues are

$$\begin{aligned} \lambda _1=-d_3-\delta _3,\quad \lambda _2=r-\beta _3-\delta _4,\quad \lambda _3=r-\delta _5. \end{aligned}$$

Here $\lambda _1$ is always negative, the sign of the other two depends on parameters. The remaining two eigenvalues are the eigenvalues of the upper left $2\times 2$ submatrix, i.e. of (17). $\square$

This result means that the disease can be fought off if the varroacide treatment is strong enough to eradicate the virus-free mites, and if the virus-carrying mites lose their virus faster than the rate at which they are born. The disease-free equilibrium is always unstable in the absence of varroacide treatment. In Ratti et al. (2015), there is no condition on the transmission rate of virus because the population is divided into virus-carrying mites and total number of mites that infest the colony. In the absence of treatment, the stability conditions for our model are in agreement with Ratti et al. (2015).

3.4 Numerical Simulations of the Model with Constant Parameters

We now perform two computer simulation experiments on the model with constant coefficients. In the first experiment, we observe the effect of different forager mortality rates on the dynamics of a colony that is infested with mites and virus. In the second experiment, we compare the dynamics of a disease-free colony with the dynamics of a mite-virus-infested colony when both are exposed to pesticides ($p>0$). We simulate the loss of foragers due to exposure to pesticides; forager mortality rate is a measure of the level to which bees are exposed to pesticides. Following Henry et al. (2012), we study the first 3 months of a beekeeping season (i.e. the spring season) encompassing the blooming period of crops such as oilseed rape, maize, etc., that are treated with pesticides and visited by bees. The parameters $\mu , \beta _{1,2,3}, d_{1,2,3},k,r,\sigma _1,\sigma _2, \alpha$ and $\gamma _{1,2,3}$ for the spring season are taken from Table 1.

Fig. 1

(Color figure online) Comparison of the dynamics of mite-virus-infested honeybee populations with no homing failure (i.e. $p=0$), a low rate of homing failure (i.e. $p=0.13$) and a high rate of homing failure (i.e. $p=0.14$). The threshold value of p is 0.134. These results are obtained with parameters fixed at the spring values (Table 1). We assume that the bees are exposed to the treated crops for 30 days (i.e. $t=5$ to $t=35$) at the beginning of spring, and the shaded areas delineate the time period of exposure

3.4.1 Simulation Experiment 1: Effect of Forager Exposure to Treated Crops on a Colony That has Fought off the Virus

We begin the simulation experiment with the bee-mite steady-state solution where virus is present initially but fought off. We investigate whether the population grows back to the steady-state level after being exposed to a treated crop (see Fig. 1). We consider a base case when the colony is not exposed to the treated crops, which means that the forager mortality due to homing failure is 0 ($p=0$). In the absence of exposure, the total bee population is constant at 17, 581 bees. For a low rate of forager mortality due to homing failure (i.e. $p=0.13$), the colony population decreases to 8, 700 bees during the exposure period. After the exposure period ends, the population starts increasing and recovers to the same level from where it started before exposure. However, it takes about a year for the solution to revert to the pre-exposure equilibrium, which is much longer than the season for which the parameters hold. For a higher rate of forager mortality due to homing failure, i.e. $p=0.14$, the population before the exposure period starts is 20, 330 and decreases quickly to 2, 385 bees by the end of the exposure period. The population rapidly goes to zero after the exposure ends.

3.4.2 Simulation Experiment 2: Comparison of the Effect of Increased Forager Loss Between a Disease-Free and a Mite-Virus-Infested Colony

In this simulation experiment, we compare the effect of exposure to treated crops on the dynamics of a disease-free colony with a mite-virus-infested colony (Fig. 2). It is observed that the disease-infested colony follows the same trajectory as the disease-free colony, but the latter curve lies above the former. For the disease-free colony in the absence of exposure, the total bee population is constant at 18, 558 bees. When the colony is exposed to pesticides ($p = 0.13$), the population decreases to 7, 586 bees. After the exposure period ends, the population increases to 12, 395 bees by the end of the spring season. For the disease-infested colony in the absence of exposure, the total bee population is constant at 13,183 bees. When the colony is exposed to pesticides ($p = 0.13$), the population decreases to 4869 bees and then remains at the same level till the end of spring. To observe the long-term effect of disease on the dynamics of the colony with increased homing failure, we need to study the case of seasonally varying parameters instead of focussing on one season.

Fig. 2

(Color figure online) Comparison of the dynamics of honeybee populations between an exposed colony that is disease-free and an exposed colony ($p=0.13$) that is infested with mites and virus. We assume that the bees are exposed to the treated crops for 30 days (i.e. $t=5$ to $t=35$) at the beginning of spring and the shaded areas delineate the time period of exposure

4 Model with Seasonally Varying Parameters

4.1 Bee-Mite Model with Periodic Coefficients

Numerical simulations suggest the existence of non-trivial disease-free periodic solutions to (25)–(29) with dependence on the model parameters. Since a formal proof of the existence of non-trivial periodic solutions seems out of reach at this point, we conjecture the existence of such solutions, as observed in simulations. We first study the stability of the mite-free periodic solution of the bee-mite model and then the complete bee-mite-virus model, using Floquet theory. This will require the stability of the non-trivial periodic solutions of the bee-only model (8)–(9) which, however, cannot be easily carried out due to the algebraic complexity of the model equations. We will show that under certain conditions on parameters, the disease-free solutions of the 3- and 5-dimensional models inherit the stability of the periodic solution of (8)–(9).

Proposition 4.1

(Stability of mite-free periodic solution) Suppose $(x_h^*(t), x_f^*(t))$ is a periodic solution of the bee-only model (8)–(9). Then $(x_h^*(t), x_f^*(t),0)$ is a stable periodic solution of (22)–(24) if (i) the periodic solution $(x_h^*(t), x_f^*(t))$ of the bee-only model is stable and (ii) $\int _0^T{(r-\delta _5)\mathrm{d}t}\le 0$.

Proof

That a positive periodic solution of (8)–(9) defines a disease-free solution of (22)–(24) is immediate from the model equations. In order to analyse its stability, we use linearization and Floquet theory. We linearize the system about the periodic solution $(x_h^*,x_f^*,0)$, i.e. we investigate the long-term behaviour of the perturbation $u:=x_h-x_h^*$, $v:=x_f-x_f^*$, $w:=n-0$.

The Jacobian of the system is obtained as

$$\begin{aligned} J(x_h^*, Fx_h^*,0)=\left[ \begin{array}{l@{\quad }l@{\quad }l} A+q(F)F^2&{}\mu \frac{\partial g}{\partial x_f^*}+q(F)&{} -\gamma _1 x_h^*\\ \sigma _1-q(F)F^2&{} -q(F)-D&{} -\gamma _2F x_h^*\\ 0&{}0 &{} r-\delta _5\\ \end{array}\right] \end{aligned}$$

where $\frac{\partial g}{\partial x_h^*}=\frac{\partial g}{\partial x_f^*}$ is defined by (18) and

$$\begin{aligned} A= & {} \mu \frac{\partial g}{\partial x_h^*}-d_1-\delta _1-\sigma _1,\\ q(F)= & {} \frac{\sigma _2 }{(1+F)^2},\\ D= & {} p+d_2+\delta _2.\\ \end{aligned}$$

Thus, the system linearized about $(x_h^*, Fx_h^*,0)$ is

$$\begin{aligned} \left[ \begin{array}{l} \dot{u}\\ \dot{v}\\ \dot{w} \end{array}\right] =&J(x_h^*, Fx_h^*,0) \left[ \begin{array}{l} u\\ v\\ w \end{array}\right] .\\ \end{aligned}$$

Let $(u_i(t),v_i(t),w_i(t))$, $i=1,2,3$, be linearly independent solutions of the linearized system with the corresponding set of initial conditions

$$\begin{aligned} u_1(0)&=1, \quad u_2(0)=0, \quad u_3(0)=0,\\ v_1(0)&=0, \quad v_2(0)=1, \quad v_3(0)=0,\\ w_1(0)&=0, \quad w_2(0)=0, \quad w_3(0)=1. \end{aligned}$$

The fundamental matrix A(t) of the linearized system over the interval $0\le t\le T$, where T is the period, is obtained as

$$\begin{aligned} A(t)=\left[ \begin{array}{lll} u_1(t)&{}u_2(t)&{}u_3(t)\\ v_1(t)&{}v_2(t)&{}v_3(t)\\ w_1(t)&{}w_2(t)&{}w_3(t) \end{array}\right] \end{aligned}$$

where

$$\begin{aligned} u_1(t)= & {} I_1\left[ \int _0^t{I_2\left( \mu g^\prime (x_f^*)+\frac{\sigma _2 x_h^{*^2}}{(x_h^*+x_f^*)^2}\right) v_1(\rho )\mathrm{d}\rho }+1\right] ,\\ u_2(t)= & {} I_1\int _0^t{I_2\left( \mu g^\prime (x_f^*)+\frac{\sigma _2 x_h^{*^2}}{(x_h^*+x_f^*)^2}\right) v_2(\rho )\mathrm{d}\rho },\\ u_3(t)= & {} I_1\int _0^t{I_2\left[ \left( \mu g^\prime (x_f^*)+\frac{\sigma _2 x_h^{*^2}}{(x_h^*+x_f^*)^2}\right) v_2(\rho )-\gamma _1 x_h^*\mathrm{e}^{\int _0^\rho {(r-\delta _5) \mathrm{d}\tau }} \right] \mathrm{d}\rho }, \\ v_1(t)= & {} I_3\int _0^t{I_4\left( \sigma _1-\frac{\sigma _2 x_f^{*^2}}{(x_h^*+ x_f^*)^2}\right) u_1(\rho )\mathrm{d}\rho },\\ v_2(t)= & {} I_3\left[ \int _0^t{I_4\left( \sigma _1-\frac{\sigma _2 x_f^{*^2}}{(x_h^*+ x_f^*)^2}\right) u_2(\rho )\mathrm{d}\rho }+1\right] ,\\ v_3(t)= & {} I_3\int _0^t{I_4\left[ \left( \sigma _1-\frac{\sigma _2 x_f^{*^2}}{(x_h^*+ x_f^*)^2}\right) u_3(\rho )-\gamma _2 x_f^*\mathrm{e}^{\int _0^\rho {(r-\delta _5) \mathrm{d}\tau }}\right] \mathrm{d}\rho },\\ w_1(t)= & {} 0,\\ w_2(t)= & {} 0,\\ w_3(t)= & {} \mathrm{e}^{\int _0^t{(r-\delta _5) \mathrm{d}\rho }}, \end{aligned}$$

and

$$\begin{aligned} I_1= & {} \mathrm{e}^{\int _0^t{\left[ \mu g^\prime (x_h^*)-d_1-\delta _1-\sigma _1+\frac{\sigma _2 x_f^{*^2}}{\left( x_h^*+x_f^*\right) ^2}\right] \mathrm{d}\rho }},\\ I_2= & {} \mathrm{e}^{-\int _0^\rho {\left[ \mu g'(x_h^*)-d_1-\delta _1-\sigma _1+\frac{\sigma _2 x_f^{*^2}}{\left( x_h^*+x_f^*\right) ^2}\right] \mathrm{d}\tau }},\\ I_3= & {} \mathrm{e}^{-\int _0^t\left[ {\frac{\sigma _2 x_h^{*^2}}{\left( x_h^*+x_f^*\right) ^2}+p+d_2+\delta _2}\right] \mathrm{d}\rho },\\ I_4= & {} \mathrm{e}^{\int _0^\rho \left[ {\frac{\sigma _2 x_h^{*^2}}{\left( x_h^*+x_f^*\right) ^2}+p+d_2+\delta _2}\right] \mathrm{d}\tau },\\ I_5= & {} \mu g\left( x_h^*+x_f^*\right) k-\frac{\beta _1 x_h^*}{x_h^*+x_f^*}-\gamma _1x_h^*. \end{aligned}$$

The transition matrix at $t=T$ is

$$\begin{aligned} C=A(T)=\left[ \begin{array}{lll} u_1(T)&{}u_2(T)&{}u_3(T)\\ v_1(T)&{}v_2(T)&{}v_3(T)\\ 0&{}0&{}\mathrm{e}^{\int _0^T{(r-\delta _5) \mathrm{d}t}} \end{array}\right] . \end{aligned}$$

One eigenvalue of the matrix is

$$\begin{aligned} \lambda _1&= \mathrm{e}^{\int _0^T{(r-\delta _5) \mathrm{d}t}}. \end{aligned}$$

The remaining two eigenvalues are the same as the eigenvalues of the transition matrix of the bee-only model (8)–(9). Therefore, the stability of $(x_h^*,x_f^*)$ carries over to the bee-mite model if $\int _0^T{(r-\delta _5)\mathrm{d}t}\le 0$. $\square$

This result indicates that the mite infestation in a colony can be fought off if (i) the cumulative death rate of mites due to treatment is greater than or equal to their birth rate, and (ii) the periodic solution of the bee-only model is stable. The mite-free periodic solution is always unstable in the absence of varroacide treatment, when $\delta _5=0$. That is, a mite invasion cannot be fought off by the bees alone as a consequence of the logistic growth assumption for mites. This generalizes the findings in Ratti et al. (2012) for the autonomous models presented there. If $(x_h^*,x_f^*,0)$ is unstable, it is not clear whether the system will converge to the trivial state or whether, for example, an endemic periodic solution will be obtained in which the bee colony persists in the presence of mites. The simulations in Eberl et al. (2014) and Ratti et al. (2012, 2015)) suggest the possibility of such an endemic periodic bee-mite solution for certain parameters. While in principle Floquet theory could be used to derive a stability condition for such a periodic solution, algebraic complexity prevented this. Instead, we study the system behaviour through numerical simulations.

4.2 Bee-Mite-Virus Model with Periodic Coefficients

Proposition 4.2

(Stability of the disease-free periodic solution) Suppose $(x_h^*(t), x_f^*(t))$ is a periodic solution of the bee-only model (8)–(9). Then, $(x_h^*(t), x_f^*(t),0,0,0)$ is a stable periodic solution of (25)–(29) if (i) the periodic solution $(x_h^*(t), x_f^*(t))$ of bee-only model is stable, (ii) $\int _0^T{(r-\beta _3-\delta _4) \mathrm{d}t}\le 0$ and (iii) $\int _0^T{(r-\delta _5) \mathrm{d}t} \le 0$.

Proof

That a positive periodic solution of (8)–(9) defines a disease-free solution of (25)–(29) is immediate from the model equations. In order to analyse its stability, we use linearization and Floquet theory. We linearize the system about the periodic solution $(x_h^*,x_f^*,0,0,0)$, i.e. we investigate the long-term behaviour of the perturbation $u:=x_h-x_h^*$, $v:=x_f-x_f^*$, $w:=y-0$, $a:=m-0$, $b:=n-0$.

The Jacobian $J(x_h^*, F x_h^*,0, 0,0)$ of the system is obtained as

$$\begin{aligned} J=\left[ \begin{array}{lllll} A+q(F) F^2&{}\mu \frac{\partial g}{\partial x_f^*}+q(F)&{} 0 &{} C &{} -\gamma _1 x_h\\ \sigma _1-q(F)F^2&{} -q(F)-D&{} 0&{}E&{} -\gamma _2 Fx_h^*\\ 0 &{} 0 &{} -d_3-\delta _3 &{} \beta _1 &{}0\\ 0 &{} 0 &{} 0 &{} r-\beta _3-\delta _4 &{} 0\\ 0&{}0 &{} 0 &{} \beta _3 &{} r-\delta _5\\ \end{array}\right] \end{aligned}$$

where

$$\begin{aligned} A= & {} \mu \frac{\partial g}{\partial x_h^*}-d_1-\delta _1-\sigma _1,\\ q(F)= & {} \frac{\sigma _2 }{(1+F)^2},\\ C= & {} \mu g\left( x_h^*+x_f^*\right) h^\prime (0)- \frac{\beta _1}{1+F}-\gamma _1 x_h,\\ D= & {} p+d_2+\delta _2,\\ E= & {} -\beta _1 \frac{F}{1+F}-\gamma _2 Fx_h^*. \end{aligned}$$

Thus, the system linearized about $(x_h^*,Fx_h^*,0,0,0)$ is

$$\begin{aligned} \left[ \begin{array}{l} \dot{u}\\ \dot{v}\\ \dot{w}\\ \dot{a}\\ \dot{b} \end{array}\right] =&J\left( x_h^*,Fx_h^*,0,0,0\right) \left[ \begin{array}{l} u\\ v\\ w\\ a\\ b \end{array}\right] .\\ \end{aligned}$$

Let $(u_i(t), v_i(t), w_i(t), a_i(t), b_i(t))$, $i=1,2,\ldots 5$ be linearly independent solutions of the linearized system with corresponding set of initial conditions

$$\begin{aligned} u_1(0)= & {} 1, \quad u_2(0)= & {} 0, \quad u_3(0)= & {} 0,\quad u_4(0)= & {} 0, \quad u_5(0)= & {} 0,\\ v_1(0)= & {} 0, \quad v_2(0)= & {} 1, \quad v_3(0)= & {} 0,\quad v_4(0)= & {} 0, \quad v_5(0)= & {} 0,\\ w_1(0)= & {} 0, \quad w_2(0)= & {} 0, \quad w_3(0)= & {} 1, \quad w_4(0)= & {} 0, \quad w_5(0)= & {} 0,\\ a_1(0)= & {} 0, \quad a_2(0)= & {} 0, \quad a_3(0)= & {} 0, \quad a_4(0)= & {} 1, \quad a_5(0)= & {} 0,\\ b_1(0)= & {} 0, \quad b_2(0)= & {} 0, \quad b_3(0)= & {} 0, \quad b_4(0)= & {} 0, \quad b_5(0)= & {} 1. \end{aligned}$$

The fundamental matrix A(t) of the linearized system over the interval $0\le t\le T$, where T is the period, is obtained as

$$\begin{aligned} A(t)=\left[ \begin{array}{lllll} u_1(t)&{}u_2(t)&{}u_3(t)&{}u_4(t)&{}u_5(t)\\ v_1(t)&{}v_2(t)&{}v_3(t)&{}v_4(t)&{}v_5(t)\\ w_1(t)&{}w_2(t)&{}w_3(t)&{}w_4(t)&{}w_5(t)\\ a_1(t)&{}a_2(t)&{}a_3(t)&{}a_4(t)&{}a_5(t)\\ b_1(t)&{}b_2(t)&{}b_3(t)&{}b_4(t)&{}b_5(t)\\ \end{array}\right] , \end{aligned}$$

where

$$\begin{aligned} u_1(t)= & {} I_1\left[ \int _0^t{-I_2\left( \mu g^\prime (x_f^*)+\frac{\sigma _2 x_h^{*^2}}{(x_h^*+x_f^*)^2}\right) v_1(\rho )\mathrm{d}\rho }+1\right] ,\\ u_2(t)= & {} I_1\int _0^t{-I_2\left( \mu g^\prime (x_f^*)+\frac{\sigma _2 x_h^{*^2}}{(x_h^*+x_f^*)^2}\right) v_2(\rho )\mathrm{d}\rho }, \\ u_3(t)= & {} I_1\int _0^t{-I_2\left( \mu g^\prime (x_f^*)+\frac{\sigma _2 x_h^{*^2}}{(x_h^*+x_f^*)^2}\right) v_3(\rho )\mathrm{d}\rho }, \\ u_4(t)= & {} I_1\int _0^t{I_2\left[ \left( \mu g^\prime (x_f^*)+\frac{\sigma _2 x_h^{*^2}}{(x_h^*+x_f^*)^2}\right) v_4(\rho )+I_5+\gamma _1 x_h^*b_4(\rho ) \right] \mathrm{d}\rho }, \\ u_5(t)= & {} I_1\int _0^t{I_2\left[ \left( \mu g^\prime (x_f^*)+\frac{\sigma _2 x_h^{*^2}}{(x_h^*+x_f^*)^2}\right) v_5(\rho )+\gamma _1 x_h^*b_5(\rho ) \right] \mathrm{d}\rho }, \\ v_1(t)= & {} I_3\int _0^t{I_4\left( \sigma _1-\frac{\sigma _2 x_f^{*^2}}{(x_h^*+x_f^*)^2}\right) u_1(\rho )\mathrm{d}\rho },\\ v_2(t)= & {} I_3\left[ \int _0^t{I_4\left( \sigma _1-\frac{\sigma _2 x_f^{*^2}}{(x_h^*+x_f^*)^2}\right) u_2(\rho )\mathrm{d}\rho }+1\right] , \\ v_3(t)= & {} I_3\int _0^t{I_4\left( \sigma _1-\frac{\sigma _2 x_f^{*^2}}{(x_h^*+x_f^*)^2}\right) u_3(\rho )\mathrm{d}\rho },\\ v_4(t)= & {} I_3\int _0^t I_4\left[ \left( \sigma _1-\frac{\sigma _2 x_f^{*^2}}{(x_h^*+x_f^*)^2}\right) u_4(\rho )+\gamma _2 x_f^*(a_4(\rho )+b_4(\rho ))\right. \\&\left. +\frac{\beta _1 x_f^*a_4(\rho )}{x_h^*+x_f^*}\right] \mathrm{d}\rho ,\\ v_5(t)= & {} I_3\int _0^t{I_4\left[ \left( \sigma _1-\frac{\sigma _2 x_f^{*^2}}{(x_h^*+x_f^*)^2}\right) u_5(\rho )+\gamma _2 x_f^*b_5(\rho )\right] \mathrm{d}\rho },\\ w_3(t)= & {} \mathrm{e}^{\int _0^t{(-d_3-\delta _3) \mathrm{d}\rho }},\\ w_4(t)= & {} -\mathrm{e}^{\int _0^t{(-d_3-\delta _3) \mathrm{d}\rho }}\int _0^t{\beta _1\mathrm{e}^{\int _0^\rho {(r-\beta _3-\delta _4+d_3+\delta _3)\mathrm{d}\tau }}\mathrm{d}\rho },\\ a_4(t)= & {} \mathrm{e}^{\int _0^t{(r-\beta _3-\delta _4) \mathrm{d}\rho }},\\ b_4(t)= & {} \mathrm{e}^{\int _0^t{(r-\delta _5) \mathrm{d}\rho }}\int _0^t{-\beta _3\mathrm{e}^{\int _0^\rho {(\delta _5-\beta _3-\delta _4)\mathrm{d}\tau }}\mathrm{d}\rho },\\ b_5(t)= & {} \mathrm{e}^{\int _0^t{(r-\delta _5) \mathrm{d}\rho }}. \end{aligned}$$

and all other variables are zero.

Here

$$\begin{aligned} I_1= & {} \mathrm{e}^{\int _0^t{\left[ \mu g^\prime (x_h^*)-d_1-\delta _1-\sigma _1+\frac{\sigma _2 x_f^{*^2}}{\left( x_h^*+x_f^*\right) ^2}\right] \mathrm{d}\rho }},\\ I_2= & {} \mathrm{e}^{-\int _0^\rho {\left[ \mu g'(x_h^*)-d_1-\delta _1-\sigma _1+\frac{\sigma _2 x_f^{*^2}}{\left( x_h^*+x_f^*\right) ^2}\right] \mathrm{d}\tau }},\\ I_3= & {} \mathrm{e}^{-\int _0^t\left[ {\frac{\sigma _2 x_h^{*^2}}{\left( x_h^*+x_f^*\right) ^2}+p+d_2+\delta _2}\right] \mathrm{d}\rho },\\ I_4= & {} \mathrm{e}^{\int _0^\rho \left[ {\frac{\sigma _2 x_h^{*^2}}{\left( x_h^*+x_f^*\right) ^2}+p+d_2+\delta _2}\right] \mathrm{d}\tau },\\ I_5= & {} \mu g\left( x_h^*+x_f^*\right) k-\frac{\beta _1 x_h^*}{x_h^*+x_f^*}-\gamma _1x_h^*. \end{aligned}$$

The transition matrix at $t=T$ is

$$\begin{aligned} C=A(T)=\left[ \begin{array}{lllll} u_1(T)&{}u_2(T)&{}u_3(T)&{}u_4(T)&{}u_5(T)\\ v_1(T)&{}v_2(T)&{}v_3(T)&{}v_4(T)&{}v_5(T)\\ 0&{}0&{}\mathrm{e}^{\int _0^T{(-d_3-\delta _3) \mathrm{d}t}}&{}w_4(T)&{}0\\ 0&{}0&{}0&{}\mathrm{e}^{\int _0^T{(r-\beta _3-\delta _4) \mathrm{d}t}}&{}0\\ 0&{}0&{}0&{}b_4(T)&{}\mathrm{e}^{\int _0^T{(r-\delta _5) \mathrm{d}t}}\\ \end{array}\right] . \end{aligned}$$

Three eigenvalues are given by

$$\begin{aligned} \lambda _1&= \mathrm{e}^{\int _0^T{(-d_3-\delta _3) \mathrm{d}t}},\\ \lambda _2&= \mathrm{e}^{\int _0^T{(r-\beta _3-\delta _4) \mathrm{d}t}},\\ \lambda _3&= \mathrm{e}^{\int _0^T{(r-\delta _5) \mathrm{d}t}}. \end{aligned}$$

The remaining two eigenvalues are the eigenvalues of the transition matrix of the bee-only model (8)–(9). Since parameters $d_3$ and $\delta _3$ are non-negative, $|\lambda _1|\le 1$. Therefore, the stability of $(x_{h}^*,x_{f}^*)$ carries over to the bee-mite-virus model if $\int _0^T{(r-\beta _3-\delta _4) \mathrm{d}t}\le 0$ and $\int _0^T{(r-\delta _5) \mathrm{d}t} \le 0$. $\square$

This result indicates that the disease infestation in a colony can be fought off if (i) the cumulative birth rate of mites is less than or equal to their death rate due to varroacides and the rate at which the virus-carrying mites lose the virus, and (ii) the periodic solution of the bee-only model is stable. As before, the disease-free periodic solution is always unstable in the absence of varroacide treatment, when $\delta _5=0$. That is, a disease invasion cannot be fought off by the bees alone as a consequence of the logistic growth assumption for mites.

4.3 Numerical Results

4.3.1 Illustration of Model Outcomes

We first show, in Figs. 3 and 4, possible simulation outcomes for the model without forager loss, i.e. $p=0$, for the parameters in Table 1, except where indicated. The periodic positive solution $(x_h(t),x_f(t))$ of the basic bee model without mites and virus that was hypothesized in Propositions 4.1 and 4.2 is depicted in Fig. 3a, showing as expected from Khoury et al. (2011) a higher hive bee population than foragers. The population is highest in summer and lowest in winter, with a period of increase in spring and a period of decrease in fall. No foragers are present during the winter months.

Fig. 3

(Color figure online) Temporal dynamics of a colony when $p=0$: a Disease-free colony. b Bee-mite coexistence without treatment. c Bee-mite co-existence when $\delta _5=1$. d Mites are fought off when $\delta _5=1.4$. (e) Colony fails after 5 years [same scenario as in c, but with increased brood maintenance coefficients K]

Fig. 4

(Color figure online) Temporal dynamics of a mite-virus-infested colony when $p=0$: a Colony dies off due to virus when $\delta _5=0.3$. b Colony fights off virus but not mites when $\delta _5=1$. c Colony fights off mites and virus when $\delta _5=1.5$

In Fig. 3b–d, mites are introduced, but the system is virus-free. In all cases periodic solutions with positive bee numbers are obtained. Without varroacide treatment, as per Proposition 4.1, the mite-free periodic solution is unstable. Instead, we find in Fig. 3b an endemic mite-infested periodic solution. The bee population is smaller than in the mite-free case of Fig. 3a, but still at comparable numbers.

We follow the same treatment strategy outlined in Ratti et al. (2015). We assume that the treatment is applied three times in the spring,

$$\begin{aligned} \delta _i(t) = {\left\{ \begin{array}{ll} \delta _i, &{} {\text { if }}30 \le t< 31, 60 \le t< 61, 90 \le t < 91 , \\ 0, &{} {\text { otherwise}}, \\ \end{array}\right. } \end{aligned}$$

where $i=1,\ldots ,5$. Since there is no detailed data available for the parameters $\delta _i$, we assume that the death rate of uninfected and infected bees due to treatment (i.e. $\delta _1,\delta _2$ and $\delta _3$) is small as compared to their natural death rates (given in Table 1). Thus, we assume $\delta _1=\delta _2=\delta _3=0.005$. We also fix $\delta _4=0.5$ and vary $\delta _5$ in the numerical experiments. Introducing treatment at a level $\delta _5=1$, smaller than the critical values as per Proposition 4.1, reduces the number of mites in the colony and increases the number of bees almost to the same level as in the mite-free case, see Fig. 3c. Increasing the varroacide treatment further to $\delta _5=1.4$, a level above the critical threshold of Proposition 4.1 for the mite-free solution, eliminates varroa and restores the mite-free periodic solution, Fig. 3d. To show that the stability of such periodic solutions is conditional on model parameters, we include in Fig. 3e in which one parameter, namely the brood maintenance coefficient K, was increased to values of 14,000, 16,000, 14,000 and 9000 in spring, summer, fall and winter, respectively: the colony appears to be working well in the presence of mites (but absence of virus) for the first 5 years, despite the bee numbers slightly decreasing from year to year. The clearest visible decline is in the winter lows. At the beginning of the 6th spring, the colony cannot grow after the winter population dropped below the critical value, around 9000, leading to fast failure.

In Fig. 4, we show solutions of the model with virus present, but still in the absence of forager losses, $p=0$. Again we used the parameters of Table 1, corresponding to the simulations of the model without virus in Fig 3b–d. In Fig. 4a, for a low level of varroa control, $\delta _5=0.3$, the colony would be able in the absence of virus to survive, attaining a periodic bee-mite coexistence simulation, but in the presence of the virus it fails after 7 years of virus build-up in the colony. Before colony failure takes place, no major effect of the diseases on the bee population is notable but bee number declines very slowly from year to year. In Fig. 4b, the simulation is shown for an increased level of varroa control, $\delta _5=1$, yet still below the critical threshold for stability of the diseases-free periodic solution as per Proposition 4.2. In this case, the mite population is not completely suppressed, but small enough such that the virus cannot take hold in the colony, i.e. the colony survives, as in Fig. 3c. In Fig. 4c, the varroa control was intensified to level that the mite is absent in the colony, $\delta _5=1.5$, and accordingly the virus cannot establish itself. This results in the diseases-free periodic solution, as per Fig. 3a.

Fig. 5

(Color figure online) Temporal dynamics of a colony when $p=0.1$: a Disease-free colony. b Bee-mite coexistence in the absence of virus and without varroacide. c Colony fights off virus but not mites at varroacide treatment level $\delta _5=1$. d Colony fights off mites and virus when treated against mites at $\delta _5=1.5$

Finally, we show simulations of the model with forager losses. We follow Henry et al. (2012) and assume that the colony experiences periods of forager loss in short period of 30 days early on in spring. We first keep the forager losses at $p=0.1$, clearly above 0.

In our first simulation, depicted in Fig. 5a, we consider again the case of a healthy colony without mites and virus and find a periodic solution as per the hypothesis of Propositions 4.1 and 4.2. The peak hive and forager bee levels in summer are rather similar than what was observed for the colony without forager losses in Fig. 3a, indicating that the colony is able to cope with the forager losses. However, during spring the number of hive bees in Fig. 5a drops clearly below the values observed in Fig. 3a, indicating that forager loss leads to accelerated recruitment of hive bees to foraging duties.

In Fig. 5b, we consider the bee-mite model without virus and varroacide treatment, as in Fig. 3b, but exposed to forager losses in early spring with $p=0.1$. The observation is similar as in the mite-free case, in that the colony is able to tolerate the moderate forager losses. The same can be found for the simulations in Fig. 5c, d, where virus is introduced in the colony and varroacide is applied at different levels. In one case, the treatment is not strong enough to completely suppress the mite population, but strong enough to keep it at levels low enough that the virus cannot take hold. In the other case, the treatment level is increased to eradicate the mite and hence also the virus. In both scenarios, the colonies is able to withstand the pressure of forager losses and accelerated recruitment of hive bees to out-of-hive duties.

Fig. 6

(Color figure online) Temporal dynamics of a colony infested with mites and virus where the virus is fought off due to the varroacide treatment (Simulation Experiment 1, case 2) if the forager mortality rate, p is a 0.166, b 0.167

Testing the model with values of $p=0.17$ and higher lead in all cases to a quick failure of the colony. We found a very narrow range for p larger than $p=0.167$ and smaller than $p=0.175$, in which a colony is able to survive for one or few years. In these instances, if colonies experience forager losses for 1 year only, they might be able to recover.

In Fig. 6, we show the simulation results for the case where varroacide treatment is high enough to fight off the virus but not to suppress the mites. We use the parameter $\delta _5=0.5$. We choose the forager loss rates to be $p=0.166$ (slightly below the critical value) and $p=0.167$ (slightly above the critical value). The critical value of p depends on the choice of the parameter $\delta _5$. In the former case, a periodic endemic solution is attained, whereas in the latter case the colony fails during the first forager loss exposure period. For all tested values of $p>0.17$, the colony is very sensitive to forager losses and fails immediately (data not shown).

4.3.2 Comparison of the Effect of Increased Forager Loss Between a Disease-Free and a Disease-Infested Colony

In this simulation series, we investigate how an increased loss of foragers due to homing failure affects the average total bee population, c.f. Fig. 7a, and loss of foragers population, c.f. Fig. 7b. Following again Henry et al. (2012), we assume that the bees are exposed to treated crops in the environment for 30 days (i.e. $t=5$ to $t=35$) at the beginning of spring every year.

Fig. 7

(Color figure online) a Comparison of average total bee population between a disease-free colony, a colony infested with mites, a colony infested with mites but treated with varroacides and a colony infested with mites and virus but treated with varroacides by varying the forager mortality due to homing failure, i.e. p from 0 to 0.5. The average total bee population is calculated over the last year. b Comparison of loss of forager population between a disease-free colony, a colony infested with mites, a colony infested with mites but treated with varroacides and a colony infested with mites and virus but treated with varroacides by varying the forager mortality due to homing failure, i.e. p from 0 to 0.5. For plotting purpose, we restricted the p range from 0 to 0.2. Note that the curve for the mite-infested but treated and the mite-virus-infested but treated case overlap with each other in (a) and (b)

In Fig. 7a, the average of the total bee population (hive bees and foragers) calculated over the last year of the simulation experiment is plotted. We vary the parameter p from 0 to 1.5 because these are the p values for which the colony survives for Fig. 2 [model (25)–(26)] with spring only parameters. We track the simulations for 20 years to capture the long-time behaviour of the system. As in Ratti et al. (2012, 2015), we assume the parameters to be seasonally constant. The parameter values for $\beta _{1,2,3},d_{1,2,3}, \mu , \sigma _1,\sigma _2,\gamma _{1,2,3}, r$ and k are those listed in Table 1. We consider two cases: Case 1: a disease-free colony and Case 2: a mite-infested but virus-free colony. Results are presented in Fig. 7. We observe that in case 1, as p increases from 0 to a critical value of 0.18, the average population decreases from 28,800 to 26,920 bees. The decrease in average population is fast for small values of p and then slows down and levels off as p increases. After p reaches the critical value ($p=0.18$), the average bee population suddenly drops to zero and stays there for all higher values of p. In case 2, there is no varroacide treatment applied, the average bee population follows the same pattern as in the case of the disease-free colony, but the population level is lower. The average bee population starts from 26,885 bees and decreases to 25,520 bees as the parameter p increases from 0 to 0.163. The population drops to 0 when the critical value $p=0.163$ is exceeded. This suggests that colonies that are stressed by a varroa infestation are more sensitive to increased forager loss than those that are free of the parasite.

We next investigate how varroacide treatment affects the dynamics of colonies infested by mites and virus. For this purpose, we follow the same treatment strategy as in Sect. 4.3.1. The parameters $\delta _1=\delta _2=\delta _3=0.005$. The varroacide control $\delta _5$ is chosen strong enough ($\delta _5=0.5$, i.e. $\delta _5(t)=0.5$ for $t=30, 60, 90$) for the mites to be eradicated. Since there is no virus present in this case, the parameter $\delta _4$ is assumed to be 0. For the virus-infested case, we choose the varroacide control for virus-free and virus-carrying mites strong enough ($\delta _4=\delta _5=0.5$, i.e. $\delta _4(t)=\delta _5(t)=0.5$ for $t=30,60,90$) for the virus to be fought off so that colony survives. The mites are not eradicated in this case.

When the colony infested with mites is treated with varroacides, the average population is maintained at a higher level as compared to the case without treatment. Also, it is important to note that the critical value of the parameter p is slightly higher (i.e. $p=0.167$) than in the case when no varroacide treatment is applied. This means that a mite-infested colony can support a slightly higher forager mortality and maintain itself at a higher population level if a sufficient varroacide treatment is applied. When the colony is infested with mites and virus and a strong enough varroacide treatment is applied, the average bee population follows the same pattern and maintains exactly the same population level as in the case of a virus-free colony treated against mites.

Figure 7b represents the effect of forager loss on the cumulative population of foragers that are lost due to homing failure. The cumulative population is calculated over the last year of the experiment. It is observed that when $p=0$ (i.e. no exposure to the pesticides) no foragers are lost from the hive. In the case of a disease-free colony, as the parameter p increases from 0 to 0.18 the forager population that is lost increases to 360,900. The population drops down to zero when the critical value of $p=0.18$ is exceeded. In the case of mite-infested colony without varroacide treatment, the forager population attains a maximum of 323,000 and drops down to zero when the critical value of $p=0.163$ is reached. In the presence of varroacide treatment, loss of the forager population in a mite-infested colony follows the same pattern and maintains exactly the same population level as in the case of a mite-virus-infested colony treated against mites. The critical population in a disease-infested colony with treatment is higher than a mite-infested colony without treatment. In the absence of forager loss, the dynamics of (i) the disease-free colony is the same as in Fig. 3a, (ii) the mite-infested colony is the same as in Fig. 3b, (iii) the mite-infested colony with treatment is similar to Fig. 3c but with higher mite load and (iv) the mite-virus-infested but treated is similar to Fig. 4d.

5 Summary and discussion

Our model is a general framework that combines the existing bee-mite-virus models without division of labour and the models based on the division of labour but do not include disease infestation. In particular, our model allows us to study the interplay between increased forager loss and infestation of the colony with varroa mites and the Acute Bee Paralysis Virus. The combined model allows us to investigate scenarios where disease leads to increased mortality of both bee classes (hive and forager bees), or where external causes of forager loss (e.g. exposure to environmental pesticides) affect a disease-infested honeybee colony. The models in Khoury et al. (2011), Kribs-Zaleta and Mitchell (2014) and Ratti et al. (2015) are special cases of our model under certain parameter conditions. For instance, our model can be reduced to the model in Khoury et al. (2011) if we assume that there is no disease present in the colony, or to the model in Kribs-Zaleta and Mitchell (2014) if we assume that there is no vector involved in the transmission of disease in the colony. The model in Ratti et al. (2015) can be obtained if we do not divide the bee population into hive bees and forager bees.

Our simulations suggest that a disease-free colony dies off if a threshold value of forager mortality due to homing failure is reached. The threshold value is slightly lower in the case of a mite infestation that is not treated with varroacides. In the presence of varroacide treatment, a mite-infested colony can tolerate a higher forager mortality due to homing failure and maintain itself at a slightly higher population level as compared to the case without varroacide treatment.

In our model, the analysis suggests that in the absence of varroacide treatment, the mite and virus-free solution is always unstable; this result is in agreement with the results for the simpler model in Ratti et al. (2015), which does not explicitly distinguish between hive and forager bees and therefore cannot be used to account for forager losses directly. In the case of instability, the solution might converge to the trivial equilibrium or to the endemic equilibrium; the outcome cannot be determined from the local analysis of the disease-free solution. Simulation experiments suggest that in a colony that is infested with only mites (no virus), the system converges to an endemic solution where bees and mites coexist, if the forager mortality is below a critical value, and the colony fails if the forager mortality is above this critical value. The bee population level throughout the year is lower as compared to the bee population in the mite-free case. Simulation experiments also suggest that in the case of a colony infested with both mites and virus with no varroacide treatment applied, the colony is not able to fight off the virus and dies off. Also this result is in agreement with the simpler model of Ratti et al. (2015), and indicates that in the absence of varroacides, the additional feature added to the model (i.e. division of labour) does not affect the stability of the disease-free equilibria.

A disease-free colony may survive as a properly working healthy colony if external stressors are not too large. Key parameters are forager mortality due to homing failure, recruitment rate of hive bees to foragers and social inhibition level. This result is in agreement with Khoury et al. (2011), in which a critical value of forager loss is calculated above which the colony fails, but below which the colony continues to function. It is not possible to analytically determine the criterion in our model because of the algebraic complexity involved.

To understand the role of forager mortality due to homing failure in a colony which is infested with disease, it is important to study the seasonal variations in colony dynamics. Seasonality is important because the dynamics of the disease-infested colony may seem to be the same as the disease-free colony in the first few years and then significantly different afterwards. Moreover, running a model for a single season simulation (i.e. a constant coefficient case) for very long time can be deceiving, which also indicates the need to incorporate seasonal variations in the model.

Based on our model and its assumptions, our analysis suggests that the mite-free equilibria can be stabilized if a sufficiently strong varroacide treatment is applied. This condition also appears in Ratti et al. (2015). In order to fight off the virus, in addition to the application of a strong enough varroacide treatment, it is necessary that the virus-carrying mites lose their virus at a rate which is higher than their maximum birth rate. This result is also observed in the simulation experiments.

Our simulations suggest that a colony that is treated to fight off ABPV will be able to tolerate forager losses that remain below the critical value for disease-free colonies, with only little effect on average bee numbers. In other words, if a colony can withstand both stressors individually, it will be able to withstand their combination, with the possible exception of a rather narrow range of parameters where a disease-free colony can tolerate forager losses but mite- and mite/ABV-infested colonies cannot, even if treated with varroacides to a level such that the disease is suppressed.

6 Conclusion

Honeybees are frequently exposed to multiple stressors simultaneously, including parasites, viruses and external factors that trigger forager losses. Mathematical modelling can be a useful tool to investigate the interplay of several such factors. We formulated such a model for honeybee colonies that are infested with Varroa destructor, infected by the Acute Bee Paralysis Virus, and exposed to increased levels of forager loss during 1 month in spring of each year. Our simulations suggest that the deadly virus can be suppressed by keeping the varroa mite, which vectors it, at low enough values by application of varroacides. They also suggest that a honeybee colony that experiences periods of increased forager loss early in the season can withstand these losses and recover to (almost) normal strength, if the losses remain below a threshold that depends on parameters. If the losses exceed this threshold the colony fails rapidly, not allowing the apiarist enough time for remedial action. The level of external forager loss that can be tolerated is only slightly higher for healthy colonies compared to colonies that are also plagued by varroa and ABPV.

In practical situations where factors that enter our model as parameters would change from year to year, recognizing the threat of colony failure due to forager loss is difficult. From a policy point of view, this would suggest that external factors that can trigger forager losses should be kept at a minimum in order to minimize the risk of local breakdown of agricultural pollination.