1 Introduction

The Western honeybee, Apis melifera, is responsible for pollinating one-third of Canadian food crops (Canadian Honey Council 2013), corresponding to an economic value to Canadian agriculture of over $2 billion annually (Canadian Honey Council 2013). The key factor in the effectiveness of honeybees is their colony size and the life span, which varies with the seasons. A honeybee colony usually consists of a single reproductive queen, 20,000–60,000 adult female worker bees, 10,000–30,000 worker brood (in the form of egg, larvae and pupae) and hundreds of male drones (Sumpter and Martin 2004). A sufficient number of adult worker bees are required to perform the tasks of brood rearing, guarding, foraging and honey production. The size of a honeybee colony and the average life span of individuals vary greatly over the year from season to season. The egg-laying rate of the queen bee is slow in spring, increases in summer and then decreases in fall. The queen bee stops laying eggs before winter (Ministry of Agriculture 2011).

The number of honeybee colony losses worldwide has been increasing rapidly since 2006 (Kevan et al. 2007; Potts et al. 2010; Engelsdorp et al. 2008). The symptoms of colony failure are different in different parts of the world, and hence, losses are designated by different names. The losses first observed in USA are called Colony Collapse Disorder (CCD). The syndrome is characterized by the disappearance of mature adult bees. The capped brood still remains in the hive. There are no dead bodies in the colony, but only an insufficient number of young adult worker bees remain to care for the hive. There is nectar, pollen and honey present in the colony, indicating that the young bees are reluctant to consume the food. In other countries, e.g., Canada and Germany, it has been observed that the colonies become so weak in the winter that they cannot emerge as healthy colonies in the spring. This is known as wintering losses (Genersch et al. 2010; Guzmán-Novoa et al. 2010). No single factor is believed to be responsible for these colony losses; various possible factors could involve weather conditions, poor diet, transportation of bees for agricultural practices, pesticides and parasites (Becher et al. 2013). One main cause is thought to be the parasitic mite Varroa destructor and the viruses it carries (Genersch et al. 2010; Conte et al. 2010; Stankus 2008).

Varroa destructor is an ectoparasitic mite that infests honeybee colonies. It is one of the haplotypes of Varroa jacobsoni, a parasite that infests the Eastern honeybee Apis cerana (Anderson and Trueman 2000). Varroa destructor is the species that parasitized Apis melifera and spread rapidly in Western countries thereafter. Varroa mites not only feed on brood and adult bees, but also carry and transmit deadly viruses from bee to bee (Bowen-Walker and Gunn 1998; Rosenkranz et al. 2010). Mites reproduce inside a honeybee brood cell. Female mites enter into the brood cell before the cell is capped. After the capping of the cell, the mite not only feeds on the developing bee but also reproduces in the cell. When the host bee leaves the cell, the mother mite leaves the cell with its progeny. The adult female mite becomes attached to the adult bee and feeds on it by squeezing between the overlapping segments on the ventral side of bee’s abdomen.

Viral infections may get injected into the bee’s body during this feeding process. When a virus-carrying mite feeds on an uninfected bee, it might release the virus into the bee’s haemolymph. Similarly when a virus-free mite feeds on an already infected bee, it can acquire the virus. There have been around 20 known honeybee viruses, of which 12 are transmitted by varroa mites (Kevan et al. 2006; Ostiguy 2004). These viruses differ in their transmission routes, virulence and impact on the host.

Our focus is on the Acute Bee Paralysis Virus (ABPV). This virus belongs to the family of Dicistroviridae along with some other viruses such as Kashmir Bee Virus (KBV) and Israeli Acute Paralysis Virus (IAPV). ABPV is frequently implicated in honeybee colony failure, especially when the colonies are infested with the parasitic mite Varroa destructor (Kevan et al. 2006). It has often been associated with wintering losses (Genersch et al. 2010; ZKBS 2012). This virus is distributed worldwide and appears to be the most common bee virus in Europe and South America (Antunez et al. 2005; Ball and Allen 1988). Adult bees infected with this virus suffer from paralysis, trembling, inability to fly and the gradual darkening and loss of hair from the thorax and abdomen before they die. Pupae that are infected with ABPV die quickly and normally do not develop into adult bees (Martin 2001; Moore et al. 2015). Varroa mites are a mechanical vector for the transmission of ABPV, i.e., unlike other honeybee viruses such as the Deformed Wing Virus (DWV) or the IAPV. ABPV does not replicate in the mites (Genersch 2010; Miranda et al. 2010; ZKBS 2012). Other transmission routes of ABPV have been suggested, but the literature is inconclusive and quantitative data that would allow a parameterization of a mathematical model are scarce. For example, Chen et al. (2006) investigated the question of vertical transmission for six viruses. While they found for five of them, including DWV, that infection of the queen implied infection of her offspring, this was not found for ABPV. Chen and Siede (2007) reports of a study in which ABPV was detected in pollen but not in the bees and their glandular secretion, suggesting that the ingestion of food which contains virus might not lead to infection. Moreover, they report that in colonies without varroa mites ABPV, if it is present, is latent, whereas the presence of varroa triggers the disease, suggesting ABPV virulence is directly related to varroa infestation, cf also Genersch (2010), Moore et al. (2015), ZKBS (2012).

A recent summary of many honeybee mathematical models (Becher et al. 2013), based on a keyword database search, divides the models into three categories: colony models, varroa models and foraging models. The level of sophistication and detail of these models and, accordingly, the level of input data required, vary widely from very simple models that can be expressed in algebraic relationship to computer simulations models consisting of several dozens of differential equations. While some of these models are very detailed with respect to honeybee biology, and while some of these models include aspects of varroa population dynamics, only very few models can be found that include mites and the diseases for which they are a vector. In particular, there are few existing papers that study models for ABPV (Eberl et al. 2010; Ratti et al. 2013; Sumpter and Martin 2004).

The first published model for the honeybee–mite–virus system in the literature was (Sumpter and Martin 2004). This is an SIR-type model, in which the overall number of mites infesting the colony is a fixed parameter but the number of mites carrying the virus is a dependent variable. The model is formulated for two viruses, ABPV and DWV, separately. The authors consider the autonomous case and study the model behavior for each season separately, based on seasonal averages for the parameters. The data requirement for this model, in terms of number of parameters, is moderate; the authors present a complete model parameter set for each season obtained from the observational and experimental literature. For ABPV, this model was modified in Eberl et al. (2010), to include brood maintenance terms reflecting that a minimum number of worker bees is always required to care for the brood in order for new bees to be born. This introduces an Allee effect with an unconditionally stable trivial equilibrium. On the other hand, the original model (Sumpter and Martin 2004) assumes that the birthrate is independent of colony strength and does not permit a trivial equilibrium, unless the death rate is higher than the birthrate, which naturally leads to collapse.

In Ratti et al. (2013) [see also (Eberl et al. 2014)], the model of Eberl et al. (2010) was extended, adding a simple growth model for the mite population dispensing with the assumption that the mite load in the colony is constant. The mite dynamics are described by a logistic equation with a carrying capacity that depends on bee colony strength which is used here as an approximate indicator of brood size. Also, while in Eberl et al. (2010), Sumpter and Martin (2004) the direct detrimental effect of mites on bee colony size was subsumed in the bee death rate, the dynamic model for the mite population (Ratti et al. 2013) distinguished between natural death and death caused by the parasite.

A current and parallel bee colony model without disease is developed in Khoury et al. (2011), where the colony is compartmentalized into hive and forager bees. This leads to a two-dimensional system of ODEs that can be discussed completely in the phase plane. The original purpose of the model was to investigate the effect of the loss of forager bees on the adaptive early recruitment of hive bees to foraging, and how this affects overall colony strength and survival. This model was used to investigate the effect of environmental pesticides on survival of strength of colonies in Henry et al. (2012), see also Henry et al. (2012), Henry (2013). In Kribs-Zaleta and Mitchell (2014), it was extended to account for an unspecified disease that is brought into the colony by the foragers. This extended model was studied in much detail analytically and numerically. The description of disease in this model is rather general and it is left open to what extent the results apply to specific diseases such as ABPV and DWV, which require both a vector and a causative agent. Another current extension of Khoury et al. (2011), although less relevant for our particular study but important in modeling work on the colony collapse phenomenon is Khoury et al. (2013), where brood size and food stores and their role in colony dynamics were explicitly considered. A generic disease model similar to Kribs-Zaleta and Mitchell (2014) is presented in Betti et al. (2014). This model explicitly accounts for food storage as does the model (Khoury et al. 2013) and assumes that in addition to worker population size, food availability can limit the birthrate. The resulting system of five ODEs is numerically studied through a sensitivity analysis, including an investigation of wintering effects, by adjusting growth rate, forager recruitment rate and food production rate to zero. Consistent with Kribs-Zaleta and Mitchell (2014), the model in Betti et al. (2014) assumes direct transmission of virus between bees, without a vector.

The models discussed above all are formulated under assumption of constant model parameters, i.e., strictly speaking only valid for at most a single season under the assumption that seasonal averages give a good description of environmental dynamics and under the assumption that the timescale of the dynamics is sufficiently fast, so that the system equilibrates quickly, in significantly less time than the duration of a season. However, these assumptions preclude the model from being used to study the fate of a mite, and possibly virus, infested colony over years. This is a severe limitation of these models as the disease process appears to be, in many cases, fundamentally a multi-season or even multi-year process. For example, wintering losses occur when a bee population is too weak at the end of fall to make it through winter in numbers that allow the colony to rebound and function properly in spring. To investigate these phenomena, a model must be able to cover the transition between seasons and span an entire year.

In this study, we build on and extend our previous work: (i) We will study the behavior of the model with seasonally varying parameters over several years. Some preliminary ad hoc simulations were included in Ratti et al. (2013). In these exploratory simulations, seasonally constant parameters were used, i.e., jump functions, which we extend here to parameters that depend continuously in time. The exploratory simulations in Ratti et al. (2013) focused on the role of two parameters: one of the honeybee population submodel and the other one of the varroa mite population submodel. In the current study, we will fix these parameters based on the earlier results and focus on the quantitative role of the initial levels of mite and virus infestations. (ii) Secondly, in Ratti et al. (2013), the important theoretical question about the stability of disease-free periodic solutions remained open. We will give an answer in this paper. (iii) Thirdly, we will extend the model by explicitly including the option to account for mite control, e.g., by varroacide application. This will allow us to investigate the question under which conditions (on parameters) vector control is a viable remedial strategy for the virus infestation.

2 Mathematical Model

2.1 Model Assumptions

Our model is based on the earlier studies discussed above (Eberl et al. 2010; Ratti et al. 2013; Sumpter and Martin 2004). Accordingly, many of the assumptions made there will be adopted here as well. Our model will also include features not accounted for in these earlier models, which will lead to additional model assumptions. A brief list of key model assumptions is provided here:

  1. 1.

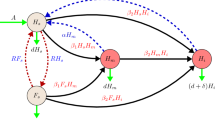
    Following Sumpter and Martin (2004), the model will be formulated in terms of the dependent variables (i) healthy and (ii) virus-infected bees, and (iii) number of mites that carry the virus. Following Ratti et al. (2013), we also include (iv) the total number of mites, virus-carrying and virus-free, as a dependent variable, which allows us to account for the dependency of the virus and its effect on the population dynamics of the vector.

  2. 2.

    The queen bee is not affected by the disease. This is an implicit assumption, which allows us to assume that the egg-laying rate of the queen is independent of mites and virus. This assumption follows Betti et al. (2014), Eberl et al. (2010), Khoury et al. (2013), Kribs-Zaleta and Mitchell (2014), Ratti et al. (2013), Sumpter and Martin (2004).

  3. 3.

    The only route of virus transmission we account for is horizontal transmission vectored by varroa mites. In accordance with Genersch (2010), Miranda et al. (2010), ZKBS (2012), the mites are assumed to be a mechanical vector only, in particular no virus replication takes place in the mites.

  4. 4.

    In accordance with Martin (2001), Moore et al. (2015), we assume that infected pupae die quickly before they develop into adult bees, and that all newly born bees are uninfected. In Ball and Allen (1988), it is suggested that mortality of brood in mite-infested colonies is associated with secondary infections by pathogenic agents. Therefore, following Sumpter and Martin (2004), we assume that only virus-carrying mites affect the rate at which brood emerge as adult bees.

  5. 5.

    Since mite reproduction depends on brood availability, we assume a carrying capacity for the mite population that depends on colony strength, as in Ratti et al. (2013). Colony strength is used here as an approximate measure of brood size. For simplicity, we use a logistic model to describe the development of the mite population.

  6. 6.

    Since worker bees are needed to allow the brood to develop to the adult stage, the birthrate is dependent on the number of bees in the colony. Since bees infected with ABPV suffer from paralysis and die quickly, we assume that only healthy bees take part in brood rearing. As in Eberl et al. (2010), we use a Hill function to describe the brood rearing term, which introduces an Allee effect.

  7. 7.

    It is assumed that healthy and sick bees both die naturally, and also due to mites feeding on them and/or infecting them with virus. Therefore, as in Ratti et al. (2013), the death rate has two components: one that depends on the mites and one that does not. In Eberl et al. (2010), Sumpter and Martin (2004), where the number of mites was a given parameter, this assumption was not necessary, as both effects could be compounded into one term. We further assume that the death rates of infected bees are higher than the death rates of uninfected bees.

  8. 8.

    In contrast to Khoury et al. (2011), Sumpter and Martin (2004), we assume that all model parameters are functions of time. This allows us to account for seasonal differences in bee biology. We assume that they are periodic functions with a period of one year to reflect seasonal patterns.

  9. 9.

    We account for varroacide treatment by introducing additional sink terms for the vectoring mites. We also include additional sink terms for the bees depending on varroacide treatment. However, we assume that the varroacide effect on the mites is stronger than its effect on the bees.

To describe the transmission of the diseases according to the assumptions 2, 3, 4 above, we follow the ABPV model originally worked out in Sumpter and Martin (2004), where also a complete set of parameters for disease dynamics is given that was inferred from observational data.

2.2 Model Equations

Our model extends (Eberl et al. 2010; Ratti et al. 2013; Sumpter and Martin 2004 by introducing the model assumptions 8 and 9 above. It reads:

$$\begin{aligned} \frac{\hbox {d}m}{\hbox {d}t}= & {} \beta _1(t) (M-m)\frac{y}{x+y}-\beta _2(t) m\frac{x}{x+y}-\delta _2 m,\end{aligned}$$
(1)
$$\begin{aligned} \frac{\hbox {d}x}{\hbox {d}t}= & {} \mu (t) g(x,t)h(m,t)-\beta _3(t) m \frac{x}{x+y}-d_1(t) x-\gamma _1 Mx-\delta _1 x,\end{aligned}$$
(2)
$$\begin{aligned} \frac{\hbox {d}y}{\hbox {d}t}= & {} \beta _3(t) m\frac{x}{x+y}-d_2(t)y-\gamma _2 My-\delta _3 y,\end{aligned}$$
(3)
$$\begin{aligned} \frac{\hbox {d}M}{\hbox {d}t}= & {} r(t)M\left( 1-\frac{M}{\alpha (t)(x+y)}\right) -\delta _2 M \end{aligned}$$
(4)

where the dependent variables are:

m,:

number of mites that carry the virus;

x,:

number of honeybees that are virus free;

y,:

number of honeybees that are infected with the virus;

M,:

number of mites that infest the colony.

The parameter \(\mu (t)\) in (2) is the maximum birthrate, specified as the number of worker bees born per day.

The function g(x, t) in (2) expresses that due to nursing, the birthrate depends on the number of worker bees. If x becomes small, essential work in the maintenance of the brood cannot be carried out anymore and no new bees are born. If x is large, bee rearing is not severely slowed down. Thus, \(g(0,\cdot )=0, \frac{\hbox {d}g(0)}{\hbox {d}x}=0, \frac{\hbox {d}g(x)}{\hbox {d}x}>0, x>0, \lim _{x\rightarrow \infty } g(x,t)=1\). A convenient formulation of such switch-like behavior is given by the sigmoidal Hill function

$$\begin{aligned} g(x,t)=\frac{x^n}{K(t)^n+x^n} \end{aligned}$$
(5)

where the parameter K(t) is the size of the bee colony at which the birthrate is half of the maximum possible rate, and \(n>1\) is an integer exponent. For \(n=1\), the same birth term as in Khoury et al. (2011) is obtained. We will use instead \(n>1\) because we assume that a sufficient number of healthy worker bees is required to rear the brood, which induces an Allee effect as in Eberl et al. (2010). If \(K=0\), then the bee birth terms of the original model in Sumpter and Martin (2004) are recovered, i.e., the brood is always reared at maximum capacity, independent of the actual bee population size. In this case, no trivial solution can be expected. Since the parameter K represents a sufficient number of healthy adult bees required to care for the brood and the brood population varies with season, the parameter K also varies with seasons.

The function h(m, t) in (2) indicates that the birthrate of bees is affected by the presence of mites that carry the virus. This behavior is particularly important for viruses like ABPV that kill infected pupae before they develop into bees. The function h(m, t) is assumed to decrease as m increases, \(h(0,t)=1, \frac{\hbox {d}h}{\hbox {d}m}(m,t)<0\) and \(\lim _{m\rightarrow \infty } h(m,t)=0\); Sumpter and Martin (2004) suggests that h(m, t) is an exponential function, \(h(m) \approx \hbox {e}^{-m k(t)}\), where k(t) is nonnegative.

The transmission of the disease is described by the terms with coefficients \(\beta _i\), as originally proposed in Sumpter and Martin (2004). Parameter \(\beta _1\) in (1) is the rate at which mites that do not carry the virus acquire it. The rate at which infected mites lose their virus to an uninfected host bee is \(\beta _2\). The rate at which uninfected bees become infected is \(\beta _3\), in bees per virus carrying mite and time.

The parameters \(d_1\) and \(d_2\) are the natural death rates for uninfected and infected honeybees, respectively. We can assume that infected bees have a shorter life span than healthy bees, thus \(d_2 > d_1\).

The last Eq. (4) is a logistic growth model for varroa mites. By r(t), we denote the maximum mite birthrate. The carrying capacity for the mites changes with the host population size, \(x+y\), and is characterized by the parameter \(\alpha (t)\) which indicates how many mites can be “sustained per bee” on average.

Mites contribute to increased bee mortality. This is considered in (2) and (3) by including death terms that depend on M; the parameters \(\gamma _{1,2}\) give the rates at which mites directly kill healthy and virus-infected bees.

The potential effects of externally applied varroacides are described by three new parameters: \(\delta _1, \delta _2\) and \(\delta _3\). The parameters \(\delta _1\) and \(\delta _3\), respectively, represent the death rates of uninfected and infected bees due to varroacides. We assume that, \(\delta _2\), the effect of varroacides on the mites that carry the virus and on the total number of mites is the same.

The parameters \(\mu , k, K,\alpha , \beta _i, d_i, \delta _i, \gamma _i\) and r are assumed to be nonnegative and periodic functions of time with a period T; in practice \(T=1\) year. Seasonal averages of the parameters \(\mu , \beta _i, d_i\) and k can be computed from the observational data given in Sumpter and Martin (2004) and for r from the data in Martin (1998), Martin (2001). A fixed set of seasonal averages for the parameter K is not available in the literature. However, we have high and low ranges of K based on Ratti et al. (2013) and we use these sets of values in this paper. The data are summarized in Table 1.

Table 1 Seasonal averages of model parameters, derived from the data in Martin (1998), Martin (2001), Ratti et al. (2013), Sumpter and Martin (2004)
Full size table

The values of \(\gamma _1\) and \(\gamma _2\) are estimated to be \(10^{-7}\) for every season, based on order of magnitude considerations. For the numerical simulations presented below, we will use these seasonal averages to construct continuous, smooth coefficient functions. The construction of such functions is not unique. While the particular choice of construction affects the solutions quantitatively, it is not a priori clear whether and to what extent construction will also affect the qualitative behavior, such as the stability of solutions. The effect of construction on the solutions is discussed and investigated in more detail in the “Appendix”, where two strategies based Piecewise Cubic Hermite Interpolating Polynomials (PCHIP) are described and compared.

3 Stability of Periodic Solutions

Numerical simulations suggest the existence of periodic solutions to (1)–(4), see below. A formal proof of the existence of such solution hinges on additional properties, which the coefficient functions must have. Since we only have at most a priori information about piecewise monotonicity of the coefficients as the seasons change, a general proof of the existence appears out of reach at this point, without introducing additional conditions on the parameters. Therefore, we conjecture the existence of periodic solutions, as observed in simulations, and aim to give conditions for their stability, particularly in the disease-free case. Although our objective is an analysis of the complete four-dimensional model (1)–(4), it is instructive to study simpler sub-models first. We begin with the mite- and virus-free model and then analyze the model where bees and mites are considered, but the virus is absent.

In the absence of mites and virus, model (1)–(4) reduces to the single differential equation

$$\begin{aligned} \dot{x}=\mu g(x,t)-d x-\delta x \end{aligned}$$
(6)

where d is the natural death rate of the bees, and \(\delta \) is the death rate at which bees die due to varroacides.

Proposition 3.1

Suppose \(x(t)=x^*(t)\) is a periodic solution of the bee-only model (6). Then, \(x=x^*\) is asymptotically stable if \(\int _0^t{(\mu g^\prime (x^*)-d-\delta )\mathrm{d}\rho }\le 0\).

Proof

Linearizing equation (6) about \(x=x^*\) gives,

$$\begin{aligned} \dot{u}=(\mu g^\prime (x^*)-d-\delta )u, \end{aligned}$$

where \(u=x-x^*\). This is a linear differential equation that can be solved with the method of integrating factors. We find

$$\begin{aligned} u(t)=c_0 \hbox {e}^{\int _0^t{(\mu g^\prime (x^*)-d-\delta )\hbox {d}\rho }}. \end{aligned}$$

In order for the periodic solution \(x=x^*\) to be asymptotically stable, the solution of the perturbed system, u(t), should go to zero. This means that the periodic solution \(x=x^*\) is stable if \(\int _0^t{(\mu g^\prime (x^*)-d-\delta )\hbox {d}\rho }\le 0\).

This result shows, as intuitively expected, that in the absence of parasites and virus, a healthy bee colony will be maintained over multiple years only if the death rate is greater than or equal to the birthrate per bee over a period of time. Otherwise, the colony will grow without bound. On the other hand, since \(x^*\equiv 0\) is a periodic solution for which the integral in the exponent is always negative, this result also shows that this trivial equilibrium is unconditionally stable, i.e., that the Allee effect of the autonomous model in Eberl et al. (2010), Ratti et al. (2013) carries over to the nonautonomous model.

Next, we consider (1)–(4) in the absence of the viral disease but potential presence of mites. The model reduces then to the two differential equations for bees and mites.

$$\begin{aligned} \frac{\hbox {d}x}{\hbox {d}t}= & {} \mu g(x)-\delta x-\gamma _1Mx, \end{aligned}$$
(7)
$$\begin{aligned} \frac{\hbox {d}M}{\hbox {d}t}= & {} (r-\delta _2)M\left( 1-\frac{rM}{(r-\delta _2)\alpha x}\right) . \end{aligned}$$
(8)

where \(\delta =d_1+\delta _1\). Here, \(d_1\) represents the natural death rate of the bees, and \(\delta _1\) is the death rate of the bees due to varroacides. The parameter \(\delta _2\) is the death rate of mites because of varroacide application.

Proposition 3.2

Suppose \(x^*(t)\) is a periodic positive solution of (6). Then, \((x^*,0)\) is a periodic solution of (7)–(8). It is stable if \(\int _0^T{(r-\delta _2)\mathrm{d}t}\le 0\) and \(\int _0^T (\mu g^\prime (x^*)-\delta )\mathrm{d}t \le 0\).

Proof

That a positive periodic solution of (6) defines a disease-free solution of (7)–(8) is immediate from the model equations. In order to analyze its stability, we use linearization and Floquet theory. We linearize the system about the periodic solution \((x^*,0)\), i.e., investigate the long-term behavior of the perturbation \(u:=x-x^*, v:=M-0\).

The Jacobian of the system is obtained as

$$\begin{aligned} J(x,M)= \left[ \begin{array}{c@{\quad }c} \mu g^{\prime }(x)-\delta -\gamma _1 M&{}-\gamma _1 x\\ \frac{rM^2}{\alpha x^2}&{}(r-\delta _2)-\frac{2rM}{\alpha x} \end{array}\right] . \end{aligned}$$

and in \((x^*,0)\), we find

$$\begin{aligned} J(x^*,0)= \left[ \begin{array}{c@{\quad }c} \mu g^{\prime }(x^*)-\delta &{}-\gamma _1 x^*\\ 0&{}r-\delta _2 \end{array}\right] . \end{aligned}$$

Thus, the linearized system about \((x^*,0)\) is

$$\begin{aligned} \left[ \begin{array}{c} \dot{u}\\ \dot{v} \end{array}\right] =&\left[ \begin{array}{c@{\quad }c} \mu g^{\prime }(x^*)-\delta &{}-\gamma _1 x^*\\ 0&{}r-\delta _2 \end{array}\right] \left[ \begin{array}{c} u\\ v \end{array}\right] .\\ \end{aligned}$$

We choose the linearly independent set of initial conditions

$$\begin{aligned} u_1(0)=1, \quad u_2(0)=0\\ v_1(0)=0, \quad v_2(0)=1 \end{aligned}$$

to find linearly independent solutions \((u_1(t),v_1(t))\) and \((u_2(t),v_2(t))\) of the linearized system.

$$\begin{aligned} u_1(t)&=\hbox {e}^{\int _0^t{(\mu g^\prime (x^*(\rho ))-\delta )\mathrm{d}\rho }},\\ v_1(t)&=0,\\ u_2(t)&=\hbox {e}^{\int _0^t{(\mu g^\prime (x^*)-\delta )\mathrm{d}\rho }}\int _0^t{-\gamma _1 x^*\hbox {e}^{\int _0^\rho {(r-\delta _2+\delta -\mu g^\prime (x^*(\tau )))\mathrm{d}\tau }}\hbox {d}\rho },\\ v_2(t)&=\hbox {e}^{\int _0^t{(r-\delta _2)\mathrm{d}\rho }}. \end{aligned}$$

The next step is to construct the fundamental matrix A(t) of the linearized system over the interval \(0\le t\le T\), where T is the period, and to determine the eigenvalues of the transition matrix

$$\begin{aligned} C=A(T)=\left[ \begin{array}{c@{\quad }c} u_1(T)&{}\quad u_2(T)\\ v_1(T)&{}\quad v_2(T) \end{array}\right] , \end{aligned}$$

which are found as

$$\begin{aligned} \lambda _1&= \hbox {e}^{\int _0^T{(\mu g^\prime (x^*)-\delta ) \mathrm{d}t}} , \quad \quad \lambda _2= \hbox {e}^{\int _0^T{(r-\delta _2) \mathrm{d}t}}. \end{aligned}$$

Stability of \((x^*,0)\) is then obtained if \(\int _0^T{(r-\delta _2)\mathrm{d}t}\le 0\) and \(\int _0^T{(\mu g^\prime (x^*)-\delta )\mathrm{d}t}\le 0\), whereas instability is implied if one of the inequalities is reversed.

This indicates that the mite infestation in a colony can be fought off if (i) the cumulative death rate of mites due to treatment is greater than or equal to their birthrate and (ii) the cumulative death rate of healthy bees is greater than or equal to their birth rate. The mite-free equilibrium is always unstable in the absence of varroacide treatment, when \(\delta _2=0\), i.e., a mite invasion cannot be fought off by the bees alone as a consequence of the logistic growth assumption for mites. This generalizes the findings in Ratti et al. (2013) for the autonomous systems. If \((x^*,0)\) is unstable, it is not clear whether the system will converge to the trivial state or whether, for example, an endemic periodic solution will be obtained in which the bee colony persists in the presence of mites. The simulations in Eberl et al. (2014), Ratti et al. (2013) suggest the possibility of such an endemic periodic bee–mite solution for certain parameters. While in principle Floquet theory could be used to derive a stability condition for such a periodic solution, algebraic complexity prevented this.

Finally, we turn to the full bee–mite–virus model

$$\begin{aligned} \frac{\hbox {d}m}{\hbox {d}t}= & {} \beta _1 (M-m)\frac{y}{x+y}-\beta _2 m \frac{x}{x+y}-\delta _2 m,\end{aligned}$$
(9)
$$\begin{aligned} \frac{\hbox {d}x}{\hbox {d}t}= & {} \mu g(x)h(m)-\beta _3 m \frac{x}{x+y}-\delta x-\gamma _1 Mx,\end{aligned}$$
(10)
$$\begin{aligned} \frac{\hbox {d}y}{\hbox {d}t}= & {} \beta _3 m\frac{x}{x+y}-\delta ^\prime y-\gamma _2 My,\end{aligned}$$
(11)
$$\begin{aligned} \frac{\hbox {d}M}{\hbox {d}t}= & {} (r-\delta _2)M\left( 1-\frac{rM}{(r-\delta _2)\alpha (x+y)}\right) , \end{aligned}$$
(12)

where \(\delta =d_1+\delta _1\) and \(\delta ^\prime =d_2+\delta _3\).

Proposition 3.3

Suppose \((0,x^*,0,0)\) is a periodic nonnegative disease-free solution of (9)–(12), where \(x^*\) is a periodic solution of the bee-only model (6). Then, \((0,x^*,0,0)\) is linearly stable if \(\int _0^T{(\mu g^\prime (x^*)-\delta ) \mathrm{d}t}\le 0\) and \(\int _0^T{(r-\delta _2) \mathrm{d}t}\le 0\).

Proof

Suppose that there exists a periodic mite-free solution \((0,x^*,0,0)\) of the bee–mite–virus model. We will again use Floquet theory to examine the stability of the linearized system.

We find the Jacobian matrix of the system as

$$\begin{aligned}&J(m,x,y,M)\\&\quad =\left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} \frac{-\beta _1 y-\beta _2 x}{x+y}-\delta _2&{} \frac{-\beta _1(M-m)y-\beta _2 my}{(x+y)^2}&{} \frac{\beta _1(M-m)x+\beta _2 mx}{(x+y)^2}&{} \frac{\beta _1y}{x+y}\\ \mu g(x)h^\prime (m)-\frac{\beta _3 x}{x+y}&{} \mu g^{\prime }(x)h(m)-\frac{\beta _3 my}{(x+y)^2}-\delta -\gamma _1 M&{} \frac{\beta _3 mx}{(x+y)^2}&{} -\gamma _1 x\\ \frac{\beta _3x}{x+y}&{} \frac{\beta _3 my}{(x+y)^2}&{} \frac{-\beta _3 mx}{(x+y)^2}-\delta ^\prime -\gamma _2M&{} -\gamma _2y\\ 0&{} \frac{rM^2}{\alpha (x+y)^2}&{} \frac{rM^2}{\alpha (x+y)^2}&{} (r-\delta _2)-\frac{2rM}{\alpha (x+y)} \end{array}\right] , \end{aligned}$$

which applied to \((0,x^*,0,0)\) reduces to

$$\begin{aligned} J(0,x^*,0,0)=\left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} -\beta _2-\delta _2&{} 0&{} 0&{} 0\\ -\beta _3&{} \mu g^{\prime }(x^*)-\delta &{} 0&{} -\gamma _1 x^*\\ \beta _3&{} 0&{} -\delta ^\prime &{} 0\\ 0&{} 0&{} 0&{} r-\delta _2 \end{array}\right] . \end{aligned}$$

The linearized system about \((0,x^*,0,0)\) is then

$$\begin{aligned} \left[ \begin{array}{c} \dot{u}\\ \dot{v}\\ \dot{w}\\ \dot{p} \end{array}\right] =&\left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} -\beta _2-\delta _2&{}\quad 0&{}\quad 0&{}\quad 0\\ -\beta _3&{}\quad \mu g^{\prime }(x^*)-\delta &{}\quad 0&{}\quad -\gamma _1 x^*\\ \beta _3&{}\quad 0&{}\quad -\delta ^\prime &{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad r-\delta _2 \end{array}\right] \left[ \begin{array}{c} u\\ v\\ w\\ p \end{array}\right] \end{aligned}$$

where \(u=m-0, v=x-x^*,w=y-0\) and \(p=M-0\). Let \((u_1(t),v_1(t),w_1(t),p_1(t)), (u_2(t),v_2(t)),(u_3(t),v_3(t),w_3(t),p_3(t))\) and \((u_4(t), v_4(t), w_4(t),p_4(t))\) denote linearly independent solutions of the linearized system, with linearly independent initial conditions

$$\begin{aligned} u_1(0)=1, \quad u_2(0)=0, \quad u_3(0)=0, \quad u_4(0)=0\\ v_1(0)=0, \quad v_2(0)=1,\quad v_3(0)=0, \quad v_4(0)=0\\ w_1(0)=0, \quad w_2(0)=0,\quad w_3(0)=1, \quad w_4(0)=0\\ p_1(0)=0, \quad p_2(0)=0,\quad p_3(0)=0, \quad p_4(0)=1 \end{aligned}$$

The fundamental matrix A(t) of the linearized system over the interval \(0\le t\le T\), where T is the period, is obtained as

$$\begin{aligned} A(t)= & {} \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} u_1(t)&{} u_2(t)&{} u_3(t)&{} u_4(t)\\ v_1(t)&{} v_2(t)&{} v_3(t)&{} v_4(t)\\ w_1(t)&{} w_2(t)&{} w_3(t)&{} w_4(t)\\ p_1(t)&{} p_2(t)&{} p_3(t)&{} p_4(t) \end{array}\right] \\= & {} \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }l} \hbox {e}^{\int _0^t{-(\beta _2+\delta _2) d\rho }}&{} 0&{} 0&{} 0\\ 0&{} \hbox {e}^{\int _0^t{(\mu g^\prime (x^*)-\delta )d\rho }}&{} 0&{} \hbox {e}^{\int _0^t{(\mu g^\prime (x^*)-\delta )d\rho }}\int _0^t\\ \\ \,&{}\,&{}\,&{}\quad -\,\gamma _1 x^*\hbox {e}^{\int _0^\rho {(r-\delta _2+\delta -\mu g^\prime (x^*))d\tau }}d\rho \\ \hbox {e}^{\int _0^t{\delta ^\prime d\rho }}\int _0^t{\beta _3 \hbox {e}^{\int _0^\rho {(\delta ^\prime -\beta _2)d\tau }}d\rho }&{} 0&{} \hbox {e}^{-\int _0^t{\delta ^\prime d\rho }}&{} 0\\ 0&{} 0&{} 0&{} \hbox {e}^{\int _0^t{(r-\delta _2)d\rho }} \end{array}\right] . \end{aligned}$$

The transition matrix \(C=A(T)\)

$$\begin{aligned} C=\left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} u_1(T)&{} u_2(T)&{} u_3(T)&{} u_4(T)\\ v_1(T)&{} v_2(T)&{} v_3(T)&{} v_4(T)\\ w_1(T)&{} w_2(T)&{} w_3(T)&{} w_4(T)\\ p_1(T)&{} p_2(T)&{} p_3(T)&{} p_4(T) \end{array}\right] , \end{aligned}$$

has eigenvalues

$$\begin{aligned} \lambda _1&= \hbox {e}^{-\int _0^T{(\beta _2+\delta _2) \mathrm{d}t}},\\ \lambda _2&= \hbox {e}^{\int _0^T{(\mu g^\prime (x^*)-\delta ) \mathrm{d}t}},\\ \lambda _3&= \hbox {e}^{-\int _0^T{\delta ^\prime \mathrm{d}t}},\\ \lambda _4&= \hbox {e}^{\int _0^T{(r-\delta _2) \mathrm{d}t}}. \end{aligned}$$

It is observed that \(\mid \lambda _1 \mid \) and \(|\lambda _3 |\) are always less than 1. Therefore, \((0,x^*,0,0)\) of the linearized model is stable if \(\int _0^T{(\mu g^\prime (x^*)-\delta ) \mathrm{d}t}\le 0\) and \(\int _0^T{(r-\delta _2) \mathrm{d}t}\le 0\).

Hence, the conditions for the virus infestation to be fought off are the same as the conditions for the eradication of mites. This indicates that in order for the honeybee colony to become disease-free, it is sufficient to fight off the mites. An important observation is that the stability of the periodic disease-free equilibrium depends on the annual average values of the parameters and not on the seasonal average values. As in the simpler bee–mite case above, algebraic complexity does not allow an analytical investigation of the behavior of the system if the disease-free solution \((0,x^*,0,0)\) becomes unstable, i.e., under which condition the colony will converge to collapse or reach a stable endemic solution. To investigate the system further, we will, therefore, resort to numerical experimentation.

4 Computer Simulations

4.1 Sample Simulations Illustrating Model Behavior

Before we conduct systematic numerical experiments to investigate the model in detail, we present some selected simulations for illustration of potential model outcomes, see Fig. 1. These are guided by the analysis carried out in the previous section.

Fig. 1
figure 1

Illustration of potential model outcomes, tracked over several years: a periodic solution describing a healthy honeybee colony in the absence of mites and virus with high K values, b the same simulation scenario as in (a) but with mites present and with enough varroa treatment to fight off the mites, c the same simulation scenario as in (b) but with insufficient varroa treatment leading to bee–mite coexistence, d failure of the bee population caused by mites only (absence of ABPV) due to insufficient varroacide treatment, e presence of ABPV leading to the failure of the colony after more than 10 years with low K values, f same scenario as in (e) but a rapid failure of the colony after 4 years due to milder varroa treatment application as compared to (e), g same scenario as in (f) but with the extent of treatment sufficient to fight off virus but not mites, h same simulation scenario as in (g) but with enough varroa treatment to eradicate the disease (mites as well as virus)

Full size image

The seasonal averages of parameters \(\beta _i, d_i,\mu , k, r\) used in Fig. 1 are given in Table 1; these have been used to determine continuous time-varying parameters as described in the “Appendix”. The seasonal averages of the parameter \(\alpha \) are chosen to be 0.4784, 0.5, 0.5, 0.4784 for spring, summer, fall and winter, respectively (see Ratti et al. 2013 for the choice of these values). Since there are various varroa treatment strategies available in the literature, there cannot be a general profile for the death rates of bees and mites due to treatment (Giovenazzo and Dubreuil 2011; Lambert et al. 2006. Often varroa treatment is applied in spring and/or fall because the brood is still small then and not much honey is present in the colony. For simplicity, we assume that the treatment is applied three times in spring,

$$\begin{aligned} \delta _i(t) = {\left\{ \begin{array}{ll} \delta _i &{} {\hbox { if }\,30 \le t < 31, 60 \le t < 61, 90 \le t < 91} \\ 0 &{} \text { otherwise} \\ \end{array}\right. } \end{aligned}$$

where \(i=1,2,3\). Since there is no concerted data available for the parameters \(\delta _i\), we assume that the death rate of uninfected and infected bees (i.e., \(\delta _1\) and \(\delta _3\)) is small as compared to their natural death rates (given in Table 1). We assume \(\delta _1=\delta _3=0.005\). The parameters that we vary for the simulations in Fig. 1 are \(\delta _2\) and the brood maintenance coefficient, K.

The starting point and reference point are in all cases, a stable periodic solution \(x^*(t)\) of (6), i.e., the model in the absence of mites and virus, according to Proposition 3.1, as in Fig. 1.a. We choose for the brood maintenance coefficient K the seasonal averages 12,000, 14,000, 12,000, 8000 for spring, summer, fall and winter, respectively.

We first show simulations of the model without virus, i.e., with initial data \(m(0)=y(0)=0\), but with varroa mites present \(M(0)=100\) (Fig. 1b). K is the same as in Fig. 1a. In Fig. 1b, the varroacide control \(\delta _2\) is chosen strong enough (i.e., \(\delta _2=1.35\), i.e., \(\delta _2(t)=1.35\) for \(t=30, 60, 90)\), according to Proposition 3.2 for the mites to be eradicated, so that the system converges to the disease- and mite-free periodic solution\((0,x^*,0,0)\). In Fig. 1c, the varroacide control is reduced \((\delta _2=1)\) such that \((0,x^*,0,0)\) looses its stability according to Proposition 3.2 and a periodic solution with bees and mites present is found. The colony strength in this case remains below \(x^*\), but the population is still strong enough to be a working colony. In Fig. 1d, the parameter \(\delta _2\) is chosen to be 0.1. The colony eventually vanishes, i.e., the unconditionally stable solution (0, 0, 0, 0) is attained after few years. Prior to failure, the peak colony strength in summer is already reducing from year to year.

For Fig. 1e–h, the seasonal averages of parameter K are 8000, 12,000, 8000, 6000 for spring, summer, fall, and winter, respectively. We illustrate now potential model outcomes in the presence of ABPV; we choose initially \(m(0)=80\). In a first simulation in Fig. 1e, the control parameter is chosen to be \(\delta _2=0.3\). After an initial transient period of 2–3 years during which the mites establish themselves in the colony, the peak colony strength in summer is approximately the same every year; the colony seems to work properly for 6–7 years and suddenly fails. In Fig. 1f, the varroacide control is reduced to 0.1, which induces a faster colony failure. In Fig. 1g, the varroacide control is increased to a level such that ABPV is fought off but the mite population still establishes itself. The varroacide control parameter is set to be \(\delta _2=1\) in this case. In Fig. 1h, finally, we choose \(\delta _2=1.35\), strong enough to eradicate both mites and virus.

The behavior observed is sensitive with respect to parameters. For example, under the parameter values for K and \(\alpha \) chosen in the simulations in Fig. 1e–h, and under conditions as in Fig. 1d, a periodic solution with mites and bees will be found, qualitatively similar as in Fig. 1c (data not shown). Under these conditions, the smallest colony strength needed for the colony to survive is reduced. In order to present a scenario of the bee–mite model where the colony collapses due to mites, as in Fig. 1d, we need to choose either high values of K or high values of the parameter \(\alpha \), to increase the number of mites to levels that can become harmful. This intricate interplay between K and \(\alpha \) in determining the fate of the colony has been studied in more detail previously in Ratti et al. (2013) and is not the focus of our current study.

The simulations presented here illustrate a wide range of potential solution behavior, in dependence of initial data and parameter, reaching from virus- and mite-free periodic solutions, over mite–bee periodic solutions, to solutions with gradual colony failure, and solutions which over years seemingly indicate a working colony and then suddenly fail. These observations motivate a number of simulation experiments in which we investigate the relationship between parameter values and long-term colony fate.

Fig. 2
figure 2

Effect of initial disease infestation (\(m_0\) and \(M_0\)) on the time at which the colony collapses (where different lines different \(M_0\) values)

Full size image

4.2 Effect of Initial Disease Infestation on the Survival of the Colony

In this first simulation experiment, we consider the system without varroacide treatment, i.e., \(\delta _i(t)\equiv 0\) for \(i=1,2,3\). We will investigate the effect of the initial mite and virus infestation level, i.e., of \(M_0\) and \(m_0\), on the time at which the colony collapses (see Fig. 2). A colony is assumed to collapse if x becomes very small, in particular, if \(x<1\); in this case, also the continuous assumption of the model is violated, i.e., the model breaks down due to small numbers. Since the trivial equilibrium has been shown to be unconditionally asymptotically stable (see Proposition 3.1), the assumption that small enough colonies imply failure seems justified.

All parameters are the same as in Sect. 4.1 with the brood maintenance coefficient K chosen to be 8000, 12,000, 8000, 6000 for spring, summer, fall and spring, respectively. We varied \(M_0\) in the range of 0 to 2000 and choose \(m_0=p M_0\) where \(0.1<p<1\). Therefore, each curve is distinguished by the ratio of \(M_0\) and \(m_0\). It was observed that when the initial mite infestation is zero, the healthy bee population obtains a strictly positive limit cycle. As the mite infestation in the colony increases, the colony eventually dies off. The higher the mite infestation, the sooner the colony vanishes. Since the bee population is not strong enough in winter to survive in the spring, the colony collapses in winter. This pattern is observed in the natural honeybee colonies as well (Engelsdorp et al. 2008) and in Ontario in particular such wintering losses have been shown to be closely associated with varroa mites (Guzmán-Novoa et al. 2010).

While the fate of the colony is robust, i.e., disease infestation implies eventual failure, the time to collapse depends heavily on the initial levels. This result suggests a window of opportunity for the adoption of remedial measures, e.g., by varroacide application. The stability criterion in the previous section indicated that the yearly compounded treatment efficacy is more important than the timing and local (in time) efficacy of treatment. This result together with the observation of the discrete nature of the failure event suggests that treatment strategies may be relatively robust. We investigate this possibility in more detail in the next experiment.

4.3 Comparison Between a System Treated with Varroacide and an Untreated One

In this simulation experiment, we compare a system without varroacide treatment (\(\delta _i\equiv 0, \forall i\)) and a system with treatment ( \(\delta _i\not \equiv 0, \forall i\)), all other parameters being the same in both cases and the same as in Sect. 4.2. We will investigate whether or not the application of varroacides can protect a colony that would otherwise die off due to the virus vectored by the mites.

As a baseline for comparison, Fig. 3a represents a mite-infested honeybee colony also infected with virus, and with no varroacide treatment. In this figure, the bee population starts increasing in spring and summer and reaches a maximum of 32,000 bees. It then starts decreasing in fall and winter to a minimum of 12,000 bees at the end of the first year. The colony appears to reach a steady maximum above 30,000 each year initially for the first three years, which indicates that it is working well. The virus is present in the colony for several years without being noticeable. After almost 4 years, the virus intensifies and has a greater effect on the bee population, reducing the number of healthy workers. The bee population decreases in spring of the fourth year but it again starts increasing in summer when the maximum birthrate increases. The maximum colony strength that years reaches about 29,000. However, the virus grows rapidly, and the colony is not able to survive the next winter and it vanishes.

Fig. 3
figure 3

a System without varroacide treatment. b System with treatment. Varroacides are applied three times in spring and fall each, with an interval of one month (with \(\delta _2=1.2\)). c System with treatment. Varroacides are applied three times in spring and fall each, with an interval of 1 month (with \(\delta _2=1.3\))

Full size image

Figure 3b, c represents a mite-infested colony infected with virus, where varroacide treatment is applied three times in spring and fall each, using different treatment-associated death rates. In Fig. 3b, the death rate of mites due to varroacides (\(\delta _2\)) is 1.2. The bee population follows a similar pattern as in Fig. 3a, i.e., increases slowly in spring and reaches a maximum of 31,000 in summer. The population starts decreasing in fall and winter attaining a minimum of 14,000 bees by the end of winter season. This pattern is repeated annually. The mite population starts increasing very slowly for the first few years and then becomes established, maintaining a steady maximum and following a limit cycle (see Fig. 4 for a magnified view of the mite population at an instance). The mite infestation level here is relatively low compared to the bee population. The virus is fought off due to the treatment, but the mites are still present in the colony, albeit at relatively low levels, compared to the colony strength. In Fig. 3c, the death rate of mites due to varroacides (\(\delta _2\)) is slightly increased to 1.3. The bee population follows a similar pattern as in Fig. 3a, b. The mite population starts increasing very slowly in the first two years, but the increase in population is negligible. The mite population is not able to establish itself further and dies off, indicating the effectiveness of the treatment in this case, in correspondence with the stability criterion found analytically (see Proposition 3.3).

Fig. 4
figure 4

Magnified version of Fig. 3b. Vertically downward arrows the times when treatment is applied and how the mite population decreases

Full size image

This result suggests that a colony which would otherwise die off due to the virus, can be protected by using varroacides. Furthermore, it can be maintained as a healthy colony with zero or very low mite population levels, depending on the efficacy of the varroacides. In other words, treatment results in control of the vector and control of the viral disease.

4.4 Effect of Varroacide Treatment on the Average Mite Population Level

In this simulation experiment, we consider a system with varroacide treatment. We investigate the effect of the death rate of mites due to treatment (\(\delta _2\)), i.e., the efficacy of the varroacide compounded over one year, on the average of the total mite population over each year, see Fig. 5. All other parameters are the same as in Sect. 4.2. The average of the mite population for each year, \(M_{av}(i)\), is calculated using the expression

$$\begin{aligned} M_{av}(i)=\frac{1}{i}\sum _{c=1}^i{\frac{\int _{a}^{b}{M(t)\mathrm{d}t}}{T}}, \quad i=1,2,3, \ldots \end{aligned}$$

where \(a=(c-1) T, b=c T\), i represents the number of years, and T is the time period.

Fig. 5
figure 5

Effect of death rate of mites due to treatment (i.e., \(\delta _2\)) on the average mite population (scale shown on the color bar)

Full size image

We vary \(\delta _2\) between 0.5 and 1.5, and track the simulations over 20 years. If the annual varroacide efficacy is small, the mite population will slowly increase and a bee–mite limit cycle with a maximum of 6000 mites will be attained. As \(\delta _2\) increases, the average mite population decreases over time. The mite population is not able to establish itself if the death rate is above a threshold value of approximately \(\delta _2=1.2661\), which is the same as calculated from the analysis of the mite- and virus-free periodic solution.

To eradicate mites from the colony, their death rate due to varroacides must be greater than a threshold value. If the death rate due to varroacides is below the threshold value, a necessary collapse of the colony is not implied, but the mite population might become established .

5 Conclusions

We studied a mathematical model of infestations of honeybee colonies with varroa mites and the ABPV with seasonally changing coefficients. Although there is still much unknown about ABPV, the literature suggests that its virulence and transmission depend primarily on Varroa destructor as a mechanical vector. Therefore, a simplifying key assumption made in our model is that ABPV is transmitted by Varroa destructor only. Our main findings can be summarized as follows:

  • In the base model without varroacide treatment, the mite- and virus-free solution is always unstable due to the logistic growth assumption that we made for varroa mites. If only mites are present, but no virus, then depending on parameters a periodic endemic solution can be found, where bees and mites are present, or the colony will fail. The bee population in an endemic bee–mite solution will remain below the size of the mite-free solution. In the presence of the virus, for parameters in realistic ranges, the colony is likely to fail rapidly after several years of slow decline.

  • In our model, the disease-free equilibrium can be stabilized by the application of varroacide with sufficient intensity. This stability criterion can be given explicitly in integral form. The success of varroacide treatment depends on the cumulative efficacy over the year, rather than a specific time course. Our computer simulations suggest that varroacide treatment, at some intermediate levels, not strong enough to completely eradicate varroa mites, can keep the disease under control. In this case, an endemic periodic solution can be found in which case the bee population remains slightly below the corresponding disease-free solution.

  • A particular difficulty in parameterizing a model like the one studied here is that normally only seasonally averaged parameter values can be obtained from available data in the literature, although it is more reasonable to assume that these parameters should vary continuously with time. We have found that different strategies to infer continuously varying parameters from seasonally averaged data lead to quantitatively different solutions, but that this has only minor impact on the qualitative long-term fate of the colony, i.e., whether it survives or fails.

  • Since our results suggest that annual cumulative efficacy of varroacide treatment is more important than the particular time course of treatment, continuous low dosage application of chemical or biological control agents might be possible. This suggests that it might be worthwhile to explore continuous, low maintenance, low-invasive, dispensing techniques as an alternative to current invasive treatment methods that might contribute to cross-contamination between colonies in an apiary. It might be possible, for example, that such dispensing methods use the natural airflow currents in the colony beehive that were studied and characterized in Sudarsan et al. (2012).