Structural and Practical Identifiability Issues of Immuno-Epidemiological Vector–Host Models with Application to Rift Valley Fever

Abstract

In this article, we discuss the structural and practical identifiability of a nested immuno-epidemiological model of arbovirus diseases, where host–vector transmission rate, host recovery, and disease-induced death rates are governed by the within-host immune system. We incorporate the newest ideas and the most up-to-date features of numerical methods to fit multi-scale models to multi-scale data. For an immunological model, we use Rift Valley Fever Virus (RVFV) time-series data obtained from livestock under laboratory experiments, and for an epidemiological model we incorporate a human compartment to the nested model and use the number of human RVFV cases reported by the CDC during the 2006–2007 Kenya outbreak. We show that the immunological model is not structurally identifiable for the measurements of time-series viremia concentrations in the host. Thus, we study the non-dimensionalized and scaled versions of the immunological model and prove that both are structurally globally identifiable. After fixing estimated parameter values for the immunological model derived from the scaled model, we develop a numerical method to fit observable RVFV epidemiological data to the nested model for the remaining parameter values of the multi-scale system. For the given (CDC) data set, Monte Carlo simulations indicate that only three parameters of the epidemiological model are practically identifiable when the immune model parameters are fixed. Alternatively, we fit the multi-scale data to the multi-scale model simultaneously. Monte Carlo simulations for the simultaneous fitting suggest that the parameters of the immunological model and the parameters of the immuno-epidemiological model are practically identifiable. We suggest that analytic approaches for studying the structural identifiability of nested models are a necessity, so that identifiable parameter combinations can be derived to reparameterize the nested model to obtain an identifiable one. This is a crucial step in developing multi-scale models which explain multi-scale data.

1 Introduction

Differential equations are powerful tools for modeling biological systems with broader applications to the fields of biomedical research and infectious disease modeling. In particular, ODEs have been a useful tool for determining the unknown parameters of theoretical models confronting experimental data. Identifiability analysis is a common methodology to determine unknown parameters in ODE models (Miao et al. 2011; Chris et al. 2011; Capaldi et al. 2012; Perasso et al. 2011). Even though identifiability analysis has been used for over the last two decades for ODE models, including structural, practical, and sensitivity-based identifiability analysis, the identifiability analyses of age-structured PDE models have not been studied (but see Perasso et al. 2011; Perasso and Razafison 2016). Here, we study structural identifiability issues for an immuno-epidemiological nested vector–host model with application to Rift Valley fever disease.

Rift Valley fever virus (Family, Bunyaviridae; genus, Phlebovirus) was originally characterized in 1931 in Kenya and has since been isolated throughout the African continent and in the Arabian Peninsula (Bird et al. 2009). The pathogen is transmitted mainly through mosquitoes and may infect several different mammal species, causing illness and death in livestock species and humans and resulting in millions of dollars of economic loss. RVFV persists between epidemic periods, with the leading hypotheses claiming that the virus either remains dormant through the transovarial transmission of the virus within the vector population or through continual amplification events within wildlife host populations (Bird et al. 2009; Manore and Beechler 2013). After being first identified in Kenya in 1931,  RVFV has largely spread throughout the African continent and has a high risk of spreading to new regions, including European Union (EU) and United States (US), through either an accidental introduction or through the use of RVFV as a biological weapon (Rolin et al. 2013).

Previous researchers have used a range of methods to model RVFV, from individual-based models to compartmental ordinary differential equations at the population level, to investigate the impact of the intervention strategies and mechanisms that lead to the persistence of RVFV outbreaks. Gaff et al. (2007, (2011) modeled RVFV disease in an ODE model with vector–host compartments to assess effectiveness of RVFV interventions. Niu et al. (2012) introduced space effects with patch-to-patch movement of species to introduce a methodology for studying the likelihood of pathogen establishment after RVFV introduction to an infection-free area. Fischer et al. (2013) investigated the effects of a temperate climate, such as the Netherlands, where both hosts and potential vectors are present. Mpeshe et al. (2011) formulated an ODE deterministic model of RVFV with a human compartment, in addition to vector–host compartments, and studied epidemiological threshold properties of reproduction number, $\mathcal R_0$, and also explored a sensitivity analysis of the model parameters. Xiao et al. (2015) recently studied the effect of both seasonality and socioeconomic status in a multi-patch model. André et al. (2003) discussed the impact of within-host pathogen and immune dynamics on the pathogen dispersal between hosts. We model RVFV within-host immune dynamics and couple it with an age-since-infection structured vector–host disease model by linking vector–host disease transmission, host recovery rate, and disease-induced death rates to the host immune dynamics (Gulbudak et al. 2016). In this paper, we are interested in the structural and practical identifiability analysis of the nested model with application to RVFV.

The nested model pertains particularly well to Rift Valley fever. The immuno-epidemiological model captures the heterogeneity that exists in the ‘macroscale’ among infected individuals in a RVFV epidemic by incorporating within-host pathogen and immune response dynamics. The immunological model captures qualitative within-host immune dynamics in the ‘microscale’by modeling IgM and IgG immune response antibodies, which are commonly measured in the laboratory (Bird et al. 2009; Jansen van Vuren and Paweska 2009). Although immuno-epidemiological models have garnered attention from scientists and mathematicians hoping to solve problems regarding host-pathogen coevolution, early diagnostics, and transmission-virulence trade-offs (Gilchrist and Sasaki 2002; Mohtashemi and Levins 2001; Alizon and Baalen 2005), the structural and practical identifiability analysis of multi-scale nested models has not been studied. We use RVFV immunological data obtained under laboratory experiments and epidemiological human data from the 2006–2007 outbreak in Kenya (CDC 2007; Munyua et al. 2010) to estimate the unknown parameter values of the nested system.

Many researchers have focused on developing methods for solving the ill-posed inverse problems generated by age-structured population models, but there has been less study on the structural and practical identifiability analysis of the age-structured models. Perasso et al. (2011) performed identifiability analysis of a nonlinear transport reaction system for a SI model, representing the spread of scrapie in a sheep flock, with realistic assumptions regarding the disease characteristics such as long and variable incubation period and asymptomatic infection. They establish an input–output(IO) relation for the model, which is based on the implicit solution of the PDE model. In another study, Perasso and Razafison (2016) investigated the identifiability of the age-dependent mortality rate of the McKendrick–VonFoerster model, where the observation is derived from a given age group of the population. They show how the non-local loopback boundary condition affects the uniqueness of the model parameters. In this study, we are interested in developing a numerical approach for a structural and practical identifiability analysis of a nested immuno-epidemiological model, which couples an ODE immunological model to an age-since-infection structured epidemiological PDE model. To our best knowledge, the identifiability analysis of a nested model, such as the model presented here, has never been studied (but for hierarchical statistical models see Lele et al. 2010), although there is a need for reliable methods for parameter estimation of immuno-epidemiological models to have comparison with experimental data and to provide accurate predictions.

This paper is organized as follows. In the next section, we present an immuno-epidemiological model, with an immunological model for IgM and IgG immune response antibodies and an epidemiological model of RVFV with an age-since-infection structure. In Sect. 3, we study the structural identifiability analysis of the immunological model by using the data from Jansen van Vuren and Paweska (2009). In Sect. 4, we develop a finite difference scheme to approximate the solutions of the immuno-epidemiological model. Then, we estimate the epidemiological parameters from the observable RVFV epidemiological data, by first fixing the immunological parameters. Next, we fit the multi-scale RVFV data to the multi-scale model introduced in this paper. In the last section, we summarize our results and give the conclusion.

2 Immuno-Epidemiological Model

In this section, we first describe a within-host pathogen and immune model, with a logistic pathogen growth rate. Then, we introduce an epidemiological model along with linking parameters. The immuno-epidemiological model links the within-host model to the epidemiological model by using the nested model framework described in Gilchrist and Sasaki (2002). The between-host model is structured with time-since-infection parameter $\tau$. Thus, the dynamics of pathogen and host immune response determines the transmission, recovery and disease-induced mortality properties of the epidemiological model.

2.1 The Immunological Model

The immunological model describes the interaction between pathogen and IgM, IgG immune response antibodies. $M(\tau )$ and $G(\tau )$ denote the within-host IgM and IgG antibody concentrations at time-since-infection $\tau$, respectively. We assume that the pathogen, $P(\tau )$, exhibits logistic growth with carrying capacity K and growth rate r. IgM and IgG immune response antibodies contribute to the elimination of the pathogen at rates $\epsilon$ and $\delta ,$ respectively. The IgM immune response antibodies proliferate at a rate proportional to the viremia level in the host, represented by the activation rate a, and decays at rate c. The IgM immune response antibodies are mainly responsible for rapid destruction of invading pathogen. B cells switch production of IgM immune response antibodies to production of a longer lasting class, IgG, at rate q. IgG immune response antibodies activate at a per-capita rate b.

$$\begin{aligned} {\hbox {Within-host model:}} {\left\{ \begin{array}{ll} \displaystyle \frac{\hbox {d}P}{\hbox {d}\tau } &{}= \left( r\left( 1- \displaystyle \frac{P(\tau )}{K}\right) -\epsilon M(\tau ) -\delta G(\tau )\right) P(\tau ) ,\\ \displaystyle \frac{\hbox {d}M}{\hbox {d}\tau } &{}= a P(\tau )M(\tau ) - (q+c)M(\tau ),\\ \displaystyle \frac{\hbox {d}G}{\hbox {d}\tau } &{}= qM(\tau ) +b G(\tau )P(\tau ). \\ \end{array}\right. } \end{aligned}$$

(1)

Table 1 Definition of the variables in the within-host model

Table 2 Definition of the parameters in the within-host model

At the initial time of infection (when $\tau =0$), there are not yet any IgG immune response antibodies, and very little first response antibodies, IgM, capable of detecting the newly presented pathogen. Over the course of the immune response, B cells will undergo immunoglobulin class switching and switch from producing IgM to IgG antibodies. Hence, the model is equipped with initial conditions: $P(0) =1,\, M(0)=0.0001,\, G(0) =0.$ The definitions of the parameters and the variables of the model are given in Tables 1 and 2.

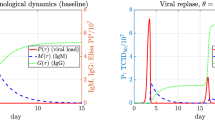
Dynamics of the novel immunological model (1) exhibits the schematically illustrated dynamics described in Bird et al. (2009). Thus either the host dies due to a drastic increase in pathogen concentration, or the pathogen is controlled by the host immune response. If $P(0) \ne K$ and $M(\tau )>0 \text { or } G(\tau )>0$ for $\tau > 0$, the immune response clears the virus, the IgM antibodies die out and the IgG antibodies reach a nonzero steady-state i.e.,

$$\begin{aligned} \displaystyle \lim _{\tau \rightarrow \infty }P(\tau )=0; \ \lim _{\tau \rightarrow \infty }M(\tau )=0 \, \text {and}\, \lim _{\tau \rightarrow \infty }G(\tau )=G^* \quad \hbox { where } G^* \ne 0 \end{aligned}$$

We present a detailed analysis of immunological model (1) in Gulbudak et al. (2016).

2.2 An Epidemiological Model of the Rift Valley Fever

Rift Valley Fever is a vector-borne, zoonotic disease. It can cause a significant economic loss due to deaths and abortions among livestock. It is mostly spread among domestic animals and humans by the bite of an infected mosquito. The sporadic outbreaks of RVFV have followed heavy rainfall and flooding in Kenya and other parts of Africa since the 1930s. Up to date, no human-to-human transmission has been seen.¹

The mosquito population is divided into two nonintersecting classes; $S_\mathrm{v}(t)$ susceptible vectors at time t and $I_\mathrm{v}(t)$ infected vectors at time t. The birth and death rates of the vector population are denoted by $\Lambda _\mathrm{v}$ and $\mu _\mathrm{v}$, respectively. Susceptible vectors become infected after a blood meal on an infected host. The density of the infected host population $i_\mathrm{H}(\tau ,t)$ is structured with both time t and time-since-infection $\tau$. The new incidences in the vector population are modeled by the term

$$\begin{aligned} S_\mathrm{v}\displaystyle \int _0^{\infty } \beta _\mathrm{H}(\tau ) i_\mathrm{H}(\tau ,t)\mathrm{d}\tau \,. \end{aligned}$$

Infectious hosts have different infectivity at different times-since-infection. Transmission rate from an infected host to a susceptible vector, $\beta _\mathrm{H}(\tau )$, is governed by the pathogen level in the infected host at $\tau$ time-since-infection. Thus, the transmission rate is linked to the infected hosts immune response dynamics, via Martcheva (2015)

$$\begin{aligned} \beta _\mathrm{H}(\tau ) = \displaystyle \frac{c_\mathrm{H} P^\nu (\tau )}{B_\mathrm{H}+ P^\nu (\tau )}, \end{aligned}$$

where $c_\mathrm{H},\,B_\mathrm{H}$ and $\nu$ are constants. The model in the vector population takes the form:

$$\begin{aligned} {\hbox {Vector Model:}} {\left\{ \begin{array}{ll} \displaystyle \frac{\hbox {d}S_\mathrm{v}}{\hbox {d}t} &{}= \Lambda _\mathrm{v} -S_\mathrm{v}\displaystyle \int _0^{\infty } \beta _\mathrm{H}(\tau ) i_\mathrm{H}(\tau ,t)\hbox {d}\tau - \mu _\mathrm{v} S_\mathrm{v},\\ \displaystyle \frac{\hbox {d}I_\mathrm{v}}{\hbox {d}t} &{}= S_\mathrm{v} \displaystyle \int _0^{\infty } \beta _\mathrm{H}(\tau ) i_\mathrm{H}(\tau ,t)\hbox {d}\tau - \mu _\mathrm{v} I_\mathrm{v}.\\ \end{array}\right. } \end{aligned}$$

(2)

The epidemiology of the RVFV between-host population is described by an SIR model. At any time, the host population (livestock population) is further divided into susceptible hosts, $S_\mathrm{H}(t)$ and recovered hosts, $R_\mathrm{H}(t)$ classes. The between host model is given by:

$$\begin{aligned} {\hbox {Between-Host Model:}} {\left\{ \begin{array}{ll} \displaystyle \frac{\hbox {d} S_\mathrm{H}}{\hbox {d} t} &{} = \Lambda - \beta _\mathrm{v} S_\mathrm{H} I_\mathrm{v} - \mu _\mathrm{H} S_\mathrm{H},\\ \displaystyle \frac{\partial i_\mathrm{H}}{\partial t} +\displaystyle \frac{\partial i_\mathrm{H}}{\partial \tau } &{}= -\left( \alpha (\tau ) + \gamma (\tau ) + \mu _\mathrm{H}\right) i_\mathrm{H}(\tau ,t),\\ i_\mathrm{H}(0,t) &{}= \beta _\mathrm{v} S_\mathrm{H} I_\mathrm{v}, \\ \displaystyle \frac{\hbox {d} R_\mathrm{H}}{\hbox {d} t} &{}= \displaystyle \int _0^{\infty } \gamma (\tau ) i_\mathrm{H}(\tau ,t)\hbox {d}\tau - \mu _\mathrm{H} R_\mathrm{H},\\ \end{array}\right. } \end{aligned}$$

(3)

where $\Lambda$ is the constant recruitment into the host population, $\mu _\mathrm{H}$ is the natural death rate, and $\beta _\mathrm{v}$ is the transmission rate from vector to host. We suppose that the disease-induced death rate, $\alpha (\tau )$, depends not only on the viral load but also on the first immune response antibodies (IgM) in the host. We assume that antibody levels are proportional to the intensity of an immune response, which is costly to the host, similar to the assumptions of previous immuno-epidemiological modelers (Gilchrist and Sasaki 2002). Thus, the disease-induced death rate, $\alpha (\tau )$, has the following linear dependence on $P(\tau )$ and $M(\tau )$

$$\begin{aligned} \alpha (\tau ) = \sigma P(\tau ) + \xi M(\tau ), \end{aligned}$$

where $\sigma$ and $\xi$ are the constants. The IgG antibodies have no effect on $\alpha (\tau )$. On the other hand, the recovery rate is proportional to the IgG levels in the host and indirectly proportional to the pathogen level. Hence,

$$\begin{aligned} \gamma (\tau ) =\displaystyle \frac{\kappa G(\tau )}{P(\tau ) +\epsilon _0 }, \end{aligned}$$

where $\kappa$ and $\epsilon _0$ are constants. Definitions of epidemiological variables, parameters, and their linking relations to the host immune response are summarized in Tables 3 and 4. A schematic illustration of the “nested model” framework for vector-borne diseases is shown in Fig. 1.

Table 3 Definition of the variables in the between-host model

Table 4 Definition of the parameters in the between-host model and their linking relation to immune response dynamics

Fig. 1

Schematic illustration of the “nested model” framework for vector-borne diseases

We study the dynamics of the epidemiological model (2)–(3) in another paper (Gulbudak et al. 2016). Here, we summarize those results. The immuno-epidemiological reproduction number of models (2)–(3) is,

$$\begin{aligned} \mathcal {R}_0 = \displaystyle \frac{\beta _\mathrm{v} \Lambda }{\mu _\mathrm{v} \mu _\mathrm{H}} \int _0^\infty \frac{\Lambda _\mathrm{v}}{\mu _\mathrm{v}}\beta _\mathrm{H}(\tau ) e^{-\displaystyle \int _0^\tau \left( \alpha (s) + \gamma (s) +\mu _\mathrm{H}\right) \hbox {d} s}\hbox {d} \tau \end{aligned}$$

(4)

The disease free equilibrium $\epsilon ^0 =\left( \ S^0_\mathrm{V}, \ I^0_\mathrm{V}, \ S^0_\mathrm{H},\ i^0_\mathrm{H}(\tau ),\ R^0_\mathrm{H}\right) = \left( \displaystyle \frac{\Lambda _\mathrm{v}}{\mu _\mathrm{v}},0,\displaystyle \frac{\Lambda }{\mu _\mathrm{H}},0,0\right)$ is locally asymptotically stable when $\mathcal {R}_0 < 1$ and unstable when $\mathcal {R}_0 >1.$ When $\mathcal {R}_0 >1$, there exists a unique locally asymptotically stable endemic equilibrium $\epsilon ^* =\left( \ S^*_\mathrm{V}, \ I^*_\mathrm{V}, \ S^*_\mathrm{H},\ i^*_\mathrm{H}(\tau ),\ R^*_\mathrm{H}\right)$ where

$$\begin{aligned} S^*_\mathrm{H}= & {} \frac{1}{\beta _\mathrm{v} \frac{S^*_\mathrm{V}}{\mu _\mathrm{v}}\int _0^\infty {\beta _\mathrm{H}(\tau )\pi (\tau )\hbox {d}\tau }}, \ i^*_\mathrm{H}(\tau )= i^*_\mathrm{H}(0)\pi (\tau ), \ R^*_\mathrm{H}=\frac{i^*_\mathrm{H}(0)}{\mu _\mathrm{H}} \int _0^\infty {\gamma (\tau )\pi (\tau )\hbox {d} \tau },\\ S^*_\mathrm{V}= & {} \frac{\Lambda _\mathrm{v}}{i^*_\mathrm{H}(0)\int _0^\infty {\beta _\mathrm{H}(\tau )\pi (\tau )\hbox {d}\tau }+\mu _\mathrm{v}},\ I^*_\mathrm{V}=\frac{S^*_\mathrm{V}}{\mu _\mathrm{v}}\int _0^\infty {\beta _\mathrm{H}(\tau )i^*_\mathrm{H}(\tau )\hbox {d}\tau }, \end{aligned}$$

and $\pi (\tau )$ is the probability of still being infectious $\tau$ time units after becoming infected, which is given by

$$\begin{aligned} \pi (\tau ) = \displaystyle e^{- \displaystyle \int _0^\tau \left( \alpha (s) +\gamma (s) + \mu _\mathrm{H}\right) \mathrm{d}s}. \end{aligned}$$

(5)

3 Parameter Estimation of the Immunological Model

We fit the immunological model to the data in Jansen van Vuren and Paweska (2009), which gives times-series RVFV viremia, IgM, and IgG immune response antibody concentrations in sheep inoculated subcutaneously with RVFV (Jansen van Vuren and Paweska 2009, Fig 7). Virus concentrations were reported as median tissue culture infectious dose (TCID$_{50}$), or the viral dilution concentration necessary to elicit cytopathic effects in 50 % of cell cultures. Antibody concentrations were reported as ELISA PP values, which are the relative percentage optical density measurements of test specimen in comparison with a mean high-positive control antigens. We extracted the data points ($\log _{10}$ of viremia levels) from the plot using MATLAB code grabit.m,² and present the data in Table 5.

Table 5 Data extracted from Figure 7 in Jansen van Vuren and Paweska (2009)

Let ${\varvec{x}} \!=\! [P ,M,G]$ be the vector of state variables, and let ${\varvec{p}} = [r, K, \epsilon ,\delta ,a, q, c, b]\,$ be the vector of model parameters, then the within-host model (1) is equivalent to

$$\begin{aligned} \begin{aligned} {\varvec{x}}'&= f({\varvec{x}}(\tau ) , {\varvec{p}}) ,\\ {\varvec{x}}(0)&= {\varvec{x}}_0\,. \\ \end{aligned} \end{aligned}$$

(6)

The parameters ${\varvec{p}}$ of the model are estimated based on the n observation $\{y_i\}_{i=1}^n$ made at times $\tau _1, \tau _2,\ldots ,\tau _n$. The data points in Table 5 are the $\log _{10}$ of the viremia levels in blood at time $\tau _i\; i=1,\ldots ,n$ ($n=11$, see Table 5). For the parameter estimation problem, we use the following statistical model as introduced in Banks et al. (2014)

$$\begin{aligned} y_i = g({\varvec{x}} (\tau _i),\hat{{\varvec{p}}}) + \varepsilon _i \end{aligned}$$

(7)

where $g({\varvec{x}} (\tau _i),\hat{{\varvec{p}}}) = P(\tau _i,\hat{{\varvec{p}}})\,$ are the viremia levels, and $\hat{{\varvec{p}}}$ are the “true” parameters we are looking for. The random variables $\varepsilon _i$ represents the measurement errors which cause the observations $g({\varvec{x}} (\tau _i),\hat{{\varvec{p}}})$ to drift away from the smooth exact path $g({\varvec{x}} (\tau ),\hat{{\varvec{p}}})$. In this study, we assume that there is no modeling error, hence the mean of the measurement errors is zero, $\mathbb {E}(\varepsilon _i) =0$. In a more general setting, the errors satisfy the following form, which allows fairly wide range of error models,

$$\begin{aligned} \varepsilon _i = g({\varvec{x}} (\tau _i),\hat{{\varvec{p}}})^{f} \epsilon _i \end{aligned}$$

(8)

where $f \ge 0$. The $\epsilon _i$ are assumed to be independent, identically distributed random variables with mean zero and finite variance $\sigma _0^2$. The mean and the variance of the random variables $y_i$ satisfy, $\mathbb {E}(y_i) = g({\varvec{x}} (\tau _i),\hat{{\varvec{p}}})$, $\hbox {Var}(y_i) = g({\varvec{x}} (\tau _i),\hat{{\varvec{p}}})^{2f} \sigma _0^2\,,$ respectively. If $f =0$, then (8) becomes $\varepsilon _i =\epsilon _i$, that is the error in the measurements are independent from the observations $g({\varvec{x}} (\tau _i),\hat{{\varvec{p}}})$, which is called absolute error. In counting populations, it is reasonable to assume that the measurement errors depends on the population size, hence in that case we set $f=1$ in (8), which is called relative error. In some cases, depending on the problem, it might be appropriate to set $f=1/2$ in (8) (Banks et al. 2014). When $f=1/2$, the error model (8) was referred to as Poisson noise in Capaldi et al. (2012).

3.1 Structural Identifiability

A first step in estimating the parameters of a model is to determine whether the problem is well posed for a given model and data. A well-posed parameter estimation problem means that the parameters of the model can be recovered uniquely from the given data set. Even in an ideal situation where the data are noise-free and there is no modeling error, the quality of parameter estimation results depends on the predictive capability of the mathematical model. If the mathematical problem is not structurally identifiable, then the parameters estimated by a numerical optimization problem might not be unique and thus be unreliable. On the other hand, a mathematical model which is structurally identifiable may not be practically identifiable (Chris et al. 2011; Cobelli and DiStefano 1980). That is, when noisy data are considered, the parameters may not be uniquely recovered. Moreover, the data might be precise, but if collected at a time interval where dynamics of the model are not captured, then the parameters might still be unidentified. Eisenberg et al. showed that a SIWR (Susceptible-Infected-Water-Recovered) model of Cholera is structurally identifiable, but it is practically unidentifiable when the environmental transmission of the cholera through the water component is very fast (Eisenberg et al. 2013).

Structural identifiability is concerned with the possibility of estimating the model parameters assuming perfect experimental data. The definition of the structural identifiability in Miao et al. (2011) is given as

Definition 3.1

A parameter set ${\varvec{p}}$ is called structurally (or uniquely) identifiable if for every ${\varvec{q}}$ in the parameter space, the equation

$$\begin{aligned} g({\varvec{x}} (\tau ) ,{\varvec{p}}) = g({\varvec{x}} (\tau ) ,{\varvec{q}}) \implies {\varvec{p}} = {\varvec{q}} \,. \end{aligned}$$

That is, any unequal parameter set yields different observations and hence the corresponding noise-free data are distinct.

It is crucial to check the structural identifiably of the model, and several methods have been proposed to perform this task. This can be done by suitable mathematical methods directly on the model without the need of any experimental data. These include Taylor series methods (Miao et al. 2011; Pohjanpalo 1978), differential algebra-based methods (Bellu et al. 2007; Eisenberg et al. 2013; Ljung and Glad 1994; Miao et al. 2011), and other methods such as the generating series approach, the direct test, and a method based on the implicit function theorem that have been reviewed in Chris et al. (2011) and Miao et al. (2011).

We will use the differential algebra approach (Bellu et al. 2007; Miao et al. 2011) to test the model (1). The differential algebra approach assumes that f and g are rational polynomial functions. One of the strengths of this approach is that if the model is unidentifiable, the identifiable parameter combinations can be obtained, which then can be used to reparametrize the model to get a structurally identifiable model (Meshkat et al. 2009). The differential algebra approach builds upon deriving the input–output equation, which contains all the structural identifiability information of the model. The input-output equations are determined from the characteristic sets which are derived by Ritt’s algorithm and depend on the ranking of the state variables and the output. We refer the reader to Meshkat et al. (2009) and Miao et al. (2011) for the details on the differential algebra approach. We briefly summarize the method with the following model (9), since our structural identifiability analysis is extensively based on this approach.

Suppose, we want to estimate the parameters of a simple immunological model, adapted from Gilchrist and Sasaki (2002) using the viremia levels in the blood as the data.

$$\begin{aligned} \begin{aligned} \displaystyle \frac{\hbox {d} P}{\hbox {d} \tau }&= \left( r -\epsilon M(\tau )\right) P(\tau ),\\ \displaystyle \frac{\hbox {d} M}{\hbox {d} \tau }&= a P(\tau )M(\tau ).\\ \end{aligned} \end{aligned}$$

(9)

The question of structural identifiability is to determine whether the model is structured to estimate the parameters uniquely given noise-free data. Within the differential algebra approach, we adapt the ranking $P< M$ of the state variables, then the model (9) yields the following input–output equation derived from the characteristic set,

$$\begin{aligned} \epsilon P'' P - \epsilon (P')^2 + \epsilon arP^3 - \epsilon aP'P^2 = 0\,. \end{aligned}$$

(10)

The characteristic set in general is not unique, but the coefficients of the normalized input–output equation contain all the identifiability information of the dynamical model (Eisenberg et al. 2013). The input–output Eq. (10) can be normalized to make it a monic differential polynomial by dividing by $\epsilon$:

$$\begin{aligned} P'' P - (P')^2 + arP^3 - aP'P^2 = 0. \end{aligned}$$

(11)

The structural identifiability can be determined from the injectivity of the coefficients $c({\varvec{p}})$ of the normalized input–output equation (Eisenberg et al. 2013).

Thus, within the differential algebra approach, the definition of the structural identifiability becomes,

Definition 3.2

Let $c({\varvec{p}})$ be the coefficients of the normalized input–output equation, then the dynamical model is structurally identifiable if and only if

$$\begin{aligned} c({\varvec{p}}) = c({\varvec{q}}) \implies {\varvec{p}} ={\varvec{q}} \end{aligned}$$

Suppose to the contrary that another set of the parameters $[q_1,q_2,q_3]$ gives the same output. Then, we would have:

$$\begin{aligned} q_1q_3 = a r \quad \hbox { and } \quad q_3 = a. \end{aligned}$$

From which we would get the parameters a and r uniquely, but $\epsilon$ can not be identified. So, the model (9) is unidentifiable. Thus, we have proved the following result.

Proposition 3.1

The model (9) is structurally unidentifiable from the observations of viremia levels in host.

The immunological model (1) is a generalization of the model (9). Following a similar analysis, we prove the following result for the model (1).

Proposition 3.2

The immunological model (1) is not structured to identify the parameters ${\varvec{p}} = [r, K, \epsilon , \delta , a, b, c, q]$ from the pathogen level observations in the host. Only the parameters $r\,, K\,, a\,, b\,,$ and the combinations of the parameters $q+c\,,$ and $\displaystyle \frac{q \delta }{\epsilon }\,$ can be identified.

Proof

To derive an input–output equation for the model (1) is more complicated. Using the Differential Algebra for Identifiability of Systems (DAISY) software, introduced in Bellu et al. (2007), we obtain the following normalized input–output equation of the model (1).

$$\begin{aligned} \begin{aligned}&P'''P^3 + P'''P^2\displaystyle \frac{K( - \epsilon q - \epsilon c + \delta q)}{ \epsilon K(a - b)}+ 4P''P'P^2 \displaystyle \frac{\epsilon K( - a + b) }{ \epsilon K(a - b)}+ 3P''P'P \frac{K(\epsilon q + \epsilon c - \delta q) }{ \epsilon K(a - b)} \\&\quad + P''P^4 \frac{\epsilon (ra - rb - a^2K + b^2K)}{ \epsilon K(a - b)} +P''P^3 \frac{( - r\epsilon q - r\epsilon c + r\delta q + 2\epsilon a q K + 2\epsilon a c K - \delta a q K - \delta q b K)}{ \epsilon K(a - b)} \\&\quad + P''P^2\frac{K( - \epsilon q^2 - 2\epsilon q c - \epsilon c^2 + \delta q^2 + \delta q c) }{ \epsilon K(a - b)}+3P'^3P+ 2P'^3\frac{K( - \epsilon q - \epsilon c + \delta q)}{ \epsilon K(a - b)} \\&\quad + P'^2P^3\frac{\epsilon ( - ra + rb + a^2K - b^2K)}{ \epsilon K(a - b)} + P'^2P^2\frac{K( - 2\epsilon a q - 2\epsilon a c + \epsilon q b + \epsilon c b + \delta a q)}{ \epsilon K(a - b)} \\&\quad + P'^2P\frac{K(\epsilon q^2 + 2\epsilon q c + \epsilon c^2 - \delta q^2 - \delta q c) }{ \epsilon K(a - b)}+ P'P^5\frac{\epsilon ( - ra^2 + rb^2 + a^2bK - ab^2K)}{ \epsilon K(a - b)} \\&\quad + P'P^4\frac{(2r\epsilon a q + 2r\epsilon a c + r\epsilon q b + r\epsilon c b - r\delta a q - 2r\delta q b - 2\epsilon a q b K - 2\epsilon a c b K + \epsilon q b^2K + \,\epsilon c b^2K + \delta a q b K) }{ \epsilon K(a - b)} \\&\quad + P'P^3\frac{\begin{array}{c}( - r\epsilon q^2 - 2r\epsilon q c- r\epsilon q b K - r\epsilon c^2 - r\epsilon c b K + r\delta q^2 + r\delta q c + r\delta q b K + \epsilon q^2bK + 2\epsilon q cbK\\ + \epsilon c^2bK - \delta q^2bK - \delta q c b K)\end{array}}{ \epsilon K(a - b)} \\&\quad + P^7\frac{r\epsilon a b(a - b) }{ \epsilon K(a - b)}+ P^6\frac{rb( - \epsilon a^2K - 2\epsilon a q - 2\epsilon a c + \epsilon a b K + \epsilon q b + \epsilon c b + \delta a q)}{ \epsilon K(a - b)} \\&\quad + P^5\frac{rb(2\epsilon a q K + 2\epsilon a c K + \epsilon q^2 + 2\epsilon q c - \epsilon q b K + \epsilon c^2 - \epsilon c b K - \delta a q K - \delta q^2 - \delta q c)}{ \epsilon K(a - b)} \\&\quad + P^4\frac{rbK( - \epsilon q^2 - 2\epsilon q c - \epsilon c^2 + \delta q^2 + \delta q c)}{ \epsilon K(a - b)} =0 \end{aligned}\nonumber \\ \end{aligned}$$

(12)

Suppose another set of parameters, ${\varvec{q}}=[q_1\,,q_2\,,q_3\,, q_4\,, q_5\,,q_6\,,q_7\,,q_8]$ produced the same output P. Since the viremia levels are equal, we compare the coefficients of the input–output equation and obtain a nonlinear system of 11 equations and derive the Groebner basis using Mathematica.

Solving the Groebner basis, we arrive at the following results,

$$\begin{aligned} r = q_1,\quad K= q_2,\quad a =q_5,\quad b=q_6,\quad q + c = q_8 +q_7 \quad \frac{q \delta }{\epsilon } = \frac{q_8 q_4}{q_3}\,. \end{aligned}$$

Thus, the model (1) is unidentifiable. Only the parameters $r\,, K\,, a\,, b\,,$ and the parameter combinations $q+c\,$ and $\displaystyle \frac{q \delta }{\epsilon }\,$ can be identified. $\square$

The Proposition 3.2 states that the parameters of the model (1) cannot be identified from the observations of viremia levels only. We would like to point out that if all the state variables were observable, in addition to viremia levels, and we were to observe IgM and IgG levels, then all parameters of the model (1) would be identified. The data given for IgM and IgG concentrations in Jansen van Vuren and Paweska (2009) are relative percentage optical density measurements from the test specimen in comparison with a mean high-positive control antigens. That is, it is not possible to use the data provided for IgM and IgG in the parameter estimations.

Fig. 2

The parameter estimates of the model (1) for 100 synthetic data generated by Poisson noise. True parameters are indicated by red stars. True parameters are $r = 5.33,\, K = 9.75 \times 10^6, \epsilon = 0.0163, \delta = 0.0079,\, a= 6.28 \times 10^{-7},\, q =0.1812,\, c=0.1155,\, b= 5.83 \times 10^{-7}.$ Note that only the parameters r, K, a and b are identified. The parameters $q,c,\epsilon$ and $\delta$ cannot be identified (Color figure online)

We perform a numerical experiment to show the theoretical results we obtained in Proposition 3.2. The viremia data in Jansen van Vuren and Paweska (2009) are given for $\log _{10}$ of the pathogen levels. But, for the numerical experiment we would like to test the structural identifiability results obtained by differential algebra approach, which requires g to be a rational function. That is, we would like to estimate the parameters of the immunological model (1) from the observations $g({\varvec{x}} (\tau _i),\hat{{\varvec{p}}}) = P(\tau _i,\hat{{\varvec{p}}})\,.$ (Note that for the practical identifiability, we take $g({\varvec{x}} (\tau _i),\hat{{\varvec{p}}}) = \log _{10} (P(\tau _i,\hat{{\varvec{p}}}))\,$ in the next section). The parameters of the model (1) are estimated using the maximum likelihood approach from 100 synthetic data generated by adding Poisson noise to the model output $g({\varvec{x}} (\tau _i),\hat{{\varvec{p}}}) = P(\tau _i,\hat{{\varvec{p}}})\,,$ at the data time points $\tau _i\,, i=1,2,\ldots ,n$ as in Table 5. That is, we generate $M=100$ synthetic data whose mean is $\mathbb {E}(y_i) = g({\varvec{x}} (\tau _i),\hat{{\varvec{p}}})$ and $\hbox {Var}(y_i) = g({\varvec{x}} (\tau _i),\hat{{\varvec{p}}})$. The true parameter values, $\hat{{\varvec{p}}}$, are shown as red stars in Fig. 2. We estimate the parameters by solving the following minimization problem for each data set

$$\begin{aligned} {\varvec{p}}_j = \displaystyle \min _{\hat{{\varvec{p}}}} \left( \displaystyle \sum _{i=1}^{n}g({\varvec{x}} (\tau _i),\hat{{\varvec{p}}}) - \displaystyle \sum _{i=1}^n y_i \ln (g({\varvec{x}} (\tau _i),\hat{{\varvec{p}}})) \right) \,, \quad j=1,2,\ldots ,100. \end{aligned}$$

(13)

The Nelder–Mead iterative algorithm is used to approximate the minimum of the cost function (13). The initial parameter values for the iterative solver are chosen randomly from a normal distribution whose mean is the true parameter values and the standard deviation is $10\,\%$ of the mean. The structural identifiability conclusion of Proposition 3.2 is consistent with the numerical experiment we performed for estimating the parameters of the model (1) (see Fig. 2). The scatter plots support the theoretical results in Proposition 3.2; only the parameters, $r\,, K\,, a\,$ can be identified and parameters $q,c,\epsilon$ and $\delta$ can not be identified. The scatter plots are inconclusive for the parameter b. The correlations between the unidentifiable parameters cannot be deduced from the scatter plots, but Proposition 3.2 gives the correlations among the unidentified parameters.

Model (1) is not structured to identify its parameters from viremia observations. In attempt to get an identifiable model, we first non-dimensionalize (1) by setting $u_1 = \displaystyle \frac{P}{K}\,, u_2 = \displaystyle \frac{\epsilon }{r}M \,, u_3 = \displaystyle \frac{\delta }{r}G$, and $t = \displaystyle \frac{\tau }{r}\,.$

$$\begin{aligned} \begin{aligned} \displaystyle \frac{\hbox {d} u_1}{\hbox {d} t}&= \left( \left( 1- u_1\right) - u_2 - u_3 \right) u_1 ,\\ \displaystyle \frac{\hbox {d} u_2}{\hbox {d} t}&= \alpha u_1 u_2 - \gamma u_2\\ \displaystyle \frac{\hbox {d} u_3}{\hbox {d} t}&= \beta u_2 + \omega u_3 u_1 \\ \end{aligned} \end{aligned}$$

(14)

where $\alpha = \displaystyle \frac{a K}{r}\,, \gamma = \displaystyle \frac{q+c}{r}, \beta = \displaystyle \frac{q \delta }{\epsilon r}\,, \omega = \displaystyle \frac{b K}{r}.$

Proposition 3.3

The non-dimensionalized model (14) is structurally identifiable from viremia observations.

Proof

Using DAISY, we get the following input–output equation of the model (14).

$$\begin{aligned} \begin{aligned}&P'''P^4+ \displaystyle \frac{( \beta - \gamma )}{(\alpha - \omega )}P'''P^3 - 4P''P'P^3+ 3\displaystyle \frac{(\gamma - \beta )}{(\alpha - \omega )}P''P'P^2\\&\quad + \displaystyle \frac{( - \alpha ^2 + \alpha + \omega ^2 - \omega ) }{(\alpha - \omega )} P''P^5 + \displaystyle \frac{(2\alpha \gamma - \alpha \beta - \gamma - \beta \omega + \beta )}{(\alpha - \omega )}P''P^4 \\&\quad + \displaystyle \frac{\gamma ( -\gamma + \beta ) }{(\alpha - \omega )}P''P^3+ 3P'^3P^2+ 2\displaystyle \frac{( - \gamma + \beta )}{(\alpha - \omega )}P'^3P + \displaystyle \frac{(\alpha ^2 - \alpha - \omega ^2 + \omega )}{(\alpha - \omega )}P'^2P^4\\&\quad + \displaystyle \frac{( - 2\alpha \gamma + \alpha \beta + \gamma \omega ) }{(\alpha - \omega )}P'^2P^3+ \displaystyle \frac{\gamma (\gamma - \beta )}{(\alpha - \omega )}P'^2P^2 +\displaystyle \frac{(\alpha ^2\omega - \alpha ^2 - \alpha \omega ^2 + \omega ^2)}{(\alpha - \omega )}P'P^6\\&\quad + \displaystyle \frac{( - 2\alpha \gamma \omega + 2\alpha \gamma + \alpha \beta \omega - \alpha \beta + \gamma \omega ^2 + \gamma \omega - 2\beta \omega )}{(\alpha - \omega )}P'P^5\\&\quad + \displaystyle \frac{(\gamma ^2\omega - \gamma ^2 - \gamma \beta \omega + \gamma \beta - \gamma \omega + \beta \omega ) }{(\alpha - \omega )}P'P^4\\&\quad + \displaystyle \frac{\alpha \omega (\alpha -\omega ) }{(\alpha - \omega )} P^8 +\displaystyle \frac{\omega ( - \alpha ^2 - 2\alpha \gamma + \alpha \beta + \alpha \omega + \gamma \omega ) }{(\alpha - \omega )} P^7\\&\quad + \displaystyle \frac{\omega (2\alpha \gamma - \alpha \beta + \gamma ^2 - \gamma \beta - \gamma \omega ) }{(\alpha - \omega )} P^6+ \displaystyle \frac{\gamma \omega ( - \gamma + \beta )}{(\alpha - \omega )} P^5=0 \end{aligned} \end{aligned}$$

(15)

Solving $c({\varvec{p}}) = c({\varvec{q}})$ for ${\varvec{p}} = [\alpha ,\gamma ,\beta ,\omega ]$ and ${\varvec{q}}=[q_1,\, q_2,\, q_3,\,q_4\,]$ using the Groebner basis in Mathematica we obtain,

$$\begin{aligned} \alpha =q_1,\quad \gamma = q_2,\quad \beta = q_3,\quad \omega = q_4. \end{aligned}$$

Thus, the model (14) is structurally identifiable. $\square$

We note that even though model (14) is structurally identifiable, in practice it is not useful. It is not clear how to normalize the data since the carrying capacity, K, of the viremia is not known. Furthermore, the parameters $r, \epsilon ,\delta ,a, q, c,$ and b cannot be derived from estimated values of $\alpha , \gamma , \beta ,$ and $\omega$. We search for another model which is structurally identifiable.

We scale the model (1) by setting $u_2 =\epsilon M \,, u_3 = \delta G$ and obtain;

$$\begin{aligned} {\hbox {Scaled Model:}} {\left\{ \begin{array}{ll} \displaystyle \frac{\hbox {d} P}{\hbox {d} \tau } &{}= \left( r\left( 1- \displaystyle \frac{P(\tau )}{K}\right) -u_2(\tau ) - u_3(\tau )\right) P(\tau ) ,\\ \displaystyle \frac{\hbox {d} u_2}{\hbox {d}\tau } &{}= a P(\tau )u_2(\tau ) - (q+c)u_2(\tau )\,,\\ \displaystyle \frac{\hbox {d}u_3}{\hbox {d} \tau } &{}= wu_2(\tau ) +b u_3(\tau )P(\tau )\,, \\ \end{array}\right. } \end{aligned}$$

(16)

where $w=\displaystyle \frac{q \delta }{\epsilon }.$ By Proposition 3.2, we see that the combination $q+c$ is identifiable, but not the parameters q and c. The parameter c denotes the exponential decay rate of the IgM immune response antibody concentration. It is suggested that the biological half life of the IgM immune response antibodies in lambs is 6 days (Watson 1992). Hence, we fix $c=\displaystyle \frac{\ln 2}{6}$.

Proposition 3.4

When c is fixed, the scaled model (16) is structurally identifiable from the viremia observations.

Proof

Using DAISY, we get the following input–output equation of the model (16).

$$\begin{aligned} \begin{aligned}&P''' P^4 + P''' P^3 \displaystyle \frac{K ( - q + w - c)}{K (a - b)} - 4 P'' P' P^3 + 3 P'' P' P^2 \displaystyle \frac{K (q - w + c)}{K (a - b)} \\&\quad + P'' P^5 \displaystyle \frac{(r a - r b - a^2 K + b^2 K)}{K (a - b)} + P'' P^4\displaystyle \frac{ ( - r q + r w - r c + 2 a q K - a w K + 2 a K c - w b K)}{K (a - b)} \\&\quad + P'' P^3 \displaystyle \frac{K ( - q^2+ q w - 2 q c + w c - c^2) }{K (a - b)} + 3 P'^3 P^2 + 2 P'^3 P\displaystyle \frac{K ( - q + w - c) }{K (a - b)} \\&\quad + P'^2 P^4 \displaystyle \frac{( - r a + r b + a^2 K - b^2 K)}{K (a - b)} + P'^2 P^3 \displaystyle \frac{K ( - 2 a q + a w - 2 a c + q b + b c) }{K (a - b)}\\&\quad +P'^2 P^2\displaystyle \frac{ K (q^2 - q w + 2 q c - w c + c^2)}{K (a - b)} + P' P^6 \displaystyle \frac{( - r a^2 + r b^2 + a^2 b K - a b^2 K)}{K (a - b)}\\&\quad + P' P^5\displaystyle \frac{ (2 r a q - r a w + 2 r a c + r q b - 2 r w b + r b c - 2 a q b K + a w b K - 2 a b K c + q b^2 K + b^2 K c)}{K (a - b)}\\&\quad + P' P^4 \displaystyle \frac{( - r q^2 + r q w - r q b K - 2r q c + r w b K + r w c - r b K c - r c^2 + q^2 b K - q w b K + 2 q b K c - w b K c + b K c^2)}{K (a - b)} \\&\quad + P^8\displaystyle \frac{ r a b (a - b) }{K (a - b)}+ P^7\displaystyle \frac{ r b ( - a^2 K - 2 a q + a w + a b K - 2 a c + q b + b c)}{K (a - b)} \\&\quad + P^6\displaystyle \frac{ r b (2 a q K - a w K + 2 a K c + q^2 - q w - q b K + 2 q c - w c - b K c + c^2)}{K (a - b)} \\&\quad + P^5 \displaystyle \frac{r b K ( - q^2 + q w - 2 q c + w c - c^2)}{K (a - b)}=0 \end{aligned} \end{aligned}$$

(17)

Solving $c({\varvec{p}}) \!=\! c({\varvec{q}})$ for ${\varvec{p}} = [r,K,a,b,q,c,w]$ and ${\varvec{q}}\!=\![q_1,\, q_2,\, q_3,\,q_4,\,q_5,\,q_6,\,q_7]$ where ${\varvec{p}}>0$ and ${\varvec{q}}>0$ we obtain,

$$\begin{aligned} r = q_1, \quad K = q_2, \quad a = q_3,\quad b = q_4,\quad q + c = q_5 +q_6, \quad w =q_7. \end{aligned}$$

Since c is fixed the scaled model (16) is globally identifiable. $\square$

Each parameter value of the immunological model (1) can be uniquely reconstructed from the unique parameter estimates of the scaled model (16) except the killing efficacy parameters $\epsilon$ and $\delta .$ Regarding these two parameters, the parameter estimate of the scaled model only provides their fraction. However, the parameters $\epsilon$ and $\delta$ are less of a concern to us, since biologically these parameters represent the average effects of multiple complex interactions occurring between antibody-pathogen recognition and the response of immune cells and cannot be easily interpreted as a single parameter.

Table 6 Parameter estimates of model (16) fitted to $\log _{10}$ of viremia levels given in Table 5

We estimate the parameters ${\varvec{p}} = [r,K,a,b,q,w]$ of model (16) from the viremia levels given in Table 5 using Nelder–Mead algorithm implemented in MATLAB. We estimate the parameters ${\varvec{p}} = [r, K, a, b, q, w]$ of model (16) by minimizing the following cost functional

$$\begin{aligned} J({\varvec{p}}) = \displaystyle \sum _{i=1}^n \omega _i (y_i - \log _{10} (P(\tau _i,{\varvec{p}}))^2\,. \end{aligned}$$

(18)

where $\omega _i$ are the weights. Initial values are fixed at $P(0) =y_1\,, M(0) = 0.0001$ and $G(0) = 0$. We present the parameter estimates which were obtained by weighted least squares in Table 6 together with the uncertainties in the estimates. Uncertainties in parameter estimates are represented in terms of the coefficient of variation (CV) which is calculated by constructing a Fisher Information Matrix using sensitivity functions. For this analysis, we first compute the sensitivity matrix ${\varvec{S}}(\tau _i,{\varvec{p}}) = \displaystyle \frac{\partial g}{\partial {\varvec{p}}}({\varvec{x}}(\tau _i),{\varvec{p}})\,,$ which is the Jacobian of the output with respect to the model parameters. Clearly, we do not have an explicit representation of the pathogen levels $P(\tau _i,{\varvec{p}})$, so we compute the sensitivity matrix ${\varvec{S}}$ by coupling the system (6) with the following system of sensitivity functions (Capaldi et al. 2012; Cintrn-Arias et al. 2009);

$$\begin{aligned} \begin{aligned} \displaystyle \frac{\hbox {d}}{\hbox {d}t} \frac{\partial {\varvec{x}} }{\partial {\varvec{p}}}&= \displaystyle \frac{\partial {\varvec{f}} }{\partial {\varvec{x}}} \frac{\partial {\varvec{x}} }{\partial {\varvec{p}}} + \frac{\partial {\varvec{f}} }{\partial {\varvec{p}}},\\ \frac{\partial {\varvec{x}} }{\partial {\varvec{p}}} ({\varvec{0}})&= {\varvec{0}} .\\ \end{aligned} \end{aligned}$$

(19)

Here, $\displaystyle \frac{\partial {\varvec{f}} }{\partial {\varvec{x}}}$ is the Jacobian matrix of the system (6). Solving the initial value problem (19) simultaneously with (6), we obtain $P(\tau _i,{\varvec{p}})$ and $\displaystyle \frac{\partial P}{\partial {\varvec{p}}}(\tau _i,{\varvec{p}})$ and then compute the sensitivity matrix ${\varvec{S}}$. If the noise in the data has independent and identical normal distribution with zero mean and unity variance, then

$$\begin{aligned} {\varvec{S}}^{T} {\varvec{S}} =F({\varvec{p}}) \end{aligned}$$

is the Fisher Information Matrix. The inverse of the Fisher Information Matrix provides a lower bound on the variance of the parameter estimates, which is known as Cramer-Rao lower bound (Petersen et al. 2001; van der Vaart 1998). Namely,

$$\begin{aligned} F^{-1}({\varvec{p}}) \le \hbox {Cov}({\varvec{p}}). \end{aligned}$$

The standard deviations of the parameter estimation can be obtained by taking the square roots of the diagonal elements of the $F^{-1}({\varvec{p}})$ matrix. We will use the standard deviations to quantify uncertainty in the parameter estimation using $F^{-1}({\varvec{p}})$ in the following way. Let $p \in {\varvec{p}}$ be the ith parameter, and $\sigma (p)$ be the standard deviation of the estimated parameter p, then

$$\begin{aligned} \sigma (p) = \sqrt{F^{-1}({\varvec{p}})_{i,i}}, \end{aligned}$$

where $F^{-1}({\varvec{p}})_{i,j}$ denotes (i, j) component of the matrix $F^{-1}({\varvec{p}})$. The coefficient variation $\hbox {CV}(p)$ of the parameter can be computed by;

$$\begin{aligned} \hbox {CV}(p) = \sigma (p)/p. \end{aligned}$$

Fig. 3

Fitting results. We plot the solutions of the model (16) for fitted parameters in Table 6. The left plot in Fig. 3 is showing the $log_{10}$ of the pathogen levels for the time-since-infection period $\tau \in [0,10]$ together with the data presented in Table 5. The right plot in Fig. 3 is presenting the dynamics of the model with fitted parameters for $\tau \in [0,30]$ and the data (red dots) (Color figure online)

3.2 Practical Identifiability

Structural identifiability is a property of the dynamical model and is independent from the accuracy of the experimental data. A parameter which is structurally identifiable may still be non-identifiable in practice. For a practically non-identifiable parameter, it might be very difficult or impossible to detect the reasons behind the non-identifiability. On the other hand, knowing that the parameter is structurally identifiable assures that the cause of the practical non-identifiability is either lack of information captured from the experimental data (too few or too noisy data) or the inability of the numerical optimization algorithm to locate the minimum of $J({\varvec{p}}).$

The parameters of the scaled model (16) are structurally identifiable, and next we test whether the parameters are identifiable in practice. For practical identifiability, we carry out Monte Carlo Simulations. Monte Carlo simulations have been widely used for practical identifiability of ODE models (Miao et al. 2011). We perform Monte Carlo simulations first by taking the estimated parameters presented in Table 6 as the true parameter set $\hat{{\varvec{p}}}$. Then, we generate $M=1000$ synthetic data by evaluating the viremia observations at the true parameter set $\hat{{\varvec{p}}}$ and adding noise at increasing levels. The Monte Carlo simulations we performed are outlined in the following steps.

• 1. Solve the scaled immunological model (16) numerically with the true parameters $\hat{{\varvec{p}}}$ and obtain the output vector ${\varvec{g}} ({\varvec{x}}(\tau _i), \hat{{\varvec{p}}}) = P(\tau _i,\hat{{\varvec{p}}})$ at the discrete data time points $\{\tau _i\}_{i=1}^n\,.$

• 2. Generate $M = 1000$ simulated data from the statistical model (7)–(8) with a given measurement error structure. Data sets are drawn from a normal distribution whose mean is the output vector obtained in step (1.) and standard deviation is the $\sigma _0 \%$ of the mean. That is, in the statistical model (7)–(8), we set $f=1$ and obtain the synthetic data points by

  $$\begin{aligned} y_i = \log _{10}\left( g({\varvec{x}} (\tau _i),\hat{{\varvec{p}}}) + g({\varvec{x}} (\tau _i),\hat{{\varvec{p}}})\epsilon _i\right) , \end{aligned}$$

  where $\hbox {Var}(\epsilon _i) = \sigma _0^2\,.$

• 3. Fit the scaled immunological model (16) to each of the M simulated data sets to estimate the parameter set ${{\varvec{p}}}_j$ for $j=1,2,\ldots , M$. That is

  $$\begin{aligned} {\varvec{p}}_j = \displaystyle \min _{{\varvec{p}}} \sum _{i=1}^n \omega _i \left( y_i - \log _{10}(g({\varvec{x}}(\tau _i),{\varvec{p}}))\right) ^2\,, \quad j=1,2,\ldots ,M\,. \end{aligned}$$

• 4. Calculate the average relative estimation error (ARE) for each parameter in the set ${\varvec{p}}$ as introduced in Miao et al. (2011),

  $$\begin{aligned} \hbox {ARE}(p^{(k)}) = 100\,\% \displaystyle \frac{1}{M} \displaystyle \sum _{j=1}^M \displaystyle \frac{| \hat{p}^{(k)} - p_j^{(k)}| }{\hat{p}^{(k)}} \end{aligned}$$

  where $p^{(k)}$ is the kth parameter in the set ${\varvec{p}}$, $\hat{p}^{(k)}$ is the kth parameter in the true parameter set $\hat{{\varvec{p}}}$, and $p_j^{(k)}$ is the kth parameter in the estimated parameter set ${\varvec{p}}_j$.

• 5. Repeat steps 1 through 4 with increasing level of noise, that is take $\sigma _0 = 0,1,5,10,$ $20\,\%.$

The computed AREs give an insight about the identifiability of the parameters of the immunological model. Since the scaled immunological model (16) is structurally identifiable, when $\sigma _0=0$, the AREs are 0 (see Table 7). That is, Monte Carlo simulations agree with the structural identifiability analysis via differential algebra approach when there is no noise in the data. As expected, increasing the noise level in the data raises the AREs. We see from Table 7 that the AREs of the parameters q and w are relatively high, showing that these two parameters are sensitive to the noise in the data. A parameter is not practically identifiable, if the ARE of that parameter is significantly high even for a reasonable level of measurement error. We say that a parameter is practically identifiable if the ARE of that parameter is less than the measurement error level. The AREs of the parameters r, K, and b are consistently below the measurement errors, so we claim that these parameters are practically identifiable. Based on the Monte Carlo simulation results presented in Table 7, we conclude that the parameters q, w, and a are not practically identifiable.

Practical identifiability of the parameters of an ODE model might be improved by increasing the data points. Next, we perform the Monte Carlo simulations with increased data time points by inserting additional time points at the midpoint between the two original time points. That is, we take the new increased data time points to be $\tau _i = \{0,0.5,1,1.5,2.2.5,\ldots ,10.5,11\}.$ The computed AREs are presented in Table 8. We observe that increasing the data points did not improve the practical identifiability of the parameters. As was shown in Lele et al. (2010), if the parameters are non-identifiable, the accuracy does not increase with the number of data points. The parameters a, q, and w are not practically identifiable. On the other hand, increasing the data points lowered the computed AREs of the identifiable parameters K and r.

Table 7 Practical identifiability analysis of parameters of the scaled immunological model (16) by Monte Carlo simulations for measurement error levels $\sigma _0 = 0,1,5,10$ and $20\,\%$

Table 8 Monte Carlo simulations of the scaled immunological model with increased data points (16)

4 Parameter Estimation of Immuno-Epidemiological Model

We develop a numerical method to fit multi-scale models to multi-scale data. For epidemiological data, we use the number of human RVFV cases reported by the CDC during the 2006–2007 outbreak in Kenya (CDC 2007) (given in Table 9). RVF is transmitted to humans mainly through direct and indirect contacts with body fluids and aerosols of infected animals during slaughtering, butchering, or assisting animal births and necropsy or laboratory procedures (Bird et al. 2009). Another route of transmission for humans is bites of infected vectors. No human-to-human cases have been seen so far. Since the majority of human infections results from handling infected animals, we model only transmission from infected host to human and augment the following human outbreak model to the system (2)–(3)

$$\begin{aligned} {\hbox {RVFV Human Model:}} {\left\{ \begin{array}{ll} \displaystyle \frac{\hbox {d} S}{\hbox {d} t} &{}= - S \displaystyle \int _0^{\infty } \beta (\tau ) i_\mathrm{H}(\tau ,t)\mathrm{d}\tau \\ \displaystyle \frac{\hbox {d} I}{\hbox {d} t} &{}= S \displaystyle \int _0^{\infty } \beta (\tau ) i_\mathrm{H}(\tau ,t)\mathrm{d}\tau ,\\ \end{array}\right. } \end{aligned}$$

(20)

where S(t) denotes the susceptible humans, and I(t) denotes the infected humans at time t. The transmission rate from an infected host to human varies according to the infectivity of the host via,

$$\begin{aligned} \beta (\tau ) = \displaystyle \frac{c_BP^\upsilon (\tau )}{B + P^\upsilon (\tau )}, \end{aligned}$$

where $c_\mathrm{B},\,B$, and $\upsilon$ are constants. Because data are the number of new cases, we fit the new human incidences $\hat{g}(t,\hat{{\varvec{p}}})$ at time t to the given data where

$$\begin{aligned} \hat{g}(t,\hat{{\varvec{p}}}) = S(t) \displaystyle \int _0^{\infty } \beta (\tau ) i_\mathrm{H}(\tau ,t)\mathrm{d}\tau , \end{aligned}$$

and $\hat{{\varvec{p}}}$ is the vector of epidemiological parameters to be fitted. We develop a finite difference scheme and combine it with a MATLAB ODE solver for the immunological model to approximate the solutions of the age-structured PDE model.

Table 9 Number of human RVF cases as reported by CDC during the 2006–2007 Kenya outbreak (CDC 2007)

4.1 Finite Difference Scheme for the Immuno-Epidemiological Model

We develop a finite difference method that discretizes both the time-since-infection variable $\tau$ and the time variable t. Let T be the final time of interest and A be the final time-since-infection. Hence, $D = \{(\tau ,t): 0\le \tau \le A,\; 0\le t \le T \}$ is the domain of the system (2)–(3). First, we discretize the domain D. Let N and M be nonnegative integers such that

$$\begin{aligned} \Delta t = \displaystyle \frac{T}{N} \quad \hbox { and } \quad \Delta \tau = \displaystyle \frac{A}{M} \quad \hbox { and } \quad \Delta t =\Delta \tau . \end{aligned}$$

We generate a square mesh and the discrete point $(\tau _k,t_n)$ of the rectangular domain D is given by $\tau _k = k\Delta t$ and $t_n = n\Delta t\,, k=1\ldots ,M,\; n=1,\ldots ,N.\,$ The approximate values at any point $(\tau _k,t_n)$ of the discretized domain are denoted by $S(t_\mathrm{n}) \approx S^n,\; i_\mathrm{H}(\tau _k,t_n) \approx i_\mathrm{H}^{k,n},\;\beta _\mathrm{H}(\tau _k) \approx \beta _\mathrm{H}^k\,.$ We approximate the time derivatives by backward Euler difference quotient and obtain the following implicit method for the system (2)–(3).

$$\begin{aligned} {\hbox {Finite Difference Algorithm:}} {\left\{ \begin{array}{ll} S_\mathrm{v}^{n+1} &{}=\displaystyle \frac{S_\mathrm{v}^n + \Delta t \Lambda _\mathrm{v}}{1 + \Delta t\displaystyle \sum \nolimits _{k=1}^M \beta _\mathrm{H}^k i_\mathrm{H}^{k,n} \Delta t+ \mu _\mathrm{v} \Delta t},\\ I_\mathrm{v}^{n+1} &{}= \displaystyle \frac{I_\mathrm{v}^n + \Delta t S_\mathrm{v}^{n+1}\displaystyle \sum \nolimits _{k=1}^M \beta _\mathrm{H}^k i_\mathrm{H}^{k,n}\Delta t }{1 + \mu _\mathrm{v} \Delta t} \\ S_\mathrm{H}^{n+1} &{}= \displaystyle \frac{S_\mathrm{H}^n + \Delta t \Lambda }{1 + \beta _\mathrm{v} I_\mathrm{v}^n \Delta t+ \mu _\mathrm{H} \Delta t} \\ i_\mathrm{H}^{k+1,n+1}&{}= \displaystyle \frac{i_\mathrm{H}^{k,n} }{1 + \left( \alpha ^k + \gamma ^k +\mu _\mathrm{H} \right) \Delta t} \\ i_\mathrm{H}^{0,n+1}&{}= \beta _\mathrm{v} S_\mathrm{H}^{n+1} I_\mathrm{v}^{n+1},\\ R_\mathrm{H}^{n+1}&{}= \displaystyle \frac{R_\mathrm{H}^n + \Delta t \displaystyle \sum \nolimits _{k=1}^M \gamma ^k i_\mathrm{H}^{k,n}\Delta t}{1 + \mu _\mathrm{H} \Delta t},\\ \end{array}\right. } \end{aligned}$$

(21)

To evaluate the linked parameters $\beta _\mathrm{H}(\tau _k),\; \alpha (\tau _k),\; \gamma (\tau _k)$, the immunological model (16) is solved using the MATLAB ODE solver ode45. Not all MATLAB ODE solvers can be set to preserve the positivity of solutions. Since it is crucial that the numerical method also preserves the positivity of the solutions, we set the function ode45 to preserve the positivity of the approximate solutions for all the numerical experiments in this paper. Integrals $\displaystyle \int _0^{\infty } \beta _\mathrm{H}(\tau ) i_\mathrm{H}(\tau ,t)\hbox {d}\tau$ and $\displaystyle \int _0^{\infty } \gamma (\tau ) i_\mathrm{H}(\tau ,t)\hbox {d}\tau$ are approximated using the right-end point rule. The nonlinear terms are linearized using a single Picard Iteration at each time level. For instance, the nonlinear term, $\beta _\mathrm{v} S_\mathrm{H}^{n+1} I_\mathrm{v}^{n+1}$, is linearized by $\beta _\mathrm{v} S_\mathrm{H}^{l+1} I_\mathrm{v}^{l}$ where l denotes the Picard Iteration counter at time $t =t_{n+1}.$ The approximate solutions obtained by the implicit method (21) converge to the solutions of the system (2)–(3) with single Picard Iteration, that is with $l=1$ (results are not shown). The order of convergence is $O(\Delta t).$ The numerical method (21) preserves the positivity of the solutions. More details about finite difference schemes for age-structured models can be found in Martcheva (2015).

Table 10 Fixed parameter values of model (2)–(3)

Structural identifiability of age-structured PDE models has not been studied as extensively as dynamical ODE systems with few exceptions in Perasso et al. (2011) and Perasso and Razafison (2016). In recent years, researchers have focused on developing methods for solving the ill-posed inverse problems generated by age-structured population models (Ackleh et al. 2005; Ackleh 1999). However, these studies did not consider the structural identifiability of the age-structured models. Analyzing the structural identifiability of the nested immuno-epidemiological models such as (2)–(3) is the topic of our current research. In this paper, we take a numerical approach and use Monte Carlo simulations for studying identifiability issues of the parameter estimation problem in a nested immuno-epidemiological model.

The parameters of importance to determine from the epidemiological data are the ones related to transmission, recovery and disease-induced death rates of the RVFV. Other epidemiological parameters such as $\Lambda _\mathrm{v},\, \Lambda ,\, \mu _\mathrm{v},\,\mu _\mathrm{H}$ and $\beta _\mathrm{v}$ are fixed to the values obtained from the literature and presented in Table 10. Studies find the median adult longevity of Aedes aegypti, a mosquito known to transmit RVFV, in the lab to be approximately 61 days (McMeniman et al. 2009). We took the average life span of the vector population to be $\mu _\mathrm{v} =\displaystyle \frac{1}{40}$ $\hbox {days}^{-1}$, intermediate between laboratory measured life span and the life span previously used to model wild populations of mosquitoes (Gaff et al. 2007, 2011). The total vector and host populations are normalized to unity, and hence the recruitment rate of the vector population is set to $\Lambda _\mathrm{v} = \displaystyle \frac{1}{40}$ $\hbox {vector} \times \hbox {days}^{-1}$. Average life span of livestock is 10 years (Gaff et al. 2011). Hence $\mu _\mathrm{H} = \displaystyle \frac{1}{365 \times 10} \hbox {days}^{-1}$ and $\Lambda = \displaystyle \frac{1}{365\times 10} \hbox {host} \times \hbox {days}^{-1}$. We suppose that initially $0.005\,\%$ of the vector population is infected and initial distribution of the infected host is $0.00001\,\%$ of the population. $85\,\%$ of the reported cases for the 2006–2007 Kenya outbreak came from only 4 districts (out of 69) in Kenya (Munyua et al. 2010); Garissa (623060), Ijara (62571), Baringo (555561), Kilifi (41109735). Initial susceptible human population is estimated to $S(0) = 2300000$ (an approximate total population of above 4 districts in Kenya). We take $\nu =1$ and $\upsilon =2$.

4.2 Fitting Epidemiological Data When the Immune Model Parameters are Fixed

To estimate the parameters of the immuno-epidemiological model, we first fix the parameters of the immunological model at the fitted values given in Table 6. The remaining parameters are fitted using a MATLAB code combining an ODE solver for the immunological model, finite difference scheme (21) for the PDE model and an optimization routine to minimize the least squares error. Hence, we estimate the parameters $\hat{{\varvec{p}}} = [\sigma , \xi , \kappa , \epsilon _0, c_\mathrm{H}, B_\mathrm{H}, c_\mathrm{B}, B]$ of the epidemiological model (2)–(3), (20) by solving the following optimization problem using the Nelder–Mead algorithm

$$\begin{aligned} \displaystyle \min _{{\varvec{\hat{p}}}} \hat{J}({\varvec{\hat{p}}}) = \displaystyle \min _{{\varvec{\hat{p}}}} \displaystyle \sum _{j=1}^{\hat{n}} \left( \hat{g}(t_j,\hat{{\varvec{p}}}) -\hat{y}_j\right) ^2\,, \end{aligned}$$

(22)

where $\hat{n} =47$, $\hat{y}_j$ are the number of new RVFV human cases at time $t_j$ as reported by CDC (2007). The fitted parameter values are presented in Table 11. In Fig. 4, the new incidences computed with the fitted values are plotted with the epidemiological data (blue bars) provided by CDC.

Fig. 4

Fitting results. The blue bars are the new incidences reported by CDC (2007) as given in Table 9. The red curve is the computed new incidences with the fitted parameters presented in Table 11. The immune parameters are fixed at the estimated values given in Table 6 (Color figure online)

Table 11 Parameter estimates of the epidemiological model (2)–(3) fitted to human incidences as reported by CDC

Table 12 Practical identifiability analysis of the epidemiological model (2)–(3) by Monte Carlo simulations

Currently, there are no analytical approaches for studying structural identifiability of nested models such as the epidemiological model we study in this paper (2)–(3). We are working on developing analytical tools to study the structural identifiability of nested models. But, within this paper we analyze the identifiability of the parameters of the nested immuno-epidemiological model (2)–(3) using Monte Carlo simulations. Monte Carlo simulations have been widely used for practical identifiability of ODE models (Miao et al. 2011). We perform Monte Carlo simulations first by taking the estimated parameters presented in Table 11 as the true parameter set $\hat{{\varvec{p}}}$ and then performed the steps (1) through (4) as explained in details in Sect. 3 with the following modifications. In step (1), $g({\varvec{x}}(\tau _i),\hat{{\varvec{p}}})$ is replaced with $\hat{g}(t_i,\hat{{\varvec{p}}})$, in step (2) we set $M=1000$, and

$$\begin{aligned} y_j = \hat{g}(t_j,\hat{{\varvec{p}}}) + \hat{g}(t_j,\hat{{\varvec{p}}})\epsilon _j \quad j=1,2,\ldots ,\hat{n} \end{aligned}$$

in step (3) we evaluated (22). The immuno-epidemiological model is approximated by the finite difference scheme (21) with $\Delta t =0.1$ (see Table 12) and $\Delta t =0.01$ (see Table 13). Monte Carlo simulations for the immuno-epidemiological PDE model are computationally expensive compared to the immunological ODE model. Computation time increases as the time step ($\Delta t$) in the finite difference scheme is refined. We performed the Monte Carlo simulations for $M=1000$ synthetic data sets for the time step $\Delta t=0.1$ (Table 12) and for $M=100$ data sets for the time step $\Delta t=0.01$ (Table 13). The parameters of the scaled immunological model (16) are fixed at the estimated values presented in Table 6. The computed AREs are presented in Tables 12 and 13 for measurement errors $\sigma _0 = 0, 1, 5, 10, 30\,\%$. The AREs of the parameters $c_\mathrm{H},\, B_\mathrm{H}$, and $c_\mathrm{B}$ increase gradually as the measurement error level increases, but remain below the measurement error level. Hence, we claim that the parameters $c_\mathrm{H},\, B_\mathrm{H}$, and $c_\mathrm{B}$ are practically identifiable. We also observe that refining the time step, $\Delta t$, in the finite difference scheme (21) did not affect the ARE values.

Table 13 Practical identifiability analysis of the epidemiological model (2)–(3) by Monte Carlo simulations

On the other hand, the ARE values of the parameters $\sigma ,\, \xi ,\, \kappa$, and $\epsilon _0$ reveal an unusual relation to the measurement error levels; the AREs do not increase as the measurement error levels increase (see Tables 12, 13). The parameters $\sigma ,\, \xi ,\, \kappa$, and $\epsilon _0$ appear in the formulation of $\pi (\tau )$ as given in (5) which is the probability of still being infectious $\tau$ time units after becoming infected. Note that the infected host population, $i_\mathrm{H}(\tau , t)$ satisfies the following relation which is derived by the method of characteristics,

$$\begin{aligned} i_H(\tau ,t) ={\left\{ \begin{array}{ll} \beta _\mathrm{v} S_\mathrm{H}(t-\tau )I_\mathrm{v}(t-\tau ) \pi (\tau ), &{} \tau < t,\\ i_\mathrm{H}(\tau -t,0)\displaystyle \frac{\pi (\tau )}{\pi (\tau -t)}, &{} \tau > t. \\ \end{array}\right. } \end{aligned}$$

(23)

Then new incidences are given as

$$\begin{aligned} \hat{g}(t,\hat{{\varvec{p}}}) = {\left\{ \begin{array}{ll} \beta _\mathrm{v} S(t) \displaystyle \int _0^{\infty } \beta (\tau ) S_\mathrm{H}(t-\tau )I_\mathrm{v}(t-\tau ) \displaystyle e^{- \displaystyle \int _0^\tau \left( \alpha (s) +\gamma (s) + \mu _\mathrm{H}\right) \hbox {d}s} \hbox {d}\tau &{} \tau < t,\\ S(t) \displaystyle \int _0^{\infty } \beta (\tau ) i_\mathrm{H}(\tau -t,0)\displaystyle \frac{ \displaystyle e^{- \displaystyle \int _0^\tau \left( \alpha (s) +\gamma (s) + \mu _\mathrm{H}\right) \hbox {d}s}}{ \displaystyle e^{- \displaystyle \int _0^{\tau -t} \left( \alpha (s) +\gamma (s) + \mu _\mathrm{H}\right) \hbox {d}s}}\hbox {d}\tau &{} \tau > t,\\ \end{array}\right. } \end{aligned}$$

(24)

We hypothesize that the strange behavior of the AREs of the parameters $\sigma ,\, \xi ,\, \kappa$, and $\epsilon _0$ is due to the fact that the measurement level error does not affect the disease-induced death rate, $\alpha (s)$, and the recovery rate, $\gamma (s)$, as much as it affects the transmission rate from an infected host to human, $\beta (\tau )$, and the transmission rate from an infected host to a vector, $\beta _\mathrm{H}(\tau )$, since they are related though the integral of a negative exponential term. We test our hypothesis with the following simplified version of (24). Assume that data are given by the following output function,

$$\begin{aligned} h(t,\hat{{\varvec{p}}}) = S(0) e^{- \left( \displaystyle \int _0^{\infty } \beta (\tau ) \pi (\tau ) \hbox {d}\tau \right) t} \displaystyle \int _0^{\infty } \beta (\tau ) \pi (\tau ) \hbox {d}\tau \end{aligned}$$

(25)

The immunological parameters are fixed at the estimated values given in Table 6, and the parameters of the transmission rate $\beta (\tau )$, $c_\mathrm{H}$, and $B_\mathrm{H}$ are fixed at the estimated values given in Table 11. We perform Monte Carlo simulations to compute the AREs of the parameters $\sigma ,\, \xi ,\, \kappa$, and $\epsilon _0$ and set the true parameters as the fitted values given in Table 11. We present the results in Table 14. We observe that the AREs of $\sigma$ increase gradually as the measurement error level increases, but the AREs of the parameters $\xi$, $\kappa$, and $\epsilon _0$ preserve the unusual behavior. Clearly, fixing the parameters $c_\mathrm{H}$ and $B_\mathrm{H}$ improved the identifiability of $\sigma$. We conclude that only parameters $c_\mathrm{H}, B_\mathrm{H}$, and $c_\mathrm{B}$ are practically identifiable when fitting the immuno-epidemiological model (2)–(3) with the immunological parameters are fixed.

Table 14 Monte Carlo simulations for the output function $h(t,\hat{{\varvec{p}}})$ given in (25)

4.3 Fitting Mutli-scale Data to Multi-scale Model

Our initial approach in fitting multi-scale data to a multi-scale model was to fit the immunological model first (18) and then use those fitted parameters in estimating the parameters of the epidemiological model (22). Next, we fit the multi-scale data to the multi-scale model simultaneously. Thus, the vector of parameters to be fitted is ${\varvec{p}}^* = [{\varvec{p}}, \; \hat{{\varvec{p}}}] = [r,K,a,b,q,w, \sigma , \xi , \kappa , \epsilon _0, c_\mathrm{H}, B_\mathrm{H}, c_\mathrm{B}, B],$ then we estimate ${\varvec{p}}^*$ by solving the following minimization problem,

$$\begin{aligned} \displaystyle \min _{{\varvec{p}}^*} J^*({\varvec{p}}^*)= & {} \min _{{\varvec{p}}, \; {\varvec{\hat{p}}}} \left( J({\varvec{p}}) + \hat{J}({\varvec{\hat{p}}}) \right) \nonumber \\= & {} \displaystyle \min _{{\varvec{p}},\;{\varvec{\hat{p}}}} \left( \displaystyle \sum _{i=1}^n \omega _i\left( \log _{10}(g({\varvec{x}}(\tau _i),{\varvec{p}})) - y_i\right) ^2 + \displaystyle \sum _{j=1}^{\hat{n}}\left( \hat{g}(t_j,\hat{{\varvec{p}}}) - \hat{y}_j\right) ^2\right) \nonumber \\ \end{aligned}$$

(26)

where $y_i$ represents the immunological data, and $\hat{y}_i$ represents the epidemiological data. To solve the optimization problem (26), we use the Nelder–Mead algorithm implemented in MATLAB which is one of the most widely used derivative-free algorithms for unconstrained optimization problems such as (26). The estimated values are presented in Table 15. The model output at the estimated values together with the data is plotted in the Fig. 5. Next, we perform Monte Carlo simulations to test the practical identifiability of the nested models (16) and (2)–(3) when both immunological and epidemiological data are available for the parameter estimation. The computed AREs of the parameters are presented in Table 16. We observe that the practical identifiability of all the parameters has improved. All the parameters of the immuno-epidemiological model are practically identifiable for multi-scale data. It is very well known that in dynamical ODE models, the identifiability of the model parameters improves as the more state variables are observed. We conclude that same phenomena hold true for the nested models (16) and (2)–(3).

Table 15 Parameter estimates of the nested immuno-epidemiological model (2)–(3) fitted to human incidences as reported by CDC and the immunological model (16) fitted to the viremia levels given in Table 5

Fig. 5

Fitting results of the parameter estimate problem (26). In the left figure, the blue bars are the new incidences reported by CDC (2007). The red curve is the computed new incidences with the fitted parameters presented in Table 15. In the right figure, the blue dots are the data given in Table  5 and the red curve is the $\log _{10}$ of the viremia levels computed with the estimated values presented in Table 15 (Color figure online)

Table 16 Practical identifiability analysis of nested immuno-epidemiological model by Monte Carlo simulations for measurement error levels $\sigma _0 = 0,1,5,10$ and $30\,\%$

5 Discussion

Models must be properly parameterized if conclusions drawn from their predictions are to be trusted. Structural identifiability issues for parameter estimation have been studied for many biological systems. From a modeling and biological perspective, it is clear that within-host dynamics have an effect on the between-host disease transmission. Hence, nested models have been developed to study host-pathogen coevolution, early diagnostics, and transmission-virulence trade-offs (Gilchrist and Sasaki 2002; Mohtashemi and Levins 2001; Alizon and Baalen 2005). In this paper, we are interested in the structural and practical identifiability analysis of nested immuno-epidemiological models, where between-host disease transmission, host recovery and disease-induced death rates are governed by within-host immune dynamics. Although there are well established theories for identifiability of dynamical systems described by ODE models, identifiability issues for structured PDE models have been a recent topic of interest. We extend the structural and practical identifiability analysis of PDE models to a multi-scale coupled model.

Regarding constructing an immunological model for arbovirus diseases, although within-host immune dynamics have the same qualitative behavior, the immune response has not been modeled with IgM and IgG antibodies which are commonly measured in the laboratory (Bird et al. 2009; Jansen van Vuren and Paweska 2009). Here, we used a novel immunological model that represents the within-host immune dynamics resulting from infection from an arbovirus disease, to estimate the unknown parameters by using RVFV time-series data obtained under experimental conditions. For the ‘macroscale’ perspective, we used 2006–2007 Kenya outbreak data (CDC 2007; Munyua et al. 2010) for RVFV human cases to determine the unknown parameter values for the immuno-epidemiological model.

We develop a finite difference scheme and combine it with a MATLAB ODE solver for the immunological model to approximate the solutions of the age-structured PDE model. In recent years, although many researchers have focused on developing methods for solving the ill-posed inverse problems generated by the age-structured population models, there have been few studies on the structural and practical identifiability of the age-structured models. In this study, we take a numerical approach for the structural and practical identifiability analysis of a nested immuno-epidemiological model, which couples an ODE immunological model to an age-since-infection structured epidemiological PDE model.

For dynamical systems described by ordinary differential equations, the state isomorphism method, the Taylor series expansion method, and the algebra-differential elimination method are mainly used for identifiability analysis. We use the differential algebra method to study the structural identifiability of the immunological model. One of the advantages of this approach is that if the model is not structurally identifiable, the method provides the identifiable parameter combinations. The parameter combinations are then used to reparametrize the system to obtain a structurally identifiable model (Meshkat et al. 2009). We show that the immunological model is not structurally identifiable for the measurements of time-series viremia concentrations in the host. Thus, we study the non-dimensionalized and scaled versions of the immunological model and prove that both are structurally globally identifiable. Although the non-dimensionalized system is structurally identifiable, we cannot use the non-dimensionalized system to reconstruct the parameter values for the immune model (1) from the uniquely estimated parameter values of non-dimensionalized system. We estimate the unique value of all key parameters in the immunological model (1) via the scaled model by fixing the biologically estimated parameter c (half life of IgM immune response antibodies). However, in practice, structural identifiability may not imply practical identifiability. Here, we also study the practical identifiability of the scaled model by Monte Carlo simulations and show that the parameters K, r, and b are practically identifiable, but the parameters $q,\, a$ and w are not practically identifiable.

After fixing parameters to the fitted values for the immunological model, we develop numerical methods to fit the observable epidemiological RVFV human data to the multi-scale model to estimate the rest of the immuno-epidemiological model parameter values. For this fitting, we use MATLAB by combining an ODE solver for the immunological model, finite difference scheme for the PDE model, and an optimizing tool to minimize the least square errors. Monte Carlo simulations suggest that only three parameters of the epidemiological model are identifiable when the immunological parameters are fixed at fitted values. Alternatively, we fit the multi-scale data to the multi-scale model simultaneously. To solve the obtained optimization problem, we use a modified Nelder–Mead algorithm $\mathtt{mfminsearch}$ implemented in MATLAB. Monte Carlo simulations for simultaneous fitting suggest that the parameters of immunological model and the parameters of the immuno-epidemiological model are practically identifiable.

We suggest developing analytical methods to study structural identifiability of nested models, and this is our current topic of research. Developing such analytical methods is a necessity especially in deriving multi-scale models that adequately explain multi-scale data. Structural identifiability analysis of unidentifiable nested model can reveal the parameter relationships, and this can further be used to reparameterize the nested (PDE) model to obtain an identifiable model. A technique that has been widely used for ODE models should be developed for nested models.

From a methodological perspective, accurate estimation of the nested model parameter values has more caveats and multi-scale nested models add one more layer complexity to these analyses in comparison with ODE models. We take a numerical approach for practical identifiability analysis of nested models. Estimation for accurate values of model parameters allows a biological system to have a satisfactory mathematical representation, which is necessary for theoretical studies confronting experiments. Structural identifiability analysis allows for clear model predictions to model parameter values.