Modelling Dominance Hierarchies Under Winner and Loser Effects

Abstract

Animals that live in groups commonly form themselves into dominance hierarchies which are used to allocate important resources such as access to mating opportunities and food. In this paper, we develop a model of dominance hierarchy formation based upon the concept of winner and loser effects using a simulation-based model and consider the linearity of our hierarchy using existing and new statistical measures. Two models are analysed: when each individual in a group does not know the real ability of their opponents to win a fight and when they can estimate their opponents’ ability every time they fight. This estimation may be accurate or fall within an error bound. For both models, we investigate if we can achieve hierarchy linearity, and if so, when it is established. We are particularly interested in the question of how many fights are necessary to establish a dominance hierarchy.

1 Introduction

Many animals spend their lives in groups that occupy the same territory with limited resources (Alcock 1993; Fero et al. 2007). In order to divide these resources, they arrange themselves into a ranking system (Hand 1986). Those with a higher rank have more chances of survival. This arrangement where everyone, or almost everyone, has a clear position in the group is called a dominance hierarchy. Individuals often establish their positions by aggressive fights between themselves. Within groups which exist permanently where new individuals arrive or are born, they generally slot into a position in the existing hierarchy (Frank 1986; Marsden 1968). We are concerned with situations where whole groups form from scratch, with individuals meeting each other for the first time, for example, in leks (Hoglund and Alatalo 1995; Kokko et al. 1998). In such situations, individuals will often enter into a series of pairwise contests, in order to establish their position within the group.

Dominance hierarchies can be linear, so that animal $A$ dominates all others, $B$ dominates all others except $A$, etc, or can be nonlinear where the position of individuals in the group is complex. They have been the subject of study by behavioural ecologists for a long time, and at first sight, it is surprising that an individual would accept a subordinate rank within a hierarchy (Allee 1951; Dugatkin 1995). However, linear hierarchies are found to be present, e.g. in birds, mammals, fish or crustaceans (Addison and Simmel 1980; Beacham 1988; Brown et al. 1997; Goessmann et al. 2000; Schjelderup-Ebbe 1922). They are also common in insects (Early and Dugatkin 2010; McDonald and Shizuka 2013; Molet et al. 2005; Monnin and Peeters 1999; Shimoji et al. 2014; Shizuka and McDonald 2012; Wilson 1971). For example in ants, Molet et al. (2005) and Monnin and Peeters (1999) showed that dominance hierarchies regulate how some workers become egg-laying ants. Using a modelling approach, Molet et al. (2005) showed that linear dominance hierarchies reduce the number of such workers. These results were found to be true in eight colonies of R. confusa.

In general, linear hierarchies are very stable; for example, when chickens were taken from their group and reintroduced days later, they reoccupied the previous place that they had in the group (Klopfer 1973).

There are many factors that influence hierarchy formation (Dugatkin 1997) which can be divided into two types: “extrinsic” and “intrinsic” factors (Dugatkin 1997; Landau 1951a, b). Intrinsic factors are related to physical attributes, which directly affect the ability of an individual to win a fight [often termed resource holding power (RHP), (Parker 1974)]. Extrinsic factors are those potentially related to psychology, for example an existing position in a hierarchy or past experience of contests. In this paper, we consider extrinsic factors in the form of winner and loser effects (denoted by $W$ and $L$, respectively), and analogously to the model developed by Dugatkin (1997) and Dugatkin and Dugatkin (2007), assume that the ability to win fights is governed by the RHP only, which is directly affected by winner and loser effects. Winner and loser effects occur when previous victories lead to an increased probability of winning and previous defeats lead to a decreased probability of winning, respectively (Beacham 2003; Hsu et al. 2006, 2009; Rutte et al. 2006). There is a lot of experimental evidence (Bakker et al. 1989; Bergman et al. 2003; Lindquist and Chase 2009; Schuett 1997) showing the presence of the loser effect in different groups of animals that lasts for several days. On the other hand, the winner effect is less common, with only some species showing it. In stickleback fish Gasterosteus aculeatus, it was observed that the loser effect lasted for twice as long as the winner effect (Bakker et al. 1989). In copperhead snakes Agkistrodon contortrix, it was observed that there was no effect after a winning experience, while the effects of losing lasted for more than one day; individuals that had previously lost did not engage in any fight (they retreated), and lost when challenged, whereas those individuals that had previously won, won six of the ten subsequent contests (Schuett 1997). There is not a large body of theory to predict the position of an individual in a linear hierarchy (Mesterton-Gibbons and Dugatkin 1995). Most such theory has considered modelling of winner and loser effects [but see (Broom and Cannings 2002, Broom 2002) for alternative models]. (Landau 1951a, b) showed that intrinsic factors such as age or size alone cannot produce hierarchies similar to ones observed in nature, pointing to the importance of extrinsic factors. Once factors such as winner and loser effects were added to the model, hierarchies similar to those found in nature were obtained. (Landau 1951a, b) considered the combined effects of winner and loser effects on hierarchy formation. Others have seen how winner and loser effects separately influence dominance hierarchy formation (Bonabeau et al. 1999; Dugatkin 1997; Dugatkin and Dugatkin 2007; Hemelrijk 2000). Dugatkin (1997) and Dugatkin and Dugatkin (2007) developed a simulation framework which explored the properties of emerging hierarchies in groups of four individuals under different assumptions about the strength of winner and loser effects. In this paper, we extend the model of Dugatkin (1997) and Dugatkin and Dugatkin (2007) and analyse their average behaviour and the temporal dynamic of the process of hierarchy formation. Dugatkin’s results are from a single observation of each combination of winner and loser effects. We are interesting in looking at the distribution of each case to ascertain whether different observations will always yield effectively the same results (in most cases they do, but there are exceptions, as we see in Sect. 3). The average is important as the logical representative of the distribution.

Working with distributions enables us to generate new statistical measures of the linearity of hierarchies such as the index of linearity, or the overlap and distinguishability between a pair of individuals, with the potential to apply these to real data. For instance, wins are easy to observe in experimental laboratory groups at least, and so for any observed group, we can work out when pairs of individuals become distinguishable and calculate the index of linearity. This paper prepares the platform for developing game-theoretical models, where levels of aggression (for example) are strategic factors, with the best choice depending upon the natural parameters, including species or habitat-specific features which affect how resources are divided (the reproductive skew).

1.1 The Dugatkin Model of Hierarchy Formation

Dugatkin (1997) and Dugatkin and Dugatkin (2007) developed a model to explore the structure of dominance hierarchies under different strengths of winner and loser effects ($W\ge 0$ and $L\in [0,1]$). The model consists of $N$ individuals who are characterised by their RHP and aggression threshold ($\theta$). The RHP value describes the ability of an individual to win an aggressive interaction, whereas $\theta$ indicates whether an individual engages in a fight in the first place. Further, it is assumed that the outcome of a fight (i.e. win or loss) influences the RHP. While a win increases an individual’s ability to win the next fight, a loss decreases it. Two models which differed in the amount of information an individual has about its opponents’ fighting abilities were analysed. The non-updated model assumes that no information about the current ability is available Dugatkin (1997), whereas the updated model assumes that information (although with varying levels of accuracy) is accessible (Dugatkin and Dugatkin 2007). In the following, we describe both models in detail.

1.1.1 The Non-updated Model

All individuals possess the same RHP initially (denoted by $\mathrm{RHP}_\mathrm{initial}$) and at each time step, two individuals, $x$ and $y$, are drawn at random to engage in an aggressive interaction. Individual $x$ decides to fight against individual $y$ at time $t$ if

$$\begin{aligned} \frac{\mathrm{RHP}_{x,t}}{\mathrm{RHP}_\mathrm{initial}}\ge \theta \end{aligned}$$

(1)

holds, and it retreats otherwise, where $\mathrm{RHP}_\mathrm{x,t}$ describes the RHP of individual $x$ at time $t$, and $\theta$ is a fixed aggression threshold. In this model, individual $x$ has no information about the current RHP of individual $y$ and simply assumes it to be equal to $\mathrm{RHP}_\mathrm{initial}$. Individual $y$ is considered similarly. Each pairwise interaction results in one of three possible outcomes:

• 1. both individuals decide to fight and $x$ wins with probability

  $$\begin{aligned} \frac{\mathrm{RHP}_{x,t}}{\mathrm{RHP}_{x,t}+\mathrm{RHP}_{y,t}} \end{aligned}$$

  (2)

  (and consequently $y$ wins with probability $1-\frac{\mathrm{RHP}_{x,t}}{\mathrm{RHP}_{x,t}+\mathrm{RHP}_{y,t}}$);

• 2. one chooses to fight and the other retreats;

• 3. both individuals retreat, which is known as a double kowtow.

The outcome of the contest is assumed to affect the RHP. If individual $x$ wins or individual $y$ retreats, then we obtain

$$\begin{aligned} \mathrm{RHP}_{x,t+1}=(1+W)\mathrm{RHP}_{x,t}. \end{aligned}$$

(3)

Similarly, if $x$ loses or retreats, then we have

$$\begin{aligned} \mathrm{RHP}_{x,t+1}=(1-L)\mathrm{RHP}_{x,t}. \end{aligned}$$

(4)

A similar dynamic holds for individual $y$. Consequently, the RHP of both individuals changes due to the outcome of their pairwise interactions, but in this model, individuals are only able to track the changes of their own RHP and assume the RHP of their opponents to be unchanged equal to $\mathrm{RHP}_\mathrm{initial}$ (this may not be entirely realistic as we touch upon in Sect. 4).

Dugatkin (1997) considered a group of four individuals and recorded the number of wins of each individual over each of the others in a single realisation of 1000 interactions. He defined $\theta =1$ (meaning that individual $x$ will fight at time $t$ if $\mathrm{RHP}_{x,t}\ge \mathrm{RHP}_\mathrm{initial}$ holds) and analysed winner and loser effects of varying strengths ($W=0;0.1;0.2;0.3;0.4;0.5$ and $L=0;0.1;0.2;0.3;0.4;0.5$, respectively).

The results obtained from this simulation can be summarised as follows. When only the winner effect was present, each individual had a clear position in the hierarchy; higher-ranked individuals were characterised by a larger total number of wins, and also the ratios of their number of wins compared to their number of losses (excluding double kowtows) against each lower-ranked individuals were high. This is true for all values of $W$. When only the loser effect was present, one individual always emerged as the dominant individual and the position of the others was unclear as subordinate individuals started retreating quickly, and so the interactions between them resulted in mutual retreat. However, increasing the winner effect for a given value of the loser effect $L$ increased the number of individuals with a clear position in the hierarchy (nevertheless the hierarchy was not always linear).

1.1.2 The Updated Model

Dugatkin and Dugatkin (2007) relaxed the (probably unrealistic) assumption that an individual has no knowledge of its opponent’s RHP. They assumed that the opponent’s RHP can be estimated and the (error-prone) estimate is drawn uniformly from the interval [$(1-\eta ) \mathrm{RHP}_{y,t};(1+\eta ) \mathrm{RHP}_{y,t}$] where $\eta$ describes the accuracy of the estimate. The case $\eta =0$ models the situation where each individual has perfect knowledge of its opponent’s RHP Dugatkin and Dugatkin (2007).

The analysis of the updated model with $\eta \,=\,0;0.25;0.75$ revealed that in all three cases, clear linear hierarchies were established (i.e. the higher-ranked individuals won more contests in total than lower-ranked individuals, and more direct contests against lower-placed individuals). Interestingly, there were almost no differences between the three cases, and thus, overestimation or underestimation of the opponent’s ability to win a fight had no impact on the establishment of linear hierarchies, as long as some ability to estimate this ability was possessed Dugatkin and Dugatkin (2007).

1.2 Our Model

In this paper, we extend the framework developed in Dugatkin (1997) and Dugatkin and Dugatkin (2007). For comparison reasons, we use the same model as that from Dugatkin (1997) and Dugatkin and Dugatkin (2007) with the only difference being in the updated model where the errors are treated differently (see Sect. 3.3). We start by analysing the average behaviour of the original model (as opposed to considering a single realisation) by recording the average number of wins of each individual over any other individual present in the population on the basis of 10,000 simulations and consider appropriate statistics to describe the properties of the emerging hierarchies. To this end, we evaluate the linearity of the hierarchy by adapting the index of linearity introduced by Kendall (1962), denoted by $K$ ($0\le K\le 1$). Values of $K$ close to one are indicative of linear hierarchies and values of $K$ close to zero indicate no linear hierarchy to be present. We calculate the index of linearity based on the averaged number of wins for all considered parameter combinations, and this systematic investigation of the model from Dugatkin (1997) revealed that a near linear hierarchy is achieved for all the analysed cases.

Besides understanding the structure of the emerging hierarchy, we are interested in understanding the temporal dynamic of the hierarchy formation; in particular, we want to explore when (or after how many interactions) a hierarchy is established. This knowledge can be of importance for experimentalists as it gives a guideline of the number of interactions that need to be observed. To do so, we firstly need to define when we consider a hierarchy as established. This will be based upon pairwise comparisons, and we will use the term “distinguishable” to indicate when two individuals can be thought to clearly occupy different positions in the hierarchy. Additionally, we are interested in the role of information in the process of hierarchy formation. Based on Dugatkin (1997) and Dugatkin and Dugatkin (2007), we consider the situations where

• (i) An individual has no information about the current RHP of its opponent,

• (ii) An individual is fully aware of the current RHP of its opponent and

• (iii) An individual can make a noisy estimate about the current RHP of its opponent.

Next for each pair of individuals and different parameter combinations, we calculate the time until both individuals are considered to be distinguishable regarding their rank in the hierarchy. We discuss our results in Sect. 3.

2 Methods

In the following, we use the above-described models to explore the properties of the process of hierarchy formation; in particular, we explore its temporal dynamic. To do so, we firstly analyse the number of wins of each individual over all other individuals present in the population after 1000 interactions (and therefore at a fixed point in time) and secondly the temporal changes in the RHP of each individual over these 1000 interactions for the non-updated and updated version of the model. We note that in both analyses, the rank of an individual is calculated differently. While in the first analysis, the rank is determined by the total number of wins, and in the second analysis, it is determined by the size of the RHP. However, the two definitions are highly correlated as Eqs. (3) and (4) guarantee that a high number of wins corresponds to a high value of RHP. All results presented in the following are based on averaging over 10,000 simulations, and we explore the same parameter constellations as in Dugatkin (1997) to allow for a direct comparison of the results. Therefore, we mainly consider groups of size four, but we have additionally analysed the behaviour of larger groups and obtained similar patterns. We occasionally comment on the results for larger group sizes in later sections.

2.1 Analysis of the Average Number of Wins

We start our analysis by determining the rank of all individual at all times $t$. Since we allow multiple contests between the individuals, it makes sense to arrange individuals according to their number of wins; the higher the number of wins, the higher the position in the hierarchy [this was the case in the models of Dugatkin (1997) and Dugatkin and Dugatkin (2007) as well]. If two individuals have the same number of wins, the rank is assigned at random. We note that an alternative way of deciding the ordering of the hierarchy would be by placing an individual above another if it had won more of their pairwise contests (although this latter definition has the significant disadvantage of sometimes not yielding an ordering). Theoretically on some occasions, these two definitions can produce different orderings of a given hierarchy, but in practice, this is very rare, and so there is no practical difference. Next we determine the matrix $\mathbf{W}=[w_{i,j}]_{i,j=1,\ldots ,N}$ which contains the average number of wins of the individual with rank $i$ over individual with rank $j$ under different strengths of the winner and loser effects, noting that there is a one-to-one correspondence between individuals and ranks. The resulting hierarchy is perfectly linear ($K=1$) if all individuals have a different number of wins and have won (lost) all of their decisive contests against those lower (higher) in the hierarchy than them. To quantify the degree of linearity, we calculate in the next step the index of linearity (Kendall 1962) using the following procedure:

• 1. From the matrix of wins $\mathbf{W}$, we construct an index matrix $\mathbf F =(f_{ij})$ where $(f_{ij}$) is the fraction of decisive interactions between individuals $i$ and $j$ (i.e. from those contests not involving a double kowtow) which were won by individual $i$ (so that $f_{ij}+f_{ji}=1$). This matrix will be called the matrix of fractions.

• 2. For this matrix F, calculate the row sum $R_i$ for $i=1...N$.

• 3. Calculate the index of linearity

  $$\begin{aligned} K=1-\frac{d}{d_\mathrm{max}}, \end{aligned}$$

  (5)

  (see Appleby 1983), where

  $$\begin{aligned} d=\frac{1}{12}N(N-1)(2N-1)-\frac{1}{2}\sum _{i=1}^{N}(R_i)^{2}, \quad d_\mathrm{max}=\frac{1}{24}(N^3-N). \end{aligned}$$

  (6)

The method used above is an adaptation of that developed by Kendall (1962). In that case, the interaction between a pair of individuals was a single contest with a unique top individual, so that exactly one of $f_{ij}$ and $f_{ji}$ was 1 and the other was 0. The parameter $d$ was the number of circular triads of matrix F, where a circular triad is a subgroup of three individuals denoted by $A,\,B$ and $C$ in a larger group which has the form $A\rightarrow B\rightarrow C\rightarrow A$ which means that $A$ dominates $B$, $B$ dominates $C$, but $C$ dominates $A$. No circular triads corresponds to a completely linear hierarchy.

Below, we show that the original definition of $d$ as the number of circular triads, in the case where there was a single contest between each pair of individuals, is a special case of our definition from (6). For the single contest case, $d$ is the total number of triples minus the total number of transitive triples (Balakrishnan and Ranganathan 2012). The number of transitive triples is $\sum \nolimits _{i=1}^{N}\left( {\begin{array}{c}R_i\\ 2\end{array}}\right)$ (see Balakrishnan and Ranganathan 2012), and so

$$\begin{aligned} d= & {} \left( {\begin{array}{c}N\\ 3\end{array}}\right) - \sum \limits _{i=1}^{N}\left( {\begin{array}{c}R_i\\ 2\end{array}}\right) \nonumber \\= & {} \frac{N(N-1)(N-2)}{6}-\frac{1}{2}\sum \limits _{i=1}^{N}(R_i)^2 +\frac{1}{2}\sum \limits _{i=1}^{N}R_i \nonumber \\= & {} \frac{N(N-1)(N-2)}{6}-\frac{1}{2}\sum \limits _{i=1}^{N}(R_i)^2 +\frac{1}{2}\frac{N(N-1)}{2} \nonumber \\= & {} \frac{N(N-1)(2N-1)}{12}-\frac{1}{2}\sum \limits _{i=1}^{N}(R_i)^2, \end{aligned}$$

(7)

which is the form for $d$ that we apply in our model for more general values of $R_{i}$ (see also de Vries 1995). For the formula (5), $d_\mathrm{max}$ corresponds to the maximum value that $d$ can take. In general, this is given by

$$\begin{aligned} d_\mathrm{max}=\frac{1}{24}(N^3-N). \end{aligned}$$

(8)

For the case where $f_{ij}$ was 0 or 1 Appleby (1983), this was also the formula for odd values of $N$, but for even values, this is not achievable, and the maximum is

$$\begin{aligned} d_\mathrm{max}=\frac{1}{24}(N^3-4N). \end{aligned}$$

(9)

In our model, we use $d_\mathrm{max}$ from (8) as this is achievable for fractional $f_{ij}$, even though our group size is generally even ($N=4$).

2.2 Analysis of the Temporal Change in RHP

It is assumed that each aggressive interaction changes the RHP of the individuals involved according to Eqs. (3) and (4). In the following, we investigate the temporal dynamic of the hierarchy formation by analysing the change in RHP for each individual over time. To do so, we define the rank of an individual at time $t \in [1,\infty ]$ based on its RHP (higher-ranked individuals have a higher RHP than lower-ranked individuals) and determine the probability distribution of the RHP values of the first, second, ..., $n$th rank based on the 10,000 simulations at each point in time. This allows us to ask how distinguishable individuals of different ranks are based on the ability to win an aggressive interaction. The degree of distinguishability between two individuals at time $t$ is determined by the overlap $\nu _{xy}(t)$ (see the grey area in Fig. 1) of the density of the RHP values, denoted by $f_x(t)$ and $f_y(t)$ (note that this overlap was termed OVL in Schmid and Schmidt 2006).

Fig. 1

Probability distributions functions of the RHP of two individuals at time $t$. The shaded area describes the overlap between the two distributions

We have $0 \le \nu _{xy}(t) \le 1, \,\forall t$ and the smaller $\nu _{xy}(t)$, the clearer the distinction between the ranks of the individuals. If there is complete overlap, then the individual with the higher rank is effectively chosen at random. In the following, we call two individuals $x$ and $y$ distinguishable if $\nu _{xy}(t)<0.1$ holds. The overlapping area $\nu _{xy}(t)$ is determined using the Kolomogorov distance $\mathop {\hbox {max}}\limits _{\forall z}|F_{x,t}(z)-F_{y,t}(z)|$ between the distributions $F_{x,t}$ and $F_{y,t}$. Assuming that the Kolmogorov distance is realised at position $z^*$, we obtain

$$\begin{aligned} \nu _{xy}(t)= & {} \int _{z^*}^{\infty } f_{y,t}(z) dz + \int _{-\infty }^{z^*} f_{x,t}(z) dz=1+(F_{x,t}(z^*)-F_{y,t}(z^*))\\= & {} 1-\mathop {\max }\limits _{\forall z}|F_{x,t}(z)-F_{y,t}(z)|. \end{aligned}$$

In our model, the values of RHP are discrete rather than continuous, but except for very early in the process (and with the single exception of the top individual when only the loser effect is present, as we discuss later), the number of possible discrete values becomes large and our discrete distribution can be approximated by a continuous distribution. We use this procedure to determine the overlap $\nu _{xy}$ for all combinations of individuals and every point in time. In this way, we are able to determine when $\nu _{xy}(t)$ falls below 0.1 for all $x, y$, and consequently when all ranks become distinguishable. We note that it is possible that $\nu _{xy}(t)$ can increase above 0.1 again (though this never in practice happens except at the very early stages of certain cases). In the following, we call the (final) time when $\nu _{xy}(t)$ falls below 0.1, a domination event.

3 Results

In the following, we assume a group of four individuals which are initialised with $\mathrm{RHP}_\mathrm{initial}=10$ and an aggression threshold $\theta =1$, unless stated otherwise. We explore the dynamics of hierarchy formation by analysing the average number of wins and the temporal change in the RHP in the non-updated model (Sect. 3.1), in the updated model with perfect assessment (Sect. 3.2) and in the updated model with imperfect assessment (Sect. 3.3).These dynamics are analysed for various combinations of winner and loser effects where both $W$ and $L$ take values from 0 up to 0.5. We show only $W$ and $L$ in the range from 0 to 0.3 in intervals of increment 0.1, as the behaviour at other values is consistent with the values shown, and 0.3 is a large value for a winner or a loser effect (see how large RHP becomes in Fig. 5a leading to predictable contest outcomes).

3.1 The Non-updated Model

We start our analysis by assuming that an individual has no information about its opponent’s RHP and therefore assumes its ability to win a fight to be $\mathrm{RHP}_\mathrm{initial}=10$ for all times.

3.1.1 Analysis of the Average Number of Wins

For different strengths of winner and loser effects, we record the average number of wins of each individual after 1000 aggressive interactions. Table 1 shows the matrix of wins $\mathbf{W}=[w_{i,j}]_{i,j=1,\ldots ,N}$ for each set of parameters. Each single entry $w_{ij}$ indicates the number of wins of individual with rank $i$ over individual with rank $j$.

Table 1 Matrices of wins $\mathbf W$ in the non-updated model for different strengths of the winner and loser effect ($W=0;0.1;0.2;0.3$ and $L=0;0.1;0.2;0.3$), $N=4,\,\varTheta =1$ and t=1000

Following our definition, it is clear that every individual has a clear rank in the hierarchy as the average numbers of wins for all individuals in all cases are different. When only the loser effect is present, all individuals in the group score except the individual that takes the last place. This is because the first to lose a fight will retreat in all subsequent contests, as its RHP is lower than $\mathrm{RHP}_\mathrm{initial}$, and therefore, Eq. (1) does not hold. Increasing the loser effect in the absence of the winner effect does not make any difference to the structure. When only the winner effect is present, all individuals in the group score and have a clear position in the hierarchy. When increasing the winner effect in the absence of the loser effect, we notice that higher-ranked individuals win an increasing fraction of the individual contests. In particular, each individual scores increasingly better against those that are lower in rank and increasingly worse against those individuals that are higher in rank.

Figure 2a shows the values of the index of linearity $K$ calculated by Eq. (5). We observe that $K$ is close to 1 for all parameter combinations considered, indicating a near linear hierarchy in almost all of the cases. Further, we see that, as expected, $K$ increases with $W$. When the loser effect is increased for a given positive value of $W$, each individual except the first placed individual does worse than before. This has a mild impact on $K$.

Fig. 2

a Index of linearity for different values of W and L, calculated from the (unrounded) values of the average number of wins from Table 1 b Change of index of linearity $K$ when the group size is increased from 4 to 9 under the influence of the loser effect only

When both winner and loser effects are present, we observe two different outcomes.

• (i) Hierarchies with a clear first and second place, a bottom individual with zero wins and the third place individual which does not differ much from the fourth place individual.

• (ii) Hierarchies with a clear first place individual, but the second place individual is not that different from the third placed one (see the case when $W=0.1$ and $L=0.3$).

These outcomes depend on the values of winner and loser effects. If we simultaneously increase winner and loser effects, we get a slight increase in the index of linearity (Fig. 2a. These results also hold for larger group sizes. Figure 2b, describes the index of linearity $K$ under the influence of the loser effect only when $N=4,5,6,7,8$.

3.1.2 Nonlinearity Due to Ties in the Final Positions

The number of wins in Table 1 is an average over 10,000 simulations, and in fact, the simulations do not always yield linear hierarchies. The fact that in every case they sometimes do is enough to demonstrate linearity on average. Nonlinearity in real dominance hierarchies can occur through a number of bottom-ranked individuals having equivalent (lack of) status, and this can also happen in our model. We now consider the probability of having a unique last-placed individual when only the loser effect is in place (this is the simplest case as we get the same structure for different values of the loser effect) and observe the large probability of ties here. The set of all possible structures with at least two individuals with zero wins will be denoted by A. When an individual has lost a contest in this version of our model, it will always concede any subsequent contest. Thus if our population enters the set A, it can never leave it, and the final dominance hierarchy will not have a unique last-placed individual. We denote all final hierarchies not in A as the set B.

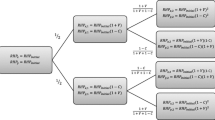
The first encounter will give us a winner denoted by $W$ and a loser denoted by $L(0)$ where $L(0)$ stands for a loser with 0 wins. This leads to a state of the population $S_\mathrm{WL(0)}$ (in our notation, we list the individuals that have fought, omitting any individual that has not engaged in a contest). Conditional on the next fight not being between the two existing individuals, we have either

• (1) A new individual fights the original loser and wins. This means that $S_\mathrm{WL(0)}$ $\mapsto$ $S_\mathrm{WWL(0)}$ with a probability $\frac{2}{5}$.

• (2) A new individual fights the original winner and loses. This means that $S_\mathrm{WL(0)}$ $\mapsto$ $S_\mathrm{WL(0)L(0)}$, an element of the set A, with a probability $\frac{1}{5}$.

• (3) A new individual fights the original winner and wins. This means that $S_\mathrm{WL(0)}$ $\mapsto$ $S_\mathrm{WL(+)L(0)}$ with a probability $\frac{1}{5}$, where $L(+)$ denotes a loser that has won a previous contest (the original winner).

• (4) The next fight is between the two new individuals. This means that $S_\mathrm{WL(0)}$ $\mapsto$ $S_\mathrm{WWL(0)L(0)}$, an element of A, with a probability $\frac{1}{5}$.

Similar working from the states $S_{WWL(0)}$ and $S_{WL(+)L(0)}$ yields the transition diagram from Fig. 3. It is easy to calculate the final probability of ending up in state A, as opposed to B, as $\frac{11}{20}$. Thus, the probability of finishing in a hierarchy with a unique last-placed individual, in set B, is $\frac{9}{20}$. Note that this does not necessarily mean that in this case, we have a linear hierarchy, because we might have a tie between the second and the third place (note that this is another way for linearity on average not to translate to linearity in every simulation).

Fig. 3

Transition probabilities between states. A represents a structure with two losers with zero wins, W is a winner that has not yet lost a fight, L(+) is a previous winner that has now lost, L(0) is a loser with no wins, and B represents all final structures with only one loser with zero wins

3.1.3 Analysis of the Temporal Change in RHP

In this section, we analyse the temporal dynamic of the change in overlap $\nu _{xy}(t)$, $x,y=1,\ldots ,4,\ x\ne y, t \ge 1$ of the probability distributions of the four ranks at time $t$. For the sake of brevity, we present the results of three different situations: i. only the loser effect is present in the population, ii. only the winner effect is present, and iii. both effects are present.

The Loser Effect Only

Figure 4a shows the probability distributions of the four ranks at time $t=500$ and $W=0, L=0.1$ and Fig. 4b the corresponding areas of overlap $\nu _{xy}(t), \ \forall \, t \le 500$. There is a clear first place individual if only the loser effect is present (we reached the same conclusion when analysing the average number of wins). Further, the second and the fourth place are distinguishable as $\nu _{24}(t)$ decreases below the threshold point 0.1 (see Fig. 4b and again the same conclusion could be drawn on the basis of Table 1). However, Fig. 4a shows clearly that the second to fourth place individuals all appear close in RHP in comparison with the dominant first individual. The areas of overlaps $\nu _{23}(t)$ and $\nu _{34}(t)$ are almost the same and the pairs corresponding to these overlaps are not distinguishable. The RHP of the top individual stays unchanged equal to $\mathrm{RHP}_\mathrm{initial}$, meaning that the top individual has distribution which takes the value 10 with probability 1. Its RHP at time $t=500$ over 10,000 simulations is shown by the vertical line $x=log(10)$ (Fig. 4a).

Fig. 4

a Probability distribution for the second, third, fourth place individuals for $W=0$ and $L=0.1$ at $t=500$. The first place does not have a distribution as it’s RHP stays unchanged and is represented by the vertical line ($x=log(10)$) b Time course of the corresponding area of overlap $\nu _{xy}(t),\,x=2,3,4,y=3,4$. $\nu _{23}(t)$ and $\nu _{34}(t)$ overlap with each other. The overlap between the top individual and the other individuals becomes close to 0 very quickly

Due to the discrete nature of the RHP, it is possible in the very early time steps that the overlap $\nu$ can decrease below 0.1 and then increase above 0.1 again (as mentioned previously) several times, but this never happens later on (in practice, theoretically this would be possible), and a dominance event is defined as the time when two individuals became distinguishable in this way for the last time. The obtained temporal dynamic in the change of the area of overlap allows us to ask when (meaning after how many fights) the dominance hierarchy is established, i.e. when the last domination event occurs.

We cannot calculate the overlap between the top individual and the other individuals in the same way, as the RHP of the top individual stays unchanged at 10. In this case, we say that the top individual will be distinguishable from the second placed individual when the $90\,\%$ quantile of the distribution of the RHP of the second individual is $<\!\!10$ (i.e. we effectively consider the probability of the second placed individual to be ten as the overlap). The same method will be used to distinguish the top individual from the third and the fourth placed individuals. For the time of domination events of other pairs of individuals, the overlap concept will be used. In the case considered the hierarchy is established quite early, 11 fights are needed for the first and the second place to become distinguishable, which is the final domination event.

It should be noted that this overlap criterion is possibly a rather conservative measure. It is based upon the comparison between randomly selected second place and third place individuals, whereas in a real hierarchy, there would be a pair of individuals in the second and third places, for example. The values of their RHP will not be independent and are likely to be negatively correlated; the better the second place does, the more likely the third place would do worse.

The Winner Effect Only

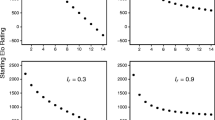
Now we consider the situation where only the winner effect is present and assume $W=0.1$ and $L=0$. We know from Table 1 that in this situation, all individuals have a clear position in the hierarchy and this result is confirmed by Fig. 5. It is clear that the area of overlap $\nu _{xy}(t)$ falls below 0.1 for all combinations of $x$ and $y$ and we are interested in when the domination event occurs.

Fig. 5

a Probability distribution for the four individuals when $W = 0.1$ and $L = 0$ at $t=500$. b Time course of the corresponding area of overlap $\nu _{xy}(t),\,x,y=1,\ldots ,4,\ x\ne y$

We note that at the start, the RHP of the different individuals can only take some discrete values causing the fluctuations of the area of overlap (see Fig. 5b). Further, from Fig. 5b, we observe that the final domination event occurs quite late. The last domination event occurs between the second and the third place individuals, which finally become distinguishable at time point $t=395$. Hence, roughly 400 fights are enough to specify the place of each individual in the hierarchy. Increasing the winner effect in the absence of the loser effect does greatly influence the time needed to establish a hierarchy.

Winner and Loser Effects

In this analysis, we assume that both the winner and loser effect are present and possess the values $W=0.3$ and $L=0.2$. We know from the matrix of wins given in Table 1 that the third place individual scores an average of approximately 1 win, whereas the last individual never wins (as it is the first one to lose and retreats afterwards). Thus, the third and the fourth place individuals are expected to have almost identical RHP, confirmed by Fig. 6. The overlapping probability distributions are concentrated around low values. We further observe that the first place individual is clearly distinguishable from the others. Interestingly, the RHP of the second place individual has a bimodal distribution. This implies that sometimes (in most cases) the second place individual is distinguishable from the third, and sometimes it is not. This phenomenon is caused by the outcomes of the very early interactions: through ‘bad luck’  the second place individual loses sufficiently many early fights and its RHP falls below 10 (implying that it will never fight another contest again), or if it wins sufficiently many early fights and its RHP will never fall below 10. Whether an individual will be in a given part of the bimodal distribution is thus determined in the early contests.

Fig. 6

a Probability distribution functions for the four individuals in the non-updated model when $W=0.3$ and $L=0.2$ at $t=500$. b Area of overlap $\nu _{xy}$ over time. $\nu _{13}(t)$ and $\nu _{14}(t)$ become close to 0 very quickly, and so are close to the $x$ axis

Based on Fig. 6b, we conclude that the second and the fourth places are distinguishable as $\nu _{24}(t)<0.1$ from a very early time. The second and the third place individuals appear to be clearly different based on the analysis of the average number of wins, with the second place individual doing much better, but the area of the overlap $\nu _{23}(t)$ decreases only to 0.18 (at $t=45$) and then stays unchanged. This means that for 82 % of hierarchies they are clearly different and for 18 %, they are effectively the same. These values (18 and 82 %) correspond to the right and left area of the bimodal distribution, respectively. We note that this result contradicts the claim of repeatability for the simulations from Dugatkin (1997) as different individual simulations will yield very different results. In general in this type of winner–loser model, this only occurs when there is bimodality in one of the individuals; in all of our cases, the second individual out of four, though it is possible for very large winner effects for this to happen for the third individual. In hierarchies with more individuals, theoretically this could happen for any individual except the first or the last.

The last pair of individuals to become distinguishable is the first and the second place, and this happens at $t=47$ (the time of the final domination event). Summarising, when both the winner and loser effect are present, the first place individual always becomes distinguishable. For $W=0.3$ and $L=0.2$, the second place individual has a bimodal distribution. In general however, if the ratio between the loser and the winner effect is sufficiently large, then the bimodal shape disappears (individuals will eventually have RHP under 10), but as the ratio becomes smaller, a small upper area appears, which is of increasing size the smaller the ratio. The times of all of the domination events for different combinations of winner and loser effects are shown in Table 2.

Table 2 The times of the domination events for the non-updated model with $\theta =1$ and various values of $W$ and $L$. $T_{xy}$ is the (final) time when $\nu _{xy}(t)$ falls below 0.1

3.2 The Updated Model with Perfect Assessment

We will now consider the hierarchy structures which emerge when each individual is aware not only of its own RHP through time, but likewise that of its opponent. This corresponds to $\eta \,=\,0$ in Dugatkin and Dugatkin (2007). All other features of the model are the same as in the previous section.

3.2.1 Analysis of the Average Number of Wins

We start by analysing the average number of wins in the updated model. Table 3 shows the matrices of wins for $W,L=0;0.1;0.2;0.3$. We observe that for every combination of $W$ and $L$, linear hierarchies are established. The strength of the winner and the loser effects do not have any significant influence on the number of wins of the first, second and third place individuals; they only affect the last place. This individual always scores zero when only the winner effect is present, but generally scores something when the loser effect or both effects are operating. This is the opposite behaviour that we get from the non-updated model.

Table 3 Matrices of wins $\mathbf W$ in the updated model for different strength of the winner and loser effect ($W=0;0.1;0.2;0.3$ and $L=0;0.1;0.2;0.3$), $N=4,\,\varTheta =1$ and 1000 aggressive interactions

3.2.2 Analysis of the Temporal Change in RHP

Following the same process as in the non-updated model, in this section we analyse the RHP values of all individuals. Firstly and in accordance with the results obtained above, we observe that for all combinations of $W$ and $L$, all ranks in the hierarchy are distinguishable (see Figs. 7, 8 and 9). Additionally, we calculate the final time when the dominance hierarchy is established and find three different outcomes depending on $W$ and $L$ values.

Fig. 7

a Probability distribution functions of RHP for the four individuals in the updated model: $t=500$, only W is present. b $\nu _{xy}$ over time when only W is present. $\nu _{14}(t)$ becomes close to 0 very quickly, and so is close to the x-axis

Fig. 8

a Probability distribution functions of RHP for the four individuals in the updated model: $t=500$, only $L$ is present. b $\nu _{xy}$ over time when only $L$ is present. $\nu _{14}(t)$ coincides with the $x$ axis after $t=1$

Fig. 9

a Probability distribution functions of RHP for the four individuals in the updated model: $t=500$, both W and L are present. b $\nu _{xy}$ through time when both W and L are present. $\nu _{14}(t),\,\nu _{13}(t),\,\nu _{14}(t)$ and $\nu _{24}(t)$ become close to 0 very quickly, and so are close to the x-axis

When only the winner effect is present (Fig. 7), on average 41 fights are necessary to establish a linear hierarchy. After this, nothing new happens to the hierarchy and the rank of the individuals. The last domination event between a pair of individuals is that between the second and the third place individuals. We note that the value of $W$ does not have any effect on the time to establish the hierarchy.

We obtained a similar pattern when only the loser effect is present (Fig. 8). Irrespective of the value of $L$, the structure is established at the point $t=44$ and the last pair to become distinguishable are the second and third place individuals.

Lastly, when winner and loser effects are both present in the population at varying strengths, hierarchies are established latest at time point $t=32$ (Fig. 9). Again, as in the two above cases, the last pair to become distinguishable are the second and third place individuals.

Table 4 shows the times of the dominance events between all pair of individuals for various values of winner and loser effects. In general, the best scenario for fast hierarchy formation is when both the winner and loser effects are present in a group of individuals as the dominance hierarchy is established earlier than when only one is present. The first pair to become distinguishable is the first and the fourth place individuals, whereas the last pair is again that of the second and the third place individuals. This is the case for all the possible values of the winner and loser effects.

Table 4 The times of the domination events for the updated model with perfect estimation: $\theta =1$, various values of $W$ and $L$. $T_{xy}$ is the (final) time when $\nu _{xy}(t)$ falls below 0.1

In the following, we consider the influence of the fighting threshold $\theta$ on the dynamics of hierarchy formation. So far we considered $\theta =1$ and from Eq. (1), it is clear that a lower fighting threshold $\theta$ means that the number of possible fights is increased. When decreasing $\theta$ to 0.8, the qualitative dynamic of the updated model is unchanged, but the time needed to establish a dominance hierarchy is increased. In particular for $0<W\le 0.2$ and $0<L\le 0.2$, the final domination events occur later than for the situation with $\theta =1$. Once we increase the values of the winner and loser effects, however, we notice that the times of the final domination event do not differ much from the previous case when $\theta =1$.

The results obtained for the updated model hold also for larger groups. Figure 10 shows the time of the domination event for each pair in a group of eight individuals. As expected, the hierarchy is established much later compared to a group of four individuals.

Fig. 10

The time of domination events between each pair of individuals in the updated model whereby, for example, the black dashed line shows the time of the domination event of the first-ranked individual with individuals of rank 2,3,...,8, for $\theta =1$, $W=0.1,\,L=0,\,N=8$ and perfect estimation

3.3 The Updated Model with Assessment Error

In this section, we relax the assumption that an individual has perfect knowledge of the RHP of its opponent. As described in Sect. 1.2, we assume that an individual assesses an opponent with a real RHP of $\mathrm{RHP}_{y,t}$ as having a value of $(1+\varepsilon ) \mathrm{RHP}_{y,t}$, where $\varepsilon$ is normally distributed with mean 0 and standard deviation 0.2 (truncated above at 1 and below at $-1$). This type of error is somewhat different to that used in Dugatkin and Dugatkin (2007), who used uniformly distributed intervals, although the results do not hugely depend upon the distribution of error used. In the following, we again consider four individuals with an aggression threshold $\theta =1$ and analyse the RHP through time. We note that the analysis of the number of wins leads to similar results as in Sect. 3.2.1 and for brevity, we exclude this.

When $\theta =1$ and $\varepsilon$ is normally distributed with mean 0 and standard deviation 0.2, linear hierarchies are formed for all combinations of $W$ and $L$. Even though the individuals can make only an approximate estimation of their opponent’s RHP with a normally distributed error $\varepsilon$, this does not have any significant effect on the linearity of the hierarchy. The only impact that $\varepsilon$ has is on the time to hierarchy establishment. In this case, the individuals need to interact more with each other (compared with the case when $\varepsilon$=0) in order to establish a linear hierarchy.

We can conclude that $\varepsilon$ stabilizes linear hierarchies, meaning that only a little information about your opponents strength is necessary in order to establish a linear hierarchy. Lowering the aggression threshold leads to a similar dynamic as described in Sect. 3.2. We still obtain linear hierarchies for all combinations of $W$ and $L$; however, the time until the hierarchy is established is increased.

Table 5 shows that for $\theta =0.8$ and imperfect information, linear hierarchies are achieved on all the analysed cases. The times of domination event depends on the values of the winner and loser effects, with an increase in the size of either effect generally reducing the time to the domination events. Comparing this with the results of the updated model with $\theta =1$ and perfect assessment from Table 4, we can see that the hierarchy generally takes longer to be established, but that the difference is not large. This is a cumulative effect of making individuals more aggressive by reducing $\theta$ and reducing the accuracy of their information; when we make one of these changes only, we find times between those from the two extremes (we have omitted tables corresponding to these cases).

Table 5 The time of domination events for the updated model with $\theta =0.8$ and imperfect estimation for various values of $W$ and $L$. $T_{xy}$ is the (final) time when $\nu _{xy}(t)$ falls below 0.1

Summarising, in this section we showed that using the updated model with different levels of accuracy, linear hierarchies are always achievable. When individuals have perfect information about their opponent’s RHP, the linear hierarchy is established earlier than when they overestimate or underestimate their opponents. More interactions are necessary in the second case, but after a certain point in time (depending on the values of the winner and the loser effects), the hierarchy is stabilized. When we lowered the aggression threshold, the linear hierarchies were established later than in the first two cases. We can conclude that the updated model with different levels of accuracy always produces linear hierarchies. The time when these are established depends upon the level of information that individuals have about others in the group, and upon the value of the aggression threshold, where the higher the threshold and the smaller the error, the shorter the time to hierarchy formation.

4 Discussion

In this paper, we explored how winner and loser effects influence dominance hierarchy formation using a simulation-based model developed first in Dugatkin (1997) and Dugatkin and Dugatkin (2007). We considered two main situations: the non-updated model, when an individual has no information about the current RHP of its opponent, and the updated model, when an individual can estimate the RHP of its opponent with various levels of accuracy. We built on the model of Dugatkin (1997) and Dugatkin and Dugatkin (2007) by providing a more complete analysis of the non-updated and updated model. All of our results are based on 10,000 simulations rather than one single realisation. In particular, we developed new statistical measures for the time when a dominance hierarchy is established.

These methods include a more detailed analysis of large numbers of interactions and an extension of the classical idea of the index of linearity $K$ (developed by Kendall 1962) to this general number of interactions. An important consideration was the time to establish the hierarchy, and we have introduced a new measure to distinguish pairs of individuals and to establish when dominance has been achieved. We have then been able to find when our hierarchy has been established for each of the different models that we consider and make comparisons between them.

The values of the index of linearity $K$ are perhaps exaggerated as a measure because high scores looks like they predict high linearity, when the reality can be more complex. We have used fractions of interactions experienced by one individual over the others where it has emerged as the winner, but this ratio is not the only important aspect; the absolute values of the number of wins is potentially important as well. For example, the ratio $20/2$ indicates more distinguishability between two individuals scoring 20 and 2 wins than the ratio $2/0.2$ for those with 2 and 0.2 wins. These low numbers can indicate an averaging which can include hierarchies with indistinguishable final individuals, although even high numbers can be the result of bimodality in RHP. One possible (simplistic) solution is to add a baseline value of wins to all table entries when calculating $K$, which necessarily will have a smaller effect, the larger the number of decisive contests.

For the non-updated model, we found different types of hierarchy formation for each of the three main cases, although the values of the index of linearity shows that almost linear hierarchies are established. When only the winner effect is present, each individual scores in the group, three of them with a high number of wins, and all interactions lead to fights. It appears that this structure is the simplest one and that it can be achieved quite early; however, our analysis of the RHP showed that up to 400 interactions are needed to establish a linear hierarchy. When only the loser effect was present, the first place individual scores a high number of wins, and all others a small number. The analysis of the RHP through time showed that the overlap between the second and the third place individuals is almost 0.4 which is much bigger than the threshold 0.1 where we consider two individuals to be distinguishable. This structure (with second and third positions indistinguishable) is established very early compared with the case when only the winner effect is present, with only 11 possible interactions needed.

When both winner and loser effects are present, we obtained a structure where the first place is always clear with an individual who has a high number of wins, and the second place has quite a high average number of wins, with a high number of wins on some simulations, and on other simulations, the number of wins does not differ much from the number of wins of the third placed individual; this corresponds with the RHP analysis where the second place individual often has a bimodal distribution of the RHP. This means that different individual simulations will yield different results, where sometimes the second place individual will be distinguishable from the third and sometimes not (this partially contradicted previous results from Dugatkin 1997), which occurs is decided very early in the process.

The non-updated model has some limitations; as in reality, the individuals could potentially approximate what the average “strength” of another individual would be at a certain time and then use this estimation when deciding whether to fight or retreat. If only the winner effect is in operation, for example, then an individual may be able to estimate the rate of increase of RHP of an average opponent just by considering the time elapsed, as the RHP of all will tend to increase. Thus, the updated model, with varying levels of accuracy, is more realistic.

For the updated model, with perfect information of the strength of the others, we conclude that a linear hierarchy is always established. The values of the winner and loser effects, and whether they are considered alone or both to be present in the group, do not have any influence on linearity. When the RHP was analysed, we calculated that the linear hierarchy is established at the time $t=41$ when only the winner effect is present, at time $t=44$ when only the loser effect is present and at $t=32$ when both the winner and the loser effect are present. If individuals do not have perfect information about the strength of their opponents, this does not have any real influence on the linearity (as was shown previously by Dugatkin and Dugatkin 2007). The only effect that it has is on the time when these linear hierarchies are established. More interactions are needed in this case than when individuals have perfect information about the RHP of others. The same results are achieved when the aggression threshold $\theta$ is lowered from 1 to 0.8, when the establishment of the dominance hierarchy occurs later than when $\theta$=1. Thus, as long as individuals know something about the strength of their opponents, a dominance hierarchy is always likely to be established in this model, and the precise model parameters have only a relatively small effect.

Our model thus predicts that for real biological populations, provided that animals can estimate the strength of their groupmates (and this estimation does not have to be accurate), then an unambiguous dominance hierarchy can be established in a relatively small number of interactions. Thus if contests are not too costly, and the group stays together for a sufficiently long time, a linear hierarchy will be formed. We predict some variation, so that when information is more reliable, or when loser effects dominate, the time to hierarchy formation will be the shortest. For the group as a whole, a short hierarchy formation phase is of course beneficial, as risk of injury and lost time and energy are minimised. If animals cannot estimate their groupmates’ strength at all, then our model predicts far longer periods of hierarchy formation often with less clear-cut results. It seems unreasonable, however, to assume that even after a number of contests animals can possess so little information. Thus it seems likely that, as often observed in real populations, linear hierarchies should form relatively quickly. Of course, it should be noted that many real populations are more complex, with group membership in a state of flux, or coalitions between groupmates (e.g. close relatives) (de Villiers et al. 2003; Silk et al. 2004), and so often our idealised conditions will not apply.

In the models considered here, and the earlier models involving winner and loser effects that they are based upon, there is no strategic element. This is in contrast to other models of dominance hierarchy formation, such as that of Broom and Cannings (2002), where individuals differed in their level of aggressiveness, and evolutionarily stable strategies were found. In future work, we plan to introduce such game-theoretical elements to our winner and loser models to consider strategic choices of the aggression threshold, for instance (in conjunction to varying rewards and costs for winning or losing different types of contests, we note that in the current model, there is no benefit to not fighting, and individuals retreat at a certain threshold due to a loss of confidence).