Electrothermal blood streaming conveying hybridized nanoparticles in a non-uniform endoscopic conduit

Abstract

The novelty of nanoparticles in transferrals of medications and biological fluids via electrokinetic mechanism has been competently recognized. Due to the impressive role of nanoparticles suspended in blood or physiological fluids in medical fields, the current research article is planned to formulate an effective mathematical model to analyze the dynamism of bloodstream infused with hybridized nanoparticles in a non-uniform endoscopic conduit (space between two coaxial tubes) under the interactivities of electroosmosis, peristalsis, and buoyancy forces. The dual impact of heat source, Joule heating, and convectively cooling wall condition is examined. The geometrical shapes (sphere, brick, cylinder, and platelet) of nanoparticles injected into blood are accounted for in the formulation of modelled equations. The blood doped with hybridized nanoparticles is regarded as an electrolyte solution. The lubrication and Debye-Hückel linearization estimations are invoked in order to linearize the flow equations. Analytical solutions for the resulting leading equations are computed by implementing an analytical approach. The amendments in the physiognomies under variations in sundry parameters are explained through the line, bar graphs, and numerical tables. Outcomes admit that the flow of ionized blood is significantly amended across the endoscopic conduit due to the electrostatic body force. Blood is warmed or cooled with positive or negative values of Joule heating parameter. Blood is cooled with augmenting volumetric concentration of hybridized nanoparticles. The trapping phenomenon is also described by designing streamline plots. The size of confined blood boluses expands due to the thin electric double layer (EDL). The novel findings of this hemodynamic simulation furnish significant applicabilities in modelling of transportation of medications and drugs, physiological fluid mixers, testing and assessment of human diseases, detection of bacteria and viruses, etc.

1 Introduction

Versatile applications of nanomaterials/nanofluids are illustrious evolutions in nanotechnology and biomedical engineering in the twenty-first century. This century is a deponent of evolution in incredible innovations of various smart devices or systems, which are smartly encountered in the diverse fields of advanced sciences. Nanofluid is a colloid formed by dispersing nanoparticles (diameter less than 100 nm) into ordinary fluids. It was reported that nanofluids possess high and exceptional thermal conductivity as compared to the base fluid. Nanoparticles are widely used in the transmission of medications, drug distribution, biomedical therapy, cancer therapy, vivo therapy, thermotherapy, laser therapy, gland tumour treatments, cryosurgery, antibacterial and antifungal agents, contrast agents [1, 2]. Several kinds of tumours, cancers, lymphoma, myelomata, and epidemic diseases are cured by the exemplary uses of nanoparticles. The conductivity of blood doped with nanoparticles improves due to free electrons that modulate the thermal state of blood flow dynamics. Due to the ample range of applications of nanoparticles in medical domains, significant research works on the dynamism of bloodstream suspended with nanoparticles or nanofibers have been conducted and reported remarkable results in recent years. The transport mechanism of blood doped with nanoparticles passing through a permeable vessel was enunciated by Gentile et al. [3]. A theoretical model for the peristaltic motion of blood mixed with copper nanoparticles in an endoscopic tube with a non-uniform cross-section was proposed by Sadaf and Malik [4]. Their results conveyed that the blood is cooled by increasing the volume fraction of nanoparticles dispersed into it. Ijaz et al. [11] established the indicative role of nanoparticles on the slip flow of blood in an inclined annulus with a blood clot. The hemodynamic properties of the bloodstream diffused with gold nanoparticles (Au NPs) through an overlapping stenosed tapered vessel were described by Elnaqeeb et al. [6]. Their results established that gold nanoparticles injected into blood significantly modulate the hemodynamical and thermal features in the flow conduit. Elmaboud et al. [7] investigated the flow of blood suspended with gold nanoparticles and pointed out that the temperature of blood rises with the volumetric concentration of gold nanoparticles, which has excellent utility in cancer therapy. Other related articles are given in [8,9,10].

Hybrid nanofluids (HNFs) are engineered by infusing two or more types of nanoparticles into a base fluid. HNFs holding hopped-up thermal conductivity have bioengineering manifestations like preventive medicine, diagnostic, orthopaedic lubrication, arthritis, anticancer and antibacterial drugs, etc. Researchers or modellers have focused on mimicking the distinctive features of hybrid nanofluids from various perspectives. Ijaz and Nadeem [11] made an examination of the flow of blood infused with hybridized nanoparticles (Ag, Al₂O₃) passing through an overlapped stenosed artery. Ijaz et al. [12] analyzed the dynamism of the bloodstream suspended with hybridized nanoparticles (Cu, CuO) through a tapered arterial network having stenosis. The blood flow conveying hybridized nanoparticles in a diseased artery with wall properties was simulated by Ijaz and Nadeem [13]. Their results revealed that hybridized nanoparticles injected into the blood play an essential role in disease prevention (arteriosclerosis). Sadaf et al. [14] scrutinized the upshot of hybridized nanoparticles on the peristaltic pumping of physiological fluid in an endoscopic tube. They observed that the hemodynamic factors are significantly altered due to the presence of an endoscope and suspension of hybridized nanoparticles. Sadaf and Abdelsalam [15] discussed the consequence of hybridized nanoparticles on the blood motion via peristalsis in an annulus with a non-uniform cross-section subject to the convective wall heating conditions. It was found that the blood boluses are not formed in the annulus for a higher Biot number. Using an analytical approach, Das et al. [16] have solved the problem of blood flow carrying hybridized nanoparticles in an inclined artery with stenosis under a uniform magnetic field. They concluded that the flow resistance reduces with higher volume volumetric concentration of hybridized nanoparticles infusing in blood. The dynamical and thermal factors of water-based hybrid nanofluids passing through an inclined channel obstructed by a porous medium in the presence of electroosmosis and peristalsis have been disclosed by Akram et al. [17]. Very recently, Sharma et al. [18] have presented a theoretical model for the unsteady flow of blood pervaded with hybridized nanoparticles (gold and alumina) in a tapered artery with multi-stenoses under the consequences of an inclined magnetic field, thermal radiation, and Joule heating. More relevant articles are referred to refs. [19,20,21,22,23].

Ongoing research on electro-hemodynamic simulation of bloodstream suspended with nanoparticles in the arterial network has opened up a new window in the medical domain. Blood is a physiological fluid that transports needed oxygen, carbon dioxide, nutrients, hormones, metabolic waste products, etc. [24]. Blood regulates cell-level metabolism, pH level, osmotic pressure, body temperature, etc. Modelling and simulating arterial blood flow doped with nanoparticles are very realistic and pertinent to cardiovascular phenomena and diseases. Abdelsalam et al. [25] have formulated a problem for the electro-osmotic flow of electrically conducting blood appending nanoparticles with different shapes via artery having both aneurysm and stenosis. Their outcomes unveiled that the blood flow rate for spherical-shaped nanoparticles is lower than other shaped nanoparticles. The flow of blood amalgamated with Au and Cu-NPs in an elastic sinusoidal channel under an AC electric field has been investigated by Mekheimer et al. [26]. Outcomes revealed that the Au-NPs are very effective as drug carriers. Nadeem et al. [27] have studied the electroosmosis endorsed blood flow through a wavy microchannel by including the consequences of Joule heating and chemical reaction. Das et al. [28, 29] have simulated a two-dimensional flow of blood assimilated with hybridized nanoparticles passing through an artery under an external magnetic field. In this direction, some other noteworthy studies are reported for the attentive readers [30,31,32,33,34,35].

The peristaltic mechanism plays a significant role in transporting biological and physiological fluids. Peristalsis is an utmost transport mechanism encountered in nature, engineering, and biomedical sciences. Peristaltic flow is generated by a continuous expansion and contraction of a flexible tube/conduit/duct which contains biofluids. This mechanism has wide manifestations in biomedical and bioengineering, such as biomimetic pumping, cardio-vascular pumping, soft robotic locomotion, urine transportation, capillary systems, blood filtration, driving of corrosive fluids, etc. [36]. Owing to excellent effectiveness of the peristaltic pumping process, it is widely deployed in biomimetic designs like drug delivery systems, bioinspired smart devices, arterial networks, etc. The peristaltic working process under the action of a magnetic field force has diverse manifestations in biomedical and engineering instruments, surgical controls, bio-magnetic therapy, bio-sensing, etc. The dynamics and thermal attributes of biological fluids with Newtonian or non-Newtonian fluid models via peristalsis have been unveiled by many researchers. Latham [37] was the pioneer who explored the mechanism of peristalsis theoretically and experimentally. After his remarkable reporting, an extensive range of peristaltic flows have been researched. Goswami et al. [38] formed a mathematical model for the electrokinetic transmission of power-law fluids through a tube with a deformable wall via peristalsis. It was disclosed that the zero-flow pressure rise directly relates to the power-law index. Tripathi et al. [39] worked on the electroosmosis endorsed peristaltic transport of non-Newtonian aqueous electrolyte in a micro-channel and derived solution in analytical form. They showed that the distribution of the pressure gradient across the channel is modulated with the strength of the electro-osmotic force. The peristaltic pumping of blood through porous microvessels, including Joule heating and different zeta potential, was demonstrated by Ranjit et al. [40]. They remarked that flow and pumping characteristics are significantly modulated by electro-osmotic parameter, zeta potential, and couple stress parameter. Manjunatha et al. [41] testified the consequences of wall slip condition and wall nature on the flow of Rabinowitsch fluid in an inclined tube with a non-uniform cross-section via peristalsis. This study found that the bolus shape enlarges with rigidity and stiffness parameters augmentation. Several other significant studies on peristaltic pumping of bio-nanofluids under electromagnetic force are mentioned in Refs. [42,43,44,45,46,47,48].

Endoscopy is a popular and robust biomedical device used to test and assess many diseases and clinical applications. The intromission of an endoscopic structure in a human body is referred as to endoscopy. Blood flow patterns and pressure features are impressively altered by inserting an endoscope through arteries or vessels. Many studies on the bio-nanofluid flow via uniform or non-uniform endoscopic geometry have been performed. Bhatti et al. [49] inspected the endoscopic effect on the peristaltic motion of blood with the Sisko fluid model conveying titanium magneto-nanoparticles in a tube with a uniform cross-section. Bhatti et al. [50] proposed a problem for the peristaltic pumping of blood through an endoscopic annulus, including the wall slip condition. They observed that the blood pressure is substantially modulated owing to the presence of an endoscope in the flow domain. A theoretical model for the flow of non-Newtonian blood suspended with nanoparticles in an endoscopic annulus via peristalsis under magnetic field impact was formulated by Abdelsalam and Bhatti [51]. Das et al. [52, 53] have recently published papers on the flow of blood conveying hybridized nanoparticles in an annulus with the implantation of an endoscopic subject to a magnetic field along with Hall currents. Their outcomes revealed that Hall currents significantly amend the hemodynamic factors in the endoscopic domain. Other foremost studies regarding peristaltic flow due to endoscopy using nanofluid models are communicated to refs. [54,55,56,57].

Electro-osmotic transport is gaining more recognition in biomechanics, electromechanical, and biomedical engineering. Electroosmosis has more ascendancy over the typical transportation induced by the pressure through microchannels or ducts. It infers an applied electric field and electrolyte liquid interplay and attributes exciting flow features. When a solid-charged surface is in contact with ionic liquids or aqueous solutions, the cations in the liquid will then be obliged to that surface, and the anions will repel from it. Due to this, an electric double layer(EDL) over the charged surface is generated. The EDL comprises an immobile Stern layer formed adjacent to the charged surface and a diffuse layer developed with mobile positive ions. The EDL with positive charges will move in the direction of the electric field, which is parallel to the charged surface. Resultantly, the bulk liquid is mobilized due to the viscous drag. This fact is well known as the electro-osmotic flow (EOF), frequently met in microfluidic devices /systems. It has a variety of potential bioengineering and biomedical manifestations such as cell culture, cell separation, tissue scaffolding, clinical procedures, cellular micro injection, biochip fabrication, microbial fuel cells in carbon capture, blood and urine diagnosis, etc. In 1809, the electro-osmotic phenomenon was first explained by Reuss [58]. After that, Wiedemann [59] submitted the theories of electro-osmotic flow phenomena. Motivating the challenging ultimatums and excellence of EOF devices, many engineers and researchers have shown their concentration on the EOF simulation of Newtonian or non-Newtonian fluids subject to various flow assumptions or constraints. The dual occurrence of electroosmosis and peristalsis frequently arises in numerous engineering and biological processes. Shit et al. [60] presented the EOF simulation of a non-Newtonian biofluid in a microchannel under a magnetic field. They pointed out that the entrapped bolus is reshaped due to the presence of electromagnetic field force. The electro-osmotic phenomena in microchannel filled with nanofluid were simulated by Tripathi et al. [61]. Their observation conveyed that the fluid pressure in the channel builds up with the applied electric field strength intensifying. Chaube et al. [62] developed a theoretical model for electro-osmotic transport via a microchannel filled with micropolar fluid. Outcomes divulged that flow and thermal features noticeably alter due to the imposition of the electro-osmotic force. Jayavel et al. [63] studied the EOF in a peristaltic microchannel filled with non-Newtonian nano-liquid. An electromagnetic simulation of an electrolyte solution induced by a peristaltic mechanism via a non-Darcy porous medium was made by Noreen et al. [64]. A two-dimensional electroosmosis endorsed peristaltic flow of a nanofluid in a channel via porous medium has been analyzed by Akram et al. [65]. It has been reported that with a growth in the thickness of EDL, the fluid motion and the pressure gradient decline. Tripathi et al. [66] have conducted a numerical simulation to comprehend the peristaltic flow of micropolar nanofluid through a vertical asymmetric microchannel in thermal radiation and a magnetic field. The entropy generation in an electroosmosis endorsed the ciliary motion of hybrid nanofluid under the impacts of buoyancy force, thermal radiation, and activation energy has been assessed by Saleem et al. [67]. In the investigation, they pointed out that the presence of activation energy and thin electric double layer (EDL) pursues mass dispersion and controls heat indulges. Saleem et al. [67] have presented a simulation of an electroosmosis-aided peristaltic flow of Casson fluid inside a heated tube. They showed that the electro-osmotic parameter is a crucial factor in manipulating the flow system’s dynamic and thermal features. Noreen et al. [69] have explored the electro-osmotic transport phenomena of bio-fluid in a wavy microchannel. They have found that the pressure gradient declines with the mean time flow rate and electro-osmotic parameter rise. A modelled problem has been demonstrated by Ranjit et al. [70] to enunciate the two-layered electrothermal flow in an asymmetric microchannel filled with a couple-stress fluid. They have noted that the temperature profile attenuates with the thickening of EDL. The EOF of non-Newtonian fluid with Jeffrey fluid model through a microchannel having a sinusoidal wall filled with a Darcy-Brinkman-Forchheimer medium under magnetic forces has been simulated by Bhatti et al. [71]. The Helmholtz-Smoluchowski parameter and magnetic field have retarding influences on the fluid- and particle-phase trajectories. Very recently, Nuwairan and Souayeh [72] have developed a mathematical model in order to demonstrate the electro-magneto-hydrodynamic peristaltic flow of blood with the suspension of gold nanoparticles and gyrotactic microorganisms in a micro-channel under the joint consequences of bioconvection, thermal radiation, and activation energy. Their results have revealed that the Helmholtz–Smoluchowski velocity amends the flow pattern inside the microchannel. Some more important relevant studies on this topic are included in refs. [73,74,75,76,77,78,79,80,81,82,83].

A comprehensive research survey evinces that minimal studies on the electro-osmotic transport of ionized blood in arterial networks have been carried out. Most of the previous studies have analyzed blood flow through arterial systems under various physiological aspects. The hemodynamical properties of ionic blood flow conveying hybridized nanoparticles under dual electroosmosis and peristalsis have not been explored earlier, which has been searched in this simulation. Another piece of the uniqueness of this modelling is the consideration of a diverging endoscopic annulus. Galvanized by inspirations described above, we intend to simulate the EOF of ionic blood with the suspension of two sorts of nanoparticles (Ag, Al₂O₃) in an endoscopic annulus with non-uniform cross-section undergoing peristalsis. The collective impact of gravitational force, heat source, Joule heating, and nanoparticles’ dimension is considered. The convectively thermal condition is imposed at the endoscopic annulus outer wall. The unsteady modelled equations are shifted to the steady-state equations via mapping from the fixed (laboratory) frame to the moving (wave) frame. The lubrication and Debye-Hückel linearization approaches are engrossed to linearize the steady-state modelled equations. The exact solutions are determined for the resulting constitutive equations. The significant outcomes from the simulation are illustrated through line and bar graphs and tables. The hybrid nano blood (Ag- Al₂O₃/blood) model is compared with the Ag-blood model via presentations.

The novelties of the current work are mentioned as follows:

• Formulation of a new mathematical model which simulates the electro-osmotic flow of blood infused with hybridized nanoparticles in a non-uniform endoscopic domain under peristalsis.

• Inclusion of joint impacts of gravitational force, heat source, Joule heating, nanoparticles’ shape, and convectively cooling arterial wall condition in the formulation of modelled equations.

• Set up closed-form solution for the flow equations by opting analytical approach.

2 Problem formulation

2.1 Physical model

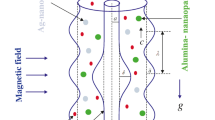
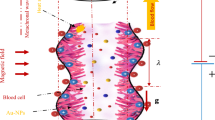
Let us consider a 2D electro-osmotic flow of incompressible blood with the suspension of hybridized nanoparticles (Ag, Al₂O₃) between two coaxial tubes (endoscopic annulus). An endoscopic tube is considered the inner tube, which is rigid, and the outer tube, which is negatively charged, propagates sinusoidally along its wall with a constant speed c. The nano blood (Ag-Al₂O₃/blood) flows in the endoscopic annulus. A cylindrical coordinate system $(\bar {R}$, $\bar {Z})$ in the laboratory frame is set to describe the flow of blood, where $\bar {R}$ is oriented along the radial direction, and $\bar {Z}$ oriented along the axial direction (axis of the endoscopic annulus). The geometrical structure of the proposed model is depicted in Fig. 1. The electric field E is applied along $\bar {Z}$-direction, which induces the EOF in the endoscopic annulus. The electrokinetic body force is $\textbf {F}_{E}=\rho _{e}\textbf {E}=\rho _{e}(E_{\bar {R}},E_{\bar {Z}})$. The thermal phenomenon is anticipated by keeping a constant temperature T₀ at the wall of the inner tube, and the outer tube wall is in contact with a cold fluid at temperature T₁, which induces a convective heat transfer coefficient h^∗. It is supposed that the blood (electrolyte solution) and hybridized nanoparticles (Ag, Al₂O₃) are in thermal equilibrium. Besides, Ag-Al₂O₃/blood has to be behaved as a single-phase fluid.

Fig. 1

Geometrical structure of the proposed model

The mathematical expression describing the endoscopic annulus is given below [4, 15, 52]:

$$\begin{array}{@{}rcl@{}} \bar{R}_{1}&=&R_{0},\\ \bar{R}_{2}&=&b(\bar{Z})+a^{\ast}\sin \frac{2\pi}{\lambda} (\bar{Z}-c \bar{t}), \end{array}$$

(1)

where R₀ denotes the inner tube radius, $b(\bar {Z})=b_{0}+\varepsilon \bar {Z}$ the outer tube radius at $\bar {Z}$, b₀ the radius of the outer tube inlet, a^∗ the wave’s amplitude, ε ≪ 1 a constant, c the wave speed, λ the wavelength, and $\bar {t}$ the time.

2.2 Electrohydrodynamics

The electric potential function in an electrolyte satisfies the Poisson equation. According to it, the electric potential Φ across the EDL is expressed as follows [20, 36, 77]:

$$\begin{array}{@{}rcl@{}} \nabla^{2}\bar{\Phi}=-\frac{\rho_{e}}{\varepsilon_{0}} \end{array}$$

(2)

in which ε₀ denotes the dielectric permittivity of the ionic blood (electrolyte), and ρ_e the net charge density of the ionic blood in a unit volume in the EDL, which is written as follows [25]:

$$\begin{array}{@{}rcl@{}} \rho_{e}=e \tilde{z} (n^{+}-n^{-}), \end{array}$$

(3)

in which e represents the charge of electron (1.6× 10^− 19C), $\tilde {z}$ the valency for both the ions (cations and anions), n⁺ and n⁻ the ionic concentrations of cations and anions in the ionic blood, respectively.

The Boltzmann distribution function for local ionic density is given below [36]:

$$\begin{array}{@{}rcl@{}} n^{\pm}=n_{0} e^{\pm \frac{e\tilde{z}\bar{\Phi}}{K_{B}T_{a}}}, \end{array}$$

(4)

where n₀ is the bulk density of cations and anions in the ionic blood, K_B the Boltzmann constant, and T_a the average temperature of the electrolyte solution (ionized blood).

In a unit volume of the ionic blood, the electric charge density is rewritten as [20, 36]:

$$\begin{array}{@{}rcl@{}} \rho_{e}=-2n_{0}\; e \;\tilde{z}\; \sinh\bigg(\frac{e \tilde{z} \tilde{\Phi}}{K_{B}T_{a}}\bigg), \end{array}$$

(5)

On the basis of (2) and (5), the Poisson-Boltzmann (PB) equation is simplified as:

$$\begin{array}{@{}rcl@{}} \nabla^{2}\bar{\Phi}=\frac{2n_{0} e \tilde{z}}{\varepsilon_{0}} \sinh\bigg(\frac{e \tilde{z} \bar{\Phi}}{K_{B}T_{a}}\bigg). \end{array}$$

(6)

To derive analytical solution, Eq. (6) is linearized via Debye-Hückel approximation in Section 2.6.

2.3 Flow equations

The equations modelling the EOF of blood infused with hybridized NPs in an endoscopic annulus under the aforementioned flow assumptions and employing Boussinesq approximation are given by [4, 15, 52, 53]:

$$\begin{array}{@{}rcl@{}} \frac{\partial\bar{U}}{\partial\bar{R}}+\frac{\bar{U}}{\bar{R}}+\frac{\partial\bar{W}}{\partial\bar{Z}}&=&0, \end{array}$$

(7)

$$\begin{array}{@{}rcl@{}} \rho_{hnf}\bigg(\frac{\partial\bar{U}}{\partial\bar{t}}+\bar{U}\frac{\partial\bar{U}}{\partial\bar{R}} +\bar{W}\frac{\partial\bar{U}}{\partial\bar{Z}}\bigg) &=&-\frac{\partial\bar{P}}{\partial\bar{R}} +\mu_{hnf}\bigg[\frac{1}{\bar{R}}\frac{\partial}{\partial\bar{R}}\bigg(\bar{R}\frac{\partial} {\partial\bar{R}}\bigg)-\frac{1}{\bar{R}^{2}}+\frac{\partial^{2}}{\partial\bar{Z}^{2}}\bigg]\bar{U}, \end{array}$$

(8)

$$\begin{array}{@{}rcl@{}} \rho_{hnf}\bigg(\frac{\partial \bar{W}}{\partial\bar{t}}+\bar{U}\frac{\partial\bar{W}}{\partial\bar{R}} +\bar{W}\frac{\partial \bar{W}}{\partial\bar{Z}}\bigg) &=&-\frac{\partial\bar{P}}{\partial\bar{Z}} +\mu_{hnf}\bigg[\frac{1}{\bar{R}}\frac{\partial}{\partial\bar{R}}\bigg(\bar{R}\frac{\partial} {\partial\bar{R}}\bigg)+\frac{\partial^{2}}{\partial\bar{Z}^{2}}\bigg]\bar{W}\\ &+&(\rho\beta)_{hnf}g(T-T_{1})+\rho_{e}E_{\bar{Z}}, \end{array}$$

(9)

$$\begin{array}{@{}rcl@{}} {(\rho c_{p})}_{hnf}\bigg(\frac{\partial T}{\partial\bar{t}}+\bar{U}\frac{\partial T} {\partial\bar{R}}+\bar{W}\frac{\partial T}{\partial\bar{Z}}\bigg) &=&\bar{k}_{hnf}\bigg(\frac{\partial^{2} T}{\partial\bar{Z}^{2}} +\frac{1}{\bar{R}} \frac{\partial\bar{T}}{\partial\bar{R}}+\frac{\partial^{2} T}{\partial\bar{R}^{2}}\bigg)+Q_{0}+ \sigma_{hnf} E_{\bar{Z}}^{2}, \end{array}$$

(10)

in which T specifies the blood temperature, $\bar {P}$ the blood pressure, ρ_hnf the density, μ_hnf the dynamic viscosity, β_hnf the thermal expansion coefficient, (ρc_p)_hnf the heat capacity, and $\bar {k}_{hnf}$ the thermal conductivity of Ag-Al₂O₃/blood, respectively, g the acceleration due to gravity, $E_{\tilde {Z}}$ the applied axial electric field component along axial direction, and Q₀ the constant heat source.

In the fixed (laboratory) frame, the worthy wall conditions are proposed as follows [15, 20, 52, 57]:

$$\begin{array}{@{}rcl@{}} &&\bar{W}=0,\; T=T_{0},\; \bar{\Phi}= 0 \;\text{at}\; \bar{R}=\bar{R}_{1},\\ &&\bar{W}=0,\; -\bar{k}_{hnf}\frac{\partial T}{\partial\bar{R}} =h^{\ast}(T- T_{1}),\; \bar{\Phi}= \bar{\Phi}_{0} \;\text{at} \;\bar{R}=\bar{R}_{2}, \end{array}$$

(11)

where h^∗ denotes the convective heat transfer coefficient.

In view of physical problems, the zero slip condition at the walls of inner and outer tubes is taken up. No electrical potential at the inner tube wall is suggested, whereas its value is considered constant at the outer tube wall. The inner tube wall is kept at temperature T₀, whereas the outer tube wall is put into contact with a cold fluid at temperature T₁, which induces a convective heat transfer phenomenon. Thermal transportation under convectively thermal wall conditions can amend the heat transfer mechanism across the wall surface. Heat transfer phenomena under convective wall conditions and electroosmosis are frequently encountered in clinical treatments such as pain relief therapies, thermal therapies, healing processes, bio-inspired transpiration cooling [83].

2.4 Thermo-physical attributes of nano blood and hybrid nano blood

The mathematical relations between thermo-physical attributes for nano blood and hybrid nano blood are expressed in Table 1, the thermo-physical attributes of blood, hybridized nanoparticles (Ag, Al₂O₃) are provided in Table 2. Furthermore, the different geometrical shapes and their shape factors are given is Table 3.

Table 1 Mathematical relations for nano blood and hybrid nano blood [1, 20, 52]

Table 2 Thermo-physical attributes of blood, silver (Ag), and alumina (Al₂O₃) [1, 20, 57]

Table 3 Geometrical shapes and shape factors of nanoparticles [15, 22, 25]

where ϕ₁ is symbolized for the solid volume fraction of silver nanoparticles (Ag NPs) and ϕ₂ the solid volume fraction of aluminium oxide nanoparticle (Ag-Al₂O₃ NPs). The suffices s₁, s₂, f, nf, hnf stand for Ag NPs, Ag-Al₂O₃ NPs, base fluid (blood), Ag-blood and hybrid Ag-Al₂O₃/blood, respectively. The hybrid nanofluid (Ag-Al₂O₃/blood) model converts to Ag-blood model by setting ϕ₂ = 0 and to pure blood model when ϕ₁ = ϕ₂ = 0.

2.5 Wave frame equations

The flow of blood is assumed to be unsteady in the laboratory (fixed) frame ($\bar {R}$, $\bar {Z}$) and it behaves as a steady-state in the wave frame ($\bar {r}$, $\bar {z}$) travelling with the wave speed c. In order to the conversion from the fixed frame (unsteady state) to the wave frame (steady-state), let us furnish the following linear transformations as [52, 53]:

$$\begin{array}{@{}rcl@{}} \bar{Z}=\bar{z}+c \bar{t}, \bar{R}=\bar{r}, \bar{W}=\bar{w}+c, \bar{U}=\bar{u}, \bar{p}(\bar{z},\bar{r})=\bar{P}(\bar{Z}, \bar{R}, \bar{t}) \end{array}$$

(12)

Invoking the transformations (12), Eqs. (7)–(10) are mapped as:

$$\begin{array}{@{}rcl@{}} \frac{\partial\bar{u}}{\partial\bar{r}}+\frac{\bar{u}}{\bar{r}}+\frac{\partial\bar{w}}{\partial\bar{z}}&=&0, \end{array}$$

(13)

$$\begin{array}{@{}rcl@{}} \rho_{hnf}\bigg[-c\frac{\partial\bar{u}}{\partial\bar{z}}+\bar{u}\frac{\partial\bar{u}}{\partial\bar{u}} +(\bar{w}+c)\frac{\partial\bar{u}}{\partial\bar{z}}\bigg] &=&-\frac{\partial\bar{p}}{\partial\bar{r}} +\mu_{hnf}\bigg[\frac{1}{\bar{r}}\frac{\partial}{\partial\bar{r}}\bigg(\bar{r}\frac{\partial\bar{u}} {\partial\bar{r}}\bigg)-\frac{\bar{u}}{\bar{r}^{2}}+\frac{\partial^{2}\bar{u}}{\partial\bar{z}^{2}}\bigg], \end{array}$$

(14)

$$\begin{array}{@{}rcl@{}} \rho_{hnf}\bigg[-c\frac{\partial \bar{w}}{\partial\bar{z}}+\bar{u}\frac{\partial\bar{w}}{\partial\bar{r}} +(\bar{w}+c)\frac{\partial \bar{w}}{\partial\bar{z}}\bigg] &=&-\frac{\partial\bar{p}}{\partial\bar{z}} +\mu_{hnf}\bigg[\frac{1}{\bar{r}}\frac{\partial}{\partial\bar{r}}\bigg(\bar{r}\frac{\partial\bar{w}} {\partial\bar{r}}\bigg)+\frac{\partial^{2}\bar{w}}{\partial\bar{z}^{2}}\bigg]\\ &+&(\rho\beta)_{hnf}(T- T_{1})+\rho_{e}E_{\bar{z}}, \end{array}$$

(15)

$$\begin{array}{@{}rcl@{}} {(\rho c_{p})}_{hnf}\bigg[-c\frac{\partial T}{\partial\bar{z}}+\bar{u}\frac{\partial T} {\partial\bar{r}}+(\bar{w}+c)\frac{\partial T}{\partial\bar{z}}\bigg] &=&\bar{k}_{hnf}\bigg(\frac{\partial^{2} T}{\partial\bar{r}^{2}} +\frac{1}{\bar{r}} \frac{\partial T}{\partial\bar{r}}+\frac{\partial^{2} T}{\partial\bar{z}^{2}}\bigg)+Q_{0}+\sigma_{hnf}E_{\bar{z}}^{2}. \end{array}$$

(16)

The boundary conditions (11) take the following form:

$$\begin{array}{@{}rcl@{}} &&\bar{w}=-c, T=T_{0}, \bar{\Phi}= 0 \;\text{at}\; \bar{r}=\bar{r}_{1},\\ &&\bar{w}=-c, -\bar{k}_{hnf}\frac{\partial T}{\partial\bar{r}} =h^{\ast}(T- T_{1}), \bar{\Phi}= \bar{\Phi}_{0} \;\text{at}\; \bar{r}=\bar{r}_{2}, \end{array}$$

(17)

2.6 Normalization and approximations

To normalize the flow Eqs. (13)–(16), let us define the non-dimensional variables as follows [4, 20, 36, 52]:

$$\begin{array}{@{}rcl@{}} &&r=\frac{\bar{r}}{b_{0}},\; z=\frac{\bar{z}}{\lambda},\; w=\frac{\bar{w}}{c}, \;u=\frac{\lambda\bar{u}}{c b_{0}}, \;t=\frac{c \bar{t}}{\lambda}, \;\delta=\frac{b_{0}}{\lambda}, \;a=\frac{a^{\ast}}{b_{0}}, \;r_{1}=\frac{\bar r_{1}}{b_{0}}=\epsilon, \;r_{2}=\frac{\bar r_{2}}{b_{0}},\\ &&\theta=\frac{T-T_{1}}{T_{0}-T_{1}}, \;p=\frac{d^{2} \bar{p}}{c \lambda \mu_{f}}, \;{\Phi}=\frac{\bar{\Phi}}{{\Phi}_{0}}, \;{\Phi}_{0}=\frac{K_{B}T_{a}}{e\tilde{z}}, \end{array}$$

(18)

in which (r, z) represents the dimensionless coordinates, (u, w) the dimensionless velocity components, t dimensionless time, a dimensionless wave number, δ the dimensionless radius of inner tube, 𝜖 amplitude ratio, r₁ and r₂ the dimensionless radii of inner and outer tubes, 𝜃 the dimensionless temperature, p the dimensionless pressure, and Φ the dimensionless electric potential.

The Poisson-Boltzmann equation (6) is linearized by $\sinh {\Phi }\approx {\Phi }$ after adopting the Debye-Hückel linearization approximation. In consequence, the analytical solution of (6) is attained. The dimensionless linearized Poisson-Boltzmann equation takes the form as:

$$\begin{array}{@{}rcl@{}} \bigg[\frac{1}{r}\frac{\partial}{\partial r}\bigg(r\frac{\partial {\Phi}}{\partial r}\bigg) +\delta^{2} \frac{\partial^{2} {\Phi}}{\partial z^{2}}\bigg]=\kappa^{2}{\Phi}, \end{array}$$

(19)

where $\kappa =b_{0} e \tilde {z}\sqrt {\frac {2n_{0}}{\epsilon _{0}K_{B}T_{a}}}=\frac {b_{0}}{\lambda _{D}}$ represents the electro-osmotic parameter or Debye-Hückel parameter which is reciprocal of EDL thickness.

On the insertion of Eqs. (19), (13)–(16) turn into:

$$\begin{array}{@{}rcl@{}} \frac{1}{r}\frac{\partial (r u)}{\partial r}+\frac{\partial w}{\partial z}&=&0, \end{array}$$

(20)

$$\begin{array}{@{}rcl@{}} Re \delta^{3}x^{\ast}_{1}\bigg(u\frac{\partial u}{\partial r}+w\frac{\partial u}{\partial z}\bigg)&=& -\frac{\partial p}{\partial r}+\delta^{2}x^{\ast}_{2}\bigg[\frac{1}{r}\frac{\partial }{\partial r}\bigg(r\frac{\partial u}{\partial r}\bigg)-\frac{u}{r^{2}} +\delta^{2}\frac{\partial^{2}u }{\partial r^{2}}\bigg], \end{array}$$

(21)

$$\begin{array}{@{}rcl@{}} Re \delta x^{\ast}_{1}\bigg(u\frac{\partial w}{\partial r}+w\frac{\partial w}{\partial z}\bigg)&=& -\frac{\partial p}{\partial z}+x^{\ast}_{2}\bigg[\frac{1}{r}\frac{\partial }{\partial r}\bigg(r\frac{\partial w}{\partial r}\bigg) +\delta^{2}\frac{\partial^{2}w}{\partial r^{2}}\bigg]+x^{\ast}_{3}Gr \theta+\kappa^{2} U_{hs}{\Phi}, \end{array}$$

(22)

$$\begin{array}{@{}rcl@{}} Re Pr \delta x^{\ast}_{5}\bigg(u\frac{\partial \theta}{\partial r} +w\frac{\partial \theta}{\partial z}\bigg)&=&x^{\ast}_{6} \bigg(\frac{\partial^{2}\theta}{\partial r^{2}} +\frac{1}{r}\frac{\partial \theta}{\partial r}+\delta^{2}\frac{\partial^{2}\theta}{\partial z^{2}}\bigg)+\chi+x^{\ast}_{4}S, \end{array}$$

(23)

where $Re=\frac {c b_{0}}{\nu _{f}}$ is the Reynolds number, $Gr=\frac {g {b_{0}^{2}}(T_{0}-T_{1})\rho _{f}\beta _{f}}{c \mu _{f}}$ the thermal Grashof number, $Pr=\frac {(\mu c_{p})_{f}}{\bar {k}_{f}}$ the Prandtl number, $S=\frac {\sigma _{f} {b_{0}^{2}}{E_{z}^{2}}}{\bar {k}_{f} (T_{0}-T_{1})}$ the Joule heating parameter, $\chi =\frac {Q_{0} {b_{0}^{2}}}{\bar {k}_{f} (T_{0}-T_{1})}$ the heat source parameter, and $U_{hs}=-\frac {\varepsilon \zeta E_{z}}{c \mu _{f}}$ the Helmholtz-Smoluchowski velocity (or maximum electro-osmotic velocity). In addition,

$$\begin{array}{@{}rcl@{}} x^{\ast}_{1}&=&(1-\phi_{2})[(1-\phi_{1})+\phi_{1} \frac{\rho_{s_{1}}}{\rho_{f}}]+\phi_{2} \frac{\rho_{s_{2}}}{\rho_{f}}, x^{\ast}_{2}=\frac{1}{(1-\phi_{1})^{2.5} (1-\phi_{2})^{2.5}},\\ x^{\ast}_{3}&=&(1-\phi_{2})[(1-\phi_{1})+\phi_{1} \frac{(\rho \beta)_{s_{1}}}{(\rho \beta)_{f}}]+\phi_{2} \frac{(\rho \beta)_{s_{2}}}{(\rho \beta)_{f}}, x^{\ast}_{4}=\frac{\sigma_{hnf}}{\sigma_{f}},\\ x^{\ast}_{5}&=&(1-\phi_{2})[(1-\phi_{1})+\phi_{1} \frac{(\rho c_{p})_{s_{1}}}{(\rho c_{p})_{f}}]+\phi_{2} \frac{(\rho c_{p})_{s_{2}}}{(\rho c_{p})_{f}}, x^{\ast}_{6}=\frac{\bar{k}_{hnf}}{\bar{k}_{f}} \end{array}$$

(24)

After employing the lubrication estimations (δ → 0, and Re → 0), Eqs. 19 and 21–23 are reduced into the following forms:

$$\begin{array}{@{}rcl@{}} &&\frac{1}{r}\frac{\partial}{\partial r}\bigg(r\frac{\partial {\Phi}}{\partial r}\bigg)=\kappa^{2}{\Phi}, \end{array}$$

(25)

$$\begin{array}{@{}rcl@{}} &&\frac{\partial p}{\partial r}=0, \end{array}$$

(26)

$$\begin{array}{@{}rcl@{}} &&-\frac{\partial p}{\partial z}+\frac{x_{1}}{r}\left[\frac{\partial}{\partial r}\left(r \frac{\partial w} {\partial r}\right)\right]+x_{2} Gr \theta+\kappa^{2} U_{hs}{\Phi}=0, \end{array}$$

(27)

$$\begin{array}{@{}rcl@{}} &&x_{4}(\frac{\partial^{2}\theta}{\partial r^{2}}+\frac{1}{r}\frac{\partial\theta}{\partial r})+\chi+x_{3}S=0, \end{array}$$

(28)

where $x_{1}=x^{\ast }_{2}$, $x_{2}=x^{\ast }_{3}$, $x_{3}=x^{\ast }_{4}$, $x_{4}=x^{\ast }_{6}$.

The dimensionless boundary conditions are prescribed as:

$$\begin{array}{@{}rcl@{}} &&w=-1,\; \theta=1,\; {\Phi}=0 \;\text{at}\; r=r_{1}=\epsilon,\\ &&w=-1, \;Bi\;\theta+x_{4}\frac{\partial \theta}{\partial r}=0, \;{\Phi}=1 \;\text{at}\; r=r_{2}=1+k z+a \sin2\pi z,\; \end{array}$$

(29)

where $k=\frac {\lambda \varepsilon }{b_{0}}$ denotes the non-uniform parameter, and $Bi=\frac {b_{0}h^{\ast }}{k_{f}}$. A larger Biot number ($Bi\to \infty$) communicates to a uniform wall thermal condition. Bi = 0 correlates to the insulated outer wall. Moreover, the outer wall is cooled convectively when Bi≠ 0 [57]. The case k < 0 designates the converging annulus, k = 0 for the uniform annulus, and k > 0 for the diverging annulus.

2.7 Analytical solution

The analytical solutions of Eqs. (25) and (37)–(28) along with the boundary conditions (29) are obtained as:

$$\begin{array}{@{}rcl@{}} {\Phi}(r,z)&=&c_{1} J_{0}(i r \kappa )+c_{2} Y_{0}(-i r \kappa), \end{array}$$

(30)

$$\begin{array}{@{}rcl@{}} \theta(r,z)&=&c_{3} \log{r}+c_{4}-\frac{r^{2}}{4 x_{4}} (S x_{3}+\chi), \end{array}$$

(31)

$$\begin{array}{@{}rcl@{}} w(r,z)&=&c_{6}+c_{5} \log{r}+\frac{r^{2}}{4 x_{1}}\left(\frac{dp}{dz}\right)+\frac{x_{2}Gr}{64 x_{1} x_{4}}[16x_{4} \{c_{3}(1-\log{r})-c_{4}\}r^{2} + (S x_{3}+\chi)r^{4}]\\ &-&\frac{U_{hs}}{x_{1}}[c_{1} \{J_{0}(i r \kappa )-1\}+c_{2} Y_{0}(-i r \kappa)], \end{array}$$

(32)

where $i=\sqrt {-1}$, J₀, Y₀ denote the first and second kind Bessel functions of zero order, respectively, and the constants c₁, c₂,..., c₆ involved in Eqs. (30)–(32) are computed using Mathematica software and mentioned in appendix.

Expressions (30)–(32) represent the electric potential, temperature, and axial velocity distributions of the ionic blood with the suspension of hybrid nanoparticles for low zeta potential, respectively.

2.8 Volumetric flow rate, stream function, and heat transfer coefficient

The volumetric flow rate F is computed as follows [53]:

$$\begin{array}{@{}rcl@{}} F=2{\int}_{r_{1}}^{r_{2}}r w(r,z) dr, \end{array}$$

(33)

which yields

$$\begin{array}{@{}rcl@{}} \frac{dp}{dz}=\frac{1}{f_{26} f_{31}}[(f_{27}+f_{28}) r_{1}-(f_{29}+f_{30}) r_{2}-f_{31}F], \end{array}$$

(34)

where f₂₆, f₂₇, f₂₈, f₂₉, f₃₀ and f₃₁ are provided in appendix.

The mean volumetric flow rate over a period of the peristaltic wave is obtained as [20]

$$\begin{array}{@{}rcl@{}} Q=F+\left(1+\frac{a^{2}}{2}+\frac{k^{2}}{3}+k-\frac{ka}{\pi}-\epsilon^{2}\right). \end{array}$$

(35)

The pressure rise per wavelength Δp, and friction forces per wavelength at the inter and outer tube walls F_i and F_o in dimensionless form, respectively, are evaluated as:

$$\begin{array}{@{}rcl@{}} {\Delta} p&=&{{\int}_{0}^{1}}\left(\frac{dp}{dz}\right)dz, \end{array}$$

(36)

$$\begin{array}{@{}rcl@{}} F_{i}&=&{{\int}_{0}^{1}}\;{r_{1}^{2}}\left(-\frac{dp}{dz}\right)dz, \end{array}$$

(37)

$$\begin{array}{@{}rcl@{}} F_{o}&=&{{\int}_{0}^{1}}\;{r_{2}^{2}}\left(-\frac{dp}{dz}\right)dz \end{array}$$

(38)

To estimate the numerical approximations of the pressure rise Δp, and frictional forces F_i and F_o, Mathematica built-in function NIntegrate is deployed.

The the stream function is defined as:

$$\begin{array}{@{}rcl@{}} u=-\frac{1}{r}\frac{\partial \psi}{\partial z}, w=\frac{1}{r}\frac{\partial \psi}{\partial r}. \end{array}$$

(39)

On integrating $w=\frac {1}{r}\frac {\partial \psi }{\partial r}$ with ψ = F at r = r₂, and the stream function ψ is extracted as, after simplification

$$\begin{array}{@{}lll@{}} \psi=F+f_{32} [24 x_{4} \{r\omega_{1}(r)+f_{33}+f_{34}\}+\omega_{2}(r)+f_{35}], \end{array}$$

(40)

where

$$\begin{array}{@{}lll@{}} {\omega_{1}}(r)&=& \kappa r [{-8c_{1}} {U_{hs 0}}{\tilde{F}_{1}}\left (;2;\frac{{r^{2}}{\kappa^{2}}}{4}\right)+8 {c_{1}} {U_{hs}}+ {r^{2}}\left(\frac{dp}{dz}\right)]\\ &-& 16 {ic_{2}} {U_{hs}} {Y_{1}}(-i r \kappa )+4 \kappa r x_{1} (2 {c_{5}} \log{r}-{c_{5}}+2 {c_{6}}), \end{array}$$

(41)

$$\begin{array}{@{}rcl@{}} \omega_{2}(r)&=& -Gr \kappa x_{2} r^{2} [r^{2}\{6 x_{4} (4 c_{3} \log{r}-5 c_{3}+4 c_{4})+(S x_{3}+ \chi)\}], \end{array}$$

(42)

where $_{0}\tilde {F}_{1}$ is the regularized confluent hypergeometric function.

The heat transfer coefficient Z^∗ at the outer wall (peristaltic wall) can be computed as [52]:

$$\begin{array}{@{}rcl@{}} Z^{\ast}&=&\frac{k_{hnf}}{k_{f}}\left(\frac{\partial r_{2}}{\partial z}\frac{\partial \theta}{\partial r}\right)_{r=r_{2}}\\ &=&[k+2\pi \;a \;\cos2\pi z][\frac{x_{4}c_{3}}{r_{2}}-\frac{r_{2}}{2}(S x_{3}+\chi)]. \end{array}$$

(43)

3 Validation of results

The following limiting cases are considered for the certification of the computed results of this simulation. The modelled problem studied by Sadaf and Abdelsalam [15] can be fetched from our present model by letting κ = 0 (omission of electro-osmotic body force) and S = 0 (devoid of Joule heating impact). Furthermore, Table 4 is furnished to show the comparison of the numerical data computed from analytical and homotopy solutions for the velocity expression w(r,z). The numerical outcomes establish the correlation of our computed analytical solution with the homotopy solution.

Table 4 Numerical values of w(r,z) for z = 0.3, k = 0.1, a = 0.1, ε = 0.2, Gr = 1, κ = 2, U_hs = 1, S = 1, χ = 1, Q = 0.5, n = 3, ϕ₁ = 0.01, ϕ₂ = 0.02

4 Analysis of results

This part is devoted to explicating the graphical and physical insight of involved flow parameters on the hemodynamic characteristics of the bloodstream in the endoscopic annulus subject to an external electric field. The change in the distributions of non-dimensional velocity and temperature, wall shear stress, heat transfer coefficient, and streamlines on varying thermal Grashof number Gr, electro-osmotic parameter κ, Helmholtz-Smoluchowski velocity U_hs, heat source parameter χ, Joule heating parameter S, Biot number B_i, non-uniform parameter k, nanoparticle volume fractions (ϕ₁, ϕ₂) is showcased in Figs. 2, 3, and 4. All numerical computations are executed by opting the prescribed values and ranges of parameters and constants associated with the flow system as [15, 20, 36, 52]: ϕ₁ = 0 − 0.1, ϕ₂ = 0 − 0.08, Gr = 0 − 10, κ = 1 − 3, U_hs = − 2 − 2, χ = 0 − 2, $B_{i}=0-\infty$, Q = − 1 − 1, k = − 0.1 − 0.1, z = 0.3, a = 0.1, and ε = 0.2. A graphical comparison is accomplished to compare hybrid blood, nano-blood, and pure blood flows. Mathematica 11 is implemented to evaluate all numerical computations and design all line and bar graphs and tables.

4.1 Velocity profile

To see the deviation in the distribution of the dimensionless axial velocity w with a change in significant parameters, viz. thermal Grashof number Gr, electro-osmotic parameter κ, Helmholtz-Smoluchowski velocity U_hs, heat source parameter χ, Joule heating parameter S, Biot number B_i, non-uniform parameter k, volume fractions (ϕ₁, ϕ₂) of nanoparticles, nanoparticles’ shape factor n, Fig. 2(a–j) are designed. In Fig. 2a, the upshot of Graphof number Gr on the axial velocity distribution is examined. It is perceived from the resulting graph that the velocity in the axial direction substantially improves near the peristaltic wall, and a counter reflection is viewed in the vicinity of the endoscopic wall for enhanced Gr for both Ag-Al₂O₃/ blood) and Ag-blood. With a rise in Gr, the buoyancy force is dominated in the flow conduit, which results in an elevation in the profile of the axial velocity. The peak axial velocity turns up near the endoscopic wall. Figure 2b expresses the variation in the distribution of the axial velocity for improving values of electro-osmotic parameter κ. For large κ, the axial velocity profile exhibits a diminutive behaviour in the zone near the peristaltic wall, and an opposite trend is manifested near the outer wall (peristaltic wall). Such fashion is shown in [36]. The electro-osmotic phenomenon can be characterized by the electro-osmotic parameter. A growth in κ (a lowering in Debye length or EDL thickness) slow down the blood motion near the peristaltic region. A thin EDL acts as a resistive factor in the EOF. Notably, the electro-osmotic parameter, which plays a crucial in electroosmosis, synchronizes the electric potential distribution in EDL and is of great applicability in designing micro-blood pumps, mixing physiological fluids (blood, saliva, etc.) with reagents. The decisive role of Helmholtz-Smoluchowski velocity U_hs in the development of the EOF adjacent to the peristaltic wall is pervaded in Fig. 2c. In graphs, it is clear that the blood motion is boosted up near the peristaltic wall and an inverse behaviour is manifested in the locality of the endoscopic wall towards changing values (from − 2 to 2) of U_hs. The blood flow in the axial direction is redistributed due to the electro-osmotic body force. Physically, U_hs < 0 interprets the axial electric field orientated in the direction of the peristaltic wave (i.e. positive z-direction). The reversely aligned axial electric field can be portrayed with regard to U_hs > 0. The electro-osmotic body force − κ²U_hsΦ is assisting for U_hs < 0 and resisting for U_hs > 0. In the case U_hs = 0, there is no electric field in the flow domain, and the modelled problem reduces to the peristaltic flow of blood. It is described that as U_hs alters from negative to positive values, the axial velocity profiles are skewed towards the peristaltic wall. Therefore, the flow dynamics of blood in an endoscopic conduit can be manipulated by imposing a properly oriented electric field. Figure 2d is graphed to inspect the out-turn of Joule heating parameter S on the distribution of the axial blood velocity. In this graph, the axial velocity profile shows enhancing trend in the vicinity of the peristaltic wall, and a counter result is witnessed in the vicinity of the endoscopic wall with augmenting S.

In Fig. 2e, the behaviour of the axial blood velocity with changing the values of heat source parameter χ is disclosed. This graph unveils that the blood velocity in the axial direction gets elevated in the zone near to the peristaltic wall, and an opposite behaviour is proclaimed in the nearer region of the endoscopic wall with enhancing deviations in χ. It is noted that the amount of heat transferred is directly proportional to the change in temperature and the transition of heat is therefore conducted from the higher region (endoscopic wall) to the lower region that leads to a declination in the blood velocity near the endoscopic wall by the augmented heat generation in the blood flow domain. In addition, nanoparticles are assembled near the charged surface (peristaltic wall), where augmented heat source parameter excites blood molecules or nanoparticles suspended into the blood to move faster in this zone. In consequence, the axial blood velocity elevates significantly near the peristaltic wall. Omission of heat source (χ = 0) provides the symmetric profile of the axial blood velocity. Figure 2f are constructed to get information regarding variation of the axial velocity w for multiple values of Biot number B_i. It is established from this plot that augmented Biot number B_i inhibits the axial velocity profile near the peristaltic wall and exhibits an inverse inclination in the region close to the endoscopic wall. The upshot of volume fractions (ϕ₁, ϕ₂) of nanoparticles on the axial velocity profile is depicted in Fig. 2g. The graphical result specifies that an enlargement in (ϕ₁, ϕ₂), the blood velocity is upraised near the peristaltic wall, and the converse impact is induced in the locality of the endoscopic wall. From this figure, it is established that the velocity values are higher for hybrid nano blood (Ag-Al₂O₃/blood) than Ag-blood. It can be concluded that the blood with infused with hybridized nanoparticles is more functional as drug carries. Moreover, the profile of the axial blood velocity shows parabolic shape, and it has increasing trend in the area of the endoscope wall irrespective of involved parameters. Table 5 portrays the outcomes of nanoparticles’ shape factor n on the axial distribution of blood velocity. As shown in this table, upon changing in shape factor n (sphere, brick, cylinder, and platelet) the axial velocity takes a reducing trend near the peristaltic wall. The blood flow considerably depends on the geometrical shape of injected nanoparticles into the blood. The magnitude of the axial blood velocity is higher for platelet shaped nanoparticles than the others. In conclusion, nanoparticles with their suitable shapes are used as nano-drug carriers in drug delivery systems.

Fig. 2

Trend of axial velocity profile with key parameters for a = 0.1, ε = 0.2, k = 0.1, z = 0.3, Q = 0.5, n = 3, ϕ₁ = 0.01, ϕ₂ = 0.02 and (a) κ = 2, U_hs = − 2, S = 1, χ = 1, B_i = 0.1. (b) Gr = 2, U_hs = − 2, S = 1, χ = 1, B_i = 0.1. (c) Gr = 2, κ = 2, S = 1, χ = 1, B_i = 0.1. (d) Gr = 2, κ = 2, U_hs = − 2, χ = 1, B_i = 0.1. (e) Gr = 2, κ = 2, U_hs = − 2, S = 1, B_i = 0.1. (f) Gr = 2, κ = 2, U_hs = − 2, S = 1, χ = 1. (g) Gr = 2, κ = 2, U_hs = − 2, S = 1, χ = 1, B_i = 0.1

Table 5 Velocity distribution w(r,z) for Gr = 2, κ = 2, U_hs = − 2, S = 1, χ = 2, B_i = 0.1, a = 0.1, ε = 0.2, k = 0.1, z = 0.3, Q = 0.5, ϕ₁ = 0.01, ϕ₂ = 0.02

4.2 Temperature profile

Figure 3a–d are framed to look into the consequences of Joule heating parameter S, heat source parameter χ, Biot number B_i, nanoparticles’ shape factor n, non-uniform parameter k, nanoparticle volume fractions ϕ₁, ϕ₂ on the distribution of the non-dimensional temperature 𝜃 of Ag-Al₂O₃/blood, and Ag-blood across the endoscopic annulus. Figure 3a is designed to outline the trend of the profile of 𝜃 against a change in Joule heating parameter S for both Ag-Al₂O₃/blood and Ag-blood flow cases. This graphical presentation exhibits that 𝜃-profile is upraised markedly due to an increment in S. The Joule heating parameter S is defined as $S=(\sigma _{f} {b_{0}^{2}}{E_{z}^{2}})/k_{f} (T_{0}-T_{1})$. From its definition, it is evident that the Joule heating parameter is quadratically related to the applied axial electric field E_z and proportional to the electrical conductivity of the blood σ_f. The blood is warmed or cooled with positive or negative values of S, as reported by Narla et al.[36]. Electrical energy is transformed to heat energy for the case of S > 0 and to sink when S < 0. S = 0 means the omission of Joule heating in the heat transfer mechanism. The Joule heating parameter S acts as a heat source or sink in the flow domain, and it exerts a revealing impact on the electro-osmotic heat transfer mechanism. Figure 3b is configured to characterize the behaviour of the blood temperature profile about multiple values of heat source parameter χ. The resulting graph demonstrates that an increment in χ leads to upliftment in the profile of the blood temperature. With positive values of χ, the ionic blood is energized. The blood temperature signifies the average kinetic energy of nanoparticles or molecules suspended in the blood. Therefore, the augmented heat generation elevates the blood temperature at a higher rate within the endoscopic conduit. The blood temperature profile attenuates moderately towards the outer wall in the ignorance of the heat source (χ = 0). In Fig. 3c, enlarging Biot number Bi receives a marked diminution in the temperature profile. A similar inclination has been proved by Das et al. [57]. The Biot number is linearly related to the convective heat transfer coefficient (h^∗) allied with the cold fluid. The heat resistance on the side attached with cold fluid is inversely connected with h^∗. For rising values of Bi, the convection resistance on the cold fluid side upsurges, and resultantly, the temperature of blood declines. The case $Bi\to \infty$ (isothermal outer wall) assigns the lower blood temperature profile, where 𝜃(r₂) = 0. This outcome has been implemented in blood transfusion in a human body, hypothermia treatment, and laser therapy [22]. The consequence of nanoparticles’ shape factor n on the blood temperature profile is explained in Fig. 3d. Results communicates that 𝜃_Sphere > 𝜃_Brick > 𝜃_Cylinder > 𝜃_Platelet. It can be documented that the blood temperature is higher for the spherical type of nanoparticles as compared to other types (brick, cylinder, and platelet). This is because spherical-shaped nanoparticles radiate a substantial amount of energy in heat, which increases the blood’s temperature. The temperature for hybrid nano blood (Ag-Al₂O₃/blood) is relatively lower than that of nano blood (Ag-blood) in the flow conduit (see in Fig. 3).

The upshot of volume fractions (ϕ₁, ϕ₂) of nanoparticles diffused in blood on the distribution of blood temperature is examined in Fig. 3e. Enlargement in (ϕ₁, ϕ₂) urges a significant attenuation in the profile of blood temperature. Physically, due to more inclusion of dissimilar nanoparticles in blood, blood’s thermal diffusivity significantly improves, resulting in fast ventilation of heat from the flow domain. Thereupon, the temperature in the blood flow noticeably abates. This trend reflects that the impulsion of hybridized nanoparticles is more acceptable than the impulsion of monotype nanoparticles into the blood due to marked enhancement in the thermal features of the blood. The main reason behind such behaviour is that as blood leaves the vicinity of the inner tube (endoscope tube), Al₂O₃ NPs close to the wall of the endoscope tube wall are warmed, and consequently, the blood temperature declines as blood swiftly migrate from the locality of the endoscope tube. A similar outcome has been documented in the study of Das et al.[57]. Moreover, Al₂O₃ NPs possess a higher atomic number, which is the prime cause of the blood temperature diminution. Therefore, the enhanced thermal characteristics are noted for Al₂O₃ NPs compared to Ag-NPs. The trend of the temperature profile for hybrid nano blood (Ag-Al₂O₃/blood), nano blood (Ag- blood), and pure blood is portrayed in Fig. 2g. As forecasted in all figures, higher temperature corresponds to Ag-Al₂O₃/blood, and lower for the Ag-blood. This is because the peristaltic wall is more flexible due to the presence of Ag-NPs, which impedes blood motion.

Fig. 3

Trend of temperature profile with key parameters for a = 0.1, ε = 0.2, k = 0.1, z = 0.3, Q = 0.5. (a) χ = 1, B_i = 0.1, n = 3, ϕ₁ = 0.01, ϕ₂ = 0.02. (b) S = 1, B_i = 0.1, n = 3, ϕ₁ = 0.01, ϕ₂ = 0.02. (c) S = 1, χ = 1, n = 3, ϕ₁ = 0.01, ϕ₂ = 0.02. (d) S = 1, χ = 1, B_i = 0.1, ϕ₁ = 0.01, ϕ₂ = 0.02. (e) S = 1, χ = 1, B_i = 0.1, n = 3. (f) S = 1, χ = 1, B_i = 0.1, n = 3

4.3 Axial pressure gradient

Figure 4a–g are plotted to show up the distribution of the non-dimensional axial pressure gradient $\frac {dp}{dz}$ with variation in the embedded parameters viz. thermal Grashof number Gr, electro-osmotic parameter κ, Helmholtz-Smoluchowski velocity U_hs, non-uniform parameter k, and nanoparticle volume fractions (ϕ₁, ϕ₂). Figure 4a delineates the alternation in the profile of $\frac {dp}{dz}$ under the change in Grashof number Gr. Plots clear that with rising thermal Grashof number Gr, the pressure gradient augments significantly. For the expansion of Gr, the buoyancy force is strongly built up in the flow conduit, which consequently contributes to aiding the axial pressure gradient. Figure 4b is drawn to predict the upshot of electro-osmotic parameter κ on the distribution of the axial pressure gradient. This graph reveals that electro-osmotic parameter κ has a diminutive impact on $\frac {dp}{dx}$-profile. The electro-osmotic force is elevated for a surge in κ, which substantially suppresses the pressure gradient profile. It is also remarked that the pressure gradient is lower for thin EDL. This interprets that the diffusion of ions in EDL significantly revises the pumping features. Examining Fig. 4c exhibits that augmented Helmholtz-Smoluchowski velocity U_hs stimulates the pressure gradient. U_hs < 0 represents the axial electric field acts along the direction of the blood flow, and U_hs < 0 corresponds to the reverse axial electric field, and U_hs = 0 signifies the omission of the electro-osmotic force. It is meant that the pressure gradient is higher if the axial electric field is opposing, and the low-pressure gradient is documented if the axial electric field is added. Thus, the pressure gradient changes with the electric potential difference due to the external axial electric field. The variation in $\frac {dp}{dz}$ with the mean volumetric flow rate Q, in Fig. 4d is outlined. Increasing values of Q urge a considerable depletion in $\frac {dp}{dz}$. The mean volumetric flow rate is defined as the velocity per unit of time through a cross-section of the annulus. An augmentation in the mean volumetric flow rate signifies that more blood is released via a cross-section of the annulus. As expected, growth in the mean volumetric flow rate induces a low-pressure gradient. Figure 4e is sketched to outline the modification in the pressure gradient distribution for variation in non-uniform parameter k on $\frac {dp}{dz}$. This figure conveys that the pressure gradient rises for change (negative to positive) in k. The line graph also conveys that the pressure gradient gets lessened in the case of the converging annulus (k < 0) as compared with the uniform annulus(k = 0) and diverging annulus (k > 0). From Fig. 4f, it is testified that expansion of nanoparticles’ solid volume fractions (ϕ₁, ϕ₂) brings about a striking elevation in the pressure gradient. This indicates that the concentration of hybridized nanoparticles can modify the pressure gradient dramatically. Figure 4g provides a comparison of the pressure gradient between hybrid nano blood (Ag-Al₂O₃/blood), nano blood (Ag-blood), and pure blood. It can be seen from these graphical views that the pressure gradient for hybrid nano blood (Ag-Al₂O₃/blood) is more prominent as compared to Ag-blood and pure blood.

Fig. 4

Trend of axial pressure gradient profile with key parameters for a = 0.1, ε = 0.2. (a) Gr = 2, κ = 2, U_hs = − 2, Q = 0.5, k = 0.1, ϕ₁ = 0.01, ϕ₂ = 0.02. (b) κ = 2, U_hs = − 2, Q = 0.5, k = 0.1, ϕ₁ = 0.01, ϕ₂ = 0.02. (c) Gr = 2, κ = 2, Q = 0.5, k = 0.1, ϕ₁ = 0.01, ϕ₂ = 0.02. (d) Gr = 2, κ = 2, U_hs = − 2, k = 0.1, ϕ₁ = 0.01, ϕ₂ = 0.02. (e) Gr = 2, κ = 2, U_hs = − 2, Q = 0.5, ϕ₁ = 0.01, ϕ₂ = 0.02. (f) Gr = 2, κ = 2, U_hs = − 2, Q = 0.5, k = 0.1. (g) Gr = 2, κ = 2, U_hs = − 2, Q = 0.5, k = 0.1

4.4 Pressure rise per wavelength

The pressure rise for each wavelength is a prime feature in a peristaltic phenomenon. The non-dimensional pressure rise per wavelength Δp versus the mean volumetric flow rate Q is depicted in Fig. 5a–f. Line graphs explain the variation in the pressure rise Δp. Figure 5a–c are outlined for exhibiting the impacts of Gr, κ, and U_hs on the pressure rise Δp. These plots reveal that the pressure rise Δp is linearly related to Gr, and U_hs and reverse inclination is noted for increasing values of κ. Physically, expansion in Gr leads to strong induction in buoyancy force in the flow regime, which encourages the pressure rise. The axial uniform electric field is notably amplified with an ascent in Helmholtz-Smoluchowski velocity U_hs. This is responsible for hiking the pressure rise Δp. Thus, the parameter U_hs is used to manipulate the pumping characteristics of EOFs. Enhanced values of electro-osmotic parameter κ substantially elevate the electrical potential, which opposes the pressure rise. Figure 5d shows a depleting behaviour in Δp in the region (0 ≤ Q ≤ 1), and it rises in the rest with increasing non-uniform parameter k. With larger values of (ϕ₁, ϕ₂), Δp strongly elevates, as exhibited in Fig. 5e. Physically, more effort is needed to pump the blood with more concentration of hybridized nanoparticles. The concentration of hybridized nanoparticles enhances the pressure rise Δp. The pressure rises Δp has an inverse linear relationship with the mean volumetric flow rate Q. Such trends have been documented in [57]. It is noting a higher-pressure rise for hybrid nano blood (Ag-Al₂O₃/blood) is recorded, and a lower one for Ag-blood and pure blood irrespective of parametric values (see Fig. 5f).

Fig. 5

Trend of pressure rise with key parameters for a = 0.1, ε = 0.2. (a) κ = 2, U_hs = − 2, k = 0.1, ϕ₁ = 0.01, ϕ₂ = 0.02. (b) Gr = 2, U_hs = − 2, k = 0.1, ϕ₁ = 0.01, ϕ₂ = 0.02. (c) Gr = 2, κ = 2, k = 0.1, ϕ₁ = 0.01, ϕ₂ = 0.02. (d) Gr = 2, κ = 2, U_hs = − 2, ϕ₁ = 0.01, ϕ₂ = 0.02. (e) Gr = 2, κ = 2, U_hs = − 2, k = 0.1. (f) Gr = 2, κ = 2, U_hs = − 2, k = 0.1

4.5 Wall frictional forces

The quantities F_i and F_o measure the frictions experienced by the blood at the walls of inner and outer tubes as it flows past the walls. Figure 6a–j are presented to illustrate the variation in the wall frictional forces (wall shears) F_i (on inner tube wall) and F_o (on outer tube wall) with change in Gr, κ, U_hs, S, ϕ₁ and ϕ₂. It is evident from these graphs that the frictional forces F_i and F_o are delinquent behaviour to the pressure rise. For higher estimation of Gr, U_hs, S, ϕ₁ and ϕ₂ strongly reduce both inner and outer wall frictional forces, and an inverse observation is noted for increasing κ. Both frictional forces are monotonically increasing with the mean volumetric flow rate Q. The buoyancy force is fostered with higher thermal Grashof number Gr, which augments the blood flow and consequently, the magnitude of both frictional forces F_i and F_o increases. Enhancing values of U_hs leads to upliftment in the electro-osmotic power, which expedites the blood flow in the conduit, and resultantly the magnitude of both frictional forces F_i and F_o is found to rise. With higher S, the electro-osmotic force is substantially elevated, due to which the magnitude of both frictional forces F_i and F_o are noticeably magnified. It is important to note that the magnitude of the friction force at the wall of the outer tube is significantly higher compared to that of the friction forces at the inner tube wall. The frictional forces on the inner and outer tube walls for hybrid nano blood (Ag-Al₂O₃/blood) are lower than Ag-blood. Higher frictional force at the arterial wall initiates several diseases in arteries which cause health hazards in the human body. Thus, injection of hybridized nanoparticles into the blood helps to reduce the frictional forces at the arterial wall.

Fig. 6

Distribution of wall frictional forces with key parameters. (a–b) varying Gr when κ = 2, U_hs = − 2, S = 1, ϕ₁ = 0.01, ϕ₂ = 0.02, ε = 0.2, a = 0.1, k = 0.1. (c–d) varying κ when Gr = 2, U_hs = − 2, S = 1, ϕ₁ = 0.01, ϕ₂ = 0.02, ε = 0.2, a = 0.1, k = 0.1. (e–f) varying U_hs when Gr = 2, κ = 2, S = 1, ϕ₁ = 0.01, ϕ₂ = 0.02, ε = 0.2, a = 0.1, k = 0.1. (g–h) varying S when Gr = 2, κ = 2, U_hs = − 2, ϕ₁ = 0.01, ϕ₂ = 0.02, ε = 0.2, a = 0.1, k = 0.1. (i–j) varying ϕ₁ and ϕ₂ when Gr = 2, κ = 2, U_hs = − 2, ε = 0.2, a = 0.1, k = 0.1

4.6 Heat transfer coefficient

The manner of the heat transfer coefficient Z^∗ at the outer tube wall of the endoscopic annulus for multiple values of S, χ, B_i, n, (ϕ₁, ϕ₂) is portrayed via Fig. 7a-g. Z^∗-profile has increasing trend for rising values of S, χ, B_i and an opponent inclination is witnessed for multiple values of n, ϕ₁, and ϕ₂. From a physical point of view, electrical dissipation is the induced kinetic energy altered into thermal energy which raises the blood temperature subject to the intensity of the applied axial electric field. The change of Joule heating parameter from S = − 1 to S = 1 leads to inflation in the distribution of the blood temperature in the endoscopic domain. Consequently, the heat transfer coefficient Z^∗ significantly increases across the outer tube wall. Joule heating is a significant agent for regulating the heat transfer mechanism. On the upswing of heat source parameter χ, the heat transfer coefficient strengthens, owing to an enhancement in heat generation propensity of the blood. The heat transfer coefficient is nearly affected by the shape factors of nanoparticles. The volumetric concentration of hybridized nanoparticles injected into the blood is directly related to the thermal diffusion of blood, which assists in the quick ventilation of heat from the flow conduit. Consequently, an increment in (ϕ₁, ϕ₂) leads to a depletion in Z^∗. The ionic blood in the flow conduit is energized with augmenting heat source parameter χ, due to which Z^∗ rises. This type of phenomenon for the existence of a heat source in the flow conduit could be beneficial in thermal therapy treatment. The heat transfer coefficient Z^∗ is marginally more significant for spherical-shaped nanoparticles than for other nanoparticles’ shapes. The heat transfer coefficient in the case of hybrid nano blood (Ag-Al₂O₃/blood) is slightly lower than that of nano blood (Ag-blood) or pure blood.

Fig. 7

Trend of heat transfer coefficient profiles with key parameters. for a = 0.1, k = 0.1, ε = 0.2, and (a) χ = 1, B_i = 0.1, n = 3, ϕ₁ = 0.1, ϕ₂ = 0.02. (b) S = 1, B_i = 0.1, n = 3, ϕ₁ = 0.1, ϕ₂ = 0.02. (c) S = 1, χ = 1, n = 3, ϕ₁ = 0.1, ϕ₂ = 0.02. (d) S = 1, B_i = 0.1, ϕ₁ = 0.01, ϕ₂ = 0.02. (e) S = 1, χ = 1, n = 3, ϕ₂ = 0.02. (f) S = 1, χ = 1, B_i = 0.1, n = 3, ϕ₁ = 0.1. (g) S = 1, χ = 1, B_i = 0.1, n = 3

4.7 Streamline pattern

Physically, streamlines connect the velocity vectors in a flow field. Streamlines split due to a stagnation point and form an enclosing bolus of fluid. The development of bolus and the disunion of streamlines are known as trapping phenomena. Figure 8a–j unveil an insight into modification in the formation of bolus and streamline structure subject to a change in Gr, κ, U_hs, n, k, and (ϕ₁, ϕ₂). Figure 8a–b are plotted to predict the consequence of thermal Grashof number Gr on streamlines. There is a significant change in size and number of entrapped boluses for a higher estimation of Gr. It is attributed that a higher thermal Grashof number modulates the size and number of trapped boluses. The streamlines for larger values of κ are graphed in Fig. 8c–d. It is inferred that the trapped bolus is contracted in size and number by mounting κ. Figure 8e–f are created to assess the alternation in streamline formation with regard to Helmholtz-Smoluchowski velocity U_hs. The corresponding graphs infer that negative U_hs makes less number of boluses, whereas positive U_hs contributes to an expansion in the trapped bolus shape. With changing shape factor n, the bolus structure has a minor modification, as displayed in Fig. 8g–j. The entrapped bolus is enhanced in number for hybrid nanofluid (Ag-Al₂O₃/blood) when compared to Ag-blood and pure blood because the dispersed nanoparticles injected into the blood swiftly migrate and circulate to form boluses (Fig. 8k–m). In Fig. 8n–p, it can be realized that with a change in k (negative to positive values), the dimension of entrapped boluses is notably amended and moved toward the peristaltic wall. It is also portrayed that the trapped bolus size is more prominent in the case of the converging non-uniform annulus (κ = − 0.1), which provides more resistance to the blood flow.

Fig. 8

Streamlines for assorted values of key parameters when a = 0.1, ε = 0.2, Q = 0.9. (a–b) κ = 2, U_hs = − 2, n = 3, k = 0.1, ϕ₁ = 0.01, ϕ₂ = 0.02. (c–d) Gr = 2, U_hs = − 2, n = 3, k = 0.1, ϕ₁ = 0.01, ϕ₂ = 0.02. (e–f) Gr = 2, κ = 2, n = 3, k = 0.1, ϕ₁ = 0.01, ϕ₂ = 0.02. (g–j) Gr = 2, κ = 2, U_hs = − 2, k = 0.1, ϕ₁ = 0.01, ϕ₂ = 0.02. (k–m) Gr = 2, κ = 2, U_hs = − 2, n = 3, k = 0.1. (n–p) Gr = 2, κ = 2, U_hs = − 2, n = 3, ϕ₁ = 0.01, ϕ₂ = 0.02

5 Conclusion

In this exploration, an improved mathematical model for the electroosmosis aided peristaltic transport of blood infused with hybridized nanoparticles (Ag, Al₂O₃) via a non-uniform endoscopic conduit has been outlined by including the cumulative impacts of thermal buoyancy force, heat source, and Joule heating. Different geometrical shapes (sphere, brick, cylinder, platelet) of implanted nanoparticles in the blood are taken into consideration in this simulation. The electric potential induced in the EDL is determined by using the Poisson-Boltzmann equation. The non-dimensional non-linear model equations are linearized by adopting lubrication and Debye-Hückel (low zeta potential) estimates. The analytical solutions of the resulting equations are achieved. The hemodynamical characteristics of the bloodstream in terms of physical parameters have been captured in detail via graphs and tables. The structure of entrapped boluses has also been outlined. The major findings of this examination are recorded as follows:

• The distribution of the axial blood velocity inflates in the locality of the peristaltic wall and q contrasting manner is showcased in the zone close to the endoscope wall due to an elevation in electro-osmotic parameter (lowering in EDL thickness).

• The blood flow expedites in the locality of the peristaltic wall whereas it declines with changing Helmholtz-Smoluchowski velocity (negative to positive values).

• Enlargement in nanoparticle’s volume fractions induces a marked alternation in the blood flow in the conduit.

• Improving the positive Joule heating parameter leads to a declination in the profile of the blood temperature.

• The blood is cooled with the growth of volume fractions of injected nanoparticles.

• The electro-osmotic body force can control the blood temperature in the endoscopic domain.

• The temperature for hybrid nano blood (Ag-Al₂O₃/blood) is higher relative to nano blood (Ag-blood), and pure blood.

• The pressure gradient is abated for electro-osmotic parameter (inverse of EDL thickness), whereas it is elevated with Helmholtz-Smoluchowski velocity.

• The pressure rise per wavelength is a monotonic decreasing function of the mean volumetric flow rate.

• With greater values of electro-osmotic parameter, the magnitude of the wall frictional forces substantially reduces.

• The heat transfer coefficient is maximum for spherical-shaped nanoparticles compared with other shapes (brick, cylinder, and platelet).

• Nanoparticles with their suitable shapes, can be used as nano-drug carriers in drug delivery systems.

• Helmholtz-Smoluchowski velocity and Debye length have impressive impacts on bolus structure.

In this research study, physiognomies of the bloodstream suspended with hybridized nanoparticles in a diverging endoscopic conduit under electro-osmotic force have been reported. Another new thing in this examination is the inclusion of injected nanoparticles’ shape factor. This theoretical study will be beneficial in capturing the hemodynamical behaviours of blood in an endoscopic arterial system. Hemodynamics and heat transport phenomena in the electro-osmotic simulation of ionic blood have an excellent perspective due to plentiful applications in electro-osmotic medical pumps, bio-micro-electromechanical systems, mechanical miniaturization systems, tissue engineering, genetic mapping, pharmacodynamics, diagnosis and treatments of cardiovascular diseases, etc. In future, this mathematical model can be extended to the electro-osmotic simulation of non-Newtonian ionic blood with non-Newtonian models, for example, Casson fluid model, Bingham plastic model, etc.

Appendix

$$\begin{array}{@{}lll@{}} c_{1}&=& \frac{Y_{0}(-i \kappa r_{1})}{J_{0}(i \kappa r_{2}) Y_{0}(-i \kappa r_{1})-J_{0}(i \kappa r_{1}) Y_{0}(-i \kappa r_{2})},\\ c_{2}&=& \frac{J_{0}(i \kappa r_{1})}{J_{0}(i \kappa r_{1}) Y_{0}(-i \kappa r_{2})-J_{0}(i \kappa r_{2}) Y_{0}(-i \kappa r_{1})},\\ f_{1}&=&B_{i}-\frac{B_{i}}{4 x_{4}}(S x_{3}+\chi)({r_{2}^{2}}-{r_{1}^{2}})-\frac{1}{2} r_{2} (S x_{3}+\chi),\\ f_{2}&=&B_{i} \log{\frac{r_{2}}{r_{1}}}+\frac{x_{4}}{r_{2}},\\ c_{3}&=&-\frac{f_{1}}{f_{2}},\\ f_{3}&=&r_{2} B_{i} [{r_{2}^{2}} \log{r_{1}}(S x_{3}+\chi)-{r_{1}^{2}} \log {r_{2}} (S x_{3}+\chi)-4 x_{4} \log{r_{2}}]\\ &+&x_{4} [2 {r_{2}^{2}} \log {r_{1}}(S x_{3}+\chi)-{r_{1}^{2}} (S x_{3}+\chi)-4 x_{4}],\\ f_{4}&=&4 x_{4} [r_{2} B_{i} \log{\frac{r_{2}}{r_{1}}}+x_{4}],\\ c_{4}&=&-\frac{f_{3}}{f_{4}},\\ f_{5}&=& - Gr \kappa x_{2} [(S x_{3}+\chi)({r_{1}^{6}} -3 {r_{2}^{2}} {r_{1}^{4}}+3 {r_{2}^{4}} {r_{1}^{2}})+{r_{2}^{6}} \chi],\\ f_{6}&=& Gr \kappa {r_{2}^{6}} S x_{2} x_{3}+192 r_{1} U x_{4} [\kappa r_{1} \{c_{1} (I_{0}(\kappa r_{1}) +I_{0}(\kappa r_{2}))\\ &+&c_{2}\left(Y_{0}(-i \kappa r_{1})+Y_{0}(-i \kappa r_{2})\right)\}-4 i c_{2} Y_{1}(-i \kappa r_{1})],\\ f_{7}&=& -192 U_{hs} x_{4} [2 c_{1} \kappa {r_{1}^{2}} {{}_{0}}\tilde{F}_{1}\left(;2;\frac{1}{4} \kappa^{2} {r_{1}^{2}}\right) +r_{2} \{c_{1} \kappa r_{2} (I_{0}(\kappa r_{1})+I_{0}(\kappa r_{2})) -4 i c_{2} Y_{1}(-i \kappa r_{2})\}],\\ f_{8}&=& -192 \kappa x_{4} [(2 x_{1} ({r_{1}^{2}}-F)+{r_{2}^{2}} \{-2 x_{1}+U_{hs} (-2 c_{1} {{}_{0}}\tilde{F}_{1}\left(;2;\frac{1}{4} \kappa^{2} {r_{2}^{2}}\right)\\ &+&c_{2} Y_{0}(-i \kappa r_{1})+c_{2} Y_{0}(-i \kappa r_{2}))\}]-12 c_{3} Gr \kappa x_{2} x_{4} [-{r_{1}^{4}}+{r_{2}^{4}}+4 {r_{2}^{2}} {r_{1}^{2}}\log{\frac{r_{1}}{r_{2}}}],\\ f_{9}&=& 192 \kappa x_{1} x_{4} [{r_{1}^{2}} (\log{\frac{r_{1}}{r_{2}}}-1)+{r_{2}^{2}} (\log{\frac{r_{1}}{r_{2}}}+1)],\\ c_{5}&=&-\frac{1}{f_{9}}(f_{5}+f_{6}+f_{7}+f_{8}),\\ f_{10}&=& Gr \kappa \chi x_{2} [{r_{1}^{8}} \log{r_{2}}+{r_{2}^{2}} {r_{1}^{6}} (3-4 \log{r_{1}})+3 {r_{2}^{4}} {r_{1}^{4}} (\log{r_{1}r_{2}}-2)+{r_{2}^{6}} {r_{1}^{2}} (3-4 \log{r_{2}})+{r_{2}^{8}} \log{r_{1}}],\\ f_{11}&=& Gr \kappa {r_{1}^{2}} S x_{2} x_{3}[{r_{1}^{6}} \log{r_{2}}+{r_{2}^{2}} {r_{1}^{4}} (3-4 \log{r_{1}})+3 {r_{2}^{4}} {r_{1}^{2}}(\log{r_{1}r_{2}}-2)+{r_{2}^{6}}(3-4 \log{r_{2}})],\\ f_{12}&=& Gr \kappa {r_{2}^{8}} S x_{2} x_{3} \log{r_{1}}+192 {r_{1}^{3}} U_{hs} x_{4} [\kappa r_{1} \{c_{1} I_{0}(\kappa r_{2}) + c_{1}(\log{r_{1}}-1)\\ &+&c_{2} Y_{0}(-i \kappa r_{2})\}+4 i c_{2} \log{r_{2}} Y_{1}(-i \kappa r_{1})],\\ f_{13}&=& -192 \kappa {r_{1}^{4}} U_{hs} x_{4} [c_{1} \log{r_{1}} I_{0}(\kappa r_{2})+c_{1} \log{r_{2}}(I_{0}(\kappa r_{1})+1)+c_{2} \log{r_{1}} Y_{0}(-i \kappa r_{2})],\\ f_{14}&=& -192 {r_{1}^{2}} U_{hs} x_{4} \log{r_{2}} [\kappa {r_{1}^{2}} \{-2c_{1} {{}_{0}}\tilde{F}_{1}\left(;2;\frac{1}{4} \kappa^{2} {r_{1}^{2}}\right) +c_{2} Y_{0}(-i \kappa r_{1})\}+4 i c_{2} r_{2} Y_{1}(-i \kappa r_{2})],\\ f_{15}&=& -192 r_{1} {r_{2}^{2}} U_{hs} x_{4} [\kappa r_{1} \{c_{1} I_{0}(\kappa r_{1})+c_{1} I_{0}(\kappa r_{2})-2 c_{1}+c_{2} Y_{0}(-i \kappa r_{1})\} +4 i c_{2} \log{r_{1}} Y_{1}(-i \kappa r_{1})],\\ f_{16}&=& 192 \kappa {r_{1}^{2}} {r_{2}^{2}} U_{hs} x_{4}[2 \log{r_{1}} \{c_{1} I_{0}(\kappa r_{1})+c_{2} Y_{0}(-i \kappa r_{1})\}-c_{2} Y_{0}(-i \kappa r_{2})],\\ f_{17}&=&384 \kappa {r_{1}^{2}} {r_{2}^{2}} U_{hs} x_{4} [-c_{1} \log{r_{1}} {{}_{0}}\tilde{F}_{1}\left(;2;\frac{1}{4} \kappa^{2} {r_{1}^{2}}\right) +\log{r_{2}} \{(c_{1} I_{0}(\kappa r_{2})+c_{2} Y_{0}(-i \kappa r_{2})\}],\\ f_{18}&=&-192 {r_{2}^{2}} U_{hs} x_{4} [2 c_{1} \kappa {r_{1}^{2}} \log{r_{2}} {{}_{0}}\tilde{F}_{1}\left(;2;\frac{1}{4} \kappa^{2} {r_{2}^{2}}\right) +r_{2} \{c_{1} \kappa r_{2}-4 i c_{2} \log{r_{1}} Y_{1}(-i \kappa r_{2})\}], \end{array}$$

$$\begin{array}{@{}rcl@{}} f_{19}&=&192 \kappa {r_{2}^{4}} U_{hs} x_{4} [c_{1} I_{0}(\kappa r_{1})-c_{1} \log{r_{1}}(I_{0}(\kappa r_{2})+1)+c_{2} Y_{0}(-i \kappa r_{1})],\\ f_{20}&=&-192 \kappa {r_{2}^{4}} U_{hs} x_{4} [-2c_{1} \log{r_{1}} {{}_{0}}\tilde{F}_{1}\left(;2;\frac{1}{4} \kappa^{2} {r_{2}^{2}}\right) +c_{1} \log{r_{2}} (I_{0}(\kappa r_{1})-1)+c_{2} \log{r_{1}} Y_{0}(-i \kappa r_{2})],\\ f_{21}&=& -192 \kappa x_{4}[c_{2} {r_{2}^{4}} U_{hs} \log{r_{2}} Y_{0}(-i \kappa r_{1})-2 {r_{2}^{2}} x_{1} (F \log{r_{1}}+{r_{1}^{2}})\\ &+&{r_{1}^{2}} x_{1} \{2 F \log{r_{2}}-{r_{1}^{2}} (\log{r_{1}}+\log{r_{2}}-1)\}],\\ f_{22}&=&12 \kappa x_{4}[-c_{3} Gr {r_{1}^{6}} x_{2} \log{r_{2}}+c_{3} Gr {r_{2}^{2}} {r_{1}^{4}} x_{2} \log{r_{1}} (4 \log{r_{1}}-3)\\ &-&32 {r_{2}^{2}} {r_{1}^{2}} x_{1}\log{r_{1}r_{2}}+16 {r_{2}^{4}} x_{1} (\log{r_{1}r_{2}}-1)],\\ f_{23}&=& 12 c_{3} Gr \kappa {r_{1}^{2}} {r_{2}^{2}} x_{2} x_{4} [{r_{2}^{2}} (4 \log{r_{1}}-3 \log{r_{2}})-4 {r_{1}^{2}} (\log{r_{1}}-1) \log{r_{2}}],\\ f_{24}&=& -12 c_{3} Gr \kappa {r_{2}^{4}} x_{2} x_{4} [4 {r_{1}^{2}} \log{\frac{r_{1}}{r_{2}}} \log{r_{2}}+{r_{2}^{2}} \log{r_{1}}],\\ f_{25}&=&192 \kappa ({r_{1}^{2}}-{r_{2}^{2}}) x_{1} x_{4} [{r_{1}^{2}} (\log{\frac{r_{1}}{r_{2}}}-1)+{r_{2}^{2}}(\log{\frac{r_{1}}{r_{2}}}+1)],\\ c_{6}&=&-\frac{1}{f_{25}}(f_{10}+f_{11}+f_{12}+f_{13}+f_{14}+f_{15}+f_{16}+f_{17}+f_{18}\\ &+&f_{19}+f_{20}+f_{21}+f_{22}+f_{23}+f_{24}),\\ f_{26}&=&\frac{1}{8 x_{1}}({r_{1}^{4}}-{r_{2}^{4}}),\\ f_{27}&=&192 c_{1} \kappa r_{1} U_{hs} x_{4} [ {{}_{0}}\tilde{F}_{1}\left(;2;\frac{1}{4} \kappa^{2} {r_{1}^{2}}\right)-1] +384 i c_{2} U_{hs} x_{4} Y_{1}(-i \kappa r_{1})-Gr \kappa {r_{1}^{5}} x_{2} (S x_{3}+\chi),\\ f_{28}&=& 6 \kappa r_{1} x_{4} [Gr {r_{1}^{2}} x_{2} (4 c_{3} \log{r_{1}}-5c_{3}+4c_{4})-16 x_{1} (2c_{5} \log{r_{1}}-c_{5}+2c_{6})],\\ f_{29}&=& 192 c_{1} \kappa r_{2} U_{hs} x_{4} [ {{}_{0}}\tilde{F}_{1}\left(;2;\frac{1}{4} \kappa^{2} {r_{2}^{2}}\right)-1] +384 i c_{2} U_{hs} x_{4} Y_{1}(-i \kappa r_{2})-Gr \kappa {r_{2}^{5}} x_{2} (S x_{3}+\chi),\\ f_{30}&=& 6 \kappa r_{2} x_{4} [Gr {r_{2}^{2}} x_{2}(4 c_{3} \log{r_{2}}-5c_{3}+4c_{4})-16 x_{1}(2 c_{5} \log{r_{2}}-c_{5}+2 c_{6})],\\ f_{31}&=&192 \kappa x_{1} x_{4},\\ f_{32}&=&\frac{1}{384 \kappa x_{1} x_{4}},\\ f_{33}&=& 16 i c_{2} r_{2} U Y_{1}(-i \kappa r_{2})-\kappa {r_{2}^{4}}\left(\frac{dp}{dz}\right),\\ f_{34}&=& 4\kappa {r_{2}^{2}}[2 c_{1} U_{hs} \{ {{}_{0}}\tilde{F}_{1}\left(;2;\frac{1}{4} \kappa^{2} {r_{2}^{2}}\right)-1\}+x_{1} (-2 c_{5} \log{r_{2}}+c_{5}-2c_{6})],\\ f_{35}&=& Gr \kappa x_{2} [6 {r_{2}^{4}} x_{4}(4 c_{3} \log{r_{2}}-5c_{3}+4c_{4})-{r_{2}^{6}}(S x_{3}+\chi)] \end{array}$$